Вулканология и сейсмология, 2020, № 6, стр. 3-25
Общий закон подобия для землетрясений
А. К. Некрасова a, *, В. Г. Кособоков a
a Институт теории прогноза землетрясений и математической геофизики РАН
117997 Москва, ул. Профсоюзная, 84/32, Россия
* E-mail: nastia@mitp.ru
Поступила в редакцию 05.07.2020
После доработки 03.08.2020
Принята к публикации 20.08.2020
Аннотация
Статья посвящена обзору многолетнего опыта отечественных и зарубежных исследователей, рассматривающих теорию самоорганизующейся критичности (SOC, Self-Organized Criticality) в применении к сейсмологическим данным. А именно ‒ Общий закон подобия для землетрясений (ОЗПЗ, в англоязычных публикациях – USLE, Unified Scaling Law for earthquakes), который, учитывая пространственное подобие множества сосредоточения эпицентров землетрясений, обобщает классический закон – соотношение Гутенберга‒Рихтера. Обоснована востребованность и актуальность использования обобщения в практических задачах, связанных с пространственно-временны́ми параметрами сейсмичности. Указаны возможные ограничения к практическому применению. Приведены различные методы оценивания значений коэффициентов USLE и примеры их практического использования.
1. ВВЕДЕНИЕ
Землетрясение – это внезапное движение внутри литосферы Земли, которое порождает сейсмические волны и сотрясения на ее поверхности. Характеристики землетрясения могут быть определены из интерпретации макросейсмического эффекта на поверхности и инструментально записанных сейсмограмм. Многочисленные подходы к определению размера очага землетрясения привели к появлению количественного определения его величины как магнитуды по инструментальным данным М [Richter, 1935; Bormann, 2011].
В своем определении магнитуды М Чарльз Рихтер использовал физически безразмерную логарифмическую шкалу, что естественно из-за иерархической организации литосферы Земли, объединяющей подвижные блоки от зерен породы размера ~10-3 м до тектонических плит размером ~106 м [Keilis-Borok, 1990]. Анализ соотношения числа землетрясений разной магнитуды в регионе привело к ставшей классической формулировке закона Гутенберга‒Рихтера [Gutenberg, Richter, 1944, 1954] –
(1)
${\text{lo}}{{{\text{g}}}_{{10}}}N\left( M \right) = a + b\left( {8 - M} \right),\,\,\,{{M}_{ - }} \leqslant M \leqslant {{M}^{ - }},$5 мая 1967 г. журнал Science опубликовал статью Бенуа Мандельброта “How long is the coast of Britain? Statistical self-similarity and fractional dimension” [Mandelbrot, 1967], которая начинается утверждением о том, что “Географические кривые настолько запутаны в своих деталях, что их длина часто бесконечна или, точнее, неопределима. Однако многие кривые статистически “самоподобны”, что означает, что каждую часть можно считать уменьшенным изображением целого. В этом случае степень сложности может быть описана величиной D, которая обладает многими свойствами “размерности”, хотя она является дробной. В частности, оно превышает значение единицы, связанное с обычными кривыми.” Идея самоподобия, основанная на рекурсивном подходе Готфрида Лейбница (1646‒1716 гг.) и работах математиков конца XIX‒начала ХХ века, нашла широкое применение в различных областях знаний, включая статистическую физику, метеорологию, гидрологию, геоморфологию, анатомию, таксономию, неврологию, лингвистику, информационные технологии, компьютерную графику, экономику, геологию, медицину, физическую космологию, инженерию, теорию хаоса, эконофизику, металлургию и социальные науки. Фундаментальные понятия “фрактала” [Mandelbrot, 1977, 1982] и “мульти-фрактала” [Mandelbrot, 1989] стали объектами целой серии популярнейших направлений научных исследований второй половины ХХ века.
Однако, следует сразу специально оговорить следующие естественные проблемы оценки коэффициента D на практике [Kossobokov, Mazhkenov, 1988; Кособоков, 2005]. Определить фрактальную размерность множества [Mandelbrot, 1982] по выборке в принципе довольно сложно, поскольку, во-первых, фрактальная размерность любого дискретного множества и, в частности, любой, пусть даже очень большой, но конечной выборки равна нулю и, во-вторых, не исключена ошибка при выборе конечного множества областей, по которым производится оценивание. Кроме того, фрактальная размерность множества одинакова во всех его точках лишь в особом классе однородных и самоподобных множеств, так называемых “монофракталах”. Наконец, в случае оценивания фрактальной размерности множества возможных эпицентров по каталогам землетрясений статистика, как правило, является представительной лишь в областях линейного размера начиная с нескольких десятков километров, а множество эпицентров аппроксимируется конечным числом событий, координаты которых известны неточно. Кроме того, очевидно, что пространственное распределение землетрясений неравномерно и a priori не ясно, насколько оно однородно и самоподобно.
1.1. Фрактальность и скейлинг
С 1980-х гг. понятия фрактал и фрактальность прочно вошли в обиход не только математиков, но и специалистов в самых разных областях науки. Слово “фрактал” образовано от латинского “fractus” и в переводе означает “состоящий из фрагментов”. Рождение фрактальной геометрии принято связывать с выходом в 1977 г. книги Мандельброта “Fractals: Form, Chance and Dimension”, в которой обобщены не только его собственные наблюдения, но и научные результаты других математиков, исследовавших геометричесие рекурсии в 1875‒1925 гг. (Вейерштрасс, Кантор, Клайн, Пуанкаре, Кох, Серпинский, Фату, Жюлиа, Хаусдорф и др.). Безусловной заслугой книги Мандельброта была демонстрация “математических монстров”, аналоги которых могут быть полезны при изучении окружающего нас мира.
Позднее, аргументируя принятую им терминологию, Бенуа Мандельброт писал [Mandelbrot, 1982]: “I coined fractal from the Latin adjective fractus. The corresponding Latin verb frangere means “to break”: to create irregular fragments. It is therefore sensible- and how appropriate for our needs! ‒ that, in addition to “fragmented” (as in fraction or refraction), fractus should also mean “irregular”, both meanings being preserved in fragment.”
“Я придумал фрактал от латинского прилагательного fractus. Соответствующий латинский глагол frangere означает “ломать”, создать неправильные обломки. Поэтому это разумно ‒ и насколько уместно для наших нужд! ‒ что, помимо “фрагментированного” (как в дробной части или преломлении), fractus также должен означать “нарушающий правила”, оба значения сохраняются во фрагменте.”
(Отметим, что толковый словарь латинского языка [Körting, 1891–1907] переводит латинский глагол frāctum как “ломать” или “разламывать”).
Определение фрактала, данное Бенуа Мандельбротом, в общих словах звучит так: “Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому” [Feder, 1988]. При этом термин “подобный” применительно к фрактальному представлению об объектах исследования употребляется не как пропорциональный с некоторым положительным или отрицательным коэффициентом, а просто “похожий”. “Подобие”, а точнее, “самоподобие” является одним из основных свойств фрактальных объектов. В самом простом случае “моно-фрактала” его небольшая часть содержит информацию обо всем объекте.
1.2. Понятие фракталов в сейсмологии. Иерархические структуры
В науках о Земле одними из первых работ, связанных с фрактальностью или скейлингом (масштабным рассмотрением), было изучение дискретности горных пород академика М.А. Садовского [Садовский, 1979], приведшее к теории автомодельности динамических геологических систем [Садовский, 1987; Садовский и др., 1987; Садовский, Писаренко, 1991]. Было сформулированно представление о разломах и блоках литосферы Земли как структуры иерархической системы. Размеры элементов этой системы определяются универсальным шагом иерархической делимости среды, а сами элементы вовлечены в сложное взаимодействие самоорганизующее ее динамику. Следует заметить, что в работе [Kagan, Knopoff, 1980] была впервые рассчитана корреляционная размерность распределения землетрясений в объеме для шести каталогов землетрясений (двух мировых и четырех региональных). Однако, в конце 1970-х гг. надежных определений параметров землетрясений было недостаточно для содержательной ревизии закона Гутенберга‒Рихтера, до которой авторам тогда не хватило буквально одного шага.
Представление о литосфере Земли как о сложной, нелинейной, самоподобной, иерархически самоорганизованной системе мобильных блоков разного размера [Keilis-Borok, 1990] является базовым фактором для современных исследований сейсмологии. В частности, это представление широко используется при изучении характерных особенностей последовательностей землетрясений различных магнитудных диапазонов в задачах поиска мест возможного возникновения сильных землетрясений [Gelfand et al., 1976; Gorsh-kov et al., 2003], прогнозирования времени их возможного возникновения [Кейлис-Борок, Кособоков, 1984; Kossobokov, 2017], группируемости сейсмических событий [Baiesi, Paczuski, 2004; Zaliapin, Ben-Zion, 2013, 2016] и оценки сейсмической опасности и рисков [Молчан и др., 1996; Некрасова и др., 2015, 2020].
Исходя из иерархической структуры разломов и блоков, независимо несколькими исследователями был сделан вывод о том, что пространственные, временны́е и энергетические характеристики сейсмичности подчиняются единому закону подобия, обобщающему соотношение Гутенберга‒Рихтера [Kossobokov, Mazhkenov, 1988; Челидзе, 1990; Смирнов, 1995]. При этом практическая задача определения параметров самоподобия сейсмического потока, как оценка фрактальной размерности природного объекта, требует принятия, вообще говоря, неоднозначных допущений, что часто приводит к спорным значениям.
В качестве примера приведем основные предположения и условия, принятые в работе [Писаренко, Голубева, 1996], посвященной одной из первых практических оценкок мульти-фрактальных параметров применительно к реальной сейсмичности.
В предположении, что существует достаточно большая, однородная сейсмическая территория, на которой справедливо предположение о сейсмичности, как о стационарном пуассоновском процессе с интенсивностью λk. При определении “средней интенсивности на единицу площади” из набора интенсивностей λ1, …, λk, …, относящихся к ячейкам площади S, величина $\frac{1}{{nS}}\sum\nolimits_{k = 1}^n {{{\lambda }_{k}}} $ не будет ни к чему сходиться при п → оо. Таким образом, “средней по площади” интенсивности не существует, а сумма $\sum\nolimits_{k = 1}^n {{{\lambda }_{k}}} $ растет пропорционально ${{n}^{{1/\alpha }}}$, а не пропорционально п. В результате сейсмический потенциал, характеризуемый интенсивностью потока землетрясений, растет при увеличении площади S пропорционально ${{S}^{{1/\alpha }}}$, где 1/α > 1, а не пропорционально площади S, хотя территория предполагается однородной в статистическом смысле. Как и при усреднении по площади, не существует “средней по времени” интенсивности. Интенсивности λk в реальности могут меняться со временем λk = λk(t), весь вопрос ‒ с какой скоростью. Если такие изменения действительно происходят, то при достаточно больших Т последовательные значения интенсивностей λk(t), λk(t + Т), относящиеся к интервалам (t, t + Т), (t + Т, t + 2Т), можно считать почти независимыми. Следовательно, усредняя интенсивности λk по такой последовательности, следует использовать нормировку ${{n}^{{1/\alpha }}}$, а не п.
Многие свойства землетрясений и разломов могут быть описаны в целом степенными cотношениями. Подробный разбор используемых в исследованиях сейсмичности степенных соотношений приведен в работе [Ben-Zion, 2008]. Показано, что модели землетрясений и разломов не соответствуют универсальной статистике степенного закона во всех областях пространства-времени. Детальные наблюдения различных величин и распределений, включая времена между последовательными событиями, распределение гипоцентров, геометрические свойства активных зон сейсмических линеаментов, закономерности фокальных механизмов, частотно-пространственные статистики, статистики форшоков и афтершоков, демонстрируют систематические отклонения от строгой инвариантности во всех диапазонах исследуемых данных. Если долгосрочное поведение системы проявляется при различных условиях различных динамических режимов, некоторые из которых имеют предпочтительные пространственно-временны́е масштабы, то масштабно-инвариантный отклик возникает только для специального подмножества параметров и условий, динамику можно понять и лучше проанализировать с точки зрения фазовых диаграмм, параметров настройки и стандартной теории критичности [Ben-Zion, 2008].
1.3. Обобщение Реньи фрактальной размерности Dq. Размерности D0, D1, D2
Для количественной оценки фрактальной размерности предложено много алгоритмов, основаных на различных математических расчетах и эмпирических оценках. Самый простой фрактальной размерностью можно назвать “размерность подобия”. Это будет, например, фрактальная размерность временны́х интервалов между последовательными сейсмическими событиями (основных толчков с исключением или включением связанных с ними зависимых событий – форшоков и афтершоков), для определения которой используют триадное канторовское множество [Mandelbrot, 1982]. Метод позволяет получить фрактальную размерность в интервале от 0 до 1. Он состоит из деления временнóго интервала T, в течение которого произошло N землетрясений, на серию из n меньших интервалов длиной t = T/n, где n = 2, 3, 4, ….. Если распределение сейсмических событий в каталоге имеет фрактальную структуру, то число интервалов R длинной t, в которых содержится хотя бы одно событие пропорционально ${{t}^{{1 - D}}}$, где D ‒ фрактальная размерность. Значение D = 1 соответствует равномерному распределению сейсмических событий по времени. Чем меньше значение параметра D, тем выше концентрация (кластеризация) землетрясений исследуемой выборки [Earthquake Research …, 2001].
В публикации [Grassberger, Procaccia, 1983] описаны алгоритмы, которые теоретически могут быть использованы (и используются очень широко в настоящее время на практике) для оценки корреляционной размерности некоторой фрактальной меры µ по выборке точек, случайно распределенных в соответствии с мерой µ.
Для практического вычисления фрактальной размерности D часто используют метод подсчета клеток [Mandelbrot, 1982; Feder, 1988], полученная оценка D0 носит название “клеточной размерности” (box dimension). При этом объем простанства, объемлющий исследуемый объект, разбивается на ячейки (в трехмерном случае – кубики) со стороной, равной l, причем при каждой следующей итерации линейный размер l изменяется. Подсчитывается минимальное число клеток, необходимых для покрытия объекта N(l), при различных значениях l. Оценка фрактальной размерности D0 определяется по формуле:
N(l) строится в зависимости от l в двойном логарифмическом масштабе (ln – натуральный логарифм). Наклон линейной апроксимации получившегося графика ‒ D0.Поскольку точки не распределены с одинаковой плотностью, некоторые клетки заполнены “гуще”, чем другие. Этот факт учитывается в обобщении оценки D0 размерностями Реньи Dq (q ≥ 0). Обобщенная размерность Реньи определяется как предел
Очевидно, что значение q = 1 особая точка. Однако, при q → 1 значение размерности Реньи сходится к пределу
2. UNIFIED SCALING LAW FOR EARTHQUAKES, USLE. ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ
Обобщения соотношения Гутенберга‒Рихтера (1), учитывающие геометрические особенности распределения землетрясений в различных публикациях, появляются под несколькими названиями, начинающимися словом “общий”, “обобщенный”, “unifited”, “universal” или “general” [Kossobokov, Mazhkenov, 1988; Челидзе, 1990; Смирнов, 1995; Bak et al., 2002; Molchan, 2020]. Поскольку эти соотношения по сути эквивалентны, далее используется аббревиатура названия статьи [Bak et al., 2002] “Unified Scaling Law for Earthquake” ‒ USLE [Kossobokov, 2020].
2.1. USLE. Формулировка
Как следствие проникновения и развития теории самоподобия, иерархических, масштабных, скейлинговых, фрактальных идей в сейсмологии, USLE был сформулирован независимо несколькими исследователями [Kossobokov, Mazhkenov, 1988; Челидзе, 1990; Смирнов, 1995; Bak et al., 2002], занимавшимися оценками статистических параметров распределений сейсмических событий. Дополнение в основное соотношение, используемое в сейсмологии ‒ закон повторяемости Гутенберга‒Рихтера (1) [Gutenberg, Richter, 1944, 1954], напрашивалось и было внесено для адекватного нормирования при переходе от региона в целом к его части. Напомним, что закон повторяемости устанавливает связь между средним числом землетрясений N(M) магнитуды M и выше в единицу времени в некоторой пространственной области.
При выборе региона для анализа параметров соотношения (1) возможны трудности, связанные с размерами выбранного региона. Особенности выполнения соотношения (1) для конкретных каталогов сейсмических событий рассмотрены в модели многомасштабной сейсмичности [Molchan et al., 1997], а концепция “характерного землетрясения” [Schwartz, Coppersmith, 1984] может объяснить невыполнение соотношения (1) в области характерного линейного размера таких событий.
Соотношение (1) в работах [Kossobokov, Mazhkenov, 1988; Кейлис-Борок и др., 1989] обобщено в виде:
(2)
$\begin{gathered} {\text{lo}}{{{\text{g}}}_{{10}}}N(M,L) = A + B(5 - M) + C{\text{lo}}{{{\text{g}}}_{{10}}}L, \\ {{M}_{ - }} \leqslant M \leqslant {{M}^{ - }}, \\ \end{gathered} $Формулировка USLE, использующая вместо числа землетрясений в определенный период времени двойственную величину ‒ время между сейсмическими событиями, была предложена в работах [Bak et al., 2002; Christensen et al., 2002] в следующем виде:
(3)
${{P}_{S}}_{{,L}}(T)\infty ~{{T}^{{ - a}}}f(x) = {{T}^{{ - a}}}f(T{{L}^{{{{d}_{f}}}}}{{S}^{{--b}}}),$“To understand the Unified Law for Earthquakes, it is essential to see what the value of x represents. The quantity LdfS–b in the scaling function represents the average number of earthquakes per unit time, with seismic moment greater than S occurring in the area size L × L. Therefore, x is a measure of the number of earthquakes happening within a time interval T. The Unified Law states that the distribution of waiting times between earthquakes depends only on this value”.
“Для того чтобы понять Общий Закон для Землетрясений, необходимо осознать, что означает параметр x. Величина LdfS–b в функции подобия представляет среднее число землетрясений с сейсмическим моментом больше S, происходящих в области размера L × L в единицу времени. Поэтому, x есть мера числа землетрясений за время T. Общий Закон утверждает, что распределение времени ожидания между землетрясениями зависит только от этого значения”.
Согласно [Corral, 2003], cформулированный таким образом принцип USLE предполагает следующие выводы для распределения сейсмических событий:
– пространственно-временнόй масштаб возникновения землетрясения является ключевым элементом, если рассматривать землетрясения в качестве критических проявлений системы;
– это первый закон, который связывает времена между последовательными землетрясениями, (фактор 1/Sb в законе Гутенберга‒Рихтера) и фрактальную размерность пространственного распределения событий df;
– USLE одинаков для всех землетрясений, независимо от их размера и местоположения, а также независимо от того, рассматриваются ли они как афтершоки, форшоки или основные события;
– согласно USLE, сразу после любого землетрясения высока вероятность наличия другого землетрясения, и эта вероятность уменьшается во времени до ${{S}^{b}}/{{L}^{{{{d}_{f}}}}}$, то есть существует время корреляции, которое зависит от размера региона и магнитуды землетрясения, и, следовательно, для любого события можно найти кластеры афтершоков в каком-либо масштабе времени, соответствующего линейному размеру региона L.
Отметим, что, согласно [Corral, 2003], выполняется эквивалентность формулировок USLE для ожидаемых интервалов времени между последовательными землетрясениями и для частоты из возникновения в рассматриваемой области линейного размер L.
А именно, если r(x, y, t) ‒ число землетрясений за единицу времени в (x, y), произошедших за время t, то зависимость от пространства и времени входит в распределение времен между последовательными событиями Dxyt(τ) только через r(x, y, t), то есть
Dxyt(τ) = Dxyt(τ| r(x, y, t)) и
где ρ(r) ‒ плотность вероятности сейсмического потока r, а μ = 〈r〉 − нормирующий коэффициент.Именно этим автором в следующей работе [Corral, 2004] поставлен вопрос о различии формулировок “universal” и “unified”. Первый термин отнесен автором к области отдельного региона, для которого USLE выполняется вплоть до максимаьного, соответствующего границам региона значения L. В то же время использование термина “unified” подразумевает автором выполнение USLE в глобальном масштабе, от любого отдельного кластера, до размеров Земли в целом. Невыполнимость второй формулировки показана для областей малых размеров L, включающих сильные землетрясения и порожденные ими “лавины” более слабых событий – афтершоков.
Анализ “универсальности” USLE, как для оценки временны́х распределений землетрясений, так и для пространственных распределений, проведен в серии работ [Molchan 2005, 2020; Molchan, Kronrod, 2007, 2009; Ben-Zion, 2008], авторы которых обращают внимание на то, что “универсальность распределения” нормированной величины τL – кажущаяся и связана с подходящей визуализацией представления распределения αLτL в log‒log шкале. В такой системе координат хорошо подтверждается согласие хвостов распределений αLτL, но скрыто расхождение распределений в области умеренных значений указанных статистик. Поведение распределений αLτL землетрясений в области малых значений имеет кажущийся степенной тренд, согласующийся с законом Омори, а в области больших значений тренд экспоненциально обрывается. Отказ от “универсальности” USLE был достаточно очевиден уже в первых публикациях, в которых полученные значения коэффициентов обшего закона для разных сейсмоактивных регионов мира значительно отличались друг от друга [Кейлис-Борок и др., 1989].
Несмотря на указанные теоретически обоснованные противоречия и сложности практического применения, основанием к использованию USLE может служить следующее предположение: в моделях коллективного поведения сложной системы эффективно применяются законы, связанные с выборочными особенностями отдельных, основных событий, которые и определяют долгосрочную реакцию системы. В идеале, эти эффективные законы должны строго устанавливаться путем изучения поведения при увеличении пространственно-временны́х масштабов и устранения на прогрессивных итерациях не относящихся к делу деталей более низких масштабов [Ben-Zion, 2008].
Методы оценивания фрактальных параметров модельных и наблюденных сейсмических каталогов определяют, какая размерность будет получена. Различные размерности, оцененные для одного и того же множества точек, могут иметь различные величины. Как будет продемонстрировано дальше, различные граничные условия для выборок с одинаковым распределением могут привести к вариациям в оценке одной и той же фрактальной размерности.
2.2. Оценки фрактальной размерности для модельных сейсмических каталогов
В пионерской работе [Кейлис‑Борок и др., 1989] предложенный авторами алгоритм оценки пространственного коэффициента распределения сейсмичеcких событий [Kossobokov, Mazhkenov, 1988] протестирован на модельных примерах искусственно сгенерированных каталогов с заранее заданными свойствами пространственно-временнóго распределения событий разных магнитуд. А именно, пространственное распределение эпицентров задавалось равномерно на плоскости (D = 2), прямой (D = 1), а также в соответствии с известными монофракталами, имеющими точно определенную теоретическую фрактальную размерность D = log10(N)/log10(n), (N > n – целые числа). Оценки коэффицентов USLE приведены для модельных примеров с распределением эпицентров на множествах размерности D в диапазоне от 1 до 2. При этом расчеты проводились для распределения эпицентров в области, полностью содержащей исследуемое множество целиком, в области, содержащей эпицентры при сдвиге ¼ модельного распределения, и в области, заполненной на ¼ и повернутой на случайный угол. Оценки коэффициентов A, B и С, приведенные в публикации [Кейлис‑Борок и др., 1989, табл. 2 ], устойчивы относительно сдвигов и поворотов и колеблются возле своих истинных модельных значений, свидетельствуя об адекватности использованного алгоритма расчета. При этом размах отклонения от истинного значения для коэффициента С связан с топологическими свойствами исследуемых множеств. В частности, самое большое отклонение от истинного значения ~13% имеет каталог, моделирующий “кладбище Серпинского”, единственного, имеющего топологическую размерность ноль и фрактальную размерность log104/log10 3 = 1.2618…. (Также следует отметить, что алгоритм расчета коэффициентов A, B и С проводился по иерархически упорядоченным квадратам со стороной L0/2i, i = 0, 1, … h – 1 для h = 7 ступеней иерархии).
В той же работе оценка пространственного распределения эпицентров для модельных каталогов, иммитирующих события в границах геоморфологически определенных линеаментов 1-го ранга Востока Средней Азии показывает, что адекватные оценки коэффициентов A, B и C могут быть получены при оценке по выборке размера близкого к реальному числу зарегистрированных в регионе сейсмических событий, что безусловно важно при переходе к расчетам для реальных сейсмоактивных регионов. При этом оценка коэффициента C для более 44 тыс. модельных событий отличается от оценок по моделям с реальным числом землетрясений магнитуды 2.78 и выше (энергетического класса К ≥ 9) на Востоке Средней Азии в период 1962‒1985 гг. и разным наклоном графика повторяемости Гутенберга‒Рихтера (b = 1 и 0.7) менее чем на 1% (C = 1.40, 1.38 и 1.37 соответственно). (Напомним, что абсолютно точная оценка C как фрактальной размерности множества сосредоточения эпицентров землетрясений возможна только при стремлении размера выборки к бесконечности, что на практике недостижимо).
Еще один модельный пример из работы [Кейлис‑Борок и др., 1989] заслуживает особого внимания как переходный шаг от монофрактала к поли- и мультифракталам. А именно, авторами в качестве носителя модельных эпицентров было рассмотрено множество, состоящее из двух наиболее простых объектов размерности 1 и 2, то есть объединение точек на прямой с точками на плоскости. Причем, баланс между числом событий, распределенных случайным образом по прямой или плоскости, задавался коэффициентом пропорциональности К, который и определял кажущуюся фрактальную размерность носителя эпицентров объединенного каталога. При значениях коэффициента К = 1/40 и 8 оценка С практически определяется лишь прямой или плоскостью, соответственно, а при значениях К в интервале от 1/4 до 4 значения параметра С изменяются и могут быть аппроксимированы степенной функцией С(К) = 1.386К–0.169, R2 = 0.991 (см. табл. 4 из работы [Кейлис‑Борок и др., 1989]). Таким образом, следует ожидать, что для неоднородного множества, объединяющего совокупность однородных носителей сейсмичности, ассоциированных с отдельными разломами сейсмоактивной территории, региональная оценка фрактальной размерности даст средневзвешенное значение фрактальных размерностей его однородных частей.
В работе [Gospodinov et al., 2010] получен набор значений стандартных фрактальных коэффициентов корреляционной размерности для моделей различных пространственных распределений. А именно, метод Монте-Карло применен для создания имитированных наборов данных о землетрясениях с равномерным пространственным распределением области G в трехмерном, двумерном и одномерном пространственных объемах. Для каждого смоделированного набора данных оценена корреляционная фрактальная размерность эпицентров D2, и проверено наличие корреляции между значениями D2 и типом пространственного распределения. Результаты анализа получены для 5000 точек. В трехмерном случае оценки выполнены для куба размером 1 × 1 × 1, а затем для объемов, соответствующих последовательному сокращению вдвое одной из его пространственных сторон три раза, т.е. до размера 0.5, 0.25 и 0.125 соответственно. Для двумерного случая начальной областью выбран квадрат 1 × 1, и, последовательно, области 1 × 0.5, 1 × 0.25 и 1 × 0.125. Для одномерного случая рассмотрено три отрезка длиной 1, 0.5, 0.25. В работе показано, что значения D2 уменьшаются при уменьшении одного из размеров выбранного объема. Поскольку авторы работы [Gospodinov et al., 2010] анализировали равномерные распределения на множестве G, можно предположить, что соответствующие значения корреляционной размерности D2 для каждого из рассмотренных объемов определяют верхние пределы возможных значений фрактальной размерности для данных о 5000 реальных землетрясений в аналогичном объеме. При этом, как считают авторы, на возможные нетривиальные фрактальные свойства реальных данных может указывать значение D2 меньшее, чем определенное ими значение корреляционной размерности D2 для простых случаев и 4-х ступеней иерархически упорядоченных объемов.
2.3. Оценки коэффициентов USLE реальных сейсмических каталогов
Основным источником фактических данных о распределении сейсмических событий служат глобальные и региональные каталоги землетрясений. С середины 1960-х годов каталоги содержат с известной погрешностью определения времени в очаге и локализации (эпицентров и гипоцентров) сейсмических событий, а также их величины (магнитуды) и предоставляют достаточно надежную информацию для проведения в настоящее время статистически значимых оценок распределений сейсмических событий и различной минимальной магнитудой как в глобальном масштабе, так и в региональном и даже локальном масштабах.
Далее будут рассмотрены более детально ограничения и сложности при оценке пространственного распределения эпицентров реальных землетрясений для отдельных регионов.
В рамках теории USLE предполагается, что сейсмические события происходят в результате подвижки по границам самоподобной иерархической структуры разломов и блоков литосферы Земли. Приведем основные принципы, которым должны удовлетворять самоподобные системы из работы [Писаренко, Голубева, 1996] и, как следствие, условия построения алгоритмов определения параметров таких систем.
Пусть сейсмоактивная область S разделена на непересекающиеся площадки Ak, $S = \bigcup\nolimits_{k = 1}^n {{{A}_{k}}} ,$ имеющие одинаковую площадь. Предположим, что на каждой из площадок Ak поток землетрясений является стационарным пуассоновским процессом с интенсивностью λk. Предположим, что {λk} являются независимыми случайными величинами, распределенными в соответствии с некоторым законом F(x). Если принять гипотезу самоподобия распределения сейсмичности по пространству в данном регионе, то естественно считать, что вид закона F(x) при изменении размера одиночной площадки Ak останется тем же, а изменится лишь масштабный, нормирующий множитель этого распределения. Если объединить n площадок, то получим: ${{С}_{n}}({{\lambda }_{{k1}}} + ...{{\lambda }_{{kn}}}) \triangleq {{\lambda }_{1}}$, где Сn ‒ некоторый нормирующий множитель, знак $ \triangleq $ обозначает эквивалентность распределений правой и левой частей, но не их равенство в буквальном смысле. Таким образом, распределение величин λk является устойчивым, а нормирующая константа имеет вид
Весьма важным условием того, что из самоподобия будет следовать устойчивость распределения интенсивностей λk, является независимость слагаемых λkn. Ясно, что при достаточно малых площадях смежные площадки могут иметь зависимые значения интенсивностей. Однако при увеличении площади можно ожидать, что эта зависимость будет ослабевать. А именно, в первом приближении можно считать, что “общая” относительная площадь двух смежных квадратов площади S обратно пропорциональна длине стороны квадрата. Таким образом, выбирая достаточно большое значение S, можно уменьшить эффект зависимости интенсивностей λ1 и λ2 на смежных площадках. Отметим, задача оценки осложняется тем, что при анализе каталога сейсмических событий наблюдаются не интенсивности λk на разных площадках, а лишь случайное число землетрясений, которое, как предполагается, имеет распределение Пуассона с параметром λk × Т, где Т ‒ время наблюдения.Приведем несколько примеров реализованных алгоритмов определения фрактальных параметров распределения сейсмических событий для одномерного случая (распределения интервалов времени между последовательными сейсмическими событиями), двумерного (определения коэффициента пространственного распределения эпицентров сейсмических событий) и трехмерного (определение коэффициента пространственного распределения гипоцентров сейсмических событий).
Распределение интервалов времени τ между последовательными сейсмическими событиями рассмотрено в работе [Molchan, 2005]. В очень общих предположениях в работе найдено, как распределение τ ведет себя вблизи 0 и на ∞. Как и предполагалось автором работы, теоретико-статистическое исследование подтвердило соответствие распределения τ закону Омори вблизи нуля и случайный пуассоновский характер основных сейсмических событий на бесконечности в асимптотическом приближении. По существу, именно эти асимптотики делают эмпирическую плотность вероятности для τ “универсальной” при построении в логарифмическом масштабе.
Трудности и причины возможных неоднозначных определений при оценке фрактальной размерности пространственного распределения эпицентров для отдельных регионов на основе реальных каталогов подробно рассмотрены в работе [Molchan, Kronrod, 2009]. А именно: 1) в стандартных подходах оценки параметра d в двумерном пространстве (на плоскости) используется сканирование территории квадратными или круговыми областями выбранного линейного размера или диаметра L, при этом результат может в большой степени зависить от значения L; 2) на результат эмпирического определения d может повлиять выбор диапазона шкал [L−, L+], так как один и тот же объект при рассмотрении в разных диапазонах масштаба может выглядеть как мультифрактальный с разными характеристиками d; 3) влияние границ области исследования или, в более общем смысле, влияние основных характеристик сейсмичности в регионе, таких как крупные разломы или разрывы сейсмичности (самоподобие может нарушаться в масштабах, сопоставимых с размером указанных неоднородностей).
В работе [Molchan, Kronrod, 2009] оценки “клеточной” ‒ d0, “информационной” ‒ d1 и “корреляционной” d2 размерностей проведены для землетрясений выделенных сейсмических областей G на территории Южной Калифорнии, Камчатской сейсмофокальной зоны, Центрально-Американской зоны субдукции, Новой Зеландии, Греции, Коста-Рики и сейсмического полигона Гарм в Средней Азии. Оценки dq для q = 0, 1, 2 выполнены для подсчета λ(dg) (числа сейсмических событий в ячейках dg с линейными размерами L). L = {Li} выбирались исходя из предварительного анализа данных сейсмического каталога каждой области G. Пример области G и выборочные результаты анализа [Molchan, Kronrod, 2009] приведены в табл. 1.
Таблица 1.
Выборочные результаты фрактального анализа из работы [Molchan, Kronrod, 2009]
| Регион G, dT |
dHG × WG × XG | mc | d0 [L−, L+] |
d1 [L−, L+] |
d2 [L−, L+] |
Характер тектонических движений |
|---|---|---|---|---|---|---|
| Южная Калифорния 1984–2002 |
<20 × 400 × 600 | 2 | 1.92 [20‒200] |
1.43 [4‒200] |
1.26 [4‒200] |
Область трансформных разломов |
| Камчатка 1962–2003 |
<90 × 180 × 720 | 3.5 | 1.99 [10‒180] |
1.81 [5‒180] |
1.69 [5‒180] |
Зона субдукции |
| Новая Зеландия 1990–2007 |
<70 × 300 × 600 | 2.5 | 1.98 [10‒100] |
1.73 [4‒150] |
1.59 [4‒150] |
Зона субдукции |
| Центральная Америка 1964–2007 |
<100 × 300 × 1500 | 4.0 | 1.97 [30‒150] |
1.77 [15‒150] |
1.66 [15‒150] |
Зона субдукции |
| Коста-Рика 1994‒2007 |
<100 × 600 × 240 | 3.2 | 1.97 [15‒120] |
1.78 [15‒120] |
1.67 [10‒120] |
Зона субдукции |
| Греция 1974‒2007 |
<70 × 400 × 600 | 3.0 | 1.97 [10‒200] |
1.78 [10‒200] |
1.63 [10‒200] |
Зона коллизии |
| Гарм 1955‒1979 |
<40 × 100 × 200 | 1.7 | 1.97 [4‒100] |
1.79 [2‒100] |
1.68 [2‒100] |
Зона коллизии |
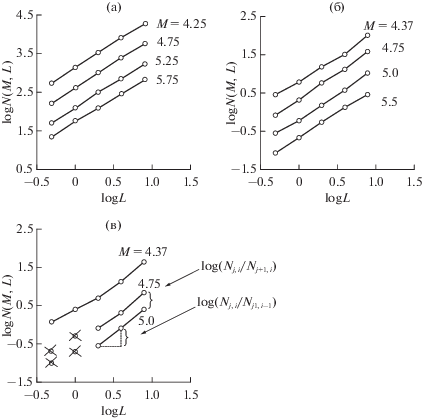
Алгоритм, предложенный и использованный в работах [Kossobokov, Mazhkenov 1988; Kosobokov, Mazhkenov, 1994; Кейлис-Борок и др., 1989], также оценивает фрактальную размерность, соответствующую корреляционному значению D2. Его модифицированная версия, алгоритм SCE (Scaling coefficient estimation), предложенная в 2002 г. для глобального картирования значений коэффициентов USLE [Nekrasova, Kossobokov, 2003; Кособоков, Некрасова, 2004], оценивает параметры A, B и C методом наименьших квадратов как коэффициенты линейной регрессии в трехмерном пространстве числа сейсмических событий Nij, подсчитанных в непересекающихся пространственных ячейках Li для сейсмических событий их энергетического (магнитудного) диапазона Mj.
Рис. 2.
Типичные наборы, Nji для выбранных регионов: а ‒ модельная выборка эпицентров на кривой Коха; б – эпицентры в районе г. Лос-Анджелес, США; в – эпицентры вблизи Токиийской агломерации, Япония [Nekrasova et al., 2015].
Перечеркнутые значения Nji ‒ “отбракованы” алгоритмом как чрезмерно отклоняющиеся от подобия, что, как правило, связано с представительностью конкретной выборки в конкретном наборе пространственной иерархии рассматриваемой области.
Еще один алгоритм оценки фрактальной размерности для множества распределения гипоцентров сейсмических событий на основе корреляционнго интеграла предложен в работе [Smirnov, 2003]. Рассмотриваются выборки расстояний от центра кластера до точки (события), принадлежащей этому кластеру в области пространства, ограниченной сферой радиуса R. Соответствующая функция распределения показывает долю событий, отстоящих от центра на расстояние меньшее или равное r. А именно, расстояние от центра кластера до его точек пропорциональна rd для расстояний из интервала [R1, R2]. При этом R1 определяется погрешностью определения положений землетрясения, а R2– либо размером кластера, либо размером пространственной ячейки, в которой оценивается d.
Для расстояний r ∈ [0, R2] функция распределения имеет вид F(r) = (r/R2)d, а плотность распределения сответственно $f(x) = \frac{d}{{{{R}_{2}}}}{{r}^{{d - 1}}}$, тогда
где NS – число известных расстояний r, а N1 = = N ‒ NS ‒ число расстояний из выборки N, для которых расстояние до центра кластера соизмеримо с погрешностью измерения положения землетрясения в каталоге [Smirnov, 2003].2.4. Параметры USLE и фрактальная размерность сейсмических линеаментов. Взаимное распределение коэффициентов USLE
Использование представлений о самоподобном блоковом строении земной коры неизбежно приводит к необходимости введения иерархии не только для блоков, но и для межблоковых промежутков – зон тектонических трещин и разломов. Между тем, для этих объектов ситуация представляется еще менее очевидной [Кочарян, 2016]. Первая оценка фрактальной размерности системы разломов и блоков была получена для сейсмически активных разломов Южной Калифорнии в работе [Okubo, Aki, 1987]. Возможный характер теоретической связи между пространственным распределением сейсмичности и фрактальной размерностью сейсмических линеаментов подразумевает одно из двух отношений конечных элементов: либо имеется фрактальное распределение разломов, каждое из которых имеет свое характерное землетрясение, либо существует фрактальное распределение землетрясений вдоль любого данного разлома [Turcotte, 1997].
Эмпирически получено соотношениe между числом землетрясений N и длиной сейсмического линеамента l, с которым они связаны N = βl –D [Turcotte, 1997]. Поскольку N = βAb ≈ βl 2b, где A ‒ площадь области разрывных нарушений [Aki, 1981], из равенства этих соотношений делается вывод о зависимости D = 2b фрактальной размерности D и коэффициентом баланса b (“b-value”) между последовательными магнитудными интервалами из закона Гутенберга‒Рихтера (1). Термин b-value известен в русской литературе как наклон графика повторяемости событий в двойном логарифмическом масштабе [Ризниченко, 1958]. В региональном масштабе многие исследователи проверяли идею о том, что фрактальное распределение частоты возникновения землетрясений, подразумеваемое соотношением Гутенберга‒Рихтера, связано с фрактальным распределением разломов (сейсмических линеаментов). Так, например, в работе [Öncel et al., 2001] проведено исследование корреляции “b-value” и D для активных сейсмических разломов на территории Японского острова Хонсю и сейсмичности с 1600 по 1997 гг. Общий вывод, сделанный в этой работе, сводится к тому, что наблюдается как положительная, так и отрицательная корреляция при рассмотрении сейсмичности и оценки фрактальной размерности сети сейсмических разломов, к которой она приурочена.
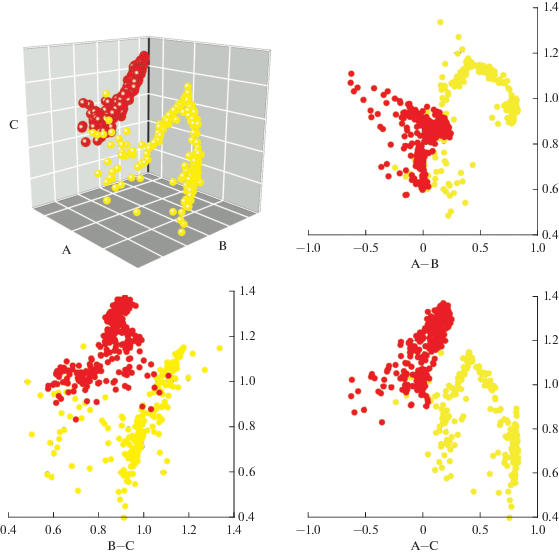
В публикациях [Nekrasova et al., 2011; Некрасова и др., 2020] приводятся примеры возможных взаимных корреляционных соотношений всех трех параметров A, B и С для USLE. Отмечено, что наблюдаемые попарные корреляции весьма нетривиальны и изменчивы не только по пространству внутри одного региона, но и во времени, отражая специфику среднесрочной изменчивости пространственно-временнóго потока землетрясений. На рис. 3 приведены примеры оценки значений коэффициентов USLE по алгоритму SCE в автономной области Фриули‒Венеция‒Джулия (Италия) на непересекающихся шестилетних временны́х интервалах. Сложное взаимное расположение в 3D значений коэффициентов USLE указывает на нетривиальность корреляционных связей между параметрами и значительное разнообразие характеристик сейсмического потока в пределах рассматриваемого региона, а также достаточно очевидно свидетельствует в пользу существенной изменчивости в динамике последовательности землетрясений во времени.
Рис. 3.
Значения коэффициентов USLE в автономной области Фриули‒Венеция‒Джулия (Италия) для шестилетних временны́х интервалов (1996‒2001 гг. ‒ желтые символы; 2011‒2017 гг. ‒ красные символы) [Некрасова и др., 2020].
При поиске в литературе данных для сравнения пространственного распределения сейсмичности с оценками фрактальной размерности геологических линеаментов следует помнить, что чаще всего для определения фрактальной размерности линейных объектов использовалась “клеточная” размерность D0. Например, реализованный алгоритм подсчета размерности Минковского в Географических информационных системах (ГИС) [Falconer, 1990]. Напомним, что значение корреляционной размерности не превышает значения “клеточной” размерности для одного и того же множества D0 ≥ D2.
В недавно опубликованном обзоре [Стаховский, 2017] предложена модель масштабной инвариантности сейсмических процессов, в рамках которой система, производящая землетрясения, воспринимается как принципиально неинтегрируемая. При этом очаг землетрясения рассматривается автором как фрактальный кластер микротрещин, который “не может быть исследован методами евклидовой геометрии”, однако, чисто гипотетически позволяет объяснить ряд особенностей сейсмического процесса.
3. USLE: ПРИМЕНЕНИЕ И РЕЗУЛЬТАТЫ
В этом разделе рассмотрены некоторые задачи, требующие анализа распределения сейсмических событий в пространственно-временнόй области, для решения которых предполагается надежность. Как показывает опыт, возможность использования предположений USLE в определенных пространственно-магнитудных и временны́х диапазонах, а также предположение о том, что хаотическое поведение может лежать в основе геотектонических процессов, довольно часто позволяют выбрать оптимально применимую методику для оценки сейсмической опасности и связанных с нею рисков. В рамках предположений о самоподобии анализ коэффициентов фрактального распределения обеспечивает простой способ описания количественно-инвариантного распределения сложных объектов или явлений по небольшому числу параметров.
Следует учитывать, что наиболее надежные характеристики сложных динамических систем можно получить лишь при значительном осреднении в крупном масштабе и с привлечением данных за максимально продолжительный период наблюдений. При этом наблюдаемая изменчивость сейсмической активности обеспечивает важные ограничения для моделирования сейсмических последовательностей. Следует отметить, что оценки параметров динамической системы в среднесрочных масштабах времени и локальных по территории зависят от методов их подсчета, так как изменчивы по времени и по пространству [Nekrasova et al., 2011; Некрасова и др., 2020].
3.1. Характеристика сейсмического потока. Контрольный параметр η
В работе [Molchan, 2020] отмечено, что сейсмический поток α (M, L, ΔT) обладает свойством USLE, если после подходящей нормировки статистики по всем ячейкам L × L α не зависит от (M, L, ΔT). Именно такая нормировка и независимость были представлены Пером Баком с соавторами [Bak et al., 2002] как контрольный параметр USLE
где τ ‒ интервал времени между последовательными сейсмическими событиями, а коэффициенты B и C ‒ из соотношения (2). Таким образом, еще раз подтверждено, что η является параметром масштабирования или нормировки сейсмического потока и, с физической точки зрения, управляет самоорганизованной нелинейной системой сейсмичности данной области так, что распределение времен между последовательными землетрясениями зависит только от этого параметра. Изменение величины η в среднесрочном масштабе времени характеризует динамику сейсмичности изучаемого региона. В публикации [Kossobokov, Nekrasova, 2017] контрольный параметр η используется для эффективной оценки динамики до и после шести сильных землетрясений в Центральной Италии, а в работе [Kossobokov, Nekrasova, 2019] аналогичное исследование применено к пространственно-временнóй окрестности девяти сильнейших (Mw ≥ 7.0) землетрясений в районе Новой Зеландии.На рис. 4 показаны изменения значений контрольного параметра η в зависимости от времени возникновения землетрясений на угловом расстоянии 2.5° от эпицентров двух сильнейших из девяти землетрясений с Mw ≥ 7.0 в Новой Зеландии с 1993 по 2018 гг. [Kossobokov, Nekrasova, 2019]. Всего при анализе пространственно-временны́х окрестностей девяти сильнейших событий в Новой Зеландии с 1993 по 2018 гг. было выделено 42 периода стабильности, характеризующихся различными уровнями средних оценок параметра 〈η〉 в скользящем временнóм окне. Из 34 случаев в девяти рассматриваемых областях уровень 〈η〉 либо в 1.25 раза был выше, чем в предыдущем (в 8 случаях), либо ниже (в 16 случаях), либо изменяется в пределах 80–120% (в остальных 10 случаях). За исключением землетрясения Mw = 7.1, 22 ноября 2004 г. к югу от островов Новой Зеландии основной толчок прерывал период стабильного значения 〈η〉 и приводил в период продолжительностью до 959 дней:
Рис. 4.
Значение контрольного параметра USLE η в зависимости от времени на угловом расстоянии 2.5° от двух сильнейших землетрясений с магнитудой Mw = 7.8 в Новой Зеландии, с 1993 по 2018 гг. [Kossobokov, Nekrasova, 2019].
Времена сильнейших событий 15.07.2009 09:22:29 в 57 км от города Те-Анау (вверху) и 13.11.2016 11:02:56 в 54 км от города Амберлей (внизу) отмечены красными треугольниками; красная и зеленая линии – значения скользящего среднего по 50 землетрясениям с М ≥ 2.5 на угловом расстоянии 2.5° и 1° соответственно.
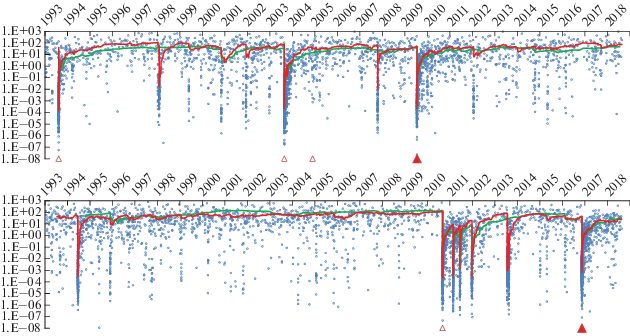
– к более низкому уровню 〈η〉 в четырех случаях (землетрясения Mw = 7.2 21 августа 2003 г., Mw = = 7.0 03 сентября 2010 г., Mw =7.0 01 сентября 2016 г. и Mw = 7.8 13 ноября 2016 г.),
– к более высокому уровню 〈η〉, только в одном случае (землетрясение Mw = 7.0 10 августа 1993 г.),
– к возвращению 〈η〉 на уровень в пределах 80–120% от уровня, прерванного основным толчком, что считается в приведенном анализе возвращением на тот же уровень (землетрясения Mw = 7.1 05 февраля 1995 г., Mw = 7.1 21 августа 2001 г., Mw = = 7.12 02 ноября 2004 г., Mw = 7.8 15 июля 2009 г.).
Таким образом, показано, что сильнейшие землетрясения могут служить причиной изменения сейсмического режима. Причем в Новой Зеландии такие землетрясения, в конечном итоге, существенно изменили сейсмический режим вблизи их местоположения в четырех случаях на более высокий и в одном случае на более низкий уровень возникновения землетрясений, а в других четырех случаях уровень контрольного параметра USLE η вернулся примерно к уровню, наблюдавшемуся до локально сильнейшего события [Kossobokov, Nekrasova, 2019].
На основе наблюдений за изменениями контрольного параметра η [Kossobokov, Nekrasova, 2017, 2019] авторами высказано предположение, что контрольный параметр η может характеризовать сейсмический поток в долгосрочной перспективе, находясь на одном из довольно устойчивых уровней своего значения и, время от времени, в среднесрочной перспективе, переключаться с одного на другой уровень в результате критического перехода, связанного, в том числе, с возникновением локально катастрофического для системы разломов и блоков землетрясения.
3.2. Декластеризации каталогов землетрясений. Поиск ближайшего соседа
Описание сейсмического потока в терминах USLE довольно быстро нашло применение в задачах декластеризации сейсмических каталогов и в настоящее время широко используются. Представление о зависимых землетрясениях фокусируется на разделении сейсмичности на группы зависимых и независимых событий, которые расположены в пространстве и времени ближе, чем можно предположить, исходя из случайных распределений. А именно, в работах [Baiesi, Paczuski, 2004; Zaliapin et al., 2008] введено понятие близости между двумя сейсмическими событиями, с помощью которого возможно определение ближайшего соседа. Близость рассчитывается как произведение двух величин, расщепляющих вклад размера (магнитуды) землетрясения ‒ величину контрольного параметра η поровну на два сомножителя: сомножитель Rij относится к пространственной области, а сомножитель Tij ‒ к временнóй области. Значения Rij и Tij определяются следующим образом:
где m – магнитуда основного толчка, ${{t}_{{ij}}} = {{t}_{j}} - {{t}_{i}}$ ‒ время взаимного влияния событий, которое является положительным, если событие j произошло после события i; а rij ≥ 0 ‒ пространственное расстояние между гипоцентрами землетрясений i и j.Согласно [Baiesi, Paczuski, 2004; Zaliapin, Ben-Zion, 2013], каждое землетрясение в каталоге соединяется со своим ближайшим соседом в соответствии с величиной “расстояния” η(i, j) = Rij × Tij (для которого, очевидно, не выполняется правило треугольника). Построенные по принципу ближайшего соседа группы отражают разнообразные вызывающие их процессы и включают в себя традиционные серии форшоков и афтершоков, а также рои и другие типы кластеризации сейсмичности. В частности, это позволяет разделить сейсмический поток на пуассоновский фон независимых событий и кластерные группы [Zaliapin, Ben-Zion, 2013]. Как уже было замечено, представление близости [Baiesi, Paczuski, 2004] основано на разложении на пространственную и временнýю составляющую контрольного параметра USLE.
При этом, оценка расстояний между ближайшими сейсмическими событиями (соседями), а также пересчет пространственных и временны́х расстояний требует предварительной оценки параметров масштабирования b и d (коэффициенты B и C USLE распределения эпицентров в пределах исследуемой области).
На рис. 5 приведен пример работы алгоритма выделения сейсмических групп [Zaliapin, Ben-Zion, 2013] для землетрясений с магнитудами M ≥ 3.0, зарегистрированных на территории Апеннинского полуострова и прилегающих территорий (каталог UCI, Updated Сatalog of Italy) в период с 1950 по 2015 гг. [Peresan, Gentili, 2018].
Рис. 5.
Реализация алгоритма “ближайшего соседа”. Пример выделения фоновых и зависимых (внутри красного контура) сейсмических событий для каталога UCI, с 1950 по 2015 гг., М ≥ 3.0 [Peresan, Gentili, 2018].
a ‒ карта плотности компонентов параметра η – R и T; б – распределение параметра η. Параметры сейсмического режима: b-value ‒ 0.9; d ‒ 1.1.
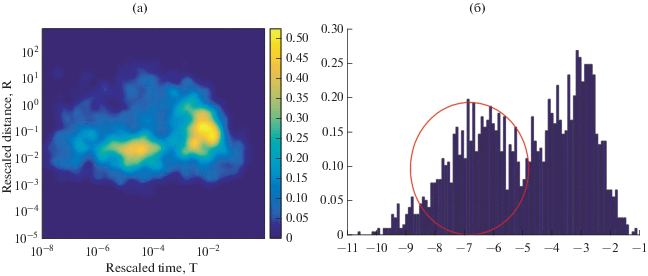
На рис. 5а представлена двумерная карта плотности компонентов параметра η на плоскости R × T, а на рис. 5б показана характерная бимодальность одномерного распределения близости ηij. Разделение событий на кластеры землетрясений (форшоки, основные события, афтершоки) выполняется путем установки соответствующего порогового значения η0. В приведенном примере такое разделение соответствует линии с наклоном 1 на двумерной карте плотности.
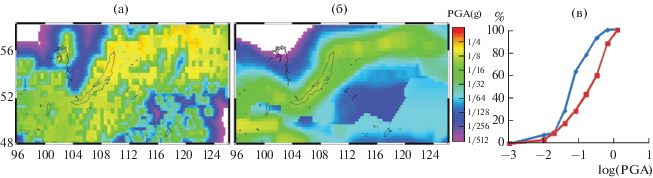
Рис. 6.
Карты PGA (в g) для окрестности озера Байкал [Nekrasova et al., 2015].
а ‒ USLE подход; б ‒ по данным окончательной карты сейсмической опасности GSHAP; в ‒ эмпирическое распределение вероятностей значений PGA в регионе (PGAUSLE ‒ красная линия с квадратами, PGAGSHAP ‒ синяя линия с ромбами, символы соответствуют g/22, g/23, g/24, g/25, g/26, g/27, g/28 и g/29).
В публикациях [Peresan, Gentili, 2018, 2020] проведен подробный сравнительный анализ выделения зависимых событий (афтершоков и форшоков) с использованием алгоритма “ближайшего соседа”, пространственно-временны́ми окнами с различными параметрами и ручным выделением афтершоков, проведенных при исследовании наиболее значимых сейсмических событий на территории итальянской провинции Фриули‒Венеция‒Джулия. Важным выводом исследований является то, что, когда пороговое значение η0 фиксировано, а все остальные параметры алгоритма не изменяются, идентификация событий “родитель/потомок” очень стабильна по отношению к Mmin, и идентифицированные кластеры остаются одинаковыми во всем диапазоне значений, что согласуется с ранее полученными результатами [Zaliapin, Ben-Zion, 2013]. Таким образом, на примерах каталогов реальных землетрясений продемонстрировано, что кластерная структура сейсмичности в рассмотренных регионах нечувствительна к неполноте каталога и изменениям в Mmin, а значит, кластерная структура сейсмичности региона может быть достаточно точно идентифицирована даже при отсутствии полного каталога сейсмических событий.
В публикациях [Peresan, Gentili, 2018, 2020] параметры b и d, аналогичные B и C в (2) и определяющие величину контрольного параметра η, получены при независимом определении коэффициентов USLE по данным каталога OGS (каталог Национального института Океанографии и экспериментальной геофизики, г. Удина, Италия) алгоритмом SCE (п. 2.3).
3.3. Картирование параметров USLE. Оценка сейсмической опасности
Представление о самоподобном распределении сейсмичности позволяют более адекватно оценить возможность редкого, однако вполне ожидаемого возникновения разрушительного землетрясения. Коэффициенты USLE, полученные для выделенной территории и характеризующие в зависимости от временнóго масштаба и целей исследования особенности сейсмического режима в долгосрочном масштабе времени или его среднесрочную изменчивость, вероятно, могут быть использованы для оценки ожидаемой максимальной магнитуды землетрясений на рассматриваемой территории.
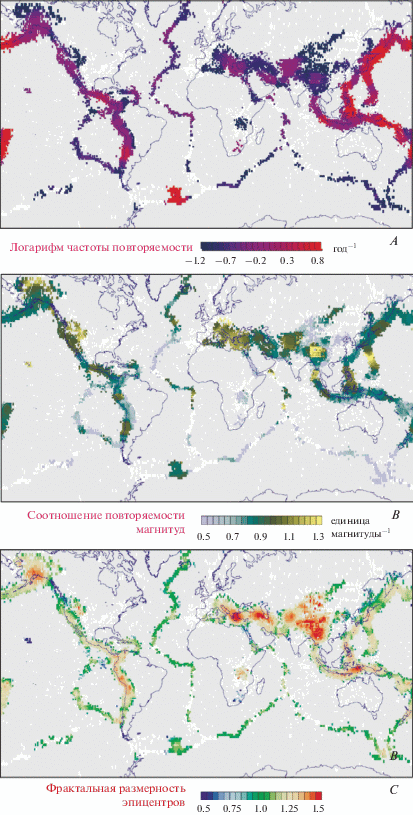
В монографии [Кособоков, 2005] приведена хронология появления карт параметров A, B и C, алгоритм для вычисления которых был представлен в п. 2.3. А именно, первые расчеты параметров повторяемости землетрясений с учетом фрактальности для ряда сейсмоактивных регионов мира в разных масштабах от глобального (западное и восточное полушария Земли) до локального (окрестность мыса Мендосино) опубликованы в работах [Kossobokov, Mazhkenov 1988; Kosobokov, Mazhkenov, 1994; Кейлис‑Борок и др., 1989]. Эти работы позволили более строго обосновать адекватность правил применения алгоритмов прогноза в разных регионах и/или диапазонах магнитуд [Долгосрочный прогноз …, 1986]. Объемы наблюденных сейсмических данных и производительность вычислительных средств позволили в дальнейшем систематически оценить параметры A, B и C из п. 2, сначала в наиболее активных [Nekrasova, Kossobokov, 2002], а затем и во всех сейсмически активных регионах мира [Kossobokov, Nekrasova, 2003; Nekrasova, Kossobokov, 2003]. Эти оценки и последующее картирование параметров А, В и С проведены модифицированным алгоритмом оценки парамеров USLE (SCE алгоритм). Глобaльные карты значений коэффициентов USLE на рис. 1 получены при оценке параметров неглубоких (с глубиной до 100 км) землетрясений по данным Глобальной базы данных о гипоцентрах землетрясений [GHDB] за 1964‒2002 гг. Расчеты выполнены во всех 9276 точках с полуцелыми географическими координатами, где показатель сейсмической активности, конкретнее, ожидаемое среднегодовое число землетрясений магнитуды от 4 и выше на площади квадрата со стороной в один градус земного меридиана из работы [Kossobokov et al., 2000] превышает 0.027, что соответствует одному событию, зарегистрированному в ячейке 1° × 1° за весь интервал времени используемого каталога. Эти точки выбраны как центры перекрывающихся квадратов со стороной 8° земного меридиана. Расчеты выполнены на пяти ступенях пространственной иерархии (пять удвоений размера от 0.5° до 8°). Заметим, что 0.5° в целом глобально соответствует точности определения эпицентров в использованном каталоге USGS-NEIC [GHDB]. Адекватные оценки параметров USLE, такие, что ошибка определения значений параметров не превосходит 0.02 были получены для 6000 ячеек. Данные Глобального картирования оценок А, В и С размещены в репозитории Международного Сейсмологического Центра и доступны для свободного использования независимыми исследователями [Nekrasova, Kossobokov, 2019].
Теоретический разбор допустимости подхода картирования параметров USLE в терминах “типичных” и “нетипичных” точек приведен в работе [Molchan, 2020]. Отмечено, что при оценке качества картируемых параметров или их сравнении важны следующие элементы использованной модели расчетов: 1) неформальный подход к пространственному картированию параметров закона повторяемости и 2) дифференцированный по магнитуде и пространству учет условий, сохраняющих подобие в повторяемости событий [Molchan, 2020]. Подчеркнуто, что картирование возможно в случае, если исходная ячейка является “типичной” в ансамбле минимальных ячеек рассматриваемого региона, а соотношение непротиворечиво в случае d (аналог C) = 2. В свою очередь, из описания SCE-алгоритма [Nekrasova et al., 2015] следует, что картирование параметров USLE проводится именно в рамках обоих отмеченных элементов применительно к каждому уровню пространственной иерархии, на котором рассматривается распределение сейсмических событий различного определенного энергетического масштаба. А именно, для каждого пространственного уровня иерархии предполагается равномерное распределение событий определенного магнитудного диапазона. Выбор размера минимальной ячейки определяется вторым предположением и связан с представительностью используемого каталога, а также с возможностями и точностью регистрации землетрясений разного размера конкретной сейсмической сетью. Так, в случае глобального картирования минимальной выбрана ячейка 1° × 1° в предположении равномерного распределения землетрясений с магнитудами от 4 до 4.75, а для ячейки 8° × 8°, предположительно выполняется равномерное распределение событий с магнитудами 6.25‒6.75.
Безусловно, что “корректное сравнение различных методов должно учитывать реальные альтернативы, связанные с сейсморайонированием. Они намного богаче предположения о равномерном распределении сейсмичности даже в областях стандартного размера” [Molchan, 2020].
В работе [Некрасова и др., 2020] представлены подход, основные принципы и методология построения карт сейсмической опасности на основе USLE, обобщающие ряд конкретных исследований для нескольких регионов мира, различающихся как по размерам территории, так и по уровню сейсмической активности [Kossobokov, Nekrasova, 2018a, b; Nekrasova et al., 2015; Parvez et al., 2014, 2017a; Некрасова, Кособоков, 2016; Некрасова и др., 2015].
В этих регионах, на основе доступных в момент исследования сейсмических данных, проведены расчет и построение карт сейсмической опасности в терминах максимальной ожидаемой магнитуды, максимального пикового ускорения грунта PGA или макросейсмической интенсивности I0. Там, где существует возможность ретроспективного анализа свидетельств о землетрясениях на исследуемой территории, например, зарегистрированные в прошлом значения PGA или I0, а также аналогичные карты сейсмической опасности, полученные альтернативными методами, проведено тестирование предлагаемых карт с использованием USLE и их сравнение с альтернативами.
В качестве примеров проверки результатов применения USLE для оценки сейсмической опасности приведем сравнение карт в терминах PGA (см. рис. 6), полученных с использованием USLE и финальных карт, полученных в рамках международной Программы Глобальной оценки сейсмической опасности (GSHAP) [Giardini et al., 1999]. Так, например, очевидно, что в районе разрозненных сейсмоактивных разломов, к востоку от верхнего сегмента Байкальской рифтовой зоны, карта на основе USLE повышает сейсмическую опасность, по сравнению с фрагментом Глобальной карты GSHAP. Также очевидно, что сейсмическая активность значительной части на территории фрагмента не учтена в расчетах ожидаемых значений PGA. Взаимная разница оценок карт, представленных на рис. 6а, б, видна при сравнении приведенных на рис. 6в эмпирических распределений вероятностей значений PGA для двух подходов.
Следует заметить, что проблемы Глобальной карты GSHAP были отмечены уже сразу после ее публикации в 1999 г. [Castaños, Lomnitz, 2002] и со временем подтвердились статистикой несоответствия ожидаемого и реализовавшегося значения PGA в период 2000‒2011 гг. Фактически все сильнейшие землетрясения магнитудой от 7.5 и выше и все 12 наиболее смертоносных сейсмических катастроф в этот период произошли в местах недооценки сейсмической опасности, причем, в большинстве случаев, недооценка была весьма значительной [Кособоков, Некрасова, 2011; Wyss et al., 2012]. Отметим, что сравнения с картами GSHAP в настоящий момент могут рассматриваться в большей степени как методологические, направленные на ревизию ставших общепринятыми представлений о вероятностной оценке сейсмической опасности и ассоциированных с нею рисков. Проект GEM [Pagani et al., 2018] должен был пересмотреть, уточнить и исправить оценки на основе опыта, накопленного за прошедшие два десятилетия. Однако, участники этого проекта, похоже, не склонны к пересмотру основных принципов оценки сейсмической опасности с привлечением альтернативных методологий, а также к обязательной проверке результатов на обучающей и контрольной выборках реальных сейсмических событий [Nekrasova et al., 2015; Kossobokov et al., 2015].
Сравнение нескольких альтернативных карт сейсмической опасности для исследуемой территории предоставляется крайне редко. Отметим в этой связи работу [Parvez et al., 2017a], где для территории Индийского штата Гуджарат проведено сравнение оригинальной карты PGAUSLE не только с картой PGAGSHAP, но и с картой, построенной на основе набирающего популярность подхода неодетерминистской оценки сейсмической опасности (Neodeterministic Seismic Hazard Assessment – NDSHA), базирующейся на компьютерной симуляции исчерпывающих сценариев возможного возникновения землетрясений с расчетом полных волновых форм и эффектов [Panza et al., 1996, 2001, 2012; Parvez et al., 2017b; Panza, Bela, 2020], Возможно, ситуация изменится в связи с проведением в настоящее время различными исследовательскими группами пересмотра глобальных и национальных карт сейсмической опасности (например, European Seismic Hazard Model 2020 ‒ ESHM20, Probabilistic Seismic Hazard Maps in Japan – PSHMJ, New Seismic Hazard Model of Italy ‒ MPS19).
3.4. Оценка параметров цикла разрушения литосферы
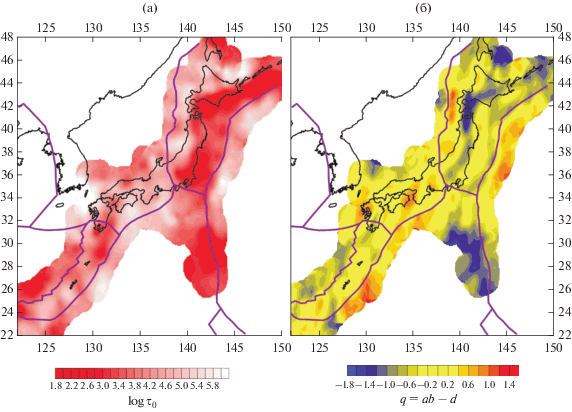
В глобальном масштабе и для ряда регионов мира с характерными геодинамическими особенностями (например, для зон субдукции и сдвиговых разломных зон) проведены оценки параметров цикла разрушения литосферы по данным каталогов землетрясенй [Smirnov, 2003; Smirnov et al., 2019]. Приведенный в 2.3 алгоритм оценки параметров фрактальной размерности для гипоцентров сейсмических событий, а также общий подход к сейсмическому режиму в терминах USLE используется авторами для определения картируемого параметра τ0 = τ(M0) – длительности цикла разрушения в области с линейным размером l0 соответствующей размеру очага землетрясения с магнитудой M0:
Авторами получена оценка характерного диапазона вариаций параметра τ(M0) в пределах от 300 до 30000 лет. Проведено сравнение значений параметра τ(M0) с характерными региональными скоростями движения плит. Отмечено, что в первом приближении средняя для региона длительность цикла разрушения литосферы обратно пропорциональна скорости тектонических деформаций в регионе. Однако подчеркивается, что даже в пределах относительно небольших регионов, значения τ0 варьируют в диапазоне двух десятичных порядков [Smirnov et al., 2019]. Это указывает на значительную неоднородность распределения скоростей деформации и прочности в пределах региона и эмпирически подтверждает современные представления об иерархичном строении геологической среды и неоднородном мозаичном характере поля напряжений.
Пример карты параметра τ0 для территории Японских островов приведен на рис. 7a. Еще один параметр, также картируемый авторами подхода ‒ q = αb − d (см. рис. 7б), показывает зависимость длительности цикла разрушения от масштаба (размера области) разрушения. Авторы считают, что в рамках модели разрушения разномасштабных дефектов среды и в предположении степенного распределения дефектов по размерам (в частности, для фрактальной геометрии системы дефектов) при αb = d и, соответственно, q = 0, закон Гутенберга‒Рихтера (1) определяется только распределением дефектов по их размерам. Отмечено, что оценки параметров цикла разрушения на региональном уровне свидетельствуют, что в фоновом режиме (при осреднении за десятилетия) длительность цикла разрушения литосферы не зависит от размера области разрушения – параметр q близок к нулю. Это означает, что в фоновом режиме процесс разрушения на разных пространственных масштабах развивается примерно с одинаковой интенсивностью, то есть вероятность разрушения элементов среды равномерно распределена по их размерам. Такая ситуация имеет место, когда поле напряжений определенным образом согласовано с “полем” прочности, т.е. вероятность разрушения дефекта (неоднородности среды) не зависит от его размера. В то же время, для отдельных областей получены значимые отклонения значения параметра q от 0, которые свидетельствуют о иерархической зависимости для процессов разрушения. А именно, если q < 0, то разрушение идет интенсивнее на старших масштабах, а при q > 0 – на младших.
4. ЗАКЛЮЧЕНИЕ
Сложность использования данных сейсмических каталогов, качество которых отличается в зависимости от местоположения, может повлиять на результаты анализа и интерпретации. Однако надежный характер расчетов на основе USLE, подтвержденный низкими значениями ошибок глобально и в рассмотренных к настоящему времени в отдельных сейсмоопасных районах, позволяет заключить обоснованность предположения о пространственном самоподобии сейсмических процессов и продолжить дальнейшие исследования фундаментальных проблем, включая оценку сейсмических рисков для населения и объектов инфраструктуры с использованием каталогов землетрясений. Необходимость использования знания о фрактальной структуре распределения землетрясений можно проиллюстрировать на простейших примерах. Так, например, коэффициент C на территории Лос-Анджелеса составляет около 1.21, как по оценкам P. Окубо и K. Аки [Okubo, Aki, 1987] для системы разломов в Южной Калифорнии, так и по расчету путем применения алгоритма SCE к данным одного из лучших региональных каталогов землетрясений; оценка повторяемости сильных землетрясений пропорционально площади по статистике всей Южной Калифорнии линейного размера ~400 км для района Лос-Анджелеса протяженностью ~40 км недооценивает частоту возникновения таких событий в (LSCA/LLA)2/(LSCA/LLA)1.21 = 100.79 = 6.2 раз. По аналогии, для Петропавловска-Камчатского, где C = = 1.26, сейсмическая опасность в 40 км окрестности города по статистике землетрясений Камчатского региона протяженностью ~700 км в случае игнорирования фрактальных свойств распределения землетрясений может быть недооценена в (LK/LPK)2/(LK/LPK)1.26 = 17.50.74 = 8.3 раз. Систематический анализ сейсмической опасности в 1140 городах и городских агломерациях в сейсмических регионах по всему миру [Nekrasova, Kossobokov, 2005] показывает, в дополнение к вышеупомянутым случаям, потенциальную недооценку в 5.4 раза для Токио (Япония), 7.2 для Сан-Франциско (США), около 20 для Улан-Удэ (Республика Бурятия, Российская Федерация) и т.д. Такое несоответствие в оценке сейсмической опасности распространяется нелинейно в ошибочные оценки рисков. Ошибка в 6 раз (в предположении B = 1) соответствует ошибке около 0.8 в магнитуде сейсмического события, которая экспоненциально возрастает в недооценке в 15 раз выделяющейся сейсмической энергии, что соответствует коэффициенту выше 4.5 в расчетах ожидаемого числа жертв землетрясения [Wyss et al., 2012].
Следует специально отметить, что оценки параметров USLE безусловно сложной динамической системы разломов и блоков литосферы Земли даже в среднесрочных масштабах времени на довольно протяженных территориях зависят от методов их подсчета, а также изменчивы как по времени, так и по пространству [Nekrasova et al., 2011]. Надежные оценки характеристик возможно получить лишь в крупном масштабе и с привлечением данных за максимально продолжительный период наблюдений после критической проверки в контрольных экспериментах. Для практики использования знаний о фрактальной природе землетрясений крайне существенно ‒ на каких отрезках времени сейсмический поток исследуемой области можно считать достаточно стационарным для анализа и интерпретаций. Этот вопрос требует тщательного специального исследования. Если окажется, что характерный интервал времени, на котором изменяется локальная интенсивность сейсмического процесса, имеет порядок нескольких десятков лет, то эти изменения необходимо учитывать в практических задачах, связанных с оценками рисков от землетрясений [Писаренко, Голубева, 1996].
Наблюдаемая изменчивость сейсмической активности накладывает важные ограничения для моделирования сейсмических последовательностей геофизиками. Результаты исследований на основе Общего закона подобия для землетрясений USLE могут использоваться с пользой для изучения разнообразия физических свойств литосферы Земли, а также для улучшения оценок локальной сейсмической опасности, включая методы прогнозирования землетрясений. Лучшее понимание USLE открывает новые горизонты в изучении процессов, связанных с возникновением землетрясений.
В заключение следует заметить, что в рамках анализа каталогов землетрясений, которые являются вторичным продуктом обработки сейсмических записей, представленные в обзоре исследования не учитывают богатейший первичный материал. Современные средства изучения сейсмических записей, возможно, уже в ближайшее время предложат лучшие средства мониторинга сейсмичности, столь необходимые как для Общего закона подобия для землетрясений, так и для оперативного прогноза сейсмической погоды, включая ожидаемые экстремальные события.
Список литературы
Долгосрочный прогноз землетрясений. Методические рекомендации / Под ред. акад. М.А. Садовского. М.: ИФЗ АН СССР, 1986. 127 с.
Кейлис-Борок В.И., Кособоков В.Г. Комплекс долгосрочных предвестников для сильнейших землетрясений мира // Землетрясения и предупреждение стихийных бедствий // 27-й Международный геологический конгресс, 4‒14 августа 1984 г., Москва, Коллоквиум С6. Т. 61. М.: Наука, 1984. С. 56‒66.
Кейлис‑Борок В.И., Кособоков В.Г., Мажкенов С.А. О подобии в пространственном распределении сейсмичности. Теория и алгоритмы интерпретации геофизических данных // Вычислительная сейсмология. Вып. 22. М.: Наука, 1989. С. 28‒40.
Кособоков В.Г., Некрасова А.К. Общий закон подобия для землетрясений: глобальная карта параметров // Анализ геодинамических и сейсмических процессов // Вычислительная сейсмология. Вып. 35. М.: ГЕОС, 2004. С. 160‒175.
Кособоков В.Г. Прогноз землетрясений и геодинамические процессы. Часть I. Прогноз землетрясений: основы, реализация, перспективы // Вычислительная сейсмология. Вып. 36. М.: ГЕОС, 2005. 179 с.
Кособоков В.Г., Некрасова А.К. Карты Глобальной программы оценки сейсмической опасности (GSHAP) ошибочны // Вопросы инженерной сейсмологии (ISSN 0132-2826). 2011. № 38(1). С. 65‒76.
Кочарян Г.Г. Геомеханика разломов. М.: ГЕОС, 2016. 424 с.
Молчан Г.М., Кронрод Т.Л., Дмитриева О.Е., Некрасова А.К. Многомасштабная модель сейсмичности в задачах сейсмического риска: Италия // Современные проблемы сейсмичности и динамики Земли // Вычислительная сейсмология. Вып. 28. М.: Наука, 1996. С. 193–224.
Некрасова А.К., Кособоков В.Г., Парвез И.А. Оценка сейсмической опасности и сейсмического риска на основе Общего закона подобия для землетрясений: Гималаи и прилегающие регионы // Физика Земли. 2015. № 2. С. 116–125.
Некрасова А.К., Кособоков В.Г. Общий закон подобия для землетрясений: Крым и Северный Кавказ // Докл. РАН. 2016. Т. 470. № 4. С. 468–470.
Некрасова А.К., Кособоков В.Г., Парвез И.А., Тао Х. Общий закон подобия для землетрясений в приложении к оценке сейсмической опасности и ассоциированных рисков // Физика Земли. 2020. № 1. С. 96‒108. https://doi.org/10.31857/S0002333720010093
Писаренко В., Голубева Т. Использование устойчивых законов в моделях сейсмичности // Современные проблемы сейсмичности и динамики Земли / Под ред. В.И. Кейлис-Борока // Вычислительная сейсмология. Вып. 28. М.: Наука, 1996. С. 153–174.
Ризниченко Ю.В. Об изучении сейсмического режима // Изв. АН СССР. Сер. геофиз. 1958. № 9. С. 1057‒1074.
Садовский М.А. Естественная кусковатость горной породы // Докл. АН СССР. 1979. Т. 247. № 4. С. 829‒831.
Садовский М.А. Автомодельность сейсмических процессов // Физические основы прогнозирования разрушения горных пород при землетрясениях. М.: Наука, 1987. С. 6-12.
Садовский М.А., Нерсесов И.Л., Писаренко В.Ф. Иерархическая дискретная структура литосферы и сейсмический процесс // Современная тектоническая активность Земли и сейсмичность. М.: Наука, 1987. С. 182‒191.
Садовский М.А., Писаренко В.Ф. Подобие в геофизике // Природа. 1991. № 1. С. 13‒23.
Смирнов В.Б. Повторяемость землетрясений и параметры сейсмического режима // Вулканология и сейсмология. 1995. № 3. С. 59‒70.
Стаховский И.Р. Масштабная инвариантность коровой сейсмичности и прогностические признаки землетрясений // УФН. 2017. Т. 187. № 5. С. 505‒524.
Челидзе Т.Л. Обобщенный фрактальный закон сейсмичности // Докл. АН СССР. 1990. Т. 314. № 5. С. 1104‒1105.
Aki K. A probabilistic synthesis of precursory phenomena, in Earthquake Prediction / Eds D.W. Simpson, P.G. Richards // An International Review, Maurice Ewing Ser. 1981. V. 4. P. 566‒574.
Baiesi M., Paczuski M. Scale-free networks of earthquakes and aftershocks // Phys. Rev. 2004. E 69. 066106.
Bak P., Christensen K., Danon L., Scanlon T. Unified Scaling Law for Earthquakes // Phys. Rev. Lett. 2002. V. 88. P. 178 501–178 504.
Ben-Zion Y. Collective behavior of earthquakes and faults: continuum-discrete transitions, progressive evolutionary changes and different dynamic regimes // Rev. Geophys. 2008. V. 46. RG4006. P. 1–70.
Bormann P. Earthquake, magnitude / Ed. H. Gupta // Encyclopedia of solid earth geophysics. Heidelberg: Springer, 2011. P. 207–217.
Castaños H., Lomnitz C. PSHA: is it science? // Eng. Geology. 2002. V. 66(3/4). P. 315–318.
Christensen K., Danon L., Scanlon T., Bak P. Unified scaling law for earthquakes // Proc Natl Acad Sci. 2002. V. 99. Suppl 1. P. 2509–2513. DOI: ISSN: 0027-8424;https://doi.org/10.1073/pnas.012581099
Corral A. Local distribution and rate fluctuation in unified scaling law for earthquakes // Phys. Rev. E. 2003. V. 68. 035102[R]. https://doi.org/10.1103/PhysRevE.68.035102
Corral A. Universal local versus unified global scaling laws in the statistics of seismicity // Physica A. 2004. V. 340. P. 590–597.
Earthquake Research and Analysis: Seismology, Seismotectonic and Earthquake // Phys. Earth and Planet. Inter. 2001. V. 125. P. 65–83.
Falconer K. Fractal geometry: mathematical foundations and applications // Chichester etc.: John Wiley, Sons [ISBN 0-471-92287-0], 1990. XXII. 288 p.
Feder J. Fractals. N. Y.: Plenum Press, 1988. 283 p. (Федер Е. Фракталы // Пер. с англ. М.: Мир, 1991. 254 с.).
Gelfand I., Guberman Sh., Keilis-Borok V., Knopoff L., Press F., Ransman E., Rotwain I., Sadovsky A. Pattern recognition applied to earthquakes epicenters in California // Phys. Earth and Planet. Inter. 1976. V. 11. P. 227‒283.
GHDB, Global Hypocenters Data Base CD-ROM // NEIC/USGS, Denver, CO, 1989 and its updates through December 2015.
Giardini D., Grünthal G., Shedlock K.M., Zhang P. The GSHAP Global Seismic Hazard Map // Annali di Geofisica. 1999. V. 42[6]. P. 1225‒1230. https://doi.org/10.4401/ag-3784
Gorshkov A., Kossobokov V., Soloviev A. Recognition of earthquake-prone areas / Eds V. Keilis-Borok, A. Soloviev // Nonlinear Dynamics of the Lithosphere and Earthquake Prediction. Heidelberg: Springer, 2003. P. 239‒310.
Gospodinov D., Marekova E., Marinov Al. Verifying the Dependence of Fractal Coefficients on Different Spatial Distributions AIP Conference Proceedings 1203. Melville, NY: AIP Publishing, 2010. V. 3. P. 731. https://doi.org/10.1063/1.3322545
Grassberger P., Procaccia I. Characterization of strange attractors // Phys. Rev. Lett. 1983. V. 50. P. 346.
Gutenberg B., Richter C.F. Frequency of earthquakes in California // Bull. Seismol. Soc. Am. 1944. V. 34. P 185‒188.
Gutenberg B., Richter C.F. Seismicity of the Earth. Princeton, N. J.: Princeton University Press, 1954. 310 p.
Kagan Y.Y., Knopoff L. Spatial distribution of earthquakes: the two-point correlation function // Geophys. J. R., Astr. Soc. 1980. V. 62. № 2. P. 303‒320. https://doi.org/10.1111/j.1365-246X.1980.tb04857.x
Keilis-Borok V.I. The lithosphere of the Earth as a nonlinear system with implications for earthquake prediction // Rev Geophys. 1990. V. 28. P. 19–34.
Körting G.C.O. Lateinisch-romanisches Wörterbuch, 1891–1907: [LRW: (Etymologisches Wörterbuch der romanischen Hauptsprachen)]. Paderborn: F. Schöningh, 1891; 2.e, vermehrte u. verbess. Aufl.: 1901 (LRW); 3.e, vermehrte u. verbess. Aufl.: 1907 (LRW).
Kosobokov V.G., Mazhkenov S.A. On similarity in the spatial distribution of seismicity / Ed. D.K. Chowdhury // Computational Seismology and Geodynamics, Am. Geophys. Un., 1, Washington, D.C.: The Union, 1994. P. 6‒15.
Kossobokov V.G., Mazhkenov S.A. Spatial characteristics of similarity for earthquake sequences: Fractality of seismicity // Lecture Notes of the Workshop on Global Geophysical Informatics with Applications to Research in Earthquake Prediction and Reduction of Seismic Risk [15 Nov.–16 Dec., 1988]. ICTP, Trieste, 1988. 15 p.
Kossobokov V.G., Keilis-Borok V.I., Turcotte D.L., Malamud B.D. Implications of a statistical physics approach for earthquake hazard assessment and forecasting // Pure Appl. Geophys. 2000. V. 157. P. 2323‒2349.
Kossobokov V., Nekrasova A. Generalized Gutenberg-Richter recurrence law // Geophysical Research Abstracts, 5, Abstracts of the Contributions of the EGS-AGU-EGU Joint Assembly, Nice, France, 06‒11 April, 2003 [CD-ROM]: EAE03-A-06597.
Kossobokov V., Peresan A., Panza G.F. Reality check: Seismic hazard models you can trust // EOS. Earth & Space Sci. News. 2015. V. 96. № 13. P. 9‒11. https://doi.org/10.1029/2015EO031919
Kossobokov V. G. Testing an earthquake prediction algorithm: The 2016 New Zealand and Chile earthquakes // Pure Appl. Geophys. 2017. V. 174. № 5. P. 1845‒1854. https://doi.org/10.1007/s00024-017-1543-9
Kossobokov V.G., Nekrasova A.K. Characterizing aftershock sequences of the recent Strong earthquakes in Central Italy // Pure Appl. Geophys. 2017. V. 174. № 10. P. 3713‒3723. https://doi.org/10.1007/s00024-017-1624-9
Kossobokov V.G., Nekrasova A.K. Aftershock Sequences of the Recent Major Earthquakes in New Zealand // Pure and Applied Geophysics. 2019. V. 176. № 1. P. 1‒23. https://doi.org/10.1007/s00024-018-2071-y
Kossobokov V.G., Nekrasova A. Earthquake Hazard and Risk Assessment based on Unified Scaling Law for Earthquakes: Greater Caucasus and Crimea // J. Seismology. 2018. V. 22. P. 1157–1169. https://doi.org/10.1007/s10950-018-9759-4
Kossobokov V.G., Nekrasova A. Earthquake Hazard and Risk Assessment based on Unified Scaling Law for Earthquakes: Altai–Sayan Region // Natural Hazards. 2018. V. 93(3). P. 1435–1449. https://doi.org/10.1007/s11069-018-3359-z
Kossobokov V. Unified Scaling Law for Earthquakes that Generalizes the Fundamental Gutenberg-Richter Relationship / Ed. H.K. Gupta // Encyclopedia of Solid Earth Geophysics, Encyclopedia of Earth Sciences Series / 2nd Edition. 2020. https://doi.org/10.1007/978-3-030-10475-7_257-1.
Mandelbrot B.B. Fractals: Form, Chance and Dimension. N. Y.: W.H. Freeman & Company, 1977. 365 p.
Mandelbrot B.B. How long is the coast of Britain? Statistical self-similarity and fractional dimension // Science. 1967. V. 156. P. 636–638.
Mandelbrot B.B. The Fractal Geometry of Nature. New York: Times Books, 1982. 468 p.
Mandelbrot B.B. Multifractal measures, especially for the geophysicist // Pure Appl. Geophys. 1989. V. 131. P. 5–42.
Molchan G., Kronrod T., Panza G.F. Multi-scale seismicity model for seismic risk // Bull. Seism. Soc. Am. 1997. V. 87. № 5. P. 1220‒1229.
Molchan G.M. Interevent time distribution of seismicity: a theoretical approach // Pure Appl. Geophys. 2005. V. 162. P. 1135‒1150.
Molchan G., Kronrod T. Seismic interevent time: A spatial scaling and multifractality // Pure Appl. Geophys. 2007. V. 164. № 1. P. 75–96.
Molchan G., Kronrod T. The fractal description of seismicity // Geophys. J. International. 2009. V. 179. № 3. P. 1787‒1799.
Molchan G.M. Fractal Seismicity and Seismic Risk // Izvestiya, Physics of the Solid Earth. 2020. V. 56. № 1. P. 66‒73. https://doi.org/10.1134/S1069351320010073
Nekrasova A., Kossobokov V. Generalizing the Gutenberg-Richter scaling law // EOS Trans. AGU. 2002. V. 83(47). Fall Meet. Suppl., Abstract NG62B-0958.
Nekrasova A., Kossobokov V. Generalized Gutenberg-Richter recurrence law: Global map of parameters // Geophysical Research Abstracts, 5. Abstracts of the Contributions of the EGS-AGU-EGU Joint Assembly, Nice, France, 06‒11 April, 2003 [CD-ROM]: EAE03-A-03801.
Nekrasova A., Kossobokov V. Unified Scaling Law for Earthquakes: Mega-cities and urban agglomerations // Eos Trans AGU. 2005. V. 86(52). Fall Meet Suppl., Abstract S23A-0229.
Nekrasova A., Kossobokov V., Aoudia A., Perezan A., Panza G.F. A Multiscale Application of the Unified Scaling Law for Earthquakes in the Central Mediterranean area and Alpine region // Pure Appl. Geophys. 2011. V. 168. P. 297‒327. Springer Basel AG. https://doi.org/10.1007/s00024-010-0163-4
Nekrasova A., Kossobokov V., Parvez I.A., Tao X. Seismic hazard and risk assessment based on the unified scaling law for earthquakes // Acta Geod Geophys. ISSN 2213-5812. 2015. V. 50. № 1. P. 21‒37. https://doi.org/10.1007/s40328-014-0082-4
Nekrasova Anastasia K., Kossobokov Vladimir G. Unified Scaling Law for Earthquakes: Global Map of Parameters // ISC’s Seismological Dataset Repository. 2019. https://doi.org/10.31905/XT753V44 http://www.isc.ac.uk/dataset_repository/recent_submissions.php
Okubo P.G., Aki K. Fractal geometry in the San Andreas Fault system // J. Geophys. Res. 1987. V. 92(B1). P. 345‒356.
Öncel A.I., Wilson T.H., Nishizawa O. Size scaling relationships in the active fault networks of Japan and their correlation with Gutenberg-Richter b-values // J. of Geophys. Res. 2001. V. 106. P. 21827‒21841. https://doi.org/10.1029/2000JB900408
Pagani M., Garcia-Pelaez J., Gee R., Johnson K., Poggi V., Styron R., Weatherill G., Simionato M., Viganò D., Danciu L., Monelli D. Global Earthquake Model [GEM] Seismic Hazard Map [version 2018.1 ‒ December 2018]. 2018. https://doi.org/10.13117/GEM-GLOBAL-SEISMIC-HAZARD-MAP-2018.1
Panza G. F., Bela J. NDSHA: A new paradigm for reliable seismic hazard assessment // Engineering Geology. 2020. https://doi.org/10.1016/j.enggeo.2019.105403
Panza G. F., Vaccari F., Costa G., Suhadolc P., Faeh D. Seismic input modelling for zoning and microzoning // Earthquake Spectra. 1996. V. 12(3). P. 529–566. https://doi.org/10.1193/1.1585896
Panza G.F., La Mura C., Peresan A., Romanelli F., Vaccari F. Chapter Three ‒ Seismic Hazard Scenarios as Preventive Tools for a Disaster Resilient Society // Advances in Geophysics. 2012. V. 53. P. 93–165. https://doi.org/10.1016/B978-0-12-380938-4.00003-3
Panza G.F., Romanelli F., Vaccari F. Seismic wave propagation in laterally heterogeneous anelastic media: theory and applications to seismic zonation // Adv. Geophys. 2001. V. 43. P. 1–95.
Parvez I., Nekrasova A.K., Kossobokov V.G. Earthquake Hazard and Risk Assessment Based on Unified Scaling Law for Earthquakes: State of Gujarat, India // Pure Appl. Geophys. 2017. V. 174. P. 1441‒1452. Springer International Publishing. https://doi.org/10.1007/s00024-017-1475-4
Parvez I.A., Magrin A., Vaccari F., Ashish, Mir R.R., Peresan A., Panza G.F. Neo-deterministic seismic hazard scenarios for India—a preventive tool for disaster mitigation // J. of Seismology. 2017. V. 21. № 6. P. 1559–1575. https://doi.org/10.1007/s10950-017-9682-0
Parvez I.A., Nekrasova A., Kossobokov V. Estimation of seismic hazard and risks for the Himalayas and surrounding regions based on Unified Scaling Law for Earthquakes // Natural Hazards. 2014. V. 71(1). P. 549–562.
Peresan A., Gentili S. Seismic clusters analysis in Northeastern Italy by the nearest-neighbor approach // Phys. of the Earth and Planet. Interiors. 2018. V. 274. P. 87–104.
Peresan A., Gentili S. Identification and characterisation of earthquake clusters: a comparative analysis for selected sequences in Italy and adjacent regions // Bollettino di Geofisica Teorica ed Applicata. 2020. V. 61. № 1. P. 57‒80. https://doi.org/10.4430/bgta0249
Richter C. F., An instrumental earthquake magnitude scale // Bull. Seismol. Soc. Am. 1935. V. 25(1). P. 1–32.
Schwartz D.P., Coppersmith K.J. Fault behavior and characteristic earthquake: Example from the Wasatch and San-Andreas fault zones // J. Geophys. Res. 1984. V. 89(B7). P. 5681‒5698.
Smirnov V.B. Estimating the Duration of the Lithospheric Failure Cycle from Earthquake Catalogs // Izvestiya, Physics of the Solid Earth. 2003. V. 39. № 10. P. 794–811. (Смирнов В.Б. Оценка длительности цикла разрушения литосферы Земли по данным каталогов землетрясений // Физика Земли. 2003. № 10. С. 13–32.)
Smirnov V.B., Ommid S., Potanina M.G., Mikhailov V.O., Petrov A.G., Shapiro N.M., Ponomarev A.V. Estimates of Lithospheric Failure Cycle Parameters from Regional Earthquake Catalogues // Izvestiya, Physics of the Solid Earth. 2019. V. 55. № 5. P. 701–718. (Смирнов В.Б., Ommi S., Потанина М.Г, Михайлов В.О., Петров А.Г., Шапиро Н.М., Пономарев А.В. Оценки параметров цикла разрушения литосферы по данным региональных каталогов землетрясений // Физика Земли. 2019. № 5. С. 3‒21.)
Turcotte D.L. Fractals and Chaos in Geology and Geophysics. Cambridge, U.K.: Cambridge Univ. Press, 1997. 398 p. https://doi.org/10.1017/CBO9781139174695
Wyss M., Nekrasova A., Kossobokov V. Errorsinexpectedhuman losses due to incorrect seismic hazard estimates // Nat Hazards. 2012. V. 62(3). P. 927–935.
Zaliapin I., Gabrielov A., Keilis-Borok V., Wong H. Clustering analysis of seismicity and aftershock identification // Phys. Rev. Lett. 2008. V. 101(1). P. 018501. https://doi.org/10.1103/PhysRevLett.101.018501
Zaliapin I., Ben-Zion Y. Earthquake clusters in southern Californi I: Identification and stability // Geophys. Res. 2013. V. 118[6]. P. 847–2864. https://doi.org/10.1002/jgrb.50179
Zaliapin I., Ben-Zion Y. A global classification and characterization of earthquake clusters // Geophysical Journal International. 2016. V. 207. № 1. P. 608–634. https://doi.org/10.1093/gji/ggw300
Дополнительные материалы отсутствуют.
Инструменты
Вулканология и сейсмология