Вулканология и сейсмология, 2021, № 3, стр. 18-28
Методика оценки вязкости магмы по морфологии лавового купола
Ю. В. Стародубцева a, b, И. С. Стародубцев a, b, c, А. Т. Исмаил-Заде a, d, *, **, И. А. Цепелев a, b, О. Э. Мельник a, e, А. И. Короткий a, b
a Институт теории прогноза землетрясений и математической геофизики РАН
117997 Москва, ул. Профсоюзная, 84/32, Россия
b Институт математики и механики им. Н.Н. Красовского УрО РАН
620990 Екатеринбург, ул. Софьи Ковалевской, 16, Россия
c Уральский федеральный университет
620002 Екатеринбург, ул. Мира, 19, Россия
d Технологический институт Карлсруэ, Институт прикладных наук о Земле
76131 Карлсруэ, ул. Аденауэрринг, 20б, Германия
e Институт механики Московского государственного университета им. М.В. Ломоносова
119192 Москва, Мичуринский просп., 1, Россия
* E-mail: aismail@mitp.ru
** E-mail: alik.ismail-zadeh@kit.edu
Поступила в редакцию 21.09.2020
После доработки 17.11.2020
Принята к публикации 11.12.2020
Аннотация
Лавовые купола образуются при извержении высоковязкой магмы. В зависимости от скорости потока и реологии магмы можно выделить несколько типов морфологических форм лавовых куполов: обелиски, лавовые выжимки, эндогенные. Вязкость магмы нелинейным образом зависит от объемной доли кристаллов и температуры. Здесь мы представляем подход к оценке вязкости магмы, основанный на сравнении наблюдаемой и смоделированных морфологических форм куполов. Рассматривается двумерная осесимметричная модель эволюции лавового купола в предположении, что вязкость лавы зависит только от объемной доли кристаллов. Кристаллизация связана с ростом температуры ликвидуса при потере магмой летучих и определяется характерным временем роста кристаллов (ВРК) и расходом лавы. Лавовые купола моделируются с использованием метода конечных объемов, реализованного в программном обеспечении Ansys Fluent для различных ВРК и размеров жерла вулкана. Для выбранного промежутка времени создается набор морфологических форм куполов (форм границы раздела между лавовым куполом и воздухом). Вычисленные таким образом формы лавовых куполов сравниваются с “наблюдаемой” формой лавового купола, полученной применением случайной модификации одной из рассчитанных форм. Для определения вязкости магмы отклонение между наблюдаемой формой купола и смоделированными формами оценивается с помощью трех функционалов на основе симметричной разности, пикового отношения сигнала к шуму и измерения индекса структурного сходства. Эти функционалы часто используются в компьютерном зрении и теории обработки изображений. Хотя каждый функционал позволяет определить минимальную разницу между смоделированными и наблюдаемыми формами купола, функционал на основе измерения индекса структурного сходства выполняет эту оценку лучше. По найденной таким образом смоделированной форме лавового купола можно оценить параметры реологической модели. Данный подход может быть распространен на трехмерный случай и использоваться для восстановления условий роста реальных лавовых куполов.
1. ВВЕДЕНИЕ
Лавовые купола возникают в результате экструзии высоковязкой магмы, образуют твердый поверхностный слой (панцирь), оставаясь подвижными и подвергаясь деформациям в течение дней или даже месяцев. Выделяются несколько типов морфологии лавового купола. При эндогенном режиме магма внедряется внутрь купола без экструзии свежей магмы на поверхности. При экзогенном режиме свежая лава изливается на поверхность, образуя различные формы куполов, таких как обелиски, лавовые выжимки, блинообразные структуры и некоторые другие (рис. 1). Обрушение лавового купола может вызвать взрывные извержения, пирокластические потоки и лахары, поэтому изучение условий роста лавовых куполов имеет важное значение для анализа опасностей и снижения риска.
Рис. 1.
Некоторые морфологические структуры лавовых куполов на вулкане Суфриер-Хиллз, Монтсеррат (фотографии [Watts et al., 2002]). a – лавовый обелиск (высотой около 40 м и шириной 35 м); б – лавовая выжимка и в – блинообразная структура (толщиной около 20 м), расположенная на обломках скальных пород.

Детальный мониторинг лавовых куполов велся на нескольких вулканах, например на Сент-Хеленс в США [Swanson et al., 1987], Пинатубо на Филиппинах [Daag et al., 1996], Унзен в Японии [Nakada et al., 1999], Сантьягуито (Санта-Мария) на Гватемале [Harris et al., 2003], Мерапи и Синабунг в Индонезии [Voight et al., 2000; Nakada et al., 2019], Суфриер-Хиллс на Монтсеррате [Watts et al., 2002; The Eruption …, 2014] и Колима в Мексике [Zobin et al., 2015]. Мониторинг позволяет картировать пространственное и временное развитие лавовых куполов и определять морфологические изменения в процессе их роста, а также определять изменение объема во времени (расход лавы).
На морфологию лавовых куполов влияют реология магмы и скорость ее поступления из канала вулкана (расход лавы, РЛ). Вязкость магмы зависит от температуры и объемной доли кристаллов, которая в свою очередь определяется кинетикой кристаллизации (характерным временем роста кристаллов, ВРК [Tsepelev et al., 2020]). При малых значениях ВРК, то есть при быстрой кристаллизации лавы, обелискообразные структуры развиваются при низких РЛ и блинообразные структуры при высоких РЛ; при больших ВРК купола имеют форму лавовых выжимок или образуют блинообразные структуры. Было показано, что охлаждение не играет существенной роли при развитии лавового купола. Это связано с тем, что если изменение количества кристаллов зависит только от температуры, то вязкость лавы увеличивается лишь в приповерхностном слое купола, а толщина температурного пограничного слоя остается небольшой по сравнению с высотой купола [Tsepelev et al., 2020]. В теле купола значительное увеличение вязкости происходит за счет кристаллизации, вызванной потерей летучих. Таким образом, по известной реологии, зависящей от ВРК, и для известного РЛ можно смоделировать эволюцию лавового купола. В то же время интерес представляет решение обратной задачи: по форме лавового купола и известному расходу восстановить реологические параметры лавы.
В данной работе предложен подход к решению такой обратной задачи, основанный на минимизации отклонения наблюдаемой и смоделированных форм лавовых куполов. Рассматривается двумерная осесимметричная модель эволюции лавового купола в предположении, что вязкость лавы зависит только от объемной доли кристаллов, а эта доля, в свою очередь, зависит от ВРК. Лавовые купола моделируются численно при различных значениях ВРК, РЛ и диаметра канала вулкана. На основе численных расчетов создается база морфологических форм куполов для выбранных временных шагов. Результаты вычислительных экспериментов (элементы базы) и данные наблюдений (в работе в качестве наблюдений строится синтетический купол) анализируются в виде двумерных изображений. Чтобы оценить вязкость магмы наблюдаемого лавового купола, осуществляется поиск минимальной разницы между наблюдаемой и смоделированными формами куполов с помощью различных функционалов, часто используемых в компьютерном зрении и теории обработки изображений. По найденной таким образом смоделированной форме лавового купола оцениваются параметры реологической модели.
2. ПОСТАНОВКА ЗАДАЧИ И МЕТОД ЧИСЛЕННОГО МОДЕЛИРОВАНИЯ ЛАВОВЫХ КУПОЛОВ
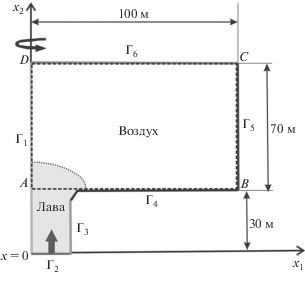
Рассматривается двумерная осесимметричная модель двухфазной несмешиваемой несжимаемой жидкости, которая аппроксимирует лаву (одна фаза) и воздух (другая фаза), разделенные подвижной границей – поверхностью лавового купола. Влияние воздушной фазы на рост лавового купола незначительно из-за большого отношения плотностей и вязкостей фаз. В модельной области $\Omega $ (рис. 2) движение лавы описывается следующим набором уравнений вместе с начальными и граничными условиями [Ismail-Zadeh, Tackley, 2010; Tsepelev et al., 2019, 2020].
Рис. 2.
Модельная область. Изогнутая стрелка указывает на условие симметрии вдоль оси x1 = 0. ${{\Gamma }_{p}}$ (p = 1, 2, 3, 4, 5, 6) представляет часть модельной границы (см. текст статьи для граничных условий). Большая черная стрелка показывает ту часть границы, через которую втекает магма. Поверхность раздела между лавой и воздухом обозначена пунктирной линией. Штриховой линией указана область, в которой сохраняются изображения в базе данных.
Мы используем уравнения Навье–Стокса с начальным условием ${\mathbf{u}}(t = 0,{\mathbf{x}}) = 0$ и уравнение неразрывности для описания динамики лавы
(1)
$\begin{gathered} \frac{{\partial (\rho {\mathbf{u}})}}{{\partial t}} + \left\langle {{\mathbf{u}},\nabla } \right\rangle (\rho {\mathbf{u}}) - \nabla \cdot \left( {\eta \left( {\nabla {\mathbf{u}} + \nabla {{{\mathbf{u}}}^{T}}} \right)} \right) = \\ = - \nabla p - \rho {\mathbf{g}}, \\ \end{gathered} $Функция $\alpha (t,{\mathbf{x}})$ принимает значение единицы для лавы и нуля для воздуха в каждой точке x и в каждый момент времени t, и эта функция переносится со скоростью u согласно уравнению адвекции
с начальным условием $\alpha (t = 0,{\mathbf{x}}) = 0,$ означающим, что в начальный момент времени вся расчетная область заполнена воздухом.Мы предполагаем, что вязкость лавы (измеряемая в Па · с) зависит от объемной доли кристаллов [Costa et al., 2009] как
(4)
$\begin{gathered} {{\eta }_{L}}(\varphi ) = {{10}^{7}}\left( {1 + {{\varphi }^{{{\delta }}}}} \right) \times \\ \times \,\,{{\left[ {1 - (1 - \xi ) \cdot {\text{erf}}\left( {\frac{{\sqrt \pi }}{{2(1 - \xi )}}\varphi (1 + {{\varphi }^{{{\gamma }}}})} \right)} \right]}^{{ - B{{\phi }_{*}}}}}, \\ \end{gathered} $(5)
$\frac{{\partial \phi }}{{\partial t}} + \nabla \cdot (\alpha \phi {\mathbf{u}}) = - \alpha \frac{{\phi - {{\phi }_{{eq}}}}}{\tau },$На границе модели $\Gamma = {{\Gamma }_{1}} \cup {{\Gamma }_{2}} \cup {{\Gamma }_{3}} \cup {{\Gamma }_{4}} \cup $ ${{\Gamma }_{5}} \cup {{\Gamma }_{6}}$ задаются следующие условия (см. рис. 2). На границе ${{\Gamma }_{1}}$ задаются условия симметрии, то есть условие непроницаемости $\left\langle {{\mathbf{u}},{\mathbf{n}}} \right\rangle = 0$ и условие свободного скольжения $\left( {\nabla {\mathbf{u}} + \nabla {{{\mathbf{u}}}^{T}}} \right){\mathbf{n}}$ – ‒ $\left\langle {\left( {\nabla {\mathbf{u}} + \nabla {{{\mathbf{u}}}^{T}}} \right){\mathbf{n}},{\mathbf{n}}} \right\rangle {\mathbf{n}} = 0.$ Предполагается, что лава плотности ${{\rho }_{L}}$ и вязкости ${{\eta }_{L}}$ поступает в модельную область через границу ${{\Gamma }_{2}}$ при заданном РЛ Q. На границах ${{\Gamma }_{3}},$ ${{\Gamma }_{4}}$ и ${{\Gamma }_{5}}$ задается условие прилипания u = 0. Воздух удаляется из модельной области через границу ${{\Gamma }_{6}}$ согласно заданному РЛ. Предполагается, что объемная доля кристаллов равна $\phi = {{\phi }_{{in}}}$ на ${{\Gamma }_{2}}$ и $\phi = 0$ на ${{\Gamma }_{6}}.$ Значения параметров модели, используемые при численном моделировании, представлены в табл. 1.
Таблица 1.
Модельные параметры и их значения
| Символ | Параметр | Значение |
|---|---|---|
| H | Высота модельной области, м | 100 |
| g | Ускорение силы тяжести, м · с–2 | 9.81 |
| ${{\eta }_{A}}$ | Вязкость воздуха, Па · с | 10–4 |
| ${{\rho }_{A}}$ | Плотность воздуха, кг · м–3 | 1 |
| ${{\rho }_{L}}$ | Плотность лавы, кг · м–3 | 2500 |
| ${{\phi }_{{in}}}$ | Начальное значение объемной доли кристаллов | 0.4 |
| ${{\phi }_{{eq}}}$ | Равновесное значение объемной доли кристаллов | 0.8 |
| ${{\phi }_{*}}$ | Cпецифическое значение объемной доли кристаллов | 0.591 |
| B | Теоретическое значение коэффициента Эйнштейна | 2.5 |
Для численного решения задачи (1)–(5) используется метод конечных объемов, реализованный в программном обеспечении Ansys Fluent. Для определения положения границы лавового купола используется метод объема жидкости (VOF) [Hirt, Nichols, 1981]. Используется неявная схема интегрирования для решения уравнений (1)–(5) с соответствующими граничными и начальными условиями. Давление дискретизируется по схеме второго порядка PRESTO! [Peyret, 1996]. Для аппроксимации оператора Лапласа мы используем численную схему второго порядка точности, а монотонные схемы используются для дискретизации конвективных членов в уравнениях [Ismail-Zadeh, Tackley, 2010]. Используется SIMPLE метод [Patankar, Spalding, 1972] для решения уравнений (1)–(2), где параметры релаксации выбираются равными 0.01 и 0.3 для скорости и давления соответственно. Для функции $\alpha $ и объемной доли кристаллов параметр релаксации выбирается равным 0.5. Учитывая большой скачок между вязкостями лавы и воздуха, выбор параметров релаксации является критическим. Временной шаг выбирается в диапазоне от 0.1 до 1 с для оптимизации скорости и обеспечения сходимости решения системы линейных алгебраических уравнений (СЛАУ), полученной после дискретизации уравнения (1). Точность в решении СЛАУ для функции $\alpha $ и объемной доли кристаллов составляет 10–6.
3. СОЗДАНИЕ БАЗЫ МОРФОЛОГИЧЕСКИХ ФОРМ И СИНТЕЗАЦИЯ НАБЛЮДАЕМОГО КУПОЛА
Создание базы морфологических форм модельных лавовых куполов рассмотрим на примере построения одного купола. Модельная область дискретизируется шестигранными ячейками (примерно 70000 ячеек). Зададим следующие значения ВРК $\tau = 5 \times {{10}^{4}}$ с, РЛ Q = 0.7 м3 с–1 и радиуса жерла вулканического извержения r = 15 м. Используя параметры, указанные в табл. 1, средствами Ansys Fluent численно решаем задачу (1)–(5) на промежутках времени, указанных в табл. 2.
Таблица 2.
Параметры модельных куполов
| Номер купола k | $\tau $, с | $r$, м | ${{t}_{k}}$, с |
|---|---|---|---|
| 1–22 | $1.8 \times {{10}^{4}}$ | $15$ | $\left\{ {3 \times {{{10}}^{4}} + k \times {{{10}}^{3}}} \right\},~k = 0,~1, \ldots ,~21$ |
| 23–44 | $5 \times {{10}^{4}}$ | $15$ | $\left\{ {3 \times {{{10}}^{4}} + k \times {{{10}}^{3}}} \right\},~k = 0,~1, \ldots ,~21$ |
| 45–92 | $5 \times {{10}^{4}}$ | 5 | $\left\{ {4 \times {{{10}}^{3}} + k \times {{{10}}^{3}}} \right\},~k = 0,~1, \ldots ,~47$ |
| 93–114 | $5 \times {{10}^{5}}$ | $15$ | $\left\{ {3 \times {{{10}}^{4}} + k \times {{{10}}^{3}}} \right\},~k = 0,~1, \ldots ,~21$ |
| 115–136 | $6 \times {{10}^{4}}$ | $15$ | $\left\{ {3 \times {{{10}}^{4}} + k \times {{{10}}^{3}}} \right\},~k = 0,~1, \ldots ,~21$ |
| 137–181 | $6 \times {{10}^{4}}$ | 5 | $\left\{ {4 \times {{{10}}^{3}} + k \times {{{10}}^{3}}} \right\},~k = 0,~1, \ldots ,~44$ |
| 182–190 | $7 \times {{10}^{4}}$ | $15$ | $\left\{ {3 \times {{{10}}^{4}} + k \times {{{10}}^{3}}} \right\},k = 0,~1, \ldots ,~8$ |
| 191–238 | $7 \times {{10}^{4}}$ | 5 | $\left\{ {4 \times {{{10}}^{3}} + k \times {{{10}}^{3}}} \right\},~k = 0,~1, \ldots ,~47$ |
| 239–260 | $8 \times {{10}^{4}}$ | $15$ | $\left\{ {3 \times {{{10}}^{4}} + k \times {{{10}}^{3}}} \right\},~k = 0,~1, \ldots ,~21$ |
| 261–308 | $8 \times {{10}^{4}}$ | 5 | $\left\{ {4 \times {{{10}}^{3}} + k \times {{{10}}^{3}}} \right\},~k = 0,~1, \ldots ,~47$ |
Рассмотрим прямоугольную область ${{\Omega }_{{ABCD}}} \subset \Omega $ с вершинами A = (0, 30), B = (100, 30), C = (100, 100), D = (0, 100). Обозначим L = $ = L(\tau ,Q,r,t) \subset {{\Omega }_{{ABCD}}}$ – область, содержащую лавовый купол, и $L{\kern 1pt} ' = {{\Omega }_{{ABCD}}}\backslash L$ – область, содержащую воздух. Назовем границу между лавой и воздухом $F = F(\tau ,Q,r,t)$ = $\left\{ {({{x}_{1}},{{x}_{2}}) \in \partial L\backslash \partial {{\Omega }_{{ABCD}}}} \right\}$ границей (или морфологической формой) лавового купола.
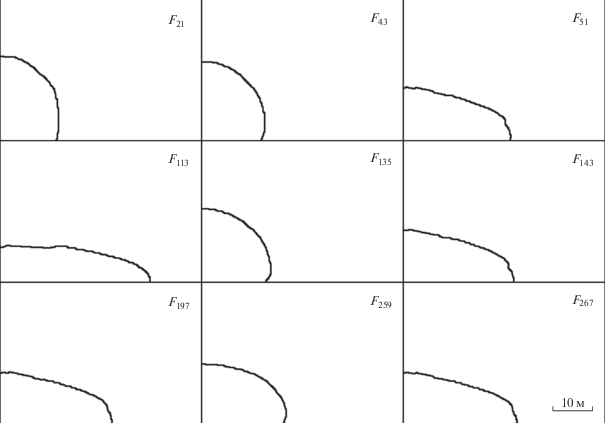
По результатам вычислительного эксперимента для момента времени ${{t}_{k}}$ находим форму купола Fk и помещаем ее в базу морфологических форм. Для организации тестового исследования морфологические формы были рассчитаны также для значений $\tau = \{ 1.8 \times {{10}^{4}},$ $6 \times {{10}^{4}},$ $7 \times {{10}^{4}},$ $8 \times {{10}^{4}},$ $5 \times {{10}^{5}}\} $ с и r = 5 м (см. табл. 2). В дальнейшем база данных может пополняться модельными формами куполов для различных параметров ВРК, РЛ и радиуса жерла вулканического извержения. На рис. 3 приведены несколько морфологических форм куполов, полученных при моделировании для различных параметров задачи. Были выбраны моменты времени, в которые площадь области L (лавового купола) примерно одинакова.
Так как основная цель работы – найти в базе данных такую форму купола, которая наилучшим способом аппроксимирует природный лавовый купол, в данном исследовании был создан также синтетический купол, в качестве возможного природного лавового купола. Для этого из базы морфологических форм выбирается любой купол, например купол с морфологической формой ${{F}_{{135}}} = F(\tau = 6 \times {{10}^{4}}\,\,{\text{с}},$ $Q = 0.7\,\,{{{\text{м}}}^{3}}\,{{{\text{с}}}^{{ - 1}}},$ $r = 15\,\,{\text{м}},$ $t = 5 \times {{10}^{4}}\,\,{\text{с}})$ (рис. 4а). Вдоль границы этого купола случайным образом вносится “зашумление”, в результате которого и получается синтетическая форма купола F* (см. рис. 4б).
Рис. 4.
Создание синтетического лавового купола: а – модельный купол F = F135, б – синтетический купол.
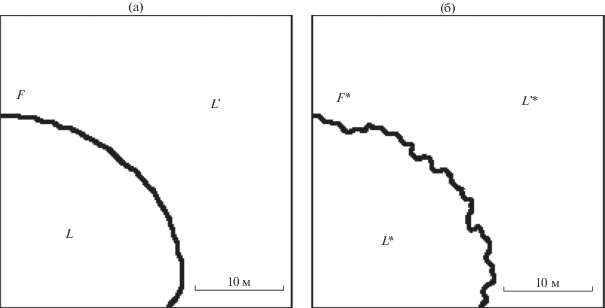
Данное зашумление производится следующим образом. В некоторой точке $a = ({{a}_{1}},{{a}_{2}}) \in F$ границы лавового купола задается случайное смещение этой точки как $a + \delta = ({{a}_{1}} + {{\delta }_{1}},{{a}_{2}} + {{\delta }_{2}}),$ где ${{\delta }_{1}},$ ${{\delta }_{2}}$ – нормально распределенные случайные величины c нулевым математическим ожиданием и стандартным отклонением, равным 1 [Венцтель, 1969]. Для каждой смещенной точки рассматривается круг ${{C}_{{a + {{\delta }}}}}\left( {\left| \varepsilon \right|} \right)$ с центром в точке $a + \delta $ и радиусом |ε|, где $\varepsilon $ – равномерно распределенная случайная величина, принимающая значения на отрезке $\left[ { - \omega ,\omega } \right],$ $\omega $ – постоянная величина; в данном случае ω = 1. Далее строится следующая область:
Таким образом, синтетический купол с границей F* получается с помощью объединения купола с границей F с множеством случайных кругов в случае неотрицательных ε и с помощью усечения синтетического купола множеством случайных кругов при отрицательных ε. Такой шум при искусственном искажении границы купола позволяет имитировать реальные искажения, которые могут быть следствием как неравномерности роста и частичным обрушением купола, так и погрешностей измерения его формы.
4. МЕТОДЫ РАСПОЗНАВАНИЯ ОБРАЗОВ
Сравнивать форму синтетического купола F* с формами лавовых куполов Fk из базы данных будем с помощью методов, используемых в теории распознавания образов [Salomon, 2007]. Представим лавовый купол в виде бинарного изображения. Для этого введем равномерное прямоугольное разбиение области ${{\Omega }_{{ABCD}}}$ на $I \times J$ ячеек ${{\Omega }_{{ij}}}\left( {{{\Omega }_{{ABCD}}} = \bigcup\nolimits_{i = 0,j = 0}^{I - 1,J - 1} {{{\Omega }_{{ij}}}} } \right).$ Каждой форме купола F поставим в соответствие прямоугольную матрицу $P(F) = \{ {{p}_{{ij}}}\} _{{i = 0,j = 0}}^{{I - 1,J - 1}}$ размера $I \times J,$ ячейки которой содержат 0, если в соответствующей ячейке ${{\Omega }_{{ij}}}$ находится более 50% воздуха, и 1 во всех остальных случаях. Оценивать близость формы синтетического купола F* и произвольной формы купола Fk из базы морфологических форм будем с помощью следующих функционалов качества.
Функционал на основе симметрической разности:
где $S( \cdot )$ (м2) – площадь области и k1 (м–2) – масштабирующий множитель.Функционал на основе метрики пикового отношения сигнала к шуму PSNR (peak signal-to-noise ratio) [Salomon, 2007]:
Функционал на основе индекса структурного сходства SSIM (structure similarity) [Wang et al., 2004]:
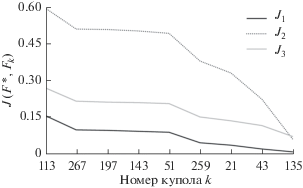
Значения функционалов вычисляются на каждом элементе базы данных, и полученный набор значений упорядочивается по убыванию. При этом то, что тот или иной функционал дает более точную оценку, основывается на информации о синтетическом куполе. Например, на рис. 5 выведены значения функционалов на элементах, представленных на рис. 3 и показано, что все три функционала достигают минимума на куполе 135. Заметим, что функционалы J1, J2 и J3 оценивают количественное отклонение модельного и синтетического куполов, в то время как функционал J3 – также структурные особенности форм куполов, хотя приводит к сложным и ресурсоемким вычислениям.
5. РЕЗУЛЬТАТЫ: ОПРЕДЕЛЕНИЕ ВЯЗКОСТИ ЛАВЫ ПО ИЗВЕСТНОЙ ФОРМЕ КУПОЛА
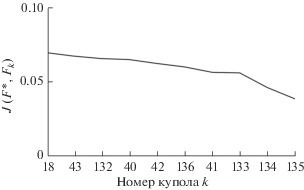
Используя описанные выше функционалы, сравним синтетический купол F* со всеми куполами Fk из базы морфологических форм. Масштабирующие множители подберем так, чтобы значения всех функционалов на элементах базы лежали на отрезке [0, 1]: k1 = 1/30, k2 = 1/25, k3 = 33, k4 = 1/14. На рис. 6 и 7 на горизонтальной оси указаны номера k куполов F из базы, на вертикальной оси указаны значения функционалов Jm(F*, F), m = 1, 2, 3. Из рис. 7 видно, что набор элементов, на которых достигаются наименьшие значения рассматриваемых функционалов, практически идентичен, наиболее близкие к синтетическому куполу F* купола – F41, F133, F134 и F135. На рис. 8 изображены синтетический купол и четыре наиболее близких модельных купола из базы данных. Время образования купола, расход лавы и размер жерла помогут с выбором близкого модельного купола.
Рис. 6.
Значения функционалов упорядочены по убыванию ${{J}_{1}}(F*,{{F}_{k}})$ (а), ${{J}_{2}}(F*,{{F}_{k}})$ (б) и ${{J}_{3}}(F*,{{F}_{k}})$ (в).
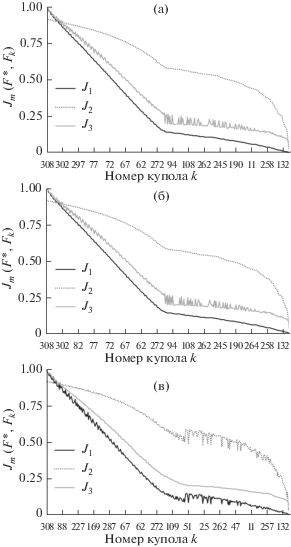
Рис. 7.
Фрагмент рис. 6 для малых значений функционалов ${{J}_{1}}(F*,{{F}_{k}})$ (а), ${{J}_{2}}(F*,{{F}_{k}})$ (б) и ${{J}_{3}}(F*,{{F}_{k}})$ (в).
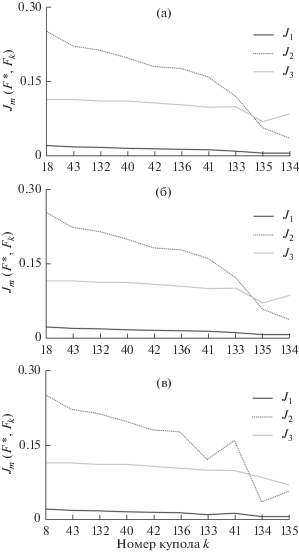
Рис. 8.
Сравнение синтетического купола F* с модельными куполами F135, F134, F133 и F41. Цветом указана модельная вязкость лавы.
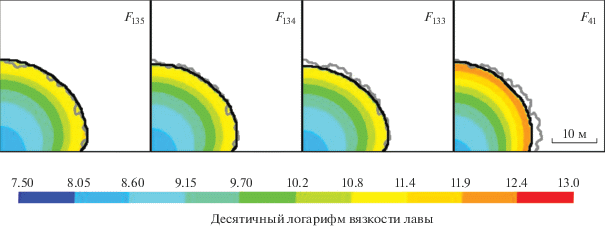
Имея информацию о том, что синтетический купол F* был получен путем “зашумления” модельного купола F135, можно сказать, что функционал на основе SSIM дает более точную оценку близости. Отметим, что для бинарного изображения функционалы J1 и J2 дают качественно схожие результаты и достаточно рассматривать один из них. Чтобы одновременно учесть качественную и количественную близость синтетического и модельного куполов можно применить линейную комбинацию описанных функционалов, тогда при подходящем выборе весовых коэффициентов можно достичь оптимальной качественной и количественной оценки. Например, рассмотрим функционал $J(F*,F)$ = $0.5\left[ {{{J}_{1}}(F*,F) + {{J}_{3}}(F*,F)} \right].$ При этом минимум такого функционала достигается для купола 135 (рис. 9). Хотя с помощью линейной комбинации функционалов можно точнее выбрать тот модельный купол, который будет минимизировать оптимальным образом природный купол, надо заметить, что на практике выбор весовых коэффициентов может представлять сложность, так как оцениваться будет природный, а не синтетический лавовый купол.
6. ОБСУЖДЕНИЕ И ЗАКЛЮЧЕНИЕ
Морфологические изменения лавовых куполов объясняются изменением вязкости магмы, вызванным дегазацией и кристаллизацией при подъеме магмы по каналу вулкана из очага извержения [Melnik, Sparks, 1999, 2005]. Быстрая скорость подъема магмы сокращает время, доступное для кристаллизации магмы, поэтому магма ведет себя как относительно маловязкая жидкость и после экструзии на поверхность растекается, образуя блинообразные морфологические структуры. С уменьшением РЛ или при малых ВРК кристаллическая магма переходит из текучего состояния к квазитвердому, образуя на поверхности лавовые выжимки и обелиски [Tsepelev et al., 2020].
Посредством решения обратной задачи можно восстановить вязкость магмы и историю роста конкретного лавового купола при наличии данных по наблюдениям его морфологии. В данной работе представлен подход к оценке вязкости магмы, основанный на сравнении наблюдаемой и смоделированных морфологических форм куполов с помощью трех функционалов, используемых в компьютерном зрении и теории обработки изображений. Хотя каждый функционал позволяет определить минимальную разницу между смоделированными и наблюдаемыми формами куполов, функционал на основе измерения индекса структурного сходства оценивает не только количественное отклонение модельных и наблюдаемого куполов, но и их структурные особенности, и тем самым выполняет оценку лучше. По найденной таким образом смоделированной форме лавового купола можно оценить параметры реологической модели и принять ее для наблюдаемого купола.
Необходимо отметить, что в данной работе в качестве наблюдаемой формы лавового купола использовалась случайная модификация одной из рассчитанных форм и оценки основывались на знании этой синтетической формы купола. В случае с природным лавовым куполом нужно рассматривать элемент базы, при котором значения функционалов минимальны, а также несколько близких к нему куполов из базы. Полученную выборку из базы требуется подвергнуть экспертной оценке.
Надо заметить, что рассматриваемая обратная задача является достаточно сложным объектом исследования как с теоретической, так и с вычислительной точек зрения [Самарский, Вабищевич, 2004; Кабанихин, 2009]. Обратные задачи являются, как правило, некорректными, т.е. неустойчивыми и могут не обладать единственностью решения. Рассматриваемая обратная задача является некорректной, она является неустойчивой (малые ошибки в исходных данных или ошибки округления могут привести к большим ошибкам в решении задачи), а также она может иметь неединственное решение. Например, при различных расходах лавы и различных характерных временах роста кристаллов может получаться похожая форма купола. Однако расход лавы можно практически определить по объему купола, и потому РЛ можно рассматривать как известную характеристику процесса. Классические методы не пригодны для решения некорректных задач. Альтернативными в этой ситуации являются различные подходы, связанные с математическими преобразованиями обратных задач [Тихонов, Арсенин, 1979]. Многие из таких подходов могут оказаться удовлетворительными при теоретическом исследовании задачи, но неудовлетворительными при ее численном решении. Другие подходы связаны с различными упрощениями обратных задач.
В данной работе для решения обратной задачи использовался подход, связанный с уточнением зависимости искомой вязкости от своих переменных и параметров, когда искомая вязкость искалась в определенном виде (в виде определенной функции) с небольшим количеством параметров. Задача фактически сводилась к поиску характерного времени роста кристаллов, от которого зависит вязкость магмы, и этот поиск осуществлялся посредством минимизации различий между наблюдаемой и смоделированными морфологическими формами лавовых куполов.
Задача предсказания формы купола и распределения напряжений в его постройке важна для оценки его устойчивости и возможности обрушения с образованием пирокластических потоков или эксплозивных извержений. В идеале настроенная на конкретный вулкан программа должна использоваться для краткосрочных и долгосрочных прогнозов сотрудниками вулканологических обсерваторий. Подобная практика применяется нефтяными компаниями для прогнозирования добычи нефти на месторождениях. Постоянная корректировка модели путем воспроизведения истории добычи нефти позволяет в этом случае делать достоверные прогнозы и определять оптимальные стратегии добычи.
При применении данной методики к реальному извержению можно учесть отклонения расчетной формы купола от измеренной не только в некоторый момент времени, но и за весь период наблюдений, задать ограничения на форму кратера, подводящего канала и петрологию магмы. Реальные лавовые купола являются трехмерными объектами. И хотя представленный в работе подход является двумерным, он может быть распространен на трехмерный случай и использоваться для восстановления условий роста природных куполов.
Список литературы
Венцтель Е.С. Теория вероятностей / 4-е изд. М.: Наука, 1969. 576 с.
Кабанихин С.И. Обратные и некорректные задачи. Новосибирск: Сибирское научное издательство, 2009. 457 с.
Самарский А.А., Вабищевич П.Н. Численные методы решения обратных задач математической физики. М.: Эдиториал УРСС, 2004. 480 с.
Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач / 2-е изд. М.: Наука, 1979. 285 с.
Costa A., Caricchi L., Bagdassarov N. A model for the rheology of particle-bearing suspensions and partially molten tocks // Geochem. Geophys. Geosys. 2009. V. 10. № 3. P. Q03010.
Daag A.S., Dolan M.T., Laguerta E. et al. Growth of a postclimactic lava dome at Pinatubo Volcano, July–October 1992 / Eds C. Newhall, R. Punongbayan // Fire and Mud. Eruptions and Lahars of Mount Pinatubo, Philippines. Seattle: University of Washington Press, 1996. P. 647–664.
Harris A.J., Rose W.I., Flynn L.P. Temporal trends in lava dome extrusion at Santiaguito 1922–2000 // Bull. Volcanol. 2003. V. 65. P. 77–89.
Hirt C.W., Nichols B.D. Volume of fluid (VOF) method for the dynamics of free boundaries // J. Comput. Phys. 1981. V. 39. № 1. P. 201–225.
Ismail-Zadeh A., Tackley P. Computational Methods for Geodynamics. Cambridge: Cambridge University Press, 2010. 313 p.
Jeffrey D., Acrivos A. The rheological properties of suspensions of rigid particles // AIChE J. 1976. V. 22. P. 417–432.
Lejeune A., Richet P. Rheology of crystal-bearing silicate melts: An experimental study at high viscosity // J. Geophys. Res. 1995. V. 100. P. 4215–4229.
Mardles E. Viscosity of suspensions and the Einstein equation // Nature. 1940. V. 145. P. 970.
Melnik O., Sparks R.S.J. Nonlinear dynamics of lava dome extrusion // Nature. 1999. V. 402. P. 37–41.
Melnik O., Sparks R.S.J. Controls on conduit magma flow dynamics during lava dome building eruptions // J. Geophys. Res. 2005. V. 110. № B2. P. B02209.
Nakada S., Shimizu H., Ohta K. Overview of the 1990–1995 eruption at Unzen Volcano // J. Volcanol. Geother. Res. 1999. V. 89. P. 1–22.
Nakada S., Zaennudin A., Yoshimoto M. et al. Growth process of the lava dome/flow complex at Sinabung Volcano during 2013–2016 // J. Volcanol. Geother. Res. 2019. V. 382. P. 120–136.
Patankar S.V., Spalding D.B. A calculation procedure for heat and mass transfer in three–dimensional parabolic flows // Int. J. Heat Mass Transfer. 1972. V. 15. P. 1787–1806.
Peyret R. Handbook of Computational Fluid Mechanics. Academic Press Limited, USA, 1996.
Salomon D. Data Compression: The Complete Reference. London: Springer, 2007.
Swanson D.A., Dzurisin D., Holcomb R.T. et al. Growth of the lava dome at Mount St Helens, Washington, (USA) 1981–1983 / Ed. J.H. Fink // The Emplacement of Silicic Domes and Lava Flows // Geol. Soc. Amer., Boulder, Special Paper 212. 1987. P. 1–16.
The Eruption of Soufrière Hills Volcano, Montserrat, from 2000 to 2010 / Eds G. Wadge, R.E.A. Robertson, B. Voight // Geol. Soc. London Mem. 2014. V. 39. https://doi.org/10.1144/M39
Tsepelev I., Ismail-Zadeh A., Melnik O. Lava dome morphology inferred from numerical modelling // Geophys. J. Inter. 2020. https://doi.org/10.1093/gji/ggaa395
Tsepelev I., Ismail-Zadeh A., Starodubtseva Y. et al. Crust development inferred from numerical models of lava flow and its surface thermal measurements // Ann. Geophys. 2019. V. 61. № 2. P. VO226. https://doi.org/10.4401/ag-7745
Voight B., Constantine E.K., Siswowidjoyo S., Torley R. Historical eruptions of Merapi volcano, Central Java, Indonesia, 1768–1998 // J. Volcanol. Geotherm. Res. 2000. V. 100. P. 69–138.
Wang Z., Bovik A.C., Sheikh H. R., Simoncelli E.P. Image quality assessment: From error visibility to structural similarity // IEEE Transactions on Image Processing. 2004. V. 13. № 4. P. 600–612.
Watts R.B., Herd R.A., Sparks R.S. J., Young S.R. Growth patterns and emplacement of the andesitic lava dome at Soufrière Hills Volcano, Montserrat / Eds T. H. Druitt, B.P. Kokelaar // The Eruption of Soufrière Hills Volcano, Montserrat, from 1995 to 1999 // Geol. Soc. London Mem. 2002. V. 21. P. 115–152.
Zobin V.M., Arámbula R., Bretón M. et al. Dynamics of the January 2013–June 2014 explosive-effusive episode in the eruption of Volcán de Colima, México: insights from seismic and video monitoring // Bull. Volcanol. 2015. V. 77. P. 31. https://doi.org/10.1007/s00445-015-0917-z
Дополнительные материалы отсутствуют.
Инструменты
Вулканология и сейсмология