Вулканология и сейсмология, 2021, № 6, стр. 14-20

ВВЕДЕНИЕ

После главного удара в очаговой зоне сильного землетрясения наблюдаются повторные подземные толчки, называемые афтершоками [Касахара, 1985]. Эмпирический закон Омори, описывающий эволюцию потока афтершоков во времени, гласит, что частота афтершоков n(t) в среднем убывает гиперболически с течением времени [Omori, 1894]. Более ста лет прошло после установления этого закона, а интерес к нему не ослабевает (см., например, [Davison, 1924; Hirano, 1924; Utsu et al., 1995; Гульельми, 2017]).

В данной статье мы предлагаем модификацию закона эволюции афтершоков. Основная идея состоит в том, что эволюция описывается дифференциальным уравнением Ферхюльста, известным также как логистическое уравнение, а отнюдь не гиперболической формулой Омори. К этой идее приводит ряд недавно опубликованных теоретических и экспериментальных работ по исследованию афтершоков [Guglielmi, 2016; Faraoni, 2020; Guglielmi, Klain, 2020; Zotov et al., 2020; Завьялов и др., 2020].

В работе [Guglielmi, 2016] предложено переформулировать закон Омори, а именно, записать его в виде дифференциального уравнения

Здесь n обозначает число афтершоков в единицу времени, σ – феноменологический параметр, названный коэффициентом деактивации очага землетрясения. На первый взгляд в этом нет большого смысла, но только на первый. В самом деле, общее решение уравнения (1) совпадает с формулой Омори. Однако запись закона в форме уравнения эволюции подсказывает нетривиальные обобщения теории. Например, можно учесть отклонения n(t) от простой гиперболы, нередко наблюдаемые на опыте. Положим σ = σ(t) и найдем общее решение уравнения (1)

Формула (2) дает возможность преодолеть ригидность классической формулы Омори. Действительно, параметры в классической формуле Омори могут изменяться от одного события (сильного землетрясения, породившего поток афтершоков) к другому, но должны оставаться неизменными в данном конкретном событии. В отличие от этого, в формуле (2) учитывается возможная нестационарность горных пород в очаге, “остывающем” после главного удара. Решение (2) сохраняет гиперболическую структуру зависимости частоты афтершоков от времени. Но при этом оно лишь учитывает, что время в очаге, образно выражаясь, течет неравномерно. При σ = const формула (2) совпадает с классической формулой Омори с точностью до обозначений.

Другой взгляд на уравнение (1) состоит в том, что его можно рассматривать как уравнение Эйлера–Лагранжа некоторой динамической системы [Faraoni, 2020]. Соответствующий лагранжиан имеет вид

Лагранжиан (3) допускает модификации. Мы воспользуемся этим, чтобы представить уравнение эволюции афтершоков в форме логистического уравнения.

Еще одно направление состоит в поиске закона пространственно-временной эволюции афтершоков [Guglielmi, Klain, 2020]. Поиск мотивирован, прежде всего, так называемым эффектом “ребристого” распространения афтершоков от эпицентра главного удара, обнаруженным недавно при участии авторов [Zotov et al., 2020; Завьялов и др., 2020]. Эффект обнаружен путем статистического исследования совокупности афтершоков от совокупности сильных землетрясений, представленных в мировых каталогах землетрясений, но он проявляется иногда и при анализе конкретных событий. Эффект “ребристости” состоит в возникновении некоего подобия волновой структуры в пространственно-временной эволюции активности (числа) сильных афтершоков в координатах время от момента главного толчка – расстояние от его эпицентра. Мы предлагаем описывать эффект “ребристого” распространения нелинейным дифференциальным уравнением в частных производных Колмогорова–Петровского–Пискунова (сокращенно КПП) [Колмогоров и др., 1937]. Во-первых, уравнение КПП имеет решения в виде бегущих волн диффузии. Это дает основу для интерпретации эффекта “ребристого” распространения афтершоков. Во-вторых, при усреднении КПП по эпицентральной зоне или в пренебрежении диффузией из КПП следует логистическое уравнение. Таким образом, мы получаем дополнительно косвенный аргумент в пользу гипотезы об уменьшении частоты афтершоков с течением времени по логистической кривой Ферхюльста, а не по гиперболе Омори.

УРАВНЕНИЕ ЭВОЛЮЦИИ

Как хорошо известно, механика Лагранжа базируется на фундаментальных законах механики Ньютона. Во многих конкретных задачах механики именно эти законы позволяют выбрать ту или иную форму лагранжиана. Но по вполне понятной причине в нашем случае практически невозможно найти лагранжиан, исходя из первых принципов. Теория афтершоков имеет сугубо феноменологический характер [Guglielmi, Klain, 2020]. Поэтому если пытаться сформулировать ее на базе уравнения Эйлера–Лагранжа, то форму лагранжиана надо угадать, руководствуясь данными наблюдений и косвенными соображениями.

Лагранжиан (3) [Faraoni, 2020], из которого следует (1), имеет непривычную структуру. Эта структура наводит на мысль, что функция L(n, $\dot {n}$) представлена в виде ряда по нечетным степеням n. При поиске более общей теории естественно попытаться, прежде всего, восстановить недостающий в (3) кубичный член вида γ²n³. После ряда проб и ошибок нами был выбран следующий лагранжиан:

Видно, что (4) переходит в лагранжиан Фараони (3) при γ = 0.

С новым лагранжианом уравнение Эйлера–Лагранжа

приобретает вид Мы получили уравнение Ферхюльста, или, как его еще называют, логистическое уравнение [Verhulst, 1838]. Оно широко используется в биологии, химии, астрофизике и других науках, включая экономику и социологию. Покажем, что уравнение Ферхюльста может быть полезным и в физике землетрясений.

Решением уравнения Ферхюльста является так называемая логистическая кривая. Напомним форму той ветви логистической кривой, которая широко используется в различных разделах науки. Это монотонно растущая функция времени (красная кривая). При t → -∞ функция асимптотически стремится к нулю, а при t → +∞ она стремится снизу к насыщению на уровне n_∞ = γ/σ.

Такое поведение несвойственно афтершокам. Однако давайте учтем, что логистическая кривая фактически состоит из двух ветвей (рис. 1). Наличие второй (зеленой) ветви обычно не принимается во внимание. Ветвь целиком располагается выше уровня насыщения n_∞ и представляет собой монотонно падающую функцию времени. При t → +∞ она асимптотически стремится сверху к уровню насыщения. Именно эта ветвь представляет интерес для описания афтершокового процесса.

Поставим задачу Коши для логистического уравнения. Выделение той или иной ветви осуществляется выбором начального условия. Мы зададим начальное условие n = n₀ при t = 0 и будем искать решения при t > 0. Нетрудно убедиться, что при n₀ < n_∞ (n_∞ < n₀) решением задачи будет нижняя (верхняя) ветвь логистической кривой. Таким образом, при постановке задачи Коши в физике афтершоков следует задавать начальные условия при дополнительном ограничении n₀ > n_∞. Более того, вполне уместно использовать сильное неравенство

В самом деле, при t → ∞ частота афтершоков асимптотически приближается сверху к фоновому (равновесному) значению n_∞. Опыт показывает, что, как правило, ${{n}_{0}} \gg {{n}_{\infty }}$ после сильного землетрясения.

ЭПОХА ОМОРИ

Итак, мы предполагаем, что эволюция афтершоков описывается логистической функцией. О правдоподобности нашей гипотезы косвенно свидетельствует опыт наблюдений. Давно известно, например, что с течением времени частота n стремится не к нулю, как это следует из закона Омори, а к некоторому равновесному (фоновому, с некоторой средней интенсивностью потока землетрясений) значению n_∞. Но более убедительным является наш опыт экспериментального изучения вариаций функции деактивации σ(t). Остановимся на этом подробнее.

Покажем, что убывание частоты афтершоков с течением времени, в целом протекающее по верхней ветви логистической функции, на первом этапе эволюции происходит по гиперболе Омори, т.е. в соответствии с формулой (2) при σ = const. Такой этап эволюции естественно назвать эпохой Омори, что мы и предложили в статье [Завьялов и др., 2020].

Предположим для простоты, что γ = const, n_∞ = const, введем обозначение

и запишем решение уравнения эволюции (6) в следующем виде:

В эпоху Омори t_∞ < t $ \ll $ 1/γ и, соответственно,

Формула (10) совпадает с формулой Омори (с точностью до обозначений).

В работе [Гульельми и др., 2019] предложен проект создания Атласа афтершоков на базе решения обратной задачи очага. Сущность обратной задачи состоит в определении коэффициента деактивации σ(t) по данным о наблюдаемой частоте афтершоков n(t). Решение обратной задачи для 20 сейсмических событий, произошедших в Калифорнии, показало, что коэффициент деактивации претерпевает сложную эволюцию, но в большинстве случаев на первых стадиях наблюдается довольно продолжительная эпоха Омори (рис. 2). Это косвенно подтверждает теорию, построенную на базе лагранжиана (4).

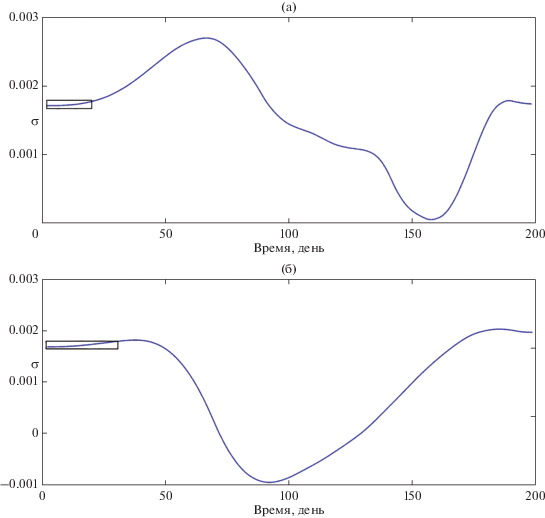
Продолжительность эпохи Омори изменяется от случая к случаю и в среднем составляет 30 дней. Обнаружена некоторая тенденция к увеличению продолжительности эпохи с ростом магнитуды главного удара.

РАСПРОСТРАНЕНИЕ АФТЕРШОКОВ

В работе [Zotov et al., 2020] было обнаружено не известное ранее явление медленного распространения афтершоков от эпицентра главного удара к периферии эпицентральной зоны (см. также [Завьялов и др., 2020]). Скорость распространения изменяется от случая к случаю в широких пределах. Ориентировочно она составляет несколько километров в час. Эта величина на три порядка меньше скоростей упругих волн в земной коре, что дает нам основание сделать предположение о распространении нелинейной диффузионной волны, возбужденной главным ударом.

Представление о бегущей волне диффузии базируется на анализе решений известного уравнения КПП [Колмогоров и др., 1937]. Пусть n(x, t) – распределение афтершоков во времени и в пространстве. Здесь x – 2D радиус-вектор, указывающий положение точки на земной поверхности относительно эпицентра главного удара. Уравнение КПП имеет вид

Здесь D – коэффициент диффузии. Разложим функцию F(n) в степенной ряд и ограничимся двумя членами: F(n) = γn – σn². Линейный член описывает тот факт, что очаг представляет собой неравновесную динамическую систему. Квадратичный член мы сохранили, ориентируясь на закон Омори в формуле (1). В результате уравнение пространственно-временной эволюции приобретает вид

Уравнение (12) обладает двумя свойствами, важными в контексте нашей темы. Во-первых, из него следует логистическое уравнение (6), если параметр D мал и можно пренебречь диффузионным членом. К логистическому уравнению можно прийти также путем усреднения (12) по эпицентральной зоне. Однако усреднение нелинейного уравнения требует специального анализа и мы не будем останавливаться на этом.

Во-вторых, уравнение имеет автомодельные решения, имеющие вид бегущей волны n(x, t) = = n(x ± Ut). Именно это обстоятельство сыграло решающую роль при выборе нами уравнения КПП в качестве управляющего уравнения. Оценку скорости распространения волны можно сделать путем анализа размерностей коэффициентов управляющего уравнения: U ∼ $\sqrt {\gamma D} .$

Известен набор частных решений одномерного нелинейного уравнения диффузии, имеющих вид бегущей волны [Polyanin, Zaitsev, 2012]. В качестве примера укажем на одно из частных решений такого рода:

Здесь C – произвольная постоянная, U = $5\sqrt {{{\gamma D} \mathord{\left/ {\vphantom {{\gamma D} 6}} \right. \kern-0em} 6}} .$

Итак, у нас наметилось перспективное направление для теоретического исследования распространения афтершоков, обнаруженного ранее в эксперименте. В этой связи следует подчеркнуть, что возможности аналитического исследования здесь довольно ограниченны. Наиболее подходящими являются численные методы решения уравнения нелинейной диффузии. При этом известные точные решения типа (13) могут быть эффективно использованы для совершенствования численных схем и для тестирования результата вычислительных процедур. Численные эксперименты дадут возможность исследовать процесс распространения афтершоков при различных граничных и начальных условиях и при различных комбинациях параметров задачи γ, σ, и D. Это, безусловно, улучшит наше понимание эволюции афтершоков во времени и в пространстве.

В заключение данного раздела следует сказать, что явление распространения афтершоков заслуживает дальнейшего экспериментального изучения. Накопленный нами опыт [Zotov et al., 2020; Завьялов и др., 2020; Guglielmi, Zotov, 2020] подсказывает, что в общем существует два режима заполнения эпицентральной зоны афтершоками – быстрый и медленный. В режиме быстрого заполнения происходит преимущественно упругое перераспределение напряжений в области очага после образования магистрального разрыва сплошности геологической среды при главном ударе. О существовании медленного режима свидетельствует эффект распространения афтершоков от эпицентра главного удара с малой скоростью в виде нелинейных диффузионных волн (“ребристая” структура). Мы планируем исследовать условия реализации того или иного режима.

ОБСУЖДЕНИЕ

Мы представили идеализированную картину эволюции афтершоков. В реальности на частоту возбуждения афтершоков влияет большое количество трудно контролируемых факторов различной природы. О нестационарности геологической среды в очаге мы упоминали выше. Среди других причин, вызывающих отклонение от идеальной картины, следует особо выделить воздействие на очаг землетрясения эндогенных и экзогенных триггеров. К ним относятся свободные колебания Земли, возбужденные главным ударом, кругосветное сейсмическое эхо, сейсмические шумы в очаге и другое [Завьялов и др., 2020].

Мы выяснили, что при постановке задачи Коши для афтершоков следует наложить ограничение n₀ > n_∞ на начальное условие. Это наводит на мысль о том, что противоположное неравенство может представлять интерес при феноменологическом описании форшоков. Вопрос требует дополнительного изучения, поскольку не вполне ясно, как моделировать возникновение главного удара в процессе нарастания интенсивности форшоков по логистической кривой. Вспомним, однако, что существуют так называемые рои землетрясений, представляющие собой тесные пространственно-временные группы сейсмических событий. В рое отсутствует главный удар. Допустим, что по той или иной причине параметр n_∞ скачком повышается, а через некоторое время возвращается к исходному значению. Такого рода включение/выключение приведет к параметрической модуляции частоты подземных толчков, причем после включения рост n(t) будет происходить по нижней (красной) ветви, а после выключения спадание n(t) будет происходить по верхней (зеленой) ветви логистической функции (см. рис. 1). Таков предварительный сценарий возникновения роя землетрясений.

Наконец, обсудим трудный вопрос о происхождении главного удара землетрясения. На рис. 2 мы видим, что параметр σ может стать на некоторое время отрицательным. Введем обозначение

При σ < 0 вместо (2) будем иметь Мы видим, что при t₂ ≥ ${{t}_{*}}$ = t₁ + Δt возникает сингулярность, которую можно гипотетически представить как образ главного удара. Величину Δt = = (n₀❬|σ|❭)^–1 естественно назвать временем ожидания главного удара. Если же t₂ < ${{t}_{*}}$, то главного удара не происходит, несмотря на то, что на некоторое время коэффициент деактивации σ становится отрицательным.

Чтобы устранить сингулярность при σ < 0, следует сохранить третий член при разложении функции F(n) в степенной ряд: F(n) = γn + |σ|n² – βn³. Здесь предполагается, что β > 0. Тогда n_max ≈ |σ|/β при t = ${{t}_{*}}$, если для простоты положить β $ \ll $ |σ|²/γ. В теории динамических систем описанную ситуацию называют взрывной неустойчивостью. Таким образом, теория предсказывает возникновение геотектонического взрыва в форме главного удара землетрясения при перемене знака коэффициента деактивации σ. Однако причина возможной перемены знака нам пока не ясна. Важное замечание касается выбора неизвестной функции в уравнении эволюции. Если развить теорию главного удара по указанной схеме, то разумно в качестве искомой функции выбрать энергию, а не частоту землетрясений.

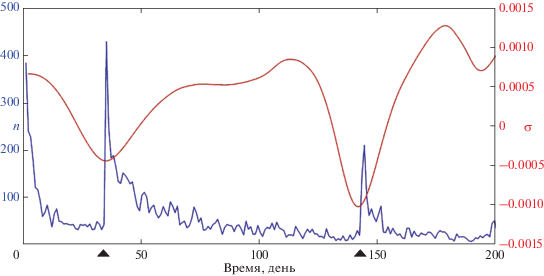
Рисунок 3 иллюстрирует возможную связь между вариациями σ(t) и вероятностью появления главных ударов [Guglielmi et al., 2020]. Рисунок получен в результате обработки данных наблюдений землетрясений Южной Калифорнии в период с 17.08.1995 по 14.03.1996 гг. Мы видим два сильных землетрясения и последующие афтершоки. Моментам возбуждения сильных землетрясений предшествовали довольно продолжительные периоды длительностью в несколько суток уменьшения значений параметра σ. Заметим, что кривая динамики коэффициента деактивации (см. рис. 3) получена путем сплайн аппроксимации. Мы проверяли влияние процедуры осреднения кривой параметра деактивации и пришли к выводу, что уменьшение коэффициента деактивации перед главным ударом связано не только с осреднением величины этого параметра по времени, но и с реальным его уменьшением перед главным ударом.

ЗАКЛЮЧЕНИЕ

Мы представили общие контуры феноменологической теории афтершоков. Судя по всему, уравнение КПП может служить основой для дальнейшего развития теории. Показано, что уравнение КПП имеет решения, имитирующие эффект медленного распространения афтершоков. Из него следует логистическое уравнение, описывающее эволюцию афтершоков, усредненных по эпицентральной зоне. Предлагаемый подход может оказаться полезным при поиске моделей форшоков, главного удара и роев землетрясений.