Журнал вычислительной математики и математической физики, 2019, T. 59, № 12, стр. 2060-2076
Алгоритмы локальной минимизации силового поля для трехмерного представления макромолекул
А. С. Аникин 1, *, О. А. Большакова 2, **, А. В. Гасников 3, 4, ***, А. Ю. Горнов 1, ****, Т. В. Ермак 5, *****, Д. В. Макаренко 3, ******, В. П. Морозов 5, *******, Б. О. Нетеребский 5, ********, П. А. Яковлев 5, *********
1 ИДСТУ СО РАН
664033 Иркутск, ул. Лермонтова, 134, Россия
2 Сириус
354349 Сочи, Олимпийский проспект, 40, Россия
3 НИУ МФТИ
141700 М.о., Долгопрудный, Институтский пер., 9, Россия
4 ИППИ РАН
127051 Москва, Бол. Каретный пер., 19, стр. 1, Россия
5 Биокад
198515 С. Петербург, ул. Связи, 34-а, Россия
* E-mail: anikin@icc.ru
** E-mail: olgab-87@yandex.ru
*** E-mail: gasnikov@yandex.ru
**** E-mail: gornov@icc.ru
***** E-mail: ermak@biocad.ru
****** E-mail: devjiu@gmail.com
******* E-mail: morozovvp@biocad.ru
******** E-mail: neterebskiy@biocad.ru
********* E-mail: yakovlev@biocad.ru
Поступила в редакцию 08.10.2018
После доработки 15.07.2019
Принята к публикации 05.08.2019
Аннотация
Большинство проблем структурной вычислительной биологии требуют решения задачи минимизации энергетической функции (силового поля), определенной на геометрии молекулы. Это позволяет определять свойства молекул, предсказывать правильное положение белковых цепей, находить лучшую состыковку молекул при предсказании комплексообразования (докинге), проверять гипотезы относительно белкового дизайна и решать многие другие задачи, возникающие при современной разработке лекарственных средств. В случае низкомолекулярных соединений (состоящих из менее чем 250 атомов) задача нахождения геометрии, минимизирующей энергетическую функцию, является достаточно хорошо решенной. Более сложной задачей является минимизация макромолекул (в частности, белков), в состав которых входят десятки тысяч атомов. Однако отличительной особенностью данных постановок задач является наличие начальных приближений, близких к искомому решению. Таким образом, исходная задача может быть сформулирована как задача невыпуклой оптимизации в пространстве порядка ${{10}^{4}}$ переменных. При этом сложность вычисления как значения функции, так и градиента, квадратична по числу переменных. В статье приводится сопоставительный анализ безградиентных методов с линейкой методов градиентного типа (градиентный спуск, быстрый градиентный спуск, метод сопряженных градиентов, квазиньютоновские методы) в GPU-реализациях (Graphical Processing Unit, графический процессор). Библ. 42. Фиг. 4. Табл. 1.
1. ВВЕДЕНИЕ
Развитие экспериментальных методов измерений в молекулярных и клеточных системах в последние десятилетия привело к значительному росту понимания биологических процессов, протекающих при различных патологических явлениях. В свою очередь это позволяет выявлять новые мишени для проведения эффективной лекарственной терапии даже для самых тяжелых заболеваний из области онкологии и аутоиммунных нарушений. Терапевтическими агентами в этом случае должны служить искусственно созданные биологические молекулы, обеспечивающие заданные функции. Обеспечение возможности рационального дизайна таких молекул, а также предсказание их свойств без проведения реального биологического эксперимента, являются одними из важнейших целей современной вычислительной биологии.
К сожалению, как недостаточные вычислительные мощности, так и фундаментальные ограничения используемых методов математического моделирования биологических систем не позволяют полностью решать эту задачу в общем случае. Для этого активно развиваются методы предсказания структуры синтетических белков, имеющие, по большей части, нефизичные основания. Другой, не менее перспективной областью является модификация природных белков с целью улучшения их характеристик или придания альтернативных свойств. Оба направления подразумевают оптимизацию геометрии исследуемых молекул с целью поиска конформации (взаимного положения всех атомов), наиболее точно соответствующей реальному состоянию биологического объекта в природе. То, что исследуемые объекты существуют при температурах, значительно превышающих ноль по шкале Кельвина, определяет постоянное движение всех компонентов молекул, вызываемых внешними возмущениями среды и, как следствие, отсутствия равновесия в действующих силах. Тем не менее практически полезно рассматривать некоторую статистически наиболее часто встречающуюся конформацию, как ту, в которой биологическая молекула проводит большую часть времени, а значит, скорее всего именно в ней способна выполнять свою основную функцию. Эта конформация логичным образом будет достигаться в минимуме потенциальной энергии молекулы, определяющейся множеством попарных взаимодействий между атомами. Природа этих взаимодействий, по большей части, лежит в области электростатики и выражается соответствующими законами, которые будут подробнее рассмотрены в разд. 2. данной статьи.
Важной особенностью рассмотренного процесса является то, что типично белок не стремится к глобальному минимуму потенциальной энергии. Связано это с тем, что белок образуется не сразу весь, а последовательно от первой аминокислоты к последней, а значит, и сворачивается не весь целиком одномоментно. Это же приводит нас к соображениям, что локально схожие последовательности аминокислот будут давать локально схожие структуры. На основе этой идеи разработаны различные методы, позволяющие получать неплохие приближения пространственных конформаций белков с использованием баз уже известных структур. Сами эти методы находятся за рамками рассмотрения данной статьи, но упомянуты для следующего важного соображения: в проблемах вычислительной биологии важной задачей становится локальная минимизация энергетического потенциала, не вызывающая значительного возмущения геометрии рассматриваемой биологической молекулы.
Другой интресующей вычислительных биологов проблемой является поиск места состыковки двух взаимодействующих белков. Данный процесс подразумевает переход молекул в альтернативные конформации, энергетически более выгодные для взаимодействия. Здесь вновь возникает задача минимизации энергии, и вновь она требует лишь локальной минимизации, поскольку поиск глобального минимума означал бы значительную “поломку” имеющейся структуры невзаимодействующих белков, что сразу нарушало бы физичность нашей модели.
Именно эти соображения стали мотивацией к данной работе, рассматривающей с точки зрения современных численных методов оптимизации задачу минимизации потенциальной энергии пространственной структуры белка в предположении, что имеются достаточно хорошие начальные приближения к нужному решению (локальному минимуму).
Структура статьи следующая. В разд. 2 приводится постановка задачи в терминах задачи невыпуклой оптимизации. В разд. 3 в хронологическом порядке приводится эволюция понимания задачи. Взрывное поведение минимизируемого потенциала при сближении атомов подсказывает, что градиентные методы должны тут плохо работать. А структура функционала позволяет эффективно пересчитывать значение энергии при шевелении одного лишь атома. Эти наблюдения приводят к безградиентному методу со случайным выбором атома для шевеления на каждом шаге. Тем не менее сравнительный анализ этого метода и градиентного спуска показал, что при наличии GPU (Graphical Processing Unit или графический процессор) на практике более эффективным оказалось использование градиентного спуска с параллелизацией вычислений на GPU (для градиентного спуска можно в полной мере использовать потенциал современных видеокарт с тысячами вычислительных ядер). В разд. 4 развивается стандартная сюжетная линия в невыпуклой оптимизации, которая сейчас активно эксплуатируется в обучении глубоких нейронных сетей [38]. Эта линия заключается в том, что если градиентные методы неплохо сходятся, то следует пробовать сделать следующий шаг – рассмотреть ускоренные (быстрые) градиентные методы, которые доказуемо дают ускорение только для выпуклых задач. А дальше можно рассмотреть и различные варианты методов сопряженных градиентов и квази-ньютоновских методов, гарантированно сходящихся только для выпуклых задач. В данном разделе приводится современный обзор результатов по скорости сходимости данных методов для выпуклых задач. В разд. 5 приведены результаты многочисленных экспериментов с методами, описанными в предыдущем разделе. В целом оценки скорости сходимости (и опыт практического использования) рассмотренных методов в выпуклом случае неплохо переносятся для данного класса задач и на невыпуклый случай, что изначально было совершенно неочевидно ввиду наличия большого числа взрывных особенностей у оптимизируемого функционала. Наиболее эффективными оказались следующие: быстрый градиентный метод Нестерова [22] со специальной стратегией выбора шага, квази-ньютоновский метод LBFGS (Limited-memory Broyden–Fletcher–Goldfarb–Shanno) с памятью 3 итерации и один из вариантов метода сопряженных градиентов Полака–Рибьера–Поляка [24]. Все методы программировались сначала на Haskell (функциональный, строго-типизированный язык программирования; создавался промышленный код; использование функционального языка практически исключало наличие возможных ошибок – при их наличии не удалось бы скомпилировать программу) с использованием библиотеки Accelerate [4] для работы с архитектурой GPU, а затем на CUDA С (набор программных средств от NVIDIA для непосредственного взаимодействия с архитектурой GPU) [11]. К сожалению, использование библиотеки Accelerate заметно (в несколько раз) дополнительно замедляло время работы программы и привносило дополнительные сложности при запуске программы на имеющемся сервере по сравнению с более стандартной в данном контексте архитектурой CUDA C [39]. Поэтому итоговый промышленный продукт был написан на CUDA C. Некоторые особенности реализации отмеченных методов (например, способ выбора шага/осуществление одномерной вспомогательной минимизации) также обсуждаются в данном разделе.
2. ПОСТАНОВКА ЗАДАЧИ
Минимизируемая геометрия белка будет представляться координатами его атомов. Для каждой из двадцати видов аминокислот, используемых при построении белков в живой природе, можно определить конкретное целое число атомов, в нее входящих. В среднем это число будет составлять около двух десятков. Каждый атом, в свою очередь, имеет три пространственные координаты $\{ {{x}_{k}},{{y}_{k}},{{z}_{k}}\} $. Далее мы будем работать в этом координатном пространстве. Обозначим через $n\;(n \sim {{10}^{4}})$ размерность этого пространства. Отметим, что в литературе часто работают и в другом пространстве: в пространстве углов и расстояний между соседними атомами(см., например, [6], [1]).
Центральное место в задаче минимизации потенциальной энергии молекулярного комплекса, разумеется, занимает приближение межатомных взаимодействий с помощью классических потенциальных сил. Различные функциональные формы, а также используемые в данных формулах коэффициенты принято называть силовыми полями [26]. Получение таких полей – тяжелая и кропотливая работа, включающая в себя многократную постановку сложных физических экспериментов и проведение квантово-механических вычислений. В связи с этим коэффициенты силовых полей могут разниться и с разным качеством описывать различные виды молекулярных систем. Тем не менее для белков, ввиду малого количества видов аминокислот (по сравнению с общим пространством допустимых органических соединений), применимы многие из этих полей: AMBER [2], CHARMM36 [7], OPLS [19] и другие.
Поле OPLS, особенно в последних редакциях, отлично зарекомендовало себя в точных оценках потенциальной энергии [31], в связи с чем именно оно было выбрано в качестве основной рабочей модели. Разберем его устройство.
В состав поля OPLS входят два вида основных взаимодействий: энергия связей и энергия несвязанных атомов. Первый вид энергетической функции рассматривает каждую связь между парой атомов как некоторый протяженный трехмерный объект, способный растягиваться (stretch), гнуться (bend) и скручиваться (torsion). Каждый из видов деформации приводит к изменению потенциальной энергии связей в соответствии с законами упругой деформации.
Так, энергию растяжения можно получить, просуммировав потенциальную энергию по всем парам связанных атомов(bonds):
Текущая длина связи представлена через $r$ и может быть легко вычислена путем вычитания координат и взятия нормы вектора. Помимо этого параметра, в данной формуле присутствуют два коэффициента: $K$ (коэффициент растяжения связи) и ${{r}_{0}}$ (равновесная длина связи). Коэффициенты являются табличными константами, определенными для каждой пары атомов, в соответствии с их типом [19].
Аналогично, используя коэффициент изгиба ${{K}_{\theta }}$ и равновесный угол ${{\theta }_{0}}$, можно ввести энергию изгиба, пользуясь всеми тройками последовательно связанных атомов:
Потенциальная энергия кручения определяется при помощи двугранного угла $\varphi $ между плоскостями, определяемыми осью вращения и двумя атомами на концах связи с разных сторон. Каждая из плоскостей задается прямой (осью вращения) и точкой (одним из краевых атомов связи). Так как кручение связи имеет периодический характер, то и энергия также будет описываться некоторым периодическим законом. В поле OPLS все четверки последовательно связанных атомов образуют последний компонент связанной энергии следующим образом:
Для вычисления потребуется 4 табличных параметра: ${{V}_{1}}$, ${{V}_{2}}$, ${{V}_{3}}$, ${{V}_{4}}$.
Помимо этой энергии, все пары атомов взаимодействуют благодаря электростатическим силам, действующим вне зависимости от наличия связи. Такие силы имеют две основные составляющие: кулоновские и силы Ван-дер-Ваальса, включающие в себя три вида слабых электромагнитных взаимодействий. Закон Кулона в хорошо известной форме учитывается в силовом поле OPLS:
Силы Ван-дер-Ваальса возникают вследствие поляризации атомов в присутствии друг друга и описываются известным потенциалом Леннарда–Джонса (потенциал 6–12), который задает экспоненциальное отталкивание на расстояниях, меньше радиуса атома, и притяжение – на расстояниях больше. Коэффициентами функции являются радиус ван-дер-ваальса атома $\sigma $ и глубина потенциальной ямы $\varepsilon $, а параметром – расстояние между атомами:
Задача минимизации потенциала полной модели силового поля OPLS окончательно будет выглядеть следующим образом:
Заметим, что набор переменных, по которым происходит оптимизация $\{ r\} $, $\{ \theta \} $, $\{ \phi \} $, однозначно определяется положениями атомов $\{ {{x}_{k}},{{y}_{k}},{{z}_{k}}\} $. Как уже отмечалось, именно в пространстве $\{ {{x}_{k}},{{y}_{k}},{{z}_{k}}\} $ далее будет решаться задача
Отметим также, что значения коэффициентов определяются структурой рассматриваемой макромолекулы, и на данный момент неизвестны какие-то красивые (компактные) способы их задания, кроме как табличным образом [19].
Для всех описанных выше функций ${{E}_{{{\text{bonds}}}}}$, ${{E}_{{{\text{bend}}}}}$, ${{E}_{{{\text{dihedrals}}}}}$ можно посчитать значение функции и градиента за $O(n)$ арифметических операций, а для ${{E}_{{{\text{cul}}}}}$, ${{E}_{{{\text{vdw}}}}}$ – за $O({{n}^{2}})$. При этом результат о сложности вычисления градиента можно получить с помощью автоматического дифференцирования [24]. Однако в данном случае лучше выписать явные формулы для расчета градиента, не требующие выгрузки в (оперативную) память дерева вычислений.
Важно отметить, что рассматривая белки в прикладных задачах, мы всегда подразумеваем наличие некоторой внешней среды, в которой они присутствуют. Обычно эта среда представляет из себя раствор электролитов, то есть молекулы воды с ионами тех или иных солей. Представлять подобный раствор можно множеством молекул, взаимодействующих с белком по тем же законам. Однако такое представление оказывается вычислительно сложным и излишним в задаче минимизации энергии белка, так что вместо явного представления растворителя можно обратиться к приближению непрерывной среды. Данное приближение дает возможность пользоваться некоторым потенциалом ${{E}_{{{\text{solvation}}}}}$, действующим между растворителем и атомами рассматриваемых макромолекул. Можно выписать расчетные формулы для ${{E}_{{{\text{solvation}}}}}$ [29], однако они достаточно громоздки, и могут быть информативными только для специалистов, поэтому здесь их не приводим. Далее будет важно только то, что функция ${{E}_{{{\text{solvation}}}}}$ локально достаточно гладкая (можно посчитать градиент), а сложность вычисления функции и ее градиента равна $O({{n}^{2}})$, что соответствует (по порядку) сложности вычисления всем остальным слагаемым. В ряде экспериментов вычисления проводились без этого слагаемого.
Задача, которую необходимо решать, может быть сформулирована следующим образом: найти в введенном координатном пространстве такую конфигурацию, которая бы минимизировала функцию $E$, если известно достаточно хорошее начальное приближение. Именно последнее предположение отличает эту статью от подавляющего большинства других работ, посвященных белковому фолдингу (см., например, [39]).
Подчеркнем, что не требуется искать глобальный минимум, как было сказано ранее, это будет неверно с физической точки зрения. Нашей же задачей станет поиск именно локального минимума, в который можно попасть из рассматриваемой точки старта. Отметим при этом, что используя различные обобщения конструкции работы [33] (например, Monotonic Basin Hopping – MBH [42]), можно пытаться строить на базе описываемых далее локально сходящихся методов, а новые методы, которые находят более глубокий минимум. Однако стоит отметить, что в подавляющем числе проведенных экспериментов не удалось сколько-нибудь существенно (больше, чем на 10% от абсолютного значения функционала в найденном локальном минимуме) улучшать найденный локальный минимум. При этом процедура MBH запускалась на GPU на 24 ч, в то время как локальная минимизация работала десятки секунд.
3. ОБСУЖДЕНИЕ ВОЗМОЖНЫХ ПОДХОДОВ К ЧИСЛЕННОМУ РЕШЕНИЮ ЗАДАЧИ
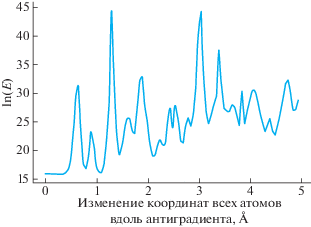
Прежде всего заметим, что рассматриваемая задача является существенно невыпуклой, особенно в окрестности начальной конфигурации. Типично, что при задании начальной конфигурации (позы) некоторые атомы оказываются неправдоподобно близко к друг другу, что приводит к огромным значениям начальной энергии ($ \sim {\kern 1pt} {{10}^{8}}$ кДж/моль вместо $ \sim {\kern 1pt} - {\kern 1pt} {{10}^{4}}$ кДж/моль в минимуме). Приведем один характерный пример. Если зафиксировать единичный вектор, направленный вдоль антиградиента функции $E$, вычисленного в начальный момент, и двигаться вдоль этого направления, то можно наблюдать следующее поведение энергии $E$ (см. фиг. 1).
Более того, из структуры оптимизируемого функционала и фиг. 1 понятно также, что оптимизируемый функционал может рассматриваться как гладкий только локально. Константа Липшица (и, тем более, константа Липшица градиента) не является равномерно ограниченной в достаточно большой, но ограниченной окрестности точки старта. Но в таком случае для минимизации такого функционала нельзя использовать градиентные методы – нет гарантий даже локальной сходимости [15], [23].
Для решения таких задач глобальной оптимизации теория рекомендует использовать безградиентные методы типа simulated annealing или марковского поиска [37], [36]. Ниже описывается подход, который был выбран изначально для решения задачи в отсутствие возможности использовать распараллеливание на GPU, но в условиях возможности использовать распараллеливание на CPU. Также предполагалось отсутствие составляющей ${{E}_{{{\text{solvation}}}}}$ в $E$. В качестве языка программирования для реализации описываемого далее (безградиентного) метода использовался (интерпретируемый) язык Python 3.
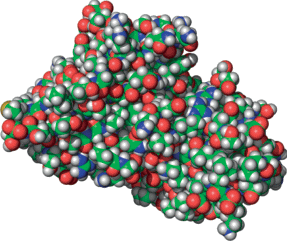
В основе предлагаемого подхода – “шевеление” на каждой итерации только одного (случайно выбранного) атома при “замороженных” остальных. Заметим, что при изменении положения одного атома пересчет ${{E}_{{{\text{stretch}}}}}$, ${{E}_{{{\text{bend}}}}}$, ${{E}_{{{\text{torsion}}}}}$ потребует $O\left( 1 \right)$ операций, поскольку затрагивает только “соседние” по химическим связям атомы (“соседние” взяты в кавычки, потому что речь идет не только о непосредственных соседях, но и о соседях через две и даже три химические связи). Обычно число таких “соседей” не больше 15. Для приближенного пересчета ${{E}_{{{\text{vdw}}}}}$ можно использовать специальные структуры данных типа Kd Tree [8], которые имеются, например, в библиотеке SciPy Python 3. Однако оптимально использовать в данном случае деревья диапазонов (Range Tree), описанные, например, в [8, гл. 5]. С помощью такой структуры данных первый пересчет ${{E}_{{{\text{vdw}}}}}$ будет занимать $O(l{{n}^{2}}n)$ операций – это время уходит на поиск ближайших пространственных соседей рассматриваемого атома. Последующие пересчеты ${{E}_{{{\text{vdw}}}}}$ при изменении положения того же атома будут занимать $O(1)$ операций. К сожалению, для небольших белков описанный способ пересчета ${{E}_{{{\text{vdw}}}}}$ не дает на практике ускорения по сравнению с явным пересчетом. Связано это с тем, что в число пространственных соседей, которых надо учитывать, для рассматриваемого атома попадают обычно десятки (а иногда и сотни) других атомов (см. фиг. 2), иначе точность аппроксимации будет недостаточной. Еще сложнее дело обстоит с ${{E}_{{{\text{cul}}}}}$.
Численные эксперименты убедительно свидетельствовали о том, что для пересчета значений ${{E}_{{{\text{cul}}}}}$ необходимо учитывать все слагаемые в сумме, которые связаны с рассматриваемым атомом. Действительно, относительный вклад в потенциал неучтенных частей ${{E}_{{{\text{vdw}}}}}$ для шара радиуса 7 A (радиус атома водорода 1 А – один ангстрем) с центром в данном атоме составляет $ \sim {\kern 1pt} {{10}^{{ - 5}}}$. Другое дело для электростатической составляющей ${{E}_{{{\text{cul}}}}}$ – для этого же шара относительный вклад будет $ \sim {\kern 1pt} {{10}^{{ - 3}}}$, что уже сопоставимо с возможной энергетической выгодой, которая получается при шевелении атома. Иначе говоря, нельзя не учитывать в электростатическом потенциале слагаемые вне шара! Поскольку всего таких слагаемых $O(n)$, то получается, что сложность пересчета ${{E}_{{{\text{cul}}}}}$ будет $O(n)$, что на два порядка больше, чем по остальным компонентам энергии. Далее излагается оригинальная конструкция, позволяющая получить амортизационную сложность пересчета ${{E}_{{{\text{cul}}}}}$ порядка $O(1)$.
Прежде всего, заметим, что на одной итерации необходимо посчитать (точнее, пересчитать) значение полной энергии при изменении положения одного атома ни один раз, а много раз, чтобы определить наилучшее положение этого атома при фиксированных положениях всех остальных атомов. Выберем число таких пересчетов порядка $n$. Покажем, как можно осуществить все эти $n$ пересчетов за время $O(n)$. Пусть на рассматриваемой итерации был выбран атом с номером $i$. Обозначим приращения положения этого атома через $\{ \delta _{i}^{x},\delta _{i}^{y},\delta _{i}^{z}\} $. Тогда за время $O(l{{n}^{2}}n)$ (см. выше) сумму ${{E}_{{{\text{cul}}}}}$ можно разбить на две неравнозначные составляющие. Первая составляющая ($O(1)$ слагаемых) будет содержать сумму по ближайшим пространственным соседям атома $i$, а вторая сумма будет содержать все, что не вошло в первую ($O\left( n \right)$ слагаемых). Вторую сумму с хорошей точностью можно заменить рядом Тейлора по $\{ \delta _{i}^{x},\delta _{i}^{y},\delta _{i}^{z}\} $ с членами до первого порядка включительно. Несложно понять, что вторая сумма есть просто линейная форма ${{C}_{x}}\delta _{i}^{x} + {{C}_{y}}\delta _{i}^{y} + {{C}_{z}}\delta _{i}^{z}$, коэффициенты которой $\left\{ {{{C}_{x}},{{C}_{y}},{{C}_{z}}} \right\}$ достаточно посчитать один раз (это можно сделать за $O(n)$ операций). Таким образом, чтобы посчитать значение $E_{{{\text{cul}}}}^{i}\left( {\delta _{i}^{x},\delta _{i}^{y},\delta _{i}^{z}} \right)$ (изменение энергии ${{E}_{{{\text{cul}}}}}$, возникшее вследствие шевеления атома $i$ на $\delta _{i}^{x},\delta _{i}^{y},\delta _{i}^{z}$) один раз нужно время $O\left( n \right)$, но чтобы посчитать $E_{{{\text{cul}}}}^{i}\left( {\delta _{i}^{x},\delta _{i}^{y},\delta _{i}^{z}} \right)$ порядка $n$ раз также нужно время $O(n)$. Получается, что среднее время на один расчет будет $O(1)$. Таким образом, пересчитать полную энергию порядка $n$ раз при изменении положения одного атома (случайно выбранного на данной итерации) можно за время $O(n)$. Это и будет стоимостью итерации, на которой приближенно ищется оптимальное положение случайно выбранного атома. Ясно, что число таких итераций (ввиду их “дешевизны”) можно сделать очень большим. Более того, если в рассматриваемой “эпохе” случайно “нарезать” исходную молекулу на приблизительно одинаковые части и выбирать независимо в каждой части атомы для шевеления (вдали от границ), то можно организовать параллельный запуск описанного выше метода. В конце каждой эпохи все части снова собираются вместе, и происходит новое (случайное и независимое) нарезание на части, начинается новая эпоха … Отметим, что для осуществления такого подхода весьма существенно, что атомы для шевеления выбираются случайно. Впрочем, немного более громоздкие рассуждения, возможно, позволят ускорить сходимость метода за счет выбора для шевеления не случайного атома, а атома, от шевеления которого может быть наибольший эффект – правило Гаусса–Саузвелла [10] (соответственно при параллельном подходе нужно будет выбирать такой атом среди атомов, принадлежащих рассматриваемой части). К сожалению, последнее (чувствительность к шевелению) можно определить лишь локально – по пересчету частных производных. Тем не менее подобно описанному выше пересчету значений функции можно показать, что с аналогичной сложностью можно пересчитывать и частные производные, поскольку пересчитывать их нужно будет только у “соседних” по химическим связям и пространству атомов. По-видимому, это общий факт, связанный с развитием идей автоматического дифференцирования [24]. Используя далее, скажем, бинарные “кучи” [17], можно поддерживать все время быстрый доступ к нужной для работы алгоритма максимальной компоненте градиента.
Описанный выше подход был реализован. К сожалению, для белков средних размеров (около 100 аминокислот) при приближении к локальному минимуму было обнаружено, что подход перестает работать заметно, не доходя до минимума, метод перестает улучшать аккуратно посчитанное значение энергии. Разбор причин этого показал, что неточность аппроксимации рядом Тейлора даже при разбиении суммы ${{E}_{{{\text{cul}}}}}$ на две, более менее, одинаковые (по числу слагаемых) подсуммы имеет порядок относительной точности ${{10}^{{ - 4}}}$–${{10}^{{ - 3}}}$, т.е. сопоставимый с возможным энергетическим выигрышем, получаемым при шевелении выбранного атома. Можно использовать квадратичную аппроксимацию, но тогда препроцессинг (вычисление коэффициентов квадратичной формы) будет довольно затратный, что не дает выигрыша.
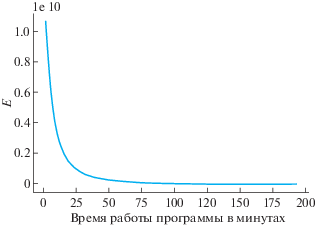
Последующие эксперименты показали, что нет необходимости пересчитывать значение энергии в $O\left( n \right)$ точках. Рассматривались следующие альтернативные стратегии: 1) выбрать случайно одну из координатных осей и посчитать значение энергии еще в двух точках на этой оси, по трем точкам построить параболу и сместить атом вдоль выбранной оси в точку минимума параболы (метод парабол); 2) аналогичный метод, но в 3D; 3) по значениям энергии в текущей точке и близкой к ней соседней точке можно оценить частную производную энергии по данной координате и далее использовать различные варианты рандомизированных покомпонентных спусков [9], [14], [35]. Эксперименты показали, что такое огрубление (неточный поиск положения атома, который был выбран для шевеления) принципиально не менят скорости сходимости. На фиг. 3 показана работа не параллельного варианта обычного покомпонентного метода с постоянным (предварительно подобранным) шагом [14] на современном ноутбуке (процессор 2.2 GHz; оперативная память 16 ГБ). Сделанное огрубление заметно уменьшает стоимость итерации, не сильно проигрывая в числе итераций. Итоговый общий выигрыш во времени работы обусловлен тем, что выписанные ранее оценки не учитывали числовые константы, которые в подходе с аппроксимацией ${{E}_{{{\text{cul}}}}}$ оказались достаточно большими.
Наблюдаемая в экспериментах хорошая работа покомпонентного типа методов наводит на мысль, что и полноградиентные методы также могут хорошо работать, несмотря на взрывные особенности функционала. Это, на самом деле, оказалось именно так. Обычный градиентный спуск в среднем за 400 итераций сходится к такому же по качеству (с точки зрения значения энергии) решению – см. фиг. 3, затрачивая на это приблизительно такое же время (5–10 ч).
На фиг. 4 и приведено сравнение времени работы безградиентного метода (варианта покомпонентного спуска) с градиентным спуском. Была выбрана конфигурация с изначально хорошим начальным условием (аналогичные результаты наблюдались и в общем случае). Представленный эксперимент проведен на стандартном ноутбуке (Intel Core i7-3630QM 2.40 GHz, 8GB) в стандартном режиме работы. Дополнительное отключение стандартных функций с целью повышения быстродействия и тюнинг операционной системы не проводились. Использовалась однопоточная реализация обоих методов на Python.
Фиг. 4.
Сравнение скорости сходимости безградиентного метода (шевеление случайного атома) с градиентным спуском.
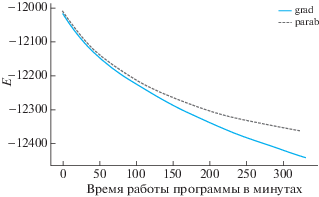
Метод, обозначенный на графике как “grad”, представляет собой реализацию градиентного спуска с адаптивным шагом.
В безградиентном методе, обозначенном как “parab”, случайным образом выбирается атом в молекуле (для шевеления) и вычисляет значение энергии при 7 различных положениях этого атома: начальное положение, и по две дополнительные позиции, симметрично расположенные относительно начального положения, вдоль каждой из трех координатных осей. По этим 7 точкам строится параболическая аппроксимация целевой функции (энергии) и вычисляется положение ее минимума. В итоге получается 8 точек, из которых выбирается та, которая доставляет минимальное значение целевой функции. Эта точка и принимается за новое положение системы атомов.
Безградиентные методы, связанные с шевелением случайно выбранного атома (и их различные модификации), могут быть распараллелены на CPU, но не более чем на несколько десятков процессоров (для белков стандартных размеров), потому что нельзя параллельно шевелить атомы, близкие к выбранному. Более того, процедура распараллеливания совсем нетривиальная. В итоге тут так и не удалось написать быстро работающую параллельную версию программы. При этом использовать в таком подходе всю мощь имеющихся GPU для ускорения расчетов по шевелению одного атома не представляет большого смысла, поскольку сложность каждого шевеления всего $O(n)$ операций. Совсем другое дело – распараллеливание вычислений ${{E}_{{{\text{vdw}}}}}$, ${{E}_{{{\text{cul}}}}}$ (и ${{E}_{{{\text{solvation}}}}}$, если учитывается) и их градиентов на GPU. Структура этих функционалов представляет собой выражение вида двойной суммы. Если задать диапазон суммирования в каждой из сумм по порядку равным числу ядер на видеокарте, то эффективный способ распараллеливания вычислений этих двойных сумм – по внешней сумме (использовалась видеокарта Tesla V100 c 5120 процессорами/ядрами (1.3 GHz) и общей оперативной памятью 32 ГБ). Именно, внешняя сумма представляет собой сумму $O\left( n \right)$ слагаемых, где каждое слагаемое в свою очередь представляет собой сумму $O\left( n \right)$ слагаемых. Каждую внутреннюю сумму вычисляет свой процессор (ядро) видеокарты.
Поскольку рассматриваемая задача является существенно невыпуклой задачей оптимизации, то можно лишь надеяться на локальную сходимость алгоритмов. Как известно, для достаточно гладких задач (не наш случай) обычный градиентный спуск будет сходиться к локальному экстремуму таким образом, что норма градиента после $N$ итераций в общем случае будет убывать как $ \sim {{N}^{{ - 1/2}}}$. При этом в классе методов первого порядка эта оценка не улучшаема [21]. Кроме того, даже если использовать методы более высокого порядка, то рассчитывать на сходимость более быструю, чем $ \sim {{N}^{{ - 1}}}$ не приходится [20]. Заметим, что обычный градиентный спуск может “застрять” в седловой точке [22], т.е. не в локальном минимуме. Тем не менее недавно было показано, что “типично” градиентный спуск сходится именно к локальному минимуму [12], [16]. Все эти результаты, однако, мало помогают в поиске наилучшего метода среди методов градиентного типа. Как показали численные эксперименты, приведенные выше оценки локальной сходимости менее информативны (полезны), чем оценки глобальной сходимости методов в выпуклом случае. Дело в том, что (типично) в некоторой окрестности (локального) минимума можно рассчитывать на то, что поведение оптимизируемой функции с хорошей точностью соответствует поведению выпуклой функции. И хотя для рассматриваемой в данной статье задачи априорно это совсем не очевидно, тем не менее, в экспериментах локально выпуклое поведение вполне подтверждалось.
Опыт использования градиентных методов для решения существенно невыпуклых задач обучения глубоких нейронных сетей [38] подсказывает, что если в экспериментах градиентные спуски неплохо работают, то можно попробовать использовать и ускоренные (быстрые/моментные) варианты градиентных спусков (см. п. 4). Более того, для специальных вариантов (универсальных – самонастраивающихся и на гладкость задачи и на ее выпуклость) ускоренных методов было доказано, что для невыпуклых задач они сходятся не хуже обычных градиентных методов, а в случае наличия локальной выпуклой структуры могут ускоряться, как это имеет место в глобально выпуклом случае [3], [15], [27]. Стоит также отметить, что ранее варианты ускоренных методов (методы типа сопряженных градиентов) уже применялись для минимизации похожих потенциалов [33]. В частности, в пакете инструментов для молекулярного моделирования Schrödinger [28] используется один из таких методов – метод Полака–Рибьера–Поляка, см. разд. 4.
Численные эксперименты по сравнению ускоренных и обычных градиентных методов для рассматриваемого класса задач невыпуклой оптимизации показали (см. полную версию статьи [5]), что ускоренные методы в целом сходятся немного быстрее. Как правило, после 300–400 итераций значение целевой функции практически уже перестает изменяться.
4. УСКОРЕННЫЕ ГРАДИЕНТНЫЕ МЕТОДЫ, МЕТОДЫ СОПРЯЖЕННЫХ ГРАДИЕНТОВ, КВАЗИНЬЮТОНОВСКИЕ МЕТОДЫ
Рассматривается общая задача безусловной выпуклой оптимизации [13]
Через ${{x}^{0}}$ обозначим точку старта. Через ${{x}_{*}}$ – решение задачи (1). Если решение задачи (1) не единственно, то под ${{x}_{*}}$ будем понимать такое решение задачи (1), которое наиболее близко к ${{x}_{0}}$ в норме с $R = {{\left\| {{{x}^{0}} - {{x}_{*}}} \right\|}_{2}}$. Будем также считать, что ${{\lambda }_{{max}}}\left( {{{\nabla }^{2}}f\left( x \right)} \right) \leqslant L$, ${{\lambda }_{{min}}}\left( {{{\nabla }^{2}}f\left( x \right)} \right) \geqslant \mu \geqslant 0$. Введем также число обусловленности $\chi = L{\text{/}}\mu $. Если $n$ достаточно большое, то самым простым численным методом решения задачи (1) будет градиентный спуск [22], [41]:
Метод (2) сходится следующим образом:
(3)
$f({{x}^{N}}) - f({{x}_{*}}) \leqslant \frac{{L{{R}^{2}}}}{2}min\left\{ {\frac{1}{N},exp\left( { - \frac{N}{\chi }} \right)} \right\}.$В общем случае для метода (2) в оценке (3) могут быть немного улучшены лишь числовые множители (перед $L$ и $\chi $).
На практике значение параметра $L$, которое нужно методу (2) для работы, как правило, не известно. К тому же, на самом деле, методу (2) и не требуется знание глобального значения этого параметра. Достаточно знать значение этого параметра на траектории метода. Возможным решением проблемы незнания $L$ является переход к методу наискорейшего спуска [41]:
(4)
$\begin{gathered} {{h}_{k}} \in \mathop {\arg \min }\limits_{h \geqslant 0} f({{x}^{k}} - h\nabla f({{x}^{k}})), \\ {{x}^{{k + 1}}} = {{x}^{k}} - {{h}_{k}}\nabla f({{x}^{k}}). \\ \end{gathered} $Переход к наискорейшему спуску принципиально не меняет оценку скорости сходимости (3).
В связи с написанным выше возникает вопрос, является ли градиентный спуск (наискорейший спуск) оптимальным методом (с точностью до числовых множителей) в классе методов вида
Ответ на этот вопрос отрицательный [40]. Оказывается, у градиентных (наискорейших) спусков есть различные ускоренные варианты. Поясним это на примере задачи квадратичной оптимизации.
Самой характерной задачей выпуклой оптимизации является задача минимизации положительно-определенной квадратичной формы:
Изучив данный класс задач, можно пытаться понять, как сходятся различные методы хотя бы локально (в окрестности минимума) в задачах выпуклой оптимизации. Кроме того, такие задачи возникают как вспомогательные подзадачи при использовании методов второго порядка (например, метода Ньютона). Известно, что для задачи выпуклой квадратичной оптимизации в оценке (5) достаточно использовать историю только с предыдущей итерации (оптимальный метод будет находиться в этом классе). Опишем его. Это метод сопряженных градиентов (первая итерация делается согласно (4)):
(6)
${{x}^{{k + 1}}} = {{x}^{k}} - {{\alpha }_{k}}\nabla f({{x}^{k}}) + {{\beta }_{k}}({{x}^{k}} - {{x}^{{k - 1}}}),$(7)
$f({{x}^{N}}) - f({{x}_{ * }}) \leqslant min\left\{ {\frac{{L{{R}^{2}}}}{{2\mathop {\left( {2N + 1} \right)}\nolimits^2 }},2L{{R}^{2}}\mathop {\left( {\frac{{\sqrt \chi - 1}}{{\sqrt \chi + 1}}} \right)}\nolimits^{2N} ,\mathop {\left( {\frac{{{{\lambda }_{{n - N + 1}}} - {{\lambda }_{1}}}}{{{{\lambda }_{{n - N + 1}}} + {{\lambda }_{1}}}}} \right)}\nolimits^2 {{R}^{2}}} \right\},$Заметим, что можно выписать явные формулы для коэффициентов ${{\alpha }_{k}}$, ${{\beta }_{k}}$. Однако на практике более распространены варианты методов сопряженных градиентов не со вспомогательной двумерной оптимизацией или с явно выписанными шагами, а со вспомогательной одномерной оптимизацией. Наиболее популярными вариантами метода сопряженных градиентов являются следующие два метода [24] (на наш взгляд исторически правильнее называть метод Полака–Рибьера методом Полака–Рибьера–Поляка):
Для задач квадратичной оптимизации оба метода эквивалентны между собой и эквивалентны методу (6). Для общих задач выпуклой оптимизации по этим методам не удалось пока получить оптимальные порядки скорости сходимости (установлен только сам факт глобальной сходимости для задач гладкой выпуклой оптимизации). Тем не менее именно эти два варианта метода сопряженных градиентов наиболее часто используются при решении практических задач [24] (в том числе не обязательно выпуклых). При этом с некоторой периодичностью (обычно период выбирают пропорционально размерности пространства, в котором происходит оптимизация) требуется перезапускать метод, обнуляя историю: вместо ${{p}^{{k + 1}}} = - \nabla f({{x}^{{k + 1}}}) + {{\beta }_{k}}{{p}^{k}}$ в момент рестарта полагают ${{p}^{{k + 1}}} = - \nabla f({{x}^{{k + 1}}})$. По-видимому, необходимость в таких рестартах обусловлена желанием “правильно сходиться” в случае оптимизации сильно выпуклых функций [25].
Для общих (не квадратичных) задач безусловной гладкой выпуклой минимизации наиболее популярным сейчас является следующий (двухшаговый) вариант быстрого (ускоренного) градиентного метода (Нестерова):
который также можно понимать как моментный метод [30]:(8)
${{x}^{{k + 1}}} = {{x}^{k}} - \frac{1}{L}\nabla f\left( {{{x}^{k}} + \frac{{k - 1}}{{k + 2}}({{x}^{k}} - {{x}^{{k - 1}}})} \right) + \frac{{k - 1}}{{k + 2}}({{x}^{k}} - {{x}^{{k - 1}}}).$Приведем также вариант моментного метода для $\mu $-сильно выпуклой функции в введенной норме [22]:
(9)
${{x}^{{k + 1}}} = {{x}^{k}} - \frac{1}{L}\nabla f\left( {{{x}^{k}} + \frac{{\sqrt L - \sqrt \mu }}{{\sqrt L + \sqrt \mu }}({{x}^{k}} - {{x}^{{k - 1}}})} \right) + \frac{{\sqrt L - \sqrt \mu }}{{\sqrt L + \sqrt \mu }}({{x}^{k}} - {{x}^{{k - 1}}}).$Оба метода (8), (9) с точностью до числовых множителей сходятся согласно первому и второму аргументу в минимуме оценки (7). Более того, можно даже объединить оба метода (8), (9) в один, сходящийся по оценке, наилучшей из двух отмеченных оценок [22]. Однако все равно требуется априорно знать параметр $\mu $. На данный момент неизвестны такие варианты быстрых (ускоренных) градиентных методов для сильно выпуклых задач, которые бы в общем случае обходились без этого знания. Отметим при этом, что незнание параметра $L$ может быть устранено вспомогательной маломерной минимизацией.
Хорошо известна (см., например, [41]) геометрическая интерпретация градиентного спуска, в основу которой положена замена исходной функции параболоидом вращения, касающимся ее графика в текущей точке. Точка, доставляющая минимум параболоиду, принимается за новое положение метода. Идея метода наискорейшего спуска заключается в подборе кривизны параболоида с помощью решения вспомогательной задачи одномерной минимизации. В методе Ньютона вместо параболоида вращения строится квадратичная аппроксимация оптимизируемой функции (на основе доступного гессиана функции, вычисленного в текущей точке), однако это приводит к необходимости решения на каждом шаге более сложной задачи – минимизации квадратичной формы (обращения матрицы/решения системы линейных уравнений).
Естественно, возникает идея построения какого-то “промежуточного” метода, с одной стороны, не требующего вычисления (и, тем более, обращения) гессиана, а с другой стороны, все-таки пытающегося как-то аппроксимировать гессиан, исходя из накопленной информации первого порядка (градиентов). В основу квазиньютоновских методов положен следующий общий принцип построения квадратичной аппроксимации: квадратичная аппроксимация должна касаться графика оптимизируемой функции в текущей точке и иметь с ней одинаковые градиенты в точке с предыдущего шага (secant equation). Существует много различных способов удовлетворить этим условиям [24]. У этих способов есть различные интерпретации, среди которых отметим понимание квазиньютоновских методов как методов переменной метрики (вариант метода сопряженных градиентов [41]). Наиболее интересными в практическом плане являются способы, которые требуют не более чем квадратичной (по размерности пространства) трудоемкости и памяти. Среди таких способов наиболее удачно себя зарекомендовал способ, приводящий в итоге к методу BFGS (Broyden-Fletcher–Goldfarb–Shanno) [24]:
В отличие от сопряженных градиентов (6) в BFGS не обязательно точно осуществлять вспомогательную одномерную оптимизацию. В целом BFGS оказался наиболее устойчивым (к вычислительным погрешностям) вариантом квазиньютоновских методов. Геометрия квазиньютоновских методов близка (но не идентична!) геометрии субградиентных методов с процедурой растяжения пространства (метод эллипсоидов, методы Шора [41]) и связана с типичным “пилообразным” поведением градиентных спусков в окрестности минимума для плохо обусловленных задач. Направления ${{\gamma }_{k}}$ и ${{\delta }_{k}}$ “подсказывают” направления растяжение/сжатие и позволяют адаптивно улучшать обусловленность задачи, правильно аккумулируя собранную информацию в ${{H}_{k}}$.
В теоретическом плане по квазиньютоновским методам на данный момент известно не так уж и много [22], [24]: глобальная скорость сходимости для гладких задач выпуклой оптимизации в общем случае не выше, чему обычных (неускоренных) градиентных методов (во всяком случае, только это пока удалось установить), а локальная скорость сходимости в случае невырожденного минимума – сверхлинейная.
Основным ограничением по использованию квазиньютоновских методов является необходимость в хранении и обновлении плотной квадратной матрицы ${{H}_{k}}$, что требует (в отличие от того, что имеет место для методов типа сопряженных градиентов) квадратичной памяти и квадратичного времени независимо от разреженности задачи. Это обстоятельство существенно ограничивает возможности по использованию таких методов для задач оптимизации с десятками тысяч переменных и более. Однако на практике используют в основном варианты таких методов с ограниченной памятью, см., например, метод LBFGS [24]. В этом случае в памяти хранится не матрица ${{H}_{k}}$, а векторы, ее порождающие. Проблема, однако, тут в том, что с ростом $k$ размер этой памяти линейно растет. Поэтому обычно последовательности векторов $\left\{ {{{\gamma }_{t}}} \right\}$ и $\left\{ {{{\delta }_{t}}} \right\}$ хранят только с $m$ последних итераций ($m$ – глубина памяти), и при этом полагают ${{H}_{{k - m}}} = I$. На практике $m$ часто выбирают совсем небольшим $m \simeq 3{\kern 1pt} - {\kern 1pt} 5$.
5. ПРОГРАММНАЯ РЕАЛИЗАЦИЯ, РЕЗУЛЬТАТЫ ВЫЧИСЛИТЕЛЬНЫХ ЭКСПЕРИМЕНТОВ
5.1. Реализация методов оптимизации
Программная реализация представленных в работе методов градиентнго типа выполнена на языке C++11 с использованием технологии параллельного программирования Nvidia CUDA [34]. Возможность работы в режимах float / double (одинарная и двойная точности) реализована с применением механизма шаблонов C++ (C++ templates), что позволило получить унифицированный программный код, максимально эффективно использующий вычислительные возможности как центрального, так и графического процессоров. Реализованный программный код скомпонован в виде разделяемой библиотеки (shared library) с соответствующим C-API (Application Programming Interface, программный интерфейс приложения), обеспечивающим возможность интеграции с другими программными модулями.
Для тестирования были отобраны следующие методы: метод сопряженных градиентов Полака–Рибьера–Поляка (CG_PRP), быстрый градиентный метод (FGM) и LBFGS (с параметром/памятью 3). С практическими деталями реализации этих методов применительно к рассматриваемому в данной статье классу задач можно познакомиться в препринте [5].
5.2. Вычислительные эксперименты
Проверка описанных выше методов оптимизации производилась в контексте алгоритмов для решения задачи предсказания белок-белковых комплексов (белок-белковый докинг). Простыми словами, данная задача может быть описана следующим образом: для имеющейся пары молекул нужно определить наиболее вероятное взаимное расположение этих молекул при образовании молекулярного комплекса белок-белок. Задача считается успешно решенной, если на выходе имеется структура комплекса, которая соответствует встречаемому в природе комплексу или очень близка к этому положению. Задача белок-белкового докинга имеет большую значимость для решения прикладных задач, связанных с разработкой лекарственных средств, основанных на белковых молекулах, так как терапевтический эффект обусловлен связыванием терапевтического белка с мишенью, а это и есть белок-белковый комплекс. Также стоит отметить, что в рамках типичного проекта по разработке лекарственного препарата, основанного на антителах, эту задачу требуется решать сотни раз.
На промежуточных этапах решения задачи белок-белкового докинга могут быть найдены, и очень часто находятся, физически-невозможные структуры комплексов, в частности, структуры со столкнувшимися атомами. Такие ситуации возникают вследствие использования грубых метрик на начальных этапах с целью ускорения процесса сканирования большого пространства решений. Следствием этой проблемы является невозможность применения наиболее физически обоснованной метрики для финального ранжирования решений – потенциальной энергии белкового комплекса. Эта метрика является наиболее обоснованной, так как меньшему значению потенциальной энергии соответствует более энергетически выгодная молекулярная структура, отсюда следует, что минимуму (либо одному из возможных минимумов) потенциальной энергии соответствует структура, встречаемая в природе. Учитывая вышесказанное, минимизация энергии является одним из важнейших этапов решения задачи докинга, так как позволяет привести структуру комплекса в физически-оправданную конформацию, а значит, и позволяет использовать энергетические метрики в качестве метрик оценки решений, что, в свою очередь, существенно повышает точность предсказаний.
Для оценки методов минимизации был использован тестовый набор для оценки точности белок-белкового докинга. Этот набор состоит из белок-белковых комплексов с достоверно известной трехмерной структурой, встречаемой в природе (нативная структура), другими словами правильный ответ уже известен. Часть данных была получена из прошедших раундов соревнований по белок-белковому докингу CAPRI (Critical Assessment of PRedicted Interactions) [18] и из курируемого набора данных для белок-белкового докинга Protein-Protein Docking Becnchmark 5.0 [32]. Для каждого комплекса с помощью алгоритмов докинга, разработанных в компании БИОКАД, были сгенерированы 499 начальных приближений, отличающихся друг от друга расположением и поворотом в трехмерном пространстве одной из молекул. То есть одна из молекул комплекса оставалась неподвижной, изменялось же расположение только второй молекулы. Кроме того, было искусственно добавлено заведомо верное расположение молекул, соответствующее нативным структурам. Так как нативной структуре комплекса соответствует минимум потенциальной энергии (E), в данном эксперименте производились минимизация всех начальных приближений, сортировка по значению E и оценка порядкового номера нативной (или очень близкой к таковой) структуры. Если близкая к нативной структура присутствует в первых 30 результатах, задача считалась успешно решенной.
Приводимые ниже результаты численных экспериментов получены на вычислительной системе, имеющей следующие характеристики:
• Ubuntu server 16.04, ×86_64
• 2 × Intel Xeon E5-2687Wv3
• 4 × Nvidia Tesla K80
• Компилятор gcc 5.4.0 с параметрами:
–std=c++11-O2-Wall-Wextra-Wpedantic-Wdouble-promotion
-Wfloat-conversion-s-DNDEBUG
• CUDA-компилятор nvcc v9.0.176 с параметрами:
–std=c++11-O3-lineinfo-Xcompiler-Wno-attributes
-gencode arch=compute_37,code=sm_37-DNDEBUG
В качестве основного режима работы реализованных алгоритмов был выбран float (одинарная точность), что обусловлено как более высоким быстродействием современных GPU при работе с вещественными числами одинарной точности, так и тем, что для требуемых расчетов float-арифметика обеспечивает достаточную точность результатов.
5.3. Результаты вычислительных экспериментов
В табл. 2 и 3, приведенных в полной версии данной статьи [5], представлены результаты вычислительных экспериментов, проведенных на тестовых данных белок-белкового докинга. Табл. 2 описывает наименьший порядковый номер (индекс) структуры, близкой к нативной, при сортировке результатов по значению потенциальной энергии. Чем меньше это число, тем точнее решена задача докинга в данном случае, при этом, если оно меньше 30, то задача считается успешно решенной. Также приведены средние значения наименьших индексов структур, близких к нативным, по которым можно судить о среднем качестве работы метода на всем тестовом наборе. Для определения близости к нативной структуре была использована метрика RMSD (Root-mean-square deviation), которая является стандартной для измерения расстояния между подобными молекулярными структурами:
Таблица 1.
Сравнение характеристик методов
| Показатели | “Шевеление” атома | Адаптивный градиентный спуск |
|---|---|---|
| Время 1 итерации, секунды | 1.2075 | 122.9814 |
| Энергия 1 итерации, кДж/моль | 0.0225 | 2.7081 |
| $ \sim \Delta $Энергии к 300 минуте, кДж/моль | $ - 347$ | $ - 413$ |
Общее время вычислительного эксперимента для трех методов занимало порядка недели в режиме параллельной работы на 4-х Nvidia Tesla K80 GPU, полная конфигурация сервера описана выше. Общее количество минимизированных структур за один эксперимент составляет 91 500: :500 начальных приближений для каждого из 61 комплекса тремя различными методами. Реальное время работы алгоритмов особенно важно, поскольку минимизация является наиболее вычислительно массивным этапом белок-белкового докинга, а в типичном процессе разработки лекарственного препарата задачу докинга, как уже упоминалось, нужно решать сотни раз. Текущая реализация позволяет произвести минимизацию 500 начальных приближений менее, чем за час на 4-х Nvidia Tesla K80 GPU, что является приемлемым временем работы.
На основании средних значений наименьших индексов структур, близких к нативным, из табл. 2 можно видеть, что методы FGM и CG_PRP показывают результаты лучше, нежели LBFGS. Тем не менее тестовый набор данных недостаточно велик для окончательного выбора одного метода. В табл. 3 можно видеть много случаев, в которых метод LBFGS показывает лучшие результаты с точки зрения абсолютного значения потенциальной энергии, тем не менее, с точки зрения решения практической задачи, решаемой в этом эксперименте, метод LBFGS ощутимо проигрывает.
Авторы выражают благодарность А.И. Голикову и Ю.Г. Етвушенко за ряд ценных замечаний, позволивших улучшить изначальный текст работы.
Список литературы
A kinematic view of loop closure / E.A. Coutsias [et al.] // J. of Computational Chemistry. 2004. V. 25. № 4. P. 510–528.
A Second Generation Force Field for the Simulation of Proteins, Nucleic Acids, and Organic Molecules / W.D. Cornell [et al.] // J. of the American Chemical Society. 1995. V. 117. № 19. P. 5179–5197.
A universal modification of the linear coupling method / S. Guminov [et al.] // Optimization Methods and Software. 2019. V. 34. № 3. P. 560–577.
Accelerate: An embedded language for accelerated array processing / M.M.T. Chakravarty [et al.]. URL: http://hackage.haskell.org/package/accelerate.
Algorithms for local minimization of 3D molecules OPLS force field / P. Yakovlev [et al.]. 2018. arXiv: 1810.03358.
Canutescu A.A., Dunbrack R.L. Cyclic coordinate descent: A robotics algorithm for protein loop closure // Protein science. 2003. V. 12. № 5. P. 963–972.
CHARMM36m: an improved force field for folded and intrinsically disordered proteins / J. Huang [et al.] // Nature Methods. 2017. V. 14. P. 71–73.
Computational geometry / M. De Berg [et al.] // Comput. geometry. Springer, 2000. P. 1–17.
Conn A.R., Scheinberg K., Vicente L.N. Introduction to derivative-free optimization. Siam, 2009. 295 p.
Coordinate descent converges faster with the Gauss-Southwell rule than random selection / J. Nutini [et al.] // Internat. Conference on Machine Learning. 2015. P. 1632–1641.
CUDA: Parallel computing platform and programming model developed by NVIDIA. URL: https://developer.nvidia.com/cuda-zone.
First-order Methods Almost Always Avoid Saddle Points / J.D. Lee [et al.]. 2017. arXiv: 1710.07406.
Gasnikov A. Universal gradient descent. 2017. arXiv: 1711.00394.
Ghadimi S., Lan G. Stochastic first-and zeroth-order methods for nonconvex stochastic programming // SIAM Journal on Optimization. 2013. V. 23. № 4. P. 2341–2368.
Ghadimi S., Lan G., Zhang H. Generalized uniformly optimal methods for nonlinear programming. 2015. arXiv: 1508.07384.
Gradient descent only converges to minimizers / J.D. Lee [et al.] // Conference on Learning Theory. 2016. P. 1246–1257.
Introduction to algorithms / T.H. Cormen [et al.]. 2nd ed. The MIT Press, 2001. 1180 p.
Janin J. Welcome to CAPRI: a critical assessment of predicted interactions // Proteins: Structure, Function, and Bioinformatics. 2002. V. 47. № 3. P. 257.
Jorgensen W.L., Maxwell D.S., Tirado-Rives J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids // J. of the American Chemical Society. 1996. V. 118. № 45. P. 11225–11236.
Lower Bounds for Finding Stationary Points I / Y. Carmon [et al.]. 2017. arXiv: 1710.11606.
Lower Bounds for Finding Stationary Points II: First-Order Methods / Y. Carmon [et al.]. 2017. arXiv: 1711.00841.
Nesterov Y. Introductory lectures on convex optimization: A basic course. Springer Science & Business Media, 2013. 236 p.
Nesterov Y., Spokoiny V. Random gradient-free minimization of convex functions // Foundat. of Comput. Math. 2017. V. 17. № 2. P. 527–566.
Nocedal J., Wright S.J. Numerical Optimization. 2nd ed. New York : Springer, 2006. 664 p. (Springer series in operations research).
O’Donoghue B., Candes E. Adaptive restart for accelerated gradient schemes // Foundations of computational mathematics. 2015. V. 15. № 3. P. 715–732.
Ponder J.W., Case D.A. Force fields for protein simulations // Advances in protein chemistry. 2003. V. 66. P. 27–85.
Primal-dual accelerated gradient descent with line search for convex and nonconvex optimization problems / Y. Nesterov [et al.]. 2018. arXiv: 1809.05895.
Protein and ligand preparation: parameters, protocols, and inuence on virtual screening enrichments / G.M. Sastry [et al.] // J. of computer-aided molecular design. 2013. V. 27. № 3. P. 221–234.
Semianalytical treatment of solvation for molecular mechanics and dynamics / W.C. Still [et al.] // J. of the American Chemical Society. 1990. V. 112. № 16. P. 6127–6129.
Su W., Boyd S., Candes E. A differential equation for modeling Nesterov’s accelerated gradient method: Theory and insights // Advances in Neural Information Processing Systems. 2014. P. 2510–2518.
Sweere A.J.M., Fraaije J.G.E.M. Accuracy Test of the OPLS-AA Force Field for Calculating Free Energies of Mixing and Comparison with PAC-MAC // J. of Chemical Theory and Computation. 2017. V. 13. № 5. P. 1911–1923.
Updates to the integrated protein–protein interaction benchmarks: docking benchmark version 5 and afinity benchmark version 2 / T. Vreven [et al.] // J. of molecular biology. 2015. V. 427. № 19. P. 3031–3041.
Wales D.J., Doye J.P. Global optimization by basin-hopping and the lowest energy structures of Lennard-Jones clusters containing up to 110 atoms // J. of Physical Chemistry A. 1997. V. 101. № 28. P. 5111–5116.
Wilt N. The CUDA Handbook: A Comprehensive Guide to GPU Programming. Pearson Education, 2013. 528 p.
Wright S.J. Coordinate descent algorithms // Math. Program. 2015. V. 151. № 1. P. 3–34.
Zhigljavsky A.A. Theory of global random search. Springer Science & Business Media, 2012. 341 p.
Zhigljavsky A., Zilinskas A. Stochastic global optimization. Springer Science & Business Media, 2008. 262 p.
Гудфеллоу Я., Иошуф Б., Курвилль А. Глубокое обучение. М.: ДМК Пресс, 2017. 652 с.
Жмуров А.А., Барсегов В.А. Моделирование биологических систем на GPU. М.: МФТИ, 2013.
Немировский А.С., Юдин Д.Б. Сложность задач и эффективность методов оптимизации. М.: Наука, 1979. 334 с.
Поляк Б.Т. Введение в оптимизацию. М.: Наука, 1983. 384 с.
Посыпкин М.А. Методы и распределенная программная инфраструктура для численного решения задачи поиска молекулярных кластеров с минимальной энергией // Вест. нижегородского ун-та им. Н.И. Лобачевского. 2010. № 1. С. 210–219.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики