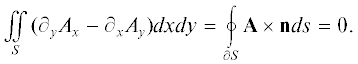Журнал вычислительной математики и математической физики, 2019, T. 59, № 2, стр. 342-354

1. ВВЕДЕНИЕ

Согласно теореме А.Н. Тихонова и А.А. Самарского [1], [2] электромагнитное поле E и H в полом волноводе постоянного сечения $S$ может быть представлено при помощи двух скалярных функций потенциалов. Такая декомпозиция электромагнитного поля оказывается возможной благодаря цилиндрической геометрии волновода, позволяющей применять теорию функций Боргниса [2], [3]. Важнейшим следствием теоремы Тихонова и Самарского является утверждение о полноте системы нормальных волн полого волновода, согласно которому любая волна, распространяющаяся в волноводе, представима как суперпозиция ТЕ и ТМ волн (см. [2], [4]).

В 1990-х годах это следствие, чрезвычайно важное для обоснования парциальных условий излучения и неполного метода Галеркина (см. [2], [5]), было обобщено на случай волновода, заполнение которого меняется на сечении, но не меняется вдоль оси волновода (см. [6]–[13]). При этом теорема о представлении поля при помощи потенциалов оказалась в тени своего следствия.

Это обстоятельство принципиально отличает вычислительную сложность спектральных задачи для полых волноводов и для волноводов, заполненных неоднородным веществом. В первом случае задачи получаются скалярными и к ним применимы хорошо разработанные методы, пригодные в равной мере и для задач акустики, и для задач квантовой механики. В случае же волновода, заполненного неоднородным веществом, приходится численно решать задачи в полной векторной постановке. Эти задачи имеют нулевое собственное значение бесконечной кратности и поэтому для их численного решения приходится прибегать к нетривиальным и трудным для компьютерной реализации приемам, например, к методу смешанных конечных элементов (см. [14]–[16]).

Следует также заметить, что для задач радиофизики наиболее интересен случай кусочно постоянного заполнения, поскольку на практике создать волновод с непрерывно меняющимся заполнением возможно только путем помещения в него слоями веществ с различными, но близкими значениями $\varepsilon $ и $\mu $. На стыках областей, заполненных различными веществами, поперечные компоненты векторных полей E и H терпят разрывы, что вносит дополнительные трудности при аппроксимации их непрерывными конечными элементами.

В настоящей статье мы хотим вернуться к задаче о представлении произвольного электромагнитного поля в волноводе с кусочно-непрерывным заполнением в ее классической постановке. Обычно, как в случае полого волновода, при введении потенциалов удается проинтегрировать часть уравнений Максвелла и уменьшить число искомых функций. Хорошо известно, что в случае волновода, заполненного неоднородным веществом, сделать это не удается. Однако мы полагаем, что главная польза от введения потенциалов должна состоять в переходе от разрывных компонент поля к непрерывным потенциалам. С этой точки зрения на введение потенциалов можно смотреть как на замену переменных, при которой от разрывных функций переходят к непрерывным.

Если направить ось $Oz$ декартовой системы координат по оси волновода и принять для краткости, что

и связь между полями и потенциалами дается формулами Каждая из этих формул представляет собой двумерный аналог декомпозиции Гельмгольца, хорошо известной в теории упругости [17]. В электродинамике для поля $\mathop {\mathbf{H}}\nolimits_ \bot $ такие потенциалы возникали при доказательстве полноты системы нормальных мод в качестве вспомогательной конструкции [11], [12]. Все четыре потенциала были введены в наших работах [18]–[20] для гладкого заполнения без коэффициентов $\tfrac{1}{\varepsilon }$ и $\tfrac{1}{\mu }$, важных только для разрывного случая. Основной результат настоящей статьи заключен в теореме 3, согласно которой любое поле в волноводе представимо при помощи этих потенциалов.

Замечание. Сама идея разделить два действия – введение потенциалов и интегрирование уравнений взята из классической механики. Как известно, в конце XIX века было потрачено много усилий на доказательство теорем Вейерштрасса о задаче трех тел и лишь в 1960-х годах Бурде случайно нашел элементарное их доказательство [21]. Как оказалось, затруднение проистекало от того, что Зундман искал регуляризующее преобразование среди канонических преобразований, а для доказательства названных теорем следовало пожертвовать гамильтоновстью этих уравнений и к тому же повысить их порядок.

2. ПОЛЕ В ЗАКРЫТОМ ВОЛНОВОДЕ

Предметом изучения в этой статье будет закрытый волновод постоянного сечения $S$ с кусочно-непрерывным заполнением $\varepsilon $ и $\mu $, не меняющимся вдоль оси волновода. Ось волновода примем за ось $Oz$. Понятие кусочной непрерывности требует некоторого уточнения.

Пусть $S$ – область на плоскости $xy$, граница которой не уходит на бесконечность и пусть линия $\Gamma $ делит ее на несколько частей ${{S}_{1}},\; \ldots \;{{S}_{K}}$, границы которых состоят из достаточно гладких дуг, чтобы можно было применять теорему Грина. Мы допускаем, что линия $\partial S \cup \Gamma $ имеет конечное число углов и самопересечений, прочие точки линии $\partial S \cup \Gamma $ будем называть регулярными точками.

Под кусочно-постоянной функцией с линией разрывов $\Gamma $ будем понимать функцию, определенную во всех частях ${{S}_{1}},\; \ldots \;{{S}_{K}}$ и не меняющую своего значения внутри каждой из этих областей. Под кусочно-непрерывной функцией будем понимать функцию, не только определенную и непрерывную во всех частях ${{S}_{1}},\; \ldots \;{{S}_{K}}$, но и допускающую доопределение по непрерывности в замыкании каждой из этих областей. Таким образом, кусочно-непрерывная функция $f$ определена во всех точках множества $\overline S $, за исключением точек линии разрыва $\Gamma $. Достаточно малую окрестность регулярной точки $p$ линии разрыва сама эта линии делит на две части, в каждой из которых $f(p)$ можно доопределить по непрерывности, однако, эти значения могут не совпадать на линии $\Gamma $, разность двух так определенных значений функции $f$ в точке $p$ будем называть скачком $f$ и обозначать как $[f]$. Кусочно-гладкой будем называть кусочно-непрерывную функцию, частные производные которой тоже являются кусочно-непрерывными функциями.

Пусть $z,t$ – еще две переменные, принимающие значения на некоторых отрезках вещественной оси, обозначим эти отрезки как $Z$ и $T$.

Определение 1. Пусть $\varepsilon ,\mu $ – кусочно-непрерывные функции на $S$, принимающее только положительные значения. Под электромагнитным полем в закрытом волноводе

с заполнением $\varepsilon ,\mu $ будем понимать векторные поля ${\mathbf{E}},{\mathbf{H}}$, компоненты которых определены на при условии, что сужение ${\mathbf{E}},\;{\mathbf{H}}$ и их частных производных по $z$ и $t$ на сечение $S$ при любых значениях $z$ и $t$ являются кусочно гладкими функциями, удовлетворяющими

1) уравнениям Максвелла

внутри волновода

2) условиям идеальной проводимости стенок волновода

в регулярных точках границы

3) условиями сопряжения

в регулярных точках границы разрыва заполнения

Замечание. Здесь и далее под ${\mathbf{n}}$ понимается единичная нормаль к соответствующей линии. Для определенности на границе волновода условимся брать внешнюю нормаль, а на границе двух областей ${{S}_{p}}$ и ${{S}_{q}}$ – внешнюю нормаль для области с меньшим номером.

Мы ни в коем случае не утверждаем, что система (2)–(4) выделяет единственное решение в рассматриваемом классе гладкости. Хорошо известно, что для выделения единственного решения нужно добавить еще дополнительные условия, например, условия излучения [2]. Однако вне зависимости от постановки задачи главная трудность, возникающая при численном решении, уже заложена в условиях (4): величины ${{E}_{z}}$ и ${{H}_{z}}$ непрерывны, а прочие компоненты этих векторных полей, напротив, разрывны. Это и создает основную проблему при численном решении уравнений Максвелла: хорошие базисные функции должны удовлетворять тем же условиям разрыва, а их очень сложно построить. Наша идея состоит в том, чтобы перейти к новым переменным, которые не терпят разрывов.

3. ПЕРЕХОД К НЕПРЕРЫВНЫМ ПЕРЕМЕННЫМ

Мы хотим выполнить переход к непрерывным переменным единообразно для всех полей в волноводе. В рамках общего подхода сразу бросается в глаза, что деление уравнений Максвелла на роторные и дивергентные естественно только для задач в трехмерных областях, как, например, задача о возбуждении поля токам в области $G \in {{\mathbb{R}}^{3}}$ с идеально проводящими стенками, изученная Вейлем и Мюллером [22]. В этой задаче противопоставление пространственных переменных $x,y,z$ и времени $t$ вполне следует геометрии задачи в $G \times T$. Для волноводных же задач, т.е. задач в $S \times Z \times T$, естественным будет противопоставление переменных $x,y$ и $z,t$. В этом случае координаты полей распадаются на две группы: четыре разрывные функции ${{E}_{x}},{{E}_{y}},{{H}_{x}},{{H}_{y}}$ и две непрерывные ${{E}_{z}},{{H}_{z}}$, а уравнения Максвелла естественно расщепляются на две системы: первая система

не содержит производных ${{H}_{z}},{{E}_{z}}$ по $x,y$, а вторая система не содержит производных ${{H}_{z}},{{E}_{z}}$ по $z,t$.

Мы хотим перейти от переменных ${{E}_{x}},{{E}_{y}},{{H}_{x}},{{H}_{y}}$ к четырем потенциалам, связанным с полями формулами (1).

Теорема 1. Пусть ${{E}_{z}},{{H}_{z}}$ – какие угодно непрерывные функции в волноводе $S \times Z \times T$, имеющие кусочно-непрерывные частные производные, причем ${{E}_{z}} = 0$ на границе волновода. Пусть потенциалы ${{u}_{e}}$ и ${{u}_{h}}$ являются классическими решениями задач Дирихле

иа потенциалы ${{v}_{e}}$ и ${{v}_{h}}$ – решениями задач НейманаиТогда поле, восстановленное по формулам (1), удовлетворяет первой подсистеме (5) уравнений Максвелла, граничным условиям (3) и условиям (4) на линии разрыва.

Замечание. Здесь и далее для оператора Лапласа ${\text{div}}(k\nabla u)$ используется обозначение ${{\Delta }_{k}}u$. Под решением краевой задачи

понимается элемент $u$ пространства Соболева $\mathop {W_{2}^{1}}\limits^0 (S)$, удовлетворяющий тождеству Если $k$ и $f$ – кусочно-непрерывные функции с разрывом на линии $\Gamma $, то в силу леммы Вейля [23] функцию $u$ можно считать дважды непрерывно-дифференцируемой в окрестности любой точки, кроме точек линии разрыва $\Gamma $. Под классическим решением мы понимаем непрерывную в $S$ функцию, имеющую кусочно-непрерывные производные. Применяя теоремы Грина к каждой из частей, на которую линия $\Gamma $ делит $S$, мы получаем В силу произвольности $v$ отсюда следует не только, что $u$ удовлетворяет в обычном смысле уравнению ${{\Delta }_{k}}u + f = 0$, но и условие на линии скачков $\Gamma $. Абсолютно аналогично доказывается, что классическое решение задачи Неймана удовлетворяет условию на линии скачков $\Gamma $.

Доказательство. (i) Начнем с проверки выполнения первой подсистемы (5) уравнений Максвелл. Подстановка выражения (1) в уравнение

дает или Это соотношение совпадает с уравнением (7). Аналогично, дает т.е. уравнение (10). Уравнение дает или т.е. уравнение (9). Наконец, уравнение дает т.е. уравнение (8). Таким образом, все четыре уравнения первой подсистемы (5) уравнений Максвелла удовлетворяются тождественно.

(ii) Обратимся теперь к проверке граничных условий на $\partial S \times Z \times T$. Условимся обозначать как ${\mathbf{\tau }}$ касательный вектор к линии и пусть для определенности

Условие означает, что Первое из этих уравнений в новых переменных означает, что Потенциалы удовлетворяют этому условию, поскольку на $\partial S \times Z \times T$. Аналогично, удовлетворяется, если на $\partial S \times Z \times T$. Таким образом, граничные условия (3) будут удовлетворены, если ${{u}_{e}},{{u}_{h}},{{E}_{z}}$ удовлетворяют условиям Дирихле, ${{v}_{e}},{{v}_{h}}$ – условиям Неймана.

(iii) Обратимся теперь к условиям (4) на линии разрыва. Так как ${{E}_{z}}$ и ${{H}_{z}}$ не имеют разрывов, эти условия сводятся к двум условиям на ${{{\mathbf{E}}}_{ \bot }}$ и двум условиям на ${{{\mathbf{H}}}_{ \bot }}$.

Первое из условий на ${{{\mathbf{E}}}_{ \bot }}$ состоит в требовании непрерывности $({{{\mathbf{E}}}_{ \bot }},{\mathbf{\tau }})$. В силу (1)

Классическое решение ${{u}_{e}}$ задачи (7) непрерывно на $\Gamma $, поэтому на $\Gamma $. Дифференцируя это соотношение по $\tau $, имеем Классическое решение ${{v}_{e}}$ задачи (9) непрерывно на $\Gamma $, а его нормальная производная удовлетворяет условию Складывая эти равенства, имеем на $\Gamma $.

Второе из условий на ${{{\mathbf{E}}}_{ \bot }}$состоит в требовании непрерывности $(\varepsilon {\mathbf{E}},{\mathbf{n}})$. В силу (1)

Поскольку потенциал ${{v}_{e}}$ является классическим решением задачи (9), он непрерывен на разрыве, откуда Потенциал же ${{u}_{e}}$ как классическое решение задачи (7) удовлетворяет условию Поэтому величина $(\varepsilon {{{\mathbf{E}}}_{ \bot }},{\mathbf{n}})$ не терпит разрыва на $\Gamma $.

Аналогично доказывается непрерывность $({{{\mathbf{H}}}_{ \bot }},{\mathbf{\tau }})$ и $(\mu {{{\mathbf{H}}}_{ \bot }},{\mathbf{n}})$.

Замечание. Обычно условия (4) ослабляют, отбросив условия на $(\varepsilon {\mathbf{E}},{\mathbf{n}})$ и $(\mu {\mathbf{H}},{\mathbf{n}})$, поскольку при определенных предположениях они могут быть выведены из остальных. Мы сохранили в определении 1 наиболее полный набор условий. Зато теперь хорошо видно, что в доказательстве теоремы 1 используются все четыре условия на нормальные производные потенциалов.

4. ДЕКОМПОЗИЦИЯ ПРОИЗВОЛЬНОГО ПОЛЯ В ВОЛНОВОДЕ

Обратим утверждение теоремы 1.

Теорема 2. Пусть $S$ – односвязная область. Если для любого поля ${\mathbf{E}},{\mathbf{H}}$ в волноводе, подпадающего под описание определения 1, задачи (7)–(10) имеют классические решения, то для этого поля с так определенными потенциалами равенство (1) оказывается верным тождеством. Указанное представление единственно с точностью до аддитивных констант.

Доказательство. Пусть ${\mathbf{E}},{\mathbf{H}}$ – произвольное поле в волноводе. Рассмотрим разности

Прежде всего заметим, что По условию теоремы поле ${\mathbf{E}},{\mathbf{H}}$ удовлетворяет уравнениям Максвелла, поэтому Но в силу (9) и поэтому Это означает, что в каждой из частей ${{S}_{n}}$, на которые $\Gamma $ делит область $S$, определена такая функция $w$, что Вспоминая теперь вывод уравнения (7), имеем или На границе области $S$или Поэтому $w$ принимает на границе области $S$ постоянное значение. В силу односвязности области $S$ его можно принять равным нулю. Наконец, на границе раздела сред величина непрерывна в силу того, что ${{u}_{e}}$ и ${{v}_{e}}$ – классические решения задач (7) и (9), а ${\mathbf{E}}$ удовлетворяет условиям сопряжения (4). Поэтому $w$ – классическое решение задачи Решение этой задачи – единственно, поэтому $w = 0$, а ${\mathbf{E}}_{ \bot }^{'} = 0$. Аналогично доказывается, что ${\mathbf{H}}_{ \bot }^{'} = 0$.

Ослабление условий доказанной теоремы требует некоторых усилий. Прежде всего докажем существование решения задач (7)–(10).

Лемма 1. Для любого поля ${\mathbf{E}},{\mathbf{H}}$ в волноводе, подпадающего под описание определения 1, обе задачи Дирихле (7) и (8) имеют обобщенное решение в $\mathop {W_{2}^{1}}\limits^0 (S)$, а обе задачи Неймана (9) и (10) имеют обобщенное решение в $W_{2}^{1}(S)$.

Доказательство. Разрешимость обеих задач Дирихле в $\mathop {W_{2}^{1}}\limits^0 (S)$ сразу следует из теоремы Рисса [24]. Большее внимание следует уделить разрешимости уравнений с условиями Неймана [24]. Напомним, что задача

разрешима в $W_{2}^{1}(S)$ тогда и только тогда, когда При этом решение определено с точностью до аддитивной константы, которую мы будем в дальнейшем опускать. Задача (9) разрешима, поскольку в силу теоремы Грина и граничных условий (3) Вообще говоря, здесь следовало учесть интеграл по $\Gamma $, однако, в силу (4) величина ${{{\text{E}}}_{ \bot }} \times n$ не терпит разрыва на границе раздела сред. Аналогично, задача (10) разрешима, поскольку в силу теоремы Грина и граничных условий (3) Здесь тоже опущен интеграл по $\Gamma $, поскольку $\mu {{{\mathbf{H}}}_{ \bot }} \cdot n$ не терпит разрыва на границе раздела сред. Таким образом, и обе задачи Неймана имеют решение в $W_{2}^{1}(S)$.

Доказанная лемма позволяет для любого электромагнитного поля в волноводе найти потенциалы в пространстве Соболева. В дальнейшем мы будем считать потенциалы элементами пространства Соболева, а их частные производные – элементами ${{L}^{2}}(S)$. Из леммы Вейля [23] следует, что вне линии раздела сред эти потенциалы можно считать дважды непрерывно дифференцируемыми функциями. Поведение потенциалов на границе раздела сред требует глубокого исследования, для наших целей не нужного. Как станет ясно из нижеследующих лемм, для наших целей вполне достаточно установить, что гладкие поля всегда допускают декомпозицию (1).

Лемма 2. Пусть $S$ – односвязная область с гладкой границей, а положительная функция $\varepsilon $ не имеет разрывов в этой области. Тогда любое гладкое векторное поле ${\mathbf{A}}$, удовлетворяющее условию

на границе $S$, можно представить в видегде $u$ и $v$ – гладкие функции из ${{C}^{2}}(S)$, удовлетворяющие на границе $\partial S$ условиямДоказательство в существенном повторяет доказательство теоремы 2. Следует также заметить, что именно в этом доказательстве и только в нем существенным образом используется односвязность $S$.

Доказательство. Задача

имеет единственное решение в $\mathop {W_{2}^{1}}\limits^0 (S)$, которое в силу леммы Вейля является классическим. Примем его за потенциал $u$. Задача имеет решение в $W_{2}^{1}(S)$, поскольку Ее решения определены с точностью до константы, примем одно из них за $v$. Положим Тогда поэтому найдется такая гладкая функция $w$, что Но тогда внутри $S$, а на границе этой области т.е. Поскольку $S$ односвязная, это означает, что $w$ не меняется вдоль границы $S$. Поэтому $w$ – решение задачи Эта задача имеет единственное классическое решение, а именно $w = {\text{const}}$. Поэтому ${\mathbf{A}}{\kern 1pt} ' = 0$.

Лемма 3. Пусть $S$ – область с гладкой границей, а положительная функция $\mu $ не имеет разрывов в этой области. Тогда любое гладкое векторное поле ${\mathbf{A}}$, удовлетворяющее условию

на границе $S$, можно представить в видегде $u$ и $v$ – гладкие функции из ${{C}^{2}}(S)$, удовлетворяющие на границе $\partial S$ условиям

Доказательство. Задача

имеет единственное решение в $\mathop {W_{2}^{1}}\limits^0 (S)$, которое в силу леммы Вейля является классическим. Примем его за потенциал $u$. Задача имеет решение в $W_{2}^{1}(S)$, поскольку Ее решения определены с точностью до константы, примем одно из них за $v$. Положим Следовательно, поэтому найдется такая гладкая функция $w$, что Но тогда внутри $S$, а на границе этой области т.е. Поэтому $w$ – решение задачи Все решения этой задачи исчерпываются семейством $w = {\text{const}}$. Поэтому ${\mathbf{A}}{\kern 1pt} ' = 0$.

Теперь можно перейти к негладкому случаю.

Теорема 3. Для любого электромагнитного поля ${\mathbf{E}},{\mathbf{H}}$ в волноводе, подпадающего под описание определения 1, найдутся такие функции

что равенство (1) оказывается верным тождеством. Указанное представление единственно с точностью до аддитивных констант.

Доказательство. Пусть задано какое-либо поле, описанное в определении 1. В силу леммы 1 по заданным ${{E}_{z}}$ и ${{H}_{z}}$ мы можем определить функции

как решения краевых задач (7)–(10). При этом ${{v}_{e}}$ и ${{v}_{h}}$ определены с точностью до аддитивной константы. Требуется доказать, что при так определенных потенциалах выполняется (1). С этой целью рассмотрим разности

(i) Для доказательства первого из этих равенств, докажем прежде всего, что

В самом деле, пусть $u$ – произвольная функция из $\mathop {W_{2}^{1}}\limits^0 (S)$. Умножим ${\mathbf{E}}_{ \bot }^{'}$ скалярно на $\varepsilon \nabla u$ и проинтегрируем по $S$: По построению ${{u}_{e}}$ – обобщенное решение задачи (7), поэтому В силу $\operatorname{div} \varepsilon {\mathbf{E}} = 0$По формуле Грина с учетом граничных условий и условий на границе раздела, последний интеграл можно переписать в виде Это означает, что в правой части равенства (14) первое слагаемое равно нулю. Второе слагаемое по теореме Грина равно нулю. Поэтому Аналогично доказывается, что (ii) Пусть $x$ – произвольная точка области $S$, не лежащая на границе раздела сред, а $U$ – столь малый круг, внутри которого $\varepsilon $ и $\mu $ не терпят разрывов. Пусть ${\mathbf{A}}$ – векторное поле, координаты ${{A}_{x}}$ и ${{A}_{y}}$ которого принадлежат $C_{0}^{\infty }(U)$. Тогда на границе круга выполняется условие поэтому в силу леммы 2 найдутся такие $u$ и $v$ из ${{C}^{2}}(U)$, что Поэтому в силу (i) В силу полноты $C_{0}^{\infty }(U)$ в ${{L}^{2}}(U)$ отсюда следует, что ${\mathbf{E}}_{ \bot }^{'} = 0$ на $U$.

Представление для $\mathop {\mathbf{H}}\nolimits_ \bot $ обосновывается тем же путем на основании леммы 3.

Доказанная теорема является прямым обобщением теоремы Тихонова и Самарского о декомпозиции поля в полом волноводе [1], в которую внесены необходимые правки на случай, когда потенциалы не являются классическими решениями соответствующих краевых задач. Как следствие этой теоремы, мы можем представить следующее утверждение, указанное Ю.В. Шестопаловым и упомянутое в [25].

Следствие 1 (Ю.В. Шестопалов, 1980 г.). Поле ${\mathbf{E}},{\mathbf{H}}$ в волноводе, подпадающее под описание определения 1, однозначно восстанавливается по заданным ${{E}_{z}}$ и ${{H}_{z}}$.

Доказательство. По заданным ${{E}_{z}}$ и ${{H}_{z}}$ можно найти потенциалы как решения задач (7)–(10), а затем по формулам (1) восстановить поле.

5. ЗАКЛЮЧЕНИЕ

Теорема 3 означает, что при переходе от переменных ${\mathbf{E}},{\mathbf{H}}$ к четырем потенциалам и двум компонентам ${{E}_{z}},{{H}_{z}}$ по формулам (1) не теряются решения уравнений Максвелла, удовлетворяющие условиям, сформулированным в определении 1. При этом условия

и заменяют нам условия на разрывах заполнения, равно как и граничные условия. Это позволяет надеяться на то, что численное решение уравнений Максвелла в новых переменных можно будет выполнять в хорошо изученных функциональных пространствах. При этом открываются новые перспективы как для создания новых численных методов расчета нормальных волн волновода, так и для доказательства не только полноты, но и базисности системы исследования нормальных волн в волноводе.

Авторы признательны А.Н. Боголюбову и участникам семинара “Математические методы в естественных науках” (МГУ, физический факультет) за постоянное внимание к их работе.