Журнал вычислительной математики и математической физики, 2019, T. 59, № 5, стр. 905-910

Быстрый алгоритм решения простейшей задачи поиска

В. Н. Малозёмов^1, *, Г. Ш. Тамасян^1, **

¹ С.-Пб гос. ун-т
199034 С.-Петербург, Университетская наб., 7/9, Россия

^* E-mail: v.malozemov@spbu.ru
^** E-mail: g.tamasyan@spbu.ru

Поступила в редакцию 23.03.2018
После доработки 11.01.2019
Принята к публикации 11.01.2019

DOI: 10.1134/S0044466919050107

Аннотация

Предлагается быстрый алгоритм решения задачи Данскина. Анализируется зависимость решения от параметров. Библ. 6. Фиг. 4. Табл. 1.

Ключевые слова: простейшая задача поиска, лемма Гиббса, быстрый алгоритм, зависимость решения от параметров.

1. ВВЕДЕНИЕ

Рассматривается простейшая задача поиска в следующей постановке. Пусть имеется $X$ единиц времени для обнаружения некоторого объекта. Объект может находиться в одном из $n$ мест, причем известна вероятность его нахождения в каждом из этих мест. Известна также вероятность обнаружения объекта, если он находится в $i$-м месте при всех $i$ от 1 до $n$. Разумеется, эта вероятность зависит от времени поиска. Требуется разбить общее время поиска $X$ на $n$ частей (по числу мест возможного нахождения объекта) так, чтобы максимизировать вероятность обнаружения объекта. Частный случай этой задачи рассмотрел Дж. М. Данскин в своей книге, посвященной теории максимина [1, с. 22–24]. С помощью леммы Гиббса он вывел необходимое условие максимума и в общих чертах описал метод решения задачи. В данной заметке предложен быстрый алгоритм решения задачи Данскина и проанализирована зависимость решения от параметров.

2. ПОСТАНОВКА ЗАДАЧИ

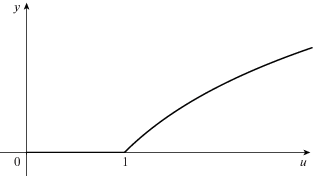
Пусть в нашем распоряжении имеется $X$ единиц времени на поиск некоторого объекта. Этот объект может находиться в одном из $n$ мест. Если объект находится в $i$-м месте, то, потратив ${{x}_{i}}$ единиц времени, мы можем обнаружить его с вероятностью $1 - {{e}^{{ - {{b}_{i}}{{x}_{i}}}}}$. Параметр ${{b}_{i}}$ можно интерпретировать как уровень условий, благоприятствующих поиску объекта в $i$-м месте. Вероятность того, что объект находится в $i$-м месте, равна ${{a}_{i}}$. Как разбить общее время поиска $X$ на сумму ${{x}_{i}}$ так, чтобы максимизировать вероятность обнаружения интересующего нас объекта?

Приходим к экстремальной задаче, которую будем называть задачей Данскина:

(1)

$\begin{array}{*{20}{c}} {F(x): = \sum\limits_{i = 1}^n \,{{a}_{i}}(1 - {{e}^{{ - {{b}_{i}}{{x}_{i}}}}}) \to max,} \\ {\sum\limits_{i = 1}^n \,{{x}_{i}} = X,\quad {{x}_{i}} \geqslant 0\quad \forall i \in 1:n.} \end{array}$

Здесь ${{a}_{i}}$, ${{b}_{i}}$, $X$ – положительные параметры.

Целевая функция $F(x)$ строго вогнута на ${{\mathbb{R}}^{n}}$, а множество планов (векторов, удовлетворяющих ограничениям экстремальной задачи) компактно. Это гарантирует существование и единственность решения задачи (1).

3. УСЛОВИЯ ОПТИМАЛЬНОСТИ. РЕШЕНИЕ ЗАДАЧИ

По лемме Гиббса [1] (см. также препринт [2]) план $x = \left( {{{x}_{1}},\; \ldots ,\;{{x}_{n}}} \right)$ задачи (1) будет оптимальным тогда и только тогда, когда при некотором вещественном $\lambda $ выполняются соотношения

(2)

${{a}_{i}}{{b}_{i}}{{e}^{{ - {{b}_{i}}{{x}_{i}}}}} = \lambda ,\quad {\text{е с л и }}\quad {{x}_{i}} > 0,$

(3)

${{a}_{i}}{{b}_{i}} \leqslant \lambda ,\quad {\text{е с л и }}\quad {{x}_{i}} = 0.$

Из (2) и (3) следует, что

(4)

${{x}_{i}} > 0,\quad {\text{е с л и }}\quad {{a}_{i}}{{b}_{i}} > \lambda ,$

(5)

${{x}_{i}} = 0,\quad {\text{е с л и }}\quad {{a}_{i}}{{b}_{i}} \leqslant \lambda .$

Действительно, при ${{a}_{i}}{{b}_{i}} \leqslant \lambda $ необходимо ${{x}_{i}} = 0$, ибо в противном случае в силу (2) получим ${{a}_{i}}{{b}_{i}} > \lambda $, что противоречит исходному условию. При ${{a}_{i}}{{b}_{i}} > \lambda $ будет ${{x}_{i}} > 0$, ибо иначе получим противоречие с (3).

На основании (2) формулу (4) можно переписать в виде

(6)

${{x}_{i}} = \frac{1}{{{{b}_{i}}}}ln\frac{{{{a}_{i}}{{b}_{i}}}}{\lambda },\quad {\text{е с л и }}\quad {{a}_{i}}{{b}_{i}} > \lambda .$

Равенство (2) гарантирует положительность $\lambda $, поэтому условия ${{a}_{i}}{{b}_{i}} > \lambda $ и ${{a}_{i}}{{b}_{i}} \leqslant \lambda $ равносильны тому, что $\tfrac{{{{a}_{i}}{{b}_{i}}}}{\lambda } > 1$ и $\tfrac{{{{a}_{i}}{{b}_{i}}}}{\lambda } \in (0,1]$. Данное замечание позволяет объединить формулы (6) и (5) следующим образом:

(7)

${{x}_{i}} = \frac{1}{{{{b}_{i}}}}l{{n}_{ + }}\frac{{{{a}_{i}}{{b}_{i}}}}{\lambda },$

где

$l{{n}_{ + }}(u) = \left\{ \begin{gathered} ln(u)\quad {\text{п р и }}\quad u > 1, \hfill \\ 0\quad {\text{п р и }}\quad u \in (0,1]. \hfill \\ \end{gathered} \right.$

График функции $y = l{{n}_{ + }}(u)$ представлен на фиг. 1.

Фиг. 1.

График функции $y = l{{n}_{ + }}(u)$.

Обозначим ${{c}_{i}} = ln{{a}_{i}}{{b}_{i}}$, $u = ln\lambda $ и покажем, что

(8)

${{x}_{i}} = \frac{1}{{{{b}_{i}}}}{{({{c}_{i}} - u)}_{ + }},\quad i \in 1:n.$

Условия $\tfrac{{{{a}_{i}}{{b}_{i}}}}{\lambda } > 1$ и $\tfrac{{{{a}_{i}}{{b}_{i}}}}{\lambda } \in (0,1]$ равносильны соответственно неравенствам ${{c}_{i}} - u > 0$ и ${{c}_{i}} - u \leqslant 0$. Согласно (7) получаем

$\begin{gathered} {{x}_{i}} = \frac{1}{{{{b}_{i}}}}({{c}_{i}} - u)\quad {\text{п р и }}\quad {{c}_{i}} - u > 0, \\ {{x}_{i}} = 0\quad {\text{п р и }}\quad {{c}_{i}} - u \leqslant 0, \\ \end{gathered} $

что равносильно (8). Параметр $u$ найдем из уравнения

(9)

$\varphi (u): = \sum\limits_{i = 1}^n \frac{1}{{{{b}_{i}}}}{{({{c}_{i}} - u)}_{ + }} = X.$

Таким образом, решение задачи (1) сводится к решению скалярного уравнения (9) и вычислению компонент оптимального плана по формуле (8).

4. ОПИСАНИЕ АЛГОРИТМА

Опишем быстрый алгоритм решения уравнения (9).

Начнем с того, что упорядочим пары $({{b}_{i}},{{c}_{i}})$, $i \in 1:n$, по невозрастанию второй компоненты. Получим последовательность

$({{\hat {b}}_{1}},{{\hat {c}}_{1}}),({{\hat {b}}_{2}},{{\hat {c}}_{2}}),\; \ldots ,\;({{\hat {b}}_{n}},{{\hat {c}}_{n}}),$

где ${{\hat {c}}_{1}} \geqslant {{\hat {c}}_{2}} \geqslant \; \ldots \; \geqslant {{\hat {c}}_{n}}$. Очевидно, что

(10)

$\varphi (u) = \sum\limits_{i = 1}^n \frac{1}{{{{{\hat {b}}}_{i}}}}{{({{\hat {c}}_{i}} - u)}_{ + }}.$

В частности,

(11)

$\varphi (u) = 0\quad {\text{п р и }}\quad u \geqslant {{\hat {c}}_{1}};$

при $u \in [{{\hat {c}}_{{k + 1}}},{{\hat {c}}_{k}}]$, $k \in 1:n - 1$, имеем

(12)

наконец,

(13)

$\varphi (u) = \sum\limits_{i = 1}^n \frac{{{{{\hat {с }}}_{i}}}}{{{{{\hat {b}}}_{i}}}} - \left( {\sum\limits_{i = 1}^n \frac{1}{{{{{\hat {b}}}_{i}}}}} \right)u\quad {\text{п р и }}\quad u \leqslant {{\hat {c}}_{n}}.$

В силу (12) получаем

$\varphi (u) - \varphi ({{\hat {с }}_{k}}) = \left( {\sum\limits_{i = 1}^k \frac{1}{{{{{\hat {b}}}_{i}}}}} \right)({{\hat {с }}_{k}} - u).$

Обозначив

${{p}_{k}} = \sum\limits_{i = 1}^k \frac{1}{{{{{\hat {b}}}_{i}}}},$

придем к формуле

(14)

$\varphi (u) = \varphi ({{\hat {c}}_{k}}) + {{p}_{k}}({{\hat {c}}_{k}} - u),\quad u \in [{{\hat {c}}_{{k + 1}}},{{\hat {c}}_{k}}],\quad k \in 1:n - 1.$

Аналогично из (13) следует, что

(15)

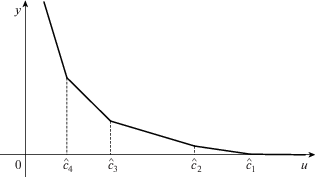
$\varphi (u) = \varphi ({{\hat {c}}_{n}}) + {{p}_{n}}({{\hat {c}}_{n}} - u),\quad u \leqslant {{\hat {c}}_{n}}.$

На основании (10), (11), (14) и (15) заключаем, что функция $\varphi (u)$ является непрерывной ломаной, выпуклой и строго убывающей от $ + \infty $ до $0$ на полуоси $( - \infty ,{{\hat {c}}_{1}})$ (см. фиг. 2).

Фиг. 2.

График ломаной $y = \varphi (u)$.

Отметим, что ломаная $\phi (u)$ на отрезке $[{{\hat {c}}_{n}},{{\hat {c}}_{1}}]$ полностью определяется своими значениями $\varphi ({{\hat {c}}_{k}})$ в узлах ${{\hat {c}}_{k}}$, $k \in 1:n$. В силу (14) эти значения связаны формулой

$\varphi ({{\hat {c}}_{{k + 1}}}) = \varphi ({{\hat {c}}_{k}}) + {{p}_{k}}({{\hat {c}}_{k}} - {{\hat {c}}_{{k + 1}}}),\quad k \in 1:n - 1.$

Обозначив ${{\varphi }_{k}} = \varphi ({{\hat {c}}_{k}})$, получим для последовательности ${{\varphi }_{1}},\; \ldots ,\;{{\varphi }_{n}}$ рекуррентное соотношение

$\begin{gathered} {{\varphi }_{1}} = 0,\quad {{p}_{0}} = 0,\quad {{p}_{k}} = {{p}_{{k - 1}}} + \frac{1}{{{{{\hat {b}}}_{k}}}}, \\ {{\varphi }_{{k + 1}}} = {{\varphi }_{k}} + {{p}_{k}}({{{\hat {c}}}_{k}} - {{{\hat {c}}}_{{k + 1}}}),\quad k \in 1:n - 1. \\ \end{gathered} $

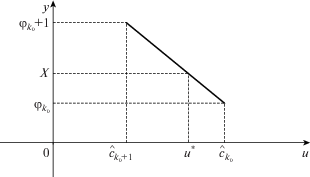
Нас интересует решение $u{\text{*}}$ уравнения $\varphi (u) = X$. Из свойств функции $\varphi (u)$ следует, что такое решение существует и единственно. Для его нахождения будем последовательно вычислять значения ${{\varphi }_{1}},\;{{\varphi }_{2}},\; \ldots $ по формулам (16), пока не встретим индекс ${{k}_{0}}$, на котором

${{\varphi }_{{{{k}_{0}}}}} < X \leqslant {{\varphi }_{{{{k}_{0}} + 1}}}.$

В этом случае $u{\text{*}}$ принадлежит отрезку $\left[ {{{{\hat {c}}}_{{{{k}_{0}} + 1}}},{{{\hat {c}}}_{{{{k}_{0}}}}}} \right]$ (см. фиг. 3).

Фиг. 3.

Локализация решения $u{\text{*}}$ уравнения $\varphi (u) = X$.

Согласно (14) имеем

(17)

$u* = {{\hat {c}}_{{{{k}_{0}}}}} - \frac{1}{{{{p}_{{{{k}_{0}}}}}}}(X - {{\varphi }_{{{{k}_{0}}}}}).$

Если ${{\varphi }_{n}} < X$, то $u* < {{\hat {c}}_{n}}$. В силу (15), $u{\kern 1pt} *$ вычисляется по той же формуле (17) при ${{k}_{0}} = n$.

На основании (8) для компонент решения $x* = (x_{1}^{ * },\; \ldots ,\;x_{n}^{ * })$ задачи (1) получаем представление

$x_{i}^{ * } = \frac{1}{{{{b}_{i}}}}{{({{c}_{i}} - u*)}_{ + }},\quad i \in 1:n.$

Замечание 1. Описанный алгоритм сходится не более, чем за $n$ шагов. И в общем случае требует сортировку элементов массива длиной $n$ и не более $6n - 2$ арифметических операций, т.е. имеет сложность порядка $O(nlo{{g}_{2}}(n))$.

Замечание 2. Используя специфику алгоритма, можно минимизировать его трудоемкость. Действительно, для последовательного нахождения значений ${{\varphi }_{k}}$, $k = 1:n$, (см. (16)) необязательно иметь всю отсортированную по невозрастанию последовательность ${{\hat {c}}_{1}} \geqslant {{\hat {c}}_{2}} \geqslant \; \ldots \; \geqslant {{\hat {c}}_{n}}$. Достаточно находить лишь одно значение из этой последовательности для каждой следующей итерации (см. [3]).

Замечание 3. В работах [4], [5] предложены алгоритмы решения скалярного уравнения вида (9), имеющие линейный порядок сложности [6]. Однако численные эксперименты показали их малую эффективность с точки зрения временных затрат (см. [3]).

5. ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ

Напомним, что параметр ${{b}_{i}}$ интерпретируется как уровень условий, благоприятствующих поиску объекта в $i$-м месте. Представляет интерес проанализировать влияние параметров ${{b}_{i}}$ на оптимальное распределение $\{ x_{i}^{ * }\} $.

Возьмем конкретные данные. Пусть $n = 4$, ${{a}_{1}} = 0.4$, ${{a}_{2}} = 0.3$, ${{a}_{3}} = 0.2$, ${{a}_{4}} = 0.1$, $X = 3$. При ${{b}_{1}} = {{b}_{2}} = {{b}_{3}} = {{b}_{4}} = 1$ оптимальное распределение $x* = (x_{1}^{ * },x_{2}^{ * },x_{3}^{ * },x_{4}^{ * })$ имеет вид

$x* = (1.327,1.039,0.634,0).$

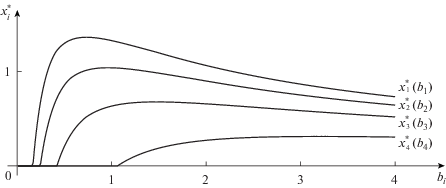
Теперь при каждом фиксированном $i \in 1:4$ будем изменять значения ${{b}_{i}}$, сохраняя остальные ${{b}_{k}}$ равными единице. На фиг. 4 изображены четыре графика, которые показывают, как изменяются $x_{i}^{ * }$ в зависимости от ${{b}_{i}}$.

Фиг. 4.

Графики зависимости $x_{i}^{ * }$ от ${{b}_{i}}$.

На каждом графике выделяются два значения параметра ${{b}_{i}}$:

$\begin{gathered} b_{i}^{0}\; - \;{\text{з н а ч е н и е }},\;{\text{д о }}\;{\text{к о т о р о г о }}\;x_{i}^{ * } = 0; \\ b_{i}^{1}\; - \;{\text{з н а ч е н и е }},\;{\text{п о с л е }}\;{\text{к о т о р о г о }}\;x_{i}^{ * }\;{\text{н а ч и н а е т }}\;{\text{у б ы в а т ь }}. \\ \end{gathered} $

В рассматриваемом случае имеем

$\begin{gathered} b_{1}^{0} = 0.167,\quad b_{2}^{0} = 0.245,\quad b_{3}^{0} = 0.421,\quad b_{4}^{0} = 1.061, \\ b_{1}^{1} = 0.734,\quad b_{2}^{1} = 0.962,\quad b_{3}^{1} = 1.475,\quad b_{4}^{1} = 3.201. \\ \end{gathered} $

В табл. 1 представлена более полная информация об изменении всего оптимального распределения $x{\text{*}}$ при изменении ${{b}_{2}}$.

Таблица 1

${{b}_{2}}$	$x_{1}^{ * }$	$x_{2}^{ * }$	$x_{3}^{ * }$	$x_{4}^{ * }$
0.245	1.693	0	1	0.307
0.484	1.416	0.832	0.723	0.029
0.723	1.342	1.009	0.649	0
0.962	1.327	1.039	0.634	0
1.5	1.356	0.982	0.662	0
2.5	1.420	0.819	0.727	0.034
4	1.479	0.644	0.785	0.092

Список литературы

Данскин Дж.М. Теория максимина и ее приложение к задачам распределения вооружения. Пер. с англ. М.: Сов. радио, 1970. 200 с.
Малоземов В.Н., Тамасян Г.Ш. Лемма Гиббса и ее приложения // Семинар “CNSA & NDO”. Избранные доклады. 10 октября 2017 г. URL: http://www.apmath.spbu.ru/cnsa/reps17.shtml#1010 (дата обращения: 01.03.2018).
Tamasyan G., Prosolupov E. Orthogonal projection of a point onto the standard simplex: algorithms analysis // Proc. 2015 Int. Conf. “Stability and Control Processes” in Memory of V. I. Zubov (SCP) (St. Petersburg, Russia, Oct. 5–9, 2015). IEEE, 2015. P. 353–356. http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=7342137
Brucker P. An $O(n)$ algorithm for quadratic knapsack problems // Oper. Res. Lett. 1984. V. 3. № 3. P. 163–166.
Maculan N., Galdino de Paula G., Jr. A linear-time median-finding algorithm for projecting a vector on the simplex of ${{\mathbb{R}}^{n}}$ // Oper. Res. Lett. 1989. V. 8. № 4. P. 219–222.
Просолупов Е.В., Тамасян Г.Ш. Оценка трудоемкости алгоритма по поиску нуля одной выпуклой кусочно-линейной функции // Дискрет. анализ и исслед. операций. 2018. Т. 25. № 2. С. 82–100.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал