Журнал вычислительной математики и математической физики, 2019, T. 59, № 5, стр. 796-821
KP1-схема ускорения внутренних итераций для уравнения переноса в трехмерной геометрии, согласованной с нодальными схемами II. Метод расщепления для решения P1-системы для ускоряющих поправок
А. М. Волощенко *
Институт прикладной математики РАН
125047 Москва, Миусская пл., 4, Россия
* E-mail: volosch@kiam.ru
Поступила в редакцию 17.09.2018
После доработки 12.12.2018
Принята к публикации 11.01.2019
Аннотация
Для решения ${{P}_{1}}$-системы для ускоряющих поправок, возникающей при построении $K{{P}_{1}}$-схемы ускорения сходимости внутренних итераций, согласованной с нодальными Linear Discontinues (LD) и Linear Best (LB)-схемами 3-го и 4-го порядка точности по пространственным переменным для уравнения переноса в трехмерной $r,\;\vartheta ,\;z$ геометрии, предложен алгоритм, основанный на использовании циклического метода расщепления (МР) в сочетании с методом прогонки для решения вспомогательных систем двухточечных уравнений. Рассмотрена модификация алгоритма на случай трехмерной $x,\;y,\;z$ геометрии. Библ. 24. Фиг. 3. Табл. 1.
ВВЕДЕНИЕ
Алгоритм ускорения итераций по интегралу рассеяния является существенным элементом численной методики решения уравнения переноса, основанной на использовании метода дискретных ординат. Расчеты полей излучения в активной зоне и радиационной защите ядерно-технических установок в неодномерных геометриях требуют значительных затрат процессорного времени. Поэтому, с практической точки зрения, разработка эффективного алгоритма ускорения для 3D геометрий является актуальной задачей, позволяя сократить время расчета типичного варианта в 3–10 и более раз.
В данной работе, являющейся 2-й частью работы [1], будет рассмотрен технически наиболее сложный элемент реализации $K{{P}_{1}}$-схемы [2] (известной также как DSA [3], [4] или ${{P}_{1}}SA$-схема [5]–[8]) ускорения внутренних итераций для практически важного случая LD и LB-схем в 3D $r,\;\vartheta ,\;z$ и $x,\;y,\;z$ геометриях, позволяющей обеспечить быструю сходимость разностного решения при сгущении пространственной сетки задачи: метод расщепления (МР) для решения ${{P}_{1}}$-системы для ускоряющих поправок.
Предложенный алгоритм реализован в 3D ${{S}_{n}}$ программе КАТРИН-2.5 из пакета программ CNCSN [9]. Он представляет собой развитие варианта МР, предложенного ранее в работе [10] для случая взвешенной алмазной (WDD) схемы.
Последовательность изложения в данной работе следующая. В разд. 2.1 сформулирован МР для решения ${{P}_{1}}$-системы для поправок, включая метод прогонки для решения вспомогательных 2-х точечных уравнений (обычный и циклический). В разд. 2.2 рассмотрен алгоритм оценки границ спектра радиальной ($\hat {R}$), азимутальной ($\hat {\Theta }$) и аксиальной ($\hat {Z}$) компонент ${{P}_{1}}$ оператора, которые используются для выбора шагов метода расщепления. В разд. 2.3 рассмотрен вопрос о выборе итерационных параметров циклического метода расщепления. В разд. 2.4 приведен численный пример, позволяющий продемонстрировать преимущества использования MP в сочетании с WLD-схемой по сравнению с использованием MP с адаптивной WDD-схемой.
Для нумерации формул используются 3 цифры: первая обозначает номер части, вторая – номер раздела, третья – номер формулы в разделе.
2.1. Алгоритм решения ${{P}_{1}}$-системы для ускоряющих поправок в $r,\;\vartheta ,\;z$ геометрии
${{P}_{1}}$-система для ускоряющих поправок для $K{{P}_{1}}$-схемы в $r,\;\vartheta ,\;z$ геометрии состоит из 16 балансных уравнений (1.2.19)–(1.2.22), шести дополнительных уравнений (1.2.26), (1.2.27) и (1.2.28); 16 дополнительных уравнений (1.2.30)–(1.2.35) и граничных условий (1.2.36)–(1.2.43) работы [1]. Эта система может быть решена итерационно с использованием, например, метода расщепления (МР) [2], [11].
В соответствии с общим подходом МР, оператор ${{P}_{1}}$-системы для ускоряющих поправок
представляется в виде суммы: где $\hat {R}$, $\hat {\Theta }$ и $\hat {Z}$ – компоненты оператора $\hat {A}$, определяющие изменение решения ${{P}_{1}}$-системы по переменным $r$, $\vartheta $ и $z$ соответственно. Более подробно о структуре операторов $\hat {R}$, $\hat {\Theta }$ и $\hat {Z}$ будет сказано ниже. Предположим также, что указанные операторы являются положительно определенными. В МР сложился следующий конструктивный способ построения итерационной схемы. Для приближенного решения уравнения (2.1.1) рассмотрим неявную двухслойную итерационную схему вида [2], [11]:(2.1.3)
${{B}_{{s + 1}}}\frac{{{{f}^{{s + 1}}} - {{f}^{s}}}}{{{{\tau }_{{s + 1}}}}} + A{{f}^{s}} = q,\quad {{B}_{s}} = \left( {E + \tau _{r}^{{(s)}}\hat {R}} \right)\left( {E + \tau _{\vartheta }^{{(s)}}\hat {\Theta }} \right)\left( {E + \tau _{z}^{{(s)}}\hat {Z}} \right),\quad s = 0,1,2, \ldots \;.$(2.1.5)
${{\partial f} \mathord{\left/ {\vphantom {{\partial f} {\partial t}}} \right. \kern-0em} {\partial t}} + Af = q.$(2.1.6)
$\begin{gathered} {{{\tilde {B}}}_{{s + 1}}}\frac{{{{f}^{{s + 1}}} - {{f}^{s}}}}{{{{{\tilde {\tau }}}_{{s + 1}}}}} + A{{f}^{s}} = q,\quad {{{\tilde {B}}}_{s}} = \left( {\omega _{z}^{{(s)}}E + \hat {R}} \right)\left( {\omega _{\vartheta }^{{(s)}}E + \hat {\Theta }} \right)\left( {\omega _{r}^{{(s)}}E + \hat {Z}} \right), \\ {{{\tilde {\tau }}}_{{s + 1}}} = {{\tau }_{{s + 1}}}\omega _{r}^{{(s + 1)}}\omega _{\vartheta }^{{(s + 1)}}\omega _{z}^{{(s + 1)}},\quad s = 0,1,2, \ldots \;. \\ \end{gathered} $(2.1.7)
$\begin{gathered} \left( {\omega _{r}^{{(s + 1)}}E + \hat {R}} \right){{\zeta }^{{s + 1/3}}} = q - A{{f}^{s}},\quad \left( {\omega _{\vartheta }^{{(s + 1)}}E + \hat {\Theta }} \right){{\zeta }^{{s + 2/3}}} = {{\zeta }^{{s + 1/3}}}, \\ \left( {\omega _{z}^{{(s + 1)}}E + \hat {Z}} \right){{\zeta }^{{s + 1}}} = {{\zeta }^{{s + 2/3}}},\quad {{f}^{{s + 1}}} = {{f}^{s}} + {{{\tilde {\tau }}}_{{s + 1}}}{{\zeta }^{{s + 1}}}. \\ \end{gathered} $Следует подчеркнуть, что исключая из оператора $\hat {A}$ с помощью дополнительных уравнений (1.2.26)–(1.2.28), (1.2.30)–(1.2.35) и граничных условий (1.2.36), (1.2.38) и (1.2.42) поправки, относящиеся к граням ячеек, можно представить его в виде, в котором присутствуют только значения поправок, отнесенные к центру ячейки. Соответственно в (2.1.7) можно считать, что единичный оператор $\hat {E}$ действует только на поправки, отнесенные к центру ячейки.
Учитывая вид поправок (1.2.17), используемых в $K{{P}_{1}}$ алгоритме, и применяя трехшаговую процедуру метода расщепления (2.1.7), получаем следующую систему для поправок на 1-м шаге $\tau _{r}^{{(s + 1)}}$:
(2.1.8)
$\begin{gathered} V\omega _{r}^{{(s + 1)}}{{\zeta }^{{0,r,s + 1/3}}}\, + \,\frac{1}{3}{{v}_{\vartheta }}{{v}_{z}}\left[ {\left( {{{A}_{{i + 1/2}}}\zeta _{{i + 1/2}}^{{0,0,s + 1/3}}\, - \,{{A}_{{i - 1/2}}}\zeta _{{i - 1/2}}^{{0,0,s + 1/3}}} \right)\, - \,C{{\zeta }^{{0,0,s + 1/3}}}} \right]\, + \,\left( {\frac{1}{3}{{\sigma }^{{11}}}V + {{M}_{r}}C{{v}_{\vartheta }}{{v}_{z}}} \right){{\zeta }^{{0,r,s + 1/3}}}\, = \\ = \;V{{Q}^{{0,r}}} - \frac{1}{3}{{v}_{\vartheta }}{{v}_{z}}\left[ {\left( {{{A}_{{i + 1/2}}}f_{{i + 1/2}}^{{0,0,s}} - {{A}_{{i - 1/2}}}f_{{i - 1/2}}^{{0,0,s}}} \right) - C{{f}^{{0,0,s}}}} \right] - \left( {{{\sigma }^{{11}}}V + {{M}_{r}}C{{v}_{\vartheta }}{{v}_{z}}} \right){{f}^{{0,r,s}}}, \\ \end{gathered} $(2.1.9)
$\begin{gathered} \left. {\mathop - \limits_{_{{_{{_{{}}}}}}} \;{{C}^{r}}{{\zeta }^{{r,0,s + 1/3}}} + C{{\delta }^{c}}{{\zeta }^{{0,0,s + 1/3}}}} \right] - {{v}_{\vartheta }}{{v}_{z}}{{\delta }^{c}}{{M}_{r}}C{{\zeta }^{{0,r,s + 1/3}}} + \left( {\frac{1}{3}{{\sigma }^{{11}}}{{V}^{r}} + M_{r}^{r}{{C}^{r}}{{v}_{\vartheta }}{{v}_{z}}} \right){{\zeta }^{{r,r,s + 1/3}}} = {{V}^{r}}{{Q}^{{r,r}}} - \\ - \;{{v}_{\vartheta }}{{v}_{z}}\frac{1}{3}\left[ {{{A}_{{i + 1/2}}}\left( {\frac{{\Delta r}}{2} - {{\delta }^{c}}} \right)f_{{i + 1/2}}^{{0,0,s}} + {{A}_{{i - 1/2}}}\left( {\frac{{\Delta r}}{2} + {{\delta }^{c}}} \right)f_{{i - 1/2}}^{{0,0,s}} - {{v}_{r}}{{f}^{{0,0,s}}} - {{C}^{r}}{{f}^{{r,0,s}}} + C{{\delta }^{c}}{{f}^{{0,0,s}}}} \right] + \\ \end{gathered} $(2.1.10)
$\begin{gathered} {{V}^{\vartheta }}\omega _{r}^{{(s + 1)}}{{\zeta }^{{\vartheta ,0,s + 1/3}}} + v_{\vartheta }^{1}{{v}_{z}}\left( {{{A}_{{i + 1/2}}}\zeta _{{i + 1/2}}^{{\vartheta ,r,s + 1/3}} - {{A}_{{i - 1/2}}}\zeta _{{i - 1/2}}^{{\vartheta ,r,s + 1/3}}} \right) + \frac{1}{3}{{\sigma }^{{00}}}{{V}^{\vartheta }}{{\zeta }^{{\vartheta ,0,s + 1/3}}} = {{V}^{\vartheta }}{{Q}^{{\vartheta ,0}}} - \Delta r{{v}_{\vartheta }}{{v}_{z}} \times \\ \times \;\left[ {\frac{1}{2}\left( {f_{{j + 1/2}}^{{0,\vartheta ,s}} + f_{{j - 1/2}}^{{0,\vartheta ,s}}} \right) - {{f}^{{0,\vartheta ,s}}}} \right] - v_{\vartheta }^{1}{{v}_{z}}\left( {{{A}_{{i + 1/2}}}f_{{i + 1/2}}^{{\vartheta ,r,s}} - {{A}_{{i - 1/2}}}f_{{i - 1/2}}^{{\vartheta ,r,s}}} \right) - {{v}_{r}}v_{\vartheta }^{1}\left( {f_{{k + 1/2}}^{{\vartheta ,z,s}} - f_{{k - 1/2}}^{{\vartheta ,z,s}}} \right) - {{\sigma }^{{00}}}{{V}^{\vartheta }}{{f}^{{\vartheta ,0,s}}}, \\ \end{gathered} $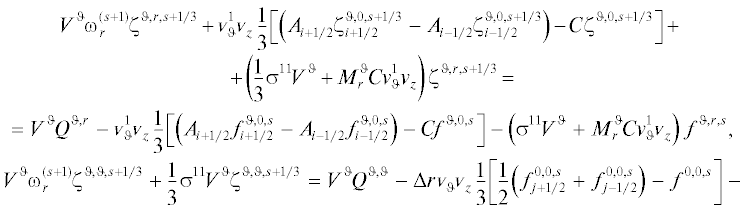
(2.1.11)
$\begin{gathered} {{V}^{z}}\omega _{r}^{{(s + 1)}}{{\zeta }^{{z,r,s + 1/3}}}\, + \,v_{z}^{1}{{v}_{\vartheta }}\frac{1}{3}{\kern 1pt} \left[ {\left( {{{A}_{{i + 1/2}}}\zeta _{{i + 1/2}}^{{z,0,s + 1/3}}\, - \,{{A}_{{i - 1/2}}}\zeta _{{i - 1/2}}^{{z,0,s + 1/3}}} \right)\, - \,C{{\zeta }^{{z,0,s + 1/3}}}} \right]\, + \,\left( {\frac{1}{3}{\kern 1pt} {{\sigma }^{{11}}}{{V}^{z}}\, + \,M_{r}^{z}Cv_{z}^{1}{{v}_{\vartheta }}} \right){\kern 1pt} {{\zeta }^{{z,r,s + 1/3}}}\, = \\ = \;{{V}^{z}}{{Q}^{{z,r}}} - v_{z}^{1}{{v}_{\vartheta }}\frac{1}{3}\left[ {\left( {{{A}_{{i + 1/2}}}f_{{i + 1/2}}^{{z,0,s}} - {{A}_{{i - 1/2}}}f_{{i - 1/2}}^{{z,0,s}}} \right) - C{{f}^{{z,0,s}}}} \right] - \left( {{{\sigma }^{{11}}}{{V}^{z}} + M_{r}^{z}Cv_{z}^{1}{{v}_{\vartheta }}} \right){{f}^{{z,r,s}}}, \\ \end{gathered} $Далее мы будем говорить, что величина относится к слою $s$, $s + 1{\text{/}}3$ и т.д., если она имеет соответствующий индекс. Следует отметить, что в рассматриваемом нами случае 3D геометрии величины $\zeta $ для дробных шагов $s + 1{\text{/}}3$ и $s + 2{\text{/}}3$ не аппроксимируют исходную нестационарную задачу (2.1.5) [15]. Для получения граничных условий по радиальной переменной для поправок $\zeta $ отметим, что из граничных условий (1.2.36) для величин $f$ в предположении (1.2.44), а также уравнения (2.1.7) следует, что:
(2.1.12)
$\begin{gathered} l_{0}^{r}\zeta _{{1/2,j,k}}^{{\beta ,0,s + 1/3}} + 3l_{1}^{r}\zeta _{{1/2,j,k}}^{{\beta ,r,s + 1/3}} = - l_{0}^{r}f_{{1/2,j,k}}^{{\beta ,0,s}} - 3l_{1}^{r}f_{{1/2,j,k}}^{{\beta ,r,s}}, \\ m_{0}^{r}\zeta _{{I + 1/2,j,k}}^{{\beta ,0,s + 1/3}} + 3m_{1}^{r}\zeta _{{I + 1/2,j,k}}^{{\beta ,r,s + 1/3}} = - m_{0}^{r}f_{{I + 1/2,j,k}}^{{\beta ,0,s}} - 3m_{1}^{r}f_{{I + 1/2,j,k}}^{{\beta ,r,s}},\quad \beta = 0,\vartheta ,z. \\ \end{gathered} $(2.1.13)
$l_{0}^{r}\zeta _{{1/2,j,k}}^{{\beta ,0,s + 1/3}} + 3l_{1}^{r}\zeta _{{1/2,j,k}}^{{\beta ,r,s + 1/3}} = 0,\quad m_{0}^{r}\zeta _{{I + 1/2,j,k}}^{{\beta ,0,s + 1/3}} + 3m_{1}^{r}\zeta _{{I + 1/2,j,k}}^{{\beta ,r,s + 1/3}} = 0,\quad \beta = 0,\vartheta ,z.$Система (2.1.8)–(2.1.11) для 16 уравнений, дополненная двумя дополнительными уравнениями для величин ${{\zeta }^{{r,0,s + 1/3}}}$и ${{\zeta }^{{r,r,s + 1/3}}}$, аналогичным (1.2.26), и четырьмя дополнительными уравнениями (1.2.30) и (1.2.31) для величин ${{\zeta }^{{\vartheta ,0,s + 1/3}}}$, ${{\zeta }^{{\vartheta ,r,s + 1/3}}}$, ${{\zeta }^{{z,0,s + 1/3}}}$ и ${{\zeta }^{{z,r,s + 1/3}}}$, а также граничными условиями (2.1.13), может быть решена прямым методом в предположении, что величины с индексом $s$ известны с предыдущего шага. Данная система состоит из трех подсистем, которые могут быть решены независимо методом прогонки [12], [2], [8] по переменной $r$, а также 8 уравнений – последних двух из подсистем уравнений (2.1.8)–(2.1.11), которые могут быть явно разрешены относительно переменных ${{\zeta }^{{0,\vartheta ,s + 1/3}}}$, ${{\zeta }^{{0,z,s + 1/3}}}$, ${{\zeta }^{{r,\vartheta ,s + 1/3}}}$, ${{\zeta }^{{r,z,s + 1/3}}}$, ${{\zeta }^{{\vartheta ,\vartheta ,s + 1/3}}}$, ${{\zeta }^{{\vartheta ,z,s + 1/3}}}$, ${{\zeta }^{{z,\vartheta ,s + 1/3}}}$ и ${{\zeta }^{{z,z,s + 1/3}}}$.
Первая подсистема относительно величин ${{\zeta }^{{0,0,s + 1/3}}}$, ${{\zeta }^{{0,r,s + 1/3}}}$, ${{\zeta }^{{r,0,s + 1/3}}}$, ${{\zeta }^{{r,r,s + 1/3}}}$, $\zeta _{{i \pm 1/2}}^{{0,r,s + 1/3}}$ и $\zeta _{{i \pm 1/2}}^{{0,0,s + 1/3}}$ состоит из двух первых уравнений в подсистемах уравнений (2.1.8) и (2.1.9) (всего 4 уравнения), дополнительных уравнений (1.2.26) для величин ${{\zeta }^{{r,0,s + 1/3}}}$и ${{\zeta }^{{r,r,s + 1/3}}}$ и граничных условий (2.1.13). Для ее решения мы должны исключить из нее величины ${{\zeta }^{{0,0,s + 1/3}}}$, ${{\zeta }^{{0,r,s + 1/3}}}$, ${{\zeta }^{{r,0,s + 1/3}}}$и ${{\zeta }^{{r,r,s + 1/3}}}$ чтобы получить двухточечную систему для величин $\zeta _{{i \pm 1/2}}^{{0,r,s + 1/3}}$ и $\zeta _{{i \pm 1/2}}^{{0,0,s + 1/3}}$ [14]. Исключая из первых двух уравнений подсистемы (2.1.9) посредством дополнительных уравнений (1.2.26) величины ${{\zeta }^{{r,0,s + 1/3}}}$и ${{\zeta }^{{r,r,s + 1/3}}}$, получим следующую систему линейных уравнений относительно ${{\zeta }^{{0,0,s + 1/3}}}$ и ${{\zeta }^{{0,r,s + 1/3}}}$:
(2.1.14)
$\begin{array}{*{20}{c}} {{{a}_{{11}}}{{\zeta }^{{0,0}}} + {{a}_{{12}}}{{\zeta }^{{0,r}}} = \sum\limits_{j = 1}^5 {c_{1}^{j}{{\zeta }_{j}}} = c_{1}^{1}\zeta _{{i + 1/2}}^{{0,0}} + c_{1}^{2}\zeta _{{i - 1/2}}^{{0,0}} + c_{1}^{3}\zeta _{{i + 1/2}}^{{0,r}} + c_{1}^{4}\zeta _{{i - 1/2}}^{{0,r}} + c_{1}^{5},} \\ {{{a}_{{21}}}{{\zeta }^{{0,0}}} + {{a}_{{22}}}{{\zeta }^{{0,r}}} = \sum\limits_{j = 1}^5 {c_{2}^{j}{{\zeta }_{j}}} = c_{2}^{1}\zeta _{{i + 1/2}}^{{0,0}} + c_{2}^{2}\zeta _{{i - 1/2}}^{{0,0}} + c_{2}^{3}\zeta _{{i + 1/2}}^{{0,r}} + c_{2}^{4}\zeta _{{i - 1/2}}^{{0,r}} + c_{2}^{5},} \end{array}$(2.1.15)
$\begin{array}{*{20}{c}} {{{\zeta }^{{0,0}}} = \sum\limits_{j = 1}^5 {x_{1}^{j}{{\zeta }_{j}}} = d_{0}^{ + }\zeta _{{i + 1/2}}^{{0,0}} + d_{0}^{ - }\zeta _{{i - 1/2}}^{{0,0}} + d_{1}^{ + }\zeta _{{i + 1/2}}^{{0,r}} + d_{1}^{ - }\zeta _{{i - 1/2}}^{{0,r}} + d,} \\ {{{\zeta }^{{0,r}}} = \sum\limits_{j = 1}^5 {x_{2}^{j}{{\zeta }_{j}}} = e_{0}^{ + }\zeta _{{i + 1/2}}^{{0,0}} + e_{0}^{ - }\zeta _{{i - 1/2}}^{{0,0}} + e_{1}^{ + }\zeta _{{i + 1/2}}^{{0,r}} + e_{1}^{ - }\zeta _{{i - 1/2}}^{{0,r}} + e,} \end{array}$(2.1.16)
${{a}_{{11}}}x_{1}^{j} + {{a}_{{12}}}x_{2}^{j} = c_{1}^{j},\quad {{a}_{{21}}}x_{1}^{j} + {{a}_{{22}}}x_{2}^{j} = c_{2}^{j},\quad j = \overline {1,5} .$(2.1.17)
$\zeta _{{i + 1/2}}^{{0,0,s + 1/3}}{{a}^{{r,\alpha }}} + \zeta _{{i - 1/2}}^{{0,0,s + 1/3}}{{b}^{{r,\alpha }}} + \zeta _{{i + 1/2}}^{{0,r,s + 1/3}}{{c}^{{r,\alpha }}} + \zeta _{{i - 1/2}}^{{0,r,s + 1/3}}{{d}^{{r,\alpha }}} = {{q}^{{r,\alpha }}},\quad \alpha = 0,r,$(2.1.18)
${{a}^{{r,r}}} = \tilde {\Sigma }_{r}^{{0,1}}e_{0}^{ + } + \frac{1}{3}{{v}_{\vartheta }}{{v}_{z}}\left( {{{A}_{{i + 1/2}}} - Cd_{0}^{ + }} \right),\quad {{b}^{{r,r}}} = \tilde {\Sigma }_{r}^{{0,1}}e_{0}^{ - } - \frac{1}{3}{{v}_{\vartheta }}{{v}_{z}}\left( {{{A}_{{i - 1/2}}} + Cd_{0}^{ - }} \right),$(2.1.19)
$\zeta _{{i + 1/2}}^{0} = \xi _{i}^{0}\zeta _{{i - 1/2}}^{0} + \eta _{i}^{0},\quad \zeta _{{i - 1/2}}^{r} = \xi _{i}^{r}\zeta _{{i - 1/2}}^{0} + \eta _{i}^{r},$(2.1.20)
$\begin{gathered} {{\xi }_{i}} = - W_{i}^{{ - 1}}{{{\mathbf{B}}}_{i}},\quad {{\eta }_{i}} = W_{i}^{{ - 1}}{{{\mathbf{Q}}}_{i}}, \\ {{W}_{i}} = \left( {\begin{array}{*{20}{c}} {a_{i}^{0} + c_{i}^{0}\xi _{{i + 1}}^{1}}&{d_{i}^{0}} \\ {a_{i}^{1} + c_{i}^{1}\xi _{{i + 1}}^{1}}&{d_{i}^{1}} \end{array}} \right),\quad {{{\mathbf{B}}}_{i}} = \left( {\begin{array}{*{20}{c}} {b_{i}^{0}} \\ {b_{i}^{1}} \end{array}} \right),\quad {{{\mathbf{Q}}}_{i}} = \left( {\begin{array}{*{20}{c}} {q_{i}^{0} - c_{i}^{0}\eta _{{i + 1}}^{1}} \\ {q_{i}^{1} - c_{i}^{1}\eta _{{i + 1}}^{1}} \end{array}} \right). \\ \end{gathered} $(2.1.21)
$\zeta _{{I + 1/2}}^{r} = \xi _{{I + 1}}^{r}\zeta _{{I + 1/2}}^{0} + \eta _{{I + 1}}^{r},\quad \xi _{{I + 1}}^{r} = - \frac{{m_{0}^{r}}}{{3m_{1}^{r}}},\quad \eta _{{I + 1}}^{r} = 0,\quad \zeta _{{1/2}}^{0} = \frac{{ - 3l_{1}^{r}\eta _{1}^{r}}}{{3l_{1}^{r}\xi _{1}^{r} + l_{0}^{r}}}.$(2.1.22)
${{\zeta }^{{r,\vartheta ,s + 1/3}}} = \left\{ {{{V}^{r}}{{Q}^{{r,\vartheta }}} - v_{{r0}}^{1}{{v}_{z}}\frac{1}{3}\left( {f_{{j + 1/2}}^{{r,0,s}} - f_{{j - 1/2}}^{{r,0,s}}} \right) + \Delta r{{v}_{z}}{{\delta }^{c}}\frac{1}{3}\left( {f_{{j + 1/2}}^{{0,0,s}} - f_{{j - 1/2}}^{{0,0,s}}} \right) + {{v}_{\vartheta }}{{v}_{z}}{{\delta }^{c}}{{M}_{\vartheta }}C{{f}^{{0,\vartheta ,s}}} - } \right.$Вторая подсистема для величин ${{\zeta }^{{\vartheta ,0,s + 1/3}}}$, ${{\zeta }^{{\vartheta ,r,s + 1/3}}}$, $\zeta _{{i \pm 1/2}}^{{\vartheta ,0,s + 1/3}}$ и $\zeta _{{i \pm 1/2}}^{{\vartheta ,r,s + 1/3}}$ состоит из двух первых уравнений в подсистеме уравнений (2.1.10), дополнительных уравнений (1.2.30) и граничных условий (2.1.13). Для ее решения исключим из нее посредством дополнительных уравнений (1.2.30) величины ${{\zeta }^{{\vartheta ,0,s + 1/3}}}$ и ${{\zeta }^{{\vartheta ,r,s + 1/3}}}$, чтобы получить двухточечную систему для величин $\zeta _{{i \pm 1/2}}^{{\vartheta ,0,s + 1/3}}$ и $\zeta _{{i \pm 1/2}}^{{\vartheta ,r,s + 1/3}}$:
(2.1.23)
$\zeta _{{i + 1/2}}^{{\vartheta ,0,s + 1/3}}{{a}^{{\vartheta ,\alpha }}} + \zeta _{{i - 1/2}}^{{\vartheta ,0,s + 1/3}}{{b}^{{\vartheta ,\alpha }}} + \zeta _{{i + 1/2}}^{{\vartheta ,r,s + 1/3}}{{c}^{{\vartheta ,\alpha }}} + \zeta _{{i - 1/2}}^{{\vartheta ,r,s + 1/3}}{{d}^{{\vartheta ,\alpha }}} = {{q}^{{\vartheta ,\alpha }}},\quad \alpha = 0,r,$(2.1.24)
${{a}^{{\vartheta ,r}}} = \tilde {\Sigma }_{r}^{{\vartheta ,1}}\frac{1}{4} + v_{\vartheta }^{1}{{v}_{z}}\frac{1}{3}\left( {{{A}_{{i + 1/2}}} - C\frac{1}{2}} \right),\quad {{b}^{{\vartheta ,r}}} = - \tilde {\Sigma }_{r}^{{\vartheta ,1}}\frac{1}{4} - v_{\vartheta }^{1}{{v}_{z}}\frac{1}{3}\left( {{{A}_{{i - 1/2}}} + C\frac{1}{2}} \right),$(2.1.25)
$\begin{gathered} {{\zeta }^{{\vartheta ,\vartheta ,s + 1/3}}} = {{\left\{ {{{V}^{\vartheta }}{{Q}^{{\vartheta ,\vartheta }}} - \Delta r{{v}_{\vartheta }}{{v}_{z}}\frac{1}{3}\left[ {\frac{1}{2}\left( {f_{{j + 1/2}}^{{0,0,s}} + f_{{j - 1/2}}^{{0,0,s}}} \right) - {{f}^{{0,0,s}}}} \right] - \left( {{{\sigma }^{{11}}}{{V}^{\vartheta }} + M_{\vartheta }^{\vartheta }Cv_{\vartheta }^{1}{{v}_{z}}} \right){{f}^{{\vartheta ,\vartheta ,s}}}} \right\}} \mathord{\left/ {\vphantom {{\left\{ {{{V}^{\vartheta }}{{Q}^{{\vartheta ,\vartheta }}} - \Delta r{{v}_{\vartheta }}{{v}_{z}}\frac{1}{3}\left[ {\frac{1}{2}\left( {f_{{j + 1/2}}^{{0,0,s}} + f_{{j - 1/2}}^{{0,0,s}}} \right) - {{f}^{{0,0,s}}}} \right] - \left( {{{\sigma }^{{11}}}{{V}^{\vartheta }} + M_{\vartheta }^{\vartheta }Cv_{\vartheta }^{1}{{v}_{z}}} \right){{f}^{{\vartheta ,\vartheta ,s}}}} \right\}} {\Sigma _{r}^{{\vartheta ,1}}}}} \right. \kern-0em} {\Sigma _{r}^{{\vartheta ,1}}}}, \\ {{\zeta }^{{\vartheta ,z,s + 1/3}}} = {{\left\{ {{{V}^{\vartheta }}{{Q}^{{\vartheta ,z}}} - {{v}_{r}}v_{\vartheta }^{1}\frac{1}{3}\left( {f_{{k + 1/2}}^{{\vartheta ,0,s}} - f_{{k - 1/2}}^{{\vartheta ,0,s}}} \right) - {{\sigma }^{{11}}}{{V}^{\vartheta }}{{f}^{{\vartheta ,z,s}}}} \right\}} \mathord{\left/ {\vphantom {{\left\{ {{{V}^{\vartheta }}{{Q}^{{\vartheta ,z}}} - {{v}_{r}}v_{\vartheta }^{1}\frac{1}{3}\left( {f_{{k + 1/2}}^{{\vartheta ,0,s}} - f_{{k - 1/2}}^{{\vartheta ,0,s}}} \right) - {{\sigma }^{{11}}}{{V}^{\vartheta }}{{f}^{{\vartheta ,z,s}}}} \right\}} {\Sigma _{r}^{{\vartheta ,1}}}}} \right. \kern-0em} {\Sigma _{r}^{{\vartheta ,1}}}}. \\ \end{gathered} $Третья подсистема для величин ${{\zeta }^{{z,0,s + 1/3}}}$, ${{\zeta }^{{z,r,s + 1/3}}}$, $\zeta _{{i \pm 1/2}}^{{z,0,s + 1/3}}$ и $\zeta _{{i \pm 1/2}}^{{z,r,s + 1/3}}$ состоит из двух первых уравнений в подсистеме уравнений (2.1.11), дополнительных уравнений (1.2.31) и граничных условий (2.1.13). Для ее решения исключим из нее посредством дополнительных уравнений (1.2.31) величины ${{\zeta }^{{z,0,s + 1/3}}}$ и ${{\zeta }^{{z,r,s + 1/3}}}$, чтобы получить двухточечную систему для величин $\zeta _{{i \pm 1/2}}^{{z,0,s + 1/3}}$ и $\zeta _{{i \pm 1/2}}^{{z,r,s + 1/3}}$:
(2.1.26)
$\zeta _{{i + 1/2}}^{{z,0,s + 1/3}}{{a}^{{z,\alpha }}} + \zeta _{{i - 1/2}}^{{z,0,s + 1/3}}{{b}^{{z,\alpha }}} + \zeta _{{i + 1/2}}^{{z,r,s + 1/3}}{{c}^{{z,\alpha }}} + \zeta _{{i - 1/2}}^{{z,r,s + 1/3}}{{d}^{{z,\alpha }}} = {{q}^{{z,\alpha }}},\quad \alpha = 0,r,$(2.1.27)
${{a}^{{z,r}}} = \tilde {\Sigma }_{r}^{{z,1}}\frac{1}{4} + v_{z}^{1}{{v}_{\vartheta }}\frac{1}{3}\left( {{{A}_{{i + 1/2}}} - C\frac{1}{2}} \right),\quad {{b}^{{z,r}}} = - \tilde {\Sigma }_{r}^{{z,1}}\frac{1}{4} - v_{z}^{1}{{v}_{\vartheta }}\frac{1}{3}\left( {{{A}_{{i - 1/2}}} + C\frac{1}{2}} \right),$(2.1.28)
$\begin{gathered} {{\zeta }^{{z,\vartheta ,s + 1/3}}} = {{\left\{ {{{V}^{z}}{{Q}^{{z,\vartheta }}} - \Delta rv_{z}^{1}\frac{1}{3}\left( {f_{{j + 1/2}}^{{z,0,s}} - f_{{j - 1/2}}^{{z,0,s}}} \right) - \left( {{{\sigma }^{{11}}}{{V}^{z}} + M_{\vartheta }^{z}Cv_{z}^{1}{{v}_{\vartheta }}} \right){{f}^{{z,\vartheta ,s}}}} \right\}} \mathord{\left/ {\vphantom {{\left\{ {{{V}^{z}}{{Q}^{{z,\vartheta }}} - \Delta rv_{z}^{1}\frac{1}{3}\left( {f_{{j + 1/2}}^{{z,0,s}} - f_{{j - 1/2}}^{{z,0,s}}} \right) - \left( {{{\sigma }^{{11}}}{{V}^{z}} + M_{\vartheta }^{z}Cv_{z}^{1}{{v}_{\vartheta }}} \right){{f}^{{z,\vartheta ,s}}}} \right\}} {\Sigma _{r}^{{z,1}}}}} \right. \kern-0em} {\Sigma _{r}^{{z,1}}}}, \\ {{\zeta }^{{z,z,s + 1/3}}} = {{\left\{ {{{V}^{z}}{{Q}^{{z,z}}} - V\frac{1}{3}\left[ {\frac{1}{2}\left( {f_{{k + 1/2}}^{{0,0,s}} + f_{{k - 1/2}}^{{0,0,s}}} \right) - {{f}^{{0,0,s}}}} \right] - {{\sigma }^{{11}}}{{V}^{z}}{{f}^{{z,z,s}}}} \right\}} \mathord{\left/ {\vphantom {{\left\{ {{{V}^{z}}{{Q}^{{z,z}}} - V\frac{1}{3}\left[ {\frac{1}{2}\left( {f_{{k + 1/2}}^{{0,0,s}} + f_{{k - 1/2}}^{{0,0,s}}} \right) - {{f}^{{0,0,s}}}} \right] - {{\sigma }^{{11}}}{{V}^{z}}{{f}^{{z,z,s}}}} \right\}} {\Sigma _{r}^{{z,1}}}}} \right. \kern-0em} {\Sigma _{r}^{{z,1}}}}. \\ \end{gathered} $(2.1.29)
$\begin{gathered} V\omega _{\vartheta }^{{(s + 1)}}{{\zeta }^{{0,r,s + 2/3}}} + \frac{1}{3}{{\sigma }^{{11}}}V{{\zeta }^{{0,r,s + 2/3}}} = V{{\zeta }^{{0,r,s + 1/3}}}, \\ V\omega _{\vartheta }^{{(s + 1)}}{{\zeta }^{{0,\vartheta ,s + 2/3}}} + \frac{1}{3}\Delta r{{v}_{z}}\left( {\zeta _{{j + 1/2}}^{{0,0,s + 2/3}} - \zeta _{{j - 1/2}}^{{0,0,s + 2/3}}} \right) + \left( {\frac{1}{3}{{\sigma }^{{11}}}V + {{M}_{\vartheta }}C{{v}_{\vartheta }}{{v}_{z}}} \right){{\zeta }^{{0,\vartheta ,s + 2/3}}} = V{{\zeta }^{{0,\vartheta ,s + 1/3}}}, \\ \end{gathered} $(2.1.30)
${{V}^{r}}\omega _{\vartheta }^{{(s + 1)}}{{\zeta }^{{r,\vartheta ,s + 2/3}}} + v_{{r0}}^{1}{{v}_{z}}\frac{1}{3}\left( {\zeta _{{j + 1/2}}^{{r,0,s + 2/3}} - \zeta _{{j - 1/2}}^{{r,0,s + 2/3}}} \right) - \Delta r{{v}_{z}}{{\delta }^{c}}\frac{1}{3}\left( {\zeta _{{j + 1/2}}^{{0,0,s + 2/3}} - \zeta _{{j - 1/2}}^{{0,0,s + 2/3}}} \right) + $(2.1.31)
${{V}^{\vartheta }}\omega _{\vartheta }^{{(s + 1)}}{{\zeta }^{{\vartheta ,\vartheta ,s + 2/3}}} + \Delta r{{v}_{\vartheta }}{{v}_{z}}\frac{1}{3}\left[ {\frac{1}{2}\left( {\zeta _{{j + 1/2}}^{{0,0,s + 2/3}} + \zeta _{{j - 1/2}}^{{0,0,s + 2/3}}} \right) - {{\zeta }^{{0,0,s + 2/3}}}} \right] + $(2.1.32)
$\begin{gathered} {{V}^{z}}\omega _{\vartheta }^{{(s + 1)}}{{\zeta }^{{z,r,s + 2/3}}} + \frac{1}{3}{{\sigma }^{{11}}}{{V}^{z}}{{\zeta }^{{z,r,s + 2/3}}} = {{V}^{z}}{{\zeta }^{{z,r,s + 1/3}}}, \\ {{V}^{z}}\omega _{\vartheta }^{{(s + 1)}}{{\zeta }^{{z,\vartheta ,s + 2/3}}} + \Delta rv_{z}^{1}\frac{1}{3}\left( {\zeta _{{j + 1/2}}^{{z,0,s + 2/3}} - \zeta _{{j - 1/2}}^{{z,0,s + 2/3}}} \right) + \left( {\frac{1}{3}{{\sigma }^{{11}}}{{V}^{z}} + M_{\vartheta }^{z}Cv_{z}^{1}{{v}_{\vartheta }}} \right){{\zeta }^{{z,\vartheta ,s + 2/3}}} = {{V}^{z}}{{\zeta }^{{z,\vartheta ,s + 1/3}}}, \\ \end{gathered} $(2.1.33)
$l_{0}^{\vartheta }\zeta _{{i,1/2,k}}^{{\beta ,0,s + 2/3}} + 3l_{1}^{\vartheta }\zeta _{{i,1/2,k}}^{{\beta ,\vartheta ,s + 2/3}} = 0,\quad m_{0}^{\vartheta }\zeta _{{i,J + 1/2,k}}^{{\beta ,0,s + 2/3}} + 3m_{1}^{\vartheta }\zeta _{{i,J + 1/2,k}}^{{\beta ,\vartheta ,s + 2/3}} = 0,\quad \beta = 0,r,z.$Система (2.1.29)–(2.1.32) для 16 уравнений, дополненная двумя дополнительными уравнениями для величин ${{\zeta }^{{\vartheta ,0,s + 2/3}}}$и ${{\zeta }^{{\vartheta ,\vartheta ,s + 2/3}}}$, аналогичным (1.2.27), и четырьмя дополнительными уравнениями (1.2.32) и (1.2.33) для величин ${{\zeta }^{{r,0,s + 2/3}}}$, ${{\zeta }^{{r,\vartheta ,s + 2/3}}}$, ${{\zeta }^{{z,0,s + 2/3}}}$ и ${{\zeta }^{{z,\vartheta ,s + 2/3}}}$, а также граничными условиями (2.1.33), может быть решена прямым методом в предположении, что величины с индексом $s + 1{\text{/}}3$ известны с предыдущего шага. Данная система состоит из трех подсистем, которые могут быть решены независимо методом прогонки по переменной $\vartheta $, а также 8 уравнений – второго и четвертого из подсистем уравнений (2.1.29)–(2.1.32), которые могут быть явно разрешены относительно переменных ${{\zeta }^{{0,r,s + 2/3}}}$, ${{\zeta }^{{0,z,s + 2/3}}}$, ${{\zeta }^{{r,r,s + 2/3}}}$, ${{\zeta }^{{r,z,s + 2/3}}}$, ${{\zeta }^{{\vartheta ,r,s + 2/3}}}$, ${{\zeta }^{{\vartheta ,z,s + 2/3}}}$, ${{\zeta }^{{z,r,s + 2/3}}}$ и ${{\zeta }^{{z,z,s + 2/3}}}$.
Первая подсистема относительно величин ${{\zeta }^{{0,0,s + 2/3}}}$, ${{\zeta }^{{0,\vartheta ,s + 2/3}}}$, ${{\zeta }^{{\vartheta ,0,s + 2/3}}}$, ${{\zeta }^{{\vartheta ,\vartheta ,s + 2/3}}}$, $\zeta _{{j \pm 1/2}}^{{0,0,s + 2/3}}$ и $\zeta _{{j \pm 1/2}}^{{0,\vartheta ,s + 2/3}}$ состоит из первого и третьего уравнений в подсистемах уравнений (2.1.29) и (2.1.31) (всего 4 уравнения), дополнительных уравнений (1.2.27) для величин ${{\zeta }^{{\vartheta ,0,s + 2/3}}}$и ${{\zeta }^{{\vartheta ,\vartheta ,s + 2/3}}}$ и граничных условий (2.1.33). Для ее решения мы должны исключить из нее величины ${{\zeta }^{{0,0,s + 2/3}}}$, ${{\zeta }^{{0,\vartheta ,s + 2/3}}}$, ${{\zeta }^{{\vartheta ,0,s + 2/3}}}$, ${{\zeta }^{{\vartheta ,\vartheta ,s + 2/3}}}$, чтобы получить двухточечную систему для величин $\zeta _{{j \pm 1/2}}^{{0,0,s + 2/3}}$ и $\zeta _{{j \pm 1/2}}^{{0,\vartheta ,s + 2/3}}$ [14]. Исключая из первого и третьего уравнений подсистемы (2.1.31) посредством дополнительных уравнений (1.2.27) величины ${{\zeta }^{{\vartheta ,0,s + 2/3}}}$и ${{\zeta }^{{\vartheta ,\vartheta ,s + 2/3}}}$ получим следующую систему линейных уравнений относительно ${{\zeta }^{{0,0,s + 2/3}}}$ и ${{\zeta }^{{0,\vartheta ,s + 2/3}}}$:
(2.1.34)
$\begin{array}{*{20}{c}} {{{a}_{{11}}}{{\zeta }^{{0,0}}} + {{a}_{{12}}}{{\zeta }^{{0,\vartheta }}} = \sum\limits_{k = 1}^5 {c_{1}^{k}{{\zeta }_{k}}} = c_{1}^{1}\zeta _{{j + 1/2}}^{{0,0}} + c_{1}^{2}\zeta _{{j - 1/2}}^{{0,0}} + c_{1}^{3}\zeta _{{j + 1/2}}^{{0,\vartheta }} + c_{1}^{4}\zeta _{{j - 1/2}}^{{0,\vartheta }} + c_{1}^{5},} \\ {{{a}_{{21}}}{{\zeta }^{{0,0}}} + {{a}_{{22}}}{{\zeta }^{{0,\vartheta }}} = \sum\limits_{k = 1}^5 {c_{2}^{k}{{\zeta }_{k}}} = c_{2}^{1}\zeta _{{j + 1/2}}^{{0,0}} + c_{2}^{2}\zeta _{{j - 1/2}}^{{0,0}} + c_{2}^{3}\zeta _{{j + 1/2}}^{{0,\vartheta }} + c_{2}^{4}\zeta _{{j - 1/2}}^{{0,\vartheta }} + c_{2}^{5},} \end{array}$(2.1.35)
$\begin{array}{*{20}{c}} {{{\zeta }^{{0,0}}} = \sum\limits_{k = 1}^5 {x_{1}^{k}{{\zeta }_{k}}} = d_{0}^{ + }\zeta _{{j + 1/2}}^{{0,0}} + d_{0}^{ - }\zeta _{{j - 1/2}}^{{0,0}} + d_{1}^{ + }\zeta _{{j + 1/2}}^{{0,\vartheta }} + d_{1}^{ - }\zeta _{{j - 1/2}}^{{0,\vartheta }} + d,} \\ {{{\zeta }^{{0,\vartheta }}} = \sum\limits_{k = 1}^5 {x_{2}^{k}{{\zeta }_{k}}} = e_{0}^{ + }\zeta _{{j + 1/2}}^{{0,0}} + e_{0}^{ - }\zeta _{{j - 1/2}}^{{0,0}} + e_{1}^{ + }\zeta _{{j + 1/2}}^{{0,\vartheta }} + e_{1}^{ - }\zeta _{{j - 1/2}}^{{0,\vartheta }} + e,} \end{array}$(2.1.36)
${{a}_{{11}}}x_{1}^{k} + {{a}_{{12}}}x_{2}^{k} = c_{1}^{k},\quad {{a}_{{21}}}x_{1}^{k} + {{a}_{{22}}}x_{2}^{k} = c_{2}^{k},\quad k = \overline {1,5} .$(2.1.37)
$\zeta _{{j + 1/2}}^{{0,0,s + 2/3}}{{a}^{{\vartheta ,\alpha }}} + \zeta _{{j - 1/2}}^{{0,0,s + 2/3}}{{b}^{{\vartheta ,\alpha }}} + \zeta _{{j + 1/2}}^{{0,\vartheta ,s + 2/3}}{{c}^{{\vartheta ,\alpha }}} + \zeta _{{j - 1/2}}^{{0,\vartheta ,s + 2/3}}{{d}^{{\vartheta ,\alpha }}} = {{q}^{{\vartheta ,\alpha }}},\quad \alpha = 0,\vartheta ,$(2.1.38)
$\begin{gathered} {{q}^{{\vartheta ,0}}} = - \Sigma _{\vartheta }^{{0,0}}d + V{{\zeta }^{{0,0,s + 1/3}}},\quad {{a}^{{\vartheta ,\vartheta }}} = \tilde {\Sigma }_{\vartheta }^{{0,1}}e_{0}^{ + } + \frac{1}{3}\Delta r{{v}_{z}}, \\ {{b}^{{\vartheta ,\vartheta }}} = \tilde {\Sigma }_{\vartheta }^{{0,1}}e_{0}^{ - } - \frac{1}{3}\Delta r{{v}_{z}},\quad {{c}^{{\vartheta ,\vartheta }}} = \tilde {\Sigma }_{\vartheta }^{{0,1}}e_{1}^{ + },\quad {{d}^{{\vartheta ,\vartheta }}} = \tilde {\Sigma }_{\vartheta }^{{0,1}}e_{1}^{ - },\quad {{q}^{{\vartheta ,\vartheta }}} = - \tilde {\Sigma }_{\vartheta }^{{0,1}}e + V{{\zeta }^{{0,\vartheta ,s + 1/3}}}, \\ \end{gathered} $(2.1.39)
$\zeta _{{j + 1/2}}^{0} = \xi _{j}^{0}\zeta _{{j - 1/2}}^{0} + \eta _{j}^{0},\quad \zeta _{{j - 1/2}}^{\vartheta } = \xi _{j}^{\vartheta }\zeta _{{j - 1/2}}^{0} + \eta _{j}^{\vartheta }$(2.1.40)
$\zeta _{{J + 1/2}}^{\vartheta } = \xi _{{J + 1}}^{\vartheta }\zeta _{{J + 1/2}}^{0} + \eta _{{J + 1}}^{\vartheta },\quad \xi _{{J + 1}}^{\vartheta } = - \frac{{m_{0}^{\vartheta }}}{{3m_{1}^{\vartheta }}},\quad \eta _{{J + 1}}^{\vartheta } = 0,\quad \zeta _{{1/2}}^{0} = \frac{{ - 3l_{1}^{\vartheta }\eta _{1}^{\vartheta }}}{{3l_{1}^{\vartheta }\xi _{1}^{\vartheta } + l_{0}^{\vartheta }}}.$При наличии периодического граничного условия на границах $\vartheta = {{\vartheta }_{0}}$ и $\vartheta = {{\vartheta }_{{end}}}$ (1.2.45) вместо граничных условий (2.1.33) следует воспользоваться периодическими граничными условиями для поправок:
(2.1.41)
$\zeta _{{i,1/2,k}}^{{\beta ,0,s + 2/3}} = \zeta _{{i,J + 1/2,k}}^{{\beta ,0,s + 2/3}},\quad \zeta _{{i,1/2,k}}^{{\beta ,\vartheta ,s + 2/3}} = \zeta _{{i,J + 1/2,k}}^{{\beta ,\vartheta ,s + 2/3}},\quad \beta = 0,r,z.$(2.1.44)
$\zeta _{{i,j,k}}^{\vartheta } = \zeta _{{i,j,k}}^{{\vartheta ,a}} + \lambda \zeta _{{i,j,k}}^{{\vartheta ,b}},$(2.1.46)
$\lambda = - \frac{{\zeta _{{i,J + 1/2,k}}^{{0,a}} - \zeta _{{i,1/2,k}}^{{0,a}}}}{{\zeta _{{i,J + 1/2,k}}^{{0,b}} - \zeta _{{i,1/2,k}}^{{0,b}}}}.$Таким образом, для получения искомого решения системы (2.1.37) с граничными условиями (2.1.41) методом циклической прогонки систему (2.1.37) приходится решать дважды с граничными условиями (2.1.42) и (2.1.43) с использованием обычной прогонки для двухточечных систем, а искомое решение получается в результате линейной комбинации (2.1.44) полученных решений. Это приводит к некоторому увеличению объема вычислений по сравнению со случаем наличия условий зеркального отражения, когда достаточно воспользоваться обычной двухточечной прогонкой.
После нахождения величин поправок для потоков на гранях ячейки $\zeta _{{j \pm 1/2}}^{{0,0,s + 2/3}}$ и $\zeta _{{j \pm 1/2}}^{{0,\vartheta ,s + 2/3}}$, поправки ${{\zeta }^{{0,0,s + 2/3}}}$, ${{\zeta }^{{0,\vartheta ,s + 2/3}}}$, ${{\zeta }^{{\vartheta ,0,s + 2/3}}}$ и ${{\zeta }^{{\vartheta ,\vartheta ,s + 2/3}}}$ для средних значений потока вычисляются по явным формулам (2.1.35) и (1.2.27). Величины ${{\zeta }^{{0,r,s + 2/3}}}$, ${{\zeta }^{{0,z,s + 2/3}}}$, ${{\zeta }^{{r,r,s + 2/3}}}$ и ${{\zeta }^{{r,z,s + 2/3}}}$ находятся по явным формулам из последних второго и четвертого уравнений подсистем (2.1.29) и (2.1.31):
(2.1.47)
$\begin{gathered} {{\zeta }^{{0,r,s + 2/3}}} = {{V{{\zeta }^{{0,r,s + 1/3}}}} \mathord{\left/ {\vphantom {{V{{\zeta }^{{0,r,s + 1/3}}}} {\Sigma _{\vartheta }^{{0,1}}}}} \right. \kern-0em} {\Sigma _{\vartheta }^{{0,1}}}},\quad {{\zeta }^{{0,z,s + 2/3}}} = {{V{{\zeta }^{{0,z,s + 1/3}}}} \mathord{\left/ {\vphantom {{V{{\zeta }^{{0,z,s + 1/3}}}} {\Sigma _{\vartheta }^{{0,1}}}}} \right. \kern-0em} {\Sigma _{\vartheta }^{{0,1}}}}, \\ {{\zeta }^{{\vartheta ,r,s + 2/3}}} = {{{{V}^{\vartheta }}{{\zeta }^{{\vartheta ,r,s + 1/3}}}} \mathord{\left/ {\vphantom {{{{V}^{\vartheta }}{{\zeta }^{{\vartheta ,r,s + 1/3}}}} {\Sigma _{\vartheta }^{{\vartheta ,1}}}}} \right. \kern-0em} {\Sigma _{\vartheta }^{{\vartheta ,1}}}},\quad {{\zeta }^{{\vartheta ,z,s + 2/3}}} = {{{{V}^{\vartheta }}{{\zeta }^{{\vartheta ,z,s + 1/3}}}} \mathord{\left/ {\vphantom {{{{V}^{\vartheta }}{{\zeta }^{{\vartheta ,z,s + 1/3}}}} {\Sigma _{\vartheta }^{{\vartheta ,1}}}}} \right. \kern-0em} {\Sigma _{\vartheta }^{{\vartheta ,1}}}},\quad \Sigma _{\vartheta }^{{\vartheta ,1}} = {{V}^{\vartheta }}\left( {\omega _{\vartheta }^{{(s + 1)}} + \frac{1}{3}{{\sigma }^{{11}}}} \right). \\ \end{gathered} $Вторая подсистема для величин ${{\zeta }^{{r,0,s + 2/3}}}$, ${{\zeta }^{{r,\vartheta ,s + 2/3}}}$, $\zeta _{{j \pm 1/2}}^{{r,0,s + 2/3}}$ и $\zeta _{{j \pm 1/2}}^{{r,\vartheta ,s + 2/3}}$ состоит из первого и третьего уравнений в подсистеме уравнений (2.1.30), дополнительных уравнений (1.2.32) и граничных условий (2.1.33). Для ее решения исключим из нее посредством дополнительных уравнений (1.2.32) величины ${{\zeta }^{{r,0,s + 2/3}}}$ и ${{\zeta }^{{r,\vartheta ,s + 2/3}}}$, а также ранее определенные величины $\zeta _{{j \pm 1/2}}^{{0,0,s + 2/3}}$ и $\zeta _{{j \pm 1/2}}^{{0,\vartheta ,s + 2/3}}$, чтобы получить двухточечную систему для величин $\zeta _{{j \pm 1/2}}^{{r,0,s + 2/3}}$ и $\zeta _{{j \pm 1/2}}^{{r,\vartheta ,s + 2/3}}$:
(2.1.48)
$\zeta _{{j + 1/2}}^{{r,0,s + 2/3}}{{a}^{{r,\alpha }}} + \zeta _{{j - 1/2}}^{{r,0,s + 2/3}}{{b}^{{r,\alpha }}} + \zeta _{{j + 1/2}}^{{r,\vartheta ,s + 2/3}}{{c}^{{r,\alpha }}} + \zeta _{{j - 1/2}}^{{r,\vartheta ,s + 2/3}}{{d}^{{r,\alpha }}} = {{q}^{{r,\alpha }}},\quad \alpha = 0,\vartheta ,$(2.1.49)
${{a}^{{r,\vartheta }}} = \tilde {\Sigma }_{\vartheta }^{{r,1}}\frac{1}{4} + v_{{r0}}^{1}{{v}_{z}}\frac{1}{3},\quad {{b}^{{r,\vartheta }}} = - \tilde {\Sigma }_{\vartheta }^{{r,1}}\frac{1}{4} - v_{{r0}}^{1}{{v}_{z}}\frac{1}{3},\quad {{c}^{{r,\vartheta }}} = \tilde {\Sigma }_{\vartheta }^{{r,1}}\frac{1}{2},\quad {{d}^{{r,\vartheta }}} = \tilde {\Sigma }_{\vartheta }^{{r,1}}\frac{1}{2},$(2.1.50)
${{\zeta }^{{r,r,s + 2/3}}} = {{{{V}^{r}}{{\zeta }^{{r,r,s + 1/3}}}} \mathord{\left/ {\vphantom {{{{V}^{r}}{{\zeta }^{{r,r,s + 1/3}}}} {\Sigma _{\vartheta }^{{r,1}}}}} \right. \kern-0em} {\Sigma _{\vartheta }^{{r,1}}}},$ ${{\zeta }^{{r,z,s + 2/3}}} = {{{{V}^{r}}{{\zeta }^{{r,z,s + 1/3}}}} \mathord{\left/ {\vphantom {{{{V}^{r}}{{\zeta }^{{r,z,s + 1/3}}}} {\Sigma _{\vartheta }^{{r,1}}}}} \right. \kern-0em} {\Sigma _{\vartheta }^{{r,1}}}}.$Третья подсистема для величин ${{\zeta }^{{z,0,s + 2/3}}}$, ${{\zeta }^{{z,\vartheta ,s + 2/3}}}$, $\zeta _{{j \pm 1/2}}^{{z,0,s + 2/3}}$ и $\zeta _{{j \pm 1/2}}^{{z,\vartheta ,s + 2/3}}$ состоит из первого и третьего уравнений в подсистеме уравнений (2.1.32), дополнительных уравнений (1.2.33) и граничных условий (2.1.33). Для ее решения исключим из нее посредством дополнительных уравнений (1.2.33) величины ${{\zeta }^{{z,0,s + 2/3}}}$ и ${{\zeta }^{{z,\vartheta ,s + 2/3}}}$, чтобы получить двухточечную систему для величин $\zeta _{{j \pm 1/2}}^{{z,0,s + 2/3}}$ и $\zeta _{{j \pm 1/2}}^{{z,\vartheta ,s + 2/3}}$:
(2.1.51)
$\zeta _{{j + 1/2}}^{{z,0,s + 2/3}}{{a}^{{z,\alpha }}} + \zeta _{{j - 1/2}}^{{z,0,s + 2/3}}{{b}^{{z,\alpha }}} + \zeta _{{j + 1/2}}^{{z,\vartheta ,s + 2/3}}{{c}^{{z,\alpha }}} + \zeta _{{j - 1/2}}^{{z,\vartheta ,s + 2/3}}{{d}^{{z,\alpha }}} = {{q}^{{z,\alpha }}},\quad \alpha = 0,\vartheta ,$(2.1.52)
${{a}^{{z,\vartheta }}}\, = \,\tilde {\Sigma }_{\vartheta }^{{z,1}}\frac{1}{4}\, + \,\Delta rv_{z}^{1}\frac{1}{3},\quad {{b}^{{z,\vartheta }}}\, = \, - {\kern 1pt} \tilde {\Sigma }_{\vartheta }^{{z,1}}\frac{1}{4}\, - \,\Delta rv_{z}^{1}\frac{1}{3},\quad {{c}^{{z,\vartheta }}}\, = \,\tilde {\Sigma }_{\vartheta }^{{z,1}}\frac{1}{2},\quad {{d}^{{z,\vartheta }}}\, = \,\tilde {\Sigma }_{\vartheta }^{{z,1}}\frac{1}{2},\quad {{q}^{{z,\vartheta }}}\, = \,{{V}^{z}}{{\zeta }^{{z,\vartheta ,s + 1/3}}},$(2.1.53)
${{\zeta }^{{z,r,s + 2/3}}} = {{{{V}^{z}}{{\zeta }^{{z,r,s + 1/3}}}} \mathord{\left/ {\vphantom {{{{V}^{z}}{{\zeta }^{{z,r,s + 1/3}}}} {\Sigma _{\vartheta }^{{z,1}}}}} \right. \kern-0em} {\Sigma _{\vartheta }^{{z,1}}}},\quad {{\zeta }^{{z,z,s + 2/3}}} = {{{{V}^{z}}{{\zeta }^{{z,z,s + 1/3}}}} \mathord{\left/ {\vphantom {{{{V}^{z}}{{\zeta }^{{z,z,s + 1/3}}}} {\Sigma _{\vartheta }^{{z,1}}}}} \right. \kern-0em} {\Sigma _{\vartheta }^{{z,1}}}}.$(2.1.54)
$V\omega _{z}^{{(s + 1)}}{{\zeta }^{{0,r,s + 1}}} + \frac{1}{3}{{\sigma }^{{11}}}V{{\zeta }^{{0,r,s + 1}}} = V{{\zeta }^{{0,r,s + 2/3}}},\quad V\omega _{z}^{{(s + 1)}}{{\zeta }^{{0,\vartheta ,s + 1}}} + \frac{1}{3}{{\sigma }^{{11}}}V{{\zeta }^{{0,\vartheta ,s + 1}}} = V{{\zeta }^{{0,\vartheta ,s + 2/3}}},$(2.1.55)
${{V}^{r}}\omega _{z}^{{(s + 1)}}{{\zeta }^{{r,r,s + 1}}} + \frac{1}{3}{{\sigma }^{{11}}}{{V}^{r}}{{\zeta }^{{r,r,s + 1}}} = {{V}^{r}}{{\zeta }^{{r,r,s + 2/3}}},\quad {{V}^{r}}\omega _{z}^{{(s + 1)}}{{\zeta }^{{r,\vartheta ,s + 1}}} + \frac{1}{3}{{\sigma }^{{11}}}{{V}^{r}}{{\zeta }^{{r,\vartheta ,s + 1}}} = {{V}^{r}}{{\zeta }^{{r,\vartheta ,s + 2/3}}},$(2.1.56)
${{V}^{\vartheta }}\omega _{z}^{{(s + 1)}}{{\zeta }^{{\vartheta ,r,s + 1}}} + \frac{1}{3}{{\sigma }^{{11}}}{{V}^{\vartheta }}{{\zeta }^{{\vartheta ,r,s + 1}}} = {{V}^{\vartheta }}{{\zeta }^{{\vartheta ,r,s + 2/3}}},\quad {{V}^{\vartheta }}\omega _{z}^{{(s + 1)}}{{\zeta }^{{\vartheta ,\vartheta ,s + 1}}} + \frac{1}{3}{{\sigma }^{{11}}}{{V}^{\vartheta }}{{\zeta }^{{\vartheta ,\vartheta ,s + 1}}} = {{V}^{\vartheta }}{{\zeta }^{{\vartheta ,\vartheta ,s + 2/3}}},$(2.1.57)
${{V}^{z}}\omega _{z}^{{(s + 1)}}{{\zeta }^{{z,r,s + 1}}} + \frac{1}{3}{{\sigma }^{{11}}}{{V}^{z}}{{\zeta }^{{z,r,s + 1}}} = {{V}^{z}}{{\zeta }^{{z,r,s + 2/3}}},\quad {{V}^{z}}\omega _{z}^{{(s + 1)}}{{\zeta }^{{z,\vartheta ,s + 1}}} + \frac{1}{3}{{\sigma }^{{11}}}{{V}^{z}}{{\zeta }^{{z,\vartheta ,s + 1}}} = {{V}^{z}}{{\zeta }^{{z,\vartheta ,s + 2/3}}},$(2.1.58)
$l_{0}^{z}\zeta _{{i,j,1/2}}^{{\beta ,0,s + 1}} + 3l_{1}^{z}\zeta _{{i,j,1/2}}^{{\beta ,z,s + 1}} = 0,\quad m_{0}^{z}\zeta _{{i,j,K + 1/2}}^{{\beta ,0,s + 1}} + 3m_{1}^{z}\zeta _{{i,j,K + 1/2}}^{{\beta ,z,s + 1}} = 0,\quad \beta = 0,r,\vartheta .$Система (2.1.54)–(2.1.57) для 16 уравнений, дополненная двумя дополнительными уравнениями для величин ${{\zeta }^{{z,0,s + 1}}}$и ${{\zeta }^{{z,z,s + 1}}}$, аналогичным (1.2.28), и четырьмя дополнительными уравнениями (1.2.34) и (1.2.35) для величин ${{\zeta }^{{r,0,s + 1}}}$, ${{\zeta }^{{r,z,s + 1}}}$, ${{\zeta }^{{\vartheta ,0,s + 1}}}$ и ${{\zeta }^{{\vartheta ,z,s + 1}}}$, а также граничными условиями (2.1.58), может быть решена прямым методом в предположении, что величины с индексом $s + 2{\text{/}}3$ известны с предыдущего шага. Данная система состоит из трех подсистем, которые могут быть решены независимо методом прогонки по переменной $z$, а также 8 уравнений – второго и третьего из подсистем уравнений (2.1.54)–(2.1.57), которые могут быть явно разрешены относительно переменных ${{\zeta }^{{0,r,s + 1}}}$, ${{\zeta }^{{0,\vartheta ,s + 1}}}$, ${{\zeta }^{{r,r,s + 1}}}$, ${{\zeta }^{{r,\vartheta ,s + 1}}}$, ${{\zeta }^{{\vartheta ,r,s + 1}}}$, ${{\zeta }^{{\vartheta ,\vartheta ,s + 1}}}$, ${{\zeta }^{{z,r,s + 1}}}$ и ${{\zeta }^{{z,\vartheta ,s + 1}}}$.
Первая подсистема относительно величин ${{\zeta }^{{0,0,s + 1}}}$, ${{\zeta }^{{0,z,s + 1}}}$, ${{\zeta }^{{z,0,s + 1}}}$, ${{\zeta }^{{z,z,s + 1}}}$, $\zeta _{{k \pm 1/2}}^{{0,0,s + 1}}$ и $\zeta _{{k \pm 1/2}}^{{0,z,s + 1}}$ состоит из первого и четвертого уравнений в подсистемах уравнений (2.1.54) и (2.1.57) (всего 4 уравнения), дополнительных уравнений (1.2.28) для величин ${{\zeta }^{{z,0,s + 1}}}$ и ${{\zeta }^{{z,z,s + 1}}}$ и граничных условий (2.1.58). Для ее решения мы должны исключить из нее величины ${{\zeta }^{{0,0,s + 1}}}$, ${{\zeta }^{{0,z,s + 1}}}$, ${{\zeta }^{{z,0,s + 1}}}$, ${{\zeta }^{{z,z,s + 1}}}$, чтобы получить двухточечную систему для величин $\zeta _{{k \pm 1/2}}^{{0,0,s + 1}}$ и $\zeta _{{k \pm 1/2}}^{{0,z,s + 1}}$ [14]. Исключая из первого и четвертого уравнений подсистемы (2.1.57) посредством дополнительных уравнений (1.2.28) величины ${{\zeta }^{{z,0,s + 1}}}$ и ${{\zeta }^{{z,z,s + 1}}}$, получаем следующую систему линейных уравнений относительно ${{\zeta }^{{0,0,s + 1}}}$ и ${{\zeta }^{{0,z,s + 1}}}$:
(2.1.59)
$\begin{array}{*{20}{c}} {{{a}_{{11}}}{{\zeta }^{{0,0}}} + {{a}_{{12}}}{{\zeta }^{{0,z}}} = \sum\limits_{i = 1}^5 {c_{1}^{i}{{\zeta }_{i}}} = c_{1}^{1}\zeta _{{k + 1/2}}^{{0,0}} + c_{1}^{2}\zeta _{{k - 1/2}}^{{0,0}} + c_{1}^{3}\zeta _{{k + 1/2}}^{{0,z}} + c_{1}^{4}\zeta _{{k - 1/2}}^{{0,z}} + c_{1}^{5},} \\ {{{a}_{{21}}}{{\zeta }^{{0,0}}} + {{a}_{{22}}}{{\zeta }^{{0,z}}} = \sum\limits_{i = 1}^5 {c_{2}^{i}{{\zeta }_{i}}} = c_{2}^{1}\zeta _{{k + 1/2}}^{{0,0}} + c_{2}^{2}\zeta _{{k - 1/2}}^{{0,0}} + c_{2}^{3}\zeta _{{k + 1/2}}^{{0,z}} + c_{2}^{4}\zeta _{{k - 1/2}}^{{0,z}} + c_{2}^{5},} \end{array}$(2.1.60)
$\begin{array}{*{20}{c}} {{{\zeta }^{{0,0}}} = \sum\limits_{i = 1}^5 {x_{1}^{i}{{\zeta }_{i}}} = d_{0}^{ + }\zeta _{{k + 1/2}}^{{0,0}} + d_{0}^{ - }\zeta _{{k - 1/2}}^{{0,0}} + d_{1}^{ + }\zeta _{{k + 1/2}}^{{0,z}} + d_{1}^{ - }\zeta _{{k - 1/2}}^{{0,z}} + d,} \\ {{{\zeta }^{{0,z}}} = \sum\limits_{i = 1}^5 {x_{2}^{i}{{\zeta }_{i}}} = e_{0}^{ + }\zeta _{{k + 1/2}}^{{0,0}} + e_{0}^{ - }\zeta _{{k - 1/2}}^{{0,0}} + e_{1}^{ + }\zeta _{{k + 1/2}}^{{0,z}} + e_{1}^{ - }\zeta _{{k - 1/2}}^{{0,z}} + e,} \end{array}$(2.1.61)
${{a}_{{11}}}x_{1}^{i} + {{a}_{{12}}}x_{2}^{i} = c_{1}^{i},\quad {{a}_{{21}}}x_{1}^{i} + {{a}_{{22}}}x_{2}^{i} = c_{2}^{i},\quad i = \overline {1,5} .$(2.1.62)
$\zeta _{{k + 1/2}}^{{0,0,s + 1}}{{a}^{{z,\alpha }}} + \zeta _{{k - 1/2}}^{{0,0,s + 1}}{{b}^{{z,\alpha }}} + \zeta _{{k + 1/2}}^{{0,z,s + 1}}{{c}^{{z,\alpha }}} + \zeta _{{k - 1/2}}^{{0,z,s + 1}}{{d}^{{z,\alpha }}} = {{q}^{{z,\alpha }}},\quad \alpha = 0,z,$(2.1.63)
${{a}^{{z,z}}} = \Sigma _{z}^{{0,1}}e_{0}^{ + } + \frac{1}{3}{{v}_{r}}{{v}_{\vartheta }},\quad {{b}^{{z,z}}} = \Sigma _{z}^{{0,1}}e_{0}^{ - } - \frac{1}{3}{{v}_{r}}{{v}_{\vartheta }},\quad {{c}^{{z,z}}} = \Sigma _{z}^{{0,1}}e_{1}^{ + },\quad {{d}^{{z,z}}} = \Sigma _{z}^{{0,1}}e_{1}^{ - },$(2.1.64)
$\zeta _{{k + 1/2}}^{0} = \xi _{k}^{0}\zeta _{{k - 1/2}}^{0} + \eta _{k}^{0},\quad \zeta _{{k - 1/2}}^{z} = \xi _{k}^{z}\zeta _{{k - 1/2}}^{0} + \eta _{k}^{z}$(2.1.65)
$\zeta _{{K + 1/2}}^{z} = \xi _{{K + 1}}^{z}\zeta _{{K + 1/2}}^{0} + \eta _{{K + 1}}^{z},\quad \xi _{{K + 1}}^{z} = - \frac{{m_{0}^{z}}}{{3m_{1}^{z}}},\quad \eta _{{K + 1}}^{z} = 0,\quad \zeta _{{1/2}}^{0} = \frac{{ - 3l_{1}^{z}\eta _{1}^{z}}}{{3l_{1}^{z}\xi _{1}^{z} + l_{0}^{z}}}.$После нахождения величин поправок для потоков на гранях ячейки $\zeta _{{k \pm 1/2}}^{{0,0,s + 1}}$ и $\zeta _{{k \pm 1/2}}^{{0,z,s + 1}}$, поправки ${{\zeta }^{{0,0,s + 1}}}$, ${{\zeta }^{{0,z,s + 1}}}$, ${{\zeta }^{{z,0,s + 1}}}$ и ${{\zeta }^{{z,z,s + 1}}}$ для средних значений потока вычисляются по явным формулам (2.1.60) и (1.2.28). Величины ${{\zeta }^{{0,r,s + 1}}}$, ${{\zeta }^{{0,\vartheta ,s + 1}}}$, ${{\zeta }^{{z,r,s + 1}}}$ и ${{\zeta }^{{z,\vartheta ,s + 1}}}$ находятся по явным формулам из второго и третьего уравнений подсистем (2.1.54) и (2.1.57):
(2.1.66)
$\begin{gathered} {{\zeta }^{{0,r,s + 1}}} = {{V{{\zeta }^{{0,r,s + 2/3}}}} \mathord{\left/ {\vphantom {{V{{\zeta }^{{0,r,s + 2/3}}}} {\Sigma _{z}^{{0,1}}}}} \right. \kern-0em} {\Sigma _{z}^{{0,1}}}},\quad {{\zeta }^{{0,\vartheta ,s + 1}}} = {{V{{\zeta }^{{0,\vartheta ,s + 2/3}}}} \mathord{\left/ {\vphantom {{V{{\zeta }^{{0,\vartheta ,s + 2/3}}}} {\Sigma _{z}^{{0,1}}}}} \right. \kern-0em} {\Sigma _{z}^{{0,1}}}}, \\ {{\zeta }^{{z,r,s + 1}}} = {{{{V}^{z}}{{\zeta }^{{z,r,s + 2/3}}}} \mathord{\left/ {\vphantom {{{{V}^{z}}{{\zeta }^{{z,r,s + 2/3}}}} {\Sigma _{z}^{{z,1}}}}} \right. \kern-0em} {\Sigma _{z}^{{z,1}}}},\quad {{\zeta }^{{z,\vartheta ,s + 1}}} = {{{{V}^{z}}{{\zeta }^{{z,\vartheta ,s + 2/3}}}} \mathord{\left/ {\vphantom {{{{V}^{z}}{{\zeta }^{{z,\vartheta ,s + 2/3}}}} {\Sigma _{z}^{{z,1}}}}} \right. \kern-0em} {\Sigma _{z}^{{z,1}}}},\quad \Sigma _{z}^{{z,1}} = {{V}^{z}}\left( {\omega _{z}^{{(s + 1)}} + \frac{1}{3}{{\sigma }^{{11}}}} \right). \\ \end{gathered} $Вторая подсистема для величин ${{\zeta }^{{r,0,s + 1}}}$, ${{\zeta }^{{r,z,s + 1}}}$, $\zeta _{{k \pm 1/2}}^{{r,0,s + 1}}$ и $\zeta _{{k \pm 1/2}}^{{r,z,s + 1}}$ состоит из первого и четвертого уравнений в подсистеме уравнений (2.1.55), дополнительных уравнений (1.2.34) и граничных условий (2.1.58). Для ее решения исключим из нее посредством дополнительных уравнений (1.2.34) величины ${{\zeta }^{{r,0,s + 1}}}$ и ${{\zeta }^{{r,z,s + 1}}}$, чтобы получить двухточечную систему для величин $\zeta _{{k \pm 1/2}}^{{r,0,s + 1}}$ и $\zeta _{{k \pm 1/2}}^{{r,z,s + 1}}$:
(2.1.67)
$\zeta _{{k + 1/2}}^{{r,0,s + 1}}{{a}^{{r,\alpha }}} + \zeta _{{k - 1/2}}^{{r,0,s + 1}}{{b}^{{r,\alpha }}} + \zeta _{{k + 1/2}}^{{r,z,s + 1}}{{c}^{{r,\alpha }}} + \zeta _{{k - 1/2}}^{{r,z,s + 1}}{{d}^{{r,\alpha }}} = {{q}^{{r,\alpha }}},\quad \alpha = 0,z,$(2.1.68)
${{a}^{{r,z}}} = \Sigma _{z}^{{r,1}}\frac{1}{4} + v_{r}^{1}{{v}_{\vartheta }}\frac{1}{3},\quad {{b}^{{r,z}}} = - \Sigma _{z}^{{r,1}}\frac{1}{4} - v_{r}^{1}{{v}_{\vartheta }}\frac{1}{3},\quad {{c}^{{r,z}}} = \Sigma _{z}^{{r,1}}\frac{1}{2},\quad {{d}^{{r,z}}} = \Sigma _{z}^{{r,1}}\frac{1}{2},\quad {{q}^{{r,z}}} = {{V}^{r}}{{\zeta }^{{r,z,s + 2/3}}},$(2.1.69)
${{\zeta }^{{r,r,s + 1}}} = {{{{V}^{r}}{{\zeta }^{{r,r,s + 2/3}}}} \mathord{\left/ {\vphantom {{{{V}^{r}}{{\zeta }^{{r,r,s + 2/3}}}} {\Sigma _{z}^{{r,1}}}}} \right. \kern-0em} {\Sigma _{z}^{{r,1}}}},\quad {{\zeta }^{{r,\vartheta ,s + 1}}} = {{{{V}^{r}}{{\zeta }^{{r,\vartheta ,s + 2/3}}}} \mathord{\left/ {\vphantom {{{{V}^{r}}{{\zeta }^{{r,\vartheta ,s + 2/3}}}} {\Sigma _{z}^{{r,1}}}}} \right. \kern-0em} {\Sigma _{z}^{{r,1}}}}.$Третья подсистема для величин ${{\zeta }^{{\vartheta ,0,s + 1}}}$, ${{\zeta }^{{\vartheta ,z,s + 1}}}$, $\zeta _{{k \pm 1/2}}^{{\vartheta ,0,s + 1}}$ и $\zeta _{{k \pm 1/2}}^{{\vartheta ,z,s + 1}}$ состоит из первого и четвертого уравнений в подсистеме уравнений (2.1.56), дополнительных уравнений (1.2.35) и граничных условий (2.1.58). Для ее решения исключим из нее посредством дополнительных уравнений (1.2.35) величины ${{\zeta }^{{\vartheta ,0,s + 1}}}$ и ${{\zeta }^{{\vartheta ,z,s + 1}}}$, чтобы получить двухточечную систему для величин $\zeta _{{k \pm 1/2}}^{{\vartheta ,0,s + 1}}$ и $\zeta _{{k \pm 1/2}}^{{\vartheta ,z,s + 1}}$:
(2.1.70)
$\zeta _{{k + 1/2}}^{{\vartheta ,0,s + 1}}{{a}^{{\vartheta ,\alpha }}} + \zeta _{{k - 1/2}}^{{\vartheta ,0,s + 1}}{{b}^{{\vartheta ,\alpha }}} + \zeta _{{k + 1/2}}^{{\vartheta ,z,s + 1}}{{c}^{{\vartheta ,\alpha }}} + \zeta _{{k - 1/2}}^{{\vartheta ,z,s + 1}}{{d}^{{\vartheta ,\alpha }}} = {{q}^{{\vartheta ,\alpha }}},\quad \alpha = 0,z,$(2.1.71)
${{a}^{{\vartheta ,z}}}\, = \,\Sigma _{z}^{{\vartheta ,1}}\frac{1}{4}\, + \,{{v}_{r}}v_{\vartheta }^{1}\frac{1}{3},\quad {{b}^{{\vartheta ,z}}}\, = \, - {\kern 1pt} \Sigma _{z}^{{\vartheta ,1}}\frac{1}{4}\, - \,{{v}_{r}}v_{\vartheta }^{1}\frac{1}{3},\quad {{c}^{{\vartheta ,z}}}\, = \,\Sigma _{z}^{{\vartheta ,1}}\frac{1}{2},\quad {{d}^{{\vartheta ,z}}}\, = \,\Sigma _{z}^{{\vartheta ,1}}\frac{1}{2},\quad {{q}^{{\vartheta ,z}}}\, = \,{{V}^{\vartheta }}{{\zeta }^{{\vartheta ,z,s + 2/3}}},$(2.1.72)
${{\zeta }^{{\vartheta ,r,s + 1}}} = {{{{V}^{\vartheta }}{{\zeta }^{{\vartheta ,r,s + 2/3}}}} \mathord{\left/ {\vphantom {{{{V}^{\vartheta }}{{\zeta }^{{\vartheta ,r,s + 2/3}}}} {\Sigma _{z}^{{\vartheta ,1}}}}} \right. \kern-0em} {\Sigma _{z}^{{\vartheta ,1}}}},\quad {{\zeta }^{{\vartheta ,\vartheta ,s + 1}}} = {{{{V}^{\vartheta }}{{\zeta }^{{\vartheta ,\vartheta ,s + 2/3}}}} \mathord{\left/ {\vphantom {{{{V}^{\vartheta }}{{\zeta }^{{\vartheta ,\vartheta ,s + 2/3}}}} {\Sigma _{z}^{{\vartheta ,1}}}}} \right. \kern-0em} {\Sigma _{z}^{{\vartheta ,1}}}}.$(2.1.73)
$f_{{k \pm 1/2}}^{{\beta ,\alpha ,s + 1}} = f_{{k \pm 1/2}}^{{\beta ,\alpha ,s}} + {{\tilde {\tau }}_{{s + 1}}}\zeta _{{k \pm 1/2}}^{{\beta ,\alpha ,s + 1}},\quad \beta = 0,r,\vartheta ,\quad \alpha = 0,z.$(2.1.74)
${{f}^{{\beta ,\alpha ,s + 1}}} = {{f}^{{\beta ,\alpha ,s}}} + {{\tilde {\tau }}_{{s + 1}}}{{\zeta }^{{\beta ,\alpha ,s + 1}}},\quad \beta = 0,r,\vartheta ,z,\quad \alpha = 0,r,\vartheta ,z.$Для расчета величин $f_{{i \pm 1/2}}^{{\beta ,\alpha ,s + 1}}$, $\beta = 0,\vartheta ,z$, $\alpha = 0,r$ и $f_{{j \pm 1/2}}^{{\beta ,\alpha ,s + 1}}$, $\beta = 0,r,z$, $\alpha = 0,\vartheta $, используемых, в частности, на следующем шаге алгоритма МР, воспользуемся системами дополнительных уравнений (1.2.26), (1.2.30), (1.2.31) и (1.2.27), (1.2.32), (1.2.33) соответственно. Для определения величин $f_{{i \pm 1/2}}^{{0,0,s + 1}}$ и $f_{{i \pm 1/2}}^{{0,r,s + 1}}$ решается система, следующая из дополнительных уравнений (1.2.26):
(2.1.75)
$f_{{i + 1/2}}^{{0,0,s + 1}}{{a}^{{r,\alpha }}} + f_{{i - 1/2}}^{{0,0,s + 1}}{{b}^{{r,\alpha }}} + f_{{i + 1/2}}^{{0,r,s + 1}}{{c}^{{r,\alpha }}} + f_{{i - 1/2}}^{{0,r,s + 1}}{{d}^{{r,\alpha }}} = {{q}^{{r,\alpha }}},\quad \alpha = 0,r,$(2.1.76)
${{a}^{{r,r}}} = \frac{1}{3}{{A}^{{r,1}}},\quad {{b}^{{r,r}}} = \frac{1}{3}{{B}^{{r,1}}},\quad {{c}^{{r,r}}} = {{A}^{{r,2}}},\quad {{d}^{{r,r}}} = {{B}^{{r,2}}},$(2.1.77)
$f_{{i + 1/2}}^{0} = \xi _{i}^{0}f_{{i - 1/2}}^{0} + \eta _{i}^{0},\quad f_{{i - 1/2}}^{r} = \xi _{i}^{r}f_{{i - 1/2}}^{0} + \eta _{i}^{r}.$(2.1.78)
$f_{{I + 1/2}}^{r} = \xi _{{I + 1}}^{r}f_{{I + 1/2}}^{0} + \eta _{{I + 1}}^{r},\quad \xi _{{I + 1}}^{r} = - \frac{{m_{0}^{r}}}{{3m_{1}^{r}}},\quad \eta _{{I + 1}}^{r} = 0,\quad f_{{1/2}}^{0} = - \frac{{3l_{1}^{r}\eta _{1}^{r}}}{{3l_{1}^{r}\xi _{1}^{r} + l_{0}^{r}}}.$Для определения величин $f_{{i \pm 1/2}}^{{\vartheta ,0,s + 1}}$ и $f_{{i \pm 1/2}}^{{\vartheta ,r,s + 1}}$ решается система, следующая из дополнительных уравнений (1.2.30):
(2.1.79)
$f_{{i + 1/2}}^{{\vartheta ,0,s + 1}}{{a}^{{r,\alpha }}} + f_{{i - 1/2}}^{{\vartheta ,0,s + 1}}{{b}^{{r,\alpha }}} + f_{{i + 1/2}}^{{\vartheta ,r,s + 1}}{{c}^{{r,\alpha }}} + f_{{i - 1/2}}^{{\vartheta ,r,s + 1}}{{d}^{{r,\alpha }}} = {{q}^{{r,\alpha }}},\quad \alpha = 0,r,$(2.1.80)
$\begin{gathered} {{a}^{{r,0}}} = \frac{1}{2},\quad {{b}^{{r,0}}} = \frac{1}{2},\quad {{c}^{{r,0}}} = \frac{3}{4},\quad {{d}^{{r,0}}} = - \frac{3}{4},\quad {{q}^{{r,0}}} = {{f}^{{\vartheta ,0}}}, \\ {{a}^{{r,r}}} = \frac{1}{4},\quad {{b}^{{r,r}}} = - \frac{1}{4},\quad {{c}^{{r,r}}} = \frac{1}{2},\quad {{d}^{{r,r}}} = \frac{1}{2},\quad {{q}^{{r,r}}} = {{f}^{{\vartheta ,r}}}. \\ \end{gathered} $Для определения величин $f_{{i \pm 1/2}}^{{z,0,s + 1}}$ и $f_{{i \pm 1/2}}^{{z,r,s + 1}}$ решается система, следующая из дополнительных уравнений (1.2.31):
(2.1.81)
$f_{{i + 1/2}}^{{z,0,s + 1}}{{a}^{{r,\alpha }}} + f_{{i - 1/2}}^{{z,0,s + 1}}{{b}^{{r,\alpha }}} + f_{{i + 1/2}}^{{z,r,s + 1}}{{c}^{{r,\alpha }}} + f_{{i - 1/2}}^{{z,r,s + 1}}{{d}^{{r,\alpha }}} = {{q}^{{r,\alpha }}},\quad \alpha = 0,r,$(2.1.82)
$\begin{gathered} {{a}^{{r,0}}} = \frac{1}{2},\quad {{b}^{{r,0}}} = \frac{1}{2},\quad {{c}^{{r,0}}} = \frac{3}{4},\quad {{d}^{{r,0}}} = - \frac{3}{4},\quad {{q}^{{r,0}}} = {{f}^{{z,0}}}, \\ {{a}^{{r,r}}} = \frac{1}{4},\quad {{b}^{{r,r}}} = - \frac{1}{4},\quad {{c}^{{r,r}}} = \frac{1}{2},\quad {{d}^{{r,r}}} = \frac{1}{2},\quad {{q}^{{r,r}}} = {{f}^{{z,r}}}. \\ \end{gathered} $Аналогично, для определения величин $f_{{j \pm 1/2}}^{{0,0,s + 1}}$ и $f_{{j \pm 1/2}}^{{0,\vartheta ,s + 1}}$ решается система, задаваемая дополнительными уравнениями (1.2.27):
(2.1.83)
$f_{{j + 1/2}}^{{0,0,s + 1}}{{a}^{{\vartheta ,\alpha }}} + f_{{j - 1/2}}^{{0,0,s + 1}}{{b}^{{\vartheta ,\alpha }}} + f_{{j + 1/2}}^{{0,\vartheta ,s + 1}}{{c}^{{\vartheta ,\alpha }}} + f_{{j - 1/2}}^{{0,\vartheta ,s + 1}}{{d}^{{\vartheta ,\alpha }}} = {{q}^{{\vartheta ,\alpha }}},\quad \alpha = 0,\vartheta ,$(2.1.84)
$\begin{gathered} {{q}^{{\vartheta ,0}}} = {{f}^{{\vartheta ,0}}} + \left( {{{A}^{{\vartheta ,0}}} + {{B}^{{\vartheta ,0}}}} \right){{f}^{{0,0}}} + \left( {{{A}^{{\vartheta ,1}}} + {{B}^{{\vartheta ,1}}}} \right){{f}^{{0,\vartheta }}}, \\ {{a}^{{\vartheta ,\vartheta }}} = \frac{1}{3}{{A}^{{\vartheta ,1}}},\quad {{b}^{{\vartheta ,\vartheta }}} = \frac{1}{3}{{B}^{{\vartheta ,1}}},\quad {{c}^{{\vartheta ,\vartheta }}} = {{A}^{{\vartheta ,2}}},\quad {{d}^{{\vartheta ,\vartheta }}} = {{B}^{{\vartheta ,2}}}, \\ \end{gathered} $(2.1.85)
$f_{{j + 1/2}}^{0} = \xi _{j}^{0}f_{{j - 1/2}}^{0} + \eta _{j}^{0},\quad f_{{j - 1/2}}^{\vartheta } = \xi _{j}^{\vartheta }f_{{j - 1/2}}^{0} + \eta _{j}^{\vartheta },$(2.1.86)
$f_{{J + 1/2}}^{\vartheta } = \xi _{{J + 1}}^{\vartheta }f_{{J + 1/2}}^{0} + \eta _{{J + 1}}^{\vartheta },\quad \xi _{{J + 1}}^{\vartheta } = - \frac{{m_{0}^{\vartheta }}}{{3m_{1}^{\vartheta }}},\quad \eta _{{J + 1}}^{\vartheta } = 0,\quad f_{{1/2}}^{0} = - \frac{{3l_{1}^{\vartheta }\eta _{1}^{\vartheta }}}{{3l_{1}^{\vartheta }\xi _{1}^{\vartheta } + l_{0}^{\vartheta }}}.$При использовании периодических граничных условий:
(2.1.87)
$f_{{1/2}}^{0} = f_{{J + 1/2}}^{0},\quad f_{{1/2}}^{\vartheta } = f_{{J + 1/2}}^{\vartheta },$Для определения величин $f_{{k \pm 1/2}}^{{r,0,s + 1}}$ и $f_{{k \pm 1/2}}^{{r,\vartheta ,s + 1}}$ решается система, следующая из дополнительных уравнений (1.2.32):
(2.1.88)
$f_{{j + 1/2}}^{{r,0,s + 1}}{{a}^{{\vartheta ,\alpha }}} + f_{{j - 1/2}}^{{r,0,s + 1}}{{b}^{{\vartheta ,\alpha }}} + f_{{j + 1/2}}^{{r,\vartheta ,s + 1}}{{c}^{{\vartheta ,\alpha }}} + f_{{j - 1/2}}^{{r,\vartheta ,s + 1}}{{d}^{{\vartheta ,\alpha }}} = {{q}^{{\vartheta ,\alpha }}},\quad \alpha = 0,\vartheta ,$(2.1.89)
$\begin{gathered} {{a}^{{\vartheta ,0}}} = \frac{1}{2},\quad {{b}^{{\vartheta ,0}}} = \frac{1}{2},\quad {{c}^{{\vartheta ,0}}} = \frac{3}{4},\quad {{d}^{{\vartheta ,0}}} = - \frac{3}{4},\quad {{q}^{{\vartheta ,0}}} = {{f}^{{r,0}}}, \\ {{a}^{{\vartheta ,\vartheta }}} = \frac{1}{4},\quad {{b}^{{\vartheta ,\vartheta }}} = - \frac{1}{4},\quad {{c}^{{\vartheta ,\vartheta }}} = \frac{1}{2},\quad {{d}^{{\vartheta ,\vartheta }}} = \frac{1}{2},\quad {{q}^{{\vartheta ,\vartheta }}} = {{f}^{{r,\vartheta }}}. \\ \end{gathered} $Для определения величин $f_{{k \pm 1/2}}^{{z,0,s + 1}}$ и $f_{{k \pm 1/2}}^{{z,\vartheta ,s + 1}}$ решается система, следующая из дополнительных уравнений (1.2.33):
(2.1.90)
$f_{{j + 1/2}}^{{z,0,s + 1}}{{a}^{{\vartheta ,\alpha }}} + f_{{j - 1/2}}^{{z,0,s + 1}}{{b}^{{\vartheta ,\alpha }}} + f_{{j + 1/2}}^{{z,\vartheta ,s + 1}}{{c}^{{\vartheta ,\alpha }}} + f_{{j - 1/2}}^{{z,\vartheta ,s + 1}}{{d}^{{\vartheta ,\alpha }}} = {{q}^{{\vartheta ,\alpha }}},\quad \alpha = 0,\vartheta ,$(2.1.91)
$\begin{gathered} {{a}^{{\vartheta ,0}}} = \frac{1}{2},\quad {{b}^{{\vartheta ,0}}} = \frac{1}{2},\quad {{c}^{{\vartheta ,0}}} = \frac{3}{4},\quad {{d}^{{\vartheta ,0}}} = - \frac{3}{4},\quad {{q}^{{\vartheta ,0}}} = {{f}^{{z,0}}}, \\ {{a}^{{\vartheta ,\vartheta }}} = \frac{1}{4},\quad {{b}^{{\vartheta ,\vartheta }}} = - \frac{1}{4},\quad {{c}^{{\vartheta ,\vartheta }}} = \frac{1}{2},\quad {{d}^{{\vartheta ,\vartheta }}} = \frac{1}{2},\quad {{q}^{{\vartheta ,\vartheta }}} = {{f}^{{z,\vartheta }}}. \\ \end{gathered} $Следует отметить, что в случае использования периодического граничного решения по переменной $\vartheta $ перенормировка решения с использованием ускоряющих поправок, в соответствии с уравнениями (1.2.17), должна производиться на обеих границах $\vartheta = {{\vartheta }_{0}}$ и $\vartheta = {{\vartheta }_{{{\text{end}}}}}$ расчетной области:
(2.1.92)
$\psi _{{1/2}}^{{\beta ,n + 1}} = \psi _{{1/2}}^{{\beta ,n + 1/2}} + \frac{1}{{4\pi }}\left( {f_{{1/2}}^{{\beta ,0}} + 3\eta f_{{1/2}}^{{\beta ,\vartheta }}} \right),\quad \psi _{{J + 1/2}}^{{\beta ,n + 1}} = \psi _{{J + 1/2}}^{{\beta ,n + 1/2}} + \frac{1}{{4\pi }}\left( {f_{{J + 1/2}}^{{\beta ,0}} + 3\eta f_{{J + 1/2}}^{{\beta ,\vartheta }}} \right),\quad \beta = 0,r,z.$Эффективность МР весьма существенно зависит от выбора параметров $\omega _{r}^{{(s + 1)}}$, $\omega _{\vartheta }^{{(s + 1)}}$ и $\omega _{z}^{{(s + 1)}}$. В отличие от метода переменных направлений для двумерной геометрии [2], [12], [15], теоретически обоснованный оптимальный выбор этих параметров отсутствует даже для случая, когда операторы $\hat {R}$, $\hat {\Theta }$ и $\hat {Z}$ являются самосопряженными, имеют положительный (отрицательный) спектр, а также перестановочны.
Однако в рассматриваемом нами общем случае гетерогенной задачи операторы $\hat {R}$, $\hat {\Theta }$ и $\hat {Z}$, вообще говоря, не перестановочны. Следовательно, результаты общей теории по выбору параметров $\omega _{r}^{{(s + 1)}}$, $\omega _{\vartheta }^{{(s + 1)}}$ и $\omega _{z}^{{(s + 1)}}$ в данном случае будут применимы лишь приближенно. Вместе с тем можно попытаться воспользоваться для выбора указанных параметров алгоритмом, аналогичным использованному ранее в симметризованном ADI алгоритме [10], который формально применим и в рассматриваемом нами случае 3D геометрии.
В следующих разделах мы рассмотрим алгоритм для оценки минимального и максимального собственных значений операторов $\hat {R}$, $\hat {\Theta }$ и $\hat {Z}$, используемых в этом подходе, и приведем соотношения для расчета итерационных параметров.
2.2. Оценка границ спектра $r$, $\vartheta $ и $z$ компонент ${{P}_{1}}$ оператора
Достаточно рассмотреть случай оператора $\hat {R}$, так как для операторов $\hat {\Theta }$ и $\hat {Z}$ используется аналогичная процедура. Прежде всего оператор $\hat {R}$ заменяется на оператор ${{\hat {R}}_{a}}$, полученный путем усреднения оператора $\hat {R}$ по переменным $\vartheta $ и $z$. Для этого вычисляются средние по переменным $\vartheta $ и $z$ значения коэффициентов ${{a}^{{r,\alpha }}}$, ${{b}^{{r,\alpha }}}$, ${{c}^{{r,\alpha }}}$ и ${{d}^{{r,\alpha }}}$, $\alpha = 0,r$, из систем (2.1.17), (2.1.18), (2.1.23), (2.1.24) и (2.1.26), (2.1.27) в точке ${{\omega }_{r}} = 0$, величин ${{A}^{{r,0}}}$, ${{A}^{{r,1}}}$, ${{A}^{{r,2}}}$, ${{B}^{{r,0}}}$, ${{B}^{{r,1}}}$ и ${{B}^{{r,2}}}$ из уравнений (1.2.26), величин $d_{0}^{ + }$, $d_{0}^{ - }$, $d_{1}^{ + }$, $d_{1}^{ - }$, $d$, $e_{0}^{ + }$, $e_{0}^{ - }$, $e_{1}^{ + }$, $e_{1}^{ - }$ и $e$ из уравнений (2.1.15). Учитываются также коэффициенты дополнительных уравнений (1.2.30) и (1.2.31). Указанные величины определяют элементы матрицы оператора ${{\hat {R}}_{a}}$, который имеет блочную структуру и может быть представлен в виде
(2.2.1)
${{\hat {R}}_{a}} = \left( {\begin{array}{*{20}{c}} {{{{\hat {C}}}_{0}}\hat {G}_{0}^{{ - 1}}}&0&0&0 \\ 0&{{{{\hat {C}}}_{0}}\hat {G}_{r}^{{ - 1}}}&0&0 \\ 0&0&{{{{\hat {C}}}_{\vartheta }}\hat {G}_{\vartheta }^{{ - 1}}}&0 \\ 0&0&0&{{{{\hat {C}}}_{z}}\hat {G}_{z}^{{ - 1}}} \end{array}} \right).$Оператор ${{\hat {C}}_{\vartheta }}$ преобразует вектор ${\mathbf{g}}_{{i \pm 1/2}}^{\vartheta } = {\text{col}}\{ g_{{i \pm 1/2}}^{{\vartheta ,0}},g_{{i \pm 1/2}}^{{\vartheta ,r}}\} $, определенный на гранях ${{r}_{{i \pm 1/2}}}$ ячеек, в вектор ${\mathbf{q}}_{i}^{\vartheta }$, состоящий из двух компонент вектора правой части ${\mathbf{q}}_{i}^{\vartheta } = {\text{col}}\{ q_{i}^{{\vartheta ,0}},q_{i}^{{\vartheta ,r}}\} $, отнесенных к центрам ячеек: ${{\hat {C}}_{\vartheta }}{{{\mathbf{g}}}^{\vartheta }} = {{{\mathbf{q}}}^{\vartheta }}$. Матрица оператора ${{\hat {C}}_{\vartheta }}$ получается усреднением по переменным $\vartheta $ и $z$ (с весом $v_{\vartheta }^{1}{{v}_{z}}$) матрицы системы (2.1.23). Оператор ${{\hat {G}}_{\vartheta }}$ преобразует вектор ${\mathbf{g}}_{{i \pm 1/2}}^{\vartheta }$ в вектор ${\mathbf{f}}_{i}^{\vartheta } = {\text{col}}\{ f_{i}^{{\vartheta ,0}},f_{i}^{{\vartheta ,r}}\} $, определенный в центрах ячеек: ${{{\mathbf{f}}}^{\vartheta }} = {{\hat {G}}_{\vartheta }}{{{\mathbf{g}}}^{\vartheta }}$. Матрица оператора ${{\hat {G}}_{\vartheta }}$ состоит из матрицы системы (1.2.30).
Оператор ${{\hat {C}}_{z}}$ преобразует вектор ${\mathbf{g}}_{{i \pm 1/2}}^{z} = {\text{col}}\{ g_{{i \pm 1/2}}^{{z,0}},g_{{i \pm 1/2}}^{{z,r}}\} $, определенный на гранях ${{r}_{{i \pm 1/2}}}$ ячеек, в вектор ${\mathbf{q}}_{i}^{z}$, состоящий из двух компонент вектора правой части ${\mathbf{q}}_{i}^{z} = {\text{col}}\{ q_{i}^{{z,0}},q_{i}^{{z,r}}\} $, отнесенных к центрам ячеек: ${{\hat {C}}_{z}}{{{\mathbf{g}}}^{z}} = {{{\mathbf{q}}}^{z}}$. Матрица оператора ${{\hat {C}}_{z}}$ получается усреднением по переменным $\vartheta $ и $z$ матрицы (с весом ${{v}_{\vartheta }}v_{z}^{1}$) системы (2.1.26). Оператор ${{\hat {G}}_{z}}$ преобразует вектор ${\mathbf{g}}_{{i \pm 1/2}}^{z}$ в вектор ${\mathbf{f}}_{i}^{z} = {\text{col}}\{ f_{i}^{{z,0}},f_{i}^{{z,r}}\} $, определенный в центрах ячеек: ${{{\mathbf{f}}}^{z}} = {{\hat {G}}_{z}}{{{\mathbf{g}}}^{z}}$. Матрица оператора ${{\hat {G}}_{z}}$ состоит из матрицы системы (1.2.31).
Для определения минимального и максимального собственных чисел ${{\lambda }_{r}}$ и ${{\Lambda }_{r}}$ оператора ${{\hat {R}}_{a}}$ может быть использован степенной метод [15], [18]:
(2.2.2)
${{\Delta }_{r}} = \mathop {\lim }\limits_{s \to \infty } \lambda _{{(s)}}^{'},\quad \lambda _{{(s + 1)}}^{'} = \frac{{\left\| {{{{\mathbf{y}}}^{{(s + 1)}}}} \right\|}}{{\left\| {{{{\mathbf{f}}}^{{(s)}}}} \right\|}},\quad {{{\mathbf{y}}}^{{(s + 1)}}} = {{\hat {R}}_{a}}{{{\mathbf{f}}}^{{(s)}}},\quad {{{\mathbf{f}}}^{{(s + 1)}}} = \frac{{{{{\mathbf{y}}}^{{(s + 1)}}}}}{{\left\| {{{{\mathbf{y}}}^{{(s + 1)}}}} \right\|}},$(2.2.3)
${1 \mathord{\left/ {\vphantom {1 {{{\lambda }_{r}}}}} \right. \kern-0em} {{{\lambda }_{r}}}} = \mathop {\lim }\limits_{s \to \infty } \lambda _{{(s)}}^{{''}},\quad \lambda _{{(s + 1)}}^{{''}} = \frac{{\left\| {{{{\mathbf{y}}}^{{(s + 1)}}}} \right\|}}{{\left\| {{{{\mathbf{f}}}^{{(s)}}}} \right\|}},\quad {{{\mathbf{y}}}^{{(s + 1)}}} = \hat {R}_{a}^{{ - 1}}{{{\mathbf{f}}}^{{(s)}}},\quad {{{\mathbf{f}}}^{{(s + 1)}}} = \frac{{{{{\mathbf{y}}}^{{(s + 1)}}}}}{{\left\| {{{{\mathbf{y}}}^{{(s + 1)}}}} \right\|}},$Для обращения операторов ${{\hat {G}}_{0}}$, ${{\hat {C}}_{0}}$, ${{\hat {G}}_{r}}$, ${{\hat {C}}_{\vartheta }}$, ${{\hat {G}}_{\vartheta }}$, ${{\hat {C}}_{z}}$, ${{\hat {G}}_{z}}$, входящих в состав оператора ${{\hat {R}}_{a}}$, используется прямой метод, аналогичный использованному при решении систем (1.2.26), (2.1.15)–(2.1.17); (1.2.30), (2.1.23); (1.2.31), (2.1.26).
При расчете максимального собственного значения по радиальной переменной на шаге $s + 1$ решается система уравнений, состоящая из трех подсистем.
Первая подсистема состоит из усредненных по переменным $z$ и $\vartheta $ уравнений (1.2.26), (2.1.15) и (2.1.17). При этом, поскольку решается задача на собственное значение, в уравнениях (2.1.15) постоянные компоненты $d$ и $e$ не учитываются. Исключая из уравнений (1.2.26) величины ${{f}^{{0,0}}}$ и ${{f}^{{0,r}}}$ посредством соотношений (2.1.15), получим двухточечную систему из двух уравнений для определения величин $f_{{i \pm 1/2}}^{{0,0,s + 1}}$ и $f_{{i \pm 1/2}}^{{0,r,s + 1}}$:
(2.2.4)
$f_{{i + 1/2}}^{{0,0,s + 1}}{{a}^{{r,\alpha }}} + f_{{i - 1/2}}^{{0,0,s + 1}}{{b}^{{r,\alpha }}} + f_{{i + 1/2}}^{{0,r,s + 1}}{{c}^{{r,\alpha }}} + f_{{i - 1/2}}^{{0,r,s + 1}}{{d}^{{r,\alpha }}} = f_{i}^{{r,\alpha ,s}}{\text{/}}\Lambda _{r}^{s},\quad \alpha = 0,r,$(2.2.5)
$\begin{gathered} {{c}^{{r,0}}} = {{A}^{{r,1}}} - \left( {{{A}^{{r,0}}} + {{B}^{{r,0}}}} \right)d_{1}^{ + } - \left( {{{A}^{{r,1}}} + {{B}^{{r,1}}}} \right)e_{1}^{ + },\quad {{d}^{{r,0}}} = {{B}^{{r,1}}} - \left( {{{A}^{{r,0}}} + {{B}^{{r,0}}}} \right)d_{1}^{ - } - \left( {{{A}^{{r,1}}} + {{B}^{{r,1}}}} \right)e_{1}^{ - }, \\ {{a}^{{r,r}}} = \frac{1}{3}{{A}^{{r,1}}} - \frac{1}{3}\left( {{{A}^{{r,1}}} + {{B}^{{r,1}}}} \right)d_{0}^{ + } - \left( {{{A}^{{r,2}}} + {{B}^{{r,2}}}} \right)e_{0}^{ + },\quad {{b}^{{r,r}}} = \frac{1}{3}{{B}^{{r,1}}} - \frac{1}{3}\left( {{{A}^{{r,1}}} + {{B}^{{r,1}}}} \right)d_{0}^{ - } - \left( {{{A}^{{r,2}}} + {{B}^{{r,2}}}} \right)e_{0}^{ - }, \\ \end{gathered} $(2.2.6)
$f_{i}^{{0,\alpha ,s + 1}} = {{\left( {f_{{i + 1/2}}^{{0,0,s + 1}}{{a}^{{r,\alpha }}} + f_{{i - 1/2}}^{{0,0,s + 1}}{{b}^{{r,\alpha }}} + f_{{i + 1/2}}^{{0,r,s + 1}}{{c}^{{r,\alpha }}} + f_{{i - 1/2}}^{{0,r,s + 1}}{{d}^{{r,\alpha }}}} \right)} \mathord{\left/ {\vphantom {{\left( {f_{{i + 1/2}}^{{0,0,s + 1}}{{a}^{{r,\alpha }}} + f_{{i - 1/2}}^{{0,0,s + 1}}{{b}^{{r,\alpha }}} + f_{{i + 1/2}}^{{0,r,s + 1}}{{c}^{{r,\alpha }}} + f_{{i - 1/2}}^{{0,r,s + 1}}{{d}^{{r,\alpha }}}} \right)} {{{v}_{i}}}}} \right. \kern-0em} {{{v}_{i}}}},\quad \alpha = 0,r.$Далее определяются компоненты собственного вектора $f_{i}^{{r,0,s + 1}}$ и $f_{i}^{{r,r,s + 1}}$ с помощью явных уравнений (1.2.26). В $r,\;\vartheta ,\;z$ геометрии для случая LD-схемы для обеспечения сходимости степенного метода оценки максимального значения собственного значения оператора по радиальной переменной вес ${{P}_{r}}$ полагается равным $P_{r}^{0} = 0.01$.
Вторая подсистема состоит из уравнений (1.2.30) и (2.1.23). Соответствующая уравнениям (1.2.30) система из двух двухточечных уравнений для определения величин $f_{{i \pm 1/2}}^{{\vartheta ,0,s + 1}}$ и $f_{{i \pm 1/2}}^{{\vartheta ,r,s + 1}}$ имеет вид
(2.2.7)
$f_{{i + 1/2}}^{{\vartheta ,0,s + 1}}{{a}^{{\vartheta ,\alpha }}} + f_{{i - 1/2}}^{{\vartheta ,0,s + 1}}{{b}^{{\vartheta ,\alpha }}} + f_{{i + 1/2}}^{{\vartheta ,r,s + 1}}{{c}^{{\vartheta ,\alpha }}} + f_{{i - 1/2}}^{{\vartheta ,r,s + 1}}{{d}^{{\vartheta ,\alpha }}} = f_{i}^{{\vartheta ,\alpha ,s}}{\text{/}}\Lambda _{r}^{s},\quad \alpha = 0,r,$(2.2.8)
${{a}^{{\vartheta ,0}}} = \frac{1}{2},\quad {{b}^{{\vartheta ,0}}} = \frac{1}{2},\quad {{c}^{{\vartheta ,0}}} = \frac{3}{4},\quad {{d}^{{\vartheta ,0}}} = - \frac{3}{4},\quad {{a}^{{\vartheta ,r}}} = \frac{1}{4},\quad {{b}^{{\vartheta ,r}}} = - \frac{1}{4},\quad {{c}^{{\vartheta ,r}}} = \frac{1}{2},\quad {{d}^{{\vartheta ,r}}} = \frac{1}{2}.$(2.2.9)
$f_{i}^{{\vartheta ,\alpha ,s + 1}} = {{\left( {f_{{i + 1/2}}^{{\vartheta ,0,s + 1}}{{a}^{{\vartheta ,\alpha }}} + f_{{i - 1/2}}^{{\vartheta ,0,s + 1}}{{b}^{{\vartheta ,\alpha }}} + f_{{i + 1/2}}^{{\vartheta ,r,s + 1}}{{c}^{{\vartheta ,\alpha }}} + f_{{i - 1/2}}^{{\vartheta ,r,s + 1}}{{d}^{{\vartheta ,\alpha }}}} \right)} \mathord{\left/ {\vphantom {{\left( {f_{{i + 1/2}}^{{\vartheta ,0,s + 1}}{{a}^{{\vartheta ,\alpha }}} + f_{{i - 1/2}}^{{\vartheta ,0,s + 1}}{{b}^{{\vartheta ,\alpha }}} + f_{{i + 1/2}}^{{\vartheta ,r,s + 1}}{{c}^{{\vartheta ,\alpha }}} + f_{{i - 1/2}}^{{\vartheta ,r,s + 1}}{{d}^{{\vartheta ,\alpha }}}} \right)} {{{v}_{i}}}}} \right. \kern-0em} {{{v}_{i}}}},\quad \alpha = 0,r.$Третья подсистема состоит из уравнений (1.2.31) и (2.1.26). Соответствующая уравнениям (1.2.31) система из двух двухточечных уравнений для определения величин $f_{{i \pm 1/2}}^{{z,0,s + 1}}$ и $f_{{i \pm 1/2}}^{{z,r,s + 1}}$ имеет вид
(2.2.10)
$f_{{i + 1/2}}^{{z,0,s + 1}}{{a}^{{z,\alpha }}} + f_{{i - 1/2}}^{{z,0,s + 1}}{{b}^{{z,\alpha }}} + f_{{i + 1/2}}^{{z,r,s + 1}}{{c}^{{z,\alpha }}} + f_{{i - 1/2}}^{{z,r,s + 1}}{{d}^{{z,\alpha }}} = f_{i}^{{z,\alpha ,s}}{\text{/}}\Lambda _{r}^{s},\quad \alpha = 0,r,$(2.2.11)
${{a}^{{z,0}}} = \frac{1}{2},\quad {{b}^{{z,0}}} = \frac{1}{2},\quad {{c}^{{z,0}}} = \frac{3}{4},\quad {{d}^{{z,0}}} = - \frac{3}{4},\quad {{a}^{{z,r}}} = \frac{1}{4},\quad {{b}^{{z,r}}} = - \frac{1}{4},\quad {{c}^{{z,r}}} = \frac{1}{2},\quad {{d}^{{z,r}}} = \frac{1}{2}.$(2.2.12)
$f_{i}^{{z,\alpha ,s + 1}} = {{\left( {f_{{i + 1/2}}^{{z,0,s + 1}}{{a}^{{z,\alpha }}} + f_{{i - 1/2}}^{{z,0,s + 1}}{{b}^{{z,\alpha }}} + f_{{i + 1/2}}^{{z,r,s + 1}}{{c}^{{z,\alpha }}} + f_{{i - 1/2}}^{{z,r,s + 1}}{{d}^{{z,\alpha }}}} \right)} \mathord{\left/ {\vphantom {{\left( {f_{{i + 1/2}}^{{z,0,s + 1}}{{a}^{{z,\alpha }}} + f_{{i - 1/2}}^{{z,0,s + 1}}{{b}^{{z,\alpha }}} + f_{{i + 1/2}}^{{z,r,s + 1}}{{c}^{{z,\alpha }}} + f_{{i - 1/2}}^{{z,r,s + 1}}{{d}^{{z,\alpha }}}} \right)} {{{v}_{i}}}}} \right. \kern-0em} {{{v}_{i}}}},\quad \alpha = 0,r.$При расчете минимального собственного значения по радиальной переменной на шаге $s + 1$ решается система уравнений, состоящая из трех подсистем.
Первая подсистема состоит из усредненных по переменным $z$ и $\vartheta $ уравнений (2.1.17):
(2.2.13)
$f_{{i + 1/2}}^{{0,0,s + 1}}{{a}^{{r,\alpha }}} + f_{{i - 1/2}}^{{0,0,s + 1}}{{b}^{{r,\alpha }}} + f_{{i + 1/2}}^{{0,r,s + 1}}{{c}^{{r,\alpha }}} + f_{{i - 1/2}}^{{0,r,s + 1}}{{d}^{{r,\alpha }}} = {{v}_{i}}f_{i}^{{r,\alpha ,s}}\lambda _{r}^{s},\quad \alpha = 0,r,$Вторая подсистема состоит из усредненных по переменным $z$ и $\vartheta $ уравнений (2.1.23):
(2.2.14)
$\zeta _{{i + 1/2}}^{{\vartheta ,0,s + 1/3}}{{a}^{{\vartheta ,\alpha }}} + \zeta _{{i - 1/2}}^{{\vartheta ,0,s + 1/3}}{{b}^{{\vartheta ,\alpha }}} + \zeta _{{i + 1/2}}^{{\vartheta ,r,s + 1/3}}{{c}^{{\vartheta ,\alpha }}} + \zeta _{{i - 1/2}}^{{\vartheta ,r,s + 1/3}}{{d}^{{\vartheta ,\alpha }}} = {{v}_{i}}f_{i}^{{\vartheta ,\alpha ,s}}\lambda _{r}^{s},\quad \alpha = 0,r.$Третья подсистема состоит из усредненных по переменным $z$ и $\vartheta $ уравнений (2.1.26):
(2.2.15)
$\zeta _{{i + 1/2}}^{{z,0,s + 1/3}}{{a}^{{z,\alpha }}} + \zeta _{{i - 1/2}}^{{z,0,s + 1/3}}{{b}^{{z,\alpha }}} + \zeta _{{i + 1/2}}^{{z,r,s + 1/3}}{{c}^{{z,\alpha }}} + \zeta _{{i - 1/2}}^{{z,r,s + 1/3}}{{d}^{{z,\alpha }}} = {{v}_{i}}f_{i}^{{z,\alpha ,s}}\lambda _{r}^{s},\quad \alpha = 0,r.$Компоненты ${{\zeta }^{{0,\vartheta }}}$, ${{\zeta }^{{0,z}}}$, ${{\zeta }^{{r,\vartheta }}}$, ${{\zeta }^{{r,z}}}$, ${{\zeta }^{{\vartheta ,\vartheta }}}$, ${{\zeta }^{{\vartheta ,z}}}$, ${{\zeta }^{{z,\vartheta }}}$ и ${{\zeta }^{{z,z}}}$ собственных векторов, отвечающих минимальному и максимальному собственным значениям оператора ${{\hat {R}}_{a}}$, стремятся к нулю и их вкладом можно пренебречь.
При использовании адаптивной коррекции весов схемы выбор весов схемы уточняется в процессе итераций. Поэтому границы спектра собственных значений операторов $\hat {R}$, $\hat {\Theta }$ и $\hat {Z}$ должны, вообще говоря, переоцениваться на каждой внутренней итерации $n$. В этом случае собственные значения и собственные вектора с предыдущей $n - 1$-й внутренней итерации используются как начальное приближение. В итоге среднее число итераций степенного метода при точности расчета собственных значений ${{\varepsilon }_{\lambda }} = {{10}^{{ - 3}}}$ обычно не велико.
2.3. Определение итерационных параметров циклического МР
В двумерном случае [17, разд. 3.4] после оценки границ собственных значений операторов $\hat {R}$ и $\hat {Z}$ для циклического ADI метода с длиной цикла $J$ рассчитываются величины, определяемые соотношениями:
(2.3.1)
$\begin{gathered} a = \sqrt {\frac{{({{\Lambda }_{r}} - {{\lambda }_{r}})({{\Lambda }_{z}} - {{\lambda }_{z}})}}{{({{\Lambda }_{r}} + {{\lambda }_{z}})({{\Lambda }_{z}} + {{\lambda }_{r}})}}} ,\quad \eta = \frac{{1 - a}}{{1 + a}},\quad b = \frac{{{{\Lambda }_{z}} + {{\lambda }_{r}}}}{{{{\Lambda }_{r}} - {{\lambda }_{r}}}}a,\quad t = \frac{{1 - b}}{{1 + b}}, \\ r = \frac{{{{\Lambda }_{z}} + {{\Lambda }_{r}}b}}{{1 + b}},\quad s = \frac{{{{\Lambda }_{z}} - {{\Lambda }_{r}}b}}{{1 + b}}, \\ \end{gathered} $(2.3.2)
${{\omega }_{{r,j}}} = \frac{{r{{\kappa }_{j}} + s}}{{1 + t{{\kappa }_{j}}}},\quad {{\omega }_{{z,j}}} = \frac{{r{{\kappa }_{j}} - s}}{{1 - t{{\kappa }_{j}}}},\quad j = 1,2, \ldots ,J,$В случае когда ${{\lambda }_{r}} = {{\lambda }_{z}} = \lambda $, ${{\Lambda }_{r}} = {{\Lambda }_{z}} = \Lambda $ соотношения (2.3.1), (2.3.2) приобретают вид:
(2.3.3)
$a = \frac{{\Lambda - \lambda }}{{\Lambda + \lambda }},\quad \eta = \frac{\lambda }{\Lambda },\quad b = 1,\quad t = 0,\quad r = \Lambda ,\quad s = 0,\quad {{\omega }_{{r,j}}} = {{\omega }_{{z,j}}} = {{\omega }_{j}} = r{{\kappa }_{j}}.$При выборе остальных параметров алгоритма: длины цикла $J$, критерия и точности сходимости итераций МР, точности расчета границ спектра операторов $\hat {R}$, $\hat {\Theta }$ и $\hat {Z}$ и т.д., позволяющих минимизировать время расчета варианта, использовался опыт задания аналогичных параметров для ADI метода в 2D геометрии [17, разд. 3.4], а также результаты численного эксперимента, в котором в качестве критерия оптимизации $K{{P}_{1}}$ алгоритма выбиралось уменьшение полного времени расчета варианта. В частности, проведенное исследование показало, что использование поточечного критерия сходимости итераций МР для каждой из компонент ${{f}^{{\alpha ,0}}}$, ${{f}^{{\alpha ,r}}}$, ${{f}^{{\alpha ,\vartheta }}}$ и ${{f}^{{\alpha ,z}}}$, ${{P}_{1}}$-системы является чрезмерным. Более приемлемым является критерий сходимости вида
(2.3.4)
$\mathop {\max }\limits_{\tilde {i},\tilde {j},\tilde {k},\gamma } \left| {\frac{{f_{{\tilde {i},\tilde {j},\tilde {k}}}^{{0,\gamma ,s + 1}} - f_{{\tilde {i},\tilde {j},\tilde {k}}}^{{0,\gamma ,s}}}}{{f_{{\tilde {i},\tilde {j},\tilde {k}}}^{{0,\gamma ,s + 1}}}}} \right| < {{\varepsilon }_{{P1}}},\quad f_{{\tilde {i},\tilde {j},\tilde {k}}}^{{0,s}} = \sqrt {{{{\sum\limits_{i \in \tilde {i},j \in \tilde {j},k \in \tilde {k}} {{{V}_{{i,j,k}}}\left( {f_{{i,j,k}}^{{0,\gamma ,s}}} \right)} }}^{2}}} ,\quad \gamma = 0,r,\vartheta ,z,$Численный эксперимент показал, что желательно использовать циклический МР с достаточно большой длиной цикла $J$ (хорошим выбором для большого класса задач является значение $J = 16$) с возрастающей последовательностью ${{\kappa }_{j}}$: ${{\kappa }_{j}} < {{\kappa }_{{j + 1}}}$. Известно [5], [19], что кинетическая часть итерации хорошо подавляет быстроменяющиеся по пространственной переменной компоненты в спектре ошибки. Основное назначение ${{P}_{1}}$ части итерации – это подавление медленно меняющихся по пространственной переменной компонент спектра ошибки, что согласуется с выбором критерия сходимости итераций МР (2.3.4) и вышеуказанной последовательностью шагов в цикле МР.
Оптимальный выбор ${{\varepsilon }_{{P1}}}$ зависит от степени монотонности используемой разностной схемы и длины цикла $J$. Численный эксперимент показал, что при $J \geqslant 8$ для LD и LB-схем в 3D расчете достаточно задать ${{\varepsilon }_{{P1}}} = 0.4$. Использование более высоких точностей ${{\varepsilon }_{{P1}}}$ может лишь незначительно уменьшить число внутренних итераций, но при этом возрастает число итераций МР и соответственно стоимость одной внутренней итерации и полное время расчета.
Численное исследование также показало, что приемлемая точность расчета границ спектра ${{\varepsilon }_{\lambda }} = {{10}^{{ - 3}}}$. Дальнейшее повышение точности расчета границ спектра практически не влияет на число итераций МР. Выход из итерационного цикла происходит либо по достижению заданной точности, либо если число итераций степенного метода превосходит некоторое предельное значение $N_{{\max }}^{\lambda }$ (обычно, $N_{{\max }}^{\lambda } = 200$).
Если число итераций МР превосходит некоторое предельное значение $N_{{\max }}^{{{\text{split}}}}$ (обычно $N_{{\max }}^{{{\text{split}}}} = \max \left( {32,J} \right)$), то осуществляется корректировка выбора шагов алгоритма МР – исходная верхняя граница спектра $\Lambda $ увеличивается в $10 \cdot {{2}^{{n - 1}}}$ раз, где $n = 1,2, \ldots $ – номер корректировки границ спектра. После корректировки верхней границы спектра итерации МР продолжаются (с использованием ранее полученного приближения для поправок) до сходимости, если не возникает необходимости в дополнительной корректировке. Корректировка верхней границы спектра производится до сходимости итераций МР, но не более 10 раз, после чего ускорение в группе отключается и используются чистые кинетические итерации.
Как показал численный эксперимент, в отличие от случая AWDD-схемы, потребность в корректировке выбора шагов алгоритма МР при использовании LD или LB-схем возникает только при решении специально подобранных задач.
Ускорение в группе отключается также по достижению некоторого максимально допустимого числа внутренних итераций (обычно, 60) в группе.
Для предотвращения возможных переполнений целесообразно также осуществлять проверку значения прогоночного коэффициента ${{\xi }^{0}}$ в уравнениях (2.1.19), (2.1.39), (2.1.64), (2.1.77) и (2.1.85). Если абсолютное значение этого коэффициента в некоторой ячейке существенно больше $1$ (в 3D коде обычно используется критерий $\left| {{{\xi }^{0}}} \right| > 2.5$), то ускоряющая коррекция решения на текущей внутренней итерации не производится.
В $r,\;\vartheta ,\;z$ геометрии на границах расчетной области по переменной $\vartheta $ обычно используется либо условие зеркального отражения, либо периодическое граничное условие. Для обеспечения стабильности алгоритма ускорения в случае LB-схемы вес ${{P}_{\vartheta }}$ по переменной $\vartheta $ выбирается равным $P_{\vartheta }^{0} = 0.99$.
2.4. Численный пример использования MP в 3D геометрии
В качестве примера приведем некоторые результаты расчетов пространственного распределения потока нейтронов с энергией E > 0.5 МэВ в РУ ВВЭР-1000/320. Продольное и поперечное сечения расчетной области приведены на фиг. 1 и 2. Для задания исходной геометрии задачи методами комбинаторной геометрии использовался геометрический модуль программы MCU [20]. Комбинаторное задание геометрии затем конвертировалось на сетку задачи c использованием метода трэйсинга (tracing) программой ConDat [21] с поддержанием локального баланса масс в пределах каждой пространственной ячейки за счет введения дополнительных смесей материалов в рамках volume fraction (VF) метода.
Фиг. 2.
Поперечное сечение сектора поворотной симметрии расчетной области РУ ВВЭР-1000/320 при $z = 26.44$ см от низа АЗ.

Расчеты выполнены для 22-х верхних нейтронных групп проблемно-ориентированной константной системы BGL1000_B7 с использованием адаптивной WDD (AWDD) схемы и LD-схемы с коррекцией отрицательных потоков путем использования, аналогично [1], адаптивной WDD-схемы по угловой переменной $\varphi $, которую обозначим как WLD-схема. В качестве критерия сходимости итераций циклического МР с длиной цикла $J = 16$ использовался поблочный критерий (2.3.4) с размером ребра блока $N = 3$ и ${{\varepsilon }_{{P1}}} = 0.4$. При решении задачи для энергетических диапазонов $E > 3$ МэВ и $0.5 < E < 3.0$ МэВ использовались квадратуры Карлсона $E{{S}_{N}}$ [22] и Лебедева ${{L}_{{N,M}}}$ [23] на сфере. Квадратура Лебедева ${{L}_{{N,M}}}$ задается посредством двух параметров: N – порядок квадратуры (число параллелей на полусфере), N = 2, 4, 6, 8; M – порядок аксиальной симметрии квадратуры: M = 1, 2, … . В качестве источника использовался потвэльный источник для 2-й компании 2-го блока Ростовской АЭС.
В табл. 1 приведены пространственные сетки, угловые приближения и расчетные времена для решения задачи на ПК на базе Intel Core i7-6950X, использующем 128 Gb оперативной памяти и 500 Gb быстрой внешней памяти на SSD устройстве.
Таблица 1
| Пространственная $r,\vartheta ,z$ сетка | Схема | Порядок квадратуры Гаусса-Лебедева или $E{{S}_{n}}$ Карлсона | Точность сходимости итераций | Суммарное число внутрен-них итераций | Расчетное время |
|---|---|---|---|---|---|
| 452 × 120 × 304 = = 16 488 960 ячеек | AWDD | ${{L}_{{14,2}}}$ при E > 3.0 МэВ, ${{L}_{{12,2}}}$ при E < 3.0 МэВ | $5 \times {{10}^{{ - 3}}}$ | 329 | 17 ч 59 мин |
| 293 × 120 × 256 = = 9 000 960 ячеек | WLD | ${{L}_{{14,2}}}$ при E > 3.0 МэВ, ${{L}_{{12,2}}}$ при E < 3.0 МэВ | ${{10}^{{ - 3}}}$ | 314 | 13 ч 55 мин |
| 293 × 120 × 256 = = 9 000 960 ячеек | WLD | $E{{S}_{{16}}}$ при E > 3.0 МэВ, $E{{S}_{{12}}}$ при E < 3.0 МэВ | ${{10}^{{ - 3}}}$ | 318 | 12 ч 54 мин |
| 293 × 120 × 256 = = 9 000 960 ячеек | WLD | ${{L}_{{12,2}}}$ при E > 3.0 МэВ, ${{L}_{{10,2}}}$ при E < 3.0 МэВ | ${{10}^{{ - 3}}}$ | 315 | 10 ч 56 мин |
| 268 × 120 × 256 = = 9 000 960 ячеек | WLD | ${{L}_{{12,2}}}$ при E > .0 МэВ, ${{L}_{{8,2}}}$ при E < 3.0 МэВ | ${{10}^{{ - 3}}}$ | 314 | 9 ч 41 мин |
Для WLD-схемы число итераций МР для данной задачи практически постоянно. Оно равно 7 и не зависит от номера итерации и группы. Для AWDD-схемы возникает необходимость в корректировке верхней границы спектра, а число итераций МР колеблется в интервале 11–31 в зависимости от номера внутренней итерации и группы. При использовании WLD-схемы возможно также дальнейшее уменьшение пространственной сетки задачи по радиальной и аксиальной переменным без потери в точности рассчитываемого функционала.
На фиг. 3 приведены азимутальные распределения потока нейтронов с энергией E > 0.5 МэВ при r = 227.50 см (внешний радиус корпуса РУ) и z = 280.06 см (центр АЗ).
Фиг. 3.
Азимутальное распределение потока нейтронов с энергией E > 0.5 МэВ при r = 227.50 см (внешний радиус корпуса РУ) и z = 280.06 см (центр АЗ).
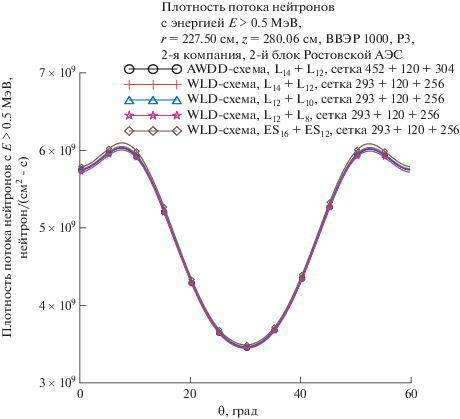
Анализ пространственных распределений в разных характерных точках задачи показывает, что оптимальный с точки зрения минимизации расчетного времени при сохранении необходимой точности расчета выбор угловой сетки задачи достигается при использовании комбинации квадратур ${{L}_{{12,2}}}$ при E > 3.0 МэВ и ${{L}_{{10,2}}}$ при $0.5 < E < 3.0$ МэВ.
2.5. Обсуждение результатов
Как показал численный эксперимент, МР в сочетании с WLD-схемой обычно сходится за 6–7 итераций и это число итераций практически не зависит от номера внутренней итерации и номера группы. Эта существенно лучший результат по сравнению с использованием МР в сочетании с адаптивной WDD (AWDD) схемой. Аналогичная ситуация наблюдается и при решении других задач. Вместе с тем использование WLD-схемы предполагает наличие больших объемов оперативной и быстрой внешней памяти для хранения рабочих массивов задачи, особенно при решении задач с большим числом групп.
Предложенный алгоритм решения ${{P}_{1}}$-системы для ускоряющих поправок используется также и для решения аналогичной ${{P}_{1}}$-системы, возникающей на каждой внешней итерации в алгоритме ускорения внешних итераций по области термализации нейтронов, а также при решении подкритической задачи [7], [24].
Список литературы
Волощенко А.М. $K{{P}_{1}}$-схема ускорения внутренних итераций для уравнения переноса в трехмерной геометрии, согласованная с нодальными схемами I. Основные уравнения и численные результаты // Ж. вычисл. матем. и матем. физ. 2019. Т. 59. № 3. С. 441.
Марчук Г.И., Лебедев В.И. Численные методы в теории переноса нейтронов. М.: Атомиздат, 1981.
Alcouffe R.E. Diffusion synthetic acceleration methods for the diamond-differenced discrete-ordinates equations // Nucl. Sci. and Eng. 1977. V. 64. № 2. P. 344.
Adams M.L., Larsen E.W. Fast iterative methods for discrete-ordinates particle transport calculations // Progress in Nuclear Energy. 2002. V. 40. Issue 1. P. 3.
Lorence L.J., Morel J.E., Larsen E.W. An ${{S}_{2}}$ synthetic acceleration method for the one-dimensional ${{S}_{N}}$ equations with linear discontinuous spatial differencing // Nucl. Sci. Eng. 1989. V. 101. № 2. P. 341.
Khalil H. A nodal diffusion technique for synthetic acceleration of nodal Sncalculations // Nucl. Sci. and Eng. 1985. V. 90. № 3. P. 263.
Voloschenko A.M. Consistent P1 synthetic acceleration scheme for transport equation in 3D geometries. // Proc. of Intern. Conf. on Mathematics and Computation, Supercomputing, Reactor Physics and Nuclear and Biological Applications. Avignon, France, September 12–15, 2005. P. 070.
Волощенко А.М., Воронков А.В., Сычугова Е.П. Согласованная ${{P}_{1}}SA$ схема ускорения внутренних и внешних итераций для уравнения переноса нейтронов и фотонов в одномерных геометриях в пакете РЕАКТОР // Препринт ИПМ им. М.В. Келдыша РАН. 1996. № 2.
CNCSN 2009: One, Two- and Three-Dimensional Coupled Neutral and Charged Particle Discrete Ordinates Parallel Multi-Threaded Code System // RSICC code package CCC-726. 2009.
Волощенко А.М. $K{{P}_{1}}$-схема ускорения внутренних итераций для уравнения переноса в двумерной геометрии, согласованная со взвешенной алмазной схемой // Ж. вычисл. матем. и матем. физ. 2009. Т. 41. № 2. С. 1.
Марчук Г.И. Методы расщепления. М.: Наука, 1988.
Самарский А.А., Николаев Е.С. Методы решения сеточных уравнений. М.: Наука, 1978.
Волощенко А.М., Кондратенко Е.П. $K{{P}_{1}}$-схема ускорения внутренних итераций, согласованная с семейством WLM-WLD схем для уравнения переноса в одномерных геометриях // Препринт ИПМ им. М.В. Келдыша АН СССР, 1986. № 197.
Voloschenko A.M. ${{P}_{1}}SA$-Scheme for Acceleration of Inner Iterations Convergence Consistent with the Weighted Nodal Scheme for Transport Equation in 1D Geometries, // Proc. of International Conference on Mathematics and Computational Methods Applied to Nuclear Science and Engineering (M&C 2011), Rio de Janeiro, RJ, Brazil, May 8–12. 2011.
Федоренко Р.П. Введение в вычислительную физику. М.: Изд. МФТИ, 1994.
Волощенко А.М. Об использовании периодических граничных условий в KP1 методе ускорения внутренних итераций // Тезисы докладов IX Российской научной конференции “Радиационная защита и радиационная безопасность в ядерных технологиях”, 24–26 октября, Обнинск, 2006. С. 39.
Волощенко А.М. KP1-схема ускорения внутренних итераций для уравнения переноса в трехмерной геометрии, согласованная со взвешенной алмазной схемой // Ж. вычисл. матем. и матем. физ. 2001. Т. 49. № 9. С. 1379.
Шишков Л.К. Методы решения диффузионных уравнений двумерного ядерного реактора. М.: Атомиздат, 1976.
Morel J.E., Manteuffel T.A. An angular multigrid acceleration technique for ${{S}_{N}}$ equations with highly forward-peaked scattering // Nucl. Sci. Eng. 1991. V. 107. № 4. P. 330.
Гуревич М.И., Шкаровский Д.А. Расчет переноса нейтронов методом Монте-Карло по программе MCU // Учебное пособие МИФИ, Москва, 2012.
Гуревич М.И., Руссков А.А., Волощенко А.М. ConDat 1.0 – программа преобразования исходных данных из комбинаторной геометрии в растровую с использованием алгоритма трейсинга (tracing). Инструкция для пользователя // Препринт ИПМ им. М.В. Келдыша РАН, № 12. 2007.
Carlson B.G. A method of characteristics and other improvements in solution methods for the transport equation // Nucl. Sci. Eng. 1976. V. 61. P. 408.
Казаков А.Н., Лебедев В.И. Квадратурные формулы типа Гаусса для сферы, инвариантные относительно группы диэдра // Труды Математического института РАН. 1994. Т. 203. С. 100.
Волощенко А.М. Адаптивные положительные аппроксимации и согласованная KP1-схема ускорения итераций для уравнения переноса в задачах радиационной защиты. Докторская диссертация, М., ИПМ им. М.В. Келдыша РАН, 2015, http://www.keldysh.ru/council/3/D00202403/voloshchenko_diss.pdf.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики



