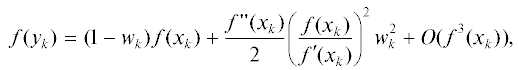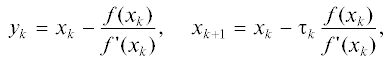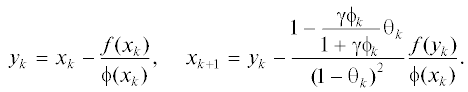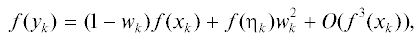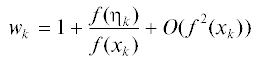Журнал вычислительной математики и математической физики, 2019, T. 59, № 6, стр. 920-936
Семейства оптимальных двух- и трехточечных итераций, не содержащих производные для решения нелинейных уравнений
Т. Жанлав 1, *, Х. Отгондорж 2, **, О. Чулуунбаатар 1, 3, ***
1 Институт математики, Монгольский Государственный университет
14201 Улан-батор, Монголия
2 Факультет прикладных наук, Монгольский Государственный университет
науки и технологии
14191 Улан-батор, Монголия
3 Объединенный институт ядерных исследований
141980 М. О., Дубна, Россия
* E-mail: tzhanlav@yahoo.com
** E-mail: otgondorj@gmail.com
*** E-mail: chuka@jinr.ru
Поступила в редакцию 09.09.2018
После доработки 16.01.2019
Принята к публикации 08.02.2019
Аннотация
В работе впервые даны необходимые и достаточные условия для двух- и трехточечных итерационных методов, не содержащих производные, чтобы иметь оптимальный порядок сходимости. Эти условия могут быть эффективно использованы не только для установления порядка сходимости итерационных методов, но и для конструкции новых методов. Более того, использование метода производящих функций позволяет конструировать широкий класс оптимальных двух- и трехточечных методов, не содержащих производные, который включает в себя много известных методов как частные случаи. Также впервые нашли аналитическую формулу для оптимального выбора параметра итераций, который позволяет увеличить порядок сходимости. Библ. 34. Табл. 6.
1. ВВЕДЕНИЕ
В настоящее время существует много итерационных методов для решения нелинейных уравнений и систем уравнений (см. [1]–[6]). В частности, необходимы методы, не содержащие производные, когда невозможно или затруднительно найти производную функции. Самый простой из них – хорошо известный метод секущих и метод Стефенсона с низким порядком сходимости. В настоящее время весьма важно получить новые оптимальные методы с восьмой степенью сходимости, потому что их индекс эффективности равен ${{8}^{{1/4}}} \approx 1.682$. Такие методы имеют приложения в экспериментальной математике, в теории чисел, в физике высоких энергий, в нелинейном процессе моделирования, в конечном элементе моделирования CAD, в 3D графике, в статистике, безопасности, в криптографии (см. [7]–[9]). В последнее десятилетие были разработаны различные двух- и трехточечные методы, не содержащие производные, с хорошими свойствами сходимости (например, см. [1]–[24], [25]–[33]). Построение итерационных методов высокого порядка сходимости стало возможным благодаря быстрому развитию компьютера, успехам компьютерной арифметики и символьных вычислений. В данной работе предлагаются некоторые семейства итерационных методов, не содержащих производные, основанных на методе производящих функций, предложенном в [5] и оптимальном выборе параметров итераций [6]. Предлагается новый и прямой подход к доказательству порядка сходимости методов без использования символьных вычислений.
Структура работы следующая. В разд. 2 рассмотрены двухточечные итерационные методы, не содержащие производные, и получены необходимые и достаточные условия для того, чтобы они были четвертого порядка сходимости. Предложены также выборы производящих функций для итерационного параметра $\tau $. В частности, получены оптимальные конечно-разностные варианты известных методов Кунга–Трауба, Кинга и Махешвари. В разд. 3 рассмотрены трехточечные итерационные методы, не содержащие производные, и получены также необходимые и достаточные условия для того, чтобы они были восьмого порядка сходимости. Предложен широкий класс оптимальных трехточечных итераций, который содержит в себе много известных методов как частные случаи. Доказана локальная сходимость методов, не используя символьных вычислений. В разд. 4 представлены результаты численных экспериментов, которые подтверждают теоретический вывод о порядке сходимости и сделаны сравнения с другими известными методами.
2. ДВУХТОЧЕЧНЫЕ ИТЕРАЦИОННЫЕ МЕТОДЫ, НЕ СОДЕРЖАЩИЕ ПРОИЗВОДНЫЕ
Рассмотрим следующие двухточечные итерации, не содержащие производные
(2.1b)
${{x}_{{k + 1}}} = {{y}_{k}} - {{\bar {\tau }}_{k}}\frac{{f({{y}_{k}})}}{{\phi ({{x}_{k}})}},$(2.2)
$f{\kern 1pt} '(x) \approx \phi (x) = \frac{{f(x + \gamma f(x)) - f(x)}}{{\gamma f(x)}},\quad \gamma \in R,$(2.6)
$\phi ({{x}_{k}}) = f{\kern 1pt} '({{x}_{k}})\left( {1 + \gamma \frac{{f{\kern 1pt} ''({{x}_{k}})}}{2}\frac{{f({{x}_{k}})}}{{f'({{x}_{k}})}}} \right) + O({{f}^{2}}({{x}_{k}})).$(2.7)
${{w}_{k}} = \frac{1}{{1 + \gamma \frac{{f{\kern 1pt} ''({{x}_{k}})}}{2}\frac{{f({{x}_{k}})}}{{f{\kern 1pt} '({{x}_{k}})}}}} + O({{f}^{2}}({{x}_{k}})) = 1 - \gamma \frac{{f{\kern 1pt} ''({{x}_{k}})}}{2}\frac{{f({{x}_{k}})}}{{f{\kern 1pt} '({{x}_{k}})}} + O({{f}^{2}}({{x}_{k}})),$(2.11)
${{\theta }_{k}} = 1 - {{w}_{k}} + \frac{1}{2}{{w}_{k}}\frac{{f{\kern 1pt} ''({{x}_{k}})f({{x}_{k}})}}{{f{\kern 1pt} '({{x}_{k}})\phi ({{x}_{k}})}} + O({{f}^{2}}({{x}_{k}})).$(2.12)
$w_{k}^{2} - (1 - \gamma \phi ({{x}_{k}})){{w}_{k}} - (1 - {{\theta }_{k}})\gamma \phi ({{x}_{k}}) = O({{f}^{2}}({{x}_{k}})).$(2.14)
${{\theta }_{k}}(\gamma {{\phi }_{k}} - {{a}_{k}}(1 + \gamma {{\phi }_{k}})) = O({{f}^{2}}({{x}_{k}})),\quad {{\phi }_{k}} = \phi ({{x}_{k}}).$(2.16)
${{w}_{k}} = 1 - \frac{{\gamma {{\phi }_{k}}}}{{1 + \gamma {{\phi }_{k}}}}{{\theta }_{k}} + O({{f}^{2}}({{x}_{k}})).$(2.17)
$f({{x}_{{k + 1}}}) = (1 - \frac{{f{\kern 1pt} '({{y}_{k}})}}{{{{\phi }_{k}}}}{{\bar {\tau }}_{k}})f({{y}_{k}}) + O(f{{({{y}_{k}})}^{2}}).$(2.18)
$f{\kern 1pt} '({{y}_{k}}) = f{\kern 1pt} '({{x}_{k}})(1 - \frac{{f{\kern 1pt} ''({{x}_{k}})f({{x}_{k}})}}{{f{\kern 1pt} '({{x}_{k}})\phi ({{x}_{k}})}}) + O({{f}^{2}}({{x}_{k}})).$(2.19)
$f{\kern 1pt} '({{y}_{k}}) = - f{\kern 1pt} '({{x}_{k}})\frac{{{{w}_{k}} + 2({{\theta }_{k}} - 1)}}{{{{w}_{k}}}} + O({{f}^{2}}({{x}_{k}})).$(2.20)
$\frac{1}{{1 - x}} = 1 + x + {{x}^{2}} + {{x}^{3}} + \ldots ,\quad {\text{|}}x{\text{|}} < 1,$(2.21)
$f{\kern 1pt} '({{y}_{k}}) = f{\kern 1pt} '({{x}_{k}})\left( {1 - \frac{2}{{1 + \gamma {{\phi }_{k}}}}{{\theta }_{k}}} \right) + O({{f}^{2}}({{x}_{k}})).$(2.22)
$f({{x}_{{k + 1}}}) = (1 - (1 - {{\hat {d}}_{k}}{{\theta }_{k}}){{\bar {\tau }}_{k}})f({{y}_{k}}) + O(f{{({{y}_{k}})}^{2}}),\quad {{\hat {d}}_{k}} = \frac{{2 + \gamma {{\phi }_{k}}}}{{1 + \gamma {{\phi }_{k}}}}.$Теперь можно доказать следующее:
Теорема 1. Пусть $f(x) \in {{C}^{3}}(I)$ и начальное приближение ${{x}_{0}}$ достаточно близко к простому нулю $x{\kern 1pt} * \in I$ функции $f(x)$. Тогда итерационный метод (2.1) имеет четвертый порядок сходимости тогда и только тогда, когда параметр ${{\bar {\tau }}_{k}}$ в (2.1) удовлетворяет условию
(2.23)
${{\bar {\tau }}_{k}} = \frac{1}{{1 - {{{\hat {d}}}_{k}}{{\theta }_{k}}}} + O({{f}^{2}}({{x}_{k}})) = 1 + {{\hat {d}}_{k}}{{\theta }_{k}} + O({{f}^{2}}({{x}_{k}})).$Доказательство. Предположим, что ${{\bar {\tau }}_{k}}$ в (2.1) удовлетворяет условию (2.23). Тогда
и $f({{y}_{k}}) = O({{f}^{2}}({{x}_{k}}))$ из-за (2.8). Следовательно, в силу (2.22), имеем т.е. порядок сходимости (2.1) равен $4$ при условии (2.23). Обратно, пусть метод (2.1) имеет четвертый порядок сходимости, то есть, (2.24) верно. Тогда из (2.24) и (2.22) следует, что $f({{y}_{k}}) = O({{f}^{2}}({{x}_{k}}))$ и $1 - (1 - {{\hat {d}}_{k}}{{\theta }_{k}}){{\bar {\tau }}_{k}} = O({{f}^{2}}({{x}_{k}}))$, т.е. ${{\bar {\tau }}_{k}}$ удовлетворяет условию (2.23).Итерационный метод (2.4) использует на каждом шаге итерации значения $f({{x}_{k}}),f({{y}_{k}})$ и $\phi ({{x}_{k}})$, поэтому он оптимален в смысле гипотезы Кунг–Трауба. Второй шаг в (2.1) можно переписать как
где(2.26)
${{\tau }_{k}} = 1 + {{\bar {\tau }}_{k}}{{\theta }_{k}} = 1 + {{\theta }_{k}} + {{\hat {d}}_{k}}\theta _{k}^{2} + O({{f}^{3}}({{x}_{k}})).$(2.29)
$H(x) = \frac{{c + ({{{\hat {d}}}_{k}}c + d)x + \omega {{x}^{2}}}}{{c + dx + b{{x}^{2}}}},\quad c + d + b \ne 0,\quad c,d,b,\omega \in R.$1. Пусть $c = 1$, $d = \beta - 2$, $b = \omega = 0$ в (2.29). Тогда получим
(2.30)
${{y}_{k}} = {{x}_{k}} - \frac{{f({{x}_{k}})}}{{\phi ({{x}_{k}})}},\quad {{x}_{{k + 1}}} = {{y}_{k}} - \frac{{1 + \left( {\beta - \frac{{\gamma {{\phi }_{k}}}}{{1 + \gamma {{\phi }_{k}}}}} \right){{\theta }_{k}}}}{{1 + (\beta - 2){{\theta }_{k}}}}\frac{{f({{y}_{k}})}}{{\phi ({{x}_{k}})}}.$2. Пусть $c = b = 1$, $d = - 2$ и $\omega = 0$ в (2.29). Тогда получим
3. Пусть $c = 1$, $\omega = d = - 1$ и $b = 0$ в (2.29). Тогда получим
Итерация (2.1) с таким выбором ${{\bar {\tau }}_{k}} = H({{\theta }_{k}})$ имеет вид(2.32)
${{y}_{k}} = {{x}_{k}} - \frac{{f({{x}_{k}})}}{{\phi ({{x}_{k}})}},\quad {{x}_{{k + 1}}} = {{y}_{k}} - \frac{{1 + \frac{1}{{1 + \gamma {{\phi }_{k}}}}{{\theta }_{k}} - \theta _{k}^{2}}}{{1 - {{\theta }_{k}}}}\frac{{f({{y}_{k}})}}{{\phi ({{x}_{k}})}}.$Следует отметить, что авторами статьи [30] была сделана попытка распространить методы Кунга и Трауба на варианты, не содержащие производные. Но полученный в [30] метод отличается от наших расширений (2.30) и (2.31).
Таким образом, используя метод производящих функций, получаем широкий класс оптимальных двухточечных методов без производных (2.1) с ${{\bar {\tau }}_{k}} = H({{\theta }_{k}})$, заданным формулой (2.29). Этот класс включает пять параметров $(\gamma ,c,d,b,\omega )$. Коэффициенты в (2.29) могут зависеть от номера итераций $k$. Следует отметить, что многие двухточечные методы, не содержащие производные, были построены в [1], [2], [7], [14]–[18]. Наш класс итераций (2.1) с параметром ${{\bar {\tau }}_{k}}$, заданный по формуле (2.29), содержит некоторые хорошо известные итерации как частные случаи. В табл. 1 перечислены некоторые из них. Только ${{\bar {\tau }}_{k}}$ в методе Рен и др. [16], [34] не принадлежит классу $H({{\theta }_{k}})$, заданному по формуле (2.29). Таким образом, можно считать, что наше семейство (2.1) с параметром, заданным по формуле (2.29), является существенным обобщением методов, предложенных в работах [2], [7], [9], [11]–[18], [20]–[23], [26], [27].
Таблица 1.
Итерационные методы
| Методы | $\mathop {\bar {\tau }}\nolimits_k $ | Частные случаи H, заданные (30) | |
|---|---|---|---|
| 1. | Методы, заданные в [18], [20] и $h(t,s) = (1 + t)(1 + s)$ [2], $P1$ в [21] | $1 + {{\hat {d}}_{k}}{{\theta }_{k}}$ | $c \ne 0,$$d = b = \omega = 0$ |
| 2. | Методы, заданные в [10], [12], [15] и $h(t,s) = \tfrac{1}{{1 - t - s}}$ [2] CTM в [15] | $\tfrac{1}{{1 - {{{\hat {d}}}_{k}}{{\theta }_{k}}}}$ | $c = 1,$$d = - {{\hat {d}}_{k}},$$b = \omega = 0$ |
| 3. | $h(t,s) = \tfrac{{1 + t}}{{1 - s}}$ [2], [34] | $\tfrac{{1 + \gamma {{\phi }_{k}} + ({{{\hat {d}}}_{k}}(1 + \gamma {{\phi }_{k}}) - 1){{\theta }_{k}}}}{{1 + \gamma {{\phi }_{k}} - {{\theta }_{k}}}}$ | $c = 1 + \gamma {{\varphi }_{k}},$$d = - 1,$$b = \omega = 0$ |
| 4. | Методы, заданные в [7] | $\tfrac{{1 + {{\phi }_{k}} + ({{{\hat {d}}}_{k}}(1 + {{\phi }_{k}}) - (2 - {{\phi }_{k}})){{\theta }_{k}}}}{{1 + {{\phi }_{k}} - (2 + {{\phi }_{k}}){{\theta }_{k}}}}$ | $c = 1 + {{\varphi }_{k}},$$d = - (2 + {{\varphi }_{k}}),$$b = - 1,$$\omega = 0$ |
| 5. | Семейство Чебышев-Халли [9] | $\tfrac{{1 + \left( {{{{\hat {d}}}_{k}} - \left( {2\alpha + \tfrac{1}{{1 + \gamma {{\phi }_{k}}}}} \right)} \right){{\theta }_{k}} + \omega \theta _{k}^{2}}}{{1 - \left( {2\alpha + \tfrac{1}{{1 + \gamma {{\phi }_{k}}}}} \right){{\theta }_{k}} + \tfrac{{2\alpha }}{{1 + \gamma {{\phi }_{k}}}}\theta _{k}^{2}}}$ | $c = 1,$$d = - \left( {2\alpha + \tfrac{1}{{1 + \gamma {{\phi }_{k}}}}} \right),$$b = \tfrac{{2\alpha }}{{1 + \gamma {{\phi }_{k}}}},$$\omega = H({{\theta }_{k}})$ |
| 6. | Метод Кунг-Трауба и метод в [11] | $\tfrac{1}{{1 - {{d}_{k}}{{\theta }_{k}} + \tfrac{1}{{1 + \gamma {{\phi }_{k}}}}\theta _{k}^{2}}}$ | $c = 1,$$d = - {{\hat {d}}_{k}},$$b = \tfrac{1}{{1 + \gamma {{\phi }_{k}}}},$$\omega = 0$ |
| 7. | Метод Потра–Птака [13], [22] | $1 + {{d}_{k}}{{\theta }_{k}} + \tfrac{{{{d}_{k}}a}}{2}\theta _{k}^{2}$ | $c = 1,$$d = b = 0,$$\omega = \tfrac{{{{{\hat {d}}}_{k}}a}}{2}$ |
| 8. | Метод типа Кинга [23] | $\tfrac{{1 + (\gamma - 1){{\theta }_{k}} - \gamma \theta _{k}^{2}}}{{1 + \left( {\gamma - 2 - \tfrac{1}{{1 - \beta {{\phi }_{k}}}}} \right){{\theta }_{k}} + \tfrac{{\gamma - 2}}{{1 - \beta {{\phi }_{k}}}}\theta _{k}^{2}}}$ | $c = 1,$$d = \gamma - 2 - \tfrac{1}{{1 - \beta {{\phi }_{k}}}},$$b = \tfrac{{2 - \gamma }}{{1 - \beta {{\phi }_{k}}}},$$a = - \gamma $ |
| 9. | Методы, заданные в [17] | $\tfrac{{1 - \tfrac{{\gamma {{\phi }_{k}}}}{{1 + \gamma {{\phi }_{k}}}}{{\theta }_{k}}}}{{1 - 2{{\theta }_{k}} + \theta _{k}^{2}}}$ | $c = b = 1,$$d = - 2,$$\omega = 0$ |
| 10. | Методы, заданные в [16] | $\tfrac{1}{{1 - {{{\hat {d}}}_{k}}{{\theta }_{k}} + a\tfrac{{1 + {{\phi }_{k}}}}{{{{\phi }_{k}}}}{{f}^{2}}({{x}_{k}})}}$ | не принадлежит к (30) |
| 11. | Методы $P2$, заданные в [21] | $\tfrac{{1 + {{\theta }_{k}}}}{{1 - \tfrac{{{{\theta }_{k}}}}{{1 + \gamma {{\phi }_{k}}}}}}$ | $c = 1,$$d = - \tfrac{1}{{1 + \gamma {{\phi }_{k}}}},$$b = \omega = 0$ |
| 12. | Методы, заданные в [27] | $\tfrac{{1 + {{\phi }_{k}} + 2{{\theta }_{k}}}}{{1 + {{\phi }_{k}} - {{\phi }_{k}}{{\theta }_{k}}}}$ | $c = 1 + {{\phi }_{k}},$$d = - {{\phi }_{k}},$$b = \omega = 0$ |
| 13. | Методы, заданные в [16] | $1 + {{\hat {d}}_{k}}{{\theta }_{k}} + \left( {{{\alpha }_{1}} + \tfrac{{{{\alpha }_{2}}}}{{{{{(1 + \gamma {{\phi }_{k}})}}^{2}}}}} \right)\theta _{k}^{2}$ | $c = 1,$$d\, = \,b\, = \,0,$$\omega \, = \,{{\alpha }_{1}}\, + \,\tfrac{{{{\alpha }_{2}}}}{{{{{(1 + \gamma {{\phi }_{k}})}}^{2}}}}$ |
Двухточечная итерация (2.1) содержит один свободный ненулевой параметр $\gamma $. Хорошо известно, что ускорение скорости сходимости достигается за счет подходящего варьирования свободного параметра на каждом шаге итерации $\gamma = {{\gamma }_{k}}$. Этот подход полезен при построении итераций высокого порядка с памятью, (см. [9], [22], [23], [25]). Теперь попытаемся найти оптимальный выбор свободного параметра с точки зрения точности. Рассмотрим разложение Тейлора функции $f({{\eta }_{k}}) = f({{x}_{k}} + \gamma f({{x}_{k}}))$ в окрестности ${{x}_{k}}$
(2.33)
$f({{\eta }_{k}}) = (1 + \gamma f{\kern 1pt} '({{x}_{k}}))f({{x}_{k}}) + \frac{{f{\kern 1pt} ''({{x}_{k}})}}{2}{{\gamma }^{2}}{{f}^{2}}({{x}_{k}}) + O({{f}^{3}}({{x}_{k}})).$(2.35)
$f({{\eta }_{k}}) = \frac{{f{\kern 1pt} ''({{x}_{k}})}}{2}\frac{{{{f}^{2}}({{x}_{k}})}}{{f'{{{({{x}_{k}})}}^{2}}}} + O({{f}^{3}}({{x}_{k}})),$(2.40)
${{\bar {\tau }}_{k}} = \frac{1}{{1 - {{{\hat {d}}}_{k}}{{\theta }_{k}}}} = 1 + {{\hat {d}}_{k}}{{\theta }_{k}} + \hat {d}_{k}^{2}\theta _{k}^{2} + O({{f}^{3}}({{x}_{k}})).$(2.42)
${{\eta }_{k}} = {{x}_{k}} - \frac{{f({{x}_{k}})}}{{f{\kern 1pt} '({{x}_{k}})}},\quad {{y}_{k}} = {{x}_{k}} - \frac{{f({{x}_{k}})}}{{{{\phi }_{k}}}},\quad {{x}_{{k + 1}}} = {{y}_{k}} - {{\bar {\tau }}_{k}}\frac{{f({{y}_{k}})}}{{{{\phi }_{k}}}}.$(2.43)
$\begin{gathered} {{\gamma }_{k}} = - \frac{1}{{N_{3}^{'}({{x}_{k}})}},\quad {{\eta }_{k}} = {{x}_{k}} + {{\gamma }_{k}}f({{x}_{k}}),\quad k = 1,2\;, \ldots , \\ {{y}_{k}} = {{x}_{k}} - \frac{{f({{x}_{k}})}}{{{{\phi }_{k}}}},\quad {{x}_{{k + 1}}} = {{y}_{k}} - {{{\bar {\tau }}}_{k}}\frac{{f({{y}_{k}})}}{{{{\phi }_{k}}}},\quad {{\phi }_{k}} = \phi ({{x}_{k}},{{\gamma }_{k}}). \\ \end{gathered} $Следует упомянуть, что иногда использовались несимметричные итерации, не содержащие производные, требующие дополнительных вычислений. Например, в [33] были предложены оптимальные итерационные семейства методов типа Кинга
(2.44)
$\begin{gathered} {{y}_{k}} = {{x}_{k}} - \frac{{f({{x}_{k}})}}{{{{\phi }_{k}}}},\quad {{\phi }_{k}} = f[{{x}_{k}},{{\eta }_{k}}],\quad {{\eta }_{k}} = {{x}_{k}} + \gamma f({{x}_{k}}), \\ {{x}_{{k + 1}}} = {{y}_{k}} - \frac{{f({{y}_{k}})}}{{f[{{y}_{k}},{{\eta }_{k}}]}}\frac{{1 + \beta {{\theta }_{k}}}}{{1 + (\beta - 1){{\theta }_{k}}}}, \\ \end{gathered} $(2.46)
${{\bar {\tau }}_{k}} = \frac{{1 + \beta {{\theta }_{k}}}}{{1 + (\beta - {{{\hat {d}}}_{k}}){{\theta }_{k}} - \frac{{(\beta - 1)\theta _{k}^{2}}}{{1 + \gamma {{\phi }_{k}}}}}},$(2.47)
$\begin{gathered} {{y}_{k}} = {{x}_{k}} - \frac{{f({{x}_{k}})}}{{{{\phi }_{k}} + \lambda f({{\eta }_{k}})}},\quad {{\eta }_{k}} = {{x}_{k}} + \gamma f({{x}_{k}}),\quad \gamma ,\lambda \in R{\backslash }\{ 0\} , \\ {{x}_{{k + 1}}} = {{y}_{k}} - \frac{{f({{y}_{k}})}}{{f[{{y}_{k}},{{\eta }_{k}}] + \lambda f({{\eta }_{k}})}}{{{\bar {\tau }}}_{k}}, \\ \end{gathered} $(2.48)
$\begin{gathered} {{{\bar {\tau }}}_{k}} = \frac{1}{{{{\theta }_{k}}}}\left( { - 1 + \frac{{\alpha + 1}}{{\alpha + \sqrt {1 - 2(\alpha + 1){{\theta }_{k}}} }}} \right)H({{\theta }_{k}}),\quad \alpha \ne - 1, \\ H(0) = 1,\quad H{\kern 1pt} '(0) = - \frac{{\alpha + 1}}{2},\quad {\text{|}}H{\kern 1pt} ''(0){\text{|}} < \infty . \\ \end{gathered} $(2.49)
$\begin{gathered} {{y}_{k}} = {{x}_{k}} - \frac{{f({{x}_{k}})}}{{{{\phi }_{k}} + \lambda f({{\eta }_{k}})}}, \\ {{x}_{{k + 1}}} = {{y}_{k}} - \frac{{f({{y}_{k}})}}{{{{\phi }_{k}} + \lambda f({{\eta }_{k}})}}{{{\bar {\tau }}}_{k}}, \\ \end{gathered} $Теорема 2. Пусть $f(x) \in {{C}^{3}}(I)$ и имеет простой нуль $x{\kern 1pt} * \in I.$ Если начальное приближение ${{x}_{0}}$ достаточно близко к $x{\kern 1pt} * \in I$, то итерационный метод (2.49) имеет оптимальную сходимость четвертого порядка, когда
(2.50)
$H(0) = 1,\quad H{\kern 1pt} '(0) = {{\hat {d}}_{k}} - \frac{{\alpha + 3}}{2},\quad {\text{|}}H{\kern 1pt} ''(0){\text{|}} < \infty .$Доказательство. Предположим, что $H(0) = a,\quad H{\kern 1pt} '(0) = b.$ Тогда из (2.48) получаем
3. ТРЕХТОЧЕЧНЫЕ ИТЕРАЦИОННЫЕ МЕТОДЫ, НЕ СОДЕРЖАЩИЕ ПРОИЗВОДНЫЕ
Рассмотрим трехточечные методы, не содержащие производные,
(3.1)
${{y}_{k}} = {{x}_{k}} - \frac{{f({{x}_{k}})}}{{\phi ({{x}_{k}})}},\quad {{z}_{k}} = {{y}_{k}} - {{\bar {\tau }}_{k}}\frac{{f({{y}_{k}})}}{{\phi ({{x}_{k}})}},\quad {{x}_{{k + 1}}} = {{z}_{k}} - {{\alpha }_{k}}\frac{{f({{z}_{k}})}}{{\phi ({{x}_{k}})}},$(3.2)
$\begin{gathered} f({{x}_{{k + 1}}}) = f({{z}_{k}}) - f'({{z}_{k}}){{\alpha }_{k}}\frac{{f({{z}_{k}})}}{{\phi ({{x}_{k}})}} + O(f{{({{z}_{k}})}^{2}}) = \\ = \left( {1 - {{\alpha }_{k}}\frac{{f{\kern 1pt} '({{z}_{k}})}}{{\phi ({{x}_{k}})}}} \right)f({{z}_{k}}) + O({{f}^{2}}({{z}_{k}})). \\ \end{gathered} $(3.4)
${{\alpha }_{k}} = \frac{{\phi ({{x}_{k}})}}{{f{\kern 1pt} '({{z}_{k}})}} + O({{f}^{4}}({{x}_{k}})).$(3.5)
$f{\kern 1pt} '({{z}_{k}}) = {{a}_{k}}f({{x}_{k}}) + {{b}_{k}}f({{y}_{k}}) + {{c}_{k}}f({{z}_{k}}) + {{d}_{k}}\phi ({{x}_{k}}) + O(f{{({{x}_{k}})}^{4}}).$(3.6)
$\begin{gathered} {{a}_{k}} + {{b}_{k}} + {{c}_{k}} = 0, \\ {{a}_{k}}{{w}_{k}} + {{b}_{k}}{{\gamma }_{k}} + {{d}_{k}} = 1, \\ {{a}_{k}}w_{k}^{2} + {{b}_{k}}\gamma _{k}^{2} + 2{{d}_{k}}\left( {{{w}_{k}} + \frac{1}{2}\gamma f({{x}_{k}})} \right) = 0, \\ {{a}_{k}}w_{k}^{3} + {{b}_{k}}\gamma _{k}^{3} + 3{{d}_{k}}\left( {w_{k}^{2} + {{w}_{k}}\gamma f({{x}_{k}}) + \frac{1}{3}{{\gamma }^{2}}{{f}^{2}}({{x}_{k}})} \right) = 0, \\ \end{gathered} $(3.8)
$\begin{gathered} {{c}_{k}} = - {{a}_{k}} - {{b}_{k}}, \\ {{d}_{k}} = 1 - {{a}_{k}}{{w}_{k}} - {{b}_{k}}{{\gamma }_{k}}, \\ {{b}_{k}} = \frac{{{{w}_{k}}({{w}_{k}} + \gamma f({{x}_{k}}))}}{{{{\gamma }_{k}}({{\gamma }_{k}} - {{w}_{k}})({{\gamma }_{k}} - {{w}_{k}} - \gamma f({{x}_{k}}))}}, \\ {{a}_{k}} = \frac{{{{\gamma }_{k}}}}{{{{w}_{k}}({{\gamma }_{k}} - {{w}_{k}})}}\frac{{({{w}_{k}} - {{\gamma }_{k}})(2{{w}_{k}} + \gamma f({{x}_{k}})) + {{{({{w}_{k}} + \gamma f({{x}_{k}}))}}^{2}}}}{{({{w}_{k}} + \gamma f({{x}_{k}}))({{w}_{k}} - {{\gamma }_{k}} + \gamma f({{x}_{k}}))}}. \\ \end{gathered} $(3.9)
$f{\kern 1pt} '({{z}_{k}}) = {{\phi }_{k}}(1 + {{a}_{k}}{{w}_{k}}\left( {\frac{{f[{{z}_{k}},{{x}_{k}}]}}{{{{\phi }_{k}}}} - 1} \right) + {{b}_{k}}{{\gamma }_{k}}\left( {\frac{{f[{{z}_{k}},{{y}_{k}}]}}{{{{\phi }_{k}}}} - 1} \right)) + O({{f}^{4}}({{x}_{k}})),$(3.10)
${{w}_{k}} = \frac{{f({{x}_{k}})}}{{{{\phi }_{k}}}}{{\tau }_{k}},\quad {{\gamma }_{k}} = ({{\tau }_{k}} - 1)\frac{{f({{x}_{k}})}}{{{{\phi }_{k}}}},\quad {{\gamma }_{k}} - {{w}_{k}} = - \frac{{f({{x}_{k}})}}{{{{\phi }_{k}}}} = {{y}_{k}} - {{x}_{k}},$(3.11)
$\frac{{{{\gamma }_{k}}}}{{{{w}_{k}} - {{\gamma }_{k}}}} = \frac{{{{y}_{k}} - {{z}_{k}}}}{{{{x}_{k}} - {{y}_{k}}}} = {{\tau }_{k}} - 1 \to {{\tau }_{k}} = \frac{{{{x}_{k}} - {{z}_{k}}}}{{{{x}_{k}} - {{y}_{k}}}},$(3.12)
${{w}_{k}} + \gamma {{f}_{k}} = \frac{{f({{x}_{k}})}}{{{{\phi }_{k}}}}({{\tau }_{k}} + \gamma {{\phi }_{k}}),\quad {{w}_{k}} - {{\gamma }_{k}} + \gamma f({{x}_{k}}) = \frac{{f({{x}_{k}})}}{{{{\phi }_{k}}}}(1 + \gamma {{\phi }_{k}}).$(3.13)
${{b}_{k}}{{\gamma }_{k}} = \frac{{{{\tau }_{k}}({{\tau }_{k}} + \gamma {{\phi }_{k}})}}{{1 + \gamma {{\phi }_{k}}}},\quad {{a}_{k}}{{w}_{k}} = (1 - {{\tau }_{k}})\frac{{2{{\tau }_{k}} + \gamma {{\phi }_{k}} + {{{({{\tau }_{k}} + \gamma {{\phi }_{k}})}}^{2}}}}{{({{\tau }_{k}} + \gamma {{\phi }_{k}})(1 + \gamma {{\phi }_{k}})}}.$(3.14)
${{\alpha }_{k}} = \frac{1}{{1 + {{a}_{k}}{{w}_{k}}\left( {\frac{{f[{{z}_{k}},{{x}_{k}}]}}{{{{\phi }_{k}}}} - 1} \right) + {{b}_{k}}{{\gamma }_{k}}\left( {\frac{{f[{{z}_{k}},{{y}_{k}}]}}{{{{\phi }_{k}}}} - 1} \right)}},$(3.15)
$\frac{{f[{{z}_{k}},{{x}_{k}}]}}{{{{\phi }_{k}}}} - 1 = \frac{1}{{{{\phi }_{k}}}}f[{{z}_{k}},{{x}_{k}},{{\xi }_{k}}]({{z}_{k}} - {{\xi }_{k}}) = - \frac{{f({{x}_{k}})}}{{\phi _{k}^{2}}}f[{{z}_{k}},{{x}_{k}},{{\xi }_{k}}]({{\tau }_{k}} + \gamma {{\phi }_{k}}),$(3.16)
$\frac{{f[{{z}_{k}},{{y}_{k}}]}}{{{{\phi }_{k}}}} - 1 = - \frac{{f({{x}_{k}})}}{{\phi _{k}^{2}}}(f[{{y}_{k}},{{z}_{k}},{{x}_{k}}] + f[{{z}_{k}},{{x}_{k}},{{\xi }_{k}}]({{\tau }_{k}} + \gamma {{\phi }_{k}})).$(3.17)
${{\alpha }_{k}} = \frac{1}{{1 - \frac{{f({{x}_{k}})}}{{\phi _{k}^{2}(1 + \gamma {{\phi }_{k}})}}{{F}_{k}}}},$Теперь найдем асимптотику для ${{\alpha }_{k}}$, заданную формулой (3.14). С этой целью используем следующие формулы
(3.18)
$\frac{{f[{{z}_{k}},{{x}_{k}}]}}{{{{\phi }_{k}}}} - 1 = - \frac{{({{{\bar {\tau }}}_{k}} + {{v}_{k}}){{\theta }_{k}}}}{{1 + {{{\bar {\tau }}}_{k}}{{\theta }_{k}}}},$(3.19)
$\frac{{f[{{z}_{k}},{{y}_{k}}]}}{{{{\phi }_{k}}}} - 1 = \frac{{1 - {{{\bar {\tau }}}_{k}} - {{v}_{k}}}}{{{{{\bar {\tau }}}_{k}}}},\quad {{v}_{k}} = {{f({{z}_{k}})} \mathord{\left/ {\vphantom {{f({{z}_{k}})} {f({{y}_{k}})}}} \right. \kern-0em} {f({{y}_{k}})}},$(3.21)
${{\alpha }_{k}} = \frac{1}{{1 + \frac{{{{A}_{1}} + {{A}_{2}} + {{A}_{3}}{{\text{v}}_{k}}}}{{(1 + \gamma {{\phi }_{k}})(1 + \gamma {{\phi }_{k}} + {{{\bar {\tau }}}_{k}}{{\theta }_{k}})(1 + {{{\bar {\tau }}}_{k}}{{\theta }_{k}}){{{\bar {\tau }}}_{k}}}}}},$(3.22a)
${{A}_{1}} = {{(1 + {{\theta }_{k}}{{\bar {\tau }}_{k}})}^{2}}{{(1 + \gamma {{\phi }_{k}} + {{\bar {\tau }}_{k}}{{\theta }_{k}})}^{2}}(1 - {{\bar {\tau }}_{k}}),$(3.22b)
${{A}_{2}} = (2 + \gamma {{\phi }_{k}} + 2{{\bar {\tau }}_{k}}{{\theta }_{k}} + {{(1 + \gamma {{\phi }_{k}} + {{\bar {\tau }}_{k}}{{\theta }_{k}})}^{2}})\bar {\tau }_{k}^{3}\theta _{k}^{2},$(3.22c)
$\begin{gathered} {{A}_{3}} = - {{(1 + {{\theta }_{k}}{{{\bar {\tau }}}_{k}})}^{2}}{{(1 + \gamma {{\phi }_{k}} + {{{\bar {\tau }}}_{k}}{{\theta }_{k}})}^{2}} + \\ + \;(2 + \gamma {{\phi }_{k}} + 2{{{\bar {\tau }}}_{k}}{{\theta }_{k}} + {{(1 + \gamma {{\phi }_{k}} + {{{\bar {\tau }}}_{k}}{{\theta }_{k}})}^{2}})\bar {\tau }_{k}^{2}\theta _{k}^{2}. \\ \end{gathered} $(3.23)
${{\bar {\tau }}_{k}} = 1 + {{\hat {d}}_{k}}{{\theta }_{k}} + {{\tilde {\beta }}_{k}}\theta _{k}^{2} + {{\tilde {\gamma }}_{k}}\theta _{k}^{3} + \cdots ,$(3.24)
$f({{y}_{k}}) = O({{f}^{2}}({{x}_{k}})),\quad f({{z}_{k}}) = O({{f}^{4}}({{x}_{k}})),\quad {{v}_{k}} = O({{f}^{2}}({{x}_{k}})).$(3.25)
${{A}_{1}} = - {{\theta }_{k}}{{(1 + \gamma {{\phi }_{k}})}^{2}}({{a}_{1}} + {{a}_{2}}{{\theta }_{k}} + {{a}_{3}}\theta _{k}^{2} + \cdots ),$(3.26)
${{A}_{2}} = \theta _{k}^{2}{{(1 + \gamma {{\phi }_{k}})}^{2}}({{b}_{1}} + {{b}_{2}}{{\theta }_{k}} + \cdots ),$(3.27)
${{A}_{3}} = - {{(1 + \gamma {{\phi }_{k}})}^{2}}({{c}_{1}} + {{c}_{2}}{{\theta }_{k}} + \cdots ),$(3.28)
$\begin{gathered} {{a}_{1}} = {{{\hat {d}}}_{k}},\quad {{a}_{2}} = \tilde {\beta } + 2\hat {d}_{k}^{2},\quad {{a}_{3}} = \tilde {\gamma } + 2\tilde {\beta }{{{\hat {d}}}_{k}} + \left( {3\hat {d}_{k}^{2} + \frac{2}{{1 + \gamma {{\phi }_{k}}}}} \right){{{\hat {d}}}_{k}}, \\ {{b}_{1}} = 1 + \frac{{{{{\hat {d}}}_{k}}}}{{1 + \gamma {{\phi }_{k}}}},\quad {{b}_{2}} = {{{\hat {d}}}_{k}} - \hat {d}_{k}^{2} + 3\hat {d}_{k}^{3},\quad {{c}_{1}} = 1,\quad {{c}_{2}} = 2{{{\hat {d}}}_{k}}. \\ \end{gathered} $(3.29)
$\frac{1}{{\left( {1 + \frac{{{{{\bar {\tau }}}_{k}}{{\theta }_{k}}}}{{1 + \gamma {{\phi }_{k}}}}} \right)(1 + {{{\bar {\tau }}}_{k}}{{\theta }_{k}}){{{\bar {\tau }}}_{k}}}} = 1 - 2{{\hat {d}}_{k}}{{\theta }_{k}} + \left( {2\hat {d}_{k}^{2} - \tilde {\beta } - \frac{1}{{1 + \gamma {{\phi }_{k}}}}} \right)\theta _{k}^{2} + O({{f}^{3}}({{x}_{k}})).$(3.30)
${{\alpha }_{k}} = 1 + {{\hat {d}}_{k}}{{\theta }_{k}} + \left( {\tilde {\beta } + \frac{1}{{1 + \gamma {{\phi }_{k}}}}} \right)\theta _{k}^{2} + \left( {\tilde {\gamma } + {{{\hat {d}}}_{k}}\tilde {\beta } - {{{\hat {d}}}_{k}} - \frac{{{{{\hat {d}}}_{k}}}}{{{{{(1 + \gamma {{\phi }_{k}})}}^{2}}}}} \right)\theta _{k}^{3} + (1 + 2{{\hat {d}}_{k}}{{\theta }_{k}}){{v}_{k}} + O({{f}^{4}}({{x}_{k}})).$(3.31)
${{\alpha }_{k}} = 1 + 2{{\theta }_{k}} + (\tilde {\beta } + 1)\theta _{k}^{2} + (\tilde {\gamma } + 2\tilde {\beta } - 4)\theta _{k}^{3} + (1 + 4{{\theta }_{k}}){{v}_{k}} + O({{f}^{4}}({{x}_{k}})),$Теорема 3. Пусть выполнены все предположения Теоремы 1. Тогда трехточечные итерационные методы (3.1) имеют 8-й порядок сходимости тогда и только тогда, когда итерационные параметры ${{\bar {\tau }}_{k}}$ и ${{\alpha }_{k}}$ задаются формулами (3.23) и (3.30) соответственно.
Доказательство. Пусть ${{\bar {\tau }}_{k}}$ и ${{\alpha }_{k}}$ задаются формулами (3.23) и (3.30) соответственно. Тогда, по теореме 1, первые два шага в (3.1) определяют оптимальный метод четвертого порядка, т.е. $f({{z}_{k}}) = O({{f}^{4}}({{x}_{k}}))$. А значение ${{\alpha }_{k}}$, заданное формулой (3.30), удовлетворяет условию (3.4). Следовательно, справедливо соотношение (3.3). Обратно, предположим, что порядок сходимости итерации (3.1) равен 8. Тогда из (3.1) и (3.3) следует, что $f({{z}_{k}}) = O({{f}^{4}}({{x}_{k}}))$ и формула (3.4). Поэтому, по теореме 1, формула (3.23) верна с некоторыми константами $\tilde {\gamma }$ и $\tilde {\beta }$. Используя аппроксимацию (3.9) в (3.4), получаем (3.14) с точностью $O({{f}^{4}}({{x}_{k}}))$. Так как (3.23) верно, то из (3.14) приходим к асимптотике (3.30).
Предположим в (3.1)
(3.32)
${{\bar {\tau }}_{k}} = H({{\theta }_{k}}) = \frac{{c + ({{{\hat {d}}}_{k}}c + d){{\theta }_{k}} + \omega \theta _{k}^{2}}}{{c + d{{\theta }_{k}} + b\theta _{k}^{2}}},\quad c + d + b \ne 0,\quad c,d,b,\omega \in R,$(3.33)
${{\alpha }_{k}} = H({{\theta }_{k}}) + \frac{1}{{1 + \gamma {{\phi }_{k}}}}\theta _{k}^{2} + {{\hat {d}}_{k}}\left( {\tilde {\beta } - \frac{2}{{1 + \gamma {{\phi }_{k}}}}} \right)\theta _{k}^{3} + (1 + 2{{\hat {d}}_{k}}{{\theta }_{k}}){{v}_{k}}.$Теперь рассмотрим следующие трехточечные итерации:
(3.34)
$\begin{gathered} {{\eta }_{k}} = {{x}_{k}} + \gamma f({{x}_{k}}),\quad {{y}_{k}} = {{x}_{k}} - \frac{{f({{x}_{k}})}}{{f[{{x}_{k}},{{\eta }_{k}}]}},\quad {{z}_{k}} = {{\psi }_{4}}({{x}_{k}},{{y}_{k}},{{\eta }_{k}}), \\ {{x}_{{k + 1}}} = {{z}_{k}} - \frac{{f({{z}_{k}})}}{{f[{{z}_{k}},{{y}_{k}}] + ({{z}_{k}} - {{y}_{k}})f[{{z}_{k}},{{y}_{k}},{{x}_{k}}] + ({{z}_{k}} - {{y}_{k}})({{z}_{k}} - {{x}_{k}})f[{{z}_{k}},{{y}_{k}},{{x}_{k}},{{\eta }_{k}}]}}. \\ \end{gathered} $Теорема 4. Пусть выполнены все предположения теоремы 1. Тогда порядок сходимости итерации (3.34) равен 8.
Доказательство. Так как ${{\psi }_{4}}$ – итерация четвертого порядка, то ${{z}_{k}}$ можно переписать как
(3.35)
${{\alpha }_{k}} = \frac{{{{\phi }_{k}}}}{{f[{{z}_{k}},{{y}_{k}}] + ({{z}_{k}} - {{y}_{k}})f[{{z}_{k}},{{y}_{k}},{{x}_{k}}] + ({{z}_{k}} - {{y}_{k}})({{z}_{k}} - {{x}_{k}})f[{{z}_{k}},{{y}_{k}},{{x}_{k}},{{\eta }_{k}}]}}.$Замечание 1. Порядок сходимости трехточечных итераций, предложенных в [12], [22]–[24], сразу следует из теоремы 4. Теорема 4 является расширением теорем, приведенных в [12], [22]–[24].
Заметим, что все существующие оптимальные трехточечные методы, не содержащие производных, могут быть переписаны в виде (3.1) однозначно.
Легко проверить, что параметры ${{\bar {\tau }}_{k}}$ и ${{\alpha }_{k}}$ в этих методах имеют одинаковую асимптотику (3.23) и (3.30) с собственными константами $\tilde {\gamma }$ и $\tilde {\beta }$. Таким образом, сходимость всех существующих оптимальных трехточечных методов, не содержащих производные, может быть доказана с использованием достаточных критериев сходимости (3.23) и (3.30) без использования символьных вычислений. Более того, применение этих достаточных условий сходимости позволяет в некоторых случаях построить новые оптимальные итерации [29]. Из табл. 1 видно, что параметр ${{\bar {\tau }}_{k}}$, входящий во всех перечисленных здесь оптимальных трехточечных методах, получается с помощью производящих функций $H({{\theta }_{k}})$, заданных формулой (3.32), за исключением метода, предложенного в [16]. Из (3.32) и (3.34) видно, что функция ${{\psi }_{4}}$ может содержать в себе некоторые свободные параметры. Это означает, что итерации (3.34) представляют широкий класс оптимальных трехточечных методов, не содержащих производные. Этот класс включает в себя многие из хорошо известных методов как частные случаи, см. [4]–[6], [9], [12]. Как и в предыдущем раз., можно варьировать $\gamma $ на каждом шаге итераций, используя информацию, полученную в предыдущем и настоящем шагах. Это позволяет увеличить порядок сходимости без использования дополнительных вычислений. А именно, получить трехточечные итерации с памятью (${{x}_{0}}$, ${{\gamma }_{0}}$ заданы). Тогда ${{\eta }_{0}} = {{x}_{0}} + {{\gamma }_{0}}f({{x}_{0}})$ и
(3.36)
$\begin{gathered} {{\gamma }_{k}} = - \frac{1}{{N_{4}^{'}({{x}_{k}})}},\quad {{\eta }_{k}} = {{x}_{k}} + {{\gamma }_{k}}f({{x}_{k}}),\quad k = 1,2,\; \ldots \\ {{y}_{k}} = {{x}_{k}} - \frac{{f({{x}_{k}})}}{{\phi ({{x}_{k}},{{\gamma }_{k}})}},\quad {{z}_{k}} = {{\psi }_{4}}({{x}_{k}},{{y}_{k}},{{\eta }_{k}}), \\ {{x}_{{k + 1}}} = {{z}_{k}} - \frac{{f({{z}_{k}})}}{{f[{{z}_{k}},{{y}_{k}}] + ({{z}_{k}} - {{y}_{k}})f[{{z}_{k}},{{y}_{k}},{{x}_{k}}] + ({{z}_{k}} - {{y}_{k}})({{z}_{k}} - {{x}_{k}})f[{{z}_{k}},{{y}_{k}},{{x}_{k}},{{\eta }_{k}}]}}. \\ \end{gathered} $4. ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ
В этом разделе приведены результаты численных экспериментов для сравнения эффективности методов. Численные расчеты, представленные здесь, были выполнены в системе Maple. Чтобы получить очень высокую точность, избежать потери значимых цифр, вычисления проводились с 300 значащими десятичными цифрами. Численные эксперименты сделаны для гладкой и негладкой функций (см. табл. 2) и при $\gamma = - 0.01$. Для проверки сходимости итераций расчетный порядок сходимости (РПС) вычислялся с помощью формулы
Таблица 2.
Нелинейные функции
| Функции | Корень | |
|---|---|---|
| 1. | ${{f}_{1}}(x) = {{e}^{{({{x}^{2}} + xcosx - 1)}}}sinx + xlog(xsinx + 1)$, [9] | $x* = 0$ |
| 2. | ${{f}_{2}}(x) = log({{x}^{2}} - 2x + 2) + {{e}^{{({{x}^{2}} - 5x + 4)}}}sin(x - 1)$, | $x* = 1$ |
| 3. | ${{f}_{3}}(x) = \left\{ \begin{gathered} x(x + 1),\quad {\text{е с л и }}\quad x < 0, \hfill \\ - 2x(x - 1),\quad {\text{е с л и }}\quad x \geqslant 0, \hfill \\ \end{gathered} \right.$ [7, 32] | $x* = 0$ $x* = 1$ $x* = - 1$ |
| 4. | ${{f}_{4}}(x) = \left| {{{x}^{2}} - 4} \right|$, [9] | $x* = \pm 2$ |
В табл. 2 приведены примеры, взятые из [9]. Третий пример с негладкой функцией (см. [7], [14], [32]) часто используется для проверки работоспособности итераций, не содержащих производных. В табл. 3–6 приведены числа итераций $(k)$, абсолютные погрешности ${\text{|}}{{x}_{k}} - x{\kern 1pt} *{\text{|}}$ и РПС для выборных методов при $\gamma = - 0.01$. Численные результаты подтверждают теоретический вывод о порядке сходимости. Из табл. 6 видно, что методы высокого порядка сходимости устойчиво работают не только для достаточно гладкой функции, но и также для негладкой функций. Отметим, что первая производная нелинейной функции ${{f}_{3}}(x)$ терпит разрыв в точке $x* = 0$, поэтому в этом случае РПС = 2 для всех предлагаемых методов (см. первую часть табл. 5, также [7]). Предлагаемые методы (3.34) могут быть успешно применены в расчетах, требующих высокую точность.
Таблица 3.
Двухточечные итерационные методы
| Методы | $\mathop {\bar {\tau }}\nolimits_k $ | k | $\left| {x{\kern 1pt} {\text{*}} - {{x}_{k}}} \right|$ | РПС |
|---|---|---|---|---|
| Численные результаты для гладкой функции ${{f}_{1}}(x)$ при ${{x}_{0}} = 1$ | ||||
| (2.1) | $c = 1,\;d = - {{\hat {d}}_{k}},\;b = - \tfrac{1}{{1 + \gamma {{\varphi }_{k}}}},\;\omega = 0$ | 4 | 0.4180e–33 | 3.99 |
| Типа Кинга [23] | $c = 1,\;d = - {{\hat {d}}_{k}},\;b = \tfrac{1}{{1 + \gamma {{\varphi }_{k}}}},\;\omega = 0$ | 5 | 0.5272e–96 | 4.00 |
| Потра-Птака [13, 22] | $c = 1,\;d = b = 0,\;\omega = \tfrac{{{{{\hat {d}}}_{k}}}}{2}$ | 5 | 0.9744e–80 | 3.99 |
| P1 [21] | $c = 1,\;b = d = \omega = 0$ | 5 | 0.1887e–65 | 4.00 |
| P2 [21] | $c = 1,\;d = - \tfrac{1}{{1 + \gamma {{\varphi }_{k}}}},\;b = \omega = 0$ | 5 | 0.1022e–95 | 4.00 |
| Чжэна [12] | $c = 1,\;d = - {{\hat {d}}_{k}},\;b = \omega = 0$ | 4 | 0.1655e–35 | 4.00 |
| (2.31) | $c = b = 1,\;d = - 2,\;\omega = 0$ | 5 | 0.1416e–95 | 4.00 |
| (2.32) | $c = 1,\;d = \omega = - 1,\;b = 0$ | 5 | 0.3838e–82 | 3.99 |
| Стефенсона | ${{x}_{{k + 1}}} = {{x}_{k}} - \tfrac{{f({{x}_{k}})}}{{\phi ({{x}_{k}})}}$ | 9 | 0.8745e–58 | 2.00 |
| Численные результаты для гладкой функции ${{f}_{2}}(x)$ при ${{x}_{0}} = 0.5$ | ||||
| (2.1) | $c = 1,\;d = - {{\hat {d}}_{k}},\;b = - \tfrac{1}{{1 + \gamma {{\varphi }_{k}}}},\;\omega = 0$ | 4 | 0.1673e–104 | 4.00 |
| Типа Кинга [23] | $c = 1,\;d = - {{\hat {d}}_{k}},\;b = \tfrac{1}{{1 + \gamma {{\varphi }_{k}}}},\;\omega = 0$ | 5 | 0.8607e–112 | 4.00 |
| Потра-Птака [13, 22] | $c = 1,\;d = b = 0,\;\omega = \tfrac{{{{{\hat {d}}}_{k}}}}{2}$ | 5 | 0.4066e–70 | 4.00 |
| P1 [21] | $c = 1,\;b = d = \omega = 0$ | 5 | 0.1325e–62 | 4.00 |
| P2 [21] | $c = 1,\;d = - \tfrac{1}{{1 + \gamma {{\varphi }_{k}}}},\;b = \omega = 0$ | 5 | 0.5680e–88 | 4.00 |
| Чжэна [12] | $c = 1,\;d = - {{\hat {d}}_{k}},\;b = \omega = 0$ | 4 | 0.4934e–58 | 3.99 |
| (2.31) | $c = b = 1,\;d = - 2,\;\omega = 0$ | 5 | 0.6144e–109 | 4.00 |
| (2.32) | $c = 1,\;d = \omega = - 1,\;b = 0$ | 5 | 0.6129e–73 | 4.00 |
| Стефенсона | ${{x}_{{k + 1}}} = {{x}_{k}} - \tfrac{{f({{x}_{k}})}}{{\phi ({{x}_{k}})}}$ | 8 | 0.4282e–30 | 2.00 |
Таблица 4.
Трехточечные итерационные методы
| Методы | ${{\bar {\tau }}_{k}} = H({{\theta }_{k}})$ | k | $\left| {x{\kern 1pt} {\text{*}} - {{x}_{k}}} \right|$ | РПС |
|---|---|---|---|---|
| выборы параметров | ||||
| Численные результаты для гладкой функции ${{f}_{1}}(x)$ при ${{x}_{0}} = 1$ | ||||
| (3.34) | $c = 1,\;d = \beta - 2,\;b = \omega = 0,\;(\beta = 2)$ | 3 | 0.1710e–38 | 8.38 |
| (3.34) | $c = b = 1,\;d = - 2,\;\omega = 0$ | 3 | 0.3900e–57 | 7.94 |
| (3.34) | $c = 1,\;d = \omega = - 1,\;b = 0$ | 3 | 0.4900e–44 | 7.99 |
| Лотфи [22] | $c = 1,\;d = b = 0,\;\omega = \tfrac{{{{{\tilde {d}}}_{k}}}}{2}$ | 3 | 0.4362e–43 | 7.99 |
| Типа Кинга [23] | $c = \omega = 1,\;d = \beta - 1 - {{\tilde {d}}_{k}},\;b = \tfrac{{2 - \beta }}{{1 + \gamma {{\varphi }_{k}}}},\;(\beta = 2)$ | 3 | 0.1024e–54 | 7.98 |
| Чжэна [12] | $c = 1,\;d = - {{\hat {d}}_{k}},\;b = \omega = 0$ | 3 | 0.5610e–62 | 7.97 |
| Шарма [14] | $c = 1,\;d = - \tfrac{1}{{1 + \gamma {{\varphi }_{k}}}},\;b = \omega = 0$ | 3 | 0.9068e–48 | 8.00 |
| Численные результаты для гладкой функции ${{f}_{2}}(x)$ при ${{x}_{0}} = 0.5$ | ||||
| (3.34) | $c = 1,\;d = \beta - 2,\;b = \omega = 0,\;(\beta = 2)$ | 3 | 0.3321e–33 | 7.96 |
| (3.34) | $c = b = 1,\;d = - 2,\;\omega = 0$ | 3 | 0.1543e–44 | 8.07 |
| (3.34) | $c = 1,\;d = \omega = - 1,\;b = 0$ | 3 | 0.4989e–36 | 7.98 |
| Лотфи [22] | $c = 1,\;d = b = 0,\;\omega = \tfrac{{{{{\tilde {d}}}_{k}}}}{2}$ | 3 | 0.2769e–35 | 7.99 |
| Типа Кинга [23] | $c = \omega = 1,\;d = \beta - 1 - {{\tilde {d}}_{k}},\;b = \tfrac{{2 - \beta }}{{1 + \gamma {{\varphi }_{k}}}},\;(\beta = 2)$ | 3 | 0.5302e–44 | 8.00 |
| Чжэна [12] | $c = 1,\;d = - {{\hat {d}}_{k}},\;b = \omega = 0$ | 3 | 0.6281e–64 | 7.97 |
| Шарма [14] | $c = 1,\;d = - \tfrac{1}{{1 + \gamma {{\varphi }_{k}}}},\;b = \omega = 0$ | 3 | 0.7441e–40 | 8.02 |
Таблица 5.
Численные результаты для негладкой функции ${{f}_{3}}(x)$. Трехточечные итерационные методы
| Методы | ${{\bar {\tau }}_{k}} = H({{\theta }_{k}})$ | k | $\left| {x{\kern 1pt} {\text{*}} - {{x}_{k}}} \right|$ | РПС |
|---|---|---|---|---|
| ${{x}_{0}} = 0.1,\;x* = 0$ | ||||
| (3.34) | $c = 1,\;d = \beta - 2,\;b = \omega = 0,\;(\beta = 2)$ | 4 | 0.7235e–30 | 2.00 |
| (3.34) | $c = b = 1,\;d = - 2,\;\omega = 0$ | 4 | 0.7186e–30 | 2.00 |
| (3.34) | $c = 1,\;d = \omega = - 1,\;b = 0$ | 4 | 0.7222e–30 | 2.00 |
| Лотфи [22] | $c = 1,\;d = b = 0,\;\omega = \tfrac{{{{{\tilde {d}}}_{k}}}}{2}$ | 4 | 0.7221e–30 | 2.00 |
| Типа Кинга [23] | $c = \omega = 1,\;d = \beta - 1 - {{\tilde {d}}_{k}},\;b = \tfrac{{2 - \beta }}{{1 + \gamma {{\varphi }_{k}}}},\;(\beta = 2)$ | 4 | 0.7185e–30 | 2.00 |
| Чжэна [12] | $c = 1,\;d = - {{\hat {d}}_{k}},\;b = \omega = 0$ | 4 | 0.7167e–30 | 2.00 |
| Шарма [14] | $c = 1,\;d = - \tfrac{1}{{1 + \gamma {{\varphi }_{k}}}},\;b = \omega = 0$ | 4 | 0.7205e–30 | 2.00 |
| ${{x}_{0}} = 5,x* = 1$ | ||||
| (3.34) | $c = 1,\;d = \beta - 2,\;b = \omega = 0,\;(\beta = 2)$ | 4 | 0.2191e–236 | 7.99 |
| (3.34) | $c = b = 1,\;d = - 2,\;\omega = 0$ | 3 | 0.8113e–39 | 7.77 |
| (3.34) | $c = 1,\;d = \omega = - 1,\;b = 0$ | 3 | 0.8754e–32 | 7.60 |
| Лотфи [22] | $c = 1,\;d = b = 0,\;\omega = \tfrac{{{{{\tilde {d}}}_{k}}}}{2}$ | 3 | 0.2144e–31 | 7.60 |
| Типа Кинга [23] | $c = \omega = 1,\;d = \beta - 1 - {{\tilde {d}}_{k}},\;b = \tfrac{{2 - \beta }}{{1 + \gamma {{\varphi }_{k}}}},\;(\beta = 2)$ | 3 | 0.2249e–37 | 7.76 |
| Чжэна [12] | $c = 1,\;d = - {{\hat {d}}_{k}},\;b = \omega = 0$ | 3 | 0.5377e–47 | 7.86 |
| Шарма [14] | $c = 1,\;d = - \tfrac{1}{{1 + \gamma {{\varphi }_{k}}}},\;b = \omega = 0$ | 3 | 0.4975e–34 | 7.67 |
| ${{x}_{0}} = - 10,\;x* = - 1$ | ||||
| (3.34) | $c = 1,\;d = \beta - 2,\;b = \omega = 0,\;(\beta = 2)$ | 4 | 0.4791e–102 | 7.99 |
| (3.34) | $c = b = 1,\;d = - 2,\;\omega = 0$ | 4 | 0.2067e–141 | 7.99 |
| (3.34) | $c = 1,\;d = \omega = - 1,\;b = 0$ | 4 | 0.9351e–112 | 7.99 |
| Лотфи [22] | $c = 1,\;d = b = 0,\;\omega = \tfrac{{{{{\tilde {d}}}_{k}}}}{2}$ | 4 | 0.5302e–110 | 7.99 |
| Типа Кинга [23] | $c = \omega = 1,\;d = \beta - 1 - {{\tilde {d}}_{k}},\;b = \tfrac{{2 - \beta }}{{1 + \gamma {{\varphi }_{k}}}},\;(\beta = 2)$ | 4 | 0.2101e–135 | 7.99 |
| Чжэна [12] | $c = 1,\;d = - {{\hat {d}}_{k}},\;b = \omega = 0$ | 4 | 0.8976e–178 | 7.99 |
| Шарма [14] | $c = 1,\;d = - \tfrac{1}{{1 + \gamma {{\varphi }_{k}}}},\;b = \omega = 0$ | 4 | 0.2099e–121 | 7.99 |
Таблица 6.
Трехточечные итерационные методы
| Методы | ${{\bar {\tau }}_{k}} = H({{\theta }_{k}})$ | k | $\left| {x{\kern 1pt} {\text{*}} - {{x}_{k}}} \right|$ | РПС |
|---|---|---|---|---|
| выборы параметров | ||||
| Численные результаты для негладкой функции ${{f}_{4}}(x)$ при ${{x}_{0}} = 3$ | ||||
| (3.34) | $c = 1,\;d = \beta - 2,\;b = \omega = 0,\;(\beta = 2)$ | 2 | 0.1365e–35 | 7.70 |
| (3.34) | $c = b = 1,\;d = - 2,\;\omega = 0$ | 2 | 0.3071e–40 | 7.79 |
| (3.34) | $c = 1,\;d = \omega = - 1,\;b = 0$ | 2 | 0.8144e–37 | 7.72 |
| Лотфи [22] | $c = 1,\;d = b = 0,\;\omega = \tfrac{{{{{\tilde {d}}}_{k}}}}{2}$ | 2 | 0.1228e–36 | 7.72 |
| Типа Кинга [23] | $c = \omega = 1,\;d = \beta - 1 - {{\tilde {d}}_{k}},\;b = \tfrac{{2 - \beta }}{{1 + \gamma {{\varphi }_{k}}}},\;(\beta = 2)$ | 2 | 0.3717e–40 | 7.80 |
| Чжэна [12] | $c = 1,\;d = - {{\hat {d}}_{k}},\;b = \omega = 0$ | 2 | 0.1675e–44 | 7.84 |
| Шарма [14] | $c = 1,\;d = - \tfrac{1}{{1 + \gamma {{\varphi }_{k}}}},\;b = \omega = 0$ | 2 | 0.2114e–38 | 7.75 |
| Стефенсона | ${{x}_{{k + 1}}} = {{x}_{k}} - \tfrac{{f({{x}_{k}})}}{{\phi ({{x}_{k}})}}$ | 6 | 0.5556e–45 | 2.00 |
5. ВЫВОДЫ
Необходимые и достаточные условия сходимости оптимальных двух- и трехточечных итерационных методов, полученных в [6], перенесены на случаи методов, не содержащих производные. Они могут быть эффективно использованы не только для установления порядка сходимости, но для изобретения новых методов. На основе метода производящих функций были предложены широкие классы оптимальных методов, которые содержат в себе много известных методов как частные случаи.
Список литературы
Liu L., Wang X. Eighth-order methods of high efficiency index for solving nonlinear equations // Appl. Math. Comput. 2010. V. 215. P. 3449–3454.
Petković M.S., Neta B., Petković L.D., Dzunić J. Multipoint methods for solving nonlinear equations // A survey, Appl. Math. Comput. 2014. V. 226. P. 635–660.
Thukral R., Petković M. S. A family of three-point methods of optimal order for solving nonlinear equations // J. Comput. Appl. Math. 2010. V. 233. P. 2278–2284.
Wang X., Liu L. New eighth-order iterative methods for solving non-linear equations // J. Comput. Appl. Math. 2010. V. 234. P. 1611–1620.
Zhanlav T., Chuluunbaatar O., Ulziibayar V. Generating function method for constructing new iterations // Appl. Math. Comput. 2017. V. 315. P. 414–423.
Жанлав Т., Улзийбаяр В., Чулуунбаатар О. Необходимые и достаточные условия сходимости двух- и трехшаговых итераций ньютоновского типа // Ж. вычисл. матем. и матем. физ. 2017. V. 57. P. 1093–1102. (English translation: Comput. Math. Math. Phys. 2017. V. 57. P. 1090–1100.)
Cordero A., Hueso J.L., Martinez E., Torregrosa J.R. A new technique to obtain derivative-free optimal iterative methods for solving nonlinear equations // J. Comput. Appl. Math. 2013. V. 252. P. 95–102.
Junjua M.D., Zafar F., Yasmin N., Akram S. A general class of derivative free with memory root solvers // Appl. Math. and Phys. 2017. V. 79. № 4. P. 19–28.
Argyros I.K., Kansal M., Kanwar V., Bajaj S. Higher-order derivative-free families of Chebyshev-Halley type methods with or without memory for solving nonlinear equations // Appl. Math. Comput. 2017. V. 315. P. 224–245.
Khattri S.K., Steihaug T. Algorithm for forming derivative-free optimal methods // Numer. Algor. 2014. V. 65. P. 809–842.
Thukral R. Eighth-order iterative methods without derivatives for solving nonlinear equations // ISRN Appl. Math. 2011 Article ID 693787, 12 pages.
Zheng Q., Li J., Huang F. An optimal Steffensen-type family for solving nonlinear equations // Appl. Math. Comput. 2011. V. 217. P. 9592–9597.
Soleymani F., Sharma R., Li X., Tohidi E. An optimized derivative-free form of the Potra-Ptak method // Math. Comput. Model. 2012. V. 56. P. 97–104.
Sharma J.R., Goyal R.K. Fourth-order derivative-free methods for solving non-linear equations // Int. J. Comput. Math. 2006. V. 83. P. 101–106.
Cordero A., Torregrosa J.R. A class of Steffensen type methods with optimal order of convergence // Appl. Math. Comput. 2011. V. 217. P. 7653–7659.
Ren H., Wu Q., Bi W. A class of two-step Steffensen type methods with fourth-order convergence // Appl. Math. Comput. 2009. V. 209. P. 206–210.
Liu Z., Zheng Q., Zhao P. A variant of Steffensen’s method of fourth-order convergence and its applications // Appl. Math. Comput. 2010. V. 216. P. 1978–1983.
Peng Y., Feng H., Li Q., Zhang X. A fourth-order derivative-free algorithm for nonlinear equations // J. Comput. Appl. Math. 2011. V. 235. P. 2551–2559.
Kansal M., Kanwar V., Bhatia S. An optimal eighth-order derivative-free family of Potra-Ptak’s method // Algorithms. 2015. V. 8. P. 309–320.
Soleymani F., Khattri S.K. Finding simple roots by seventh-and eighth-order derivative-free methods // Inter. J. Mathematical Models and Methods in Applied Sciences, 2012. V. 6. P. 45–52.
Thukral R. A family of three-point derivative-free methods of eighth-order for solving nonlinear equations // J. Mod. Meth. Numer. Math. 2012. V. 3. P. 11–21.
Lotfi T., Soleymani F., Ghorbanzadeh M., Assari P. On the construction of some tri-parametric iterative methods with memory // Numer. Algor. 2015. V. 70. P. 835–845.
Sharifi S., Siegmund S., Salimi M. Solving nonlinear equations by a derivative-free form of the King’s family with memory // Calcolo. 2016. V. 53. P. 201–215.
Sharma J.R., Guha R.K., Gupta P. Some efficient derivative free methods with memory for solving nonlinear equations // Appl. Math. Comput. 2012. V. 219. P. 699–707.
Behl R., Gonzalez D., Maroju P., Motsa S.S. An optimal and efficient general eighth-order derivative-free scheme for simple roots // J. Comput. Appl. Math. 2018. V. 330. P. 666–675.
Soleymani F. Optimal fourth-order iterative methods free from derivative // Miskolc Mathematical Notes. 2011. V. 12. P. 255–264.
Khattri S.K., Agarwal R.P. Derivative-free optimal iterative methods // Comput. Meth. in Appl. Math. 2010. V. 10. P. 368–375.
Zhanlav T., Otgondorj Kh. A new family of optimal eighth-order methods for solving nonlinear equations // American Journal of Comput and Applied Math. 2018. V. 8. 1. P. 15–19.
Zafar F., Yasmin N., Kutbi M. A., Zeshan M. Construction of Tri-parametric derivative free fourth order with and without memory iterative method // J. Nonlinear Sci. Appl. 2016. V. 9. P. 1410–1423.
Soleymani F., Vanani S.K. Optimal Steffensen-type methods with eighth order of convergence // Comput. Math. Appl. 2011. V. 62. P. 4619–4626.
Soleymani F. On a bi-parametric class of optimal eighth-order derivative-free methods // Int. J. Pure. Appl. Math. 2011. V. 72. P. 27–37.
Kansal M., Kanwar V., Bhatia S. Efficient derivative-free variants of Hansen-Patrick’s family with memory for solving nonlinear equations // Numer. Algor. 2016. V. 73. P. 1017–1036.
Chicharro F.I., Cordero A., Torregrosa J.R., Vassileva M.P. King-Type derivative-free iterative families: Real and memory dynamics // Complexity. 2017. V. 2017. P. 2713145, 15 pages.
Petković M.S., Ilic S., Dzunić J. Derivative-free two-point methods with and without memory for solving nonlinear equations // Appl. Math. Comput. 2010. V. 217. P. 1887–1895.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики