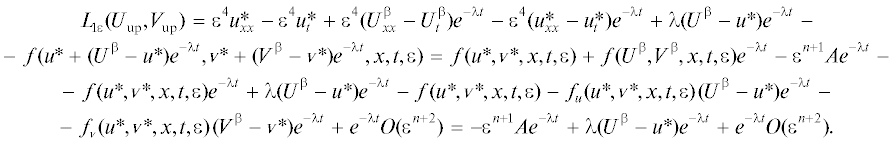Журнал вычислительной математики и математической физики, 2019, T. 59, № 7, стр. 1184-1200

Существование и устойчивость периодического решения типа фронта в двухкомпонентной системе параболических уравнений

А. А. Мельникова^*

МГУ, физический факультет
119991 Москва, Ленинские горы, Россия

Поступила в редакцию 14.06.2018
После доработки 10.02.2019
Принята к публикации 11.03.2019

DOI: 10.1134/S0044466919070111

Аннотация

Рассматривается периодическое решение типа фронта для сингулярно возмущенной системы параболических уравнений. Систему можно рассматривать как математическую модель, описывающую резкое изменение физических характеристик пространственно-неоднородных сред. Подобные модели используются для описания процессов в экологии, биофизике, химической кинетике, физике горения и других областях. Доказана теорема существования решения типа фронта и установлена асимптотическая устойчивость периодического решения. Описан алгоритм построения асимптотического приближения решения. Библ. 28. Фиг. 2.

Ключевые слова: периодическое решение, внутренний переходный слой, устойчивость, сингулярное возмущение.

ВВЕДЕНИЕ

В работе исследуются решения типа движущегося фронта для нелинейной системы параболических уравнений. Систему можно рассматривать как математическую модель, описывающую резкое изменение физических характеристик пространственно-неоднородных сред. Модели такого типа используются в химической кинетике (см. [1]–[3]), биофизике (см. [4]), экологии (см. [5], [6]), физике сверхпроводников (см. [7]) и других областях и изучаются как аналитическими методами (см. [1], [2], [8]), так и в численных экспериментах (см. [3], [4]).

При моделировании переходных процессов решение модельной системы имеет вид движущегося фронта. В областях много больших, чем ширина фронта, появляются решения с резкими градиентами. Применение численных методов в данных задачах ограничено за счет значительной численной неустойчивости решений описанного типа. Появляется необходимость в аналитическом исследовании.

В работе исследуется двухкомпонентная система параболических уравнений, которая может применяться для моделирования неоднородных сред, параметры которых меняются со временем. Например, похожая модель используется для моделирования урбоэкосистем (см. [5], [6]). Цель работы состоит в доказательстве существования решения с внутренним переходным слоем для нового типа систем сингулярно возмущенных уравнений. Для этого используются асимптотические методы, а именно, теория контрастных структур (см. [9]). С исследованиями по решениям с внутренними переходными слоями для разных типов задач можно ознакомиться в работах [10]–[13].

Для достижения поставленной цели в работе решены следующие задачи: определены условия, при которых существует решение заявленного вида, доказана теорема существования решения для постановки с периодическими условиями по времени и в случае начальной задачи по времени, доказана устойчивость решения периодической задачи, представлен алгоритм получения асимптотического приближения решения типа фронта.

Доказательство теоремы существования опирается на работы Пао по системам параболических уравнений (см. [14], [15]) и проведено по методу дифференциальных неравенств (см. [16]–[18]).

Работа имеет следующую структуру. В разд. 1 описана постановка краевой задачи для системы двух параболических уравнений с периодическими условиями по времени. В разд. 2 предложен алгоритм получения асимптотического приближения решения. При этом существенно используются результаты для системы уравнений в стационарном случае (см. [16]). В разд. 3 сформулирована и доказана теорема существования решения с внутренним переходным слоем для периодической задачи. В разд. 4 доказаны асимптотическая устойчивость и локальная единственность решения периодической задачи.

1. ПОСТАНОВКА ЗАДАЧИ

Рассмотрим задачу

(1)

$\begin{array}{*{20}{c}} {{{\varepsilon }^{4}}({{u}_{{xx}}} - {{u}_{t}}) = f(u,\text{v},x,t,\varepsilon ),\quad {{\varepsilon }^{2}}({{\text{v}}_{{xx}}} - {{\text{v}}_{t}}) = g(u,\text{v},x,t,\varepsilon ),\quad x \in (0;L),\quad t \in {{\mathbb{R}}^{ + }},} \\ {{{u}_{x}}(0,t,\varepsilon ) = {{u}_{x}}(L,t,\varepsilon ) = 0,\quad {{\text{v}}_{x}}(0,t,\varepsilon ) = {{\text{v}}_{x}}(L,t,\varepsilon ) = 0,\quad t \in {{\mathbb{R}}^{ + }},} \end{array}$

с условиями

(2)

$u(x,t,\varepsilon ) = u(x,t + T,\varepsilon ),\quad \text{v}(x,t,\varepsilon ) = \text{v}(x,t + T,\varepsilon ),\quad x \in [0;L],\quad t \in {{\mathbb{R}}^{ + }},$

где $\varepsilon > 0$ – малый параметр, функции $f(u,\text{v},x,t,\varepsilon )$ и $g(u,\text{v},x,t,\varepsilon )$ достаточно гладкие и $T$-периодические по переменной $t$.

Целью работы является доказательство теоремы существования решения в виде периодического фронта задачи (1), (2), получение алгоритма построения асимптотического приближения решения, доказательство локальной единственности и асимптотической устойчивости решения.

Требование гладкости функций $f$ и $g$ связано с предполагаемым порядком точности асимптотического приближения. Для построения асимптотики порядка $n$ требуется, чтобы функции $f(u,\text{v},x,t,\varepsilon )$ и $g(u,\text{v},x,t,\varepsilon )$ принадлежали классу ${{C}^{{n + 3}}}$.

Предполагается, что выполнены следующие условия.

(H₁) Уравнение $f(u,\text{v},x,t,0) = 0$ имеет ровно три корня относительно переменной $u$: $u = {{\varphi }^{l}}(\text{v},x,t)$, $u = {{\varphi }^{0}}(\text{v},x,t)$, $u = {{\varphi }^{r}}(\text{v},x,t)$, такие что ${{\varphi }^{l}}(\text{v},x,t) < {{\varphi }^{0}}(\text{v},x,t) < {{\varphi }^{r}}(\text{v},x,t)$ всюду в области $\{ (\text{v},x,t) \in {{I}_{\text{v}}} \times [0;L] \times {{\mathbb{R}}^{ + }}\} $; причем ${{f}_{u}}({{\varphi }^{{l,r}}}(\text{v},x,t),\text{v},x,t,0) > 0$, и ${{f}_{u}}({{\varphi }^{0}}(\text{v},x,t),\text{v},x,t,0) < 0$. (Здесь ${{I}_{\text{v}}}$ – некоторая область изменения переменной $\text{v}$.)

(H₂) Каждое из уравнений ${{h}^{{l,r}}}(\text{v},x,t): = g({{\varphi }^{{l,r}}}(\text{v},x,t),\text{v},x,t,0) = 0$, имеет единственное решение $\text{v} = {{\text{v}}^{{l,r}}}(x,t) \in {{I}_{\text{v}}}$; причем неравенства ${{\text{v}}^{l}}(x,t) < {{\text{v}}^{r}}(x,t)$ и $h_{\text{v}}^{{l,r}}({{\text{v}}^{{l,r}}}(x,t),x,t) > 0$ выполнены всюду в области $\{ (x,t):[0;L] \times {{\mathbb{R}}^{ + }}\} $.

(H₃) Неравенства ${{f}_{\text{v}}}(u,\text{v},x,t,0) < 0$ и ${{g}_{u}}(u,\text{v},x,t,0) < 0$ выполнены всюду в области $\{ (u,\text{v},x,t) \in {{I}_{u}} \times {{I}_{\text{v}}} \times [0;L] \times {{\mathbb{R}}^{ + }}\} $.

(H₄) Существует единственное $T$-периодическое решение ${{\text{v}}_{0}}(t)$, ${{x}_{0}}(t)$ системы уравнений

(3)

$\begin{array}{*{20}{c}} {J(\text{v},x,t): = \int\limits_{{{\text{v}}^{l}}\left( {x,t} \right)}^\text{v} {{{h}^{l}}} \left( {\text{v}{\kern 1pt} {\text{'}},x,t} \right)d\text{v}{\kern 1pt} {\text{'}} + \int\limits_\text{v}^{{{\text{v}}^{r}}\left( {x,t} \right)} {{{h}^{r}}} \left( {\text{v}{\kern 1pt} {\text{'}},x,t} \right)d\text{v}{\kern 1pt} {\text{'}} = 0,} \\ {Y(\text{v},x,t): = \int\limits_{{{\varphi }^{l}}\left( {\text{v},x,t} \right)}^{{{\varphi }^{r}}\left( {\text{v},x,t} \right)} f (u,\text{v},x,t,0)du = 0,} \end{array}$

определенное в области $\{ x(t) \in (0;L),\;\text{v}(t) \in ({{\text{v}}^{l}}(x,t),{{\text{v}}^{r}}(x,t)),\;(x,t) \in [0;L] \times {{\mathbb{R}}^{ + }}\} $.

(H₅) Определитель Якоби системы уравнений (3) удовлетворяет неравенству $\tfrac{{D(J,Y)}}{{D(\text{v},x)}}\left( {{{\text{v}}_{0}}(t),{{x}_{0}}(t)} \right) < 0$, $t \in {{\mathbb{R}}^{ + }}$.

Исследуется вопрос существования периодического решения системы уравнений (1), (2) в форме движущегося фронта. Подобная задача с другим дифференциальным оператором и без периодических условий решена в работе [19]. Решение типа фронта в каждый момент времени $t \in {{\mathbb{R}}^{ + }}$ имеет внутренний переходный слой в малой окрестности некоторой точки $x = {{x}_{{tr}}}(t) \in (0;L)$. Условия ${{H}_{1}}$ и ${{H}_{2}}$ определяют устойчивые корни вырожденной системы (1) (системы (1) при $\varepsilon = 0$), между которыми образуется переходный слой. Предполагается, что при $x < {{x}_{{tr}}}(t)$ решение близко к корням ${{\varphi }^{l}}(\text{v},x,t)$, ${{\text{v}}^{l}}(x,t)$ вырожденной системы (1), а при $x > {{x}_{{tr}}}(t)$ – близко к корням ${{\varphi }^{r}}(\text{v},x,t)$, ${{\text{v}}^{r}}(x,t)$ для $u$ и $\text{v}$ компонент соответственно.

Физический смысл условия ${{H}_{3}}$ в задачах химической кинетики, где величины $u$ и $\text{v}$ имеют смысл концентраций веществ, состоит в том, как изменение концентрации одной из компонент влияет на скорость изменения второй составляющей системы. Предполагая, что производные ${{f}_{\text{v}}}$, ${{g}_{u}}$ сохраняют знак во всей области изменения переменных, возможны четыре варианта комбинаций знаков производных ${{f}_{\text{v}}}$, ${{g}_{u}}$, из которых в данной работе рассматривается один. В случае разных знаков производных изменится способ построения верхнего и нижнего решений в методе доказательства теоремы существования (см. [21]).

Условие ${{H}_{4}}$ определяет зависимость от времени положения фронта в нулевом приближении по малому параметру. Опираясь на исследования об устойчивости контрастных структур (см., например, [20]), можно предположить, что условие ${{H}_{5}}$ на знак якобиана системы уравнений (3) связано с устойчивостью решения с внутренним переходным слоем для случая системы уравнений. Знак якобиана определяет устойчивость ступеньки, идущей от меньшего корня вырожденной системы к большему. Однако обоснование этого утверждения выходит за рамки данной работы.

2. АСИМПТОТИЧЕСКОЕ ПРИБЛИЖЕНИЕ

Точка локализации фронта $({{x}_{{tr}}},t)$ описывает некоторую кривую $x = {{x}_{{tr}}}(t)$ на плоскости $(x,t)$, которая определяет положение внутреннего слоя на сегменте $[0;L]$ в момент времени $t$. Кривая $x = {{x}_{{tr}}}(t)$ разделяет область ${{\bar {D}}_{T}}:(x,t) \in [0;L] \times {{\mathbb{R}}^{ + }}$ на две подобласти $\bar {D}_{T}^{l}$ и $\bar {D}_{T}^{r}$: $\bar {D}_{T}^{l}:(x,t) \in $ $ \in \;[0;{{x}_{{tr}}}(t)] \times {{\mathbb{R}}^{ + }}$, $\bar {D}_{T}^{r}:(x,t) \in [{{x}_{{tr}}}(t);L] \times {{\mathbb{R}}^{ + }}$.

Составим асимптотическое приближение решения по методу Васильевой с соответствующей модификацией для задач с внутренними слоями (см. [22]) отдельно в областях $\bar {D}_{T}^{l}$ и $\bar {D}_{T}^{r}$:

$u = \left\{ \begin{gathered} {{u}^{l}},\quad (x,t) \in \bar {D}_{T}^{l}, \hfill \\ {{u}^{r}},\quad (x,t) \in \bar {D}_{T}^{r}; \hfill \\ \end{gathered} \right.\quad \text{v} = \left\{ \begin{gathered} {{\text{v}}^{l}},\quad (x,t) \in \bar {D}_{T}^{l}, \hfill \\ {{\text{v}}^{r}},\quad (x,t) \in \bar {D}_{T}^{r}. \hfill \\ \end{gathered} \right.$

Решение представляется суммой функций, каждая из которых описывает кривую решения на определенной части сегмента $[0;L]$. Функции ${{u}^{{l,r}}}$, ${{\text{v}}^{{l,r}}}$ имеют вид

(4)

$\begin{gathered} {{u}^{{l,r}}} = {{{\bar {u}}}^{{l,r}}}(x,t,\varepsilon ) + {{Q}^{{l,r}}}u(\xi ,t,\varepsilon ) + {{M}^{{l,r}}}u(\sigma ,t,\varepsilon ) + {{P}^{{l,r}}}u({{\zeta }_{{l,r}}},\varepsilon ) + {{R}^{{l,r}}}u({{\eta }_{{l,r}}},\varepsilon ), \\ {{\text{v}}^{{l,r}}} = {{{\bar {v}}}^{{l,r}}}(x,t,\varepsilon ) + {{Q}^{{l,r}}}\text{v}(\xi ,t,\varepsilon ) + {{M}^{{l,r}}}\text{v}(\sigma ,t,\varepsilon ) + {{P}^{{l,r}}}\text{v}({{\zeta }_{{l,r}}},\varepsilon ) + {{R}^{{l,r}}}\text{v}({{\eta }_{{l,r}}},\varepsilon ). \\ \end{gathered} $

Здесь функции ${{\bar {u}}^{{l,r}}}(x,t,\varepsilon )$, ${{\bar {v}}^{{l,r}}}(x,t,\varepsilon )$ представляют регулярную часть решения; ${{Q}^{{l,r}}}u(\xi ,t,\varepsilon )$, ${{Q}^{{l,r}}}\text{v}(\xi ,t,\varepsilon )$, ${{M}^{{l,r}}}u(\sigma ,t,\varepsilon )$, ${{M}^{{l,r}}}\text{v}(\sigma ,t,\varepsilon )$ описывают внутренний переходный слой, ${{P}^{{l,r}}}u({{\zeta }_{{l,r}}},\varepsilon )$, ${{P}^{{l,r}}}\text{v}({{\zeta }_{{l,r}}},\varepsilon )$, ${{R}^{{l,r}}}u({{\eta }_{{l,r}}},\varepsilon )$, ${{R}^{{l,r}}}\text{v}({{\eta }_{{l,r}}},\varepsilon )$ – функции пограничного слоя, описывающие решение в окрестности точек $x = 0$ и $x = L$. Мы используем переменные переходного слоя $\xi = {{\varepsilon }^{{ - 1}}}(x - {{x}_{{tr}}})$, $\sigma = {{\varepsilon }^{{ - 2}}}(x - {{x}_{{tr}}})$ и переменные пограничного слоя ${{\zeta }_{l}} = x{\text{/}}\varepsilon $, ${{\zeta }_{r}} = (L - x){\text{/}}\varepsilon $, ${{\eta }_{l}} = x{\text{/}}{{\varepsilon }^{2}}$, ${{\eta }_{r}} = (L - x){\text{/}}{{\varepsilon }^{2}}$.

Функции в представлениях (4) ищем в виде рядов по степеням малого параметра $\varepsilon $, например: ${{\bar {u}}^{l}}(x,t,\varepsilon ) = \bar {u}_{0}^{l}(x,t) + \varepsilon \bar {u}_{1}^{l}(x,t) + {{\varepsilon }^{2}}\bar {u}_{2}^{l}(x,t) + \ldots + {{\varepsilon }^{n}}\bar {u}_{n}^{l}(x,t) + \ldots \;.$ Члены этих рядов могут быть получены по стандартной процедуре (см. [22]) отдельно справа и слева от точки ${{x}_{{tr}}}$.

Задача рассматривается в области $x \in [0;L]$, соответствено области изменения переменных $\xi $ и $\sigma $: $\xi \in [ - {{x}_{{tr}}}{\text{/}}\varepsilon ;(L - {{x}_{{tr}}}){\text{/}}\varepsilon ]$ и $\sigma \in [ - {{x}_{{tr}}}{\text{/}}\varepsilon ;(L - {{x}_{{tr}}}){\text{/}}{{\varepsilon }^{2}}]$, а области изменения переменных ${{\zeta }_{{l,r}}}$ и ${{\eta }_{{l,r}}}$ $:{{\zeta }_{{l,r}}} \in [0;L{\text{/}}\varepsilon ]$ и ${{\eta }_{{l,r}}} \in [0;L{\text{/}}{{\varepsilon }^{2}}]$.

Параметр $\varepsilon $ появляется в модельных задачах после нормировки на характерный масштаб области изменения переменной $x$ и его малость означает, что ширина фронта много меньше размеров области. Назначение погранслойных рядов в том, чтобы совместно с регулярной частью удовлетворять граничным условиям. Известно (см. [22]), что в подобных задачах функции пограничного слоя экспоненциально затухают с ростом погранслойной переменной. Тем самым они существенны лишь в малых окрестностях граничных точек – так называемых пограничных слоях и стремятся к нулю быстрее любой степени $\varepsilon $ вне малой окрестности граничных точек. Аналогичные рассуждения справдливы для функций переходного слоя.

Предполагая, что асимптотика строится при $\varepsilon \to 0$, можно использовать допущение, что $L{{\varepsilon }^{{ - 1}}} \to + \infty $ и область изменения переменных ${{\zeta }_{{l,r}}}$ и ${{\eta }_{{l,r}}}$: ${{\zeta }_{{l,r}}},{{\eta }_{{l,r}}} \in \left[ {0; + \infty } \right)$. Аналогично, получаем область изменения переменных $\xi $ и $\sigma $: $\xi ,\sigma \in ( - \infty ; + \infty )$.

Для функций переходного слоя потребуем выполнения условия убывания на бесконечности

(5)

$\begin{gathered} Q_{i}^{{l,r}}u(\xi ,t) \to 0,\quad Q_{i}^{{l,r}}\text{v}(\xi ,t) \to 0\quad {\text{п р и }}\quad \xi \to \mp \infty , \\ M_{i}^{{l,r}}u(\sigma ,t) \to 0,\quad M_{i}^{{l,r}}\text{v}(\sigma ,t) \to 0\quad {\text{п р и }}\quad \sigma \to \mp \infty ,\quad i = 0,1, \ldots ;\quad t \in {{\mathbb{R}}^{ + }}. \\ \end{gathered} $

Функции пограничных слоев также должны удовлетворять условию убывания к нулю при ${{\zeta }_{{l,r}}},{{\eta }_{{l,r}}} \to + \infty $.

Обозначим через ${{\text{v}}_{{tr}}}(t)$ значение, которое принимает $\text{v}$-компонента решения в точке $x = {{x}_{{tr}}}(t)$ в каждый момент времени $t \in {{\mathbb{R}}^{ + }}$.

На плоскости $(x,t)$ кривая $x = {{x}_{{tr}}}(t)$ определяется равенством $u({{x}_{{tr}}}(t),t) = {{\varphi }^{0}}({{\text{v}}_{{tr}}}(t),{{x}_{{tr}}}(t),t)$.

Функции ${{u}^{l}}$ и ${{u}^{r}}$, ${{\text{v}}^{l}}$ и ${{\text{v}}^{r}}$ сшиваются непрерывно в точке $x = {{x}_{{tr}}}$:

(6)

${{\bar {v}}^{l}}({{x}_{{tr}}}(t),t,\varepsilon ) + {{Q}^{l}}\text{v}(0,t,\varepsilon ) + {{M}^{l}}\text{v}(0,t,\varepsilon ) = {{\bar {v}}^{r}}({{x}_{{tr}}}(t),t,\varepsilon ) + {{Q}^{r}}\text{v}(0,t,\varepsilon ) + {{M}^{r}}\text{v}(0,t,\varepsilon ) = {{\text{v}}_{{tr}}}(t);$

(7)

${{\bar {u}}^{l}}({{x}_{{tr}}}(t),t,\varepsilon ) + {{Q}^{l}}u(0,t,\varepsilon ) + {{M}^{l}}u(0,t,\varepsilon ) = {{\bar {u}}^{r}}({{x}_{{tr}}}(t),t,\varepsilon ) + {{Q}^{r}}u(0,t,\varepsilon ) + {{M}^{r}}u(0,t,\varepsilon ){{\varphi }^{0}}({{\text{v}}_{{tr}}}(t),{{x}_{{tr}}}(t),t).$

Функции ${{\text{v}}_{{tr}}}(t)$ и ${{x}_{{tr}}}(t)$ представляются рядами по степеням параметра $\varepsilon $:

(8)

${{\text{v}}_{{tr}}}(t) = {{\text{v}}_{0}}(t) + \varepsilon {{\text{v}}_{1}}(t) + {{\varepsilon }^{2}}{{\text{v}}_{2}}(t) + \ldots ,$

(9)

${{x}_{{tr}}}(t) = {{x}_{0}}(t) + \varepsilon {{x}_{1}}(t) + {{\varepsilon }^{2}}{{x}_{2}}(t) + \ldots \;.$

При этом производные рядов (4) также непрерывны на кривой $x = {{x}_{{tr}}}(t)$ (условие ${{C}^{1}}$-сшивания)

(10)

$\varepsilon \frac{{\partial {{{\bar {v}}}^{l}}}}{{\partial x}}({{x}_{{tr}}}(t),t,\varepsilon ) + \frac{{\partial {{Q}^{l}}\text{v}}}{{\partial \xi }}(0,t,\varepsilon ) + {{\varepsilon }^{{ - 1}}}\frac{{\partial {{M}^{l}}\text{v}}}{{\partial \sigma }}(0,t,\varepsilon ) = \varepsilon \frac{{\partial {{{\bar {v}}}^{r}}}}{{\partial x}}({{x}_{{tr}}}(t),t,\varepsilon ) + \frac{{\partial {{Q}^{r}}\text{v}}}{{\partial \xi }}(0,t,\varepsilon ) + {{\varepsilon }^{{ - 1}}}\frac{{\partial {{M}^{r}}\text{v}}}{{\partial \sigma }}(0,t,\varepsilon );$

(11)

${{\varepsilon }^{2}}\frac{{\partial {{{\bar {u}}}^{l}}}}{{\partial x}}({{x}_{{tr}}}(t),t,\varepsilon ) + \varepsilon \frac{{\partial {{Q}^{l}}u}}{{\partial \xi }}(0,t,\varepsilon ) + \frac{{\partial {{M}^{l}}u}}{{\partial \sigma }}(0,t,\varepsilon ) = {{\varepsilon }^{2}}\frac{{\partial {{{\bar {u}}}^{r}}}}{{\partial x}}({{x}_{{tr}}}(t),t,\varepsilon ) + \varepsilon \frac{{\partial {{Q}^{r}}u}}{{\partial \xi }}(0,t,\varepsilon ) + \frac{{\partial {{M}^{r}}u}}{{\partial \sigma }}(0,t,\varepsilon ).$

В дальнейшем в некоторых случаях мы будем опускать аргумент у функций ${{x}_{{tr}}}(t)$ и ${{\text{v}}_{{tr}}}(t)$.

Пограничные функции ${{P}^{{l,r}}}u({{\zeta }_{{l,r}}},\varepsilon )$, ${{P}^{{l,r}}}\text{v}({{\zeta }_{{l,r}}},\varepsilon )$, ${{R}^{{l,r}}}u({{\eta }_{{l,r}}},\varepsilon )$, ${{R}^{{l,r}}}\text{v}({{\eta }_{{l,r}}},\varepsilon )$ строятся стандартным способом (см. [22]). Ряды пограничных функций не содержат членов нулевого порядка, что характерно для задачи Неймана, ряды ${{P}^{{l,r}}}u({{\zeta }_{{l,r}}},\varepsilon )$, ${{P}^{{l,r}}}\text{v}({{\zeta }_{{l,r}}},\varepsilon )$ начинаются с членов порядка $\varepsilon $, ряды ${{R}^{{l,r}}}u({{\eta }_{{1,2}}},\varepsilon )$ – с членов порядка ${{\varepsilon }^{2}}$, а ряды ${{R}^{{l,r}}}\text{v}\left( {{{\eta }_{{l,r}}},\varepsilon } \right)$ – с членов порядка ${{\varepsilon }^{4}}$. Функции $P_{i}^{{l,r}}u({{\zeta }_{{l,r}}})$, $P_{i}^{{l,r}}\text{v}({{\zeta }_{{l,r}}})$ экспоненциально убывают при ${{\zeta }_{{l,r}}} \to + \infty $, а функции $R_{i}^{{l,r}}u({{\eta }_{{l,r}}})$, $R_{i}^{{l,r}}\text{v}({{\eta }_{{l,r}}})$ экспоненциально убывают при ${{\eta }_{{l,r}}} \to + \infty $. Умножим все пограничные функции на срезающие функции (см. [23]), в результате чего пограничные функции станут равными нулю вне некоторых конечных окрестностей граничных точек и, таким образом, не войдут в левые части равенств (2), (7) и в равенства (10), (11).

2.1. Регулярная часть решения

Функции регулярной части $\bar {u}_{k}^{{l,r}}(x,t)$, $\bar {v}_{k}^{{l,r}}(x,t)$, $k = 0,\;1,\; \ldots $, определяются из следующих систем уравнений:

$\begin{array}{*{20}{c}} {{{\varepsilon }^{4}}\left( {\frac{{{{\partial }^{2}}{{{\bar {u}}}^{{l,r}}}}}{{\partial {{x}^{2}}}} - \frac{{\partial {{{\bar {u}}}^{{l,r}}}}}{{\partial t}}} \right) = f({{{\bar {u}}}^{{l,r}}},{{{\bar {v}}}^{{l,r}}},x,t,\varepsilon ),} \\ {{{\varepsilon }^{2}}\left( {\frac{{{{\partial }^{2}}{{{\bar {v}}}^{{l,r}}}}}{{\partial {{x}^{2}}}} - \frac{{\partial {{{\bar {v}}}^{{l,r}}}}}{{\partial t}}} \right) = g({{{\bar {u}}}^{{l,r}}},{{{\bar {v}}}^{{l,r}}},x,t,\varepsilon ),\quad x \in [0;L],\quad t \in {{\mathbb{R}}^{ + }}.} \end{array}$

В системы подставляем функции ${{\bar {u}}^{{l,r}}}$ и ${{\bar {v}}^{{l,r}}}$ в виде рядов ${{\bar {u}}^{{l,r}}}(x,t) = \bar {u}_{0}^{{l,r}}(x,t) + \varepsilon \bar {u}_{1}^{{l,r}}(x,t) + \ldots $ $ \ldots + \;{{\varepsilon }^{n}}\bar {u}_{n}^{{l,r}}(x,t) + \ldots $, ${{\bar {v}}^{{l,r}}}(x,t) = \bar {v}_{0}^{{l,r}}(x,t) + \varepsilon \bar {v}_{1}^{{l,r}}(x,t) + \ldots + {{\varepsilon }^{n}}\bar {v}_{n}^{{l,r}}(x,t) + \ldots $, приравниваем коэффициенты при одинаковых степенях $\varepsilon $ и получаем уравнения для определения $\bar {u}_{k}^{{l,r}}(x,t)$, $\bar {v}_{k}^{{l,r}}(x,t)$, $k = 0,\;1,\; \ldots $ .

Функции $\bar {u}_{0}^{{l,r}}(x,t)$, $\bar {v}_{0}^{{l,r}}(x,t)$ удовлетворяют вырожденной системе (1)

$f(\bar {u}_{0}^{{l,r}},\bar {v}_{0}^{{l,r}},x,t,0) = 0,\quad g(\bar {u}_{0}^{{l,r}},\bar {v}_{0}^{{l,r}},x,t,0) = 0,$

решения которой определены условиями ${{H}_{1}}$ и ${{H}_{2}}$

$\begin{gathered} \bar {v}_{0}^{l}(x,t) = {{\text{v}}^{l}}(x,t),\quad \bar {v}_{0}^{r}(x,t) = {{\text{v}}^{r}}(x,t); \\ \bar {u}_{0}^{l}(x,t) = {{\varphi }^{l}}({{\text{v}}^{l}}(x,t),x,t,0) = :{{{\bar {\varphi }}}^{l}}(x,t),\quad \bar {u}_{0}^{r}(x,t) = {{\varphi }^{r}}({{\text{v}}^{r}}(x,t),x,t,0) = :{{{\bar {\varphi }}}^{r}}(x,t). \\ \end{gathered} $

Функции $\bar {u}_{k}^{{l,r}}(x,t)$ и $\bar {v}_{k}^{{l,r}}(x,t)$ при $k \geqslant 1$ определяются из линейных систем

(12)

$\bar {f}_{u}^{{l,r}}(x,t)\bar {u}_{k}^{{l,r}} + \bar {f}_{\text{v}}^{{l,r}}(x,t)\bar {v}_{k}^{{l,r}} = \bar {F}_{k}^{{l,r}}(x,t),\quad \bar {g}_{u}^{{l,r}}(x,t)\bar {u}_{k}^{{l,r}} + \bar {g}_{\text{v}}^{{l,r}}(x,t)\bar {v}_{k}^{{l,r}} = \bar {G}_{k}^{{l,r}}(x,t).$

Здесь

$\bar {f}_{u}^{l}(x,t) = {{f}_{u}}({{\bar {\varphi }}^{l}}(x,t),{{\text{v}}^{l}}(x,t),x,t,0),\quad \bar {f}_{u}^{r}(x,t) = {{f}_{u}}({{\bar {\varphi }}^{r}}(x,t),{{\text{v}}^{r}}(x,t),x,t,0),$

аналогичный смысл имеют обозначения $\bar {f}_{\text{v}}^{{l,r}}(x,t)$, $\bar {g}_{u}^{{l,r}}(x,t)$, $\bar {g}_{\text{v}}^{{l,r}}(x,t)$, а $\bar {F}_{k}^{{l,r}}(x,t)$ и $\bar {G}_{k}^{{l,r}}(x,t)$ – известные на $k$-м шаге функции, рекуррентно выражающиеся через $\bar {u}_{i}^{{l,r}}(x,t),$ $\bar {v}_{i}^{{l,r}}(x,t)$ с номерами $i < k$.

Системы (12) разрешимы единственным образом, поскольку определители ${{\Delta }^{{l,r}}}(x,t) = $ $ = \bar {f}_{u}^{{l,r}}(x,t)\bar {g}_{\text{v}}^{{l,r}}(x,t) - \bar {f}_{\text{v}}^{{l,r}}(x,t)\bar {g}_{u}^{{l,r}}(x,t) = \bar {f}_{u}^{{l,r}}(x,t)h_{\text{v}}^{{l,r}}(x,t) > 0$ отличны от нуля всюду на сегменте $[0;L]$ по условиям ${{H}_{1}}$ и ${{H}_{2}}$.

2.2. Функции переходного слоя

Перепишем дифференциальные операторы системы (1) в переменных $(\xi ,t)$ и $(\sigma ,t)$. Например, оператор ${{\varepsilon }^{4}}\left( {\tfrac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}} - \tfrac{\partial }{{\partial t}}} \right)$ в переменных $(\xi ,t)$ принимает вид

${{\varepsilon }^{2}}\tfrac{{{{\partial }^{2}}}}{{\partial {{\xi }^{2}}}} + {{\varepsilon }^{3}}\tfrac{{d{{x}_{{tr}}}}}{{dt}}\tfrac{\partial }{{\partial \xi }} - {{\varepsilon }^{4}}\tfrac{\partial }{{\partial t}}.$

Уравнения для функций $Q_{i}^{{l,r}}u(\xi ,t)$, $Q_{i}^{{l,r}}\text{v}(\xi ,t)$, $i = 0,\;1,\; \ldots $, получаются по методу Васильевой с соответствующей модификацией для систем уравнений (см. [19], [22]). Будем приравнивать коэффициенты при одинаковых степенях $\varepsilon $ в обеих частях равенств

(13)

${{\varepsilon }^{2}}\frac{{{{\partial }^{2}}{{Q}^{{l,r}}}u}}{{\partial {{\xi }^{2}}}} - {{\varepsilon }^{4}}\frac{{\partial {{Q}^{{l,r}}}u}}{{\partial t}} + {{\varepsilon }^{3}}W\frac{{\partial {{Q}^{{l,r}}}u}}{{\partial \xi }} = {{Q}^{{l,r}}}f,\quad \frac{{{{\partial }^{2}}{{Q}^{{l,r}}}\text{v}}}{{\partial {{\xi }^{2}}}} - {{\varepsilon }^{2}}\frac{{\partial {{Q}^{{l,r}}}\text{v}}}{{\partial t}} + \varepsilon W\frac{{\partial {{Q}^{{l,r}}}\text{v}}}{{\partial \xi }} = {{Q}^{{l,r}}}g,$

считая, что функции ${{Q}^{{l,r}}}u$, ${{Q}^{{l,r}}}\text{v}$ – это ряды по степеням параметра $\varepsilon $. Здесь

$\begin{gathered} {{Q}^{{l,r}}}f: = f({{{\bar {u}}}^{{l,r}}}(\varepsilon \xi + {{x}_{{tr}}}) + {{Q}^{{l,r}}}u,\;{{{\bar {v}}}^{{l,r}}}(\varepsilon \xi + {{x}_{{tr}}}) + {{Q}^{{l,r}}}\text{v},\;\varepsilon \xi + {{x}_{{tr}}},\;t,\;\varepsilon ) - \\ - \;f({{{\bar {u}}}^{{l,r}}}(\varepsilon \xi + {{x}_{{tr}}}),\;{{{\bar {v}}}^{{l,r}}}(\varepsilon \xi + {{x}_{{tr}}}),\;\varepsilon \xi + {{x}_{{tr}}},\;t,\;\varepsilon ). \\ \end{gathered} $

Обозначение ${{Q}^{{l,r}}}g$ имеет тот же смысл. Через $W$ обозначена производная $d{{x}_{{tr}}}{\text{/}}dt$, которая определяет скорость фронта.

Уравнения для функций $M_{i}^{{l,r}}u(\sigma ,t)$, $M_{i}^{{l,r}}\text{v}(\sigma ,t)$, $i = 0,\;1,\; \ldots $, получаются приравниванием коэффициентов при ${{\varepsilon }^{i}}$ в разложениях обеих частей равенств

(14)

$\frac{{{{\partial }^{2}}{{M}^{{l,r}}}u}}{{\partial {{\sigma }^{2}}}} - {{\varepsilon }^{4}}\frac{{\partial {{M}^{{l,r}}}u}}{{\partial t}} + {{\varepsilon }^{2}}W\frac{{\partial {{M}^{{l,r}}}u}}{{\partial \sigma }} = {{M}^{{l,r}}}f,\quad \frac{1}{{{{\varepsilon }^{2}}}}\frac{{{{\partial }^{2}}{{M}^{{l,r}}}\text{v}}}{{\partial {{\sigma }^{2}}}} - {{\varepsilon }^{2}}\frac{{\partial {{M}^{{l,r}}}\text{v}}}{{\partial t}} + W\frac{{\partial {{M}^{{l,r}}}\text{v}}}{{\partial \sigma }} = {{M}^{{l,r}}}g,$

где

$\begin{gathered} {{M}^{{l,r}}}f: = f({{{\bar {u}}}^{{l.r}}} + {{Q}^{{l,r}}}u + {{M}^{{l,r}}}u,\;{{{\bar {v}}}^{{l,r}}} + {{Q}^{{l,r}}}\text{v} + {{M}^{{l,r}}}\text{v},\;{{\varepsilon }^{2}}\sigma + {{x}_{{tr}}},\;t,\;\varepsilon ) - \\ - \;f({{{\bar {u}}}^{{l.r}}} + {{Q}^{{l,r}}}u,\;{{{\bar {v}}}^{{l,r}}} + {{Q}^{{l,r}}}\text{v},\;{{\varepsilon }^{2}}\sigma + {{x}_{{tr}}},\;t,\;\varepsilon ). \\ \end{gathered} $

Обозначение ${{M}^{{l,r}}}g$ имеет тот же смысл. Заметим, что для функций ${{\bar {u}}^{{l,r}}}$ и ${{\bar {v}}^{{l,r}}}$ аргумент $x$ заменяется на ${{\varepsilon }^{2}}\sigma + {{x}_{{tr}}}$, а для ${{Q}^{{l,r}}}u$, ${{Q}^{{l,r}}}\text{v}$ аргумент $\xi $ заменяется на $\varepsilon \sigma $.

2.3. Функции переходного слоя нулевого порядка

Сформулируем задачи для функций $M_{0}^{{l,r}}\text{v}(\sigma ,t)$ и $M_{1}^{{l,r}}\text{v}(\sigma ,t)$. Уравнения получаются из (14) и условий (5)

$\frac{{{{\partial }^{2}}M_{i}^{l}\text{v}}}{{\partial {{\sigma }^{2}}}} = 0,\quad \sigma \leqslant 0,\quad \frac{{{{\partial }^{2}}M_{i}^{r}\text{v}}}{{\partial {{\sigma }^{2}}}} = 0,\quad \sigma \geqslant 0,\quad M_{i}^{l}\text{v}( - \infty ,t) = 0,\quad M_{i}^{r}\text{v}( + \infty ,t) = 0,\quad i = 0,1.$

Здесь и далее переменная $t \in {{\mathbb{R}}^{ + }}$ рассматривается как параметр. Задачи имеют только тривиальные решения $M_{0}^{{l,r}}\text{v}(\sigma ,t) \equiv 0$, $M_{1}^{{l,r}}\text{v}(\sigma ,t) \equiv 0$.

Систему уравнений для функций $Q_{0}^{{l,r}}u(\xi ,t)$ и $Q_{0}^{{l,r}}\text{v}(\xi ,t)$ получаем из (13)

(15)

$f({{\bar {\varphi }}^{{l,r}}}({{x}_{{tr}}}(t),t) + Q_{0}^{{l,r}}u,\;{{\text{v}}^{{l,r}}}({{x}_{{tr}}}(t),t) + Q_{0}^{{l,r}}\text{v},\;{{x}_{{tr}}}(t),\;t,\;0) = 0,$

(16)

$\frac{{{{\partial }^{2}}Q_{0}^{{l,r}}\text{v}}}{{\partial {{\xi }^{2}}}} = g({{\bar {\varphi }}^{{l,r}}}({{x}_{{tr}}}(t),t) + Q_{0}^{{l,r}}u,\;{{\text{v}}^{{l,r}}}({{x}_{{tr}}}(t),t) + Q_{0}^{{l,r}}\text{v},\;{{x}_{{tr}}}(t),\;t,\;0).$

Здесь индекс “$l$” соответствует $\xi \leqslant 0$, а индекс “$r$” – условию $\xi \geqslant 0$.

Из равенств (15) по условию ${{H}_{1}}$ получаем уравнения

(17)

${{\bar {\varphi }}^{{l,r}}}({{x}_{{tr}}}(t),t) + Q_{0}^{{l,r}}u(\xi ,t) = {{\varphi }^{{l,r}}}({{\text{v}}^{{1,r}}}({{x}_{{tr}}}(t),t) + Q_{0}^{{l,r}}\text{v}(\xi ,t),\;{{x}_{{tr}}}(t),\;t).$

Подставим выражения (17) в уравнения (16) и получим уравнения для функций $Q_{0}^{{l,r}}\text{v}$:

(18)

$\begin{gathered} \frac{{{{\partial }^{2}}Q_{0}^{l}\text{v}}}{{\partial {{\xi }^{2}}}} = {{h}^{l}}({{\text{v}}^{l}}({{x}_{{tr}}}(t),t) + Q_{0}^{l}\text{v},{{x}_{{tr}}}(t),t),\quad \xi \leqslant 0, \\ \frac{{{{\partial }^{2}}Q_{0}^{r}\text{v}}}{{\partial {{\xi }^{2}}}} = {{h}^{r}}({{\text{v}}^{r}}({{x}_{{tr}}}(t),t) + Q_{0}^{r}\text{v},{{x}_{{tr}}}(t),t),\quad \xi \geqslant 0, \\ \end{gathered} $

где ${{h}^{l}}(\text{v},x,t)$, ${{h}^{r}}(\text{v},x,t)$ – это функции, определенные условием ${{H}_{2}}$.

Граничные условия для $Q_{0}^{{l,r}}\text{v}$ при $\xi = 0$ получаются из (2), а условия на бесконечности – из (5)

(19)

$\begin{array}{*{20}{c}} {Q_{0}^{l}\text{v}(0,t) = {{\text{v}}_{{tr}}}(t) - {{\text{v}}^{l}}({{x}_{{tr}}}(t),t),\quad Q_{0}^{r}\text{v}(0,t) = {{\text{v}}_{{tr}}}(t) - {{\text{v}}^{r}}({{x}_{{tr}}}(t),t),} \\ {Q_{0}^{l}\text{v}( - \infty ,t) = 0,\quad Q_{0}^{r}\text{v}( + \infty ,t) = 0.} \end{array}$

Применим метод понижения степени в задачах (18)–(19) и придем к уравнениям первого порядка с условиями (19) при $\xi = 0$

$\begin{array}{*{20}{c}} {\frac{{\partial Q_{0}^{l}\text{v}}}{{\partial \xi }} = \sqrt 2 {\kern 1pt} \mathop {\left( {\int\limits_{{{\text{v}}^{l}}({{x}_{{tr}}}(t),t)}^{{{\text{v}}^{l}}({{x}_{{tr}}}(t),t) + Q_{0}^{l}\text{v}} {{h}^{l}}(\text{v},{{x}_{{tr}}}(t),t)d\text{v}} \right)}\nolimits^{1/2} ,\quad \xi \leqslant 0,} \\ {\frac{{\partial Q_{0}^{r}\text{v}}}{{\partial \xi }} = \sqrt 2 {\kern 1pt} \mathop {\left( {\int\limits_{{{\text{v}}^{3}}({{x}_{{tr}}}(t),t)}^{{{\text{v}}^{r}}({{x}_{{tr}}}(t),t) + Q_{0}^{r}\text{v}} {{h}^{r}}(\text{v},{{x}_{{tr}}}(t),t)d\text{v}} \right)}\nolimits^{1/2} ,\quad \xi \geqslant 0.} \end{array}$

Для функций $Q_{0}^{{l,r}}u(\xi ,t)$ и $Q_{0}^{{l,r}}\text{v}(\xi ,t)$ имеют место экспоненциальные оценки (см. [24])

(20)

$\left| {Q_{0}^{{l,r}}u(\xi )} \right| \leqslant Cexp( - \kappa \left| \xi \right|),\quad \left| {Q_{0}^{{l,r}}\text{v}(\xi )} \right| \leqslant Cexp( - \kappa \left| \xi \right|),$

где $C$ и $\kappa $ – здесь и далее положительные числа, не зависящие от $\varepsilon $.

Уравнения для функций $M_{0}^{{l,r}}u(\sigma ,t)$ получаются из первого уравнения (14) (мы использовали равенство (17), взятое при $\xi = 0$ и уравнения (19))

(21)

$\frac{{{{\partial }^{2}}M_{0}^{{l,r}}u}}{{\partial {{\sigma }^{2}}}} = f({{\varphi }^{{l,r}}}({{\text{v}}_{{tr}}}(t),{{x}_{{tr}}}(t),t) + M_{0}^{{l,r}}u,{{\text{v}}_{{tr}}}(t),{{x}_{{tr}}}(t),t,0).$

Начальные условия для функций $M_{0}^{{l,r}}u(\sigma ,t)$ получаются из (7) в нулевом порядке разложения по степеням $\varepsilon $, а условия на бесконечности – из (5)

(22)

$M_{0}^{{l,r}}u(0,t) = {{\varphi }^{0}}({{\text{v}}_{{tr}}}(t),{{x}_{{tr}}}(t),t) - {{\varphi }^{{l,r}}}({{\text{v}}_{{tr}}}(t),{{x}_{{tr}}},t),\quad M_{0}^{{l,r}}u( \mp \infty ,t) = 0.$

Решения задач (21), (22) можно получить из уравнений первого порядка

$\frac{{\partial M_{0}^{l}u}}{{\partial \sigma }} = \sqrt 2 {\kern 1pt} \mathop {\left( {\int\limits_{{{\varphi }^{l}}\left( {{{\text{v}}_{{tr}}},{{x}_{{tr}}},t} \right)}^{{{\varphi }^{l}}\left( {{{\text{v}}_{{tr}}},{{x}_{{tr}}},t} \right) + M_{0}^{l}u(\sigma ,t)} f (u,{{\text{v}}_{{tr}}},{{x}_{{tr}}},t,0)du} \right)}\nolimits^{1/2} ,\quad \sigma \leqslant 0,$

$\frac{{\partial M_{0}^{r}u}}{{\partial \sigma }} = \sqrt 2 {\kern 1pt} \mathop {\left( {\int\limits_{{{\varphi }^{r}}\left( {{{\text{v}}_{{tr}}},{{x}_{{tr}}},t} \right)}^{{{\varphi }^{r}}\left( {{{\text{v}}_{{tr}}},{{x}_{{tr}}},t} \right) + M_{0}^{r}u(\sigma ,t)} f (u,{{\text{v}}_{{tr}}},{{x}_{{tr}}},t,0)du} \right)}\nolimits^{1/2} ,\quad \sigma > 0.$

Функции $M_{0}^{{l,r}}u(\sigma ,t)$ имеют экспоненциальные оценки (см. [24])

(23)

$\left| {M_{0}^{{l,r}}u(\sigma )} \right| \leqslant Cexp( - \kappa \left| \sigma \right|).$

Введем обозначения, которые будут использованы ниже:

$\begin{array}{*{20}{c}} {{{\Phi }_{l}}(\xi ,t,{{\text{v}}_{{tr}}},{{x}_{{tr}}}): = \frac{{\partial Q_{0}^{l}\text{v}}}{{\partial \xi }},\quad {{\Phi }_{r}}(\xi ,t,{{\text{v}}_{{tr}}},{{x}_{{tr}}}): = \frac{{\partial Q_{0}^{r}\text{v}}}{{\partial \xi }};} \\ {{{\Psi }_{l}}(\sigma ,t,{{\text{v}}_{{tr}}},{{x}_{{tr}}}): = \frac{{\partial M_{0}^{l}u}}{{\partial \sigma }},\quad {{\Psi }_{r}}(\sigma ,t,{{\text{v}}_{{tr}}},{{x}_{{tr}}}): = \frac{{\partial M_{0}^{r}u}}{{\partial \sigma }}.} \end{array}$

Запишем равенства (10), (11), учитывая представление функций ${{\bar {u}}^{{l,\text{v}}}}$, ${{\bar {v}}^{{l,\text{v}}}}$, ${{Q}^{{l,r}}}u$, ${{Q}^{{l,r}}}\text{v}$, ${{M}^{{l,r}}}\text{v}$, ${{M}^{{l,r}}}\text{v}$ в виде рядов

(24)

$\begin{gathered} \mathop {\left. {{{\Phi }_{l}}} \right|}\nolimits_{\xi = 0} - \mathop {\left. {{{\Phi }_{r}}} \right|}\nolimits_{\xi = 0} + \sum\limits_{i = 0} {{{\varepsilon }^{{i + 1}}}} \mathop {{\kern 1pt} \left( {\frac{{\partial{ \bar {v}}_{i}^{l}}}{{\partial x}} - \frac{{\partial{ \bar {v}}_{i}^{r}}}{{\partial x}}} \right)}\nolimits_{x = {{x}_{{tr}}}} + \sum\limits_{i = 1} {{{\varepsilon }^{i}}} \mathop {{\kern 1pt} \left( {\frac{{\partial Q_{i}^{l}\text{v}}}{{\partial \xi }} - \frac{{\partial Q_{i}^{r}\text{v}}}{{\partial \xi }}} \right)}\nolimits_{\xi = 0} + \sum\limits_{i = 2} {{{\varepsilon }^{{i - 1}}}} {\kern 1pt} \mathop {\left( {\frac{{\partial M_{i}^{l}\text{v}}}{{\partial \sigma }} - \frac{{\partial M_{i}^{r}\text{v}}}{{\partial \sigma }}} \right)}\nolimits_{\sigma = 0} = 0, \\ \mathop {\left. {{{\Psi }_{l}}} \right|}\nolimits_{\sigma = 0} - \mathop {\left. {{{\Psi }_{r}}} \right|}\nolimits_{\sigma = 0} + \sum\limits_{i = 0} {{{\varepsilon }^{{i + 2}}}} \mathop {{\kern 1pt} \left( {\frac{{\partial{ \bar {u}}_{i}^{l}}}{{\partial x}} - \frac{{\partial{ \bar {u}}_{i}^{r}}}{{\partial x}}} \right)}\nolimits_{x = {{x}_{{tr}}}} + \sum\limits_{i = 1} {{{\varepsilon }^{{i + 1}}}} {\kern 1pt} \mathop {\left( {\frac{{\partial Q_{i}^{l}u}}{{\partial \xi }} - \frac{{\partial Q_{i}^{r}u}}{{\partial \xi }}} \right)}\nolimits_{\xi = 0} + \sum\limits_{i = 1} {{{\varepsilon }^{i}}} \mathop {{\kern 1pt} \left( {\frac{{\partial M_{i}^{l}u}}{{\partial \sigma }} - \frac{{\partial M_{i}^{r}u}}{{\partial \sigma }}} \right)}\nolimits_{\sigma = 0} = 0. \\ \end{gathered} $

Функции ${{x}_{{tr}}}$ и ${{\text{v}}_{{tr}}}$ в выражениях (24) разложим в ряды (9) и (8) и приравняем коэффициенты при одинаковых степенях $\varepsilon $. Для нулевого порядка получим равенства

${{\Phi }_{l}}(0,t,{{\text{v}}_{0}},{{x}_{0}}) - {{\Phi }_{r}}(0,t,{{\text{v}}_{0}},{{x}_{0}}) = 0,\quad {{\Psi }_{l}}(0,t,{{\text{v}}_{0}},{{x}_{0}}) - {{\Psi }_{r}}(0,t,{{\text{v}}_{0}},{{x}_{0}}) = 0,$

справедливые в силу условия ${{H}_{4}}$.

Введем непрерывные функции $\Phi (\xi ,t)$ и $\Psi (\sigma ,t)$ по формулам

(25)

$\Phi (\xi ,t) = \left\{ \begin{gathered} {{\Phi }_{l}}(\xi ,t,{{\text{v}}_{0}}(t),{{x}_{0}}(t)),\quad \xi \leqslant 0, \hfill \\ {{\Phi }_{r}}(\xi ,t,{{\text{v}}_{0}}(t),{{x}_{0}}(t)),\quad \xi \geqslant 0; \hfill \\ \end{gathered} \right.\quad \Psi (\sigma ,t) = \left\{ \begin{gathered} {{\Psi }_{l}}(\sigma ,t,{{\text{v}}_{0}}(t),{{x}_{0}}(t)),\quad \sigma \leqslant 0, \hfill \\ {{\Psi }_{r}}(\sigma ,t,{{\text{v}}_{0}}(t),{{x}_{0}}(t)),\quad \sigma \geqslant 0. \hfill \\ \end{gathered} \right.$

2.4. Функции переходного слоя n-го порядка

Функции переходного слоя следующих порядков определяются по алгоритму, описанному в работе [16].

Предполагается, что члены асимптотических рядов с номерами $i = \overline {0,n - 1} $ уже известны.

Введем обозначения

$\begin{gathered} {{{\tilde {\varphi }}}^{{l,r}}}(\xi ,t): = {{\varphi }^{{l,r}}}({{\text{v}}^{{l,r}}}({{x}_{{tr}}},t) + Q_{0}^{{l,r}}\text{v}(\xi ,t),{{x}_{{tr}}},t,0), \\ \tilde {h}_{\text{v}}^{{l,r}}(\xi ,t): = h_{\text{v}}^{{l,r}}({{{\tilde {\varphi }}}^{{l,r}}}\left( {\xi ,t} \right),\bar {v}_{0}^{{l,r}}({{x}_{{tr}}},t) + Q_{0}^{{l,r}}\text{v}(\xi ,t),{{x}_{{tr}}},t,0), \\ \end{gathered} $

${{\hat {f}}_{u}}(\sigma ,t): = \left\{ \begin{gathered} {{f}_{u}}({{\varphi }^{l}}({{\text{v}}_{{tr}}},{{x}_{{tr}}},t) + M_{0}^{l}u(\sigma ,t),{{\text{v}}_{{tr}}},{{x}_{{tr}}},t,0),\quad \sigma \leqslant 0, \hfill \\ {{f}_{u}}({{\varphi }^{r}}({{\text{v}}_{{tr}}},{{x}_{{tr}}},t) + M_{0}^{r}u(\sigma ,t),{{\text{v}}_{{tr}}},{{x}_{{tr}}},t,0),\quad \sigma \geqslant 0. \hfill \\ \end{gathered} \right.$

Обозначения $\tilde {f}_{u}^{{l,r}}(\xi ,t)$, $\tilde {g}_{u}^{{l,r}}(\xi ,t)$ имеют тот же смысл.

Функции $M_{n}^{{l,r}}\text{v}(\sigma ,t)$ определяются из следующих задач:

$\frac{{{{\partial }^{2}}M_{n}^{{l,r}}\text{v}}}{{\partial {{\sigma }^{2}}}} = m_{n}^{{l,r}}g(\sigma ,t),\quad M_{n}^{{l,r}}\text{v}( \mp \infty ,t) = 0,$

где функции $m_{n}^{{l,r}}g(\sigma ,t)$ известны на $n$-м шаге.

Задачи для определения функций $Q_{n}^{{l,r}}\text{v}(\xi ,t)$ выглядят следующим образом:

$\frac{{{{\partial }^{2}}Q_{n}^{{l,r}}\text{v}}}{{\partial {{\xi }^{2}}}} = \tilde {h}_{\text{v}}^{{l,r}}(\xi ,t)Q_{n}^{{l,r}}\text{v} + H_{n}^{{l,r}}(\xi ,t),\quad Q_{n}^{{l,r}}\text{v}(0,t) = - \bar {v}_{n}^{{l,r}}({{x}_{{tr}}},t) - M_{n}^{{l,r}}\text{v}(0,t),\quad Q_{n}^{{l,r}}\text{v}( \mp \infty ,t) = 0,$

где $H_{n}^{{l,r}}(\xi ,t)$ – известные функции. Решения задач для функций $Q_{n}^{{l,r}}\text{v}(\xi ,t)$ могут быть записаны в явном виде:

$Q_{n}^{{l,r}}\text{v}(\xi ,t) = - {{\Phi }_{{l,r}}}(\xi ,t)\Phi _{{l,r}}^{{ - 1}}(0,t)(\bar {v}_{n}^{{l,r}}({{x}_{{tr}}},t) + M_{n}^{{l,r}}\text{v}(0,t)) + {{\Phi }_{{l,r}}}(\xi ,t)\int\limits_0^\xi {\Phi _{{l,r}}^{{ - 2}}} ({{\xi }_{1}},t)d{{\xi }_{1}}\int\limits_{ \mp \infty }^{{{\xi }_{1}}} {{{\Phi }_{{l,r}}}} ({{\xi }_{2}},t)H_{n}^{{l,r}}({{\xi }_{2}},t)d{{\xi }_{2}}.$

Функции $Q_{n}^{{l,r}}u(\xi ,t)$ связаны с $Q_{n}^{{l,r}}\text{v}(\xi ,t)$ равенствами

$Q_{n}^{{l,r}}u + \bar {u}_{n}^{{l,r}}({{x}_{{tr}}},t) = \tilde {\varphi }_{\text{v}}^{{l,r}}(\xi ,t)(Q_{n}^{{l,r}}\text{v} + \bar {v}_{n}^{{l,r}}({{x}_{{tr}}},t)) + q_{n}^{{l,r}}f(\xi ,t),$

где $q_{n}^{{l,r}}f(\xi ,t)$ известны на $n$-м шаге.

Функции $M_{n}^{{l,r}}u(\sigma ,t)$ являются решениями задач

(26)

$\frac{{{{\partial }^{2}}M_{n}^{{l,r}}u}}{{\partial {{\sigma }^{2}}}} - \hat {f}_{u}^{{l,r}}(\sigma ,t)M_{n}^{{l,r}}u = F_{n}^{{l,r}}(\sigma ,t),\quad M_{n}^{{l,r}}u(0,t) = \chi _{n}^{{l,r}}(t),\quad M_{n}^{{l,r}}u( \mp \infty ,t) = 0,$

причем функции $F_{n}^{{l,r}}(\xi ,t)$, $\chi _{n}^{{l,r}}(t)$ известны на $n$-м шаге.

Решения задач (26) могут быть записаны в явной форме:

$M_{n}^{{l,r}}u(\sigma ,t) = - {{\Psi }_{{l,r}}}(\sigma ,t)\Psi _{{l,r}}^{{ - 1}}(0,t)\chi _{n}^{{l,r}}(0,t) + {{\Psi }_{{l,r}}}(\sigma ,t)\int\limits_0^\sigma {\Psi _{{l,r}}^{{ - 2}}} ({{\sigma }_{1}},t)d{{\sigma }_{1}}\int\limits_{ \mp \infty }^{{{\sigma }_{1}}} {{{\Psi }_{{l,r}}}} ({{\sigma }_{2}},t)F_{n}^{{l,r}}({{\sigma }_{2}},t)d{{\sigma }_{2}}.$

Из вида функций $Q_{n}^{{l,r}}u(\xi ,t)$, $Q_{n}^{{( \mp )}}\text{v}(\xi ,t)$, $M_{n}^{{( \mp )}}u(\sigma ,t)$, $M_{n}^{{( \mp )}}u(\sigma ,t)$, $n = 1,\;2,\; \ldots $, следует, что для них имеют место экспоненциальные оценки типа (20) и (23).

2.5. Система уравнений для функций ${{\text{v}}_{n}}(t)$, ${{x}_{n}}(t)$

Соберем в равенствах (24) слагаемые порядка ${{\varepsilon }^{n}}$ с учетом разложения функций ${{x}_{{tr}}}(t)$ и ${{\text{v}}_{{tr}}}(t)$ в ряды (9) и (8). Обозначим через ${{S}_{n}}(t)$ и ${{T}_{n}}(t)$ слагаемые, не содержащие ${{x}_{n}}$ и ${{\text{v}}_{n}}$. Система уравнений относительно ${{x}_{n}}$ и ${{\text{v}}_{n}}$ имеет вид

(27)

$\begin{gathered} \frac{{\partial ({{\Phi }_{l}} - {{\Phi }_{r}})}}{{\partial \text{v}}}(0,t,{{\text{v}}_{0}},{{x}_{0}}){{\text{v}}_{n}} + \frac{{\partial ({{\Phi }_{l}} - {{\Phi }_{r}})}}{{\partial x}}(0,t,{{\text{v}}_{0}},{{x}_{0}}){{x}_{n}} + {{S}_{n}}(t) = 0, \\ \frac{{\partial ({{\Psi }_{l}} - {{\Psi }_{r}})}}{{\partial \text{v}}}(0,t,{{\text{v}}_{0}},{{x}_{0}}){{\text{v}}_{n}} + \frac{{\partial ({{\Psi }_{l}} - {{\Psi }_{r}})}}{{\partial x}}(0,t,{{\text{v}}_{0}},{{x}_{0}}){{x}_{n}} + {{T}_{n}}(t) = 0. \\ \end{gathered} $

Система уравнений (27) имеет единственное решение, поскольку ее определитель совпадает с якобианом системы уравнений (3), отличным от нуля по условнию ${{H}_{5}}$.

2.6. Формальная асимптотика $n$-го порядка

Составим конечную сумму, представляющую собой формальное асимптотическое приближение $n$-го порядка по малому параметру. Предположим, что члены рядов (4), (9), (8) определены до номера $n$, а также известны функции $M_{{n + 1}}^{{l,r}}\text{v}$, $M_{{n + 2}}^{{l,r}}\text{v}$, $R_{{n + 1}}^{{l,r}}\text{v}$, $R_{{n + 2}}^{{l,r}}\text{v}$.

Обозначим через $\text{v}_{n}^{{tr}}(t)$ и ${{X}_{n}}(t)$ частичные суммы рядов ${{\text{v}}_{{tr}}}$ и ${{x}_{{tr}}}$

(28)

${{X}_{n}}(t) = \sum\limits_{i = 0}^n {{{\varepsilon }^{i}}{{x}_{i}}(t)} ,\quad \text{v}_{n}^{{tr}}(t) = \sum\limits_{i = 0}^n {{{\varepsilon }^{i}}{{\text{v}}_{i}}(t)} .$

Введем обозначения ${{\xi }_{n}} = {{\varepsilon }^{{ - 1}}}(x - {{X}_{n}}(t))$, ${{\sigma }_{n}} = {{\varepsilon }^{{ - 2}}}(x - {{X}_{n}}(t)).$

Кривая ${{X}_{n}}(t)$ разделяет область ${{\bar {D}}_{T}}:\left\{ {(x,t) \in [0,L] \times (0,T]} \right\}$ на две подобласти $\bar {D}_{n}^{l}$ и $\bar {D}_{n}^{r}$ ($\bar {D}_{n}^{l}:\left\{ {(x,t) \in [0,{{X}_{n}}(t)] \times (0,T]} \right\}$ и $\bar {D}_{n}^{r}:\left\{ {(x,t) \in [{{X}_{n}}(t),L] \times (0,T]} \right\}$).

Составим суммы $U_{n}^{l}$, $V_{n}^{l}$, $U_{n}^{r}$, $V_{n}^{r}$:

(29)

$\begin{gathered} U_{n}^{{l,r}}(x,t,\varepsilon ) = \sum\limits_{i = 0}^n {{{\varepsilon }^{i}}} (\bar {u}_{i}^{{l,r}}(x) + Q_{i}^{{l,r}}u({{\xi }_{n}},t) + M_{i}^{{l,r}}u({{\sigma }_{n}},t) + P_{i}^{{l,r}}u({{\zeta }_{{l,r}}}) + R_{i}^{{l,r}}u({{\eta }_{{l,r}}})),\quad (x,t) \in \bar {D}_{n}^{{l,r}}, \\ V_{n}^{{l,r}}(x,t,\varepsilon ) = \sum\limits_{i = 0}^n {{{\varepsilon }^{i}}} (\bar {v}_{i}^{{l,r}}(x) + Q_{i}^{{l,r}}\text{v}({{\xi }_{n}},t) + M_{i}^{{l,r}}\text{v}({{\sigma }_{n}},t) + P_{i}^{{l,r}}\text{v}({{\zeta }_{{l,r}}}) + R_{i}^{{l,r}}\text{v}({{\eta }_{{l,r}}})) + \\ + \;\sum\limits_{i = n + 1}^{n + 2} {{{\varepsilon }^{i}}} (M_{i}^{{l,r}}\text{v}({{\sigma }_{n}},t) + R_{i}^{{l,r}}\text{v}({{\eta }_{{l,r}}})),\quad (x,t) \in \bar {D}_{n}^{{l,r}}. \\ \end{gathered} $

В этих суммах ряды ${{x}_{{tr}}}$ и ${{\text{v}}_{{tr}}}$, которые входят в выражения для $Q$ и M-функций заменены на частичные суммы ${{X}_{n}}(t)$ и $\text{v}_{n}^{{tr}}(t)$ (см. (28)) этих рядов.

Определим функции ${{U}_{n}}(x,t,\varepsilon )$ и ${{V}_{n}}(x,t,\varepsilon )$ равенствами

${{U}_{n}}(x,t,\varepsilon ) = \left\{ \begin{gathered} U_{n}^{l}(x,t,\varepsilon ),\quad (x,t) \in \bar {D}_{n}^{l}, \hfill \\ U_{n}^{r}(x,t,\varepsilon ),\quad (x,t) \in \bar {D}_{n}^{r}, \hfill \\ \end{gathered} \right.\quad {{V}_{n}}(x,t,\varepsilon ) = \left\{ \begin{gathered} V_{n}^{l}(x,t,\varepsilon ),\quad (x,t) \in \bar {D}_{n}^{l}, \hfill \\ V_{n}^{r}(x,t,\varepsilon ),\quad (x,t) \in \bar {D}_{n}^{r}. \hfill \\ \end{gathered} \right.$

Функции ${{U}_{n}}$ и ${{V}_{n}}$ по построению удовлетворяют уравнениям (1) с точностью $O({{\varepsilon }^{{n + 1}}})$ всюду в области ${{\bar {D}}_{T}}$, за исключением кривой ${{X}_{n}}(t)$, а на кривой они и их производные терпят разрыв.

3. ОБОСНОВАНИЕ АСИМПТОТИКИ

Теорема 1. При выполнении условий ${{H}_{1}}$–${{H}_{5}}$ при достаточно малых $\varepsilon > 0$ существует периодическое решение $u(x,t,\varepsilon )$, $\text{v}(x,t,\varepsilon )$ задачи (1), (2), для которого функции ${{U}_{n}}(x,t,\varepsilon )$, ${{V}_{n}}(x,t,\varepsilon )$ являются равномерным на отрезке $[0;L]$ асимптотическим приближением с точностью порядка $O({{\varepsilon }^{{n + 1}}})$, т.е. при $(x,t) \in [0;L] \times (0; + \infty )$ выполняются неравенства

$\left| {u(x,t,\varepsilon ) - {{U}_{n}}(x,t,\varepsilon )} \right| \leqslant C{{\varepsilon }^{{n + 1}}},\quad \left| {\text{v}(x,t,\varepsilon ) - {{V}_{n}}(x,t,\varepsilon )} \right| \leqslant C{{\varepsilon }^{{n + 1}}},$

где $C$ – положительная постоянная, не зависящая от $\varepsilon $.

Доказательство. Составим периодические функции ${{U}^{\alpha }}(x,t,\varepsilon )$, ${{V}^{\alpha }}(x,t,\varepsilon )$ и ${{U}^{\beta }}(x,t,\varepsilon )$, ${{V}^{\beta }}(x,t,\varepsilon )$ называемые соответственно верхним и нижним решениями задачи (1), (2), таким образом, чтобы при достаточно малых $\varepsilon $ они удовлетворяли следующим условиям.

Условие 1. ${{U}^{\alpha }}(x,t,\varepsilon ) \leqslant {{U}^{\beta }}(x,t,\varepsilon )$, ${{V}^{\alpha }}(x,t,\varepsilon ) \leqslant {{V}^{\beta }}(x,t,\varepsilon )$, $(x,t) \in {{\bar {D}}_{T}}$.

Условие 2. При $(x,t) \in {{\bar {D}}_{T}}$ выполнены неравенства

$\begin{gathered} {{L}_{{1\varepsilon }}}({{U}^{\beta }},\text{v}): = {{\varepsilon }^{4}}U_{{xx}}^{\beta } - {{\varepsilon }^{4}}U_{t}^{\beta } - f({{U}^{\beta }},\text{v},x,t,\varepsilon ) < 0 < {{L}_{{1\varepsilon }}}({{U}^{\alpha }},\text{v})\quad {\text{п р и }}\quad {{V}^{\alpha }} \leqslant \text{v} \leqslant {{V}^{\beta }}, \\ {{L}_{{2\varepsilon }}}(u,{{V}^{\beta }}): = {{\varepsilon }^{2}}V_{{xx}}^{\beta } - {{\varepsilon }^{2}}V_{t}^{\beta } - g(u,{{V}^{\beta }},x,t,\varepsilon ) < 0 < {{L}_{{2\varepsilon }}}(u,{{V}^{\alpha }})\quad {\text{п р и }}\quad {{U}^{\alpha }} \leqslant u \leqslant {{U}^{\beta }}. \\ \end{gathered} $

Условие 3.

$\begin{gathered} \mathop {\left. {\frac{{\partial {{U}^{\beta }}}}{{\partial x}}{\kern 1pt} } \right|}\nolimits_{x = 0} \leqslant 0 \leqslant \mathop {\left. {\frac{{\partial {{U}^{\alpha }}}}{{\partial x}}{\kern 1pt} } \right|}\nolimits_{x = 0} ,\quad \mathop {\left. {\frac{{\partial {{V}^{\beta }}}}{{\partial x}}{\kern 1pt} } \right|}\nolimits_{x = 0} \leqslant 0 \leqslant \mathop {\left. {\frac{{\partial {{V}^{\alpha }}}}{{\partial x}}{\kern 1pt} } \right|}\nolimits_{x = 0} , \\ \mathop {\left. {\frac{{\partial {{U}^{\alpha }}}}{{\partial x}}{\kern 1pt} } \right|}\nolimits_{x = L} \leqslant 0 \leqslant \mathop {\left. {\frac{{\partial {{U}^{\beta }}}}{{\partial x}}{\kern 1pt} } \right|}\nolimits_{x = L} ,\quad \mathop {\left. {\frac{{\partial {{V}^{\alpha }}}}{{\partial x}}{\kern 1pt} } \right|}\nolimits_{x = L} \leqslant 0 \leqslant \mathop {\left. {\frac{{\partial {{V}^{\beta }}}}{{\partial x}}{\kern 1pt} } \right|}\nolimits_{x = L} . \\ \end{gathered} $

Верхнее решение строится отдельно слева и справа от точки $x = {{X}_{\beta }}(t)$, а для нижнего решения точка сшивки определяется функцией $x = {{X}_{\alpha }}(t)$. Эти функции задаются равенствами

(30)

${{X}_{\beta }}(t) = \sum\limits_{i = 0}^{n + 1} {{{\varepsilon }^{i}}{{x}_{i}}(t)} - {{\varepsilon }^{{n + 1}}}\delta (t) = {{X}_{{n + 1}}}(t) - {{\varepsilon }^{{n + 1}}}\delta (t),\quad {{X}_{\alpha }}(t) = {{X}_{{n + 1}}}(t) + {{\varepsilon }^{{n + 1}}}\delta (t),$

где функция $\delta (t)$ положительна и будет определена ниже.

Кривая ${{X}_{\beta }}(t)$ разделяет область ${{\bar {D}}_{T}}$ на две подобласти $\bar {D}_{\beta }^{l}$ и $\bar {D}_{\beta }^{r}$. Верхнее решение задачи (1), (2) составляется отдельно в этих подобластях

${{U}^{\beta }}(x,t,\varepsilon ) = \left\{ \begin{gathered} U_{\beta }^{l}(x,t,\varepsilon ),\quad (x,t) \in \bar {D}_{\beta }^{l}, \hfill \\ U_{\beta }^{r}(x,t,\varepsilon ),\quad (x,t) \in \bar {D}_{\beta }^{r}, \hfill \\ \end{gathered} \right.\quad {{V}^{\beta }}(x,t,\varepsilon ) = \left\{ \begin{gathered} V_{\beta }^{l}(x,t,\varepsilon ),\quad (x,t) \in \bar {D}_{\beta }^{l}, \hfill \\ V_{\beta }^{r}(x,t,\varepsilon ),\quad (x,t) \in \bar {D}_{\beta }^{r}. \hfill \\ \end{gathered} \right.$

Аналогично, нижнее решение состоит из двух частей $U_{\alpha }^{l}(x,t,\varepsilon )$, $U_{\alpha }^{r}(x,t,\varepsilon )$ и $V_{\alpha }^{l}(x,t,\varepsilon )$, $V_{\alpha }^{r}(x,t,\varepsilon )$, которые строятся отдельно в областях $\bar {D}_{\alpha }^{l}$ и $\bar {D}_{\alpha }^{r}$.

Функции ${{U}^{{\alpha ,\beta }}}(x,t,\varepsilon )$ и ${{V}^{{\alpha ,\beta }}}(x,t,\varepsilon )$ непрерывны в области $\bar {D}$, со следующими условиями в точках сшивки ${{X}_{{\alpha ,\beta }}}$:

(31)

$\begin{array}{*{20}{c}} {V_{{\alpha ,\beta }}^{l}({{X}_{{\alpha ,\beta }}}(t),t,\varepsilon ) = V_{{\alpha ,\beta }}^{r}({{X}_{{\alpha ,\beta }}}(t),t,\varepsilon ) = {{\text{v}}_{{\alpha ,\beta }}}(t),} \\ {U_{{\alpha ,\beta }}^{l}({{X}_{{\alpha ,\beta }}}(t),t,\varepsilon ) = U_{{\alpha ,\beta }}^{r}({{X}_{{\alpha ,\beta }}}(t),t,\varepsilon ) = {{\varphi }^{0}}({{\text{v}}_{{\alpha ,\beta }}}(t),{{X}_{{\alpha ,\beta }}}(t),t).} \end{array}$

Здесь

(32)

${{\text{v}}_{\alpha }}(t) = \text{v}_{{n + 1}}^{{tr}}(t) - {{\varepsilon }^{{n + 1}}}\mu (t),\quad {{\text{v}}_{\beta }}(t) = \text{v}_{{n + 1}}^{{tr}}(t) + {{\varepsilon }^{{n + 1}}}\mu (t),$

$\text{v}_{{n + 1}}^{{tr}}(t)$ – это частичная сумма ряда ${{\text{v}}_{{tr}}}(t)$ (см. (28)), а функция $\mu (t)$ будет выбрана ниже.

Если нижнее и верхнее решения на кривых ${{X}_{\alpha }}(t)$, ${{X}_{\beta }}(t)$ не являются гладкими, то должно выполняться условие 4:

$\begin{array}{*{20}{c}} {\mathop {\left( {\frac{{\partial U_{\beta }^{l}}}{{\partial x}} - \frac{{\partial U_{\beta }^{r}}}{{\partial x}}} \right)}\nolimits_{x = {{X}_{\beta }}(t)} \geqslant 0,\quad \mathop {\left( {\frac{{\partial V_{\beta }^{l}}}{{\partial x}} - \frac{{\partial V_{\beta }^{r}}}{{\partial x}}} \right)}\nolimits_{x = {{X}_{\beta }}(t)} \geqslant 0;} \\ {\mathop {\left( {\frac{{\partial U_{\alpha }^{l}}}{{\partial x}} - \frac{{\partial U_{\alpha }^{r}}}{{\partial x}}} \right)}\nolimits_{x = {{X}_{\alpha }}(t)} \leqslant 0,\quad \mathop {\left( {\frac{{\partial V_{\alpha }^{l}}}{{\partial x}} - \frac{{\partial V_{\alpha }^{r}}}{{\partial x}}} \right)}\nolimits_{x = {{X}_{\alpha }}(t)} \leqslant 0.} \end{array}$

Функции $U_{\beta }^{l}$, $U_{\beta }^{r}$ и $V_{\beta }^{l}$, $V_{\beta }^{r}$ составляются на основе асимптотического приближения ($n + 1$)-го порядка. Обозначим через $K_{{\alpha ,\beta }}^{{l,r}}u$ и $K_{{\alpha ,\beta }}^{{l,r}}\text{v}$ добавки к асимптотике. Функции $K_{{\alpha ,\beta }}^{{l,r}}u$ и $K_{{\alpha ,\beta }}^{{l,r}}\text{v}$ имеют вид

${{K}^{{l,r}}}u(x,t,\varepsilon ) = {{\varepsilon }^{{n + 1}}}({{\tilde {u}}^{{l,r}}}(x,t) + \tilde {Q}_{{n + 1}}^{{l,r}}u(\xi ,t) + \tilde {M}_{{n + 1}}^{{l,r}}u(\sigma ,t))) + {{\varepsilon }^{{n + 2}}}exp( - \gamma {{\zeta }_{{l,r}}}),$

$\begin{gathered} {{K}^{l}}\text{v}(x,t,\varepsilon ) = {{\varepsilon }^{{n + 1}}}({{{\tilde {v}}}^{l}}(x,t) + \tilde {Q}_{{n + 1}}^{l}\text{v}(\xi ,t)) + {{\varepsilon }^{{n + 2}}} + {{\varepsilon }^{{n + 2}}}exp( - \gamma {{\zeta }_{l}}) + \\ + \;{{\varepsilon }^{{n + 3}}}\tilde {M}_{{n + 3}}^{l}\text{v}(\sigma ,t) + {{\varepsilon }^{{n + 2}}}{{\omega }_{0}}(t) + {{\varepsilon }^{{n + 3}}}{{\omega }_{1}}(t), \\ \end{gathered} $

${{K}^{r}}\text{v}(x,t,\varepsilon ) = {{\varepsilon }^{{n + 1}}}({{\tilde {v}}^{r}}(x,t) + \tilde {Q}_{{n + 1}}^{r}\text{v}(\xi ,t)) + {{\varepsilon }^{{n + 2}}} + {{\varepsilon }^{{n + 2}}}exp( - \gamma {{\zeta }_{r}}) + {{\varepsilon }^{{n + 3}}}\tilde {M}_{{n + 3}}^{r}\text{v}(\sigma ,t),$

где $\gamma $ – положительная константа. Функции $U_{{\alpha ,\beta }}^{{l,r}}(x,t,\varepsilon )$ и $V_{{\alpha ,\beta }}^{{l,r}}(x,t,\varepsilon )$ определяются формулами

(33)

$U_{\beta }^{{l,r}} = \mathop {\left. {U_{{n + 1}}^{{l,r}}} \right|}\nolimits_{{{\xi }_{\beta }},{{\sigma }_{\beta }}} + \mathop {\left. {{{K}^{{l,r}}}u} \right|}\nolimits_{{{\xi }_{\beta }},{{\sigma }_{\beta }}} ,\quad U_{\alpha }^{{l,r}} = \mathop {\left. {U_{{n + 1}}^{{l,r}}} \right|}\nolimits_{{{\xi }_{\alpha }},{{\sigma }_{\alpha }}} - \mathop {\left. {{{K}^{{l,r}}}u} \right|}\nolimits_{{{\xi }_{\alpha }},{{\sigma }_{\alpha }}} .$

(34)

$V_{\beta }^{{l,r}} = \mathop {\left. {V_{{n + 1}}^{{l,r}}} \right|}\nolimits_{{{\xi }_{\beta }},{{\sigma }_{\beta }}} + \mathop {\left. {{{K}^{{l,r}}}\text{v}} \right|}\nolimits_{{{\xi }_{\beta }},{{\sigma }_{\beta }}} ,\quad V_{\alpha }^{{l,r}} = \mathop {\left. {V_{{n + 1}}^{{l,r}}} \right|}\nolimits_{{{\xi }_{\alpha }},{{\sigma }_{\alpha }}} - \mathop {\left. {{{K}^{{l,r}}}\text{v}} \right|}\nolimits_{{{\xi }_{\alpha }},{{\sigma }_{\alpha }}} .$

Растянутые переменные ${{\xi }_{\beta }}$, ${{\sigma }_{\beta }}$ и ${{\xi }_{\alpha }}$, ${{\sigma }_{\alpha }}$ вводятся по формулам ${{\xi }_{{\alpha ,\beta }}} = {{\varepsilon }^{{ - 1}}}(x - {{X}_{{\alpha ,\beta }}}(t))$, ${{\sigma }_{{\alpha ,\beta }}} = {{\varepsilon }^{{ - 2}}}(x - {{X}_{{\alpha ,\beta }}}(t))$.

Функции $U_{{n + 1}}^{{l,r}}$, $V_{{n + 1}}^{{l,r}}$ в суммах (33), (34) являются асимптотическими приближениями (29) порядка $(n + 1)$, с той разницей, что аргументы функций переходного слоя ${{\xi }_{{n + 1}}}$ и ${{\sigma }_{{n + 1}}}$ заменены на ${{\xi }_{{\alpha ,\beta }}}$ и ${{\sigma }_{{\alpha ,\beta }}}$, а величины ${{X}_{{n + 1}}}(t)$, $\text{v}_{n}^{{tr}}(t)$ заменены на ${{X}_{{\alpha ,\beta }}}(t)$, ${{\text{v}}_{{\alpha ,\beta }}}(t)$ (см. (30), (32)).

Функции ${{\tilde {u}}^{{l,r}}}(x,t)$, ${{\tilde {v}}^{{l,r}}}(x,t)$ определяются из следующей системы уравнений:

(35)

$\bar {f}_{u}^{{l,r}}(x,t){{\tilde {u}}^{{l,r}}} + \bar {f}_{\text{v}}^{{l,r}}(x,t){{\tilde {v}}^{{l,r}}} = A,\quad \bar {g}_{u}^{{l,r}}(x,t){{\tilde {u}}^{{l,r}}} + \bar {g}_{\text{v}}^{{l,r}}(x,t){{\tilde {v}}^{{l,r}}} = B,$

где $A$ и $B$ – некоторые положительные числа. Системы (35) разрешимы единственным образом, поскольку определитель ${{\Delta }^{{l,r}}}(x,t) = \bar {f}_{u}^{{l,r}}(x,t)h_{\text{v}}^{{1,3}}(x,t) > 0$ отличен от нуля всюду на сегменте $[0;L]$ по условиям ${{H}_{1}}$ и ${{H}_{2}}$.

Функции $\tilde {Q}_{{n + 1}}^{{l,r}}u$, $\tilde {Q}_{{n + 1}}^{{l,r}}\text{v}$, $\tilde {M}_{{n + 1}}^{{l,r}}u$, $\tilde {M}_{{n + 3}}^{{l,r}}\text{v}$ направлены на устранение невязок, возникающих в результате модификации регулярной части асимптотики порядка $(n + 1)$, т.е. добавок ${{\tilde {u}}^{{l,r}}}$ и ${{\tilde {v}}^{{l,r}}}$ и изменения граничных условий для функций переходного слоя за счет равенств (31).

Функции $\tilde {Q}_{{n + 1}}^{{l,r}}\text{v}\left( {\xi ,t} \right)$ определяются из уравнений

$\frac{{{{\partial }^{2}}\tilde {Q}_{{n + 1}}^{{l,r}}\text{v}}}{{\partial {{\xi }^{2}}}} = \tilde {h}_{\text{v}}^{{l,r}}(\xi ,t)\tilde {Q}_{{n + 1}}^{{l,r}}\text{v} + \tilde {h}_{\text{v}}^{{l,r}}(\xi ,t){{\tilde {v}}^{{l,r}}}({{X}_{{n + 1}}},t) + \tilde {g}_{u}^{{l,r}}(\xi ,t){{(\tilde {f}_{u}^{{l,r}}(\xi ,t))}^{{ - 1}}}A - B,$

с граничными условиями $\tilde {Q}_{{n + 1}}^{{l,r}}\text{v}(0,t) = - {{\tilde {v}}^{{l,r}}}({{X}_{{n + 1}}}(t),t)$, $\tilde {Q}_{{n + 1}}^{{l,r}}\text{v}( \mp \infty ,t) = 0$.

Функции $\tilde {Q}_{{n + 1}}^{{l,r}}u(\xi ,t)$ определяются равенствами

${{\tilde {u}}^{{l,r}}}({{X}_{{n + 1}}}(t),t) + \tilde {Q}_{{n + 1}}^{{l,r}}u(\xi ,t) = \tilde {\varphi }_{\text{v}}^{{l,r}}(\xi ,t)({{\tilde {v}}^{{l,r}}}({{X}_{{n + 1}}}(t),t) + \tilde {Q}_{{n + 1}}^{{l,r}}\text{v}(\xi ,t)) + {{(\tilde {f}_{u}^{{l,r}}(\xi ,t))}^{{ - 1}}}A.$

Функции $\tilde {M}_{{n + 1}}^{{l,r}}u$ определяются из задач

$\begin{array}{*{20}{c}} {\frac{{{{\partial }^{2}}\tilde {M}_{{n + 1}}^{{l,r}}u}}{{\partial {{\sigma }^{2}}}} - {{{\hat {f}}}_{u}}(\sigma ,t)\tilde {M}_{{n + 1}}^{{l,r}}u = ({{{\hat {f}}}_{u}}(\sigma ,t){{{(\tilde {f}_{u}^{{l,r}}(0,t))}}^{{ - 1}}} - 1)A,} \\ {\tilde {M}_{{n + 1}}^{{l,r}}u(0,t) = - {{{(\tilde {f}_{u}^{{l,r}}(0,t))}}^{{ - 1}}}A,\quad \tilde {M}_{{n + 1}}^{{l,r}}u( \mp \infty ,t) = 0.} \end{array}$

Функции $\tilde {M}_{{n + 3}}^{{l,r}}\text{v}(\sigma ,t)$ задаются уравнениями $\tfrac{{{{\partial }^{2}}\tilde {M}_{{n + 3}}^{{l,r}}\text{v}}}{{\partial {{\sigma }^{2}}}} = \tilde {m}_{{n + 1}}^{{l,r}}g(\sigma ,t)$ с условиями $\tilde {M}_{{n + 3}}^{{l,r}}\text{v}( \mp \infty ,t) = 0$, где $\tilde {m}_{{n + 1}}^{{l,r}}g(\sigma ,t)$ – известные функции.

Введение функций ${{\omega }_{{0,1}}}(t)$ позволяет обеспечить непрерывность $\text{v}$-компоненты верхнего решения. Эти функции задаются равенствами: ${{\omega }_{0}}(t) = M_{{n + 2}}^{r}\text{v}(0,t) - M_{{n + 2}}^{l}\text{v}(0,t)$, ${{\omega }_{1}}(t) = M_{{n + 3}}^{r}\text{v}(0,t) - $ $ - \;M_{{n + 3}}^{l}\text{v}(0,t) + \tilde {M}_{{n + 3}}^{r}\text{v}(0,t) - \tilde {M}_{{n + 3}}^{l}\text{v}(0,t)$.

Наконец, величины $\mu (t)$ и $\delta (t)$ являются решениями системы уравнений

(36)

$\frac{{\partial J}}{{\partial \text{v}}}\left( {{{\text{v}}_{0}},{{x}_{0}},t} \right)\mu + \frac{{\partial J}}{{\partial x}}\left( {{{\text{v}}_{0}},{{x}_{0}},t} \right)( - \delta ) = {{A}_{2}},\quad \frac{{\partial Y}}{{\partial \text{v}}}\left( {{{\text{v}}_{0}},{{x}_{0}},t} \right)\mu + \frac{{\partial Y}}{{\partial x}}\left( {{{\text{v}}_{0}},{{x}_{0}},t} \right)( - \delta ) = {{B}_{2}},$

где

${{A}_{2}}: = {{A}_{1}} + {{\Phi }^{{ - 1}}}(0,t)\int\limits_{ - \infty }^{ + \infty } \Phi (\xi ,t)(B - {{\tilde {g}}_{u}}(\xi ,t)\tilde {f}_{u}^{{ - 1}}(\xi ,t)A)d\xi ,$

${{B}_{2}}: = {{B}_{1}} + A{{\Psi }^{{ - 1}}}(0,t)({{\varphi }^{r}}({{\text{v}}_{0}}(t),{{x}_{0}}(t),t) - {{\varphi }^{l}}({{\text{v}}_{0}}(t),{{x}_{0}}(t),t)),$

функции $\Phi (\xi ,t)$, $\Psi (\sigma ,t)$ определены выражениями (25), ${{A}_{1}}$, ${{B}_{1}}$ – некоторые положительные числа. Выберем $B > A\tilde {g}_{u}^{{l,r}}(\xi ,t){{(\tilde {f}_{u}^{{l,r}}(\xi ,t))}^{{ - 1}}}$ и поскольку $\Phi (\xi ,t) > 0$, ${{\Psi }^{{ - 1}}}(0,t) > 0$, ${{\varphi }^{r}}({{\text{v}}_{0}}(t),{{x}_{0}}(t),t) - $ $ - \;{{\varphi }^{l}}({{\text{v}}_{0}}(t),{{x}_{0}}(t),t) > 0$ (по условию ${{H}_{1}}$), то ${{A}_{2}} > 0$, ${{B}_{2}} > 0$.

Решение системы (36) имеет вид

$\mu (t) = \mathop {\left( {\mathop {\left. {\frac{{D(J,Y)}}{{D(\text{v},x)}}} \right|}\nolimits_{{{\text{v}}_{0}},{{x}_{0}}} } \right)}\nolimits^{ - 1} \left( {\frac{{\partial Y}}{{\partial x}}\left( {{{\text{v}}_{0}},{{x}_{0}},t} \right){{A}_{2}} - \frac{{\partial J}}{{\partial x}}\left( {{{\text{v}}_{0}},{{x}_{0}},t} \right){{B}_{2}}} \right),$

$\delta (t) = \mathop {\left( {\mathop {\left. {\frac{{D(J,Y)}}{{D(\text{v},x)}}{\kern 1pt} } \right|}\nolimits_{{{\text{v}}_{0}},{{x}_{0}}} } \right)}\nolimits^{ - 1} \left( {\frac{{\partial Y}}{{\partial \text{v}}}\left( {{{\text{v}}_{0}},{{x}_{0}},t} \right){{A}_{2}} - \frac{{\partial J}}{{\partial \text{v}}}\left( {{{\text{v}}_{0}},{{x}_{0}},t} \right){{B}_{2}}} \right),$

где определитель $\mathop {\left. {\tfrac{{D(J,Y)}}{{D(\text{v},x)}}{\kern 1pt} } \right|}\nolimits_{{{\text{v}}_{0}},{{x}_{0}}} < 0$ по условию ${{H}_{5}}$. Можно показать, что функция $\delta (t)$ положительна (см. [16]).

Построенные функции ${{U}^{{\alpha ,\beta }}}$, ${{V}^{{\alpha ,\beta }}}$ удовлетворяют условиям 1–4.

Условие 1 упорядоченности выполняется на отрезке $[0;L]$ за счет выбора функции $\delta (t) > 0$ и положительных функций ${{\tilde {u}}^{{l,r}}}(x)$, ${{\tilde {v}}^{{l,r}}}(x)$. Также при проверке условия 1 используются экспоненциальные оценки функций переходного слоя. С подробными выкладками можно ознакомиться в работе [16] (п. 3.2).

По способу построения функции ${{U}^{\beta }}(x,t,\varepsilon )$, ${{V}^{\beta }}(x,t,\varepsilon )$ и ${{U}^{\alpha }}(x,t,\varepsilon )$, ${{V}^{\alpha }}(x,t,\varepsilon )$ удовлетворяют равенствам:

${{L}_{{1\varepsilon }}}({{U}^{\beta }},{{V}^{\beta }}) = - {{\varepsilon }^{{n + 1}}}A + O({{\varepsilon }^{{n + 2}}}) < 0,\quad {{L}_{{1\varepsilon }}}({{U}^{\alpha }},{{V}^{\alpha }}) = {{\varepsilon }^{{n + 1}}}A + O({{\varepsilon }^{{n + 2}}}) > 0,$

${{L}_{{2\varepsilon }}}({{U}^{\beta }},{{V}^{\beta }}) = - {{\varepsilon }^{{n + 1}}}B + O({{\varepsilon }^{{n + 2}}}) < 0,\quad {{L}_{{2\varepsilon }}}({{U}^{\alpha }},{{V}^{\alpha }}) = {{\varepsilon }^{{n + 1}}}B + O({{\varepsilon }^{{n + 2}}}) > 0.$

В силу условия ${{H}_{3}}$ данные выражения доказывают выполнение неравенств условия 2.

В граничных точках отрезка $[0;L]$ частные производные функций ${{U}^{\beta }}$, ${{V}^{\beta }}$ и ${{U}^{\alpha }}$, ${{V}^{\alpha }}$ по переменной $x$ имеют вид

$\frac{{\partial {{U}^{\beta }}}}{{\partial x}}(0,t,\varepsilon ) = {{\varepsilon }^{{n + 1}}}\left( { - \gamma + \frac{{\partial {{{\tilde {u}}}_{l}}}}{{\partial x}}(0,t)} \right) + O({{\varepsilon }^{{n + 2}}}),\quad \frac{{\partial {{U}^{\alpha }}}}{{\partial x}}(0,t,\varepsilon ) = {{\varepsilon }^{{n + 1}}}\left( {\gamma - \frac{{\partial {{{\tilde {u}}}_{l}}}}{{\partial x}}(0,t)} \right) + O({{\varepsilon }^{{n + 2}}}).$

Неравенства условия 3 выполняются для функций ${{U}^{\beta }}$, ${{U}^{\alpha }}$ при $x = 0$ за счет выбора достаточно большого положительного $\gamma $. Аналогично проверяются остальные неравенства условия 3.

Можно показать, что для функций ${{U}^{\beta }}(x,t,\varepsilon )$, ${{V}^{\beta }}(x,t,\varepsilon )$ при $x = {{X}_{\beta }}(t)$ и для функций ${{U}^{\alpha }}(x,t,\varepsilon )$, ${{V}^{\alpha }}(x,t,\varepsilon )$ при $x = {{X}_{\alpha }}(t)$ справедливы равенства

$\mathop {\left( {\frac{{\partial U_{\beta }^{l}}}{{\partial x}} - \frac{{\partial U_{\beta }^{r}}}{{\partial x}}} \right)}\nolimits_{x = {{X}_{\beta }}} = {{\varepsilon }^{{n - 1}}}{{B}_{1}} + O({{\varepsilon }^{n}}) > 0,\quad \mathop {\left( {\frac{{\partial V_{\beta }^{l}}}{{\partial x}} - \frac{{\partial V_{\beta }^{r}}}{{\partial x}}} \right)}\nolimits_{x = {{X}_{\beta }}} = {{\varepsilon }^{n}}{{A}_{1}} + O({{\varepsilon }^{{n + 1}}}) > 0,$

$\mathop {\left( {\frac{{\partial U_{\alpha }^{l}}}{{\partial x}} - \frac{{\partial U_{\alpha }^{r}}}{{\partial x}}} \right)}\nolimits_{x = {{X}_{\alpha }}} = - {{\varepsilon }^{{n - 1}}}{{B}_{1}} + O({{\varepsilon }^{n}}) < 0,\quad \mathop {\left( {\frac{{\partial V_{\alpha }^{l}}}{{\partial x}} - \frac{{\partial V_{\alpha }^{r}}}{{\partial x}}} \right)}\nolimits_{x = {{X}_{\alpha }}} = - {{\varepsilon }^{n}}{{A}_{1}} + O({{\varepsilon }^{{n + 1}}}) < 0.$

Условие 4 выполняется.

Согласно статье [15, теорема 2.2] существование верхнего и нижнего решений – непрерывных и гладких в области ${{\bar {D}}_{T}}$ функций, гарантирует существование классического решения задачи (1), (2). Доказательство основано на принципе максимума для верхнего и нижнего решений из класса ${{C}^{{2,1}}}({{\bar {D}}_{T}})$. В данном случае функции ${{U}^{\beta }}(x,t,\varepsilon )$, ${{V}^{\beta }}(x,t,\varepsilon )$ и ${{U}^{\alpha }}(x,t,\varepsilon )$, ${{V}^{\alpha }}(x,t,\varepsilon )$ принадлежат классу ${{C}^{{1,1}}}({{\bar {D}}_{T}})$, если в условии 4 выполнено равенство. Тогда можно повторить рассуждения работы [15], основываясь на принципе максимума для функций из ${{C}^{{1,1}}}({{\bar {D}}_{T}})$, доказанном в работе [25]. Если же функции ${{U}^{\beta }}(x,t,\varepsilon )$, ${{V}^{\beta }}(x,t,\varepsilon )$ и ${{U}^{\alpha }}(x,t,\varepsilon )$, ${{V}^{\alpha }}(x,t,\varepsilon )$ принадлежат классу ${{C}^{{0,0}}}({{\bar {D}}_{T}}) \cap {{C}^{{2,1}}}(D_{T}^{l} \cup D_{T}^{r})$ и имеют единственную точку разрыва производной, тогда для доказательства можно использовать принцип максимума из работы [26, лемма 4].

Приведенные рассуждения утверждают справедливость теоремы 1.

4. ЛОКАЛЬНАЯ ЕДИНСТВЕННОСТЬ И УСТОЙЧИВОСТЬ РЕШЕНИЯ ПЕРИОДИЧЕСКОЙ ЗАДАЧИ

4.1. Существование решения начально-краевой задачи

Рассмотрим систему уравнений (1) с начальными условиями по времени

(37)

Определим функции ${{U}_{{{\text{up}}}}}(x,t,\varepsilon )$, ${{V}_{{{\text{up}}}}}(x,t,\varepsilon )$ и ${{U}_{{{\text{down}}}}}(x,t,\varepsilon )$, ${{V}_{{{\text{down}}}}}(x,t,\varepsilon )$ равенствами

(38)

$\begin{array}{*{20}{c}} {{{U}_{{{\text{up}}}}}(x,t,\varepsilon ) = u{\kern 1pt} {\text{*}}(x,t,\varepsilon ) + ({{U}^{\beta }}(x,t,\varepsilon ) - u{\text{*}}(x,t,\varepsilon )){{e}^{{ - \lambda t}}},} \\ {{{U}_{{{\text{down}}}}}(x,t,\varepsilon ) = u{\kern 1pt} {\text{*}}(x,t,\varepsilon ) + ({{U}^{\alpha }}(x,t,\varepsilon ) - u{\text{*}}(x,t,\varepsilon )){{e}^{{ - \lambda t}}},} \\ {{{V}_{{{\text{up}}}}}(x,t,\varepsilon ) = \text{v}{\kern 1pt} {\text{*}}(x,t,\varepsilon ) + ({{V}^{\beta }}(x,t,\varepsilon ) - \text{v}{\text{*}}(x,t,\varepsilon )){{e}^{{ - \lambda t}}},} \\ {{{V}_{{{\text{down}}}}}(x,t,\varepsilon ) = \text{v}{\kern 1pt} {\text{*}}(x,t,\varepsilon ) + ({{V}^{\alpha }}(x,t,\varepsilon ) - \text{v}{\text{*}}(x,t,\varepsilon )){{e}^{{ - \lambda t}}}.} \end{array}$

Здесь ${{U}^{\alpha }}$, ${{V}^{\alpha }}$ и ${{U}^{\beta }}$, ${{V}^{\beta }}$ – это нижнее и верхнее решения задачи (1), (2), заданные выражениями (34). Через $u{\text{*}}(x,t,\varepsilon )$, $\text{v}{\kern 1pt} {\text{*}}(x,t,\varepsilon )$ обозначено некоторое решение задачи (1), (2), лежащие между ${{U}^{\alpha }}$, ${{U}^{\beta }}$ и ${{V}^{\alpha }}$, ${{V}^{\beta }}$ соответственно (решение существует согласно теореме 1).

Теорема 2. При выполнении условий ${{H}_{1}}$–${{H}_{5}}$ для произвольных достаточно гладких начальных функций ${{u}_{{{\text{init}}}}}(x)$, ${{\text{v}}_{{{\text{init}}}}}(x)$ таких, что

${{U}_{{{\text{down}}}}}(x,0,\varepsilon ) < {{u}_{{{\text{init}}}}}(x) < {{U}_{{{\text{up}}}}}(x,0,\varepsilon ),\quad {{V}_{{{\text{down}}}}}(x,0,\varepsilon ) < {{\text{v}}_{{{\text{init}}}}}(x) < {{V}_{{{\text{up}}}}}(x,0,\varepsilon ),\quad x \in [0;L],$

существует решение $u(x,t,\varepsilon )$, $\text{v}(x,t,\varepsilon )$ начально-краевой задачи (37), лежащее между верхним и нижним решениями ${{U}_{{{\text{down}}}}}(x,t,\varepsilon )$, ${{U}_{{{\text{up}}}}}(x,t,\varepsilon )$ для $u$-компоненты и ${{V}_{{{\text{down}}}}}(x,t,\varepsilon )$, ${{V}_{{{\text{up}}}}}(x,t,\varepsilon )$ – для $\text{v}$-компоненты при $x \in [0;L]$ и $t \in (0; + \infty )$:

${{U}_{{{\text{down}}}}}(x,t,\varepsilon ) < u(x,t,\varepsilon ) < {{U}_{{{\text{up}}}}}(x,t,\varepsilon ),\quad {{V}_{{{\text{down}}}}}(x,t,\varepsilon ) < \text{v}(x,t,\varepsilon ) < {{V}_{{{\text{up}}}}}(x,t,\varepsilon ).$

Доказательство. Воспользуемся определением верхнего и нижнего решений, введенным в разд. 3, исключая условие периодичности. Можно показать, что функции ${{U}_{{{\text{up}}}}}(x,t,\varepsilon )$, ${{V}_{{{\text{up}}}}}(x,t,\varepsilon )$ и ${{U}_{{{\text{down}}}}}(x,t,\varepsilon )$, ${{V}_{{{\text{down}}}}}(x,t,\varepsilon )$ являются верхним и нижним решениями задачи (37). В работах [27], [28] аналогичное утверждение доказано для случая уравнения реакция-диффузия с разрывной неоднородностью.

Условие 1 выполняется на сегменте $x \in [0;L]$, так как по способу построения функций ${{U}^{{\alpha ,\beta }}}(x,t,\varepsilon )$ справедливо равенство ${{U}_{{{\text{up}}}}}(x,t,\varepsilon ) - {{U}_{{{\text{down}}}}}(x,t,\varepsilon ) = {{e}^{{ - \lambda t}}}({{U}^{\beta }}(x,t,\varepsilon ) - {{U}^{\alpha }}(x,t,\varepsilon )) \geqslant 0$. Аналогичное равенство справедливо для ${{V}^{{\alpha ,\beta }}}(x,t,\varepsilon )$.

Функции ${{U}_{{{\text{up}}}}}(x,t,\varepsilon )$, ${{V}_{{{\text{up}}}}}(x,t,\varepsilon )$ и ${{U}_{{{\text{down}}}}}(x,t,\varepsilon )$, ${{V}_{{{\text{down}}}}}(x,t,\varepsilon )$ удовлетворяют неравенствам условия 2. Неравенство ${{L}_{{1\varepsilon }}}({{U}_{{{\text{up}}}}},\text{v}) < 0$ достаточно проверить при $\text{v} = {{V}_{{{\text{up}}}}}$ в силу условия ${{H}_{3}}$:

В ходе преобразования мы использовали утверждение теоремы 1 и равенство ${{L}_{{1\varepsilon }}}({{U}^{\beta }},{{V}^{\beta }}) = - {{\varepsilon }^{{n + 1}}}A + {{e}^{{ - \lambda t}}}O({{\varepsilon }^{{n + 2}}})$. Согласно теореме 1 разность $\left( {{{U}^{\beta }} - u{\text{*}}} \right)$ является величиной порядка $O({{\varepsilon }^{{n + 1}}})$. Можно выбрать $\lambda > 0$ достаточно малым и получить

${{L}_{{1\varepsilon }}}({{U}_{{{\text{up}}}}},{{V}_{{{\text{up}}}}}) = - {{\varepsilon }^{{n + 1}}}A{{e}^{{ - \lambda t}}} + \lambda O({{\varepsilon }^{{n + 1}}}){{e}^{{ - \lambda t}}} + {{e}^{{ - \lambda t}}}O({{\varepsilon }^{{n + 2}}}) < 0.$

Аналогичным образом, можно показать, что неравенства условия 2 выполняются для дифференциальных операторов ${{L}_{{1\varepsilon }}}({{U}_{{{\text{down}}}}},{{V}_{{{\text{down}}}}})$, ${{L}_{{2\varepsilon }}}({{U}_{{{\text{up}}}}},{{V}_{{{\text{up}}}}})$, ${{L}_{{2\varepsilon }}}({{U}_{{{\text{down}}}}},{{V}_{{{\text{down}}}}})$.

В граничных точках сегмента $[0;L]$ для функции ${{U}_{{{\text{up}}}}}(x,t,\varepsilon )$ выполнено равенство:

$\frac{{\partial {{U}_{{{\text{up}}}}}}}{{\partial x}}(0,t,\varepsilon ) = \frac{{\partial u{\kern 1pt} {\text{*}}}}{{\partial x}}(0,t,\varepsilon )(1 - {{e}^{{ - \lambda t}}}) + {{e}^{{ - \lambda t}}}\frac{{\partial {{U}^{\beta }}}}{{\partial x}}(0,t) \leqslant 0,$

$\frac{{\partial {{U}_{{up}}}}}{{\partial x}}(L,t,\varepsilon ) = \frac{{\partial u{\kern 1pt} {\text{*}}}}{{\partial x}}(L,t,\varepsilon )(1 - {{e}^{{ - \lambda t}}}) + {{e}^{{ - \lambda t}}}\frac{{\partial {{U}^{\beta }}}}{{\partial x}}(L,t,\varepsilon ) \geqslant 0,$

согласно граничным условиям для периодических решений задачи $($1), (2) и методу построения функции ${{U}^{\beta }}(x,t,\varepsilon )$. Таким образом, для функции ${{U}_{{{\text{up}}}}}(x,t,\varepsilon )$ выполнено условие 3. Аналогично можно показать, что функции ${{V}_{{{\text{up}}}}}(x,t,\varepsilon )$ и ${{U}_{{{\text{down}}}}}(x,t,\varepsilon )$, ${{V}_{{{\text{down}}}}}(x,t,\varepsilon )$ также удовлетворяют условию 3.

Пользуясь теоремой 3.1 из работы [15] и рассуждениями, аналогичными приведенным в доказательстве теоремы 1, можно показать, что из существования нижних ${{U}_{{{\text{down}}}}}(x,t,\varepsilon )$, ${{V}_{{{\text{down}}}}}(x,t,\varepsilon )$ и верхних ${{U}_{{{\text{up}}}}}(x,t,\varepsilon )$, ${{V}_{{{\text{up}}}}}(x,t,\varepsilon )$ решений задачи (37) следует, что решение $u(x,t,\varepsilon )$, $\text{v}(x,t,\varepsilon )$ задачи (37) существует и удовлетворяет неравенствам: ${{U}_{{{\text{down}}}}}(x,t,\varepsilon ) \leqslant u(x,t,\varepsilon ) \leqslant {{U}_{{{\text{up}}}}}(x,t,\varepsilon )$, ${{V}_{{{\text{down}}}}}(x,t,\varepsilon ) \leqslant \text{v}(x,t,\varepsilon ) \leqslant {{V}_{{{\text{up}}}}}(x,t,\varepsilon )$, $\quad x \in [0;L]$, $t \in (0; + \infty )$. Теорема доказана.

Теорема 3. Пусть выполнены условия ${{H}_{1}}$–${{H}_{5}}$. Тогда гладкое периодическое решение задачи (1), (2), для которого суммы (29) являются асимптотическим приближением, единственно и асимптотически устойчиво по Ляпунову с областью влияния по крайней мере $[{{U}^{\alpha }},{{U}^{\beta }}]$ для $u$-компоненты и $[{{V}^{\alpha }},{{V}^{\beta }}]$ для $\text{v}$-компоненты.

Доказательство. Выберем начальные функции ${{u}_{{{\text{init}}}}}(x)$, ${{\text{v}}_{{{\text{init}}}}}(x)$ задачи (37) таким образом, чтобы выполнялись неравенства

(39)

${{U}^{\alpha }}(x,0,\varepsilon ) < {{u}_{{{\text{init}}}}}(x) < {{U}^{\beta }}(x,0,\varepsilon ),\quad {{V}^{\alpha }}(x,0,\varepsilon ) < {{\text{v}}_{{{\text{init}}}}}(x) < {{V}^{\beta }}(x,0,\varepsilon ),\quad x \in [0;L].$

Из равенств (38) следует, что ${{U}_{{{\text{down}}}}}(x,0,\varepsilon ) = {{U}^{\alpha }}(x,0,\varepsilon )$, ${{U}_{{{\text{up}}}}}(x,0,\varepsilon ) = {{U}^{\beta }}(x,0,\varepsilon )$ и ${{V}_{{{\text{down}}}}}(x,0,\varepsilon ) = {{V}^{\alpha }}(x,0,\varepsilon )$, ${{V}_{{{\text{up}}}}}(x,0,\varepsilon ) = {{V}^{\beta }}(x,0,\varepsilon )$. Таким образом, функции ${{u}_{{{\text{init}}}}}(x)$ и ${{\text{v}}_{{{\text{init}}}}}(x)$, удовлетворяющие неравенствам (39), лежат между нижним и верхним решениями ${{U}_{{{\text{down}}}}}$, ${{U}_{{{\text{up}}}}}$ и ${{V}_{{{\text{down}}}}}$, ${{V}_{{{\text{up}}}}}$ при $x \in [0;L]$. Условия теоремы 2 выполнены и существует единственное решение $u(x,t,\varepsilon )$, $\text{v}(x,t,\varepsilon )$ начальной задачи (37), лежащее между ${{U}_{{{\text{down}}}}}(x,t,\varepsilon )$, ${{U}_{{{\text{up}}}}}(x,t,\varepsilon )$ и ${{V}_{{{\text{down}}}}}(x,t,\varepsilon )$, ${{V}_{{{\text{up}}}}}(x,t,\varepsilon )$.

Функции ${{U}_{{{\text{down}}}}}(x,t,\varepsilon )$, ${{U}_{{{\text{up}}}}}(x,t,\varepsilon )$ сходятся к функции $u{\kern 1pt} {\text{*}}(x,t,\varepsilon )$ при $t \to + \infty $. В этом случае функция $u(x,t,\varepsilon )$ также стремится к $u{\text{*}}(x,t,\varepsilon )$. Поскольку решение $u(x,t,\varepsilon )$ задачи (37) единственно, то функция $u{\text{*}}(x,t,\varepsilon )$ является единственным решением задачи (1), (2), расположенным между ${{U}^{\alpha }}(x,t,\varepsilon )$ и ${{U}^{\beta }}(x,t,\varepsilon )$. Аналогично для $\text{v}$-компоненты функция $\text{v}{\kern 1pt} *(x,t,\varepsilon )$ является единственным решением задачи (1), (2), расположенным между ${{V}^{\alpha }}(x,t,\varepsilon )$ и ${{V}^{\beta }}(x,t,\varepsilon ).$

Отсюда следует, что если неравенства (39) выполнены, то справедливы предельные равенства

$\mathop {lim}\limits_{t \to + \infty } \left| {u(x,t,\varepsilon ) - u{\kern 1pt} {\text{*}}(x,t,\varepsilon )} \right| = 0,\quad \mathop {lim}\limits_{t \to + \infty } \left| {\text{v}(x,t,\varepsilon ) - \text{v}{\kern 1pt} {\text{*}}(x,t,\varepsilon )} \right| = 0$

и периодическое решение $u{\kern 1pt} {\text{*}}(x,t,\varepsilon )$, $\text{v}{\kern 1pt} {\text{*}}(x,t,\varepsilon )$ локально устойчиво по Ляпунову с областью влияния, по крайней мере, $[{{U}^{\alpha }},{{U}^{\beta }}]$ для $u$-компоненты и $[{{V}^{\alpha }},{{V}^{\beta }}]$ для $\text{v}$-компоненты.

5. ПРИМЕР

Приведем пример модельной системы, для которой выполнены условия ${{H}_{1}}$–${{H}_{5}}$, и выпишем асимптотическое приближение нулевого порядка. Задача имеет вид

${{\varepsilon }^{4}}({{u}_{{xx}}} - {{u}_{t}}) = (u + 0.125\text{v} + 0.5x - 1)(u - (4 + \varepsilon x(cos(2\pi t) + 2)))(u - ( - 4 + \varepsilon x(cos(2\pi t) + 2))),$

${{\varepsilon }^{2}}({{\text{v}}_{{xx}}} - {{\text{v}}_{t}}) = \text{v} - 0.5(0.25u + 3)(x + 1.4)(cos(2\pi t) + 2),\quad x \in (0;2),\quad t \in {{\mathbb{R}}^{ + }},$

${{u}_{x}}(0,t,\varepsilon ) = {{u}_{x}}(2,t,\varepsilon ) = 0,\quad {{\text{v}}_{x}}(0,t,\varepsilon ) = {{\text{v}}_{x}}(2,t,\varepsilon ) = 0,\quad t \in {{\mathbb{R}}^{ + }}.$

Для функций регулярной части нулевого порядка получаем следующие выражения:

$\begin{gathered} \bar {u}_{0}^{l}(x,t) = - 4,\quad \bar {v}_{0}^{l}(x,t) = (x + 1.4)(cos(2\pi t) + 2), \\ \bar {u}_{0}^{r}(x,t) = 4,\quad \bar {v}_{0}^{r}(x,t) = 2(x + 1.4)(cos(2\pi t) + 2). \\ \end{gathered} $

Положение фронта с точностью $O(\varepsilon )$ определяется функцией ${{x}_{0}}(t)$:

${{x}_{0}}(t) = \frac{{27.2}}{{3cos(2\pi t) + 14}} - 1.4.$

Запишем выражение для $\text{v}$-компоненты решения с точностью $O(\varepsilon )$:

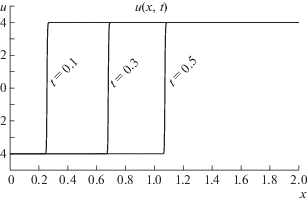
$\text{v}(x,t) = \left\{ \begin{gathered} (x + 1.4)(cos(2\pi t) + 2) + ({{\text{v}}_{0}}(t) - {{\text{v}}^{1}}({{x}_{0}}(t),t))exp((x - {{x}_{0}}(t)){\text{/}}\varepsilon ) + \hfill \\ + \;\varepsilon (cos(2\pi t) + 2)exp( - x{\text{/}}\varepsilon ),\quad 0 \leqslant x \leqslant {{x}_{0}}(t); \hfill \\ 2(x + 1.4)(cos(2\pi t) + 2) + ({{\text{v}}_{0}}(t) - {{\text{v}}^{3}}({{x}_{0}}(t),t))exp( - (x - {{x}_{0}}(t)){\text{/}}\varepsilon ) - \hfill \\ - \;2\varepsilon (cos(2\pi t) + 2)exp( - (2 - x){\text{/}}\varepsilon ),\quad {{x}_{0}}(t) \leqslant x \leqslant 2. \hfill \\ \end{gathered} \right.$

График функции $\text{v}(x,t)$ представлен на фиг. 1.

Фиг. 1.

График $\text{v}$-компоненты решения с точностью $O(\varepsilon )$ в различные моменты времени. Параметр $\varepsilon = 0.2$.

Введем функцию $\tilde {u}(\sigma ,t)$:

$\tilde {u}(\sigma ,t) = \left\{ {\begin{array}{*{20}{l}} { - 4 + M_{0}^{l}(\sigma ,t),\quad x \leqslant {{x}_{0}}(t),} \\ {4 + M_{0}^{r}(\sigma ,t),\quad x \geqslant {{x}_{0}}(t).} \end{array}} \right.$

Функция $\tilde {u}(\sigma ,t)$ в данном примере определяется из задачи

$\frac{{{{\partial }^{2}}\tilde {u}}}{{\partial {{\sigma }^{2}}}} = (\tilde {u} + 0.125{{\text{v}}_{0}}(t) + 0.5{{x}_{0}}(t) - 1)(\tilde {u} - 4)(\tilde {u} + 4),$

$\tilde {u}(0,t) = 1 - 0.125{{\text{v}}_{0}}(t) - 0.5{{x}_{0}}(t),\quad \tilde {u}( - \infty ,t) = - 4,\quad \tilde {u}( + \infty ,t) = 4,$

где ${{\text{v}}_{0}}(t) = 13.6(1 - 8{{(3cos(2\pi t) + 14)}^{{ - 1}}})$. (Задача для $\tilde {u}(\sigma ,t)$ получается из уравнений (21) с условиями (22).)

Тогда приближенное решение для $u$-компоненты при $\varepsilon \to 0$ можно записать в виде

$u(x,t) = \tilde {u}((x - {{x}_{0}}(t)){\text{/}}{{\varepsilon }^{2}},t) + O(\varepsilon ).$

График решения представлен на фиг. 2.

Фиг. 2.

График $u$-компоненты решения с точностью $O(\varepsilon )$ в различные моменты времени. Параметр $\varepsilon = 0.2$.

Список литературы

Wu S.L., Zhao H.Q. Traveling fronts for a delayed reaction-diffusion system with a quiescent stage // Commun. Nonlinear Sci. Numer. Simul. 2011. V. 16. № 9. P. 3610–3621.
Larralde H., Araujo M., Havlin S. Diffusion-reaction kinetics for A + B – C for one-dimensional systems with initially separated reactants // Phys. Rev. A. 1992. V. 46. № 10. P. 855–859.
Kessler D., Levine H. Fluctuation-induced diffusive instabilities // Nat. Mater. 1998. V. 394. P. 556–558.
Prum R.O., Williamson S. Reaction-diffusion models of within-feather pigmentation patterning // Proc. R. Soc. B Biol. Sci. 2002. V. 269. № 1493. P. 781–792.
Levashova N., Melnikova A., Sidorova A., Semina A. Autowave mechanisms of structure formation in urban ecosystems as the process of self-organization in active media // Commun. Appl. Math. Comput. 2017. V. 31. № 1. P. 32–42.
Сидорова А.Э., Левашова Н.Т., Мельникова А.А., Дерюгина Н.Н., Семина А.Е. Автоволновая самоорганизация в неоднородных природно-антропогенных экосистемах // Вестн. Московского университета. Серия 3: Физика, астрономия. 2016. Т. № 6. С. 39–45.
Orlov A., Levashova N., Burbaev T. The use of asymptotic methods for modelling of the carriers wave functions in the Si/SiGe heterostructures with quantum-confined layers // J. Phys.: Conf. Ser. 2015. V. 586. № 012003.
Ham Y. Internal layer oscillations in FitzHugh-Nagumo equation // J. Comput. Appl. Math. 1999. V. 103. P. 287–295.
Бутузов В.Ф., Васильева А.Б., Нефедов Н.Н. Асимптотическая теория контрастных структур (обзор) // Автоматика и телемехан. 1997. № 7. С. 4–32.
Левашова Н.Т., Нефедов Н.Н., Орлов А.О. Стационарное уравнение реакции-диффузии с разрывным реактивным членом // Ж. вычисл. матем. и матем. физ. 2017. Т. 57. № 5. С. 854–866.
Lukyanenko D., Nefedov N., Nikulin E., Volkov V. Use of asymptotics for new dynamic adapted mesh construction for periodic solutions with an interior layer of reaction-diffusion-advection equations // Lect. Notes in Comp. Sc. 2017. V. 10187. P. 107–118.
Melnikova A., Levashova N., Lukyanenko D. Front dynamics in an activator-inhibitor system of equations // Lect. Notes in Computer Science. 2017. V. 10187. P. 492–499.
Мельникова А.А., Чэнь М. Существование и асимптотика автоволнового решения системы уравнений // Ж. вычисл. матем. и матем. физ. 2018. Т. 58. № 5. С. 705–715.
Pao C.V. Nonlinear Parabolic and Elliptic Equations. New York: Plenum Press, 1992. P. 56–69.
Pao C.V. Periodic solutions of parabolic systems with nonlinear boundary conditions // J. Math. Anal. Appl. 1999. V. 234. № 2. P. 695–716.
Бутузов В.Ф., Левашова Н.Т., Мельникова А.А. Контрастная структура типа ступеньки в сингулярно возмущенной системе уравнений с различными степенями малого параметра // Ж. вычисл. матем. и матем. физ. 2012. Т. 52. № 11. С. 1983–2003.
Nefedov N.N. An asymptotic method of differential inequalities for the investigation of periodic contrast structures: existence, asymptotics, and stability // Differ. Equations. 2000. V. 36. № 2. P. 298–305.
Nefedov N. Comparison principle for reaction-diffusion-advection problems with boundary and internal layers // Lect. Notes in Comp. Sc. 2013. V. 8236. P. 62–72.
Левашова Н.Т., Мельникова А.А. Контрастная структура типа ступеньки в сингулярно возмущенной системе параболических уравнений // Дифференц. ур-ния. 2015. Т. 51. № 3. С. 339–358.
Васильева А.Б. Об устойчивости контрастных структур // Матем. моделирование. 1991. Т. 3. № 4. С. 114–123.
Левашова Н.Т., Мельникова А.А., Быцюра С.В. Применение метода дифференциальных неравенств для обоснования решения системы параболических уравнений в виде движущегося фронта //Моделирование и анализ информационных систем. 2016. Т. 23. № 3. С. 317–325.
Васильева А.Б., Бутузов В.Ф. Асимптотические методы в теории сингулярных возмущений. М.: Высш. школа, 1990. С. 27–34.
Бутузов В.Ф. Контрастные структуры типа всплеска в параболической системе двух сингулярно возмущенных уравнений // Ж. вычисл. матем. и матем. физ. 1997. Т. 37. № 4. С. 415–428.
Васильева А.Б., Плотников А.А. Асимптотическая теория сингулярно возмущенных задач. М.: Физический факультет МГУ, 2008. С. 38–42.
Dong G. Nonlinear Partial Differential Equations of Second Order. Providence, Rhode Island, 2008.
Levashova N., Nefedov N., Nikolaeva O., Orlov A., Panin A. The solution with internal transition layer of the reaction-diffusion equation in case of discontinuous reactive and diffusive terms // Mathematical Methods in the Applied Sciences. 2018. V. 41. № 18. P. 1–15.
Орлов А.О., Нефедов Н.Н., Левашова Н.Т. Решение вида контрастной структуры параболической задачи реакция-диффузия в среде с разрывными характеристиками // Дифференц. ур-ния. 2018. Т. 54. № 5. С. 673–690.
Левашова Н.Т., Нефедов Н.Н., Орлов А.О. Асимптотическая устойчивость стационарного решения многомерного уравнения реакция-диффузия с разрывным источником // Ж. вычисл. матем. и матем. физ. 2019. Т. 59. № 4. С. 76–85.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал