Журнал вычислительной математики и математической физики, 2020, T. 60, № 11, стр. 1881-1897
Бигармоническая задача с препятствием: гарантированные и вычисляемые оценки ошибок для приближенных решений
Д. Е. Апушкинская 1, 2, *, С. И. Репин 3, 4, **
1 Saarland University
66041 Saarbrücken, P.O. Box 151150, Germany
2 РУДН
117198 Москва, ул. Миклухо-Маклая, 6, Россия
3 ПОМИ РАН
191023 Санкт-Петербург, Фонтанка 27, Россия
4 University of Jyväskylä
40014 Jyväskylä, P.O. Box 35 (Agora), Finland
* E-mail: darya@math.uni-sb.de
** E-mail: repin@pdmi.ras.ru
Поступила в редакцию 17.06.2020
После доработки 17.06.2020
Принята к публикации 07.07.2020
Аннотация
В статье рассматривается эллиптическое вариационное неравенство, возникающее в задаче с препятствием для бигармонического оператора. Изучаются оценки разности между точным решением (минимайзером) соответствующей вариационной задачи и произвольной функцией из энергетического класса, которая удовлетворяет поставленным краевым условиям и ограничениям, связанным с препятствием. Используя общую теорию, построенную для выпуклых вариационных задач, получено тождество, одна часть которого характеризует величину отклонения функции (аппроксимации) от точного решения, а другая является вычисляемой величиной (она зависит только от данных задачи и известных функций). Использование этого тождества в практических вычислениях позволяет оценить качество полученных приближенных решений. Использующаяся в тождестве мера отклонения от точного решения содержит различные слагаемые. Два из них задаются нормами разности между точными решениями прямой и двойственной вариационных задач и их аппроксимациями соответственно. Два других, вообще говоря, не представимы в виде норм и являются нелинейными мерами, которые обращаются в ноль, если коинцедентное множество, построенное по приближенному решению, удовлетворяет некоторым условиям (например совпадает с точным коинцедентным множеством). Тождество верно для любых допустимых (конформных) аппроксимаций прямой переменной, но содержит некоторые ограничения на двойственную переменную. В статье показано, что эти ограничения могут быть сняты, но при этом тождество заменяется на неравенство. Последнее дает явно вычисляемую мажоранту величины отклонения от точного решения данной нелинейной задачи для любых аппроксимаций прямой и двойственной вариационных задач. Приводится ряд примеров, которые иллюстрируют установленные тождества и неравенства. Библ. 29. Фиг. 5. Табл. 3.
1. ВВЕДЕНИЕ
Пусть $\Omega $ – ограниченная область в пространстве ${{\mathbb{R}}^{d}}$ с липшицевой границей $\partial \Omega $ и единичной внешней нормалью $\nu $, а $\varphi $ – заданная функция (препятствие) в ${{C}^{2}}(\bar {\Omega })$ такая, что $\varphi \leqslant 0$ на $\partial \Omega $. Далее будем использовать стандартные обозначения для функциональных пространств Лебега и Соболева. Через ${{g}_{ \oplus }}$ обозначим $\max \{ g,0\} $.
Рассматривается вариационная задача ($\mathcal{P}$): минимизировать функционал
(1.1)
$J(v) = \int\limits_\Omega \,\left( {\frac{1}{2}{{{\left| {\Delta v} \right|}}^{2}} - fv} \right)dx$Задача ($\mathcal{P}$) называется задачей с препятствием для бигармонического оператора. Она имеет множество приложений в теории упругости (равновесный контакт без трения упругих пластин или балок над жестким препятствием) и в механике жидкостей (течение несжимаемой жидкости с малым числом Рейнольдса на плоскости). Стандартным образом (см., например, [1], [2]) мы получаем, что задача ($\mathcal{P}$) имеет единственное решение $u$, которое удовлетворяет п.в. в $\Omega $ соотношениям:
(1.2)
${{\Delta }^{2}}u \geqslant f,\quad u \geqslant \varphi ,\quad ({{\Delta }^{2}}u - f)(u - \varphi ) = 0.$В частности, из известных работ [3] и [4] вытекает следующая априорная гладкость решения:
(1.3)
$u \in H_{{{\text{loc}}}}^{3}(\Omega ) \cap W_{{{\text{loc}}}}^{{2,\infty }}(\Omega )\quad {\text{и}}\quad \Delta u \in W_{{{\text{loc}}}}^{{2,\infty }}(\Omega ).$В общем случае область $\Omega $ разделяется на две подобласти ${{\Omega }_{0}}$ и ${{\Omega }_{\varphi }}$, где решение $u$ обладает различными свойствами. В ${{\Omega }_{0}}$ выполняется уравнение ${{\Delta }^{2}}u = f$, а в ${{\Omega }_{\varphi }}$ решение $u$ совпадает с препятствием (это множество принято называть коинцедентным). Граница между множествами заранее неизвестна, поэтому задача $\mathcal{P}$ относится к классу задач со свободными границами.
Задача с препятствием для бигармонического оператора активно изучалась различными авторами, начиная с пионерских работ Ландау и Лифшица [5], Фрезе [4], [6], Чиматти [7], Стампаккьи [8], Брезиса и Стампаккьи [8]. Упомянем также известные монографии Дуво и Лионса [10] и Родригеса [11], где приведены примеры изгибающихся пластин, расположенных над препятствиями. Заметим также, что подавляющее большинство исследований задач с препятствием для уравнений четвертого порядка были в основном посвящены либо описанию регулярности минимайзеров, либо свойствам соответствующих свободных границ (см. [3], [4], [6], [7], [12–13], [14]).
Аппроксимационные методы для бигармонической задачи с препятствием разрабатывались в рамках методов вычислений для вариационных неравенств (см., например, [15]–[19]) и соответствующих задач оптимального управления [20], [21]. Таким образом, в принципе понятно, как построить последовательность приближений, сходящихся к точному решению нашей нелинейной вариационной задачи.
В данной статье нас интересует другая проблема. Нашей целью является получение гарантированной и полностью вычисляемой оценки расстояния (измеряемого в терминах естественной энергетической нормы) между точным решением $u \in \mathbb{K}$ и любым приближенным решением $v \in \mathbb{K}$. Для получения такой оценки будет использоваться метод, который использовался в работе [22] при выводе гарантированных оценок разности между точным решением линейной бигармонической задачи и произвольной функцией из энергетического допустимого класса. В [23]–[26] и в некоторых других публикациях этот метод применялся к ряду задач с препятствиями для эллиптических операторов второго порядка. Мы показываем, что предлагаемая методика оказывается весьма эффективной и в случае операторов более высокого порядка. Она позволяет установить естественную меру ошибки (которая характеризует отклонение произвольной функции из соответствующего энергетического пространства от точного решения) и получить полностью вычисляемые оценки этой меры.
2. ОЦЕНКИ ОТКЛОНЕНИЯ ОТ ТОЧНОГО РЕШЕНИЯ
2.1. Общий вид тождества для меры ошибки
Рассмотрим функциональные пространства
Нетрудно видеть, что функционал $J$ в задаче (1.1) представим в виде
где оператор $\Lambda $ и функционалы $G$ и $F$ определяются следующим образом:(2.2)
$I{\kern 1pt} {\text{*}}(n{\kern 1pt} {\text{*}}): = - G{\kern 1pt} {\text{*}}(n{\kern 1pt} {\text{*}}) - F{\kern 1pt} {\text{*}}( - \Lambda {\kern 1pt} {\text{*}}n{\kern 1pt} {\text{*}})$Учитывая соотношение двойственности $J(u) = I{\kern 1pt} {\text{*}}(p{\kern 1pt} {\text{*}})$ (которое выполнено для данной вариационной задачи) и тождества (7.2.13)–(7.2.14) из [28], получаем для любых $v \in \mathbb{K}$ и $n{\kern 1pt} * \in N{\kern 1pt} *$ следующие соотношения:
(2.3)
$J(v) - J(u) = J(v) - I{\kern 1pt} {\text{*}}(p{\kern 1pt} {\text{*}}) = {{\mathcal{D}}_{G}}(\Lambda v,p{\kern 1pt} {\text{*}}) + {{\mathcal{D}}_{F}}(v, - \Lambda {\kern 1pt} {\text{*}}p{\kern 1pt} {\text{*}}),$(2.4)
$I{\kern 1pt} {\text{*}}(p{\kern 1pt} {\text{*}}) - I{\kern 1pt} {\text{*}}(n{\kern 1pt} {\text{*}}) = J(u) - I{\kern 1pt} {\text{*}}(n{\kern 1pt} {\text{*}}) = {{\mathcal{D}}_{G}}(\Lambda u,n{\kern 1pt} {\text{*}}) + {{\mathcal{D}}_{F}}(u, - \Lambda {\kern 1pt} {\text{*}}n{\kern 1pt} {\text{*}}).$ и
и  обозначают так называемые составные функционалы (compound functionals), которые определяются соотношениями
обозначают так называемые составные функционалы (compound functionals), которые определяются соотношениями
(2.5)
${{\mathcal{D}}_{G}}(\Lambda {v},n{\kern 1pt} {\text{*}}) = G(\Lambda {v}) + G{\kern 1pt} {\text{*}}(n{\kern 1pt} {\text{*}}) - (\Lambda {v},n{\kern 1pt} {\text{*}}),$(2.6)
${{\mathcal{D}}_{F}}(v, - \Lambda {\kern 1pt} {\text{*}}n{\kern 1pt} {\text{*}}) = F(v) + F{\kern 1pt} {\text{*}}(n{\kern 1pt} {\text{*}}) + \left\langle {\Lambda n{\kern 1pt} {\text{*}},v} \right\rangle ,$Из соотношений (2.3), (2.4) следует тождество (“error identity”, см. подробное изложение в [27])
(2.7)
${{\mathcal{D}}_{G}}(\Lambda v,p{\kern 1pt} {\text{*}}) + {{\mathcal{D}}_{F}}(v, - \Lambda {\kern 1pt} {\text{*}}p{\kern 1pt} {\text{*}}) + {{\mathcal{D}}_{G}}(\Lambda u,n{\kern 1pt} {\text{*}}) + {{\mathcal{D}}_{F}}(u, - \Lambda {\kern 1pt} {\text{*}}n{\kern 1pt} {\text{*}}) = {{\mathcal{D}}_{G}}(\Lambda v,n{\kern 1pt} {\text{*}}) + {{\mathcal{D}}_{F}}(v, - \Lambda {\kern 1pt} {\text{*}}n{\kern 1pt} {\text{*}}),$Тождество (2.7) выполняется для любой вариационной задачи с функционалом вида (2.1). Установим его вид в терминах рассматриваемой задачи. Нетрудно видеть, что $G{\kern 1pt} *:N{\kern 1pt} * \to \mathbb{R}$ определяется равенством $G{\kern 1pt} {\text{*}}(n{\kern 1pt} {\text{*}}): = \tfrac{1}{2}{{\left\| {n{\kern 1pt} *} \right\|}^{2}}$ (здесь и далее $\left\| {\, \cdot \,} \right\|$ обозначает норму в пространствах ${{L}_{2}}(\Omega )$ для скалярных, векторных и матричных функций). Поэтому первые слагаемые, стоящие в правых частях (2.3) и (2.4), вычисляются довольно просто:
(2.8)
${{\mathcal{D}}_{G}}(\Lambda v,p{\kern 1pt} *) = \frac{1}{2}{{\left\| {\nabla \nabla v - p{\kern 1pt} *} \right\|}^{2}} = \frac{1}{2}{{\left\| {\nabla \nabla (v - u)} \right\|}^{2}}{\kern 1pt} ,$(2.9)
${{\mathcal{D}}_{G}}(\Lambda u,n{\kern 1pt} *) = \frac{1}{2}{{\left\| {\nabla \nabla u - n{\kern 1pt} *} \right\|}^{2}} = \frac{1}{2}{{\left\| {p{\kern 1pt} * - n{\kern 1pt} *} \right\|}^{2}}.$Вычисление вторых слагаемых в правых частях (2.3) и (2.4) потребует значительных усилий.
Для вычисления $\left\langle {v{\kern 1pt} *,v} \right\rangle $ необходимо ввести промежуточное гильбертовое пространство $\mathcal{V}: = {{L}^{2}}(\Omega )$. Очевидно, что $\mathcal{V}$ обладает свойством $V \subset \mathcal{V} \subset V{\kern 1pt} *$. Если $v{\kern 1pt} * \in \mathcal{V}$, то произведение $\left\langle {v{\kern 1pt} *,v} \right\rangle $ отождествляется со скалярным произведением в пространстве $\mathcal{V}$, т.е.
В соответствии с определением сопряженного функционала для $n{\kern 1pt} * \in N$ мы имеем
Предположим, что функция $n{\kern 1pt} *$ удовлетворяет дополнительному условию
(2.10)
$n{\kern 1pt} * \in H(\Omega ,\operatorname{div} \operatorname{Div} ): = \left\{ {m{\kern 1pt} * \in N{\kern 1pt} *:\operatorname{div} \operatorname{Div} m{\kern 1pt} * \in {{L}^{2}}(\Omega )} \right\}.$(2.11)
$\int\limits_\Omega \,(fv - n{\kern 1pt} *:\nabla \nabla v)dx = \int\limits_\Omega \,(fv + \nabla v \cdot \operatorname{Div} n{\kern 1pt} *{\kern 1pt} )dx.$(2.12)
$0 = \int\limits_{\partial \Omega } \,(\operatorname{Div} n{\kern 1pt} {\text{*}} \cdot \nu )vds = \int\limits_\Omega \,{\text{div}}({v}\operatorname{Div} n{\kern 1pt} *{\kern 1pt} )dx = \int\limits_\Omega \,(\operatorname{Div} n{\kern 1pt} * \cdot \nabla {v} + {v}\operatorname{div} \operatorname{Div} n{\kern 1pt} *{\kern 1pt} )dx,$Таким образом,
(2.13)
$F{\kern 1pt} *{\kern 1pt} ( - \Lambda {\kern 1pt} *{\kern 1pt} n{\kern 1pt} *{\kern 1pt} ) = \mathop {sup}\limits_{{v} \in \mathbb{K}} \left\{ {\int\limits_\Omega \,(f - \operatorname{div} \operatorname{Div} n{\kern 1pt} *{\kern 1pt} ){v}dx} \right\}\quad \forall n{\kern 1pt} * \in H(\Omega ,\operatorname{div} {\text{Div}}).$(2.14)
$Q_{ \ominus }^{*}: = \left\{ {m{\kern 1pt} * \in H(\Omega ,\operatorname{div} \operatorname{Div} )\left| {\int\limits_\Omega \,(f - \operatorname{div} \operatorname{Div} m{\kern 1pt} *{\kern 1pt} )wdx} \right. \leqslant 0\;\;\forall w \in {{V}^{ + }}(\Omega )} \right\}.$Поэтому составной функционал ${{\mathcal{D}}_{F}}({v}, - \Lambda {\kern 1pt} *{\kern 1pt} n{\kern 1pt} *{\kern 1pt} )$ конечен тогда и только тогда, когда условие
выполняется почти везде в $\Omega $.Следовательно, для $n{\kern 1pt} * \in H(\Omega ,\operatorname{div} \operatorname{Div} )$, удовлетворяющего условию (2.15), функционал ${{\mathcal{D}}_{F}}({v}, - \Lambda {\kern 1pt} *{\kern 1pt} n{\kern 1pt} *{\kern 1pt} )$ принимает вид
(2.16)
${{\mathcal{D}}_{F}}({v}, - \Lambda {\kern 1pt} *{\kern 1pt} n{\kern 1pt} *{\kern 1pt} ) = \int\limits_\Omega \,(f - \operatorname{div} \operatorname{Div} n{\kern 1pt} *)(\varphi - {v})dx.$Теперь необходимо вычислить ${{\mathcal{D}}_{F}}({v}, - \Lambda {\kern 1pt} *{\kern 1pt} p{\kern 1pt} *{\kern 1pt} )$ для любой функции ${v} \in \mathbb{K}$. Мы не можем воспользоваться предыдущей формулой, поскольку $p{\kern 1pt} *$, вообще говоря, не удовлетворяет условию (2.10). Действительно, согласно (1.3) мы знаем только, что $\operatorname{div} \operatorname{Div} p{\kern 1pt} *$ является интегрируемой с квадратом функцией на множестве ${{\Omega }_{0}}$ (где $u > \varphi $ и выполняется условие $\operatorname{div} \operatorname{Div} p{\kern 1pt} * = f$) и на коинцедентном множестве ${{\Omega }_{\varphi }} = \{ u = \varphi \} = \Omega {\backslash }{{\Omega }_{0}}$. Для всей области это, вообще говоря, неверно. Поэтому мы используем другой метод. Положив $v = u$ в соотношении (2.3), получим равенство
из которого следует, что(2.17)
${{\mathcal{D}}_{F}}(v, - \Lambda {\kern 1pt} *{\kern 1pt} p{\kern 1pt} *{\kern 1pt} ) = \int\limits_{{{\Gamma }_{u}}} \,[\operatorname{Div} p{\kern 1pt} {\text{*}} \cdot {{\nu }_{{{{\Gamma }_{u}}}}}](u - {v})ds + \int\limits_{\{ u = \varphi \} } \,(f - \operatorname{div} \operatorname{Div} p{\kern 1pt} *{\kern 1pt} )(u - {v})dx,$Объединяя (2.3)–(2.9) и (2.16), (2.17), мы получаем конкретные выражения для мер, стоящих в левой части (2.7). Для любой функции $v \in \mathbb{K}$ имеем
(2.18)
$\mu (v): = {{\mathcal{D}}_{G}}(\Lambda v,p{\kern 1pt} *{\kern 1pt} ) + {{\mathcal{D}}_{F}}(v, - \Lambda {\kern 1pt} *{\kern 1pt} p{\kern 1pt} *{\kern 1pt} ) = \frac{1}{2}{{\left\| {\nabla \nabla (u - {v})} \right\|}^{2}} + {{\mu }_{\varphi }}({v}),$(2.19)
${{\mu }_{\varphi }}({v}): = \int\limits_{\{ u = \varphi \} } \,(\operatorname{div} \operatorname{Div} \nabla \nabla u - f)({v} - u)dx - \int\limits_{{{\Gamma }_{u}}} \,[\operatorname{Div} \nabla \nabla u \cdot {{\nu }_{{{{\Gamma }_{u}}}}}]({v} - u)ds.$(2.20)
$\int\limits_\Omega \,\left\{ {\nabla \nabla u:\nabla \nabla ({v} - u) - f({v} - u)} \right\}dx \geqslant 0\quad \forall v \in \mathbb{K}.$Нетрудно видеть, что ${{\mu }_{\varphi }}(v) = 0$, если ${{\Omega }_{\varphi }} \subset \{ x \in \Omega \,|\,v(x) = \varphi (x)\} $, т.е. если точное коинцедентное множество содержится внутри приближенного, определенного при помощи функции $v$. В других случаях эта мера будет положительной. Таким образом, меру ${{\mu }_{\varphi }}(v)$ можно рассматривать, как некоторую характеристику того, насколько точно множество $\{ v = \varphi \} $ аппроксимирует коинцидентное множество ${{\Omega }_{\varphi }}$. Конечно, эта характеристика весьма слабая и не дает желаемой информации о границе ${{\Gamma }_{u}}$. Однако в рамках стандартного вариационного подхода получить более подробную информацию о свободной границе не представляется возможным. Действительно, в силу равенства $\mu (v) = J(v) - J(u)$ мера $\mu (v)$ стремится к нулю на любой минимизирующей последовательности и является наиболее сильной среди всех мер, которые обладают таким свойством.
Аналогичным образом получаем, что если $p{\kern 1pt} *$ – максимайзер двойственной вариационной задачи (2.2), а $n{\kern 1pt} * \in H(\Omega ,\operatorname{div} {\text{Div}})$ – его аппроксимация, удовлетворяющая условию (2.15), то соответствующая мера отклонения имеет вид
(2.21)
$\mu {\kern 1pt} *{\kern 1pt} (n{\kern 1pt} *{\kern 1pt} ): = {{\mathcal{D}}_{G}}(\Lambda u,n{\kern 1pt} *{\kern 1pt} ) + {{\mathcal{D}}_{F}}(u, - \Lambda {\kern 1pt} *{\kern 1pt} n{\kern 1pt} *{\kern 1pt} ) = \frac{1}{2}{{\left\| {p{\kern 1pt} {\text{*}} - n{\kern 1pt} *} \right\|}^{2}} + \mu _{\varphi }^{*}(n{\kern 1pt} *{\kern 1pt} ),$(2.22)
$\mu _{\varphi }^{*}(n{\kern 1pt} *{\kern 1pt} ): = \int\limits_{{{\Omega }_{0}}} \,(f - \operatorname{div} \operatorname{Div} n{\kern 1pt} *)(\varphi - u)dx.$Равенства (2.7), (2.13), (2.16), (2.18) и (2.21) приводят к следующему результату:
Теорема 2.1. Для любой функции $n{\kern 1pt} * \in H(\Omega ,{\text{div}}\,{\text{Div}})$, удовлетворяющей условию (2.15), и для любой функции $v \in \mathbb{K}$ выполняется тождество
(2.23)
$\mu ({v}) + \mu {\kern 1pt} *{\kern 1pt} (n{\kern 1pt} *{\kern 1pt} ) = \frac{1}{2}{{\left\| {\nabla \nabla {v} - n{\kern 1pt} *} \right\|}^{2}} + \int\limits_\Omega \,(f - \operatorname{div} \operatorname{Div} n{\kern 1pt} *{\kern 1pt} )(\varphi - {v}){\kern 1pt} dx,$2.2. Расширение допустимого множества для $n{\kern 1pt} *$
Тождество (2.23) дает простое выражение для вычисления полной меры ошибки, но оно выполняется лишь для функций $n{\kern 1pt} * \in H(\Omega ,\operatorname{div} {\text{Div}})$, удовлетворяющих условию (2.15). Это функциональное множество является довольно узким и неудобным для практического использования. Покажем, как можно преодолеть этот недостаток и расширить допустимое множество для $n{\kern 1pt} *$.
Лемма 2.1. Для любой функции $\tilde {n}{\kern 1pt} * \in H(\Omega ,\operatorname{div} {\text{Div}})$ выполняется проекционное неравенство
(2.24)
$\mathop {inf}\limits_{n{\kern 1pt} * \in Q_{ \ominus }^{ * }} \left\| {n{\kern 1pt} {\text{*}} - \tilde {n}{\kern 1pt} *} \right\| \leqslant {{C}_{{{{F}_{\Omega }}}}}\left\| {{{{(f - \operatorname{div} \operatorname{Div} \tilde {n}{\kern 1pt} *{\kern 1pt} )}}_{ \oplus }}} \right\|,$Доказательство. Для любой функции ${{m}^{*}} \in H(\Omega ,\operatorname{div} {\text{Div}})$ выполняется равенство
Поэтому имеем(2.25)
$\mathop {inf}\limits_{n{\kern 1pt} * \in Q_{ \ominus }^{ * }} \frac{1}{2}{{\left\| {n{\kern 1pt} {\text{*}} - \tilde {n}{\kern 1pt} *} \right\|}^{2}} = \mathop {inf}\limits_{n{\kern 1pt} * \in N*} \mathop {sup}\limits_{w \in {{V}^{ + }}(\Omega )} \int\limits_\Omega \,\left( {\frac{1}{2}{{{\left| {n{\kern 1pt} {\text{*}} - \tilde {n}{\kern 1pt} *} \right|}}^{2}} + fw - n{\kern 1pt} *:\nabla \nabla w} \right)dx.$Поиск инфимума по $n{\kern 1pt} * \in N{\kern 1pt} {\text{*}}$ сводится к алгебраической задаче, решение которой почти везде в $\Omega $ удовлетворяет уравнению $n{\kern 1pt} * = \tilde {n}{\kern 1pt} {\text{*}} + \nabla \nabla w$. Используя его и интегрируя по частям, мы получаем
(2.26)
$\begin{gathered} \mathop {inf}\limits_{n{\kern 1pt} * \in Q_{ \ominus }^{ * }} \frac{1}{2}{{\left\| {n{\kern 1pt} {\text{*}} - \tilde {n}{\kern 1pt} *} \right\|}^{2}} = \mathop {sup}\limits_{w \in {{V}^{ + }}(\Omega )} \int\limits_\Omega \,\left( { - \frac{1}{2}{{{\left| {\nabla \nabla w} \right|}}^{2}} + fw - \tilde {n}{\kern 1pt} *:\nabla \nabla w} \right)dx = \\ = \mathop {sup}\limits_{w \in {{V}^{ + }}(\Omega )} \int\limits_\Omega \,\left( { - \frac{1}{2}{{{\left| {\nabla \nabla w} \right|}}^{2}} + (f - \operatorname{div} \operatorname{Div} \tilde {n}{\kern 1pt} *{\kern 1pt} )w} \right)dx \leqslant \mathop {sup}\limits_{w \in {{V}^{ + }}(\Omega )} \int\limits_\Omega \,\left( { - \frac{1}{2}{{{\left| {\nabla \nabla w} \right|}}^{2}} + {{{(f - \operatorname{div} \operatorname{Div} \tilde {n}{\kern 1pt} *{\kern 1pt} )}}_{ \oplus }}w} \right)dx. \\ \end{gathered} $(2.27)
$\left\| w \right\| \leqslant {{C}_{{{{F}_{\Omega }}}}}\left\| {\nabla w} \right\| \leqslant C_{{{{F}_{\Omega }}}}^{2}\left\| {\nabla \nabla w} \right\|$(2.28)
$\int\limits_\Omega \,{{(\operatorname{div} \operatorname{Div} \tilde {n}{\kern 1pt} {\text{*}} + f)}_{ \oplus }}wdx \leqslant C_{{{{F}_{\Omega }}}}^{2}\left\| {{{{(f - \operatorname{div} \operatorname{Div} \tilde {n}{\kern 1pt} *{\kern 1pt} )}}_{ \oplus }}} \right\|\left\| {\nabla \nabla w} \right\|.$Вводя обозначение $t: = \left\| {\nabla \nabla w} \right\|$ и объединяя (2.26) с (2.28), мы видим, что супремум в (2.26) можно оценить сверху величиной
2.3. Мажоранта меры отклонения от точного решения
Теперь мы используем лемму 2.1 и тождество (2.23) для получения оценки, которая выполняется для $\tilde {n}{\kern 1pt} * \in H(\Omega ,\operatorname{div} {\text{Div}})$. Прежде всего надо преобразовать выражения для меры $\mu {\kern 1pt} *{\kern 1pt} (n{\kern 1pt} *{\kern 1pt} )$, определенной соотношением (2.21). При помощи неравенства Юнга (с параметром $\beta $) получаем следующую оценку снизу для $\mu {\kern 1pt} *{\kern 1pt} (n{\kern 1pt} *{\kern 1pt} )$:
(2.29)
$\begin{gathered} \mu {\kern 1pt} *{\kern 1pt} (n{\kern 1pt} *{\kern 1pt} ) = \frac{1}{2}{{\left\| {p{\kern 1pt} {\text{*}} - n{\kern 1pt} {\text{*}} + \tilde {n}{\kern 1pt} {\text{*}} - \tilde {n}{\kern 1pt} *} \right\|}^{2}} + \int\limits_{\Omega {\backslash }\{ u = \varphi \} } \,(f - \operatorname{div} \operatorname{Div} (n{\kern 1pt} {\text{*}} - \tilde {n}{\kern 1pt} {\text{*}} + \tilde {n}{\kern 1pt} *{\kern 1pt} ))(\varphi - u)dx \geqslant \\ \, \geqslant \mu _{\beta }^{*}(\tilde {n}{\kern 1pt} *{\kern 1pt} ) + \frac{1}{2}\left( {1 - \frac{1}{\beta }} \right){{\left\| {\tilde {n}{\kern 1pt} {\text{*}} - n{\kern 1pt} *} \right\|}^{2}} - \int\limits_{\Omega {\backslash }\{ u = \varphi \} } \,(\varphi - u)\operatorname{div} \operatorname{Div} (n{\kern 1pt} {\text{*}} - \tilde {n}{\kern 1pt} *{\kern 1pt} )dx, \\ \end{gathered} $(2.30)
$\begin{gathered} \mu (v) + \mu {\kern 1pt} *{\kern 1pt} (n{\kern 1pt} *{\kern 1pt} ) = \frac{1}{2}{{\left\| {\nabla \nabla v - n{\kern 1pt} *} \right\|}^{2}} + \int\limits_\Omega \,(f - \operatorname{div} \operatorname{Div} \tilde {n}{\kern 1pt} *{\kern 1pt} )(\varphi - v)dx + \\ + \;\int\limits_\Omega \,(f - \operatorname{div} \operatorname{Div} (n{\kern 1pt} {\text{*}} - \tilde {n}{\kern 1pt} *{\kern 1pt} ))(\varphi - v){\kern 1pt} dx \leqslant \frac{1}{2}(1 + \beta ){{\left\| {\nabla \nabla v - \tilde {n}{\kern 1pt} *} \right\|}^{2}} + \frac{1}{2}\left( {1 + \frac{1}{\beta }} \right){{\left\| {n{\kern 1pt} {\text{*}} - \tilde {n}{\kern 1pt} *} \right\|}^{2}} + \\ + \;\int\limits_\Omega \,(f - \operatorname{div} \operatorname{Div} \tilde {n}{\kern 1pt} *)(\varphi - {v})dx - \int\limits_\Omega \,(\varphi - {v})\operatorname{div} \operatorname{Div} (n{\kern 1pt} {\text{*}} - \tilde {n}{\kern 1pt} *{\kern 1pt} )dx. \\ \end{gathered} $Объединяя выражения (2.29) и (2.30), перенося члены
(2.31)
$\begin{gathered} \mu ({v}) + \mu _{\beta }^{*}(\tilde {n}{\kern 1pt} *{\kern 1pt} ) \leqslant \frac{1}{2}(1 + \beta ){{\left\| {\nabla \nabla {v} - \tilde {n}{\kern 1pt} *} \right\|}^{2}} + \int\limits_\Omega \,(f - \operatorname{div} \operatorname{Div} \tilde {n}{\kern 1pt} *{\kern 1pt} )(\varphi - {v})dx + \\ \, + \frac{1}{\beta }{{\left\| {n{\kern 1pt} {\text{*}} - \tilde {n}{\kern 1pt} *} \right\|}^{2}} + \int\limits_\Omega \,({v} - u)\operatorname{div} \operatorname{Div} (n{\kern 1pt} {\text{*}} - \tilde {n}{\kern 1pt} *)dx. \\ \end{gathered} $Последовательное применение неравенства Гёльдера и неравенства Юнга (с параметром $\beta $) к последнему слагаемому в правой части (2.31) приводит к неравенству
(2.32)
$\int\limits_\Omega \,({v} - u)\operatorname{div} \operatorname{Div} (n{\kern 1pt} {\text{*}} - \tilde {n}{\kern 1pt} *){\kern 1pt} dx \leqslant \frac{\beta }{2}{{\left\| {\nabla \nabla (u - {v})} \right\|}^{2}} + \frac{1}{{2\beta }}{{\left\| {n{\kern 1pt} {\text{*}} - \tilde {n}{\kern 1pt} *} \right\|}^{2}}{\kern 1pt} .$Соотношения (2.31), (2.32) и (2.24) дают требуемую оценку (2.33), правая часть которой содержит только известные функции и может быть явно вычислена.
Теорема 2.2. Для любых ${v} \in \mathbb{K}$ и $\tilde {n}{\kern 1pt} * \in H(\Omega ,{\text{div}}\,{\text{Div}})$ полная мера отклонения этих функций от точных решений прямой и двойственной задач ($u$ и $p{\kern 1pt} *$ соответственно) удовлетворяет оценке
(2.33)
$\frac{{1 - \beta }}{2}({{\left\| {\nabla \nabla (u - {v})} \right\|}^{2}} + {{\left\| {p{\kern 1pt} {\text{*}} - \tilde {n}{\kern 1pt} *} \right\|}^{2}}) + {{\mu }_{\varphi }}({v}) + \mu _{\varphi }^{*}(\tilde {n}{\kern 1pt} *{\kern 1pt} ) \leqslant \mathfrak{M}({v},\tilde {n}{\kern 1pt} *,f,\varphi ,\beta ),$Замечание 2.1. В (2.29)–(2.32) мы использовали неравенство Юнга с одной и той же постоянной $\beta $. Вообще говоря, в разных оценках можно использовать разные положительные постоянные. При этом получится более точное (но и более громоздкое) выражение для мажоранты $\mathfrak{M}$, которое мы здесь не приводим.
3. ПРИМЕРЫ
Обсудим два примера, которые иллюстрируют, как работают тождество (2.23) и оценка (2.33) для полной меры ошибки.
Сначала мы рассмотрим одномерную модельную задачу, для которой известно точное решение, и, следовательно, мы можем явно посчитать ошибки аппроксимации, соответствующие прямой и двойственной переменным. В обсуждаемом примере приближенное решение имеет существенно меньшее коинцидентное множество, чем точное решение. Однако и в этом случае тождество для полной меры ошибки справедливо и оценки ошибок, вычисленные для регуляризованного двойственного приближения оказываются довольно точными.
В качестве второго примера мы рассмотрим взаимодействие с плоским препятствием упругой радиально симметричной пластины с закрепленным краем. Полученные результаты совпадают с соответствующими результатами для одномерной задачи и подтверждают справедливость тождества (2.23).
Очевидный интерес представляет применение полученных оценок в случаях, когда приближенные решения строятся с помощью некоторых стандартных (например, FEM) аппроксимаций бигармонической задачи с препятствием. Однако такая деятельность выходит за рамки данной статьи.
3.1. Модельная одномерная задача
Пусть $\Omega = ( - 1,1)$, $\varphi \equiv - 1$ и $f \equiv c$. Если положить $c = - 1152$, то минимайзер задачи (1.1) имеет вид
 .
.
Рассмотрим функцию
В качестве аппроксимации потока выберем сначала функцию
(3.2)
${{\mu }_{\varphi }}({{v}_{1}}) = \int\limits_{ - 0.5}^{0.5} \,(\operatorname{div} \operatorname{Div} \nabla \nabla \varphi - f)({{{v}}_{1}} - \varphi )dx - [u{\kern 1pt} '{\kern 1pt} '{\kern 1pt} '( - 0.5)]({{{v}}_{1}} - u){{{\text{|}}}_{{x = - 0.5}}} - [u{\kern 1pt} '{\kern 1pt} '{\kern 1pt} '(0.5)]{{\left. {({{v}_{1}} - u)} \right|}_{{x = 0.5}}} = 152.89.$Мера $\mu {\kern 1pt} *{\kern 1pt} (n{\kern 1pt} *{\kern 1pt} )$ вычисляется в соответствии с (2.21) и (2.22):
(3.3)
$\frac{1}{2}{{\left\| {p{\kern 1pt} {\text{*}} - n{\kern 1pt} *} \right\|}^{2}} = \int\limits_{0.5}^1 \,{{(p{\kern 1pt} {\text{*}} - n{\kern 1pt} *)}^{2}}dx \simeq 74.74,$(3.4)
$\mu _{\varphi }^{*}(n{\kern 1pt} *{\kern 1pt} ) = 2\int\limits_{0.5}^1 \,(f - n{\kern 1pt} '{\kern 1pt} ')(\varphi - u)dx \simeq 156.78.$Теперь мы выберем $\tilde {n}{\kern 1pt} *$ так, чтобы эта функция удовлетворяла условию (2.10), но $\tilde {n}{\kern 1pt} *$ не удовлетворяла условию (2.15). Зададим $\tilde {n}{\kern 1pt} *$ в виде
Непосредственные вычисления показывают, что
Напомним, что для $\Omega = ( - 1,1)$ имеем ${{C}_{{{{F}_{\Omega }}}}} = 4{\text{/}}{{\pi }^{2}}$. Таким образом, согласно (2.33) для любого $\beta \in (0,1]$ мажоранта $\mathfrak{M}({{v}_{1}},\tilde {n}{\kern 1pt} *,f,\varphi ,\beta )$ принимает вид
Принимая во внимание (3.1) и (3.2), для левой части неравенства (2.33) получаем выражение $524.95 - 150.06\beta $. Таким образом, это неравенство приобретает вид (для $\beta \in (0,1]$)
(3.6)
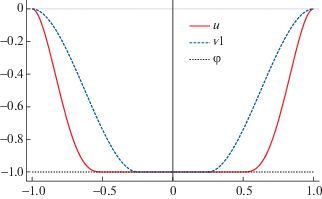
$524.95 - 150.06{\kern 1pt} \beta \leqslant 352.44 + 33.08{\kern 1pt} \beta + 189.22{\kern 1pt} \frac{1}{\beta }.$Далее мы рассмотрим серию приближенных решений (см. фиг. 4)
Фиг. 4.
Минимайзер $u$ и функции ${{v}_{\varepsilon }}$ с ${{\varepsilon }_{1}} = 0.35$, ${{\varepsilon }_{2}} = 0.15$ и ${{\varepsilon }_{3}} = 0$.

Аппроксимации $n_{\varepsilon }^{*}$ потока точного решения $p{\kern 1pt} *$ строится путем сглаживания второй производной функции ${{v}_{\varepsilon }}$ (которая заменяет $\nabla \nabla {{v}_{\varepsilon }}$) так, чтобы $(n_{\varepsilon }^{*}){\kern 1pt} '{\kern 1pt} ' \in {{L}^{2}}( - 1,1)$ (что соответствует условию $n_{\varepsilon }^{*} \in H({\text{div}}\,{\text{Div}},\Omega )$). В частности, если взять
В табл. 1 приведены результаты расчетов для слагаемых, входящих в состав $\mu ({{v}_{\varepsilon }})$, которые были вычислены для $\varepsilon = 0.05j$, $j = 7,5,3,1$ и $0$. Оба слагаемых (квадратичное и нелинейное) убывают при $\varepsilon \to 0$, однако первое остается положительным (поскольку последовательность приближенных решений не стремится к точному решению $u$), а второе стремится к нулю (потому что соответствующая последовательность приближенных коинцедентных множеств стремится к точному множеству ${{\Omega }_{\varphi }}$). Нетрудно видеть, что сумма этих двух слагаемых (которая составляет меру $\mu ({{v}_{\varepsilon }})$) в точности равна отклонению $J({{v}_{\varepsilon }})$ от точного минимума прямой вариационной задачи. В последнем столбце табл. 1 показан относительный вклад в ошибку нелинейной меры ${{\mu }_{\varphi }}({{v}_{\varepsilon }})$, который определяется формулой
Таблица 1.
Компоненты меры $\mu ({{v}_{\varepsilon }})$
| $\varepsilon $ | $\tfrac{1}{2}{{\left\| {\nabla \nabla (u - {{{v}}_{\varepsilon }})} \right\|}^{2}}$ | ${{\mu }_{\varphi }}({{{v}}_{\varepsilon }})$ | $J({{{v}}_{\varepsilon }}) - J(u)$ | $k({{{v}}_{\varepsilon }})\;[\% ]$ |
|---|---|---|---|---|
| 0.35 | 134.060 | 250.280 | 384.340 | 65.12 |
| 0.25 | 125.156 | 152.889 | 278.044 | 54.99 |
| 0.15 | 109.904 | 68.192 | 178.096 | 38.29 |
| 0.05 | 81.474 | 9.852 | 91.326 | 1.06 |
| 0.00 | 57.600 | 0 | 57.60 | 0 |
Табл. 2 содержит аналогичные данные, относящиеся к мере $\mu {\kern 1pt} *{\kern 1pt} (n_{\varepsilon }^{*})$. Как и в случае меры ${{\mu }_{\varphi }}({{v}_{\varepsilon }})$ и квадратичный и нелинейный члены убывают при $\varepsilon \to 0$. Однако здесь нелинейная мера не стремится к нулю. Эта мера контролирует нарушение уравнения $\operatorname{div} \operatorname{Div} n{\kern 1pt} * = f$ на множестве ${{\Omega }_{0}}$. Функция $n_{\varepsilon }^{*}$ не удовлетворяет этому уравнению ни при каком $\varepsilon $, поэтому $\mu {\kern 1pt} *{\kern 1pt} (n_{\varepsilon }^{*}) > 0$. Более того, в этом случае мера $\mu _{\varphi }^{*}(n_{\varepsilon }^{*})$ существенно превышает первое слагаемое, что видно по коэффициенту
Таблица 2.
Компоненты меры $\mu {\kern 1pt} *{\kern 1pt} (n_{\varepsilon }^{*})$
| $\varepsilon $ | $\tfrac{1}{2}{{\left\| {p{\kern 1pt} {\text{*}} - {{n}_{\varepsilon }}} \right\|}^{2}}$ | $\mu _{\varphi }^{ * }(n_{\varepsilon }^{ * })$ | $I{\kern 1pt} {\text{*}}(p{\kern 1pt} {\text{*}}) - I{\kern 1pt} {\text{*}}(n_{\varepsilon }^{ * })$ | $k(n_{\varepsilon }^{ * })\;[\% ]$ |
|---|---|---|---|---|
| 0.35 | 119.444 | 422.937 | 542.381 | 77.98 |
| 0.25 | 109.443 | 400.119 | 509.562 | 78.52 |
| 0.15 | 95.972 | 357.378 | 453.349 | 78.83 |
| 0.05 | 78.510 | 270.053 | 348.563 | 77.48 |
| 0.00 | 68.571 | 192 | 260.571 | 73.68 |
Табл. 3 иллюстрирует тождество (2.23). Первые две колонки соответствуют двум слагаемым, образующим правую часть (2.23). Здесь, через $\mathcal{N}({{v}_{\varepsilon }},n_{\varepsilon }^{*})$ обозначается член $\int_{ - 1}^1 \,(f - (n_{\varepsilon }^{*}){\kern 1pt} '{\kern 1pt} ')(\varphi - {{v}_{\varepsilon }})dx$ (который соответствует слагаемому $\int_\Omega \,(f - \operatorname{div} \operatorname{Div} n_{\varepsilon }^{*})(\varphi - {{v}_{\varepsilon }})dx$ в тождестве). Сумма этих слагаемых приведена в третьем столбце. Она в точности совпадает с суммой мер (которые приведены в табл. 1, 2). Отметим, что величины, стоящие в первых двух столбцах табл. 3, вычисляются непосредственно по функциям ${{v}_{\varepsilon }}$ и $n_{\varepsilon }^{*}$. Эти функции можно рассматривать, как приближенные решения, построенные при помощи какой-либо вычислительной процедуры. Таблица показывает, что сумма
Таблица 3.
Компоненты тождества (2.23), вычисленные для ${{v}_{\varepsilon }}$ и $n_{\varepsilon }^{*}$ при различных $\varepsilon $
| $\varepsilon $ | $\tfrac{1}{2}{{\left\| {\nabla \nabla {{{v}}_{\varepsilon }} - n_{\varepsilon }^{ * }} \right\|}^{2}}$ | $\mathcal{N}({{{v}}_{\varepsilon }},n_{\varepsilon }^{ * })$ | пр. часть (2.23) | $\mu ({{{v}}_{\varepsilon }}) + \mu {\kern 1pt} {\text{*}}(n_{\varepsilon }^{ * })$ |
|---|---|---|---|---|
| 0.35 | 10.049 | 916.672 | 926.721 | 926.721 |
| 0.25 | 14.629 | 772.978 | 787.606 | 787.606 |
| 0.15 | 22.472 | 608.973 | 631.445 | 631.445 |
| 0.05 | 37.094 | 402.796 | 439.890 | 439.890 |
| 0.00 | 49.371 | 268.800 | 318.171 | 318.171 |
3.2. Изгиб круглой пластины
Пусть $\Omega = {{B}_{3}} \subset {{\mathbb{R}}^{2}}$, где ${{B}_{3}}$ обозначает открытый шар с центром в начале координат и радиусом $3$. В этом случае задачу $\mathcal{P}$ можно рассматривать как упрощенный вариант задачи об изгибе упругой круглой пластины, жестко закрепленной по краям над плоским препятствием $\varphi \equiv - 1$ под действием внешней силы $f$. Упрощение заключается в том, что мы заменяем тензор упругих постоянных на единичный тензор, что в контексте рассматриваемых вопросов не играет существенной роли. Положим
Отметим, что для выбранных данных можно явно определить точное решение задачи. В полярных координатах $(r,\theta )$ минимайзер имеет следующий вид:
Очевидно, что ${{\Delta }^{2}}u = {{f}_{0}}$ в ${{B}_{3}}{\backslash }{{B}_{1}}$, $u \geqslant - 1$ в ${{B}_{3}}$ и $u(3,\theta ) = \tfrac{{\partial u}}{{\partial r}}(3,\theta ) = 0$ для всех $\theta \in [0,2\pi )$. Простые вычисления показывают, что
В качестве $v$ зададим функцию
После проведения непосредственных вычислений меры (2.18) мы получаем
(3.7)
$\mu ({{v}_{2}}) = \frac{1}{2}{{\left\| {\nabla \nabla (u - {{v}_{2}})} \right\|}^{2}} + {{\mu }_{\varphi }}({{v}_{2}}) = \frac{1}{2}{{\left\| {\nabla \nabla (u - {{v}_{2}})} \right\|}^{2}} \simeq 157.19.$Положим
Вычисляя меру ошибки $\mu {\kern 1pt} *(\hat {n}{\kern 1pt} *)$, определяемую выражениями (2.21) и (2.22), получаем
(3.8)
$\mu {\kern 1pt} *(\hat {n}{\kern 1pt} *{\kern 1pt} ) = \frac{1}{2}{{\left\| {p{\kern 1pt} {\text{*}} - \hat {n}{\kern 1pt} *} \right\|}^{2}} + \int\limits_{{{B}_{3}}{\backslash }{{B}_{1}}} {(f - \operatorname{div} \operatorname{Div} \hat {n}{\kern 1pt} *{\kern 1pt} )} {\kern 1pt} ( - 1 - u)rdrd\theta \simeq 14.84 + 63.46 \simeq 78.30.$(3.9)
$\mu ({{v}_{2}}) + \mu {\kern 1pt} *{\kern 1pt} (\hat {n}{\kern 1pt} *{\kern 1pt} ) \simeq 157.19 + 78.30 = 235.49.$При вычислении слагаемых в правой части тождества (2.23) мы используем только функции ${{v}_{2}}$ и $\hat {n}{\kern 1pt} *$ (известные аппроксимации точных решений). Сумма этих слагаемых дает такое же значение, как и (3.9):
Список литературы
Lions J.-L., Stampacchia G. Variational inequalities // Comm. Pure Appl. Math. 1967. V. 20. P. 493–519.
Lions J.-L. Quelques Méthodes de Résolution des Problèmes aux Limites Non Linéaires. Dunod; Gauthier-Villars, Paris, 1969.
Caffarelli L.A., Friedman A. The obstacle problem for the biharmonic operator // Ann. Scuola Norm. Sup. Pisa Cl. Sci. (2.1). 1979. V. 6. № 1. P. 151–184.
Frehse J. On the regularity of the solution of the biharmonic variational inequality // Manuscripta Math. 1973. V. 9. P. 91–103.
Landau L.D., Lifshitz E.M. Theory of Elasticity. Course of Theoretical Physics, Vol. 7. Translated by J. B. Sykes and W. H. Reid Pergamon Press, London-Paris-Frankfurt; Addison-Wesley Publishing Co., Inc., Reading, Mass., 1959.
Frehse J. Zum Differenzierbarkeitsproblem bei Variationsungleichungen höherer Ordnung // Abh. Math. Sem. Univ. Hamburg. 1971. V. 36. P. 140–149.
Cimatti G. The constrained elastic beam // Meccanica – J. Italian Assoc. Theoret. Appl. Mech. 1973. V. 8. P. 119–124.
Stampacchia G. Su una disequazione variazionale legata al comportamento elastoplastico delle travi appoggiate agli estremi // Boll. Un. Mat. Ital. (2.1). 1975. V. 11. № 3 suppl. P. 444–454.
Brézis H., Stampacchia G. Remarks on some fourth order variational inequalities // Ann. Scuola Norm. Sup. Pisa Cl. Sci. (2.1). 1977. V. 4. № 2. P. 363–371.
Duvaut G., Lions J.-L. Inequalities in Mechanics and Physics. Translated from the French by C.W. John, Grundlehren der Mathematischen Wissenschaften, 219 Springer-Verlag, Berlin-New York, 1976.
Rodrigues J.-F. Obstacle Problems in Mathematical Physics. North-Holland Mathematics Studies. V. 134. North-Holland Publishing Co., Amsterdam, 1987.
Caffarelli L.A., Friedman A., Torelli A. The two-obstacle problem for the biharmonic operator // Pacific J. Math. 1982. V. 103. № 2. P. 325–335.
Schild B. On the coincidence set in biharmonic variational inequalities with thin obstacles // Ann. Scuola Norm. Sup. Pisa Cl. Sci. (2.1). 1986. V. 13. № 4. P. 559–616.
Aleksanyan G. Regularity of the free boundary in the biharmonic obstacle problem // Calc. Var. Partial Differential Equations. 2019. V. 58. https://doi.org/10.1007/s00526-019-1638-5
Brenner S.C., Sung L.-Y., Zhang H., Zhang Y. A quadratic ${{C}^{0}}$ interior penalty method for the displacement obstacle problem of clamped Kirchhoff plates // SIAM J. Numer. Anal. 2012. V. 50. № 6. P. 3329–3350.
Glowinski R., Marini L.D., Vidrascu M. Finite-element approximations and iterative solutions of a fourth-order elliptic variational inequality // IMA J. Numer. Anal. 1984. V. 4. № 2. P. 127–167.
Glowinski R. Numerical Methods for Nonlinear Variational Problems. Springer Series in Computational Physics Springer-Verlag, New York, 1984.
Haslinger J., Hlaváček I., Nečas J. A unified approach to a posteriori error estimation using element residual methods // Handb. Numer. Anal., IV. 1996. P. 313–485.
Ito K., Kunisch K. An augmented Lagrangian technique for variational inequalities // Appl. Math. Optim. 1990. V. 21. № 3. P. 223–241.
Adams D.R., Hrynkiv V., Lenhart S. Optimal control of a biharmonic obstacle problem // Around the research of Vladimir Maz’ya. III. Int. Math. Ser. (N. Y.) 2010. V. 13. P. 1–24.
Ito K., Kunisch K. Optimal control of elliptic variational inequalities // Appl. Math. Optim. 2000. V. 41. № 3. P. 343–364.
Neittaanmäki P., Repin S.I. A posteriori error estimates for boundary-value problems related to the biharmonic operator // East-West J. Numer. Math. 2001. V. 9. № 2. P. 157–178.
Repin S.I. Estimates of deviations from exact solutions of elliptic variational inequalities // Зап. научн. сем. ПОМИ. 2000. V. 271. С. 188–203.
Repin S. A Posteriori Estimates for Partial Differential Equations. Radon Series on Computational and Applied Mathematics. V. 4. Walter de Gruyter GmbH & Co. KG, Berlin, 2008.
Repin S., Valdman J. Error identities for variational problems with obstacles // ZAMM Z. Angew. Math. Mech. 2018. V. 98. № 4. P. 635–658.
Apushkinskaya D.E., Repin S.I. Thin obstacle problem: estimates of the distance to the exact solution // Interfaces Free Bound. 2018. V. 20. № 4. P. 511–531.
Repin S.I. Two-sided estimates of deviation from exact solutions of uniformly elliptic equations // Proceedings of the St. Petersburg Mathematical Society, Vol. IX. Amer. Math. Soc. Transl. Ser. 2. 2003. V. 209. P. 143–171.
Neittaanmäki P., Repin S. Reliable Methods for Computer Simulation. Studies in Mathematics and its Applications. V. 33. Elsevier Science B.V., Amsterdam, 2004.
Ekeland I., Temam R. Convex Analysis and Variational Problems. North-Holland Publishing Co., Amsterdam-Oxford; American Elsevier Publishing Co., Inc., New York, 1976.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики