Журнал вычислительной математики и математической физики, 2020, T. 60, № 2, стр. 171-176

Декомпозиционная реализация схемы горнера для вычисления значений многомерных многочленов

А. П. Афанасьев^1, *, С. М. Дзюба^2, **

¹ ИППИ РАН
127994 Москва, Большой Каретный пер., 19, стр. 1, Россия

² ТвГТУ
170026 Тверь, наб. Афанасия Никитина, 22, Россия

^* E-mail: apa@iitp.ru
^** E-mail: sdzyuba@mail.ru

Поступила в редакцию 26.06.2017
После доработки 02.09.2019
Принята к публикации 17.10.2019

DOI: 10.31857/S0044466920020027

Полный текст (PDF)

Аннотация

Приведена декомпозиционная реализация схемы Горнера для вычисления значений многомерных многочленов, сводящая задачу к вычислению по схеме Горнера последовательности значений одномерных многочленов. Изучена возможность использования этой схемы в распределенной компьютерной среде. В качестве примера работы схемы рассмотрена проблема построения приближенных аналитических решений дифференциальных уравнений с полиномиальной правой частью. Библ. 11. Фиг. 1. Табл. 1.

Ключевые слова: многомерные многочлены, схема Горнера, декомпозиция вычислительного процесса, дифференциальные уравнения с полиномиальной правой частью.

1. ВВЕДЕНИЕ

Рассмотрим многомерный многочлен

(1.1)

${{p}_{n}}({\mathbf{x}}) = \sum\limits_{{{i}_{1}} = 0}^N \, \ldots \sum\limits_{{{i}_{n}} = 0}^N \,{{a}_{{{{i}_{1}} \ldots {{i}_{n}}}}}x_{1}^{{{{i}_{1}}}} \ldots x_{n}^{{{{i}_{n}}}},$

где ${\mathbf{x}} = ({{x}_{1}}, \ldots ,{{x}_{n}})$ есть $n$-мерный действительный вектор, ${{a}_{{{{i}_{1}} \ldots {{i}_{n}}}}}$ – постоянные действительные коэффициенты многочлена и $N$ – некоторое натуральное число, представляющее собой максимальную степень, которая достигается по крайней мере по одному из переменных ${{x}_{1}}, \ldots ,{{x}_{n}}$.

Проблема вычисления значений многочлена (1.1) достаточно актуальна. Этими многочленами описываются различные математические объекты такие, как правые части обыкновенных дифференциальных уравнений, ограничения задач нелинейного программирования, начальные и граничные условия задач математической физики и многие другие (см., например, [1]–[4]).

Хорошо известно, что вычисление значений многочленов вида (1.1) одного переменного удобно осуществлять с помощью схемы Горнера, позволяющей во многих случаях уменьшить верхнюю оценку ошибки вычислений (см., например, [1], [5]–[7]). Что касается многомерных многочленов, то на сегодняшний день известны несколько вычислительных алгоритмов, реализующих различные обобщения схемы Горнера (см., например, [1], [8]–[11]). Здесь помимо преимуществ одномерной схемы появляется возможность декомпозиции вычислительного процесса. Так, например, в работе [9] показано, что при наличии $O(N)$ процессоров вычислительный процесс может быть декомпозирован на $O(lo{{g}_{2}}(N)lo{{g}_{2}}(n))$ шагов параллельных вычислений.

В работах [10], [11] приведена и подробно изучена еще одна из возможных реализаций схемы Горнера. В этих работах схема Горнера сводится к преобразованию исходного многочлена и его представления в виде комбинации мономов. Однако результаты этих работ не учитывают и не используют тот факт, что одномерная схема Горнера хорошо изучена; в частности, в настоящее время существуют весьма эффективные программы для вычисления значений одномерных многочленов. Более того, в [10], [11] не рассматривается вопрос о распараллеливании и декомпозиции вычислительного процесса.

Целью настоящей работы является построение декомпозиционной реализации схемы Горнера для вычисления значений многомерных многочленов (1.1). Особое внимание будет уделено описанию соответствующего алгоритма, ориентированного на сведение вычислительного процесса к последовательно-параллельному вычислению значений одномерных многочленов.

2. ДЕКОМПОЗИЦИОННАЯ РЕАЛИЗАЦИЯ СХЕМЫ ГОРНЕРА

Схема Горнера для одномерных многочленов хорошо известна и изучается во многих работах (см., например, [5]). Суть ее состоит в следующем.

Рассмотрим действительный одномерный многочлен

(2.1)

${{p}_{1}}(x) = \sum\limits_{i = 0}^N \,{{a}_{i}}{{x}^{i}},$

где ${{a}_{i}}$ – некоторые действительные числа и $x$ – действительное переменное. Согласно [5] схема Горнера для многочлена (2.1) имеет следующий вид:

(2.2)

${{p}_{1}}(x) = (( \ldots (({{a}_{N}}x + {{a}_{{N - 1}}})x + {{a}_{{N - 2}}})x + \ldots + {{a}_{2}})x + {{a}_{1}})x + {{a}_{0}}.$

Рассмотрим обобщение схемы Горнера для многочлена (1.1). При ${{i}_{1}} = 0, \ldots ,N$ определим функции $({{x}_{2}}, \ldots ,{{x}_{n}}) \to {{\alpha }_{{{{i}_{1}}}}}({{x}_{2}}, \ldots ,{{x}_{n}})$. Для этого положим

(2.3)

${{\alpha }_{{{{i}_{1}}}}}({{x}_{2}}, \ldots ,{{x}_{n}}) = \sum\limits_{{{i}_{2}} = 0}^N \, \ldots \sum\limits_{{{i}_{n}} = 0}^N \,{{a}_{{{{i}_{1}}{{i}_{2}} \ldots {{i}_{n}}}}}x_{2}^{{{{i}_{2}}}} \ldots x_{n}^{{{{i}_{n}}}},\quad {{i}_{1}} = 0, \ldots ,N.$

Тогда имеем

(2.4)

$\begin{gathered} {{p}_{n}}({\mathbf{x}}) = (( \ldots (({{\alpha }_{N}}({{x}_{2}}, \ldots ,{{x}_{n}}){{x}_{1}} + {{\alpha }_{{N - 1}}}({{x}_{2}}, \ldots ,{{x}_{n}})){{x}_{1}} + {{\alpha }_{{N - 2}}}({{x}_{2}}, \ldots ,{{x}_{n}})){{x}_{1}} + \ldots + {{\alpha }_{2}}({{x}_{2}}, \ldots ,{{x}_{n}})){{x}_{1}} + \\ \, + {{\alpha }_{1}}({{x}_{2}}, \ldots ,{{x}_{n}})){{x}_{1}} + {{\alpha }_{0}}({{x}_{2}}, \ldots ,{{x}_{n}}). \\ \end{gathered} $

Каждая функция $({{x}_{2}}, \ldots ,{{x}_{n}}) \to {{\alpha }_{{{{i}_{1}}}}}({{x}_{2}}, \ldots ,{{x}_{n}})$, задаваемая равенством (2.3), является многомерным многочленом переменных ${{x}_{2}}, \ldots ,{{x}_{n}}$. Для вычисления значений этих многочленов при ${{i}_{1}},\;{{i}_{2}} = 0, \ldots ,N$ определим функции $({{x}_{3}}, \ldots ,{{x}_{n}}) \to {{\alpha }_{{{{i}_{1}}{{i}_{2}}}}}({{x}_{3}}, \ldots ,{{x}_{n}})$. Для этого положим

${{\alpha }_{{{{i}_{1}}{{i}_{2}}}}}({{x}_{3}}, \ldots ,{{x}_{n}}) = \sum\limits_{{{i}_{3}} = 0}^N \, \ldots \sum\limits_{{{i}_{n}} = 0}^N \,{{a}_{{{{i}_{1}}{{i}_{2}}{{i}_{3}} \ldots {{i}_{n}}}}}x_{3}^{{{{i}_{3}}}} \ldots x_{n}^{{{{i}_{n}}}},\quad {{i}_{1}},{{i}_{2}} = 0, \ldots ,N.$

Тогда имеем

$\begin{gathered} {{\alpha }_{{{{i}_{1}}}}}({{x}_{2}}, \ldots ,{{x}_{n}}) = (( \ldots (({{\alpha }_{{{{i}_{1}}N}}}({{x}_{3}}, \ldots ,{{x}_{n}}){{x}_{2}} + {{\alpha }_{{{{i}_{1}},N - 1}}}({{x}_{3}}, \ldots ,{{x}_{n}})){{x}_{2}} + \\ + \;{{\alpha }_{{{{i}_{1}},N - 2}}}({{x}_{3}}, \ldots ,{{x}_{n}})){{x}_{2}} + \ldots + {{\alpha }_{{{{i}_{1}}2}}}({{x}_{3}}, \ldots ,{{x}_{n}})){{x}_{2}} + {{\alpha }_{{{{i}_{1}}1}}}({{x}_{3}}, \ldots ,{{x}_{n}})){{x}_{2}} + {{\alpha }_{{{{i}_{1}}0}}}({{x}_{3}}, \ldots ,{{x}_{n}}), \\ {{i}_{1}} = 0, \ldots ,N. \\ \end{gathered} $

Действуя аналогичным образом, для произвольного значения $k = 1, \ldots ,n - 1$ положим

${{\alpha }_{{{{i}_{1}} \ldots {{i}_{k}}}}}({{x}_{{k + 1}}}, \ldots ,{{x}_{n}}) = \sum\limits_{{{i}_{{k + 1}}} = 0}^N \, \ldots \sum\limits_{{{i}_{n}} = 0}^N \,{{a}_{{{{i}_{1}} \ldots {{i}_{k}}{{i}_{{k + 1}}} \ldots {{i}_{n}}}}}x_{{k + 1}}^{{{{i}_{{k + 1}}}}} \ldots x_{n}^{{{{i}_{n}}}},\quad {{i}_{1}}, \ldots ,{{i}_{k}} = 0, \ldots ,N.$

Тогда несложно заметить, что для определения функций $({{x}_{k}}, \ldots ,{{x}_{n}}) \to {{\alpha }_{{{{i}_{1}} \ldots {{i}_{{k - 1}}}}}}({{x}_{k}}, \ldots ,{{x}_{n}})$ при ${{i}_{1}}, \ldots ,{{i}_{{k - 1}}} = 0, \ldots ,N$ справедливо рекуррентное соотношение

(2.5)

$\begin{gathered} {{\alpha }_{{{{i}_{1}} \ldots {{i}_{{k - 1}}}}}}({{x}_{k}}, \ldots ,{{x}_{n}}) = (( \ldots (({{\alpha }_{{{{i}_{1}} \ldots {{i}_{{k - 1}}}N}}}({{x}_{{k + 1}}}, \ldots ,{{x}_{n}}){{x}_{k}} + {{\alpha }_{{{{i}_{1}} \ldots {{i}_{{k - 1}}},N - 1}}}({{x}_{{k + 1}}}, \ldots ,{{x}_{n}})){{x}_{k}} + \\ + \;{{\alpha }_{{{{i}_{1}} \ldots {{i}_{{k - 1}}},N - 2}}}({{x}_{{k + 1}}}, \ldots ,{{x}_{n}})){{x}_{k}} + \ldots + {{\alpha }_{{{{i}_{1}} \ldots {{i}_{{k - 1}}}2}}}({{x}_{{k + 1}}}, \ldots ,{{x}_{n}})){{x}_{k}}{{\alpha }_{{{{i}_{1}} \ldots {{i}_{{k - 1}}}1}}}({{x}_{{k + 1}}}, \ldots ,{{x}_{n}})){{x}_{k}} + \\ \, + {{\alpha }_{{{{i}_{1}} \ldots {{i}_{{k - 1}}}0}}}({{x}_{3}}, \ldots ,{{x}_{n}}),\quad {{i}_{1}}, \ldots ,{{i}_{{k - 1}}} = 0, \ldots ,N. \\ \end{gathered} $

При этом

(2.6)

$\begin{gathered} {{\alpha }_{{{{i}_{1}} \ldots {{i}_{{n - 1}}}}}}({{x}_{n}}) = \sum\limits_{{{i}_{n}} = 0}^N \,{{a}_{{{{i}_{1}} \ldots {{i}_{n}}}}}x_{n}^{{{{i}_{n}}}} = (( \ldots (({{a}_{{{{i}_{1}} \ldots {{i}_{{n - 1}}}N}}}{{x}_{n}} + {{a}_{{{{i}_{1}} \ldots {{i}_{{n - 1}}},N - 1}}}){{x}_{n}} + {{a}_{{{{i}_{1}} \ldots {{i}_{{n - 1}}},N - 2}}}){{x}_{n}} + \ldots + {{a}_{{{{i}_{1}} \ldots {{i}_{{n - 1}}}2}}}){{x}_{n}} + \\ \, + {{a}_{{{{i}_{1}} \ldots {{i}_{{n - 1}}}1}}}){{x}_{n}} + {{\alpha }_{{{{i}_{1}} \ldots {{i}_{{n - 1}}}0}}},\quad {{i}_{1}}, \ldots ,{{i}_{{n - 1}}} = 0, \ldots ,N. \\ \end{gathered} $

Таким образом, имеем соотношения (2.4)–(2.6), определяющие обобщенную схему Горнера для вычисления значений многочлена (1.1).

Обобщенная схема Горнера во многих случаях позволяет упростить вычисления. Прямым подсчетом устанавливается, что вычисление значений многочлена (1.1) по схеме (2.4)–(2.6) эквивалентно вычислению значений

$\mathcal{N} = \sum\limits_{i = 0}^{n - 1} \,{{(N + 1)}^{i}}$

одномерных многочленов. Более того, число умножений по обобщенной схеме Горнера равно

$H(N,n) = {{(N + 1)}^{n}} - 1.$

Число же умножений по “тривиальному” алгоритму (т.е. алгоритму прямого вычисления по формуле (1.1) при условии, что величина ${{y}^{k}}$ вычисляется как ${{y}^{k}} = y{{y}^{{k - 1}}}$) равно

$T(N,n) = n{{(N + 1)}^{n}} + nN.$

Уже только это говорит о том, что чем больше значения $n$ и $N$, тем эффективнеe становится использование обобщенной схемы Горнера.

Процесс вычисления значений многочлена (1.1) по предложенной выше схеме сводится к процессу вычисления значений одномерных многочленов. Вычисление же значений одномерных многочленов по схеме Горнера в настоящее время реализовано на самом высоком уровне (см., например, [1], [5]–[7]).

3. АЛГОРИТМ

Для реализации описанной выше обобщенной схемы Горнера будем использовать следующий алгоритм, состоящий из $n$ шагов и ориентированный на декомпозицию вычислительного процесса.

Шаг 1. Здесь осуществляется вычисление значений функций ${{x}_{n}} \to {{\alpha }_{{{{i}_{1}} \ldots {{i}_{{n - 1}}}}}}({{x}_{n}})$ по формуле (2.6). Каждая из этих функций, очевидно, может строиться независимо. Поэтому процесс построения может быть естественным образом декомпозирован на параллельное вычисление значений всех этих функций.

Шаги $2, \ldots ,n - 1.$ На данных шагах для $k = n - 1, \ldots ,2$ по формуле (2.5) вычисляются значения функций $({{x}_{k}}, \ldots ,{{x}_{n}}) \to {{\alpha }_{{{{i}_{1}} \ldots {{i}_{{k - 1}}}}}}({{x}_{k}}, \ldots ,{{x}_{n}}).$ Как и на шаге 1, каждая из этих функций может строиться независимо, т.е. здесь процесс построения в общем случае также может быть естественным образом декомпозирован на параллельное вычисление значений всех этих функций.

Шаг $n.$ Данный шаг наиболее простой: на нем по формуле (2.4) вычисляются значения функции ${\mathbf{x}} \to {{p}_{n}}({\mathbf{x}}).$

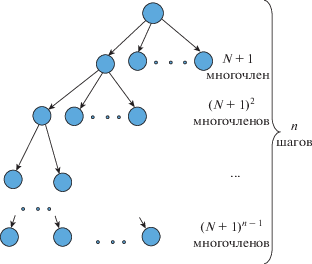
Условная схема организации работы описанного выше алгоритма приведена на фиг. 1. Как видно из фиг. 1, при наличии ${{(N + 1)}^{{n - 1}}}$ процессоров значения всех одномерных многочленов на каждом шаге алгоритма могут быть вычислены параллельно. Следовательно, вычисление значений многочлена (1.1) эквивалентно вычислению значений $n$ одномерных многочленов.

Фиг. 1.

Условная схема работы алгоритма.

В общем случае значение ${{(N + 1)}^{{n - 1}}}$ может быть достаточно велико. Поэтому наиболее эффективно представленный алгоритм может быть реализован в распределенной компьютерной среде с большим числом независимых узлов.

4. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С ПОЛИНОМИАЛЬНОЙ ПРАВОЙ ЧАСТЬЮ

В качестве одного из важнейших примеров использования обобщенной схемы Горнера обратимся к проблеме построения приближенных аналитических решений дифференциальных уравнений с полиномиальной правой частью.

Рассмотрим систему обыкновенных дифференциальных уравнений, векторная запись которой имеет вид

(4.1)

${\mathbf{\dot {x}}} = {{{\mathbf{p}}}_{n}}({\mathbf{x}}),$

где ${\mathbf{x}}(t) = ({{x}_{1}}(t), \ldots ,{{x}_{n}}(t))$ – действительная векторная функция действительного переменного $t$, а ${{{\mathbf{p}}}_{n}} = ({{p}_{1}}, \ldots ,{{p}_{n}})$ – действительная векторная функция, каждый элемент которой ${{p}_{i}}$ является многомерным многочленом переменных ${{x}_{1}}, \ldots ,{{x}_{n}}$.

Для построения решения ${\mathbf{x}} = \xi (t)$ системы (4.1) с начальным условием

$\xi (0) = {{\xi }_{0}}$

удобно учитывать специальный вид правой части данной системы (см., например, [1]–[4]). Наиболее простым и естественным является метод построения приближенного аналитического решения с использованием его разложения в ряд Тейлора (см., например, [1], [2]). В этом случае имеем

$\xi (t) = {{\xi }_{0}} + \sum\limits_{i = 1}^l \,{{\psi }_{i}}({{\xi }_{0}}){{t}^{i}} + o({\text{|}}t{{{\text{|}}}^{l}}),$

где ${{\psi }_{i}}({{\xi }_{0}})$ – соответствующие векторные многомерные многочлены компонент вектора ${{\xi }_{0}}$ (см., например, [1], [2]). Другими словами, с некоторой заданной точностью, определяющей количество слагаемых $l$, решение ${\mathbf{x}} = \xi (t)$ можно аппроксимировать приближенным равенством

(4.2)

$\xi (t) \approx {{\xi }_{0}} + \sum\limits_{i = 1}^l \,{{\psi }_{i}}({{\xi }_{0}}){{t}^{i}}.$

Соотношение (4.2) дает приближение к решению $\xi (t)$ в виде времени $t$ и векторного многомерного многочлена вектора ${{\xi }_{0}}$. Однако, как известно, радиус сходимости ряда

$\sum\limits_{i = 1}^l \,{{\psi }_{i}}({{\xi }_{0}}){{t}^{i}}$

во многих случаях достаточно мал. Поэтому оценки значений функции $\xi (t)$ будем строить по формуле

(4.3)

${{\xi }_{{j + 1}}} = {{\xi }_{j}} + \sum\limits_{i = 1}^l \,{{\psi }_{i}}({{\xi }_{j}}){{h}^{i}},\quad j = 0, \ldots ,J,$

где $h$ – шаг по $t$.

Для вычисления значений каждого из многочленов ${{\psi }_{i}}$ в формуле (4.3) нами использовалась обобщенная схема Горнера, как с декомпозицией вычислительного процесса, так и без декомпозиции. Вычислительные эксперименты, проведенные на типовых уравнениях (уравнение Ван-дер-Поля, система Лоренца и др.), показали, что использование декомпозиции в сочетании с обобщенной схемой Горнера позволяет при сохранении точности сократить время расчетов в несколько раз.

Для иллюстрации сказанного обратимся к проблеме построения решений системы Лоренца

(4.4)

$\dot {x} = \sigma (y - x),\quad \dot {y} = rx - y - xz,\quad \dot {z} = xy - bz,$

при классических значениях параметров данной системы:

$\sigma = 10,\quad r = 28,\quad b = 8{\text{/}}3.$

Для начального условия

$x(0) = 1,\quad y(0) = 1,\quad z(0) = 1$

вычисления проводились для $J = 1000$ с шагом $h = 0.01$ на кластере параллельных вычислений (4 процессора). В ходе вычислительного эксперимента осуществлялась эмуляция мантиссы в сто десятичных знаков (использовалась библиотека MPFR (https://en.wikipedia.org/wiki/GNU_MPFR)). Данные о времени вычислительного процесса сведены в табл. 1.

Таблица 1

Число членов разложения $l$	Декомпозиция	Время вычисл.
$30$	Да	2.401 с
$30$	Нет	4.541 с
$40$	Да	5.589 с
$40$	Нет	14.802 с

Система (4.3) является системой с полилинейной правой частью; поэтому для нее максимальная степень многочлена ${{\psi }_{i}}$ равна $i$ (см., например, [1]). Несложный анализ табл. 1 показывает, что использование декомпозиционной реализации обобщенной схемы Горнера даже в простейшем случае сокращает время вычислений. Разница во времени начинает увеличиваться уже при переходе с $l = 30$ до $l = 40$.

5. ОБСУЖДЕНИЕ

Отличительной особенностью описанной в настоящей работе обобщенной схемы Горнера является очевидная возможность декомпозиции вычислительного процесса. При этом сама обобщенная схема Горнера (даже без декомпозиции вычислительного процесса) во многих случаях позволяет уменьшить верхнюю оценку ошибки по сравнению с прямым вычислением многочлена.

Алгоритм, реализующий эту схему, сводится к последовательно-параллельному вычислению значений одномерных многочленов. Отличительная особенность такой реализации состоит в том, что здесь возможна очевидная декомпозиция вычислительного процесса, которая может быть осуществлена в распределенной компьютерной среде.

Список литературы

Афанасьев А.П. Продолжение траекторий в оптимальном управлении. Труды ИСА РАН. М.: КомКнига, 2006.
Афанасьев А.П., Тарасов А.С. Квазианалитическое решение систем дифференциальных уравнений с полиномиальными правыми частями // Сб. трудов ИСА РАН “Пробл. вычисл. в распределенной среде: распределенные приложения, коммуникационные системы, матем. модели и оптимизация”. Т. 25. С. 165–183. М.: КомКнига, 2006.
Афанасьев А.П., Дзюба С.М. Метод построения приближенных аналитических решений систем обыкновенных дифференциальных уравнений с полиномиальной правой частью // Ж. вычисл. матем. и матем. физ. 2015. Т. 55. № 10. С. 1694–1702.
Афанасьев А.П., Дзюба С.М. Построение минимальных множеств дифференциальных уравнений с полиномиальной правой частью // Дифференц. ур-ния. 2015. Т. 51. № 11. С. 1411–1419.
Мак-Кракен Д., Дорн У. Численные методы и программирование на ФОРТРАНЕ. М.: Мир, 1977.
Левитин А.В. Схема Горнера и возведение в степень // Алгоритмы. Введение в разработку и анализ. С. 284–291. М.: Вильямс, 2006.
Cormen T.H., Leiserson C.E., Rivest R.L., Stein C. Introduction to the algorithms. New York: MIT Press and McGraw-Hill, 2009.
Диканев Т.В. Вычисление полинома от нескольких переменных // http://www.tvd-home.ru/numerical/polynom
Dowling M.L. A fast parallel Horner algorithm // SIAM J. Comp. 1990. Vol. 19. No. 1. P. 133–142.
Peña J.M., Sauer T. On the multivariate Horner scheme // SIAM J. Numer Anal. 2000. Vol. 37. No. 4. P. 1186–1197.
Peña J.M., Sauer T. On the multivariate Horner scheme II: Running Error Analysis // Computing (Vienna/New York). 2000. Vol. 65. P. 313–322.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал