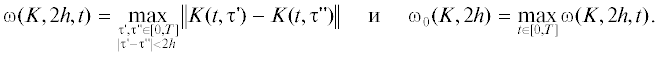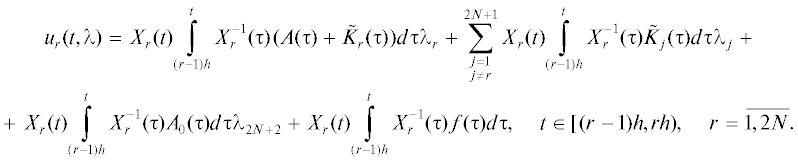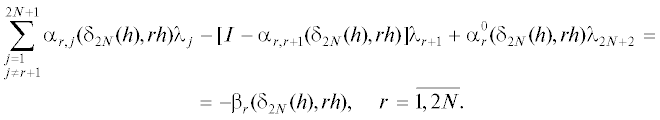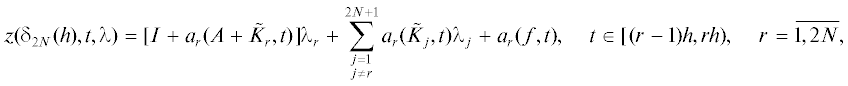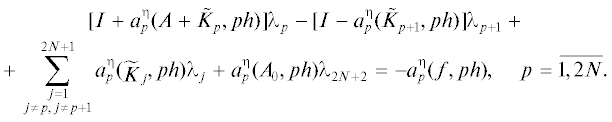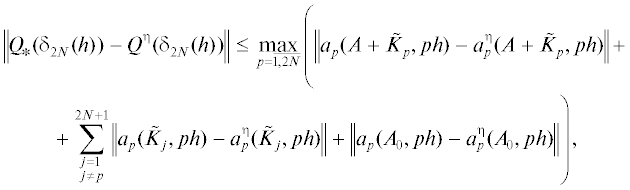Журнал вычислительной математики и математической физики, 2020, T. 60, № 2, стр. 197-215

1. ВВЕДЕНИЕ

Задачи управления, называемые краевыми задачами с параметрами, а также задачами идентификации параметров для систем обыкновенных дифференциальных и интегродифференциальных уравнений с параметрами, активно исследуются в работах многих авторов [1]–[6]. Для решения этих классов задач они использовали методы из качественной теории дифференциальных уравнений, вариационного исчисления и теории оптимизации, метод верхних и нижних решений и т.д.

Несмотря на это, вопросы нахождения эффективных критериев однозначной разрешимости и построения численных алгоритмов нахождения оптимальных решений задач управления для систем обыкновенных дифференциальных и интегродифференциальных уравнений с параметрами все еще остается открытым.

В настоящей работе мы предлагаем численно-приближенный метод решения исследуемой задачи управления и проверяем сходимость, устойчивость и точность предлагаемого метода.

Рассмотрим задачу управления для интегродифференциального уравнения с параметром

Здесь $(n \times n)$-матрицы $A(t)$ и $K(t,\tau )$ непрерывны на $[0,T]$ и $[0,T] \times [0,T]$ соответственно; $(n \times l)$-матрица ${{A}_{0}}(t)$ непрерывна на $[0,T]$, $n$ вектор-функция $f(t)$ непрерывна на $[0,T]$; $\left\| x \right\| = \mathop {max}\limits_{i = \overline {1,n} } \left| {{{x}_{i}}} \right|$.

Пусть $C([0,T],{{R}^{n}})$ обозначает пространство непрерывных функций $x:[0,T] \to {{R}^{n}}$ с нормой ${{\left\| x \right\|}_{1}} = \mathop {max}\limits_{t \in [0,T]} \left\| {x(t)} \right\|.$

Решением задачи управления (1.1), (1.2) является пара $(x{\text{*}}(t),\mu {\text{*}}),$ где функция $x{\text{*}}(t) \in C([0,T],{{R}^{n}})$ непрерывно дифференцируема на $(0,T)$, а параметр $\mu {\text{*}} \in {{R}^{l}}$, удовлетворяет интегродифференциальному уравнению (1.1) и граничному условию (1.2).

В [7]–[11] была рассмотрена следующая задача:

На основе метода параметризации [12] критерии разрешимости и однозначной разрешимости (1.1)', (1.2)' установлены в [7]–[10]. Алгоритмы методa параметризации для решения этой проблемы предложены в [9]–[11].

Мы распространяем методы и результаты из [11] на задачу управления (1.1), (1.2). Интервал $[0,T]$ делится на $2N$ частей с шагом $h > 0:2Nh = T.$ Уравнение (1.1) заменяется нагруженным дифференциальным уравнением (см. [7]–[11], [13]–[16]), и задача (1.1), (1.2) аппроксимируется задачей с параметром для нагруженного дифференциального уравнения. Результаты из [13] и непрерывность ядра $K(t,\tau )$ на $[0,T] \times [0,T]$ дают равномерную сходимость решений аппроксимирующей задачи к решению задачи (1.1), (1.2) на $[0,T]$ при $h \to 0$.

Показано, что сходимость относительно $h$ имеет четвертый порядок, если данные задачи (1.1), (1.2) достаточно гладкие. Для аппроксимирующей задачи управления составлена система линейных алгебраических уравнений относительно произвольных векторов нового общего решения [11]. Доказано, что число обусловленности этой системы возрастает линейно относительно $2N$, если аппроксимирующая задача управления корректно разрешима. Это свойство системы обеспечивает ее стабильную разрешимость. Задачи Коши для обыкновенных дифференциальных уравнений на подынтервалах являются основными вспомогательными задачами в предлагаемых методах. Если мы выберем приближенный метод для решения этих задач, то мы получаем приближенный метод решения задачи управления (1.1), (1.2). Численные методы, используемые для решения задач Коши, дают численные методы решения задачи (1.1), (1.2).

2. АППРОКСИМАЦИЯ ЗАДАЧИ УПРАВЛЕНИЯ (1.1), (1.2) ЗАДАЧЕЙ УПРАВЛЕНИЯ ДЛЯ СПЕЦИАЛЬНЫХ НАГРУЖЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПАРАМЕТРОМ

Aппроксимируем задачу управления для интегродифференциальных уравнений (1.1), (1.2) задачей управления для нагруженных дифференциальных уравнений.

Определение 2.1. Задача управления (1.1), (1.2) называется корректно разрешимой, если для произвольной пары $(f(t),d)$ с $f(t) \in C([0,T],{{R}^{n}})$ и $d \in {{R}^{{n + l}}}$ она имеет единственное решение $(x{\text{*}}(t),\mu {\text{*}})$, и выполняется неравенство

где $\gamma $ – константа, не зависящая от $f(t)$ и $d$.

Число $\gamma $ называется константой корректной разрешимости задачи управления (1.1), (1.2).

Положим $\alpha = \mathop {max}\limits_{t \in [0,T]} \left\| {A(t)} \right\|$, $\beta = \mathop {max}\limits_{(t,\tau ) \in [0,T] \times [0,T]} \left\| {K(t,\tau )} \right\|$ и ${{\alpha }_{0}} = \mathop {max}\limits_{t \in [0,T]} \left\| {{{A}_{0}}(t)} \right\|$.

Далее берем $h > 0:$ $2Nh = T$ и вводим обозначения:

${{\tilde {K}}_{j}}(t) = \tfrac{{4h}}{3}K(t,(j - 1)h)$ для четных $j$ и

${{\tilde {K}}_{j}}(t) = \tfrac{{2h}}{3}K(t,(j - 1)h)$ для нечетных $j,$ где $j = 2,3,...,2N,$

${{\tilde {K}}_{1}}(t) = \tfrac{h}{3}K(t,0),$ ${{\tilde {K}}_{{2N + 1}}}(t) = \tfrac{h}{3}K(t,T).$

Пусть

Тогда аппроксимирующую задачу с параметром можно записать в виде:

Решением задачи управления (2.1), (2.2) является пара $(z{\text{*}}(t),v{\text{*}})$, где функция $z{\text{*}}(t) \in C([0,T],{{R}^{n}})$ непрерывно дифференцируема на $(0,T)$, а параметр $v{\text{*}} \in {{R}^{l}}$, удовлетворяет нагруженному уравнению (2.1) и граничному условию (2.2).

Определение 2.2. Задача управления (2.1), (2.2) называется корректно разрешимой, если для произвольной пары $(f(t),d)$ с $f(t) \in C([0,T],{{R}^{n}})$ и $d \in {{R}^{{n + l}}},$ она имеет единственное решение $(z{\text{*}}(t),v{\text{*}})$, и выполняется неравенство

где $\chi $ – константа, не зависящая от $f(t)$ и $d$.

Число $\chi $ называется константой корректной разрешимости задачи управления (2.1), (2.2).

Следующие два утверждения устанавливают взаимосвязь между исходной задачей управления для интегродифференциального уравнения с параметром (1.1), (1.2) и аппроксимирующей задачей управления для нагруженного дифференциального уравнения с параметром (2.1), (2.2).

Теорема 2.1. Пусть задача управления (1.1), (1.2) корректно разрешима с константой $\gamma $ и справедливо неравенство

Тогда задача (2.1), (2.2) корректно разрешима с константойигде $(z{\text{*}}(t),v{\text{*}})$ и $(x{\text{*}}(t),\mu {\text{*}})$ – решения задач (2.1), (2.2) и (1.1), (1.2) соответственно.

Доказательство. Найдем решение задачи управления (2.1), (2.2), применяя метод последовательных приближений. Положим ${{z}^{{(0)}}}(t) = x{\text{*}}(t)$, ${{v}^{{(0)}}} = \mu {\text{*}}$ и найдем последующие приближения ${{z}^{{(k)}}}(t)$, ${{v}^{{(k)}}}$, $k = 1,2,...,$ решая задачи управления для интегродифференциального уравнения с параметром

где

Отметим, что представление функции $F({{z}^{{(k - 1)}}},t)$ получено из

после специального преобразования, в силу следующего соотношения:

По предположению, задача управления (1.1), (1.2) имеет единственное решение для произвольной пары $(f(t),d)$ с $f(t) \in C([0,T],{{R}^{n}})$ и $d \in {{R}^{{n + l}}}$. Очевидно, что для ${{z}^{{(k - 1)}}}(t) \in C([0,T],{{R}^{n}})$, ${{v}^{{(k - 1)}}} \in {{R}^{{n + l}}}$, функция $F({{z}^{{(k - 1)}}},t)$ также принадлежит $C([0,T],{{R}^{n}})$.

Поэтому для произвольных $k = 1,2,...$ существует единственное решение ${{y}^{{(k)}}}(t)$ задачи (2.5), (2.6).

Пусть

Очевидно, что для любого $k = 1,2,...$ пара $({{\Delta }^{{(k)}}}(t),{{\Theta }^{{(k)}}})$ является единственным решением задачи с параметром Следовательно, принимая во внимание корректную разрешимость задачи управления (1.1), (1.2) с константой $\gamma ,$ из (2.6), (2.7) имеем Используем обозначения для разностей первой суммы (2.9) и применяем общеизвестную теорему о среднем значении для разностей второй суммы (2.9). После непосредственных вычислений мы получим следующие оценки: Тогда уравнение (2.7) дает Из (2.10) и (2.11) получаем

Так как согласно (2.3), ${{q}_{1}}(h,\gamma ,{{\omega }_{0}}) < 1$, оценки (2.12) обеспечивают равномерную сходимость последовательности $\{ {{\dot {z}}^{{(k)}}}(t)\} $, $k = 1,2,...$, на $(0,T)$ при $k \to \infty $ к функции $y(t)$, непрерывной на $(0,T)$.

Последовательность $\{ {{z}^{{(k)}}}(t)\} $, $k = 1,2,...$, равномерно сходится на $[0,T]$ при $k \to \infty $ к функции $z{\text{*}}(t)$, непрерывной на $[0,T]$ и непрерывно дифференцируемой на $(0,T)$, и последовательность $\{ {{v}^{{(k)}}}\} $, $k = 1,2,...$, сходится при $k \to \infty $ к ${{v}^{{\text{(}}}}{{{\text{*}}}^{{\text{)}}}} \in {{R}^{l}}$. Более того, $\dot {z}{\text{*}}(t) = y(t)$.

Очевидно, что пара $(z{\text{*}}(t),v{\text{*}})$ удовлетворяет граничному условию (2.2). Покажем, что эта пара также удовлетворяет нагруженному дифференциальному уравнению с параметром (2.1). Для $k = 1,2,...$ пара $({{z}^{{(k)}}}(t),{{v}^{{(k)}}})$ является единственным решением задачи (2.5), (2.6), и

Переходя в (2.13) к пределу при $k \to \infty $ и учитывая соотношение получаем Итак, пара $(z{\text{*}}(t),v{\text{*}})$ является решением задачи управления (2.1), (2.2). Неравенства в сочетании с (2.10)–(2.12) дают Перейдем теперь к пределу при $k \to \infty $ и получим оценку (2.5), которая в сочетании с неравенством приводит к оценке где

Отсюда следует оценка (2.4).

Теперь нам осталось показать единственность $(z{\text{*}}(t),v{\text{*}})$. Пусть пара $(\tilde {z}(t),\tilde {v})$ является другим решением задачи управления (2.1), (2.2). Тогда, аналогично (2.12), легко получаем

Следовательно, неравенство ${{q}_{1}}(h,\gamma ,{{\omega }_{0}}) < 1$ приводит к $\tilde {z}(t) = z{\text{*}}(t)$ для всех $t \in [0,T]$ и $\tilde {v} = v{\text{*}}$, и $\tilde {z}(t) = \dot {z}{\text{*}}(t)$ для всех $t \in (0,T)$. Теорема 2.1 доказана.

Теорема 2.2. Пусть задача управления (2.1), (1.2) корректно разрешима с константой $\chi ,$ и справедливо неравенство

Тогда задача управления (1.1), (1.2) корректно разрешима с константойигде $(x{\text{*}}(t),\mu {\text{*}})$ и $(z{\text{*}}(t),v{\text{*}})$ – решения задач управления (1.1), (1.2) и (2.1), (2.2) соответственно.

Доказательство. Положим ${{x}^{{(0)}}}(t) = z{\text{*}}(t)$, ${{\mu }^{{(0)}}} = v{\text{*}}$ и определим последующие приближения ${{x}^{{(k)}}}(t)$, ${{\mu }^{{(k)}}}$, $k = 1,2,...$, из задач с параметром:

Так как задача (2.17), (2.18) корректно разрешима с константой $\chi ,$ равномерная сходимость последовательности $\{ {{x}^{{(k)}}}(t)\} $, $k = 1,2,...$, на $[0,T]$ при $k \to \infty ,$ и сходимость последовательности $\{ {{\mu }^{{(k)}}}\} $, $\quad k = 1,2,...,$ при $k \to \infty ,$ доказывается так же, как в теореме 2.1.

Оставшаяся часть доказательства с небольшими изменениями аналогична доказательству теоремы 2.1. И мы опускаем здесь его. Теорема 2.2 доказана.

3. ${{\delta }_{{2N}}}(h)$ ОБЩЕЕ РЕШЕНИЕ И КОРРЕКТНАЯ РАЗРЕШИМОСТЬ ЗАДАЧИ УПРАВЛЕНИЯ ДЛЯ НАГРУЖЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С ПАРАМЕТРОМ

В данном разделе мы представляем новое общее решение нагруженного дифференциального уравнения с параметром (2.1) и исследуем однозначную разрешимость задачи управления (2.1), (2.2).

Пусть $C([0,T],h,{{R}^{{2Nn}}})$ обозначает пространство систем функций $z[t] = ({{z}_{1}}(t),{{z}_{2}}(t), \ldots ,$ ${{z}_{{2N}}}(t)),$ где ${{z}_{r}}:[(r - 1)h,rh) \to {{R}^{n}}$ непрерывны и имеют конечные левосторонние пределы $\mathop {lim}\limits_{t \to rh - 0} {{z}_{r}}(t)$ для всех $r = \overline {1,2N} ,$ с нормой ${{\left\| {z{\kern 1pt} [\, \cdot \,]{\kern 1pt} } \right\|}_{2}} = \mathop {max}\limits_{r = \overline {1,2N} } \mathop {sup}\limits_{t \in [(r - 1)h,rh)} \left\| {{{z}_{r}}(t)} \right\|.$

Пусть $(z(t),v)$ – решение нагруженного дифференциального уравнения с параметром (2.1) и ${{z}_{r}}(t)$ – сужение функции $z(t)$ на подынтервал $[(r - 1)h,rh)$, т.е. ${{z}_{r}}(t) = z(t),$ $t \in [(r - 1)h,rh)$, $r = \overline {1,2N} .$ Тогда пара $(z[t],v)$, где система функций $z[t] = ({{z}_{1}}(t),{{z}_{2}}(t), \ldots ,{{z}_{{2N}}}(t))$ принадлежит $C([0,T],h,{{R}^{{2Nn}}})$ и $v \in {{R}^{l}},$ удовлетворяет системе нагруженных дифференциальных уравнений с параметром

где $z(2Nh)$ – значение функции $z(t)$ в правом конце интервала: $t = 2Nh = T.$

Тройка $(\tilde {z}[t],\tilde {z}(2Nh),v)$ с $\tilde {z}[t] = ({{\tilde {z}}_{1}}(t),{{\tilde {z}}_{2}}(t),...,{{\tilde {z}}_{{2N}}}(t)) \in C([0,T],h,{{R}^{{2Nn}}})$, $\tilde {z}(2Nh) \in {{R}^{n}}$, и $v \in {{R}^{l}},$ удовлетворяющая уравнению (3.1), называется решением уравнения (3.1).

Введем параметры ${{\lambda }_{r}} = {{z}_{r}}((r - 1)h),$ $r = \overline {1,2N} ,$ ${{\lambda }_{{2N + 1}}} = z(2Nh)$, и ${{\lambda }_{{2N + 2}}} = v$. Делая замену ${{u}_{r}}(t) = {{z}_{r}}(t) - {{\lambda }_{r}}$ на каждом $r$-м интервале $[(r - 1)h,rh),$ мы получим систему обыкновенных дифференциальных уравнений с параметрами

и начальные условия При фиксированном $\hat {\lambda } = ({{\hat {\lambda }}_{1}},{{\hat {\lambda }}_{2}}, \ldots ,{{\hat {\lambda }}_{{2N + 1}}},{{\hat {\lambda }}_{{2N + 2}}}) \in {{R}^{{(2N + 1)n + l}}},$ задача Коши (3.2), (3.3) имеет единственное решение ${{u}_{r}}(t,\hat {\lambda })$ на подынтервале $[(r - 1)h,rh),$ $r = \overline {1,2N} ,$ и система функций $u[t,\hat {\lambda }] = ({{u}_{1}}(t,\hat {\lambda }),{{u}_{2}}(t,\hat {\lambda }), \ldots ,{{u}_{{2N}}}(t,\hat {\lambda }))$ принадлежит $C([0,T],h,{{R}^{{2Nn}}}).$

Система функций $u[t,\hat {\lambda }]$ называется решением задач Коши (3.2), (3.3) с $\lambda = \hat {\lambda }.$

Система  нагруженных дифференциальных уравнений с параметром (3.1) эквивалентна задачам Коши с параметрами (3.2), (3.3) в следующем смысле. Пусть тройка $(\tilde {z}[t] = ({{\tilde {z}}_{1}}(t),{{\tilde {z}}_{2}}(t),...,{{\tilde {z}}_{{2N}}}(t)),\tilde {z}(2Nh),\tilde {v})$ является решением уравнения (3.1). Выберем параметры: ${{\tilde {\lambda }}_{r}} = {{\tilde {z}}_{r}}((r - 1)h),$ $r = \overline {1,2N} ,$ ${{\tilde {\lambda }}_{{2N + 1}}} = \tilde {z}(2Nh)$, и ${{\tilde {\lambda }}_{{2N + 2}}} = \tilde {v}$. Тогда система функций $u[t,\widetilde \lambda ] = ({{u}_{1}}(t,\widetilde \lambda ),{{u}_{2}}(t,\widetilde \lambda ), \ldots ,{{u}_{{2N}}}(t,\widetilde \lambda ))$, где ${{u}_{r}}(t,\widetilde \lambda ) = {{\tilde {z}}_{r}}(t) - {{\tilde {\lambda }}_{r}}$, $r = \overline {1,2N} $, является решением задач Коши (3.2), (3.3) с $\lambda = \widetilde \lambda = ({{\widetilde \lambda }_{1}},{{\widetilde \lambda }_{2}},...,{{\widetilde \lambda }_{{2N + 1}}},{{\widetilde \lambda }_{{2N + 2}}}) \in {{R}^{{(2N + 1)n + l}}}$. И обратно, если система функций $u[t,\lambda {\text{*}}] = ({{u}_{1}}(t,\lambda {\text{*}}),{{u}_{2}}(t,\lambda {\text{*}}), \ldots ,{{u}_{{2N}}}(t,\lambda {\text{*}})) \in C([0,T],h,{{R}^{{2Nn}}})$ является решением задач Коши (3.2), (3.3) с $\lambda = \lambda {\text{*}} = (\lambda _{1}^{*},\lambda _{2}^{*},...,\lambda _{{2N + 1}}^{*},\lambda _{{2N + 2}}^{*}) \in {{R}^{{(2N + 1)n + l}}}$, тогда тройка $(z{\text{*}}[t] = (z_{1}^{*}(t),z_{2}^{*},...,z_{{2N}}^{*}(t)),{{z}^{*}}(2Nh),{{v}^{*}})$ с $z_{r}^{*}(t) = \lambda _{r}^{*} + {{u}_{r}}(t,\lambda {\text{*}})$, $r = \overline {1,2N} $, $z{\text{*}}(2Nh) = \lambda _{{2N + 1}}^{*}$, и $v{\text{*}} = \lambda _{{2N + 2}}^{*}$ является решением уравнения (3.1).

Теперь мы вводим новое общее решение нагруженного дифференциального уравнения с параметром [11].

Определение 3.1. Пусть $u[t,\lambda ] = ({{u}_{1}}(t,\lambda ),{{u}_{2}}(t,\lambda ),...,{{u}_{{2N}}}(t,\lambda ))$ – решение задач Коши (3.2), (3.3) с $\lambda = ({{\lambda }_{1}},{{\lambda }_{2}},...,{{\lambda }_{{2N + 1}}},{{\lambda }_{{2N + 2}}}) \in {{R}^{{(2N + 1)n + l}}}$.

Тогда пара $(z({{\delta }_{{2N}}}(h),\lambda ,t),v({{\delta }_{{2N}}}(h),\lambda ))$, где функция $z({{\delta }_{{2N}}}(h),\lambda ,t)$ и параметр $v({{\delta }_{{2N}}}(h),\lambda )$ заданы равенствами

называется ${{\delta }_{{2N}}}(h)$ общим решением нагруженного дифференциального уравнения с параметром (2.1).

Согласно oпределению 3.1, ${{\delta }_{{2N}}}(h)$ общее решение зависит от $2N + 2$ произвольных векторов ${{\lambda }_{r}} \in {{R}^{n}}$, $r = \overline {1,2N + 1} $, ${{\lambda }_{{2N + 2}}} \in {{R}^{l}}$, и удовлетворяет нагруженному дифференциальному уравнению с параметром (2.1) для всех $t \in (0,T){\backslash }\{ ph,p = \overline {1,2N - 1} \} .$

Пусть ${{X}_{r}}(t)$ – фундаментальное решение обыкновенного дифференциального уравнения

Тогда единственное решение задачи Коши (3.2), (3.3) можно записать в виде

Следовательно, из (3.5) мы получим следующее представление ${{\delta }_{{2N}}}(h)$ общего решения:

с где $I$ – единичная матрица размерности $n.$

Здесь $(n \times n)$ – матрицы ${{\alpha }_{{r,j}}}({{\delta }_{{2N}}}(h),t)$, $\quad r = \overline {1,2N} ,$ $\quad j = \overline {1,2N + 1} ,$ $(n \times l)$ – матрицы $\alpha _{r}^{0}({{\delta }_{{2N}}}(h),t)$, $\quad r = \overline {1,2N} ,$ и $n$ вектора ${{\beta }_{r}}({{\delta }_{{2N}}}(h),t)$, $\quad r = \overline {1,2N} ,$ называются коэффициентами и правыми частями общего решения ${{\delta }_{{2N}}}(h)$ соответственно.

Если пара $(z(t),v)$ является решением уравнения (2.1), и $z[t] = ({{z}_{1}}(t),{{z}_{2}}(t),...,{{z}_{{2N}}}(t))$ – система функций, составленная из сужений функции $z(t)$ на подынтервалах $[(r - 1)h,rh),$ $r = \overline {1,2N} ,$ то имеют место следующие уравнения:

Эти уравнения называются условиями непрерывности для решения уравнения (2.1).

Общее решение ${{\delta }_{{2N}}}(h)$ позволяет нам свести разрешимость задачи (2.1), (1.2) к разрешимости системы линейных алгебраических уравнений относительно ${{\lambda }_{r}} \in {{R}^{n}},$ $r = \overline {1,2N + 1} ,\;\,{{\lambda }_{{2N + 2}}} \in {{R}^{l}}.$

Подставляя соответствующие выражения ${{\delta }_{{2N}}}(h)$ общего решения в граничное условие (2.2) и условия непрерывности (3.13) и (3.14), мы получим систему линейных алгебраических уравнений:

Обозначим через ${{Q}_{*}}({{\delta }_{{2N}}}(h)):{{R}^{{(2N + 1)n + l}}} \to {{R}^{{(2N + 1)n + l}}}$ матрицу, соответствующую левой части системы уравнений (3.15), (3.16) и запишем систему в виде где ${{F}_{*}}({{\delta }_{{2N}}}(h)) = ( - d,{{\beta }_{1}}({{\delta }_{{2N}}}(h),h),$ ${{\beta }_{2}}({{\delta }_{{2N}}}(h),2h), \ldots ,{{\beta }_{{2N}}}({{\delta }_{{2N}}}(h),2Nh)) \in {{R}^{{(2N + 1)n + l}}}$.

Используя свойства общего решения ${{\delta }_{{2N}}}(h)$, легко проверить, что разрешимость задачи с параметром (2.1), (2.2) эквивалентна разрешимости системы (3.17).

Поэтому общеизвестные теоремы линейной алгебры приводят к следующим двум утверждениям.

Теорема 3.1. Задача управления (2.1), (2.2) разрешима тогда и только тогда, когда вектор ${{F}_{ * }}({{\delta }_{{2N}}}(h))$ ортогонален ядру транспонированной матрицы $({{Q}_{*}}({{\delta }_{{2N}}}(h))){\text{'}},$ т.е. равенство

справедливо для $\forall \zeta \in Ker({{Q}_{*}}({{\delta }_{{2N}}}(h))){\text{'}},$ где $( \cdot , \cdot )$ – скалярное произведение в ${{R}^{{(2N + 1)n + l}}}.$

Теорема 3.2. Задача управления (2.1), (2.2) корректно разрешима тогда и только тогда, когда матрица ${{Q}_{*}}({{\delta }_{{2N}}}(h))$ обратима.

Кроме того, общее решение ${{\delta }_{{2N}}}(h)$ и оценка $\left\| {{{{[{{Q}_{*}}({{\delta }_{{2N}}}(h))]}}^{{ - 1}}}} \right\|$ позволяют нам определить константу корректной разрешимости задачи (2.1), (2.2). Предположим, что матрица ${{Q}_{*}}({{\delta }_{{2N}}}(h))$ обратима, и

В этом случае уравнение (3.17) имеет единственное решение $\lambda {\text{*}} = - {{[{{Q}_{*}}({{\delta }_{{2N}}}(h))]}^{{ - 1}}}{{F}_{*}}({{\delta }_{{2N}}}(h))$, и пара $(z{\text{*}}(t),v{\text{*}})$, где функция $z{\text{*}}(t) = z({{\delta }_{{2N}}}(h),\lambda {\text{*}},t)$ и парaметр $v{\text{*}}\;{\text{ = }}\;v({{\delta }_{{2N}}}(h),\lambda {\text{*}}),$ является единственным решением задачи управления (2.1), (2.2). Равенства (3.9)–(3.12) и соотношения (см. (14) в [7, с. 1152]) позволяют установить оценки Правую часть уравнения (3.17) можно оценить в виде с

Неравенства (3.18), (3.20)–(3.23) и (3.24) приводят к оценке

где Оценки (3.25) и (3.26) означают: с

Итак, задача управления (2.1), (2.2) корректно разрешима с константой $\chi $.

Выберем $h \in [0,{{h}_{0}})$: $2Nh = T$ с ${{h}_{0}}$, удовлетворяющим неравенству (2.15), тогда из теоремы 2.2 мы определяем $\gamma $.

Формулы (3.9)–(3.12), определяющие коэффициенты и правые части ${{\delta }_{{2N}}}(h)$ общего решения, содержат фундаментальные матрицы ${{X}_{r}}(t)$, $r = \overline {1,2N} $. Отметим, что довольно сложно построить фундаментальные матрицы для систем обыкновенных дифференциальных уравнений с переменными коэффициентами. Поэтому ниже мы предлагаем численные и приближенные методы для построения ${{\delta }_{{2N}}}(h)$ общего решения.

Рассмотрим задачи Коши для обыкновенных дифференциальных уравнений на подынтервалах:

где $P(t)$ – квадратная матрица или вектор размерности $n$, непрерывная (или непрерывен) на $[0,T]$.

Обозначим через ${{a}_{r}}(P,t)$ единственное решение задачи Коши (3.28). Очевидно, что

Теперь, принимая в рассмотрение (3.29), мы можем определить коэффициенты и правые части ${{\delta }_{{2N}}}(h)$ общего решения следующими уравнениями:

Используя (3.30)–(3.33), мы построим общее решение ${{\delta }_{{2N}}}(h)$ нагруженного дифференциального уравнения с параметром (2.1) в следующем виде:

4. МЕТОДЫ РЕШЕНИЯ ЗАДАЧИ УПРАВЛЕНИЯ (1.1), (1.2). СХОДИМОСТЬ, УСТОЙЧИВОСТЬ И ТОЧНОСТЬ

Метод, предлагаемый в настоящем разделе, основан на аппроксимации задачи управления (1.1), (1.2) задачами с параметром для нагруженных дифференциальных уравнений (2.1), (2.2). Алгоритм метода представлен ниже.

Поскольку равномерная непрерывность $K(t,\tau )$ на $[0,T] \times [0,T]$ приводит к

то решение аппроксимирующей задачи с параметром (2.1), (2.2) равномерно сходится к решению исходной задачи управления (1.1), (1.2) на $[0,T]$ при $h \to 0$.

Здесь требовалaсь только непрерывность $A(t),$ ${{A}_{0}}(t)$ и $f(t)$ на $[0,T]$ и $K(t,\tau )$ на $[0,T] \times [0,T]$ соответственно. В следующем утверждении, при большей гладкости этих данных, устанавливается точность аппроксимации решения задачи управления (1.1), (1.2) решениями задачи с параметром (2.1), (2.2).

Теорема 4.1. Предположим, что: a) задача (1.1), (1.2) корректно разрешима с константой $\gamma ;$ б) матрицы $A(t)$, ${{A}_{0}}(t)$ и вектор $f(t)$ имеют непрерывные производные ${{A}^{{(k)}}}(t)$, $A_{0}^{{(k)}}(t)$ и ${{f}^{{(k)}}}(t)$, $k = \overline {1,3} $, на $[0,T];$ в) матрица $K(t,\tau )$ имеет непрерывные частные производные $K_{{t,\tau }}^{{(k,i)}}(t,\tau )$, $k = \overline {1,3} $, $i = \overline {1,4} $, на $[0,T] \times [0,T]$. Тогда существует ${{h}_{0}} > 0$ такое, что для всех $h \in (0,{{h}_{0}}]:$ $2Nh = T$, задача с параметром (2.1), (2.2) имеет единственное решение $(z{\text{*}}(t),v{\text{*}})$, и

где $(x{\text{*}}(t),\mu {\text{*}})$ – единственное решение задачи с параметром (1.1), (1.2).

Доказательство. Корректная разрешимость задачи управления (1.1), (1.2) и гладкость данных уравнения (1.1) обеспечивает существование непрерывной производной ${{[x{\text{*}}(t)]}^{{(4)}}}$ на $[0,T]$.

Выбираем

Поскольку непрерывность матрицы $K(t,\tau )$ на замкнутой области приводит к ее равномерной непрерывности на $[0,T] \times [0,T],$ для существует число ${{h}_{0}} \in (0,{{h}_{1}}]$ такое, что выполняется оценка для всех $\tau {\text{'}} \in [0,T]$ и $\tau {\text{''}} \in [0,T]$, удовлетворяющих неравенству $\left| {\tau {\text{'}} - \tau {\text{''}}} \right| < 2{{h}_{0}}$.

Итак, условие (2.3) выполнено: ${{q}_{1}}(h,\gamma ,{{\omega }_{0}}) = \tfrac{1}{2} < 1$ для $h \in (0,{{h}_{0}}]$: $2Nh = T$.

Неравенство (4.2) приводит к ${{\omega }_{0}}(K,2h) < \tfrac{1}{{4Tmax(\gamma ,(\alpha + \beta T + {{\alpha }_{0}})\gamma + 1)}}$.

Согласно теореме 2.1, задача управления (2.1), (2.2) корректно разрешима с константой $\chi = 2max(\gamma ,(\alpha + \beta T + {{\alpha }_{0}})\gamma + 1)$ для всех $h \in (0,{{h}_{0}}]$: $2Nh = T$. Поэтому пара $(\Delta (t),\Theta )$ с $\Delta (t) = z{\text{*}}(t) - x{\text{*}}(t)$ и $\Theta = v{\text{*}} - \mu {\text{*}}$ является единственным решением задачи с параметром

Так как задача (4.3), (4.4) корректно разрешима с константой $2max(\gamma ,(\alpha + \beta T + {{\alpha }_{0}})\gamma + 1)$, справедливо неравенство Следовательно, применяя оценки погрешности метода Симпсона [2, с. 132], мы установим оценку (4.1). Теорема 4.1 доказана.

Вернемся к общему решению ${{\delta }_{{2N}}}(h)$ нагруженных дифференциальных уравнений (2.1) и выражениям (3.34)–(3.36).

Подставляя соответствующие выражения $z({{\delta }_{{2N}}}(h),t,\lambda )$ и $v({{\delta }_{{2N}}}(h),\lambda )$ в граничное условие (2.2) и условия непрерывности решения в точках ${{t}_{p}} = ph$, $p = 1,2,...,2N$, затем умножая обе части граничного условия на $h > 0$, мы получаем следующую систему линейных алгебраических уравнений:

Обозначим через ${{Q}_{*}}({{\delta }_{{2N}}}(h)):$ ${{R}^{{n(2N + 1) + l}}} \to {{R}^{{n(2N + 1) + l}}}$ матрицу, соответствующую левой части системы уравнений (4.6), (4.7) и запишем ее в виде где ${{F}_{*}}({{\delta }_{{2N}}}(h)) = ( - hd,{{a}_{1}}(f,h),{{a}_{2}}(f,2h),...,{{a}_{{2N}}}(f,2Nh)) \in {{R}^{{n(2N + 1) + l}}}$.

Как было показано в [13], число обусловленности является одним из наиболее основных характеристик для системы линейных алгебраических уравнений. Это число, определяемое как произведение норм матрицы системы и ее обратной, демонстрирует как изменение коэффициентов и правых частей системы влияют на изменение решения системы. Для определения числа обусловленности по формуле (4.8), мы оцениваем $\left\| {{{Q}_{*}}({{\delta }_{{2N}}}(h))} \right\|$ и $\left\| {{{{[{{Q}_{*}}({{\delta }_{{2N}}}(h))]}}^{{ - 1}}}} \right\|$.

Учитывая $\mathop {max}\limits_{t \in [0,T]} \left\| {A(t)} \right\| = \alpha $, $\mathop {max}\limits_{t \in [0,T]} \left\| {{{A}_{0}}(t)} \right\| = {{\alpha }_{0}}$, $\mathop {max}\limits_{(t,\tau ) \in [0,T] \times [0,T]} \left\| {K(t,\tau )} \right\| = \beta $, имеем

Поэтому норма матрицы ${{Q}_{*}}({{\delta }_{{2N}}}(h))$ не зависит от числа разбиения $2N.$

Теорема 4.2. Предположим, что задача (2.1), (2.2) корректно разрешима с константой $\chi $. Тогда существует число ${{h}_{1}} > 0$ такое, что для всех $h \in (0,{{h}_{1}}]:$ $2Nh = T$, $(n(2N + 1) + l) \times (n(2N + 1) + l)$ – матрица ${{Q}_{*}}({{\delta }_{{2N}}}(h))$ обратима, и справедлива оценка

Доказательство. Применяя Лемму из [12, с. 39], вычислим норму ${{[{{Q}_{ * }}({{\delta }_{{2N}}}(h))]}^{{ - 1}}}.$ Выбираем $\varepsilon = 1$ и ${{h}_{1}} \in (0,{{h}_{0}}]$, удовлетворяющими неравенству

Рассмотрим систему линейных алгебраических уравнений с $h \in (0,{{h}_{1}}]:$ $2Nh = T$ и $b = ({{b}_{1}},{{b}_{2}},...,{{b}_{{2N + 1}}})$. Для произвольной ${{b}^{ - }} = ({{b}_{2}},{{b}_{3}},...,{{b}_{{2N + 1}}}) \in {{R}^{{n2N}}}$, построим непрерывную на $[0,T]$ функцию ${{f}_{{{{b}^{ - }}}}}(t)$, удовлетворяющую следующим соотношениям:

1) $\tfrac{1}{h}{{a}_{r}}({{f}_{{{{b}^{ - }}}}},rh) = {{b}_{{r + 1}}},$ $r = \overline {1,2N} ;\quad $

2) $\mathop {max}\limits_{t \in [(r - 1)h,rh]} \left\| {{{f}_{{{{b}^{ - }}}}}(t)} \right\| \leqslant 2\left\| {{{b}^{ - }}} \right\| = 2\mathop {max}\limits_{r = \overline {1,2N} } \left\| {{{b}_{{r + 1}}}} \right\|$.

Используя Лемму на каждом интервале $[(r - 1)h,rh],$ $r = \overline {1,2N} ,$ мы получим непрерывную функцию $f_{r}^{b}(t)$ со следующими свойствами:

a) $f_{r}^{b}((r - 1)h) = 0$, $f_{r}^{b}(rh) = 0$;

б) $\mathop {max}\limits_{t \in [(r - 1)h,rh]} \left\| {f_{r}^{b}(t)} \right\| \leqslant 2\left\| {{{b}_{{r + 1}}}} \right\|$;

в) $\tfrac{1}{h}{{a}_{r}}(f_{r}^{b},rh) = {{b}_{{r + 1}}}$, $r = \overline {1,2N} $.

Определим неизвестную функцию равенствами: ${{f}_{{{{b}^{ - }}}}}(t) = f_{r}^{b}(t)$, $t \in [(r - 1)h,rh]$, $r = \overline {1,2N} $. Обозначим через $({{z}_{b}}(t),{{v}_{b}})$ единственное решение задачи (2.1), (2.2) с $f(t) = {{f}_{{{{b}^{ - }}}}}(t)$ и $d = {{b}_{1}}$, и обозначим через ${{\lambda }^{b}} = (\lambda _{1}^{b},\lambda _{2}^{b},...,\lambda _{{2N + 1}}^{b},\lambda _{{2N + 2}}^{b})$ решение уравнения (4.11).

Так как задача (2.1), (2.2) корректно разрешима с константой $\chi $, и $\lambda _{r}^{b} = {{z}_{b}}[(r - 1)h]$, $r = \overline {1,2N + 1} $, $\lambda _{{2N + 2}}^{b} = {{v}_{b}}$, имеем

Учитывая, что $b$ является произвольным вектором из ${{R}^{{n(2N + 1) + l}}}$, из (4.12) мы получим оценку (4.10). Теорема 4.2 доказана.

Итак, если задача (2.1), (2.2) корректно разрешима с константой $\chi $, тогда неравенства (4.9) и (4.12) приводят к оценке

для $h \in (0,{{h}_{1}}]:2Nh = T$.

Следовательно, число обусловленности системы (4.8) растет линейно относительно $2N$, если задача с параметром (1.1), (1.2) корректно разрешима. Это свойство обеспечивает устойчивость решения системы (4.6), (4.7) (см. [13]).

Предположим, что мы решаем задачи Коши для обыкновенных дифференциальных уравнений (3.28) на подынтервалах приближенным или численным методом. Обозначим через $a_{r}^{\eta }(P,t)$, $r = \overline {1,2N} ,$ решение (3.28). Здесь $\eta > 0$ показывает ошибку применяемого метода. Таким образом, вместо (4.6), (4.7) мы решаем следующую систему линейных алгебраических уравнений:

Запишем вышеуказанную систему (4.14), (4.15) в виде Справедливы следующие неравенства: Задача (2.1), (2.2) корректно разрешима тогда и только тогда, когда матрица ${{Q}_{*}}({{\delta }_{{2N}}}(h))$ обратима. Применяя (4.17) и оценку ошибки метода, который мы выбрали для решения задач Коши (3.28), получаем Отсюда, если матрица ${{Q}^{\eta }}({{\delta }_{{2N}}}(h))$ обратима и $\left\| {{{{[{{Q}^{\eta }}({{\delta }_{{2N}}}(h))]}}^{{ - 1}}}} \right\|{{\varepsilon }_{0}}(\eta ) < 1$, то теорема 4 из [16, с. 212] обеспечивает обратимость матрицы ${{Q}_{*}}({{\delta }_{{2N}}}(h))$.

Рассмотрим уравнения (4.8) и (4.16) при условиях теоремы 4.2. Предположим, что имеет место (4.19), неравенство

и $\tfrac{{2\chi }}{h}{{\varepsilon }_{0}}(\eta ) < 1,$ тогда, согласно теореме 4 из [13, с. 212], матрица ${{Q}^{\eta }}({{\delta }_{{2N}}}(h))$ также будет обратима, и уравнения (4.8) и (4.16) имеют соответствующие единственные решения: Применяя неравенства (4.10), (4.18), (4.19) и (4.20), мы получаем оценки

Устойчивость вычислений при решении задач Коши (3.28) и системы (4.14), (4.15), корректная разрешимость задачи управления (1.1), (1.2), а также сходимость $(z{\text{*}}(t),v{\text{*}})$ к $(x{\text{*}}(t),\mu {\text{*}})$ обеспечивают устойчивость предлагаемого метода. Отметим, что для составления системы (4.14), (4.15), нам нужны значения решения задачи (3.28) только в конечных точках подынтервалов. Решаем задачу с параметром (2.1), (2.2), используя

Алгоритм A

Шаг 1. Решаем задачи Коши

и находим $a_{r}^{\eta }(A + {{\tilde {K}}_{r}},rh)$, $a_{r}^{\eta }({{\tilde {K}}_{j}},rh)$, $a_{r}^{\eta }({{A}_{0}},rh)$, и $a_{r}^{\eta }(f,rh)$, где $r = \overline {1,2N} $, $j \ne r$, $j = \overline {1,2N + 1} ;$

Шаг 2. Составляем систему линейных алгебраических уравнений (4.14), (4.15);

Шаг 3. Решаем систему (4.14), (4.15) и находим параметр ${{\lambda }^{\eta }} = (\lambda _{1}^{\eta },\lambda _{2}^{\eta },...,\lambda _{{2N + 1}}^{\eta },\lambda _{{2N + 2}}^{\eta }) \in {{R}^{{n(2N + 1) + l}}}$. Заметим, что элементы ${{\lambda }^{\eta }}$ являются приближенными значениями решения задачи с параметром (2.1), (2.2) в точках нагружения $[0,T]$: $\lambda _{r}^{\eta } = {{z}^{\eta }}((r - 1)h)$, $r = \overline {1,2N + 1} ,$ и $\lambda _{{2N + 2}}^{\eta } = {{v}^{\eta }}$.

Шаг 4. Формируем функцию

Решаем задачи Коши и вычисляем значения решения ${{z}^{\eta }}(t)$ в оставшихся точках $[(r - 1)h,rh]$, $r = \overline {1,2N} .$

Ниже мы представляем численные результаты.

Пример. Рассмотрим линейную задачу управления для интегродифференциального уравнения

Случай 1. Для $l = 1$ исходные данные задачи имеют следующий вид:

Случай 2. Для $l = 2$ исходные данные задачи имеют следующий вид:

Случай 3. Для $l = 3$ исходные данные задачи имеют следующий вид:

Возьмем шаг $h = 0.1$ и разделим $[0,1]$ на 10 частей. Заменим интегральное слагаемое уравнения (4.25) с помощью формулы Симпсона:

Таким образом, мы получим задачу с параметром для нагруженного дифференциального уравнения, где нагруженная часть определяется правой частью (4.27). Применяя алгоритм $A,$ находим численное решение этой задачи. Обозначим через $(\tilde {x},\tilde {\mu }) = ({{\tilde {x}}_{1}},{{\tilde {x}}_{2}},\tilde {\mu }){\text{'}}$, $(\hat {x},\hat {\mu }) = ({{\hat {x}}_{1}},{{\hat {x}}_{2}},{{\hat {\mu }}_{1}},{{\hat {\mu }}_{2}}){\text{'}}$, и $(\bar {x},\bar {\mu }) = ({{\bar {x}}_{1}},{{\bar {x}}_{2}},{{\bar {\mu }}_{1}},{{\bar {\mu }}_{2}},{{\bar {\mu }}_{3}}){\text{'}}$ численные решения задачи (4.25), (4.26) для $l = 1$, $l = 2,$ и $l = 3$ соответственно.

Задачи Коши для обыкновенного дифференциального уравнения на подынтервалах решаются методом Рунге-Кутты четвертого порядка с шагом ${{h}_{1}} = 0.025.$

Используя компьютерную систему MathCad15 и применяя предложенный выше алгоритм, мы получим значения численного решения задачи (4.25), (4.26) для трех случаев. Результаты для $k = \overline {0,40} $ представлены в следующей табл. 1.

В первом случае точным решением задачи (4.25), (4.26) является пара $(x{\text{*}}(t),\mu {\text{*}})$ с $x{\text{*}}(t) = \left( {\begin{array}{*{20}{c}} {{{t}^{2}} - 9} \\ {t + 7} \end{array}} \right)$ и $\mu {\text{*}} = 9$. Справедлива оценка

Во втором случае точным решением задачи (4.25), (4.26) является пара $(x{\text{*}}(t),\mu {\text{*}})$ с $x{\text{*}}(t) = \left( {\begin{array}{*{20}{c}} {{{t}^{2}} - 9} \\ {t + 7} \end{array}} \right)$ и $\mu {\text{*}} = \left( {\begin{array}{*{20}{c}} 1 \\ { - 5} \end{array}} \right).$ Справедлива следующая оценка:

В третьем случае точным решением задачи (4.25), (4.26) является пара $(x{\text{*}}(t),\mu {\text{*}})$ с $x{\text{*}}(t) = \left( {\begin{array}{*{20}{c}} {{{t}^{2}} - 9} \\ {t + 7} \end{array}} \right)$ и $\mu {\text{*}} = (1, - 5,9){\text{'}}$. Справедлива следующая оценка:

Авторы искренне признательны рецензентам за их тщательное чтение рукописи, полезные замечания и предложения.