Журнал вычислительной математики и математической физики, 2020, T. 60, № 3, стр. 351-368

Новая методика формулировки алгоритмов разделения области

В. И. Агошков^1, 2, *

¹ ИВМ РАН
119333 Москва, ул. Губкина, 8, Россия

² МГУ
119991 Москва, Ленинские горы, Россия

^* E-mail: agoshkov@m.inm.ras.ru

Поступила в редакцию 05.08.2019
После доработки 23.10.2019
Принята к публикации 18.11.2019

DOI: 10.31857/S0044466920030023

Полный текст (PDF)

Аннотация

Предлагается новая методика построения алгоритмов разделения области, которая базируется на теории оптимального управления, результатах теории обратных и некорректных задач, применении сопряженных уравнений и современных итерационных процессах. Отметим, что в данной методике построения алгоритмов разделения области допустимо рассмотрение широкого класса задач математической физики (в т.ч. с несимметричными операторами, с преобладающими конвективными частями операторов и др.). Библ. 32. Фиг. 3.

Ключевые слова: алгоритмы разделения области, оптимальное управления, обратные задачи, сопряженные уравнения.

ВВЕДЕНИЕ

В 70-е–80-е годы XX века наблюдался значительный рост научных работ, посвященных методам разделения области (Э.И. Матеева, Б.В. Пальцев [1], Л.Б. Цвик [2], В.В. Смелов [3], В.Г. Осмоловский, В.Я. Ривкинд [4], В.Э. Кацнельсон, В.В. Меньшиков [5], Ю.А. Кузнецов [6], А.М. Мацокин [7], В.И. Агошков [8]–[10], В.И. Агошков, В.И. Лебедев [11], Р. Гловивский [12], O. Видлунд [13], А. Фишлер [14], М. Дрыя [15], [16], А. Квартерони, С. Ландриани [17], Т. Чен [18] и др.). В значительной части этих работ построение алгоритмов разделения области осуществляется двумя подходами: а) формулировкой алгоритмов в терминах исходных “непрерывных” задач; б) формулировкой алгоритмов для аппроксимаций исходных задач по методу конечных элементов. В большинстве этих работ метод разделения области исследуется в применении либо к модельным задачам, либо к задачам с симметричными операторами. Однако заметим, что многие прикладные задачи включают уравнения с операторами: несимметричными, с малыми параметрами при старших производных, с коэффициентами, вырождающимися на границе, с преобладающей кососимметричной частью, с преобладающей “конвективной” составляющей оператора, с нелинейными и др. Одной из областей математической физики, в которой наблюдаются подобные задачи, является гидродинамика, в частности, океанология. По-видимому, не будет большой ошибкой сказать, что теоретических результатов по методу разделения области для задач с такими операторами еще мало. Кроме того, в данных задачах даже при наличии теоретических результатов последнее слово все же остается за экспериментальной проверкой, выводы которой могут значительно отличаться от заключений теории.

Опишем некоторые из методологий построения алгоритмов разделения области. B настоящее время известно, что для конструирования самых различных алгоритмов разделения области, их анализа и оптимизации весьма плодотворными оказались специальные граничные операторы – операторы Пуанкаре–Стеклова, введенные в работе [19]. С помощью этих операторов исходную задачу (после простых преобразований) можно свести решению абстрактного уравнения $B\tilde {u} = \psi $, рассматриваемого на $\gamma $-множестве точек, которое разбивает область $D$ на подобласти ${{D}_{i}}$. Используя свойства операторов Пуанкаре–Стеклова, можно сделать ряд утверждений о свойствах оператора $B$. А это дает возможность применить для решения уравнения $B\tilde {u} = \psi $ подходящий итерационный алгоритм. Таким образом, используя современную теорию итерационных методов, мы получаем множество алгоритмов решения уравнения $B\tilde {u} = \psi $. Если же теперь выписать этапы реализации этих методов в терминах исходной задачи или в векторно-матричной форме, то получим соответствующие множества алгоритмов разделения области.

Далее, здесь мы имеем два пути построения алгоритмов разделения области. Первый состоит в том, что все построения проводятся в терминах задач без осуществления их конечномерных аппроксимаций, т.е. в терминах “непрерывных” задач. И только после того, как алгоритм разделения области полностью выписан, можно применить конечномерную аппроксимацию этапов его реализации (метод конечных разностей, метод конечных элементов и др.). При этом можно надеяться, что если сформулированный алгоритм сходится, а выбранная аппроксимация является достаточно точной, то и практическая реализация алгоритма разделения области даст сходящийся процесс решения исходной задачи. Кроме того, большинство выводов и заключений также может сохраниться. При таком подходе исследование влияния погрешностей аппроксимаций можно отнести к проблеме устойчивости алгоритмов.

Второй путь состоит в следующем. После формулировки задачи сразу же осуществляется ее аппроксимация, например, методом конечных элементов. И затем уже при рассмотрении конечномерных аппроксимаций задачи вводятся операторы Пуанкаре–Стеклова и осуществляется весь процесс построения алгоритма разделения области. Здесь, в отличие от первого пути, все рассуждения в основном проводятся в конечномерных пространствах выбранных финитных базисных функций, и в итоге мы получим алгоритм, который можем практически реализовывать при численном счете на ЭВМ.

Новая методика построения алгоритмов разделения области, предлагаемая в настоящей работе, базируется на теории оптимального управления, результатах теории обратных и некорректных задач, применении сопряженных уравнений и современных итерационных процессах [20]–[23]. Идея этой методики состоит в следующем. После введения внутренней границы, разделяющей исходную область, на ней записываются условия сшивки для решений подзадач в подобластях. Затем некоторые из условий сшивки записываются через “граничные функции”, которые объявляются “управлениями” и подлежат отысканию вместе с решениями в подобластях. В качестве “уравнений замыкания” принимается вторая часть условий сшивки, которые записываются на внутренней границе “в смысле наименьших квадратов” (возможно, с введением различного рода регуляризаций). Таким образом, получаем задачу оптимального управления, которая решается уже известными методами (см. [24]–[26]) и в результате получаем итерационные алгоритмы разделения области. В определенном смысле такой подход к построению методов разделения области можно трактовать как применение “метода квазирешений В.К. Иванова” с введением регуляризации по Тихонову для отыскания “граничных функций”, задаваемых на внутренней границе разделения областей. Отмечаем, что в данной методике построения алгоритмов разделения области допустимо рассмотрение широкого класса задач математической физики (в т.ч. с несимметричными операторами, с преобладающими “конвективными частями операторов” и др.). Поскольку “уравнения замыкания” записываются “в смысле наименьших квадратов” и вся задача сводится к минимизации выпуклого квадратичного функционала, то при решении этой экстремальной задачи сопряженные операторы и задачи возникают естественным образом. Отметим, что данная методика применима к задачам с операторами различных типов, порядков и с различным числом независимых переменных.

Для определенности основную часть исследований мы будем проводить для задачи конвекции-диффузии температуры $T$ в океане (море), а затем сделаем замечания относительно возможности применения предлагаемых методов и подходов к другим подзадачам.

1. МЕТОД РАЗДЕЛЕНИЯ ОБЛАСТИ ДЛЯ УРАВНЕНИЯ КОНВЕКЦИИ–ДИФФУЗИИ

1.1. Постановка задачи

Пусть рассматривается полная система уравнений и краевых условий, задающая математическую модель гидротермодинамики (общей циркуляции) океана или моря в $D \times (0,\bar {t})$, где $D \subset {{\mathbb{R}}^{3}}$, $\bar {t} < \infty $. Пусть для аппроксимации этой модели по временной переменной $t \in [0,\bar {t}]$ применяется метод расщепления и получена полудискретная модель, состоящая из “основных подзадач” (температура, соленость, вектора скорости). Теперь для решения одной из этих подзадач сформулируем итерационные алгоритмы, которые представляют собой методы разделения области. Пусть рассматривается задача вида:

$\begin{gathered} {{T}_{t}} + \left( {\bar {U},{\mathbf{Grad}}} \right)T - {\mathbf{Div}}\left( {{{\nu }_{T}}\,{\mathbf{Grad}}\,T} \right) = {{f}_{T}}\quad {\text{в}}\quad D \times ({{t}_{0}},{{t}_{1}}), \\ T = T\left( 0 \right)\quad {\text{при}}\quad t = {{t}_{0}}\quad {\text{в}}\quad D, \\ \end{gathered} $

(1)

$\begin{gathered} \bar {U}_{n}^{{( - )}}T - {{\nu }_{T}}\frac{{\partial T}}{{\partial z}} + {{\gamma }_{T}}(T - {{T}_{a}}) = {{Q}_{T}} + \bar {U}_{n}^{{( - )}}{{d}_{T}}\quad {\text{на}}\quad {{\Gamma }_{s}} \times ({{t}_{0}},{{t}_{1}}), \\ \frac{{\partial T}}{{\partial {{N}_{T}}}} = 0\quad {\text{на}}\quad {{\Gamma }_{{w,c}}} \times ({{t}_{0}},{{t}_{1}}), \\ \end{gathered} $

$\begin{gathered} \bar {U}_{n}^{{( - )}}T + \frac{{\partial T}}{{\partial {{N}_{T}}}} = \bar {U}_{n}^{{( - )}}{{d}_{T}} + {{Q}_{T}}\quad {\text{на}}\quad {{\Gamma }_{{w,op}}} \times ({{t}_{0}},{{t}_{1}}), \\ \frac{{\partial T}}{{\partial {{N}_{T}}}} = 0\quad {\text{на}}\quad {{\Gamma }_{H}} \times ({{t}_{0}},{{t}_{1}}) \\ \end{gathered} $

с заданными $\bar {U},{{f}_{T}},...,{{d}_{T}},{{Q}_{T}}$. Здесь $\bar {U} \equiv (u,v,w)$ – вектор скорости, ${{\nu }_{T}} \geqslant 0,$ ${{\gamma }_{T}} \geqslant 0$, а границу области $\Gamma \equiv \partial D$ мы будем представлять как объединение четырех непересекающихся частей ${{\Gamma }_{S}}$, ${{\Gamma }_{{w,op}}}$, ${{\Gamma }_{{w,c}}}$, ${{\Gamma }_{H}}$, где ${{\Gamma }_{S}} \equiv \Omega $ – “невозмущенная поверхность”, ${{\Gamma }_{{w,op}}}$ – жидкая (открытая) часть вертикальной боковой границы, ${{\Gamma }_{{w,c}}}$ – твердая часть вертикальной боковой границы, ${{\Gamma }_{H}}$ – дно океана.

Единичный вектор внешней нормали к $\Gamma $ обозначаем через ${\mathbf{N}} \equiv $ (${{N}_{1}},{{N}_{2}},{{N}_{3}})$. Отмечаем, что ${\mathbf{N}} = \left( {0,0, - 1} \right)$ на ${{\Gamma }_{S}}$ и ${\mathbf{N}}$ $ = $ (${{N}_{1}}$, ${{N}_{2}}$, 0) на ${{\Gamma }_{w}} = {{\Gamma }_{{w,op}}} \cup {{\Gamma }_{{w,c}}}$ при этом вектор ${\mathbf{n}} \equiv $ (${{N}_{1}}$,${{N}_{2}})$ $ \equiv $ (${{n}_{1}}$, ${{n}_{2}})$ является единичным вектором внешней нормали к $\partial \Omega $. Выражение компонентов ${{N}_{1}},\;{{N}_{2}},\;{{N}_{3}}$ определяется выбираемым параметрическим представлением той или иной части границы. Таким образом, $\frac{{\partial T}}{{\partial {{N}_{T}}}} = {\mathbf{N}} \cdot {{\nu }_{T}}$.

При рассмотрении вектора скорости ${\mathbf{U}} = (u,v,w)$ на границе $\Gamma $ мы будем обозначать его составляющую по нормали через ${{U}_{n}}$: ${{U}_{n}} = $ ${\mathbf{U}} \cdot {\mathbf{N}} = u{{N}_{1}} + v{{N}_{2}} + w{{N}_{3}}.$ И пусть далее

$U_{n}^{{( + )}} \equiv \frac{{\left| {{{U}_{n}}} \right| + {{U}_{n}}}}{2},\quad U_{n}^{{( - )}} \equiv \frac{{\left| {{{U}_{n}}} \right| - {{U}_{n}}}}{2}.$

Отмечаем, что ${{U}_{n}} = U_{n}^{{( + )}} - U_{n}^{{( - )}}$ на $\Gamma $.

Пусть область $D$ разделена кусочно-гладкой липшицевой поверхностью ${{\Gamma }_{{in}}}$ на две подобласти ${{D}_{1}}$, ${{D}_{2}}$ так, что границы $\partial {{D}_{1}}$, $\partial {{D}_{2}}$ будут также липшицевыми. Характеристические функции ${{\Gamma }_{{in}}}$ обозначим ${{m}_{{in}}}$. В частности это означает, что на $\partial {{D}_{1}}$, $\partial {{D}_{2}}$ почти всюду существуют нормали к этим границам и отсутствуют “нулевые углы” на $\partial {{D}_{1}}$, $\partial {{D}_{2}}$.

Пусть $T \equiv {{T}_{1}}$, ${{T}_{{(0)}}} \equiv T_{{(0)}}^{{(1)}}$ в ${{D}_{1}}$, $T \equiv {{T}_{2}}$, ${{T}_{{(0)}}} \equiv T_{{(0)}}^{{(2)}}$ в ${{D}_{2}}$ $\forall t \in \left( {{{t}_{0}},{{t}_{1}}} \right)$ (обозначения для других коэффициентов и функций для упрощения обозначений оставляем прежними).

Если на границах $\partial {{D}_{i}},\;i = 1,2$, граничные условия для ${{T}_{i}},\;i = 1,2$, “порождаются” соответствующими граничными условиями из (1), то остановимся на условиях, которые надо задавать на “искусственно” введенной границе разделения областей ${{\Gamma }_{{in}}}$ $\forall t \in \left( {{{t}_{0}},{{t}_{1}}} \right)$. Если требовать, чтобы:

${{T}_{i}} \in {{L}_{2}}\left( {{{D}_{i}} \times \left( {{{t}_{0}},{{t}_{1}}} \right)} \right);\quad \left| {{\mathbf{Grad}}\,{{T}_{i}}} \right| \in \left| {{\mathbf{div}}\left( {{{\nu }_{T}}\,{\mathbf{grad}}\,{{T}_{i}}} \right)} \right| \in {{L}_{2}}\left( {{{D}_{i}} \times \left( {{{t}_{0}},{{t}_{1}}ht)} \right),\quad i = 1,2} \right.,$

то естественным является введение условий сопряжения вида

(2)

${{T}_{1}} = {{T}_{2}},\quad \frac{{\partial {{T}_{1}}}}{{\partial {{N}_{{T,1}}}}} = - \frac{{\partial {{T}_{2}}}}{{\partial {{N}_{{T,2}}}}}\quad {\text{на}}\quad {{\Gamma }_{{in}}} \times \left( {{{t}_{0}},{{t}_{1}}} \right).$

(В настоящей работе используются известные вещественные лебегово пространство ${{L}_{2}}(D)$ и пространства $W_{2}^{1}(D)$ Соболева С.Л. и их подпространства (см., например, [27], [28]).)

Но можно требовать также выполнения следующих условий:

(3)

${{T}_{1}} = {{T}_{2}},\quad U_{{n,1}}^{{\left( - \right)}}{{T}_{1}} + \frac{{\partial {{T}_{1}}}}{{\partial {{N}_{{T,1}}}}} = - \left( {U_{{n,2}}^{{\left( - \right)}}{{T}_{2}} + \frac{{\partial {{T}_{2}}}}{{\partial {{N}_{{T,2}}}}}} \right),$

где $U_{{n,i}}^{{\left( - \right)}} \equiv U_{n}^{{\left( - \right)}}$ при подходе к ${{\Gamma }_{{in}}}$ из ${{D}_{i}},\;i = 1,2$, $\bar {n} \equiv {{n}_{1}}$ – вектор внешней нормали к $\partial {{D}_{1}}$.

Как мы увидим ниже, введение условий в форме (3) также имеет свои преимущества при обобщенных постановках задач в ${{D}_{i}} \times ({{t}_{0}},{{t}_{1}}),$ $i = 1,2$.

Задача (1) может быть записана на каждом из множеств ${{D}_{1}} \times ({{t}_{0}},{{t}_{1}})$,${{D}_{2}} \times ({{t}_{0}},{{t}_{1}})$ (т.е. в форме (1) при $D \equiv {{D}_{i}},\;i = 1,2$) и условий сопряжений вида

(4)

где ${{N}_{{T,i}}}$ – внешняя к ${{\Gamma }_{{in}}}$ конормаль к ${{D}_{i}},\;(i = 1,2)$, а ${{\Gamma }_{{in}}}$ – общая часть границ для $\partial {{D}_{1}},\;\partial {{D}_{2}}$, разделяющая $D$ на ${{D}_{1}},\;{{D}_{2}}$ (обратим внимание на то, что ${{\Gamma }_{{in}}}$ может быть составлена из нескольких частей $\Gamma _{{in}}^{k},$, $k = 1,2,..,$ $k < \infty $, несоприкасающихся друг с другом!)

Пусть вводится “дополнительная неизвестная” $v$ (“управление”) на ${{\Gamma }_{{in}}} \times ({{t}_{0}},{{t}_{1}})$ как

(5)

$v \equiv U_{{n,1}}^{{\left( - \right)}}{{T}_{1}} + \frac{{\partial {{T}_{1}}}}{{\partial {{N}_{{T,1}}}}}\quad {\text{на}}\quad {{\Gamma }_{{in}}} \times ({{t}_{0}},{{t}_{1}}),$

подлежащая определению вместе с ${{T}_{1}},\;{{T}_{2}}$. Отмечаем, что в силу (4) имеем

(6)

$U_{{n,2}}^{{\left( - \right)}}{{T}_{2}} + \frac{{\partial {{T}_{2}}}}{{\partial {{N}_{{T,2}}}}} = - v\quad {\text{на}}\quad {{\Gamma }_{{in}}} \times ({{t}_{0}},{{t}_{1}}).$

В качестве уравнения замыкания задачи будем рассматривать первое равенство из (4) и вводим следующий “функционал стоимости”:

(7)

${{J}_{\alpha }}\left( v \right) \equiv {{J}_{\alpha }}\left( {{{T}_{1}}\left( v \right),{{T}_{2}}\left( v \right),v} \right) \equiv \frac{\alpha }{2}\int\limits_{{{\Gamma }_{{in}}}} \,\int\limits_{{{t}_{0}}}^{{{t}_{1}}} \,{{m}_{{in}}}\mathop {(v - {{v}^{{(0)}}})}\nolimits^2 d\Gamma dt + \frac{1}{2}\int\limits_{{{\Gamma }_{{in}}}} \,\int\limits_{{{t}_{0}}}^{{{t}_{1}}} \,{{m}_{{in}}}\mathop {({{T}_{1}} - {{T}_{2}})}\nolimits^2 d\Gamma dt,$

где $\alpha = {\text{const}} \geqslant 0$ – “параметр регуляризации”, ${{v}^{{(0)}}}$ – заданная функция (“приближение” к $v$ и возможно принять ${{v}^{{(0)}}} \equiv 0$), ${{m}_{{in}}}$ – характеристическая функция множества ${{\Gamma }_{{in}}}$. Для определенности считаем, что ${{v}^{{(0)}}} \equiv 0,$ $v \equiv 0$ на $(\Gamma {\backslash }{{\Gamma }_{{in}}}) \times ({{t}_{0}},{{t}_{1}})$.

Ставится следующая

Задача. Найти функцию ${{T}_{i}},(i = 1,2)$ в ${{D}_{i}} \times ({{t}_{0}},{{t}_{1}})$, удовлетворяющую (1)–(6) при $D \equiv {{D}_{i}},$ $(i = 1,2)$ и функцию $v$ такие, что функционал (7) принимает наименьшее значение:

(8)

$\mathop {inf}\limits_v {{J}_{\alpha }}\left( v \right).$

Если найти решение данной экстремальной задачи $v \equiv v(\alpha )$ при $\alpha = {{\alpha }_{i}},\;i = 1,2, \ldots ({{\alpha }_{1}} > $ $ > \;{{\alpha }_{2}} > \ldots > {{\alpha }_{k}} \to + 0,k \to \infty )$, то при определенных условиях функцию $v(\alpha )$ и порождаемые ею функции ${{T}_{1}}(\alpha ) \equiv {{T}_{2}}(v(\alpha ))$:

${{T}_{1}} \cong {{T}_{1}}\left( {v\left( \alpha \right)} \right),\quad {{T}_{2}} \cong {{T}_{2}}\left( {v\left( \alpha \right)} \right),\quad v \cong v\left( \alpha \right),$

можно принять в качестве приближенного решения исходной задачи.

1.2. Вариационные уравнения

Запишем необходимое условие минимума функционала в (8), для этого вычислим его первую вариацию $\delta {{J}_{\alpha }}$:

$\delta {{J}_{\alpha }} = \alpha \int\limits_{{{t}_{0}}}^{{{t}_{1}}} \,\int\limits_{{{\Gamma }_{{in}}}} \,{{m}_{{in}}}(v - {{v}^{{(0)}}})\delta vd\Gamma dt + \int\limits_{{{\Gamma }_{{in}}}} \,\int\limits_{{{t}_{0}}}^{{{t}_{1}}} \,{{m}_{{in}}}({{T}_{1}} - {{T}_{2}})\delta {{T}_{1}}d\Gamma dt + \int\limits_{{{\Gamma }_{{in}}}} \,\int\limits_{{{t}_{0}}}^{{{t}_{1}}} \,{{m}_{{in}}}({{T}_{2}} - {{T}_{1}})\delta {{T}_{2}}d\Gamma dt,$

при этом функции $\delta {{T}_{i}}$, $i = 1,\;2$, будут удовлетворять следующим системам:

$\begin{gathered} {{(\delta {{T}_{i}})}_{t}} + \left( {\bar {U},{\mathbf{Grad}}} \right)\delta {{T}_{i}} - {\mathbf{Div}}\left( {{{\nu }_{T}}{\mathbf{Grad}}\delta {{T}_{i}}} \right) = 0\quad {\text{в}}\quad D \times \left( {{{t}_{0}},{{t}_{1}}} \right),\quad \delta {{T}_{i}} = 0\quad {\text{при}}\quad t = {{t}_{0}}\quad {\text{в}}\quad D, \\ U_{n}^{{( - )}}\delta {{T}_{i}} - {{\nu }_{T}}\frac{{\partial \delta {{T}_{i}}}}{{\partial z}} + {{\gamma }_{T}}\delta {{T}_{i}} = 0\quad {\text{на}}\quad {{\Gamma }_{s}} \times ({{t}_{0}},{{t}_{1}}),\quad U_{n}^{{( - )}}\delta {{T}_{i}} + \frac{{\partial \delta {{T}_{i}}}}{{\partial {{N}_{T}}}} = 0\quad {\text{на}}\quad {{\Gamma }_{{w,op}}} \times ({{t}_{0}},{{t}_{1}}), \\ \end{gathered} $

$\begin{gathered} \frac{{\partial \delta {{T}_{i}}}}{{\partial {{N}_{T}}}} = 0\quad {\text{на}}\quad {{\Gamma }_{{w,c}}} \times ({{t}_{0}},{{t}_{1}}),\quad \frac{{\partial \delta {{T}_{i}}}}{{\partial {{N}_{T}}}} = 0\quad {\text{на}}\quad {{\Gamma }_{H}} \times ({{t}_{0}},{{t}_{1}}), \\ U_{{n,1}}^{{( - )}}\delta {{T}_{1}} + \frac{{\partial \delta {{T}_{1}}}}{{\partial {{N}_{{T,1}}}}} = - \left( {U_{{n,2}}^{{( - )}}\delta {{T}_{2}} + \frac{{\partial \delta {{T}_{2}}}}{{\partial {{N}_{{T,2}}}}}} \right) = \delta v, \\ \end{gathered} $

где $D = {{D}_{1}}$ или $D = {{D}_{2}}$, а граничные условия на ${{\Gamma }_{s}},\;{{\Gamma }_{{w,c}}},\;{{\Gamma }_{{w,op}}}$ ставятся на тех частях $\partial {{D}_{1}},\;\partial {{D}_{2}}$, которые имеют пересечения положительной меры с частями ${{\Gamma }_{s}},\;{{\Gamma }_{{w,c}}},\;{{\Gamma }_{{w,op}}}$ границы $\Gamma \equiv \partial D$ всей области $D$.

Введем следующие “сопряженные задачи” $(i = 1,2)$:

$ - {\kern 1pt} {{(T_{i}^{*})}_{t}}\, - \,{\text{Div}}({\mathbf{U}}T_{i}^{*})\, - \,{\text{Div}}({{\nu }_{T}}\operatorname{Grad} T_{i}^{*})\, = \,0\quad {\text{в}}\quad {{D}_{i}}\, \times \,({{t}_{0}},{{t}_{1}}),\quad T_{i}^{*}\, = \,0\quad {\text{при}}\quad t\, = \,{{t}_{1}}\quad {\text{в}}\quad {{D}_{i}},$

(9)

$\begin{gathered} {\mathbf{U}}_{n}^{{( + )}}T_{i}^{*} - {{\nu }_{T}}\frac{{\partial T_{i}^{*}}}{{\partial z}} + {{\gamma }_{T}}T_{i}^{*} = 0\quad {\text{на}}\quad {{\Gamma }_{s}} \times ({{t}_{0}},{{t}_{1}}),\quad {\mathbf{U}}_{n}^{{( + )}}T_{i}^{*} + \frac{{\partial T_{i}^{*}}}{{\partial {{N}_{T}}}} = 0\quad {\text{на}}\quad {{\Gamma }_{{w,op}}} \times ({{t}_{0}},{{t}_{1}}), \\ \frac{{\partial T_{i}^{*}}}{{\partial N}} = 0\quad {\text{на}}\quad ({{\Gamma }_{H}} \cup {{\Gamma }_{{w,c}}}) \times ({{t}_{0}},{{t}_{1}}),\quad {\mathbf{U}}_{n}^{{( + )}}T_{1}^{*} + \frac{{\partial T_{1}^{*}}}{{\partial {{N}_{{T,1}}}}} = {{m}_{{in}}}({{T}_{1}} - {{T}_{2}})\quad {\text{на}}\quad {{\Gamma }_{{in}}} \times ({{t}_{0}},{{t}_{1}}), \\ \end{gathered} $

${\mathbf{U}}_{n}^{{( + )}}T_{2}^{*} + \frac{{\partial T_{2}^{*}}}{{\partial {{N}_{{T,2}}}}} = {{m}_{{in}}}({{T}_{2}} - {{T}_{1}})\quad {\text{на}}\quad {{\Gamma }_{{in}}} \times ({{t}_{0}},{{t}_{1}}).$

Несложно показать, что $\delta {{J}_{\alpha }}$ может быть представлена в следующем виде:

(10)

$\begin{gathered} \delta {{J}_{\alpha }} = \alpha \int\limits_{{{t}_{0}}}^{{{t}_{1}}} \,\int\limits_{{{\Gamma }_{{in}}}} \,(v - {{v}^{{(0)}}})\delta vd\Gamma dt + \int\limits_{{{\Gamma }_{{in}}}} \,\int\limits_{{{t}_{0}}}^{{{t}_{1}}} \,{{m}_{{in}}}T_{1}^{*}\left( {\bar {U}_{{n,1}}^{{( - )}}\delta {{T}_{1}} + \frac{{\partial \delta {{T}_{1}}}}{{\partial {{N}_{{T,1}}}}}} \right)d\Gamma dt + \\ \, + \int\limits_{{{\Gamma }_{{in}}}} \,\int\limits_{{{t}_{0}}}^{{{t}_{1}}} \,{{m}_{{in}}}T_{2}^{*}\left( {\bar {U}_{{n,2}}^{{( - )}}\delta {{T}_{2}} + \frac{{\partial \delta {{T}_{2}}}}{{\partial {{N}_{{T,2}}}}}} \right)d\Gamma dt = \\ \, = \alpha \int\limits_{{{\Gamma }_{{in}}}} \,\int\limits_{{{t}_{0}}}^{{{t}_{1}}} {{m}_{{in}}}\,(v - {{v}^{{(0)}}})\delta vd\Gamma dt + \int\limits_{{{\Gamma }_{{in}}}} \,\int\limits_{{{t}_{0}}}^{{{t}_{1}}} \,{{m}_{{in}}}(T_{1}^{*} - T_{2}^{*})\delta vd\Gamma dt. \\ \end{gathered} $

В силу произвольности выбора $\delta v$ из (10) получаем уравнение Эйлера (“необходимое условие оптимальности”, “вариационное уравнение”) вида

(11)

$\alpha {{m}_{{in}}}(v - {{v}^{{(0)}}}) + {{m}_{{in}}}(T_{1}^{*} - T_{2}^{*}) = 0\quad {\text{на}}\quad {{\Gamma }_{{in}}} \times ({{t}_{0}},{{t}_{1}}).$

Таким образом, решение задачи (8): ${{T}_{i}} = T$ в ${{D}_{i}} \times ({{t}_{0}},{{t}_{1}}),\;i = 1,2$, $v$ на ${{\Gamma }_{{in}}} \times ({{t}_{0}},{{t}_{1}})$ удовлетворяет системе уравнений (1)–(5) при $(D \equiv {{D}_{i}}) \times ({{t}_{0}},{{t}_{1}})$ $\left( {i = 1,2} \right)$, (9),(11).

Приведенные выше задачи в их “классических постановках” (т.е. когда все уравнения выполняются почти всюду на соответствующих множествах точек) можно записать в обобщенных постановках, а также как “операторные уравнения”. Так, введем следующие вещественные гильбертовы пространства [27]:

${{L}_{2}}\left( {({{t}_{0}},{{t}_{1}}) \times D} \right) \equiv \mathbb{H}:\mathop {\left( {\varphi ,\psi } \right)}\nolimits_H \equiv \left( {\varphi ,\psi } \right) = \int\limits_{{{t}_{0}}}^{{{t}_{1}}} \,\int\limits_D \,\varphi \psi dDdt,$

$W_{2}^{{0,1}}\left( {({{t}_{0}},{{t}_{1}}) \times D} \right) \equiv {{L}_{2}}\left( {({{t}_{0}},{{t}_{1}});W_{2}^{1}\left( D \right)} \right) \equiv Y:\mathop {\left( {\varphi ,\psi } \right)}\nolimits_Y = \left( {\varphi ,\psi } \right) + \int\limits_{{{t}_{0}}}^{{{t}_{1}}} \,\int\limits_D \,{\mathbf{Grad}}\,\varphi \cdot {\mathbf{Grad}}\,\psi dDdt,$

$W\left( {({{t}_{0}},{{t}_{1}}) \times D} \right) \equiv W:\mathop {\left\| \varphi \right\|}\nolimits_W = \mathop {\left( {\mathop {\left\| \varphi \right\|}\nolimits_Y^2 + \mathop {\left\| {\frac{{\partial \varphi }}{{\partial t}}} \right\|}\nolimits_{{{Y}^{ * }}}^2 } \right)}\nolimits^{1/2} ,$

где

$Y{\text{*}} = {{L}_{2}}\left( {({{t}_{0}},{{t}_{1}});(W_{2}^{1}(D)){\text{*}}} \right),$

$W_{2}^{1}\left( {({{t}_{0}},{{t}_{1}}) \times D} \right) \equiv W_{2}^{1}:\mathop {\left( {\varphi ,\psi } \right)}\nolimits_{W_{2}^{1}} = \mathop {\left( {\varphi ,\psi } \right)}\nolimits_Y + \left( {\frac{{\partial \varphi }}{{\partial t}},\frac{{\partial \psi }}{{\partial t}}} \right).$

Отметим, что если $\varphi \in W$, то $\varphi \in C\left( {[{{t}_{0}},{{t}_{1}}],{{L}_{2}}\left( D \right)} \right)$ (см. [27]) и

$_{{t \in [{{t}_{0}},{{t}_{1}}]}}max\mathop {\left\| \varphi \right\|}\nolimits_{{{L}_{2}}\left( D \right)} \leqslant C\mathop {\left\| \varphi \right\|}\nolimits_W ,\quad C = {\text{const}} < \infty .$

Пусть также

${{V}_{0}} = \left\{ {\varphi \in W:\varphi = 0\;{\text{при}}\;t = {{t}_{0}}\;{\text{почти}}\;{\text{всюду}}\;{\text{в}}\;D} \right\},$

${{V}_{1}} = \left\{ {\varphi \in W:\varphi = 0\;{\text{при}}\;t = {{t}_{1}}\;{\text{почти}}\;{\text{всюду}}\;{\text{в}}\;D} \right\}.$

Предполагается, что нормы во всех введенных пространствах порождаются соответствующими скалярными произведениями. Пусть в дальнейшем такие же пространства введены также при $D \equiv {{D}_{1}}$ и $D \equiv {{D}_{2}}$.

Введем следующие билинейные формы:

$\begin{gathered} {{a}_{i}}\left( {\varphi ,\psi } \right) \equiv - \left( {\varphi ,\frac{{\partial \psi }}{{\partial t}}} \right) - \left( {\varphi ,{\text{Div}}(\bar {U}\psi )} \right) + \int\limits_{{{t}_{0}}}^{{{t}_{1}}} \,\int\limits_D \,{{\nu }_{T}}\operatorname{Grad} \varphi \cdot {\mathbf{Grad}}\,\psi dDdt + \\ \, + \int\limits_{{{t}_{0}}}^{{{t}_{1}}} \,\left( {\int\limits_{{{\Gamma }_{{in}}}} \,U_{{n,i}}^{{( + )}}\varphi \psi d\Gamma + \int\limits_{{{\Gamma }_{{w,op}}}} \,U_{{n,i}}^{{( + )}}\varphi \psi d\Gamma + \int\limits_{{{\Gamma }_{s}}} \,{{\gamma }_{T}}\varphi \psi d\Gamma } \right)dt + \int\limits_{{{D}_{i}}} \,\mathop {\left. {\varphi \cdot \psi } \right|}\nolimits_{t = {{t}_{1}}} dD \\ {\text{при}}\quad \varphi ,\psi \in W\quad {\text{или}}\quad \varphi \in Y,\quad \psi \in {{V}_{1}},\quad i = 1,2, \\ \end{gathered} $

${{B}_{1}}\left( {v,\psi } \right) \equiv \int\limits_{{{t}_{0}}}^{{{t}_{1}}} \,\int\limits_{{{\Gamma }_{{in}}}} \,U_{{n,1}}^{{( - )}}v\psi d\Gamma dt\quad \forall \psi \in W\quad {\text{или}}\quad \psi \in {{V}_{1}},$

${{B}_{2}}\left( {v,\psi } \right) \equiv \int\limits_{{{t}_{0}}}^{{{t}_{1}}} \,\int\limits_{{{\Gamma }_{{in}}}} \,U_{{n,2}}^{{( - )}}v\psi d\Gamma dt\quad \forall \psi \in W\quad {\text{или}}\quad \psi \in {{V}_{1}}.$

Тогда задача для ${{T}_{1}},\;{\kern 1pt} {{T}_{2}}$ в обобщенных постановках формулируется так: найти ${{T}_{i}} \in \mathop {{{W}_{2}}}\nolimits^{0,1} ({{D}_{i}} \times ({{t}_{0}},{{t}_{1}})),\;i = 1,2$, такие, что выполнены соотношения вида

(12)

${{a}_{i}}\left( {{{T}_{i}},\psi } \right) = {{\mathcal{F}}_{i}}\left( \psi \right) + {{B}_{i}}\left( {v,\psi } \right)\quad \forall \psi \in {{V}_{1}}(({{t}_{0}},{{t}_{1}}) \times {{D}_{i}}),\quad i = 1,2,$

где

$\begin{gathered} {{\mathcal{F}}_{i}}\left( \psi \right) \equiv \int\limits_{{{t}_{0}}}^{{{t}_{1}}} \,\int\limits_{{{D}_{i}}} \,{{f}_{T}}\psi dDdt + \int\limits_{{{D}_{i}}} \,\mathop {\left. {T\left( 0 \right)\psi } \right|}\nolimits_{t = {{t}_{0}}} dD + \int\limits_{{{t}_{0}}}^{{{t}_{1}}} \,\int\limits_{{{\Gamma }_{S}}} \,{{\gamma }_{T}}{{T}_{a}}\psi dDd\Gamma dt + \\ + \;\int\limits_{{{t}_{0}}}^{{{t}_{1}}} \,\int\limits_{{{\Gamma }_{{w,op}}}} \,(U_{{n,i}}^{{( - )}}dT + {{Q}_{T}})\psi d\Gamma dt,\quad i = 1,2,\quad {\text{при}}\quad \psi \in W\quad {\text{или}}\quad \psi \in {{V}_{1}}. \\ \end{gathered} $

Обобщенная постановка задачи в $D \times ({{t}_{0}},{{t}_{1}})$ есть: найти функцию $T \in W_{2}^{{0,1}}(D \times ({{t}_{0}},{{t}_{1}})),$ удовлетворяющую (12) при $i = 1,2$ (при переобозначении ${{T}_{i}} \equiv T,$ ${{D}_{i}} \equiv D$) и выполнении первого условия из (4). Второе условие из (4) при этом оказывается естественным и оно рассматривается как равенство в $W_{2}^{{ - 1/2}}({{\Gamma }_{{in}}} \times ({{t}_{0}},{{t}_{1}})) \equiv (W_{2}^{{1/2}}({{\Gamma }_{{in}}} \times ({{t}_{0}},{{t}_{1}})){\text{*}})$. Введем операторы ${{L}_{i}},\;{{B}_{i}},\;{{C}_{i}}$ и функции ${{F}_{i}},\;i = 1,2$, определяемые в виде

$\mathop {\left( {{{L}_{i}}\varphi ,\psi } \right)}\nolimits_{{{L}_{2}}\left( {{{D}_{i}} \times \left( {{{t}_{0}},{{t}_{1}}} \right)} \right)} \equiv {{a}_{i}}\left( {\varphi ,\psi } \right)\quad \forall \varphi \in W_{2}^{{0,1}}({{D}_{i}} \times ({{t}_{0}},{{t}_{1}})),\quad \forall t \in W_{2}^{1}({{D}_{i}} \times ({{t}_{0}},{{t}_{1}})),$

$\mathop {\left( {{{B}_{i}}\varphi ,\psi } \right)}\nolimits_{{{L}_{2}}\left( {{{\Gamma }_{{in}}} \times \left( {{{t}_{0}},{{t}_{1}}} \right)} \right)} \equiv {{B}_{i}}\left( {v,\psi } \right)\quad \forall W_{2}^{1}\left( {{{D}_{i}} \times ({{t}_{0}},{{t}_{1}})} \right),$

${{C}_{i}}\varphi \equiv \mathop {\left. \varphi \right|}\nolimits_{{{\Gamma }_{{in}}}} \quad {\text{почти}}\;{\text{всюду}}\;{\text{на}}\quad ({{t}_{0}},{{t}_{1}})\quad \forall \varphi \in W_{2}^{{0,1}}({{D}_{i}} \times ({{t}_{0}},{{t}_{1}})),$

$\mathop {\left( {{{F}_{i}},\psi } \right)}\nolimits_{{{L}_{2}}\left( {{{D}_{i}} \times ({{t}_{0}},{{t}_{1}})} \right)} \equiv {{\mathcal{F}}_{i}}\left( \psi \right)\quad \forall \psi \in W_{2}^{1}\left( {{{D}_{i}} \times ({{t}_{0}},{{t}_{1}})} \right).$

Заметим, что оператор ${{C}_{i}}$ есть оператор взятия следа на ${{\Gamma }_{{in}}}$ при $t \in ({{t}_{0}},{{t}_{1}})$ у функции $\varphi \in W_{2}^{{0,1}}({{D}_{i}} \times ({{t}_{0}},{{t}_{1}}))$. Сузим область определения оператора ${{L}_{i}}$, приняв ее равной пространству $W_{2}^{1}({{D}_{i}} \times ({{t}_{0}},{{t}_{1}}))$, плотному в $W_{2}^{{0,1}}({{D}_{i}} \times ({{t}_{0}},{{t}_{1}})),$ $i = 1,2$. При этом за сужением операторов оставляем прежние обозначения ${{L}_{i}},\;i = 1,2$.

Теперь задачи для $\left\{ {{{T}_{i}}} \right\}$ можно записать в форме операторых уравнений:

(13)

${{L}_{i}}{{T}_{i}} = {{F}_{i}} + {{B}_{i}}v\quad {\text{в}}\quad V_{1}^{*},\quad {{C}_{1}}{{T}_{1}} = {{C}_{2}}{{T}_{2}}\quad {\text{почти}}\;{\text{всюду}}\;{\text{на}}\quad ({{t}_{0}},{{t}_{1}}) \times {{\Gamma }_{{in}}}.$

Далее, для операторов ${{L}_{i}},\;i = 1,2$, справедливо свойство положительной определенности:

$\begin{gathered} \left( {{{L}_{i}}\varphi ,\varphi } \right) = {{a}_{i}}\left( {\varphi ,\varphi } \right) = \int\limits_{{{t}_{0}}}^{{{t}_{1}}} \,\int\limits_{{{D}_{i}}} \,{{\nu }_{T}}\mathop {\left| {{\mathbf{Grad}}\,\varphi } \right|}\nolimits^2 dDdt + \\ + \;\int\limits_{{{t}_{0}}}^{{{t}_{1}}} \,\left[ {\int\limits_{{{\Gamma }_{s}}} \,{{\gamma }_{T}}{{\varphi }^{2}}d\Gamma + \int\limits_{{{\Gamma }_{{w,op}}} \cup {{\Gamma }_{s}}} \,\frac{1}{2}(U_{{n,i}}^{{( + )}} + U_{{n,i}}^{{( - )}}){{\varphi }^{2}}d\Gamma + \int\limits_{{{\Gamma }_{i}}} \,\frac{1}{2}(U_{{n,i}}^{{( + )}} + U_{{n,i}}^{{( - )}}){{\varphi }^{2}}d\Gamma } \right]dt + \\ + \;\frac{1}{2}\int\limits_{{{D}_{i}}} \,\left( {\mathop {\left. {{{\varphi }^{2}}} \right|}\nolimits_{t = {{t}_{0}}} + \mathop {\left. {{{\varphi }^{2}}} \right|}\nolimits_{t = {{t}_{1}}} } \right)dD \geqslant {{C}_{i}}\int\limits_{{{t}_{0}}}^{{{t}_{1}}} \,\int\limits_{{{D}_{i}}} \,\mathop {\left| \varphi \right|}\nolimits^2 dDdt,\quad {{C}_{i}} = {\text{const}} > 0,\quad i = 1,2. \\ \end{gathered} $

Следовательно, эти операторы обратимы.

Исключая ${{T}_{i}}$ из первого уравнения из (13): ${{T}_{i}} = L_{i}^{{ - 1}}\left( {{{F}_{i}} + {{B}_{i}}v} \right),$ $i = 1,2$, и подставляя во второе уравнение из (13), получаем

${{C}_{1}}L_{1}^{{ - 1}}\left( {{{F}_{1}} + {{B}_{1}}v} \right) = {{C}_{2}}L_{2}^{{ - 1}}\left( {{{F}_{2}} + {{B}_{2}}v} \right)$

или

(14)

$Av = g\quad {\text{в}}\quad {{L}_{2}}(({{t}_{0}},{{t}_{1}}) \times {{\Gamma }_{{in}}}),$

где

$A \equiv ({{C}_{1}}L_{1}^{{ - 1}}{{B}_{1}} - {{C}_{2}}L_{2}^{{ - 1}}{{B}_{2}}),\quad g \equiv {{C}_{2}}L_{2}^{{ - 1}}{{F}_{2}} - {{C}_{1}}L_{1}^{{ - 1}}{{F}_{1}}.$

Справдливо следующее

Утверждение 1. Оператор $A$ как оператор, действующий в ${{L}_{2}}\left( {\left( {{{t}_{0}},{{t}_{1}}} \right) \times {{\Gamma }_{{in}}}} \right)$ является непрерывным.

Доказательство. Пусть $v \in {{L}_{2}}(({{t}_{0}},{{t}_{1}}) \times {{\Gamma }_{{in}}})$. Тогда функция $\varphi \equiv L_{i}^{{ - 1}}{{B}_{i}}v$ принадлежит по крайней мере пространству $W_{2}^{1}({{D}_{i}})$ почти всюду на $\left( {{{t}_{0}},{{t}_{1}}} \right)$ (и даже пространству $W_{2}^{{1 + \varepsilon }}({{D}_{i}})$, где величина $\varepsilon > 0$ зависит от величины наименьшего угла в ${{D}_{i}}$, который в силу липшицевости ${{D}_{i}}$ положителен). Тогда функция ${{C}_{i}}\varphi $ принадлежит $W_{2}^{{1/2}}({{\Gamma }_{{in}}})$ почти всюду на $({{t}_{0}},{{t}_{1}})$, при этом

$\mathop {\left\| {{{C}_{i}}{{\varphi }_{i}}} \right\|}\nolimits_{W_{2}^{{1/2}}\left( {{{\Gamma }_{{in}}}} \right)} \left( t \right) \leqslant C\mathop {\left\| {{{\varphi }_{i}}} \right\|}\nolimits_{W_{2}^{1}\left( {{{D}_{i}}} \right)} \left( t \right)\quad {\text{почти}}\;{\text{всюду}}\;{\text{на}}\quad \left( {{{t}_{0}},{{t}_{1}}} \right),$

где $C = {\text{const}} < \infty $. Но тогда из последнего соотношения получаем

$\int\limits_{{{t}_{0}}}^{{{t}_{1}}} \,\mathop {\left\| {{{C}_{i}}{{\varphi }_{i}}} \right\|}\nolimits_{W_{2}^{{1/2}}\left( {{{\Gamma }_{{in}}}} \right)}^2 \left( t \right)dt \leqslant C\int\limits_{{{t}_{0}}}^{{{t}_{1}}} \,\mathop {\left\| {{{\varphi }_{i}}} \right\|}\nolimits_{W_{2}^{1}\left( {{{D}_{i}}} \right)}^2 \left( t \right)dt \leqslant \widetilde C\int\limits_{{{t}_{0}}}^{{{t}_{1}}} \,\mathop {\mathop {\left\| v \right\|}\nolimits^2 }\nolimits_{{{L}_{2}}\left( {{{\Gamma }_{{in}}}} \right)} dt,\quad \widetilde C = {\text{const}} < \infty .$

Следовательно, оператор $A$ является суммой двух ограниченных (а значит, и непрерывных) операторов, что и доказывает утверждение.

Замечание. В действительности решения ${{\varphi }_{i}},\;i = 1,2$, и функции $\left\{ {{{C}_{i}}\varphi } \right\}$ могут обладать “дополнительной гладкостью” и, возможно, установление полной непрерывности оператора $A$. Однако установление этого свойства $A$ носит скорее теоретический интерес, так как численное решение рассматриваемых здесь задач осуществляется часто при аппроксимации производных $\partial {\text{/}}\partial t$ по той или иной разностной схеме с последующим применением, например, метода разделения области. В результате таких процедур операторы, аналогичные введенному здесь оператору $A$, будут заведомо вполне непрерывными, и некоторые из “этих процедур” мы рассмотрим ниже.

Некоторые другие свойства оператора $A$, связанные с тривиальностью его ядра, будут рассмотрены в следующем разделе. Здесь лишь отмечаем, что используя введенный оператор $A$, мы можем представить ${{J}_{\alpha }}\left( v \right)$ как регуляризованный функционал

(15)

${{J}_{\alpha }}\left( v \right) = \frac{\alpha }{2}\int\limits_{{{\Gamma }_{{in}}}} \,\int\limits_{{{t}_{0}}}^{{{t}_{1}}} \,{{m}_{{in}}}\mathop {(v - {{v}^{{\left( 0 \right)}}})}\nolimits^2 d\Gamma dt + \frac{1}{2}\int\limits_{{{\Gamma }_{{in}}}} \,\int\limits_{{{t}_{0}}}^{{{t}_{1}}} \,\mathop {\left| {Av - g} \right|}\nolimits^2 d\Gamma dt,$

где $\left( {Av - g} \right) = {{T}_{1}} - {{T}_{2}}.$

Представление функционала ${{J}_{\alpha }}\left( v \right)$ в такой форме полезно при исследовании всей поставленной задачи, изучении метода разделения области в применении к этой задаче, формулировке итерационных алгоритмов ее решения (т.е. различных модификаций метода разделения области) и др. Некоторые из этих алгоритмов будут рассмотрены ниже, а здесь мы выпишем лишь уравнение Эйлера, которому удовлетворяет решение задачи минимизации ${{J}_{\alpha }}\left( v \right)$:

(16)

${{\mathcal{A}}_{\alpha }}v \equiv \alpha {{m}_{{in}}}v + A{\kern 1pt} {\text{*}}Av = {{g}_{\alpha }} \equiv (A{\kern 1pt} {\text{*}}g + \alpha {{m}_{{in}}}{{v}^{{\left( 0 \right)}}})\quad {\text{в}}\quad {{L}_{2}}({{\Gamma }_{{in}}} \times ({{t}_{0}},{{t}_{1}})),$

которое при $\alpha = 0$ есть второе уравнение из (4), записанное в смысле наименьших квадратов. Если $\alpha > 0$, то оператор ${{\mathcal{A}}_{\alpha }}$ самосопряжен и положительно определен в ${{L}_{2}}({{\Gamma }_{{in}}} \times ({{t}_{0}},{{t}_{1}}))$, а при $\alpha \geqslant 0$ он неотрицателен и компактен, если компактен $A$.

1.3. Разрешимость задач

Изучим вопрос о разрешимости задач (1), (4), (5), (16).

Если $\alpha > 0$, то, как хорошо известно, уравнение (16) имеет единственное решение, а значит, и задачи (1), (4), (5) будут также однозначно разрешимы. Поэтому наибольший интерес представляет случай $\alpha = 0$.

Теорема. Задача об определении ${{T}_{1}},\;{{T}_{2}},\;v$ однозначно и плотно разрешима.

Рассмотрим сначала однородную задачу (1) при $D = {{D}_{i}},$ $i = 1,2$, при выполнении условий

${{T}_{1}} = {{T}_{2}},\quad \left( {U_{{n,1}}^{{( - )}}{{T}_{1}} + \frac{{\partial {{T}_{1}}}}{{\partial {{N}_{{T,1}}}}}} \right) = - \left( {U_{{n,2}}^{{( - )}}{{T}_{2}} + \frac{{\partial {{T}_{2}}}}{{\partial {{N}_{{T,2}}}}}} \right) = v\quad {\text{на}}\quad ({{t}_{0}},{{t}_{1}}) \times {{\Gamma }_{{in}}}.$

Рассматривая данную задачу в $({{t}_{0}},{{t}_{1}}) \times (D = {{D}_{1}} \cup {{D}_{2}} \cup {{\Gamma }_{{in}}})$ (пусть даже с неизвестной $v$) для $T = {{T}_{i}}$ в $({{t}_{0}},{{t}_{1}}) \times {{D}_{i}},\;i = 1,2$, заключаем, что $T \equiv 0$ в $({{t}_{0}},{{t}_{1}}) \times D$. Это означает, что ${{T}_{i}} = 0$ в $({{t}_{0}},{{t}_{1}}) \times {{D}_{i}},\;i = 1,2$, а также, что $v = 0$. Таким образом, однородная задача (1), (4), (5) (или (16)) при $\alpha = 0$ имеет только тривиальное решение, что означает: обратная задача об определении ${{T}_{1}},\;{{T}_{2}},\;v$ однозначно разрешима, а также ${\text{Ker}}\left( A \right) = {\text{Ker}}(AA{\kern 1pt} {\text{*}}) = \left\{ 0 \right\}$.

Рассмотрим теперь однородную задачу (9) при условиях

(17)

$\left( {U_{{n,1}}^{{( + )}}T_{1}^{*} + \frac{{\partial T_{1}^{*}}}{{\partial {{N}_{{T,1}}}}}} \right) = {{m}_{{in}}}w,\quad \left( {U_{{n,2}}^{{( + )}}T_{2}^{*} + \frac{{\partial T_{2}^{*}}}{{\partial {{N}_{{T,2}}}}}} \right) = - {{m}_{{in}}}w\quad {\text{на}}\quad ({{t}_{0}},{{t}_{1}}) \times {{\Gamma }_{{in}}}$

(пока с неизвестной $w$) и при выполнении условия (см. (16)) при $\alpha = 0$:

${{m}_{{in}}}(T_{1}^{*} - T_{2}^{*})\quad {\text{на}}\quad ({{t}_{0}},{{t}_{1}}) \times {{\Gamma }_{{in}}}.$

Снова полагая $T{\text{*}} \equiv T_{i}^{*}$ в $({{t}_{0}},{{t}_{1}}) \times {{D}_{i}},\;i = 1,2$, и $T{\text{*}} = T_{1}^{*} = T_{2}^{*}$ на $({{t}_{0}},{{t}_{1}}) \times {{\Gamma }_{{in}}}$, имеем однородную задачу для $T{\text{*}}$ в $({{t}_{0}},{{t}_{1}}) \times D$. Следовательно, $T{\text{*}} \equiv 0$ в $({{t}_{0}},{{t}_{1}}) \times {{D}_{i}}$ и $w = 0$ (17). Таким образом, однородная сопряженная задача и уравнение $A{\kern 1pt} *{\kern 1pt} w = 0$ при $A{\text{*}} = B_{1}^{*}\mathop {(L_{1}^{{ - 1}})}\nolimits^* C_{1}^{*} + B_{2}^{*}\mathop {(L_{2}^{{ - 1}})}\nolimits^* C_{2}^{*}$ имеют только тривиальные разделения и ${\text{Ker}}(A{\kern 1pt} {\text{*}}) = \left\{ 0 \right\}$. А тогда рассматриваемая обратная задача об определении ${{T}_{1}},\;{{T}_{2}},\;v$ плотно разрешима и

$lim{{J}_{\alpha }} \to 0,\quad \left( {{{T}_{1}}\left( \alpha \right) - {{T}_{2}}\left( \alpha \right)} \right) \to 0\quad {\text{при}}\quad \alpha \to + 0$

(см. [8]). Если же выполнены условия существования “классического решения” ${{T}_{1}},\;{{T}_{2}},\;v$ данной обратной задачи, то также

${{T}_{1}}\left( \alpha \right) \to T,\quad {{T}_{2}}\left( \alpha \right) \to T\quad {\text{на}}\quad ({{t}_{0}},{{t}_{1}}) \times {{\Gamma }_{{in}}}\quad {\text{при}}\quad \alpha \to + 0.$

При наличии у классического решения некоторой дополнительной гладкости справедлива оценка вида

$\mathop {\left( {\int\limits_{{{t}_{0}}}^{{{t}_{1}}} \,\int\limits_{{{\Gamma }_{{in}}}} \,\left( {\mathop {\left( {v - \frac{{\partial {{T}_{1}}\left( \alpha \right)}}{{\partial {{N}_{{T,1}}}}}} \right)}\nolimits^2 + \mathop {\left( {v - \frac{{\partial {{T}_{2}}\left( \alpha \right)}}{{\partial {{N}_{{T,2}}}}}} \right)}\nolimits^2 } \right)d\Gamma dt} \right)}\nolimits^{1/2} \leqslant C\sqrt \alpha \quad {\text{при}}\quad \alpha \to + 0,$

где $C = {\text{const}} < \infty $.

Приведенные выше утверждения следуют из общих положений теории задач вариационной ассимиляции данных, изложенных в [24], [25].

1.4. Итерационные алгоритмы методов разделения области

Суть излагаемого в настоящей работе подхода к формулировке алгоритмов метода разделения области заключается в формулировке подходящего итерационного процесса для операторных уравнений в применении к уравнению (16) и выписывание его в терминах операторов исходных задач.

Так, один из простейших итерационных процессов решения [24] является следующим:

(18)

${{v}_{{k + 1}}} = {{v}_{k}} - {{\tau }_{k}}({{\mathcal{A}}_{\alpha }}{{v}_{k}} - {{g}_{\alpha }}),\quad k = 0,1,2,...,$

где $\{ {{\tau }_{k}}\} $ – параметры итерационного процесса. Известно, (см. [24], [29]), что если ${{\tau }_{k}} = \tau $ $\forall k$ и

$0 < \tau < \frac{2}{{2\alpha + \mathop {\left\| A \right\|}\nolimits^2 }}$

(чего всегда можно добиться считая $\tau $ “достаточно малым”), то процесс сходится.

Если считать, что ${{v}_{k}}$ уже определено, а ${{\tau }_{k}} \equiv \tau $ задано, то вычисление ${{v}_{{k + 1}}}$ осуществляется согласно (18) и, как легко заметить, эквивалентно вычислению ${{v}_{{k + 1}}}$ по следующей формуле:

${{v}_{{k + 1}}} = {{v}_{k}} - {{\tau }_{k}}(\alpha ({{v}_{k}} - {{v}^{{\left( 0 \right)}}}) + {{m}_{{in}}}(T_{{1,k}}^{*} - T_{{2,k}}^{*}))\quad {\text{на}}\quad ({{t}_{0}},{{t}_{1}}) \times {{\Gamma }_{{in}}},$

где $T_{{1,k}}^{*},\;T_{{2,k}}^{*}$ – решения сопряженных задач (9) в $({{t}_{0}},{{t}_{1}}) \times {{D}_{1}},\;({{t}_{0}},{{t}_{1}}) \times {{D}_{2}}$ при ${{T}_{1}} \equiv {{T}_{{1,k}}},$ ${{T}_{2}} \equiv {{T}_{{2,k}}}$ – решение (1) в $D \equiv {{D}_{1}},$ $D \equiv {{D}_{2}}$ и $v \equiv {{v}_{k}}$.

Как уже сказано выше, данный процесс сходится при достаточно малых ${{\tau }_{k}} \equiv \tau > 0,$ $k = 1,2,...,$ и любом $\alpha > 0$.

В силу наличия свойств однозначной и плотной разрешимости в рассматриваемой обратной задаче можно при достаточно малом $\alpha > 0$ выбирать $\tau $ в виде [24]

${{\tau }_{k}} = \frac{1}{2}\frac{{\int\limits_{{{\Gamma }_{{in}}}} \,\int\limits_{{{t}_{0}}}^{{{t}_{1}}} \,\mathop {({{T}_{{1,k}}} - {{T}_{{2,k}}})}\nolimits^2 d\Gamma dt}}{{\int\limits_{{{\Gamma }_{{in}}}} \,\int\limits_{{{t}_{0}}}^{{{t}_{1}}} \,\mathop {(T_{{1,k}}^{*} - T_{{2,k}}^{*})}\nolimits^2 d\Gamma dt}}.$

Как показала практика решений ряда задач, такой выбор ${{\tau }_{k}}$ значительно ускоряет скорость сходимости рассматриваемого итерационного процесса [24], [25].

В качестве другого примера решения (16) приведем здесь метод минимальных невязок. По форме он имеет тот же вид (18), однако, параметр ${{\tau }_{k}}$ выбирается по формуле (см. [29])

${{\tau }_{k}} = \frac{{({{\mathcal{A}}_{\alpha }}{{\xi }_{k}},{{\xi }_{k}})}}{{\mathop {\left\| {{{\mathcal{A}}_{\alpha }}{{\xi }_{k}}} \right\|}\nolimits^2 }},$

где скалярное произведение и норма в ${{L}_{2}}({{\Gamma }_{{in}}} \times ({{t}_{0}},{{t}_{1}}))$, а также

${{\xi }_{k}} = {{\mathcal{A}}_{\alpha }}{{v}_{k}} - A{\kern 1pt} {\text{*}}g = A{\kern 1pt} {\text{*}}\quad \left( {A{{v}_{k}} - g} \right)$

есть функция невязки.

Реализация данного алгоритма в форме метода разделения области состоит в следующем: если ${{v}_{k}}$ вычислено, то как и в предыдущем алгоритме

1) решаем прямые задачи в ${{D}_{i}} \times ({{t}_{0}},{{t}_{1}})$ при ${v} \equiv {{{v}}_{k}}$,

2) решаем сопряженные задачи в ${{D}_{i}} \times ({{t}_{0}},{{t}_{1}}),$ $i = 1,2$,

3) вычисляем ${{\xi }_{k}} = {{T}_{{1,k}}} - {{T}_{{2,k}}},$ $A{\kern 1pt} {\text{*}}{{\xi }_{k}} = T_{{1,k}}^{*} - T_{{2,k}}^{*}$ на ${{\Gamma }_{{in}}} \times ({{t}_{0}},{{t}_{1}})$,

4) вычисляем ${{\tau }_{k}}$:

${{\tau }_{k}} = \frac{{\int\limits_{{{t}_{0}}}^{{{t}_{1}}} \,\int\limits_{{{\Gamma }_{{in}}}} \,(T_{{1,k}}^{*} - T_{{2,k}}^{*})({{T}_{{1,k}}} - {{T}_{{2,k}}})dtd\Gamma }}{{\int\limits_{{{t}_{0}}}^{{{t}_{1}}} \,\int\limits_{{{\Gamma }_{{in}}}} \,\mathop {\left| {T_{{1,k}}^{*} - T_{{2,k}}^{*}} \right|}\nolimits^2 dtd\Gamma }}.$

Относительно скорости сходимости этого алгоритма легко распространить утверждения о скорости сходимости метода минимальных невязок (см. [29]).

1.5. Алгоритм разделения области для полудискретной модели

Во многих случаях приближенное решение (1) осуществляется при предварительной аппроксимации (1) по переменной t и переходе от задачи (1) к ее полудискретному аналогу. Так, предположим, что величина $\Delta t \equiv {{t}_{1}} - {{t}_{0}}$ достаточно мала и введем для определнности следующее приближение:

$\mathop {\left. {{{T}_{t}}} \right|}\nolimits_{t \equiv {{t}_{1}}} \equiv {{T}_{t}}({{t}_{1}}) \cong (T({{t}_{1}}) - T({{t}_{0}})){\text{/}}\Delta t.$

Подставляя его в (1) вместо первого уравнения, записанного при $t = {{t}_{1}}$, получаем уравнение вида (“стационарное уравнение конвекции-диффузии”):

(19)

$\left( {\bar {U},{\mathbf{Grad}}} \right)T - {\mathbf{Div}}\left( {{{\nu }_{T}}\,{\mathbf{Grad}}\,T} \right) + bT = {{F}_{T}}\quad {\text{в}}\quad D,$

где $b = 1{\text{/}}\Delta t,$ ${{F}_{T}} = {{f}_{T}}({{t}_{1}}) + T\left( 0 \right){\text{/}}\Delta t,...,\bar {U} = \bar {U}({{t}_{1}}),$ $T \equiv {{T}_{1}} \cong T({{t}_{1}})$.

Уравнение (19) рассматривается при граничных условиях из (1), соответственно уже на множествах ${{\Gamma }_{s}},...,{{\Gamma }_{H}}$ и условиях (4) на ${{\Gamma }_{{in}}}$.

Решение задачи для (19) может быть осуществлено аналогично тому, как это сделано выше для (1).

Согласно (5) вводим “дополнительное неизвестное” $v$, определенное на ${{\Gamma }_{{in}}}$ при $t = {{t}_{1}}$, которое необходимо определить вместе с ${{T}_{i}}$ в ${{D}_{i}},$ $i = 1,2$, рассматривая первое из равенств (4) как “уравнение замыкания”.

Приближенное решение задачи об отыскании ${{T}_{i}}$ в ${{D}_{i}},$ $i = 1,2$, и $v$ на ${{\Gamma }_{{in}}}$ осуществляется “вариационным методом”, переходя от требования “${{T}_{1}} = {{T}_{2}}$ на ${{\Gamma }_{{in}}}$” к экстремальной задаче (8), где функционал ${{J}_{\alpha }}$ есть

${{J}_{\alpha }}\left( v \right) = \frac{\alpha }{2}\int\limits_{{{\Gamma }_{{in}}}} \,{{m}_{{in}}}\mathop {(v - {{v}^{{\left( 0 \right)}}})}\nolimits^2 d\Gamma + \frac{1}{2}\int\limits_{{{\Gamma }_{{in}}}} \,{{m}_{{in}}}\mathop {({{T}_{1}} - {{T}_{2}})}\nolimits^2 d\Gamma ,$

где смысл $\alpha ,\;{{v}^{{\left( 0 \right)}}},\;{{m}_{{in}}}$ тот же, что и в (7).

Дальнейшее изучение и решение экстремальной задачи осуществляется как и ранее (при очевидных упрощениях). Отметим, что здесь справедливо

Утверждение 2. Оператор $A = ({{C}_{1}}L_{1}^{{ - 1}}{{B}_{1}} - {{C}_{2}}L_{2}^{{ - 1}}{{B}_{2}})$ является компактным в ${{L}_{2}}({{\Gamma }_{{in}}})$.

Доказательство. Каждая из функций ${{T}_{i}} \equiv L_{i}^{{ - 1}}{{B}_{i}}v,$ $i = 1,2$, здесь принадлежит $W_{2}^{1}({{D}_{i}})$. Следовательно, $({{C}_{i}}{{T}_{i}}) \in W_{2}^{{1/2}}({{\Gamma }_{{in}}})$. Но $W_{2}^{{1/2}}t({{\Gamma }_{{in}}})$ компактно вложено в ${{L}_{2}}({{\Gamma }_{{in}}})$, следовательно, операторы ${{C}_{i}}L_{i}^{{ - 1}}{{B}_{i}},$ $i = 1,2$, и оператор $A$ компактен в ${{L}_{2}}({{\Gamma }_{{in}}})$.

Следствие. “Обратная задача” об определении ${{T}_{i}}$ в ${{D}_{i}},\;i = 1,2$, и $v$ на ${{\Gamma }_{{in}}}$ при использовании условия замыкания вида “${{T}_{1}} = {{T}_{2}}$ на ${{\Gamma }_{{in}}}$” некорректна.

Численное решение рассматриваемой здесь экстремальной задачи можно осуществить, привлекая простейший итерационный алгоритм (18). В результате получаем следующий метод разделения области для стационарного уравнения конвекции-диффузии.

Пусть $v \equiv {{v}_{k}}$ уже определено. Тогда

1. В ${{D}_{i}}$ определяется функция $T_{i}^{k}$ как решение уравнения

$(\bar {U},{\mathbf{Grad}}){{T}_{i}} - {\mathbf{Div}}({{\nu }_{T}}\,{\mathbf{Grad}}\,{{T}_{i}}) + b{{T}_{i}} = {{F}_{T}}\quad {\text{в}}\quad {{D}_{i}},\quad i = 1,2,$

при условиях

${{U}_{{n,1}}}{{T}_{1}} + \frac{{\partial {{T}_{1}}}}{{\partial {{N}_{{T,1}}}}} = v,\quad {{U}_{{n,2}}}{{T}_{2}} + \frac{{\partial {{T}_{2}}}}{{\partial {{N}_{{T,2}}}}} = - v\quad {\text{на}}\quad {{\Gamma }_{{in}}}$

(остальные граничные условия на $\partial {{D}_{i}}{\backslash }{{\Gamma }_{{in}}}$ “очевидны”).

2. Решаем сопряженные задачи:

$ - {\mathbf{Div}}({\mathbf{U}}T_{i}^{*}) - {\mathbf{Div}}({{\nu }_{T}}\,{\mathbf{Grad}}\,T_{i}^{*}) + bT_{i}^{*} = 0\quad {\text{в}}\quad {{D}_{i}},\quad i = 1,2,$

при условиях

$U_{n}^{{( + )}}T_{1}^{*} + \frac{{\partial T_{1}^{*}}}{{\partial {{N}_{{T,1}}}}} = {{m}_{{in}}}({{T}_{1}} - {{T}_{2}}),\quad U_{n}^{{( + )}}T_{2}^{*} + \frac{{\partial T_{2}^{*}}}{{\partial {{N}_{{T,2}}}}} = {{m}_{{in}}}({{T}_{2}} - {{T}_{1}})\quad {\text{на}}\quad {{\Gamma }_{{in}}}.$

3. Находим новое приближение ${{v}_{{k + 1}}}$

${{v}_{{k + 1}}} = {{v}_{k}} - {{\tau }_{k}}(\alpha ({{v}_{k}} - {{v}^{{(0)}}}) + {{m}_{{in}}}(T_{1}^{*} - T_{2}^{*}))\quad {\text{на}}\quad {{\Gamma }_{{in}}},$

где параметр ${{\tau }_{k}}$ вычисляется по формуле

${{\tau }_{k}} = \frac{1}{2}\frac{{\int\limits_{{{\Gamma }_{{in}}}} \,\mathop {({{T}_{1}} - {{T}_{2}})}\nolimits^2 d\Gamma }}{{\int\limits_{{{\Gamma }_{{in}}}} \,\mathop {(T_{1}^{*} - T_{2}^{*})}\nolimits^2 d\Gamma }}.$

Сформулированный алгоритм разделения области сходится, если в качестве $\left\{ {{{\tau }_{k}}} \right\}$ выбирать “достаточно” малый положительный параметр $\tau $, причем

$\sum\limits_{i = 1}^2 \,\mathop {\left\| {{{T}_{i}} - {{T}_{{i,k}}}} \right\|}\nolimits_{W_{2}^{1}\left( {{{D}_{i}}} \right)} + \mathop {\left\| {v - {{v}_{k}}} \right\|}\nolimits_{{{L}_{2}}\left( {{{\Gamma }_{{in}}}} \right)} \to 0\quad {\text{при}}\quad \alpha \to + 0\quad {\text{и}}\quad k \to \infty $

(см., например, изложение рассуждений для алгоритма разделения области применительно к (1)).

1.6. Результаты численных экспериментов и обсуждение

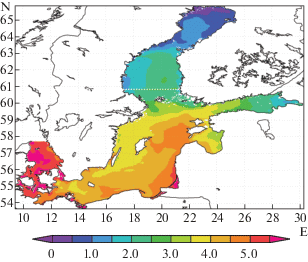
Для проверки эффективности использования метода разделения области был проведен ряд численных экспериментов, результаты которых будут представлены ниже. Исследования были проведены для разделения акватории Балтийского моря на две части. Рассмотрим метод разделения области, представленный в п. 1.5, в сравнении с решением задачи [30] без его применения. Результаты численных экспериментов для обоих случаев приведены ниже.

Результаты расчета для акватории без использования метода разделения области представлены на фиг. 1. Результаты расчета для области с применением алгоритма разделения области представлены на фиг. 2. Внутренняя граница ${{\Gamma }_{{in}}}$ для метода разделения области была выбрана между Ботническим заливом и остальной частью моря. Сравнивая результаты расчетов, изображенных на фиг. 1 и 2 , можно сделать вывод о том, что введение границы раздела двух областей оказывает слабое влияние на результаты расчета. Небольшая ошибка, до 0.5 градусов, возникает только на самой границе раздела.

Фиг. 1.

Температура на поверхности без использования метода разделения области, °С.

Фиг. 2.

Температура на поверхности с использованием метода разделения области, °С.

Разрезы по границе раздела областей представлены на фиг. 3. Здесь по вертикали отложена глубина, по горизонтали градусы восточной долготы. Граница раздела областей обозначена на фиг. 2 пунктирной линией. Расчет без использования метода разделения области представлен на фиг. 3а, то же значение температуры, но рассчитанной с использованием метода разделения области, представлено на 3б. Разность этих значений изображена на 3в.

Фиг. 3.

Профиль температуры по глубине на границе Γ_in: а) без использования метода разделения области; б) с применением метода разделения области; в) разница между полученными температурами, °С.

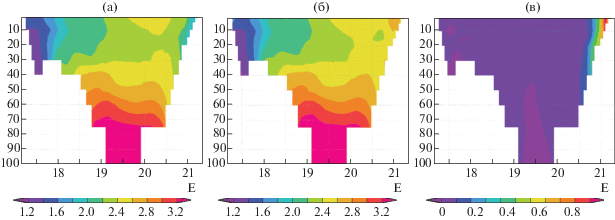
Проведенные численные эксперименты без и с использованием метода разделения области для задачи о распространении тепла в акватории Балтийского моря показывают хорошее соответствие результатов. Так, представленное на фиг. 3 сравнение температур на внутренней границе ${{\Gamma }_{{in}}}$ иллюстрирует почти полное их совпадение. Схожие результаты наблюдаются и во всей акватории, что подтверждается на фиг. 1 и 2 . Тем не менее в отдельных частях границы наблюдается значительно большее расхождение результатов, вплоть до 1 градуса. Это может быть вызвано тем, что в данной части границы наблюдается значительно большее, по сравнению с остальной частью, преобладание конвективной части над диффузионной. Для решения данной проблемы, возможно, требуется некоторая корректировка метода для устранения обнаруженного эффекта.

Таким образом, результаты расчетов свидетельствуют о возможности применения метода разделения области. При этом применяемый итерационный алгоритм показывает достаточно быструю сходимость. Однако метод требует модификации для расширения области его применения.

2. О ДРУГИХ ПОДХОДАХ К ФОРМУЛИРОВКЕ АЛГОРИТМОВ РАЗДЕЛЕНИЯ ОБЛАСТИ НА ОСНОВЕ НОВОЙ МЕТОДИКИ

Сделаем несколько замечаний о других подходах к построению методов разделения области, отличных от примененных в предыдущих разделах.

1. Пусть, например, рассматривается задача (1). При формулировке алгоритма разделения области ранее мы вводили дополнительное неизвестное согласно (5), тогда первое условие из (4) бралось в качестве “уравнения замыкания”. Но можно было бы поступить и так: дополнительное неизвестное вводится как ${{T}_{1}} = {{T}_{2}} = v$ на ${{\Gamma }_{{in}}}$, а в качестве уравнения замыкания принимается второе из условий (4). Дальнейшие шаги по построению алгоритмов разделения области такие же, как и ранее: уравнение замыкания записывается в смысле наименьших квадратов на ${{\Gamma }_{{in}}}$ (в подходящей норме), вводится регуляризованная экстремальная задача, выписываются вариационные уравнения, …, формируется алгоритм разделения области, соответствующий итерационному процессу решения уравнения.

2. Важным (как с теоретической точки зрения, так и для практической реализации алгоритмов) является выбор подходящего пространства и подходящей нормы в нем, в которых рассматривается уравнение замыкания. Так ранее, при рассмотрении (1) требование ${{T}_{1}} = {{T}_{2}}$ на ${{\Gamma }_{{in}}}$ мы рассматривали в ${{L}_{2}}$ (${{\Gamma }_{{in}}}$), что удобно при численной реализации формулируемых алгоритмов разделения области. Однако операторы $A$, $A{\kern 1pt} {\text{*}}$ в уравнениях (14), (16) здесь часто являются компактными, что необходимо учитывать при применении к этим уравнениям. Поэтому здесь, например, уравнение замыкания можно было бы рассматривать как равенство в $W_{2}^{{1/2}}({{\Gamma }_{{in}}})$ $\forall t$. Если же вводить дополнительное неизвестное как ${{T}_{1}} = {{T}_{2}} = {v}$ на ${{\Gamma }_{{in}}}$, то второе условие из (4) записывается как равенство в $W_{2}^{{ - 1/2}}({{\Gamma }_{{in}}})$ $\forall t$. Можно предположить, что операторы $A$, $A{\kern 1pt} {\text{*}}$ здесь будут не только ограниченными, но и положительно-определенными, что сразу же открывает новые возможности по формулировке быстро сходящихся итерационных алгоритмов. Однако нетрудно заметить, что в данных алгоритмах возникает дополнительный этап их реализации, связанный с вычислением норм в $W_{2}^{{1/2}}({{\Gamma }_{{in}}})$ $\forall t$, $W_{2}^{{ - 1/2}}({{\Gamma }_{{in}}})$ $\forall t$. При рассмотрении задачи (1) вычисление этих норм сводится к решению дополнительной задачи в ${{D}_{i}},\;i = 1,2$, для уравнения Лапласа (для упрощения изложения мы этот вопрос здесь не обсуждаем).

При применении описанных подходов к задаче для функции уровня $\xi $ в математической модели гидротермодинамики океана и моря (см., например, [30], [31]), помимо представленного ранее алгоритма, можно поступить следующим образом. Во всех наших подзадачах вместо

$\frac{{\partial T}}{{\partial t}},\;...,\;\frac{{\partial \xi }}{{\partial t}}$

вводятся их аппроксимации:

$\mathop {\left. {\frac{{\partial T}}{{\partial t}}} \right|}\nolimits_{{{t}_{j}}} \cong \frac{{T({{t}_{j}}) - T({{t}_{{j - 1}}})}}{{\Delta {{t}_{j}}}},\;...,\mathop {\left. {\;\frac{{\partial \xi }}{{\partial t}}} \right|}\nolimits_{{{t}_{j}}} \cong \frac{{\xi ({{t}_{j}}) - i({{t}_{{j - 1}}})}}{{\Delta {{t}_{j}}}}.$

После этого для ${{\xi }_{j}} \cong \xi ({{t}_{j}})$ получим эллиптическую задачу второго порядка, к которой применимы уже обычные подходы и алгоритмы, сформулированные, например, для (1).

Введение аппроксимаций задач по $t$ можно осуществить во всех подзадачах сформулированной ранее схемы расщепления, а не рассматривать эволюционные задачи по $t$.

Заметим также, что наличие свойств однозначной и плотной разрешимостей задачи при $\alpha = 0$ позволяет решать исходную задачу в $D \times \left( {0,\bar {t}} \right)$ методом разделения области последовательно в $D \times ({{t}_{{j - 1}}},{{t}_{j}})$, $j = 1,2,...,J$ (ранее этот метод рассматривался для определенности в $D \times ({{t}_{0}},{{t}_{1}})$.

4. Остановимся еще раз на проблеме учета свойства компактности оператора A.

В представленных выше алгоритмах разделения области для уравнения конвекции-диффузии мы в качестве дополнительного неизвестного (управления) брали значение

$U_{{n,1}}^{{( - )}}{{T}_{1}} + \frac{{\partial {{T}_{1}}}}{{\partial {{N}_{{T,1}}}}} = - \left( {U_{{n,2}}^{{( - )}}{{T}_{2}} + \frac{{\partial {{T}_{2}}}}{{\partial {{N}_{{T,2}}}}}} \right) = v$

функции $T$ на поверхности раздела, а условием сшивки выбиралось (фактически) равенство функций ${{T}_{i}},\;i = 1,2$, на поверхностях раздела. Такой подход эквивалентен рассмотрению на поверхности раздела некоторого уравнения $Av = g$ для $v$ с компактным, как правило, оператором $A$. Далее, от этого уравнения осуществляется переход к регуляризованному уравнению $A{\kern 1pt} {\text{*}}Av = A{\kern 1pt} {\text{*}}g$ (метод Тихонова, метод квазирешений с регуляризацией) и к последним применяется какой-либо итерационный процесс. При численной аппроксимации задач, реализующих этот процесс, вводятся дополнительные погрешности. А согласно классическим результатам теории некорректно поставленных задач выбор параметра $\alpha $ и число итераций необходимо согласовывать с вносимыми погрешностями численной аппроксимации. Иначе итерационный процесс может расходиться. На это обстоятельство в классических методах разделения области для эллиптических задач с симметричными операторами не обращается внимание и автору неизвестны работы с обсуждением этого вопроса. Вероятно, одной из причин этого является то, что часто исходная задача сразу аппроксимируется по методу конечных элементов, методу конечных разностей и т.д., а затем рассматривается метод разделения области в дискретных пространствах. Само уже уравнение $Av = g$ (как предельный аналог некоторых дискретных уравнений на поверхности раздела) вообще не вводится и не изучаются его свойства. Одним из подходов здесь является введение дискретных переобуславливателей с целью ускорения сходимости итерационных алгоритмов.

5. При формулировке алгоритмов разделения области для рассматриваемых нами задач в качестве функции управления можно было бы брать след искомых решений на поверхности раздела, а равенство конормальных производных на этой поверхности принимать за условие замыкания (см., например, работы Агошкова В.И., Лебедева В.И. по теории операторов Пуанкаре-Стеклова и методам разделения областей). Однако в данном случае оператор $A$ в уравнении $Au = g$, как правило, является неограниченным и формулировка итерационных алгоритмов в применении непосредственно к этому уравнению вызывает известные трудности. Чтобы преодолеть эти трудности, можно поступить несколькими способами: один из них заключается в рассмотрении уравнения $Au = g$ и итерационных алгоритмов для него в специальных шкалах функциональных пространств, в которых оператор $A$ был бы уже ограниченным. Другой способ состоит в введении переобуславливателей на “непрерывном дифференциальном уровне” и переходе от $Au = g$ к новому уравнению, но уже с ограниченным оператором. Наконец, можно сначала перейти от рассматриваемых задач к их конечномерным аппроксимациям (методам конечных разностей и т.д.) и переходу от $Au = g$ к уравнению ${{A}_{h}}{{u}_{h}} = {{g}_{h}}$ в конечномерном пространстве. Здесь норма $\left\| {{{A}_{h}}} \right\|$ будет конечна, но будет расти при уменьшении шагов сеток, увеличении числа базисных функций и т.п. Поэтому здесь снова можно ввести переобуславливатели (но теперь уже на дискретном уровне), чтобы ускорить сходимость формулируемых итерационных алгоритмов. Можно и не вводить переобуславливатели, но тогда будет наблюдаться зависимость скорости сходимости алгоритмов от размеров шагов разностных сеток и т.д.

Однако отметим, что применение указанных выше подоходов к решению задач конвекции-диффузии и многих других задач геофизической гидротермодинамики весьма затруднительно (а иногда совсем проблематично), т.к. операторы этих задач, как правило, несимметричны, часто некоэрцитивны и т.д.

6. Сформулированные выше подходы могут быть распространены на задачи порядка $2k$.

Так, пусть рассматриваются билинейные нормы вида

$\begin{gathered} {{a}_{i}}\left( {u,v} \right) = \sum\limits_{\left| p \right|,\left| q \right| \leqslant k} \,\int\limits_{{{D}_{i}}} \,{{a}_{{pq}}}\left( x \right){{D}^{p}}u{{D}^{q}}{v}dx,\quad i = 1,2, \\ a\left( {u,v} \right) = {{a}_{1}}\left( {u,{v}} \right) + {{a}_{2}}\left( {u,{v}} \right), \\ \end{gathered} $

где ${{D}^{p}}u \equiv \partial {{u}^{p}}{\text{/}}\partial x_{1}^{{{{p}_{1}}}}...\partial x_{n}^{{{{p}_{n}}}}$ – производная порядка $p$ функции $u$ (в смысле распределений), $\left| p \right| = {{p}_{1}} + {{p}_{2}} + ... + {{p}_{n}}$, $p = \left( {{{p}_{1}},{{p}_{2}},...,{{p}_{n}}} \right)$, ${{D}_{i}}$ – есть гладкое ограниченное подмножество ${{R}^{n}}$, $i = 1,2$, $D = {{D}_{1}} \cup {{D}_{2}} \cup {{\Gamma }_{{in}}}$, ${{\Gamma }_{{in}}}$ – “внутренняя граница”, разделяющая $D$ на ${{D}_{1}},\;{{D}_{2}}$, ${{a}_{{p,q}}}(x)$ являются достаточно гладкими.

Считаем, что форма ${{a}_{i}}\left( {u,v} \right)$ является $W_{2}^{k}({{D}_{i}})$ ограниченной и $W_{2}^{k}({{D}_{i}})$ коэрцитивной, $i = 1,2$, тогда как форма $a\left( {u,v} \right)$ является $W_{2}^{k}\left( D \right)$ ограниченной и $W_{2}^{k}\left( D \right)$ коэрцитивной.

Введем оператор ${{L}_{i}}$, соответствующий форме ${{a}_{i}}\left( {u,v} \right)$ и определяемый соотношением

${{L}_{i}}u = \sum\limits_{\left| p \right|,\left| q \right| \leqslant k} \,\mathop {\left( { - 1} \right)}\nolimits^q {{D}^{q}}({{a}_{{pq}}}(x){{D}^{p}}u)$

с областью определения

$D({{L}_{i}}) = \{ u:u \in W_{2}^{k}({{D}_{i}}),\;{{L}_{i}}u \in {{L}_{2}}({{D}_{i}})\} .$

Для определенности пусть на внешней части границы $\partial {{D}_{i}}{\backslash }\partial {{\Gamma }_{{in}}}$ функция $u \in D({{L}_{i}})$ удовлетворяет следующим граничным условиям: $\gamma _{j}^{{\left( i \right)}}u = 0$ на $\partial {{D}_{i}}{\backslash }\partial {{\Gamma }_{{in}}},$ $0 \leqslant j \leqslant k - 1$, где ${{\gamma }_{j}}u = {{\partial }^{j}}u{\text{/}}\partial {{n}^{j}}$ – производная по нормали к $\partial {{D}_{i}}$ порядка $j$ к функции $u$ (при $j = 0$ функция $\gamma _{0}^{{\left( i \right)}}u = 0$ есть сужение и на $\partial {{D}_{i}}$ – “след” функции и на $\partial {{D}_{i}}$: $\gamma _{0}^{{\left( i \right)}}u \equiv u{\text{/}}\partial {{D}_{i}}$”).

Справедлива следующая формула Грина (см. [32]):

$\begin{gathered} {{a}_{i}}(u,v) = \mathop {({{L}_{i}}u,v)}\nolimits_{{{L}_{2}}\left( {{{D}_{i}}} \right)} + \sum\limits_{0 \leqslant j \leqslant k - 1} \,\int\limits_{\partial {{D}_{i}}} \,\delta _{{2k - 1 - j}}^{{\left( i \right)}}u\gamma _{j}^{{\left( i \right)}}vd\Gamma , \\ \forall u \in D({{L}_{i}}),\quad v \in W_{2}^{k}({{D}_{i}}), \\ \end{gathered} $

где ${{\delta }_{j}}$ – дифференциальные операторы порядка $j$ ($k \leqslant j \leqslant 2k - 1$).

Пусть оператор L определяется в виде

$Lu \equiv {{L}_{i}}u\quad {\text{в}}\quad {{D}_{i}},\quad i = 1,2,$

с областью определения $D\left( L \right)$:

$D(L) \equiv \{ u:u \in W_{2}^{k}(D),\;Lu \in {{L}_{2}}(D),\;{{\gamma }_{j}}u = 0\;{\text{на}}\;\partial D,\;0 \leqslant j \leqslant k - 1\} .$

Данный оператор соответствует форме $a\left( {u,{v}} \right)$, и формула Грина здесь имеет вид

$a\left( {u,v} \right) = \mathop {\left( {Lu,v} \right)}\nolimits_{{{L}_{2}}\left( D \right)} + \sum\limits_{0 \leqslant j \leqslant k - 1} \,\int\limits_{\partial D} \,{{\delta }_{{2k - 1 - j}}}u{{\gamma }_{j}}vd\Gamma ,\quad \forall u \in D\left( L \right),\quad v \in W_{2}^{k}\left( D \right).$

Привлекая приведенные выше формулы Грина, форму $a\left( {u,{v}} \right)$ можно представить также в следующей форме:

$\begin{gathered} a\left( {u,v} \right) = \sum\limits_{i = 1}^2 \,{{a}_{i}}\left( {u,v} \right) = \sum\limits_{i = 1}^2 \,\mathop {\left( {{{L}_{i}}u,v} \right)}\nolimits_{{{L}_{2}}\left( {{{D}_{i}}} \right)} + \sum\limits_{i = 1}^2 \,\left( {\sum\limits_{0 \leqslant j \leqslant k - 1} \,\int\limits_{\partial {{D}_{i}}/\partial {{\Gamma }_{{in}}}} \,\delta _{{2k - 1 - j}}^{{\left( i \right)}}u\gamma _{j}^{{\left( i \right)}}vd\Gamma } \right) + \\ + \;\sum\limits_{0 \leqslant j \leqslant k - 1} \,\left( {\int\limits_{{{\Gamma }_{{in}}}} \,(\delta _{{2k - 1 - j}}^{{\left( 1 \right)}}{{u}^{{\left( 1 \right)}}} + \delta _{{2k - 1 - j}}^{{\left( 2 \right)}}{{u}^{{\left( 2 \right)}}}){{\gamma }_{j}}vd\Gamma } \right),\quad \forall u \in D\left( L \right),\quad \forall v \in W_{2}^{k}\left( D \right), \\ \end{gathered} $

где ${{u}^{i}} \equiv u$ в ${{D}_{i}},$ $i = 1,2$ ${{\gamma }_{j}}v = \gamma _{j}^{{(1)}}v = \gamma _{j}^{{(2)}}v$ $\forall v \in W_{2}^{k}\left( D \right)$.

Пусть в последующем

$\begin{gathered} \mathop {W_{2}^{k}}\limits^{^{ \circ }} (D) = \{ u:u \in W_{2}^{k}(D),\;{{\gamma }_{j}}u = 0\;{\text{на}}\;\partial D\;{\text{при}}\;0 \leqslant j \leqslant k - 1\} , \\ \mathop {W_{2}^{k}}\limits^{^{ \circ }} ({{D}_{i}}) = \{ u:u \in W_{2}^{k}({{D}_{i}}),\;{{\gamma }_{j}}u = 0\;{\text{на}}\;\partial {{D}_{i}}{\backslash }{{\Gamma }_{{in}}}\;{\text{при}}\;0 \leqslant j \leqslant k - 1\} ,\quad i = 1,2. \\ \end{gathered} $

Очевидно, что приведенные выше формулы Грина справедливы (с очевидными упрощениями их формы) при ${v} \in \mathop {W_{2}^{k}}\limits^{^{ \circ }} ({{D}_{1}}), \ldots ,{v} \in \mathop {W_{2}^{k}}\limits^{^{ \circ }} {\kern 1pt} \left( D \right).$

Пусть задана функция $f \in {{L}_{2}}\left( D \right)$ и пусть ${{f}_{i}} \equiv f$ в $D$, $i = 1,2$.

Рассмотрим теперь исходную задачу в $D$: требуется найти $u \in D\left( L \right) \cap \mathop {W_{2}^{k}}\limits^{^{ \circ }} \left( D \right)$, т.ч.

$Lu = f\;{\text{в}}\;D.$

Эта задача эквивалентна следующей вариационной задаче (см. [32]): найти $u \in D\left( L \right)$, т.ч.

$a\left( {u,{v}} \right) = \mathop {\left( {f,{v}} \right)}\nolimits_{{{L}_{2}}\left( D \right)} \quad \forall {v} \in \mathop {W_{2}^{k}}\limits^{^{ \circ }} {\kern 1pt} \left( D \right).$

Как следует из изложенного выше, решение $u$ этих задач на “внутренней границе” ${{\Gamma }_{{in}}}$ (границе раздела $D$ на подобласти ${{D}_{1}}$, ${{D}_{2}}$) необходимо и достаточно удовлетворяет условиям сшивки:

$\begin{gathered} {{\gamma }_{j}}{{u}^{1}} = {{\gamma }_{j}}{{u}^{2}}\quad {\text{на}}\quad {{\Gamma }_{{in}}}, \\ \delta _{{2k - 1 - j}}^{1}{{u}^{1}} + \delta _{{2k - 1 - j}}^{2}{{u}^{2}}\quad {\text{на}}\quad {{\Gamma }_{{in}}},\quad 0 \leqslant j \leqslant k - 1, \\ \end{gathered} $

где ${{u}^{{\left( i \right)}}} \equiv u\;{\text{в}}\;{{D}_{i}},\;i = 1,2.$

Имея данные условия, можно предложить алгоритм разделения области решения “исходной задачи” $D$. Так, например, рассматриваются следующие задачи в подобластях ${{D}_{i}}$: найти ${{u}_{i}} \in D({{L}_{i}}) \cap \mathop {W_{2}^{k}}\limits^{^{ \circ }} {\kern 1pt} ({{D}_{i}}),$ $i = 1,2,$ т.ч.

(20)

${{L}_{i}}{{u}_{i}} = f\quad {\text{в}}\quad {{D}_{i}}$

или что равносильно

(21)

$a\left( {{{u}_{i}},{v}} \right) = \left( {{{f}_{i}},{v}} \right)\quad \forall {v} \in \mathop {W_{2}^{k}}\limits^{^{ \circ }} ({{D}_{i}})$

при выполнении условий вида

(22)

$\begin{gathered} {{\gamma }_{j}}{{u}_{1}} = {{\gamma }_{j}}{{u}_{2}}\quad {\text{на}}\quad {{\Gamma }_{{in}}}, \\ \delta _{{2k - 1 - j}}^{{\left( 1 \right)}}{{u}_{1}} = - \delta _{{2k - 1 - j}}^{{\left( 2 \right)}}{{u}_{2}} \equiv {{V}_{j}}\quad {\text{на}}\quad {{\Gamma }_{{in}}},\quad 0 \leqslant j \leqslant k - 1. \\ \end{gathered} $

Будем считать функции $\{ {{V}_{j}}\} $ “дополнительными неизвестными”, тогда как соотношение (22) рассматриваем как “уравнение замыкания”. Ставится “обратная задача” вида: найти ${{u}_{i}}$ в ${{D}_{i}},$ и “граничные функции” $\{ {{V}_{j}}\} $, т.ч. выполнены уравнения (20) (или 21) и равенства (22).

Дальнейшее изучение этой задачи и ее приближенное решение осуществляется уже “известными подходами и методами”. Так, условия (22) записываются в “смысле наименьших квадратов”, например,

(23)

$\mathop {inf}\limits_{\left\{ {{{V}_{j}}} \right\}} \left\| {{{\gamma }_{j}}{{u}_{1}} - {{\gamma }_{j}}{{u}_{2}}} \right\|_{{{{L}_{2}}\left( {{{\Gamma }_{{in}}}} \right)}}^{2},\quad 0 \leqslant j \leqslant k - 1.$

От требований (23) переходим к экстремальной задаче вида

$\mathop {inf}\limits_{\left\{ {{{V}_{j}}} \right\}} {{J}_{\alpha }}\left( {\mathbf{V}} \right),$

где $\bar {V} = ({{V}_{0}},{{V}_{1}},...,{{V}_{{k - 1}}})$ – “вектор управлений”,

${{J}_{\alpha }}\left( {\mathbf{V}} \right) \equiv \sum\limits_{j = 0}^{k - 1} \,\mathop {{{\alpha }_{j}}\left\| {{{V}_{j}} - V_{j}^{{\left( 0 \right)}}} \right\|}\nolimits_{{{L}_{2}}\left( {{{\Gamma }_{{in}}}} \right)}^2 + \sum\limits_{j = 0}^{k - 1} \,{{\beta }_{j}}\mathop {\left\| {{{\gamma }_{j}}{{u}_{1}} - {{\gamma }_{j}}{{u}_{2}}} \right\|}\nolimits_{{{L}_{2}}\left( {{{\Gamma }_{{in}}}} \right)}^2 ,$

${{u}_{i}}$ – есть решение задачи (20), (23), ${{\alpha }_{j}} \geqslant 0$ – параметры регуляризаций, ${{\alpha }_{j}} > 0$ – заданные “весовые коэффициенты”, $\{ V_{j}^{0}\} $ – заданные функции (например, $V_{j}^{0} \equiv 0,$ $\forall j$).

Исследование этой экстремальной задачи можно осуществить на основе общей методологии из [24] с привлечением теории сопряженных уравнений. А формулируя итерационный алгоритм ее решения (см. [24]), мы получим соответствующий алгоритм разделения области решения исходной задачи.

7. Итак, в настоящем разделе мы представили некоторые предложения по развитию алгоритмов и подходов решения краевых задач методами разделения области. Более детальное изучение этих алгоритмов и подходов вероятно целесообразно изучать, конкретизируя рассматриваемую задачу.

Так, в работе [31] на основе предлагаемых подходов сформулированы и исследованы (теоремы разрешимости, о сходимости и др.) методы разделения области для уравнений мелкой воды (как представителя гиперболических систем 1-го порядка) и для эллиптических уравнений 4-го порядка.

Численные эксперименты, результаты которых приводятся здесь, проведены Лезиной Н.Р., с любезного согласия которой они представлены здесь. Автор благодарит Лезину Н.Р. за данную помощь.

Список литературы

Матеева Э.И., Пальцев Б.В. О разделении области при решении краевых задач для уравнения Пуассона в областях сложной формы // Ж. вычисл. матем. и матем. физ. 1973. Т. 13. № 6. С. 1441–1452.
Цвик Л.Б. Обобщение алгоритма Шварца на случай областей, сопряженных без налегания // Докл. АН СССР. 1975. Т. 224. № 2. С. 309–312.
Смелов В.В. Принцип итерирования по подобластям в задачах с уравнением переноса // Ж. вычисл. матем. и матем. физ. 1981. Т. 21. № 6. С. 131–143.
Осмоловский В.Г., Ривкинд В.Я. О методе разделения областей для эллиптических уравнений с разрывными коэффициентами // Ж. вычисл. матем. и матем. физ. 1981. Т. 21. № 1. С. 35–39.
Канцельсон В.Э., Меньшиков В.В. Об одном аналоге альтернирующего метода Шварца // Теория функций, функциональный анализ и их приложения. Х.: Изд-во Харьк. ун-та, 1973. Вып. 17. С. 206–215.
Кузнецов Ю.А. Итерационные методы в подпространствах. М.: ОВМ АН СССР, 1984.
Мацокин А.М. Метод фиктивных компонент и модифицированный аналог метода Шварца // Вычисл. методы линейной алгебры. Новосибирск, 1980.
Агошков В.И. Метод разделения области в задачах гидродинамики. I. Задача о плоской циркуляции в океане. М.: Препринт/ОВМ АН СССР. 1985. № 96.
Агошков В.И. Метод разделения области в задачах гидродинамики. II. Задача о распределении температуры. М.: Препринт/ОВМ АН СССР. 1986. № 118.
Агошков В.И. Метод разделения области в задачах гидродинамики. III. Задача для уравнения переноса. М.: Препринт/ОВМ АН СССР. М., 1986. № 120.
Агошков В.И., Лебедев В.И. Операторы Пуанкаре–Стеклова и методы разделения области в вариационных задачах // Вычисл. процессы и системы. Вып. 2. М.: Наука, 1985. С. 173–227.
Glovinsky R. Domain decomposition methods for nonlinear problems in fluid dynamics // Rapports de Recherche, INRIA. Paris, 1982.
Wildlund O.B. Iterative Methods for Elliptic Problems oп Regions Partitioned into Substructures and the Biharmonic Dirichlet Problem. Preprint, 1983.
Fischler A. Resolution du pгobleme de Stokes par une methode de decomposition de domaines. Application a la simulation numerique d’ecoulements de Navier–Stokes de fluides incompressibles en elements finis // These pour l’obtention du diplome de docteur de 3e cycle L’Universite Pierre et Marie Curie. Paris, 1985. V. 6.
Дрыя М. Метод разделения области решения вариационно-разностных систем для эллиптических задач // Вариационно-разностные методы в математической физике. М.: ОВМ АН СССР, 1984. С. 46–57.
Dryja M. A capacitance matrix method for Dicichlet pгoblem oп polygon region // Numer. Math. 1982. V. 39. P. 51–64.
Quarteroni A., Landriani G.S. Domain Decomposition Preconditioners for the Spectral Collocation Method/Istituto di Analisi Numecica del Consiglio Nazionale delle Ricerche. Pavia, 1987.
Chan T.F. Analysis of preconditioners for domain decomposition // SIAM J. Numer. Anal. 1987. V. 24. P. 382–390.
Лебедев В.И., Агошков В.И. Операторы Пуанкаре–Стеклова и их приложения в анализе. М.: ОВМ АН СССР, 1983.
Ягола А.Г. О выборе параметра регуляризации при решении некорректных задач в рефлексивных пространствах // Ж. вычисл. матем. и матем. физ. 1980. Т. 20. № 3. С. 586–596.
Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М.: Наука, 1979. 285 с.
Иванов В.К., Васин В.В., Танана В.П. Теория линейных некорректных задач и ее приложения. М.: Наука, 1978. 206 с.
Денисов А.М. Введение в теорию обратных задач. М.: Изд-во МГУ, 1994. 208 с.
Агошков В.И. Методы оптимального управления и сопряженных уравнений в задачах математической физики. М.: ИВМ РАН, 2016. 244 с.
Агошков В.И. Методы решения обратных задач и задач вариационной ассимиляции данных наблюдений в проблемах крупномасштабной динамики океанов и морей. М.: ИВМ РАН, 2016. 192 с.
Васильев Ф.П. Методы решения экстремальных задач. М.: Наука, 1981. 400 с.
Лионс Ж.-Л., Мадженес Э. Неоднородные граничные задачи и их приложения / Пер. с франц. Л.С. Франка; под ред. В.В. Грушина. М.: Мир, 1971. 372 с.
Темам Р. Уравнения Навье–Стокса. М.: Мир, 1981. 408 с.
Марчук Г.И. Методы вычислительной математики. М.: Наука, 1980. 608 с.
Марчук Г.И., Дымников В.П., Залесный В.Б. Математические модели в геофизической гидродинамике и численные методы их реализации. Л.: Гидрометеоиздат, 1987. 296 с.
Агошков В.И. Методы разделения области в задачах гидротермодинамики океанов и морей. М.: ИВМ РАН, 2017. 188 с.
Обен Ж.-П. Приближенное решение эллиптических краевых задач. М.: Мир, 1977. 384 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал