Журнал вычислительной математики и математической физики, 2020, T. 60, № 4, стр. 725-737
Метод разностных потенциалов для эволюционных уравнений с лакунами
С. В. Петропавловский 1, С. В. Цынков 2, *
1 Национальный исследовательский университет
“Высшая школа экономики”
101000 Москва, ул. Мясницкаая, 20, Россия
2 Department of Mathematics, North Carolina State University
Box 8205NC 27695 Raleigh, USA
* E-mail: tsynkov@math.ncsu.edu
Поступила в редакцию 14.11.2019
После доработки 14.11.2019
Принята к публикации 16.12.2019
Аннотация
Предложен граничный метод для расчета нестационарного распространения волн в трехмерном пространстве. Излагаемый подход базируется на методе разностных потенциалов и принципе Гюйгенса, позволяющем реализовать обновление решения на границе рассеивателя, используя лишь определенный фиксированный по времени интервал. Библ. 7. Фиг. 4.
1. ВВЕДЕНИЕ
Граничные методы решения задач математической физики давно и успешно используются для решения, в основном, эллиптических задач. Главное преимущество граничной постановки – снижение размерности исходной задачи на единицу путем перехода к уравнениям для неизвестных величин, заданных лишь на границе области, в которой требуется найти решение [1]. Непосредственное обобщение такого подхода на нестационарные задачи наталкивается на очевидную трудность: граница для эволюционной задачи представляет собой пространственно-временнóе многообразие – прямое произведение пространственной границы области и отрезка времени, на котором требуется найти решение, – причем с ростом времени интегрирования эта граница разрастается, заставляя хранить и решать все большее количество переменных и уравнений [2]. На практике подобный подход оказывается неприменим уже при малых временах интегрирования.
В данной работе представлен граничный метод решения некоторых гиперболических уравнений, свободный от указанного недостатка. Мы рассматриваем уравнения, для которых выполняется принцип Гюйгенса, т.е., иными словами, решения которых обладают конечной памятью “назад” по времени. Последнее эквивалентно наличию лакун в решении данных уравнений, т.е. областей пространства-времени, где решения обращаются в ноль по окончании работы источника (правой части уравнения), порождающего данное решение. Практически важными примерами подобных уравнений являются трехмерное волновое уравнение с постоянными коэффициентами и система Максвелла в вакууме. Ограниченная во времени зависимость решений этих уравнений позволяет разбить интервал интегрирования на небольшие части и продвигаться по времени шагами фиксированной длительности, последовательно обновляя решение некоторых граничных уравнений. Тем самым удается совместить преимущества граничной формулировки (снижение размерности по пространственным переменным на единицу) с алгоритмом обновления решения в духе обычной разностной схемы для эволюционного уравнения. За счет снижения размерности построенный алгоритм оказывается более эффективным с точки зрения вычислительной сложности, чем традиционное решение эволюционного уравнения с помощью явной разностной схемы (это свойство выполняется начиная с определенной длительности расчета).
Другой особенностью предлагаемого подхода является способ сведения и особенно решения граничной задачи. Традиционный подход базируется на дискретизации интегралов, взятых по границе, и решении возникающей алгебраической системы. Для областей со сложной геометрией указанный прием может вызвать значительные вычислительные сложности. Дополнительная трудность связана с сингулярностью ядер в фигурирующих свертках. В нашем изложении мы опираемся на метод разностных потенциалов [3], позволяющий вычислять возникающие свертки путем решения вспомогательной задачи, поставленной в геометрически простой области (скажем, кубе), с помощью любой подходящей разностной схемы на простейшей прямоугольной сетке. Последнее обстоятельство обеспечивает легкость реализации алгоритма, возможность контролировать и увеличивать точность расчета путем использования схем повышенной точности и другие преимущества, присущие конечно-разностному подходу. При этом никакой потери точности, связанной с аппроксимацией криволинейных границ/граничных условий на прямоугольной сетке, не происходит.
В данной работе мы описываем метод, используя для демонстрации внешнюю задачу для трехмерного волнового уравнения. Иными словами, мы решаем задачу рассеяния волн на препятствии с произвольно сложной формой границы, интересуясь отраженным полем. Применительно к задачам рассеяния дополнительным преимуществом любого граничного метода, в частности, описанного ниже, служит точный учет условия излучения на бесконечности. При использовании объемных методов интегрирования условия излучения на бесконечности заменяются специально построенными для этой цели искусственными краевыми условиями на внешней границе расчетной области, см., например, [4]. Кроме того, в наших расчетах мы используем разностную схему повышенного (четвертого) порядка точности, что позволяет эффективно бороться с проявлениями так называемой численной дисперсии.
В разд. 2 представлена общая идея метода в непрерывной формулировке. Основным моментом здесь является схема продвижения во времени небольшими шагами. Разд. 3 содержит детали дискретизации алгоритма. В разд. 4 приводятся результаты тестового расчета.
2. ИДЕЯ МЕТОДА
Рассмотрим внешнюю задачу для трехмерного волнового уравнения с постоянными коэффициентами
(2.1)
${{\square }_{c}}u = 0,\quad ({\mathbf{x}},t) \in {{\mathbb{R}}^{3}}{\backslash }\Omega \times (0,T],$(2.3)
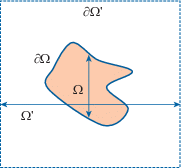
$\mathop {\left. u \right|}\nolimits_{t = 0} = \mathop {\left. {\partial u{\text{/}}\partial t} \right|}\nolimits_{t = 0} = 0,$Рассмотрим несколько бóльшую вспомогательную область $\Omega {\text{'}} \supset \Omega $ такую, что разность 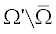 (черта над $\Omega $ означает замыкание) содержит в себе, в частности, расчетную область, где требуется
найти решение поставленной задачи. Без потери общности будем предполагать, что $\Omega {\text{'}}$ представляет собой параллелепипед. Выберем также некоторую запаздывающую функцию
Грина (фундаментальное решение) $G({\mathbf{x}},t)$ уравнения (2.1). Применим формулу Грина к четырехмерной области
(черта над $\Omega $ означает замыкание) содержит в себе, в частности, расчетную область, где требуется
найти решение поставленной задачи. Без потери общности будем предполагать, что $\Omega {\text{'}}$ представляет собой параллелепипед. Выберем также некоторую запаздывающую функцию
Грина (фундаментальное решение) $G({\mathbf{x}},t)$ уравнения (2.1). Применим формулу Грина к четырехмерной области 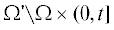 , $t \leqslant T$ (см. [5]):
, $t \leqslant T$ (см. [5]):
(2.4)
$ + \;\mathop \smallint \limits_{{{{\Gamma }}_{t}}} \left\{ {\frac{{\partial u}}{{\partial {\mathbf{n}}}}\left( {{\mathbf{y}},t{\kern 1pt} '} \right)G\left( {{\mathbf{x}} - y,t - t{\kern 1pt} '} \right) - u\left( {{\mathbf{y}},t{\kern 1pt} {\text{'}}} \right)\frac{{\partial G}}{{\partial {\mathbf{n}}}}\left( {{\mathbf{x}} - {\mathbf{y}},t - t{\kern 1pt} '} \right)} \right\}dt{\kern 1pt} {\text{'}}d{{S}_{{\mathbf{y}}}} + $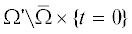 , и ненулевым временам ${{\Gamma }_{t}} \equiv \partial \Omega \times (0,t]$ и $\Gamma _{t}^{'} \equiv \partial \Omega {\text{'}} \times (0,t]$, причем $\Gamma _{t}^{'}$ отвечает пространственно-временнóй границе вспомогательной области $\Omega {\text{'}}$.
, и ненулевым временам ${{\Gamma }_{t}} \equiv \partial \Omega \times (0,t]$ и $\Gamma _{t}^{'} \equiv \partial \Omega {\text{'}} \times (0,t]$, причем $\Gamma _{t}^{'}$ отвечает пространственно-временнóй границе вспомогательной области $\Omega {\text{'}}$.
Первый член в (2.4) равняется нулю из-за однородных граничных условий (2.3). Последний интеграл в формуле (2.4) берется по пространственно-временнóй границе вспомогательной области $\Gamma _{t}^{'} \equiv \partial \Omega {\text{'}} \times (0,t]$ и равняется нулю при условии, что выбранная функция Грина есть фундаментальное решение трехмерного волнового уравнения, распространяющееся в пустом пространстве, т.е.
(2.5)
$G({\mathbf{x}},t) = \frac{1}{{4\pi {\text{|}}{\mathbf{x}}{\text{|}}}}\delta (t - \left| {\mathbf{x}} \right|{\text{/}}c).$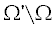 через его значения (и значения его нормальной производной) на границе рассеивателя
$\Omega $ во все предыдущие моменты времени.
через его значения (и значения его нормальной производной) на границе рассеивателя
$\Omega $ во все предыдущие моменты времени.
По аналогии с формулой (2.4) вводится потенциал Кальдерона с плотностью ${{\xi }_{{{{\Gamma }_{t}}}}} = ({{\xi }_{0}},{{\xi }_{1}})$, определенной на ${{\Gamma }_{t}}$:
(2.6)
${{{\mathbf{P}}}_{{\tilde {\Omega }}}}{{\xi }_{{{{\Gamma }_{t}}}}}({\mathbf{x}},t) = \int\limits_{{{\Gamma }_{t}}} \,\left\{ {{{\xi }_{1}}({\mathbf{y}},t{\text{'}})G({\mathbf{x}} - {\mathbf{y}},t - t{\text{'}}) - {{\xi }_{0}}({\mathbf{y}},t{\text{'}})\frac{{\partial G}}{{\partial {\mathbf{n}}}}({\mathbf{x}} - {\mathbf{y}},t - t{\text{'}})} \right\}dt{\text{'}}d{{S}_{{\mathbf{y}}}},$Сравнивая формулы (2.4) и (2.6), нетрудно заметить, что функции ${{\xi }_{0}}$ и ${{\xi }_{1}}$ можно интерпретировать как след на $\partial \Omega $ уходящего из $\Omega {\text{'}}$ решения и его нормальной производной. Доказывается, см. [3], что пара ${{\xi }_{{{{\Gamma }_{t}}}}} = ({{\xi }_{0}},{{\xi }_{1}})$ действительно является следом уходящего решения тогда и только тогда, когда ${{\xi }_{{{{\Gamma }_{t}}}}}$ удовлетворяет граничному уравнению с проектором (ГУП):
(2.7)
${{{\mathbf{P}}}_{{{{\Gamma }_{t}}}}}{{\xi }_{{{{\Gamma }_{t}}}}} = {{\xi }_{{{{\Gamma }_{t}}}}}.$Таким образом, ГУП (2.7) совместно с граничным условием (2.8) являются эквивалентной граничной формулировкой исходной системы (2.2) с искомой величиной ${{\xi }_{{{{\Gamma }_{t}}}}}$ (возможно, только одной неизвестной компонентой в случае условий Дирихле и Неймана). Размерность задачи при этом снижается на единицу по сравнению с исходной системой. По найденной плотности ${{\xi }_{{{{\Gamma }_{t}}}}}$ решение $u({\mathbf{x}},t)$ в трехмерной области $\tilde {\Omega } = {{\mathbb{R}}^{3}}{\backslash }\Omega $ восстанавливается по формуле (2.6).
Подчеркнем, что интегрирование в формуле (2.6) проводится по (2 + 1)-мерному многообразию и в случае геометрически сложного рассеивателя
$\Omega $ может представлять вычислительно нетривиальную задачу. В этой связи удобно использовать
другое, эквивалентное представление потенциала Кальдерона. Рассмотрим функцию $w({\mathbf{x}},t)$, определенную на ${{\mathbb{R}}^{3}}{\backslash }\Omega \times (0,t]$ и такую, что ${\mathbf{T}}{{{\mathbf{r}}}_{{{{\Gamma }_{t}}}}}w = {{\xi }_{{{{\Gamma }_{t}}}}}$, $w({\mathbf{x}},0) = \tfrac{{\partial w({\mathbf{x}},0)}}{{\partial t}} = 0$. Иными словами, от функции $w({\mathbf{x}},t)$ требуется лишь то, чтобы ее след и след ее нормальной производной на ${{\Gamma }_{t}}$ совпадал с ${{\xi }_{{{{\Gamma }_{t}}}}}$, а также выполнялись указанные начальные условия. В остальном эта функция произвольна,
в частности, она не обязана быть решением волнового уравнения (2.1), т.е. в общем случае ${{\square }_{c}}w \ne 0$ на ${{\mathbb{R}}^{3}}{\backslash }\Omega \times (0,t]$. На практике функцию $w({\mathbf{x}},t)$ можно построить продолжением с границы ${{\Gamma }_{t}}$ с помощью ряда Тейлора, где необходимые производные второго и более высоких порядков
вычисляются с помощью исходного уравнения (2.1), см. разд. 2. Применяя формулу Грина к данной функции на 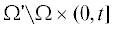 и разрешая получающееся соотношение относительно интересующей нас величины (2.6),
нетрудно убедиться, что потенциал Кальдерона можно представить в следующем виде:
и разрешая получающееся соотношение относительно интересующей нас величины (2.6),
нетрудно убедиться, что потенциал Кальдерона можно представить в следующем виде:
(2.9)
${{{\mathbf{P}}}_{{\tilde {\Omega }}}}{{\xi }_{{{{\Gamma }_{t}}}}}({\mathbf{x}},t) = w({\mathbf{x}},t) - v({\mathbf{x}},t),\quad {\mathbf{x}} \in \tilde {\Omega },$Подчеркнем еще раз, что ВЗ (2.10) решается в простой (прямоугольной) вспомогательной области $\Omega {\text{'}}$ без “дырки”, отвечающей рассеивателю $\Omega $; вся информация о геометрии этого объекта (возможно, сложной и не совпадающей с линиями декартовой сетки), а также граничных условиях на нем содержится в функции $w(x,t)$ и переходит в правую часть (2.10) и далее в формулу (2.9). Данное обстоятельство позволяет использовать конечно-разностный метод на простейших прямоугольных сетках для расчета объектов сложной геометрической формы без какой-либо потери точности, связанной с несовпадением границ объекта с линиями сетки.
Представим теперь, что нам требуется найти решение задачи указанным методом в конечный момент времени $t = T$. С ростом $T$ граница ${{\Gamma }_{T}} = \partial \Omega \times (0,T]$, где определена плотность ${{\xi }_{{{{\Gamma }_{T}}}}}$, увеличивается линейно, и уже при умеренных $T$ метод становится практически неприменимым из-за необходимости хранения и решения уравнения относительно разрастающейся со временем величины ${{\xi }_{{{{\Gamma }_{T}}}}}$.
Для того, чтобы снять это ограничение, разобъем интервал $(0,T]$ на $K$ частей длины ${{T}_{0}}$, $K{{T}_{0}} = T$, и на каждой парциальной пространственно-временной границе
Фиг. 2.
(a) Разбиение во времени, конус зависимости решения. (б) Лакуна в решении. По горизонтальной оси условно отложено трехмерное пространство.
Однако легко заметить, что для выбранной функции Грина (2.5) интегрирование в потенциале Кальдерона (2.6) осуществляется по пересечению светового конуса с вершиной в точке границы ${{\Gamma }_{k}}$ и поверхности рассеивателя $\Omega $ в предыдущие моменты времени, см. фиг. 2а, где для демонстрации положено $k = K$. Рассматривая все точки из ${{\Gamma }_{K}}$, где мы интересуемся плотностью ${{\xi }_{{{{\Gamma }_{K}}}}}$, данное пересечение не пусто максимум в течение времени $2{{T}_{0}}$, отсчитывая назад от последнего (наиболее позднего) момента времени множества ${{\Gamma }_{K}}$ (т.е. для случая, изображенного на рисунке, $t = T$), при условии, что размер разбиения принят равным
Иными словами, при условии (2.11) плотности ${{\xi }_{{{{\Gamma }_{s}}}}}$, отвечающие более ранним элементам разбиения ${{\Gamma }_{s}}$, $s = 1,...,K - 2$, никак не влияют на плотность, определенную на элементе ${{\Gamma }_{K}}$. То же самое можно объяснить на языке лакун решения волнового уравнения в свободном пространстве, когда решение, порожденное источником (правой частью), локализованным в пространстве-времени на границе предыдущего элемента разбиения (${{\Gamma }_{1}}$ на фиг. 2б), заведомо уходит из области $\Omega $ за время (2.11). Таким образом, глубина зависимости решения уравнения (2.7) ограничена назад одним элементом разбиения, что позволяет построить рекуррентную схему обновления плотности:(2.12)
${{{\mathbf{P}}}_{{{{\Gamma }_{k}}}}}{{\xi }_{{{{\Gamma }_{k}}}}} + {{{\mathbf{R}}}_{{{{\Gamma }_{k}}}}}{{\xi }_{{{{\Gamma }_{{k - 1}}}}}} = {{\xi }_{{{{\Gamma }_{k}}}}},$(2.13)
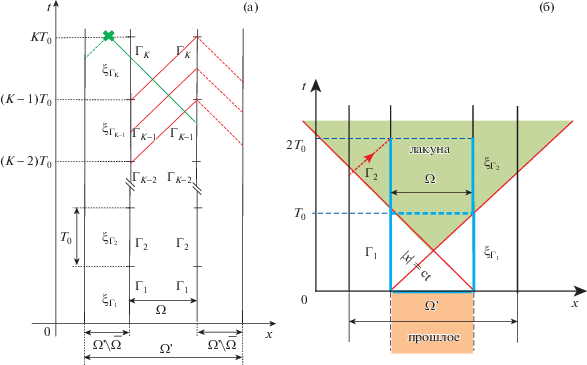
${{{\mathbf{R}}}_{{{{\Gamma }_{k}}}}}{{\xi }_{{{{\Gamma }_{{k - 1}}}}}}({\mathbf{x}},t) = {\mathbf{T}}{{{\mathbf{r}}}_{{{{\Gamma }_{k}}}}}\int\limits_{{{\Gamma }_{{k - 1}}}} \,\left\{ {{{\xi }_{1}}({\mathbf{y}},t{\kern 1pt} {\text{'}})G({\mathbf{x}} - {\mathbf{y}},t - t{\kern 1pt} {\text{'}}) - {{\xi }_{0}}({\mathbf{y}},t{\kern 1pt} {\text{'}})\frac{{\partial G}}{{\partial {\mathbf{n}}}}({\mathbf{x}} - {\mathbf{y}},t - t{\kern 1pt} {\text{'}})} \right\}dt{\kern 1pt} {\text{'}}d{{S}_{{\mathbf{y}}}}$Фиг. 3.
Сетка, покрывающая вспомогательную область $\Omega {\text{'}}$. Зелеными точками обозначены узлы, составляющие дискретную границу рассеивателя $\gamma $. Желтыми квадратами условно обозначен шаблон разностной схемы [6].
Парциальные плотности ${{\xi }_{{{{\Gamma }_{k}}}}}$ и ${{\xi }_{{{{\Gamma }_{{k - 1}}}}}}$ удобно разложить в ряд на ${{\Gamma }_{k}}$ и ${{\Gamma }_{{k - 1}}}$ по системе каких-либо базисных функций
(2.14)
${{\xi }_{{{{\Gamma }_{{k - 1}}}}}} = \sum\limits_s \,c_{{0,s}}^{{({\text{I}})}}{{\psi }_{{0,s}}} + c_{{1,s}}^{{({\text{I}})}}{{\psi }_{{1,s}}},\quad {{\xi }_{{{{\Gamma }_{k}}}}} = \sum\limits_s \,c_{{0,s}}^{{({\text{II}})}}{{\psi }_{{0,s}}} + c_{{1,s}}^{{({\text{II}})}}{{\psi }_{{1,s}}},$Укажем также, что ядро интегралов (2.6) и (2.13) с учетом явного вида (2.5) инвариантно относительно сдвигов во времени. Поэтому с учетом использования одного и того же базиса для всех элементов разбиения результат действия операторов (2.6) и (2.13) на базисные элементы на множестве ${{\Gamma }_{k}}$ (левая часть уравнения (2.12)) можно рассчитать на любых двух смежных элементах разбиения длительностью ${{T}_{0}}$, например, ${{\Gamma }_{1}}$ и ${{\Gamma }_{2}}$, и обозначить результат через ${{{\mathbf{P}}}_{{{{\Gamma }_{{{{T}_{0}}}}}}}}{{\psi }_{s}}$ и ${{{\mathbf{R}}}_{{{{\Gamma }_{{{{T}_{0}}}}}}}}{{\psi }_{s}}$. При этом уравнение (2.7) примет вид
(2.15)
${{{\mathbf{P}}}_{{{{\Gamma }_{{{{T}_{0}}}}}}}}{{\xi }_{{{{\Gamma }_{k}}}}} + {{{\mathbf{R}}}_{{{{\Gamma }_{{{{T}_{0}}}}}}}}{{\xi }_{{{{\Gamma }_{{k - 1}}}}}} = {{\xi }_{{{{\Gamma }_{k}}}}}.$(2.16)
$\sum\limits_s \,c_{{0,s}}^{{({\text{II}})}}\underbrace {\left\{ {{{{\mathbf{P}}}_{{{{\Gamma }_{{{{T}_{0}}}}}}}} - {\mathbf{I}}} \right\}}_{{{{\mathbf{Q}}}_{{{{\Gamma }_{{{{T}_{0}}}}}}}}}{{\psi }_{{0,s}}} + c_{{1,s}}^{{({\text{II}})}}\underbrace {\left\{ {{{{\mathbf{P}}}_{{{{\Gamma }_{{{{T}_{0}}}}}}}} - {\mathbf{I}}} \right\}}_{{{{\mathbf{Q}}}_{{{{\Gamma }_{{{{T}_{0}}}}}}}}}{{\psi }_{{1,s}}} = - \sum\limits_s \,c_{{0,s}}^{{({\text{I}})}}{{{\mathbf{R}}}_{{{{\Gamma }_{{{{T}_{0}}}}}}}}{{\psi }_{{0,s}}} + c_{{1,s}}^{{({\text{I}})}}{{{\mathbf{R}}}_{{{{\Gamma }_{{{{T}_{0}}}}}}}}{{\psi }_{{1,s}}},$3. ДИСКРЕТИЗАЦИЯ
Введем на вспомогательной области $\Omega {\text{'}}$ (параллелепипиде) прямоугольную сетку с шагом $h$ по каждому пространственному измерению. Еще раз подчеркнем, что хотя разностное решение задачи определено и требуется лишь вне препятствия $\Omega $, мы тем не менее рассматриваем дискретизацию всей области $\Omega $. Заметим также, что граница объекта $\partial \Omega $ может не совпадать с линиями введенной прямоугольной сетки. Решением задачи будем интересоваться в дискретные моменты времени с шагом $\tau $, т.е., иными словами, введем сетку на четырехмерной области $\Omega {\text{'}} \times [0,T]$ с указанными шагами. Для дискретизации уравнения (2.2) воспользуемся компактной разностной схемой четвертого порядка точности с шаблоном, состоящим из $3 \times 3 \times 3 \times 3 = 81$ точек:
(3.1)
$\Delta {{u}^{{n + 1}}} - \frac{{{{u}^{{n + 1}}}}}{{\theta {{\tau }^{2}}{{c}^{2}}}} = 2\left( {\Delta {{u}^{n}} - \frac{{{{u}^{n}}}}{{\theta {{\tau }^{2}}{{c}^{2}}}}} \right) - \left( {\Delta {{u}^{{n - 1}}} - \frac{{{{u}^{{n - 1}}}}}{{\theta {{\tau }^{2}}{{c}^{2}}}}} \right) - \frac{1}{\theta }\Delta {{u}^{n}},$Обозначим через ${{\mathbb{N}}_{m}}$ точки сетки, принадлежащие данному 81-точечному шаблону с центром в узле сетки $m$. Введем, далее, несколько требуемых в дальнейшем подмножеств пространственно-временной
прямоугольной сетки, покрывающей $\Omega {\text{'}} \times [0,T]$. Именно, обозначим через ${{\mathbb{M}}^{ - }}$ и ${{\mathbb{M}}^{ + }}$ подмножества узлов сетки, попадающих в области 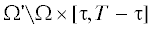 и $\Omega \times [0,T]$ соответственно. Таким образом, ${{\mathbb{M}}^{ - }}$ и ${{\mathbb{M}}^{ + }}$ представляют собой узлы сетки, лежащие вне и внутри объекта $\Omega $ во все моменты времени $t \in [0,T]$; узлы, попадающие на границу препятствия $\partial \Omega $, включаются в ${{\mathbb{M}}^{ + }}$. При этом центр шаблона ${{\mathbb{N}}_{m}}$ находится внутри областей
и $\Omega \times [0,T]$ соответственно. Таким образом, ${{\mathbb{M}}^{ - }}$ и ${{\mathbb{M}}^{ + }}$ представляют собой узлы сетки, лежащие вне и внутри объекта $\Omega $ во все моменты времени $t \in [0,T]$; узлы, попадающие на границу препятствия $\partial \Omega $, включаются в ${{\mathbb{M}}^{ + }}$. При этом центр шаблона ${{\mathbb{N}}_{m}}$ находится внутри областей 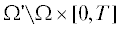 и $\Omega \times [0,T]$, если $m \in {{\mathbb{M}}^{ - }}$ и $m \in {{\mathbb{M}}^{ + }}$ соответственно.
и $\Omega \times [0,T]$, если $m \in {{\mathbb{M}}^{ - }}$ и $m \in {{\mathbb{M}}^{ + }}$ соответственно.
Пусть ${{\gamma }^{ + }}$ обозначает подмножество узлов, удовлетворяющих одновременно двум условиям: эти узлы
принадлежат шаблону ${{\mathbb{N}}_{m}}$ с центром $m \in {{\mathbb{M}}^{ - }}$ и лежат внутри $\Omega $. Аналогично, подмножество ${{\gamma }^{ - }}$ обозначает узлы, принадлежащие шаблону ${{\mathbb{N}}_{m}}$ с центром $m \in {{\mathbb{M}}^{ + }}$ и лежащие вне $\Omega $. Объединение ${{\gamma }^{ + }} \cup {{\gamma }^{ - }} \equiv \gamma $ образует тонкий слой узлов, охватывающий пространственно-временную границу $\Gamma $ рассеивателя $\Omega $ и заменяющий $\Gamma $ в дискретной постановке, см. фиг. 3. Рассмотрим также множества ${{\mathbb{N}}^{ + }} = \bigcup\nolimits_{m \in {{\mathbb{M}}^{ + }}}^{} {{{\mathbb{N}}_{m}}} $ и ${{\mathbb{N}}^{ - }} = \bigcup\nolimits_{m \in {{\mathbb{M}}^{ - }}}^{} {{{\mathbb{N}}_{m}}} $, включающие все точки шаблона ${{\mathbb{N}}_{m}}$, когда центр последнего пробегает все точки из ${{\mathbb{M}}^{ + }}$ или ${{\mathbb{M}}^{ - }}$ соответственно. В частности, ${{\mathbb{N}}^{ - }}$ содержит точки на границе $\partial \Omega {\text{'}}$, первый и последний слои по времени $t = \{ 0,T\} $ внутри области 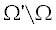 , а также подмножество ${{\gamma }^{ + }}$. Объединение ${{\mathbb{N}}^{0}} = {{\mathbb{N}}^{ + }} \cup {{\mathbb{N}}^{ - }}$ есть набор всех точек сетки, которые попадают в шаблон ${{\mathbb{N}}_{m}}$, когда $m \in {{\mathbb{M}}^{ + }} \cup {{\mathbb{M}}^{ - }}$.
, а также подмножество ${{\gamma }^{ + }}$. Объединение ${{\mathbb{N}}^{0}} = {{\mathbb{N}}^{ + }} \cup {{\mathbb{N}}^{ - }}$ есть набор всех точек сетки, которые попадают в шаблон ${{\mathbb{N}}_{m}}$, когда $m \in {{\mathbb{M}}^{ + }} \cup {{\mathbb{M}}^{ - }}$.
Все введенные выше (под)множества узлов отвечали сетке, покрывающей всю пространственно-временную область $\Omega {\text{'}} \times [0,T]$, отвечающую конечному моменту времени $T$. Очевидно, что все эти конструкции можно определить и на любой части $\Omega {\text{'}} \times [0,t]$, $t < T$, снабдив их подстрочным индексом $t$. В частности, множество ${{\gamma }_{t}}$ является дискретным аналогом границы ${{\Gamma }_{t}}$ из разд. 2.
3.1. Разностные потенциалы
Введем сеточную функцию ${{\xi }_{{{{\gamma }_{t}}}}}$, определенную на сеточной границе ${{\gamma }_{t}}$. Рассмотрим также сеточную функцию ${{w}^{{(h)}}}$, определенную в точках $\mathbb{N}_{t}^{0}$ и такую, что ее след на ${{\gamma }_{t}}$ совпадает с ${{\xi }_{{{{\gamma }_{t}}}}}$:
Оператор взятия следа ${\mathbf{Tr}}_{{{{\gamma }_{t}}}}^{{(h)}}$, введенный выше, осуществляет сужение сеточной функции с множества $\mathbb{N}_{t}^{0}$ на дискретную границу ${{\gamma }_{t}} \subset \mathbb{N}_{t}^{0}$. Обозначим через $\square _{c}^{{(h)}}$ дискретный оператор Лапласа, отвечающий избранной разностной схеме. По аналогии с формулой (2.10) построим “правую часть”, дополненную нулем для узлов сетки внутри рассеивателя $\Omega $:Определим разностный потенциал с плотностью ${{\xi }_{{{{\gamma }_{t}}}}}$ как сеточную функцию, заданную на $\mathbb{N}_{t}^{ - }$, по следующему правилу:
(3.2)
${{{\mathbf{P}}}_{{\mathbb{N}_{t}^{ - }}}}{{\xi }_{{{{\gamma }_{t}}}}} = {{\left. {{{w}^{{(h)}}}} \right|}_{{\mathbb{N}_{t}^{ - }}}} - \;{{{\mathbf{G}}}^{{(h)}}}\left( {\square \mathop {\left. {_{c}^{{(h)}}{{w}^{{(h)}}}} \right|}\nolimits_{\mathbb{M}_{t}^{ - }} } \right),$(3.3)
$\square _{c}^{{(h)}}{{v}^{{(h)}}} = \;\square \mathop {\left. {_{c}^{{(h)}}{{w}^{{(h)}}}} \right|}\nolimits_{\mathbb{M}_{t}^{ - }} $(3.4)
$n{{P}_{{{{\gamma }_{t}}}}}{{\xi }_{{{{\gamma }_{t}}}}}\;\mathop = \limits^{{\text{def}}} \;{\mathbf{Tr}}_{{{{\gamma }_{t}}}}^{{(h)}}{{{\mathbf{P}}}_{{\mathbb{N}_{t}^{ - }}}}{{\xi }_{{{{\gamma }_{t}}}}}.$Можно показать, что конечно-разностное граничное уравнение с проектором (ГУП) [ср. c (2.7)]
(3.5)
${{{\mathbf{P}}}_{{{{\gamma }_{t}}}}}{{\xi }_{{{{\gamma }_{t}}}}} = {{\xi }_{{{{\gamma }_{t}}}}}$Как и в непрерывной формулировке, разностное ГУП (3.5), определенное на дискретной границе ${{\gamma }_{t}}$, эквивалентно заменяет собой разностное волновое уравнение ${{\left. {\square _{c}^{{(h)}}u_{{\mathbb{N}_{t}^{ - }}}^{{(h)}}} \right|}_{{\mathbb{M}_{t}^{ - }}}} = 0$ с нулевыми начальными условиями, рассматриваемое на множестве $\mathbb{N}_{t}^{ - }$, т.е. вне рассеивателя $\Omega $.
Очевидно, существует множество решений ${{\xi }_{{{{\gamma }_{t}}}}}$ разностного ГУП (3.5), т.к. существует множество решений $u_{{\mathbb{N}_{t}^{ - }}}^{{(h)}}$ разностного волнового уравнения $\square _{c}^{{(h)}}u_{{\mathbb{N}_{t}^{ - }}}^{{(h)}}$ во внешних по отношению к рассеивателю узлах $\mathbb{M}_{t}^{ - }$. Для выбора требуемого решения уравнение (3.5) должно быть дополнено соответствующим условием, следующим из граничного условия на рассеивателе (2.2). Однако условия (2.2) поставлены на аналитической границе ${{\Gamma }_{t}}$, а не на ее дискретном аналоге ${{\gamma }_{t}}$, где рассматривается уравнение (3.5). Поэтому требуется некоторая дополнительная процедура, позволяющая перенести информацию о граничном условии с ${{\Gamma }_{t}}$ на ${{\gamma }_{t}}$.
3.2. Продолжение граничных данных
Пусть плотность ${{\left. {{{\xi }_{{{{\Gamma }_{t}}}}} = ({{\xi }_{0}},{{\xi }_{1}})} \right|}_{{{{\Gamma }_{t}}}}}$ на аналитической границе ${{\Gamma }_{t}}$ задана. Определим в окрестности ${{\Gamma }_{t}}$ функцию $v = v({\mathbf{x}},t)$ с помощью ряда Тейлора с конечным числом слагаемых $P$:
(3.6)
$v({\mathbf{x}},t) = \sum\limits_{p = 0}^P \,\frac{1}{{p!}}\frac{{{{\partial }^{p}}v}}{{\partial {{{\mathbf{n}}}^{p}}}}({{{\mathbf{x}}}_{0}},t){{\rho }^{p}}.$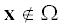 , и $\rho = - {\text{|}}{\mathbf{x}} - {{{\mathbf{x}}}_{0}}{\text{|}}$, если ${\mathbf{x}} \in \Omega $.
, и $\rho = - {\text{|}}{\mathbf{x}} - {{{\mathbf{x}}}_{0}}{\text{|}}$, если ${\mathbf{x}} \in \Omega $.
Производные по внешней к $\partial \Omega $ нормали в (3.6) определяются следующим образом. Для $p = 0$ полагаем $v({{{\mathbf{x}}}_{0}},t) = {{\xi }_{0}}({{{\mathbf{x}}}_{0}},t)$, для $p = 1$ кладем $\tfrac{{\partial v}}{{\partial {\mathbf{n}}}}({{{\mathbf{x}}}_{0}},t) = {{\xi }_{1}}({{{\mathbf{x}}}_{0}},t)$. Такой выбор отвечает тому, что ${\mathbf{T}}{{{\mathbf{r}}}_{{{{\Gamma }_{t}}}}}v = {{\xi }_{{{{\Gamma }_{t}}}}}$. Производные более высокого порядка вычисляются при помощи волнового уравнения (2.1), рассматриваемого в локальной ортогональной системе координат с центром в точке ${{{\mathbf{x}}}_{0}}$. Эта система выбирается так, чтобы две из осей лежали в касательной плоскости, а третья ось совпадала с нормалью ${\mathbf{n}}$ (с точностью до знака последней). В таком случае трехмерный лапласиан в точке ${{{\mathbf{x}}}_{0}}$ можно записать в следующем виде:
где оператор содержит тангенциальные производные и, возможно, производную по n порядка не выше первого. Например, если $\partial \Omega $ является сферой, то в сферических координатах имеем(3.7)
$\frac{{{{\partial }^{2}}v}}{{\partial {{{\mathbf{n}}}^{2}}}}({{{\mathbf{x}}}_{0}},t) = \frac{1}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}v}}{{\partial {{t}^{2}}}}({{{\mathbf{x}}}_{0}},t) - {\mathbf{L}}v({{{\mathbf{x}}}_{0}},t).$Если плотность ${{\xi }_{{{{\Gamma }_{t}}}}}$ отвечает какому-либо решению $u({\mathbf{x}},t)$ волнового уравнения, т.е. если ${{\xi }_{0}}$ и ${{\xi }_{1}}$ являются следом этого решения и его нормальной производной на ${{\Gamma }_{t}}$, то функция $v({\mathbf{x}},t)$, построенная согласно (3.6), аппроксимирует данное решение с точностью $\mathcal{O}({\text{|}}\rho {{{\text{|}}}^{{P + 1}}})$. Формально данная техника переноса граничных данных может быть применена к любой паре функций ${{\xi }_{{{{\Gamma }_{t}}}}} = {{\left. {({{\xi }_{0}},{{\xi }_{1}})} \right|}_{{{{\Gamma }_{t}}}}}$, не выбранных согласованно и не являющихся следом какого-либо решения и его производной. В этом случае правило (3.6) просто определяет новую функцию. В рамках излагаемого подхода нас интересует продолжение (3.6) в узлы дискретной границы ${{\gamma }_{t}}$, расположенные вблизи точной границы ${{\Gamma }_{t}}$. Обозначим это продолжение следующим образом:
где ${\mathbf{Ex}}$ есть оператор продолжения, определенный формулами (3.6), (3.7). В частности, таким образом можно продолжить на ${{\gamma }_{t}}$ любой базисный элемент ${{\psi }_{{0,s}}}$, ${{\psi }_{{1,s}}}$, заданный на точной границе ${{\Gamma }_{t}}$, т.е. рассчитать сеточные функции ${\mathbf{Ex}}{{\psi }_{{0,s}}}$, ${\mathbf{Ex}}{{\psi }_{{1,s}}}$.3.3. Схема обновления решения во времени
Рассмотрим разбиение границы во времени, описанное в разд. 2, но примененное теперь к дискретной границе $\gamma $. Обозначим через ${{{\mathbf{P}}}_{{{{\gamma }_{{{{T}_{0}}}}}}}}$ разностный аналог оператора ${{{\mathbf{P}}}_{{{{\Gamma }_{{{{T}_{0}}}}}}}}$, определяемый формулой (3.4). Разностный аналог ${{{\mathbf{R}}}_{{{{\Gamma }_{{{{T}_{0}}}}}}}}$ определим следующим образом:
(3.9)
${{{\mathbf{R}}}_{{{{\gamma }_{{{{T}_{0}}}}}}}}{{\xi }_{{{{\gamma }_{{{{T}_{0}}}}}}}}\;\mathop = \limits^{{\text{def}}} \;\mathop {{\mathbf{Tr}}}\nolimits_{{{\gamma }_{{({{T}_{0}},2{{T}_{0}}]}}}}^{(h)} {{{\mathbf{P}}}_{{\mathbb{N}_{{2{{T}_{0}}}}^{ - }}}}{{\xi }_{{{{\gamma }_{{{{T}_{0}}}}}}}},$(3.10)
${\mathbf{Q}}_{{{{\gamma }_{{{{T}_{0}}}}}}}^{{(0)}}{\mathbf{c}}_{0}^{{({\text{II}})}} + {\mathbf{Q}}_{{{{\gamma }_{{{{T}_{0}}}}}}}^{{(1)}}{\mathbf{c}}_{1}^{{({\text{II}})}} = - {\mathbf{R}}_{{{{\gamma }_{{{{T}_{0}}}}}}}^{{(0)}}{\mathbf{c}}_{0}^{{({\text{I}})}} - {\mathbf{R}}_{{{{\gamma }_{{{{T}_{0}}}}}}}^{{(1)}}{\mathbf{c}}_{1}^{{({\text{I}})}},$Столбцы матриц в (3.10) отвечают отдельным элементам используемого базиса:
(3.11)
$\begin{gathered} {\mathbf{Q}}_{{{{\gamma }_{{{{T}_{0}}}}}}}^{{(0)}} = [\underbrace {{{{\mathbf{P}}}_{{{{\gamma }_{{{{T}_{0}}}}}}}}{\mathbf{Ex}}{{\psi }_{{0,1}}} - {\mathbf{Ex}}{{\psi }_{{0,1}}}}_{{\text{столбец}}\;{\text{\# }}\;1} \ldots \underbrace {{{{\mathbf{P}}}_{{{{\gamma }_{{{{T}_{0}}}}}}}}{\mathbf{Ex}}{{\psi }_{{0,s}}} - {\mathbf{Ex}}{{\psi }_{{0,s}}}}_{{\text{столбец}}\;{\text{\# }}\;s} \ldots \underbrace {{{{\mathbf{P}}}_{{{{\gamma }_{{{{T}_{0}}}}}}}}{\mathbf{Ex}}{{\psi }_{{0,S}}} - {\mathbf{Ex}}{{\psi }_{{0,S}}}}_{{\text{столбец}}\;{\text{\# }}\;S}], \\ {\mathbf{Q}}_{{{{\gamma }_{{{{T}_{0}}}}}}}^{{(1)}} = [{{{\mathbf{P}}}_{{{{\gamma }_{{{{T}_{0}}}}}}}}{\mathbf{Ex}}{{\psi }_{{1,1}}} - {\mathbf{Ex}}{{\psi }_{{1,1}}} \ldots {{{\mathbf{P}}}_{{{{\gamma }_{{{{T}_{0}}}}}}}}{\mathbf{Ex}}{{\psi }_{{1,s}}} - {\mathbf{Ex}}{{\psi }_{{1,s}}} \ldots {{{\mathbf{P}}}_{{{{\gamma }_{{{{T}_{0}}}}}}}}{\mathbf{Ex}}{{\psi }_{{1,S}}} - {\mathbf{Ex}}{{\psi }_{{1,S}}}], \\ \end{gathered} $(3.12)
$\begin{gathered} {\mathbf{R}}_{{{{\gamma }_{{{{T}_{0}}}}}}}^{{(0)}} = [\underbrace {{{{\mathbf{R}}}_{{{{\gamma }_{{{{T}_{0}}}}}}}}{\mathbf{Ex}}{{\psi }_{{0,1}}}}_{{\text{столбец}}\;{\text{\# }}\;1} \ldots \underbrace {{{{\mathbf{R}}}_{{{{\gamma }_{{{{T}_{0}}}}}}}}{\mathbf{Ex}}{{\psi }_{{0,s}}}}_{{\text{столбец}}\;{\text{\# }}\;s} \ldots \underbrace {{{{\mathbf{R}}}_{{{{\gamma }_{{{{T}_{0}}}}}}}}{\mathbf{Ex}}{{\psi }_{{0,S}}}}_{{\text{столбец}}\;{\text{\# }}\;S}], \\ {\mathbf{R}}_{{{{\gamma }_{{{{T}_{0}}}}}}}^{{(1)}} = [{{{\mathbf{R}}}_{{{{\gamma }_{{{{T}_{0}}}}}}}}{\mathbf{Ex}}{{\psi }_{{1,1}}} \ldots {{{\mathbf{R}}}_{{{{\gamma }_{{{{T}_{0}}}}}}}}{\mathbf{Ex}}{{\psi }_{{1,s}}} \ldots {{{\mathbf{R}}}_{{{{\gamma }_{{{{T}_{0}}}}}}}}{\mathbf{Ex}}{{\psi }_{{1,S}}}]. \\ \end{gathered} $После того как матрицы (3.11), (3.12) посчитаны, рекуррентное соотношение (3.10) решается совместно с граничным условием на рассеивателе в виде (2.17) относительно неизвестных коэффициентов. Это решение ищется в смысле наименьших квадратов методом QR-разложения матриц ${\mathbf{Q}}_{{{{\gamma }_{{{{T}_{0}}}}}}}^{{(0)}}$, ${\mathbf{Q}}_{{{{\gamma }_{{{{T}_{0}}}}}}}^{{(1)}}$, поскольку, как правило, число строк матриц (3.11), (3.12) значительно превосходит число столбцов и система относительно неизвестных коэффициентов является переопределенной. При этом наиболее вычислительно нагруженную часть решения, QR-разложение, достаточно выполнить только один раз перед началом расчета, так что рекуррентное обновление коэффициентов в (3.10) сводится к обратной подстановке в методе QR-разложения.
Также отметим, что, поскольку матрицы не содержат в себе информацию о конкретном граничном условии на рассеивателе $\Omega $, они универсально подходят для любого типа рассеивания. То есть, чтобы пересчитать задачу с другим типом граничного условия на $\partial \Omega $, достаточно решить рекуррентное соотношение (3.10) с новым типом граничного условия (2.17) без относительно “дорогого” перерасчета матриц (3.11), (3.12).
4. ЧИСЛЕННЫЙ ЭКСПЕРИМЕНТ
Для демонстрации работы описанного метода рассмотрим задачу рассеяния плоской волны на сфере радиуса ${{R}_{0}} = 1$ см. Эта классическая задача имеет аналитическое решение в виде ряда, см. [5], с которым мы и будем сравнивать численное решение. В качестве падающего излучения возьмем не одну, а сумму двух плоских волн с несоизмеримыми угловыми частотами, ${{\omega }_{1}} = 3$ c–1 и ${{\omega }_{2}} = {{\omega }_{1}}{\text{/}}\sqrt 2 $, получая тем самым апериодическое во времени решение. Отметим, что для избранных частот длина волны падающего излучения является величиной порядка диаметра рассеивателя $2{{R}_{0}}$. Решением будем интересоваться в сферическом слое вокруг рассеивателя ${{R}_{0}} < r < {{R}_{1}}$, где ${{R}_{1}} = 1.5$ см.
В качестве вспомогательной области $\Omega {\text{'}}$ возьмем куб ${{[ - {{R}_{2}},{{R}_{2}}]}^{3}}$, ${{R}_{2}} > {{R}_{1}}$, такой, что за максимальное время расчета вспомогательной задачи $2{{T}_{0}}$ волны, отраженные от внешней границы $\partial \Omega {\text{'}}$, не успеют достичь расчетной области ${{R}_{0}} < r < {{R}_{1}}$, см. фиг. 2б. Нетрудно проверить, что для этого величина ${{R}_{2}}$ должна удовлетворять условию $2{{R}_{2}} - {{R}_{0}} - {{R}_{1}} > 2c{{T}_{0}}$. Такой выбор размера вспомогательной области позволяет поставить произвольные граничные условия на $\partial \Omega {\text{'}}$ вместо каких-либо приближенных условий излучения и получить решение ВЗ (3.3) в интервале времени $[0,2{{T}_{0}}]$ на ${{R}_{0}} < r < {{R}_{1}}$ как если бы ВЗ решалась в неограниченной области. Отметим, что подобный прием позволяет точно, без какого-либо приближения, смоделировать процесс ухода отраженных волн в бесконечность и является существенным преимуществом излагаемого метода. Возможность этого обусловлена коротким временем расчета ВЗ (максимум $2{{T}_{0}}$ секунд), необходимым для формирования матриц (3.11), (3.12).
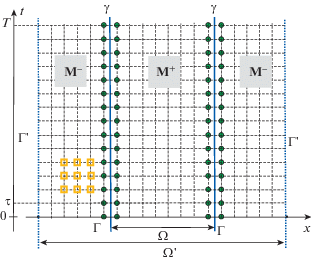
Построенная таким образом область $\Omega {\text{'}}$ покрывается прямоугольной сеткой, на которой алгоритм реализуется в рамках упомянутой разностной схемы четвертого порядка [6]. Уменьшая шаг сетки, можно проследить за сходимостью алгоритма, см. фиг. 4. Из данного рисунка видно, что двоичный логарифм ошибки уменьшается на четыре при измельчении сетки вдвое, что подтверждает правильную работу алгоритма. Заметим также, что на данном рисунке представлен результат достаточно длительного расчета: конечный момент ${{T}_{{{\text{sim}}}}}$ отвечает времени, за которое сигнал пересечет шар $r \leqslant {{R}_{0}}$ около 6000 раз. При этом никаких признаков возрастания ошибки со временем не наблюдается.
Фиг. 4.
Двоичный логарифм ошибки численного решения на двух последовательных сетках для трех типов граничных условий. Граничное условие III рода выбирается в виде $u + \tfrac{{\partial u}}{{\partial n}} = 0$.
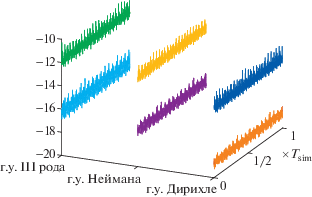
Отметим также, что для построения базиса ${{\psi }_{{0,s}}}$, ${{\psi }_{{1,s}}}$ используется прямое произведение полиномов Чебышева ${{T}_{n}}(t)$ (по времени) и сферических гармоник ${{Y}_{{lm}}}(\vartheta ,\varphi )$ (для разложения по границе $\Omega $, т.е. по сфере). Как показал эксперимент, максимального порядка $n = 10$ и $l = 12$ хватает с большим запасом для результатов с уровнем точности, представленным на фиг. 4.
5. ЗАКЛЮЧЕНИЕ
В работе предложен алгоритм расчета нестационарных процессов распространения волн, позволяющий: (i) понизить размерность задачи на единицу за счет сведения к граничной формулировке (ii) производить расчеты для областей сложной геометрической формы, пользуясь обычными разностными схемами на простейших прямоугольных сетках без какой-либо потери точности, связанной с аппроксимацией границ (iii) точно учитывать условия излучения для внешних задач (iv) эффективно использовать возможности параллелизации вычислений.
Обсудим следствия (i) и (iv) более подробно. Очевидно, что обновление решения на элементе разбиения длины ${{T}_{0}}$ согласно (3.10) занимает меньше времени, чем продвижение решения на это же время с помощью какой-либо явной разностной схемы, в силу того, что размерность задачи в первом случае на единицу меньше. Однако чтобы начать решать рекуррентное соотношение (3.10), требуется рассчитать матрицы, фигурирующие в (3.10). Это наиболее вычислительно длительная часть алгоритма, т.к. на этом этапе приходится решать $4S$ задач на протяжении времени максимум $2{{T}_{0}}$. Из-за этого обстоятельства при небольших временах расчета обычная явная схема справится с заданием быстрее, чем предложенный алгоритм. При более длительных временах затраты времени на вычисление матриц ${\mathbf{Q}}_{{{{\gamma }_{{{{T}_{0}}}}}}}^{{(0)}}$, ${\mathbf{Q}}_{{{{\gamma }_{{{{T}_{0}}}}}}}^{{(1)}}$, ${\mathbf{R}}_{{{{\gamma }_{{{{T}_{0}}}}}}}^{{(0)}}$, ${\mathbf{R}}_{{{{\gamma }_{{{{T}_{0}}}}}}}^{{(1)}}$ будут скомпенсированы более быстрым, чем в случае явной схемы, продвижением согласно (3.10). Таким образом, существует время расчета, начиная с которого предложенный алгоритм становится выгоднее самого очевидного, простого и быстрого решения – продвижения с помощью явной разностной схемы. Также важно отметить, что матрицы ${\mathbf{Q}}_{{{{\gamma }_{{{{T}_{0}}}}}}}^{{(0)}}$, ${\mathbf{Q}}_{{{{\gamma }_{{{{T}_{0}}}}}}}^{{(1)}}$, ${\mathbf{R}}_{{{{\gamma }_{{{{T}_{0}}}}}}}^{{(0)}}$, ${\mathbf{R}}_{{{{\gamma }_{{{{T}_{0}}}}}}}^{{(1)}}$ рассчитываются параллельно, т.к. их столбцы независимы друг от друга. Чем больше ядер, узлов и т.д. задействовано в этом расчете, тем меньшее время потребуется на данный расчет, и тем скорее (при меньших временах расчета) описанный алгоритм окажется эффективнее явной схемы. Укажем также, что подробное исследование описанного метода применительно к внутренним задачам представлено в работе [7].
Дальнейшее развитие метода связано с обобщением на систему Максвелла, а также на объекты с произвольной формой границы с использованием подходящих сплайнов.
Список литературы
Kleinman R.E., Roach G.F. Boundary integral equations for the three-dimensional Helmholtz equation // SIAM Rev. 1974. V. 16. P. 214–236.
Sayas F.-J. Retarded Potentials and Time Domain Boundary Integral Equations. A Road Map. Switzerland: Springer Series in Computational Mathematics. Vol. 50. Springer, 2016.
Рябенький В.С. Метод разностных потенциалов и его приложения. М.: Физматлит, 2002.
Софронов И.Л. О применении прозрачных граничных условий в задачах аэроакустики // Матем. моделирование, 2007. Т. 19. № 8. С. 105–112.
Морс Ф.M., Фешбах Г. Методы теоретической физики. Т. 2. М.: ИЛ, 1960.
Smith F., Tsynkov S., Turkel E. Compact High Order Accurate Schemes for the Three Dimensional Wave Equation // J. Sci. Comput. 2019. V. 81. Is. 3. P. 1181–1209.
Petropavlovsky S., Tsynkov S., Turkel E. A method of boundary equations for unsteady hyperbolic problems in 3D // J. Comp. Phys. 2018. V. 365. P. 294–323.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики