1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 60, № 4, 2020

Журнал вычислительной математики и математической физики, 2020, T. 60, № 4, стр. 752-764

Применение кода несветай к решению трехмерных задач высотной аэродинамики

В. А. Титарев *, **

ФИЦ ИУ РАН
119333 Москва, ул. Вавилова, 40, Россия

* E-mail: titarev@ccas.ru
** E-mail: titarev@mail.ru

Поступила в редакцию 21.10.2019
После доработки 21.10.2019
Принята к публикации 16.12.2019

Полный текст (PDF)

Аннотация

Приводится обзор возможностей кода Несветай в приложении к задачам обтекания тел сложной формы высокоскоростным потоком одноатомного газа для больших высот полета. Описаны неявный численный метод решения на произвольной неструктурированной сетке и двухуровневый подход к организации параллельных вычислений. Представлены сравнения с известными кодами MONACO и SMILE, реализующими метод прямого статистического моделирования. Библ. 48. Фиг. 7.

Ключевые слова: кинетическое уравнение, S-модель, разреженный газ, вычислительная аэродинамика, неструктурированная сетка, суперкомпьютерные расчеты.

ВВЕДЕНИЕ

В последние годы благодаря развитию численных методов и быстрому росту производительности суперЭВМ все более популярными становятся методы моделирования пространственных задач механики разреженного газа, основанные на прямом численном решении кинетического уравнения Больцмана с точным либо модельным оператором столкновений. Привлекательной стороной данного подхода является возможность разработки эффективных методов решения типа Годунова [1] второго порядка точности, применимых как для стационарных, так и для нестационарных течений. Соответствующие пакеты программ разрабатываются рядом коллективов, например [2]–[6]. Для решения сложных прикладных (промышленных) задач особенно привлекательной кажется возможность использования кинетических уравнений с приближенными (модельными) операторами столкновений [7]–[9]. Методы решения модельных уравнений обладают гораздо большей вычислительной эффективностью и гибкостью, обеспечивая в большинстве случае приемлемую точность счета.

Цель настоящей работы – представить краткий обзор существующих возможностей универсального программного кода Несветай [10] (Несветай – название реки в Ростовской области России) в приложении к задачам численного моделирования обтекания тел сложной формы высокоскоростным потоком одноатомного разреженного газа на больших высотах полета. Данный код разрабатывается автором на протяжении последних лет [11]–[15] и реализует схемы типа С.К. Годунова, адаптированные для решения трехмерного кинетического уравнения с приближенным (модельным) оператором столкновений Е.М. Шахова [8] (S-модель).

Основными особенностями кода Несветай являются использование как многоблочных структурированных, так и полностью неструктурированных сеток в физическом и фазовом пространствах, быстрый неявный метод дискретизации по времени для решения стационарных задач, поддержка одноуровневой и двухуровневой OpenMP + MPI модели параллельных вычислений, что позволяет проводить вычисления на системах с десятками тысяч x86 ядер.

1. РАСЧЕТНЫЕ УРАВНЕНИЯ

Рассматривается внешнее обтекание трехмерного тела потоком одноатомного разреженного газа. Невозмущенный поток характеризуется числовой плотностью ${{n}_{\infty }}$, давлением ${{p}_{\infty }}$, температурой ${{T}_{\infty }}$, скоростью ${{u}_{\infty }}$ и вязкостью ${{\mu }_{\infty }}$. Состояние одноатомного газа описывается функцией распределения молекул по скоростям $f = f(t,{\mathbf{x}},\xi )$, где $({{\xi }_{1}},{{\xi }_{2}},{{\xi }_{3}})$ – компоненты вектора молекулярной скорости по направлениям $({{x}_{1}},{{x}_{2}},{{x}_{3}})$ соответственно, $t$ – физическое время. Кинетическое уравнение Больцмана для $f(t,{\mathbf{x}},\xi )$ с S-модельным оператором столкновений [8] записывается в виде

(1)
$\begin{gathered} \frac{{\partial f}}{{\partial t}} + {{\xi }_{\alpha }}\frac{{\partial f}}{{\partial {{x}_{\alpha }}}} = J,\quad J = \nu ({{f}^{ + }} - f),\quad \nu = \frac{p}{\mu }, \\ {{f}_{M}} = \frac{n}{{{{{(2\pi {{R}_{g}}T)}}^{{3/2}}}}}{{e}^{{ - {{c}^{2}}}}},\quad {{f}^{ + }} = {{f}_{M}}\left[ {1 + \frac{4}{5}(1 - {\text{Pr}}){{S}_{\alpha }}{{c}_{\alpha }}\left( {{{c}^{2}} - \frac{5}{2}} \right)} \right], \\ {{S}_{i}} = \frac{1}{n}\int {{{c}_{i}}{{c}^{2}}fd\xi } ,\quad {\mathbf{c}} = \frac{{\xi - {\mathbf{u}}}}{{\sqrt {2{{R}_{g}}T} }}. \\ \end{gathered} $
Здесь ${\text{Pr}}$ – число Прандтля (${\text{Pr}} = 1$ соответствует модели БГК [7]), ${{R}_{g}}$ – газовая постоянная. Предполагается суммирование по греческим индексам. Зависимость вязкости от температуры предполагается в виде степенного закона с показателем $\omega $

(2)
$\mu (T) = {{\mu }_{\infty }}\mathop {\left( {\frac{T}{{{{T}_{\infty }}}}} \right)}\nolimits^\omega .$

Макроскопические параметры, такие как числовая $n$ и массовая $\rho $ плотности, вектор средней скорости ${\mathbf{u}} = ({{u}_{1}},{{u}_{2}},{{u}_{3}})$, давление $p$, температура $T$ и поток тепла ${\mathbf{q}} = ({{q}_{1}},{{q}_{2}},{{q}_{3}})$ выражаются через функцию распределения в виде интегралов ($m$ – масса молекулы):

(3)
$\begin{gathered} n = \int {fd\xi } ,\quad n{\mathbf{u}} = \int {\xi fd\xi } ,\quad \frac{3}{2}mn{{R}_{g}}T + \frac{1}{2}mn{{u}^{2}} = \frac{1}{2}m\int {{{\xi }^{2}}fd\xi } , \\ {\mathbf{q}} = \frac{1}{2}m\int {{\mathbf{v}}{{v}^{2}}fd\xi } ,\quad {\mathbf{v}} = \xi - {\mathbf{u}},\quad \rho = mn,\quad p = \rho {{R}_{g}}T. \\ \end{gathered} $

Граничные условия формулируются следующим образом. На поверхности тела предполагаем условие диффузного рассеяния молекул с полной тепловой аккомодацией при температуре поверхности ${{T}_{w}}$:

(4)
$\begin{array}{*{20}{c}} {f = {{f}_{w}} = \frac{{{{n}_{w}}}}{{{{{(2\pi {{R}_{g}}{{T}_{w}})}}^{{3/2}}}}}exp\left( { - \frac{{{{\xi }^{2}}}}{{2{{R}_{g}}{{T}_{w}}}}} \right).} \end{array}$
Для простоты в настоящей работе температура поверхности полагается постоянной и заданной условиями задачи. Плотность отраженных частиц ${{n}_{w}}$ определяется из условия непротекания. На бесконечности вверх по течению задается условие невозмущенного потока
$f = {{f}_{\infty }}(\xi ) = \frac{{{{n}_{\infty }}}}{{{{{(2\pi {{R}_{g}}{{T}_{\infty }})}}^{{3/2}}}}}exp\left( { - \frac{{{{{(\xi - {{{\mathbf{u}}}_{\infty }})}}^{2}}}}{{2{{R}_{g}}{{T}_{\infty }}}}} \right).$
Принималось, что вниз по потоку функция распределения близка к локально-максвелловской с параметрами, определяемыми решением задачи.

Начальное значение функции распределения $f(0,{\mathbf{x}},\xi )$ полагается равным локально-максвелловской функции с заданным полем распределения плотности, скорости и температуры газа.

2. ЧИСЛЕННЫЙ МЕТОД РЕШЕНИЯ

В настоящей работе используется метод дискретных ординат с сетками произвольного типа как в физическом, так и в скоростном пространствах. Данная особенность метода отличает его от большинства описанных в литературе методов решения кинетического уравнения и обеспечивает большую гибкость и эффективность в решении задач внешнего обтекания тел сложной формы. Введем в скоростном пространстве ограниченную расчетную области и сетку с узлами ${{\xi }_{j}} = ({{\xi }_{{1j}}},{{\xi }_{{2j}}},{{\xi }_{{3j}}})$. Общее количество узлов сетки обозначим через ${{N}_{\xi }}$. Функции ${\mathbf{f}}$, ${{{\mathbf{f}}}^{{({\mathbf{S}})}}}$ будем задавать в центрах ячеек скоростной сетки, интерпретируя их как векторы длины ${{N}_{\xi }}$ с компонентами

${{f}_{j}} = f(t,{\mathbf{x}},{{\xi }_{j}}),\quad f_{j}^{{(S)}} = {{f}^{{(S)}}}(t,{\mathbf{x}},{{\xi }_{j}}).$
Кинетическое уравнение (1) переписывается в виде системы из ${{N}_{\xi }}$ уравнений и в векторной форме имеет вид
(5)
$\frac{\partial }{{\partial t}}{\mathbf{f}} + \frac{\partial }{{\partial {{x}_{\alpha }}}}\left( {{{\Xi }_{\alpha }} \circ {\mathbf{f}}} \right) = {\mathbf{J}},\quad {\mathbf{J}} = \nu ({{{\mathbf{f}}}^{{(S)}}} - {\mathbf{f}}).$
Здесь ${{\Xi }_{k}}$ – вектор, компонентами которого являются $k$-компонента молекулярной скорости во всех узлах сетки: ${{\Xi }_{k}} = {{({{\xi }_{{k1}}},{{\xi }_{{k2}}},{{\xi }_{{k3}}}, \ldots {{\xi }_{{k{{N}_{\xi }}}}})}^{{\text{T}}}};$ через $ \circ $ обозначена операция покомпонентного умножения двух векторов: $c = a \circ b$ – вектор с компонентами ${{c}_{i}} = {{a}_{i}}{{b}_{i}}$.

Система (5) записана в консервативной форме. Число уравнений определяется размерностью сетки в скоростном пространстве и может быть достаточно большим (десятки и даже сотни тысяч уравнений). Для решения (5) будем использовать специальный вариант противопоточной ТВД схемы типа С.К. Годунова.

Расчетная область в физических переменных разбивается на контрольные объемы (ячейки) ${{V}_{i}}$ тетраэдальной, пирамидальной, гексаэдральной или призматической формы. Каждая из ячеек образована несколькими треугольными или четырехугольными гранями ${{A}_{{li}}}$, где $l$ – номер грани. Общее количество ячеек равняется ${{N}_{{{\text{space}}}}}$. Интегрирование системы (5) по ячейке ${{V}_{i}}$ и стандартная аппроксимация интегралов от потоков и правой части приводит к полудискретной схеме для значений функции распределения ${{{\mathbf{f}}}_{i}}$

(6)
$\begin{array}{*{20}{c}} {\frac{{\partial {{{\mathbf{f}}}_{i}}}}{{\partial t}} = {{{\mathbf{R}}}_{i}} = - \frac{1}{{{\text{|}}{{V}_{i}}{\text{|}}}}\sum\limits_{l = 1} \,{{\Phi }_{{li}}} + {{{\mathbf{J}}}_{i}},\quad {{\Phi }_{{li}}} = \int\limits_{{{A}_{{li}}}} \,({{\xi }_{{li}}} \circ {\mathbf{f}})dS,} \end{array}$
где компоненты вектора ${{\xi }_{{li}}}$ равны значениям проекции вектора молекулярной скорости на внешнюю единичную нормаль к грани $l$ пространственной ячейки ${{V}_{i}}$.

Процедура нахождения потока ${{\Phi }_{{li}}}$ для грани $l$ ячейки ${{V}_{i}}$ на произвольной неструктурированной сетке подробно описана в [11], [12], [14], [15] и состоит из двух этапов. На первом этапе для достижения второго порядка аппроксимации по пространству применяется процедура реконструкции решения на гранях сетки по известным средним значениям в ячейках [16]–[18]. В общем случае значения ${{{\mathbf{f}}}_{{li}}}$ функции распределения на внутренней стороне грани $l$ ячейки ${{V}_{i}}$ вычисляются по средним значениям в ячейке ${{V}_{i}}$ и ее соседях по формуле

${{{\mathbf{f}}}_{{li}}} = {{{\mathbf{f}}}_{i}} + {\mathbf{f}}_{{li}}^{{{\text{cor}}}}.$
Для вычисления поправки ${\mathbf{f}}_{{li}}^{{{\text{cor}}}}$ могут использоваться два подхода. В наиболее общем способе поправка выражается с помощью метода наименьших квадратов, записанного в локальной системе координат [19], [20], через средние значения в ячейках шаблона реконструкции ${{V}_{{{{m}_{i}}}}}$ по формуле
(7)
${\mathbf{f}}_{{li}}^{{{\text{cor}}}} = \psi _{i}^{{3d}}\left( {\sum\limits_{m = 0}^M \,{{g}_{{iml}}}{{{\mathbf{f}}}_{{{{m}_{i}}}}} - {{{\mathbf{f}}}_{i}}} \right).$
Коэффициенты ${{g}_{{iml}}}$ определяются только геометрией сетки и находятся на этапе инициализации счета. Данный способ в дальнейшем обозначается TVD3D. Пример шаблонов реконструкции для метода наименьших квадратов приведен на фиг. 1. Для гексаэдральных сеток возможно использование локально-одномерного подхода, в котором значения поправки находятся интерполяцией вдоль сеточных линий в направлении нормали к грани:
(8)
${\mathbf{f}}_{{li}}^{{{\text{cor}}}} = \psi _{{li}}^{{1d}}({{{\mathbf{S}}}_{L}},{{{\mathbf{S}}}_{R}}){{\Delta }_{l}},$
где ${{\Delta }_{l}}$ – расстояние от центра ячейки $i$ до центра грани $l$; ${{{\mathbf{S}}}_{L}}$ и ${{{\mathbf{S}}}_{R}}$ – левая и правая оценки наклона решения. Данный способ обозначается как TVD1D. Для обоих типов реконструкции функция $\psi $ – т.н. ограничитель наклонов, используемый для подавления паразитных осцилляций на разрывах. Как правильно, используется ограничитель наклонов типа minmod [16], [21].

Фиг. 1.

Примеры шаблонов реконструкции для метода TVD3D (7) на неструктурированной пространственной сетке с ячейками произвольной формы.

Важной частью численного метода является алгоритм аппроксимации граничных условий. Чтобы обеспечить расчет граничного условия зеркального отражения от плоскости симметрии, скоростная сетка строится таким образом, чтобы обеспечить попадание вектора скорости отраженной молекулы ${{\xi }_{1}} = \xi - 2{{\xi }_{n}}{\mathbf{n}}$ в узел скоростной сетки. После этого расчет граничного условия тривиален: $f(t,{\mathbf{x}},\xi ) = f(t,{\mathbf{x}},{{\xi }_{1}})$. Для всех граней ячеек сетки, лежащих на поверхности тела, интегрированием по $\xi $ при заданной температуре поверхности ${{T}_{w}}$ вычисляется плотность отраженных молекул ${{n}_{w}}$ таким образом, чтобы обеспечивалось точное выполнение условия непротекания.

На втором этапе полученные значения функции распределения ${{{\mathbf{f}}}^{ - }}$, ${{{\mathbf{f}}}^{ + }}$ с двух сторон каждой грани сетки используются для нахождения окончательного значения ${{\Phi }_{{li}}}$ путем решения задачи Римана для линейного уравнения в направлении, перпендикулярном грани:

(9)
${{\Phi }_{{li}}} = \frac{1}{2}{{\xi }_{{li}}} \circ \left[ {{{{\mathbf{f}}}^{ - }} + {{{\mathbf{f}}}^{ + }} - {\text{sign}}({{\xi }_{{li}}}) \circ ({{{\mathbf{f}}}^{ + }} - {{{\mathbf{f}}}^{ - }})} \right]{\text{|}}{{A}_{{li}}}{\text{|}},$
где ${\text{|}}{{A}_{{li}}}{\text{|}}$ – площадь грани. Помимо точной формулы (9), может использоваться приближенное решение, основанное на подходе Русанова [22], в котором в качестве оценки скорости используется максимальное по модулю значение молекулярной скорости. Для граней сетки, лежащих на границах расчетной области в физическом пространстве, значение ${{{\mathbf{f}}}^{ + }}$ находится из граничного условия.

Вычисление модельного (приближенного) интеграла столкновений ${\mathbf{J}}$ (индексы сетки по пространству и шага времени опущены для простоты) требует знания макроскопических величин. Пусть ${{b}_{j}}$ – веса квадратурной формулы второго порядка точности. Непосредственная аппроксимация выражений (3) для макропараметров газа имеет вид

(10)
$({\mathbf{U}},{\mathbf{q}}) = \left( {n,n{\mathbf{u}},\frac{3}{2}nT + n{{{\mathbf{u}}}^{2}},{\mathbf{q}}} \right) = \sum\limits_{j = 1}^{{{N}_{\xi }}} \,{{\left( {1,\xi ,{{\xi }^{2}},\frac{1}{2}{\mathbf{v}}{{v}^{2}}} \right)}_{j}}\,{{f}_{j}}{{b}_{j}}.$
Численное интегрирование полудискретной схемы (6) с весами $1$, $\xi $, ${{\xi }^{2}}$ приводит к дискретному аналогу уравнений сохранения массы, импульса и энергии:
(11)
$\frac{\partial }{{\partial t}}{\mathbf{U}} + {{D}_{h}}(\Pi ) = {{\epsilon }_{{{\text{Kn}}}}},\quad {{\epsilon }_{{{\text{Kn}}}}} = \sum\limits_{j = 1}^{{{N}_{\xi }}} \,(1,\xi ,{{\xi }^{2}})_{j}^{{\text{T}}}{{J}_{j}}{{b}_{j}}.$
Здесь $\Pi $ – тензор физических потоков. При точном интегрировании по $\xi $ численный метод должен быть консервативен, так что ${{\epsilon }_{{{\text{Kn}}}}} \equiv {\mathbf{0}}$. Однако при подстановке значений (10) в уравнения (11) получается неконсервативная схема [23], причем величина ошибки обратно пропорциональна числу Кнудсена ${\text{|}}{{\epsilon }_{{{\text{Kn}}}}}{\text{|}} \approx \tfrac{1}{{{\text{Kn}}}}O(\Delta {{\xi }^{2}})$. Для проведения расчетов с большим числом шагов по времени или малыми числами Кнудсена необходимо обеспечить выполнение условия ${\text{|}}{{\epsilon }_{{{\text{Kn}}}}}{\text{|}} = 0$.

Основная идея используемого метода расчета макроскопических величин [23] состоит в прямой аппроксимации условий на модельный интеграл столкновений, использовавшихся в [8] при выводе S-модели. Вектор простых переменных ${\mathbf{W}} = {{(n,{\mathbf{u}},T,{\mathbf{q}})}^{{\text{T}}}}$ находится из системы уравнений

(12)
${\mathbf{H}}({\mathbf{W}}) = \sum\limits_{j = 1}^{{{N}_{\xi }}} \,\mathop {\left( {\begin{array}{*{20}{c}} 1 \\ \xi \\ {{{\xi }^{2}}} \\ {{\mathbf{v}}{{v}^{2}}} \end{array}} \right)}\nolimits_j {{({{f}^{{(S)}}} - f)}_{j}}{{b}_{j}} + \left( {\begin{array}{*{20}{c}} 0 \\ {\mathbf{0}} \\ 0 \\ {2Pr{\mathbf{q}}} \end{array}} \right) = 0.$
Для каждой пространственной ячейки $i$ система из восьми уравнений (12) решается методом Ньютона
(13)
$\begin{array}{*{20}{c}} {M({{{\mathbf{W}}}^{{s - 1}}})({{{\mathbf{W}}}^{s}} - {{{\mathbf{W}}}^{{s - 1}}}) = - {\mathbf{H}}({{{\mathbf{W}}}^{{s - 1}}}),\quad M = \frac{{\partial {\mathbf{H}}}}{{\partial {\mathbf{W}}}},\quad s = 1,2, \ldots .} \end{array}$
В качестве начального приближения используются значения, полученные по формулам (10). В специальном случае ${\text{Pr}} = 1$ последние три уравнения могут быть опущены и система (12) сводится к процедуре, предложенной в [24], [25].

Медленной частью метода Ньютона является вычисление в системе (12) матрицы Якоби $M$, представляющей из себя дискретные суммы от производных ${{f}^{{(S)}}}$ по макроскопическим переменным. Точное вычисление $M$ требует существенных затрат машинного времени, особенно для более сложных кинетических моделей, таких как модель Рыкова двухатомного газа [9]. Если перейти в выражении для $M$ от численного интегрирования к точному (аналитическому), то можно получить приближенное аналитическое представление $M$ через макропараметры газа [11], [26]. Использование приближенной формулы для $M$ существенно уменьшает затраты машинного времени, несмотря на потерю квадратичной сходимости итераций.

Для дискретизации по времени в работе используется неявная одношаговая схема без итераций на верхнем слое по времени, которая выводится из (6) обычным образом:

(14)
$\frac{{\Delta {{{\mathbf{f}}}_{i}}}}{{\Delta t}} = {\mathbf{R}}_{i}^{{n + 1}} = {\mathbf{R}}_{i}^{n} + \mathop {\left( {\frac{{\partial {\mathbf{R}}}}{{\partial {\mathbf{f}}}}} \right)}\nolimits_i^n \Delta {{{\mathbf{f}}}_{i}},\quad \Delta {{{\mathbf{f}}}_{i}} = {\mathbf{f}}_{i}^{{n + 1}} - {\mathbf{f}}_{i}^{n}.$

Для вычисления приращения функции распределения по времени проводится приближенная линеаризация (14)

${\mathbf{\Phi }}_{{li}}^{{n + 1}} \approx {\mathbf{\Phi }}_{{li}}^{n} + \frac{{\partial {\mathbf{\Phi }}_{{li}}^{n}}}{{\partial {\mathbf{f}}_{i}^{n}}} \circ \Delta {{{\mathbf{f}}}_{i}} + \frac{{\partial {\mathbf{\Phi }}_{{li}}^{n}}}{{\partial {\mathbf{f}}_{{{{i}_{l}}}}^{n}}} \circ \Delta {{{\mathbf{f}}}_{{{{i}_{l}}}}},\quad {\mathbf{J}}_{i}^{{n + 1}} \approx {\mathbf{J}}_{i}^{n} - \nu _{i}^{n}\Delta {{{\mathbf{f}}}_{i}}.$
Здесь ${{{\mathbf{f}}}_{{{{i}_{l}}}}}$ – значение функции распределения в ячейке с индексом ${{i}_{l}}$, являющейся соседней к ячейке ${{V}_{i}}$ через грань $l$. При дальнейших упрощениях будем полагать, что в левой части численный поток аппроксимируется противопоточной схемой первого порядка с использованием точного распада разрыва, либо подхода Русанова. Группируя члены и выделяя в явном виде коэффициент перед $\Delta {{{\mathbf{f}}}_{i}}$, получаем
(15)
${{{\mathbf{d}}}_{i}} \circ \Delta {{{\mathbf{f}}}_{i}} + \Delta t\sum\limits_l \,{{{\mathbf{c}}}_{{li}}} \circ \Delta {{{\mathbf{f}}}_{{{{i}_{l}}}}} = \Delta t{\mathbf{R}}_{i}^{n}.$
Величина ${\mathbf{R}}_{i}^{n}$ находится со вторым порядком точности по известным значениям на нижнем временном слое ${{t}^{n}}$. Для решения (15) используется приближенная факторизация разреженной матрицы системы на основе подхода, предложенного в [27], [28] для уравнений газодинамики. После чего значения $\Delta {{{\mathbf{f}}}_{i}}$ находятся с помощью обычного обратного и прямого хода метода LU.

Для более эффективного и надежного построения решения задач обтекания тел сложной трехмерной формы высокоскоростным потоком разреженного газа в базовый численный метод были внесены два улучшения. Первое улучшение состоит в способе построения неравномерной адаптивной сетки в скоростном пространстве [14], [15]. Около $\xi = {{U}_{\infty }}$ (набегающий поток) и $\xi = 0$ (поверхность тела) вводятся кубические подобласти, в которых используется кубическая сетка с $\Delta \xi = 0.5\sqrt {2{{R}_{g}}{{T}_{\infty }}} $ и $\Delta \xi = 0.5\sqrt {2{{R}_{g}}{{T}_{w}}} $ соответственно. В остальной части области используются пирамиды и тетраэдры, размер которых плавно растет до $ \approx {\kern 1pt} 0.5\sqrt {2{{R}_{g}}{{T}_{{sw}}}} $, где ${{T}_{{sw}}}$ – оценка температуры за фронтом ударной волны. Как правило, сетка строится в четверти пространства с учетом плоскостей симметрии задачи, после чего препроцессор комплекса Несветай отражает ее в недостающие части расчетной области в скоростном пространстве. Описанный способ построения скоростной сетки требует некоторого знания о решаемой задаче, но при этом он значительно проще, чем адаптивная сетка типа восьмеричного дерева, используемая в работах [4], [5].

Второе улучшение численного метода состоит в использовании неоднородной дискретизации по физическому пространству. Как правило, для расчета высокоскоростных задач внешнего обтекания предпочтительными являются структурированные расчетные сетки со сгущением к поверхности. Однако для тел сложной формы такие сетки могут содержать небольшое количество ячеек плохого качества, например, сильно скошенных ячеек. Опыт проведения расчетов показывает, что наиболее надежной из схем второго порядка является подход TVD3D на основе метода наименьших квадратов, однако его использование может приводить к потере формальной сходимости к стационарному решению. Метод TVD1D обеспечивает повышенную точность в наиболее нагруженных областях поверхности тела и обеспечивает формальную сходимость к стационарному решению, однако может приводить к нефизическим значениям макроскопических величин в плохих ячейках сетки.

В настоящей работе предлагается использовать адаптивное переключение между методами TVD1D и TVD3D. Основным является метод TVD1D. По мере продвижения решения к стационарному режиму программный код Несветай создает список проблемных ячеек по критерию падения значения температуры ниже некоторого заранее предписанного малого значения, и переключает реконструкцию в этих ячейках на метод TVD3D. В результате получающийся численный метод формально сходится в интегральной норме без появления нефизических значений температуры.

В целом процедура построения решения состоит из следующих шагов. Сначала поле течения инициализируется значениями макропараметров набегающего потока, либо с помощью построения решения уравнений Навье–Стокса вязкого газа с помощью стороннего кода, например [29], [30]. После этого строится предварительное кинетическое решение с помощью метода первого порядка точности и модели БГК. Окончательное решение получается с помощью использования полученной функции распределения как начального условия для схемы второго порядка точности и S-модели. Описанный алгоритм позволяет проводить расчеты для произвольно больших чисел Маха набегающего потока.

3. ПРОГРАММНЫЙ КОМПЛЕКС НЕСВЕТАЙ

В состав пакет программ Несветай [13] входят вычислительное ядро, кинетический решатель и препроцессоры сетки. Вычислительное ядро представляет собой набор классов и модулей, реализующих базовые операции, необходимые для проведения расчетов: процедуры чтения пространственных сеток в различных форматах, построение информации о связности сетки; алгоритмы реконструкции скалярных функций методом наименьших квадратов на произвольной сетке; процедуры вывода пространственных и поверхностных данных в формате Tecplot. Кинетический решатель является надстройкой над ядром и реализует разностную схему решения кинетического уравнения. Препроцессоры используются для разбиения расчетной сетки при параллельных вычислениях. Общий объем кода – 20 000 строк на Фортран 2003/2008 с элементами объектно-ориентированного программирования. В качестве основного средства разработки используется среда Microsoft Visual Studio и компилятор Intel Fortran, входящий в состав пакета Intel Parallel Studio.

Одна из ключевых особенностей программного комплекса – использование двухуровневой модели параллельных вычислений OpenMP + MPI, которая активно развивается в последние годы в приложении к газодинамическим расчетам, см., например, [31], [32].

Каждый уровень параллельной реализации в Несветай основан на декомпозиции расчетной сетки. На верхнем уровне используется технология MPI обмена данными между узлами суперЭВМ. При распределении вычислений между узлами суперЭВМ может использоваться как декомпозиция расчетной сетки в скоростном пространстве, так и традиционная для вычислительной аэродинамики декомпозиции сетки в физическом пространстве. На нижнем уровне организации параллельных вычислений всегда используется разбиение сетки в физическом пространстве на блоки и использование технологии OpenMP. Для большинства частей метода решения достаточно использовать простые циклы OMP с динамической балансировкой. Однако параллельная многопоточная реализация метода LU-SGS решения системы уравнений для приращения функции распределения требует специальных изменений метода решения для того, чтобы скорость сходимости к стационарному решению не ухудшалась.

Таким образом, реализация OpenMPт подхода позволяет использовать на узле суперЭВМ произвольную комбинацию MPI процессов и OpenMP нитей. В дальнейшем при проведении расчетов основным будет являться вариант MPI-разбиения в пространстве скоростей, как более удобный с практической точки зрения. Отметим, что, по-видимому, впервые разбиение скоростной сетки для MPI-вычислений использовалось для решения точного уравнения Больцмана с помощью явной разностной схемы в работе [33].

Результаты тестирования масштабируемости параллельной версии кода Несветай на различных российских суперЭВМ могут быть найдены в работах [12], [14], [34]. Наилучшими по числу задействованных процессоров являются расчеты на системе РСК “Петастрим” [35], установленной в cуперкомпьютерном центре “Политехнический” СПбПУ Петра Великого. Каждый узел данного кластера состоит из одного сопроцессора Intel Xeon Phi 5120D (60 физических ядер, 240 гиперпотоков, частота 1.053 ГГц, 8 Гб ОЗУ). При проведении расчетов с использованием до 256 узлов (61 440 гиперпотока) была получена эффективность около 75%, что находится на уровне лучших примеров из вычислительной аэродинамики [31], [32].

4. ПРИМЕРЫ РАСЧЕТОВ

При анализе результатов cтепень разреженности газа характеризуется параметром разреженности $\delta $, который обратно пропорционален числу Кнудсена ${\text{Kn}}$, определенному по длине свободного пробега ${{\lambda }_{\infty }}$ в набегающем потоке газа и заданному масштабу длины ${{l}_{\infty }}$:

$\delta = \frac{{{{l}_{\infty }}{{p}_{\infty }}}}{{{{\mu }_{\infty }}{{v}_{\infty }}}} = \frac{8}{{5\sqrt \pi }}\frac{1}{{{\text{Kn}}}},\quad {\text{Kn}} = \frac{{{{\lambda }_{\infty }}}}{{{{l}_{\infty }}}},\quad {{v}_{\infty }} = \sqrt {2{{R}_{g}}{{T}_{\infty }}} .$

В качестве первой тестовой задачи рассматриваются результаты расчета обтекания плоского круглого цилиндра радиуса 6 дюймов (${{r}_{{{\text{cyl}}}}} = 0.1524$ м) потоком аргона [15], [34]. Задача решалась для скорости набегающего потока ${{U}_{8}} = 6585$ м/c, температуры потока ${{T}_{\infty }} = 200$ K и температуры поверхности ${{T}_{w}} = 1500$ К. Использовались два значения плотности набегающего потока ${{\rho }_{\infty }} = 1.127 \times {{10}^{{ - 6}}}$ кг/м$^{3}$ и $2.818 \times {{10}^{{ - 5}}}$ кг/м$^{3}$, которые при выборе ${{l}_{\infty }} = {{r}_{{{\text{cyl}}}}}$ соответствуют значениям параметра разреженности $\delta = 1.6$, $40$. Соответствующие числа Кнудсена равны ${\text{Kn}} = 0.56$, $0.0225$. Во всех случаях показатель степени в законе вязкости $\omega = 0.734$. Число Прандтля принималось равным ${\text{Pr}} = 2{\text{/}}3$. Использовавшаяся сетка в физическом пространстве состояла из $115 \times 40$ ячеек в плоскости $x - y$ и 3 ячеек по оси z. Высота первой ячейки в пристеночном слое равнялась ${{h}_{n}} = {{10}^{{ - 4}}}{{r}_{{{\text{cyl}}}}}$. Неравномерная скоростная сетка со сгущением к $\xi = 0$ и $\xi = {{U}_{\infty }}$ состояла из 35 720 узлов. Решение задачи потребовало 1000–3000 ядро-часов машинного времени в зависимости от значения $\delta $.

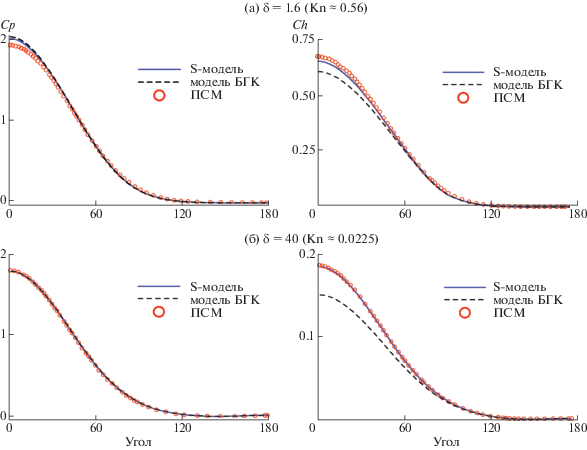
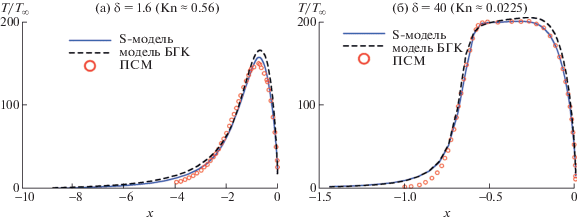
На фиг. 2 приведено сравнениe распределений коэффициентов давления и теплоотдачи по поверхности цилиндра, полученных с помощью решения модельных кинетических уравнений Е.М. Шахова и БГК с результатами работы [36] по расчету обтекания цилиндра с помощью кода MONACO [37], основанному на методе прямого статистического моделирования (ПСМ). Видно согласование расчетов по методу ПСМ и модельному уравнению Е.М. Шахова для всех значений $\delta $; максимальное различие в точке торможения составляет не более 2%. Использование модели БГК приводит к довольно заметной ошибке в коэффициенте теплоотдачи для $\delta = 40$. На фиг. 3 приведено сравнение профилей температуры на линии торможения в поле течения. В целом результаты расчетов по S-модели и методу ПСМ достаточно близки за исключением “хвоста” ударной волны. Использование модели БГК приводит к довольно заметной ошибке в “ступеньке” профиля температуры за фронтом ударной волны при $\delta = 40$.

Фиг. 2.

Распределение коэффициентов давления ${{c}_{p}}$, трения ${{c}_{f}}$ и теплоотдачи ${{c}_{h}}$ по поверхности цилиндра при обтекании аргоном для ${{{\text{M}}}_{\infty }} = 25$. Сплошная линия – расчет по S-модели, штриховая – по модели БГК, кружочки – расчет методом прямого статистического моделирования (ПСМ), взятый из [36].

Фиг. 3.

Сравнение профилей безразмерной температуры вдоль $T{\text{/}}{{T}_{\infty }}$ линии торможения при обтекании цилиндра аргоном для ${{{\text{M}}}_{\infty }} = 25$. Обозначения как на фиг. 2.

В работе [38] для задачи обтекания круглого цилиндра проводилось сравнение результатов расчета по S-модели с решением точного уравнения Больцмана с законом вязкости, соответствующим закону взаимодействия твердых сфер. Было получено хорошее согласие распределения поверхностных коэффициентов для ${{{\text{M}}}_{\infty }} = 10$. Вычисления проводились как с помощью кода Несветай, так и кодом UFS [2], [4]. Смотри также [39], [40].

Таким образом, в данных расчетах впервые показана хорошая точность S-модельного кинетического уравнения в задачах высокоскоростного обтекания затупленных тел, включая задачу расчета теплообмена на поверхности.

В качестве второй тестовой задачи рассматривается обтекание трехмерной модели воздушно-космического аппарата (ВКА) ЦАГИ потоком воздуха на больших высотах полета без учета внутренних степеней свободы. Модель ВКА имеет сложную форму и состоит из фюзеляжа с затупленным носком, двух крыльев, вертикального киля и щитка. Общая длина тела со щитком составляет 10 м. Вследствие своей геометрической сложности, необходимости использовать пространственную сетку с большим количеством плохих ячеек и скоростную сетку для набегающего потока под углом атаки задача построения решения служит отличным тестом. Для прикладных (инженерных) расчетов критически важной является возможность гарантированно получить ответ (решение) за небольшое время счета.

Принципиальная возможность построения численного решения данной задачи кодом Несветай для чисел Маха набегаюшего потока ${{{\text{M}}}_{\infty }} \geqslant 10$ и различных углов атаки была продемонстрирована автором в работах [14], [15], [34]. Это стало возможным благодаря использованию комбинации адаптивной скоростной сетки и эффективного неявного метода. В настоящей работе время решения задачи значительно уменьшено благодаря использованию в коде Несветай неоднородной аппроксимации оператора переноса на пространственной сетке.

Для оценки фактической точности счета проводится сравнение с результатами вычислений по коду [41]–[46], который реализует одну из современных схем метода прямого численного моделирования. В расчетах кодом SMILE параметры потока соответствовали воздуху (показатель адиабаты $\gamma = 1.4$, ${{R}_{g}} = 287.6$ Дж/(кг К)) с “замороженными” внутренними степенями свободы для заданной высоты $H$, числа Маха ${{{\text{M}}}_{\infty }}$ и угла атаки $\alpha $. Используемая в данных расчетах физическая модель, строго говоря, не является эквивалентной S-модели, поэтому представленные сравнения результатов носят оценочный характер. Вычисления кодом SMILE были выполнены Е.А. Бондарем, П.В. Ващенковым и А.А. Шевыриным (ИТПМ им. С.А. Христиановича СО РАН).

В [34], [47] было получено удовлетворительное согласие между расчетом Несветай и расчетом SMILE с “замороженными” внутренними степенями свободы для параметров задачи $H = 90$ км, ${{{\text{M}}}_{\infty }} = 10$ и $\alpha = 25$. В настоящей работе решение строится для более реалистичных условий $H = 100$ км и ${{{\text{M}}}_{\infty }} = 25$. Соответствующие параметры набегающего потока для воздуха ${{\rho }_{\infty }} = 5.550 \times {{10}^{{ - 7}}}$ кг/м3, ${{p}_{\infty }} = 0.0319$ Pa, ${{U}_{\infty }} = 7092$ м/c, ${{T}_{\infty }} = 199.34$ K, температура поверхности принималась равной ${{T}_{w}} = 300$ К (в работах [34], [47] использовалось ${{T}_{w}} = 1500$ K). Число Прандтля в уравнении (1) принималось равным ${\text{Pr}} = 0.71$. Параметр разреженности $\delta = 5.43$ на основе характерного размера ${{l}_{\infty }} = 1$ м. Используемый в SMILE алгоритм расчета столкновений приблизительно соответствует закону вязкости (2) с параметрами ${{\mu }_{\infty }} = 1.74 \times {{10}^{{ - 5}}}$, $\omega = 0.734$; эти значения констант в законе вязкости использовались и в расчете кодом Несветай.

Детальное описание параметров расчетных сеток в физическом пространстве приведено в [47]. Код SMILE использует многоуровневую декартову расчетную сетку, адаптированную к областями большой неравновесности течения, таких как фронты ударных волн и пристеночные области. Для кода Несветай используется сеточная модель в физическом пространстве на основе многоблочной расчетной сетки, состоящей из 159 блоков с общим числом ячеек 568 тысяч, см. фиг. 4. Высота первой ячейки у поверхности тема равнялась ${{10}^{{ - 3}}}$ м. Расчетная сетка в скоростном пространстве строилась аналогично случаю расчета обтекания цилиндра и содержала 32 144 узлa, так что полное число степеней свободы (ячеек в 6-мерной расчетной сетке) равнялось 18 миллиардам. Решение задачи кодом Несветай потребовало 5000 ядро-часов машинного времени.

Фиг. 4.

Расчетная сетка в физическом пространстве для задачи обтекания ВКА.

На фиг. 5, 6 представлено сравнение результатов счета для ${{c}_{p}}$, ${{c}_{h}}$. Видно хорошее согласие для коэффициента давления, в то время как для наиболее сложной в расчете величины, коэффициента теплопередачи ${{c}_{h}}$, на носке модели расчет SMILE дает несколько большее пиковое значение ${{c}_{h}} = 0.77$ по сравнению с ${{c}_{h}} = 0.65$ из расчета кодом Несветай. Полученное отличие в 16% можно объяснить использованием существенно отличающихся расчетных уравнений, сеток и численных методов. В целом получено хорошее согласие для расчета по S-модели и методом ПСМ для задачи обтекания трехмерного тела сложной формы и большой скорости набегающего потока.

Фиг. 5.

Сравнение распределения коэффициента давления ${{c}_{p}}$ для $H = 100$ км, $\alpha = 25$ и ${{{\text{M}}}_{\infty }} = 25$. Слева – SMILE, справа – Несветай.

Фиг. 6.

Сравнение распределения коэффициента теплопередачи ${{c}_{h}}$ для $H = 100$ км, $\alpha = 25$ и ${{{\text{M}}}_{\infty }} = 25$. Слева – SMILE, справа – Несветай.

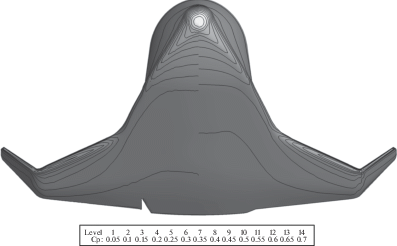
На фиг. 7 представлены линии уровня безразмерного давления, полученные с помощью кода Несветай. В целом видна типичная картинка обтекания тела скоростным потоком разреженного газа, включающая в себя формирующуюся отошедшую ударную волну и донную область с возвратным течением. Отношение давления в области торможения вблизи носка тела к давлению в донной области более 20 000. Несмотря на это, программный комплекс Несветай позволяет построить решение задачи.

Фиг. 7.

Линии уровня безразмерного давления $p{\text{/}}{{p}_{\infty }}$, полученные расчетом с помощью кода Несветай для $H = 100$ км, $\alpha = 25$ и ${{{\text{M}}}_{\infty }} = 25$.

ЗАКЛЮЧЕНИЕ

В работе приведено описание текущих возможностей моделирования задач внешнего обтекания тел скоростным потоком разреженного газа с помощью пакета параллельных программ Несветай, разрабатываемого автором на протяжении ряда лет в отделе Механики ФИЦ “Информатика и управление” РАН. Представленные результаты демонстрируют хорошую точность и надежность программы и ее применимость к расчету обтекания тел сложной формы до чисел Маха ${{{\text{M}}}_{\infty }}$ = 25 с использованием современных российских суперЭВМ.

Автор выражает благодарность своим коллегам Е.М. Шахову и А.А. Фроловой за конструктивные обсуждения и Е.А. Бондарю, П.В. Ващенкову и А.А. Шевырину (ИТПМ им. С.А. Христиановича СО РАН) за предоставленные результаты вычислений с помощью пакета SMILE. Работа выполнена с использованием ресурсов суперкомпьютерного комплекса МГУ им. М.В. Ломоносова [48], МСЦ РАН, cуперкомпьютерного центра “Политехнический” СПбПУ Петра Великого и МФТИ.

Список литературы

  1. Годунов С.К. Разностный метод численного расчета разрывных решений уравнений гидродинамики // Матем. сборник. 1959. Т. 47. № 89. С. 271–306.

  2. Kolobov V.I., Arslanbekov R.R., Aristov V.V., Frolova A.A., Zabelok S.A. Unified solver for rarefied and continuum flows with adaptive mesh and algorithm refinement // J. Comput. Phys. 2007. V. 223. C. 589–608.

  3. Аникин Ю.А., Клосс Ю.Ю., Мартынов Д.В., Черемисин Ф.Г. Компьютерное моделирование и анализ эксперимента Кнудсена 1910 года // Нано- и микросистемная техника. 2010. № 8. С. 6–14.

  4. Arslanbekov R.R., Kolobov V.I., Frolova A.A. Kinetic solvers with adaptive mesh in phase space // Physical Review E. 2013. V. 88. № 6. P. 063301.

  5. Baranger C., Claudel J., Herouard N., Mieussens L. Locally refined discrete velocity grids for stationary rarefied flow simulations // J. Comput. Phys. 2014. V. 257. P. 572–593.

  6. Dimarco G., Loubere R., Narski J. Towards an ultra efficient kinetic scheme. Part III: High-performance computing // J. Comput. Phys. 2015. V. 284. P. 22–39.

  7. Bhatnagar P. L., Gross E. P., Krook M. A model for collision processes in gases. I. Small amplitude processes in charged and neutral one-component systems // Phys. Rev. 1954. V. 94. № 3. P. 511–525.

  8. Шахов Е.М. Об обобщении релаксационного кинетического уравнения Крука // Изв. АН СССР. Механ. жидкости и газа. 1968. № 5. С. 142–145.

  9. Рыков В.А. Модельное кинетическое уравнение для газа с вращательными степенями свободы // Изв. АН СССР. Механ. жидкости и газа. 1975. № 6. С. 107–115.

  10. Титарев В.А. Программный комплекс моделирования трехмерных течений одноатомного разреженного газа Несветай-3Д // Свидетельство о государственной регистрации программы для ЭВМ 20176616295 от 06.06.2017, 2017.

  11. Титарев В.А. Неявный численный метод расчета пространственных течений разреженного газа на неструктурированных сетках // Ж. вычисл. матем. и матем. физ. 2010. Т. 50. № 10. С. 1811–1826.

  12. Titarev V.A., Dumbser M., Utyuzhnikov S.V. Construction and comparison of parallel implicit kinetic solvers in three spatial dimensions // J. Comput. Phys. 2014. V. 256. P. 17–33.

  13. Титарев В.А. Программный комплекс Несветай-3Д моделирования пространственных течений одноатомного разреженного газа // Наука и образование. МГТУ им. Н.Э. Баумана. Элект. журнал. 2014. № 6. С. 124–154.

  14. Titarev V.A. Numerical modeling of high-speed rarefied gas flows over blunt bodies using model kinetic equations // European Journal of Mechanics / B Fluids, Special Issue on Non-equilibrium Gas Flows. 2017. V. 64. P. 112–117.

  15. Titarev V.A. Application of model kinetic equations to hypersonic rarefied gas flows // Computers & Fluids, Special issue “Nonlinear flow and transport”. 2018. V. 169. P. 62–70.

  16. Колган В.П. Применение принципа минимальных значений производной к построению конечно-разностных схем для расчета разрывных течений газовой динамики // Уч. зап. ЦАГИ. 1972. Т. 3. № 6. С. 68–77.

  17. Kolgan V.P. Application of the principle of minimizing the derivative to the construction of finite-difference schemes for computing discontinuous solutions of gas dynamics // J. Comput. Phys. 2011. V. 230. № 7. P. 2384–2390.

  18. van Leer B. Towards the ultimate conservative difference scheme V: a second order sequel to Godunov’ method // J. Comput. Phys. 1979. V. 32. P. 101–136.

  19. Dumbser M., Käser M. Arbitrary high order non-oscillatory finite volume schemes on unstructured meshes for linear hyperbolic systems // J. Comput. Phys. 2007. V. 221. № 2. P. 693–723.

  20. Dumbser M., Käser M., Titarev V.A., Toro E.F. Quadrature-free non-oscillatory finite volume schemes on unstructured meshes for nonlinear hyperbolic systems // J. Comput. Phys. 2007. V. 226. P. 204–243.

  21. Barth T.J., Frederickson P.O. Higher order solution of the Euler equations on unstructured grids using quadratic reconstruction // AIAA paper no. 90-0013, 28th Aerospace Sciences Meeting, 1990.

  22. Русанов В.В. Расчет взаимодействия нестационарных ударных волн с препятствиями // Ж. вычисл. матем. и матем. физ. 1961. Т. 1. № 2. С. 267–279.

  23. Titarev V.A. Conservative numerical methods for model kinetic equations // Computers and Fluids. 2007. V. 36. № 9. P. 1446–1459.

  24. Mieussens L. Discrete-velocity models and numerical schemes for the Boltzmann-BGK equation in plane and axisymmetric geometries // J. Comput. Phys. 2000. V. 162. № 2. P. 429–466.

  25. Gusarov A.V., Smurov I. Gas-dynamic boundary conditions of evaporation and condensation: numerical analysis of the Knudsen layer //Phys. Fluids. 2002. V. 14. № 12. P. 4242–4255.

  26. Титарев В.А. Численный метод расчета двухмерных нестационарных течений разреженного газа в областях произвольной формы // Ж. вычисл. матем. и матем. физ. 2009. Т. 49. V. 7. P. 1255–1270.

  27. Yoon S., Jameson A. Lower-Upper Symmetric-Gauss-Seidel Method for the Euler and Navier–Stokes Equations // AIAA Journal. 1988. V. 26. № 9. P. 1025–1026.

  28. Men’shov I.S., Nakamura Y. An implicit advection upwind splitting scheme for hypersonic air flows in thermochemical nonequilibrium // A Collection of Technical Papers of 6th Int. Symp. on CFD, volume 2, page 815. Lake Tahoe, Nevada, 1995.

  29. Petrov M.N., Tambova A.A., Titarev V.A., Utyuzhnikov S.V., Chikitkin A.V. FlowModellium software package for calculating high-speed flows of compressible fluid // Comput. Math. & Math. Phys. 2018. V. 58. № 11. P. 1865–1886.

  30. Chikitkin A., Petrov M., Titarev V., Utyuzhnikov S. Parallel versions of implicit LU-SGS method // A Special Issue of Lobachevskii Journal of Mathematics on “Parallel Structure of Algorithms”. 2018. V. 39. № 4. P. 503–512.

  31. Абалакин И.В., Бахвалов П.А., Горобец А.В., Дубень А.П., Козубская Т.К. Параллельный программный комплекс NOISETTE для крупномасштабных расчетов задач аэродинамики и аэроакустики // Вычис. методы и программирование. 2012. Т. 13. № 3. С. 110–125.

  32. Gorobets A.V. Parallel Algorithm of the NOISEtte Code for CFD and CAA Simulations // Lobachevskii Journal of Mathematics. 2018. V. 39. № 4. P. 524–532.

  33. Аристов В.В., Забелок C.A. Детерминистический метод решения уравнения Больцмана с параллельными вычислениями // Ж. вычисл. матем. и матем. физ. 2002. Т. 42. № 3. С. 425–437.

  34. Титарев В.А. Численное моделирование пространственных течений разреженного газа с использованием суперЭВМ // Диссертация д-ра физ.-мат. наук., ФИЦ ИУ РАН, М., 2018.

  35. Semin A., Druzhinin E., Mironov V., Shmelev A., Moskovsky A. The Performance Characterization of the RSC PetaStream Module // Lecture Notes in Computer Science, V. 8488. P. 420–429. 29th Internat. Conference, ISC 2014, Leipzig, Germany, 2014.

  36. Lofthouse A.J. Nonequilibrium Hypersonic Aerothermodynamics Using the Direct Simulation Monte-Carlo and Navier–Stokes Models // Ph. D. thesis. The University of Michigan, 2008.

  37. Dietrich S., Boyd I.D. Scalar and parallel optimized implementation of the direct simulation Monte-Carlo method // J. Comput. Phys. 1996. V. 126. № 2. P. 328–342.

  38. Frolova A.A., Titarev V.A. Recent progress on supercomputer modelling of high-speed rarefied gas flows using kinetic equations // Supercomput. Frontiers and Innovat. 2018. V. 5. № 3. P. 117–121.

  39. Фролова А.А., Титарев В.А. Кинетические методы решения нестационарных задач со струйными течениями // Матем. и матем. моделирование. 2018. № 4. С. 27–44.

  40. Титарев В.А., Фролова А.А. Применение модельных кинетических уравнений для расчетов сверх- и гиперзвуковых течений молекулярного газа // Известия РАН. Механ. жидкости и газа. 2018. № 4. С. 95–112.

  41. Kashkovsky A.V., Bondar Ye.A., Zhukova G.A., Ivanov M.S., Gimelshein S.F. Object-oriented software design of real gas effects for the DSMC method // 24th International Symposium on Rarefied Gas Dynamics. AIP Conference Proc. 2004. V. 762. P. 583–588.

  42. Ivanov M.S., Kashkovsky A.V., Gimelshein S.F., Markelov G.N., Alexeenko A.A., Bondar Ye.A., Zhukova G.A., Nikiforov S.B., Vashenkov P.V. SMILE System for 2D/3D DSMC computations // Proc. of 25th Int. Symp. On RGD., P. 539–544. Publishing House of the Siberian Branch of the Russian Academy of Sciences, 2007.

  43. Ivanov M., Kashkovsky A., Vashchenkov P., Bondar Y. Parallel object-oriented software system for DSMC modeling of high-altitude aerothermodynamic problems // 27th internat. symposium on rarefied gas dynamics. AIP Conference Proc. 2010. V. 1333. P. 211–218.

  44. Шоев Г.В., Бондарь Е.А., Облапенко Г.П., Кустова Е.В. Разработка и апробация методики численного моделирования термически неравновесных диссоциирующих течений в Ansys Fluent // Теплофиз. и аэромехан. 2016. Т. 23. № 2 (98). С. 159–171.

  45. Шевырин А.А., Бондарь Е.А., Калашников С.Т., Хлыбов В.И., Дегтярь В.Г. Прямое статистическое моделирование разреженного высокоэнтальпийного течения около капсулы RAM C-II // Теплофиз. высоких температур. 2016. Т. 54. № 3. С. 408–414.

  46. Molchanova A., Kashkovsky A., Bondar Ye. Surface recombination in the direct simulation Monte-Carlo method // Phys. of Fluids. 2018. V. 30. P. 107105.

  47. Titarev V.A., Frolova A.A., Rykov V.A., Vashchenkov P.V., Shevyrin A.A., Bondar Ye.A. Comparison of the Shakhov kinetic equation and DSMC method as applied to space vehicle aerothermodynamics // J. Comput. & Applied Math. 2020. V. 364. P. 1–12.

  48. Voevodin Vl., Antonov A., Nikitenko D., Shvets P., Sobolev S., Sidorov I., Stefanov K., Voevodin Vad., Zhumatiy S. Supercomputer Lomonosov-2: Large Scale, Deep Monitoring and Fine Analytics for the User Community // Supercomput. Frontiers and Innovat. 2019. V. 6. № 2. P. 4–11.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал