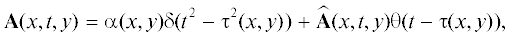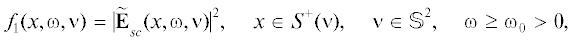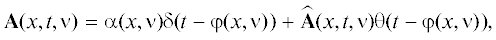Журнал вычислительной математики и математической физики, 2020, T. 60, № 6, стр. 1074-1092

1. ВВЕДЕНИЕ

В настоящей статье дается обзор работ по бесфазовым обратным задачам для дифференциальных уравнений. Объясним вначале, что означает термин “бесфазовая обратная задача”. Он означает, что рассматривается решение дифференциального уравнения, которое является комплексно-значной функцией, следовательно, эта функция представима в тригонометрической форме через ее модуль и аргумент (фазу), но в обратной задаче в качестве данных задачи задается только модуль решения на некотором множестве, а фаза не задается. Впервые на важность исследования подобных задач указали французские физики-математики К. Шадан (K. Chadan) и П. Сабатье (P.C. Sabatier) в книге [1], посвященной исследованию обратной задачи об определении потенциала в уравнении Шрёдингера по данным рассеяния. Эта задача изучалась многими отечественными и зарубежными авторами в предположении, что может быть измерено полное рассеянное поле, т.е. его модуль и фаза. Однако, как указали К. Шадан и П. Сабатье, в физических экспериментах на ускорителях при высоких энергиях (частотах) фазу решения измерить невозможно. Несколько позже Р. Ньютон (R. Newton) указал [2], что при высоких энергиях можно измерять только поперечное сечение рассеяния, которое определяется через квадрат модуля рассеянного поля. В связи с этим в книгах [1], [2] было отмечена важность изучения бесфазовой обратной задачи квантовой теории рассеяния. Хорошо известно, что чем выше частота излучения, тем более мелкие характеристики неоднородной среды (порядка длины волны) могут быть найдены на основе физических экспериментов. Необходимость изучения нано-структур материалов, структур биологических клеток приводят к рассмотрению бесфазовых обратных задач.

2. БЕСФАЗОВЫЕ ОБРАТНЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЯ ШРЁДИНГЕРА

Рассмотрим уравнение Шрёдингера

в котором $q(x)$ – переменный коэффициент, называемый потенциалом, $F(x)$ – заданная функция, ${\text{|}}k{\text{|}}$ – частота колебаний, связанная с энергией $E$ формулой ${\text{|}}k{\text{|}} = \sqrt E $. Прямая задача для уравнения (2.1) заключается в построении функции $u = u(x,k)$, являющейся решением уравнения (2.1), удовлетворяющим на бесконечности условию излучения равномерно по всем направлениям. Обычно при этом предполагается, что и потенциал, и функция $F(x)$ достаточно быстро убывают на бесконечности. В дальнейшем, для простоты изложения, будем полагать, что потенциал $q(x)$ является финитной функцией, т.е. он равен нулю вне некоторой конечной области $\Omega $, в качестве которой, также для простоты, возьмем шар радиуса $R$, а именно, $\Omega = \{ x \in {{\mathbb{R}}^{3}}\,{\text{|}}\,\left| x \right| < R\} $. Границу $\Omega $ обозначим через $S$.

Ниже в качестве прямой задачи будут рассматриваться только 2 варианта ее постановки.

1. Пусть $F(x) = \delta (x - y)$. Этот случай соответствует точечному источнику излучения, сосредоточенному в точке $y \in {{\mathbb{R}}^{3}}$. При этом решение задачи (2.1), (2.2), отвечающее нулевому потенциалу $q(x) = 0$, дается формулой

Представим решение задачи (2.1), (2.2) в виде Тогда функция ${{u}_{{sc}}}(x,k,y)$ описывает поле, рассеянное на потенциале $q(x)$, и удовлетворяет уравнению и условию излучения

2. Пусть $F(x) = 0$. Тогда существует решение однородного уравнения (2.1) с нулевым потенциалом вида плоской волны

в котором $\nu $ – произвольный единичный вектор. Здесь и далее символом $( \cdot )$ обозначается скалярное произведение векторов. Представим решение однородного уравнения (2.1) в виде При этом функция ${{u}_{{sc}}}(x,k,\nu )$ удовлетворяет уравнению, аналогичному уравнению (2.5), а именно, уравнению и условию излучения (2.6).

Обратная задача квантовой теории рассеяния заключается в отыскании потенциала $q(x)$ по некоторой информации о рассеянном поле. Теория этой задачи развивалась на протяжении последнего столетия, начиная с одномерного случая, когда $x \in \mathbb{R}$, в предположении, что задано комплекснозначное рассеянное поле, т.е. его модуль и фаза. В связи с отмеченным в работах [1], [2] фактом невозможности экспериментально измерить фазу рассеянного поля на высоких частотах, в литературе появились исследования возможности отыскания фазы решения по его заданному модулю. Теоремы единственности о восстановлении фазы по модулю решения были установлены в работах [3]–[10], как для уравнения Шрёдингера, так и для волнового уравнения. Однако эти теоремы не дают конструктивного алгоритма построения фазы, а значит, и решения обратной задачи.

Первые результаты по решению бесфазовых обратных задач для уравнения Шрёдингера появились в 2015 г. в работах М.В. Клибанова, В.Г. Романова [11], [12] и Р.Г. Новикова [13]–[15]. Представленные в этих работах подходы различны. В работах М.В. Клибанова и В.Г. Романова в качестве инициирующих источников излучения используются либо точечные источники [11], либо плоские волны, идущие из бесконечности [12], а информация о модуле рассеянного поля задается на границе области $\Omega $. Использование высокочастотной асимптотики поля сводит исходную задачу к задаче рентгеновской томографии. В работах Р.Г. Новикова используются плоские волны в качестве инициирующего воздействия и рассматривается поведение поля в дальней зоне (при ${\text{|}}x{\text{|}} \to \infty $). Основная идея этих работ заключается в построении фазы по модулю рассеянного [13] или полного поля [14], и сведении, таким образом, бесфазовой обратной задачи к классической постановке. В работе [15] изучается бесфазовая обратная задача на прямой. Ниже мы остановимся на результатах, представленных в работах [11], [12] и [13], [14], более подробно.

Начнем с работы [11]. Предположения о потенциале в ней следующие:

Рассматривается следующая постановка задачи.

Задача 1. Для $F(x) = \delta (x - y)$ задан модуль рассеянного поля ${{u}_{{sc}}}(x,k,y)$ для всех $x,y \in S$ и всех частот $k$, начиная с некоторой ${{k}_{0}} > 0$, т.е. задана функция

Требуется по этой функции найти $q(x)$ в $\Omega $.

Основной результат в исследовании этой задачи связан со следующей теоремой, установленной в [11].

Теорема 1. При выполнении условий (2.10) имеет место асимптотическое равенство

в котором $L(x,y)$ – отрезок прямой, соединяющей точки $x$ и $y$, а $d\sigma $ – элемент длины.

Данные обратной задачи и предположение (2.10) о неотрицательности $q(x)$ позволяют найти интегралы по всевозможным отрезкам $L(x,y)$:

В результате возникает хорошо известная задача рентгеновской томографии об определении функции по ее интегралам вдоль прямых (см. [16]–[18]). Существует много устойчивых алгоритмов ее решения, которые дают прекрасные результаты по визуализации искомой функции. Отметим, что для решения исходной бесфазовой задачи достаточно знать функцию $f(x,k,y)$ только для тех $x,\;y$, которые лежат в сечениях поверхности $S$ семейством параллельных плоскостей.

Идея доказательства теоремы 1 основана на рассмотрении задачи Коши для гиперболического уравнения, связанного с уравнением (2.1) формальным преобразованием Фурье по временной переменной. Эта задача имеет вид

Для задачи Коши (2.14) справедлива

Лемма 1. При выполнении условий (2.10) для решения задачи (2.14) имеет место равенство

в котором $\theta (t)$ – функция Хевисайда: $\theta (t) = 1$ для $t \geqslant 0$ и $\theta (t) = 0$ для $t < 0$, а функция $\tilde {w}(x,t,y)$ – дважды непрерывно дифференцируема по всем аргументам при $t \geqslant {\text{|}}x - y{\text{|}}$ и, кроме того,

Представление (2.15) и формула (2.16) были впервые получены в [19] (см. также [20], [21]) для функций $q(x) \in C({{\mathbb{R}}^{3}})$. В работе [11] установлена дважды непрерывная дифференцируемость функции $\tilde {w}(x,t,y)$.

Формальное преобразование Фурье

сводит задачу (2.14) к задаче (2.1), (2.2) с $F(x) = \delta (x - y)$. При этом Существование преобразований (2.17), (2.18) следует из работ Б. Вайнберга [22], [23], в которых доказывается экспоненциальное убывание по времени решений гиперболических уравнений в любой области, ограниченной по пространственным переменным. Интегрирование по частям в формуле (2.18), использование формулы (2.16) и свойств гладкости функции $\tilde {w}(x,t,y)$, указанных в лемме 1, приводит к асимптотической формуле (2.12).

В работе [12] рассматривается рассеянное поле, инициируемое плоской волной (2.7). Ставится и изучается следующая бесфазовая обратная

Задача 2. Задан модуль рассеянного поля ${{u}_{{sc}}}(x,k,\nu )$ для всех $x \in S$, $\nu \in {{\mathbb{S}}^{2}}$ и всех частот $k$, начиная с некоторой ${{k}_{0}} > 0$, т.е. задана функция

Требуется по функции ${{f}_{1}}(x,k,\nu )$ найти $q(x)$ в $\Omega $.

При исследовании этой задачи в [12] доказана следующая теорема об асимптотическом поведении решения прямой задачи (2.6)–(2.9).

Теорема 2. При выполнении условий (2.10) имеет место асимптотическое равенство

в котором $L(x,\nu )$ – отрезок прямой, выходящей из точки $x$ в направлении вектора $ - \nu $, а $d\sigma $ – элемент длины.

Теорема 2 вытекает из изучения следующей задачи Коши для нестационарного уравнения:

Решение этой задачи связано с решением задачи (2.6)–(2.9) преобразованием, аналогичным (2.18) (с заменой в нем $y$ на $\nu $).

Лемма 2. При выполнении условий (2.10) решение задачи (2.21) обладает свойством $\tilde {w}(x,t,\nu ) \equiv 0$ для $t < x \cdot \nu $, при каждом фиксированном $\nu $ является дважды непрерывно дифференцируемой функцией аргументов $x,\;t$ в области $t \geqslant x \cdot \nu $ и, кроме того,

Лемма 2 обосновывает теорему 2. При этом используются аргументы, аналогичные приведенным выше для задачи 1.

Теорема 2: данные (2.19) обратной задачи позволяют найти интегралы по всевозможным отрезкам $L(x,\nu )$:

В результате опять приходим к задаче рентгеновской томографии об определении функции $q(x)$ по ее интегралам вдоль всевозможных прямых.

В работе [13] рассматривается решение однородного уравнения (2.1) в ${{\mathbb{R}}^{d}}$, $d \geqslant 2$, в дальней зоне (при ${\text{|}}x{\text{|}} \to \infty $), инициированное плоской волной ${{e}^{{ikx \cdot \nu }}}$, $\nu \in {{\mathbb{S}}^{{d - 1}}}$. Это решение имеет вид

в котором $c(d,{\text{|}}k{\text{|}})$ – некоторая комплекснозначная постоянная, а $\ell = x/{\text{|}}x{\text{|}} \in {{\mathbb{S}}^{{d - 1}}}$. Классическая обратная задача рассеяния заключается в определении потенциала $q(x)$ по $f(k,\nu ,\ell )$, называемой амплитудной функцией. В обратной бесфазовой задаче кажется естественным рассмотреть задачу об определении потенциала по модулю этой функции. Однако она допускает множество решений. В [24] показано, что потенциалы $q(x)$ и $q(x - y)$, $y \in {{\mathbb{R}}^{d}}$, имеют амплитудные функции, модули которых совпадают для всех $k,\;\nu ,\;\ell $. В связи с этим в [13] рассмотрена следующая постановка бесфазовой обратной задачи.

Задача 3. Пусть $f(k,\nu ,\ell )$, ${{f}_{1}}(k,\nu ,\ell )$, ${{f}_{2}}(k,\nu ,\ell )$ – амплитудные функции, отвечающие потенциалам $q(x)$, $q(x) + {{q}_{1}}(x)$, $q(x) + {{q}_{2}}(x)$ соответственно и финитные потенциалы ${{q}_{1}}(x)$ и ${{q}_{2}}(x)$ известны и не равны тождественно друг другу. Пусть, далее, заданы

требуется найти $q(x)$ по данным (2.23).

Основной результат работы [13] состоит в доказательстве теореме единственности для задачи 3 и построению конструктивных формул, определяющих потенциал $q(x)$. Фактически эти формулы восстанавливают фазу амплитудной функции $f(k,\nu ,\ell )$. Теорема единственности, вытекающая из теоремы 2.1 [13], формулируется таким образом.

Теорема 3. Пусть $q,{{q}_{1}},{{q}_{2}} \in {{L}^{\infty }}({{\mathbb{R}}^{d}})$ и $\operatorname{supp} q \subset \Omega $, $\operatorname{supp} {{q}_{j}} \subset {{\Omega }_{j}}$, $\Omega \cap {{\Omega }_{j}} = \not {0}$, $j = 1,2$. Тогда данные обратной задачи 3 однозначно определяют $q(x)$.

Заметим, что в этой статье не предполагается знакопостоянство потенциала $q(x)$ в области $\Omega $, более того, этот потенциал может быть комплекснозначным.

В статье [14] установлено, что модуль полного поля ${{u}^{ + }}(x,k,\nu )$, определенного формулой (2.22), заданный при фиксированных $k$ и $\nu $ вне области $\Omega $, позволяет однозначно найти амплитудную функцию $f(k,\nu ,\ell )$ для $\ell \ne \nu $. Более точно, чтобы найти $f(k,\nu ,\ell )$ при фиксированном $\ell $ достаточно задать фукцию ${\text{|}}{{u}^{ + }}(x,k,\nu ){{{\text{|}}}^{2}}$ для значений $x$, лежащих на полубесконечной прямой $x = s\ell $, $s \in (R,\infty )$ (при этом предполагается, что $\Omega \subset \{ {\text{|}}x{\text{|}} \leqslant R\} $). Таким образом, бесфазовая информация о полном поле сводит обратную задачу к классической обратной задаче рассеяния.

Кроме того, в работе [14] рассмотрено решение уравнения (2.1) при $F(x) = \delta (x - y)$, $y \in {{\mathbb{R}}^{d}}{\backslash }\Omega $, удовлетворяющее условию излучения (2.2). Обозначим его ${{R}^{ + }}(x,k,y)$. Для этого решения установлен следующий результат: функция ${\text{|}}{{R}^{ + }}(x,k,y){{{\text{|}}}^{2}}$, заданная для $x = - s\nu $, $s \in (R,\infty )$, однозначно определяет функцию ${{u}^{ + }}(y,k,\nu )$. Этот результат также сводит бесфазовую обратную задачу с данными о полном поле, инициированным точечными источниками, к классической обратной задаче рассеяния.

Некоторые подходы к численному решению бесфазовых обратных задач изложены в работах [3]–[7], [25]–[28].

3. ОБОБЩЕННОЕ УРАВНЕНИЕ ГЕЛЬМГОЛЬЦА

Рассмотрим обобщенное уравнение Гельмгольца

в котором $n(x) > 0$ – коэффициент преломления среды, связанный со скоростью распространения волн $c(x)$ соотношением $n(x) = 1{\text{/}}n(x)$. Уравнение (3.1) возникает, если к волновому уравнению формально применить преобразование Фурье по временной переменной $t$. Уравнение (3.2) описывает распространение акустических волн в неоднородной среде. Это уравнение возникает также для описания отдельных компонент решения уравнений электродинамики и упругости в тех случаях, когда свойства среды не зависят от одной из пространственных переменных. При определенных условиях уравнение (3.1) хорошо описывает распространение ведущей компоненты электромагнитных волн (см. [29]). Уравнение (3.1) соответствует периодическим по времени колебаниям с частотой $k$.

В дальнейшем будем полагать, что коэффициент $n(x)$ вне области $\Omega = \{ x \in {{\mathbb{R}}^{3}}\,|\,{\text{|}}x{\text{|}} < R\} $ совпадает с $1$ и является ${{C}^{m}}({{\mathbb{R}}^{3}})$ гладкой функцией при достаточно большом $m$, т.е.

Обратные бесфазовые задачи для уравнения (3.1) впервые были рассмотрены в работах [30]–[32]. В статье [30] изучен случай, когда волны инициируются точечным источником, сосредоточенным в точке $y \in {{\mathbb{R}}^{3}}$, точнее, когда $F(x) = \delta (x - y)$ в уравнении (3.1). В этом случае в однородной среде при $n(x) \equiv 1$ решение этого уравнения, удовлетворяющее условию излучения (2.2), имеет вид Обозначим через ${{u}_{{sc}}}(x,k,y) = u(x,k,y) - {{u}_{0}}(x,k,y)$ волну, рассеянную на неоднородности, локализованной в $\Omega $. Пусть $S = \{ {\text{|}}x{\text{|}} = R\} $ – граница $\Omega $, ${{k}_{0}}$ – некоторая положительная постоянная.

Задача 4. Задана функция

найти $n(x)$.

В [30] эта задача изучена при следующем предположении.

Предположение 1. Риманова метрика $d\tau = n(x){\text{|}}dx{\text{|}}$, ${\text{|}}dx{\text{|}} = {{(dx_{1}^{2} + dx_{2}^{2} + dx_{3}^{2})}^{{1/2}}}$, является простой, т.е. любые две точки $x,y \in {{\mathbb{R}}^{3}}$ можно соединить единственной геодезической линией $\Gamma (x,y)$.

С введенной римановой метрикой связаны геодезические расстояния $\tau (x,y)$ между точками $x,y$. В однородной среде ($n(x) \equiv 1$) они вычисляются по формуле ${{\tau }_{0}}(x,y) = {\text{|}}x - y{\text{|}}$. Физический смысл геодезического расстояния $\tau (x,y)$ – время пробега сигнала между точками $x$ и $y$ в среде, скорость распространения сигналов в которой равна $1{\text{/}}n(x)$. Хорошо известно, что $\tau (x,y)$ является решением уравнения эйконала

удовлетворяющим условию Геодезические линии $\Gamma (x,y)$ – характеристики уравнения эйконала. Чтобы их найти, достаточно проинтегрировать некоторую систему обыкновенных дифференциальных уравнений (см., например, [20]).

Теорема 4. Пусть выполнены условия (3.3) при $m = 15$ и предположение 1 о простоте римановой метрики. Тогда данные (3.5) однозначно определяют $\tau (x,y)$ для всех $x,y \in S$.

Эта теорема сводит задачу 4 к хорошо известной обратной кинематической задаче об определении скорости $c(x) = 1{\text{/}}n(x)$ в области $\Omega $ по заданным временам пробега сигнала между произвольными точками ее границы.

История обратной кинематической задачи насчитывает уже более 100 лет. Впервые она была рассмотрена для шаровой области в предположении сферической симметрии среды в работе Герглотца [33] в 1905 г. Вытекающий из этой работы алгоритм построения решения был затем широко использован геофизиками для обработки сейсмических данных о землетрясениях и на его основе были получены первоначальные представления о скоростях распространения продольных и поперечных упругих волн в глубоких слоях Земли и о самой структуре Земли. На основе проведенных исследований были введены в рассмотрение основные структурные элементы: земная кора, мантия, ядро Земли. Однако построенные для разных частей Земли скоростные разрезы (найденные в предположении сферической симметрии) отличались друг от друга (в пределах порядка 10%), что свидетельствовало о том, что на самом деле скорости распространения волн зависят не только от глубины, но и от географических координат. Первый результат в исследовании трехмерной обратной кинематической задачи был получен для ее линеаризованного варианта в работе [34]. В дальнейшем на его основе был создан вычислительный алгоритм для построения двумерного скоростного строения верхней мантии Земли (см. работы [35]–[37]), фактически он был положен затем в основу сейсмической томографии.

В предположении 1 для нелинейной обратной кинематической задачи впервые теорема о единственности и устойчивости ее решения была получена Р.Г. Мухометовым в работе [38] для двумерного пространства. Затем она была обобщена на пространства более высокой размерности в работах [39]–[41].

Основу доказательства теоремы 4 составляет асимптотическая формула при $k \to \infty $ для решения задачи (3.1), (2.2). Она, в свою очередь, базируется на рассмотрении структуры фундаментального решения для неоднородного волнового уравнения (3.2). Эта структура исследована в книге [42] для общих линейных гиперболических уравнений в предположении о простоте римановой метрики, определяемой главной частью уравнения. В работе [30] структура решения конкретизирована на рассматриваемое уравнение (3.2). А именно, для задачи

доказана следующая лемма (соответствует Theorem 2 в [30]).

Лемма 3. Пусть выполнены предположения теоремы 4. Тогда для любого $T > 0$ и любого фиксированного $y$ существует единственное решение $v(x,t,y)$ задачи (3.8), представимое в области $D(y,T) = \{ (x,t)\,|\,0 < t \leqslant T - \tau (x,y)\} $ в виде

в котором функция $A(x,y) > 0$, $\theta (t)$ – функция Хевисайда, а функция $\hat {v}(x,t,y) \in {{C}^{2}}(D{\text{*}}(y,T))$, $D{\text{*}}(y,T) = \{ (x,t)\,|\,\tau (x,y) \leqslant t \leqslant T - \tau (x,y)\} $.

Из этой леммы и преобразования Фурье

путем интегрирования по частям, находится асимптотическая формула Следовательно, Здесь ${{\tau }_{0}}(x,y) = {\text{|}}x - y{\text{|}}$. Из формул (3.11), (3.5) находится следующее представление для данных обратной задачи: Зафиксируем в этой формуле $x \in S$ и $y \in S$. Тогда функция $f(x,k,y)$ становится функцией одной переменной $k$. Если она имеет предел при $k \to \infty $, то это означает, что $\tau (x,y) = {{\tau }_{0}}(x,y)$. В противном случае, эта функция является почти периодической и можно вычислить ее период, следовательно, величину $\psi (x,y) = \tau (x,y) - {{\tau }_{0}}(x,y)$ и затем по ней найти $\tau (x,y)$. Таким образом, по данным обратной задачи можно найти $\tau (x,y)$ для всех $x,y \in S$, что и приводит к теореме 4.

В той же работе [30] рассмотрена и другая постановка бесфазовой обратной задачи.

Задача 5. Задана функция

найти $n(x)$.

Из формулы (3.10) следует, что по информации (3.13) можно вычислить

Поэтому обратная задача 5 сводится к задаче об определении $n(x)$ по $A(x,y)$, $x,y \in S$. Функция $A(x,y)$ выражается в явном виде через якобиан преобразования $J(x,y) = \partial \zeta {\text{/}}\partial x$ римановых координат $\zeta = ({{\zeta }_{1}},{{\zeta }_{2}},{{\zeta }_{3}})$ точки $x$ относительно фиксированной $y$ в декартовые. Эта формула имеет вид В свою очередь $\zeta = \zeta (x,y)$ вычисляется по формуле $\zeta = - n(y){{\nabla }_{y}}{{\tau }^{2}}(x,y){\text{/}}2$. Таким образом, $A(x,y)$ зависит от $n(x)$ нелинейно. В работе [25] изучен линейный вариант задачи об определении $n(x)$ по $A(x,y)$, $x,y \in S$. А именно, в предположении, что $\beta (x) = n(x) - 1$ удовлетворяет условию для функции $\tau (x,y)$ использовано линейное приближение из которого найдена приближенная формула для вычисления В результате для функции $a(x) = \Delta \beta (x)$ возникает задача интегральной геометрии о восстановлении $a(x)$ через интегралы от нее по всем прямым, соединяющим точки $S$, с весовой функцией $s(1 - s)$. Эта задача решается однозначно в каждом сечении области $\Omega $ плоскостями ${{x}_{3}} = {\text{const}}.$ По найденной функции $a(x)$ искомый коэффициент $\beta (x)$ затем вычисляется как решение следующей задачи Дирихле:

В работе [31], при тех же предположениях о функции $n(x)$, что и в [30], исследована задача об определении $n(x)$ по данным рассеяния для уравнения (3.1), когда в этом уравнении $F(x) = 0$, а инициирующая волна является плоской и имеет вид (2.7). Тогда рассеянное поле определяется равенством ${{u}_{{sc}}}(x,k,\nu ) = u(x,k,\nu ) - {{u}_{0}}(x,k,\nu )$. Пусть ${{S}^{ + }}(\nu ) = \{ x \in S\,|\,x \cdot \nu > 0\} $. Обратная задача ставится следующим образом.

Задача 6. Задана функция

найти $n(x)$.

Пусть $y = y(\nu ) = - R\nu \in S$ и $\Sigma (\nu )$ – касательная плоскость к $S$ в точке $y(\nu )$, т.е. $\Sigma (\nu ) = \{ x\,|\,x \cdot \nu + R = 0\} $. Определим функцию $\varphi (x,\nu )$ следующим образом: $\varphi (x,\nu ) = x \cdot \nu $ для $x$, лежащих в полупространстве $x \cdot \nu + R \leqslant 0$, а для $x$, удовлетворяющих неравенству $x \cdot \nu + R > 0$, как то решение задачи Коши для уравнения эйконала

которое продолжается гладким образом (с сохранением непрерывности функции и ее производных) через $\Sigma (\nu )$.

Задача 6 исследована при следующем предположении.

Предположение 2. Геодезические линии римановой метрики $d\tau = n(x){\text{|}}dx{\text{|}}$, ${\text{|}}dx{\text{|}} = {{(dx_{1}^{2} + dx_{2}^{2} + dx_{3}^{2})}^{{1/2}}}$ ${\text{|}}dx{\text{|}} = {{(dx_{1}^{2} + dx_{2}^{2} + dx_{3}^{2})}^{{1/2}}}$, обладают следующими свойствами регулярности:

1) через каждую точку $x \in {{\mathbb{R}}^{3}}$ проходит единственная геодезическая $\Gamma (x,\nu )$, которая продолжается до плоскости $\Sigma (\nu )$ и ортогональна к ней,

2) геодезические линии, ортогональные $\Sigma (\nu )$, нигде не пересекаются.

Лемма 4. Пусть выполнены предположение 2 и условия (3.3) с $m = 15$. Тогда для любого $\nu \in {{\mathbb{S}}^{2}}$ существует единственное решение $u(x,t,\nu )$ задачи (3.1) при $F(x) = 0$, представимое в виде $u(x,k,\nu ) = exp(ikx \cdot \nu ) + {{u}_{{sc}}}(x,k,\nu )$, в котором ${{u}_{{sc}}}(x,k,\nu )$ удовлетворяет условию излучения (2.6), и для этого решения имеет место асимптотическая формула

В этой формуле $A{\kern 1pt} {\text{*}}(x,\nu ) > 0$ – гладкая функция $x \in {{\mathbb{R}}^{3}}$.

С помощью этой леммы находится асимптотическая формула для данных обратной задачи

При фиксированных $x \in {{S}^{ + }}(\nu )$ и $\nu \in {{\mathbb{S}}^{2}}$ формула (3.17) позволяет найти $\varphi (x,\nu )$, а значит, и вычислить для $x \in {{S}^{ + }}(\nu )$ время пробега $\tau (x,\nu ) = \varphi (x,\nu ) + R$ вдоль геодезической $\Gamma (x,\nu )$. Таким образом, обратная задача 6 сводится к следующей задаче: для любого $\nu \in {{\mathbb{S}}^{2}}$ заданы времена пробега сигнала от точек $x \in {{S}^{ + }}(\nu )$ до плоскости $\sum {(\nu )} $, найти $n(x)$. Эта задача отличается от обратной кинематической задачи лишь формой задания данных. Фактически метод доказательства единственности решения задачи и получения оценок его устойчивости в данном случае совпадает с методом, использованным в работах [38]–[41].

В [31] рассмотрена также постановка обратной бесфазовой задачи, когда вместо информации о модуле рассеянного поля задается подобная же информация о полном поле. Ее исследование выполнено в линейном приближении.

В статье [32] наряду с изложением некоторых геометрических вопросов, связанных с исследованием обратных задач для дифференциальных уравнений, сформулирована бесфазовая обратная задача для уравнения

При этом предполагается, что и решение уравнения (3.18) удовлетворяет условию излучения (2.2). Решение задачи (3.18), (2.2), отвечающее случаю $n(x) = 1,$ $q(x) = 0$, имеет вид Пусть ${{u}_{{sc}}}(x,k,y) = u(x,k,y) - {{u}_{0}}(x,k,y)$.

Задача 7. Задана функция

найти $n(x)$ и $q(x)$.

Эта задача исследована в статье [43]. Доказано, что при выполнении условий (3.19) и предположения 1 задача 7 может быть сведена к последовательному решению двух задач: 1) обратной кинематической задаче для определения $n(x)$ внутри $\Omega $ и 2) решению задачи интегральной геометрии на геодезических $\Gamma (x,y)$ римановой метрики $d\tau = n(x){\text{|}}dx{\text{|}}$ для отыскания $q(x)$. Обе эти задачи были изучены ранее в работах [38]–[41]. Для них установлены теоремы единственности решения и оценки его устойчивости.

В статье [44] для задачи 4 установлена следующая теорема единственности.

Теорема 5. Пусть предположение 1 и условия (3.3) выполнены. Тогда для любых фиксированных $x,y \in S$ числа $A(x,y)$ и $\tau (x,y)$, входящие в асимптотическую формулу (3.10), $f(x,y,k)$, заданная для всех $x,y \in S$, $k \in (a,b)$, однозначно определяет коэффициент $n(x)$.

В статье [45] доказано, что задание при фиксированных $x,y \in S$ функции $f(x,k,y)$ для $k \in (a,b)$, $0 < a < b$, однозначно определяет ее для всех $k$.

В работе [46] рассмотрены постановки бесфазовых обратных задач для уравнений Шрёдингера и Гельмгольца, использующие интерференцию волн. В этом случае задается модуль полного поля, возникающего в результате взаимодействия полей от точечного источника $y \in S$ и некоторого сопряженного источника $y{\text{*}}$, расположенного вне $\Omega $ с противоположной стороны. Более детально о таких постановках задач рассказано в следующем разделе. Именно для уравнений электродинамики и были впервые введены в рассмотрение такие бесфазовые обратные задачи.

4. УРАВНЕНИЯ МАКСВЕЛЛА

В работах [47]–[51] рассмотрены различные постановки бесфазовых обратных задач для стационарных уравнений электродинамики, отвечающих изотропным и простейшим анизотропным средам. Ниже приводится обзор постановок задач и полученных результатов. Исследование обратных задач для уравнений электродинамики началось с работ А.Н. Тихонова и Л. Каньяра (L. Cagniard) [52]–[54]. Развитый в них метод магнито-теллурических зондирований широко использовался геофизиками при изучении проводимости верхних слоев земной коры. Трехмерные обратные задачи электродинамики начали интенсивно изучаться с 80-х годов прошлого столетия. В работах [55]–[65] исследованы вопросы единственности и устойчивости решения многих обратных задач.

Рассмотрим нестационарную систему уравнений Максвелла

в которой $\varepsilon (x)$ – положительная функция, называемая коэффициентом диэлектрической проницаемости среды, ${{\mu }_{0}}$ – некоторая положительная постоянная, ${\mathbf{j}}(x,t)$ – сторонний ток, ${\mathbf{E}}$ и ${\mathbf{H}}$ – векторы электрической и магнитной напряженностей соответственно. Всюду в дальнейшем принимается, что вне области $\Omega = \{ x \in {{\mathbb{R}}^{3}}\,|\,{\text{|}}x{\text{|}} < R\} $, $R > 0$, коэффициент $\varepsilon (x) \in {{C}^{\infty }}({{\mathbb{R}}^{3}})$ совпадает с заданной положительной постоянной ${{\varepsilon }_{0}}$. Пусть, как и ранее, $S = \{ x \in {{\mathbb{R}}^{3}}\,|\,{\text{|}}x{\text{|}} = R\} $ – граница области $\Omega $. Обозначим через $c(x) = 1{\text{/}}\sqrt {\varepsilon (x){{\mu }_{0}}} $ скорость распространения электромагнитных волн, и через ${{c}_{0}} = 1{\text{/}}\sqrt {{{\varepsilon }_{0}}{{\mu }_{0}}} $ – ее значение в однородной среде. Введем также индексы рефракции $n(x) = 1{\text{/}}c(x)$, ${{n}_{0}} = 1{\text{/}}{{c}_{0}}$ для неоднородной и однородной сред соответственно.

В случае когда сторонний ток представляет собой периодическую по времени функцию ${\mathbf{j}}(x,t) = {{{\mathbf{j}}}_{0}}(x){{e}^{{ - \omega t}}}$, существуют периодические по времени решения уравнений (4.1) вида ${\mathbf{E}}(x,t) = \widetilde {\mathbf{E}}(x){{e}^{{ - \omega t}}}$, ${\mathbf{H}}(x,t) = \widetilde {\mathbf{H}}(x){{e}^{{ - \omega t}}}$, в котором $\widetilde {\mathbf{E}}(x)$, $\widetilde {\mathbf{H}}(x)$ являются решением системы уравнений

Для дальнейшего удобно использовать векторный потенциал $\widetilde {\mathbf{A}}$, через который $\widetilde {\mathbf{E}}$, $\widetilde {\mathbf{H}}$ выражаются по формулам: При этом уравнение для $\widetilde {\mathbf{A}}$ является решением уравнения Условие излучения для $\widetilde {\mathbf{A}}(x)$ можно записать в виде в котором ${{n}_{0}} = 1{\text{/}}{{c}_{0}} = \sqrt {{{\varepsilon }_{0}}{{\mu }_{0}}} $.

Пусть ${{{\mathbf{j}}}_{0}}(x)$ соответствует точечному диполю, помещенному в точку $y$ и имеющему направление ${{{\mathbf{j}}}^{0}} \in {{\mathbb{S}}^{2}}$, т.е. ${{{\mathbf{j}}}_{0}}(x) = {{{\mathbf{j}}}^{0}}\delta (x - y)$. Тогда в однородной среде (при $\varepsilon (x) = {{\varepsilon }_{0}}$) решение задачи (4.4), (4.5) имеет вид

Функции ${{\widetilde {\mathbf{E}}}^{0}}(x,\omega ,y)$, ${{\widetilde {\mathbf{H}}}^{0}}(x,\omega ,y)$, соответствующие этому случаю, вычисляются по формулам (4.3), в которых надо положить $\widetilde {\mathbf{A}} = {{\widetilde {\mathbf{A}}}^{0}}(x,\omega ,y)$.

Наряду с функциями $\widetilde {\mathbf{E}}(x,\omega ,y)$, $\widetilde {\mathbf{E}}(x,\omega ,y)$, введем функции

соответствующие рассеянному полю.

В работе [47] изучена следующая задача.

Задача 8. Задан квадрат модуля вектора ${{\widetilde {\mathbf{E}}}_{{sc}}}(x,\omega ,y)$ для всех $x,y \in S$ и всех частот $\omega $, начиная с некоторой частоты ${{\omega }_{0}}$, т.е. задана функция

найти $\varepsilon (x)$.

Исследование этой задачи основано на изучении асимптотики функции ${{\widetilde {\mathbf{E}}}_{{sc}}}(x,\omega ,y)$ при $\omega \to \infty $. Прежде всего из формулы (4.3) следует асимптотическая формула

в которой ${{\tau }_{0}}(x,y) = {{n}_{0}}{\text{|}}x - y{\text{|}}$ – время пробега электромагнитной волны между точками $x$ и $y$ в однородной среде, ${\mathbf{j}}_{ \bot }^{0} = {{{\mathbf{j}}}^{0}} - {{\nu }^{0}}({{{\mathbf{j}}}^{0}} \cdot {{\nu }^{0}})$ – проекция вектора ${{{\mathbf{j}}}^{0}}$ на плоскость, ортогональную единичному вектору ${{\nu }^{0}} = (x - y){\text{/|}}x - y{\text{|}}$.

Примем, что риманова метрика $d\tau = n(x){\text{|}}dx{\text{|}}$, $n(x) = \sqrt {\varepsilon (x){{\mu }_{0}}} $, является простой, т.е. любые две точки $x$, $y$ в ${{\mathbb{R}}^{3}}$ могут быть соединены единственной геодезической $\Gamma (x,y)$. Обозначим через $\tau (x,y)$ риманово расстояние между точками $x$ и $y$.

Для вывода асимптотики функции $\widetilde {\mathbf{A}}(x,\omega ,y)$ при $\omega \to \infty $ используется то обстоятельство, что эта функция при $y \in S$ совпадает с образом Фурье по $t$ решения ${\mathbf{A}}(x,t,y)$ задачи Коши

Структура решения функции ${\mathbf{A}}(x,t,y)$ изучена в [66]. Следующая лемма вытекает из выполненного исследования.

Лемма 5. Пусть $\varepsilon (x) \in {{C}^{\infty }}({{\mathbb{R}}^{3}})$, совпадает с заданной положительной постоянной ${{\varepsilon }_{0}}$ вне $\Omega $ и метрика $d\tau = n(x){\text{|}}dx{\text{|}}$, $n(x) = \sqrt {\varepsilon (x){{\mu }_{0}}} $, является простой. Тогда решение задачи (4.9) может быть представлено в виде

в котором $\alpha (x,y)$, ${{\tau }^{2}}(x,y)$ и $\widehat {\mathbf{A}}(x,t,y)$ – бесконечно дифференцируемые функции и $\theta (t)$ – функция Хевисайда.

Так как

то из (4.10), (4.11) следует, что Из формул (4.3), (4.12) вытекает асимптотическая формула в которой ${{\alpha }_{ \bot }}(x,y) = \alpha (x,y) - (\alpha (x,y) \cdot \nu (x,y))\nu (x,y)$ – проекция вектора $\alpha (x,y)$ на плоскость, ортогональную единичному вектору $\nu (x,y = \nabla \tau (x,y){\text{/}}n(x)$. Тогда из формул (4.8), (4.13) следует равенство Положим в этой формуле $x \in S$, $y \in S$, $x \ne y$. Используя данные (4.7) обратной задачи 8, находим, что Зафиксируем в этой формуле $x$ и $y$. Тогда получим функцию только одной переменной $\omega $, которая является почти периодической функцией этой переменной. Так как (см. [47]) множитель при косинусе в формуле (4.14) отличен от нуля, можно найти период этой функции, т.е. найти разность $\tau (x,y) - {{\tau }_{0}}(x,y) = \psi (x,y)$. Следовательно, можно найти и $\tau (x,y) = \psi (x,y) + {{\tau }_{0}}(x,y)$ для всех $x,y \in S$, $x \ne y$. Тогда мы приходим к обратной кинематической задаче: найти $n(x)$ внутри $\Omega $ по заданным временам пробега $\tau (x,y)$ между любыми точками $x$ и $y$, лежащими на ее границе. В результате приходим к теореме единственности решения задачи 8.

Теорема 6. При выполнении условий леммы 5 информация (4.7) однозначно определяет решение задачи 8.

Заметим, что бесконечная дифференцируемость коэффициента диэлектрической проницаемости $\varepsilon (x)$ на самом деле не является существенной и может быть заменена требованием конечной гладкости этого коэффициента.

Наибольший интерес представляет, конечно, не сама теорема единственности, а редукция обратной задачи 8 к обратной кинематической задаче, что открывает конструктивный путь ее решения.

В работе [48] рассмотрен случай, когда электромагнитное поле возбуждается плоской волной, идущей из бесконечности. При ${{{\mathbf{j}}}_{0}}(x) = 0$ и $\varepsilon (x) = {{\varepsilon }_{0}}$, уравнение (4.4) имеет решения вида

в котором единичные векторы ${{{\mathbf{j}}}^{0}}$ и ν ортогональны друг другу, ${{\varphi }_{0}}(x,\nu ) = {{n}_{0}}x \cdot \nu $. При этом ${\text{div}}{{\widetilde {\mathbf{A}}}^{0}} = 0$. Тогда В рассматриваемом случае векторы $\widetilde {\mathbf{E}}(x,\omega ,\nu )$, $\widetilde {\mathbf{H}}(x,\omega ,\nu )$ удовлетворяют однородной системе уравнений (4.2). Представим их в виде

Сформулируем задачу об определении коэффициента диэлектрической проницаемости для этого случая.

Задача 9. Пусть задан модуль вектора ${{\widetilde {\mathbf{E}}}_{{sc}}}(x,\omega ,\nu )$ как функция точки $x \in {{S}^{ + }}(\nu ) = \{ x \in S\,|\,x \cdot \nu > 0\} $ и параметров $\omega $ и $\nu $ для всех $\nu \in {{\mathbb{S}}^{2}}$ и всех частот $\omega $, начиная с некоторой частоты ${{\omega }_{0}} > 0$, т.е. задана функция

требуется по этой функции найти $\varepsilon (x)$ внутри $\Omega $.

Определим, как и при исследовании задачи 6, $\Sigma (\nu )$ как касательная плоскость к $S$ в точке $y(\nu ) = - R\nu \in S$ и функцию $\varphi (x,\nu ) = {{\varphi }_{0}}(x,\nu )$ для $x$, лежащих в полупространстве $x \cdot \nu + R \leqslant 0$, а для $x$, удовлетворяющих неравенству $x \cdot \nu + R > 0$, как то решение задачи Коши для уравнения эйконала

которое остается непрерывно дифференцируемым при переходе через плоскость $\Sigma (\nu )$.

Рассмотрим решение задачи Коши для гиперболической системы

Образ Фурье по $t$ этого решения совпадает с функцией $\widetilde {\mathbf{A}}(x,\omega ,\nu )$, через которую векторы $\widetilde {\mathbf{E}}(x,\omega ,\nu )$ и $\widetilde {\mathbf{H}}(x,\omega ,\nu )$ находятся по формулам (4.3). Для решения задачи (4.17) имеет место

Лемма 7. Пусть выполнено предположение 2 о регулярности геодезических линий римановой метрики $d\tau = n(x){\text{|}}dx{\text{|}}$, положительный индекс рефракции $n(x)$ принадлежит ${{C}^{\infty }}({{\mathbb{R}}^{3}})$ и ${\text{supp}}(n(x) - {{n}_{0}}) \subset \Omega $.Тогда существует решение задачи (4.17), представимое в виде

в котором $\alpha (x,\nu )$ и $\varphi (x,\nu )$ являются ${{C}^{\infty }}({{\mathbb{R}}^{3}})$ гладкими функциями, причем $\alpha (x,\nu ) = {{{\mathbf{j}}}^{0}}$ для $x \cdot \nu + R \leqslant 0$, $\theta (t)$ – функция Хевисайда, а $\widehat {\mathbf{A}}(x,t,\nu )$ является ${{C}^{\infty }}$-гладкой функцией переменных $x,t$ в области $t \geqslant \varphi (x,\nu )$.

Из этой леммы вытекает асимптотическая формула

В результате для функции находится формула в которой ${{\alpha }_{ \bot }}(x,\nu ) = \alpha (x,\nu ) - (\alpha (x,\nu ) \cdot \nu )\nu $. Тогда формула (4.16) приводит при $\omega \to \infty $ к равенству Зафиксируем $x \in {{S}^{ + }}(\nu )$ и $\nu \in {{\mathbb{S}}^{2}}$. Тогда ${{f}_{1}}{\text{/}}{{\omega }^{2}}$ является функцией только одной переменной $\omega $, почти периодической по этой переменной. Поэтому при больших $\omega $ можно найти период этой функции, т.е. найти разность $\varphi (x,\nu ) - {{\varphi }_{0}}(x,\nu ) = \psi (x,\nu )$. Следовательно, можно найти и $\varphi (x,\nu ) = \psi (x,\nu ) + {{\varphi }_{0}}(x,\nu )$ для всех $x \in {{S}^{ + }}(\nu )$, $\nu \in {{\mathbb{S}}^{2}}$. По функции $\varphi (x,\nu )$ находится $\tau (x,\nu ) = \varphi (x,\nu ) + R{{n}_{0}}$ для $x \in {{S}^{ + }}(\nu )$, $\nu \in {{\mathbb{S}}^{2}}$. Поэтому возникает уже встречавшийся ранее вариант обратной кинематической задачи: найти $n(x)$ по заданным для всех $\nu \in {{\mathbb{S}}^{2}}$ геодезическим расстояниям от точек $x \in {{S}^{ + }}(\nu )$ до плоскости $\Sigma (\nu )$. Отсюда следует теорема единственности.

Теорема 7. При выполнении условий леммы 7 информация (4.16) однозначно определяет решение задачи 9.

Характерной особенностью рассмотренных выше бесфазовых обратных задач является то, что на границе $S$ области $\Omega $ задается модуль рассеянного поля, инициированного либо точечными источниками, либо плоскими волнами, падающими из бесконечности. Но измерять рассеянное поле часто довольно затруднительно, проще измерить модуль полного поля. Одна из таких постановок с заданием модуля полного поля для уравнения Гельмгольца была рассмотрена выше (задача 5) в линейном приближении. В работе [49] предложено, как изменить постановку прямой задачи, чтобы обратная безфазовая проблема при измерении модуля полного поля обладала бы такими же свойствами, как и при измерении рассеянного поля, а именно, допускала бы сведение ее к той же хорошо изученной обратной кинематической задаче. Рассматривается случай, когда поле инициируется двумя встречными плоскими волнами, падающими из бесконечности.

Задача 10. Пусть электромагнитное поле инициируется плоскими волнами вида (4.15), падающими на неоднородность, локализованную в $\Omega $, из направлений, определяемых векторами $\nu $ и $ - \nu $, и имеющими одинаковую поляризацию ${{{\mathbf{j}}}^{0}}$. Пусть, далее, задан квадрат модуля суммы векторов $\widetilde {\mathbf{E}}(x,\omega ,\nu )$ и $\widetilde {\mathbf{E}}(x,\omega , - \nu )$ как функция точки $x \in {{S}^{ + }}(\nu ) = \{ x \in S\,|\,x \cdot \nu > 0\} $ и параметров $\omega $ и $\nu $ для всех $\nu \in {{\mathbb{S}}^{2}}$ и всех частот $\omega $, начиная с некоторой частоты ${{\omega }_{0}} > 0$, т.е. задана функция

найти $\varepsilon (x)$ внутри $\Omega $.

В предположениях леммы 7 для вектора $\widetilde E(x,\omega ,\nu )$ действует представление (4.18), а $\widetilde E(x,\omega , - \nu ) = {{{\mathbf{j}}}^{0}}exp( - i\omega {{\phi }_{0}}(x,\nu ))$ для $x \in {{S}^{ + }}(\nu )$. Поэтому при $\omega \to \infty $ имеет место равенство

Из равенства (4.22) с помощью описанной ранее процедуры находится $\varphi (x,\nu )$, а затем и $\tau (x,\nu )$ для всех $x \in {{S}^{ + }}(\nu )$ и $\nu \in {{\mathbb{S}}^{2}}$. Тем самым задача 10 приводится к той же обратной кинематической задаче, что и в предыдущем случае.

В работе [50] рассмотрена постановка бесфазовой обратной задачи с интерферирующими волнами, вызванными точечным источником ${{{\mathbf{j}}}^{0}}\delta (x - y)$ и сопряженным ${{{\mathbf{j}}}^{0}}\delta (x - z(y))$, сосредоточенным в точке $z(y)$, определяемой формулой $z(y) = y\ell $. Число $\ell $ зависит от геометрических параметров проблемы. Постановка задачи в этом случае немного изменяется. А именно, предполагается, что носитель разности $\varepsilon (x) - {{\varepsilon }_{0}}$ принадлежит области ${{\Omega }_{0}} = \{ x \in {{\mathbb{R}}^{3}}\,|\,{\text{|}}x{\text{|}} < {{R}_{0}}\} $, которая содержится в $\Omega = \{ x \in {{\mathbb{R}}^{3}}\,|\,{\text{|}}x{\text{|}} < R\} $, причем $R > {{R}_{0}}\sqrt 2 $. Граница $\Omega $ по-прежнему обозначается через $S$, а через $S(y)$ обозначается та часть $S$, на которую проектируется ${{\Omega }_{0}}$ при освещении ее пучком света, исходящим из точки $y$, т.е. $S(y) = \{ x \in S\,|\,{\text{|}}x - y{\text{|}} \geqslant 2\sqrt {{{R}^{2}} - R_{0}^{2}} , - y \cdot (x - y) \geqslant 2({{R}^{2}} - R_{0}^{2})$. При условии $R > {{R}_{0}}\sqrt 2 $ множество $S(y)$, очевидно, принадлежит полусфере $\{ x \in S\,|\,{\text{|}}x - y{\text{|}} > R\sqrt 2 $. Параметр $\ell $ выбирается так, чтобы множество $S(y)$ принадлежало той части $S$, которая освещается источником света, помещенным в точку $z(y)$. Достаточным для этого является выполнение условия $\ell > {{R}^{2}}{\text{/}}({{R}^{2}} - 2R_{0}^{2})$.

Задача 11. Пусть функция

задана для всех $y \in S$, $x \in S(y)$ и $\omega \geqslant {{\omega }_{0}} > 0$. Требуется по функции ${{f}_{3}}(x,\omega ,y)$ найти $\varepsilon (x)$ внутри ${{\Omega }_{0}}$.

Основной результат изучения этой задачи заключается в следующей теореме.

Теорема 8. Если риманова метрика $d\tau = n(x){\text{|}}dx{\text{|}}$ является простой, то данные (4.23) однозначно определяют длины геодезических линий $\Gamma (x,y)$ для всех $x,y \in S$.

В работе [51] рассмотрена система уравнений Максвелла, соответствующая анизотропной среде

В уравнениях (4.24) $\varepsilon (x) = {\text{diag}}({{\varepsilon }_{1}}(x),{{\varepsilon }_{1}}(x),{{\varepsilon }_{2}}(x))$ – положительно-определенная диагональная матрица. Предполагается, что ${{\varepsilon }_{1}}(x) \ne {{\varepsilon }_{2}}(x)$ для всех $x \in {{\mathbb{R}}^{3}}$, и ${{\varepsilon }_{1}}(x) = \varepsilon _{1}^{0}$, ${{\varepsilon }_{2}}(x) = \varepsilon _{2}^{0}$ вне области $\Omega = \{ x \in {{\mathbb{R}}^{3}}\,|\,{\text{|}}x{\text{|}} < R\} $. Здесь $\varepsilon _{1}^{0}$, $\varepsilon _{2}^{0}$ – заданные положительные числа.

В рассматриваемом случае для нестационарной системы уравнений Максвелла существуют две характеристические поверхности $t = {{\varphi }^{{(j)}}}(x)$, $j = 1,2$, в которых ${{\varphi }^{{(j)}}}(x)$ определены равенствами (см. [67]):

В соответствии с этим с уравнениями (4.24) связаны две римановы метрики: и в каждой точке $x \in {{\mathbb{R}}^{3}}$ существуют две скорости распространения волн ${{v}^{{(1)}}}$ и ${{v}^{{(2)}}}$. Первая из этих скоростей изотропна по отношению к направлению распространения волны, ${{v}^{{(1)}}}(x) = {{({{\mu }_{0}}{{\varepsilon }_{1}}(x))}^{{ - 1/2}}}$, вторая ${{v}^{{(2)}}}$ анизотропна, она зависит от $x$ и единичного вектора $\nu = ({{\nu }_{1}},{{\nu }_{2}},{{\nu }_{3}}) \in {{\mathbb{S}}^{2}}$, определяющего направление волны, $\nu = dx{\text{/|}}dx{\text{|}}$, и находится по формуле

В однородной среде (при ${{\varepsilon }_{1}} \equiv \varepsilon _{1}^{0}$, ${{\varepsilon }_{2}} \equiv \varepsilon _{2}^{0}$) существуют решения уравнений (4.25) и (4.26) вида

В формулах (4.29) $\nu = ({{\nu }_{1}},{{\nu }_{2}},{{\nu }_{3}}) = (sin\vartheta \cos \phi ,sin\vartheta sin\phi ,cos\vartheta )$, $\phi \in [0,2\pi )$, $\vartheta \in [0,\pi ]$, ${{\ell }^{0}}(\nu ) = (n_{2}^{0}{{\nu }_{1}},n_{2}^{0}{{\nu }_{2}},n_{1}^{0}{{\nu }_{3}})$ ${{\ell }^{0}}(\nu ) = (n_{2}^{0}{{\nu }_{1}},n_{2}^{0}{{\nu }_{2}},n_{1}^{0}{{\nu }_{3}})$, $n_{1}^{0} = {{({{\mu }_{0}}\varepsilon _{1}^{0})}^{{1/2}}}$, $n_{2}^{0} = {{({{\mu }_{0}}\varepsilon _{2}^{0})}^{{1/2}}}$. Поэтому в однородной среде существуют решения уравнений (4.24) типа плоских волн двух мод, которые являются образами Фурье бегущих плоских волн, найденных в [67]: Здесь ${{({{\epsilon }^{0}})}^{{ - 1}}}$ – матрица, обратная к матрице ${{\epsilon }^{0}} = {\text{diag}}(\varepsilon _{1}^{0},\varepsilon _{1}^{0},\varepsilon _{2}^{0})$.

Далее рассматривается задача о падении волн (4.30) и (4.32), падающих из бесконечности на неоднородность, сосредоточенную в области $\Omega $. Решение системы (4.24) представляется в виде

в  котором  $\widetilde {\mathbf{E}}_{{sc}}^{{(j)}}$, $\widetilde {\mathbf{H}}_{{sc}}^{{(j)}}$  отвечают  рассеянному  полю.  Пусть  $S$  –  граница  $\Omega $.  Обозначим через $S_{ + }^{{(j)}}(\nu ) = \{ x \in S\,|\,{{\varphi }^{{(0,j)}}}(x,\nu ) > 0\} $ и ${{\mathbb{S}}^{2}}({{\vartheta }_{0}})$ – шаровой пояс единичной сферы ${{\mathbb{S}}^{2}}({{\vartheta }_{0}}) = \{ \nu \in {{\mathbb{S}}^{2}}\,|\,\nu _{1}^{2} + \nu _{2}^{2} = {{\sin }^{2}}\vartheta \geqslant {{n}^{2}}{{\vartheta }_{0}} > 0\} $ ${{\mathbb{S}}^{2}}({{\vartheta }_{0}}) = \{ \nu \in {{\mathbb{S}}^{2}}\,|\,\nu _{1}^{2} + \nu _{2}^{2} = {{\sin }^{2}}\vartheta \geqslant {{n}^{2}}{{\vartheta }_{0}} > 0\} $.

Задача 12. Найти ${{\varepsilon }_{1}}(x)$, ${{\varepsilon }_{2}}(x)$ в области $\Omega $ по следующей информации: для $j = 1,2$ на $S_{ + }^{{(j)}}(\nu )$ заданы квадраты модуля суммы двух векторов ${{\widetilde {\mathbf{E}}}^{{(j)}}}(x,\omega ,\nu )$ и ${{\widetilde {\mathbf{E}}}^{{(j)}}}(x,\omega , - \nu )$ для всех $\nu \in {{\mathbb{S}}^{2}}({{\vartheta }_{0}})$ и всех частот $\omega $, больших некоторой фиксированной частоты ${{\omega }_{0}}$, т.е. заданы функции ${{F}_{j}}(x,\omega ,\nu )$ такие, что

Исследование задачи 12 проведено в [51] при условии, что выполнены некоторые предположения об элементах матрицы $\varepsilon (x)$ и римановых метриках $d{{\tau }^{{(j)}}}$, $j = 1,2$, определенных формулами (4.27), (4.28). Эти предположения заключаются в том, что ${{\varepsilon }_{j}}(x) \in {{C}^{{15}}}({{\mathbb{R}}^{3}})$, $j = 1,2$, и, кроме того, среда является слабо градиентной, т.е. величины ${\text{|}}\nabla {{\varepsilon }_{j}}(x){\text{|}}$, $j = 1.2$, достаточно малы. Принимается также, что для геодезических ${{\Gamma }_{j}}(x,\nu )$, отвечающих метрикам (4.27), (4.28), выполнено аналогичное ранее сделанному предположению 2 предположение о регулярности.

Предположение 3. Геодезические линии ${{\Gamma }_{j}}(x,\nu )$, $j - 1,2$, римановых метрик (4.27), (4.28) обладают следующими свойствами регулярности:

1) через каждую точку $x \in {{\mathbb{R}}^{3}}$ проходит единственная геодезическая ${{\Gamma }_{j}}(x,\nu )$, которая продолжается до плоскости ${{\Sigma }_{j}}(\nu )$ и ортогональна к ней,

2) геодезические линии ${{\Gamma }_{j}}(x,\nu )$, ортогональные ${{\Sigma }_{j}}(\nu )$, нигде не пересекаются.

При выполнении условий гладкости и регулярности установлены асимптотические формулы для функций ${{F}_{j}}(x,\omega ,\nu )$, $j = 1,2$, вполне аналогичные формуле (4.22). Из этих формул следует, что данные (4.36) обратной задачи однозначно определяют римановы расстояния ${{\tau }_{j}}(x,\nu )$, $j = 1,2$, для всех $x \in S_{ + }^{{(j)}}(\nu )$ и $\nu \in {{\mathbb{S}}^{2}}({{\vartheta }_{0}})$.

Таким образом, задача 12 сводится к рассмотрению следующей задачи: найти коэффициенты ${{\varepsilon }_{1}}(x)$ и ${{\varepsilon }_{2}}(x)$ по заданным временам пробега ${{\tau }_{j}}(x,\nu )$, $j = 1,2$, от точек $x \in S_{ + }^{{(j)}}(\nu )$ до точек плоскости ${{\Sigma }_{j}}(\nu )$ для всех $\nu \in {{\mathbb{S}}^{2}}({{\vartheta }_{0}})$. Эта задача распадается на две подзадачи: найти ${{\varepsilon }_{1}}(x)$ по ${{\tau }_{1}}(x,\nu )$, а затем найти ${{\varepsilon }_{2}}(x)$ по ${{\tau }_{2}}(x,\nu )$ при уже известном коэффициенте ${{\varepsilon }_{1}}(x)$. Каждая из этих задач является недоопределенной в том смысле, что времена пробега ${{\tau }_{j}}(x,\nu )$ для значений $\nu $, лежащих вне шарового пояса ${{\mathbb{S}}^{2}}({{\vartheta }_{0}})$, не заданы. К настоящему времени нет результатов, связанных с вопросами единственности и устойчивости решения этих задач, если ${{\vartheta }_{0}} \ne 0$. При ${{\vartheta }_{0}} = 0$ первая из задач совпадает с классической обратной кинематической задачей (правда, в несколько измененной параметризации задачи) и решение ее единственно и устойчиво. Решая ее, можно однозначно найти ${{\varepsilon }_{1}}(x)$. Что касается второй задачи, то она остается открытой для исследования.

В статье [51] обе подзадачи изучены в линейном приближении: предполагается, что каждая из функций ${{\varepsilon }_{j}}(x)$ мало отличается от соответствующей постоянной $\varepsilon _{j}^{0}$. Определение ${{\varepsilon }_{j}}(x)$ для $j = 1,2$ сведено, в линейном приближении, к обычным задачам рентгеновской томографии.

Некоторые численные методы решения бесфазовых обратных задач для уравнений электродинамики представлены в работах [25], [68], [69].