1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 60, № 7, 2020

Журнал вычислительной математики и математической физики, 2020, T. 60, № 7, стр. 1143-1150

Эвристический адаптивный быстрый градиентный метод в задачах стохастической оптимизации

А. В. Огальцов 1, А. И. Тюрин 1, *

1 НИУ ВШЭ
101000 Москва, ул. Мясницкая, 20, Россия

* E-mail: atyurin@hse.ru

Поступила в редакцию 07.10.2019
После доработки 12.11.2019
Принята к публикации 10.03.2020

Полный текст (PDF)

Аннотация

Приводится эвристический стохастический адаптивный ускоренный градиентный метод. Показывается, что на практике предложенный алгоритм имеет высокую скорость сходимости по сравнению с популярными сейчас методами оптимизации. Кроме того, приводится обоснование данного метода и описываются трудности, которые не позволяют на данный момент получить оптимальные оценки для предложенного алгоритма. Библ. 28. Фиг. 1.

Ключевые слова: быстрый градиентный метод, стохастическая оптимизация, адаптивная оптимизация.

1. ВВЕДЕНИЕ

В данной работе представлен эвристический алгоритм стохастической оптимизации, который является обобщением быстрого градиентного метода [1]. Методы стохастической оптимизации в последнее время являются популярными по той причине, что они позволяют уменьшать сложность подсчета градиента, что является очень важным, так как существуют примеры функций, в которых невозможно за разумное время подсчитать градиент оптимизируемой функции хотя бы в одной точке [2], [3]. Помимо этого, в задачах стохастической оптимизации [4] в силу формулировки самой задачи единственный разумный способ получить направление спуска – это сэмлирование векторов, которые имеют несмещенные по отношению к истинному градиенту направления. Данный подход также популярен в глубинном обучении [3], в задачах, которые имеют вид суммы функций [4]. Стоит подчеркнуть, что сложность подсчета стохастического градиента, как правило, можно регулировать. Отметим, что неускоренный вариант предложенного алгоритма имеется в работе [5].

Задача по поиску адаптивного быстрого градиентного метода со стохастическим градиентом по-прежнему является актуальной. Насколько нам известно, данная проблема является нерешенной. Отметим, что в данном направлении активно идет работа. В работе [6] предложили метод, который одновременно хорошо работает на гладких и негладких задачах, однако, данный метод не является ускоренным, шаг метода выбирается таким образом, что он не возрастает, в то время, как в нашем методе шаг метода подбирается адаптивно, может возрастать и убывать. В работе [7] предложили объединить стохастический неускоренный градиентный метод и правило Армихо [8], в результате авторы доказали, что их метод имеет скорость сходимости неускоренного градиентного метода, но это им удалось, используя специальные предположения об оптимизационной задаче. В работе [9] предложено доказательство вариации метода Adagrad [10] для случая, когда функция гладкая и невыпуклая, но как и в [6] шаг метода не возрастает, т.е. метод не является полностью адаптивным, не настраивается на локальную гладкость. Аналогичная проблема возникает в работах [11], [12], но только там авторы предлагают ускоренные варианты градиентного метода и более гибкие шаги внутри алгоритмов, в работе [12] методы зависят от оценки расстояния от начальной точки до оптимальной точки (размерности решения). Большую работу по поиску адаптивного стохастического быстрого градиентного метода сделали в работе [13]. В данной работе предложен адаптивный стохастический метод для вариационных неравенств, доказательство сходимости которого основано на теории эмпирических процессов [14], [15]. Отметим, что неускоренный градиентный метод является частным случаем метода, решающего вариационные неравенства, в то время как ускоренный градиентный метод получить из работы [13] нельзя. Кроме того, в [13] есть ограничение на максимальное значение шага метода, что немного упрощает анализ предложенных в [13] алгоритмов.

К сожалению, нам пока так и не удалось получить теоретические оценки для предложенного метода. В данной работе приведены эксперименты (см. раздел 4), которые показывают, что в задачах машинного обучения с логистической регрессией, нейронной сетью и сверточной нейронной сетью предложенный алгоритм имеет более быструю скорость сходимости, чем Adagrad [10] и Adam [16]. Кроме того, в разд. 3 мы приводим некоторое обоснование нашего алгоритма и объясняем некоторые детали, которые нам не позволяют до конца доказать сходимость метода в оптимальной форме.

2. АДАПТИВНЫЙ БЫСТРЫЙ СТОХАСТИЧЕСКИЙ ГРАДИЕНТНЫЙ МЕТОД

Опишем сначала общую постановку задачи выпуклой оптимизации [1]. Пусть определена функция $f(x):Q \to \mathbb{R}$ и дана произвольная норма $\left\| {\, \cdot \,} \right\|$ в ${{\mathbb{R}}^{n}}$. Сопряженная норма определяется следующим образом:

${{\left\| \lambda \right\|}_{*}}\;\mathop = \limits^{{\text{def}}} \;\mathop {max}\limits_{\left\| \nu \right\| \leqslant 1;\nu \in {{\mathbb{R}}^{n}}} \left\langle {\lambda ,\nu } \right\rangle \quad \forall \lambda \in {{\mathbb{R}}^{n}}.$
Будем полагать, что

1) $Q \subseteq {{\mathbb{R}}^{n}}$, выпуклое, замкнутое;

2) $f(x)$ – непрерывная, гладкая и выпуклая функции на $Q$;

3) $f(x)$ ограничена снизу на $Q$ и достигает своего минимума в некоторой точке (необязательно единственной) ${{x}_{*}} \in Q$.

Рассмотрим следующую задачу оптимизации:

$f(x) \to \mathop {min}\limits_{x \in Q} .$

Введем два понятия: прокс-функция и дивергенция Брэгмана [17].

Определение 1. $d(x){\kern 1pt} :\;Q \to \mathbb{R}$ называется прокс-функцией, если $d(x)$ непрерывно дифференцируемая на $\operatorname{int} Q$ и $d(x)$ является 1-сильно выпуклой относительно нормы $\left\| {\, \cdot \,} \right\|$ на $\operatorname{int} Q$$.$

Определение 2. Дивергенцией Брэгмана называется

$V(x,y)\;\mathop = \limits^{{\text{def}}} \;d(x) - d(y) - \left\langle {\nabla d(y),x - y} \right\rangle ,$
где $d(x)$ – произвольная прокс-функция.

Определение 3. Стохастическим $(\delta ,L)$-оракулом будем называть оракул, который на запрашиваемую точку $y \in Q$ дает пару $\left( {{{f}_{\delta }}(y),\nabla {{f}_{\delta }}(y;\xi )} \right)$ такую, что

$0 \leqslant f(x) - {{f}_{\delta }}(y) - \left\langle {\nabla {{f}_{\delta }}(y),x - y} \right\rangle \leqslant \frac{L}{2}{{\left\| {x - y} \right\|}^{2}} + \delta \quad \forall x \in Q,$
$\mathbb{E}\left[ {\nabla {{f}_{\delta }}(y;\xi )} \right] = \nabla {{f}_{\delta }}(y)\quad \forall y \in Q,$
$\mathbb{E}\left[ {exp\left( {\frac{{\left\| {\nabla {{f}_{\delta }}(y;\xi ) - \nabla {{f}_{\delta }}(y)} \right\|_{*}^{2}}}{{{{\sigma }^{2}}}}} \right)} \right] \leqslant exp(1)\quad \forall y \in Q,$
где ${{\sigma }^{2}} > 0$ и $\xi $ – произвольная случайная величина.

Отметим, что концепция стохастического $(\delta ,L)$-оракула основана на концепции $(\delta ,L)$-оракула [18]–[20].

Замечание 1. В определении 3 можно дополнительно потребовать случайность не только градиента, но и самой функции, т.е., чтобы стохастический $(\delta ,L)$-оракул возвращал вместо неслучайного ${{f}_{\delta }}(y)$ значения функции некоторое случайное значение ${{f}_{\delta }}(y;\xi )$.

Определим константу ${{R}_{Q}}$ такую, что

${{R}_{Q}} \geqslant \mathop {max}\limits_{x,y \in Q} \left\| {x - y} \right\|.$
Будем считать, что ${{R}_{Q}} < \infty $.

В методе, который мы предложим далее, будем оценивать истинный градиент на каждом шаге с помощью некоторого количества $\nabla {{f}_{\delta }}(y;{{\xi }_{j}})$, $j \in [1 \ldots {{m}_{{k + 1}}}]$, используя технику mini-batch (см., например, [21]).

Обозначим

(1)
${{\tilde {\nabla }}^{{{{m}_{{k + 1}}}}}}{{f}_{\delta }}(y)\;\mathop = \limits^{{\text{def}}} \;\frac{1}{{{{m}_{{k + 1}}}}}\sum\limits_{j = 1}^{{{m}_{{k + 1}}}} \,\nabla {{f}_{\delta }}(y;{{\xi }_{j}}).$

Пусть $\kappa $ – константа регулярности из [22] для $({{\mathbb{R}}^{n}},{{\left\| {\, \cdot \,} \right\|}_{*}})$. Для некоторых простых случаев верно следующее: если ${{\left\| {\, \cdot \,} \right\|}_{*}} = {{\left\| {\, \cdot \,} \right\|}_{2}}$, то $\kappa = 1$. Более того, если ${{\left\| {\, \cdot \,} \right\|}_{*}} = {{\left\| {\, \cdot \,} \right\|}_{q}}$, $q \in [2,\infty ]$, то $\kappa = min\left[ {q - 1,2ln(n)} \right]$. Сделаем следующее обозначение: $\widetilde \Omega \;\mathop = \limits^{{\text{def}}} \;2\kappa + 4\Omega \sqrt \kappa + 2{{\Omega }^{2}}$.

Далее будет использоваться в алгоритме константа ${{L}_{0}} \geqslant 0$, которая имеет смысл предположительной “локальной”, константы Липшица градиента в точке ${{x}_{0}}$. Рассмотрим адаптивный зеркальный вариант метода подобных треугольников со стохастическим $(a,L)$-оракулом.

Алгоритм 1 (Теоретический вариант)

Дано: ${{x}_{0}}$ – начальная точка, $\epsilon $ – желаемая точность решения, $\delta $, $L$ – константы из $(\delta ,L)$-оракула, $\beta $ – доверительный уровень, ${{L}_{0}}$ (${{L}_{0}} \leqslant L$), ${{\sigma }^{2}}$ – константа из определения 3.

Алгоритм: Возьмем

$N: = \left\lceil {\frac{{2\sqrt 3 \sqrt L {{R}_{Q}}}}{{\sqrt \varepsilon }}} \right\rceil ,\quad \Omega : = \sqrt {6ln\frac{N}{\beta }} .$

0-шаг:

${{y}_{0}}: = {{x}_{0}},\quad {{u}_{0}}: = {{x}_{0}},\quad {{\alpha }_{0}}: = 0,\quad {{A}_{0}}: = {{\alpha }_{0}}.$

k + 1-шаг:

${{j}_{{k + 1}}}: = 0.$

Пока не выполнится неравенство

(2)
${{f}_{\delta }}({{x}_{{k + 1}}}) \leqslant {{f}_{\delta }}({{y}_{{k + 1}}}) + \left\langle {{{{\tilde {\nabla }}}^{{{{m}_{{k + 1}}}}}}{{f}_{\delta }}({{y}_{{k + 1}}}),{{x}_{{k + 1}}} - {{y}_{{k + 1}}}} \right\rangle + \frac{{{{L}_{{k + 1}}}}}{2}{{\left\| {{{x}_{{k + 1}}} - {{y}_{{k + 1}}}} \right\|}^{2}} + \frac{{3{{\sigma }^{2}}\widetilde \Omega }}{{{{L}_{{k + 1}}}{{m}_{{k + 1}}}}} + \delta $

повторять:

$\begin{gathered} {{L}_{{k + 1}}}: = {{2}^{{{{j}_{{k + 1}}} - 1}}}{{L}_{k}},\quad {{\alpha }_{{k + 1}}}: = \frac{{1 + \sqrt {1 + 4{{A}_{k}}{{L}_{{k + 1}}}} }}{{2{{L}_{{k + 1}}}}},\quad {{A}_{{k + 1}}}: = {{A}_{k}} + {{\alpha }_{{k + 1}}}, \\ {{y}_{{k + 1}}}: = \frac{{{{\alpha }_{{k + 1}}}{{u}_{k}} + {{A}_{k}}{{x}_{k}}}}{{{{A}_{{k + 1}}}}},\quad {{m}_{{k + 1}}}: = \left\lceil {\frac{{3{{\sigma }^{2}}\tilde {\Omega }{{\alpha }_{{k + 1}}}}}{\epsilon }} \right\rceil . \\ \end{gathered} $

Сгенерировать i.i.d. ${{\xi }_{j}}$ ($j = 1,...,{{m}_{{k + 1}}}$) и посчитать ${{\tilde {\nabla }}^{{{{m}_{{k + 1}}}}}}{{f}_{\delta }}({{y}_{{k + 1}}})$.

$\begin{gathered} {{\phi }_{{k + 1}}}(x)\;\mathop = \limits^{{\text{def}}} \;V(x,{{u}_{k}}) + {{\alpha }_{{k + 1}}}\left( {{{f}_{\delta }}({{y}_{{k + 1}}}) + \left\langle {{{{\tilde {\nabla }}}^{{{{m}_{{k + 1}}}}}}{{f}_{\delta }}({{y}_{{k + 1}}}),x - {{y}_{{k + 1}}}} \right\rangle } \right) \\ {{u}_{{k + 1}}}: = \mathop {argmin}\limits_{x \in Q} {{\phi }_{{k + 1}}}(x),\quad {{x}_{{k + 1}}}: = \frac{{{{\alpha }_{{k + 1}}}{{u}_{{k + 1}}} + {{A}_{k}}{{x}_{k}}}}{{{{A}_{{k + 1}}}}},\quad {{j}_{{k + 1}}}: = {{j}_{{k + 1}}} + 1. \\ \end{gathered} $

Конец алгоритма.

Гипотеза 1. Пусть ${{x}_{*}}$ – ближайшая точка минимума к точке ${{x}_{0}}$ в смысле дивергенции Брэгмана, точность $\delta = \mathcal{O}({{\epsilon }^{{3/2}}}).$ Тогда для предложенного алгоритма с вероятностью $1 - \mathcal{O}(\beta )$ выполнено равенство

$f({{x}_{N}}) - f({{x}_{*}}) = \mathcal{O}(\epsilon ).$

3. ОБОСНОВАНИЕ АЛГОРИТМА

Приведем обоснование данного алгоритма. Предложенный алгоритм базируется на следующих градиентных методах [5], [20], [23]. Для адаптивного быстрого градиентного метода с $(\delta ,L)$-оракулом можно получить следующие оценки сходимости [5], [20], [23]:

$f({{x}_{N}}) - f({{x}_{*}}) \leqslant \mathcal{O}\left( {\frac{{LR_{Q}^{2}}}{{{{N}^{2}}}} + N\delta } \right).$
В то время, как для стохастического быстрого градиентного метода с $(\delta ,L)$-оракулом можно получить оценки вида [20]:
$f({{x}_{N}}) - f({{x}_{*}}) \leqslant \mathcal{O}\left( {\frac{{LR_{Q}^{2}}}{{{{N}^{2}}}} + \frac{{\sigma {{R}_{Q}}}}{{\sqrt N }}} \right).$
Соответственно ожидаемая оценка для адаптивного стохастического быстрого градиентного метода с $(\delta ,L)$-оракулом должна иметь вид

$f({{x}_{N}}) - f({{x}_{*}}) \leqslant \mathcal{O}\left( {\frac{{LR_{Q}^{2}}}{{{{N}^{2}}}} + N\delta + \frac{{\sigma {{R}_{Q}}}}{{\sqrt N }}} \right).$

Основная проблема по доказательству гипотезы 1, которая возникает в данный момент, связана с проблемой “выборки с отклонением” [24]. В доказательствах методов оптимизации со стохастическим градиентом (см. (1)) ключевым образом используется тот факт, что стохастический градиент имеет несмещенное математическое ожижание по отношению к настоящему градиенту. В алгоритме из разд. 2 это не так. Стоит обратить внимание, что наш метод является адаптивным и настраивается на локальную гладкость, делая проверку (2). Получается, что во внутреннем цикле, когда мы подбираем шаг метода, мы сначала генерируем mini-batch, а затем mini-batch проверяем на то, подходит ли он в неравенстве (2). Таким образом, мы неявно делаем процедуру “выборки с отклонением” [24] и соответственно возникает смещение сгенерированного стохастического градиента.

Стоит отметить, что возникали различные попытки перестроения алгоритма, но нам так и не удалось решить проблему “выборки с отклонением”.

В алгоритме 1 из разд. 2 в процедуре подбора параметра ${{L}_{{k + 1}}}$ мы каждый раз генерируем мини-батч. Возможный способ решения проблемы “выборки с отклонением” – это генерировать мини-батч один раз до процедуры подбора параметра ${{L}_{{k + 1}}}$ (см. алгоритм 2 из разд. 4). К сожалению, данный способ описания алгоритма приводит к другой проблеме. По аналогии с [20] в процессе доказательства возникает выражение вида

$\sum\limits_{k = 0}^{N - 1} \,{{\alpha }_{{k + 1}}}\left\langle {{{{\tilde {\nabla }}}^{{{{m}_{{k + 1}}}}}}{{f}_{\delta }}({{y}_{{k + 1}}}) - \nabla {{f}_{\delta }}({{y}_{{k + 1}}}),x - {{u}_{k}}} \right\rangle .$
Основной задачей является найти некоторые хорошие оценки сверху на данную сумму. В работе [20] данные оценки получены и доказано, что с “большой вероятностью” верно следующее неравенство:
$\sum\limits_{k = 0}^{N - 1} \,{{\alpha }_{{k + 1}}}\left\langle {{{{\tilde {\nabla }}}^{{{{m}_{{k + 1}}}}}}{{f}_{\delta }}({{y}_{{k + 1}}}) - \nabla {{f}_{\delta }}({{y}_{{k + 1}}}),x - {{u}_{k}}} \right\rangle \leqslant \mathcal{O}\left( {\frac{{\sigma {{R}_{Q}}}}{{\sqrt N }}} \right).$
Для доказательства данного неравенства использовались неравенства типа Азума–Хефдинга ([20], [25], Лемма 7.11) и тот факт, что ${{\alpha }_{{k + 1}}}$ являются неслучайными и условное математическое ожидание мини-батча равно настоящему градиенту. Для случая, когда мы один раз фиксируем мини-батч, возникает проблема с тем, что ${{\alpha }_{{k + 1}}}$ получаются случайные и скоррелированные с мини-батчем, поэтому стандартные неравенства типа Азума–Хефдинга ([20], Лемма 7.11) нам применить не удается.

В следующем разделе мы проводим численные эксперименты на различных задачах оптимизации. Мы показываем, что на практике практический вариант предложенного алгоритма (см. алгоритм 2 из разд. 4) работает лучше, чем популярные алгоритмы Adagrad [10] и Adam [16].

4. ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ

Начнем с описания отличия теоретического варианта (алгоритм 1) и практического варианта (алгоритм 2).

1. На практике мы не всегда можем знать константу $L$ и более того константа ${{R}_{Q}}$ может быть не ограничена, поэтому заранее точно определить $N$ из алгоритма 1 мы не можем, поэтому на практике будем предполагать, что $\tilde {\Omega } = 1$.

2. В практическом варианте константу ${{m}_{{k + 1}}}$ мы оцениваем, используя ${{L}_{k}}$, а не константу ${{L}_{{k + 1}}}$. Это позволяет нам эффективнее делать подбор параметра ${{L}_{{k + 1}}}$ за счет того, что количество ${{m}_{{k + 1}}}$ слагаемых при подсчете mini-batch не меняется.

3. Для многих классов оптимизируемых функций, которые включают в себя логистическую регрессию, нейронные сети и сверточные нейронные сети, сложность подсчета функции имеет тот же порядок сложности, что и подсчет градиента [26]. Соответственно значение функции так же оценивается, используя технику mini-batch (см. замечание 1):

$f_{\delta }^{{{{m}_{{k + 1}}}}}(y)\;\mathop = \limits^{{\text{def}}} \;\frac{1}{{{{m}_{{k + 1}}}}}\sum\limits_{j = 1}^{{{m}_{{k + 1}}}} \,\nabla {{f}_{\delta }}(y;{{\xi }_{j}}).$
Теоретические рассмотрения предыдущих глав статьи приводят к практической версии алгоритма 2. Было проведено три серии экспериментов. Оптимизация всех функций происходила относительно евклидовой нормы ${{\left\| {\, \cdot \,} \right\|}_{2}}$ c $V(x,y) = \tfrac{1}{2}\left\| {x - y} \right\|_{2}^{2}$, множество $Q = {{\mathbb{R}}^{n}}$. Начальные параметры алгоритма 2 для всех экспериментов оставались одинаковыми: верхняя оценка дисперсии градиента $\sigma _{0}^{2} = 0.1$, точность $\epsilon = 0.002$, константа ${{L}_{0}} = 1$. В экспериментах использовались следующие наборы данных.

1. MNIST [27], состоящий из изображений рукописных цифр размера $28 \times 28$ пикселей.

2. CIFAR [28], состоящий из цветных изображений размера $3 \times 32 \times 32$ пикселей, каждое из которых принадлежит к одному из 10 классов.

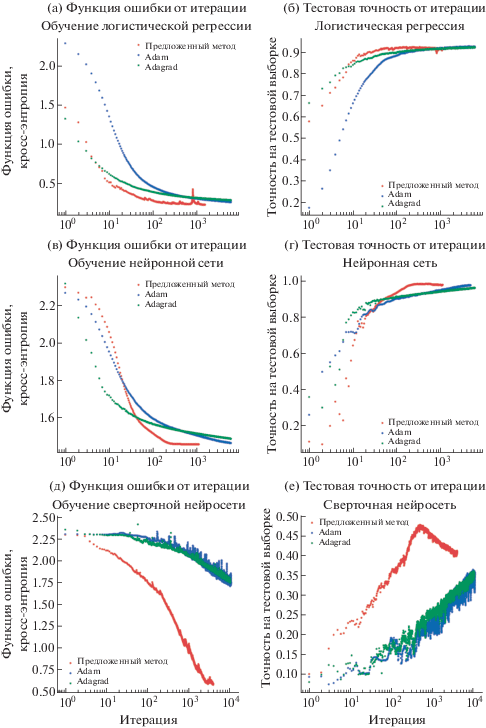
В первых двух сериях экспериментов использовался набор данных MNIST. Эксперименты заключаются в обучении логистической регрессии (линейный классификатор с выпуклой функцией потерь) и двухслойной нейронной сети с размером скрытых слоев 1000 (нелинейный классификатор с невыпуклой функцией потерь). В случае логистической регрессии количество оптимизируемых параметров равнялось 7850, а в случае двухслойной нейронной сети уже 795010. Оптимизация проводилась при помощи предложенного алгоритма, а также при помощи наиболее распространенных на сегодняшний день адаптивных алгоритмов Adam [16] и AdaGrad [10]. Для Adagrad и Adam использовались стандартные параметры: размер батча 128, $lr = 0.001$. Сравнение проводилось по скорости изменения функции потерь от итерации обучения и по изменению точности классификации на тестовой выборке. Результаты сравнения для логистической регрессии находятся на фиг. 1а, б, а для нейронной сети на фиг. 1в, г. В обоих случаях предложенный метод превосходит упомянутые выше как по скорости сходимости функции ошибки, так и по достигнутой точности.

Фиг. 1.

Численные эксперименты.

В третьей серии экспериментов небольшая свeрточная нейронная сеть обучалась предсказанию класса картинки на наборе данных CIFAR. Использовалась следующая архитектура свeрточной нейросети.

1. По матрице изображения ($3 \times 32 \times 32$) проходим окном свeртки размера $3 \times 6 \times 5$. Веса свeртки являются настраиваемыми параметрами.

2. После свeртки по полученному изображению проходит так называемый MaxPooling – это окно размера $2 \times 2$, которое оставляет максимальный попавший в него элемент, а остальные зануляет.

3. Далее снова проходим по результату предыдущего шага окном свeртки размера $6 \times 16 \times 5$.

4. Далее идут три последовательных полносвязных слоя с убывающим размером: 400, 120, 84.

Общее число параметров данной нейросети – 62 000. В этой серии экспериментов результаты работы предложенного метода также сравнивались с Adagrad и Adam (фиг. 1д, е). Алгоритм 2 также показал лучшие результаты.

Алгоритм 2 (Практический вариант)

Дано: ${{x}_{0}}$ – начальная точка, константы $\epsilon > 0$, ${{L}_{0}} > 0$ и $\sigma _{0}^{2} > 0$.

Алгоритм:

0-шаг:

${{y}_{0}}: = {{x}_{0}},\quad {{u}_{0}}: = {{x}_{0}},\quad {{\alpha }_{0}}: = 0,\quad {{A}_{0}}: = {{\alpha }_{0}}.$

k + 1-шаг:

${{\tilde {\alpha }}_{{k + 1}}} = \frac{{1 + \sqrt {1 + 4{{A}_{k}}{{L}_{k}}} }}{{2{{L}_{k}}}},\quad {{m}_{{k + 1}}}: = \left\lceil {\frac{{3\sigma _{0}^{2}{{{\tilde {\alpha }}}_{{k + 1}}}}}{\epsilon }} \right\rceil ,\quad {{j}_{{k + 1}}}: = 0,$
сгенерировать i.i.d. ${{\xi }_{j}}$ ($j = 1,...,{{m}_{{k + 1}}}$).

Пока не выполнится неравенство

(3)
$f_{\delta }^{{{{m}_{{k + 1}}}}}({{x}_{{k + 1}}}) \leqslant f_{\delta }^{{{{m}_{{k + 1}}}}}({{y}_{{k + 1}}}) + \left\langle {{{{\tilde {\nabla }}}^{{{{m}_{{k + 1}}}}}}{{f}_{\delta }}({{y}_{{k + 1}}}),{{x}_{{k + 1}}} - {{y}_{{k + 1}}}} \right\rangle + \frac{{{{L}_{{k + 1}}}}}{2}{{\left\| {{{x}_{{k + 1}}} - {{y}_{{k + 1}}}} \right\|}^{2}} + \frac{\epsilon }{{{{L}_{{k + 1}}}{{\alpha }_{{k + 1}}}}}$

повторять:

$\begin{gathered} {{L}_{{k + 1}}}: = {{2}^{{{{j}_{{k + 1}}} - 1}}}{{L}_{k}},\quad {{\alpha }_{{k + 1}}}: = \frac{{1 + \sqrt {1 + 4{{A}_{k}}{{L}_{{k + 1}}}} }}{{2{{L}_{{k + 1}}}}},\quad {{A}_{{k + 1}}}: = {{A}_{k}} + {{\alpha }_{{k + 1}}}, \\ {{y}_{{k + 1}}}: = \frac{{{{\alpha }_{{k + 1}}}{{u}_{k}} + {{A}_{k}}{{x}_{k}}}}{{{{A}_{{k + 1}}}}}. \\ \end{gathered} $

Посчитать $\mathop {\widetilde \nabla }\nolimits^{{{m}_{{k + 1}}}} {{f}_{\delta }}({{y}_{{k + 1}}})$ и $f_{\delta }^{{{{m}_{{k + 1}}}}}({{y}_{{k + 1}}})$:

$\begin{gathered} {{\phi }_{{k + 1}}}(x)\;\mathop = \limits^{{\text{def}}} \;V(x,{{u}_{k}}) + {{\alpha }_{{k + 1}}}\left( {f_{\delta }^{{{{m}_{{k + 1}}}}}({{y}_{{k + 1}}}) + \left\langle {{{{\tilde {\nabla }}}^{{{{m}_{{k + 1}}}}}}{{f}_{\delta }}({{y}_{{k + 1}}}),x - {{y}_{{k + 1}}}} \right\rangle } \right) \\ {{u}_{{k + 1}}}: = \mathop {argmin}\limits_{x \in Q} {{\phi }_{{k + 1}}}(x),\quad {{x}_{{k + 1}}}: = \frac{{{{\alpha }_{{k + 1}}}{{u}_{{k + 1}}} + {{A}_{k}}{{x}_{k}}}}{{{{A}_{{k + 1}}}}},\quad {{j}_{{k + 1}}}: = {{j}_{{k + 1}}} + 1. \\ \end{gathered} $

Посчитать $f_{\delta }^{{{{m}_{{k + 1}}}}}({{x}_{{k + 1}}})$.

Конец алгоритма.

Список литературы

  1. Нестеров Ю.Е. Введение в выпуклую оптимизацию. М.: МЦНМО, 2010. 262 с.

  2. Goodfellow I., Bengio Y., Courville A. Deep learning. MIT press. 2016.

  3. Krizhevsky A., Sutskever I., Hinton G. Imagenet classification with deep convolutional neural networks // In Advances in neural information processing systems. 2012. P. 1097–1105.

  4. Гасников А.В., Двуреченский П.Е., Усманова И.Н. О нетривиальности быстрых (ускоренных) рандомизированных методов // Труды МФТИ. 2016. Т. 8. № 2. С. 67–100.

  5. Гасников А.В. Современные численныe методы оптимизации. Метод универсального градиентного спуска // e-print. arXiv:1711.00394. 2018.

  6. Bach F., Levy K.Y. A universal algorithm for variational inequalities adaptive to smoothness and noise // COLT, 2019.

  7. Vaswani S., Mishkin A., Laradji I., Schmidt M., Gidel G., Lacoste-Julien S. Painless Stochastic Gradient: interpolation, line-search, and convergence rates // NIPS, 2019.

  8. Nocedal J., Wright S. Numerical optimization. Springer Science & Business Media. 2006.

  9. Ward R., Wu X., Bottou L. AdaGrad stepsizes: sharp convergence over nonconvex landscapes, from any initialization // ICML, 2019.

  10. Duchi J., Hazan E., Singer Y. Adaptive subgradient methods for online learning and stochastic optimization // Journal of Machine Learning Research. 2011. V. 12. № Jul. P. 2121–2159.

  11. Deng Q., Cheng Y., Lan G. Optimal adaptive and accelerated stochastic gradient descent // e-print. arXiv:1810.00553. 2018.

  12. Levy K.Y., Yurtsever A., Cevher V. Online adaptive methods, universality and acceleration // NIPS, 2018.

  13. Iusem A.N., Jofre A., Oliveira R.I., Thompson P. Variance-based extragradient methods with line search for stochastic variational inequalities // SIAM J. Optimizat. 2019. V. 29. № 1. P. 175–206.

  14. Boucheron S., Lugosi G., Massart P. Concentration inequalities: A nonasymptotic theory of independence. Oxford University Press. 2013.

  15. Panchenko D. Symmetrization approach to concentration inequalities for empirical processes // The Annals of Probability. 2003. V. 31. № 4. P. 2068–2081.

  16. Kingma D.P., Ba J. Adam: a method for stochastic optimization // ICLR, 2015.

  17. Gupta M.D., Huang T. Bregman distance to l1 regularized logistic regression // ICPR, 2008.

  18. Devolder O., Glineur F., Nesterov Yu. First-order methods with inexact oracle: the strongly convex case // CORE Discussion Paper 2013/16. 2013. URL: https://www.uclouvain.be/cps/ucl/doc/core/documents/coredp2013_16web.pdf.

  19. Devolder O., Glineur F., Nesterov Yu. First-order methods of smooth convex optimization with inexact oracle // Math. Program. 2014. V. 146. № 1–2. P. 37–75.

  20. Devolder O. Exactness, inexactness and stochasticity in first-order methods for largescale convex optimization. PhD thesis. CORE UCL, 2013.

  21. Li M., Zhang T., Chen Y., Smola A.J. Efficient mini-batch training for stochastic optimization // ACM, 2014.

  22. Juditsky A., Nemirovski A. Large deviations of vector-valued martingales in 2-smooth normed spaces // e-print. arXiv:0809.0813. 2008.

  23. Gasnikov A., Tyurin A. Fast gradient descent for convex minimization problems with an oracle producing a (δ, L)-model of function at the requested point // Computational Mathematics and Mathematical Physics. 2019. V. 59. № 7. P. 1085–1097.

  24. Robert C., Casella G. Monte Carlo statistical methods. Springer Science & Business Media. 2013.

  25. Lan G., Nemirovski A., Shapiro A. Validation analysis of mirror descent stochastic approximation method // Math. Program. 2012. V. 134. № 2. P. 425–458.

  26. Griewank A. On automatic differentiation // Mathematical Programming: recent developments and applications. 1989. V. 6. № 6. P. 83–107.

  27. LeCun Y., Bottou L., Bengio Y., Haffner P. Gradient-based learning applied to document recognition // Proceedings of the IEEE. 1998. V. 86. № 11. P. 2278–2324.

  28. Krizhevsky A. Learning Multiple Layers of Features from Tiny Images. PhD thesis. University of Toronto, 2009.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал