1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 61, № 10, 2021

Журнал вычислительной математики и математической физики, 2021, T. 61, № 10, стр. 1672-1683

Расчет осаждения струи капельной влаги моментным методом

В. Н. Котеров 1, *, Р. И. Романенко 2, **

1 ФИЦ ИУ РАН
119333 Москва, Вавилова, 44, корп. 2, Россия

2 МФТИ(ГУ)
141701 Долгопрудный, М.о., Институтский пер., 9, Россия

* E-mail: vkoterov@yandex.ru
** E-mail: romanenko.ri@phystech.edu

Поступила в редакцию 03.02.2021
После доработки 07.03.2021
Принята к публикации 09.06.2021

Полный текст (PDF)

Аннотация

На примере задачи расчета осаждения шлейфа мелкодисперсной капельной влаги, образованного компактным источником в потоке воздуха, проводится верификация моментного метода приближенного решения уравнения переноса и диффузии полидисперсной среды. Формулируется способ замыкания бесконечной цепочки моментных уравнений. Результаты расчетов уравнения переноса и диффузии сравниваются с расчетами, выполненными по двухмоментному и трехмоментному приближениям. Библ. 15. Фиг. 8. Табл. 1.

Ключевые слова: полидисперсная среда, уравнение переноса и диффузии, капельная влага, метод моментов.

1. ВВЕДЕНИЕ

Задачи расчета переноса воздушным потоком капельной влаги уже давно рассматриваются, например, при математическом моделировании зарождения и формирования осадков в облачных структурах. Подобные задачи возникают также при попытках описания распространения аэрозолей, распыляемых наземным или воздушным источниками. Еще одно интересное явление, к которому имеет отношение настоящая работа, – это возникновение и интенсивный перенос капельной влаги в нижних бьефах крупных гидроэлектростанций при работе их водосбросных сооружений. Математическая модель (см. [1]–[6]), описывающая данное явление, включает, в частности, блок расчета распространения капельной влаги в потоке воздуха. Перенос капельной влаги достаточно аккуратно описывается уравнением переноса и диффузии, которому удовлетворяет функция распределения капель по их размерам. При этом, однако, необходимо рассматривать четырехмерное пространство (три пространственные координаты, плюс переменная, определяющая радиусы капель), что на практике требует длительных расчетов с использованием высокопроизводительных вычислительных комплексов. Для сокращения расчетного времени в модели (см. [1]–[6]) была использована приближенная методика, основанная на применении метода моментов, в двухмоментном и трехмоментном приближении.

Настоящая работа посвящена верификации моментного метода расчета уравнения переноса и диффузии капельной влаги путем сравнения результатов расчетов моментных уравнений с “точным” расчетом уравнения переноса и диффузии. При этом рассматривается одна из простейших задач в двумерной пространственной постановке, а именно, расчет осаждения двумерного (плоского) шлейфа мелкодисперсной капельной влаги, образованного компактным источником в потоке воздуха.

2. ПОСТАНОВКА ЗАДАЧИ

Рассмотрим плоский шлейф осаждающейся капельной влаги, образованный компактным неподвижным источником, находящимся на высоте H над подстилающей поверхностью в однородном потоке воздуха, имеющем скорость U0 (фиг. 1).

Фиг. 1.

Схема плоского капельного шлейфа, образованного неподвижным источником влаги в потоке воздуха.

Будем полагать, что количество жидкой фазы, содержащейся в единице объема среды невелико, а влияние процессов испарения/конденсации, сопровождающихся поглощением/выделением скрытой теплоты испарения, пренебрежимо мало. В этом случае можно считать, что функция распределения f(a) капель по размерам (радиусам a) удовлетворяет следующему уравнению переноса и диффузии:

(1)
$\frac{{\partial f}}{{\partial t}} + \frac{{\partial {{U}_{0}}f}}{{\partial x}} + \frac{{\partial {{w}_{s}}f}}{{\partial z}} + \frac{{\partial{ \dot {a}}f}}{{\partial a}} = \frac{\partial }{{\partial x}}{{A}_{x}}\frac{{\partial f}}{{\partial x}} + \frac{\partial }{{\partial z}}{{A}_{z}}\frac{{\partial f}}{{\partial z}},\quad q = \mathop \smallint \limits_0^\infty \,f(a){\kern 1pt} da.~$
Здесь и далее q – масса воды в единице объема (так называемая водность среды), ws – скорость осаждения капель в гравитационном поле, $\dot {a}$ – скорость изменения радиуса капель, Ax и Az – коэффициенты горизонтальной и вертикальной турбулентной диффузии, принимаемые далее постоянными.

Задача рассматривается в области x ≥ 0, z ≥ 0, a ≥ 0. Наличие источника капельной влаги, образующего водно-воздушный шлейф, учитывается следующим краевым условием:

(2)
$f = {{f}_{0}}b(a{\text{/}}{{a}_{m}})\delta (z{\text{/}}H - 1)\quad {\text{при}}\quad x = 0,\quad \mathop \smallint \limits_0^\infty \,b(a{\kern 1pt} ')da{\kern 1pt} ' = 1,\quad \mathop \smallint \limits_0^\infty \delta (z{\kern 1pt} {\text{'}} - 1)dz{\kern 1pt} ' = 1.$
Здесь b(a/am) – нормированное на единицу распределение источника капельной влаги по радиусам капель (am – мода распределения), δ(z/H – 1) – нормированная на единицу достаточно узкая финитная функция, описывающая распределение функции f в начальном сечении шлейфа (H – высота источника над подстилающей поверхностью), f0 – нормировочный множитель.

Так как погонный расход жидкости источника капельной влаги Q0 (фиг. 1) определяется выражением

${{Q}_{0}} = {{U}_{0}}\int_0^\infty {q(0,z)dz} ,\quad q(0,z) = \int_0^\infty {f(a,0,z)da} ,\quad {\text{то}}\quad {{f}_{0}} = {{Q}_{0}}{\text{/}}({{U}_{0}}{{a}_{m}}H).$

На подстилающей поверхности (z = 0) выставляется условие $\partial f{\text{/}}\partial z = 0$, и расчетная величина осадков h, выпадающих на подстилающую поверхность, вычисляется по формуле

$h = \frac{1}{{{{\rho }_{w}}}}\mathop \smallint \limits_0^\infty \,{{w}_{s}}f(a)da.$
Здесь и далее ρw – плотность воды.

На открытом участке границы, через который может происходить диффузия капельной влаги (при $x \to \infty $), выставляется модельное “мягкое” условие ${{\partial }^{2}}f{\text{/}}\partial {{x}^{2}} = 0$. Аналогичное условие ${{\partial }^{2}}f{\text{/}}\partial {{z}^{2}} = 0$ выставляется и при $z \to \infty $.

Наконец, при a = 0 можно считать, что “поток капель” $\dot {a}f(a) = 0$, а при a → ∞ величина f → 0. В рассматриваемой задаче, впрочем, будет считаться, что изменение размеров капель происходит только за счет так называемого процесса гравитационной коагуляции. В этом случае “скорость потока капель в пространстве их радиусов” $\dot {a} \geqslant 0$, и условие f → 0 при a → ∞ можно не учитывать.

Для окончательной формулировки задачи необходимо указать зависимость скорости осаждения капель ws от их радиуса a, а также выражение для скорости изменения размеров капель $\dot {a}$.

2.1. Скорость осаждения капель в гравитационном поле

Эта величина для капель (или твердых частиц) достаточно малого радиуса может быть вычислена по формуле Стокса (см., например, [7]):

(3)
${{w}_{s}} = {{w}_{{St}}}(a) \equiv k{{a}^{2}},\quad k = \frac{2}{9}\frac{g}{{{{\nu }_{a}}}}\left( {\frac{{{{\rho }_{w}}}}{{{{\rho }_{a}}}} - 1} \right),$
где g – ускорение свободного падения, νa – кинематическая вязкость газа, ρw и ρa – плотности жидкости и газа соответственно. Для капель воды в воздухе параметр k в формуле (3) составляет величину порядка 108 1/(м⋅с).

Формула (3) справедлива лишь для капель или твердых частиц достаточно малого размера, когда скорость их осаждения такова, что число Рейнольдса $\operatorname{Re} (a) = 2a{{w}_{s}}(a){\text{/}}{{\nu }_{a}} < 1$ (см. [7]). При $\operatorname{Re} (a) \geqslant 1$ используются различные полуэмпирические формулы, основанные на формуле Стокса (3), но с поправками, зависящими от числа Рейнольдса Re. Например, согласно [8],

(4)
${{w}_{s}}(a) = \frac{{{{w}_{{St}}}(a)}}{{1 + 0.15\operatorname{Re} {{{(a)}}^{{0.687}}}}}.$

Отметим также, что очень крупные капли вначале испытывают значительную деформацию, а затем могут начинать дробиться. В результате максимальный радиус капель не превышает 2.5–3 мм, а их скорость осаждения 9–10 м/с (см. [9]).

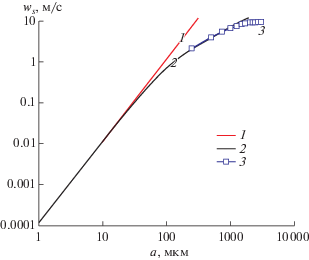
На фиг. 2 представлена зависимость скорости осаждения ws капли воды в воздухе от радиуса капли a. Видно, что формула Стокса удовлетворительно работает лишь для капель радиуса a ≤ ≤ 50–100 мкм, а формула (3) для a ≤ 1000–1500 мкм.

Фиг. 2.

Скорость осаждения капель воды в воздухе: 1 – формула Стокса (3), 2 – формула (4), 3 – данные [9].

В настоящей работе, в отличие от [1]–[6], будет рассматриваться только мелкодисперсная капельная влага, осаждаемая в режиме Стокса.

2.2. Скорость изменения размеров капель

Изменение размеров капель в процессе их переноса потоком воздуха происходит, в основном, за счет процессов конденсации/испарения и процесса коагуляции, в частности, гравитационной коагуляции – укрупнения капель в процессе их движения за счет “поглощения” более мелких капель. Крупные капли c a ≥ 103 мкм, скорость движения которых относительно воздуха достаточно высока, могут также дробиться на более мелкие. Известно, что механизм изменения размеров капель за счет конденсации/испарения существенен для капель достаточно малого радиуса (a ≤ 50 мкм, см., например, [10]). Для капель с размерами 50 мкм < a < 103 мкм, которые будут рассматриваться далее, основную роль должна играть гравитационная коагуляция. Точное выражение для скорости изменения радиусов капель за счет этого процесса достаточно сложное (см., например, [10], [11]). Однако известны приближенные формулы, применяемые, например, при моделировании переноса капельной влаги в облачных структурах. В частности, в метеорологии известна следующая теоретическая формула для изменения массы M капли в результате процесса гравитационной коагуляции (см. [12]):

$dM{\text{/}}dt = \pi {{a}^{2}}{{w}_{s}}(a){{\rho }_{w}}q\tilde {E},\quad \tilde {E} = {\text{const,}}$
где $\tilde {E}$ – безразмерная величина, которую можно назвать средней вероятностью/коэффициентом захвата/коагуляции крупной каплей более мелких капель. Так как $M = (4{\text{/}}3)\pi {{\rho }_{w}}{{a}^{3}}$, то отсюда немедленно следует: $\dot {a} = \tilde {K}{{w}_{s}}(a)q$, $\tilde {K} = \tilde {E}{\text{/}}(4{{\rho }_{w}})$. Если скорость осаждения капель рассчитывается по формуле Стокса, то

$\dot {a} = K{{a}^{2}}q,\quad K = k\tilde {K} = k\tilde {E}{\text{/}}(4{{\rho }_{w}}).$

По порядку величины (значение $\tilde {E}$ принято равным 0.4) в рассматриваемых случаях (капли воды в воздухе) K ≈ 104 м2/(кг⋅с).

1.3. Формулировка задачи в безразмерной форме

Приведем уравнение (1) и краевое условие (2) к безразмерной форме, для чего представим переменные в следующем виде (штрихи помечают безразмерные переменные):

$\begin{gathered} x = H\frac{{{{U}_{0}}}}{{ka_{m}^{2}}}x{\kern 1pt} {\text{'}},\quad z = Hz{\kern 1pt} {\text{'}},\quad t = {{T}_{0}}t{\kern 1pt} {\text{'}},\quad a = {{a}_{m}}a{\kern 1pt} {\text{'}}, \\ f = {{f}_{0}}f{\kern 1pt} {\text{'}},\quad q = {{f}_{0}}{{a}_{m}}q{\kern 1pt} {\text{'}},\quad \dot {a} = Ka_{m}^{3}{{f}_{0}}\dot {a}{\kern 1pt} {\text{'}},\quad h = \frac{1}{{{{\rho }_{w}}}}ka_{m}^{3}{{f}_{0}}h{\kern 1pt} {\text{'}}, \\ \end{gathered} $
где am – мода распределения источника капельной влаги, ${{T}_{0}} = H{\text{/}}(ka_{m}^{2})$ – характерное время процесса, $\dot {a}{\kern 1pt} '$ и $h{\kern 1pt} '$– безразмерная скорость изменения размеров капель и безразмерная скорость выпадения капельной влаги на подстилающую поверхность. Подставляя данные выражения в (1) и (2), получаем (штрихи у безразмерных переменных далее везде опущены):
(5)
$\frac{{\partial f}}{{\partial t}} + \frac{{\partial f}}{{\partial x}} - {{a}^{2}}\frac{{\partial f}}{{\partial z}} + {{\varepsilon }_{{\dot {a}}}}\frac{{\partial{ \dot {a}}f}}{{\partial a}} = {{\varepsilon }_{{{{A}_{x}}}}}\frac{{{{\partial }^{2}}f}}{{\partial {{x}^{2}}}} + {{\varepsilon }_{{{{A}_{z}}}}}\frac{{{{\partial }^{2}}f}}{{\partial {{z}^{2}}}},\quad \dot {a} = {{a}^{2}}q,\quad q = \mathop \smallint \limits_0^\infty \,f(a)da,$
(6)
$f = b(a)\delta (z - 1)\quad {\text{при}}\quad x = 0,$
где ${{\varepsilon }_{{\dot {a}}}},\;{{\varepsilon }_{{{{A}_{x}}}}},\;{{\varepsilon }_{{{{A}_{z}}}}}$ – параметры подобия, определяющие влияние гравитационной коагуляции, горизонтальной и вертикальной диффузии, соответственно, на процесс осаждения шлейфа. Они следующим образом связаны с определяющими параметрами задачи:

${{\varepsilon }_{{\dot {a}}}} = \frac{{K{{Q}_{0}}}}{{k{{a}_{m}}{{U}_{0}}}},\quad {{\varepsilon }_{{{{A}_{x}}}}} = \frac{{{{A}_{x}}}}{{H{{U}_{0}}}}\frac{{{{w}_{s}}({{a}_{m}})}}{{{{U}_{0}}}},\quad {{\varepsilon }_{{{{A}_{z}}}}} = \frac{{{{A}_{z}}}}{{H{{U}_{0}}}}\frac{{{{U}_{0}}}}{{{{w}_{s}}({{a}_{m}})}},\quad {{w}_{s}}({{a}_{m}}) = ka_{m}^{2}.$

Так как обычно ${{w}_{s}}({{a}_{m}}){\text{/}}{{U}_{0}} \ll 1$, то ${{\varepsilon }_{{{{A}_{x}}}}} \ll {{\varepsilon }_{{{{A}_{z}}}}}$, т.е. процессом продольной диффузии часто можно пренебрегать по сравнению с вертикальной диффузией.

В расчетах будем принимать, что функция δ, задающая пространственное распределение функции f в начальном сечении x = 0 шлейфа, имеет вид гауссовой функции

$\delta (z - 1) = \frac{1}{{{{\Delta }}\sqrt \pi }}\exp \left[ { - {{{\left( {\frac{{z - 1}}{{{\Delta }}}} \right)}}^{2}}} \right],$
где Δ – характерная безразмерная полуширина шлейфа в его начальном сечении.

Безразмерная скорость выпадения жидкости на подстилающую поверхность вычисляется так:

$h = \mathop \smallint \limits_0^\infty \,{{a}^{2}}f(a)da\quad {\text{при}}\quad z = 0.$

3. МОМЕНТНЫЙ МЕТОД

Введем моменты функции распределения капель по размерам (n – порядок момента):

${{f}_{n}} = \mathop \smallint \limits_0^\infty \,{{a}^{n}}f(a)da,\quad n = 0,1,...\;.$

Отметим, что нулевой и первый моменты функции распределения связаны с водностью q и со средним размером капель $\bar {a}$ следующим образом:

${{f}_{0}} = q,\quad {{f}_{1}} = q\bar {a},\quad \bar {a} = \mathop \smallint \limits_0^\infty \,af(a)da{\text{/}}\mathop \smallint \limits_0^\infty \,f(a)da.$

Второй момент f2 совместно с двумя первыми определяет дисперсию D функции распределения и стандартное отклонение σ размеров капель от среднего значения:

$D = \mathop \smallint \limits_0^\infty \,{{(a - \bar {a})}^{2}}f(a)da = {{f}_{2}} - f_{1}^{2}{\text{/}}{{f}_{0}},\quad \sigma = \sqrt D .$

Помножим уравнение (5) на an и проинтегрируем по всем возможным размерам капель a. Тогда можно получить следующие моментные уравнения:

(7)
$\frac{{\partial {{f}_{n}}}}{{\partial t}} + \frac{{\partial {{f}_{n}}}}{{\partial x}} - \frac{{\partial {{f}_{{n + 2}}}}}{{\partial z}} - n{{\varepsilon }_{{\dot {a}}}}{{f}_{0}}{{f}_{{n + 1}}} = {{\varepsilon }_{{{{A}_{x}}}}}\frac{{{{\partial }^{2}}{{f}_{n}}}}{{\partial {{x}^{2}}}} + {{\varepsilon }_{{{{A}_{z}}}}}\frac{{{{\partial }^{2}}{{f}_{n}}}}{{\partial {{z}^{2}}}},\quad n = 0,1, \ldots ~\;.$

Цепочка моментных уравнений (7), обрываемая на каком-нибудь значении n = N, оказывается не замкнутой, так как в эти уравнения входят моменты ${{f}_{{N + 1}}}$ и ${{f}_{{N + 2}}}$ , порядок которых выше N. Однако на основе (7) могут быть построены приближенные модели процесса переноса капельной влаги, позволяющие, в частности, рассчитывать распределения водности среды и интенсивность осадков, выпадающих на подстилающую поверхность.

Оборвем цепочку уравнений (7) на некотором значении n = N (N будет назваться номером приближения), и запишем ее в следующем виде:

$\frac{{\partial {{f}_{n}}}}{{\partial t}} + \frac{{\partial {{f}_{n}}}}{{\partial x}} - \frac{{\partial {{f}_{{n + 2}}}}}{{\partial z}} - n{{\varepsilon }_{{\dot {a}}}}{{f}_{0}}{{f}_{{n + 1}}} = {{\varepsilon }_{{{{A}_{x}}}}}\frac{{{{\partial }^{2}}{{f}_{n}}}}{{\partial {{x}^{2}}}} + {{\varepsilon }_{{{{A}_{z}}}}}\frac{{{{\partial }^{2}}{{f}_{n}}}}{{\partial {{z}^{2}}}},\quad n = 0,1, \ldots ,N - 2,$
(8)
$\frac{{\partial {{f}_{{N - 1}}}}}{{\partial t}} + \frac{{\partial {{f}_{{N - 1}}}}}{{\partial x}} - \frac{{\partial {{\eta }_{{N - 1}}}{{{\bar {a}}}^{2}}{{f}_{{N - 1}}}}}{{\partial z}} - (N - 1){{\varepsilon }_{{\dot {a}}}}{{f}_{0}}{{f}_{N}} = {{\varepsilon }_{{{{A}_{x}}}}}\frac{{{{\partial }^{2}}{{f}_{{N - 1}}}}}{{\partial {{x}^{2}}}} + {{\varepsilon }_{{{{A}_{z}}}}}\frac{{{{\partial }^{2}}{{f}_{{N - 1}}}}}{{\partial {{z}^{2}}}},$
$\frac{{\partial {{f}_{N}}}}{{\partial t}} + \frac{{\partial {{f}_{N}}}}{{\partial x}} - \frac{{\partial {{\eta }_{N}}{{{\bar {a}}}^{2}}{{f}_{N}}}}{{\partial z}} - N{{\varepsilon }_{{\dot {a}}}}{{\zeta }_{N}}{{f}_{1}}{{f}_{N}} = {{\varepsilon }_{{{{A}_{x}}}}}\frac{{{{\partial }^{2}}{{f}_{N}}}}{{\partial {{x}^{2}}}} + {{\varepsilon }_{{{{A}_{z}}}}}\frac{{{{\partial }^{2}}{{f}_{N}}}}{{\partial {{z}^{2}}}}.$
Здесь введены следующие обозначения:

(9)
${{\eta }_{n}} = \frac{{{{f}_{{n + 2}}}}}{{{{{\bar {a}}}^{2}}{{f}_{n}}}} = \frac{{{{f}_{{n + 2}}}f_{0}^{2}}}{{{{f}_{n}}f_{1}^{2}}} = \frac{{\int\limits_0^\infty {{{a}^{{n + 2}}}fda} {{{\left( {\int\limits_0^\infty {fda} } \right)}}^{2}}}}{{\int\limits_0^\infty {{{a}^{n}}fda} {{{\left( {\int\limits_0^\infty {afda} } \right)}}^{2}}}},\quad {{\zeta }_{n}} = \frac{{{{f}_{0}}{{f}_{{n + 1}}}}}{{{{f}_{1}}{{f}_{n}}}} = \frac{{\int\limits_0^\infty {fda} \,\int\limits_0^\infty {{{a}^{{n + 1}}}fda} }}{{\int\limits_0^\infty {afda} \,\int\limits_0^\infty {{{a}^{n}}fda} }}.$

Заметим, что, согласно (9), ζ1 = η0. Отметим также, что если в дробно-рациональных функционалах (9) полагать f = f0δ(a – a0) (где δ – дельта-функция Дирака, а a0 = const), то все ηn = 1 и ζn = 1.

Систему уравнений (8) можно замкнуть, указав приближенную зависимость функционалов ${{\eta }_{{N - 1}}}$, ηN и ζN от моментов f0, …, fN. Для решения этой задачи постулируем какую-нибудь физически оправданную аналитическую зависимость функции распределения f(a) от радиуса капель a и от (N + 1)-го дополнительного параметра. Сама эта функциональная зависимость должна оставаться неизменной в рассматриваемом процессе, но параметры в ней, конечно, могут меняться с течением времени.

Удобно постулировать следующую параметрическую зависимость:

(10)
$f = \frac{{{{f}_{0}}}}{{{{a}_{m}}}}F(\xi ;{{g}_{0}},...,{{g}_{{N - 2}}}),\quad \xi = \frac{a}{{{{a}_{m}}}},\quad \mathop \smallint \limits_0^\infty \,F(\xi ;{{g}_{0}},...,{{g}_{{N - 2}}})d\xi = 1,$
где f0 = q – водность среды, а F – так называемая функция распределения, “нормированная на единицу”. В качестве нормировочной величины am удобно выбрать моду функции распределения. Величины f0, am, g0, …, ${{g}_{{N - 2}}}$ являются теми дополнительными параметрами, о которых шла речь в предыдущем абзаце.

Вычисляя моменты, из (10) имеем

(11)
${{f}_{n}} = {{f}_{0}}a_{m}^{n}{{\alpha }_{n}}({{g}_{0}}, \ldots ,{{g}_{{N - 2}}}),\quad {{\alpha }_{n}}({{g}_{0}}, \ldots ,{{g}_{{N - 2}}}) = \mathop \smallint \limits_0^\infty {{\xi }^{n}}F(\xi ;{{g}_{0}}, \ldots ,{{g}_{{N - 2}}})d\xi ,\quad n = 1,~2,...,N.$

Из (9) и (11), учитывая, что α0 = 1, получаем

(12)
${{\eta }_{n}} = \frac{{{{\alpha }_{{n + 2}}}({{g}_{0}},...,{{g}_{{N - 2}}})}}{{{{\alpha }_{n}}({{g}_{0}},...,{{g}_{{N - 2}}})\,\alpha _{1}^{2}({{g}_{0}},...,{{g}_{{N - 2}}})}},\quad {{\zeta }_{n}} = \frac{{{{\alpha }_{{n + 1}}}({{g}_{0}},...,{{g}_{{N - 2}}})}}{{{{\alpha }_{1}}({{g}_{0}},...,{{g}_{{N - 2}}})\,{{\alpha }_{n}}({{g}_{0}},...,{{g}_{{N - 2}}})}}.$

Соотношения (11) можно свести к следующей системе (N – 1)-го уравнения для (N – 1)-го параметра g0, …, ${{g}_{{N - 2}}}$:

(13)
$\frac{{{{f}_{n}}f_{0}^{{n - 1}}}}{{f_{1}^{n}}} = \frac{{{{\alpha }_{n}}({{g}_{0}},...,{{g}_{{N - 2}}})}}{{\alpha _{1}^{n}({{g}_{0}},...,{{g}_{{N - 2}}})}},\quad n = 2,~3,...,N.$

Разрешив эту систему уравнений и воспользовавшись (12), получим окончательно искомые зависимости параметров ηn и ζn от моментов fn в виде

(14)
${{\eta }_{n}} = {{\eta }_{n}}\left( {\frac{{{{f}_{2}}{{f}_{0}}}}{{f_{1}^{2}}},...,\frac{{{{f}_{N}}f_{0}^{{N - 1}}}}{{f_{1}^{N}}}} \right),\quad {{\zeta }_{n}} = {{\zeta }_{n}}\left( {\frac{{{{f}_{2}}{{f}_{0}}}}{{f_{1}^{2}}},...,\frac{{{{f}_{N}}f_{0}^{{N - 1}}}}{{f_{1}^{N}}}} \right).$

Рассмотрим далее два низших приближения: приближение двух моментов (N = 1) и приближение трех моментов (N = 2).

Система уравнений (8) в приближении двух моментов (N = 1) имеет следующий вид:

(15)
$\begin{gathered} \frac{{\partial {{f}_{0}}}}{{\partial t}} + \frac{{\partial {{f}_{0}}}}{{\partial x}} - \frac{{\partial {{\eta }_{0}}{{{\bar {a}}}^{2}}{{f}_{0}}}}{{\partial z}} = {{\varepsilon }_{{{{A}_{x}}}}}\frac{{{{\partial }^{2}}{{f}_{0}}}}{{\partial {{x}^{2}}}} + {{\varepsilon }_{{{{A}_{z}}}}}\frac{{{{\partial }^{2}}{{f}_{0}}}}{{\partial {{z}^{2}}}}, \\ \frac{{\partial {{f}_{1}}}}{{\partial t}} + \frac{{\partial {{f}_{1}}}}{{\partial x}} - \frac{{\partial {{\eta }_{1}}{{{\bar {a}}}^{2}}{{f}_{1}}}}{{\partial z}} - {{\varepsilon }_{{\dot {a}}}}{{\eta }_{0}}f_{1}^{2} = {{\varepsilon }_{{{{A}_{x}}}}}\frac{{{{\partial }^{2}}{{f}_{1}}}}{{\partial {{x}^{2}}}} + {{\varepsilon }_{{{{A}_{z}}}}}\frac{{{{\partial }^{2}}{{f}_{1}}}}{{\partial {{z}^{2}}}},\quad \bar {a} = {{f}_{1}}{\text{/}}{{f}_{0}}. \\ \end{gathered} $

В приближении трех моментов (N = 2)

$\frac{{\partial {{f}_{0}}}}{{\partial t}} + \frac{{\partial {{f}_{0}}}}{{\partial x}} - \frac{{\partial {{f}_{2}}}}{{\partial z}} = {{\varepsilon }_{{{{A}_{x}}}}}\frac{{{{\partial }^{2}}{{f}_{0}}}}{{\partial {{x}^{2}}}} + {{\varepsilon }_{{{{A}_{z}}}}}\frac{{{{\partial }^{2}}{{f}_{0}}}}{{\partial {{z}^{2}}}},$
(16)
$\frac{{\partial {{f}_{1}}}}{{\partial t}} + \frac{{\partial {{f}_{1}}}}{{\partial x}} - \frac{{\partial {{\eta }_{1}}{{{\bar {a}}}^{2}}{{f}_{1}}}}{{\partial z}} - {{\varepsilon }_{{\dot {a}}}}{{f}_{0}}{{f}_{2}} = {{\varepsilon }_{{{{A}_{x}}}}}\frac{{{{\partial }^{2}}{{f}_{1}}}}{{\partial {{x}^{2}}}} + {{\varepsilon }_{{{{A}_{z}}}}}\frac{{{{\partial }^{2}}{{f}_{1}}}}{{\partial {{z}^{2}}}},$
$\frac{{\partial {{f}_{2}}}}{{\partial t}} + \frac{{\partial {{f}_{2}}}}{{\partial x}} - \frac{{\partial {{\eta }_{2}}{{{\bar {a}}}^{2}}{{f}_{2}}}}{{\partial z}} - 2{{\varepsilon }_{{\dot {a}}}}{{\zeta }_{2}}{{f}_{1}}{{f}_{2}} = {{\varepsilon }_{{{{A}_{x}}}}}\frac{{{{\partial }^{2}}{{f}_{2}}}}{{\partial {{x}^{2}}}} + {{\varepsilon }_{{{{A}_{z}}}}}\frac{{{{\partial }^{2}}{{f}_{2}}}}{{\partial {{z}^{2}}}},\quad \bar {a} = {{f}_{1}}{\text{/}}{{f}_{0}}.$

Для замыкания систем (15) и (16) воспользуемся приближенным аналитическим выражением для распределения капель жидкой фазы в двухфазной среде. Известны различные формулы, аппроксимирующие экспериментальные функции распределения. В частности, типовые распределения капель в облаках и туманах довольно хорошо аппроксимируются следующей колоколообразной функцией (см., например, [13]):

(17)
$F(\xi ;s,p) = \frac{1}{C}{{\xi }^{p}}\exp \left( { - \frac{p}{s}{{\xi }^{s}}} \right),\quad C = \frac{1}{s}{{\left( {\frac{s}{p}} \right)}^{{(p + 1)/s}}}\Gamma \left( {\frac{{p + 1}}{s}} \right),$
где p и s – эмпирические параметры, а ${{\Gamma }}(x) = \int_0^\infty {{{\eta }^{{x - 1}}}{{e}^{{ - \eta }}}d\eta } $ – полная гамма-функция.

Моменты αn от “нормированной на единицу” функции распределения (17) имеют следующий вид:

${{\alpha }_{n}}(s,p) = \mathop \smallint \limits_0^\infty \,{{\xi }^{n}}F(\xi ;s,p)d\xi = {{\left( {\frac{s}{p}} \right)}^{{n/s}}}\Gamma \left( {\frac{{n + p + 1}}{s}} \right){\text{/}}\Gamma \left( {\frac{{p + 1}}{s}} \right),$
и дробно-рациональные функционалы (12) легко вычисляются:

(18)
${{\eta }_{n}}(s,p) = \frac{{{{\alpha }_{{n + 2}}}(s,p)}}{{{{\alpha }_{n}}(s,p)\alpha _{1}^{2}(s,p)}},\quad {{\zeta }_{n}}(s,p) = \frac{{{{\alpha }_{{n + 1}}}(s,p)}}{{{{\alpha }_{1}}(s,p){{\alpha }_{n}}(s,p)}}.$

3.1. Приближение двух моментов

В двухмоментном приближении (N = 1) пространственно-временные распределения водности среды q = f0 и среднего радиуса капель $\bar {a} = {{f}_{1}}{\text{/}}{{f}_{0}}$ описываются двумя уравнениями (15). При этом параметры s и p в (17) должны быть фиксированными, а дробно-рациональные функционалы ${{\eta }_{0}} = {{\alpha }_{2}}{\text{/}}\alpha _{1}^{2}$ и ${{\eta }_{1}} = {{\alpha }_{3}}{\text{/}}\alpha _{1}^{3}$ – постоянными (табл. 1). Величины η0 и η1 имеют порядок единицы. Их зависимость от s и p достаточно слабая.

Таблица 1.

Зависимость величин α1, α2, η0, η1 от параметров функции распределения (17) капель по радиусам

(s, p) (2, 2) (2, 3) (2, 4) (3, 8)
α1(s, p) 1.12837917 1.08540188 1.06384608 1.03166095
α2(s, p) 1.5 1.33333333 1.25 1.125
η0(s, p) 1.17809725 1.13176848 1.10446616 1.05700864
η1(s, p) 1.57079633 1.41471060 1.32535940 1.17445404

Скорость выпадения жидкости на подстилающую поверхность в приближении двух моментов вычисляется так:

$h = {{\eta }_{0}}{{\bar {a}}^{2}}{{f}_{0}}(t,x,0).$

3.2. Приближение трех моментов

В приближении трех моментов (N = 2) будем считать, что параметр s в (17) фиксирован, а параметр p, определяющий дисперсию функции распределения, может изменяться. Тогда, согласно (13), (14), входящие в (16) дробно-рациональные функционалы η1, η2 и ζ2 будут зависеть только от следующей комбинации трех моментов: $x = {{f}_{2}}{{f}_{0}}{\text{/}}f_{1}^{2}.$ При этом данная величина может быть связана с параметром p функции распределения (17) уравнением (см. (13))

$\frac{{{{f}_{2}}{{f}_{0}}}}{{f_{1}^{2}}} = \frac{{{{\alpha }_{2}}(s,p)}}{{\alpha _{1}^{2}(s,p)}}.$

Обратив эту зависимость (напомним, что s – фиксировано) и использовав результат в (18), получим искомые выражения дробно-рациональных функционалов от первых трех моментов функции распределения в виде

(18)
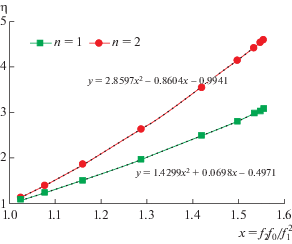
${{\eta }_{1}} = {{\eta }_{1}}(s,\;{{f}_{2}}{{f}_{0}}{\text{/}}f_{1}^{2}),\quad {{\eta }_{2}} = {{\eta }_{2}}(s,\;{{f}_{2}}{{f}_{0}}{\text{/}}f_{1}^{2}),\quad {{\zeta }_{2}} = {{\zeta }_{2}}(s,\;{{f}_{2}}{{f}_{0}}{\text{/}}f_{1}^{2}).$

На фиг. 3 и 4 приведены рассчитанные с помощью электронных таблиц Exel графики функций (18) для случая s = 2. Там же представлены квадратичные зависимости, хорошо аппроксимирующие данные кривые.

Фиг. 3.

Зависимости η1 и η2 от первых трех моментов при s = 2. Штриховые кривые – квадратичные аппроксимации.

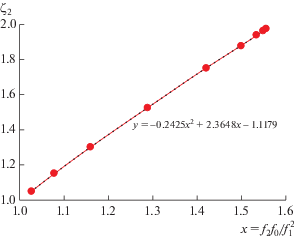
Фиг. 4.

Зависимость ζ2 от первых трех моментов при s = 2. Штриховая кривая – квадратичная аппроксимация.

Скорость выпадения жидкости на подстилающую поверхность в приближении трех моментов определяется вторым моментом функции распределения:

$h = {{f}_{2}}(t,x,0).$

При постановке краевой задачи для моментных уравнений в сечении x = 0 должны быть заданы пространственные распределения всех моментов, входящих в рассматриваемое приближения моментного метода. Далее в конкретных расчетах примем, что в начальном сечении x = 0 функция распределения  f  капель по размерам имеет вид (6), причем $b(a) = F(a;s,p)$ (см. (17)). Тогда в сечении x = 0

${{f}_{n}}(z) = \left( {\mathop \smallint \limits_0^\infty \,{{a}^{n}}b(a)da} \right)\delta (z - 1) = {{\alpha }_{n}}(s,p)\delta (z - 1),\quad n = 0,1,...,N.$

4. РЕЗУЛЬТАТЫ РАСЧЕТОВ. ВЫВОДЫ

Для численного интегрирования уравнения переноса и диффузии в настоящей работе используется вычислительная методика, предложенная в [14] и применявшаяся, например, в работе [15]. Достоинства этой методики состоят не в экономичности и высокой скорости счета (что до некоторой степени компенсируется все возрастающей производительностью современных ЭВМ), а в простоте реализации и высокой универсальности.

На фиг. 5–7 приведены результаты расчетов описанной выше задачи как в “точной” постановке (1), так и с использованием двухмоментного приближения (15) и трехмоментного приближения (16). Расчеты проведены при разных значениях параметра гравитационной коагуляции ${{\varepsilon }_{{\dot {a}}}}$. Во всех расчетах ${{\varepsilon }_{{Ax}}} = 0$, ${{\varepsilon }_{{Az}}} = 0.3$.

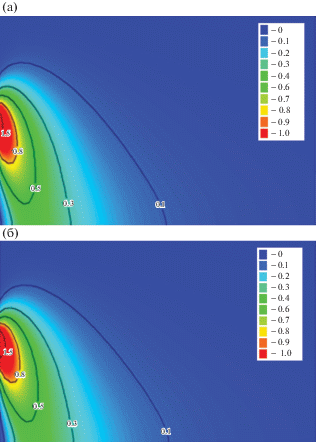
Фиг. 5.

Распределение водности в стационарном шлейфе капельной влаги при ${{\varepsilon }_{{\dot {a}}}} = 1$: (а) – “точное” решение; (б) – двухмоментное приближение.

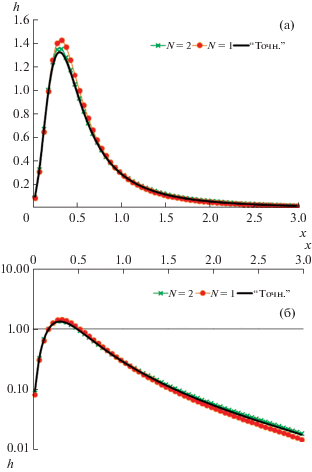
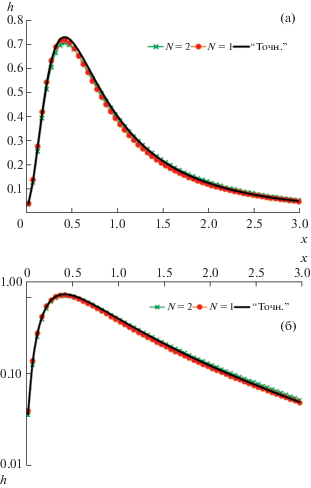
Фиг. 6.

Стационарные осадки на подстилающую поверхность в обычном (а) и логарифмическом (б) масштабе: “точное” решение (“Точн.”), двухмоментное приближение (N = 1), трехмоментное приближение (N = 2). Параметр ${{\varepsilon }_{{\dot {a}}}} = 0$.

Фиг. 7.

То же, что на фиг. 6, но при ${{\varepsilon }_{{\dot {a}}}} = 1$.

Расчетное распределение водности в стационарном шлейфе капельной влаги при ${{\varepsilon }_{{\dot {a}}}} = 1$ представлено на фиг. 5.

Сравнение “точного” решения с расчетами по двухмоментному и трехмоментному приближению для трех различных значений ${{\varepsilon }_{{\dot {a}}}}$ приведено на фиг. 6–8.

Фиг. 8.

То же, что на фиг. 6, но при ${{\varepsilon }_{{\dot {a}}}} = 2$.

Видно, что моментный метод в целом дает неплохие не только качественные, но и количественные результаты. Во всяком случае, при ${{\varepsilon }_{{\dot {a}}}} \leqslant 1$ даже низшее, двухмоментное приближение вполне приемлемо. Видно также, что использование трехмоментного приближения заметно уменьшает разницу между точным и приближенным решением при ${{\varepsilon }_{{\dot {a}}}} > 1$ (особенно вдали от источника капельной влаги).

В заключение отметим, что согласно данным, приведенным в пп. 2.1 и 2.2, параметр коагуляции ${{\varepsilon }_{{\dot {a}}}} = 1$ при значениях ${{a}_{m}} = 100$ мкм, ${{Q}_{0}} = 10$ кг/(м с), и ${{U}_{0}} = 10$ м/с.

Список литературы

  1. Котеров В.Н., Архипов Б.В., Беликов В.В., Солбаков В.В., Федосов В.Е. Численное моделирование образования и переноса капельной влаги в нижнем бьефе гидроузла при работе водосборов трамплинного типа // Гидротехническое строительство. 2007. Вып. 7. С. 17–27.

  2. Котеров В.Н., Архипов Б.В., Беликов В.В., Солбаков В.В. Образование и перенос капельной влаги в нижнем бьефе гидроузла // Матем. моделирование. 2008. Т. 20. № 5. С. 78–92.

  3. Котеров В.Н., Беликов В.В. Исследование и моделирование тепловой конвекции воздуха и переноса локальных осадков при работе эксплуатационного водосброса Саяно-Шушенской ГЭС в зимний период // Гидротехническое строительство. 2012. № 3. С. 62–70.

  4. Беликов В.В., Котеров В.Н. Численное моделирование переноса капельной влаги, генерируемой работой водосброса № 1 Богучанской ГЭС в период наполнения водохранилища зимой 2012 г. // Гидротехническое строительство. 2014. № 5. С. 16–26.

  5. Беликов В.В., Котеров В.Н. Прогноз влияния водно-ледяного облака за водосбросами № 1 и № 2 Богучанской ГЭС на сооружения гидроузла в условиях аварийной эксплуатации в зимний период // Гидротехническое строительство. 2015. № 6. С. 40–51.

  6. Беликов В.В., Котеров В.Н. Проблемы брызгового обледенения и образования техногенных осадков в нижних бьефах высоконапорных гидроузлов. Теория и практика математического моделирования природных и техногенных процессов. М.: Янус-К, 2016. 152 с.

  7. Дж. Бэтчелор. Введение в динамику жидкости. М.: Мир, 1973. 758 с.

  8. Winterwerp J.C. A simple model for turbulence induced flocculation of cohesive sediment // J. Hydraulic Res. 1997. V. 36. № 3. P. 309–326.

  9. ГОСТ Р 53613-2009 (МЭК 60721-2-2:1988) Воздействие природных внешних условий на технические изделия. Общая характеристика. Осадки и ветер.

  10. Качурин Л.Г. Физические основы воздействия на атмосферные процессы. Л.: Гидрометеоиздат, 1973. 366 с.

  11. Колдоба А.В., Повещенко Ю.А., Самарская Е.А., Тишкин В.Ф. Методы математического моделирования окружающей среды. М.: Наука, 2000. 254 с.

  12. Халтинер Дж., Мартин Ф. Динамическая и физическая метеорология. М.: Изд-во Иностр. лит., 1960. 435 с.

  13. Качурин Л.Г. Физические основы воздействия на атмосферные процессы. Л.: Гидрометеоиздат, 1973. 366 с.

  14. Котеров В.Н., Кочерова А.С., Кривцов В.М. Об одной методике расчета течений несжимаемой жидкости // Ж. вычисл. матем. и матем. физ. 2002. Т. 42. № 4. С. 550–558.

  15. Зубов В.И., Инякин В.А., Котеров В.Н., Кривцов В.М. Численное моделирование пространственных турбулентных течений газа в сложных сопловых устройствах // Ж. вычисл. матем. и матем. физ. 2005. Т. 45. № 10. С. 1871–1886.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал