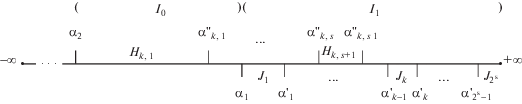Журнал вычислительной математики и математической физики, 2021, T. 61, № 2, стр. 345-362

1. ВВЕДЕНИЕ

Рассматривается стандартная задача сортировки набора из $n$ элементов линейно упорядоченного множества с помощью попарных сравнений. Подробное введение в проблематику представлено в [1, гл. 3], [2, п. 5.3], [3, Ch. 2].

Алгоритм сортировки можно изобразить в виде бинарного корневого дерева с ориентацией ребер в направлении от корня. Такое дерево обычно называется деревом сравнений, а также деревом решений или бинарной решающей диаграммой. Внутренняя вершина дерева соответствует операции сравнения некоторых двух элементов. В зависимости от результата сравнения алгоритм осуществляет переход по одному из ребер к следующей вершине. Концевая вершина (лист) дерева соответствует полученному в результате сравнений упорядочению входного набора. Сложностью алгоритма называется глубина дерева – максимальное расстояние в ребрах между корнем и листом.

Естественно ограничить рассмотрение алгоритмами, не выполняющими избыточных сравнений (т.е. сравнений, не добавляющих новой информации о порядке элементов). В соответствующих таким алгоритмам деревьях каждая возможная перестановка связана ровно с одним листом. В частности, деревья для сортировки $n$-элементного набора имеют ровно $n!$ листьев.

Пусть $S(n)$ означает минимальную сложность алгоритма сортировки $n$-элементного набора. Поскольку глубина дерева с $m$ листьями не меньше $logm$, имеет место простая нижняя оценка

$loge \approx 1.443$. (Здесь и далее по тексту основание у двоичных логарифмов опускается.) Более того, поскольку даже средняя глубина дерева по всем его листьям не превосходит $logm$, то оценка (1) действительна и для сложности сортировки в среднем по всем $n!$ возможным перестановкам входного набора (см. также [1]–[3]). Подобные нижние оценки называются теоретико-информационными.

С точки зрения верхней оценки, в целом лучшим среди известных остается метод Форда–Джонсона [4] (метод бинарных вставок), предложенный более 60 лет назад. Он приводит к соотношению

где константа $c$ в зависимости от $n$ варьируется от $log(3e{\text{/}}8) \approx 0.028$ (в благоприятном случае $n \sim {{2}^{k}}{\text{/}}3$) до $log[3{\text{/}}(4ln2)] \approx 0.114$ (в неблагоприятном случае $n \sim ln2 \times {{2}^{k}}{\text{/}}3$). Метод бинарных вставок доказуемо оптимален при $n \leqslant 15$ и при некоторых больших $n$ (см. [5]). Усовершенствование метода, предложенное в [6] около 1980 г., позволяет уточнить константу в неблагоприятном случае до $c \approx 0.105$. Достаточно большую работу по сглаживанию неравномерности оценок метода бинарных вставок проделали авторы [7]. По результатам этой работы можно указать константу для неблагоприятного случая где-то в пределах $0.06 < c < 0.07$, точнее сказать трудно¹¹. Для сложности сортировки в среднем оценки сближены гораздо сильнее. Константа в верхней границе сложности недавно была понижена до $c \approx 0.032$ при любом $n$ (см. [8], [9]).

Метод Форда–Джонсона основан на процедурах вставки элементов в линейно упорядоченное множество. Вставка каждого элемента выполняется отдельно. Эффективность метода обеспечивается путем подбора мощности целевого множества, близкой к степени двойки.

Однако известно, что совместная вставка даже двух элементов выполняется быстрее, чем раздельная, если мощность $n$ целевого множества находится в пределах ${{2}^{k}} < n < \tfrac{{17}}{{14}} \times {{2}^{k}} - 1$ (см. [10], [11], а также [2]). Еще выгоднее может быть группировка элементов по 4 или 5 с последующей их сортировкой до вставки (см. [6]). Высокая эффективность метода работы [8] (с точки зрения средней сложности) также достигается за счет того, что часть вставок выполняется совместно для пар элементов.

В развитие этой идеи мы предлагаем алгоритм групповой вставки большого числа элементов, организованный в некотором смысле как система массового обслуживания. Этот подход перекликается с концепцией массового производства (частично упорядоченных наборов), которой следуют лучшие известные алгоритмы выбора элемента заданного порядка (см. [12], [13]). Предлагаемый метод позволяет приблизить сложность вставки, приходящуюся на один элемент, к теоретико-информационной нижней границе, т.е. $logn + o(1)$ при любом $n$. Как следствие, на методе сортировки с помощью групповых вставок достигается оценка

Разумеется, такая же оценка справедлива и для сложности сортировки в среднем.

Изложение построено следующим образом. В разд. 2 дается краткая справка о методе Форда–Джонсона. В разд. 3 приводятся некоторые элементарные соображения, лежащие в основе предлагаемого метода. Обобщенная концепция метода групповой вставки изложена в разд. 4. Центральная часть метода – стратегия выбора элементов для сравнений – описана в разд. 5. В разд. 6 представлены основные заключения о сложности групповой вставки и сортировки.

2. МЕТОД БИНАРНЫХ ВСТАВОК

Операцию сравнения элементов ${{e}_{1}}$ и ${{e}_{2}}$ будем обозначать через ${{e}_{1}}\,?\,{{e}_{2}}$, а отношение порядка – неравенствами ${{e}_{1}} < {{e}_{2}}$ или ${{e}_{1}} > {{e}_{2}}$. Если элементы ${{e}_{1}}$ и ${{e}_{2}}$ совпадают, то операция сравнения все равно возвращает либо ${{e}_{1}} < {{e}_{2}}$, либо ${{e}_{1}} > {{e}_{2}}$. Без ограничения общности можно считать, что все элементы входного набора различны. Для краткости линейно упорядоченный набор элементов далее будем называть цепочкой. Под длиной цепочки будем понимать число элементов в ней. Номер элемента цепочки при нумерации с 1 в порядке возрастания будем называть рангом.

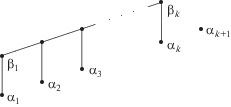
Напомним суть метода бинарных вставок (см. [4], а также [2]): все элементы разбиваются на пары, внутри пар выполняются сравнения, большие элементы пар сортируются. В результате получается частичный порядок, диаграмма²² которого изображена на фиг. 1: элементы в парах обозначены через ${{\alpha }_{i}},{{\beta }_{i}}$, где ${{\beta }_{i}} > {{\alpha }_{i}}$, нумерация в порядке возрастания ${{\beta }_{i}}$. В нечетном случае $n = 2k + 1$ один из элементов не имеет пары, он обозначен через ${{\alpha }_{{k + 1}}}$.

По построению элементы ${{\alpha }_{1}},{{\beta }_{1}},{{\beta }_{2}}, \ldots ,{{\beta }_{k}}$ образуют цепочку. Далее проводится последовательная вставка оставшихся элементов ${{\alpha }_{i}}$ в эту цепочку. Первым вставляется элемент ${{\alpha }_{3}}$ с помощью двух сравнений, затем элемент ${{\alpha }_{2}}$ – также за два сравнения; далее вставляются все элементы, для которых достаточно трех сравнений (это ${{\alpha }_{5}}$ и ${{\alpha }_{4}}$ в таком порядке) и т.д. Всякий раз вставка элемента выполняется в цепочку длины ${{2}^{j}} - 1$, где $j = 2,3, \ldots $, разве что в финальной серии вставок используется цепочка неполной длины.

Можно проверить, что $j$ сравнений достаточно для вставки каждого из элементов ${{\alpha }_{i}}$ с номерами ${{u}_{{j - 1}}} < i \leqslant {{u}_{j}}$, где ${{u}_{j}} = \tfrac{{{{2}^{{j + 1}}} + {{{( - 1)}}^{j}}}}{3}$. Таким образом, сложность $f(n)$ сортировки $n$-элементного набора методом Форда–Джонсона при $\left\lfloor {{{2}^{{k + 1}}}{\text{/}}3} \right\rfloor \leqslant n < \left\lfloor {{{2}^{{k + 2}}}{\text{/}}3} \right\rfloor $ описывается выражением

Эту формулу удобно переписать в асимптотическом виде. Пусть $n = \tau \times {{2}^{{k + 1}}}{\text{/}}3$, где $\tau \in [1,2)$. Тогда Коэффициент в скобках при линейном члене принимает максимальное значение $log(8{\text{/}}3) \approx 1.415$ при $\tau = 1$, а минимальное значение $log(4eln2{\text{/}}3) \approx 1.329$ – при $\tau = 2ln2$. Более подробный анализ метода, см. в [4], [2].

Введем стандартное обозначение $M(m,n)$ для сложности слияния двух цепочек длины $m$ и $n$. Одним из результатов работы Шульте–Мёнтинга [6] является оценка $M(5,n) \leqslant 5k - 8$ при $n \leqslant \tfrac{{319}}{{448}} \times {{2}^{k}} - O(1)$. Она демонстрирует возможность вставки пятерки элементов в цепочку длины $n$ за $5k - 8 + S(5) = 5k - 1$ сравнений, т.е. со средней сложностью $k - 1{\text{/}}5$ на один элемент. Поэтому в общем случае часть вставок финальной серии метода Форда–Джонсона, а именно, вставку элементов с номерами после ${{u}_{{k - 1}}}$, выгодно произвести в цепочку меньшей длины со средней сложностью $k - 1{\text{/}}5$ вместо $k$. Это наблюдение приводит к уточнению оценки (3) для всех $n$, за исключением очень близко расположенных к точкам последовательности $\{ {{2}^{i}}{\text{/}}3\} $. Максимальное значение конcтанты в оценке сложности (2) при этом понижается до $c \approx 0.105$. Аналогичный результат получен в [7] весьма сложным способом: вместо вставок в финальной стадии алгоритма используются слияния длинных цепочек методом Кристена (см. [14]), но при этом оценка для неблагоприятного случая улучшена значительно.

3. ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ

Для удобства изложения введем еще несколько понятий. В задачах слияния или вставки более длинную цепочку будем называть главной. Множество элементов главной цепочки, расположенных между некоторыми элементами $\alpha $ и $\beta $, назовем интервалом и обозначим через $(\alpha ,\beta )$: если $Z$ – главная цепочка, то $(\alpha ,\beta ) = \{ z \in Z\,{\text{|}}\,\alpha < z < \beta \} $. В качестве концов интервала также допускаются условные элементы $ \pm \infty $: по определению, $ - \infty < \alpha < + \infty $ выполнено для всех $\alpha $. В отличие от длины цепочки, длину интервала определим как увеличенное на единицу число элементов в нем, т.е. как число возможностей для вставки нового элемента. Для длины будем использовать обозначение $\left| {(\alpha ,\beta )} \right|$.

Обозначим через $Q(a)$ максимальное число $n$, при котором вставка элемента в интервал длины $n$ выполняется со сложностью не более $a$ или, иначе говоря, $M(1,n - 1) \leqslant a$. Тривиально,

Аналогично, через $P(a)$ обозначим максимальное $n$ такое, что $M(2,n - 1) \leqslant 2a$: в аргументе функции $P$ записываем число сравнений, приходящееся на один элемент вставляемой пары. Известно (см. [10], [11]), что

Пусть $M(m \times k,n)$ означает сложность слияния $m$ цепочек длины $k$ с цепочкой длины $n$. Введем обозначения ${{Q}_{m}}(a)$ и ${{P}_{m}}(a)$ для максимального числа $n$, при котором $M(m \times 1,n - 1) \leqslant am$ и соответственно $M(m \times 2,n - 1) \leqslant 2am$.

По определению, ${{Q}_{1}}(a) = Q(a)$ и ${{P}_{1}}(a) = P(a)$. Также очевидно, что ${{Q}_{m}}(a) \geqslant Q(a) - m + 1$ и ${{P}_{m}}(a) \geqslant P(a) - 2(m - 1)$.

Первое следствие, оправдывающее введение функции ${{Q}_{m}}$, можно извлечь из (5). Поскольку ${{Q}_{2}}(a) \geqslant P(a - 1{\text{/}}2)$,

Таким образом, ${{Q}_{2}}(a)$ может быть существенно больше, чем $Q(a)$.

При $m = 1$ осмысленны только полуцелые аргументы у функций ${{P}_{m}}(a)$ и ${{Q}_{{2m}}}(a)$. Скажем, ${{P}_{1}}(r - 1{\text{/}}4) = {{P}_{1}}(r - 1{\text{/}}2) \approx \tfrac{6}{7} \times {{2}^{r}}$, $r \in \mathbb{N}$. Однако с ростом $m$ открываются новые возможности. Для разминки и иллюстрации основной идеи предлагаемого далее метода выведем оценку

В главной цепочке длины $\left\lceil {\tfrac{{51}}{{56}} \times {{2}^{r}}} \right\rceil - 4m$ выберем элемент $\alpha $ ранга $\left\lceil {\tfrac{{17}}{{56}} \times {{2}^{r}}} \right\rceil - 2m + 1$. Тогда интервал $( - \infty ,\alpha )$ имеет длину не более ${{Q}_{2}}(r - 3{\text{/}}2) - 2(m - 1)$, согласно (6), а интервал $(\alpha , + \infty )$ – не более $P(r - 1) - 2(m - 1)$, согласно (5).

Произвольная пара ${{\beta }_{0}} < {{\beta }_{1}}$ обрабатывается следующим образом. Сравниваем ${{\beta }_{0}}$ с $\alpha $. Если ${{\beta }_{0}} > \alpha $, то пара вставляется в интервал $(\alpha , + \infty )$ за $2(r - 1)$ сравнений методом из [10], [11]. Иначе, пара разбивается: элемент ${{\beta }_{1}}$ вставляется в главную цепочку бинарным методом за $r$ сравнений, а элемент ${{\beta }_{0}}$ помещается во временное хранилище – контейнер. Если контейнер был пуст, то переходим к обработке следующей пары. Но если в контейнере оказалось 2 элемента, вставляем их в интервал $( - \infty ,\alpha )$ за $2r - 3$ сравнений.

По мере выполнения вставок главная цепочка и ее подынтервалы удлиняются. Выбор длин интервалов с запасом $2(m - 1)$ обеспечивает возможность вставки в них элементов всех $m$ обрабатываемых пар за планируемое число сравнений: соответственно $2(r - 3{\text{/}}2)$ для двух элементов в интервал $( - \infty ,\alpha )$ и $2(r - 1)$ – для пар в интервал $(\alpha , + \infty )$.

После того, как обработка всех пар завершена, в контейнере еще может оставаться один элемент. Тривиальным способом он вставляется в цепочку за $r - 1$ сравнений.  Тогда общее число сравнений, выполняемых алгоритмом, в худшем случае оценивается как $m + m(r + r - 3{\text{/}}2) + 1{\text{/}}2 = 2m(r - 1{\text{/}}4) + 1{\text{/}}2$. Соотношение (7) доказано.

4. ОБЩИЙ МЕТОД

В этом разделе мы опишем общий вид предлагаемого метода групповой вставки вместе со средствами его анализа, попутно вводя необходимые понятия.

Операцию сравнения в любом методе вставки или слияния можно рассматривать как шаг разбиения главной цепочки на все меньшие интервалы, в которых локализуются вставляемые элементы или группы элементов. Это дает возможность рекурсивного построения алгоритма: задача слияния с длинной цепочкой с помощью нескольких сравнений сводится к слияниям с более короткими цепочками.

Опишем основные принципы метода групповой вставки упорядоченных пар элементов в главную цепочку. В главной цепочке выделяются интервалы, которые называются финишными. Вставка элемента или пары элементов в финишный интервал выполняется подходящим алгоритмом из доставляющих оценки (4)–(6). Для некоторых финишных интервалов предусмотрены контейнеры. Как в простом примере выше, любой контейнер имеет емкость 2 элемента. Когда в контейнере оказывается два элемента, то выполняется их совместная вставка в соответствующий интервал.

Пары обрабатываются по очереди. Для результата обработки пары могут быть следующие возможности: пара попадает в финишный интервал и применяется метод из [10], [11] для окончательной вставки ее в главную цепочку, либо пара в какой-то момент разбивается и элементы обрабатываются по отдельности.

Судьба одиночных элементов может быть следующей: либо элемент попадает в финишный интервал и вставляется в главную цепочку бинарным методом, либо элемент помещается в контейнер. Если в контейнере нет других элементов, то работа продолжается с новой парой. Иначе выполняется обработка двух элементов из контейнера.

После того, как все пары подверглись обработке, любой из вставляемых элементов либо включен в главную цепочку, либо находится один в некотором контейнере. Алгоритм завершается тем, что каждый из оставшихся в контейнерах элементов вставляется в свой интервал тривиальным бинарным методом.

Удельной сложностью обработки одной пары назовем число сравнений, приходящихся на элементы пары, в наихудшем случае при условии, что ни один из элементов пары не остался в контейнере (для этого можно предположить, что все контейнеры не пусты). В ходе подсчета сложности одно сравнение, выполняемое при совместной обработке пары элементов, засчитывается как полсравнения каждому элементу. Удельная сложность вставки пары в примере из предыдущего раздела равна $2(k - 1{\text{/}}4)$.

Итоговую сложность алгоритма групповой вставки можно оценить сверху как

где $\rho $ – удельная сложность, $m$ – число вставляемых объектов, $n$ – длина исходной цепочки, а $C$ – общее число контейнеров. Избыточное число сравнений при вставке последнего элемента в контейнере здесь оценивается грубо как $log(n + 2m)$; более аккуратное рассуждение привело бы к оценке $O(1)$; в реальных алгоритмах эта величина не превосходит 1, как в примере из разд. 3.

Теперь введем комплексное понятие стратегии сравнений. Пусть задан некоторый числовой набор ${{y}_{1}}, \ldots ,{{y}_{d}} \in \mathbb{R}$ с условием $0 \leqslant {{y}_{1}} < \ldots < {{y}_{d}} < 1$. Вводятся величины ${{p}_{{r,i}}}$, характеризующие длину интервала ${{J}_{{r,i}}}$, вставка пары в который возможна с удельной сложностью $2(r + {{y}_{i}})$. Наряду с величинами ${{p}_{{r,j}}}$ будем также использовать удельные величины ${{x}_{{r,j}}} = {{p}_{{r,j}}} \times {{2}^{{ - r}}}$.

При любом $i = 1,2, \ldots ,d$ и $r \geqslant {{r}_{0}}$ задается сокращенное дерево сравнений ${{T}_{{r,i}}}$ для вставки пары в интервал ${{J}_{{r,i}}}$. Под сокращенным деревом мы понимаем поддерево обычного дерева сравнений. Концевые вершины ${{T}_{{r,i}}}$ соответствуют вызову процедуры вставки в интервалы меньшей длины, назовем эти интервалы терминальными. Разбиение пары допускается только в концевых вершинах дерева. Так определенные сокращенные деревья сравнений описывают сведение задачи вставки в длинный интервал к задачам меньшей размерности.

Концевой вершине дополнительно ставятся в соответствие ограничения на длины терминальных интервалов, обеспечивающие выполнение оценки удельной сложности вставки пары в интервал ${{J}_{{r,i}}}$. Если при концевой вершине на расстоянии $s$ от корня выполняется вставка пары в терминальный интервал $(\alpha {\kern 1pt} ',\alpha {\kern 1pt} '{\kern 1pt} ')$, то ограничение имеет вид ${\text{|}}{\kern 1pt} (\alpha {\kern 1pt} ',\alpha {\kern 1pt} '{\kern 1pt} '){\kern 1pt} {\text{|}} \leqslant {{p}_{{l,j}}}$, где $l + {{y}_{j}} + s{\text{/}}2 \leqslant r + {{y}_{i}}$. Для одиночного элемента $\beta $, вставляемого в $(\alpha {\kern 1pt} ',\alpha {\kern 1pt} '{\kern 1pt} ')$, ограничение может выглядеть либо как ${\text{|}}{\kern 1pt} (\alpha {\kern 1pt} ',\alpha {\kern 1pt} '{\kern 1pt} '){\kern 1pt} {\text{|}} \leqslant {{p}_{{l,j}}}$, либо как ${\text{|}}{\kern 1pt} (\alpha {\kern 1pt} ',\alpha {\kern 1pt} '{\kern 1pt} '){\kern 1pt} {\text{|}} \leqslant {{2}^{l}}$. В первом случае вклад этого элемента в удельную сложность оценивается как $l + {{y}_{j}} + s{\text{/}}2 + 1{\text{/}}2$, а во втором – как $l + s{\text{/}}2$. Сумма оценок для двух элементов пары не должна превосходить $2(r + {{y}_{i}})$.

Будем считать, что ранги элементов $\alpha {\kern 1pt} '$, $\alpha {\kern 1pt} '{\kern 1pt} '$ также выражаются линейными комбинациями величин ${{p}_{{l,j}}}$. Некоторые ограничения могут при этом тривиально выполняться (например, в случае тождественности правой и левой частей неравенств). Множество оставшихся определим как систему ограничений стратегии.

Итак, под стратегией сравнений будем понимать семейство деревьев (фактически алгоритмов) ${{T}_{{r,i}}}$ и систему ограничений, обеспечивающую удельную сложность $2(r + {{y}_{i}})$ вставки пар в интервалы ${{J}_{{r,i}}}$. Глубиной стратегии назовем максимальную глубину деревьев ${{T}_{{r,i}}}$.

Если минимальная удельная сложность вставки пары по всем терминальным интервалам в алгоритме с деревом сравнений ${{T}_{{r,i}}}$ равна $2(r{\kern 1pt} '\; + {{y}_{j}})$, то положим ${{w}_{{r,i}}} = r - r{\kern 1pt} '\; + 1$.

Мы ограничим рассмотрение однородными стратегиями – такими, в которых очередной элемент интервала ${{J}_{{r,i}}}$, выбираемый для сравнения, делит интервал ${{J}_{{r,i}}}$ в отношении, не зависящем от $r$ (с точностью до целочисленного округления). Тогда при любом $i$ все деревья ${{T}_{{r,i}}}$ подобны некоторому дереву ${{T}_{i}}$. Можно считать, что внутренней вершине ${{T}_{i}}$ приписана пара $(y,\Delta )$, $y \in \{ 0,1\} $, $\Delta \in \mathbb{R}$, кодирующая сравнение ${{\beta }_{y}}\,?\,\alpha $, где $({{\beta }_{0}},{{\beta }_{1}})$ – вставляемая пара, а $\alpha $ – элемент ранга $\Delta \left| {{{J}_{{r,i}}}} \right|$ в интервале ${{J}_{{r,i}}}$. В однородной стратегии ${{w}_{{r,i}}} = {{w}_{i}}$ при всех $r$. Величину $ma{{x}_{i}}{{w}_{i}}$ назовем шириной однородной стратегии. Ширина стратегии характеризует максимальную разницу сложности вставки между исходным интервалом и его терминальными подынтервалами. Ниже под стратегией всюду понимается однородная стратегия.

Далее в выкладках позволим длинам интервалов и рангам элементов цепочки принимать нецелые значения, под которыми будут пониматься округления до ближайшего целого в ту или иную сторону. В случае утверждения о сложности вставки в интервал нецелой длины $x$ будем требовать выполнение этого утверждения для интервала длины $\left\lceil x \right\rceil $.

Наша ближайшая цель – построить переход от стратегии к конкретному алгоритму. В предположении существования пределов ${{z}_{i}} = li{{m}_{{r \to \infty }}}{{x}_{{r,i}}}$ ограничения стратегии можно переписать в терминах предельных величин ${{z}_{i}}$ и перейти к задаче линейного программирования. Ниже следуют описание и обоснование корректности такого перехода.

Пусть на множестве последовательностей $d$-мерных вещественных векторов ${{x}_{0}},{{x}_{1}}, \ldots \in {{\mathbb{R}}^{d}}$, ${{x}_{j}} = ({{x}_{{j,1}}},{{x}_{{j,2}}}, \ldots ,{{x}_{{j,d}}})$, определена система $\sigma $ нормированных линейных неравенств ширины $w$ вида

при всех $t \geqslant 0$. Здесь ${{a}_{{i,j,k}}},\;{{b}_{k}}$ – вещественные коэффициенты. С помощью формальной подстановки ${{x}_{{j,i}}} = {{z}_{i}}$ для всех $i$, $j$ в (9) получим приведенную системуотносительно переменных ${{z}_{i}}$.

Система (10) определяет симплекс $T(\sigma )$ в пространстве ${{\mathbb{R}}^{d}}$. Для произвольного параметра $\varepsilon \geqslant 0$ определим вложенный симплекс ${{T}^{\varepsilon }}(\sigma ) \subset T(\sigma )$ системой неравенств

Будем говорить, что подпоследовательность ${{x}_{l}},{{x}_{{l + 1}}}, \ldots ,{{x}_{{l'}}}$ удовлетворяет (9), если ограничения (9) выполнены для всех $t = l,$$l + 1, \ldots ,l{\kern 1pt} '\; + w - 1$ при подходящем доопределении последовательности векторами ${{x}_{{l' + 1}}}, \ldots ,{{x}_{{l' + w - 1}}}$.

Далее через $\left\| {\, \cdot \,} \right\|$ обозначается ${{l}_{\infty }}$-норма в векторном пространстве (максимум модуля координат вектора), а через $\left\langle { \cdot , \cdot } \right\rangle $ – евклидово скалярное произведение векторов. Нам понадобится простой факт о скорости приближения к заранее известному решению задачи (9).

Лемма 1. Пусть $u \in {{T}^{\varepsilon }}(\sigma )$, $v \in T(\sigma )$ и $0 < \varepsilon < \left\| {v - u} \right\|$. Тогда на отрезке $[u,v]$ найдется удовлетворяющая системе неравенств $\sigma $ (9) ширины $w$ последовательность $\{ {{x}_{i}}\} $ с началом ${{x}_{0}} = {{x}_{1}} = \ldots = {{x}_{{w - 1}}} = u$, сходящаяся к точке $v$ со скоростью

Доказательство. Определим ${{\varepsilon }_{i}} = \varepsilon {{(1 - \varepsilon \Delta )}^{i}}$. При $i \geqslant 1$ и $j = 0,1, \ldots ,w - 1$ положим

По построению

Таким образом, оценка (12) выполняется. Осталось проверить, что построенная последовательность удовлетворяет системе $\sigma $.

В силу ${{x}_{{lw}}} = {{x}_{{lw + 1}}} = \ldots = {{x}_{{lw + w - 1}}} \in [u,v] \subset T(\sigma )$ неравенства (9) выполнены при всех $t = lw$, где $l \in \mathbb{N}$.

Покажем, что ${{x}_{{lw}}} \in {{T}^{{{{\varepsilon }_{l}}}}}(\sigma )$. При $l = 0$ это гарантировано условием леммы. Обозначим ${{a}_{k}} = ({{a}_{{1,k}}}, \ldots ,{{a}_{{d,k}}})$. Тогда при $l > 1$ и при любом $k = 1,2, \ldots ,K$, согласно (14), имеет место

в силу линейности скалярного произведения.

Пусть $lw < t < (l + 1)w$. В этом случае в левых частях неравенств (9) используются только координаты векторов ${{x}_{{lw}}}$ и ${{x}_{{(l + 1)w}}}$. Тогда с помощью (13) и с учетом ${{x}_{{lw}}} \in {{T}^{{{{\varepsilon }_{l}}}}}(\sigma )$ при любом $k = 1,2, \ldots ,K$ получаем

Следовательно, построенная последовательность удовлетворяет системе неравенств $\sigma $.

Сформулируем основной результат раздела. Обозначим

В частности, $\pi (a) = \tfrac{{17}}{{14}}$ при $0 \leqslant a < \tfrac{1}{2}$ и $\pi (a) = \tfrac{{12}}{7}$ при $\tfrac{1}{2} \leqslant a < 1$, согласно (5).

Лемма 2. Пусть для некоторого набора ${{y}_{1}}, \ldots ,{{y}_{d}} \in \mathbb{R}$, где $0 \leqslant {{y}_{1}} < \ldots < {{y}_{d}} < 1$, имеется стратегия сравнений глубины $h$ и ширины $w$, задающая систему ограничений $\sigma $ (9) на ${{x}_{{r,i}}}$, где ${{x}_{{r,i}}} \times {{2}^{r}}$ – нижняя оценка длины интервала, вставка упорядоченной пары в который выполняется с удельной сложностью $2(r + {{y}_{i}})$. Пусть $v = ({{v}_{1}}, \ldots ,{{v}_{d}}) \in T(\sigma )$, $u = ({{u}_{1}}, \ldots ,{{u}_{d}}) \in {{T}^{\varepsilon }}(\sigma )$, где $0 < \varepsilon < \left\| {v - u} \right\|$, причем ${{u}_{i}} < {{v}_{i}}$ и ${{u}_{i}} \leqslant \pi ({{y}_{i}})$ для всех $i = 1,2, \ldots ,d$. Обозначим ${{u}_{{\min }}} = \min \{ {{u}_{i}}\} $. Тогда для любого $r \in \mathbb{N}$ и любых $m \in \mathbb{N}$, $\varphi > 0$, удовлетворяющих условию

выполняетсягде $i = 1,2, \ldots ,d$ и $R = \left\| {v - u} \right\|$.

Доказательство. Зададимся некоторым значением $r$ и допустимой парой параметров $m$ и $\varphi $. Положим $L = \left\lfloor {\tfrac{\varphi }{{(h + 1)(d + 1)}}} \right\rfloor $ и $q = r - L$. Из (16) и (15) вытекает $m \leqslant \tfrac{6}{7} \times {{2}^{{r - \varphi }}}$, откуда $r > \varphi \geqslant L$. Следовательно, $q > 0$.

Пусть $\delta \in (0,\varepsilon )$ – параметр, который будет выбран позже. На отрезке $[u,v]$ выберем точку $v{\kern 1pt} ' = (1 - \delta {\text{/}}\varepsilon )v + (\delta {\text{/}}\varepsilon )u$. То, что $v{\kern 1pt} ' \in {{T}^{\delta }}(\sigma )$, проверяется рассуждением из леммы 1: при любом $k = 1,2, \ldots ,K$

По определению ширина системы ограничений не превосходит ширину соответствующей ей стратегии; можно считать, что обе величины равны $w$. Рассмотрим $\sigma {\kern 1pt} '$ – систему, получающуюся из $\sigma $ вычитанием $\delta $ из правых частей неравенств (9). Тогда имеем $v{\kern 1pt} ' \in T(\sigma {\kern 1pt} ')$ и $u \in {{T}^{{\varepsilon - \delta }}}(\sigma {\kern 1pt} ')$. Применяя лемму 1 к системе $\sigma {\kern 1pt} '$, построим последовательность $\{ {{x}_{l}} = ({{x}_{{l,1}}}, \ldots ,{{x}_{{l,d}}})\} $, сходящуюся к $v{\kern 1pt} '$, с началом ${{x}_{q}} = \ldots = {{x}_{{q + w - 1}}} = u$.

Обозначим ${{X}_{{l,i}}} = {{x}_{{q + l,i}}} \times {{2}^{{q + l}}}$. По условию заданная стратегия сравнений обеспечивает удельную сложность $2(q + l + {{y}_{i}})$ вставки пары в интервал длины ${{X}_{{l,i}}}$. Покажем индукцией по $dl + i$, что для вставки $m$ пар в интервал длины

можно построить алгоритм той же удельной сложности $2(q + l + {{y}_{i}})$ с ${{c}_{{dl + i}}} \leqslant (dl + i) \times {{2}^{{(dl + i)(h + 1)}}}$ контейнерами. (Напомним, что под интервалом длины $X_{{l,i}}^{'}$ понимается интервал длины $\left\lceil {X_{{l,i}}^{'}} \right\rceil $.)

Убедимся, что $X_{{l,i}}^{'} > 0$. Действительно, согласно (16),

Теперь проверим, что запас по длине и число контейнеров достаточны для вставки, затем обеспечим выполнение ограничений (9) для подпоследовательности векторов $x_{{q + l}}^{'}$, $0 \leqslant l \leqslant L$, с компонентами $x_{{q + l,i}}^{'} = X_{{l,i}}^{'} \times {{2}^{{ - (q + l)}}}$.

При $0 \leqslant l \leqslant w - 1$ (база индукции) требуемое гарантируется условиями леммы на ${{u}_{i}}$: длины интервалов находятся в области применения оценок (5). В этом случае контейнеры не нужны. Для вставки $m$ пар требуется запас длины $2m - 2$ по отношению к (5) с возможными дополнительными поправками: 1 на округление длины интервала до $\left\lceil {X_{{0,i}}^{'}} \right\rceil $ и 1 на ошибку (15) при предельном переходе по отношению к (5). Поэтому взятый в (18) запас минимум в $2m$ достаточен.

При $l \geqslant w$, отталкиваясь от разбиения интервала длины ${{X}_{{l,i}}}$ на подынтервалы в соответствии со стратегией, построим разбиение интервала длины $X_{{l,i}}^{'}$. По существу задача состоит в том, чтобы распределить запас длины ${{2}^{{(dl + i)h}}} \times 2m$ между подынтервалами. Будем передвигаться по дереву сравнений от корня к произвольному листу. Пусть в очередной вершине выполняется сравнение с элементом³³ $\alpha $ главной цепочки, и $(\alpha {\kern 1pt} ',\alpha {\kern 1pt} '{\kern 1pt} ')$ – минимальный интервал, включающий $\alpha $, границы которого либо являются элементами предшествующих сравнений, либо границами исходного интервала. Тогда запас длины интервала $(\alpha {\kern 1pt} ',\alpha {\kern 1pt} '{\kern 1pt} ')$ поделим поровну между интервалами $(\alpha {\kern 1pt} ',\alpha )$ и $(\alpha ,\alpha {\kern 1pt} '{\kern 1pt} ')$. В итоге, поскольку дерево сравнений имеет глубину $h$, любой из подынтервалов, образованный точками сравнений, получит запас длины не менее ${{2}^{{(dl + i - 1)h}}} \times 2m$ – по индуктивному предположению, достаточный запас для вставки пары с удельной сложностью $2(q + l{\kern 1pt} '\; + {{y}_{j}})$ или одиночного элемента – с удельной сложностью⁴⁴ $q + l{\kern 1pt} '\; + {{y}_{j}} + 1{\text{/}}2$, где $l{\kern 1pt} ' < l$ или $j < i$. Разумеется, запас выбирается в пределах длины подынтервала, чтобы она оставалась положительной. Также заметим, что терминальные интервалы в алгоритме имеют удельную сложность вставки пары не менее $q + l - w \geqslant q$, поэтому рекурсивный вызов алгоритма (вставки в терминальный интервал) возможен. Формально не исключается случай, когда стратегия предполагает вставку одиночного элемента во внутренний подынтервал с удельной сложностью не менее $q + l + {{y}_{i}} + 1{\text{/}}2$. В этой ситуации просто вызывается алгоритм вставки в исходный интервал стартовой длины $X_{{l,i}}^{'}$.

С использованием разбиения интервала длины $X_{{l,i}}^{'}$ разбиение интервала длины $\left\lceil {X_{{l,i}}^{'}} \right\rceil $ строится простым округлением рангов всех внутренних элементов разбиения до ближайших целых чисел сверху. При этом длины любых подынтервалов исходного разбиения, в том числе терминальных, изменяются менее чем на 1, т.е. превращаются в округления до ближайших целых сверху или снизу. Таким образом, учет округлений не приводит к изменению оценки удельной сложности алгоритма.

Оценим достаточное число контейнеров. Дерево сравнений имеет не более ${{2}^{h}}$ листьев, каждому соответствует до двух терминальных интервалов, вставка в которые по предположению индукции выполняется алгоритмами, использующими не более $2{{c}_{{dl + i - 1}}}$ контейнеров. Еще не более ${{2}^{{h + 1}}} + 1$ контейнеров может понадобиться для обслуживания непосредственно терминальных интервалов и исходного интервала. Получаем

Теперь проверим выполнение ограничений $\sigma $ для $x_{{l,i}}^{'}$. Формально положим $x_{{l,i}}^{'} = {{x}_{{j,i}}}$ при $j > r$. Определим $\delta = {{2}^{{\varphi - r + 1}}}m.$ По условию (16) имеет место $\delta < \varepsilon {\text{/}}2$. Кроме того, в силу (18) и определений параметров $\varphi $ и $\delta $ выполнено $x_{{l,i}}^{'} - {{x}_{{j,i}}} \in ( - \delta ,0]$ для всех $j \geqslant q$. Значит, при всех $t \geqslant q$ и любом $k = 1,2, \ldots ,K$ получаем

Таким образом, последовательность $\{ x_{l}^{'} = (x_{{l,1}}^{'}, \ldots ,x_{{l,d}}^{'})\} $ удовлетворяет системе ограничений $\sigma $ при $t \geqslant q$. Тем самым доказан индуктивный переход: вставка в интервал длины $X_{{L,i}}^{'}$ действительно выполняется с удельной сложностью $2(r + {{y}_{i}})$ сравнений.

Остается проверить оценку (17). Выбором параметра $L$ обеспечено

Из леммы 1 следует где также использовалось известное неравенство ${{(1 - x)}^{{1/x}}} \leqslant {{e}^{{ - 1}}}$ при $x \in (0,1)$. Теперь (17) получается подстановкой (19) и (20) в оценку (8), в которой можно положить $n + 2m \leqslant {{X}_{{L,i}}} = {{x}_{{r,i}}} \times {{2}^{r}} < {{2}^{{r + 2}}}$, поскольку из теоретико-информационных соображений ${{x}_{{r,i}}} \leqslant {{2}^{{{{y}_{i}} + 1/2}}} < 4$.

Оценки в обеих леммах весьма грубы: точность приносится в жертву простоте или общности изложения. В частности, существенно меньшее число контейнеров требуется конкретной стратегии, к которой будет применяться лемма 2.

5. УНИВЕРСАЛЬНАЯ СТРАТЕГИЯ

В этом разделе строится стратегия сравнений для доказательства асимптотической оценки высокой точности. Известно (и вполне очевидно), что для построения оптимального алгоритма сортировки некоторого частично упорядоченного множества желательно, чтобы при каждом сравнении множество возможных доупорядочиваний разбивалось на две примерно равные части в зависимости от результата сравнения. Такой ход мысли ведет к градиентному методу: сначала выполняем некоторое число сравнений, руководствуясь делением множества исходов как можно точнее пополам; затем полученный частичный порядок обрабатываем каким-то простым способом.

Теоретико-информационная нижняя оценка сложности вставки пары в интервал длины $n - 1$ составляет $log[n(n - 1){\text{/}}2] < 2(logn - 1{\text{/}}2)$. Представим идеальный случай, предположив, что с удельной сложностью $2a$ пару можно вставить в интервал длины $Y(a) = (1 - \lambda ) \times {{2}^{{a + 1/2}}}$ при любом достаточно большом $a$, где $\lambda \geqslant 0$ – не зависящий от $a$ параметр, который будет определен позднее.

Рассмотрим одну из градиентных стратегий для алгоритма вставки пары ${{\beta }_{0}} < {{\beta }_{1}}$ в интервал длины $Y(a)$. Стратегия характеризуется параметром $s \in \mathbb{N}$. Сразу заметим, что при построении стратегии длины интервалов считаются действительными числами: необходимость округления до целых учитывается при переходе от стратегии к алгоритму леммой 2.

Сначала отдельно рассмотрим задачу выбора очередного элемента для сравнения. Пусть в результате серии сравнений частичный порядок таков, что элемент ${{\beta }_{1}}$ принадлежит интервалу ${{I}_{1}}$, а ${{\beta }_{0}}$ принадлежит интервалу ${{I}_{0}} \cup {{I}_{1}}$, где ${{I}_{0}} \cap {{I}_{1}} = \emptyset $ и ${\text{|}}{{I}_{0}}{\text{|}} = b\,{\text{|}}{{I}_{1}}{\text{|}}$. Тогда наилучший выбор для сравнения с ${{\beta }_{0}}$ – это элемент⁵⁵ $\alpha $, имеющий ранг $(b{\text{/}}2 + 1{\text{/}}4)\,{\text{|}}{{I}_{1}}{\text{|}}$, считая от левого края интервала ${{I}_{0}}$. (Если $b > 1{\text{/}}2$, то $\alpha \in {{I}_{0}}$.) А наилучший выбор для сравнения с ${{\beta }_{1}}$ – это элемент $\alpha '$ ранга $\sqrt {{{b}^{2}} + b + 1{\text{/}}2} \,{\text{|}}{{I}_{1}}{\text{|}}$ (фиг. 2). Вообще, если бы мы хотели разбить множество исходов в отношении $x:(1 - x)$, то для сравнения c ${{\beta }_{0}}$ и ${{\beta }_{1}}$ нужно было бы выбрать соответственно элементы ранга $x(b + 1{\text{/}}2){\kern 1pt} {\text{|}}{{I}_{1}}{\kern 1pt} {\text{|}}$ или ранга $\sqrt {{{b}^{2}} + x(2b + 1)} {\kern 1pt} {\text{|}}{{I}_{1}}{\kern 1pt} {\text{|}}$.

Исходное разбиение. Не ограничивая общности, считаем, что первое сравнение имеет вид ${{\beta }_{1}}\,?\,{{\alpha }_{1}}$, тогда в качестве ${{\alpha }_{1}}$ следует взять элемент ранга $Y(a - 1{\text{/}}2) = (1 - \lambda ) \times {{2}^{a}}$. Если ${{\beta }_{1}} < {{\alpha }_{1}}$, то вызывается алгоритм вставки пары в интервал $( - \infty ,{{\alpha }_{1}})$ длины $Y(a - 1{\text{/}}2)$. Иначе, выполняем сравнение ${{\beta }_{0}}\,?\,{{\alpha }_{2}}$, где ${{\alpha }_{2}}$ – элемент оптимального ранга $(1 - \lambda )\tfrac{{\sqrt 2 + 1}}{4} \times {{2}^{a}}$. Причина, по которой второе сравнение выполняется с элементом ${{\beta }_{0}}$, будет разъяснена чуть позже.

Если ${{\beta }_{0}} < {{\alpha }_{2}}$, то элемент ${{\beta }_{0}}$ вставляется в интервал $( - \infty ,{{\alpha }_{2}})$ с удельной сложностью $a - 2 + log(\sqrt 2 + 1)$, а элемент ${{\beta }_{1}}$ вставляется в интервал $({{\alpha }_{1}}, + \infty )$ длины $(1 - \lambda )(\sqrt 2 - 1) \times {{2}^{a}}$ с удельной сложностью $a + log(\sqrt 2 - 1)$. Следовательно, в этом случае вставка пары выполняется за $2a$ удельных сравнений.

Если же ${{\beta }_{0}} > {{\alpha }_{2}}$, то ${{\beta }_{1}} \in {{I}_{1}}$ и ${{\beta }_{0}} \in {{I}_{0}} \cup {{I}_{1}}$, где ${{I}_{1}} = ({{\alpha }_{1}}, + \infty )$ и ${{I}_{0}} = ({{\alpha }_{2}},{{\alpha }_{1}})$. Пусть $b = {\text{|}}{{I}_{0}}{\text{|/|}}{{I}_{1}}{\text{|}} = \tfrac{{2\sqrt 2 + 1}}{4}$. С помощью $s$ сравнений, разбивая каждый раз множество исходов пополам, мы локализуем ${{\beta }_{1}}$ в одном из ${{2}^{s}}$ подынтервалов интервала ${{I}_{1}}$. В соответствии с приведенными выше формулами границами этих подынтервалов являются элементы $\mathop {\alpha '}\nolimits_k $ ранга ${{b}_{k}}\; \cdot \;{\text{|}}{{I}_{1}}{\text{|}}$, ${{b}_{k}} = \sqrt {{{b}^{2}} + k(2b + 1) \times {{2}^{{ - s}}}} $, $k = 0,1, \ldots ,{{2}^{s}} - 1$, и условная точка $\alpha _{{{{2}^{s}}}}^{'} = + \infty $. Обозначим подынтервал $(\alpha _{{k - 1}}^{'},\alpha _{k}^{'})$ через ${{J}_{k}}$. Общая схема разбиения показана на фиг. 3.

Пусть элемент ${{\beta }_{1}}$ определен в интервал ${{J}_{k}}$. Следующий этап – вставка элемента ${{\beta }_{0}}$. По очереди сравниваем его с элементами $\alpha _{{k,1}}^{{''}}, \ldots ,\alpha _{{k,s + 1}}^{{''}}$, определяемыми следующим образом. Положим $\alpha _{{k,0}}^{{''}} = {{\alpha }_{2}}$. Обозначим через ${{H}_{{k,j}}}$ интервал $(\alpha _{{k,j - 1}}^{{''}},\alpha _{{k,j}}^{{''}})$. Длина интервала ${{H}_{{k,j}}}$ выбирается равной

Если ${{\beta }_{0}} > \alpha _{{k,1}}^{{''}}$, то выполняем сравнение ${{\beta }_{0}}\,?\,\alpha _{{k,2}}^{{''}}$; если ${{\beta }_{0}} > \alpha _{{k,2}}^{{''}}$, то сравниваем ${{\beta }_{0}}$ с $\alpha _{{k,3}}^{{''}}$ и т.д. Как только ${{\beta }_{0}} < \alpha _{{k,j}}^{{''}}$, элементы ${{\beta }_{0}}$ и ${{\beta }_{1}}$ вставляются независимо в интервалы ${{H}_{{k,j}}}$ и ${{J}_{k}}$ с суммарной удельной сложностью $2a - s - 2 - j$. В этом случае общая удельная сложность вставки пары составит $2a$.

Наконец, если ${{\beta }_{0}} > \alpha _{{k,s + 1}}^{{''}}$, то оба элемента ${{\beta }_{0}},\;{{\beta }_{1}}$ принадлежат интервалу $(\alpha _{{k,s + 1}}^{{''}},\alpha _{k}^{'})$. Хотелось бы вставить пару в этот интервал ценой $2a - 2s - 3$ сравнений. Это было бы возможно в случае, когда, скажем, $\alpha _{{k,s + 1}}^{{''}} = {{\alpha }_{{k - 1}}}$. Но равенство, вообще говоря, не выполняется, и интервал оказывается длиннее требуемого. Оценим превышение длины. Интервал ${{J}_{k}}$ имеет длину

Тогда из (21) следует, что Значит, сумма длин интервалов ${{H}_{{k,j}}}$ при фиксированном $k$ равна Получаем Следовательно,

Полученная оценка понадобится чуть позже. Теперь мы модифицируем описанную выше стратегию сравнений, позволив некоторое отступление от идеала, т.е. деления множества исходов ровно пополам. А именно, мы изменим распределение длин подынтервалов ${{J}_{k}}$ внутри интервала ${{I}_{1}}$, уменьшив (оценочную) сложность вставки элементов в каждый из них, тем самым увеличив допустимую сложность вставки в интервалы ${{H}_{{k,j}}}$ и удлинив их. Для этого у нас имеется резерв – использовать для сложности вставки элемента простую оценку $Q(a)$ вместо $Y(a - 1{\text{/}}2)$, которая лучше, когда значение $a$ близко снизу к целому числу⁶⁶. Длина интервала ${{I}_{1}}$ не будет изменена.

Заметим, что длины интервалов ${{J}_{k}}$ с ростом $k$ изменяются в пределах от $\tfrac{{2b + 1}}{{2b}} \times {{2}^{{ - s}}}{\kern 1pt} {\text{|}}{{I}_{1}}{\text{|}}$ до $\tfrac{{2b + 1}}{{2b + 2}} \times {{2}^{{ - s}}}{\kern 1pt} {\text{|}}{{I}_{1}}{\text{|}}$ (см. (22)). В силу $b < 1$ выполнено $\left[ {\tfrac{2}{3},\tfrac{4}{3}} \right] \subset \left[ {1 - \tfrac{1}{{2b + 1}},1 + \tfrac{1}{{2b + 1}}} \right]$, поэтому при любом (достаточно большом) $a$ часть интервалов ${{J}_{k}}$ имеет длину, близкую к степени двойки. Выполненное вторым сравнение ${{\beta }_{0}}\,?\,{{\alpha }_{2}}$ преследовало именно цель уменьшения показателя $b$ до величины меньше 1.

Коррекция разбиения. На этом шаге мы вносим поправки в длины интервалов ${{J}_{k}}$ и ${{H}_{{k,j}}}$, корректируя стратегию, и одновременно дискретизируем задачу (новые интервалы будут обозначаться как $J_{k}^{*}$ и $H_{{k,j}}^{*}$). Введем параметр дискретизации $d \in 2\mathbb{N}$ и положим ${{y}_{i}} = i{\text{/}}d$, $i = 0,1, \ldots ,d - 1$. По-прежнему мы ищем оценку длины интервала, достаточной для вставки пары с удельной сложностью $2(r + {{y}_{i}})$, в виде $Y(r + {{y}_{i}}) = (1 - \lambda ) \times {{2}^{{r + {{y}_{i}} + 1/2}}}$.

Задавшись некоторым $a = r + {{y}_{i}}$, $r \in \mathbb{N}$, опишем модификацию исходного разбиения. Четность параметра $d$ позволяет выбрать элемент ${{\alpha }_{1}}$ для первого сравнения так же, как и в идеальной схеме. Но сложность вставки элемента в интервал ${{I}_{1}} = ({{\alpha }_{1}}, + \infty )$ теперь приходится оценить как $a + \left\lceil {dlog(\sqrt 2 - 1)} \right\rceil {\text{/}}d < a + log(\sqrt 2 - 1) + 1{\text{/}}d$. Как следствие, вместо ${{\alpha }_{2}}$ приходится выбирать элемент $\alpha _{2}^{*}$ ранга не выше $(1 - \lambda ) \times {{2}^{{a - 2 - \left\lceil {dlog(\sqrt 2 - 1)} \right\rceil /d}}}$. Руководствуясь соображением последующего применения леммы 2, создадим дополнительный запас сложности $1{\text{/}}d$ на втором сравнении и выберем в качестве $\alpha _{2}^{*}$ элемент чуть меньшего ранга:

Тогда, используя неравенство ${{e}^{x}} \geqslant 1 + x$, получаем Следовательно, При $d$ достаточно большом, ${\text{|}}I_{0}^{*}{\text{|}} < {\text{|}}{{I}_{1}}{\text{|}}$.

Выполним перераспределение интервалов ${{J}_{k}}$ внутри ${{I}_{1}}$. Введем параметр $\mu > 0$. Потребуем, чтобы удельная сложность вставки элемента в $J_{k}^{*}$ была меньше сложности вставки в ${{J}_{k}}$ в идеальной стратегии хотя бы на $\left( {2 - \tfrac{k}{{{{2}^{s}}}}} \right)\mu $ сравнений, $k = 1,2, \ldots ,{{2}^{s}}$. Напомним, что в идеальной стратегии сложность оценивается как $log[{\kern 1pt} {\text{|}}{{J}_{k}}{\text{|/}}(1 - \lambda )]$. Прибегать к неравномерности сужения вынуждает эффект смещения правых границ интервалов ${{J}_{k}}$. При равномерном сужении в $1 + \mu $ раз, ввиду ${\text{|}}{{I}_{0}}{\text{|}} < {\text{|}}{{I}_{1}}{\text{|}}$, компенсация этого смещения, вообще говоря, была бы затруднена при малых $k$: сумма длин интервалов ${{H}_{{k,j}}}$ выросла бы примерно на $\mu \,{\text{|}}{{I}_{0}}{\text{|}}$, тогда как точка $\alpha _{{k + 1}}^{'}$ (правая граница интервала ${{J}_{k}}$) могла бы сместиться вправо приблизительно на $\mu \,{\text{|}}{{I}_{1}}{\text{|}}$. Поэтому для интервалов с большими номерами выбирается меньший коэффициент сужения.

Сужение. Мы собираемся сузить почти все интервалы ${{J}_{k}}$, но это сужение будет компенсировано расширением небольшого числа интервалов, длины которых близки к степеням двойки, с опорой на простую оценку (4). Сначала оценим сверху величину ${{\theta }_{p}}$ общего сужения интервалов с номерами от $p$ до ${{2}^{s}}$. Перед этим заметим, что для величины ${{b}_{k}}$ выполняются простые соотношения (проверяются возведением в квадрат)

С учетом дискретизации длину суженного интервала $J_{k}^{*}$ можно выбрать в пределах Исходя из пессимистического предположения, что все интервалы сужаются, снова используя неравенство ${{e}^{x}} \geqslant 1 + x$, а также (22) и (28), получаем В частности, для суммарного сужения всех интервалов ${{J}_{k}}$ имеем оценку а при $p \geqslant 2$ – оценку поскольку ${{p}^{2}}{\text{/}}{{2}^{s}} \leqslant p \leqslant 2(p - 1)$ и $\tfrac{{2b + 1}}{{4(b + 1)}} < b = \tfrac{{2\sqrt 2 + 1}}{4}$.

Расширение. Теперь оценим снизу величину возможной компенсации. Если

то сложность вставки элемента пары в интервал ${{J}_{k}}$ в идеальной стратегии пока оценивалась как минимум в $l + 2\mu $. Тем не менее длину интервала можно увеличить до ${{2}^{l}}$, при этом уменьшив оценку сложности по меньшей мере на $2\mu $, что и требуется.

Сначала проверим, что если $\lambda $ и $\mu $ не слишком велики, то при некотором $l \in \mathbb{N}$ справедливо

При $\mu \ll \lambda $ для этого достаточно выполнения условия ${\text{|}}{{J}_{1}}{\text{|/|}}{{J}_{{{{2}^{s}}}}}{\text{|}} \geqslant \tfrac{2}{{1 - \lambda }}$. Используя (22) и (28), выводим где также использовались простые неравенства $\tfrac{1}{{1 + x}} \geqslant 1 - x$ и $(1 - x)(1 - y) \geqslant 1 - x - y$, справедливые при $x,y \geqslant 0$. Подстановкой численных значений легко проверяется, что полученная оценка превосходит $\tfrac{2}{{1 - \lambda }}$, скажем, при любых $s \geqslant 10$ и $\lambda \leqslant 1{\text{/}}50$.

Итак, некоторый отрезок $g = [(1 - \lambda ) \times {{2}^{{l + 2\mu }}},{{2}^{l}}]$ лежит внутри отрезка $\left[ {{\kern 1pt} {\text{|}}{{J}_{{{{2}^{s}}}}}{\text{|}},{\text{|}}{{J}_{1}}{\text{|}}} \right]$. Оценим возможное увеличение длины только для тех интервалов ${{J}_{k}}$, длины которых оказались в $g$. Напомним, что длины интервалов монотонно убывают с ростом $k$ (см. (22)). Длину отрезка $g$ оценим снизу с помощью (22) и справедливого при $0 \leqslant x \leqslant 1$ неравенства ${{2}^{x}} \leqslant 1 + x$ как

Теперь оценим сверху разность длин соседних интервалов:

Следовательно, при любом $k$

Легко проверить, что если множество точек делит отрезок длины $L$ на подотрезки с длинами не более $\Delta $, то сумма расстояний от этих точек до границы отрезка не меньше $\tfrac{{L(L - \Delta )}}{{2\Delta }}$. Подставляя в эту формулу значения $L$ и $\Delta $, приходим к оценке

Так мы оценили снизу максимум суммарного возможного расширения интервалов ${{J}_{k}}$ с длинами из отрезка $g$ (до длины ${{2}^{l}}$).

Компенсация сужения остальных интервалов ${{J}_{k}}$ осуществима при $\tfrac{{L(L - \Delta )}}{{2\Delta }} \geqslant {{\theta }_{1}}$. Используя (30), достаточное для этого условие можно теперь записать как

Пока ограничимся тривиальным замечанием: при достаточно большом $s$ можно задать параметры в виде⁷⁷ $d \asymp {{2}^{s}}$, $\lambda \asymp {{2}^{{ - s/2}}}$, $\mu \asymp {{2}^{{ - s}}}$ так, что (35) будет удовлетворено.

Сведение. Пришло время проверить, позволяют ли предпринятые меры компенсировать дефицит длины интервалов ${{H}_{{k,j}}}$, отраженный в соотношении (25). Обратим внимание на изменение условий, в которых выполнялась оценка (25). Для величины $Y(a - s - 3{\text{/}}2)$ используется прежняя оценка, но при этом произошло удлинение интервала ${{I}_{0}}$ (см. (27)), а правая граница интервала ${{J}_{k}}$ могла сместиться правее на величину, оцененную сверху как ${{\theta }_{{k + 1}}}$ (см. (31)).

Таким образом, мы требуем, чтобы при любом $k$ прирост суммарной длины интервалов ${{H}_{{k,j}}}$ составил не менее

где $\delta \,{\text{|}}{{I}_{1}}{\text{|}}$ – дополнительный запас, который потребуется позже для применения леммы 2.

По построению, ${\text{|}}H_{{k,j}}^{*}{\text{|}} \geqslant {\text{|}}{{H}_{{k,j}}}{\text{|}} \times {{2}^{{\left( {2 - \tfrac{k}{{{{2}^{s}}}}} \right)\mu - \tfrac{1}{d}}}}$ с учетом поправки на дискретизацию. Поэтому, подставляя (24) и используя (28), получаем

Используя эту оценку, а также (27) и (31), достаточное для выполнения (36) условие можно записать как

Положим $d = {{2}^{s}}$ и $\delta = {{2}^{{ - s}}}$. Тогда, чтобы удовлетворить (37), можно выбрать $\mu = 30 \times {{2}^{{ - s}}}$ (принимаем, что $s \geqslant 10$). Условие (35) при этом будет выполнено, например, если $\lambda = 20 \times {{2}^{{ - s/2}}} + 64 \times {{2}^{{ - s}}}$. Обеспечивающее (32) частное условие $\lambda \leqslant 1{\text{/}}50$ выполнено при любом $s \geqslant 20$.

Описание стратегии. Фиксируя выбранные значения параметров $d,\;\delta ,\;\mu ,\;\lambda $, получаем стратегию вставки с системой ограничений, которую обозначим через $\sigma [s]$. Стратегия заключается в том, что элементы главной цепочки, участвующие в сравнениях, разбивают цепочку на интервалы, вставка в которые выполняется с такой сложностью, которая получается в вышеприведенном расчете. Опишем систему ограничений стратегии.

Пусть $p(a)$ является оценкой длины интервала с удельной сложностью вставки пары $2a$ сравнений, а ${{p}_{c}}(J)$ – оценкой длины интервала с удельной сложностью вставки элемента на $c$ выше, что и в некоторый интервал $J$ из построенного ранее разбиения. Для вставки в некоторые интервалы $J$ мы выбираем оценки типа $Q(a)$, а для остальных вставок – оценки типа $p(a)$ при подходящих $a$.

Первое сравнение, в силу выбора элемента ${{\alpha }_{1}}$, не порождает ограничений. Для второго сравнения вводится неравенство

Здесь мы используем запас сложности, обеспеченный выбором элемента $\alpha _{2}^{*}$ (см. (26)), и можем позволить вставку в интервал ${{I}_{1}}$ с чуть большей удельной сложностью. Это понадобится только для формального удовлетворения условиям применения леммы 2.

Следующие $s$ сравнений, локализующие ${{\beta }_{1}}$ в одном из интервалов $J_{k}^{*}$, относятся к внутренним вершинам дерева сравнений. Для того чтобы обеспечить в дальнейшем вставку элемента ${{\beta }_{1}}$ в любой из этих интервалов с заданной сложностью, вводится ограничение

Ограничение всего одно, так как длины интервалов $J_{k}^{*}$, $k > 1$, мы можем задать свободно, выбирая подходящим образом пограничные элементы $\alpha _{k}^{{'*}}$, тогда только длина интервала $J_{1}^{*}$ будет определяться длиной остальных интервалов.

Длины интервалов $H_{{k,j}}^{*}$ тоже устанавливаются свободно (выбором элементов для сравнений), и лишь вставки после $2s + 3$ сравнений порождают ограничения вида

где ${{I}_{{ - 1}}} = ( - \infty ,\alpha _{2}^{*})$.

Таким образом, система ограничений $\sigma [s]$ складывается из (38)–(40) при всевозможных $a = r + i{\text{/}}d$. Для перехода к форме записи из определения стратегии следует в указанных неравенствах заменить выражения $p(x)$ и ${{p}_{c}}(J)$ величинами ${{p}_{{r,i}}}$ или числовыми значениями в случаях, когда применяется оценка $Q(a)$.

Глубина стратегии с системой ограничений $\sigma [s]$ равна $2s + 3$. Проверим, что ширина (стратегии и, следовательно, системы $\sigma [s]$) не превосходит $s + 4$. Действительно,

согласно (26) (напомним, что $p(a) = Y(a)$). Далее, в силу (29) и (22) Наконец, из (23) следует Таким образом, если $p(a) = {{p}_{{r{\kern 1pt} ',i{\kern 1pt} '}}}$, то при перезаписи (38)–(40) в терминах величин ${{p}_{{r,i}}}$, среди этих величин будут встречаться только такие, для которых $r \geqslant r{\kern 1pt} '\; - s - 3$.

Лемма 3. Пусть $s \geqslant 20$, $d = {{2}^{s}}$, $\mu = 30 \times {{2}^{{ - s}}}$, $\lambda = 20 \times {{2}^{{ - s/2}}} + 64 \times {{2}^{{ - s}}}$ и $\varepsilon = \tfrac{1}{{25 \times {{2}^{s}}}}$. Пусть также ${{y}_{i}} = i{\text{/}}d$ и ${{v}_{i}} = (1 - \lambda ) \times {{2}^{{{{y}_{i}} + 1/2}}}$. Тогда

$({\text{i}})$ $v = ({{v}_{0}}, \ldots ,{{v}_{{d - 1}}}) \in T(\sigma [s]);$

$({\text{ii}})$ $u = v{\text{/}}2 \in {{T}^{\varepsilon }}(\sigma [s]).$

Доказательство. Первая часть леммы уже доказана, так как сама стратегия подогнана под заданное решение. Остается проверить (ii).

Напомним, что при переходе к канонической системе (9) мы переписываем неравенства в терминах переменных ${{x}_{{r,i}}} = {{p}_{{r,i}}} \times {{2}^{{ - r}}}$ и выполняем нормировку, а для перехода к приведенной системе (10) производится подстановка ${{x}_{{r,i}}} = {{z}_{i}}$.

Пусть $p(a) = {{p}_{{r{\kern 1pt} ',i{\kern 1pt} '}}}$. Выполним предварительную нормировку неравенств (38)–(40) домножением на ${{2}^{{ - r{\kern 1pt} '}}}$ и перепишем их в терминах величин ${{x}_{{r,i}}}$. Полученные неравенства обозначим через (38')–(40'). Оценим сумму абсолютных величин коэффициентов при ${{x}_{{r,i}}}$ в каждом из этих неравенств для определения итоговых коэффициентов нормировки.

Вклад от слагаемого $p(a)$ в каждую сумму коэффициентов равен $1$. Тогда вклад любого из слагаемых $p(a - 1{\text{/}}2)$, ${{p}_{{1/d}}}({{I}_{1}})$, ${{p}_{0}}({{I}_{{ - 1}}})$ и ${{p}_{0}}({{H}_{{k,1}}})$ не выше $1$, вклад $p(a - s - 3{\text{/}}2)$ не превосходит ${{2}^{{ - s - 1}}}$, при любом $j$ вклад слагаемого ${{p}_{0}}({{H}_{{k,j + 1}}})$ вдвое меньше, чем у ${{p}_{0}}({{H}_{{k,j}}})$. Поскольку ${\text{|}}J_{k}^{*}{\text{|}} \leqslant {\text{|}}{{J}_{1}}{\text{|}} \leqslant {{2}^{{a - s}}}$, согласно (22), то вклад каждого из слагаемых ${{p}_{0}}(J_{k}^{*})$ не превосходит ${{2}^{{ - s}}}$. Эти оценки означают, что суммы коэффициентов при ${{x}_{{r,i}}}$ в неравенствах (38'), (39') и (40') не превосходят соответственно 3, 3 и 5.

Теперь оценим запас, с которым вектор $u$ удовлетворяет приведенным неравенствам (38')–(40'). По построению для основного решения $v$ приведенное неравенство (38') выполнялось бы и при замене ${{p}_{{1/d}}}({{I}_{1}})$ на ${{p}_{0}}({{I}_{1}})$ в (38). Таким образом, правая часть (38) при ${{p}_{{r,i}}} = {{v}_{i}} \times {{2}^{r}}$ превосходит левую на величину не менее

После нормировки (делением не более, чем на $3 \times {{2}^{a}}$) и подстановки $u$ вместо $v$ величина запаса в приведенном неравенстве (38') сокращается не более, чем в $6 \times {{2}^{a}}$ раз, и остается не меньшей, чем $\tfrac{1}{{24 \times {{2}^{s}}}} > \varepsilon $.

Оценим свободный член, возникающий в (39') из-за того, что для сложности вставки в некоторые интервалы $J_{k}^{*}$ используется оценка $Q(a)$. Число таких интервалов не меньше $\left\lfloor {L{\text{/}}\Delta } \right\rfloor $ (см. выше), а применяемая оценка имеет величину ${{2}^{l}} \geqslant {\text{|}}{{J}_{{{{2}^{s}}}}}{\text{|}} \geqslant {{2}^{{a - s - 2}}}$, согласно (32) и (22). Поэтому, используя значения $L$ и $\Delta $ из (33) и (34), заключаем, что свободный член в правой части (39') не меньше

При подстановке $u$ вместо $v$ в приведенное неравенство (39') все члены сокращаются вдвое, тогда и свободный член можно уменьшить наполовину, т.е. на $\tfrac{1}{{6 \times {{2}^{{s/2}}}}} > \varepsilon $ с учетом нормировки.

Каждое из неравенств (40) при ${{p}_{{r,i}}} = {{v}_{i}} \times {{2}^{r}}$ выполняется с заложенным в сумму длин интервалов $H_{{k,j}}^{*}$ запасом

(см. (36)). При нормировке (делением не более, чем на $5 \times {{2}^{a}}$) и подстановке $u$ вместо $v$ запас сокращается не более чем в $10 \times {{2}^{a}}$ раз, до величины не менее $\varepsilon = \tfrac{1}{{25 \times {{2}^{s}}}}$.

Следовательно, при уменьшении свободных членов в приведенных неравенствах (38')–(40') на $\varepsilon $ вектор $u$ остается решением системы.

6. СОРТИРОВКА

Теорема 1. При любом $a \geqslant 2$ и ${{2}^{{a/4}}} \leqslant m \leqslant {{2}^{{a/2}}}$ выполнено

где $\gamma $ мало, например, $\gamma = \tfrac{1}{5}$.

Доказательство. Воспользуемся результатом леммы 3 и применим лемму 2. Значения всех параметров заимствуются из леммы 3. Имеем $v \in T(\sigma [s])$ и $u \in {{T}^{\varepsilon }}(\sigma [s])$ для системы ограничений $\sigma [s]$ глубины $h = 2s + 3$ и ширины $w \leqslant s + 4$. При этом справедливо ${{u}_{i}} < {{2}^{{{{y}_{i}} - 1/2}}} < \pi ({{y}_{i}})$ (см. (5)). Кроме того, $\varepsilon < 1 - \lambda < R = \left\| {v - u} \right\| < \sqrt 2 $. При $a < 100$ неравенство (41) заведомо выполнено при достаточно больших значениях константы под знаком “$O$”. Поэтому считаем, что $a \geqslant 100$. Положим $\varphi = log\left( {\tfrac{{m\varepsilon }}{{4{{a}^{2}}}}} \right)$ и $s = \left\lceil {2\gamma loga} \right\rceil $. Если $\gamma \leqslant 1{\text{/}}4$, то при этом $m\varepsilon \geqslant {{2}^{{a/4}}}{\text{/}}(50{{a}^{{2\gamma }}}) \geqslant 4{{a}^{2}}$, следовательно, $\varphi > 0$. Условие (16) леммы 2 выполнено автоматически.

Пусть $r + {{y}_{i}} \leqslant a - \tfrac{{(a + 2)\varphi \times {{2}^{\varphi }}}}{m} \leqslant r + {{y}_{i}} + \tfrac{1}{d}$, где $r \in \mathbb{N}$. С помощью леммы 2 получаем оценку

если, скажем, $\gamma \leqslant 1/5$.

Следствие 1. При любом $a \geqslant 2$ и ${{2}^{{a/4}}} \leqslant m \leqslant {{2}^{{a/2}}}$ выполнено

Реализованное доказательство главного технического результата (теорема 1) довольно громоздко. Поэтому для большей ясности приведем неформальное резюме схемы рассуждения.

1. Построим некоторую идеальную серию сравнений, всякий раз выполняя деление множества исходов пополам. К сожалению, она не дает сведения к подобной задаче меньшей размерности.

2. Отступление от идеала (поправочный коэффициент $\lambda $) позволяет разбалансировать длины интервалов, используя оценку (4) для сложности вставки, близкой к целому числу, и получить сходящийся рекурсивный алгоритм.

3. Дискретизация (параметр $d$) вводится, чтобы перейти от континуального к конечному семейству алгоритмов. В приведенном доказательстве шаги 2 и 3 совмещены. В результате мы имеем алгоритм с хорошей оценкой сложности, но который рекурсивно сводится к себе самому.

4. Обеспечим прогрессивный рост качества оценки сложности с увеличением размерности задачи, стартуя из точки, в которой оценка тривиально выполняется (лемма 2).

С технической стороны доказательство состоит в контролируемом учете поправок из трех источников: неравномерности разбиения, дискретизации и малой размерности.

Отметим, что даже упрощенный вариант стратегии из разд. 5 с выбором $s = 1$ и глубиной 6, только не универсальный, а с подбором оптимальных разбиений при каждом $i$, позволил бы улучшить результаты метода бинарных вставок при всех достаточно больших $n$. Однако для получения более точной оценки приходится выбирать параметр $s$ растущим. Главный содержательный результат формулирует следующая

Теорема 2. При любых $n$ выполняется равенство

Доказательство. Начинаем как в методе бинарных вставок. Разобьем набор из $n$ элементов на пары, упорядочим их и выполним сортировку старших элементов пар (они образуют главную цепочку). На это требуется $n{\text{/}}2 + S(n{\text{/}}2)$ сравнений. Пусть младшие элементы пар обозначаются через ${{\alpha }_{i}}$ с нумерацией в порядке возрастания ранга старших элементов в главной цепочке (фиг. 1).

Вставим первые ${{n}_{0}} = n{\text{/}}logn$ из младших элементов в главную цепочку методом бинарных вставок, потратив на это $n + O({{n}_{0}})$ сравнений. Оставшиеся элементы разобьем на группы по $m \approx \sqrt n {\text{/}}logn$ штук: группа с номером $k$ содержит элементы ${{\alpha }_{{{{n}_{0}} + (k - 1)m + 1}}},{{\alpha }_{{{{n}_{0}} + (k - 1)m + 2}}}, \ldots ,{{\alpha }_{{{{n}_{0}} + km}}}$. Группы вставляются в главную цепочку по очереди в порядке возрастания номеров методом следствия 1. Последняя группа может содержать менее $m$ элементов – их вставляем тривиальным бинарным методом.

Группа с номером $t$ должна быть вставлена в интервал длины ${{L}_{t}} = 2({{n}_{0}} + tm) - m$. Согласно следствию 1, при некотором ${{\rho }_{t}} = log{{L}_{t}} + O(lo{{g}^{{ - 1/5}}}n)$ выполнено ${{Q}_{m}}({{\rho }_{t}}) \geqslant {{L}_{t}}$. Поэтому сложность вставки $t$-й группы не превосходит ${{\rho }_{t}}m$.

Представим идеализированный случай, когда элемент ${{\alpha }_{k}}$ мог бы быть вставлен в главную цепочку за $log(2k - 1)$ сравнений. Тогда, если вставлять элементы в порядке возрастания номеров, было бы затрачено $log\prod\nolimits_{k = 1}^{\left\lceil {n/2} \right\rceil } (2k - 1) = log(n!) - log((n{\text{/}}2)!) - n{\text{/}}2 + O(logn)$ сравнений.

В групповом методе мы тратим на вставку элемента ${{\alpha }_{k}}$ не более $log(2k + m) + O(lo{{g}^{{ - 1/5}}}n) = log(2k - 1) + O(lo{{g}^{{ - 1/5}}}n)$ $log(2k + m) + O(lo{{g}^{{ - 1/5}}}n) = log(2k - 1) + O(lo{{g}^{{ - 1/5}}}n)$ сравнений при ${{n}_{0}} < k < n{\text{/}}2 - m$ и не более $log(2k - 1) + O(1)$ сравнений при $k \leqslant {{n}_{0}}$ и $k \geqslant n{\text{/}}2 - m$. Общее превышение сложности вставки по отношению к идеализированной ситуации тогда можно оценить как

Получаем рекуррентное соотношение или, если выразить через величины $s(n) = S(n) - log(n!)$, Отсюда следует $s(n) = O(nlo{{g}^{{ - 1/5}}}n)$.