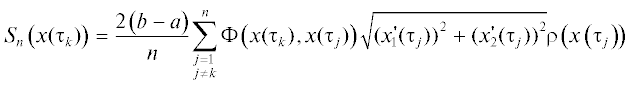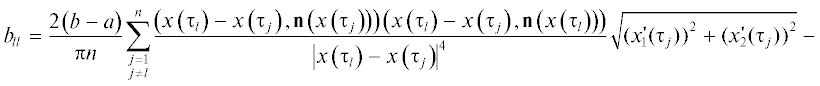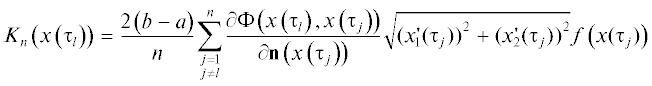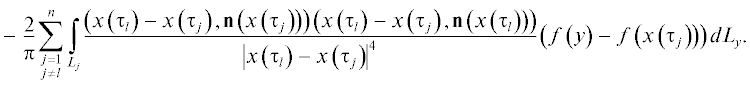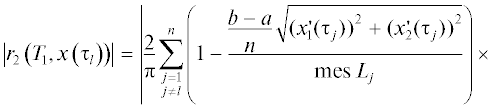1. На главную
  2. Электронные версии
  3. Журнал вычислительной математики и математической физики
  4. T. 61, № 6, 2021

Журнал вычислительной математики и математической физики, 2021, T. 61, № 6, стр. 936-950

Обоснование метода коллокации для интегрального уравнения внешней краевой задачи дирихле для уравнения Лапласа

М. Н. Бахшалыева 1, *, Э. Г. Халилов 1, **

1 Азербайджанский государственный университет нефти и промышленности
AZ 1010 Баку, пр. Азадлыг 20, Азербайджан

* E-mail: mehpara.bakhshalieva@mail.ru
** E-mail: elnurkhalil@mail.ru

Поступила в редакцию 07.05.2020
После доработки 18.08.2020
Принята к публикации 18.11.2020

Полный текст (PDF)

Аннотация

Рассматривается криволинейное интегральное уравнение внешней краевой задачи Дирихле для уравнения Лапласа. Дан новый метод построения квадратурной формулы для сингулярного интеграла, и на основе этого метода построена квадратурная формула для нормальной производной логарифмического потенциала двойного слоя. В определенно выбранных точках уравнение заменяется системой алгебраических уравнений, при этом устанавливается существование и единственность решения этой системы. Доказывается сходимость решения этой системы к точному решению интегрального уравнения и указывается скорость сходимости метода. Библ. 21.

Ключевые слова: криволинейный сингулярный интеграл, метод коллокации, краевая задача Дирихле, уравнение Лапласа, метод граничных интегральных уравнений.

1. ВВЕДЕНИЕ И ПОСТАНОВКИ ЗАДАЧИ

Пусть $D \subset {{R}^{2}}$ – ограниченная область с дважды непрерывно дифференцируемой границей $L$, а $f$ – заданная непрерывная функция на $L$.

Рассмотрим внешнюю краевую задачу Дирихле для уравнения Лапласа: найти функцию $u \in {{C}^{{\left( 2 \right)}}}({{R}^{2}}{{\backslash }}\bar {D}) \cap C({{R}^{2}}{{\backslash }}D)$, удовлетворяющую уравнению Лапласа $\Delta u = 0$ в ${{R}^{2}}{{\backslash }}\bar {D}$, условию излучения Зоммерфельда

$\left( {\frac{x}{{\left| x \right|}},\;\operatorname{grad} u\left( x \right)} \right) = o\left( {\frac{1}{{{{{\left| x \right|}}^{{1/2}}}}}} \right),\quad x \to \infty ,$
равномерно по всем направлениям $x{\text{/}}\left| x \right|$ и граничному условию

$u\left( x \right) = f\left( x \right)\quad {\text{на}}\quad L.$

Известно, что одним из методов решения внешней краевой задачи Дирихле для уравнения Лапласа является ее приведение к криволинейному интегральному уравнению. Основное преимущество применения метода интегральных уравнений к исследованию внешних краевых задач заключается в том, что подобный подход позволяет свести задачу, поставленную для неограниченной области, к задаче для ограниченной области меньшей размерности. Так как интегральные уравнения в замкнутом виде решаются лишь в очень редких случаях, первостепенное значение приобретает разработка приближенных методов решения интегральных уравнений с соответствующим теоретическим обоснованием.

В [1, с. 115–116] показано, что если решение $u\left( x \right)$ внешней краевой задачи Дирихле для уравнения Лапласа имеет нормальную производную в смысле равномерной сходимости, то неизвестная нормальная производная $\rho \left( x \right) = \frac{{\partial u\left( x \right)}}{{\partial{ \vec {n}}\left( x \right)}}$, $x \in L$, удовлетворяет интегральному уравнению II рода

(1.1)
$\rho + \tilde {K}\rho = Tf$
и интегральному уравнению I рода
(1.2)
$S\rho = - f + Kf,$
где $n\left( x \right)$ – единичная внешняя нормаль в точке $x \in L$,
$\left( {S\rho } \right)\left( x \right) = 2\int\limits_L {\Phi (x,y)\rho (y)d{{L}_{y}}} ,\quad \left( {K\rho } \right)\left( x \right) = 2\int\limits_L {\frac{{\partial \Phi (x,y)}}{{\partial n(y)}}\rho (y)d{{L}_{y}}} ,$
$\left( {\tilde {K}\rho } \right)\left( x \right) = 2\int\limits_L {\frac{{\partial \Phi (x,y)}}{{\partial n(x)}}\rho (y)d{{L}_{y}}} ,\quad \left( {Tf} \right)\left( x \right) = 2\frac{\partial }{{\partial n\left( x \right)}}\left( {\int\limits_L {\frac{{\partial \Phi (x,y)}}{{\partial n(y)}}f(y)d{{L}_{y}}} } \right),\quad x \in L,$
а $\Phi (x,y)$ – фундаментальное решение уравнения Лапласа, т.е.

$\Phi (x,y) = \frac{1}{{2\pi }}\ln \frac{1}{{\left| {x - y} \right|}},\quad x,y \in {{R}^{2}},\quad x \ne y.$

Несмотря на разрешимости интегральных уравнений (1.1) и (1.2), эти уравнения не имеют единственного решения. Однако Бертон и Миллер (см. [2]) доказали, что интегральное уравнение II рода

(1.3)
$\rho + \tilde {K}\rho - i\eta S\rho = Tf - i\eta \left( {Kf - f} \right),$
полученное из линейных комбинаций уравнений (1.1) и (1.2), разрешимо единственным образом в пространстве $C\left( L \right)$, где $\eta \ne 0$ – произвольное действительное число, а через $C\left( L \right)$ обозначено пространство всех непрерывных функций на $L$ с нормой ${{\left\| \varphi \right\|}_{\infty }} = \mathop {\max }\limits_{x \in L} \left| {\varphi \left( x \right)} \right|$.

Запишем уравнение (1.3) в виде

(1.4)
$\rho \left( x \right) + \left( {A\rho } \right)\left( x \right) = \left( {Bf} \right)\left( x \right),$
где

$\left( {A\rho } \right)\left( x \right) = \left( {\tilde {K}\rho } \right)\left( x \right) - i\eta \left( {S\rho } \right)\left( x \right),\quad \left( {Bf} \right)\left( x \right) = \left( {Tf} \right)\left( x \right) - i\eta \left( {\left( {Kf} \right)\left( x \right) - f\left( x \right)} \right),\quad x \in L.$

Известно, что внешнюю краевую задачу Дирихле для уравнения Лапласа можно привести к различным интегральным уравнениям, приближенные решения которых исследованы, например, в [3]–[5]. Уравнение (1.4) имеет то преимущество, что его решение является нормальной производной в смысле равномерной сходимости решения внешней краевой задачи Дирихле для уравнения Лапласа на $L$. При этом функция

$u\left( x \right) = \int\limits_L {\left\{ {f\left( y \right)\frac{{\partial \Phi \left( {x,y} \right)}}{{\partial n\left( y \right)}} - \rho \left( y \right)\Phi \left( {x,y} \right)} \right\}d{{S}_{y}}} {\kern 1pt} ,\quad x \in {{R}^{2}}{{\backslash }}\bar {D},$
является решением внешней краевой задачи Дирихле.

Отметим, что в [6] дано обоснование метода коллокации для интегрального уравнения (1.4) внешней краевой задачи Дирихле для уравнения Гельмгольца в трехмерном пространстве. А в [7] исследовано приближенное решение интегрального уравнения

$\rho + K\rho - i\eta S\rho = 2f$
внешней краевой задачи Дирихле для уравнения Гельмгольца и, используя значения в определенных точках функции $f$, проведены численные расчеты. Кроме того, в [7] отмечено, что можно исследовать также приближенное решение уравнения (1.4) и провести численные расчеты. Однако построенный Ляпуновым контрпример показывает (см. [8, с. 89–90]), что для потенциала двойного слоя с непрерывной плотностью производная, вообще говоря, не существует. Поэтому вычислить значение функции $\left( {Bf} \right)\left( x \right)$ в определенных точках не представляется возможным. Следует указать, что в [9], рассматривая нормальную производную потенциала двойного слоя как сильный сингулярный интеграл (см. [9, с. 115–116]), т.е. понимая интеграл в смысле конечного значения по Адамару, построена квадратурная формула для нормальной производной потенциала двойного слоя при дополнительно налагаемом условии на плотность $f$ (см. [9, с. 290]). Однако известно, что при этом условии выражение для нормальной производной потенциала двойного слоя может быть представлено в виде с сингулярным интегралом (см. [1, с. 68], [9, с. 100], [10]), т.е. интеграл $\left( {Tf} \right)\left( x \right)$ существует в смысле главного значения Коши.

В настоящей работе, рассматривая нормальную производную потенциала двойного слоя как интеграл в смысле главного значения Коши, построена квадратурная формула для $\left( {Tf} \right)\left( x \right)$, $x \in L$. Кроме того, с помощью построенных квадратурных формул для интегралов $\left( {A\rho } \right)\left( x \right)$ и $\left( {Bf} \right)\left( x \right)$ дано обоснование метода коллокации для уравнения (1.4).

2. КВАДРАТУРНАЯ ФОРМУЛА ДЛЯ ОДНОГО КЛАССА КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ

Предположим, что кривая $L$ задана параметрическим уравнением $x\left( t \right) = \left( {{{x}_{1}}\left( t \right),{{x}_{2}}\left( t \right)} \right)$, $t \in \left[ {a,b} \right]$. Разобьем промежуток $\left[ {a,b} \right]$ на $n > 2{{M}_{1}}\left( {b - a} \right){\text{/}}d$ равных частей: ${{t}_{k}} = a + \frac{{\left( {b - a} \right)k}}{n}$, $k = \overline {0,n} $, где ${{M}_{1}} = \mathop {\max }\limits_{t \in \left[ {a,b} \right]} \sqrt {{{{(x_{1}^{'}(t))}}^{2}} + {{{(x_{2}^{'}(t))}}^{2}}} < + \infty $ (см. [11, с. 560–561]) и $d$ – стандартный радиус (см. [11, с. 19], [12, с. 400]). В качестве опорных точек возмем $x\left( {{{\tau }_{k}}} \right)$, $k = \overline {1,n} $, где ${{\tau }_{k}} = a + \frac{{\left( {b - a} \right)\left( {2k - 1} \right)}}{{2n}}$. Тогда кривая $L$ разбивается на элементарные части: $L = \bigcup\nolimits_{l = 1}^n {{{L}_{l}}} $, где ${{L}_{k}} = \left\{ {x\left( t \right)\,:{{t}_{{k - 1}}} \leqslant t \leqslant {{t}_{k}}} \right\}$.

Известно, что (см. [13])

(1) $\forall k \in \left\{ {1,\;2,\; \ldots ,\;n} \right\}$: ${{r}_{k}}(n)\sim {{R}_{k}}(n)$ ($a\left( n \right)\sim b\left( n \right) \Leftrightarrow {{C}_{1}} \leqslant \frac{{a\left( n \right)}}{{b\left( n \right)}} \leqslant {{C}_{2}}$,  где  C1  и C2  – положительные постоянные, не зависящие от n), где ${{r}_{k}}\left( n \right) = \min \left\{ {\left| {x\left( {{{\tau }_{k}}} \right) - x\left( {{{t}_{{k - 1}}}} \right)} \right|,\left| {x\left( {{{t}_{k}}} \right) - x\left( {{{\tau }_{k}}} \right)} \right|} \right\}$ и ${{R}_{k}}\left( n \right) = \max \left\{ {\left| {x\left( {{{\tau }_{k}}} \right) - x\left( {{{t}_{{k - 1}}}} \right)} \right|,\left| {x\left( {{{t}_{k}}} \right) - x\left( {{{\tau }_{k}}} \right)} \right|} \right\}$;

(2) $\forall k \in \left\{ {1,\;2,\; \ldots ,\;n} \right\}$: ${{R}_{k}}\left( n \right) \leqslant d{\text{/}}2$;

(3) $\forall k,j \in \left\{ {1,\;2,\; \ldots ,\;n} \right\}$: ${{r}_{j}}\left( n \right)\sim {{r}_{k}}\left( n \right)$;

(4) $r\left( n \right)\sim R\left( n \right)\sim 1{\text{/}}n$, где $R\left( n \right) = \mathop {\max }\limits_{k = \overline {1,\,n} } {{R}_{k}}\left( n \right)$, $r\left( n \right) = \mathop {\min }\limits_{k = \overline {1,n} } {{r}_{k}}\left( n \right)$.

Лемма 1 (см. [14]). Существуют такие постоянные $C_{0}^{'} > 0$ и $C_{1}^{'} > 0$, не зависящие от $n$, для которых при $\forall k,j \in \left\{ {1,\;2,\; \ldots ,\;n} \right\}$, $j \ne k$, и $\forall y \in {{L}_{j}}$ справедливы следующие неравенства:

(2.1)
$C_{0}^{'}\left| {y - x\left( {{{\tau }_{k}}} \right)} \right| \leqslant \left| {x\left( {{{\tau }_{j}}} \right) - x\left( {{{\tau }_{k}}} \right)} \right| \leqslant C_{1}^{'}\left| {y - x\left( {{{\tau }_{k}}} \right)} \right|.$

Для функции $\varphi (x) \in C\left( L \right)$ вводим модуль непрерывности вида

$\omega (\varphi ,\delta ) = \delta \mathop {\sup }\limits_{\tau \geqslant \delta } \frac{{\bar {\omega }(\varphi ,\tau )}}{\tau },\quad \delta > 0,$
где . Кроме того, рассмотрим матрицу ${{A}^{n}} = \left( {{{a}_{{lj}}}} \right)_{{l,j = 1}}^{n}$ с элементами

${{a}_{{lj}}} = 0\quad {\text{при}}\quad l = j;$
${{a}_{{lj}}} = 2\frac{{b - a}}{n}\left( {\frac{{\partial \Phi \left( {x({{\tau }_{l}}),x({{\tau }_{j}})} \right)}}{{\partial n\left( {x({{\tau }_{l}})} \right)}} - i\eta \Phi \left( {x({{\tau }_{l}}),x({{\tau }_{j}})} \right)} \right)\sqrt {{{{(x_{1}^{'}({{\tau }_{j}}))}}^{2}} + {{{(x_{2}^{'}({{\tau }_{j}}))}}^{2}}} \quad {\text{при}}\quad l \ne j.$

Теорема 1. Выражение

(2.2)
${{A}_{n}}\left( {x({{\tau }_{l}})} \right) = \sum\limits_{j = 1}^n {{{a}_{{lj}}}\rho \left( {x({{\tau }_{j}})} \right)} $
в опорных точках $x\left( {{{\tau }_{l}}} \right)$, $l = \overline {1,n} $, является квадратурной формулой для интеграла $\left( {A\rho } \right)\left( x \right)$, причем (здесь и далее через М будем обозначать положительные постоянные, разные в различных неравенствах)

$\mathop {\max }\limits_{l = \overline {1,n} } \left| {A\left( {x\left( {{{\tau }_{l}}} \right)} \right) - {{A}_{n}}\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right| \leqslant М\left( {\omega \left( {\rho ,1{\text{/}}n} \right) + {{{\left\| \rho \right\|}}_{\infty }}\frac{{\ln n}}{n}} \right).$

Доказательство. В [13] доказано, что выражения

и
в опорных точках $x\left( {{{\tau }_{k}}} \right)$, $k = \overline {1,n} $, являются квадратурными формулами для интегралов $\left( {S\rho } \right)\left( x \right)$ и $\left( {\tilde {K}\rho } \right)\left( x \right)$, соответственно, причем
$\mathop {\max }\limits_{k = \overline {1,n} } \left| {\left( {S\rho } \right)\left( {x\left( {{{\tau }_{k}}} \right)} \right) - {{S}_{n}}\left( {x\left( {{{\tau }_{k}}} \right)} \right)} \right| \leqslant M\left( {\omega \left( {\rho ,1{\text{/}}n} \right) + {{{\left\| \rho \right\|}}_{\infty }}\frac{{\ln n}}{n}} \right),$
$\mathop {\max }\limits_{k = \overline {1,n} } \left| {\left( {\tilde {K}\rho } \right)\left( {x\left( {{{\tau }_{k}}} \right)} \right) - {{{\tilde {K}}}_{n}}\left( {x\left( {{{\tau }_{k}}} \right)} \right)} \right| \leqslant M\left( {\omega \left( {\rho ,1{\text{/}}n} \right) + {{{\left\| \rho \right\|}}_{\infty }}\frac{{\ln n}}{n}} \right).$
Отсюда получаем, что выражение (2.2) в опорных точках $x\left( {{{\tau }_{l}}} \right)$, $l = \overline {1,n} $, является квадратурной формулой для интеграла $\left( {A\rho } \right)\left( x \right)$, причем
$\mathop {\max }\limits_{l = \overline {1,n} } \left| {A\left( {x\left( {{{\tau }_{l}}} \right)} \right) - {{A}_{n}}\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right| \leqslant M\left( {\omega \left( {\rho ,1{\text{/}}n} \right) + {{{\left\| \rho \right\|}}_{\infty }}\frac{{\ln n}}{n}} \right).$
Теорема доказана.

Очевидно, что существует натуральное число ${{n}_{0}}$ такое, что

$\sqrt {R\left( n \right)} \leqslant \min \left\{ {1,d{\text{/}}2} \right\}\quad \forall n > {{n}_{0}}.$

Пусть

${{P}_{l}} = \left\{ {j\,|\,1 \leqslant j \leqslant n,\;\left| {x\left( {{{\tau }_{l}}} \right) - x\left( {{{\tau }_{j}}} \right)} \right| \leqslant \sqrt {R\left( n \right)} } \right\},\quad {{Q}_{l}} = \left\{ {j\,|\,1 \leqslant j \leqslant n,\;\left| {x\left( {{{\tau }_{l}}} \right) - x\left( {{{\tau }_{j}}} \right)} \right| > \sqrt {R\left( n \right)} } \right\}.$

Рассмотрим матрицу${{B}^{n}} = \left( {{{b}_{{lj}}}} \right)_{{l,j = 1}}^{n}$ с элементами

$ - \;\frac{{b - a}}{{\pi n}}\sum\limits_{j \in {{Q}_{{\,l}}}} {\frac{{\left( {n\left( {x\left( {{{\tau }_{j}}} \right)} \right),n\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right)}}{{{{{\left| {x\left( {{{\tau }_{j}}} \right) - x\left( {{{\tau }_{l}}} \right)} \right|}}^{2}}}}\sqrt {{{{(x_{1}^{'}({{\tau }_{j}}))}}^{2}} + {{{(x_{2}^{'}({{\tau }_{j}}))}}^{2}}} } + i\eta \quad {\text{при}}\quad l = \overline {1,n} ;$
${{b}_{{l\,j}}} = - \,\,\frac{{2\left( {b - a} \right)}}{n}\,\left[ {\frac{{\left( {x\left( {{{\tau }_{l}}} \right) - x\left( {{{\tau }_{j}}} \right),\,n\left( {x\left( {{{\tau }_{j}}} \right)} \right)} \right)\,\left( {x\left( {{{\tau }_{l}}} \right) - x\left( {{{\tau }_{j}}} \right),\,n\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right)}}{{\pi \,{{{\left| {x\left( {{{\tau }_{l}}} \right) - x\left( {{{\tau }_{j}}} \right)} \right|}}^{4}}}} + } \right.$
$ + \;\left. {i\eta \frac{{\partial \Phi \left( {x\left( {{{\tau }_{l}}} \right),x\left( {{{\tau }_{j}}} \right)} \right)}}{{\partial n\left( {x\left( {{{\tau }_{j}}} \right)} \right)}}} \right]\sqrt {{{{(x_{1}^{'}({{\tau }_{j}}))}}^{2}} + {{{(x_{2}^{'}({{\tau }_{j}}))}}^{2}}} \quad {\text{при}}\quad j \in {{P}_{l}}\quad {\text{и}}\quad j \ne l;$
${{b}_{{lj}}} = - \frac{{2\left( {b - a} \right)}}{n}\left[ {\frac{{\left( {x\left( {{{\tau }_{l}}} \right) - x\left( {{{\tau }_{j}}} \right),n\left( {x\left( {{{\tau }_{j}}} \right)} \right)} \right)\left( {x\left( {{{\tau }_{l}}} \right) - x\left( {{{\tau }_{j}}} \right),n\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right)}}{{\pi {{{\left| {x\left( {{{\tau }_{l}}} \right) - x\left( {{{\tau }_{j}}} \right)} \right|}}^{4}}}} - } \right.$
$ - \frac{{\left( {n\left( {x\left( {{{\tau }_{j}}} \right)} \right),n\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right)}}{{2\pi {{{\left| {x\left( {{{\tau }_{j}}} \right) - x\left( {{{\tau }_{l}}} \right)} \right|}}^{2}}}} + \left. {i\eta \frac{{\partial \Phi \left( {x\left( {{{\tau }_{l}}} \right),x\left( {{{\tau }_{j}}} \right)} \right)}}{{\partial n\left( {x\left( {{{\tau }_{j}}} \right)} \right)}}} \right]\sqrt {{{{(x_{1}^{'}({{\tau }_{j}}))}}^{2}} + {{{(x_{2}^{'}({{\tau }_{j}}))}}^{2}}} \quad {\text{при}}\quad j \in {{Q}_{l}}.$

Теорема 2. Пусть функция $f$ непрерывно дифференцируема на $L$ и

$\int\limits_0^d {\frac{{\omega ({\text{grad}}\,f,t)}}{t}dt < \infty } .$
Тогда выражение
(2.3)
${{\left( {Bf} \right)}^{n}}\left( {x\left( {{{\tau }_{l}}} \right)} \right) = \sum\limits_{j = 1}^n {{{b}_{{lj}}}f\left( {x\left( {{{\tau }_{j}}} \right)} \right)} $
в опорных точках $x\left( {{{\tau }_{l}}} \right)$, $l = \overline {1,n} $, является квадратурной формулой для интеграла $\left( {Bf} \right)\left( x \right)$, причем

$\mathop {\max }\limits_{l = \overline {1,n} } \left| {\left( {Bf} \right)\left( {x\left( {{{\tau }_{l}}} \right)} \right) - {{{\left( {Bf} \right)}}^{n}}\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right| \leqslant M\left[ {\frac{{{{{\left\| f \right\|}}_{\infty }} + {{{\left\| {{\text{grad}}\,f} \right\|}}_{\infty }}}}{{\sqrt n }} + \int\limits_0^{1/\sqrt n } {\frac{{\omega ({\text{grad}}\,f,t)}}{t}dt} } \right].$

Доказательство. В [13] доказано, что выражение

в опорных точках $x\left( {{{\tau }_{l}}} \right)$, $l = \overline {1,n} $, является квадратурной формулой для интеграла $\left( {Kf} \right)\left( x \right)$, причем
$\mathop {\max }\limits_{l = \overline {1,n} } \left| {\left( {Kf} \right)\left( {x\left( {{{\tau }_{l}}} \right)} \right) - {{K}_{n}}\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right| \leqslant M\left( {\omega \left( {f,1{\text{/}}n} \right) + {{{\left\| f \right\|}}_{\infty }}\frac{{\ln n}}{n}} \right).$
Тогда, принимая во внимание неравенство
(2.4)
$\omega \left( {f,1{\text{/}}n} \right) \leqslant \frac{{{{{\left\| {{\text{grad}}\,f} \right\|}}_{\infty }}}}{n},$
получаем, что
$\mathop {\max }\limits_{l = \overline {1,n} } \left| {\left( {Kf} \right)\left( {x\left( {{{\tau }_{l}}} \right)} \right) - {{K}_{n}}\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right| \leqslant M\left( {{{{\left\| {\operatorname{grad} f} \right\|}}_{\infty }} + {{{\left\| f \right\|}}_{\infty }}} \right)\frac{{\ln n}}{n}.$
Теперь построим квадратурную формулу для интеграла $\left( {Tf} \right)\left( x \right)$.

В [10] доказано, что

$\left( {Tf} \right)\left( x \right) = {{T}_{1}}\left( x \right) + {{T}_{2}}\left( x \right),$
где
${{T}_{1}}\left( x \right) = - \frac{2}{\pi }\int\limits_L {\frac{{\left( {x - y,n(y)} \right)\left( {x - y,n(x)} \right)}}{{{{{\left| {x - y} \right|}}^{4}}}}} \left( {f(y) - f(x)} \right)d{{L}_{y}}$
и
${{T}_{2}}\left( x \right) = \frac{1}{\pi }\int\limits_L {\frac{{\left( {n(y),n(x)} \right)}}{{{{{\left| {x - y} \right|}}^{2}}}}\left( {f(y) - f(x)} \right)d{{L}_{y}}} ,\quad x \in L,$
причем интеграл ${{T}_{2}}\left( x \right)$ существует в смысле главного значения Коши.

Построим квадратурную формулу для интеграла ${{T}_{1}}\left( x \right)$. Выражение

(2.5)
в опорных точках $x\left( {{{\tau }_{l}}} \right)$, $l = \overline {1,n} $, является квадратурной формулой для интеграла ${{T}_{1}}\left( x \right)$. Оценим погрешность квадратурной формулы (2.5). Очевидно, что
${{T}_{1}}\left( {x\left( {{{\tau }_{l}}} \right)} \right) - {{T}_{1}}^{n}\left( {x\left( {{{\tau }_{l}}} \right)} \right) = - \frac{2}{\pi }\int\limits_{{{L}_{l}}} {\frac{{\left( {x\left( {{{\tau }_{l}}} \right) - y,n(y)} \right)\left( {x\left( {{{\tau }_{l}}} \right) - y,n\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right)}}{{{{{\left| {x\left( {{{\tau }_{l}}} \right) - y} \right|}}^{4}}}}\left( {f\left( y \right) - f\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right)} {\kern 1pt} d{{L}_{y}} - $
$ \times \;\left( {\operatorname{mes} {{L}_{j}} - \frac{{b - a}}{n}\sqrt {{{{(x_{1}^{'}({{\tau }_{j}}))}}^{2}} + {{{(x_{2}^{'}({{\tau }_{j}}))}}^{2}}} } \right)\left( {f\left( {x({{\tau }_{j}})} \right) - f\left( {x({{\tau }_{l}})} \right)} \right) - $
$ \times \;\left( {x\left( {{{\tau }_{l}}} \right) - x\left( {{{\tau }_{j}}} \right),n\left( {x\left( {{{\tau }_{j}}} \right)} \right)} \right)\left( {x\left( {{{\tau }_{l}}} \right) - x\left( {{{\tau }_{j}}} \right),n\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right)\left( {f\left( y \right) - f\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right)d{{L}_{y}} - $
Слагаемые выражения в правой части последнего равенства обозначим через ${{r}_{1}}\left( {{{T}_{1}},x\left( {{{\tau }_{l}}} \right)} \right)$, ${{r}_{2}}\left( {{{T}_{1}},x\left( {{{\tau }_{l}}} \right)} \right)$, ${{r}_{3}}\left( {{{T}_{1}},x\left( {{{\tau }_{l}}} \right)} \right)$, ${{r}_{4}}\left( {{{T}_{1}},x\left( {{{\tau }_{l}}} \right)} \right)$ и ${{r}_{5}}\left( {{{T}_{1}},x\left( {{{\tau }_{l}}} \right)} \right)$ соответственно.

Так как функция $f(x)$ непрерывно дифференцируема, то существует такая точка $y* = x + \theta (y - x)$ (здесь $\theta = ({{\theta }_{1}},{{\theta }_{2}})$ и ${{\theta }_{1}},{{\theta }_{2}} \in \left( {0,1} \right)$), что

(2.6)
$f(y) - f(x) = (\operatorname{grad} f(y*),y - x),\quad x,y \in L.$
Тогда, применяя неравенство
$\left| {\left( {x - y,n\left( y \right)} \right)} \right| \leqslant M{{\left| {x - y} \right|}^{2}}$
и формулу вычисления криволинейного интеграла, имеем

$\left| {{{r}_{1}}\left( {{{T}_{1}},x\left( {{{\tau }_{l}}} \right)} \right)} \right| \leqslant M{{\left\| {\operatorname{grad} f} \right\|}_{\infty }}{{\left( {R\left( n \right)} \right)}^{2}}.$

Учитывая неравенство

$\left| {\sqrt {{{{(x_{1}^{'}(t))}}^{2}} + {{{(x_{2}^{'}(t))}}^{2}}} - \sqrt {{{{(x_{1}^{'}({{\tau }_{j}}))}}^{2}} + {{{(x_{2}^{'}({{\tau }_{j}}))}}^{2}}} } \right| \leqslant MR\left( n \right)\quad \forall t \in \left[ {{{t}_{{j - 1}}},{{t}_{j}}} \right],$
получаем, что
(2.7)
$\begin{gathered} \left| {1 - \frac{{\frac{{b - a}}{n}\sqrt {{{{(x_{1}^{'}({{\tau }_{j}}))}}^{2}} + {{{(x_{2}^{'}({{\tau }_{j}}))}}^{2}}} }}{{\operatorname{mes} {{L}_{j}}}}} \right| = \frac{{\left| {\int\limits_{{{t}_{{j - 1}}}}^{{{t}_{j}}} {\left( {\sqrt {{{{(x_{1}^{'}(t))}}^{2}} + {{{(x_{2}^{'}(t))}}^{2}}} - \sqrt {{{{(x_{1}^{'}({{\tau }_{j}}))}}^{2}} + {{{(x_{2}^{'}({{\tau }_{j}}))}}^{2}}} } \right)} dt} \right|}}{{\operatorname{mes} {{L}_{j}}}} \leqslant \\ \leqslant \;M\frac{{\frac{{b - a}}{n}R\left( n \right)}}{{\frac{{b - a}}{n}{{m}_{1}}}} \leqslant MR\left( n \right), \\ \end{gathered} $
где ${{m}_{1}} = \mathop {\min }\limits_{t \in \left[ {a,b} \right]} \sqrt {{{{(x_{1}^{'}(t))}}^{2}} + {{{(x_{2}^{'}(t))}}^{2}}} > 0$ (см. [11, с. 560–561]). Тогда, принимая во внимание (2.1), (2.6) и (2.7), получаем

$\left. {\mathop \times \limits_{\mathop {}\limits_{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}^{} }^{} \;\int\limits_{{{L}_{j}}} {\frac{{\left( {x\left( {{{\tau }_{l}}} \right) - x\left( {{{\tau }_{j}}} \right),n\left( {x\left( {{{\tau }_{j}}} \right)} \right)} \right)\left( {x\left( {{{\tau }_{l}}} \right) - x\left( {{{\tau }_{j}}} \right),n\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right)}}{{{{{\left| {x\left( {{{\tau }_{l}}} \right) - x\left( {{{\tau }_{j}}} \right)} \right|}}^{4}}}}\left( {f\left( {x\left( {{{\tau }_{j}}} \right)} \right) - f\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right)d{{L}_{y}}} } \right| \leqslant $
$ \leqslant \;M{{\left\| {\operatorname{grad} f} \right\|}_{\infty }}R\left( n \right).$

Пусть $y \in {{L}_{j}}$ и $j \ne l$. Тогда, учитывая (2.1) и (2.6), получаем

$\left| {\frac{{\left( {x\left( {{{\tau }_{l}}} \right) - y,n\left( y \right)} \right)\left( {x\left( {{{\tau }_{l}}} \right) - y,n\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right) - \left( {x\left( {{{\tau }_{j}}} \right) - x\left( {{{\tau }_{l}}} \right),n\left( {x\left( {{{\tau }_{j}}} \right)} \right)} \right)\left( {x\left( {{{\tau }_{j}}} \right) - x\left( {{{\tau }_{l}}} \right),n\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right)}}{{{{{\left| {x\left( {{{\tau }_{l}}} \right) - y} \right|}}^{4}}}} \times } \right.$
$\left. {\mathop \times \limits_{\mathop {}\limits_{_{{_{{}}}}} }^{} \;\left( {f\left( y \right) - f\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right)} \right| = $
$ = \;\left| {\left( {f\left( y \right) - f\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right)\left( {\frac{{\left( {\left( {y - x\left( {{{\tau }_{j}}} \right),n\left( y \right)} \right) + \left( {x\left( {{{\tau }_{j}}} \right) - x\left( {{{\tau }_{l}}} \right),n\left( y \right) - n\left( {x\left( {{{\tau }_{j}}} \right)} \right)} \right)} \right)\left( {y - x\left( {{{\tau }_{l}}} \right),n\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right)}}{{{{{\left| {x\left( {{{\tau }_{l}}} \right) - y} \right|}}^{4}}}} + } \right.} \right.$
$\left. {\left. { + \;\frac{{\left( {x\left( {{{\tau }_{j}}} \right) - x\left( {{{\tau }_{l}}} \right),n\left( {x\left( {{{\tau }_{j}}} \right)} \right)} \right)\left( {\left( {y - x\left( {{{\tau }_{j}}} \right),n\left( {x\left( {{{\tau }_{l}}} \right)} \right) - n\left( y \right)} \right) + \left( {y - x\left( {{{\tau }_{j}}} \right),n\left( y \right)} \right)} \right)}}{{{{{\left| {x\left( {{{\tau }_{l}}} \right) - y} \right|}}^{4}}}}} \right)} \right| \leqslant $
$ \leqslant \;M{{\left\| {\operatorname{grad} f} \right\|}_{\infty }}R\left( n \right).$

Следовательно,

$\left| {{{r}_{3}}\left( {{{T}_{1}},x\left( {{{\tau }_{l}}} \right)} \right)} \right| \leqslant M{{\left\| {{\text{grad}}\,\rho } \right\|}_{\infty }}R\left( n \right).$

Принимая во внимание (2.1) и (2.6), получаем, что если $y \in {{L}_{j}}$ и $j \ne l$, то

$\begin{gathered} \left| {\left( {x\left( {{{\tau }_{j}}} \right) - x\left( {{{\tau }_{l}}} \right),n\left( {x\left( {{{\tau }_{j}}} \right)} \right)} \right)\left( {x\left( {{{\tau }_{j}}} \right) - x\left( {{{\tau }_{l}}} \right),n\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right)\left( {f\left( y \right) - f\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right)} \right| \times \\ \times \;\left| {\frac{1}{{{{{\left| {x\left( {{{\tau }_{l}}} \right) - y} \right|}}^{4}}}} - \frac{1}{{{{{\left| {x\left( {{{\tau }_{l}}} \right) - x\left( {{{\tau }_{j}}} \right)} \right|}}^{4}}}}} \right| \leqslant M{{\left\| {\operatorname{grad} f} \right\|}_{\infty }}\frac{{R\left( n \right)}}{{\left| {x\left( {{{\tau }_{l}}} \right) - y} \right|}} \\ \end{gathered} $
и
$\left| {\frac{{\left( {x\left( {{{\tau }_{j}}} \right) - x\left( {{{\tau }_{l}}} \right),n\left( {x\left( {{{\tau }_{j}}} \right)} \right)} \right)\left( {x\left( {{{\tau }_{j}}} \right) - x\left( {{{\tau }_{l}}} \right),n\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right)}}{{{{{\left| {x\left( {{{\tau }_{l}}} \right) - x\left( {{{\tau }_{j}}} \right)} \right|}}^{4}}}}\left( {f\left( y \right) - f\left( {x\left( {{{\tau }_{j}}} \right)} \right)} \right)} \right| \leqslant M{{\left\| {\operatorname{grad} f} \right\|}_{\infty }}\frac{{R\left( n \right)}}{{\left| {x\left( {{{\tau }_{l}}} \right) - y} \right|}}.$
Тогда
$\left| {{{r}_{4}}\left( {{{T}_{1}},x\left( {{{\tau }_{l}}} \right)} \right)} \right| \leqslant M{{\left\| {\operatorname{grad} f} \right\|}_{\infty }}R\left( n \right)\left| {\ln R\left( n \right)} \right|$
и

$\left| {{{r}_{5}}\left( {{{T}_{1}},x\left( {{{\tau }_{l}}} \right)} \right)} \right| \leqslant M{{\left\| {\operatorname{grad} f} \right\|}_{\infty }}R\left( n \right)\left| {\ln R\left( n \right)} \right|$.

Суммируя полученные оценки для выражений ${{r}_{j}}\left( {{{T}_{1}},x\left( {{{\tau }_{l}}} \right)} \right)$, $j = \overline {1,5} $, находим

$\mathop {\max }\limits_{l = \overline {1,n} } \left| {{{T}_{1}}\left( {x\left( {{{\tau }_{l}}} \right)} \right) - T_{1}^{n}\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right| \leqslant M{{\left\| {\operatorname{grad} f} \right\|}_{\infty }}R\left( n \right)\left| {\ln \left( {R\left( n \right)} \right)} \right|.$

Теперь построим квадратурную формулу для интеграла ${{T}_{2}}\left( x \right)$. Выражение

(2.8)
$T_{2}^{n}\left( {x\left( {{{\tau }_{l}}} \right)} \right) = \frac{{b - a}}{{\pi n}}\sum\limits_{j \in {{Q}_{{\,l}}}} {\frac{{\left( {n\left( {x\left( {{{\tau }_{j}}} \right)} \right),n\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right)}}{{{{{\left| {x\left( {{{\tau }_{j}}} \right) - x\left( {{{\tau }_{l}}} \right)} \right|}}^{2}}}}} \sqrt {{{{(x_{1}^{'}({{\tau }_{j}}))}}^{2}} + {{{(x_{2}^{'}({{\tau }_{j}}))}}^{2}}} \left( {f\left( {x({{\tau }_{j}})} \right) - f\left( {x({{\tau }_{l}})} \right)} \right)$
в опорных точках $x\left( {{{\tau }_{l}}} \right)$, $l = \overline {1,n} $, является квадратурной формулой для интеграла ${{T}_{2}}\left( x \right)$. Оценим погрешность квадратурной формулы (2.8). Очевидно, что
${{T}_{2}}\left( {x\left( {{{\tau }_{l}}} \right)} \right) - T_{2}^{n}\left( {x\left( {{{\tau }_{l}}} \right)} \right) = \frac{1}{\pi }\sum\limits_{j \in {{Q}_{l}}} {\frac{{\left( {n\left( {x\left( {{{\tau }_{j}}} \right)} \right),n\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right)}}{{{{{\left| {x\left( {{{\tau }_{l}}} \right) - x\left( {{{\tau }_{j}}} \right)} \right|}}^{2}}}} \times } $
$ \times \;\left( {\operatorname{mes} {{L}_{j}} - \frac{{b - a}}{n}\sqrt {{{{(x_{1}^{'}({{\tau }_{j}}))}}^{2}} + {{{(x_{2}^{'}({{\tau }_{j}}))}}^{2}}} } \right)\left( {f\left( {x({{\tau }_{j}})} \right) - f\left( {x({{\tau }_{l}})} \right)} \right) + $
$ + \;\frac{1}{\pi }\sum\limits_{j \in {{Q}_{l}}} {\int\limits_{{{L}_{j}}} {\left( {\frac{{f\left( y \right) - f\left( {x\left( {{{\tau }_{l}}} \right)} \right)}}{{{{{\left| {x\left( {{{\tau }_{l}}} \right) - y} \right|}}^{2}}}}\left( {n\left( y \right),n\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right) - \frac{{f\left( {x\left( {{{\tau }_{j}}} \right)} \right) - f\left( {x\left( {{{\tau }_{l}}} \right)} \right)}}{{{{{\left| {x\left( {{{\tau }_{l}}} \right) - x\left( {{{\tau }_{j}}} \right)} \right|}}^{2}}}}\left( {n\left( {x\left( {{{\tau }_{j}}} \right)} \right),n\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right)} \right)} d{{L}_{y}}} + $
$ + \;\frac{1}{\pi }\int\limits_{\bigcup\limits_{j \in {{P}_{l}}} {{{L}_{j}}} } {\frac{{f\left( y \right) - f\left( {x\left( {{{\tau }_{l}}} \right)} \right)}}{{{{{\left| {x\left( {{{\tau }_{l}}} \right) - y} \right|}}^{2}}}}\left( {n\left( y \right),n\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right)d{{L}_{y}}} .$
Слагаемые выражения в правой части последнего равенства обозначим через ${{r}_{1}}\left( {{{T}_{2}},x\left( {{{\tau }_{l}}} \right)} \right)$, ${{r}_{2}}\left( {{{T}_{2}},x\left( {{{\tau }_{l}}} \right)} \right)$ и ${{r}_{3}}\left( {{{T}_{2}},x\left( {{{\tau }_{l}}} \right)} \right)$ соответственно.

Принимая во внимание (2.1), (2.6) и (2.7), получаем

$\left| {r{}_{1}\left( {{{T}_{2}},x\left( {{{\tau }_{l}}} \right)} \right)} \right| = \left| {\frac{1}{\pi }\sum\limits_{j \in {{Q}_{l}}} {\left( {1 - \frac{{\frac{{b - a}}{n}\sqrt {{{{(x_{1}^{'}({{\tau }_{j}}))}}^{2}} + {{{(x_{2}^{'}({{\tau }_{j}}))}}^{2}}} }}{{\operatorname{mes} {{L}_{j}}}}} \right)} \times } \right.$
$\left. {\mathop \times \limits_{\mathop {}\limits_{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}^{} }^{} \;\int\limits_{{{L}_{j}}} {\frac{{\left( {n\left( {x\left( {{{\tau }_{j}}} \right)} \right),n\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right)}}{{{{{\left| {x\left( {{{\tau }_{l}}} \right) - x\left( {{{\tau }_{j}}} \right)} \right|}}^{2}}}}\left( {f\left( {x\left( {{{\tau }_{j}}} \right)} \right) - f\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right)d{{L}_{y}}} } \right| \leqslant $
$ \leqslant \;M{{\left\| {\operatorname{grad} f} \right\|}_{\infty }}R(n)\int\limits_{\sqrt {R(n)} }^{{\text{diam}}L} {\frac{{dt}}{t}} \leqslant M{{\left\| {\operatorname{grad} f} \right\|}_{\infty }}R(n)\left| {\ln R(n)} \right|.$

Пусть $y \in {{L}_{j}}$, $j \in {{Q}_{l}}$. Тогда

$\left| {\frac{{f\left( y \right) - f\left( {x\left( {{{\tau }_{l}}} \right)} \right)}}{{{{{\left| {x\left( {{{\tau }_{l}}} \right) - y} \right|}}^{2}}}}\left( {n\left( y \right),n\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right) - \frac{{f\left( {x\left( {{{\tau }_{j}}} \right)} \right) - f\left( {x\left( {{{\tau }_{l}}} \right)} \right)}}{{{{{\left| {x\left( {{{\tau }_{l}}} \right) - x\left( {{{\tau }_{j}}} \right)} \right|}}^{2}}}}\left( {n\left( {x\left( {{{\tau }_{j}}} \right)} \right),n\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right)} \right| \leqslant $
$ \leqslant \;\left| {\frac{{\left( {f\left( y \right) - f\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right)\left( {n\left( y \right),n\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right)\left( {{{{\left| {x\left( {{{\tau }_{l}}} \right) - x\left( {{{\tau }_{j}}} \right)} \right|}}^{2}} - {{{\left| {x\left( {{{\tau }_{l}}} \right) - y} \right|}}^{2}}} \right)}}{{{{{\left| {x\left( {{{\tau }_{l}}} \right) - y} \right|}}^{2}}{{{\left| {x\left( {{{\tau }_{l}}} \right) - x\left( {{{\tau }_{j}}} \right)} \right|}}^{2}}}}} \right| + $
$ + \;\frac{{\left| {\left( {f\left( y \right) - f\left( {x\left( {{{\tau }_{j}}} \right)} \right)} \right)\left( {n\left( y \right),n\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right)} \right|}}{{{{{\left| {x\left( {{{\tau }_{l}}} \right) - x\left( {{{\tau }_{j}}} \right)} \right|}}^{2}}}} + \frac{{\left| {\left( {f\left( {x\left( {{{\tau }_{j}}} \right)} \right) - f\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right)\left( {n\left( y \right) - n\left( {x\left( {{{\tau }_{j}}} \right)} \right),n\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right)} \right|}}{{{{{\left| {x\left( {{{\tau }_{l}}} \right) - x\left( {{{\tau }_{j}}} \right)} \right|}}^{2}}}} \leqslant $
$ \leqslant \;M{{\left\| {\operatorname{grad} f} \right\|}_{\infty }}\frac{{R\left( n \right)}}{{{{{\left| {x\left( {{{\tau }_{l}}} \right) - y} \right|}}^{2}}}}.$
Отсюда находим

$\left| {{{r}_{2}}\left( {{{T}_{2}},x\left( {{{\tau }_{l}}} \right)} \right)} \right| \leqslant M{{\left\| {\operatorname{grad} f} \right\|}_{\infty }}R\left( n \right)\int\limits_{\sqrt {R(n)} }^{{\text{diam}}L} {\frac{{dt}}{{{{t}^{2}}}}} \leqslant M{{\left\| {\operatorname{grad} f} \right\|}_{\infty }}\sqrt {R\left( n \right)} .$

Так как существует такая точка $\tilde {y}\left( l \right) = x\left( {{{\tau }_{l}}} \right) + \theta \left( {y - x\left( {{{\tau }_{l}}} \right)} \right)$ (здесь $\theta = ({{\theta }_{1}},{{\theta }_{2}})$ и ${{\theta }_{1}},{{\theta }_{2}} \in \left( {0,1} \right)$), что

(2.9)
$f\left( y \right) - f\left( {x\left( {{{\tau }_{l}}} \right)} \right) = \left( {\operatorname{grad} f\left( {\tilde {y}\left( l \right)} \right),y - x\left( {{{\tau }_{l}}} \right)} \right),\quad y \in \bigcup\limits_{j \in {{P}_{l}}} {{{L}_{j}}} ,$
то выражение $r_{3}^{{}}\left( {{{T}_{3}},x\left( {{{\tau }_{l}}} \right)} \right)$ можно представить в виде

${{r}_{3}}\left( {{{T}_{3}},x\left( {{{\tau }_{l}}} \right)} \right) = \frac{1}{\pi }\int\limits_{\bigcup\limits_{j \in {{P}_{l}}} {{{L}_{j}}} } {\frac{{\left( {\operatorname{grad} f\left( {\tilde {y}\left( l \right)} \right),y - x\left( {{{\tau }_{l}}} \right)} \right)}}{{{{{\left| {x\left( {{{\tau }_{l}}} \right) - y} \right|}}^{2}}}}\left( {n\left( y \right) - n\left( {x\left( {{{\tau }_{l}}} \right)} \right),n\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right)d{{L}_{y}} + } $
$ + \;\frac{1}{\pi }\int\limits_{\bigcup\limits_{j \in {{P}_{l}}} {{{L}_{j}}} } {\frac{{\left( {\operatorname{grad} f\left( {\tilde {y}\left( l \right)} \right) - \operatorname{grad} f\left( {x\left( {{{\tau }_{l}}} \right)} \right),y - x\left( {{{\tau }_{l}}} \right)} \right)}}{{{{{\left| {x\left( {{{\tau }_{l}}} \right) - y} \right|}}^{2}}}}d{{L}_{y}}} + \frac{1}{\pi }\int\limits_{\bigcup\limits_{j \in {{P}_{l}}} {{{L}_{j}}} } {\frac{{\left( {\operatorname{grad} f\left( {x\left( {{{\tau }_{l}}} \right)} \right),y - x\left( {{{\tau }_{l}}} \right)} \right)}}{{{{{\left| {x\left( {{{\tau }_{l}}} \right) - y} \right|}}^{2}}}}d{{L}_{y}}} .$

Пусть $y \in \partial \left( {\bigcup\nolimits_{j \in {{P}_{l}}}^{} {{{L}_{j}}} } \right)$. Очевидно, что существуют натуральные числа $s \in {{P}_{l}}$ и $m \in {{Q}_{l}}$ такие, что $y \in \partial {{L}_{s}}$ и $y \in \partial {{L}_{m}}$. Отсюда имеем

$\left| {x\left( {{{\tau }_{l}}} \right) - y} \right| \leqslant \left| {x\left( {{{\tau }_{l}}} \right) - x\left( {{{\tau }_{s}}} \right)} \right| + \left| {x\left( {{{\tau }_{s}}} \right) - y} \right| \leqslant \sqrt {R\left( n \right)} + R\left( n \right)$
и

$\left| {x\left( {{{\tau }_{l}}} \right) - y} \right| \geqslant \left| {x\left( {{{\tau }_{l}}} \right) - x\left( {{{\tau }_{m}}} \right)} \right| - \left| {x\left( {{{\tau }_{m}}} \right) - y} \right| > \sqrt {R\left( n \right)} - R\left( n \right).$

Следовательно,

(2.10)
$\sqrt {R\left( n \right)} - R\left( n \right) < \left| {x\left( {{{\tau }_{l}}} \right) - y} \right| \leqslant \sqrt {R\left( n \right)} + R\left( n \right)\quad \forall y \in \partial \left( {\bigcup\limits_{j \in {{P}_{l}}} {{{L}_{j}}} } \right).$
Тогда
$\begin{gathered} \left| {\int\limits_{\bigcup\limits_{j \in {{P}_{l}}} {{{L}_{j}}} } {\frac{{\left( {\operatorname{grad} f\left( {\tilde {y}\left( l \right)} \right),y - x\left( {{{\tau }_{l}}} \right)} \right)}}{{{{{\left| {x\left( {{{\tau }_{l}}} \right) - y} \right|}}^{2}}}}\left( {n\left( y \right) - n\left( {x\left( {{{\tau }_{l}}} \right)} \right),n\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right)d{{L}_{y}}} } \right| \leqslant \\ \leqslant \;M{{\left\| {\operatorname{grad} f} \right\|}_{\infty }}\int\limits_0^{\sqrt {R\left( n \right)} + R(n)} {dt} \leqslant M{{\left\| {\operatorname{grad} f} \right\|}_{\infty }}\sqrt {R\left( n \right)} . \\ \end{gathered} $
Кроме того, принимая во внимание неравенство (2.9), находим

$\left| {\int\limits_{\bigcup\limits_{j \in {{P}_{l}}} {{{L}_{j}}} } {\frac{{\left( {\operatorname{grad} f\left( {\tilde {y}\left( l \right)} \right) - \operatorname{grad} f\left( {x\left( {{{\tau }_{l}}} \right)} \right),y - x\left( {{{\tau }_{l}}} \right)} \right)}}{{{{{\left| {x\left( {{{\tau }_{l}}} \right) - y} \right|}}^{2}}}}d{{L}_{y}}} } \right| \leqslant M\int\limits_0^{\sqrt {R\left( n \right)} + R(n)} {\frac{{\omega (\operatorname{grad} f,t)}}{t}dt.} $

Известно (см. [11, с. 19], [12, с. 400–401]), что для любой точки $x \in L$ окрестность ${{L}_{d}}(x) = \left\{ {y \in L{\text{:}}\;\left| {y - x} \right| < d} \right\}$ пересекается с прямой, параллельной нормали $n(x)$, в единственной точке, либо вообще не пересекается, т.е. множество ${{L}_{d}}(x)$ однозначно проектируется на промежуток ${{\Omega }_{d}}(x)$, лежащий на касательной прямой $\Gamma (x)$ к $L$ в точке$x$. На куске ${{L}_{d}}\left( {x\left( {{{\tau }_{l}}} \right)} \right)$ выберем локальную прямоугольную систему координат $(u,{v})$ с началом в точке $x\left( {{{\tau }_{l}}} \right)$, где ось ${v}$ направим вдоль нормали $n\left( {x\left( {{{\tau }_{l}}} \right)} \right)$, а ось $u$ направим вдоль положительного направления касательной прямой $\Gamma \left( {x\left( {{{\tau }_{l}}} \right)} \right)$. Известно, что при этом координаты точек $x\left( {{{\tau }_{l}}} \right)$ будут $\left( {0,\;0} \right)$. Кроме того, в этих координатах окрестность ${{L}_{d}}\left( {x\left( {{{\tau }_{l}}} \right)} \right)$ можно задать уравнением ${v} = g(u)$, $u \in {{\Omega }_{d}}\left( {x\left( {{{\tau }_{l}}} \right)} \right)$, причем

$g \in {{C}^{{\left( 2 \right)}}}\left( {{{\Omega }_{d}}\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right)\quad {\text{и}}\quad g(0) = 0,\quad g{\text{'}}(0) = 0.$

Через ${{\Omega }_{l}}$ обозначим проекцию множества $\bigcup\nolimits_{j \in {{P}_{l}}}^{} {{{L}_{j}}} $ на касательную прямую $\Gamma \left( {x\left( {{{\tau }_{l}}} \right)} \right)$. Пусть ${{d}_{l}} = \mathop {\min }\limits_{\tilde {y} \in \partial {{\Omega }_{l}}} \left| {x\left( {{{\tau }_{l}}} \right) - \tilde {y}} \right|$. Так как

$\int\limits_{\bigcup\limits_{j \in {{P}_{l}}} {{{L}_{j}}} } {\frac{{\left( {\operatorname{grad} f\left( {x\left( {{{\tau }_{l}}} \right)} \right),y - x\left( {{{\tau }_{l}}} \right)} \right)}}{{{{{\left| {x\left( {{{\tau }_{l}}} \right) - y} \right|}}^{2}}}}d{{L}_{y}}} = \int\limits_{\bigcup\limits_{j \in {{P}_{l}}} {{{L}_{j}}} } {\frac{{\left( {{{y}_{1}} - {{x}_{1}}\left( {{{\tau }_{l}}} \right)} \right)\frac{{\partial f\left( {x\left( {{{\tau }_{l}}} \right)} \right)}}{{\partial {{x}_{1}}}} + \left( {{{y}_{2}} - {{x}_{2}}\left( {{{\tau }_{l}}} \right)} \right)\frac{{\partial f\left( {x\left( {{{\tau }_{l}}} \right)} \right)}}{{\partial {{x}_{2}}}}}}{{{{{\left( {{{y}_{1}} - {{x}_{1}}\left( {{{\tau }_{l}}} \right)} \right)}}^{2}} + {{{\left( {{{y}_{2}} - {{x}_{2}}\left( {{{\tau }_{l}}} \right)} \right)}}^{2}}}}d{{L}_{y}}} ,$
то по формуле вычисления криволинейного интеграла получаем, что
$\int\limits_{\bigcup\limits_{j \in {{P}_{l}}} {{{L}_{j}}} } {\frac{{\left( {{\text{grad}}\,f\left( {x\left( {{{\tau }_{l}}} \right)} \right),y - x\left( {{{\tau }_{l}}} \right)} \right)}}{{{{{\left| {x\left( {{{\tau }_{l}}} \right) - y} \right|}}^{2}}}}d{{L}_{y}}} = \frac{{\partial f\left( {x\left( {{{\tau }_{l}}} \right)} \right)}}{{\partial {{x}_{1}}}}\int\limits_{ - {{d}_{l}}}^{{{d}_{l}}} {\frac{{du}}{u}} + $
(2.11)
$ + \;\frac{{\partial f\left( {x\left( {{{\tau }_{l}}} \right)} \right)}}{{\partial {{x}_{2}}}}\int\limits_{ - {{d}_{l}}}^{{{d}_{l}}} {\frac{{g\left( u \right)}}{{{{u}^{2}} + {{{\left( {g\left( u \right)} \right)}}^{2}}}}\sqrt {1 + {{{\left( {g{\text{'}}\left( u \right)} \right)}}^{2}}} } du + \frac{{\partial f\left( {x\left( {{{\tau }_{l}}} \right)} \right)}}{{\partial {{x}_{1}}}}\int\limits_{ - {{d}_{l}}}^{{{d}_{l}}} {\frac{{u\left( {\sqrt {1 + {{{\left( {g{\text{'}}\left( u \right)} \right)}}^{2}}} - 1} \right)}}{{{{u}^{2}} + {{{\left( {g\left( u \right)} \right)}}^{2}}}}du + } $
$ + \;\frac{{\partial f\left( {x\left( {{{\tau }_{l}}} \right)} \right)}}{{\partial {{x}_{1}}}}\int\limits_{ - {{d}_{l}}}^{{{d}_{l}}} {u\left( {\frac{1}{{{{u}^{2}} + {{{\left( {g\left( u \right)} \right)}}^{2}}}} - \frac{1}{{{{u}^{2}}}}} \right)du + } \int\limits_{{{\Omega }_{l}}\backslash \left( { - {{d}_{l}},{{d}_{l}}} \right)} {\frac{{\frac{{\partial f\left( {x\left( {{{\tau }_{l}}} \right)} \right)}}{{\partial {{x}_{1}}}}u + \frac{{\partial f\left( {x\left( {{{\tau }_{l}}} \right)} \right)}}{{\partial {{x}_{2}}}}g\left( u \right)}}{{{{u}^{2}} + {{{\left( {g\left( u \right)} \right)}}^{2}}}}\sqrt {1 + {{{\left( {g{\text{'}}\left( u \right)} \right)}}^{2}}} du} .$
Первое слагаемое в правой части равенства (2.11) существует в смысле главного значения Коши и равно нулю. Кроме того, учитывая неравенства
$\left| {g{\text{'}}(u)} \right| \leqslant M\left| u \right|$
и
$\left| {g(u)} \right| = \left| {g(u) - g(0)} \right| \leqslant M{{\left| u \right|}^{2}},$
имеем
$\left| {\frac{{\partial f\left( {x\left( {{{\tau }_{l}}} \right)} \right)}}{{\partial {{x}_{2}}}}\int\limits_{ - {{d}_{l}}}^{{{d}_{l}}} {\frac{{g\left( u \right)}}{{{{u}^{2}} + {{{\left( {g\left( u \right)} \right)}}^{2}}}}\sqrt {1 + {{{\left( {g{\text{'}}\left( u \right)} \right)}}^{2}}} } du} \right| \leqslant M{{\left\| {\operatorname{grad} f} \right\|}_{\infty }}\sqrt {R\left( n \right)} ,$
$\left| {\frac{{\partial f\left( {x\left( {{{\tau }_{l}}} \right)} \right)}}{{\partial {{x}_{1}}}}\int\limits_{ - {{d}_{l}}}^{{{d}_{l}}} {\frac{{u{\kern 1pt} \left( {\sqrt {1 + {{{\left( {g{\text{'}}\left( u \right)} \right)}}^{2}}} - 1} \right)}}{{{{u}^{2}} + {{{\left( {g\left( u \right)} \right)}}^{2}}}}du} } \right| \leqslant M{{\left\| {\operatorname{grad} f} \right\|}_{\infty }}R\left( n \right)$
и

$\left| {\frac{{\partial f\left( {x\left( {{{\tau }_{l}}} \right)} \right)}}{{\partial {{x}_{1}}}}\int\limits_{ - {{d}_{l}}}^{{{d}_{l}}} {u\left( {\frac{1}{{{{u}^{2}} + {{{\left( {g\left( u \right)} \right)}}^{2}}}} - \frac{1}{{{{u}^{2}}}}} \right)du} } \right| \leqslant M{{\left\| {\operatorname{grad} f} \right\|}_{\infty }}R\left( n \right).$

Прежде всего существует точка ${{\tilde {y}}_{*}} \in {{\Omega }_{l}}$ такая, что ${{d}_{l}} = \left| {x\left( {{{\tau }_{l}}} \right) - {{{\tilde {y}}}_{*}}} \right|$. Обозначим через ${{y}_{*}} \in \partial \left( {\bigcup\nolimits_{j \in {{P}_{l}}}^{} {{{L}_{j}}} } \right)$ прообраз точки ${{\tilde {y}}_{*}}$, а через $\alpha \left( {a,b} \right)$ угол между векторами a и b. Применяя неравенство (2.10), получаем, что

${{d}_{l}} = \left| {x\left( {{{\tau }_{l}}} \right) - {{y}_{*}}} \right|\cos \alpha \left( {{{y}_{*}} - x\left( {{{\tau }_{l}}} \right),{{{\tilde {y}}}_{*}} - x\left( {{{\tau }_{l}}} \right)} \right) = \left| {x\left( {{{\tau }_{l}}} \right) - {{y}_{*}}} \right|\sqrt {1 - {{{\cos }}^{2}}\alpha \left( {{{y}_{*}} - x\left( {{{\tau }_{l}}} \right),n\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right)} \geqslant $
(2.12)
$\begin{gathered} \geqslant \;\left| {x\left( {{{\tau }_{l}}} \right) - {{y}_{*}}} \right|\,\sqrt {1 - {{M}^{2}}{{{\left| {x\left( {{{\tau }_{l}}} \right) - {{y}_{*}}} \right|}}^{2}}} \geqslant \left( {\sqrt {R\left( n \right)} - R(n)} \right)\sqrt {1 - {{M}^{2}}{{{\left( {\sqrt {R\left( n \right)} + R(n)} \right)}}^{2}}} \geqslant \\ \geqslant \;\left( {\sqrt {R\left( n \right)} - R(n)} \right)\sqrt {1 - {{M}^{2}}{{{\left( {2\sqrt {R\left( n \right)} } \right)}}^{2}}} = \left( {\sqrt {R\left( n \right)} - R(n)} \right)\sqrt {\left( {1 - 2M\sqrt {R\left( n \right)} } \right)\left( {1 + 2M\sqrt {R\left( n \right)} } \right)} \geqslant \\ \end{gathered} $
$ \geqslant \;\left( {\sqrt {R\left( n \right)} - R(n)} \right)\left( {1 - 2M\sqrt {R\left( n \right)} } \right) \geqslant \sqrt {R\left( n \right)} - (1 + 2M)R(n).$
Принимая во внимание неравенство (2.12) для последнего слагаемого в правой части равенства (2.11), получаем

$\left| {\int\limits_{{{\Omega }_{l}}\backslash \left( { - {{d}_{l}},{{d}_{l}}} \right)} {\frac{{\frac{{\partial f\left( {x\left( {{{\tau }_{l}}} \right)} \right)}}{{\partial {{x}_{1}}}}u + \frac{{\partial f\left( {x\left( {{{\tau }_{l}}} \right)} \right)}}{{\partial {{x}_{2}}}}f\left( u \right)}}{{{{u}^{2}} + {{{\left( {g\left( u \right)} \right)}}^{2}}}}\sqrt {1 + {{{\left( {g{\text{'}}\left( u \right)} \right)}}^{2}}} du} } \right| \leqslant $
$ \leqslant \;M{{\left\| {\operatorname{grad} f} \right\|}_{\infty }}\int\limits_{\sqrt {R\left( n \right)} - R\left( n \right)\left( {1 + 2M} \right)}^{\sqrt {R\left( n \right)} + R\left( n \right)} {\frac{{dt}}{t}} = M{{\left\| {\operatorname{grad} f} \right\|}_{\infty }}\ln \frac{{\sqrt {R\left( n \right)} + R\left( n \right)}}{{\sqrt {R\left( n \right)} - R\left( n \right)\left( {1 + 2M} \right)}} = $
$ = \;M{{\left\| {\operatorname{grad} f} \right\|}_{\infty }}\ln \left( {1 + \frac{{R\left( n \right)\left( {2 + 2M} \right)}}{{\sqrt {R\left( n \right)} - R\left( n \right)\left( {1 + 2M} \right)}}} \right) \leqslant $
$ \leqslant \;M{{\left\| {\operatorname{grad} f} \right\|}_{\infty }}\frac{{R\left( n \right)\left( {2 + 2M} \right)}}{{\sqrt {R\left( n \right)} - R\left( n \right)\left( {1 + 2M} \right)}} \leqslant M{{\left\| {\operatorname{grad} f} \right\|}_{\infty }}\sqrt {R\left( n \right)} .$

В результате находим

$\left| {\frac{1}{\pi }\int\limits_{\bigcup\limits_{j \in {{P}_{l}}} {{{L}_{j}}} } {\frac{{\left( {\operatorname{grad} f\left( {x\left( {{{\tau }_{l}}} \right)} \right),y - x\left( {{{\tau }_{l}}} \right)} \right)}}{{{{{\left| {x\left( {{{\tau }_{l}}} \right) - y} \right|}}^{2}}}}d{{L}_{y}}} } \right| \leqslant M{{\left\| {\operatorname{grad} f} \right\|}_{\infty }}\sqrt {R\left( n \right)} .$

Следовательно,

$\left| {{{r}_{3}}\left( {{{T}_{2}},x\left( {{{\tau }_{l}}} \right)} \right)} \right| \leqslant M\left[ {{{{\left\| {\operatorname{grad} f} \right\|}}_{\infty }}\sqrt {R\left( n \right)} + \int\limits_0^{\sqrt {R\left( n \right)} + R\left( n \right)} {\frac{{\omega (\operatorname{grad} f,t)}}{t}dt} } \right].$

Суммируя полученные оценки для выражений ${{r}_{1}}\left( {{{T}_{2}},x\left( {{{\tau }_{l}}} \right)} \right)$, ${{r}_{2}}\left( {{{T}_{2}},x\left( {{{\tau }_{l}}} \right)} \right)$ и ${{r}_{3}}\left( {{{T}_{2}},x\left( {{{\tau }_{l}}} \right)} \right)$, имеем

$\mathop {\max }\limits_{l = \overline {1,n} } \left| {{{T}_{2}}\left( {x\left( {{{\tau }_{l}}} \right)} \right) - T_{2}^{n}\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right| \leqslant M\left[ {{{{\left\| {\operatorname{grad} f} \right\|}}_{\infty }}\sqrt {R\left( n \right)} + \int\limits_0^{\sqrt {R\left( n \right)} + R\left( n \right)} {\frac{{\omega (\operatorname{grad} f,t)}}{t}dt} } \right].$

В итоге, принимая во внимание построенные квадратурные формулы для интегралов ${{T}_{1}}\left( x \right)$, ${{T}_{2}}\left( x \right)$ и оценки их погрешностей, получаем, что выражение

в опорных точках $x\left( {{{\tau }_{l}}} \right)$, $l = \overline {1,n} $, является квадратурной формулой для интеграла $\left( {Tf} \right)\left( x \right)$, причем, учитывая соотношение $R\left( n \right)\sim \frac{1}{n}$, имеем

$\mathop {\max }\limits_{l = \overline {1,n} } \left| {\left( {Tf} \right)\left( {x\left( {{{\tau }_{l}}} \right)} \right) - {{{\left( {Tf} \right)}}^{n}}\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right| \leqslant M\left[ {\frac{{{{{\left\| {\operatorname{grad} f} \right\|}}_{\infty }}}}{{\sqrt n }} + \int\limits_0^{1/\sqrt n } {\frac{{\omega (\operatorname{grad} f,t)}}{t}dt} } \right].$

В результате, принимая во внимание построенные квадратурные формулы для интегралов $\left( {Kf} \right)\left( x \right)$, $\left( {Tf} \right)\left( x \right)$ и оценки их погрешностей, получаем доказательство теоремы.

Замечание 1. Отметим, что методом построения квадратурной формулы для интеграла ${{T}_{2}}\left( x \right)$ можно построить квадратурную формулу и для других сингулярных интегралов по кривой Ляпунова.

Замечание 2. Данный метод для построения квадратурной формулы для сингулярного интеграла в отличие от других известных методов (см., например, [15]–[18]) обладает тем преимуществом, что очень простым способом можно вычислить коэффициенты этой квадратурной формулы.

Замечание 3. Как видно, если $f \equiv {\text{const}}$, то ${{\left( {Tf} \right)}^{n}}\left( {x\left( {{{\tau }_{l}}} \right)} \right) = 0$  $\forall \;l = \overline {1,n} $, и по теореме Гаусса (см. [12, с. 452])

$\int\limits_L {\frac{{\left( {x - y,n\left( y \right)} \right)}}{{{{{\left| {x - y} \right|}}^{2}}}}} d{{L}_{y}} = - \pi ,\quad x \in L,$
а значит, $\left( {Tf} \right)\left( x \right) = 0$, $x \in L$. Следовательно, в классе постоянных функций $f$ выполняется равенство
${{\left( {Tf} \right)}^{n}}\left( {x\left( {{{\tau }_{l}}} \right)} \right) = \left( {Tf} \right)\left( {x\left( {{{\tau }_{l}}} \right)} \right) = 0\quad \forall l = \overline {1,n} ,$
т.е. построенная квадратурная формула для нормальной производной логарифмического потенциала двойного слоя является эффективным.

3. ОБОСНОВАНИЕ МЕТОДА КОЛЛОКАЦИИ

Пусть ${{C}^{n}}$ – пространство $n$-мерных векторов ${{z}^{n}} = {{(z_{1}^{n},\; \ldots ,\;z_{n}^{n})}^{{\text{т}}}}$, $z_{l}^{n} \in C$, $l = \overline {1,n} $, с нормой $\left\| {{{z}^{n}}} \right\| = \mathop {\max }\limits_{l = \overline {1,n} } \left| {z_{l}^{n}} \right|$, где запись “${{a}^{{\text{т}}}}$” означает транспонировку вектора $a$. Используя квадратурные формулы (2.2) и (2.3), интегральное уравнение (1.4) заменяем системой алгебраических уравнений относительно $z_{l}^{n}$ – приближенных значений $\rho \left( {x\left( {{{\tau }_{l}}} \right)} \right)$, $l = \overline {1,n} $, которую запишем в виде

(3.1)
$({{I}^{n}} + {{A}^{n}}){{z}^{n}} = {{B}^{n}}{{f}^{n}},$
где ${{I}^{n}}$ – единичный оператор на пространстве ${{C}^{n}}$, ${{f}^{n}} = {{p}^{n}}f$, а ${{p}^{n}}:C\left( L \right) \to {{C}^{n}}$ – линейный ограниченный оператор, определяемый формулой
${{p}^{n}}f = {{\left( {f\left( {x\left( {{{\tau }_{1}}} \right)} \right),\; \ldots ,\;f\left( {x\left( {{{\tau }_{n}}} \right)} \right)} \right)}^{{\text{т}}}}$
и называемый оператором простого сноса.

Теорема 3. Пусть $f$ – непрерывно дифференцируемая функция на $L$ и

$\int\limits_0^d {\frac{{\omega (\operatorname{grad} f,t)}}{t}dt < \infty } .$
Тогда уравнения (1.4) и (3.1) имеют единственные решения ${{\rho }_{*}} \in C\left( L \right)$ и $z_{*}^{n} \in {{C}^{n}}$ $\left( {n \geqslant {{n}_{0}}} \right)$ соответственно, и $\left\| {z_{*}^{n} - {{p}^{n}}{{\rho }_{*}}} \right\| \to 0$ при $n \to \infty $ с оценкой скорости сходимости

$\left\| {z_{*}^{n} - {{p}^{n}}{{\rho }_{*}}} \right\| \leqslant M\left[ {\omega \left( {\operatorname{grad} f,1{\text{/}}n} \right) + \frac{{{{{\left\| f \right\|}}_{\infty }} + {{{\left\| {\operatorname{grad} f} \right\|}}_{\infty }}}}{{\sqrt n }} + \int\limits_0^{1/\sqrt n } {\frac{{\omega \left( {\operatorname{grad} f,t} \right)}}{t}dt} } \right].$

Доказательство. Отметим, что здесь мы будем пользоваться теоремой Г.М. Вайникко о сходимости для линейных операторных уравнений (см. [19]), при этом обозначения и необходимые определения и предложения возьмем из [19]. Теперь проверим выполнение условий теоремы 4.2 из [19]. В [2] доказано, что ${\text{Ker}}\left( {I + A} \right) = \left\{ 0 \right\}$, где $I$ – единичный оператор на пространстве $C\left( L \right)$. Кроме того, операторы ${{I}^{n}} + {{A}^{n}}$ фредгольмовы с нулевым индексом и операторы ${{p}^{n}}:C\left( L \right) \to {{C}^{n}}$ линейны и ограничены. Принимая во внимание способ разбиения кривой $L$ на элементарные части, получаем, что

$\mathop {\lim }\limits_{n \to \infty } \left\| {{{p}^{n}}\varphi } \right\| = \mathop {\lim }\limits_{n \to \infty } \mathop {\max }\limits_{l = \overline {1,n} } \left| {\varphi \left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right| = \mathop {\max }\limits_{x \in L} \left| {\varphi \left( x \right)} \right| = {{\left\| \varphi \right\|}_{\infty }}\quad \forall \;\varphi \in C\left( L \right).$

Следовательно, система операторов простого сноса $P = \{ {{p}^{n}}\} $ является связывающей для пространств $C\left( L \right)$ и ${{C}^{n}}$. Тогда из теоремы 2 получаем, что по определению 1.1 из [19] ${{B}^{n}}{{f}^{n}}\mathop \to \limits^P Bf$. Кроме того, из теоремы 1 получаем, что по определению 2.1 из [19] ${{I}^{n}} + {{A}^{n}}\mathop \to \limits^{PP} I + A$. Так как по определению 3.2 из [19] ${{I}^{n}} \to I$ устойчиво, то по предложению 3.5 и по определению 3.3 из [19] осталось проверить условие компактности, которое, ввиду предложения 1.1 из [19], равносильно условию: $\forall \{ {{z}^{n}}\} $, ${{z}^{n}} \in {{C}^{n}}$, $\left\| {{{z}^{n}}} \right\| \leqslant M$ существует относительно компактная последовательность $\{ {{A}_{n}}{{z}^{n}}\} \subset C\left( L \right)$ такая, что

$\left\| {{{A}^{n}}{{z}^{n}} - {{p}^{n}}\left( {{{A}_{n}}{{z}^{n}}} \right)} \right\| \to 0\quad {\text{при}}\quad n \to \infty .$

В качестве $\{ {{A}_{n}}{{z}^{n}}\} $ выберем последовательность

$\left( {{{A}_{n}}{{z}^{n}}} \right)\left( x \right) = \left( {{{{\tilde {K}}}_{n}}{{z}^{n}}} \right)\left( x \right) - i\eta \left( {{{S}_{n}}{{z}^{n}}} \right)\left( x \right),$
где

$\left( {{{S}_{n}}{{z}^{n}}} \right)\left( x \right) = 2\sum\limits_{j = 1}^n {z_{j}^{n}\int\limits_{{{L}_{j}}} {\Phi \left( {x,y} \right)d{{L}_{y}},} } \quad \left( {{{{\tilde {K}}}_{n}}{{z}^{n}}} \right)\left( x \right) = 2\sum\limits_{j = 1}^n {z_{j}^{n}\int\limits_{{{L}_{j}}} {\frac{{\partial \Phi \left( {x,y} \right)}}{{\partial{ \vec {n}}\left( x \right)}}d{{L}_{y}},\quad x \in L} } .$

Возьмем любые точки $x{\text{'}},x{\text{''}} \in L$ такие, что $\left| {x{\text{'}} - x{\text{''}}} \right| = \delta < \min \left\{ {1,d} \right\}{\text{/}}2$. Очевидно, что

$\left| {\left( {{{S}_{n}}{{z}^{n}}} \right)\left( {x{\text{'}}} \right) - \left( {S{{z}^{n}}} \right)\left( {x{\text{''}}} \right)} \right| \leqslant 2\left\| {{{z}^{n}}} \right\|\int\limits_L {\left| {\Phi \left( {x{\text{'}},y} \right) - \Phi \left( {x{\text{''}},y} \right)} \right|} d{{L}_{y}} \leqslant $
$ \leqslant \;2\left\| {{{z}^{n}}} \right\|\int\limits_{{{L}_{{\delta /2}}}\left( {x{\text{'}}} \right)} {\left| {\Phi \left( {x{\text{'}},y} \right)} \right|} d{{L}_{y}} + 2\left\| {{{z}^{n}}} \right\|\int\limits_{{{L}_{{\delta /2}}}\left( {x{\text{''}}} \right)} {\left| {\Phi \left( {x{\text{''}},y} \right)} \right|} d{{L}_{y}} + $
$ + \;2\left\| {{{z}^{n}}} \right\|\int\limits_{{{L}_{{\delta /2}}}\left( {x{\text{'}}} \right)} {\left| {\Phi \left( {x{\text{''}},y} \right)} \right|} d{{L}_{y}} + 2\left\| {{{z}^{n}}} \right\|\int\limits_{{{L}_{{\delta /2}}}\left( {x{\text{''}}} \right)} {\left| {\Phi \left( {x{\text{'}},y} \right)} \right|} d{{L}_{y}} + $
$ + \;2\left\| {{{z}^{n}}} \right\|\int\limits_{{{L}_{d}}\left( {x{\text{'}}} \right)\backslash \left( {{{L}_{{\delta /2}}}\left( {x{\text{'}}} \right) \cup {{L}_{{\delta /2}}}\left( {x{\text{''}}} \right)} \right)} {\left| {\Phi \left( {x{\text{'}},y} \right) - \Phi \left( {x{\text{''}},y} \right)} \right|} d{{L}_{y}} + 2\left\| {{{z}^{n}}} \right\|\int\limits_{L\backslash {{L}_{d}}\left( {x{\text{'}}} \right)} {\left| {\Phi \left( {x{\text{'}},y} \right) - \Phi \left( {x{\text{''}},y} \right)} \right|} d{{L}_{y}}.$
Используя формулу вычисления криволинейного интеграла, имеем
$\int\limits_{{{L}_{{\delta /2}}}\left( {x{\text{'}}} \right)} {\left| {\Phi \left( {x{\kern 1pt} ',y} \right)} \right|} d{{L}_{y}} = \frac{1}{{2\pi }}\int\limits_{{{L}_{{\delta /2}}}\left( {x{\text{'}}} \right)} {\ln \frac{1}{{\left| {x{\text{'}} - y} \right|}}} d{{L}_{y}} \leqslant M\int\limits_0^{\delta /2} {\left| {\ln t} \right|dt} \leqslant M\delta \left| {\ln \delta } \right|,$
$\int\limits_{{{L}_{{\delta /2}}}\left( {x{\text{''}}} \right)} {\left| {\Phi \left( {x{\text{''}},y} \right)} \right|} d{{L}_{y}} \leqslant M\delta \left| {\ln \delta } \right|,$
$\int\limits_{{{L}_{{\delta /2}}}\left( {x{\text{'}}} \right)} {\left| {\Phi \left( {x{\text{''}},y} \right)} \right|} d{{L}_{y}} = \frac{1}{{2\pi }}\int\limits_{{{L}_{{\delta /2}}}\left( {x{\text{'}}} \right)} {\ln \frac{1}{{\left| {x{\text{''}} - y} \right|}}} d{{L}_{y}} \leqslant \frac{1}{{2\pi }}\int\limits_{{{L}_{{\delta /2}}}\left( {x{\text{'}}} \right)} {\ln \frac{1}{{\left| {x{\text{'}} - y} \right|}}} d{{L}_{y}} \leqslant M\delta \left| {\ln \delta } \right|$
и

$\int\limits_{{{L}_{{\delta /2}}}\left( {x{\text{''}}} \right)} {\left| {\Phi \left( {x{\text{'}},y} \right)} \right|} d{{L}_{y}} \leqslant M\delta \left| {\ln \delta } \right|.$

Так как для любого $y \in {{L}_{d}}(x{\text{'}}){{\backslash }}({{L}_{{\delta /2}}}(x{\text{'}}) \cup {{L}_{{\delta /2}}}(x{\text{''}}))$

$\left| {x{\text{'}} - y} \right| \leqslant \left| {x{\text{'}} - x{\text{''}}} \right| + \left| {x{\text{''}} - y} \right| \leqslant 3\left| {x{\text{''}} - y} \right|,$
$\left| {x{\text{''}} - y} \right| \leqslant 3\left| {x{\text{'}} - y} \right|,$
то
$\left| {\Phi \left( {x{\text{'}},y} \right) - \Phi \left( {x{\text{''}},y} \right)} \right| = \frac{1}{{2\pi }}\left| {\ln \frac{{\left| {x{\text{''}} - y} \right|}}{{\left| {x' - y} \right|}}} \right| = \frac{1}{{2\pi }}\left| {\ln \left( {1 + \frac{{\left| {x{\text{''}} - y} \right| - \left| {x{\text{'}} - y} \right|}}{{\left| {x{\text{'}} - y} \right|}}} \right)} \right| \leqslant $
$ \leqslant \;M\frac{{\left| {x{\text{''}} - y} \right| - \left| {x{\text{'}} - y} \right|}}{{\left| {x{\text{'}} - y} \right|}} \leqslant M\frac{{\left| {x{\text{'}} - x{\text{''}}} \right|}}{{\left| {x' - y} \right|}} \leqslant \frac{{M\delta }}{{\left| {x{\text{'}} - y} \right|}}\quad \forall y \in {{L}_{d}}(x{\text{'}}){{\backslash }}({{L}_{{\delta /2}}}(x{\text{'}}) \cup {{L}_{{\delta /2}}}(x{\text{''}})),$
а значит,
$\int\limits_{{{L}_{d}}\left( {x{\text{'}}} \right)\backslash \left( {{{L}_{{\delta /2}}}\left( {x{\text{'}}} \right) \cup {{L}_{{\delta /2}}}\left( {x{\text{''}}} \right)} \right)} {\left| {\Phi \left( {x{\text{'}},y} \right) - \Phi \left( {x{\text{''}},y} \right)} \right|} d{{L}_{y}} \leqslant M\delta \int\limits_{{{L}_{d}}\left( {x{\text{'}}} \right)\backslash \left( {{{L}_{{\delta /2}}}\left( {x{\text{'}}} \right) \cup {{L}_{{\delta /2}}}\left( {x{\text{''}}} \right)} \right)} {\frac{{d{{L}_{y}}}}{{\left| {x{\text{'}} - y} \right|}}} \leqslant M\delta \int\limits_\delta ^d {\frac{{dt}}{t}} \leqslant M\delta \left| {\ln \delta } \right|.$
Очевидно, что
$\int\limits_{L\backslash {{L}_{d}}\left( {x{\text{'}}} \right)} {\left| {\Phi \left( {x{\text{'}},y} \right) - \Phi \left( {x{\text{''}},y} \right)} \right|} d{{L}_{y}} \leqslant M\delta .$
Суммируя выше полученные оценки, находим

$\left| {\left( {{{S}_{n}}{{z}^{n}}} \right)\left( {x{\text{'}}} \right) - \left( {{{S}_{n}}{{z}^{n}}} \right)\left( {x{\text{''}}} \right)} \right| \leqslant M\delta \left| {\ln \delta } \right|.$

Так как

$\frac{{\partial \Phi \left( {x,y} \right)}}{{\partial{ \vec {n}}\left( x \right)}} = \frac{1}{{2\pi }}\frac{{\left( {y - x,n\left( x \right)} \right)}}{{{{{\left| {x - y} \right|}}^{2}}}},$
тогда, поступая точно также, как и в доказательстве теоремы 3.1 из [20], нетрудно показать, что

$\left| {\left( {{{{\tilde {K}}}_{n}}{{z}^{n}}} \right)\left( {x{\text{'}}} \right) - \left( {{{{\tilde {K}}}_{n}}{{z}^{n}}} \right)\left( {x{\text{''}}} \right)} \right| \leqslant M\delta \left| {\ln \delta } \right|.$

В результате

(3.2)
$\left| {\left( {{{A}_{n}}{{z}^{n}}} \right)\left( {x{\text{'}}} \right) - \left( {{{A}_{n}}{{z}^{n}}} \right)\left( {x{\text{''}}} \right)} \right| \leqslant M\delta \left| {\ln \delta } \right|,$
а значит, $\{ {{A}_{n}}{{z}^{n}}\} \subset C\left( L \right)$. Относительная компактность последовательности $\{ {{A}_{n}}{{z}^{n}}\} $ следует из теоремы Арцеля. Действительно, равномерная ограниченность непосредственно вытекает из условия $\left\| {{{z}^{n}}} \right\| \leqslant M$, а равностепенная непрерывность следует из оценки (3.2). Кроме того, поступая точно также, как и в [13], получаем, что
$\left\| {{{A}^{n}}{{z}^{n}} - {{p}^{n}}\left( {{{A}_{n}}{{z}^{n}}} \right)} \right\| \to 0\quad {\text{при}}\quad n \to \infty .$
Тогда, применяя теорему 4.2 из [19], получаем, что уравнения (1.4) и (3.1) имеют единственные решения ${{\rho }_{*}} \in C\left( L \right)$ и $z_{*}^{n} \in {{C}^{n}}$ ($n \geqslant {{n}_{0}}$) соответственно, причем
${{c}_{1}}{{\delta }_{n}} \leqslant \left\| {z_{*}^{n} - {{p}^{n}}{{\rho }_{*}}} \right\| \leqslant {{c}_{2}}{{\delta }_{n}},$
где

${{c}_{1}} = 1{\text{/}}\mathop {\sup }\limits_{n \geqslant {{n}_{0}}} \left\| {{{I}^{n}} + {{A}^{n}}} \right\| > 0,\quad {{c}_{2}} = \mathop {\sup }\limits_{n \geqslant {{n}_{0}}} \left\| {{{{({{I}^{n}} + {{A}^{n}})}}^{{ - 1}}}} \right\| < \infty ,$
${{\delta }_{n}} = \mathop {\max }\limits_{l = \overline {1,n} } \left| {{{\rho }_{*}}\left( {x\left( {{{\tau }_{l}}} \right)} \right) + \left( {{{A}^{n}}{{\rho }_{*}}} \right)\left( {x\left( {{{\tau }_{l}}} \right)} \right) - \left( {{{B}^{n}}f} \right)\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right|.$

Так как

${{\rho }_{*}}\left( {x\left( {{{\tau }_{l}}} \right)} \right) = \left( {Bf} \right)\left( {x\left( {{{\tau }_{l}}} \right)} \right) - \left( {A{{\rho }_{*}}} \right)\left( {x\left( {{{\tau }_{l}}} \right)} \right),$
то, принимая во внимание оценки погрешности квадратурных формул (2.2) и (2.3), имеем

$\begin{gathered} {{\delta }_{n}} = \mathop {\max }\limits_{l = \overline {1,n} } \left| {\left( {{{{\left( {A{{\rho }_{*}}} \right)}}^{n}}\left( {x\left( {{{\tau }_{l}}} \right)} \right) - \left( {A{{\rho }_{*}}} \right)\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right) + \left( {\left( {Bf} \right)\left( {x\left( {{{\tau }_{l}}} \right)} \right) - {{{\left( {Bf} \right)}}^{n}}\left( {x\left( {{{\tau }_{l}}} \right)} \right)} \right)} \right| \leqslant \\ \leqslant \;M\left( {\omega \left( {{{\rho }_{*}},1{\text{/}}n} \right) + {{{\left\| {{{\rho }_{*}}} \right\|}}_{\infty }}\frac{{\ln n}}{n} + \frac{{{{{\left\| f \right\|}}_{\infty }} + {{{\left\| {\operatorname{grad} f} \right\|}}_{\infty }}}}{{\sqrt n }} + \int\limits_0^{1/\sqrt n } {\frac{{\omega (\operatorname{grad} f,t)}}{t}dt} } \right). \\ \end{gathered} $

Так как ${{\rho }_{*}} = {{\left( {I + A} \right)}^{{ - 1}}}\left( {Bf} \right)$, то, учитывая следствие 1 из [10], находим

${{\left\| {{{\rho }_{*}}} \right\|}_{\infty }} \leqslant \left\| {{{{\left( {I + A} \right)}}^{{ - 1}}}} \right\|\left( {{{{\left\| {Tf} \right\|}}_{\infty }} + \left| \eta \right|{{{\left\| {Kf} \right\|}}_{\infty }} + {{{\left\| f \right\|}}_{\infty }}} \right) \leqslant M\left( {{{{\left\| f \right\|}}_{\infty }} + {{{\left\| {\operatorname{grad} f} \right\|}}_{\infty }} + \int\limits_0^{{\text{diam}}L} {\frac{{\omega \left( {\operatorname{grad} f,t} \right)}}{t}} dt} \right).$
Кроме того, очевидно, что
$\begin{gathered} \omega \left( {{{\rho }_{*}},1{\text{/}}n} \right) = \omega \left( {Bf - A{{\rho }_{*}},1{\text{/}}n} \right) \leqslant \omega \left( {Bf,1{\text{/}}n} \right) + \omega \left( {A{{\rho }_{*}},1{\text{/}}n} \right) \leqslant \omega \left( {Tf,1{\text{/}}n} \right) + \\ + \;\left( {1 + \left| \eta \right|} \right)\left( {\omega \left( {Kf,1{\text{/}}n} \right) + \omega \left( {f,1{\text{/}}n} \right)} \right) + \omega \left( {\tilde {K}{{\rho }_{*}},1{\text{/}}n} \right) + \left( {1 + \left| \eta \right|} \right)\omega \left( {S{{\rho }_{*}},1{\text{/}}n} \right). \\ \end{gathered} $
Тогда, принимая во внимание следствие 2 из [10] и неравенства (2.4),
$\omega \left( {Kf,1{\text{/}}n} \right) \leqslant M{{\left\| f \right\|}_{\infty }}\frac{{\ln n}}{n},\quad \omega \left( {S{{\rho }_{*}},1{\text{/}}n} \right) \leqslant M{{\left\| {{{\rho }_{*}}} \right\|}_{\infty }}\frac{{\ln n}}{n},\quad \omega \left( {\tilde {K}{{\rho }_{*}},1{\text{/}}n} \right) \leqslant M{{\left\| {{{\rho }_{*}}} \right\|}_{\infty }}\frac{{\ln n}}{n},$
находим, что
$\omega \left( {{{\rho }_{*}},1{\text{/}}n} \right) \leqslant M\left( {{{{\left\| f \right\|}}_{\infty }}\frac{{\ln n}}{n} + \omega \left( {\operatorname{grad} f,1{\text{/}}n} \right) + {\text{ }}\int\limits_o^{1/n} {\frac{{\omega \left( {\operatorname{grad} f,t} \right)}}{t}dt + } {\kern 1pt} \frac{1}{n}\int\limits_{1/n}^{{\text{diam}}L} {\frac{{\omega \left( {\operatorname{grad} f,t} \right)}}{{{{t}^{2}}}}dt} } \right).$
Так как (см. [21, с. 55])
$\int\limits_o^{1/n} {\frac{{\omega \left( {\operatorname{grad} f,t} \right)}}{t}dt + } {\kern 1pt} \frac{1}{n}\int\limits_{1/n}^{{\text{diam}}L} {\frac{{\omega \left( {\operatorname{grad} f,t} \right)}}{{{{t}^{2}}}}dt} \leqslant M\omega \left( {\operatorname{grad} f,1{\text{/}}n} \right),$
то

$\omega \left( {{{\rho }_{*}},1{\text{/}}n} \right) \leqslant M\left( {{{{\left\| f \right\|}}_{\infty }}\frac{{\ln n}}{n} + \omega \left( {\operatorname{grad} f,1{\text{/}}n} \right)} \right).$

В результате получаем

${{\delta }_{n}} \leqslant M\left( {\omega \left( {\operatorname{grad} f,1{\text{/}}n} \right) + \frac{{{{{\left\| f \right\|}}_{\infty }} + {{{\left\| {\operatorname{grad} f} \right\|}}_{\infty }}}}{{\sqrt n }} + \int\limits_0^{1/\sqrt n } {\frac{{\omega \left( {\operatorname{grad} f,t} \right)}}{t}dt} } \right).$
Теорема доказана.

Список литературы

  1. Колтон Д., Кресс Р. Методы интегральных уравнений в теории рассеяния. М.: Мир, 1987. 311 с.

  2. Burton A.J., Miller G.F. The application of integral equation methods to the numerical solution of some exterior boundary–value problems // Proceed. Royal Soc. London. 1971. V. A323. P. 201–220.

  3. Каширин А.А., Смагин С.И. О численном решении задач Дирихле для уравнения Гельмгольца методом потенциалов // Ж. вычисл. матем. и матем. физ. 2012. Т. 52. № 8. С. 1492–1505.

  4. Мусаев Б.И., Халилов Э.Г. О приближенном решении одного класса граничных интегральных уравнений методом коллокации // Тр. Института математики и механики АН Азербайджана. 1998. Т. 9 (17). С. 78–84.

  5. Colton D., Kress R. Iterative methods for solving the exterior Dirichlet problem for the Helmholtz equation with applications to the inverse scattering problem for low frequency acoustic waves // J. Math. Analys. Appl. 1980. V. 77. P. 60–72.

  6. Халилов Э.Г. Обоснование метода коллокации для одного класса поверхностных интегральных уравнений // Матем. заметки. 2020. Т. 107. № 4. С. 604–622.

  7. Kress R. Boundary integral equations in time-harmonic acoustic scattering // Math. Computer Model. 1991. V. 15. № 3–5. P. 229–243.

  8. Гюнтер Н.М. Теория потенциала и ее применение к основным задачам математической физики. М.: Гостехиздат, 1953. 415 с.

  9. Лифанов И.К. Метод сингулярных интегральных уравнений и численный эксперимент. М.: ТОО “Янус”, 1995. 521 с.

  10. Халилов Э.Г., Бахшалыева М.Н. О производной логарифмического потенциала двойного слоя // Вестник Томского государственного университета. Математика и механ. 2019. № 62. С. 38–54.

  11. Мусхелешвили Н.И. Сингулярные интегральные уравнения. М.: Физматлит, 1962. 599 с.

  12. Владимиров В.С. Уравнения математической физики. М.: Наука, 1976. 527 с.

  13. Khalilov E.H., Bakhshaliyeva M.N. Quadrature formulas for simple and double layer logarithmic potentials // Proceed. IMM of NAS of Azerbaijan. 2019. V. 45. № 1. P. 155–162.

  14. Кустов Ю.А., Мусаев Б.И. Кубатурная формула для двумерного сингулярного интеграла и ее приложения // Деп. в ВИНИТИ. № 4281–81. 60 с.

  15. Алиев Р.А. Новый конструктивный метод решения сингулярных интегральных уравнений // Матем. заметки. 2006. Т. 79. № 6. С. 803–824.

  16. Бесаева З.В., Хубежты Ш.С. Приближенное решение сингулярного интегрального уравнения с применением рядов Чебышева // Владикавказский матем. ж. 2016. Т. 18. № 4. С. 15–22.

  17. Шешко М.А., Шешко С.М. Сингулярное интегральное уравнение с ядром Коши на сложном контуре // Дифференц. ур-ния. 2011. Т. 47. № 9. С. 1331–1343.

  18. Li-xia Cao. Regularization method for complete singular integral equation with Hilbert kernel on open arcs // Proc. of the 2nd Internat. Conf. Systems Engineer. Model. (ICSEM-13). 2013. P. 0997–01000.

  19. Вайникко Г.М. Регулярная сходимость операторов и приближенное решение уравнений // Итоги науки и техн. Матем. анализ. 1979. Т. 16. С. 5–53.

  20. Халилов Э.Г. Обоснование метода коллокации для интегрального уравнения смешанной краевой задачи для уравнения Гельмгольца // Ж. вычисл. матем. и матем. физ. 2016. Т. 56. № 7. С. 1340–1348.

  21. Гусейнов А.И., Мухтаров Х.Ш. Введение в теорию нелинейных сингулярных интегральных уравнений. М.: Наука, 1980. 416 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал