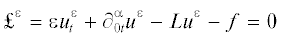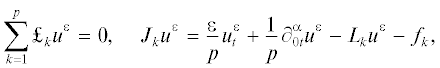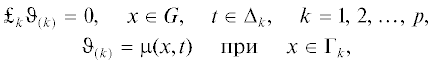Журнал вычислительной математики и математической физики, 2021, T. 61, № 7, стр. 1082-1100

Локально-одномерная схема для первой начально-краевой задачи для многомерного уравнения конвекции–диффузии дробного порядка

А. А. Алиханов^1, *, М. Х. Бештоков^2, **, М. Х. Шхануков-Лафишев^2, ***

¹ ФГАОУ ВО “Северо-Кавказский федеральный университет”
355017 Ставрополь, ул. Пушкина, 1, Россия

² ИПМатем. и автоматизации, КБНЦ РАН
360004 Нальчик, ул. Шортанова, 89а, Россия

^* E-mail: alikhanov-tom@yandex.ru
^** E-mail: beshtokov-murat@yandex.ru
^*** E-mail: lafishev@yandex.ru

Поступила в редакцию 14.09.2020
После доработки 26.11.2020
Принята к публикации 11.03.2021

DOI: 10.31857/S0044466921070024

Полный текст (PDF)

Аннотация

Исследуется первая краевая задача для уравнения конвекции–диффузии дробного порядка. Построена локально-одномерная разностная схема. С помощью принципа максимума получена априорная оценка в равномерной метрике. Доказаны устойчивость и сходимость рассматриваемой разностной схемы. Построен алгоритм приближенного решения локально-одномерной разностной схемы. Проведены численные расчеты, иллюстрирующие полученные теоретические результаты в работе. Библ. 32. Табл. 2.

Ключевые слова: дифференциальное уравнение в частных производных, уравнение конвекции–диффузии, производная дробного порядка, дробная производная по времени в смысле Капуто, локально-одномерная разностная схема, устойчивость и сходимость разностных схем.

ВВЕДЕНИЕ

В последние годы возрос интерес к исследованию дифференциальных уравнений дробного порядка, в которых неизвестная функция содержится под знаком производной дробного порядка. Интегралы и производные нецелого порядка и дробные интегро-дифференциальные уравнения находят множество применений в современных исследованиях в теоретической физике, механике и прикладной математике. Для описания структуры неупорядоченных сред и протекающих в них процессов широко используется теория фракталов (см. [1]–[17]). Примерами неупорядоченных сред являются пористые тела. При этом фракталами могут быть поровое пространство, скелет породы, поверхность скелета породы и т.д. В случае, когда пространство представляет собой фрактал с размерностью Хаусдорфа–Безиковича ${{d}_{f}}$, погруженный в сплошную среду с размерностью $d$ ($d \geqslant {{d}_{f}}$, $d = 2,\;3$), для описания движения примеси в потоке однородной среды используется дифференциальное уравнение дробного порядка (см. [18]).

Перенос, описываемый операторами с дробными производными, на больших расстояниях от источника приводит к совершенно иному поведению относительно малых концентраций по сравнению с классической диффузией. Эти малые концентрации, или “далекие хвосты распределений”, при дробной диффузии подчинены степенному закону убывания, и их существование может заставить пересмотреть существующие ранее представления о безопасности, базирующиеся на представлениях об экспоненциальной скорости затухания (см. [19], [20]).

В [21, с. 199] и [22] дается описание геометрии облаков, размеры которых заключены в широком диапазоне от 1 до $1.2 \times {{10}^{6}}$ км². Выяснено, что периметр облака связан с фрактальной размерностью облака $D = 1.35 \pm 0.05$. Заметим, что порядок дробной производной связан с размерностью фрактала (см. [3], [4], [14]).

В [23] найдена связь между порядком дробной производной и фрактальной размерностью.

В [24] рассматривается локально-одномерная схема для решения линейных и квазилинейных уравнений параболического типа с любым числом $р$ пространственных переменных, пригодная для произвольной области $G$. Доказана равномерная устойчивость локально-одномерной схемы по правой части, краевым и начальным данным. Показано, что локально-одномерные схемы дают точность $O({{h}^{2}} + \tau ).$

В [25] рассмотрена локально-одномерная схема для уравнения теплопроводности с дробной по времени производной без учета движения самой среды. Построена экономичная аддитивная схема в области сложной формы. Показано, что построенная схема обладает свойством суммарной аппроксимации $\psi = O(h_{\alpha }^{2} + \tau )$ в регулярных узлах, в нерегулярных узлах $\psi = O(1)$, где ${{h}_{\alpha }}$ и $\tau $ – шаги сетки по направлению ${{x}_{\alpha }}$ и времени $t$.

Построению локально-одномерных схем для численного решения различных краевых задач для уравнения параболического типа c дробной производной по времени в многомерной области посвящены работы [5], [25]–[27], в которых априорные оценки были получены лишь при условии, когда $\tfrac{1}{2} < \alpha < 1$.

В настоящей работе рассмотрено построение локально-одномерной (экономичной) разностной схемы для численного решения первой краевой задачи для уравнения переноса пассивных примесей дробного порядка в многомерном случае, основная идея которого состоит в сведении перехода со слоя на слой к последовательному решению ряда одномерных задач по каждому из координатных направлений. Построена локально-одномерная разностная схема. С помощью принципа максимума получена априорная оценка для решения задачи в разностной трактовке, откуда следует равномерная сходимость локально-одномерной схемы в классе достаточно гладких решений при $0 < \alpha < 1$, где $\alpha $ – порядок дробной производной. Построен алгоритм решения локально-одномерной разностной схемы. Проведены численные эксперименты.

1. ПОСТАНОВКА ПЕРВОЙ НАЧАЛЬНО-КРАЕВОЙ ЗАДАЧИ

В замкнутом цилиндре ${{\bar {Q}}_{T}} = \bar {G} \times [0 \leqslant t \leqslant T]$, основанием которого является $p$-мерный прямоугольный параллелепипед $G = {\text{\{ }}x = ({{x}_{1}},\; \ldots ,\;{{x}_{p}}):0 < {{x}_{k}} < {{l}_{k}},\;k = 1,\;2,\; \ldots ,\;p{\text{\} }}$ с границей $\Gamma $, $\bar {G} = G \cup \Gamma $, рассмотрим следующую начально-краевую задачу:

(1.1)

$\partial _{{0t}}^{\alpha }u = Lu + f(x,t),\quad (x,t) \in {{Q}_{T}},$

(1.2)

${{\left. u \right|}_{{\text{Г}}}} = \mu (x,t),\quad 0 \leqslant t \leqslant T,$

(1.3)

$u(x,0) = {{u}_{0}}(x),\quad x \in \bar {G},\quad \bar {G} = G \cup \Gamma ,$

где

$\partial _{{0t}}^{\alpha }u = \tfrac{1}{{{\text{Г}}(1 - \alpha )}}\int\limits_0^t {\tfrac{{\partial u(x,\eta )}}{{\partial \eta }}} \tfrac{{d\eta }}{{{{{(t - \eta )}}^{\alpha }}}},\quad 0 < \alpha < 1,$

есть дробная производная Капуто порядка $\alpha $,

$L = \sum\limits_{k = 1}^p {{{L}_{k}}} ,\quad {{L}_{k}}u = \frac{\partial }{{\partial {{x}_{k}}}}\left( {{{\Theta }_{k}}(x,t)\frac{{\partial u}}{{\partial {{x}_{k}}}}} \right) + {{r}_{k}}(x,t)\frac{{\partial u}}{{\partial {{x}_{k}}}} - {{q}_{k}}(x,t)u,\quad k = 1,\;2,\; \ldots ,\;p,$

$u(x,t)$ – концентрация примеси в точке $x$ в момент времени $t$,

${{\Theta }_{k}}(x,t)$ – коэффициент турбулентной диффузии по направлениям ${{x}_{k}}$,

${{r}_{k}}(x,t)$ – компоненты вектора скорости воздушных потоков по направлениям ${{x}_{k}}$,

$0 < {{c}_{0}} \leqslant {{\Theta }_{k}}(x,t),\quad {{q}_{k}}(x,t) \leqslant {{c}_{1}},\quad \left| {{{r}_{k}}(x,t)} \right| \leqslant {{c}_{2}},$

${{c}_{0}},{{c}_{1}},{{c}_{2}} - {\text{положительные}}\;{\text{постоянные}},\quad {{Q}_{T}} = G \times (0 < t \leqslant T],\quad k = 1,\;2,\; \ldots ,\;p,$

$x = ({{x}_{1}},\; \ldots ,\;{{x}_{p}}),\quad x{\text{'}} = ({{x}_{1}},\; \ldots ,\;{{x}_{{k - 1}}},{{x}_{{k + 1}}},\; \ldots ,\;{{x}_{p}}).$

В дальнейшем будем предполагать, что коэффициенты уравнения и граничных условий (1.1)–(1.3) удовлетворяют необходимым по ходу изложения условиям, обеспечивающим нужную гладкость решения $u(x,t)$ в цилиндре ${{Q}_{T}}$.

Локально-одномерные разностные схемы для уравнения диффузии дробного порядка в многомерной области для случая, когда оператор $Lu = \sum\nolimits_{k = 1}^p {{{L}_{k}}} u,$ ${{L}_{k}}u = \tfrac{{\partial {{u}^{2}}}}{{\partial x_{k}^{2}}}$, рассмотрены в [5], а для случая, когда оператор ${{L}_{k}}u = \tfrac{\partial }{{\partial {{x}_{k}}}}\left( {{{k}_{k}}\tfrac{{\partial u}}{{\partial {{x}_{k}}}}} \right)$ с краевыми условиями III рода, рассмотрены в [27].

В той же области вместо задачи (1.1)–(1.3) рассмотрим следующую задачу с малым параметром $\varepsilon $:

(1.4)

$\varepsilon u_{t}^{\varepsilon } + \partial _{{0t}}^{\alpha }{{u}^{\varepsilon }} = L{{u}^{\varepsilon }} + f(x,t),\quad (x,t) \in {{Q}_{T}},$

(1.5)

${{\left. {{{u}^{\varepsilon }}} \right|}_{{\text{Г}}}} = \mu (x,t),\quad 0 \leqslant t \leqslant T,$

(1.6)

${{u}^{\varepsilon }}(x,0) = {{u}_{0}}(x),\quad x \in \bar {G},$

где $\varepsilon = {\text{const}} > 0.$

Так как при $t = 0$ начальные условия для уравнения (1.1) и (1.4) совпадают, то в окрестности $t = 0$ у производной $u_{t}^{\varepsilon }$ не возникает особенности типа пограничного слоя (см. [28], [29, с. 10]).

Покажем, что ${{u}^{\varepsilon }} \to u$ в некоторой норме при $\varepsilon \to 0$. Обозначим $\tilde {z} = {{u}^{\varepsilon }} - u$ и подставим ${{u}^{\varepsilon }} = \tilde {z} + u$ в задачу (1.4)–(1.6). Тогда получим

(1.7)

$\varepsilon \mathop {\tilde {z}}\nolimits_t + \partial _{{0t}}^{\alpha }\tilde {z} = L\tilde {z} + \tilde {f}(x,t),\quad (x,t) \in {{Q}_{T}},$

(1.8)

${{\left. {\tilde {z}} \right|}_{{\text{Г}}}} = 0,\quad 0 \leqslant t \leqslant T,$

(1.9)

$\tilde {z}(x,0) = 0,\quad x \in \bar {G},\quad \bar {G} = G + {\text{Г}},$

где $\tilde {f}(x,t) = - \varepsilon \tfrac{{\partial u}}{{\partial t}}$.

Для получения априорной оценки воспользуемся методом энергетических неравенств. Умножим уравнение (1.7) скалярно на $\tilde {z}$ и получим энергетическое тождество

(1.10)

$\left( {\varepsilon \frac{{\partial{ \tilde {z}}}}{{\partial t}},\tilde {z}} \right) + \left( {\partial _{{0t}}^{\alpha }\tilde {z},\tilde {z}} \right) = \left( {\sum\limits_{k = 1}^p {\frac{\partial }{{\partial {{x}_{k}}}}} \left( {{{\Theta }_{k}}(x,t)\frac{{\partial{ \tilde {z}}}}{{\partial {{x}_{k}}}}} \right),\tilde {z}} \right) + \left( {\sum\limits_{k = 1}^p {{{r}_{k}}} (x,t)\frac{{\partial{ \tilde {z}}}}{{\partial {{x}_{k}}}},\tilde {z}} \right) - \left( {\sum\limits_{k = 1}^p {{{q}_{k}}} (x,t)\tilde {z},\tilde {z}) + (\tilde {f}(x,t),\tilde {z}} \right).$

Будем пользоваться скалярным произведением и нормой

$(u,{v}) = \int\limits_G u {v}dx,\quad (u,u) = \left\| u \right\|_{0}^{2},\quad \left\| u \right\|_{{{{L}_{2}}(0,{{l}_{k}})}}^{2} = \int\limits_0^{{{l}_{k}}} {{{u}^{2}}} (x,t)d{{x}_{k}}.$

Далее через ${{M}_{i}}$, $i = 1,\;2,\; \ldots $, обозначаются положительные постоянные, зависящие только от входных данных рассматриваемой задачи.

Используя лемму 1 из [30], преобразуем интегралы, входящие в тождество (1.10):

(1.11)

$\left( {\varepsilon \frac{{\partial{ \tilde {z}}}}{{\partial t}},\tilde {z}} \right) = \frac{\varepsilon }{2}\frac{\partial }{{\partial t}}\left\| {\tilde {z}} \right\|_{0}^{2},$

(1.12)

$\begin{gathered} \left( {\partial _{{0t}}^{\alpha }\tilde {z},\tilde {z}} \right) = \left( {\frac{1}{p}\sum\limits_{k = 1}^p {\partial _{{0t}}^{\alpha }} \tilde {z},\tilde {z}} \right) = \frac{1}{p}\int\limits_G {\sum\limits_{k = 1}^p {\tilde {z}} } \partial _{{0t}}^{\alpha }\tilde {z}dx = \frac{1}{p}\sum\limits_{k = 1}^p {\int\limits_G {\tilde {z}} \partial _{{0t}}^{\alpha }\tilde {z}dx} = \frac{1}{p}\sum\limits_{k = 1}^p {\int\limits_{G'} {\left( {\int\limits_0^{{{l}_{k}}} {\tilde {z}} \partial _{{0t}}^{\alpha }\tilde {z}d{{x}_{k}}} \right)} } dx{\text{'}} \geqslant \\ \geqslant \frac{1}{{2p}}\sum\limits_{k = 1}^p {\int\limits_{G'} {\left( {\int\limits_0^{{{l}_{k}}} {\partial _{{0t}}^{\alpha }} \mathop {\tilde {z}}\nolimits^2 d{{x}_{k}}} \right)} } dx{\text{'}} = \frac{1}{{2p}}\sum\limits_{k = 1}^p {\int\limits_{G'} {\partial _{{0t}}^{\alpha }} } \left\| {\tilde {z}} \right\|_{{{{L}_{2}}(0,{{l}_{k}})}}^{2}dx{\text{'}} = \frac{1}{{2p}}\sum\limits_{k = 1}^p {\partial _{{0t}}^{\alpha }} \left\| {\tilde {z}} \right\|_{0}^{2} = \frac{1}{2}\partial _{{0t}}^{\alpha }\left\| {\tilde {z}} \right\|_{0}^{2}, \\ \end{gathered} $

(1.13)

$\begin{gathered} \left( {\sum\limits_{k = 1}^p {\frac{\partial }{{\partial {{x}_{k}}}}\left( {{{\Theta }_{k}}(x,t)\frac{{\partial{ \tilde {z}}}}{{\partial {{x}_{k}}}}} \right)} ,\tilde {z}} \right) = \sum\limits_{k = 1}^p {\int\limits_{G'} {{{\Theta }_{k}}} } (x,t)\tilde {z}\left. {\frac{{\partial{ \tilde {z}}}}{{\partial {{x}_{k}}}}} \right|_{0}^{{{{l}_{k}}}}dx{\text{'}} - \sum\limits_{k = 1}^p {\int\limits_G {{{\Theta }_{k}}} } (x,t){{\left( {\frac{{\partial{ \tilde {z}}}}{{\partial {{x}_{k}}}}} \right)}^{2}}dx = \\ = - \sum\limits_{k = 1}^p {\int\limits_G {{{\Theta }_{k}}} } (x,t){{\left( {\frac{{\partial{ \tilde {z}}}}{{\partial {{x}_{k}}}}} \right)}^{2}}dx \leqslant - {{c}_{0}}\left\| {{{{\tilde {z}}}_{x}}} \right\|_{0}^{2}, \\ \end{gathered} $

где $u_{x}^{2} = \sum\nolimits_{k = 1}^p {u_{{{{x}_{k}}}}^{2}} $, $G{\text{'}} = \left\{ {x{\text{'}} = ({{x}_{1}},\; \ldots ,\;{{x}_{{k - 1}}},{{x}_{{k + 1}}},\; \ldots ,\;{{x}_{p}}):0 < {{x}_{k}} < {{l}_{k}}} \right\}$, $dx{\text{'}} = d{{x}_{1}}\; \cdots \;d{{x}_{{k - 1}}}d{{x}_{{k + 1}}} \cdots \;d{{x}_{p}}$.

Далее, для оценки слагаемых в правой части применим $\varepsilon $-неравенство Коши

(1.14)

$\begin{gathered} \left( {\sum\limits_{k = 1}^p {{{r}_{k}}} (x,t)\frac{{\partial{ \tilde {z}}}}{{\partial {{x}_{k}}}},\tilde {z}} \right) = \int\limits_G {\sum\limits_{k = 1}^p {{{r}_{k}}} } (x,t)\frac{{\partial{ \tilde {z}}}}{{\partial {{x}_{k}}}}\tilde {z}dx = \sum\limits_{k = 1}^p {\int\limits_G {{{r}_{k}}} } (x,t)\frac{{\partial{ \tilde {z}}}}{{\partial {{x}_{k}}}}\tilde {z}dx \leqslant \\ \leqslant \;{{\varepsilon }_{1}}\sum\limits_{k = 1}^p {\int\limits_G {{{{\left( {\frac{{\partial{ \tilde {z}}}}{{\partial {{x}_{k}}}}} \right)}}^{2}}} } dx + M_{1}^{{{{\varepsilon }_{1}}}}\sum\limits_{k = 1}^p {\int\limits_G {{{{\tilde {z}}}^{2}}} } dx, \\ \end{gathered} $

(1.15)

$\left( {\tilde {f}(x,t),\tilde {z}} \right) \leqslant \frac{1}{2}\left\| {\tilde {f}} \right\|_{0}^{2} + \frac{1}{2}\left\| {\tilde {z}} \right\|_{0}^{2}.$

Учитывая преобразования (1.11)–(1.15), из (1.10) получаем неравенство

(1.16)

$\frac{\varepsilon }{2}\frac{\partial }{{\partial t}}\left\| {\tilde {z}} \right\|_{0}^{2} + \frac{1}{2}\partial _{{0t}}^{\alpha }\left\| {\tilde {z}} \right\|_{0}^{2} + {{c}_{0}}\left\| {{{{\tilde {z}}}_{x}}} \right\|_{0}^{2} + {{c}_{0}}\left\| {\tilde {z}} \right\|_{0}^{2} \leqslant {{\varepsilon }_{1}}\left\| {{{{\tilde {z}}}_{x}}} \right\|_{0}^{2} + M_{2}^{{{{\varepsilon }_{1}}}}\left\| {\tilde {z}} \right\|_{0}^{2} + \frac{1}{2}\left\| {\tilde {f}} \right\|_{0}^{2}.$

Выбирая ${{\varepsilon }_{1}} = \tfrac{{{{c}_{0}}}}{2}$, из неравенства (1.16) находим

(1.17)

$\varepsilon \frac{\partial }{{\partial t}}\left\| {\tilde {z}} \right\|_{0}^{2} + \partial _{{0t}}^{\alpha }\left\| {\tilde {z}} \right\|_{0}^{2} + \left\| {{{{\tilde {z}}}_{x}}} \right\|_{0}^{2} + \left\| {\tilde {z}} \right\|_{0}^{2} \leqslant {{M}_{3}}\left\| {\tilde {z}} \right\|_{0}^{2} + {{M}_{4}}\left\| {\tilde {f}} \right\|_{0}^{2}.$

Проинтегрируем (1.17) по $\tau $ от 0 до $t$, тогда получим

(1.18)

$\varepsilon \left\| {\tilde {z}} \right\|_{0}^{2} + D_{{0t}}^{{\alpha - 1}}\left\| {\tilde {z}} \right\|_{0}^{2} + \int\limits_0^t {\left( {\left\| {\tilde {z}} \right\|_{0}^{2} + \left\| {{{{\tilde {z}}}_{x}}} \right\|_{0}^{2}} \right)d\tau } \leqslant {{M}_{5}}\int\limits_0^t {\left\| {\tilde {z}} \right\|_{0}^{2}} d\tau + {{M}_{6}}\int\limits_0^t {\left\| {\tilde {f}} \right\|_{0}^{2}} d\tau ,$

где $D_{{0t}}^{{\alpha - 1}}u = \tfrac{1}{{\Gamma (1 - \alpha )}}\int_0^t {\tfrac{{ud\tau }}{{{{{(t - \tau )}}^{\alpha }}}}} $ – дробный интеграл Римана–Лиувилля порядка $1 - \alpha $, $0 < \alpha < 1$.

В (1.18) покажем, что $\int_0^t {\left\| {\tilde {z}} \right\|_{0}^{2}} d\tau = D_{{0t}}^{{ - \alpha }}\left( {D_{{0t}}^{{\alpha - 1}}\left\| {\tilde {z}} \right\|_{0}^{2}} \right)$:

(1.19)

$\begin{gathered} D_{{0t}}^{{ - \alpha }}\left( {D_{{0t}}^{{\alpha - 1}}\left\| {\tilde {z}} \right\|_{0}^{2}} \right) = \frac{1}{{\Gamma (\alpha )\Gamma (1 - \alpha )}}\int\limits_0^t {\frac{{d\tau }}{{{{{(t - \tau )}}^{{1 - \alpha }}}}}} \int\limits_0^\tau {\frac{{\left\| {\tilde {z}} \right\|_{0}^{2}ds}}{{{{{(\tau - s)}}^{\alpha }}}}} = \frac{1}{{\Gamma (\alpha )\Gamma (1 - \alpha )}}\int\limits_0^t {\left\| {\tilde {z}} \right\|_{0}^{2}} ds\int\limits_s^\tau {\frac{{d\tau }}{{{{{(t - \tau )}}^{{1 - \alpha }}}{{{(\tau - s)}}^{\alpha }}}}} = \\ = \frac{1}{{\Gamma (\alpha )\Gamma (1 - \alpha )}}\int\limits_0^t {\left\| {\tilde {z}} \right\|_{0}^{2}} {\kern 1pt} ds\int\limits_0^\infty {\frac{{d{v}}}{{(1 + {v}){{{v}}^{\alpha }}}}} = \frac{{B(1 - \alpha ,\alpha )}}{{\Gamma (\alpha )\Gamma (1 - \alpha )}}\int\limits_0^t {\left\| {\tilde {z}} \right\|_{0}^{2}} d\tau = \int\limits_0^t {\left\| {\tilde {z}} \right\|_{0}^{2}} d\tau , \\ \end{gathered} $

где $D_{{0t}}^{{ - \alpha }}u = \tfrac{1}{{\Gamma (\alpha )}}\int_0^t {\tfrac{{ud\tau }}{{{{{(t - \tau )}}^{{1 - \alpha }}}}}} $ – дробный интеграл Римана–Лиувилля порядка $\alpha $, $0 < \alpha < 1$.

Учитывая (1.19), из (1.18) получаем

(1.20)

$\varepsilon \left\| {\tilde {z}} \right\|_{0}^{2} + D_{{0t}}^{{\alpha - 1}}\left\| {\tilde {z}} \right\|_{0}^{2} + \int\limits_0^t {\left( {\left\| {\tilde {z}} \right\|_{0}^{2} + \left\| {{{{\tilde {z}}}_{x}}} \right\|_{0}^{2}} \right)d\tau } \leqslant {{M}_{5}}D_{{0t}}^{{ - \alpha }}\left( {D_{{0t}}^{{\alpha - 1}}\left\| {\tilde {z}} \right\|_{0}^{2}} \right) + {{M}_{6}}\int\limits_0^t {\left\| {\tilde {f}} \right\|_{0}^{2}d\tau } .$

С помощью леммы 2 (см. [30]) из (1.20) получаем неравенство

(1.21)

$\varepsilon \left\| {\tilde {z}} \right\|_{0}^{2} + D_{{0t}}^{{\alpha - 1}}\left\| {\tilde {z}} \right\|_{0}^{2} + \left\| {\tilde {z}} \right\|_{{2,{{Q}_{t}}}}^{2} + \left\| {{{{\tilde {z}}}_{x}}} \right\|_{{2,{{Q}_{t}}}}^{2} \leqslant {{M}_{7}}\int\limits_0^t {\left\| {\tilde {f}} \right\|_{0}^{2}} d\tau = {{\varepsilon }^{2}}{{M}_{7}}\int\limits_0^t {\left\| {{{u}_{\tau }}} \right\|_{0}^{2}} d\tau = O({{\varepsilon }^{2}}),$

где $M$ – зависит только от входных данных задач (1.1)–(1.3), $\left\| {{{{\tilde {z}}}_{x}}} \right\|_{{2,{{Q}_{t}}}}^{2} = \int_0^t {\left\| {{{{\tilde {z}}}_{x}}} \right\|_{0}^{2}d\tau } $.

Из априорной оценки (1.21) следует сходимость ${{u}^{\varepsilon }}$ к $u$ при $\varepsilon \to 0$ в норме $\left\| {\tilde {z}} \right\|_{1}^{2} = \varepsilon \left\| {\tilde {z}} \right\|_{0}^{2} + D_{{0t}}^{{\alpha - 1}}\left\| {\tilde {z}} \right\|_{0}^{2} + \left\| {\tilde {z}} \right\|_{{2,{{Q}_{t}}}}^{2} + \left\| {{{{\tilde {z}}}_{x}}} \right\|_{{2,{{Q}_{t}}}}^{2}$. Поэтому при малом $\varepsilon $ решение задачи (1.4)–(1.6) будем принимать за приближенное решение первой краевой задачи для уравнения конвекции–диффузии дробного порядка (1.1)–(1.3).

2. ПОСТРОЕНИЕ ЛОКАЛЬНО-ОДНОМЕРНОЙ СХЕМЫ (ЛОС)

Пространственную сетку выберем равномерной по каждому направлению $O{{x}_{k}}$ с шагом ${{h}_{k}} = \tfrac{{{{l}_{k}}}}{{{{N}_{k}}}}$, $k = 1,\;2,\; \ldots ,\;p$:

${{\bar {\omega }}_{{{{h}_{k}}}}} = \left\{ {x_{k}^{{({{i}_{k}})}} = {{i}_{k}}{{h}_{k}}:{{i}_{k}} = 0,\;1,\; \ldots ,\;{{N}_{k}},{{h}_{k}} = \frac{{{{l}_{k}}}}{{{{N}_{k}}}},k = 1,\;2,\; \ldots ,\;p} \right\},\quad \bar {\omega } = \prod\limits_{k = 1}^p {{{{\bar {\omega }}}_{{{{h}_{k}}}}}} .$

На отрезке $0 \leqslant t \leqslant T$ введем равномерную сетку

$\bar {\omega }_{\tau }^{'} = \left\{ {0,{{t}_{{j + \tfrac{k}{p}}}} = \left( {j + \frac{k}{p}} \right)\tau ,\;j = 0,\;1,\; \ldots ,\;{{j}_{0}} - 1,\;\tau = \frac{T}{{{{j}_{0}}}},\;k = 1,\;2,\; \ldots ,\;p} \right\},$

содержащую, наряду с узлами ${{t}_{j}} = j\tau ,$ фиктивные узлы ${{t}_{{j + \tfrac{k}{p}}}}$, $k = 1,\;2,\; \ldots ,\;p - 1$. Будем обозначать через $\omega _{\tau }^{'}$ множество узлов сетки $\bar {\omega }_{\tau }^{'}$, для которых $t > 0$.

На равномерной сетке ${{\bar {\omega }}_{{h\tau }}}$ по аналогии с [31] уравнению (1.4) поставим в соответствие цепочку “одномерных” уравнений, для этого перепишем уравнение (1.4) в виде

или

где ${{f}_{k}}(x,t)$, $k = 1,\;2,\; \ldots ,\;p$, – произвольные функции, обладающие той же гладкостью, что и $f(x,t)$, и удовлетворяющие условию $\sum\nolimits_{k = 1}^p {{{f}_{k}}} = f$.

На каждом полуинтервале ${{\Delta }_{k}} = \left( {{{t}_{{j + \tfrac{{k - 1}}{p}}}},{{t}_{{j + \tfrac{k}{p}}}}} \right]$, $k = 1,\;2,\; \ldots ,\;p$, будем последовательно решать задачи

(2.1)

полагая при этом

(2.2)

$\begin{gathered} {{\vartheta }_{{(1)}}}(x,0) = {{u}_{0}}(x),\quad {{\vartheta }_{{(1)}}}(x,{{t}_{j}}) = {{\vartheta }_{{(p)}}}(x,{{t}_{j}}),\quad j = 1,\;2,\; \ldots ,\;{{j}_{0}} - 1, \\ {{\vartheta }_{{(k)}}}\left( {x,{{t}_{{j + \tfrac{{k - 1}}{p}}}}} \right) = {{\vartheta }_{{(k - 1)}}}\left( {x,{{t}_{{j + \tfrac{{k - 1}}{p}}}}} \right),\quad k = 2,\;3,\; \ldots ,\;p, \\ \end{gathered} $

где ${{{\text{Г}}}_{k}}$ – множество граничных точек по направлению ${{x}_{k}}.$

Аналогично [31, с. 401], получим для уравнения (2.1) номера $k$ монотонную схему второго порядка аппроксимации по ${{h}_{k}}$, для которой справедлив принцип максимума при любых $\tau $ и ${{h}_{k}}$, $k = 1,\;2,\; \ldots ,\;p$. Для этого рассмотрим уравнение (2.1) при фиксированном $k$ с возмущенным оператором ${{\tilde {L}}_{k}}$:

(2.3)

$\frac{\varepsilon }{p}{{\vartheta }_{t}} + \frac{1}{p}\partial _{{0t}}^{\alpha }{{\vartheta }_{{(k)}}} = {{\tilde {L}}_{k}}{{\vartheta }_{{(k)}}} + {{f}_{k}},\quad t \in {{\Delta }_{k}},\quad k = 1,\;2,\; \ldots ,\;p,$

где

${{\tilde {L}}_{k}}{{\vartheta }_{{(k)}}} = {{\chi }_{k}}\frac{\partial }{{\partial {{x}_{k}}}}\left( {{{\Theta }_{k}}(x,t)\frac{{\partial {{\vartheta }_{{(k)}}}}}{{\partial {{x}_{k}}}}} \right) + {{r}_{k}}(x,t)\frac{{\partial {{\vartheta }_{{(k)}}}}}{{\partial {{x}_{k}}}} - {{q}_{k}}(x,t){{\vartheta }_{{(k)}}},$

${{\chi }_{k}} = \tfrac{1}{{1 + {{R}_{k}}}}$, ${{R}_{k}} = 0.5{{h}_{k}}\tfrac{{\left| {{{r}_{k}}} \right|}}{{{{\Theta }_{k}}}}$ – разностное число Рейнольдса.

Каждое из уравнений (2.3) заменим разностной схемой

(2.4)

$\begin{gathered} \frac{\varepsilon }{p}y_{{\bar {t}}}^{{j + \tfrac{k}{p}}} + \frac{1}{p}\frac{1}{{{\text{Г}}(2 - \alpha )}}\sum\limits_{s = 1}^{pj + k} {\left( {t_{{j + \tfrac{{k - s + 1}}{p}}}^{{1 - \alpha }} - t_{{j + \tfrac{{k - s}}{p}}}^{{1 - \alpha }}} \right)} y_{{\overline t }}^{{\tfrac{s}{p}}} = {{{\tilde {\Lambda }}}_{k}}\left( {{{\sigma }_{k}}{{y}^{{j + \tfrac{k}{p}}}} + (1 - {{\sigma }_{k}}){{y}^{{j + \tfrac{{k - 1}}{p}}}}} \right) + \varphi _{k}^{{j + \tfrac{k}{p}}}, \\ x \in {{\omega }_{h}},\quad k = 1,\;2,\; \ldots ,\;p, \\ {{\left. {{{y}^{{j + \tfrac{k}{p}}}}} \right|}_{{{{\gamma }_{{h,k}}}}}} = {{\mu }^{{j + \tfrac{k}{p}}}},\quad j = 0,\;1,\; \ldots ,\;{{j}_{0}} - 1, \\ y(x,0) = {{u}_{0}}(x),\quad x \in \bar {G}, \\ \end{gathered} $

где

$\frac{1}{{{\text{Г}}(1 - \alpha )}}\int\limits_0^{{{t}_{{j + \tfrac{k}{p}}}}} {\frac{{\partial u(x,\eta )}}{{\partial \eta }}} \frac{{d\eta }}{{{{{\left( {{{t}_{{j + \tfrac{k}{p}}}} - \eta } \right)}}^{\alpha }}}} = \frac{1}{{{\text{Г}}(2 - \alpha )}}\sum\limits_{s = 1}^{pj + k} {\left( {t_{{j + \tfrac{{k - s + 1}}{p}}}^{{1 - \alpha }} - t_{{j + \tfrac{{k - s}}{p}}}^{{1 - \alpha }}} \right)} u_{{\overline t }}^{{\tfrac{s}{p}}} + O\left( {\frac{\tau }{p}} \right),$

$y_{{\overline t }}^{{\tfrac{s}{p}}} = \frac{{{{y}^{{\tfrac{s}{p}}}} - {{y}^{{\tfrac{{s - 1}}{p}}}}}}{{\tfrac{\tau }{p}}},\quad {{\mu }^{{j + \tfrac{k}{p}}}} = \mu \left( {x,{{t}_{{j + \tfrac{k}{p}}}}} \right),\quad \varphi _{k}^{{j + \tfrac{k}{p}}} = {{f}_{k}}\left( {x,{{t}_{{j + \tfrac{k}{p}}}}} \right),\quad k = 1,\;2,\; \ldots ,\;p,$

${{\sigma }_{k}}$ – произвольные параметры, ${{\gamma }_{{h,k}}}$ – множество граничных по направлению ${{x}_{k}}$ узлов,

$x \in {{\bar {\omega }}_{h}} = \left\{ {{{x}_{i}} = \left( {{{i}_{1}}{{h}_{1}},\; \ldots ,\;{{i}_{p}}{{h}_{p}}} \right) \in \bar {G},\;{{i}_{k}} = 0,\;1,\; \ldots {{N}_{k}},{{h}_{k}} = \frac{{{{l}_{k}}}}{{{{N}_{k}}}}} \right\},$

${{\tilde {\Lambda }}_{k}}{{y}^{{j + \tfrac{k}{p}}}} = {{\chi }_{k}}{{\left( {{{a}_{k}}y_{{\bar {x}}}^{{j + \tfrac{k}{p}}}} \right)}_{{{{x}_{k}}}}} + b_{k}^{ + }a_{k}^{{( + 1)}}y_{{{{x}_{k}}}}^{{j + \tfrac{k}{p}}} + b_{k}^{ - }{{a}_{k}}y_{{\mathop {\bar {x}}\nolimits_k }}^{{j + \tfrac{k}{p}}} - {{d}_{k}}{{y}^{{j + \tfrac{k}{p}}}},$

$d_{k}^{{j + \tfrac{k}{p}}} = q\left( {{{x}_{i}},{{t}^{{j + \tfrac{k}{p}}}}} \right),\quad {{a}^{{( + 1)}}} = {{a}_{{i + 1}}},\quad a_{i}^{j} = \Theta \left( {{{x}_{{i - 1/2}}},\bar {t}} \right),\quad \bar {t} = {{t}_{{j + \tfrac{1}{2}}}},$

$r_{k}^{ + } = 0.5\left( {{{r}_{k}} + \left| {{{r}_{k}}} \right|} \right) \geqslant 0,\quad r_{k}^{ - } = 0.5\left( {{{r}_{k}} - \left| {{{r}_{k}}} \right|} \right) \leqslant 0,\quad b_{k}^{ + } = \frac{{r_{k}^{ + }}}{{{{\Theta }_{k}}}},\quad b_{k}^{ - } = \frac{{r_{k}^{ - }}}{{{{\Theta }_{k}}}},\quad {{r}_{k}} = r_{k}^{ + } + r_{k}^{ - },$

3. ПОГРЕШНОСТЬ АППРОКСИМАЦИИ ЛОС

Перейдем к изучению погрешности аппроксимации (невязки) локально-одномерной схемы и убедимся в том, что каждое в отдельности уравнение (2.4) номера $k$ не аппроксимирует уравнение (1.4), но сумма погрешностей аппроксимации:

$\psi = {{\psi }_{1}} + \; \ldots \; + {{\psi }_{p}},$

стремится к нулю при $\tau $ и $\left| h \right|$, стремящимся к нулю.

Будем считать ${{\sigma }_{k}} = 1$, $k = 1,\;2,\; \ldots ,\;p$. Пусть $u = u(x,t)$ – решение задачи (1.4)–(1.6), а ${{y}^{{j + \tfrac{k}{p}}}}$ – решение разностной задачи (2.4). Характеристикой точности локально-одномерной схемы является разность ${{y}^{{j + 1}}} - {{u}^{{j + 1}}} = {{z}^{{j + 1}}}$. Промежуточные значения ${{y}^{{j + \tfrac{k}{p}}}}$ будем сравнивать с ${{u}^{{j + \tfrac{k}{p}}}} = u\left( {x,{{t}_{{j + \tfrac{k}{p}}}}} \right)$, полагая ${{z}^{{j + \tfrac{k}{p}}}} = {{y}^{{j + \tfrac{k}{p}}}} - {{u}^{{j + \tfrac{k}{p}}}}$. Подставляя ${{y}^{{j + \tfrac{k}{p}}}} = {{z}^{{j + \tfrac{k}{p}}}} + {{u}^{{j + \tfrac{k}{p}}}}$ в разностное уравнение (2.4), получаем

(3.1)

$\frac{\varepsilon }{p}z_{{\bar {t}}}^{{j + \tfrac{k}{p}}} + \frac{1}{p}\frac{1}{{\Gamma (2 - \alpha )}}\sum\limits_{s = 1}^{pj + k} {\left( {t_{{j + \tfrac{{k - s + 1}}{p}}}^{{1 - \alpha }} - t_{{j + \tfrac{{k - s}}{p}}}^{{1 - \alpha }}} \right)} z_{{\bar {t}}}^{{\tfrac{s}{p}}} = {{\tilde {\Lambda }}_{k}}{{z}^{{j + \tfrac{k}{p}}}} + \psi _{k}^{{j + \tfrac{k}{p}}},$

(3.2)

${{\left. {{{z}^{{j + \tfrac{k}{p}}}}} \right|}_{{{{\gamma }_{{h,k}}}}}} = 0,\quad z(x,0) = 0,$

где

$\psi _{k}^{{j + \tfrac{k}{p}}} = {{\tilde {\Lambda }}_{k}}{{u}^{{j + \tfrac{k}{p}}}} + \varphi _{k}^{{j + \tfrac{k}{p}}} - \frac{1}{p}\frac{1}{{\Gamma (2 - \alpha )}}\sum\limits_{s = 1}^{pj + k} {\left( {t_{{j + \tfrac{{k - s + 1}}{p}}}^{{1 - \alpha }} - t_{{j + \tfrac{{k - s}}{p}}}^{{1 - \alpha }}} \right)u_{{\bar {t}}}^{{\tfrac{s}{p}}}} - \frac{\varepsilon }{p}u_{t}^{{j + \tfrac{k}{p}}}.$

Обозначив через

(3.3)

${{\mathop \psi \limits^ \circ }_{k}} = {{\left( {{{L}_{k}}u + {{f}_{k}} - \frac{\varepsilon }{p}{{u}_{t}} - \frac{1}{p}\partial _{{0t}}^{\alpha }u} \right)}^{{j + \tfrac{1}{2}}}}$

и, замечая, что

$\sum\limits_{k = 1}^p {{{{\mathop \psi \limits^ \circ }}_{k}}} = 0,$

если

$\sum\limits_{k = 1}^p {{{f}_{k}}} = f,$

представим ${{\psi }_{k}} = \psi _{k}^{{j + \tfrac{k}{p}}}$ в виде

${{\psi }_{k}} = {{\mathop \psi \limits^ \circ }_{k}} + {{\mathop \psi \limits^* }_{k}},$

где

$\psi _{k}^{{j + \tfrac{k}{p}}} = \left( {{{{\tilde {\Lambda }}}_{k}}{{u}^{{j + \tfrac{k}{p}}}} - {{L}_{k}}{{u}^{{j + \tfrac{1}{2}}}}} \right) + \left( {\varphi _{k}^{{j + \tfrac{k}{p}}} - f_{k}^{{j + \tfrac{1}{2}}}} \right) - \left( {\frac{1}{p}\Delta _{{0{{t}_{{j + \tfrac{k}{p}}}}}}^{\alpha }{{u}^{{j + \tfrac{k}{p}}}} - \frac{1}{p}\mathop {(\partial _{{0t}}^{\alpha }u)}\nolimits^{j + \tfrac{1}{2}} } \right) - $

$ - \;\left( {\frac{\varepsilon }{p}u_{{\bar {t}}}^{{j + \tfrac{k}{p}}} - \frac{\varepsilon }{p}u_{t}^{{j + \tfrac{1}{2}}}} \right) + {{\mathop \psi \limits^ \circ }_{k}} = {{\mathop \psi \limits^ \circ }_{k}} + {{\mathop \psi \limits^* }_{k}},$

${{\mathop \psi \limits^* }_{k}} = \left( {{{{\tilde {\Lambda }}}_{k}}{{u}^{{j + \tfrac{k}{p}}}} - {{L}_{k}}{{u}^{{j + \tfrac{1}{2}}}}} \right) + \left( {\varphi _{k}^{{j + \tfrac{k}{p}}} - f_{k}^{{j + \tfrac{1}{2}}}} \right) - \left( {\frac{1}{p}\Delta _{{0{{t}_{{j + \tfrac{k}{p}}}}}}^{\alpha }{{u}^{{j + \tfrac{k}{p}}}} - \frac{1}{p}\mathop {(\partial _{{0t}}^{\alpha }u)}\nolimits^{j + \tfrac{1}{2}} } \right) - \left( {\frac{\varepsilon }{p}u_{{\bar {t}}}^{{j + \tfrac{k}{p}}} - \frac{\varepsilon }{p}u_{t}^{{j + \tfrac{1}{2}}}} \right).$

Ясно, что ${{\mathop \psi \limits^* }_{k}} = O(h_{k}^{2} + \tau )$, так как каждая из схем (2.4) номера $k$ аппроксимирует в обычном смысле соответствующее уравнение (2.3), т.е. ${\text{|}}{\kern 1pt} {\text{|}}{\kern 1pt} {{\mathop \psi \limits^* }_{k}}{\kern 1pt} {\text{|}}{\kern 1pt} {\text{|}}$ стремится к нулю (в некоторой норме) при $\left| h \right| \to 0$, $\tau \to 0$. Таким образом, ЛОС (2.4) обладает суммарной аппроксимацией

${{\mathop \psi \limits^* }_{k}} = O(h_{k}^{2} + \tau ),\quad {{\mathop \psi \limits^ \circ }_{k}} = O(1),\quad \sum\limits_{k = 1}^p {{{{\mathop \psi \limits^ \circ }}_{k}}} = 0,$

$\psi = \sum\limits_{k = 1}^p {{{\psi }_{k}}} = \sum\limits_{k = 1}^p {\left( {{{{\mathop \psi \limits^ \circ }}_{k}} + {{{\mathop \psi \limits^* }}_{k}}} \right)} = \sum\limits_{k = 1}^p {{{{\mathop \psi \limits^* }}_{k}}} = O\left( {{{{\left| h \right|}}^{2}} + \tau } \right).$

4. УСТОЙЧИВОСТЬ ЛОС

Получим априорную оценку в сеточной норме $C$ для решения разностной задачи (2.4), выражающую устойчивость локально-одномерной схемы по начальным данным и правой части. Исследование устойчивости разностной схемы (2.4) будем проводить с помощью принципа максимума (см. [31, с. 226]), для чего решение задачи (2.4) представим в виде суммы

$y = \bar {y} + {v},$

где $\bar {y}$ – решение однородных уравнений (2.4) с неоднородными краевыми и начальными условиями

${{\left. {{{{\bar {y}}}^{{j + \tfrac{k}{p}}}}} \right|}_{{{{\gamma }_{{h,k}}}}}} = {{\mu }^{{j + \tfrac{k}{p}}}},$

$\bar {y}(x,0) = {{u}_{0}}(x),$

${v}$ – решение неоднородных уравнений (2.4) с однородными краевыми и начальными условиями

(4.1)

$\begin{gathered} \frac{\varepsilon }{p}\mathop {\bar {y}}\nolimits_{\bar {t}}^{j + \tfrac{k}{p}} + \frac{1}{p}\frac{1}{{{\text{Г}}(2 - \alpha )}}\sum\limits_{s = 1}^{pj + k} {\left( {t_{{j + \tfrac{{k - s + 1}}{p}}}^{{1 - \alpha }} - t_{{j + \tfrac{{k - s}}{p}}}^{{1 - \alpha }}} \right)\bar {y}_{t}^{{\tfrac{s}{p}}}} = {{{\tilde {\Lambda }}}_{k}}{{{\bar {y}}}^{{j + \tfrac{k}{p}}}}, \\ {{\left. {{{{\bar {y}}}^{{j + \tfrac{k}{p}}}}} \right|}_{{{{\gamma }_{{h,k}}}}}} = {{\mu }^{{j + \tfrac{k}{p}}}}, \\ \bar {y}(x,0) = {{u}_{0}}(x), \\ \end{gathered} $

(4.2)

$\begin{gathered} \frac{\varepsilon }{p}{v}_{{\bar {t}}}^{{j + \tfrac{k}{p}}} + \frac{1}{p}\frac{1}{{{\text{Г}}(2 - \alpha )}}\sum\limits_{s = 1}^{pj + k} {\left( {t_{{j + \tfrac{{k - s + 1}}{p}}}^{{1 - \alpha }} - t_{{j + \tfrac{{k - s}}{p}}}^{{1 - \alpha }}} \right){v}_{{\overline t }}^{{\tfrac{s}{p}}}} = {{{\tilde {\Lambda }}}_{k}}{{{v}}^{{j + \tfrac{k}{p}}}} + \varphi _{k}^{{j + \tfrac{k}{p}}}, \\ {{\left. {{{{v}}^{{j + \tfrac{k}{p}}}}} \right|}_{{{{\gamma }_{{h,k}}}}}} = 0, \\ {v}(x,0) = 0. \\ \end{gathered} $

Получим оценку для $\bar {y}$, записав уравнение (4.1) в канонической форме. В точке $P = P\left( {{{x}_{{{{i}_{k}}}}},{{t}_{{j + \tfrac{k}{p}}}}} \right)$ имеем

(4.3)

$\begin{gathered} \left[ {\frac{\varepsilon }{\tau } + \frac{\gamma }{{{{\tau }^{\alpha }}}} + \frac{{{{\chi }_{k}}{{a}_{{k,{{i}_{k}} + 1}}}}}{{h_{k}^{2}}} + \frac{{{{\chi }_{k}}{{a}_{{k,{{i}_{k}}}}}}}{{h_{k}^{2}}} + \frac{{b_{k}^{ + }{{a}_{{k,{{i}_{k}} + 1}}}}}{{{{h}_{k}}}} - \frac{{b_{k}^{ - }{{a}_{{k,{{i}_{k}}}}}}}{{{{h}_{k}}}} + {{d}_{k}}} \right]\bar {y}_{{{{i}_{k}}}}^{{j + \tfrac{k}{p}}}\, = \,\frac{{{{\chi }_{k}}{{a}_{{k,{{i}_{k}} + 1}}}}}{{h_{k}^{2}}}\bar {y}_{{{{i}_{k}} + 1}}^{{j + \tfrac{k}{p}}}\, + \,\frac{{{{\chi }_{k}}{{a}_{{k,{{i}_{k}}}}}}}{{h_{k}^{2}}}\mathop {\bar {y}}\nolimits_{{{i}_{k}} - 1}^{j + \tfrac{k}{p}} \, + \,\frac{{b_{k}^{ + }{{a}_{{k,{{i}_{k}} + 1}}}}}{{{{h}_{k}}}}\bar {y}_{{{{i}_{k}} + 1}}^{{j + \tfrac{k}{p}}}\, - \\ - \;\frac{{b_{k}^{ - }{{a}_{{k,{{i}_{k}}}}}}}{{{{h}_{k}}}}\bar {y}_{{{{i}_{{k - 1}}}}}^{{j + \tfrac{k}{p}}} + \left[ {\frac{\varepsilon }{\tau } + \frac{\gamma }{{{{\tau }^{\alpha }}}}(2 - {{2}^{{1 - \alpha }}})} \right]\mathop {\bar {y}}\nolimits_{{{i}_{k}}}^{j + \tfrac{{k - 1}}{p}} + \frac{1}{\tau }\frac{1}{{{\text{Г}}(2 - \alpha )}}\left[ {\left( {t_{{j + \tfrac{k}{p}}}^{{1 - \alpha }} - t_{{j + \tfrac{{k - 1}}{p}}}^{{1 - \alpha }}} \right)\bar {y}_{{{{i}_{k}}}}^{0}} \right. + \\ + \;\left( { - t_{{j + \tfrac{k}{p}}}^{{1 - \alpha }} + 2t_{{j + \tfrac{{k - 1}}{p}}}^{{1 - \alpha }} - t_{{j + \tfrac{{k - 2}}{p}}}^{{1 - \alpha }}} \right)\mathop {\bar {y}}\nolimits_{{{i}_{k}}}^{\tfrac{1}{p}} + \; \ldots \; + \left. {\left( { - t_{{\tfrac{3}{p}}}^{{1 - \alpha }} + 2t_{{\tfrac{2}{p}}}^{{1 - \alpha }} - t_{{\tfrac{1}{p}}}^{{1 - \alpha }}} \right)\bar {y}_{{{{i}_{k}}}}^{{j + \tfrac{{k - 2}}{p}}}} \right], \\ \end{gathered} $

где $\gamma = \tfrac{1}{{{{p}^{{1 - \alpha }}}{\text{Г}}(2 - \alpha )}}$.

Справедлива следующая (см. [5])

Лемма. Пусть $l = pj + k - 1 \geqslant 1$, тогда имеет место неравенство

(4.4)

$ - t_{{j + \tfrac{k}{p}}}^{{1 - \alpha }} + 2t_{{j + \tfrac{{k - 1}}{p}}}^{{1 - \alpha }} - t_{{j + \tfrac{{k - 2}}{p}}}^{{1 - \alpha }} > 0,\quad j = 0,\;1,\; \ldots ,\;{{j}_{0}} - 1,\quad k = 2,\;3,\; \ldots ,\;p.$

В [31] доказан принцип максимума и получены априорные оценки для решения сеточного уравнения общего вида

$A(P)y(P) = \sum\limits_{Q \in {\text{Ш'}}(P)} B (P,Q)y(Q) + F(P),\quad P \in \Omega ,$

$y(P) = \mu (P)\quad {\text{при}}\quad P \in S,$

где $P$, $Q$ – узлы сетки $\Omega $ + S, ${\text{Ш'}}(P)$ – окрестность узла $P$, не содержащего самого узла $P$. Коэффициенты $A(P)$, $B(P,Q)$ удовлетворяют условиям

(4.5)

$A(P) > 0,\quad B(P,Q) > 0,\quad D(P) = A(P) - \sum\limits_{Q \in {\text{Ш'}}(P)} B (P,Q) \geqslant 0.$

Обозначим через $P(x,t{\text{'}})$, где $x \in {{\omega }_{h}}$, $t{\text{'}} \in \omega _{\tau }^{'}$, узел $(p + 1)$-мерной сетки $\Omega = {{\omega }_{h}} \times \omega _{\tau }^{'}$, через $S$ $ - $ границу $\Omega $, состоящую из узлов $P$($x$,0) при $x \in {{\bar {\omega }}_{h}}$ и узлов $P\left( {x,{{t}_{{j + \tfrac{k}{p}}}}} \right)$ при ${{t}_{{j + \tfrac{k}{p}}}} \in \omega _{\tau }^{'}$ и $x \in {{\gamma }_{{h,k}}}$ для всех $k = 1,\;2,\; \ldots ,p$ и $j = 0,\;1,\; \ldots ,\;{{j}_{0}}$.

Справедливы следующие теоремы (см. [32]).

Теорема 1 (см. [32, с. 344]). Пусть коэффициенты уравнения

(*)

$A(P)y(P) = \sum\limits_{Q \in {\text{Ш'}}(P)} B (P,Q)y(Q) + F(P),\quad P \in \Omega ,$

удовлетворяют условиям

$A(P) > 0,\quad B(P,Q) \geqslant 0,\quad D(P) > 0,\quad P \in \mathop \omega \limits^* ,$

$A(P) > 0,\quad B(P,Q) > 0,\quad D(P) = F(P) = 0,\quad P \in \mathop \omega \limits^ \circ ,$

где $\mathop \omega \limits^ \circ $ – некоторое связное подмножество множества $\omega $, а $\mathop \omega \limits^* $ – дополнение $\mathop \omega \limits^ \circ $ до $\omega $.

Тогда для решения задачи (*) справедлива оценка

${{\left\| y \right\|}_{C}} \leqslant {{\left\| {\frac{{F(P)}}{{D(P)}}} \right\|}_{{C*}}},$

где

${{\left\| f \right\|}_{C}} = \mathop {max}\limits_{P \in \omega } \left| {f(P)} \right|,\quad {{\left\| f \right\|}_{{C*}}} = \mathop {max}\limits_{P \in \omega *} \left| {f(P)} \right|.$

Теорема 2 (см. [32, с. 347]). Если выполнены условия

$D{\text{'}}{\kern 1pt} \left( {{{P}_{{(n + 1)}}}} \right) > 0\quad для\;всех\quad {{P}_{{(n + 1)}}} \in \omega ,\quad A\left( {{{P}_{{(n + 1)}}}} \right) > 0,\quad B\left( {{{P}_{{(n + 1)}}},Q} \right) \geqslant 0$

для всех $Q \in {\text{Ш}}_{n}^{{''}}$, $Q \in {\text{Ш}}_{{n + 1}}^{'}$,

$\sum\limits_{Q \in {\text{Ш}}_{n}^{{''}}} B \left( {{{P}_{{(n + 1)}}},Q} \right) > 0,\quad \frac{1}{{D{\text{'}}\left( {{{P}_{{(n + 1)}}}} \right)}}\sum\limits_{Q \in {\text{Ш}}_{n}^{{''}}} B \left( {{{P}_{{(n + 1)}}},Q} \right) \leqslant 1 + {{c}_{1}}\tau ,$

где ${{c}_{1}} = {\text{const}} > 0$ не зависит от $\tau $, $h$.

Тогда для решения задачи

$A\left( {{{P}_{{(n + 1)}}})y({{P}_{{(n + 1)}}}} \right) = \sum\limits_{Q \in {\text{Ш}}_{{n + 1}}^{'}} B ({{P}_{{(n + 1)}}},Q)y(Q) + \Phi \left( {{{P}_{{(n + 1)}}}} \right),$

где

${{P}_{{(n + 1)}}} = P\left( {x,{{t}_{{n + 1}}}} \right),$

$\Phi ({{P}_{{(n + 1)}}}) = \sum\limits_{Q \in {\text{Ш}}_{n}^{'}} B ({{P}_{{(n + 1)}}},Q)y(Q) + F\left( {{{P}_{{(n + 1)}}}} \right),$

$D{\text{'}}({{P}_{{(n + 1)}}}) = A\left( {{{P}_{{(n + 1)}}}} \right) - \sum\limits_{Q \in {\text{Ш}}_{т}^{{''}}} B \left( {{{P}_{{(n + 1)}}},Q} \right),$

справедлива оценка

${{\left\| {{{y}_{{n + 1}}}} \right\|}_{{{{C}_{h}}}}} \leqslant {{e}^{{{{c}_{1}}{{t}_{n}}}}}\left( {{{{\left\| {{{y}_{0}}} \right\|}}_{{{{C}_{h}}}}} + \sum\limits_{k = 1}^{n + 1} \tau {{{\left\| {{{{\tilde {F}}}_{k}}} \right\|}}_{{{{C}_{h}}}}}} \right).$

Проверим выполнимость условий теоремы 1, опираясь на лемму. Тогда, учитывая положительность выражений, стоящих в круглых скобках, имеем, что коэффициенты уравнения (4.3) в точке $P = P\left( {{{x}_{{{{i}_{k}}}}},{{t}_{{j + \tfrac{k}{p}}}}} \right)$ удовлетворяют условиям (4.5) и $D(P) = 0$.

Из теоремы 2 следует, что для решения задачи (4.1) верна оценка

(4.6)

${{\left\| {{{{\bar {y}}}^{j}}} \right\|}_{C}} \leqslant {{\left\| {{{u}_{0}}} \right\|}_{C}} + \mathop {max}\limits_{0 < t' \leqslant j\tau } {{\left\| {\mu (x,t{\text{'}})} \right\|}_{{{{C}_{\gamma }}}}},$

где

${{\left\| y \right\|}_{C}} = \mathop {max}\limits_{x \in {{{\bar {\omega }}}_{h}}} \left| y \right|,\quad {{\left\| y \right\|}_{{{{C}_{\gamma }}}}} = \mathop {max}\limits_{x \in {{\gamma }_{h}}} \left| y \right|.$

Переходим к оценке функции ${v}$. Уравнение (4.2) перепишем в виде

(4.7)

$\begin{gathered} \left( {\frac{\varepsilon }{p} + \frac{1}{p}\frac{1}{{{\text{Г}}(2 - \alpha )}}\mathop {\left( {\frac{\tau }{p}} \right)}\nolimits^{1 - \alpha } } \right){v}_{{\bar {t}}}^{{j + \tfrac{k}{p}}} = {{{\tilde {\Lambda }}}_{k}}{{{v}}^{{j + \tfrac{k}{p}}}} + \tilde {\varphi }_{k}^{{j + \tfrac{k}{p}}}, \\ {{\left. {{{{v}}^{{j + \tfrac{k}{p}}}}} \right|}_{{{{\gamma }_{{h,k}}}}}} = 0, \\ {v}(x,0) = 0, \\ \end{gathered} $

где

$\tilde {\varphi }_{k}^{{j + \tfrac{k}{p}}} = {{\varphi }^{{j + \tfrac{k}{p}}}} - \frac{1}{p}\frac{1}{{{\text{Г}}(2 - \alpha )}}\sum\limits_{s = 1}^{pj + k - 1} {\left( {t_{{j + \tfrac{{k - s + 1}}{p}}}^{{1 - \alpha }} - t_{{j + \tfrac{{k - s}}{p}}}^{{1 - \alpha }}} \right){v}_{{\overline t }}^{{\tfrac{s}{p}}}} .$

Уравнение (4.7) приведем к каноническому виду

$\begin{gathered} \left[ {\frac{\varepsilon }{\tau } + \frac{\gamma }{{{{\tau }^{\alpha }}}} + \frac{{{{\chi }_{{{{i}_{k}}}}}{{a}_{{k,{{i}_{k}} + 1}}}}}{{h_{k}^{2}}} + \frac{{{{\chi }_{{{{i}_{k}}}}}{{a}_{{k,{{i}_{k}}}}}}}{{h_{k}^{2}}} + \frac{{b_{k}^{ + }{{a}_{{k,{{i}_{k}} + 1}}}}}{{{{h}_{k}}}} - \frac{{b_{k}^{ - }{{a}_{{k,{{i}_{k}}}}}}}{{{{h}_{k}}}} + {{d}_{k}}} \right]{v}_{{{{i}_{k}}}}^{{j + \tfrac{k}{p}}} = \\ = \;\frac{1}{{h_{k}^{2}}}\left[ {{{\chi }_{{{{i}_{k}}}}}{{a}_{{k,{{i}_{k}} + 1}}}\nu _{{{{i}_{k}} + 1}}^{{j + \tfrac{k}{p}}} + {{\chi }_{{{{i}_{k}}}}}{{a}_{{k,{{i}_{k}}}}}\nu _{{{{i}_{k}} - 1}}^{{j + \tfrac{k}{p}}}} \right] + \frac{{b_{k}^{ + }{{a}_{{k,{{i}_{k}} + 1}}}}}{{{{h}_{k}}}}\nu _{{{{i}_{k}} + 1}}^{{j + \tfrac{k}{p}}} - \frac{{b_{k}^{ - }{{a}_{{k,{{i}_{k}}}}}}}{{{{h}_{k}}}}\nu _{{{{i}_{k}} - 1}}^{{j + \tfrac{k}{p}}} + \Phi \left( {{{P}_{{j + \tfrac{k}{p}}}}} \right), \\ \end{gathered} $

где

$\Phi \left( {{{P}_{{j + \tfrac{k}{p}}}}} \right) = \left[ {\frac{\varepsilon }{\tau } + \frac{\gamma }{{{{\tau }^{\alpha }}}}\left( {2 - {{2}^{{1 - \alpha }}}} \right)} \right]{v}_{{{{i}_{k}}}}^{{j + \tfrac{{k - 1}}{p}}} + \bar {\varphi }_{k}^{{j + \tfrac{k}{p}}},$

$\bar {\varphi }_{k}^{{j + \tfrac{k}{p}}} = \varphi _{k}^{{j + \tfrac{k}{p}}} + \frac{1}{{{\text{Г}}(2 - \alpha )}}\frac{1}{\tau }\left( {t_{{\tfrac{2}{p}}}^{{1 - \alpha }} - t_{{\tfrac{1}{p}}}^{{1 - \alpha }}} \right){v}_{{{{i}_{k}}}}^{{j + \tfrac{{k - 2}}{p}}} - \frac{1}{\tau }\frac{1}{{{\text{Г}}(2 - \alpha )}}\sum\limits_{s = 1}^{pj + k - 2} {\left( {t_{{j + \tfrac{{k - s + 1}}{p}}}^{{1 - \alpha }} - t_{{j + \tfrac{{k - s}}{p}}}^{{1 - \alpha }}} \right)} \left( {{v}_{{{{i}_{k}}}}^{{\tfrac{s}{p}}} - {v}_{{{{i}_{k}}}}^{{\tfrac{{s - 1}}{p}}}} \right).$

Проверим выполнимость условий теоремы 2

(4.8)

$\begin{gathered} D{\text{'}}({{P}_{{(k)}}}) = A({{P}_{{(k)}}}) - \sum\limits_{Q \in {\text{Ш}}_{k}^{'}(P)} B \left( {{{P}_{{(k)}}},Q} \right) = \frac{\varepsilon }{\tau } + \frac{\gamma }{{{{\tau }^{\alpha }}}} + {{d}_{k}} \geqslant \frac{\varepsilon }{\tau } + \frac{\gamma }{{{{\tau }^{\alpha }}}} > 0, \\ {{P}_{{(k)}}} = P\left( {x,{{t}_{{j + \tfrac{k}{p}}}}} \right),\quad A({{P}_{{(k)}}}) > 0,\quad B\left( {{{P}_{{(k)}}},Q} \right) > 0, \\ \end{gathered} $

для всех $Q \in {\text{Ш}}_{{k - 1}}^{{''}}$, $Q \in {\text{Ш}}_{k}^{'}$,

$\sum\limits_{Q \in {\text{Ш}}_{{k - 1}}^{{''}}} B \left( {{{P}_{{(k)}}},Q} \right) = \frac{\varepsilon }{\tau } + \frac{\gamma }{{{{\tau }^{\alpha }}}}\left( {2 - {{2}^{{1 - \alpha }}}} \right) > 0,$

$\frac{1}{{D{\text{'}}{\kern 1pt} \left( {{{P}_{{(k)}}}} \right)}}\sum\limits_{Q \in {\text{Ш}}_{{k - 1}}^{{''}}} B \left( {{{P}_{{(k)}}},Q} \right) = \frac{{\tfrac{\varepsilon }{\tau } + \tfrac{{\gamma (2 - {{2}^{{1 - \alpha }}})}}{{{{\tau }^{\alpha }}}}}}{{\tfrac{\varepsilon }{\tau } + \tfrac{\gamma }{{{{\tau }^{\alpha }}}}}} \leqslant 1,$

где ${\text{Ш'}}\left( {P\left( {x,{{t}_{{j + \tfrac{k}{p}}}}} \right)} \right) = {\text{Ш}}_{k}^{'} + {\text{Ш}}_{{k - 1}}^{'}$, ${\text{Ш}}_{k}^{'}$ – множество узлов $Q = Q(\xi ,{{t}_{k}}) \in {\text{Ш'}}\left( {P\left( {x,{{t}_{k}}} \right)} \right)$, ${\text{Ш}}_{{k - 1}}^{'}$ – множество узлов $Q = Q(\xi ,{{t}_{{k - 1}}}) \in {\text{Ш'}}\left( {P\left( {x,{{t}_{{k - 1}}}} \right)} \right)$.

На основании теоремы 2, в силу (4.8), получаем оценку для ${v}$

(4.9)

${{\left\| {{{{v}}^{{j + \tfrac{k}{p}}}}} \right\|}_{C}} \leqslant \frac{1}{{\tfrac{\varepsilon }{\tau } + \tfrac{\gamma }{{{{\tau }^{\alpha }}}}}}{{\left\| {\bar {\varphi }_{k}^{{j + \tfrac{k}{p}}}} \right\|}_{C}} + \frac{{\tfrac{\varepsilon }{\tau } + \tfrac{{\gamma (2 - {{2}^{{1 - \alpha }}})}}{{{{\tau }^{\alpha }}}}}}{{\tfrac{\varepsilon }{\tau } + \tfrac{\gamma }{{{{\tau }^{\alpha }}}}}}{{\left\| {{{{v}}^{{j + \tfrac{{k - 1}}{p}}}}} \right\|}_{C}}.$

Оценим ${{\left\| {\bar {\varphi }_{k}^{{j + \tfrac{k}{p}}}} \right\|}_{C}}$, где

(4.10)

$\begin{gathered} \bar {\varphi }_{k}^{{j + \tfrac{k}{p}}} = \varphi _{k}^{{j + \tfrac{k}{p}}} + \frac{1}{{{\text{Г}}(2 - \alpha )}}\frac{1}{\tau }\left( {t_{{\tfrac{2}{p}}}^{{1 - \alpha }} - t_{{\tfrac{1}{p}}}^{{1 - \alpha }}} \right){v}_{{{{i}_{k}}}}^{{j + \tfrac{{k - 2}}{p}}} - \frac{1}{p}\frac{1}{{{\text{Г}}(2 - \alpha )}}\sum\limits_{s = 1}^{pj + k - 2} {\left( {t_{{j + \tfrac{{k - s + 1}}{p}}}^{{1 - \alpha }} - t_{{j + \tfrac{{k - s}}{p}}}^{{1 - \alpha }}} \right){v}_{{\overline t }}^{{\tfrac{s}{p}}}} = \\ = \;\varphi _{k}^{{j + \tfrac{k}{p}}} + \frac{1}{\tau }\frac{1}{{{\text{Г}}(2 - \alpha )}}\left[ {\left( {t_{{j + \tfrac{k}{p}}}^{{1 - \alpha }} - t_{{j + \tfrac{{k - 1}}{p}}}^{{1 - \alpha }}} \right)} \right.{v}_{{{{i}_{k}}}}^{0} + \left( { - t_{{j + \tfrac{k}{p}}}^{{1 - \alpha }} + 2t_{{j + \tfrac{{k - 1}}{p}}}^{{1 - \alpha }} - t_{{j + \tfrac{{k - 2}}{p}}}^{{1 - \alpha }}} \right){v}_{{{{i}_{k}}}}^{{\tfrac{1}{p}}} + \; \ldots \; + \\ + \;\left. {\left( { - t_{{\tfrac{3}{p}}}^{{1 - \alpha }} + 2t_{{\tfrac{2}{p}}}^{{1 - \alpha }} - t_{{\tfrac{1}{p}}}^{{1 - \alpha }}} \right){v}_{{{{i}_{k}}}}^{{j + \tfrac{{k - 2}}{p}}}} \right]. \\ \end{gathered} $

Так как, в силу леммы, выражения, стоящие в круглых скобках положительны, то из (4.10) получаем оценку

(4.11)

${{\left\| {\bar {\varphi }_{k}^{{j + \tfrac{k}{p}}}} \right\|}_{C}} \leqslant {{\left\| {\varphi _{k}^{{j + \tfrac{k}{p}}}} \right\|}_{C}} + \frac{{\gamma ({{2}^{{1 - \alpha }}} - 1)}}{{{{\tau }^{\alpha }}}}\mathop {max}\limits_{0 \leqslant s \leqslant k - 2} {{\left\| {{{{v}}^{{j + \tfrac{s}{p}}}}} \right\|}_{C}}.$

С помощью (4.11) из (4.9) находим

(4.12)

$\mathop {max}\limits_{0 \leqslant s \leqslant k} {{\left\| {{{{v}}^{{j + \tfrac{s}{p}}}}} \right\|}_{C}} \leqslant \mathop {max}\limits_{0 \leqslant s \leqslant k - 1} {{\left\| {{{{v}}^{{j + \tfrac{s}{p}}}}} \right\|}_{C}} + \frac{\tau }{{\varepsilon + \gamma {{\tau }^{{1 - \alpha }}}}}\mathop {max}\limits_{0 \leqslant s \leqslant k} {{\left\| {\varphi _{k}^{{j + \tfrac{s}{p}}}} \right\|}_{C}}.$

Просуммировав (4.12) сначала по $k = 1,\;2,\; \ldots ,\;p$, затем по $j{\text{'}} = 0,\;1,\; \ldots ,\;j$, получим оценку

(4.13)

${{\left\| {{{{v}}^{{j + 1}}}} \right\|}_{C}} \leqslant {{\left\| {{{{v}}^{0}}} \right\|}_{C}} + \sum\limits_{j' = 0}^j {\frac{\tau }{{\varepsilon + \gamma {{\tau }^{{1 - \alpha }}}}}} \sum\limits_{k = 1}^p {\mathop {max}\limits_{0 \leqslant s \leqslant k} } {{\left\| {\varphi _{k}^{{j' + \tfrac{s}{p}}}} \right\|}_{C}}.$

Из (4.6) и (4.13) следует окончательная оценка

(4.14)

${{\left\| {{{y}^{{j + 1}}}} \right\|}_{C}} \leqslant {{\left\| {{{y}^{0}}} \right\|}_{C}} + \mathop {max}\limits_{0 < t' \leqslant {{t}_{{j + 1}}}} {{\left\| {\mu (x,t{\text{'}})} \right\|}_{{{{C}_{\gamma }}}}} + \sum\limits_{j' = 0}^j {\frac{\tau }{{\varepsilon + \gamma {{\tau }^{{1 - \alpha }}}}}} \sum\limits_{k = 1}^p {\mathop {max}\limits_{0 \leqslant s \leqslant k} } {{\left\| {\varphi _{k}^{{j' + \tfrac{s}{p}}}} \right\|}_{C}}.$

Таким образом, справедлива

Теорема 3. Локально-одномерная схема (2.4) устойчива по начальным данным и правой части, так что для решения задачи (2.4) справедлива оценка (4.14).

5. РАВНОМЕРНАЯ СХОДИМОСТЬ ЛОС

Чтобы использовать свойство $\sum\nolimits_{k = 1}^p {\mathop {{{\psi }_{k}}}\limits^ \circ } = 0$, $\mathop \psi \limits^ \circ = O(1)$, представим по аналогии с [31] решение задачи для погрешности (3.1), (3.2) в виде суммы

(5.1)

${{z}_{{(k)}}} = {{{v}}_{{(k)}}} + {{\eta }_{{(k)}}},\quad {{z}_{{(k)}}} = {{z}^{{j + \tfrac{k}{p}}}},$

где ${{\eta }_{{(k)}}}$ определяется условиями

(5.2)

$\begin{gathered} \frac{\varepsilon }{p}\eta _{{\bar {t}}}^{{j + \tfrac{k}{p}}} + \frac{1}{p}\frac{1}{{{\text{Г}}(2 - \alpha )}}\sum\limits_{s = 1}^{pj + k} {\left( {t_{{j + \tfrac{{k - s + 1}}{p}}}^{{1 - \alpha }} - t_{{j + \tfrac{{k - s}}{p}}}^{{1 - \alpha }}} \right)\eta _{{\overline t }}^{{\tfrac{s}{p}}}} = {{\mathop \psi \limits^ \circ }_{k}},\quad x \in {{\omega }_{h}} + {{\gamma }_{{h,k}}},\quad k = 1,\;2,\; \ldots ,\;p, \\ \eta (x,0) = 0. \\ \end{gathered} $

Функция ${{{v}}_{{(k)}}}$ определяется условиями

(5.3)

$\begin{gathered} \frac{\varepsilon }{p}{v}_{{\bar {t}}}^{{j + \tfrac{k}{p}}} + \frac{1}{p}\frac{1}{{{\text{Г}}(2 - \alpha )}}\sum\limits_{s = 1}^{pj + k} {\left( {t_{{j + \tfrac{{k - s + 1}}{p}}}^{{1 - \alpha }} - t_{{j + \tfrac{{k - s}}{p}}}^{{1 - \alpha }}} \right){v}_{{\overline t }}^{{\tfrac{s}{p}}}} = {{{\tilde {\Lambda }}}_{k}}{{{v}}_{{(k)}}} + {{{\tilde {\psi }}}_{k}}, \\ {{\left. {{{{v}}_{{(k)}}}} \right|}_{{{{\gamma }_{{h,k}}}}}} = - {{\eta }_{{(k)}}},\quad {v}(x,0) = 0, \\ \end{gathered} $

где

$\mathop {\widetilde \psi }\nolimits_k = \mathop {{{\psi }_{k}}}\limits^* + {{\tilde {\Lambda }}_{k}}{{\eta }_{{(k)}}},\quad \mathop {{{\psi }_{k}}}\limits^* = O(h_{k}^{2} + \tau ).$

Покажем, что

${{\eta }^{{j + \tfrac{k}{p}}}} = O\left( {\tfrac{\tau }{{\varepsilon + \gamma {{\tau }^{{1 - \alpha }}}}}} \right),\quad k = 1,\;2,\; \ldots ,\;p,\quad j = 0,\;1,\; \ldots ,\;{{j}_{0}} - 1.$

Ради простоты рассмотрим двумерный случай ($p = 2$). Сначала положим $j = 0$, т.е. рассмотрим первый слой $(0,{{t}_{1}}]$. Тогда задача (5.2) примет вид

$\frac{\varepsilon }{2}\eta _{{\bar {t}}}^{{\tfrac{k}{2}}} + \frac{1}{2}\frac{1}{{{\text{Г}}(2 - \alpha )}}\sum\limits_{s = 1}^k {\left( {t_{{\tfrac{{k - s + 1}}{2}}}^{{1 - \alpha }} - t_{{\tfrac{{k - s}}{2}}}^{{1 - \alpha }}} \right)\eta _{{\overline t }}^{{\tfrac{s}{2}}}} = \mathop {{{\psi }_{k}}}\limits^ \circ ,\quad k = 1,2.$

Пусть $k = 1$, тогда получим

(5.4)

$\frac{\varepsilon }{2}\eta _{{\bar {t}}}^{{\tfrac{1}{2}}} + \frac{1}{2}\frac{1}{{{\text{Г}}(2 - \alpha )}}t_{{\tfrac{1}{2}}}^{{1 - \alpha }}\eta _{{\overline t }}^{{\tfrac{1}{2}}} = \mathop {{{\psi }_{1}}}\limits^ \circ \,.$

При $k = 2$ получаем

(5.5)

$\frac{\varepsilon }{2}\eta _{{\bar {t}}}^{1} + \frac{1}{2}\frac{1}{{{\text{Г}}(2 - \alpha )}}\left[ {\left( {t_{1}^{{1 - \alpha }} - t_{{\tfrac{1}{2}}}^{{1 - \alpha }}} \right)\eta _{{\overline t }}^{{\tfrac{1}{2}}} + t_{{\tfrac{1}{2}}}^{{1 - \alpha }}\eta _{{\bar {t}}}^{1}} \right] = \mathop {{{\psi }_{2}}}\limits^ \circ \,.$

Складывая выражения (5.4) и (5.5), получаем

(5.6)

$\frac{\varepsilon }{2}\eta _{{\bar {t}}}^{{\tfrac{1}{2}}} + \frac{\varepsilon }{2}\eta _{{\bar {t}}}^{1} + \frac{1}{2}\frac{1}{{{\text{Г}}(2 - \alpha )}}\frac{1}{{{{\tau }^{\alpha }}}}\left[ {\left( {1 - \frac{1}{{{{2}^{{1 - \alpha }}}}}} \right){{\eta }^{{\tfrac{1}{2}}}} + \frac{1}{{{{2}^{{1 - \alpha }}}}}{{\eta }^{1}}} \right] = 0.$

Из (5.4) находим

(5.7)

${{\eta }^{{\tfrac{1}{2}}}} = \frac{\tau }{{\varepsilon + \gamma {{\tau }^{{1 - \alpha }}}}}\mathop {{{\psi }_{1}}}\limits^ \circ = - \frac{\tau }{{\varepsilon + \gamma {{\tau }^{{1 - \alpha }}}}}\mathop {{{\psi }_{2}}}\limits^ \circ ,$

где $\gamma = \tfrac{1}{{{{2}^{{1 - \alpha }}}\Gamma (2 - \alpha )}}$.

Выражая ${{\eta }^{1}}$ из (5.6) и учитывая (5.7), получаем

(5.8)

${{\eta }^{{\tfrac{1}{2}}}},{{\eta }^{1}} = O\left( {\frac{\tau }{{\varepsilon + \gamma {{\tau }^{{1 - \alpha }}}}}} \right).$

Допустим, что при $j = n$ выполнено условие

(5.9)

${{\eta }^{{\tfrac{1}{2}}}},{{\eta }^{1}},{{\eta }^{{1 + \tfrac{1}{2}}}},\; \ldots ,\;{{\eta }^{{n + 1}}} = O\left( {\frac{\tau }{{\varepsilon + \gamma {{\tau }^{{1 - \alpha }}}}}} \right).$

Опираясь на допущение (5.9), покажем, что аналогичное условие выполнено и при $j = n + 1$. Для чего запишем уравнение (5.2) при $j = n + 1$, $p = 2$:

(5.10)

$\frac{\varepsilon }{2}\eta _{{\bar {t}}}^{{n + 1 + \tfrac{k}{2}}} + \frac{1}{2}\frac{1}{{{\text{Г}}(2 - \alpha )}}\sum\limits_{s = 1}^{2(n + 1) + k} {\left( {t_{{n + 1 + \tfrac{{k - s + 1}}{2}}}^{{1 - \alpha }} - t_{{n + 1 + \tfrac{{k - s}}{2}}}^{{1 - \alpha }}} \right)\eta _{{\overline t }}^{{\tfrac{s}{2}}}} = \mathop {{{\psi }_{k}}}\limits^ \circ ,\quad k = 1,\;2.$

Полагая в (5.10) $k = 1$, находим

(5.11)

$\begin{gathered} {{\tau }^{{1 - \alpha }}}\left[ {\mathop {\left( {n + \frac{3}{2}} \right)}\nolimits^{1 - \alpha } - 2{{{\left( {n + 1} \right)}}^{{1 - \alpha }}} + \mathop {\left( {n + \frac{1}{2}} \right)}\nolimits^{1 - \alpha } } \right]{{\eta }^{{\tfrac{1}{2}}}} + \\ + \;{{\tau }^{{1 - \alpha }}}\left[ {{{{\left( {n + 1} \right)}}^{{1 - \alpha }}} - 2\mathop {\left( {n + \frac{1}{2}} \right)}\nolimits^{1 - \alpha } + {{n}^{{1 - \alpha }}}} \right]{{\eta }^{1}} + \; \cdots \; - {\text{Г}}(2 - \alpha )\left( {\varepsilon - \frac{{{{\tau }^{{1 - \alpha }}}}}{{{\text{Г}}(2 - \alpha )}}(1 - {{2}^{\alpha }})} \right){{\eta }^{{n + 1}}} + \\ + \;{\text{Г}}(2 - \alpha )(\varepsilon + \gamma {{\tau }^{{1 - \alpha }}}){{\eta }^{{n + \tfrac{3}{2}}}} = 2{\text{Г}}(2 - \alpha )\tau \mathop {{{\psi }_{1}}}\limits^ \circ \,. \\ \end{gathered} $

Откуда с учетом (5.9) и достаточной ограниченности коэффициентов при ${{\eta }^{{\tfrac{1}{2}}}},{{\eta }^{1}},\; \ldots ,\;{{\eta }^{{n + \tfrac{3}{2}}}}$ находим ${{\eta }^{{n + \tfrac{3}{2}}}} = O\left( {\tfrac{\tau }{{\varepsilon + \gamma {{\tau }^{{1 - \alpha }}}}}} \right)$.

Положим теперь в (5.10) $k = 2$, затем сложим полученное таким образом выражение с выражением (5.11) с учетом равенства

$\mathop {{{\psi }_{1}}}\limits^ \circ \; + \mathop {{{\psi }_{2}}}\limits^ \circ = 0.$

Тогда получим

(5.12)

${{\eta }^{{\tfrac{1}{2}}}},{{\eta }^{1}},\; \ldots ,\;{{\eta }^{{n + 1}}},{{\eta }^{{n + \tfrac{3}{2}}}},{{\eta }^{{n + 2}}} = O\left( {\frac{\tau }{{\varepsilon + \gamma {{\tau }^{{1 - \alpha }}}}}} \right).$

Итак, равенство (5.12) выполнено при любом значении $j$. Аналогично можно показать, что

${{\eta }^{{j + \tfrac{k}{p}}}} = O\left( {\frac{\tau }{{\varepsilon + \gamma {{\tau }^{{1 - \alpha }}}}}} \right),\quad k = 1,\;2,\; \ldots ,\;p,\quad j = 0,\;1,\; \ldots ,\;{{j}_{0}} - 1.$

Для оценки решения задачи (5.3) воспользуемся теоремой 3:

(5.13)

${{\left\| {{{{v}}^{{j + 1}}}} \right\|}_{C}} \leqslant \mathop {max}\limits_{0 < j' + \tfrac{k}{p} \leqslant j + 1} {{\left\| {{{\eta }^{{j' + \tfrac{k}{p}}}}} \right\|}_{{{{C}_{\gamma }}}}} + \sum\limits_{j' = 0}^j {\frac{\tau }{{\varepsilon + \gamma {{\tau }^{{1 - \alpha }}}}}} \sum\limits_{k = 1}^p {\mathop {max}\limits_{0 \leqslant s \leqslant k} } {{\left\| {\tilde {\psi }_{k}^{{j' + \tfrac{s}{p}}}} \right\|}_{C}},$

где ${{\tilde {\psi }}_{k}} = \mathop {{{\psi }_{k}}}\limits^* \; + {{\tilde {\Lambda }}_{k}}{{\eta }_{{(k)}}}$.

Если существуют непрерывные в замкнутой области ${{\bar {Q}}_{T}}$ производные $\tfrac{{{{\partial }^{4}}u}}{{\partial x_{k}^{2}\partial x_{\nu }^{2}}}$, $k \ne \nu $, то

${{\tilde {\Lambda }}_{k}}{{\eta }_{{(k)}}} = - \frac{\tau }{{\varepsilon + \gamma {{\tau }^{{1 - \alpha }}}}}{{a}_{k}}{{\tilde {\Lambda }}_{k}}\left( {\mathop {{{\psi }_{{k + 1}}}}\limits^ \circ \; + \; \ldots \; + \mathop {{{\psi }_{p}}}\limits^ \circ } \right) = O\left( {\frac{\tau }{{\varepsilon + \gamma {{\tau }^{{1 - \alpha }}}}}} \right),$

${{a}_{k}}$ – известные постоянные.

Тогда из оценки (5.13) находим, что

${{\left\| {{{{v}}^{{j + 1}}}} \right\|}_{C}} \leqslant M\left( {\frac{\tau }{{\varepsilon + \gamma {{\tau }^{{1 - \alpha }}}}} + p\frac{\tau }{{\varepsilon + \gamma {{\tau }^{{1 - \alpha }}}}}\sum\limits_{j' = 0}^j {\left( {{{h}^{2}} + \frac{\tau }{{\varepsilon + \gamma {{\tau }^{{1 - \alpha }}}}}} \right)} } \right) \leqslant M\left( {\frac{{{{h}^{2}}}}{{\varepsilon + {{\tau }^{{1 - \alpha }}}}} + \frac{\tau }{{{{{(\varepsilon + {{\tau }^{{1 - \alpha }}})}}^{2}}}}} \right),\quad h = \mathop {max}\limits_{1 \leqslant k \leqslant p} {{h}_{k}}.$

Откуда получаем

${{\left\| {{{z}^{{j + 1}}}} \right\|}_{C}} \leqslant {{\left\| {{{\eta }^{{j + 1}}}} \right\|}_{C}} + {{\left\| {{{{v}}^{{j + 1}}}} \right\|}_{C}} \leqslant O\left( {\frac{{{{h}^{2}}}}{{\varepsilon + {{\tau }^{{1 - \alpha }}}}} + \frac{\tau }{{{{{(\varepsilon + {{\tau }^{{1 - \alpha }}})}}^{2}}}}} \right).$

Итак, справедлива теорема

Теорема 4. Пусть задача (1.4)–(1.6) имеет единственное непрерывное решение $u(x,t)$ в ${{\bar {Q}}_{T}}$ при всех значениях $\varepsilon $ и существуют непрерывные в ${{\bar {Q}}_{T}}$ производные

$\frac{{{{\partial }^{2}}u}}{{\partial {{t}^{2}}}},\;\frac{{{{\partial }^{4}}u}}{{\partial x_{k}^{2}\partial x_{\nu }^{2}}},\;\frac{{{{\partial }^{3}}u}}{{\partial x_{k}^{2}\partial t}},\;\frac{{{{\partial }^{{2 + \alpha }}}u}}{{\partial x_{k}^{2}\partial {{t}^{\alpha }}}},\;\frac{{{{\partial }^{2}}f}}{{\partial x_{k}^{2}}},\quad 1 \leqslant k,\quad \nu \leqslant p,\quad k \ne \nu ,\quad 0 < \alpha < 1,$

тогда решение разностной задачи (2.4) равномерно сходится к решению дифференциальной задачи (1.1)–(1.3) со скоростью

$O\left( {\tfrac{{{{h}^{2}}}}{{\varepsilon + {{\tau }^{{1 - \alpha }}}}} + \tfrac{\tau }{{{{{(\varepsilon + {{\tau }^{{1 - \alpha }}})}}^{2}}}} + \varepsilon } \right),\quad {{h}^{2}} = o(\varepsilon + {{\tau }^{{1 - \alpha }}}),\quad \tau = o({{(\varepsilon + {{\tau }^{{1 - \alpha }}})}^{2}}),$

где $\varepsilon - $ малый параметр.

Очевидно, что скорость сходимости будет определяться наилучшим образом, если

$\frac{{{{h}^{2}}}}{{\varepsilon + {{\tau }^{{1 - \alpha }}}}} + \frac{\tau }{{{{{(\varepsilon + {{\tau }^{{1 - \alpha }}})}}^{2}}}} = \varepsilon .$

Пусть $\varepsilon = {{\tau }^{\gamma }}$, тогда из последнего получаем

${{h}^{2}}({{\tau }^{\gamma }} + {{\tau }^{{1 - \alpha }}}) + \tau = {{\tau }^{\gamma }}\mathop {({{\tau }^{\gamma }} + {{\tau }^{{1 - \alpha }}})}\nolimits^2 $

или

$\tau \leqslant {{\tau }^{\gamma }}\mathop {({{\tau }^{\gamma }} + {{\tau }^{{1 - \alpha }}})}\nolimits^2 .$

Следовательно,

$min\left\{ {\gamma ,1 - \alpha } \right\} = \frac{{1 - \gamma }}{2},$

откуда получаем, что

(5.14)

$\varepsilon = \left\{ \begin{gathered} {{\tau }^{{\tfrac{1}{3}}}},\quad 0 < \alpha \leqslant \tfrac{2}{3}, \hfill \\ {{\tau }^{{2\alpha - 1}}},\quad \tfrac{2}{3} < \alpha < 1. \hfill \\ \end{gathered} \right.$

Тогда справедливо

Следствие. Если $\varepsilon $ определяется из условия (5.14), тогда решение разностной задачи (2.4) равномерно сходится к решению дифференциальной задачи (1.1)–(1.3) со скоростью

$O\left( {\frac{{{{h}^{2}}}}{{{{\tau }^{{\tfrac{1}{3}}}}}} + {{\tau }^{{\tfrac{1}{3}}}}} \right),\quad {\text{если}}\quad 0 < \alpha \leqslant \frac{2}{3},$

$O\left( {\frac{{{{h}^{2}}}}{{{{\tau }^{{1 - \alpha }}}}} + {{\tau }^{{2\alpha - 1}}}} \right),\quad {\text{если}}\quad \frac{2}{3} < \alpha < 1.$

При $\alpha \to 1$ получаем, что решение разностной задачи (2.4) равномерно сходится к решению дифференциальной задачи (1.1)–(1.3) со скоростью $O({{h}^{2}} + \tau )$.

6. АЛГОРИТМ ЧИСЛЕННОГО РЕШЕНИЯ

Для численного решения поставленной задачи (1.1)–(1.3) выпишем расчетные формулы ($0 \leqslant {{x}_{k}} \leqslant {{l}_{k}}$, $k = 1,\;2$, $p = 2$):

(6.1)

$\begin{gathered} \varepsilon \frac{{\partial u}}{{\partial t}} + \partial _{{0t}}^{\alpha }u = \frac{\partial }{{\partial {{x}_{1}}}}\left( {{{\Theta }_{1}}({{x}_{1}},{{x}_{2}},t)\frac{{\partial u}}{{\partial {{x}_{1}}}}} \right) + \frac{\partial }{{\partial {{x}_{2}}}}\left( {{{\Theta }_{2}}({{x}_{1}},{{x}_{2}},t)\frac{{\partial u}}{{\partial {{x}_{2}}}}} \right) + {{r}_{1}}({{x}_{1}},{{x}_{2}},t)\frac{{\partial u}}{{\partial {{x}_{1}}}} + \\ + \;{{r}_{2}}({{x}_{1}},{{x}_{2}},t)\frac{{\partial u}}{{\partial {{x}_{2}}}} - {{q}_{1}}({{x}_{1}},{{x}_{2}},t)u({{x}_{1}},{{x}_{2}},t) - {{q}_{2}}({{x}_{1}},{{x}_{2}},t)u({{x}_{1}},{{x}_{2}},t) + f({{x}_{1}},{{x}_{2}},t), \\ \end{gathered} $

(6.2)

$\left\{ \begin{gathered} u(0,{{x}_{2}},t) = {{\mu }_{{11}}}({{x}_{2}},t),\quad u({{l}_{1}},{{x}_{2}},t) = {{\mu }_{{12}}}({{x}_{2}},t), \hfill \\ u({{x}_{1}},0,t) = {{\mu }_{{21}}}({{x}_{1}},t),\quad u({{x}_{1}},{{l}_{2}},t) = {{\mu }_{{22}}}({{x}_{1}},t), \hfill \\ \end{gathered} \right.$

(6.3)

$u({{x}_{1}},{{x}_{2}},0) = {{u}_{0}}({{x}_{1}},{{x}_{2}}).$

Рассмотрим сетку $x_{k}^{{({{i}_{k}})}} = {{i}_{k}}{{h}_{k}}$, $k = 1,\;2$, ${{t}_{j}} = j\tau $, где ${{i}_{k}} = 0,\;1,\; \ldots ,\;{{N}_{k}}$, ${{h}_{k}} = {{l}_{k}}{\text{/}}{{N}_{k}}$, $j = 0,\;1,\; \ldots ,\;m$, $\tau = T{\text{/}}m$. Вводим один дробный шаг ${{t}_{{j + \tfrac{1}{2}}}} = {{t}_{j}} + 0.5\tau $. Обозначим через $y_{{{{i}_{1}},{{i}_{2}}}}^{{j + \tfrac{k}{p}}} = {{y}^{{j + \tfrac{k}{p}}}} = y({{i}_{1}}{{h}_{1}},{{i}_{2}}{{h}_{2}},(j + 0.5k)\tau )$ $y_{{{{i}_{1}},{{i}_{2}}}}^{{j + \tfrac{k}{p}}} = {{y}^{{j + \tfrac{k}{p}}}} = y({{i}_{1}}{{h}_{1}},{{i}_{2}}{{h}_{2}},(j + 0.5k)\tau )$, $k = 1,\;2$, сеточную функцию.

Напишем локально-одномерную схему

(6.4)

$\begin{gathered} \varepsilon \tfrac{{{{y}^{{j + \tfrac{1}{2}}}} - {{y}^{j}}}}{\tau } + \tfrac{1}{2}\tfrac{1}{{{\text{Г}}(2 - \alpha )}}\sum\limits_{s = 1}^{2j + 1} {\left( {t_{{j + \tfrac{{2 - s}}{2}}}^{{1 - \alpha }} - t_{{j + \tfrac{{1 - s}}{2}}}^{{1 - \alpha }}} \right)y_{{\overline t }}^{{\tfrac{s}{2}}}} = {{{\tilde {\Lambda }}}_{1}}{{y}^{{j + \tfrac{1}{2}}}} + {{\varphi }_{1}}, \hfill \\ \varepsilon \tfrac{{{{y}^{{j + 1}}} - {{y}^{{j + \tfrac{1}{2}}}}}}{\tau } + \tfrac{1}{2}\tfrac{1}{{{\text{Г}}(2 - \alpha )}}\sum\limits_{s = 1}^{2j + 2} {\left( {t_{{j + \tfrac{{3 - s}}{2}}}^{{1 - \alpha }} - t_{{j + \tfrac{{2 - s}}{2}}}^{{1 - \alpha }}} \right)y_{{\overline t }}^{{\tfrac{s}{2}}}} = {{{\tilde {\Lambda }}}_{2}}{{y}^{{j + 1}}} + {{\varphi }_{2}}, \hfill \\ \end{gathered} $

(6.5)

$\begin{gathered} y_{{0,{{i}_{2}}}}^{{j + \tfrac{1}{2}}} = {{\mu }_{{11}}}\left( {{{i}_{2}}{{h}_{2}},{{t}_{{j + \tfrac{1}{2}}}}} \right),\quad y_{{{{N}_{1}},{{i}_{2}}}}^{{j + \tfrac{1}{2}}} = {{\mu }_{{12}}}\left( {{{i}_{2}}{{h}_{2}},{{t}_{{j + \tfrac{1}{2}}}}} \right), \hfill \\ y_{{{{i}_{1}},0}}^{{j + 1}} = {{\mu }_{{21}}}\left( {{{i}_{1}}{{h}_{1}},{{t}_{{j + 1}}}} \right),\quad y_{{{{i}_{1}},{{N}_{2}}}}^{{j + 1}} = {{\mu }_{{22}}}\left( {{{i}_{1}}{{h}_{1}},{{t}_{{j + 1}}}} \right), \hfill \\ \end{gathered} $

(6.6)

$\begin{gathered} y_{{{{i}_{1}},{{i}_{2}}}}^{0} = {{u}_{0}}\left( {{{i}_{1}}{{h}_{1}},{{i}_{2}},{{h}_{2}}} \right), \\ {{{\tilde {\Lambda }}}_{k}}{{y}^{{j + \tfrac{k}{p}}}} = {{\varkappa }_{k}}{{\left( {{{a}_{k}}y_{{\mathop {\bar {x}}\nolimits_k }}^{{j + \tfrac{k}{p}}}} \right)}_{{{{x}_{k}}}}} + b_{k}^{ + }a_{k}^{{( + 1)}}y_{{{{x}_{k}}}}^{{j + \tfrac{k}{p}}} + b_{k}^{ - }{{a}_{k}}y_{{\mathop {\bar {x}}\nolimits_k }}^{{j + \tfrac{k}{p}}} - {{d}_{k}}{{y}^{{j + \tfrac{k}{p}}}},\quad k = 1,\;2, \\ {{\varphi }_{k}} = \tfrac{1}{2}f({{x}_{1}},{{x}_{2}},{{t}_{{j + 0.5k}}})\quad {\text{или}}\quad {{\varphi }_{1}} = 0,\quad {{\varphi }_{2}} = f({{x}_{1}},{{x}_{2}},{{t}_{{j + 1}}}). \\ \end{gathered} $

Приведем расчетные формулы для решения задачи (6.4)–(6.6).

На первом этапе находим решение $y_{{{{i}_{1}},{{i}_{2}}}}^{{j + \tfrac{1}{2}}}$. Для этого при каждом значении ${{i}_{2}} = \overline {1,{{N}_{2}} - 1} $ решается следующая задача:

(6.7)

$\begin{gathered} {{A}_{{1({{i}_{1}},{{i}_{2}})}}}y_{{{{i}_{1}} - 1,{{i}_{2}}}}^{{j + \tfrac{1}{2}}} - {{C}_{{1({{i}_{1}},{{i}_{2}})}}}y_{{{{i}_{1}},{{i}_{2}}}}^{{j + \tfrac{1}{2}}} + {{B}_{{1({{i}_{1}},{{i}_{2}})}}}y_{{{{i}_{1}} + 1,{{i}_{2}}}}^{{j + \tfrac{1}{2}}} = - F_{{1({{i}_{1}},{{i}_{2}})}}^{{j + \tfrac{1}{2}}},\quad 0 < {{i}_{1}} < {{N}_{1}}, \\ y_{{0,{{i}_{2}}}}^{{j + \tfrac{1}{2}}} = {{\mu }_{{11}}}\left( {{{i}_{2}}{{h}_{2}},{{t}_{{j + \tfrac{1}{2}}}}} \right),\quad y_{{{{N}_{1}},{{i}_{2}}}}^{{j + \tfrac{1}{2}}} = {{\mu }_{{12}}}\left( {{{i}_{2}}{{h}_{2}},{{t}_{{j + \tfrac{1}{2}}}}} \right), \\ \end{gathered} $

где

${{A}_{{1({{i}_{1}},{{i}_{2}})}}} = \frac{{{{{({{\varkappa }_{1}})}}_{{{{i}_{1}},{{i}_{2}}}}}{{{({{a}_{1}})}}_{{{{i}_{1}},{{i}_{2}}}}}}}{{h_{1}^{2}}} - \frac{{{{{(b_{1}^{ - })}}_{{{{i}_{1}},{{i}_{2}}}}}{{{({{a}_{1}})}}_{{{{i}_{1}},{{i}_{2}}}}}}}{{{{h}_{1}}}},$

${{B}_{{1({{i}_{1}},{{i}_{2}})}}} = \frac{{{{{({{\varkappa }_{1}})}}_{{{{i}_{1}},{{i}_{2}}}}}{{{({{a}_{1}})}}_{{{{i}_{1}} + 1,{{i}_{2}}}}}}}{{h_{1}^{2}}} + \frac{{{{{(b_{1}^{ + })}}_{{{{i}_{1}},{{i}_{2}}}}}{{{({{a}_{1}})}}_{{{{i}_{1}} + 1,{{i}_{2}}}}}}}{{{{h}_{1}}}},$

${{C}_{{1({{i}_{1}},{{i}_{2}})}}} = {{A}_{{1({{i}_{1}},{{i}_{2}})}}} + {{B}_{{1({{i}_{1}},{{i}_{2}})}}} + \frac{\varepsilon }{\tau } + \frac{1}{{2{{\tau }^{\alpha }}{\text{Г}}(2 - \alpha )}} + \frac{1}{p}{{d}_{{1({{i}_{1}},{{i}_{2}})}}},$

$F_{{1({{i}_{1}},{{i}_{2}})}}^{{j + \tfrac{1}{2}}} = \frac{\varepsilon }{\tau }y_{{{{i}_{1}},{{i}_{2}}}}^{j} + \frac{1}{{2{{\tau }^{\alpha }}{\text{Г}}(2 - \alpha )}}y_{{{{i}_{1}},{{i}_{2}}}}^{j} + \frac{1}{{\tau {\text{Г}}(2 - \alpha )}}\sum\limits_{s = 1}^{2j} {\left( {t_{{j + \tfrac{{2 - s}}{2}}}^{{1 - \alpha }} - t_{{j + \tfrac{{1 - s}}{2}}}^{{1 - \alpha }}} \right)y_{{\overline t }}^{{\tfrac{s}{2}}}} + {{\varphi }_{1}}_{{({{i}_{1}},{{i}_{2}})}}.$

На втором этапе находим решение $y_{{{{i}_{1}},{{i}_{2}}}}^{{j + 1}}.$ Для этого, как и в первом случае, при каждом значении ${{i}_{1}} = \overline {1,{{N}_{1}} - 1} $ решается задача

$\begin{gathered} {{A}_{{2({{i}_{1}},{{i}_{2}})}}}y_{{{{i}_{1}},{{i}_{2}} - 1}}^{{j + 1}} - {{C}_{{2({{i}_{1}},{{i}_{2}})}}}y_{{{{i}_{1}},{{i}_{2}}}}^{{j + 1}} + {{B}_{{2({{i}_{1}},{{i}_{2}})}}}y_{{{{i}_{1}},{{i}_{2}} + 1}}^{{j + 1}} = - F_{{2({{i}_{1}},{{i}_{2}})}}^{{j + 1}},\quad 0 < {{i}_{2}} < {{N}_{2}}, \\ y_{{{{i}_{1}},0}}^{{j + 1}} = {{\mu }_{{21}}}\left( {{{i}_{1}}{{h}_{1}},{{t}_{{j + 1}}}} \right),\quad y_{{{{i}_{1}},{{N}_{2}}}}^{{j + 1}} = {{\mu }_{{22}}}\left( {{{i}_{1}}{{h}_{1}},{{t}_{{j + 1}}}} \right), \\ \end{gathered} $

(6.8)

$\begin{gathered} {{A}_{{2({{i}_{1}},{{i}_{2}})}}} = \frac{{{{{({{\varkappa }_{2}})}}_{{{{i}_{1}},{{i}_{2}}}}}{{{({{a}_{2}})}}_{{{{i}_{1}},{{i}_{2}}}}}}}{{h_{2}^{2}}} - \frac{{{{{(b_{2}^{ - })}}_{{{{i}_{1}},{{i}_{2}}}}}{{{({{a}_{2}})}}_{{{{i}_{1}},{{i}_{2}}}}}}}{{{{h}_{2}}}}, \\ {{B}_{{2({{i}_{1}},{{i}_{2}})}}} = \frac{{{{{({{\varkappa }_{2}})}}_{{{{i}_{1}},{{i}_{2}}}}}{{{({{a}_{2}})}}_{{{{i}_{1}},{{i}_{2}} + 1}}}}}{{h_{2}^{2}}} + \frac{{{{{(b_{2}^{ + })}}_{{{{i}_{1}},{{i}_{2}}}}}{{{({{a}_{2}})}}_{{{{i}_{1}},{{i}_{2}} + 1}}}}}{{{{h}_{2}}}}, \\ \end{gathered} $

$\begin{gathered} {{C}_{{2({{i}_{1}},{{i}_{2}})}}} = {{A}_{{2({{i}_{1}},{{i}_{2}})}}} + {{B}_{{2({{i}_{1}},{{i}_{2}})}}} + \frac{\varepsilon }{\tau } + \frac{1}{{2{{\tau }^{\alpha }}{\text{Г}}(2 - \alpha )}} + \frac{1}{p}{{d}_{{2({{i}_{1}},{{i}_{2}})}}}, \\ F_{{2({{i}_{1}},{{i}_{2}})}}^{{j + 1}} = \frac{\varepsilon }{\tau }y_{{{{i}_{1}},{{i}_{2}}}}^{{j + \tfrac{1}{2}}} + \frac{1}{{2{{\tau }^{\alpha }}{\text{Г}}(2 - \alpha )}}y_{{{{i}_{1}},{{i}_{2}}}}^{{j + \tfrac{1}{2}}} + \frac{1}{{\tau {\text{Г}}(2 - \alpha )}}\sum\limits_{s = 1}^{2j + 1} {\left( {t_{{j + \tfrac{{3 - s}}{2}}}^{{1 - \alpha }} - t_{{j + \tfrac{{2 - s}}{2}}}^{{1 - \alpha }}} \right)y_{{\overline t }}^{{\tfrac{s}{2}}}} + {{\varphi }_{{2({{i}_{1}},{{i}_{2}})}}}. \\ \end{gathered} $

Каждая из задач (6.7), (6.8) решается методом прогонки (см. [32]).

7. ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ

Коэффициенты уравнения и граничных условий задачи (1.1)–(1.3) подбираются таким образом, чтобы точным решением задачи была функция $u(x,t) = {{t}^{3}}(x_{1}^{4} - {{l}_{1}}x_{1}^{3})(x_{2}^{4} - {{l}_{2}}x_{2}^{3})$.

Ниже в табл. 1 и 2 при уменьшении размера сетки приведены максимальное значение погрешности ($z = y - u$) и порядок сходимости в норме ${{\left\| {\, \cdot \,} \right\|}_{{C(\mathop {\bar {w}}\nolimits_{h\tau } )}}}$, где ${{\left\| y \right\|}_{{C({{{\bar {w}}}_{{h\tau }}})}}} = \mathop {max}\limits_{({{x}_{i}},{{t}_{j}}) \in {{{\bar {w}}}_{{h\tau }}}} \left| y \right|$ при $0 < \alpha < 1$, когда ${{h}^{2}} = \tau $. Погрешность уменьшается в соответствии с порядком аппроксимации