Журнал вычислительной математики и математической физики, 2021, T. 61, № 8, стр. 1353-1362

1. ВВОДНАЯ ИНФОРМАЦИЯ

Настоящая статья посвящена исследованию временной асимптотики среднего потока частиц, рассеивающихся с размножением в случайной среде. С этой целью разработано осреднение соответствующих аналитических и численно-статистических оценок (т.е. оценок метода Монте-Карло), получаемых для детерминированных реализаций среды.

Известно (см., например, [1]), что плотность потока частиц $\Phi (t,{\mathbf{r}},{\mathbf{v}})$ в системе, образованной размножающей средой в области ${\mathbf{D}}$, в достаточно широких условиях является асимптотически экспоненциальной по времени $t$

Временнáя постоянная $\lambda $ является ведущим характеристическим числом соответствующего однородного стационарного кинетического уравнения: Здесь $\Phi \equiv \Phi ({\mathbf{r}},{\mathbf{v}})$ – стационарная плотность потока (характеристическая функция уравнения (1.1)), $\Phi {\text{'}} \equiv \Phi ({\mathbf{r}},{\mathbf{v}}{\text{'}})$; $\sigma \equiv \sigma ({\mathbf{r}},{\mathbf{v}})$ – полное сечение (коэффициент ослабления); $\sigma = {{\sigma }_{s}} + {{\sigma }_{f}} + {{\sigma }_{c}}$, ${{\sigma }_{s}}$ — сечение рассеяния, ${{\sigma }_{f}}$ – сечение деления (${{w}_{s}}$, ${{w}_{f}}$ – соответствующие индикатрисы), ${{\sigma }_{c}}$ – сечение поглощения; $\nu $ – число частиц, вылетающих из точки деления; ${\mathbf{v}} = {v}\omega $ – вектор скорости, $\omega $ – единичный вектор направления, ${v} = \left| {\mathbf{v}} \right|$; ${\mathbf{r}}$ – пространственная точка.

С целью построения и исследования алгоритмов метода Монте-Карло далее в качестве соответствующей уравнению (1.1) (см., например, [2]) математической модели процесса переноса используется однородная обрывающаяся с вероятностью единица цепь Маркова, состояниями которой являются фазовые точки последовательных “столкновений частицы с элементами вещества”, т.е. точки, в которых происходят мгновенные изменения скорости частицы. Указанная цепь Маркова ${{x}_{0}}$, ${{x}_{1}}$, …, ${{x}_{N}}$ рассматривается в фазовом пространстве $X = R \times V \times T$ координат, скоростей и времени, т.е. ${{x}_{n}} = ({{{\mathbf{r}}}_{n}},{{{\mathbf{v}}}_{n}},{{t}_{n}})$, где ${{{\mathbf{r}}}_{n}}$ – точка $n$-го столкновения, ${{{\mathbf{v}}}_{n}}$ – скорость непосредственно перед столкновением, а ${{t}_{n}} = {{t}_{{n - 1}}} + \left| {{{{\mathbf{r}}}_{{n - 1}}} - {{{\mathbf{r}}}_{n}}} \right|{\text{/}}\left| {{{{\mathbf{v}}}_{{n - 1}}}} \right|$ – время “жизни” сталкивающейся частицы. Рассматриваемая цепь определяется плотностью $f(x)$ распределения начального столкновения ${{x}_{0}}$ и плотностью $k(x{\text{'}},x)$ перехода из состояния $x{\text{'}}$ в $x$, причем предполагается, что

т.е. цепь обрывается с вероятностью единица, и среднее число переходов конечно. Условие (1.2) выполняется, например, для ограниченной системы (см. [2], [3]). Субстохастическое ядро $k(x{\text{'}},x)$ получается (см. [2], [3]) из характеризации процесса переноса, которая определяет и уравнение (1.1). Отношения ${{\sigma }_{s}}(x){\text{/}}\sigma (x)$, ${{\sigma }_{f}}(x){\text{/}}\sigma (x)$ и ${{\sigma }_{c}}(x){\text{/}}\sigma (x)$ равны вероятностям рассеяния, деления и поглощения непосредственно после столкновения в фазовой точке $x$, а плотность распределения длины $\ell $ свободного пробега из ${\mathbf{r}}{\text{'}}$ в ${\mathbf{r}}$ равна $p(\ell ) = \sigma (r(\ell ))exp( - {{\tau }_{{{\text{op}}}}}(\ell ))$, где ${{\tau }_{{{\text{op}}}}}(\ell )$ – оптическая длина пробега (см. [2], [3]). Видно, что плотность столкновений $\varphi (x) = \sum\nolimits_{n = 0}^\infty {{{\varphi }_{n}}} (x)$, где ${{\varphi }_{n}}(x)$ – плотность распределения столкновений номера $n$, представляет собой ряд Неймана для интегрального уравнения II рода где $K$ – интегральный оператор с ядром $k( \cdot , \cdot )$. Как указано, например, в [2], [3], несмотря на наличие в ядре $k(x{\text{'}},x)$ обобщенных множителей $\delta ({\mathbf{v}}{\text{'/}}{\kern 1pt} {\text{|}}{\mathbf{v}}{\text{'|}} - ({\mathbf{r}} - {\mathbf{r}}{\text{'}}){\text{/|}}{\mathbf{r}} - {\mathbf{r}}{\text{'|}})$ и $\delta \left( {t - t{\text{'}} - \left| {{\mathbf{r}} - {\mathbf{r}}{\text{'}}{\kern 1pt} } \right|{\text{/}}\left| {{\mathbf{v}}{\text{'}}{\kern 1pt} } \right|} \right)$, оператор $K$ можно рассматривать действующим из ${{L}_{1}}(X)$ в ${{L}_{1}}(X)$ тем более, что в рассматриваемой задаче все функции неотрицательны. При выполнении условия (1.2) имеем ${{\left\| K \right\|}_{{{{L}_{1}}}}} < 1$, и, следовательно, спектральный радиус оператора $\rho (K) < 1$.

Используемая обычно в теории переноса интенсивность излучения $\Phi (x)$ (плотность потока частиц) связана с плотностью столкновений соотношением $\varphi (x) = \sigma (x)\Phi (x)$. Метод Монте-Карло, как правило, используется для оценки линейных функционалов вида ${{J}_{h}} = (\varphi ,h) = (\sigma \Phi ,h)$, $h \in {{L}_{\infty }}$. Для построения весовых алгоритмов метода Монте-Карло используется цепь Маркова с начальной плотностью ${{f}_{0}}(x)$ и плотностью перехода $p(x{\text{'}},x)$, содержащей указанные обобщенные множители, например, цепь столкновений для других значений параметров $\sigma $, ${{\sigma }_{s}}$, ${{\sigma }_{f}}$, ${{\sigma }_{c}}$. При этом вводятся вспомогательные веса по формулам

Если выполняются “условия несмещенности”: то (см. [2], [3]) Если, кроме того, $\rho ({{K}_{p}}) < 1$, где ${{K}_{p}}$ – оператор с ядром ${{k}^{2}}(x{\text{'}},x){\text{/}}p(x{\text{'}},x)$, и ${{f}^{2}}{\text{/}}{{f}_{0}} \in {{L}_{1}}(X)$, то $D\xi < + \infty $. Случайная величина $\xi $ называется оценкой по столкновениям для функционала ${{J}_{h}}$.

Отметим, что новая скорость обычно моделируется следующим образом: с вероятностью ${{\sigma }_{s}}(x{\text{'}}){\text{/}}\sigma (x{\text{'}})$ – согласно индикатрисе ${{w}_{s}}({\mathbf{v}}{\text{'}} \to {\mathbf{v}};{\mathbf{r}}{\text{'}})$, а с вероятностью ${{\sigma }_{f}}(x{\text{'}}){\text{/}}\sigma (x{\text{'}})$ – согласно ${{w}_{f}}({\mathbf{v}}{\text{'}} \to {\mathbf{v}};{\mathbf{r}}{\text{'}})$; для построения весовой модификации номер типа моделирования (т.е. типа столкновения) вводится в число координат фазового пространства (см. [2], [3]).

2. ОЦЕНКА ВЕЛИЧИНЫ $\lambda $

В этом разделе рассматриваются два подхода к оценке временной константы $\lambda $ размножения частиц, которая определяет асимптотику $Cexp(\lambda t)$ функции $\Phi $ в детерминированной среде (см., например, [1]). Известно (см. [1]), что если величину $\lambda {\text{/}}{v}$ (${v}$ – скорость частицы) добавить к сечению поглощения, то система становится критической, т.е. $\lambda $ – характеристическое число уравнения (1.1).

2.1. Дифференцируя уравнение (1.1) в операторном виде $k$ раз по $\tau $, получаем

или ${{R}_{1}}{{\Phi }^{{(k)}}} = - (k{\text{/}}{v}){{\Phi }^{{(k - 1)}}}$. Следовательно, При выполнении стандартных спектральных свойств резольвентного оператора (см. [1]) имеем $k{{\Phi }^{{(k - 1)}}}{\text{/}}{{\Phi }^{{(k)}}} \to {{\tau }_{1}}$, $k \to \infty $. Отсюда получаем следующий предельный вид уравнения (2.1): Таким образом, Для оценки производных по $\tau $ от линейного функционала $J$ моделируется цепь столкновений с параметрами $\tau = 0$, $\nu \equiv 1$, причем ${{Q}_{n}} = {{\tilde {\nu }}_{n}}exp( - \tau {{t}_{n}})$, где ${{t}_{n}}$ – полное время пробега частицы до ${{r}_{n}}$ и ${{\tilde {\nu }}_{n}}$ – вес, учитывающий деления для простейшей модификации процесса без ветвления (см. [2]). Отсюда Поскольку $\tau {\text{/}}{v}$ добавляется к сечению поглощения, то величина $\left\| {{{K}_{p}}} \right\|$, модифицированная заменами ${{\sigma }_{f}} \mapsto {{\sigma }_{f}} + {{\sigma }_{c}}$, $\nu \mapsto \nu {{\sigma }_{f}}{\text{/}}({{\sigma }_{f}} + {{\sigma }_{c}})$, может быть сделана меньше единицы выбором достаточно большого $\tau $. Нетрудно обосновать здесь несмещенность соответствующих оценок ${{\xi }^{{(k)}}}$ производных ${{J}^{{(k)}}}$ и конечность их дисперсий при $\left\| {{{K}_{p}}} \right\| < 1$ на основе векторного подхода; условия конечности дисперсий менее ограничительны, если моделируется ветвление (см. [3]).

Рассмотренный подход был сформулирован в [4] и детально разработан в [5]. Его недостатком является необходимость трудоемких расчетов кратных производных ${{\xi }^{{(k)}}}$, дисперсии которых весьма сильно возрастают при увеличении $k$ в реальных задачах. Тем не менее в [5] на основе дополнительного вычисления производных от оценок $\lambda $ по значениям кусочно-постоянной случайной функции $\sigma (\tau )$ были получены достаточно точные тестовые оценки величин ${\text{E}}\lambda $, ${\text{D}}\lambda $ для модельной сферически-симметричной системы; они будут использованы в разд. 4 настоящей работы.

Далее сформулирован более универсальный подход к оценке величины $\lambda $ на основе использования функции Грина по параметру времени $t$.

2.2. Пусть ${{\varphi }_{0}}(x;{{{\mathbf{r}}}_{0}},{{{\mathbf{v}}}_{0}})$ — плотность столкновений (по аргументу $x$) от одного столкновения в точке $({{{\mathbf{r}}}_{0}},{{{\mathbf{v}}}_{0}},0)$, т.е. для $f(x) = \delta ({\mathbf{r}} - {{{\mathbf{r}}}_{0}})\delta ({\mathbf{v}} - {{{\mathbf{v}}}_{0}})\delta (t)$.

Функционал

можно представить в виде (см. [5]) где Предполагается, что $f({\mathbf{r}},{\mathbf{v}}, - t) \equiv 0$, и вследствие этого $F({\mathbf{r}},{\mathbf{v}}, - t) \equiv 0$, при $t > 0$.

Символом $f_{t}^{{(m)}}$ далее обозначается $m$-кратная производная от функции $f$ по $t$.

Лемма 1 (см. [2]). Пусть точка $({{{\mathbf{r}}}_{0}},{{{\mathbf{v}}}_{0}})$ распределена для ${{t}_{0}} \equiv 0$ с плотностью ${{f}_{0}}({\mathbf{r}},{\mathbf{v}})$, выполняются условия (1.3),

и $F(x) < C < + \infty $. Тогда выполняется соотношение ${{J}^{{(m)}}}(t) = E\xi _{t}^{{(m)}}$, гдепричем $D\xi _{t}^{{(m)}} < + \infty $, $m = 0,\;1,\; \ldots ,\,n$.

Отметим, что в [2] оценка типа $\xi $ (т.е. $\xi _{t}^{{(m)}}$ при $m = 0$) используется для решения нестационарных задач оптического зондирования с реальными источниками излучения. В настоящей работе, следуя [5], на основе $\xi $ и $\xi {\text{'}}$ со вспомогательной плотностью $f(x)$ строятся оценки параметра $\lambda $ экспоненциальной асимптотики потока частиц по времени.

Известно, что при выполнении довольно общих условий в случае источника, локализованного в точке $({{{\mathbf{r}}}_{0}},{{{\mathbf{v}}}_{0}},0)$, имеет место асимптотическое при $t \to \infty $ соотношение (см. [1])

где $\lambda $ – ведущее характеристическое число уравнения (1.1). Эти условия, в частности, имеют место для односкоростного процесса переноса частиц в ограниченной среде с достаточно быстро убывающей по времени плотностью источника. Сказанное выше дает возможность построить оценку величины $\lambda $.

Теорема 1. Если выполняются соотношения

соотношение (2.4) и условия леммы 1, то

Доказательство. Прямое интегрирование с учетом леммы 1 и соотношений (2.4), (2.5) дает равенства

причем $\varepsilon (t)$, ${{\varepsilon }_{1}}(t) \to 0$ для $t \to + \infty $. Интегрируя функцию $J{\text{'}}(t)$ в пределах $({{\tau }_{0}}, + \infty )$ при ${{\tau }_{0}} \to \infty $ для $\lambda < 0$, получаем В случае $\lambda > 0$ тот же результат получается путем введения дополнительного поглощения с коэффициентом $\sigma _{c}^{{(0)}} > \lambda {\text{/}}{v}$. Это завершает доказательство теоремы 1.

3. ОЦЕНКА СРЕДНЕГО ПОТОКА ЧАСТИЦ В СТОХАСТИЧЕСКОЙ СРЕДЕ

3.1. Для простоты изложения далее рассматривается односкоростной процесс переноса частиц; предполагается, что $\sigma \equiv \sigma (r)$ – случайное поле, причем отношения ${{\sigma }_{s}}{\text{/}}\sigma $, ${{\sigma }_{f}}{\text{/}}\sigma $, а также индикатрисы рассеяния и деления фиксированы.

Если ${{h}_{0}}(r) = {{I}_{{\mathbf{D}}}}(r){\text{/}}\sigma (r)$, где ${{I}_{{\mathbf{D}}}}$ – индикатор области ${\mathbf{D}}$, то функционал $J(t,\sigma )$ представляет собой полный поток частиц в области ${\mathbf{D}}$ для заданного момента времени $t$. Предполагая гауссовость случайной величины $\lambda (\sigma )$ и равномерность (по $\sigma $) предельного перехода $J(t,\sigma ){{ \to }_{{t \to \infty }}}C(\sigma ){{{\text{e}}}^{{\lambda (\sigma )t}}}$, можно оценить асимптотику функции ${\text{E}}J(t,\sigma ) = {{J}_{t}}$ при $t \to \infty $:

где $a = {\text{E}}\lambda (\sigma )$, ${{d}^{2}} = {\text{D}}\lambda (\sigma )$ – математическое ожидание и дисперсия соответствующей величины. При этом также предполагается, что множители $C(\sigma )$ и ${{{\text{e}}}^{{\lambda (\sigma )t}}}$ в асимптотике слабо коррелированы и, следовательно, $C \approx {\text{E}}C(\sigma )$. Сделанные предположения являются естественными, например, для малого случайного возмущения многослойной (многокомпонентной) среды при условии $d \ll \left| a \right|$; их эффективность проверена в настоящей работе тестовыми расчетами (см. далее разд. 4). Используя интегральную формулу (2.3.15), № 11, из [6], далее получаем Следовательно, можно предположить, что Отметим, что формулы (3.1), (3.2) могут служить основой для численных исследований конкретных вариантов задачи. Определяемый формулой (3.1) закон роста среднего числа частиц можно назвать “сверхэкспоненциальным”. Более общее и практически удобное определение сверхэкспоненциальности можно связать с увеличением коэффициента роста $n(t + \Delta t){\text{/}}n(t)$ при увеличении $t$.

В реальных задачах выполняется соотношение $ - \infty < {{\lambda }_{1}} < \lambda (\sigma ) < {{\lambda }_{2}} < + \infty $; следовательно, полученная асимптотика, по-видимому, может аппроксимировать ${{J}_{t}}$ лишь в некотором интервале $0 < {{T}_{1}} \leqslant t \leqslant {{T}_{2}} < + \infty $; в связи с этим требуются дополнительные численные исследования.

3.2. Практически важными здесь являются величины E$\lambda (\sigma )$ и D$\lambda (\sigma )$. Логически простейший (прямой) способ их оценки методом Монте-Карло состоит в реализации достаточно точных оценок величины $J{\kern 1pt} {\text{'}}(t,\sigma ){\text{/}}J(t,\sigma )$ для выборки $\sigma $ достаточно большого объема. Однако такой способ может быть слишком трудоемким для реалистических моделей среды и процесса переноса. Поэтому в [7] для построения рандомизированного алгоритма используется соотношение ($J(t,\sigma )$ заменяется на $J(\sigma )$):

где ${{\tilde {J}}_{0}}$ – предварительная статистическая оценка величины ${\text{E}}J(\sigma )$, которую здесь можно детерминировать. Простейшая (элементарная) несмещенная рандомизированная оценка величины ${{\lambda }_{n}}$ на основе леммы 1 строится путем реализации $n + 1$ условно независимых траекторий частиц для выбранного значения $\sigma :{{\lambda }_{n}} = {\text{E}}{{\tilde {\lambda }}_{n}}$, где

С помощью аналогичного разложения строится оценка величины ${\text{E}}{{\lambda }^{2}}(\sigma )$ (см. [7]). Видно, что ${{\tilde {\lambda }}_{0}}$ из (3.3) представляет собой статистическую оценку величины $J_{t}^{'}{\text{/}}{{J}_{t}}$. В данном случае значения $J_{t}^{'}$ и ${{J}_{t}}$ оцениваются методом двойной рандомизации (см. [3]) одновременно. Для определенности сформулируем это в виде отдельного утверждения.

Лемма 2. В условиях леммы 1 справедливо равенство

где ${{\tilde {J}}_{t}}$, $\tilde {J}_{t}^{'}$ – соответствующие статистические оценки, получаемые методом двойной рандомизации.

Для каждой реализации среды здесь можно строить лишь одну траекторию частиц, используя (2.3) для $m = 0;\;1$. Если трудоемкость моделирования среды существенно превосходит трудоемкость моделирования траектории, то целесообразно строить $r$ условно-независимых траекторий для каждой реализации среды. Оптимальное значение $r$ оценивается при этом по аналогии с параметром метода расщепления (см. [9]).

Отметим, что дисперсия величины $\tilde {J}_{t}^{'}{\text{/}}{{\tilde {J}}_{t}}$ оценивается сверху с помощью линеаризации дроби по формуле

3.3. В [5] построен алгоритм оценки величин ${\text{E}}\lambda $, ${\text{D}}\lambda $ для среды со случайной кусочно-постоянной плотностью $\rho $ на основе разложения $\lambda (\rho )$ в ряд Тейлора по $({{\rho }_{1}},\; \ldots ,\;{{\rho }_{m}})$ в точке $({\text{E}}{{\rho }_{1}},\; \ldots ,\;{\text{E}}{{\rho }_{m}})$, причем для дисперсии был использован отрезок ряда до первого порядка включительно, а для математических ожиданий – до второго. В предположении независимости случайных величин ${\text{\{ }}{{\rho }_{i}}{\text{\} }}$ выполняются соотношения

Оценку дисперсии можно уточнить, используя слагаемые второго порядка; в рассмотренном далее примере это уточнение оказалось несущественным. Таким образом, оценка (3.6) сводится к оценке производных первого и второго порядков от $\lambda $ по ${{\rho }_{i}}$.

После замены $\lambda $ на итерационное резольвентное приближение (см. п. 2.1) такие оценки определяются смешанными производными

Величины (3.7) можно вычислять, как указано в [5], используя метод Монте-Карло со вспомогательными весами, соответствующими вариациям параметров $\tau $ и ${\text{\{ }}{{\rho }_{i}}{\text{\} }}$, $i = 1,\;2,\; \ldots ,\;n$.

Полученные таким образом результаты можно независимо контролировать более трудоемкими расчетами на основе (3.3).

4. РЕЗУЛЬТАТЫ РАСЧЕТОВ

4.1. Для проведения тестовых расчетов рассматривался односкоростной процесс переноса частиц в сферически-симметричной среде с кусочно-постоянной случайной плотностью $\rho = \rho (r)$ в шаре радиуса $R = 7.72043$ с макроскопическими сечениями $\rho {{\sigma }^{{(0)}}}$, $\rho \sigma _{s}^{{(0)}}$, $\rho \sigma _{f}^{{(0)}}$, где

Для построения реализации среды шар делится на $m$ одинаковых по объему сферических слоев; в каждом слое случайная величина $\rho \equiv {{\rho }_{i}}$ выбирается независимо и равномерно на отрезке $[1 - \varepsilon ,\;1 + \varepsilon ]$.

Для построения эффективного алгоритма метода Монте-Карло на основе леммы 2 в сформулированную модель было введено поглощение с постоянным неслучайным коэффициентом ${{\sigma }_{c}}{\text{/}}{v}$, который приводит к замене $\lambda \mapsto \lambda - {{\sigma }_{c}}{\text{/}}{v}$ $\forall \sigma $. Отметим, что такой прием является универсальным и может существенно повысить эффективность весового метода, исключая необходимость ветвления моделируемых траекторий, как это рассмотрено далее.

Используя уравнение переноса (см. [2], [3]), можно сделать замену

В численном эксперименте моделировался процесс переноса с константами $\sigma _{s}^{ * } = {{\sigma }_{s}}$, $\sigma _{f}^{ * } = {{\sigma }_{f}} + {{\sigma }_{c}}$, $\nu {\kern 1pt} * = 1$. Вспомогательные веса при этом определяются формулой ${{Q}_{n}} = {{[\nu {{\sigma }_{f}}{\text{/}}({{\sigma }_{f}} + {{\sigma }_{c}})]}^{{{{n}_{1}}}}}$, где ${{n}_{1}}$ – число делений, предшествующих данному столкновению (см. [5]). Было использовано значение ${{\sigma }_{c}} = 0.059$, для которого $\nu {{\sigma }_{f}}{\text{/}}({{\sigma }_{f}} + {{\sigma }_{c}}) < 1$ и тем самым (см. [2], [3]) $\rho ({{K}_{p}}) < 1$ $\forall \sigma $. Плотность распределения первых столкновений взята в виде где ${{f}_{d}}({\mathbf{r}}) = Csin(\unicode{230} (\rho )r){\text{/}}r$ – улучшенное диффузионное приближение к пространственной характеристической функции для $\sigma = 1$, $\unicode{230} (1) = 0.3739866$ (см. [8]). Для оценки величин ${\text{E}}\lambda $, ${\text{D}}\lambda $ полагали также $h({\mathbf{r}},{\mathbf{v}}) = {{h}_{0}}({\mathbf{r}}){\text{/}}\sigma ({\mathbf{r}})$, где ${{h}_{0}}({\mathbf{r}}) = sin(\unicode{230} (\rho )r){\text{/}}r$, причем (см. [8]) При этом ${{J}_{t}} = (\Phi ,{{h}_{0}}{{f}_{{\text{t}}}}{\text{/}}{{f}_{0}})$, т.е. вычисляется функционал от потока частиц. Расчеты показали, что использование таких функциональных параметров алгоритма существенно улучшает сходимость в (2.6) сравнительно с ${{f}_{d}}({\mathbf{r}}) \equiv {{\left( {\tfrac{4}{3}\pi {{R}^{3}}} \right)}^{{ - 1}}}$ и даже сравнительно с вариантом, в котором $f({\mathbf{r}},t)$ определяется формулой (4.1), а $h({\mathbf{r}},{\mathbf{v}}) \equiv 1$. Нетрудно проверить, что для сформулированных выше характеристик вычислительной модели выполняются условия леммы 1.

Соответствующие оценки величин ${\text{E}}\lambda $ и $\sqrt {{\text{D}}\lambda } $ приведены в первых двух столбцах табл. 1. Они были получены с помощью распределенных вычислений в ССКЦ СО РАН (Siberian Supercomputer Center SB RAS). Эти оценки определялись на основе установления двух значащих цифр при возрастании $t$ и $n$ с учетом статистической погрешности. Окончательные результаты получены осреднением оценок для моментов времени $t = 17,\;18,\;19,\;20$ при $n = 4$ для $m = 2$ и $n = 2$ для $m = 6$. Это соответствует улучшению свойств оценок при $m \to \infty $. В качестве погрешности этих оценок приведены среднеквадратические отклонения.

В [5] для рассматриваемой задачи были реализованы также формулы (3.6), которые с учетом равенства $\lambda (\bar {\rho }) = 0$ здесь имеют вид

Полученные таким образом результаты приведены в двух последних столбцах табл. 1. Их можно рассматривать как тестовые для $\varepsilon = 0.1$, а также для $\varepsilon = 0.3$ при $m = 1;\;6$.

4.2. На фиг. 1 приведены графики оценки логарифмической производной (3.4) для $m = 6$ при $\varepsilon = 0.1;\;0.3$. Точками обозначены соответствующие значения оценки (3.4), полученные с помощью распределенных вычислений в ССКЦ СО РАН. Приведенные интервальные погрешности представляют собой оценки вида (3.5) среднеквадратических погрешностей. Прямые на фиг. 1 линейно аппроксимируют функцию

Точечные оценки этой функции дают возможность вычислить соответствующие регрессионные (для $15 \leqslant {{t}_{i}} \leqslant 20$) оценки $\tilde {\alpha }$, $\tilde {\beta }$ коэффициентов линейной аппроксимации $y(t) \approx \beta t + \alpha $ по известным (см. [10]) формулам В рассматриваемой задаче случайные величины ${\text{\{ }}{{y}_{i}}{\text{\} }}$ положительно коррелированы, поэтому

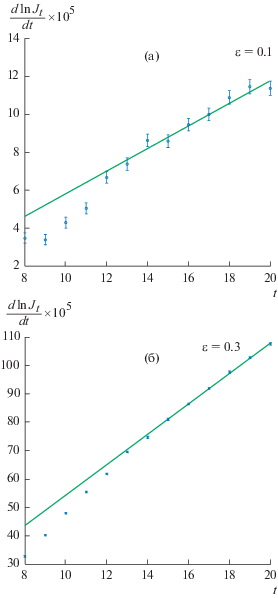
Анализ полученных на этой основе оценок дисперсий с учетом неполной зависимости величин ${\text{\{ }}{{y}_{i}}{\text{\} }}$ показал, что оценки среднеквадратической погрешности величин $\tilde {\alpha }$, $\tilde {\beta }$ можно вычислять по формулам $\sigma (\tilde {\alpha }) \approx 2\sqrt {{{{\text{D}}}_{\alpha }}} $, $\sigma (\tilde {\beta }) \approx 2\sqrt {{{{\text{D}}}_{\beta }}} $. Аналитические и регрессионные оценки коэффициентов линейной аппроксимации функции $dln{{J}_{t}}{\text{/}}dt$ приведены в табл. 2. Необходимые при этом значения величин $a = {\text{E}}\lambda $, ${{d}^{2}} = {\text{D}}\lambda $ определялись по формулам (4.2) (см. табл. 1 и табл. 7 из [3]).

Таким образом, можно констатировать, что здесь в интервале $15 \leqslant t \leqslant 20$ аналитическая оценка показателя экспоненциальной асимптотики потока частиц по времени является удовлетворительной. Более точное соответствие статистических оценок коэффициентов их аналитическим значениям при $\varepsilon = 0.1$ можно объяснить лучшей гауссовостью распределения $\lambda (\sigma )$ для этого варианта задачи, согласно теории малых возмущений.

В заключение сделаем замечание о возможности более широкого применения полученных результатов. Они показывают, что скорость роста среднего числа частиц произвольной природы (например, микроорганизмов) при их распределенном размножении в случайной среде может быть сверхэкспоненциальной (см. разд. 3). Это соответствует увеличению коэффициента роста чисел ${\text{\{ }}{{n}_{i}}{\text{\} }}$ частиц в фиксированные равноотстоящие моменты времени ${\text{\{ }}{{t}_{i}}{\text{\} }}$, т.е. увеличению отношения ${{n}_{{i + 1}}}{\text{/}}{{n}_{i}}$. Однако, если такое увеличение наблюдается экспериментально, то это можно связать с распределенностью “очага” размножения. В частности, согласно статистике ВОЗ (см. [11]) именно так развивалась пандемия COVID-19 в целом по всему миру с 09.03.2020 по 21.03.2020. Соответствующая численность (по дням) с погрешностью, не превышающей 2%, аппроксимируется по формуле типа (3.1) следующим образом:

Сравнение отдельных значений численности дано в табл. 3.