Журнал вычислительной математики и математической физики, 2021, T. 61, № 9, стр. 1536-1544

1. ВВЕДЕНИЕ

Задачи для нелинейных уравнений в частных производных составляют важный класс задач теоретической и математической физики (см. [1]–[3]). Среди этих задач значительное место занимают задачи, связанные с распространением возмущений различной природы, а именно, задачи для нелинейных уравнений гиперболического типа. Наряду с прямыми задачами, состоящими в определении таких возмущений, возникают обратные задачи, связанные с восстановлением параметров модели. Случай квазилинейных гиперболических уравнений рассматривался в [4]–[9] (в [4]–[6] указаны более ранние работы).

В настоящей работе рассмотрены обратные задачи, восходящие по постановке к известным задачам из [10] [11, с. 42], но в отличие от них не сводящиеся к линейным интегральным уравнениям типа Вольтерра I или II рода. В качестве исходных данных для восстановления нелинейной скорости распространения волн рассмотрены доступные в наблюдениях период и амплитуда установившихся колебаний. Близкие по постановке обратные задачи для стационарных колебаний для системы уравнений мелкой воды и уравнения КдВ (см. [1]–[3], [12]) рассмотрены в [13]–[15].

Волновое уравнение

описывает широкий класс процессов распространения колебаний в неоднородной среде. Случай $k = 1$ соответствует распространению волн без рассеяния, случай $k = 2$ – распространению с коэффициентом отражения, равным $ - a{\kern 1pt} '(x){\text{/}}a(x)$. Наряду с прямыми задачами, в которых при некоторых дополнительных условиях и известной функции $a(x)$ требуется найти функцию $u(x,t)$, возможна постановка обратных задач. В этих задачах по дополнительным данным о решении прямой задачи требуется восстановить $a(x)$.

Уравнение (1) справедливо в рамках линейной теории, когда силы напряжения линейно зависят от деформаций (в терминах теории упругости). Очевидно, что возникает потребность рассматривать процессы, где такая зависимость нелинейна. Простейшим уравнением, обобщающим (1) на случай нелинейной однородной среды, является уравнение

Функцию $a(u)$ считаем четной, и пусть $a{\kern 1pt} '(u) > 0$ при $u > 0$.

Уравнение (2) допускает решения в виде бегущих волн. Среди таких решений наиболее просто как в лабораторных экспериментах, так и в натурных наблюдениях изучать установившиеся колебания, которые мы будем также называть стационарными волнами. Построим такое решение для уравнения (2) при $k = 1$. Запишем (2) в виде

и рассмотрим установившееся решение После подстановки $q(\xi )$ в (3) находим что после разделения переменных дает Интегрируя последнее равенство и полагая постоянную интегрирования равной нулю, что не ограничивает общности рассмотрения, получаем откуда приходим к равенству

Нетрудно заметить, что последнее равенство определяет гамильтонову систему с гамильтонианом

и энергией $E$. Как известно, при определенных свойствах функции $a(y)$ (например, $a{\kern 1pt} '{\kern 1pt} '(y) > 0$) существуют ограниченные фазовые траектории этой системы, зависящие от параметра $c$, т.е. стационарные решения вида $q = q(\xi ,c)$.

Установившиеся решения, другими словами, периодические колебания, характеризуются двумя величинами: периодом и амплитудой, которые, в свою очередь, зависят от энергии $E$. Изменяя энергию системы, можно получить параметрическую зависимость периода колебаний от амплитуды. Действительно, возвращаясь к (4), получаем

откуда для четной функции $a(y)$, делая $y$ независимой переменной, находим где $T(Y)$ – период колебаний, $Y$ – амплитуда, а контурный интеграл считается по замкнутой фазовой траектории. Полагаем, что период $T$ и амплитуда $Y$ являются величинами, доступными в измерениях. Равенство (4) соответствует переходу от параметрической зависимости периода и амплитуды от энергии $E$ к явной.

Пусть теперь зависимость $T(Y)$ известна на $[0,h]$, и требуется найти $a(y)$. Такую задачу будем называть обратной по отношению к прямой задаче для уравнения (2), а четную, гладкую на $[0,h]$, функцию $a(y)$ такую, что $a{\kern 1pt} '(y) > 0$ при $y > 0$, удовлетворяющую уравнению (5), – ее решением. Эта обратная задача является, с одной стороны, простейшей в своем классе, с другой стороны, к ней сводится задача из более широкого класса, в частности, задача восстановления в (2) коэффициента вида $a(u,x)$.

2. ЕДИНСТВЕННОСТЬ РЕШЕНИЯ ОБРАТНОЙ ЗАДАЧИ ($k$ = 1)

Очевидно, что (5) может быть записано в форме нелинейного функционального уравнения типа Вольтерра I рода относительно $a(y)$:

Лемма 1. Пусть $a \in {{C}^{2}}[0,h]$. Тогда $T \in {{C}^{1}}(0,h]$.

Доказательство. Рассмотрим несобственный интеграл

где $y(a)$ – фун кция, обратная к $a(y)$ при $y \in [0,h]$, $c > {{a}_{0}}$, ${{a}_{0}} = a(0)$, и $y{\kern 1pt} '(a) \to + \infty $ при $a \to {{a}_{0}}$. Разобьем (7) на два слагаемых: Очевидно, что первый интеграл имеет под интегралом особенность при $a = {{a}_{0}}$. Но любой интеграл вида является сходящимся при $n \in \mathbb{N}$, так как а последовательность интегралов монотонно возрастает по ${{\varepsilon }_{m}}$ при монотонной последовательности $\{ {{\varepsilon }_{m}}\} \to + 0$. Следовательно, первый интеграл дифференцируем по $c > {{a}_{1}}$.

Второй интеграл имеет под интегралом особенность типа $1{\text{/}}\sqrt x $ и может быть взят по частям:

Ясно, что последнее выражение дифференцируемо по $c > {{a}_{1}}$, и, следовательно, интеграл (7) дифференцируем по $Y > 0$, так как $c = a(Y)$.

Пример 1. Пусть ${{a}^{2}}(y) = a_{0}^{2} + a_{2}^{2}{{y}^{2}}$, ${{a}_{2}} > 0$. Тогда

Полагая $T(0) = li{{m}_{{Y \to 0}}}T(Y) = 2\pi {\text{/}}{{a}_{2}}$, получаем гладкую на отрезке $[0,h]$ функцию $T(Y)$.

Из этого примера следует, что ${{a}_{0}}$ условиями обратной задачи, вообще говоря, не определяется. Поэтому полагаем ${{a}_{0}} > 0$ известной величиной.

Замечание. Поведение функции $T$ в нуле зависит от поведения функции $a$ в нуле; при этом функция $T$ может быть как дифференцируемой, так и нет в этой точке. Например, если $a{\kern 1pt} '{\kern 1pt} '(0) > 0$, $a \in {{C}^{3}}[0,h]$, то $T \in {{C}^{1}}[0,h]$. Более детальное изучение аналитических свойств интеграла (6) выходит за рамки настоящей статьи.

Теорема 1. Пусть $T \in {{C}^{1}}[0,h]$. Тогда на $[0,h]$ существует не более одного решения обратной задачи.

Доказательство. Преобразуем исходное уравнение (6). Домножим его на $c{\text{/}}\sqrt {{{v}^{2}} - {{c}^{2}}} $ и проинтегрируем обе части по $c$. При этом, используя прием Дирихле, имеем

откуда следует равенство

Дальнейшее доказательство единственности проведем от противного, а именно, допустим, что найдется точка ${{y}_{0}} \in [0,h)$, число $\delta > 0$ и решения обратной задачи ${{a}_{1}}(y),\;{{a}_{2}}(y)$ такие, что ${{a}_{1}}(y) = {{a}_{2}}(y) = a(y)$ при $y \leqslant {{y}_{0}}$ (возможно, ${{y}_{0}} = 0$), и ${{a}_{1}}(y) \ne {{a}_{2}}(y)$ при ${{y}_{0}} < y < {{y}_{0}} + \delta \leqslant h$. Тогда для разности обратных функций ${{y}_{1}}(a) \ne {{y}_{2}}(a)$ при $a({{y}_{0}}) \leqslant a \leqslant a({{y}_{0}}) + \varepsilon $, где $\varepsilon > 0$ достаточно мало, из (8) имеем

где $M$ не зависит от $\varepsilon $. В точке ${{a}_{*}} = \mathop {{\text{argmax}}}\nolimits_{c \in [{{a}_{0}},a]} \left| {{{y}_{1}}(c) - {{y}_{2}}(c)} \right|$ приходим к противоречию в силу произвольности выбора $\varepsilon $.

3. СУЩЕСТВОВАНИЕ РЕШЕНИЯ ОБРАТНОЙ ЗАДАЧИ ($k$ = 1)

Справедлива следующая теорема существования в малом обратной задачи для случая $k = 1$.

Теорема 2. Пусть $T \in {{C}^{1}}[0,h]$, $T(Y) > 0$ при $Y \in [0,h]$. Тогда найдется точка ${{h}_{0}} \in (0,h]$ такая, что на $[0,{{h}_{0}}]$ существует строго монотонная функция $a \in {{C}^{1}}[0,{{h}_{0}}]$ (решение уравнения (5)), такая, что $a(0) = {{a}_{0}}$, $a{\kern 1pt} '(0) = 0$.

Доказательство. Рассмотрим последовательность ${{\{ {{y}_{n}}(a)\} }_{{n \in \mathbb{N}}}}$, определяемую равенством

при $a \in [{{a}_{0}},{{a}_{\varepsilon }}]$, ${{a}_{\varepsilon }} = {{a}_{0}} + \varepsilon $, $\varepsilon \leqslant \delta $. Повторяя рассуждения теоремы 1, для $n \geqslant 2$ получаем откуда при $M = \sqrt {2{{a}_{0}} + \delta } ma{{x}_{{y \in [0,h]}}}\left| {T{\kern 1pt} '(y)} \right|$ имеем рекуррентную оценку Из нее следует, что функциональный ряд равномерно сходится на отрезке $[{{a}_{0}},{{a}_{\varepsilon }}]$ к непрерывной функции $y(a)$ при достаточно малом $\varepsilon $ в силу признака Вейерштрасса, поскольку любая функция ${{y}_{n}} \in C[{{a}_{0}},{{a}_{\varepsilon }}]$, причем ${{y}_{n}}({{a}_{0}}) = 0$ для всех $n \in \mathbb{N}$.

Докажем последнее по индукции. Так как ${{y}_{0}} = {\text{const}}$, то из (9) при ${{a}_{0}} < a \leqslant {{a}_{\varepsilon }}$ следует, что $2\pi {{y}_{1}}(a) = T({{y}_{0}})\sqrt {{{a}^{2}} - a_{0}^{2}} ,$ и, доопределив ${{y}_{1}}(a)$ при $a = {{a}_{0}}$ как ${{y}_{1}}({{a}_{0}}) = 0$, получаем, что ${{y}_{1}} \in C[{{a}_{0}},{{a}_{\varepsilon }}]$.

Пусть ${{y}_{n}} \in C[{{a}_{0}},{{a}_{\varepsilon }}]$, $n > 1$. Разобьем интеграл в (9) на сумму двух:

Аналогично лемме 1 доказываем, что функция ${{y}_{{n + 1}}}(a)$ непрерывна при любом $a \in [{{a}_{1}},{{a}_{\varepsilon }}]$, причем Доопределив ${{y}_{{n + 1}}}({{a}_{0}}) = 0$, получаем, что ${{y}_{{n + 1}}} \in C[{{a}_{0}},{{a}_{\varepsilon }}]$.

Итак, доказано, что найдется такой отрезок $[{{a}_{0}},{{a}_{\varepsilon }}]$, что на нем определена непрерывная функция $y(a)$, удовлетворяющая уравнению (8). Аналогично лемме 1 доказываем, что $y \in {{C}^{1}}[{{a}_{0}},{{a}_{\varepsilon }}]$.

Докажем, что $y{\kern 1pt} '(a) > 0$ при $a \in ({{a}_{0}},{{a}_{0}} + \varepsilon ]$ и, более того,

Для этого продифференцируем (8), предварительно проинтегрировав интеграл по частям: В результате получаем где $F \in {{C}^{1}}[{{a}_{0}},{{a}_{\varepsilon }}]$ – известная функция, причем величина $F({{a}_{0}})$ конечна. Равенство (10) является уравнением Абеля II рода относительно функции $\varphi {\kern 1pt} '(v)$ и, таким образом, имеет непрерывное на $[{{a}_{0}},{{a}_{\varepsilon }}]$ решение. Отсюда следует, что $\varphi \in {{C}^{1}}[{{a}_{0}},{{a}_{\varepsilon }}]$ и $\varphi ({{a}_{0}}) = 0$.

Из структуры функции $y(a)$ следует, что

при $a \in ({{a}_{0}},{{a}_{\varepsilon }}]$, и, таким образом, $y{\kern 1pt} '(a) > 0$, если $\varepsilon $ достаточно мало. Очевидно, что при этом на отрезке $[{{a}_{0}},y({{a}_{\varepsilon }})]$ существует гладкая монотонная функция $a(y)$, обратная к $y(a)$, причем

Теперь, когда доказана монотонность функции $y(a)$, остается доказать, что $a(y)$ является решением уравнения (5). Для этого домножим (8) на $v{\text{/}}\sqrt {{{u}^{2}} - {{v}^{2}}} $ и проинтегрируем по отрезку $[{{a}_{0}},u]$, воспользовавшись приемом Дирихле. Взяв полученный при этом интеграл по частям, имеем

В результате последующего дифференцирования получаем Положим $Y = y(u)$. Учитывая монотонность функции $y({v})$ для обратной к ней функции $a(y)$, окончательно приходим к равенству

Пример 2. Нетривиальный пример дает зависимость $T(Y) = 2\pi cosY$. Нетрудно проверить, что решением уравнения (5) при ${{a}_{0}} = 1$ является $a(y) = 1{\text{/}}cosy$. Таким образом, решение обратной задачи существует при выполнении условия $T(Y) > 0$.

4. ЕДИНСТВЕННОСТЬ РЕШЕНИЯ ОБРАТНОЙ ЗАДАЧИ ($k$ = 2)

Повторяя рассуждения из разд. 1, приходим к следующему равенству:

Покажем, что и в этом случае физическая система, описываемая (3), допускает периодические колебания. Выберем в (11) знак $ + $, тогда с учетом монотонности и четности $a(q)$ получаем решение $q(\xi )$, возрастающее от значения $ - {{a}^{{ - 1}}}(c)$ до ${{a}^{{ - 1}}}(c)$ на интервале $(\xi ( - c),\xi (c))$, где и $y = {{a}^{{ - 1}}}$ – функция, обратная к функции $a$.

Доопределим функцию $y(\xi )$ в точках $ \pm \xi (c)$ по непрерывности, положив $y( \pm \xi (c)) = \pm {{a}^{{ - 1}}}(c)$. Очевидно, что при этом $y{\kern 1pt} '( \pm \xi (c)) = + \infty $. Такое построение для ОДУ (11) можно продолжить на всей числовой прямой $\mathbb{R} \mathrel\backepsilon \xi $. В итоге приходим к стационарному решению $y(\xi )$ (волновому процессу с обострением) (см. фиг. 1) с периодом $4\xi (c)$ и амплитудой ${{a}^{{ - 1}}}(c)$.

Поставим следующую обратную задачу: по периоду $X(Y)$, как функции амплитуды $Y$, найти функцию $a(y)$ (см. разд. 1). Полагая $c = a(Y)$, из (12) получаем относительно $a(y)$ основное уравнение обратной задачи:

Лемма 2. Пусть $a \in {{C}^{2}}[0,h]$. Тогда $X \in {{C}^{2}}(0,h]$ и $X{\kern 1pt} '(Y) > 0$ при $Y \in (0,h]$.

Доказательство. Формальное дифференцирование (13) дает

где функция $T(Y)$ определяется равенством (6). Из леммы 1 следует, что $T \in {{C}^{1}}(0,h]$, откуда следует утверждение леммы.

Пример 3. Рассмотрим ${{a}^{2}}(y) = a_{0}^{2} + a_{2}^{2}{{y}^{2}}$. Несложные вычисления дают $X(Y) = \pi {{a}_{2}}{{Y}^{2}}$. Отсюда следует, что ${{a}_{0}}$ данными обратной задачи, вообще говоря, не определяется. Кроме того, $X(Y)$ имеет при $Y = 0$ нуль порядка не менее второго, если функция $a(y)$ достаточно гладкая.

Теорема 3. Пусть $X \in {{C}^{2}}[0,h]$, и пусть решение обратной задачи $a(y)$ известно при $y \in [0,\varepsilon ]$, $0 < \varepsilon < h$. Тогда обратная задача имеет не более одного решения на $[0,h]$.

Доказательство. Допустим, что при $y > \varepsilon $ существуют ${{a}_{1}}(y) \ne {{a}_{2}}(y)$, что эквивалентно существованию ${{y}_{1}}(a) \ne {{y}_{2}}(a)$ при $a > {{a}_{\varepsilon }}$, ${{a}_{\varepsilon }} = {{a}_{i}}(\varepsilon )$, $i = 1,2$. Продифференцируем (13) и запишем полученное уравнение в виде

Для разности ${{y}_{1}}({v}) - {{y}_{2}}({v}) = z({v})$ имеем Отсюда при $v \in [{{a}_{\varepsilon }},b]$, $b = mi{{n}_{{i = 1,2}}}\{ {{a}_{i}}(h)\} $ вытекает следующая оценка: т.е. где величины $m,{{M}_{1}},{{M}_{2}} > 0$ и не зависят от $v$. При достаточно малой разности ${v} - {{a}_{\varepsilon }} \leqslant \delta $ из этой оценки в точке $v{\kern 1pt} * = \mathop {{\text{argmax}}}\nolimits_{{v} \in [{{a}_{\varepsilon }},{{a}_{\varepsilon }} + \delta ]} \left| {z{\kern 1pt} '({v})} \right|$ имеем В силу произвольности выбора $\delta > 0$ приходим к противоречию.

5. ЧИСЛЕННОЕ РЕШЕНИЕ ОБРАТНЫХ ЗАДАЧ ДЛЯ $k = 1,2$

Исходное уравнение (5) обратной задачи в случае $k = 1$ имеет под интегралом интегрируемую особенность, что затрудняет непосредственное использование (5). Получим эквивалентное функциональное уравнение, лишенное этого недостатка.

Обратимся к уравнению (8) и проинтегрируем левую часть по частям:

Возвращаясь к переменной $y$, имеем Сделаем замену ${{Z}^{2}}(Y) = {{a}^{2}}(Y) - a_{0}^{2}$ и окончательно получим следующее функциональное уравнение:

Это функциональное уравнение не является уравнением типа Вольтерра II рода, поскольку выражение под интегралом не локально. Однако (14) является эволюционным уравнением, что вытекает из следующего нелокального дифференциального уравнения:

Численное решение этого дифференциального уравнения можно построить, например, методом ломаных, единственность этого решения следует из результатов разд. 2. Очевидно, что построенное таким образом решение имеет наибольшую область определения, в то время как решение, построенное методом последовательных приближений для (14) этого, вообще говоря, не гарантирует. Данное обстоятельство полностью подтвердилось при проведении вычислительных экспериментов.

Опираясь на свойство эволюционности уравнения (14), в настоящей работе был применен следующий дискретный алгоритм нахождения функции $Z(y)$. Для выражения под интегралом в (14) использовалась формула прямоугольников на равномерной сетке, что приводило к рекуррентному вычислению ${{z}_{n}} = Z({{y}_{n}})$, $n = 1,2, \ldots ,N$:

Для функции $T(y)$, заданной приближенно, при вычислении $T{\kern 1pt} '({{y}_{n}})$ осуществлялась соответствующая регуляризация.

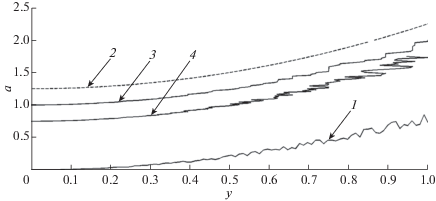
Результаты численного моделирования представлены на фиг. 2 для $T(y) = 2\pi cos(y)$, точное решение $a(y) = 1{\text{/}}cos(y)$, $y \in [0,\pi {\text{/}}2)$. Относительная погрешность задания $T(y)$ по норме ${{C}_{h}}[0,\pi {\text{/}}2]$ составляла $10\% $.

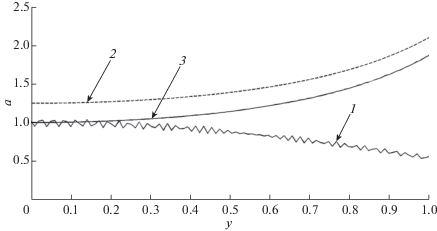
Очевидно, что обратная задача при $k = 2$ является хуже обусловленной, чем при $k = 1$, поскольку уравнение (13) однократным дифференцированием не приводится к функциональному уравнению II рода. Однако в результате интегрирования (13) по частям удается получить интегральное уравнение I рода с особенностью в ядре типа $1{\text{/}}\sqrt x $. Основным моментом при построении численного алгоритма является аналитически точное вычисление квадратур с особенностью.

Проинтегрировав (13) по частям, имеем

откуда на равномерной сетке ${{a}_{k}} = {{a}_{0}} + kh$, $k = 0,1, \ldots ,N$, получаем рекуррентное уравнение на $\{ {{y}_{n}}\} $, $n = 1,2, \ldots ,N$:

Результаты численного моделирования представлены на фиг. 3. Поскольку на приближенных данных $X({{y}_{n}})$ сеточная функция ${{y}_{n}} = y({{a}_{n}})$ оказывается не монотонной, то графическое изображение функции ${{a}_{n}} = a({{y}_{n}})$ носит весьма причудливый характер. С учетом необходимой монотонности $\{ {{y}_{n}}\} $ результат решения также представлен на фиг. 3. Относительная погрешность задания $X(y)$ по норме ${{C}_{h}}[0,\pi {\text{/}}2]$ составляла $2.5\% $.