Журнал вычислительной математики и математической физики, 2021, T. 61, № 9, стр. 1508-1527
Об аналитическом и численном решении одномерных уравнений холодной плазмы
О. С. Розанова 1, *, Е. В. Чижонков 1, **
1 Московский государственный университет им. М.В. Ломоносова
119899 Москва, Ленинские горы, Россия
* E-mail: rozanova@mech.math.msu.su
** E-mail: chizhonk@mech.math.msu.su
Поступила в редакцию 24.08.2020
После доработки 24.08.2020
Принята к публикации 07.04.2021
Аннотация
Для моделирования колебаний холодной плазмы как в нерелятивистском случае, так и с учетом релятивизма, предложены и обоснованы численные алгоритмы высокой точности. Спецификой подхода является использование лагранжевых переменных для приближенного решения задачи, сформулированной в эйлеровых переменных. Основной результат представлен теоремами о сходимости предложенных алгоритмов относительно малых параметров дискретизации независимых эйлеровых переменных. Численные эксперименты наглядно иллюстрируют полученные теоретические результаты. В частности, проведено моделирование известного эффекта опрокидывания плазменных колебаний и подтверждено, что он имеет характер градиентной катастрофы. Библ. 19. Фиг. 4.
ВВЕДЕНИЕ
Гидродинамическая модель “холодной” плазмы хорошо известна и подробно описана в учебниках и монографиях по физике плазмы. Она является oдной из простейших моделей, в которой плазма рассматривается как релятивистская электронная жидкость, в пренебрежении столкновительными и рекомбинационными эффектами, а также движением ионов. В настоящее время внимание к этой модели обусловлено, в первую очередь, задачами, связанными с распространением сверхмощных коротких лазерных импульсов в плазме (см. [1], [2]). В процессе движения импульс возбуждает позади кильватерную плазменную волну, которая представляет собой волну плотности заряда, распространяющуюся в направлении движения импульса и ограниченную в поперечном направлении. Предсказанный первоначально теоретически эффект возбуждения кильватерной плазменной волны лазерным импульсом в дальнейшем получил подтверждение в ряде экспериментов, где было проведено исследование пространственной структуры кильватерных полей.
При математическом моделировании процессов в бесстолкновительной холодной плазме наиболее часто используются два подхода – Лагранжа и Эйлера: метод частиц, позволяющий отслеживать их индивидуальные траектории, и гидродинамическое описание на базе уравнений с частными производными (см., например, [3], [4]). В рамках обоих подходов хорошо известен эффект опрокидывания колебаний (см. [5]). В первом случае критерием опрокидывания колебаний является пересечение траекторий электронов, а во втором – обращение в бесконечность функции, описывающей плотность электронов. В [6] имеется физическое обоснование появления сингулярности плотности среды при пересечении траекторий частиц. С математической точки зрения это явление означает появление сильной (дельтаобразной) сингулярности у фун ции, описывающей плотность среды, и также описано на примере некоторых моделей, например, газовой динамики “без давления”.
По существу, кильватерные волны в плазме, инициируемые лазерными импульсами, тесно связаны с колебаниями, возникающими вследствие неоднородности плотности заряда, которая формирует начальное электрическое поле специальной формы. В [7] проанализированы две различные постановки задачи Коши для уравнений, описывающих плоские одномерные свободные электронные колебания в холодной плазме. Для нерелятивистского случая результат указанной работы позволяет разделить начальные данные задачи Коши, описывающей плоские одномерные нерелятивистские электронные колебания в холодной плазме, на два класса. Один – порождает гладкое $2\pi $-периодическое решение на бесконечном интервале времени, а другой – приводит к образованию сингулярности в течение уже первого периода колебаний. Для релятивистской постановки в общем случае разделить начальные данные задачи Коши на два класса аналогичным образом, т.е. получить критерий образования особенности, удается только для промежутка времени, соответствующего первому колебанию. Настоящая работа базируется на результатах о существовании решения дифференциальных задач для обеих постановок (см. [7]).
Статья организована следующим образом. В разд. 1 ставится задача о колебаниях плазмы в общем трехмерном случае и осуществляется редукция полной системы для случая одномерных плоских колебаний для релятивистского и нерелятивистского случаев. В разд. 2 предложен и проанализирован численный алгоритм без учета релятивистских эффектов, включая условия регулярности получаемой эйлеровой сетки и положительности функции электронной плотности. Раздел 3 посвящен релятивистскому случаю. С учетом возникновения у решения градиентной катастрофы, сначала определена область определения приближенного решения, т.е. “зона ответственности” численного метода во времени, а затем предложен и проанализирован он сам. При обосновании корректности численного алгоритма особое внимание уделяется отличиям от нерелятивистского случая, разобранного разд. 2. В разд. 4 рассмотрена процедура возврата к эйлеровым переменным, основанная на эрмитовой кубической интерполяции, а также сформулированы и доказаны теоремы о сходимости предложенных алгоритмов относительно малых параметров дискретизации независимых эйлеровых переменных. Раздел 5 посвящен численным иллюстрациям полученных теоретических результатов. В частности, при использовании предложенного подхода проведено моделирование известного эффекта опрокидывания плазменных колебаний и подтверждено, что он имеет характер градиентной катастрофы. В заключение систематизированы результаты проведенных исследований.
1. ПОСТАНОВКА ЗАДАЧИ О ПЛАЗМЕННЫХ КОЛЕБАНИЯХ
Система уравнений гидродинамики “холодной” плазмы, включающая гидродинамические уравнения совместно с уравнениями Максвелла, в векторной форме имеет вид (см., например, [8]–[11])
(1)
$\begin{array}{*{20}{c}} {\frac{{\partial n}}{{\partial t}} + \operatorname{div} (n{\mathbf{v}}) = 0,\quad \frac{{\partial {\mathbf{p}}}}{{\partial t}} + \left( {{\mathbf{v}} \cdot \nabla } \right){\mathbf{p}} = e\left( {{\mathbf{E}} + \frac{1}{c}\left[ {{\mathbf{v}} \times {\mathbf{B}}} \right]} \right),} \\ {\gamma = \sqrt {1 + \frac{{{\text{|}}{\mathbf{p}}{{{\text{|}}}^{2}}}}{{{{m}^{2}}{{c}^{2}}}}} ,\quad {\mathbf{v}} = \frac{{\mathbf{p}}}{{m\gamma }},} \\ {\frac{1}{c}\frac{{\partial {\mathbf{E}}}}{{\partial t}} = - \frac{{4\pi }}{c}en{\mathbf{v}} + \operatorname{rot} {\mathbf{B}},\quad \frac{1}{c}\frac{{\partial {\mathbf{B}}}}{{\partial t}} = - \operatorname{rot} {\mathbf{E}},\quad \operatorname{div} {\mathbf{B}} = 0,} \end{array}$С целью построения численного решения плоских одномерных релятивистских плазменных колебаний базовые уравнения (1) можно существенно упростить.
Будем обозначать независимые переменные в декартовой системе координат обычным образом $(x,y,z)$ и примем допущения, что:
– решение определяется только $x$-компонентами вектор-функций ${\mathbf{p}},\;{\mathbf{v}},\;{\mathbf{E}}$;
– зависимость в этих функциях от переменных $y$ и $z$ отсутствует, т.е. $\partial {\text{/}}\partial y = \partial {\text{/}}\partial z = 0$.
Тогда из системы (1) получим
(2)
$\begin{array}{*{20}{c}} {\frac{{\partial n}}{{\partial t}} + \frac{\partial }{{\partial x}}(n{{v}_{x}}) = 0,\quad \frac{{\partial {{p}_{x}}}}{{\partial t}} + {{v}_{x}}\frac{{\partial {{p}_{x}}}}{{\partial x}} = e{{E}_{x}},} \\ {\gamma = \sqrt {1 + \frac{{p_{x}^{2}}}{{{{m}^{2}}{{c}^{2}}}}} ,\quad {{v}_{x}} = \frac{{{{p}_{x}}}}{{m\gamma }},\quad \frac{{\partial {{E}_{x}}}}{{\partial t}} = - 4\pi en{{v}_{x}}.} \end{array}$Введем безразмерные величины
(3)
$\begin{array}{*{20}{c}} {\frac{{\partial N}}{{\partial \theta }} + \frac{\partial }{{\partial \rho }}(NV) = 0,\quad \frac{{\partial P}}{{\partial \theta }} + E + V\frac{{\partial P}}{{\partial \rho }} = 0,} \\ {\gamma = \sqrt {1 + {{P}^{2}}} ,\quad V = \frac{P}{\gamma },\quad \frac{{\partial E}}{{\partial \theta }} = NV.} \end{array}$Из первого и последнего уравнений (3) следует
Это соотношение справедливо как при отсутствии плазменных колебаний ($N \equiv 1,E \equiv 0$), так и при их наличии. Поэтому отсюда имеем более простое выражение для электронной плотности $N(\rho ,\theta )$:Воспользовавшись им в (3), приходим к уравнениям, описывающим плоские одномерные релятивистские плазменные колебания (см. [12]):
(5)
$\frac{{\partial P}}{{\partial \theta }} + V\frac{{\partial P}}{{\partial \rho }} + E = 0,\quad \frac{{\partial E}}{{\partial \theta }} + V\frac{{\partial E}}{{\partial \rho }} - V = 0,\quad V = \frac{P}{{\sqrt {1 + {{P}^{2}}} }},$Ниже мы будем изучать в полуплоскости $\{ (\rho ,\theta ):\rho \in \mathbb{R},\;\theta > 0\} $ численное решение задачи Коши для (4), (5) с начальными условиями
Можно также рассмотреть систему (5) в упрощенном (нерелятивистском) приближении. А именно, в предположении малости скорости электронов $V$ имеет место представление $P = V + \frac{{{{V}^{3}}}}{2} + O({{V}^{5}})$, $V \to 0$. Таким образом, с точностью до кубически малых слагаемых мы можем считать, что $P = V$. Это предположение позволяет записать (5) в виде
(7)
$\frac{{\partial V}}{{\partial \theta }} + V\frac{{\partial V}}{{\partial \rho }} + E = 0,\quad \frac{{\partial E}}{{\partial \theta }} + V\frac{{\partial E}}{{\partial \rho }} - V = 0,$Системы (5) и (7) относятся к гиперболическому типу. Известно, что для таких систем существует локально по времени единственное решение задачи Коши того же класса, что и начальные данные (см. [13]).
2. РЕШЕНИЕ НЕРЕЛЯТИВИСТСКИХ УРАВНЕНИЙ
Прежде, чем описывать алгоритм решения задачи (4), (7) с начальными условиями (8), напомним основные результаты из [7].
2.1. Вспомогательные сведения
Для нерелятивистских уравнений принципиально важной является теорема существования глобального по времени решения (см. [7]).
Утверждение 2.1. Пусть начальные данные (8) принадлежат классу ${{C}^{2}}(\mathbb{R})$. Для существования и единственности непрерывно дифференцируемого по обеим переменным $2\pi $-периодического по времени при всех $\theta > 0$ решения $V(\theta ,\rho ),\;E(\theta ,\rho )$ задачи (7), (8) необходимо и достаточно, чтобы в каждой точке $\rho \in ( - \infty ,\infty )$ было выполнено неравенство
Если же существует хотя бы одна точка $\rho $, для которой выполняется неравенство, противоположное (9), то в течение конечного времени производные решения обращаются в бесконечность.Следствие. Если необходимое и достаточное условие существования решения (9) выполнено в начальный момент времени, то оно сохраняется во времени и пространстве, т.е. для произвольной точки $(\rho ,\theta )$ справедливо
(10)
${{\left( {\frac{{\partial V(\rho ,\theta )}}{{\partial \rho }}} \right)}^{2}} + 2\frac{{\partial E(\rho ,\theta )}}{{\partial \rho }} - 1 < 0.$Даже если условие (9) не выполнено, то сами функции $V(\rho ,\theta )$ и $E(\rho ,\theta )$ все равно остаются ограниченными, в силу равенства ${{V}^{2}} + {{E}^{2}} = V_{0}^{2}({{\rho }_{0}}) + E_{0}^{2}({{\rho }_{0}}) = {\text{const}}$, справедливого для произвольной характеристики системы (7), стартующей из точки ${{\rho }_{0}}$. Отсюда следует, что разрушение решения может иметь только вид градиентной катастрофы.
Следует отметить, что, в силу соотношения (4), из (10) вытекают строгая положительность и отделенность от нуля функции электронной плотности:
Таким образом, из приведенной информации следует, что решение задачи (4), (7) с начальными условиями (8) полностью характеризуется поведением функций $V(\rho ,\theta ),$ $E(\rho ,\theta )$ и их пространственных производных (градиентов).
В дальнейшем нам потребуется решение вспомогательной задачи для функций $W(\theta )$ и $D(\theta )$ с вещественными начальными данными:
(11)
$\begin{array}{*{20}{c}} {W{\kern 1pt} ' = - D - {{W}^{2}},\quad D{\kern 1pt} ' = (1 - D)W,} \\ {W(0) = \beta ,\quad D(0) = \alpha .} \end{array}$Легко убедиться в том, что фазовые траектории системы (11) представляют собой кривые второго порядка (эллипсы, параболы или гиперболы, в зависимости от начальных данных). Нас будет интересовать явный вид решения в случае ограниченности фазовых траекторий, т.е. эллипсов.
Полученные ниже формулы (12), (13) были известны ранее (см. [14], а также [12]), однако мы приведем наиболее естественный геометрический способ их получения, основанный на эллиптической параметризации.
Утверждение 2.2. Пусть величина $s = (1 - \alpha ){\text{/}}\sqrt {{{\alpha }^{2}} + {{\beta }^{2}}} $ удовлетворяет условию $s > 1$, тогда решение (11) имеет вид
(12)
$W(\theta ) = \frac{{cos(\theta + {{\theta }_{2}})}}{{s + sin(\theta + {{\theta }_{2}})}},\quad D(\theta ) = \frac{{sin(\theta + {{\theta }_{2}})}}{{s + sin(\theta + {{\theta }_{2}})}},$(13)
$cos{{\theta }_{2}} = \frac{\beta }{{\sqrt {{{\alpha }^{2}} + {{\beta }^{2}}} }},\quad sin{{\theta }_{2}} = \frac{\alpha }{{\sqrt {{{\alpha }^{2}} + {{\beta }^{2}}} }}.$Доказательство. Воспользуемся следующими представлениями искомых функций:
(14)
$W(\theta ) = r(\theta )cos\varphi (\theta ),\quad D(\theta ) = r(\theta )sin\varphi (\theta ).$(15)
$\begin{array}{*{20}{c}} {r{\kern 1pt} 'cos\varphi - r\varphi {\kern 1pt} 'sin\varphi = - rsin\varphi - {{r}^{2}}co{{s}^{2}}\varphi ,} \\ {r{\kern 1pt} 'sin\varphi + r\varphi {\kern 1pt} 'cos\varphi = - rcos\varphi - {{r}^{2}}cos\varphi sin\varphi .} \end{array}$(16)
$\varphi {\kern 1pt} ' = 1,\quad {\text{т}}.{\text{е}}.\quad \varphi (\theta ) = \theta + {{\theta }_{2}}.$Заметим, что константа $1{\text{/}}s < 1$ играет роль эксцентриситета эллипса, таким образом, условие $s > 1$ гарантирует корректность формул (12) в произвольный момент времени $\theta $. Утверждение доказано.
Наконец, для завершения подготовки к численному решению нерелятивистских уравнений отметим, что пространственные частные производные решения системы (7):
2.2. Численный алгоритм
По сути, излагаемый ниже метод является методом характеристик, однако его конструкцию весьма удобно привести в терминах лагранжева описания среды, т.е. используя понятия частиц и их траекторий.
Определим для нахождения численного решения на прямой $\rho \in ( - \infty ,\infty )$ произвольную сетку в начальный момент времени $\theta = 0$:
состоящую из $M$ узлов. В каждый узел ${{\rho }_{k}}(\theta = 0)$, 1 < k < M, поместим частицу, маркированную лагранжевой координатой $\rho _{k}^{L}$.Напомним, что траектория каждой частицы характеризуется двумя параметрами: лагранжевой координатой ${{\rho }^{L}}$ и функцией смещения $R({{\rho }^{L}},\theta )$, которые совместно определяют эйлерову координату $\rho ({{\rho }^{L}},\theta )$, т.е. местонахождение частицы в момент времени $\theta $:
Перепишем систему уравнений (7) в более удобной форме:
(22)
$\frac{{dV(\rho ,\theta )}}{{d\theta }} = - E(\rho ,\theta ),\quad \frac{{dE(\rho ,\theta )}}{{d\theta }} = V(\rho ,\theta ),$(24)
$R({{\rho }^{L}},\theta ) = E(\rho ,\theta ) \equiv E({{\rho }^{L}} + R({{\rho }^{L}},\theta ),\theta ).$(25)
$\frac{{dV(\rho _{k}^{L},\theta )}}{{d\theta }} = - R(\rho _{k}^{L},\theta ),\quad \frac{{dR(\rho _{k}^{L},\theta )}}{{d\theta }} = V(\rho _{k}^{L},\theta ),\quad k = 1,2, \ldots ,M.$Воспользуемся равенствами (21) и (24) для получения недостающих начальных условий к системам вида (25). В узле ${{\rho }_{k}}$ при $\theta = 0$ определено ${{E}_{0}}({{\rho }_{k}})$, т.е. выполнено ${{\rho }_{k}} = \rho _{k}^{L} + {{E}_{0}}({{\rho }_{k}})$, откуда для частицы, помеченной лагранжевой координатой $\rho _{k}^{L}$, сразу следуют начальные условия
(26)
$V(\rho _{k}^{L},\theta = 0) = {{V}_{0}}({{\rho }_{k}}),\quad R(\rho _{k}^{L},\theta = 0) = {{E}_{0}}({{\rho }_{k}}),\quad k = 1,2, \ldots ,M.$Однако решение задачи (25), (26) не позволяет найти пространственные производные искомых функций $V$ и $E$, что делает невозможным определение функции электронной плотности $N$ в соответствии с (4). Чтобы избежать этого недостатка, достаточно переформулировать задачу (19), (20), записанную в эйлеровых переменных, также в лагранжевы переменные, используя рассуждения, изложенные выше. Формальные преобразования дают уравнения
(27)
$\frac{{dW(\rho _{k}^{L},\theta )}}{{d\theta }} = - D(\rho _{k}^{L},\theta ) - {{W}^{2}}(\rho _{k}^{L},\theta ),\quad \frac{{dD(\rho _{k}^{L},\theta )}}{{d\theta }} = (1 - D(\rho _{k}^{L},\theta ))W(\rho _{k}^{L},\theta )$(28)
$W(\rho _{k}^{L},\theta = 0) = {{W}_{0}}({{\rho }_{k}}) \equiv {{\beta }_{k}},\quad D(\rho _{k}^{L},\theta = 0) = {{D}_{0}}({{\rho }_{k}}) \equiv {{\alpha }_{k}},$Теперь с помощью решения задачи (27), (28) и соотношения (21) для каждой частицы
можно в эйлеровой точке пространства $({{\rho }_{k}}(\theta ),\theta )$ определить значение электронной плотностиТаким образом, предлагаемый численный алгоритм заключается в точном (аналитическом) нахождении в узлах переменной эйлеровой сетки (29) решений уравнений (25) с условиями (26) для $k = 1,2, \ldots ,M$:
(30)
$\begin{array}{*{20}{c}} {V(\rho _{k}^{L},\theta ) = {{A}_{k}}cos(\theta + {{\theta }_{1}}),\quad R(\rho _{k}^{L},\theta ) = {{A}_{k}}sin(\theta + {{\theta }_{1}}),} \\ {{{A}_{k}} = \sqrt {V_{0}^{2}({{\rho }_{k}}) + E_{0}^{2}({{\rho }_{k}})} ,\quad cos{{\theta }_{1}} = {{V}_{0}}({{\rho }_{k}}){\text{/}}{{A}_{k}},\quad sin{{\theta }_{1}} = {{E}_{0}}({{\rho }_{k}}){\text{/}}{{A}_{k}}.} \end{array}$Далее необходимо обсудить вопросы о корректности предлагаемых формул и восстановлении функций, найденных в узлах переменной эйлеровой сетки, для произвольных значений $\rho $ между этими узлами.
Важным для ответа на первый вопрос является
Утверждение 2.3. Пусть выполнены условия утверждения 2.1, тогда эйлеровы траектории частиц ${{\rho }_{k}}(\theta ),1 \leqslant k \leqslant M,$ определяемые соотношением (29), не пересекутся ни при каком $\theta > 0$.
Доказательство. Применим формулу (21) для двух бесконечно близких частиц с координатами ${{\rho }^{L}}$ и ${{\rho }^{L}} + \Delta {{\rho }^{L}}$ соответственно, получим
(31)
$T({{\rho }^{L}},\theta ) \equiv \mathop {\left( {\frac{{\partial R({{\rho }^{L}},\theta )}}{{\partial {{\rho }^{L}}}}} \right)}\nolimits^2 + \mathop {\left( {\frac{{\partial V({{\rho }^{L}},\theta )}}{{\partial {{\rho }^{L}}}}} \right)}\nolimits^2 < 1.$(32)
$\frac{d}{{d\theta }}\left( {\frac{{\partial V({{\rho }^{L}},\theta )}}{{\partial {{\rho }^{L}}}}} \right) = - \frac{{\partial R({{\rho }^{L}},\theta )}}{{\partial {{\rho }^{L}}}},\quad \frac{d}{{d\theta }}\left( {\frac{{\partial R({{\rho }^{L}},\theta )}}{{\partial {{\rho }^{L}}}}} \right) = \frac{{\partial V({{\rho }^{L}},\theta )}}{{\partial {{\rho }^{L}}}},$С этой целью рассмотрим выражение $\partial \rho ({{\rho }^{L}},\theta ){\text{/}}\partial {{\rho }^{L}}$, следующее из (21). Отметим, что в произвольный момент времени $\theta $ его обратная величина в точности совпадает со значением электронной плотности, т.е.
Теперь воспользуемся тем, что при $\theta = 0$ электронная плотность выражается формулой
Это дает возможность выразить искомую величину:Следствие. Порядок лагранжевых частиц (29) сохраняется во времени, т.е. для произвольного $\theta \geqslant 0$ справедливо
Рассмотрим теперь вопрос о положительности электронной плотности $N(\rho ,\theta )$ в узлах сетки ${{\rho }_{k}}(\theta ),k = 1,2, \ldots ,M$. Имеет место
Утверждение 2.4. Пусть выполнены условия утверждения 2.1, тогда в произвольный момент времени $\theta \geqslant 0$ в произвольном узле сетки ${{\rho }_{k}}(\theta )$, $k = 1,2, \ldots ,M$, выполнено неравенство
Доказательство. В каждом узле эйлеровой сетки
значение электронной плотности определено формулой В свою очередь, значения $D(\rho _{k}^{L},\theta )$ порождаются решением системы (27), (28), т.е. даются формулами (12), (13).Обратим внимание, что условие $s > 1$, т.е. неравенство $1 - 2D(0) - {{W}^{2}}(0) > 0$ эквивалентно выполнению условий утверждения 2.1 (неравенству (9)) и, кроме того, сохраняется во времени. Другими словами, в произвольный момент времени $\theta \geqslant 0$ справедливо
что можно проверить простой подстановкой формул (12). Отсюда, в свою очередь, следует неравенство $D(\theta ) < 1{\text{/}}2$, которое с учетом (4) приводит к искомой оценке снизу для электронной плотности. Утверждение доказано.Следует отметить, что из формул (12) можно получить также оценку сверху для электронной плотности вида
Рассмотрим вопрос о регулярности эйлеровой сетки ${{\rho }_{k}}(\theta ),\quad k = 1,2, \ldots ,M,$ получаемой в процессе численного алгоритма. С этой целью удобно проанализировать функцию расстояний между соседними частицами
Утверждение 2.5. Пусть выполнены условия утверждения 2.1, тогда в произвольный момент времени $\theta > 0$ для соседних узлов эйлеровой сетки ${{\rho }_{k}}(\theta ),\;k = 1,2, \ldots ,M,$ выполнен закон сохранения заряда
(35)
$\int\limits_{{{\rho }_{k}}(\theta )}^{{{\rho }_{{k + 1}}}(\theta )} \,N(\rho ,\theta )d\rho = \int\limits_{{{\rho }_{k}}(0)}^{{{\rho }_{{k + 1}}}(0)} \,N(\rho ,\theta = 0)d\rho .$Доказательство. Рассмотрим функцию
(36)
${{h}_{k}}(\theta ) - [E({{\rho }_{{k + 1}}},\theta ) - E({{\rho }_{k}},\theta )] = {{h}_{k}}(0) - [E({{\rho }_{{k + 1}}},0) - E({{\rho }_{k}},0)].$Следствие. Для функции расстояния между частицами в произвольный момент времени $\theta > 0$ справедливы неравенства
Кроме того, из утверждения 2.5 явно следует рекомендация выбирать начальную эйлерову сетку ${{\rho }_{k}}(0)$, $k = 1,2, \ldots ,M$, таким образом, чтобы интегралы в правой части соотношения (35) были примерно равны и достаточно малы. Это несложно сделать, учитывая начальные данные (8) и формулу для плотности (4).
Суммируя приведенное описание численного алгоритма и результаты, связанные с анализом его корректности, подчеркнем, что для решения исходной задачи (4), (7), (8), записанной в эйлеровых переменных, удобно перейти в лагранжевы переменные и использовать явные формулы для вычисления искомых функций в точках ${{\rho }_{k}}(\theta )$, $k = 1,2, \ldots ,M$, принадлежащих траекториям частиц. Этого вполне достаточно для исследования большинства постановок. Однако вполне возможно возникновение ситуаций, когда требуется определить решение в заданных эйлеровых точках $(\rho ,\theta )$, которые не обязаны принадлежать рассчитываемым траекториям частиц.
В этом случае в момент времени $\theta $ необходимо определить сначала интервал $[{{\rho }_{k}}(\theta ),{{\rho }_{{k + 1}}}(\theta )]$, которому принадлежит заданное значение $\rho $, а затем с помощью процедуры интерполяции найти приближенное значение. Учитывая, что в узлах эйлеровой сетки ${{\rho }_{k}}(\theta )$, $k = 1,2, \ldots ,M$, имеются не только значения функций $V(\rho ,\theta )$ и $E(\rho ,\theta )$, но и значения их пространственных производных, представляется весьма удобным применение в этих целях эрмитовой кубической интерполяции. Необходимые формулы и оценки погрешностей будут приведены в разд. 4 (см. также [16]).
3. РЕШЕНИЕ РЕЛЯТИВИСТСКИХ УРАВНЕНИЙ
Прежде, чем описывать алгоритм решения задачи (4), (5) с начальными условиями (6), напомним ее основные свойства, а также отличия от нерелятивистского случая.
3.1. Существование решения и уравнения в лагранжевых переменных
Система уравнений (5) также является гиперболической, и для нее справедливы общие результаты о локальном существовании гладкого решения задачи Коши и характере возникновении особенностей, отмеченные ранее (см. [13]). В рассматриваемом случае эти результаты можно уточнить (см. [7]):
Утверждение 3.1. Пусть начальные данные (6) принадлежат классу ${{C}^{2}}(\mathbb{R})$ и выражение $2\sqrt {1 + P_{0}^{2}(\rho )} + E_{0}^{2}(\rho )$ не равно тождественно константе. Тогда, если существует хотя бы одна точка ${{\rho }_{0}}$, для которой выполняется неравенство
Выполнение для всех $\rho $ условия
обеспечивает сохранение гладкости решения, по крайней мере, в течение одного полупериода $T(\rho )$ на каждой характеристике, т.е. до момента времени ${{t}_{*}} = \mathop {min}\limits_{\rho \in \mathbb{R}} T(\rho )$, ${{t}_{ * }} \geqslant \pi $.Следует отметить, что начальные данные (6) рассматриваются на всей прямой, поэтому условие отличия от константы выражения $2\sqrt {1 + P_{0}^{2}(\rho )} + E_{0}^{2}(\rho )$ следует воспринимать, в первую очередь, как конечность области или ограниченность энергии исследуемого решения. Тем более, что даже в этом случае типичным является возникновение градиентной катастрофы у решения системы (5). Действительно, из ее системы характеристик:
(37)
$\frac{{dP}}{{d\theta }} = - E,\quad \frac{{dE}}{{d\theta }} = \frac{P}{{\sqrt {1 + {{P}^{2}}} }},\quad \frac{{d\rho }}{{d\theta }} = \frac{P}{{\sqrt {1 + {{P}^{2}}} }},$(38)
$2\sqrt {1 + {{P}^{2}}} + {{E}^{2}} = 2\sqrt {1 + P_{0}^{2}({{\rho }_{0}})} + E_{0}^{2}({{\rho }_{0}}) = {\text{const}}$Утверждение 3.2. У любого решения задачи Коши (5), (6), для которого $2\sqrt {1 + P_{0}^{2}(\rho )} + E_{0}^{2}(\rho )$ не равно тождественно константе, являющегося сколь угодно малым отклонением от положения равновесия $P = 0$, $E = 0$, производные решения в течение конечного времени обращаются в бесконечность.
Суммируя вышесказанное, подчеркнем, что в отличие от нерелятивистского случая численное решение задачи (4), (5) с начальными условиями (6) имеет смысл обсуждать только на конечном временном интервале. Причем получаемое решение, как правило, будет завершаться градиентной катастрофой, т.е. обращением в бесконечность функции электронной плотности.
По этой причине представляется вполне разумным подход к численному решению, основанный на использовании лагранжевых переменных, как в разд. 2. С этой целью переформулируем соответствующим образом исходную постановку (4)–(6). Уравнения динамики лагранжевых частиц для $k = 1,2, \ldots ,M$ примут следующий вид:
(39)
$\frac{{dP(\rho _{k}^{L},\theta )}}{{d\theta }} = - R(\rho _{k}^{L},\theta ),\quad \frac{{dR(\rho _{k}^{L},\theta )}}{{d\theta }} = \frac{{P(\rho _{k}^{L},\theta )}}{{\sqrt {1 + {{P}^{2}}(\rho _{k}^{L},\theta )} }} \equiv V(\rho _{k}^{L},\theta ),$(40)
$P(\rho _{k}^{L},\theta = 0) = {{P}_{0}}({{\rho }_{k}}),\quad R(\rho _{k}^{L},\theta = 0) = {{E}_{0}}({{\rho }_{k}}),\quad k = 1,2, \ldots ,M.$Дополним полученную постановку для функций $P(\rho ,\theta )$ и $E(\rho ,\theta )$ задачей для их производных:
(41)
$\frac{{dQ}}{{d\theta }} = - D - \frac{{{{Q}^{2}}}}{{{{{(1 + {{P}^{2}})}}^{{3/2}}}}},\quad \frac{{dD}}{{d\theta }} = (1 - D)\frac{Q}{{{{{(1 + {{P}^{2}})}}^{{3/2}}}}}.$(42)
$Q(\rho _{k}^{L},\theta = 0) = {{P}_{0}}({{\rho }_{k}}),\quad D(\rho _{k}^{L},\theta = 0) = {{E}_{0}}({{\rho }_{k}}),\quad k = 1,2, \ldots ,M.$Подчеркнем различие между задачами Коши в релятивистском (41), (42) и нерелятивистском (27), (28) случаях: уравнения (27) не зависят от функций $V(\rho _{k}^{L},\theta ),\;R(\rho _{k}^{L},\theta )$, поэтому их решения находятся отдельно от (25); в свою очередь, уравнения (41) зависят от функции $P(\rho _{k}^{L},\theta )$, поэтому их решения можно определить только при совместном решении с (39).
3.2. Численный алгоритм и особенности его использования
Преобразование исходной гиперболической постановки (4)–(6) к задаче Коши для системы обыкновенных дифференциальных уравнений (39)–(42) порождает численный метод нахождения искомых переменных в точках траекторий лагранжевых частиц $({{\rho }_{k}}(\theta ),\theta )$, где ${{\rho }_{k}}(\theta ) = \rho _{k}^{L} + R(\rho _{k}^{L},\theta ),\;k = 1,2, \ldots ,M.$
При наличии у решения достаточной гладкости по переменной $\theta $ весьма удобным представляется использование классического метода Рунге–Кутты четвертого порядка точности (см. [16]), в противном случае (меньшей гладкости) следует применять схемы меньшего порядка точности вплоть до метода Эйлера. В любом случае, в силу использования приближенного метода интегрирования, формируется его погрешность, поэтому для дальнейшего важно, что даже при отсутствии ошибок округлений мы будем оперировать в узлах эйлеровой сетки не точными значениями искомых функций $F({{\rho }_{k}},{{\theta }^{n}})$, как в нерелятивистском случае, а их приближениями ${{F}_{k}}({{\theta }^{n}})$, которые в общем случае удовлетворяют асимптотическому равенству
(43)
$\left| {{{F}_{k}}({{\theta }^{n}}) - F({{\rho }_{k}},{{\theta }^{n}})} \right| = O({{\tau }^{p}}),\quad p > 0,\quad k = 1,2, \ldots ,M,$Отметим также, что устойчивость интегрирования по времени уравнений для импульса и электрического поля полностью определяется равенством (38). Аналогичное свойство для уравнений, описывающих динамику их производных, отсутствует, поэтому при начальных условиях, не приводящих к пересечению лагранжевых траекторий в нерелятивистском случае, в релятивистском случае эти траектории пересекаются. Такая ситуация приводит к возникновению разрыва у функции $E(\rho ,\theta )$, и, как его следствие, сингулярности функции электронной плотности в соответствии с (4). Поэтому в процессе вычислений необходимо постоянно контролировать сохранение стартового порядка частиц, т.е. условия ${{\rho }_{k}}({{\theta }^{n}}) < {{\rho }_{{k + 1}}}({{\theta }^{n}})$ для всех $k = 1,2, \ldots ,M - 1.$ Нарушение этого условия хотя бы для одного значения $k$ означает прекращение процесса колебаний (невозможность дальнейшего применения модели), обозначаемое термином “опрокидывание” (breaking). Вышесказанное означает, что наблюдение или исследование решения с конкретными начальными данными имеет смысл только до наступления момента опрокидывания, т.е. релятивистский аналог утверждения 2.3 справедлив только локально во времени. По этой причине далее будем иметь в виду, что численный метод применяется на ограниченном интервале времени $\theta \in [0,{{\theta }_{{br}}}]$, пока искомое решение задачи (4)–(6) существует, единственно и ограничено вместе с необходимыми производными. Другими словами, далее предполагается, что на отрезке $[0,{{\theta }_{{br}}}]$ порядок лагранжевых частиц не изменяется, т.е. выполнено неравенство
(44)
${{\left( {\frac{{\partial P(\rho ,\theta )}}{{\partial \rho }}} \right)}^{2}} + 2\frac{{\partial E(\rho ,\theta )}}{{\partial \rho }} - 1 < 0.$В этих предположениях справедливо
Утверждение 3.3. Пусть выполнено условие (44) и погрешность численного алгоритма имеет вид (43), тогда при достаточно малом $\tau $ в произвольный момент времени ${{\theta }^{n}}$ из отрезка $[0,{{\theta }_{{br}}}]$ в произвольном узле сетки ${{\rho }_{k}}(\theta ),\;k = 1,2, \ldots ,M,$ выполнено неравенство
Доказательство. В каждом узле эйлеровой сетки
Ответ на вопрос о регулярности эйлеровой сетки ${{\rho }_{k}}({{\theta }^{n}})$, $k = 1,2, \ldots ,M$, получаемой в процессе численного алгоритма дает
Утверждение 3.4. Пусть погрешность алгоритма численного интегрирования имеет вид (43) и на отрезке $[0,{{\theta }_{{br}}}]$ порядок лагранжевых частиц не изменяется, тогда при достаточно малом $\tau $ в произвольный момент времени ${{\theta }^{n}}$ из отрезка $[0,{{\theta }_{{br}}}]$ для соседних узлов эйлеровой сетки ${{\rho }_{k}}({{\theta }^{n}})$, $k = 1,2, \ldots ,M$, выполнен закон сохранения заряда
(46)
$\int\limits_{{{\rho }_{k}}({{\theta }^{n}})}^{{{\rho }_{{k + 1}}}({{\theta }^{n}})} \,N(\rho ,{{\theta }^{n}})d\rho = \int\limits_{{{\rho }_{k}}(0)}^{{{\rho }_{{k + 1}}}(0)} \,N(\rho ,\theta = 0)d\rho + O({{\tau }^{p}}),\quad p > 0.$Доказательство. Рассмотрим функцию, получаемую в процессе вычислений,
(47)
${{h}_{k}}({{\theta }^{n}}) - [E({{\rho }_{{k + 1}}},{{\theta }^{n}}) - E({{\rho }_{k}},{{\theta }^{n}})] = {{h}_{k}}(0) - [E({{\rho }_{{k + 1}}},0) - E({{\rho }_{k}},0)] + O({{\tau }^{p}}).$Следствие. Для функции расстояния между частицами в произвольный момент времени ${{\theta }^{n}}$ из отрезка $[0,{{\theta }_{{br}}}]$ справедливы неравенства
Кроме того, из утверждения 3.4 явно следует рекомендация выбирать начальную эйлерову сетку ${{\rho }_{k}}(0)$, $k = 1,2, \ldots ,M$, таким образом, чтобы интегралы в правой части соотношения (46) были примерно равны и достаточно малы. Это несложно сделать, учитывая начальные данные (6) и формулу для плотности (4).
С помощью выражений, использовавшихся при доказательстве утверждения 3.4, можно оценить величину скачка функции $E(\rho ,\theta )$ в момент опрокидывания колебаний. Действительно, предположим, что траектории двух соседних частиц пересеклись, т.е. для некоторого $k$ из диапазона $1 \leqslant k \leqslant M - 1$ выполнено ${{h}_{k}}({{\theta }^{n}}) = {{\rho }_{{k + 1}}}({{\theta }^{n}}) - {{\rho }_{k}}({{\theta }^{n}}) = 0$, тогда из выражения (47) следует
(48)
$[E({{\rho }_{k}},{{\theta }^{n}})] = - ({{\rho }_{{k + 1}}}(0) - {{\rho }_{k}}(0)) + ({{E}_{0}}({{\rho }_{{k + 1}}}) - {{E}_{0}}({{\rho }_{k}})) + O({{\tau }^{p}}).$Суммируя приведенное описание численного алгоритма и результаты, связанные с анализом его корректности, подчеркнем, что для решения исходной задачи (5), (6), записанной в эйлеровых переменных, удобно перейти в лагранжевы переменные и использовать приближенные методы интегрирования по времени для вычисления искомых функций в точках ${{\rho }_{k}}({{\theta }^{n}})$, $k = 1,2, \ldots ,M$, принадлежащих траекториям частиц. Этого вполне достаточно для исследования большинства постановок. Однако вполне возможно возникновение ситуаций, когда требуется определить решение в заданных эйлеровых точках $(\rho ,\theta )$, которые не обязаны принадлежать рассчитываемым траекториям частиц.
В этом случае в момент времени ${{\theta }^{n}}$ необходимо определить сначала интервал $[{{\rho }_{k}}({{\theta }^{n}}),{{\rho }_{{k + 1}}}({{\theta }^{n}})]$, которому принадлежит заданное значение $\rho $, а затем с помощью процедуры интерполяции найти приближенное значение. Учитывая, что в узлах эйлеровой сетки ${{\rho }_{k}}({{\theta }^{n}}),\quad k = 1,2, \ldots ,M,$ имеются не только значения функций $P(\rho ,\theta )$ и $E(\rho ,\theta )$, но и значения их пространственных производных, представляется весьма удобным применение в этих целях эрмитовой кубической интерполяции. Необходимые формулы и оценки погрешностей будут приведены в следующем разделе.
4. ЭРМИТОВА КУБИЧЕСКАЯ ИНТЕРПОЛЯЦИЯ И РЕЗУЛЬТАТЫ О СХОДИМОСТИ
Отметим, что использование кубической интерполяции требует от решения большей гладкости, чем ${{C}^{2}}(\mathbb{R})$, однако при условии ограниченности решения и его первых производных в развитии во времени потери начальной гладкости не происходит (см. [13]). Поэтому погрешность интерполируемых данных в общем случае зависит от гладкости начальных функций.
Если в узлах сетки известны не только значения достаточно гладкой функции, но и значения ее производных, удобным способом ее приближенного представления является эрмитова кубическая интерполяция. Вывод необходимых формул и оценок погрешностей приведен в [17], практические детали использования, включая необходимые программы, хорошо описаны в [16]. Далее нам потребуется известное (см. [17])
Утверждение 4.1. Пусть на отрезке $[a,b]$ длины $h > 0$ задана функция $f(x)$ такая, что $\mathop {max}\limits_{[a,b]} \left| {{{f}^{{(4)}}}(x)} \right| = {{A}_{4}} < \infty $, и по значениям $f(a),\;f(b),\;f{\kern 1pt} '(a),\;f{\kern 1pt} '(b)$ построен ее эрмитов кубический интерполянт
(49)
$C(x) = f(a)[{{y}^{2}}(2y - 3) + 1] + f(b){{y}^{2}}(2y - 3) + f{\kern 1pt} '(a)hy{{(y - 1)}^{2}} + f{\kern 1pt} '(b)h{{y}^{2}}(y - 1),$(50)
$\left| {{{f}^{{(l)}}}(x) - {{C}^{{(l)}}}(x)} \right| \leqslant {{C}_{l}}{{h}^{{4 - l}}}{{A}_{4}},\quad l = 0,1,2,3,$Обратим внимание, что приведенный интерполянт с разумной точностью приближает не только саму функцию, но еще и три ее производных, что может оказаться полезным для приложений. Кроме того, представляет интерес вычислительная устойчивость сплайна (49). Справедливо
Утверждение 4.2. Пусть в эрмитовом кубическом интерполянте $C(x)$, построенном на отрезке $[a,b]$ длины $h > 0$, величины $f(a),\;f(b),\;f{\kern 1pt} '(a),\;f{\kern 1pt} '(b)$ заданы с возмущениями так, что
(51)
${\text{|}}C(x) - {{C}_{*}}(x){\kern 1pt} {\text{|}} \leqslant {{\varepsilon }_{a}} + {{\varepsilon }_{b}} + \frac{{4h}}{{27}}({{\delta }_{a}} + {{\delta }_{b}}),\quad {\text{|}}C{\kern 1pt} '(x) - С_{*}^{'}(x){\kern 1pt} {\text{|}} \leqslant \frac{3}{{2h}}({{\varepsilon }_{a}} + {{\varepsilon }_{b}}) + {{\delta }_{a}} + {{\delta }_{b}}.$Доказательство. Явная формула для разности эрмитовых кубических интерполянтов, построенных по точным и возмущенным значениям,
Следствие. Из утверждений 4.1 и 4.2 вытекает оценка близости точного и приближенного значений функции $f(x)$, полученного с помощью возмущенного интерполянта $\forall x \in [a,b]$,
(52)
${\text{|}}{\kern 1pt} f(x) - {{C}_{*}}(x){\kern 1pt} {\text{|}} \leqslant {{C}_{0}}{{h}^{4}}{{A}_{4}} + {{\varepsilon }_{a}} + {{\varepsilon }_{b}} + \frac{{4h}}{{27}}({{\delta }_{a}} + {{\delta }_{b}}).$Подчеркнем, что в (52) слагаемые в правой части имеют различное происхождение, а именно: возмущение точных значений функции и ее производных в концах отрезка и замена гладкой функции внутри отрезка на кубический многочлен.
Используя оценки выше, можно привести окончательные результаты о сходимости численных алгоритмов из разд. 2 и 3. Для численного решения нерелятивистских уравнений справедлива
Теорема 1. Пусть выполнены условия утверждения 2.1, тогда в произвольный момент времени $\theta \geqslant 0$ формулы (12) и (30) в предположении отсутствия ошибок округлений дают точное решение задачи (4), (7), (8) в узлах эйлеровой сетки (29).
Если начальные данные (8) принадлежат классу ${{C}^{5}}(\mathbb{R})$, то для $\forall \rho \in [{{\rho }_{1}}(\theta ),{{\rho }_{M}}(\theta )]$ значения функций $V(\rho ,\theta ),$ $E(\rho ,\theta ),$ $N(\rho ,\theta )$ можно восстановить с точностью $O({{h}^{4}}),$ где $h = \mathop {max}\limits_{1 \leqslant k \leqslant M - 1} ({{\rho }_{{k + 1}}}(\theta ) - {{\rho }_{k}}(\theta ))$. При этом значения электронной плотности будут при достаточно малых $h$ удовлетворять оценке $N(\rho ,\theta ) \geqslant 1{\text{/}}2$.
Доказательство. Численный алгоритм для решения задачи (4), (7) с начальными условиями (8), изложенный в разд. 2, позволяет в произвольный момент времени $\theta > 0$ получать точные (в предположении отсутствия ошибок округлений) значения функций $V(\rho ,\theta ),$ $E(\rho ,\theta ),$ $N(\rho ,\theta )$ в узлах эйлеровой сетки ${{\rho }_{k}}(\theta )$, $k = 1,2, \ldots ,M$, которые принадлежат характеристикам системы уравнений (7).
Согласно утверждениям 2.3 и 2.5, эта сетка будет невырожденной, т.е. порядок узлов будет сохраняться и длины отрезков ${{h}_{k}}(\theta )$ будут равномерно ограничены. Это необходимо, когда точка $(\rho ,\theta )$, в которой требуется найти решение задачи, не принадлежит множеству узлов получаемой в процессе вычислений сетки. В такой ситуации необходимо определить отрезок $[a,b] \equiv [{{\rho }_{{k + 1}}}(\theta ),{{\rho }_{k}}(\theta )]$, которому принадлежит заданное $\rho $, и по известным в концах отрезка значениям функции и производной построить эрмитов кубический интерполянт.
Далее применяется неравенство (52), в котором параметры $\varepsilon $ и $\delta $ играют роль вычислительной погрешности и поэтому могут быть опущены. Требование принадлежности начальных данных к классу ${{C}^{5}}(\mathbb{R})$ диктуется принадлежностью функции $D(\rho ,\theta )$ к классу ${{C}^{4}}(\mathbb{R})$, так как электронная плотность вычисляется по формуле
Напомним, что при решении релятивистских уравнений численный алгоритм предусматривает решение задачи Коши по времени с точностью $O({{\tau }^{p}}),p > 0$, где $\tau $ – параметр дискретизации по времени. Это приводит к тому, что значения искомых функций $P(\rho ,\theta ),$ $E(\rho ,\theta ),$ $N(\rho ,\theta )$ вычисляются не просто в узлах эйлеровой сетки ${{\rho }_{k}}({{\theta }^{n}}),k = 1,2, \ldots M,$ принадлежащих характеристикам, но еще и с погрешностями $O({{\tau }^{p}})$. Кроме того, в релятивистском случае отсутствует глобальная по времени теорема существования решения, т.е. можно обсуждать сходимость численного алгоритма только до наступления градиентной катастрофы. Поэтому для численного решения релятивистских уравнений справедлива
Теорема 2. Пусть погрешность численного интегрирования задачи Коши (39)–(42) имеет вид (43), на отрезке $[0,{{\theta }_{{br}}}]$ порядок лагранжевых частиц не изменяется и выполнено условие локального по времени существования решения (44), тогда при достаточно малом $\tau $ в произвольный момент времени ${{\theta }^{n}}$ из отрезка $[0,{{\theta }_{{br}}}]$ в узлах эйлеровой сетки (29) справедлива оценка погрешности
(53)
$\left| {{{F}_{k}}({{\theta }^{n}}) - F({{\rho }_{k}},{{\theta }^{n}})} \right| = O({{\tau }^{p}}),\quad p > 0,\quad k = 1,2, \ldots ,M,$Если начальные данные (6) принадлежат классу ${{C}^{5}}(\mathbb{R})$, то в произвольный момент времени ${{\theta }^{n}} \in [0,{{\theta }_{{br}}}]$ и в произвольной точке пространства $\rho \in [{{\rho }_{1}}({{\theta }^{n}}),{{\rho }_{M}}({{\theta }^{n}})]$ значения функций $P(\rho ,\theta ),$ $E(\rho ,\theta ),$ $N(\rho ,\theta )$ можно восстановить с точностью $O({{h}^{4}} + {{\tau }^{p}}),\;p > 0$, где $h = \mathop {max}\limits_k ({{\rho }_{{k + 1}}}(\theta ) - {{\rho }_{k}}(\theta ))$. При этом значения электронной плотности при достаточно малых $h$ и $\tau $ будут удовлетворять оценке $N(\rho ,\theta ) \geqslant 1{\text{/}}2$.
Доказательство. Численный алгоритм для решения задачи (4), (5) с начальными условиями (6), изложенный в разд. 3, позволяет в произвольный момент времени ${{\theta }^{n}} \in [0,{{\theta }_{{br}}}]$ получать значения функций $V(\rho ,\theta )$, $E(\rho ,\theta )$, $N(\rho ,\theta )$ с точностью $O({{\tau }^{p}}),\;p > 0$, в узлах эйлеровой сетки ${{\rho }_{k}}({{\theta }^{n}}),\;k = 1,2, \ldots ,M$, которые принадлежат характеристикам системы уравнений (5) в дискретные моменты времени ${{\theta }^{n}}$.
Согласно предположению о локальной гладкости решения и утверждению 3.4, на отрезке $[0,{{\theta }_{{br}}}]$ эта сетка будет невырожденной, т.е. порядок узлов будет сохраняться при любом ${{\theta }^{n}}$ и длины отрезков ${{h}_{k}}({{\theta }^{n}})$ будут равномерно ограничены. Это необходимо, когда точка $(\rho ,{{\theta }^{n}})$, в которой требуется найти решение задачи, не принадлежит множеству узлов получаемой в процессе вычислений сетки. В такой ситуации необходимо определить отрезок $[a,b] \equiv [{{\rho }_{{k + 1}}}({{\theta }^{n}}),{{\rho }_{k}}({{\theta }^{n}})]$, которому принадлежит заданное $\rho $, и по вычисленным с точностью $O({{\tau }^{p}}),\;p > 0$, в концах отрезка значениям функции и производной построить эрмитов кубический интерполянт.
Далее применяется неравенство (52), в котором параметры $\varepsilon $ и $\delta $ играют роль погрешности численного интегрирования задачи Коши (39)–(42), т.е. при достаточно малом $\tau $ имеют порядок $O({{\tau }^{p}}),\;p > 0$. Требование принадлежности начальных данных к классу ${{C}^{5}}(\mathbb{R})$ диктуется принадлежностью функции $D(\rho ,\theta )$ к классу ${{C}^{4}}(\mathbb{R})$, так как электронная плотность вычисляется по формуле
5. ЧИСЛЕННЫЕ ИЛЛЮСТРАЦИИ
В качестве начальных условий выберем функции
(54)
${{E}_{0}}(\rho ) = \mathop {\left( {\frac{{{{a}_{*}}}}{{{{\rho }_{*}}}}} \right)}\nolimits^2 \rho exp\left\{ { - 2\frac{{{{\rho }^{2}}}}{{\rho _{*}^{2}}}} \right\},\quad {{P}_{0}}(\rho ) = {{V}_{0}}(\rho ) = 0.$В качестве рабочей области локализации колебаний выберем отрезок $[ - d,d]$ при $d = 4.5{{\rho }_{ * }}$. В этом случае амплитуды колебаний частиц на границах будут по порядку величины совпадать с машинной точностью, в силу $\exp \{ - 2{{d}^{2}}{\text{/}}\rho _{*}^{2}\} \approx 2.58 \times {{10}^{{ - 18}}}$, т.е. приграничные характеристики с большой степенью точности будут совпадать с прямыми $\rho \approx \pm d$. Начальную сетку удобно выбрать равномерной ${{\rho }_{k}}(\theta = 0) = kh - d,$ $k = 0,1, \ldots ,M,$ $h = 2d{\text{/}}M$.
В качестве иллюстрации нерелятивистского алгоритма из разд. 2 возьмем точные формулы (30) и (12) и вычислим значения функций $V(\rho ,\theta )$, $E(\rho ,\theta )$, $W(\rho ,\theta )$, $D(\rho ,\theta )$ в узлах переменной эйлеровой сетки (29) в моменты времени $\theta = n\tau ,$ $n \geqslant 0$, на отрезке $[0,20\pi ]$. Сравним полученные значения с результатом численного интегрирования задачи Коши (25)–(28) классическим методом Рунге–Кутты 4-го порядка точности в те же моменты времени при $\tau = h$.
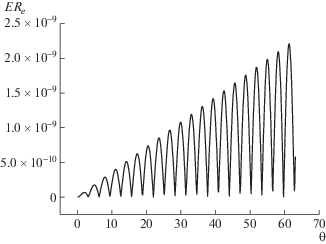
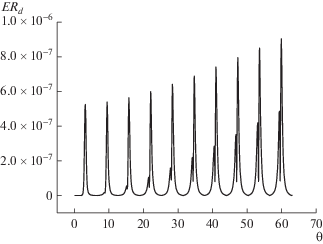
На фиг. 1 и 2 приведены зависимости от времени максимальной по области абсолютной погрешности для функций электрического поля и электронной плотности при $\tau = h = 0.01$. Обратим внимание, что верхняя граница погрешностей на обоих графиках растет практически линейно по времени. Эта тенденция не меняется, если провести вычисления с другими параметрами дискретизации. Например, при $\tau = h = 0.1$ вид графиков неотличим от представленных, зато сами значения погрешностей в полном соответствии с теорией методов Рунге–Кутты ровно в ${{10}^{4}}$ раз больше. Следует также отметить, что абсолютные значения погрешностей электрического поля и электронной плотности отличаются примерно на три порядка. Это указывает на то, что функция электронной плотности является наиболее трудной (чувствительной) для вычислений. Обратим также внимание, что, начиная с некоторого периода, становятся заметными “провалы” в погрешности, соответствующие тождественно нулевым значениям функции $D(\rho ,\theta )$ на отрезке $[ - d,d]$ в некоторые моменты времени ${{\theta }^{n}}$, что полностью соответствует формулам (12) при $\beta = 0$.
В качестве иллюстрации релятивистского алгоритма из разд. 3 приведем расчет эффекта опрокидывания при $\tau = h = 0.01$.
Так как начальные условия в силу утверждения 3.1 обеспечивают существование решения более, чем в течение одного периода, а утверждение 3.2 гарантирует нам наблюдение за градиентной катастрофой решения, то в соответствии с теоретическим анализом в процессе колебаний можно отметить две тенденции. Первая из них заключается в том, что колебания плотности вне начала координат несколько опережают по фазе колебания плотности в точке $\rho = 0$, и от периода к периоду этот фазовый сдвиг увеличивается. Вторая тенденция более наглядна: с течением времени происходит постепенное формирование абсолютного максимума плотности, расположенного вне начала координат. На фиг. 3 пунктиром изображено изменение во времени электронной плотности в начале координат, а сплошной линией – динамика максимального по области значения. Сначала колебания носят регулярный характер, т.е. глобальные по области максимумы и минимумы плотности сменяют друг друга через половину периода и располагаются в начале координат. После седьмого регулярного (центрального) максимума в момент времени $\theta \approx 42.2$ возникает новая структура – максимум электронной плотности вне начала координат, тогда как в окрестности начала координат продолжают наблюдаться регулярные колебания. Вновь возникший максимум в момент времени $\theta \approx 48.8$ возрастает по величине примерно в два раза и на следующем периоде (в $\theta \approx 55.1$) на его месте возникает дельтаобразная сингулярность электронной плотности.
Фиг. 3.
Динамика плотности электронов в релятивистском расчете: максимум по области (сплошная линия) и в начале координат (пунктирная линия).

На фиг. 4 изображены пространственные распределения импульса $P$ и электрического поля $E$ в момент опрокидывания $\theta \approx 55.1$, когда абсолютный максимум плотности вне начала координат стал неограниченным, а траектории пары соседних частиц пересеклись. Отметим, что в силу структуры уравнений (5) их решения будут оставаться нечетными функциями координат в случае, если таким свойством обладают начальные данные. Начальные данные (54) именно таковы, поэтому мы привели результаты численных расчетов только на положительной полуоси.
Фиг. 4.
Пространственное распределение импульса и электрического поля в момент опрокидывания в релятивистском расчете.
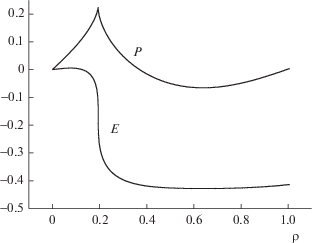
Видно, что в окрестности максимума плотности у компоненты скорости образуется разрыв производной (слабый разрыв), но не самой функции, тогда как у функции электрического поля образуется сильный разрыв. Именно такие качественные характеристики $P$ и $E$ обеспечивают опрокидывание колебаний. Важно отметить, что опрокидывание носит характер “градиентной катастрофы”, т.е. сами функции $P$ и $E$ при этом остаются ограниченными.
Следует отметить, что представленные результаты расчетов замечательно согласуются с данными, полученными с помощью других идейно отличающихся алгоритмов (см. [12]), использующих как лагранжевы, так и эйлеровы переменные.
ЗАКЛЮЧЕНИЕ
В настоящей работе для одномерных плоских уравнений холодной плазмы на основе теорем существования решений, подробные доказательства которых приведены в [19], построены и обоснованы новые численные алгоритмы. Особенностью подхода является использование лагранжевых переменных, что фактически эквивалентно методу характеристик для исходной постановки в эйлеровых переменных.
При пренебрежении релятивистскими эффектами получены аналитические выражения для искомых функций в точках, принадлежащих траекториям лагранжевых частиц, т.е. характеристикам системы уравнений (7). В случае учета эффектов релятивизма заменой аналитическим формулам является численное интегрирование стандартной задачи Коши для системы обыкновенных дифференциальных уравнений, приводящее как к определению самих характеристик системы (5), так и к значениям искомого решения в точках характеристик. В обоих случаях, если необходимо вычисление решения в точках, не принадлежащих траекториям лагранжевых частиц, прилагаются формулы и оценки погрешностей эрмитовой кубической интерполяции, включая оценки вычислительной устойчивости. Результатом работы являются теоремы о сходимости предложенных алгоритмов относительно малых параметров дискретизации независимых эйлеровых переменных.
Проведенные вычислительные эксперименты полностью согласуются с полученными теоретическими результатами о сходимости алгоритмов в нерелятивистском и релятивистском случаях. В частности, при использовании предложенного подхода проведено моделирование известного эффекта опрокидывания плазменных колебаний и подтверждено, что он имеет характер градиентной катастрофы.
Полученные результаты могут быть использованы при численном моделировании лазер-плазменных взаимодействий, когда требуется высокая точность расчетов, а также для развития теории численных методов решения гиперболических систем.
Список литературы
Esarey E., Schroeder C.B., Leemans W.P. Physics of laser-driven plasma-based electron accelerators // Rev. Mod. Phys. 2009. V. 81. P. 1229.
Bulanov S.V., Esirkepov T.Zh., Hayashi Y. et al. On some theoretical problems of laser wake-field accelerators // J. Plasma Phys. 2016. V. 82. № 3. P. 905820308.
Birdsall C.K., Langdon A.B. Plasma physics via computer simulation. New York: McGraw-Hill Inc., 1985.
Днестровский Ю.Н., Костомаров Д.П. Математическое моделирование плазмы. М.: Наука, 1982.
Dawson J.M. Nonlinear electron oscillations in a cold plasma // Phys. Rev. 1959. V. 113. № 2. P. 383–387.
Зельдович Я.Б., Мышкис А.Д. Элементы математической физики. М.: Наука, 1973. С. 86–94.
Розанова О.С., Чижонков Е.В. О существовании глобального решения одной гиперболической задачи // Докл. АН. Математика, информатика, процессы управления. 2020. V. 492. № 1. P. 97–100.
Силин В.П. Введение в кинетическую теорию газов. М.: Наука, 1971. С. 119.
Александров А.Ф., Богданкевич Л.С., Рухадзе А.А. Основы электродинамики плазмы. М.: Высш. школа, 1978. С. 55–60.
Гинзбург В.Л., Рухадзе А.А. Волны в магнитоактивной плазме. М.: Наука, 1975. С. 46–51.
Силин В.П., Рухадзе А.А. Электромагнитные свойства плазмы и плазмоподобных сред. Изд. 2-е испр. М.: Книжный дом “ЛИБРОКОМ”, 2012. С. 104–110.
Чижонков Е.В. Математические аспекты моделирования колебаний и кильватерных волн в плазме. М.: Физматлит, 2018. С. 50–72.
Dafermos C.M. Hyperbolic Conservation Laws in Continuum Physics. The 4th Ed., Berlin-Heidelberg: Springer, 2016. P. 221–225.
Чижонков Е.В. К моделированию электронных колебаний в плазменном слое // Ж. вычисл. матем. и матем. физ. 2011. Т. 51. № 3. С. 456–469.
Davidson R.C. Methods in nonlinear plasma theory. New York: Acad. Press, 1972. P. 33–53.
Kahaner D., Moler C., Nash S. Numerical Methods and Software. New Jersey: Prentice-Hall Inter., Inc., 1989. P. 100–114.
Schultz M.H. Spline Analysis. New York: Prentice-Hall Inter., Inc., 1973. P. 24–39.
Sheppard C.J.R. Cylindrical lenses – focusing and imaging: a review Invited // Appl. Opt. 2013. V. 52. № 4. P. 538–545.
Rozanova O.S., Chizhonkov E.V. On the conditions for the breaking of oscillations in a cold plasma // Z. Angew. Math. Phys. 2021. V. 72. P. 13.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики