Журнал вычислительной математики и математической физики, 2022, T. 62, № 1, стр. 12-22

1. ВВЕДЕНИЕ И ПОСТАНОВКА ЗАДАЧИ

В данной работе рассматривается следующая задача квадратичной минимизации без ограничений:

где пространства $F$ и $H$ предполагаются гильбертовыми, элемент $f \in F$ фиксирован, а оператор $\mathcal{A}$ линеен и ограничен: $\mathcal{A} \in \mathcal{L}(H \to F)$. Основной целью является поиск нормального решения ${{u}_{*}}$ задачи (1.1): Предполагается, что известны некоторые приближения ${{\mathcal{A}}_{n}} \in \mathcal{L}(H \to F)$, ${{f}_{n}} \in F$, сходящиеся к точным данным $\mathcal{A}$, $f$ при $n \to \infty $, и по ним требуется построить соответствующую последовательность элементов ${{u}_{n}} \in H$, сильно сходящуюся в пространстве $H$ к нормальному решению ${{u}_{*}}$.

Задачи такого типа исследовались ранее во множестве работ и, вообще говоря, относятся к классу некорректных задач, в которых малые возмущения исходных данных могут приводить к значительным возмущениям решения. Такое свойство задачи делает невозможным ее устойчивое численное решение без привлечения дополнительной априорной информации (см. [1]) и специальных численных методов, использующих эту информацию. Так, например, в случае, если известно компактное множество, содержащее точное решение ${{u}_{ * }}$, элементы ${{u}_{n}}$ можно строить с помощью метода квазирешений В.К. Иванова (см. [2]). В случае, когда известны уровни погрешностей ${{h}_{n}}$, ${{\sigma }_{n}}$ из оценок

можно использовать метод регуляризации А.Н. Тихонова (см. [3]), метод М.М. Лаврентьева (см. [4]), обобщенный метод невязки (см. [5]), обобщенный принцип невязки (см. [6]), методы итеративной регуляризации (см. [7]) и многие другие (см. [8]–[11]). При этом одним из обязательных требований при обосновании сходимости ${{\left\| {{{u}_{n}} - {{u}_{*}}} \right\|}_{H}} \to 0$ является сходимость последовательностей $\{ {{h}_{n}}\} $ и $\{ {{\sigma }_{n}}\} $ к нулю при $n \to \infty $.

Однако при решении прикладных задач далеко не всегда легко найти компакт, которому принадлежит искомое решение ${{u}_{*}}$, и нередко приходится иметь дело с такими приближенными операторами, для которых 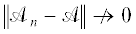при $n \to \infty $. Данное явление наблюдается в случае, когда оператор $\mathcal{A}$ является некомпактным, а вычислитель должен оперировать лишь с конечномерными операторами ${{\mathcal{A}}_{n}}$, как, например, при решении задачи граничного управления для волнового уравнения (см. [12], [13]). Одним из возможных методов решения задач такого вида является вариационный метод М.М. Потапова (см. [14]), для обоснованного применения которого требуется априорная информация об истокопредставимости точного нормального решения ${{u}_{*}} = \mathcal{A}{\kern 1pt} *{{v}_{*}}$ с известным значением ${{r}_{ * }}$ из оценки нормы источника: $\left\| {{{v}_{*}}} \right\| \leqslant {{r}_{*}}$. Для реализации вариационного метода не требуется знание уровней погрешностей ${{h}_{n}}$ и ${{\sigma }_{n}}$, однако отыскание правильных и приемлемых для вычислений, т.е. не сильно завышенных значений оценочной константы ${{r}_{*}}$, является достаточно трудной проблемой. В настоящей работе предлагается подход, использующий информацию об уровнях погрешностей, подобную (1.2), но которая по сравнению с (1.2) может быть доступна для более широкого класса задач из-за изменения операторных норм.

Пусть наряду с $H$ и $F$ имется еще одна пара гильбертовых пространств ${{H}^{ - }}$ и ${{F}^{ + }}$ таких, что имеют место непрерывные и плотные вложения ${{H}^{ - }} \subset H$ и $F \subset {{F}^{ + }}$. Соответствующие операторы вложения обозначим через ${{\mathcal{B}}^{ - }}$ и ${{\mathcal{B}}^{ + }}$:

Пусть вместо (1.2) известны уровни $h_{n}^{ + },\;h_{n}^{ - },\;{{\sigma }_{n}},\;\sigma _{n}^{ + }$ следующих погрешностей: Понятно, что условия (1.4), (1.5) являются более мягкими по сравнению с (1.2) и совпадают с (1.2) в случае ${{H}^{ - }} = H$ и ${{F}^{ + }} = F$. При наличии априорной информации вида (1.4), (1.5) для построения элементов ${{u}_{n}}$ можно воспользоваться модификацией обобщенного метода невязки (см. [15]) или модификацией обобщенного принципа невязки (см. [16]). В данной работе будет предложен метод, являющийся модификацией регуляризованного градиентного метода (см. [17]), настроенной на информационные условия (1.3)–(1.5). Этот метод, на наш взгляд, более удобен для численной реализации при решении задач квадратичной минимизации вида (1.1), чем подходы, предложенные ранее в [15], [16].

Изложение будет организовано следующим образом: сначала будет описана предлагаемая вычислительная процедура, затем мы сформулирем основные предположения, необходимые для доказательства сходимости, и приведем это доказательство. Наконец, будет приведен пример задачи граничного управления волновым уравнением, при конечномерной аппроксимации которой возникают серьезные затруднения с обоснованием сходимости классического регуляризованного градиентного метода (см. [17]), поскольку 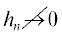в условиях (1.2). В то же время при соответствующем выборе вспомогательных пространств ${{H}^{ - }}$ и ${{F}^{ + }}$ для тех же самых аппроксимаций в этом примере будут выполняться условия (1.3)–(1.5), а также и предположения H1–H4, достаточные для сходимости представленного в данной работе итерационного процесса.

2. ОПИСАНИЕ МЕТОДА

В качестве начальных приближений выбираются произвольные элементы ${{g}_{0}} \in {{H}^{ - }}$ и ${{w}_{0}} = ({{u}_{0}},{{\psi }_{0}}) \in H \times F$. Следующие приближения ${{g}_{n}} \in {{H}^{ - }}$, ${{w}_{n}} = ({{u}_{n}},{{\psi }_{n}}) \in H \times F,$ $n = 1,2, \ldots ,$ строятся по правилам

Здесь $\left\| {(u,\psi )} \right\|_{{H \times F}}^{2} = \left\| u \right\|_{H}^{2} + \left\| \psi \right\|_{F}^{2}$, а градиенты $(T_{n}^{ - }){\kern 1pt} '(g)$ и $(T_{n}^{ + }){\kern 1pt} '(u,\psi )$ функционалов А.Н. Тихонова $T_{n}^{ - }(g)$ и $T_{n}^{ + }(u,\psi )$ вычисляются по обычным правилам: Параметрами метода (2.1)–(2.8) являются шаги $\beta _{n}^{ \mp } > 0$ градиентного спуска, штрафные коэффициенты ${{\Theta }_{n}} > 0$ и параметры регуляризации $\alpha _{n}^{ \mp } > 0$. Элементы ${{g}_{n}},{{\psi }_{n}}$ и величины ${{\mu }_{n}}$ играют вспомогательную роль, а главный интерес для нас будут представлять предельные свойства компонент ${{u}_{n}}$ при $n \to \infty $.

3. ОСНОВНЫЕ ПРЕДПОЛОЖЕНИЯ

Сформулируем требования к исходным и приближенным данным задачи (1.1) и параметрам метода (2.1)–(2.8).

H1. Задача (1.1) имеет решение, т.е. ${{U}_{ * }} \ne \emptyset $.

H2. Пространства $H$, ${{H}^{ - }}$, $F$, ${{F}^{ + }}$ являются гильбертовыми и имеют место непрерывные и всюду плотные вложения ${{H}^{ - }} \subset H$ и $F \subset {{F}^{ + }}$, реализуемые в (1.3) операторами ${{\mathcal{B}}^{ \mp }}$.

H3. Справедливы оценки погрешностей (1.4), (1.5) с известными уровнями погрешностей $h_{n}^{ + },\;h_{n}^{ - },\;{{\sigma }_{n}},\;\sigma _{n}^{ + }$, причем

H4. Параметры метода $\beta _{n}^{ \mp },\;{{\Theta }_{n}},\;\alpha _{n}^{ \mp }$ положительны и удовлетворяют следующим условиям, в том числе условиям согласования с уровнями погрешностей:

Подразумевается, что неравенства в (3.1) и (3.3) должны выполняться для всех достаточно больших номеров $n$.

4. ВСПОМОГАТЕЛЬНЫЕ СВЕДЕНИЯ

Сначала докажем липшицевость точных функционалов и получим оценки погрешности для их градиентов.

Лемма 1. Пусть выполнены предположения H2, H3. Тогда функционал $J(u) = $ $ = \left\| {\mathcal{A}{{\mathcal{B}}^{ - }}u - f} \right\|_{F}^{2}:{{H}^{ - }} \to \mathbb{R}$ имеет липшицев градиент

и справедлива следующая оценка погрешности приближения его градиента градиентом функционала ${{J}_{n}}(u) = \left\| {{{\mathcal{A}}_{n}}{{\mathcal{B}}^{ - }}u - {{f}_{n}}} \right\|_{F}^{2}:{{H}^{ - }} \to \mathbb{R}$: с постоянной $C > 0,$ не зависящей от $n$ и $u$. Градиенты функционалов ${{P}_{n}}(\psi )$ и $I(u,\psi ) = \left\| {{{\mathcal{B}}^{ + }}[\psi - (\mathcal{A}u - f)]} \right\|_{{{{F}^{ + }}}}^{2}:H \times F \to \mathbb{R}$ также будут липшиц-непрерывны: и, кроме того, будет справедлива следующая оценка погрешности приближения градиента $I{\kern 1pt} '(u,\psi )$ градиентом функционала ${{I}_{n}}(u,\psi ) = \left\| {{{\mathcal{B}}^{ + }}[\psi - ({{\mathcal{A}}_{n}}u - {{f}_{n}})]} \right\|_{{{{F}^{ + }}}}^{2}:H \times F \to \mathbb{R}$: с постоянной $C > 0,$ не зависящей от $n$, $u$ и $\psi $.

Доказательство. Свойства липшиц-непрерывности (4.1) и (4.4) следуют непосредственно из вида градиентов:

Выражение для градиента $P_{n}^{'}(\psi )$ приведено в (2.8). Если ${{\left\| \psi \right\|}_{F}} > {{\mu }_{n}},$ то ${{\mu }_{n}}\psi {\text{/}}{{\left\| \psi \right\|}_{F}}$ является проекцией ${{\mathcal{P}}_{n}}\psi $ точки $\psi $ на шар ${{B}_{{{{\mu }_{n}}}}} = \{ \psi \in F\,{\text{|}}\,{{\left\| \psi \right\|}_{F}} \leqslant {{\mu }_{n}}\} $, т.e. Оценка (4.3) очевидна для элементов $\psi ,\varphi \in {{B}_{{{{\mu }_{n}}}}}.$ Если $\psi \in {{B}_{{{{\mu }_{n}}}}},$ а $\varphi \notin {{B}_{{{{\mu }_{n}}}}},$ то $P_{n}^{'}(\psi ) = 0$ и с учетом определения проекции и (4.6) будем иметь Если же оба элемента $\psi $ и $\varphi $ находятся вне шара ${{B}_{{{{\mu }_{n}}}}}$, то Преобразуем второе слагаемое из правой части (4.7): Заметим, что в силу характеристического свойства проекции каждое из двух скалярных произведений, присутствующих в правой части (4.8), неположительно, поэтому а тогда из (4.7) получаем искомое свойство (4.3).

Для получения оценки погрешности (4.2) используем неравенство треугольника и условия (1.4), (1.5):

где для некоторой, не зависящей от n и u постоянной C > 0$.$

Докажем теперь оценку погрешности (4.5) для градиента функционала $I(u,\psi )$:

При оценке второго слагаемого учитываем (1.4) и (1.5): Первое слагаемое оценивается следующим образом: Из этих двух оценок, используя неравенство $\sqrt {1 + x} \leqslant \sqrt x + 1,$ получаем, что где Лемма 1 доказана.

Докажем, что значения ${{\mu }_{n}}$ из (2.2) являются верхними аппроксимациями точной нижней грани ${{\mu }_{ * }}$ в исходной задаче (1.1):

Лемма 2. При выполнении условий H1–H4 справедливы соотношения

Доказательство. Cвойство доминирования (4.10) следует из определения нижней грани (4.9), неравенства треугольника, а также (1.4), (1.5) и (2.2):

Доказательство сходимости (4.11) в целом аналогично доказательству сходимости регуляризованного градиентного метода из [18, с. 846–852], однако следует учесть, что задача минимизации (1.1), рассматриваемая на пространстве $u \in {{H}^{ - }} \subset H,$ может не иметь решения. Рассмотрим минимизаторы ${{{v}}_{n}}$ точных аналогов функционалов $T_{n}^{ - }(g)$ из (2.1):

Заметим, что существует последовательность элементов $v_{n}^{ - } \in {{H}^{ - }}$ такая, что Для доказательства существования таких элементов достаточно рассмотреть вспомогательные задачи минимизации и взять в качестве $v_{n}^{ - }$ их решения. При этом, используя плотность вложения ${{H}^{ - }} \subset H$ и сходимость $\alpha _{n}^{ - } \to 0,$ получаем соотношения (4.14).

Применяя неравенство треугольника и условие (1.4), запишем соотношения

где Оценим ${{Q}_{n}}$ с помощью неравенств ${{(a + b)}^{2}} \leqslant 2{{a}^{2}} + 2{{b}^{2}}$ и $2ab \leqslant {{a}^{2}} + {{b}^{2}}$: Заметим, что последнее слагаемое в правой части (4.16) является неположительным в силу первого условия из (3.1). Кроме того, из оптимальности элемента ${{v}_{n}}$ в задаче (4.13) следует неравенство $\left\| {\mathcal{A}{{v}_{n}} - f} \right\|_{F}^{2} \leqslant \left\| f \right\|_{F}^{2}$, поэтому Элементы $v_{n}^{ - }$ в задаче (4.13) являются допустимыми, поэтому В силу (4.14) правая часть (4.18) при $n \to \infty $ стремится к $\left\| {\mathcal{A}{{u}_{*}} - f} \right\|_{F}^{2} = \mu _{*}^{2}$, следовательно, из (4.15), (4.17) и (4.18) имеем В то же время верна аналогичная (4.12) оценка которая вместе с (4.19) влечет сходимость

Далее по той же схеме, что и в [18, с. 846–852], проводится доказательство сходимости ${{\left\| {{{v}_{n}} - {{g}_{n}}} \right\|}_{{{{H}^{ - }}}}} \to 0.$ При этом используются условия согласования параметров (3.1), (3.2), оценки для констант Липшица и погрешностей из леммы 1, а также теорема 16 из [18, с. 197].

Для завершения доказательства сходимости (4.11) запишем следующие неравенства:

Правая часть (4.21) при $n \to \infty $ стремится к ${{\mu }_{*}}$ в силу (4.20) и имеющейся сходимости ${{\left\| {{{v}_{n}} - {{g}_{n}}} \right\|}_{{{{H}^{ - }}}}} \to 0,$ поэтому что вместе с (4.10) приводит к (4.11). Лемма 2 доказана.

5. ДОКАЗАТЕЛЬСТВО СХОДИМОСТИ МЕТОДА

Сформулируем основное утверждение о сходимости метода.

Теорема. Пусть выполняются условия H1–H4. Тогда компоненты ${{u}_{n}}$ элементов ${{w}_{n}} = ({{u}_{n}},{{\psi }_{n}})$, построенных с помощью итерационного процесса (2.1)–(2.5), сильно сходятся к нормальному решению ${{u}_{*}}$ задачи (1.1):

Доказательство. Рассмотрим минимизаторы ${{q}_{n}} = ({{z}_{n}},{{\varphi }_{n}})$ функционала Тихонова с точными данными $\mathcal{A}$ и $f$, аналогичного функционалу (2.4):

Элемент ${{w}_{*}} = ({{u}_{*}},\mathcal{A}{{u}_{*}} - f),$ порожденный нормальным решением ${{u}_{ * }}$ задачи (1.1), является в (5.2) допустимым и, кроме того, поэтому ${{P}_{n}}(\mathcal{A}{{u}_{*}} - f)\mathop = \limits^{(2.5)} 0$, а тогда Оценивая левую часть (5.3) снизу поочередно каждым из слагаемых, получаем следующие три соотношения: В силу (5.6) последовательность ${{q}_{n}} = ({{z}_{n}},{{\varphi }_{n}})$ ограничена в пространстве $H \times F,$ поэтому без ограничения общности ее можно считать слабо в $H \times F$ сходящейся к некоторому элементу $({{z}_{0}},{{\varphi }_{0}}).$ В то же время, согласно (5.4), имеется сильная сходимость Поскольку предел единственен, из слабой сходимости в $H \times F$ следует слабая сходимость в $H \times {{F}^{ + }}$, линейный оператор $\mathcal{A}:H \to F$ непрерывен и вложение $F \subset {{F}^{ + }}$ также непрерывно, то в пределе получается равенство Из (5.5), определения (2.5) штрафной функции ${{P}_{n}}$ и утверждения (4.11) леммы 2 имеем Используя слабую сходимость ${{\varphi }_{n}} \to {{\varphi }_{0}}$ в $F$ и слабую полунепрерывность снизу нормы $\parallel \cdot {{\parallel }_{F}},$ получаем соотношения В задаче (1.1) элемент ${{u}_{*}}$ является оптимальным, а ${{z}_{0}}$ – допустимым, поэтому а тогда из (5.9), (5.10) следует существование предела и условие ${{z}_{0}} \in {{U}_{*}},$ т.е. оптимальность компоненты ${{z}_{0}}$ в задаче (1.1). Отсюда в силу свойства Радона–Рисса имеем сильную сходимость ${{\varphi }_{n}} \to {{\varphi }_{0}} = \mathcal{A}{{z}_{0}} - f$ в пространстве $F$. Используя ортогональное разложение $f = {{f}_{R}} + {{f}_{N}}$, в котором ${{f}_{R}} \in \overline {R(\mathcal{A})} $, ${{f}_{N}} \in N(\mathcal{A}{\kern 1pt} *),$ получаем Из плотности $R(\mathcal{A})$ в $\overline {R(\mathcal{A})} $ следует, что $\mu _{*}^{2} = \left\| {{{f}_{N}}} \right\|_{F}^{2}$, а следовательно, будет выполняться цепочка равенств $\left\| {\mathcal{A}{{z}_{0}} - {{f}_{R}}} \right\|_{F}^{2} + \left\| {{{f}_{N}}} \right\|_{F}^{2} = \left\| {\mathcal{A}{{z}_{0}} - f} \right\|_{F}^{2} = \mu _{*}^{2} = \left\| {{{f}_{N}}} \right\|_{F}^{2}$, т.е. $\mathcal{A}{{z}_{0}} - {{f}_{R}} = 0$ или, что то же самое, Поэтому ${{\left\| {{{\varphi }_{n}} + {{f}_{N}}} \right\|}_{F}} \to 0$ при $n \to \infty .$ Тогда после перехода к верхнему пределу в развернутой записи неравенства (5.6) получаем соотношение Напомним, что ${{u}_{*}}$ – нормальное решение задачи (1.1), ${{z}_{0}} \in {{U}_{*}}$ – некоторое ее решение и ${{z}_{n}} \to {{z}_{0}}$ слабо в $H.$ По этим причинам справедливы подобные (5.9) соотношения и, тем самым, существует предел норм В силу единственности нормального решения задачи (1.1) имеем равенство ${{z}_{0}} = {{u}_{*}},$ а значит, и сильную сходимость ${{\left\| {{{z}_{n}} - {{u}_{*}}} \right\|}_{H}} \to 0$ при $n \to \infty .$ Кроме того, из сходимости ${{\left\| {{{\varphi }_{n}} - {{\varphi }_{0}}} \right\|}_{F}} \to 0$ и (5.7) следует, что

Сходимость ${{\left\| {{{q}_{n}} - {{w}_{n}}} \right\|}_{H}} \to 0$ доказывается абсолютно аналогично (см. [18]). При этом используются условия согласования параметров (3.3), (3.4), оценка (4.5) из леммы 1, а также теорема 16 из [18, с. 197]. В результате получаем сильную сходимость

и, тем более, сходимость (5.1) первых компонент ${{u}_{n}}$ пар ${{w}_{n}} = ({{u}_{n}},{{\varphi }_{n}}).$ Теорема доказана.

6. ПРИМЕР

Приведем пример, иллюстрирующий расширенные возможности применения предложенной модификации по сравнению с классическим регуляризованным градиентным методом. Рассмотрим управляемую систему, описываемую волновым уравнением:

Определим оператор, ставящий в соответствие каждому граничному управлению $u = u(t)$ следы обобщенного решения и его производной по $t$ в конечный момент времени $T$: где ${{L}^{2}}(0,l)$ – гильбертово пространство Лебега, ${{H}^{{ - 1}}}(0,l) = (H_{0}^{1}(0,l)){\kern 1pt} *$, а $H_{0}^{1}(0,l)$ – подпространство функций из пространства Соболева ${{H}^{1}}(0,l) = W_{2}^{1}(0,l)$, обращающихся в нуль на концах отрезка $[0,l]$. Известно (см. [19]), что оператор $\mathcal{A}$ имеет замкнутый бесконечномерный образ $R(\mathcal{A})$ и, следовательно, не может быть приближен конечномерными операторами в классическом смысле (1.2), поэтому для устойчивого численного решения задачи (1.1) обоснованное применение классического регуляризованного градиентного метода не представляется возможным. В то же время при выборе пространств в силу компактности вложений ${{H}^{ - }} \subset H$ и $F \subset {{F}^{ + }},$ осуществляемых операторами ${{\mathcal{B}}^{ - }}$ и ${{\mathcal{B}}^{ + }},$ операторы управления $\mathcal{A}{{\mathcal{B}}^{ - }}:{{H}^{ - }} \to F$ и ${{\mathcal{B}}^{ + }}\mathcal{A}:H \to {{F}^{ + }}$ станут компактными, и их можно будет приблизить конечномерными операторами с оценками погрешностей вида (1.4). Соответствующие аппроксимации могут быть построены, например, на базе разностных схем, а оценки погрешностей во вспомогательных парах пространств можно получить, действуя по аналогии с [20].