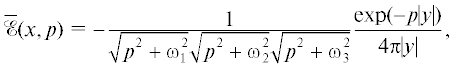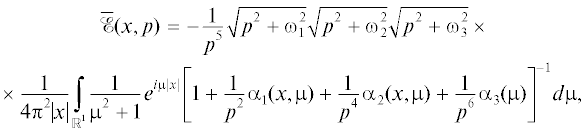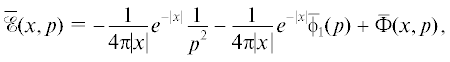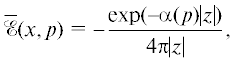Журнал вычислительной математики и математической физики, 2022, T. 62, № 10, стр. 1639-1661
Локальная разрешимость, разрушение и гёльдеровская регулярность решений некоторых задач Коши для нелинейных уравнений теории волн в плазме. I. Формулы Грина
М. О. Корпусов 1, *, Е. А. Овсянников 1, **
1 МГУ им. М.В. Ломоносова
119991 Москва, Ленинские горы, 1, Россия
* E-mail: korpusov@gmail.com
** E-mail: evg.bud@yandex.ru
Поступила в редакцию 29.11.2021
После доработки 11.03.2022
Принята к публикации 11.04.2022
- EDN: MFWGAE
- DOI: 10.31857/S0044466922090071
Аннотация
В статье дается вывод трех нелинейных уравнений из теории ионно-звуковых и дрейфовых волн в плазме. Затем строится фундаментальное решение общей линейной части выведенных нелинейных уравнений и изучаются его свойства гладкости. После этого строится вторая формула Грина в ограниченной области, из которой получается третья формула Грина в ограниченной области. Наконец, в определенном классе функций строятся два варианта третьих формул Грина во всем пространстве. Библ. 30.
Ключевые слова: нелинейные уравнения соболевского типа, фундаментальное решение, формулы Грина.
1. ВВЕДЕНИЕ
В работе мы рассмотрим задачи Коши для следующих трех нелинейных уравнений, объединенных общей линейной частью:
(1.1)
$\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\left( {\Delta u(x,t) - u(x,t)} \right) + \sum\limits_{j = 1}^3 \,\omega _{j}^{2}\frac{{{{\partial }^{2}}u(x,t)}}{{\partial x_{j}^{2}}} + \frac{{\partial {{u}^{2}}(x,t)}}{{\partial t}} = 0,$(1.2)
$\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\left( {\Delta u(x,t) - u(x,t)} \right) + \sum\limits_{j = 1}^3 \,\omega _{j}^{2}\frac{{{{\partial }^{2}}u(x,t)}}{{\partial x_{j}^{2}}} + \frac{{\partial {\kern 1pt} {\text{|}}{{D}_{x}}u{\kern 1pt} {{|}^{2}}(x,t)}}{{\partial t}} = 0,$(1.3)
$\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\left( {\Delta u(x,t) - u(x,t)} \right) + \sum\limits_{j = 1}^3 \,\omega _{j}^{2}\frac{{{{\partial }^{2}}u(x,t)}}{{\partial x_{j}^{2}}} - \frac{{{{\partial }^{2}}{{u}^{2}}(x,t)}}{{\partial {{t}^{2}}}} = 0,$
$u(x,t) \in \mathbb{C}_{b}^{{(2 + 2)}}((1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}};{{\mathbb{R}}^{3}} \times [0,T]) \cap {{\mathbb{C}}^{{(2)}}}([0,T];{{\mathbb{C}}^{{2 + \alpha }}}({{\mathbb{R}}^{3}})),\quad \alpha \in (0,1),$
для начальных функций
${{u}_{0}}(x) \in {{\mathbb{C}}^{{2 + \alpha }}}((1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{2}}/2}}};{{\mathbb{R}}^{3}}),\quad \alpha \in (0,1),\quad {{\beta }_{2}}\; \geqslant \;{{\beta }_{1}}\; \geqslant \;0,$
${{u}_{1}}(x) \in {{\mathbb{C}}^{{2 + \alpha }}}((1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{3}}/2}}};{{\mathbb{R}}^{3}}),\quad \alpha \in (0,1),\quad {{\beta }_{3}}\; \geqslant \;{{\beta }_{1}}\; \geqslant \;0.$
Причем для нелинейных уравнений (1.1) и (1.2) мы докажем существование непродолжаемых
решений, а для уравнения (1.3) существование локального во времени решения. Для соответствующей задачи Коши для
уравнения (1.1) энергетическим методом, развитым в работах [1]–[4], мы получим достаточные условия разрушения решения за конечное время и получим оценку
сверху на время разрушения решения. Для соответствующей задачи Коши для уравнения (1.3) методом нелинейной емкости С.И. Похожаева [5] мы получим результат о разрушении решений за конечное время и два результата об
отсутствии даже локальных решений, а также получим оценку сверху для времени разрушения
решения.
Настоящая работа продолжает наши исследования, начатые в работах [6]–[14]. Особо отметим нашу работу [15], в которой, в частности, были изучены задачи Коши для соответствующих уравнениям (1.1) и (1.3) $1 + 1$–мерные уравнения следующего вида:
$\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\left( {{{u}_{{xx}}}(x,t) - u(x,t)} \right) + {{\omega }^{2}}\frac{{{{\partial }^{2}}u(x,t)}}{{\partial {{x}^{2}}}} + \frac{{\partial ({\text{|}}u{\kern 1pt} {{{\text{|}}}^{q}}u)(x,t)}}{{\partial t}} = 0,$
$\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\left( {{{u}_{{xx}}}(x,t) - u(x,t)} \right) + {{\omega }^{2}}\frac{{{{\partial }^{2}}u(x,t)}}{{\partial {{x}^{2}}}} - \frac{{{{\partial }^{2}}{{u}^{2}}(x,t)}}{{\partial {{t}^{2}}}} = 0,\quad \omega > 0,$
где $q > 0$, $\omega > 0$.
В этой работе изучались вопросы локальной разрешимости и разрушения классических решений задач Коши за конечное время.
В нашей работе, состоящей из трех частей, мы последовательно развиваем теорию потенциала для линейной части уравнений (1.1)–(1.3). Отметим, что теория потенциала для уравнения С.Л. Соболева была рассмотрена в работе [16]. Затем теория потенциала развивалась для более сложных уравнений в работах [17]–[19] (см. также работу [20]).
Отметим, что уравнения (1.1)–(1.3) относятся к нелинейным уравнениям соболевского типа. Для уравнений соболевского типа разработаны специальные методы исследования. Например, в работах [21]–[23] методом вырожденных полугрупп Г.А. Свиридюка были исследованы в достаточно общей форме разнообразные задачи для уравнений соболевского типа.
2. ДРЕЙФОВЫЕ ВОЛНЫ В ПЛАЗМЕ. ВЫВОД УРАВНЕНИЙ
В этом разделе мы приведем вывод рассматриваемых ниже нелинейных уравнений дрейфовых волн в плазме во внешнем магнитном поле (см. работы [24]–[27]).
Пусть ${{{\mathbf{B}}}_{0}} = {{B}_{0}}{{{\mathbf{e}}}_{3}}$ и $\{ O,{{{\mathbf{e}}}_{1}},{{{\mathbf{e}}}_{2}},{{{\mathbf{e}}}_{3}}\} $ – это прямоугольная правая декартова система координат. Рассмотрим систему уравнений квазистационарного электрического поля:
(2.1)
$\begin{gathered} \operatorname{div} {\mathbf{D}} = - 4\pi {{n}_{e}},\quad {\mathbf{E}} = - \nabla \phi ,\quad {\mathbf{D}} = {\mathbf{E}} + 4\pi {\mathbf{P}}, \\ {{n}_{e}} = {{n}_{{1e}}} + {{n}_{{2e}}},\quad {{n}_{{1e}}} = {{n}_{0}}\exp \left( {\frac{{e\phi }}{{k{{T}_{e}}}}} \right), \\ \end{gathered} $(2.2)
$\begin{gathered} {\mathbf{v}} = - \frac{c}{{{{B}_{0}}}}\left\{ { - [\nabla \phi ,{{{\mathbf{e}}}_{3}}] + \frac{1}{{{{\omega }_{B}}}}\frac{\partial }{{\partial t}}{{\nabla }_{ \bot }}\phi } \right\} + {{v}_{3}}{{{\mathbf{e}}}_{3}},\quad {\mathbf{v}} = ({{v}_{1}},{{v}_{2}},{{v}_{3}}), \\ \frac{{\partial {{v}_{3}}}}{{\partial t}} = - \frac{e}{M}\frac{{\partial \phi }}{{\partial {{x}_{3}}}},\quad \frac{{\partial {\mathbf{P}}}}{{\partial t}} = e{{n}_{0}}{\mathbf{v}}, \\ \end{gathered} $(2.4)
$\frac{{\partial {{n}_{{2e}}}}}{{\partial t}} + {{m}_{0}}{\text{|}}\nabla \phi {\kern 1pt} {{{\text{|}}}^{2}} = 0,$(2.6)
$\frac{{u_{A}^{2}}}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\left( {\Delta \phi - 4\pi {{n}_{0}}\exp \left( {\frac{{e\phi }}{{k{{T}_{e}}}}} \right)} \right) + \frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}{{\Delta }_{ \bot }}\phi + \omega _{B}^{2}\frac{{{{\partial }^{2}}\phi }}{{\partial x_{3}^{2}}} + 4\pi e\frac{{u_{A}^{2}}}{{{{c}^{2}}}}{{q}_{0}}\frac{{\partial {{\phi }^{2}}}}{{\partial t}} = 0,$(2.7)
$\frac{{u_{A}^{2}}}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\left( {\Delta \phi - 4\pi {{n}_{0}}\exp \left( {\frac{{e\phi }}{{k{{T}_{e}}}}} \right)} \right) + \frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}{{\Delta }_{ \bot }}\phi + \omega _{B}^{2}\frac{{{{\partial }^{2}}\phi }}{{\partial x_{3}^{2}}} + 4\pi e\frac{{u_{A}^{2}}}{{{{c}^{2}}}}{{q}_{0}}\frac{{\partial {\kern 1pt} |{\kern 1pt} \nabla \phi {\kern 1pt} {{|}^{2}}}}{{\partial t}} = 0,$(2.8)
$\frac{{u_{A}^{2}}}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\left( {\Delta \phi - 4\pi {{n}_{0}}\exp \left( {\frac{{e\phi }}{{k{{T}_{e}}}}} \right)} \right) + \frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}{{\Delta }_{ \bot }}\phi + \omega _{B}^{2}\frac{{{{\partial }^{2}}\phi }}{{\partial x_{3}^{2}}} = 0,$
$\Delta : = {{\Delta }_{ \bot }} + \frac{{{{\partial }^{2}}}}{{\partial x_{3}^{2}}},\quad {{\Delta }_{ \bot }}: = \frac{{{{\partial }^{2}}}}{{\partial x_{1}^{2}}} + \frac{{{{\partial }^{2}}}}{{\partial x_{2}^{2}}},$
$u_{A}^{2}: = \frac{{B_{0}^{2}}}{{4\pi {{n}_{0}}M}},\quad \omega _{B}^{2} = {{\left( {\frac{{e{{B}_{0}}}}{{Mc}}} \right)}^{2}},$
${{u}_{A}}$– альфвеновская скорость ионов. В предположении, что температура ионов ${{T}_{i}} \ll {{T}_{e}}$, можно сделать в уравнениях (2.6) и (2.7) частичную линеаризацию
(2.9)
$\exp \left( {\frac{{e\phi }}{{k{{T}_{e}}}}} \right) \simeq 1 + \frac{{e\phi }}{{k{{T}_{e}}}},$(2.10)
$\exp \left( {\frac{{e\phi }}{{k{{T}_{e}}}}} \right) \simeq 1 + \frac{{e\phi }}{{k{{T}_{e}}}} + \frac{1}{2}{{\left( {\frac{{e\phi }}{{k{{T}_{e}}}}} \right)}^{2}}.$(2.11)
$\frac{{u_{A}^{2}}}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\left( {\Delta \phi - \frac{{4\pi {{n}_{0}}e}}{{k{{T}_{e}}}}\phi } \right) + \frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}{{\Delta }_{ \bot }}\phi + \omega _{B}^{2}\frac{{{{\partial }^{2}}\phi }}{{\partial x_{3}^{2}}} + 4\pi e\frac{{u_{A}^{2}}}{{{{c}^{2}}}}{{q}_{0}}\frac{{\partial {{\phi }^{2}}}}{{\partial t}} = 0.$(2.12)
$\frac{{u_{A}^{2}}}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\left( {\Delta \phi - \frac{{4\pi {{n}_{0}}e}}{{k{{T}_{e}}}}\phi } \right) + \frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}{{\Delta }_{ \bot }}\phi + \omega _{B}^{2}\frac{{{{\partial }^{2}}\phi }}{{\partial x_{3}^{2}}} + 4\pi e\frac{{u_{A}^{2}}}{{{{c}^{2}}}}{{q}_{0}}\frac{{\partial {\kern 1pt} |{\kern 1pt} \nabla \phi {\kern 1pt} {{|}^{2}}}}{{\partial t}} = 0.$(2.13)
$\frac{{u_{A}^{2}}}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\left( {\Delta \phi - \frac{{4\pi {{n}_{0}}}}{{k{{T}_{e}}}}\phi - \frac{{2\pi {{n}_{0}}{{e}^{2}}}}{{{{{(k{{T}_{e}})}}^{2}}}}{{\phi }^{2}}} \right) + \frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}{{\Delta }_{ \bot }}\phi + \omega _{B}^{2}\frac{{{{\partial }^{2}}\phi }}{{\partial x_{3}^{2}}} = 0.$3. ИОННО-ЗВУКОВЫЕ ВОЛНЫ В ПЛАЗМЕ. ВЫВОД УРАВНЕНИЙ
Уравнения ионно-звуковых волн выводятся в предположении, что температура ионов ${{T}_{i}}$ много меньше температуры электронов ${{T}_{e}}$. Это более подробно изложено в работе [28]. Тогда для скорости ионов справедлива следующая формула:
Дополним полученное уравнение (3.1) уравнениями электрической части системы уравнений Максвелла в квазистационарном приближении(3.2)
$\operatorname{div} {\mathbf{D}} = - 4\pi {{n}_{e}},\quad {\mathbf{D}} = - \nabla \phi + 4\pi {\mathbf{P}},$(3.5)
$\frac{{\partial {{n}_{{2e}}}}}{{\partial t}} + {{m}_{0}}{\kern 1pt} |{\kern 1pt} \nabla \phi {\kern 1pt} {{|}^{2}}\; = 0,$(3.7)
$\frac{{{{\partial }^{2}}{\mathbf{P}}}}{{\partial {{t}^{2}}}} = - \frac{{{{e}^{2}}{{n}_{0}}}}{M}\nabla \phi .$(3.8)
$\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\left( {{{\Delta }_{3}}\phi - 4\pi {{n}_{0}}\exp \left( {\frac{{e\phi }}{{k{{T}_{e}}}}} \right)} \right) + \omega _{{pi}}^{2}{{\Delta }_{3}}\phi + 4\pi {{q}_{0}}\frac{{\partial {{\phi }^{2}}}}{{\partial t}} = 0.$(3.9)
$\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\left( {{{\Delta }_{3}}\phi - 4\pi {{n}_{0}}\exp \left( {\frac{{e\phi }}{{k{{T}_{e}}}}} \right)} \right) + \omega _{{pi}}^{2}{{\Delta }_{3}}\phi + 4\pi {{q}_{0}}\frac{{\partial {\kern 1pt} {\text{|}}\nabla \phi {\kern 1pt} {{{\text{|}}}^{2}}}}{{\partial t}} = 0,$(3.10)
$\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\left( {{{\Delta }_{3}}\phi - 4\pi {{n}_{0}}\exp \left( {\frac{{e\phi }}{{k{{T}_{e}}}}} \right)} \right) + \omega _{{pi}}^{2}{{\Delta }_{3}}\phi = 0,$
${{\Delta }_{3}} = \frac{{{{\partial }^{2}}}}{{\partial x_{1}^{2}}} + \frac{{{{\partial }^{2}}}}{{\partial x_{2}^{2}}} + \frac{{{{\partial }^{2}}}}{{\partial x_{3}^{2}}},\quad {{\omega }_{{pi}}} = {{\left( {\frac{{4\pi {{e}^{2}}{{n}_{0}}}}{M}} \right)}^{{1/2}}}.$
Далее для уравнений (3.8) и (3.9) воспользуемся частичной линеаризацией (2.9), а для
уравнения (3.10) воспользуемся упрощением (2.10). Тогда уравнения (3.8), (3.9) и (3.10) перейдут в следующие уравнения:
(3.11)
$\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\left( {{{\Delta }_{3}}\phi - \frac{{4\pi {{n}_{0}}e}}{{k{{T}_{e}}}}\phi } \right) + \omega _{{pi}}^{2}{{\Delta }_{3}}\phi + 4\pi {{q}_{0}}\frac{{\partial {{\phi }^{2}}}}{{\partial t}} = 0,$(3.12)
$\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\left( {{{\Delta }_{3}}\phi - \frac{{4\pi {{n}_{0}}e}}{{k{{T}_{e}}}}\phi } \right) + \omega _{{pi}}^{2}{{\Delta }_{3}}\phi + 4\pi {{q}_{0}}\frac{{\partial {\kern 1pt} |{\kern 1pt} \nabla \phi {\kern 1pt} {{|}^{2}}}}{{\partial t}} = 0,$(3.13)
$\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\left( {{{\Delta }_{3}}\phi - \frac{{4\pi {{n}_{0}}e}}{{k{{T}_{e}}}}\phi - \frac{{2\pi {{n}_{0}}{{e}^{2}}}}{{{{{(k{{T}_{e}})}}^{2}}}}{{\phi }^{2}}} \right) + \omega _{{pi}}^{2}{{\Delta }_{3}}\phi = 0.$4. ОБОЗНАЧЕНИЯ
Символом $[x,y]$ мы обозначаем отрезок, соединяющий точки $x,y \in {{\mathbb{R}}^{3}}$:
Символом ${\text{|}}a,b{\text{|}}$ при $a,b \in {{\mathbb{R}}^{1}}$ мы обозначаем следующее множество:
${\text{|}}a,b{\kern 1pt} {\text{|}} = \left\{ \begin{gathered} [a,b],\quad {\text{если}}\quad a\;\leqslant \;b; \hfill \\ [b,a],\quad {\text{если}}\quad b\;\leqslant \;a. \hfill \\ \end{gathered} \right.$
Символом ${{\mathbb{C}}^{{(m)}}}[0,T]$ при $m \in \mathbb{N}$ мы обозначаем линейное пространство непрерывно дифференцируемых функций, причем производные в граничных точках $t = 0$ и $t = T$ понимаются в смысле односторонних пределов.
В работе мы будем пользоваться обозначениями из [29]. Символом ${{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}})$ мы обозначаем пространство непрерывных и ограниченных функций, норма которого имеет следующий вид:
${\text{|}}{\kern 1pt} f{\kern 1pt} {{{\text{|}}}_{0}}: = \mathop {\sup }\limits_{x \in {{\mathbb{R}}^{3}}} {\text{|}}{\kern 1pt} f(x){\kern 1pt} {\text{|}}.$
Символом $\mathbb{C}_{b}^{{(k)}}({{\mathbb{R}}^{3}})$ при $k \in \mathbb{N} \cup \{ 0\} $ мы обозначаем банахово пространство функций, у которых существуют, непрерывны и ограничены
все частные производные по координатам $x = ({{x}_{1}},{{x}_{2}},{{x}_{3}}) \in {{\mathbb{R}}^{3}}$ и ограничена следующая норма:
${\text{|}}{\kern 1pt} f{\kern 1pt} {{{\text{|}}}_{k}} = \sum\limits_{|\beta |\leqslant k} {{\left| {{{D}^{\beta }}f(x)} \right|}_{0}},\quad D_{x}^{\beta } = \frac{{{{\partial }^{{{{\beta }_{1}}}}}}}{{\partial x_{1}^{{{{\beta }_{1}}}}}}\frac{{{{\partial }^{{{{\beta }_{2}}}}}}}{{\partial x_{2}^{{{{\beta }_{2}}}}}}\frac{{{{\partial }^{{{{\beta }_{3}}}}}}}{{\partial x_{3}^{{{{\beta }_{3}}}}}},$
$\beta = ({{\beta }_{1}},{{\beta }_{2}},{{\beta }_{3}}) \in \mathbb{Z}_{ + }^{3},\quad {\text{|}}\beta {\text{|}} = {{\beta }_{1}} + {{\beta }_{2}} + {{\beta }_{3}}.$
Символом ${{\mathbb{C}}^{\alpha }}({{\mathbb{R}}^{3}})$ мы обозначаем линейное подпространство функций из банахова пространства ${{\mathbb{C}}_{b}}({{\mathbb{R}}^{3}}),$ для которых конечна норма
${\text{|}}{\kern 1pt} f{\kern 1pt} {{{\text{|}}}_{\alpha }}: = {\text{|}}{\kern 1pt} f{\kern 1pt} {{{\text{|}}}_{0}} + {{[f]}_{\alpha }},\quad {{[f]}_{\alpha }}: = \mathop {\sup }\limits_{x \ne y} \frac{{{\text{|}}{\kern 1pt} f(x) - f(y){\kern 1pt} {\text{|}}}}{{{\text{|}}x - y{\kern 1pt} {{{\text{|}}}^{\alpha }}}},\quad \alpha \in (0,1).$
Символом ${{\mathbb{C}}^{{k + \alpha }}}({{\mathbb{R}}^{3}})$ при $k \in \mathbb{N} \cup \{ 0\} $ мы обозначаем линейное пространство функций из банахова пространства $\mathbb{C}_{b}^{{(k)}}({{\mathbb{R}}^{3}}),$ для которых конечна норма:
${\text{|}}{\kern 1pt} f{\kern 1pt} {{{\text{|}}}_{{k + \alpha }}}: = {\text{|}}{\kern 1pt} f{\kern 1pt} {{{\text{|}}}_{k}} + \sum\limits_{|\beta | = k} \,{{[D_{x}^{\beta }f(x)]}_{\alpha }}.$
Кроме того, мы систематически будем использовать банаховы пространства абстрактных
функций $\mathbb{C}([0,T];\mathbb{B}),$ ${{\mathbb{C}}^{{(1)}}}([0,T];\mathbb{B})$ и ${{\mathbb{C}}^{{(2)}}}([0,T];\mathbb{B})$, где $\mathbb{B}$ – банахово пространство относительно нормы $|\, \cdot \,{{|}_{\mathbb{B}}}$. Линейное пространство $\mathbb{C}([0,T];\mathbb{B}) \ni f(t)$ определяется следующими свойствами:
$f(t):\;[0,T] \to \mathbb{B},\quad {\text{|}}{\kern 1pt} f({{t}_{2}}) - f({{t}_{1}}){\kern 1pt} {{{\text{|}}}_{\mathbb{B}}} \to + 0\quad {\text{при}}\quad {\text{|}}{{t}_{2}} - {{t}_{1}}{\kern 1pt} {\text{|}} \to + 0,\quad {{t}_{1}},{{t}_{2}} \in [0,T].$
Линейное пространство ${{\mathbb{C}}^{{(1)}}}([0,T];\mathbb{B})$ определяется как такое подпространство линейного пространства $\mathbb{C}([0,T];\mathbb{B}),$ что существует сильная производная
$\frac{{df}}{{dt}}(t) \in \mathbb{C}([0,T];\mathbb{B}),\quad {{\left| {\frac{{f(t + \Delta t) - f(t)}}{{\Delta t}} - \frac{{df}}{{dt}}(t)} \right|}_{\mathbb{B}}} \to + 0\quad {\text{при}}\quad {\text{|}}\Delta t{\kern 1pt} {\text{|}} \to + 0.$
Линейное пространство ${{\mathbb{C}}^{{(2)}}}([0,T];\mathbb{B})$ определяется индуктивным образом. Линейные пространства $\mathbb{C}([0,T];\mathbb{B}),$ ${{\mathbb{C}}^{{(1)}}}([0,T];\mathbb{B})$ и ${{\mathbb{C}}^{{(2)}}}([0,T];\mathbb{B})$ являются банаховыми относительно соответствующих норм
${{\left\| {f(t)} \right\|}_{T}}: = \mathop {\sup }\limits_{t \in [0,T]} {\text{|}}{\kern 1pt} f(t){\kern 1pt} {{{\text{|}}}_{\mathbb{B}}},\quad {{\left\| {f(t)} \right\|}_{{1,T}}}: = \mathop {\sup }\limits_{t \in [0,T]} {\text{|}}{\kern 1pt} f(t){\kern 1pt} {{{\text{|}}}_{\mathbb{B}}} + \mathop {\sup }\limits_{t \in [0,T]} {{\left| {\frac{{df}}{{dt}}(t)} \right|}_{\mathbb{B}}},$
${{\left\| {f(t)} \right\|}_{{2,T}}}: = \mathop {\sup }\limits_{t \in [0,T]} {\text{|}}{\kern 1pt} f(t){\kern 1pt} {{{\text{|}}}_{\mathbb{B}}} + \mathop {\sup }\limits_{t \in [0,T]} {{\left| {\frac{{df}}{{dt}}(t)} \right|}_{\mathbb{B}}} + \mathop {\sup }\limits_{t \in [0,T]} {{\left| {\frac{{{{d}^{2}}f}}{{d{{t}^{2}}}}(t)} \right|}_{\mathbb{B}}}.$
Символом $\mathbb{C}_{b}^{{(m + n)}}({{\mathbb{R}}^{3}} \times [0,T])$ мы обозначаем такие функции $f(x,t),$ что
для всех $k = \overline {0,n} $ и ${\text{|}}\beta {\text{|}}\;\leqslant \;m,$ причем все смешанные производные коммутируют. Аналогичным образом определяется ${{\mathbb{C}}^{{(2 + 2)}}}(\bar {\Omega } \times [0,T]),$ где $\Omega \subset {{\mathbb{R}}^{3}}$ – ограниченная область. Символом $\mathbb{C}_{0}^{{(2 + 2)}}({{\mathbb{R}}^{3}} \times [0,T])$ мы обозначаем такие функции $f(x,t),$ что имеют место следующие соотношения:
для всех $k = \overline {0,2} $ и ${\text{|}}\beta {\kern 1pt} {\text{|}}\;\leqslant \;2,$ причем $f(x,T) = f{\kern 1pt} '(x,T) = 0$ и для каждого $t \in [0,T]$ носитель функции $f(x,t)$ компактен в ${{\mathbb{R}}^{3}}$.
В работе мы систематически будем использовать весовые аналоги пространств непрерывных и ограниченных функций, а также весовые пространства Гёльдера. Символом $\mathbb{C}_{b}^{{(m + n)}}((1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{\gamma /2}}};{{\mathbb{R}}^{3}} \times [0,T])$ при $m,n \in \mathbb{N} \cup \{ 0\} $ мы обозначаем такие функции, что
${{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{\gamma /2}}}f(x,t) \in \mathbb{C}_{b}^{{(m + n)}}({{\mathbb{R}}^{3}} \times [0,T]),\quad \gamma \; \geqslant \;0.$
Символом ${{\mathbb{C}}^{{k + \alpha }}}((1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{\gamma /2}}};{{\mathbb{R}}^{3}})$ мы обозначаем такие функции $f(x),$ что
${{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}^{{\gamma /2}}}f(x) \in {{\mathbb{C}}^{{k + \alpha }}}({{\mathbb{R}}^{3}}),\quad \gamma \; \geqslant \;0,\quad k \in \mathbb{N} \cup \{ 0\} ,\quad \alpha \in (0,1).$
Отметим, что справедлива следующая
Лемма 4.1. Если ${{\beta }_{1}}\; \geqslant \;0$ и $\alpha \in (0,1),$ то имеет место следующее вложение:
${{\mathbb{C}}^{{(2)}}}([0,T];{{\mathbb{C}}^{{2 + \alpha }}}((1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}};{{\mathbb{R}}^{3}})) \subset {{\mathbb{C}}^{{(2)}}}([0,T];{{\mathbb{C}}^{{2 + \alpha }}}({{\mathbb{R}}^{3}})) \cap \mathbb{C}_{b}^{{(2 + 2)}}((1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{)}^{{{{\beta }_{1}}/2}}};{{\mathbb{R}}^{3}} \times [0,T]).$
Символами $\mathcal{D}{\kern 1pt} '({{\mathbb{R}}^{3}}),$ $\mathcal{D}{\kern 1pt} '({{\mathbb{R}}^{3}} \times (0,T))$ мы обозначаем пространства обобщенных функций, соответствующие пространствам основных функций $\mathcal{D}({{\mathbb{R}}^{3}}),$ $\mathcal{D}({{\mathbb{R}}^{3}} \times (0,T))$. Символом ${{L}^{p}}({{\mathbb{R}}^{3}})$ при $p \in [1, + \infty )$ мы обозначаем пространства Лебега, для нормы которых используем обозначение
${{\left\| f \right\|}_{p}} = {{\left( {\int\limits_{{{\mathbb{R}}^{3}}} {\text{|}}{\kern 1pt} f(x){\kern 1pt} {{{\text{|}}}^{p}}{\kern 1pt} dx} \right)}^{{1/p}}}.$
Наконец, символом ${{H}^{2}}(\Omega ),$ где $\Omega \subset {{\mathbb{R}}^{3}}$ – область, мы обозначаем пространство С.Л. Соболева
${{H}^{2}}(\Omega ) = \{ f(x):f(x) \in {{L}^{2}}(\Omega ),\;{{D}_{{{{x}_{j}}}}}f(x) \in {{L}^{2}}(\Omega ),\;D_{{{{x}_{j}}{{x}_{k}}}}^{2}f(x) \in {{L}^{2}}(\Omega )\} $
при $j,k \in \overline {1,3} $. Кроме того, символом ${{D}_{x}}f(x)$ мы обозначаем ковектор градиент наравне с более привычным обозначением ${{\nabla }_{x}}f(x)$, причем ${\text{|}}{{D}_{x}}f(x){\text{|}}$ или ${\text{|}}{{\nabla }_{x}}f(x){\text{|}}$ – евклидова норма этих ковекторов.
5. ФУНДАМЕНТАЛЬНОЕ РЕШЕНИЕ
Рассмотрим следующее уравнение в смысле $\mathcal{D}{\kern 1pt} '({{\mathbb{R}}^{4}})$:
$\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\left( {\Delta \mathcal{E} - \mathcal{E}} \right) + \omega _{1}^{2}{{\mathcal{E}}_{{{{x}_{1}}{{x}_{1}}}}} + \omega _{2}^{2}{{\mathcal{E}}_{{{{x}_{2}}{{x}_{2}}}}} + \omega _{3}^{2}{{\mathcal{E}}_{{{{x}_{3}}{{x}_{3}}}}} = \delta (x)\delta (t).$
Рассмотрим преобразование Лапласа от обеих частей этого равенства и получим следующее
равенство:
Одним из решений этого уравнения является следующее:
${\text{|}}y{\kern 1pt} {\text{|}}: = {{\left( {\frac{{x_{1}^{2}}}{{{{p}^{2}} + \omega _{1}^{2}}} + \frac{{x_{2}^{2}}}{{{{p}^{2}} + \omega _{2}^{2}}} + \frac{{x_{3}^{2}}}{{{{p}^{2}} + \omega _{3}^{2}}}} \right)}^{{1/2}}}.$
Воспользуемся следующим равенством:
$\exp ( - {\text{|}}x{\kern 1pt} {\text{|}}\alpha ) = \frac{\alpha }{\pi }\int\limits_{{{\mathbb{R}}^{1}}} \frac{{{{e}^{{i\mu |x|}}}}}{{{{\mu }^{2}} + {{\alpha }^{2}}}}{\kern 1pt} d\mu .$
Получим следующее равенство:
где
$\begin{gathered} A(x,\mu ,p): = {{\mu }^{2}}({{p}^{2}} + \omega _{1}^{2})({{p}^{2}} + \omega _{2}^{2})({{p}^{2}} + \omega _{3}^{2}) + \\ + \;{{p}^{2}}({{p}^{2}} + \omega _{2}^{2})({{p}^{2}} + \omega _{3}^{2})\frac{{x_{1}^{2}}}{{{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}}} + {{p}^{2}}({{p}^{2}} + \omega _{1}^{2})({{p}^{2}} + \omega _{3}^{2})\frac{{x_{2}^{2}}}{{{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}}} + {{p}^{2}}({{p}^{2}} + \omega _{1}^{2})({{p}^{2}} + \omega _{2}^{2})\frac{{x_{3}^{2}}}{{{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}}}. \\ \end{gathered} $
Выражение для $A(x,p,\mu )$ можно преобразовать к следующему виду:
(5.2)
$\begin{gathered} A(x,\mu ,p) = {{p}^{6}}({{\mu }^{2}} + 1) + {{p}^{4}}\left( {(\omega _{1}^{2} + \omega _{2}^{2} + \omega _{3}^{2}){{\mu }^{2}} + (\omega _{2}^{2} + \omega _{3}^{2})\frac{{x_{1}^{2}}}{{{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}}} + (\omega _{1}^{2} + \omega _{3}^{2})\frac{{x_{2}^{2}}}{{{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}}} + (\omega _{1}^{2} + \omega _{2}^{2})\frac{{x_{3}^{2}}}{{{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}}}} \right) + \\ \, + {{p}^{2}}\left( {(\omega _{1}^{2}\omega _{2}^{2} + \omega _{2}^{2}\omega _{3}^{2} + \omega _{3}^{2}\omega _{1}^{2}){{\mu }^{2}} + \omega _{2}^{2}\omega _{3}^{2}\frac{{x_{1}^{2}}}{{{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}}} + \omega _{1}^{2}\omega _{3}^{2}\frac{{x_{2}^{2}}}{{{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}}} + \omega _{1}^{2}\omega _{2}^{2}\frac{{x_{3}^{2}}}{{{\text{|}}x{\text{|}}{{{\kern 1pt} }^{2}}}}} \right) + \omega _{1}^{2}\omega _{2}^{2}\omega _{3}^{2}{{\mu }^{2}} = \\ \, = {{p}^{6}}({{\mu }^{2}} + 1)\left[ {1 + \frac{1}{{{{p}^{2}}}}{{\alpha }_{1}}(x,\mu ) + \frac{1}{{{{p}^{4}}}}{{\alpha }_{2}}(x,\mu ) + \frac{1}{{{{p}^{6}}}}{{\alpha }_{3}}(\mu )} \right], \\ \end{gathered} $(5.3)
${{\alpha }_{1}}(x,\mu ): = \frac{1}{{{{\mu }^{2}} + 1}}\left[ {(\omega _{1}^{2} + \omega _{2}^{2} + \omega _{3}^{2}){{\mu }^{2}} + (\omega _{2}^{2} + \omega _{3}^{2})\frac{{x_{1}^{2}}}{{{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}}} + (\omega _{1}^{2} + \omega _{3}^{2})\frac{{x_{2}^{2}}}{{{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}}} + (\omega _{1}^{2} + \omega _{2}^{2})\frac{{x_{3}^{2}}}{{{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}}}} \right],$(5.4)
${{\alpha }_{2}}(x,\mu ): = \frac{1}{{{{\mu }^{2}} + 1}}\left[ {(\omega _{1}^{2}\omega _{2}^{2} + \omega _{2}^{2}\omega _{3}^{2} + \omega _{3}^{2}\omega _{1}^{2}){{\mu }^{2}} + \omega _{2}^{2}\omega _{3}^{2}\frac{{x_{1}^{2}}}{{{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}}} + \omega _{1}^{2}\omega _{3}^{2}\frac{{x_{2}^{2}}}{{{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}}} + \omega _{1}^{2}\omega _{2}^{2}\frac{{x_{3}^{2}}}{{{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}}}} \right],$(5.5)
${{\alpha }_{3}}(\mu ): = \frac{{{{\mu }^{2}}}}{{{{\mu }^{2}} + 1}}\omega _{1}^{2}\omega _{2}^{2}\omega _{3}^{2}.$
Предположим, что $\operatorname{Re} p = \sigma \; \geqslant \;R > 0$ при достаточно большом $R > 0,$ тогда будет справедливо следующее разложение в ряд:
${{\left[ {1 + \frac{1}{{{{p}^{2}}}}{{\alpha }_{1}}(x,\mu ) + \frac{1}{{{{p}^{4}}}}{{\alpha }_{2}}(x,\mu ) + \frac{1}{{{{p}^{6}}}}{{\alpha }_{3}}(\mu )} \right]}^{{ - 1}}} = \sum\limits_{k = 0}^{ + \infty } \,{{( - 1)}^{k}}{{\left[ {{{\alpha }_{1}}(x,\mu ) + \frac{1}{{{{p}^{2}}}}{{\alpha }_{2}}(x,\mu ) + \frac{1}{{{{p}^{4}}}}{{\alpha }_{3}}(\mu )} \right]}^{k}}\frac{1}{{{{p}^{{2k}}}}}.$
Заметим, что
$\begin{gathered} \bar {\phi }(p): = \frac{1}{{{{p}^{5}}}}\sqrt {{{p}^{2}} + \omega _{1}^{2}} {\kern 1pt} \sqrt {{{p}^{2}} + \omega _{2}^{2}} {\kern 1pt} \sqrt {{{p}^{2}} + \omega _{3}^{2}} = \frac{1}{{{{p}^{2}}}}\sqrt {1 + \frac{{\omega _{1}^{2}}}{{{{p}^{2}}}}{\kern 1pt} } \sqrt {1 + \frac{{\omega _{2}^{2}}}{{{{p}^{2}}}}} {\kern 1pt} \sqrt {1 + \frac{{\omega _{3}^{2}}}{{{{p}^{2}}}}} = \\ \, = \frac{1}{{{{p}^{2}}}} + \sum\limits_{{{k}_{1}} + {{k}_{2}} + {{k}_{3}}\, \geqslant \,1} \left( {\begin{array}{*{20}{c}} {1{\text{/}}2} \\ {{{k}_{1}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {1{\text{/}}2} \\ {{{k}_{2}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {1{\text{/}}2} \\ {{{k}_{3}}} \end{array}} \right)\frac{{\omega _{1}^{{2{{k}_{1}}}}\omega _{2}^{{2{{k}_{2}}}}\omega _{3}^{{2{{k}_{3}}}}}}{{{{p}^{{2{{k}_{1}} + 2{{k}_{2}} + 2{{k}_{3}} + 2}}}}}. \\ \end{gathered} $
Тогда выражение для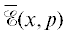 
можно переписать в следующем виде:
${{\phi }_{1}}(p): = \sum\limits_{{{k}_{1}} + {{k}_{2}} + {{k}_{3}}\, \geqslant \,1} \left( {\begin{array}{*{20}{c}} {1{\text{/}}2} \\ {{{k}_{1}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {1{\text{/}}2} \\ {{{k}_{2}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {1{\text{/}}2} \\ {{{k}_{3}}} \end{array}} \right)\frac{{\omega _{1}^{{2{{k}_{1}}}}\omega _{2}^{{2{{k}_{2}}}}\omega _{3}^{{2{{k}_{3}}}}}}{{{{p}^{{2{{k}_{1}} + 2{{k}_{2}} + 2{{k}_{3}} + 2}}}}},$
$\bar {\Phi }(x,p) = - \bar {\phi }(p)\frac{1}{{4{{\pi }^{2}}{\text{|}}x{\kern 1pt} {\text{|}}}}\int\limits_{{{\mathbb{R}}^{1}}} \frac{1}{{{{\mu }^{2}} + 1}}{{e}^{{i\mu |x|}}}\sum\limits_{k = 1}^{ + \infty } \,{{( - 1)}^{k}}{{\left[ {{{\alpha }_{1}}(x,\mu ) + \frac{1}{{{{p}^{2}}}}{{\alpha }_{2}}(x,\mu ) + \frac{1}{{{{p}^{4}}}}{{\alpha }_{3}}(\mu )} \right]}^{k}}\frac{1}{{{{p}^{{2k}}}}}{\kern 1pt} d\mu .$
Применяя обратное преобразование Лапласа, получаем следующее выражение для фундаментального
решения:
(5.6)
$\begin{gathered} \mathcal{E}(x,t) = - t\theta (t)\frac{{{{e}^{{ - |x|}}}}}{{4\pi {\text{|}}x{\kern 1pt} {\kern 1pt} {\text{|}}}} - {{\phi }_{1}}(t)\frac{{{{e}^{{ - |x|}}}}}{{4\pi {\text{|}}x{\kern 1pt} {\text{|}}}} + \Phi (x,t), \\ \Phi (x,t): = - \frac{{\theta (t)}}{{4{{\pi }^{2}}{\text{|}}x{\kern 1pt} {\text{|}}}}\sum\limits_{k = 1}^{ + \infty } \frac{{{{{( - 1)}}^{k}}}}{{(2k - 1)!}}\int\limits_{{{\mathbb{R}}^{1}}} {\kern 1pt} d\mu {\kern 1pt} \frac{{{{e}^{{i\mu |x|}}}}}{{{{\mu }^{2}} + 1}}\phi (t) * {{\left[ {{{\alpha }_{1}}(x,\mu ){\text{id}} + {{\alpha }_{2}}(x,\mu )t{\kern 1pt} * + \frac{1}{6}{{\alpha }_{3}}(\mu ){{t}^{3}}{\kern 1pt} * } \right]}^{k}}{{t}^{{2k - 1}}}, \\ \end{gathered} $(5.7)
$\phi (t): = \theta (t)\sum\limits_{{{k}_{1}} + {{k}_{2}} + {{k}_{3}}\, \geqslant \,0} \left( {\begin{array}{*{20}{c}} {1{\text{/}}2} \\ {{{k}_{1}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {1{\text{/}}2} \\ {{{k}_{2}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {1{\text{/}}2} \\ {{{k}_{3}}} \end{array}} \right)\omega _{1}^{{2{{k}_{1}}}}\omega _{2}^{{2{{k}_{2}}}}\omega _{3}^{{2{{k}_{3}}}}\frac{{{{t}^{{2{{k}_{1}} + 2{{k}_{2}} + 2{{k}_{3}} + 1}}}}}{{(2{{k}_{1}} + 2{{k}_{2}} + 2{{k}_{3}} + 1)!}},$(5.8)
${{\phi }_{1}}(t): = \theta (t)\sum\limits_{{{k}_{1}} + {{k}_{2}} + {{k}_{3}}\, \geqslant \,1} \left( {\begin{array}{*{20}{c}} {1{\text{/}}2} \\ {{{k}_{1}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {1{\text{/}}2} \\ {{{k}_{2}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {1{\text{/}}2} \\ {{{k}_{3}}} \end{array}} \right)\omega _{1}^{{2{{k}_{1}}}}\omega _{2}^{{2{{k}_{2}}}}\omega _{3}^{{2{{k}_{3}}}}\frac{{{{t}^{{2{{k}_{1}} + 2{{k}_{2}} + 2{{k}_{3}} + 1}}}}}{{(2{{k}_{1}} + 2{{k}_{2}} + 2{{k}_{3}} + 1)!}}.$Лемма 5.1. Если $x \ne 0,$ то справедливы следующие равенства:
(5.9)
$\mathcal{E}(x,0) = 0,\quad \frac{{\partial{ \mathcal{E}}}}{{\partial t}}(x,0) = - \frac{{\exp ( - {\text{|}}x{\kern 1pt} {\text{|}})}}{{4\pi {\text{|}}x{\kern 1pt} {\text{|}}}},\quad \frac{{{{\partial }^{2}}\mathcal{E}}}{{\partial {{t}^{2}}}}(x,0) = 0.$Доказательство. Доказательство основано на явном виде (5.6) фундаментального решения $\mathcal{E}(x,t)$.
6. ОЦЕНКИ ФУНДАМЕНТАЛЬНОГО РЕШЕНИЯ
Точно так же, как в работе [18], может быть получено следующее представление для фундаментального решения (5.6):
(6.1)
$\begin{gathered} \mathcal{E}(x,t) = - t\theta (t)\frac{{{{e}^{{ - |x|}}}}}{{4\pi {\text{|}}x{\kern 1pt} {\text{|}}}} - {{\phi }_{1}}(t)\frac{{{{e}^{{ - |x|}}}}}{{4\pi {\text{|}}x{\kern 1pt} {\text{|}}}} + \Phi (x,t), \\ \Phi (x,t): = \frac{{\theta (t)}}{{4{{\pi }^{2}}{\text{|}}x{\kern 1pt} {\text{|}}}}\sum\limits_{k = 1}^{ + \infty } \frac{{{{{( - 1)}}^{k}}}}{{(2k - 1)!}}\int\limits_{C_{\varepsilon }^{ + }(i)} dz{\kern 1pt} \frac{{{{e}^{{iz|x|}}}}}{{{{z}^{2}} + 1}}\phi (t) * {{\left[ {{{\alpha }_{1}}(x,z){\text{id}} + {{\alpha }_{2}}(x,z)t{\kern 1pt} * + \frac{1}{6}{{\alpha }_{3}}(z){{t}^{3}}{\kern 1pt} * } \right]}^{k}}{{t}^{{2k - 1}}}, \\ \end{gathered} $
${{\alpha }_{1}}(x,z): = \frac{1}{{{{z}^{2}} + 1}}\left[ {(\omega _{1}^{2} + \omega _{2}^{2} + \omega _{3}^{2}){{z}^{2}} + (\omega _{2}^{2} + \omega _{3}^{2})\frac{{x_{1}^{2}}}{{{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}}} + (\omega _{1}^{2} + \omega _{3}^{2})\frac{{x_{2}^{2}}}{{{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}}} + (\omega _{1}^{2} + \omega _{2}^{2})\frac{{x_{3}^{2}}}{{{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}}}} \right],$
(6.2)
${{\alpha }_{2}}(x,z): = \frac{1}{{{{z}^{2}} + 1}}\left[ {(\omega _{1}^{2}\omega _{2}^{2} + \omega _{2}^{2}\omega _{3}^{2} + \omega _{3}^{2}\omega _{1}^{2}){{z}^{2}} + \omega _{2}^{2}\omega _{3}^{2}\frac{{x_{1}^{2}}}{{{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}}} + \omega _{1}^{2}\omega _{3}^{2}\frac{{x_{2}^{2}}}{{{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}}} + \omega _{1}^{2}\omega _{2}^{2}\frac{{x_{3}^{2}}}{{{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}}}} \right],$
${{\alpha }_{3}}(z): = \frac{{{{z}^{2}}}}{{{{z}^{2}} + 1}}\omega _{1}^{2}\omega _{2}^{2}\omega _{3}^{2},$
а функции $\phi (t)$ и ${{\phi }_{1}}(t)$ определены равенствами (5.7) и (5.8). Из явного вида функций ${{\alpha }_{1}}(x,z),$ ${{\alpha }_{2}}(x,z)$ при условиях, что ${\text{|}}z - i{\kern 1pt} {\text{|}} = \varepsilon $, $\varepsilon \in (0,1)$ и $x \ne (0,0,0)$ вытекают следующие оценки:
(6.3)
$\left| {\frac{{\partial {{\alpha }_{1}}(x,z)}}{{\partial {{x}_{j}}}}} \right|\;\leqslant \;\frac{{{{c}_{1}}(\varepsilon )}}{{{\text{|}}x{\kern 1pt} {\text{|}}}},\quad \left| {\frac{{\partial {{\alpha }_{2}}(x,z)}}{{\partial {{x}_{j}}}}} \right|\;\leqslant \;\frac{{{{c}_{2}}(\varepsilon )}}{{{\text{|}}x{\kern 1pt} {\text{|}}}},$
$\left| {\frac{{{{\partial }^{2}}{{\alpha }_{1}}(x,z)}}{{\partial {{x}_{j}}\partial {{x}_{k}}}}} \right|\;\leqslant \;\frac{{{{c}_{3}}(\varepsilon )}}{{{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}}},\quad \left| {\frac{{{{\partial }^{2}}{{\alpha }_{2}}(x,z)}}{{\partial {{x}_{j}}\partial {{x}_{k}}}}} \right|\;\leqslant \;\frac{{{{c}_{4}}(\varepsilon )}}{{{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}}},$
(6.4)
$\left| {\frac{{{{\partial }^{3}}{{\alpha }_{1}}(x,z)}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial {{x}_{l}}}}} \right|\;\leqslant \;\frac{{{{c}_{5}}(\varepsilon )}}{{{\text{|}}x{\kern 1pt} {{{\text{|}}}^{3}}}},\quad \left| {\frac{{{{\partial }^{3}}{{\alpha }_{2}}(x,z)}}{{\partial {{x}_{j}}\partial {{x}_{k}}\partial {{x}_{l}}}}} \right|\;\leqslant \;\frac{{{{c}_{6}}(\varepsilon )}}{{{\text{|}}x{\kern 1pt} {{{\text{|}}}^{3}}}}$(6.5)
$\mathcal{E}(x,t) \in {{\mathbb{C}}^{{(m + n)}}}({{\mathbb{R}}^{3}}{{\backslash }}\{ 0\} \times [0, + \infty ))\quad {\text{для всех}}\quad m,n \in \mathbb{N} \cup \{ 0\} .$(6.6)
$\begin{gathered} \left| {\frac{{{{\partial }^{m}}\mathcal{E}(x,t)}}{{\partial {{t}^{m}}}}} \right|\;\leqslant \;\frac{{{{A}_{0}}(T,{{R}_{0}},\varepsilon )}}{{{\text{|}}x{\kern 1pt} {\text{|}}}},\quad \left| {\frac{{{{\partial }^{{m + 1}}}\mathcal{E}(x,t)}}{{\partial {{t}^{m}}\partial {{x}_{j}}}}} \right|\;\leqslant \;\frac{{{{A}_{1}}(T,{{R}_{0}},\varepsilon )}}{{{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}}}, \\ \left| {\frac{{{{\partial }^{{m + 2}}}\mathcal{E}(x,t)}}{{\partial {{t}^{m}}\partial {{x}_{j}}\partial {{x}_{k}}}}} \right|\;\leqslant \;\frac{{{{A}_{2}}(T,{{R}_{0}},\varepsilon )}}{{{\text{|}}x{\kern 1pt} {{{\text{|}}}^{3}}}},\quad \left| {\frac{{{{\partial }^{{m + 3}}}\mathcal{E}(x,t)}}{{\partial {{t}^{m}}\partial {{x}_{j}}\partial {{x}_{k}}\partial {{x}_{l}}}}} \right|\;\leqslant \;\frac{{{{A}_{3}}(T,{{R}_{0}},\varepsilon )}}{{{\text{|}}x{\kern 1pt} {{{\text{|}}}^{4}}}} \\ \end{gathered} $(6.7)
$\left| {\frac{{{{\partial }^{m}}\mathcal{E}(x,t)}}{{\partial {{t}^{m}}}}} \right|\;\leqslant \;{{B}_{0}}(T,{{R}_{0}},\varepsilon )\frac{{{{e}^{{ - (1 - \varepsilon )|x|}}}}}{{{\text{|}}x{\kern 1pt} {\text{|}}}},$
$\left| {\frac{{{{\partial }^{{m + 1}}}\mathcal{E}(x,t)}}{{\partial {{t}^{m}}\partial {{x}_{j}}}}} \right|\;\leqslant \;{{B}_{1}}(T,{{R}_{0}},\varepsilon )\frac{{{{e}^{{ - (1 - \varepsilon )|x|}}}}}{{{\text{|}}x{\kern 1pt} {\text{|}}}},$
$\left| {\frac{{{{\partial }^{{m + 2}}}\mathcal{E}(x,t)}}{{\partial {{t}^{m}}\partial {{x}_{j}}\partial {{x}_{k}}}}} \right|\;\leqslant \;{{B}_{2}}(T,{{R}_{0}},\varepsilon )\frac{{{{e}^{{ - (1 - \varepsilon )|x|}}}}}{{{\text{|}}x{\kern 1pt} {\text{|}}}},$
(6.8)
$\left| {\frac{{{{\partial }^{{m + 3}}}\mathcal{E}(x,t)}}{{\partial {{t}^{m}}\partial {{x}_{j}}\partial {{x}_{k}}\partial {{x}_{l}}}}} \right|\;\leqslant \;{{B}_{3}}(T,{{R}_{0}},\varepsilon )\frac{{{{e}^{{ - (1 - \varepsilon )|x|}}}}}{{{\text{|}}x{\kern 1pt} {\text{|}}}}$Лемма 6.1. Для всех $(x,t) \in {{\mathbb{R}}^{3}}{{\backslash }}\{ 0\} \times [0,T]$ при $T > 0$ частные производные в оценках (6.6)–(6.8) коммутируют.
Доказательство. Доказательство основано на свойстве гладкости (6.5).
7. ВТОРАЯ ФОРМУЛА ГРИНА
Пусть $u(x,t),{v}(x,t) \in {{\mathbb{C}}^{{(2 + 2)}}}(\bar {\Omega } \times [0,T])$. Тогда справедливы следующие равенства:
(7.1)
$\begin{gathered} v\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\Delta u = \frac{\partial }{{\partial t}}\left( {v\Delta \frac{{\partial u}}{{\partial t}}} \right) - \frac{\partial }{{\partial t}}\left( {\Delta u\frac{{\partial v}}{{\partial t}}} \right) + \operatorname{div} \left( {\frac{{{{\partial }^{2}}v}}{{\partial {{t}^{2}}}}\nabla u} \right) - \operatorname{div} \left( {u\nabla \frac{{{{\partial }^{2}}v}}{{\partial {{t}^{2}}}}} \right) + u\Delta \frac{{{{\partial }^{2}}v}}{{\partial {{t}^{2}}}} = \frac{\partial }{{\partial t}}\left( {v\Delta \frac{{\partial u}}{{\partial t}}} \right) - \\ \, - \frac{\partial }{{\partial t}}\left( {\Delta u\frac{{\partial v}}{{\partial t}}} \right) + \operatorname{div} \left( {v\nabla \frac{{{{\partial }^{2}}u}}{{\partial {{t}^{2}}}}} \right) - \operatorname{div} \left( {u\nabla \frac{{{{\partial }^{2}}v}}{{\partial {{t}^{2}}}}} \right) + \frac{\partial }{{\partial t}}\operatorname{div} \left( {\frac{{\partial v}}{{\partial t}}\nabla u} \right) - \frac{\partial }{{\partial t}}\operatorname{div} \left( {v\nabla \frac{{\partial u}}{{\partial t}}} \right) + u\Delta \frac{{{{\partial }^{2}}v}}{{\partial {{t}^{2}}}}, \\ \end{gathered} $(7.2)
$\begin{gathered} v\frac{{{{\partial }^{2}}u}}{{\partial {{t}^{2}}}} = \frac{\partial }{{\partial t}}\left( {v\frac{{\partial u}}{{\partial t}}} \right) - \frac{{\partial v}}{{\partial t}}\frac{{\partial u}}{{\partial t}} = \frac{\partial }{{\partial t}}\left( {v\frac{{\partial u}}{{\partial t}}} \right) - \frac{\partial }{{\partial t}}\left( {u\frac{{\partial v}}{{\partial t}}} \right) + u\frac{{{{\partial }^{2}}v}}{{\partial {{t}^{2}}}}, \\ v\frac{{{{\partial }^{2}}u}}{{\partial x_{j}^{2}}} = \frac{\partial }{{\partial {{x}_{j}}}}\left( {v\frac{{\partial u}}{{\partial {{x}_{j}}}}} \right) - \frac{\partial }{{\partial {{x}_{j}}}}\left( {u\frac{{\partial {v}}}{{\partial {{x}_{j}}}}} \right) + u\frac{{{{\partial }^{2}}v}}{{\partial x_{j}^{2}}}\quad {\text{при}}\quad j = 1,2,3. \\ \end{gathered} $
$\mathfrak{M}_{{x,t}}^{t}[u](x,t) = {{\mathfrak{M}}_{{x,t}}}[u](x,t) = \frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\left( {\Delta u(x,t) - u(x,t)} \right) + \sum\limits_{j = 1}^3 \,\omega _{j}^{2}\frac{{{{\partial }^{2}}u(x,t)}}{{\partial x_{j}^{2}}}.$
Из равенств (7.1) и (7.2) вытекает вторая формула Грина
$\begin{gathered} \int\limits_0^t {\kern 1pt} \int\limits_\Omega \left[ {v(\xi ,\tau ){{\mathfrak{M}}_{{\xi ,\tau }}}[u](\xi ,\tau ) - u(\xi ,\tau ){{\mathfrak{M}}_{{\xi ,\tau }}}[v](\xi ,\tau )} \right]{\kern 1pt} d\xi {\kern 1pt} d\tau = \\ = \int\limits_0^t {\kern 1pt} \int\limits_{\partial \Omega } \left[ {v(\xi ,\tau ){{\mathfrak{N}}_{{\xi ,\tau }}}[u](\xi ,\tau ) - u(\xi ,\tau ){{\mathfrak{N}}_{{\xi ,\tau }}}[v](\xi ,\tau )} \right]{\kern 1pt} d{{S}_{\xi }}{\kern 1pt} d\tau + \\ \end{gathered} $
(7.3)
$\begin{gathered} + \;\int\limits_\Omega \left[ {v(\xi ,t)\left[ {\Delta \frac{{\partial u}}{{\partial \tau }}(\xi ,t) - \frac{{\partial u}}{{\partial \tau }}(\xi ,t)} \right] - v(\xi ,0)\left[ {\Delta \frac{{\partial u}}{{\partial \tau }}(\xi ,0) - \frac{{\partial u}}{{\partial \tau }}(\xi ,0)} \right]} \right]{\kern 1pt} d\xi - \\ \, - \int\limits_\Omega \left[ {\frac{{\partial v}}{{\partial \tau }}(\xi ,t)\left[ {\Delta u(\xi ,t) - u(\xi ,t)} \right] - \frac{{\partial v}}{{\partial \tau }}(\xi ,0)\left[ {\Delta u(\xi ,0) - u(\xi ,0)} \right]} \right]{\kern 1pt} d\xi + \\ \end{gathered} $
$\begin{gathered} + \;\int\limits_{\partial \Omega } \left[ {\frac{{\partial v}}{{\partial \tau }}(\xi ,t)\frac{{\partial u}}{{\partial {{n}_{\xi }}}}(\xi ,t) - \frac{{\partial v}}{{\partial \tau }}(\xi ,0)\frac{{\partial u}}{{\partial {{n}_{\xi }}}}(\xi ,0)} \right]{\kern 1pt} {\kern 1pt} d{{S}_{\xi }} - \\ - \;\int\limits_{\partial \Omega } \left[ {v(\xi ,t)\frac{{{{\partial }^{2}}u}}{{\partial \tau \partial {{n}_{\xi }}}}(\xi ,t) - v(\xi ,0)\frac{{{{\partial }^{2}}u}}{{\partial \tau \partial {{n}_{\xi }}}}(\xi ,0)} \right]{\kern 1pt} {\kern 1pt} d{{S}_{\xi }}, \\ \end{gathered} $
где мы ввели обозначения
(7.4)
${{\mathfrak{N}}_{{\xi ,\tau }}}[u](\xi ,\tau ) = \mathfrak{N}_{{\xi ,\tau }}^{t}[u](\xi ,\tau ) = \frac{{{{\partial }^{2}}}}{{\partial {{\tau }^{2}}}}\frac{{\partial u}}{{\partial {{n}_{\xi }}}} + \omega _{1}^{2}\frac{{\partial u}}{{\partial {{\xi }_{1}}}}\cos ({{n}_{\xi }},{{e}_{1}}) + \omega _{2}^{2}\frac{{\partial u}}{{\partial {{\xi }_{2}}}}\cos ({{n}_{\xi }},{{e}_{2}}) + \omega _{3}^{2}\frac{{\partial u}}{{\partial {{\xi }_{3}}}}\cos ({{n}_{\xi }},{{e}_{3}}).$Теорема 1. Для любых функций $u(x,t),{v}(x,t) \in {{\mathbb{C}}^{{(2 + 2)}}}(\bar {\Omega } \times [0,T])$ при $t \in [0,T]$ справедливо равенство (7.3).
8. ТРЕТЬЯ ФОРМУЛА ГРИНА В ОГРАНИЧЕННОЙ ОБЛАСТИ
Пусть $u(\xi ,\tau ) \in {{\mathbb{C}}^{{(2 + 2)}}}(\bar {\Omega } \times [0,T])$ и $(x,t) \in \Omega \times (0,T]$ – фиксированная точка. Тогда найдется такое $\delta > 0,$ что $O(x,\delta ) \subset \Omega $. Введем следующее обозначение:
Применим вторую формулу Грина (7.3) к области ${{\Omega }_{\delta }}$ и функциям $u(\xi ,\tau )$, ${v}(\xi ,\tau ) = \mathcal{E}(x - \xi ,t - \tau ) \in $ $ \in {{\mathbb{C}}^{{(2 + 2)}}}({{\bar {\Omega }}_{\delta }} \times [0,t])$ для любого $t \in (0,T]$. Тогда она примет следующий вид:
$\begin{gathered} \int\limits_0^t {\kern 1pt} \int\limits_{{{\Omega }_{\delta }}} \left[ {v(\xi ,\tau ){{\mathfrak{M}}_{{\xi ,\tau }}}[u](\xi ,\tau ) - u(\xi ,\tau ){{\mathfrak{M}}_{{\xi ,\tau }}}[v](x - \xi ,t - \tau )} \right]{\kern 1pt} d\xi {\kern 1pt} d\tau = \\ \, = \int\limits_0^t {\kern 1pt} \int\limits_{\partial {{\Omega }_{\delta }}} \left[ {v(\xi ,\tau ){{\mathfrak{N}}_{{\xi ,\tau }}}[u](\xi ,\tau ) - u(\xi ,\tau ){{\mathfrak{N}}_{{\xi ,\tau }}}[v](x - \xi ,t - \tau )} \right]{\kern 1pt} d{{S}_{\xi }}{\kern 1pt} d\tau + \\ + \;\int\limits_{{{\Omega }_{\delta }}} \left[ {v(\xi ,t)\left[ {\Delta \frac{{\partial u}}{{\partial \tau }}(\xi ,t) - \frac{{\partial u}}{{\partial \tau }}(\xi ,t)} \right] - v(\xi ,0)\left[ {\Delta \frac{{\partial u}}{{\partial \tau }}(\xi ,0) - \frac{{\partial u}}{{\partial \tau }}(\xi ,0)} \right]} \right]{\kern 1pt} d\xi - \\ \end{gathered} $
(8.1)
$\, - \int\limits_{{{\Omega }_{\delta }}} \left[ {\frac{{\partial v}}{{\partial \tau }}(\xi ,t)\left[ {\Delta u(\xi ,t) - u(\xi ,t)} \right] - \frac{{\partial v}}{{\partial \tau }}(\xi ,0)\left[ {\Delta u(\xi ,0) - u(\xi ,0)} \right]} \right]{\kern 1pt} d\xi + $
$\begin{gathered} + \;\int\limits_{\partial {{\Omega }_{\delta }}} \left[ {\frac{{\partial v}}{{\partial \tau }}(\xi ,t)\frac{{\partial u}}{{\partial {{n}_{\xi }}}}(\xi ,t) - \frac{{\partial v}}{{\partial \tau }}(\xi ,0)\frac{{\partial u}}{{\partial {{n}_{\xi }}}}(\xi ,0)} \right]{\kern 1pt} {\kern 1pt} d{{S}_{\xi }} - \int\limits_{\partial {{\Omega }_{\delta }}} \left[ {v(\xi ,t)\frac{{{{\partial }^{2}}u}}{{\partial \tau \partial {{n}_{\xi }}}}(\xi ,t) - v(\xi ,0)\frac{{{{\partial }^{2}}u}}{{\partial \tau \partial {{n}_{\xi }}}}(\xi ,0)} \right]{\kern 1pt} {\kern 1pt} d{{S}_{\xi }}, \\ {{\mathfrak{M}}_{{x,t}}}[w](x,t) = {{\Delta }_{x}}\frac{{{{\partial }^{2}}w(x,t)}}{{\partial {{t}^{2}}}} + \sum\limits_{j = 1}^3 \,\omega _{j}^{2}\frac{{{{\partial }^{2}}w(x,t)}}{{\partial x_{j}^{2}}}, \\ {{\mathfrak{N}}_{{x,t}}}[w](x,t) = \frac{\partial }{{\partial {{n}_{x}}}}\frac{{{{\partial }^{2}}w(x,t)}}{{\partial {{t}^{2}}}} + \sum\limits_{j = 1}^3 \,\omega _{j}^{2}\frac{{\partial w(x,t)}}{{\partial {{x}_{j}}}}\cos ({{n}_{x}},{{e}_{j}}). \\ \end{gathered} $
Последовательно рассмотрим слагаемые в левой и в правой частях равенства (8.1). Рассмотрим
следующий интеграл:
${{I}_{{1\delta }}}: = \int\limits_0^t {\kern 1pt} \int\limits_{O(x,\delta )} {\kern 1pt} v(\xi ,\tau ){{\mathfrak{M}}_{{\xi ,\tau }}}[u](\xi ,\tau ){\kern 1pt} d\xi {\kern 1pt} d\tau .$
В силу оценки (6.6) справедлива следующая оценка:
$\left| {{{I}_{{1\delta }}}} \right|\;\leqslant \;{{A}_{0}}(T,{{R}_{0}},\varepsilon )\mathop {\sup }\limits_{(x,t) \in \overline \Omega \otimes [0,T]} \left| {{{\mathfrak{M}}_{{x,t}}}[u](x,t)} \right|{{\delta }^{2}} \to + 0\quad {\text{при}}\quad \delta \to + 0.$
Поэтому имеем
(8.2)
$\int\limits_0^t {\kern 1pt} \int\limits_{{{\Omega }_{\delta }}} \,v(\xi ,\tau ){{\mathfrak{M}}_{{\xi ,\tau }}}[u](\xi ,\tau ){\kern 1pt} d\xi {\kern 1pt} d\tau \to \int\limits_0^t {\kern 1pt} \int\limits_\Omega \,v(\xi ,\tau ){{\mathfrak{M}}_{{\xi ,\tau }}}[u](\xi ,\tau ){\kern 1pt} d\xi {\kern 1pt} d\tau \quad {\text{при}}\quad \delta \to + 0.$
${{\mathfrak{M}}_{{\xi ,\tau }}}[v](x - \xi ,t - \tau ) = 0\quad {\text{при}}\quad (\xi ,\tau ) \in {{\bar {\Omega }}_{\delta }} \times [0, + \infty ),$
то поэтому
(8.3)
$\int\limits_0^t {\kern 1pt} \int\limits_{{{\Omega }_{\delta }}} u(\xi ,\tau ){{\mathfrak{M}}_{{\xi ,\tau }}}[v](x - \xi ,t - \tau ){\kern 1pt} d\xi {\kern 1pt} d\tau = 0.$
${{I}_{{2\delta }}}: = \int\limits_0^t {\kern 1pt} \int\limits_{\partial O(x,\delta )} v(\xi ,\tau ){{\mathfrak{N}}_{{\xi ,\tau }}}[u](\xi ,\tau ){\kern 1pt} d{{S}_{\xi }}{\kern 1pt} d\tau .$
В силу оценки (6.6) справедлива следующая оценка:
$\left| {{{I}_{{2\delta }}}} \right|\;\leqslant \;{{A}_{0}}(T,{{R}_{0}},\varepsilon )\mathop {\sup }\limits_{(x,t) \in \overline \Omega \otimes [0,T]} \left| {{{\mathfrak{N}}_{{x,t}}}[u](x,t)} \right|\delta \to + 0\quad {\text{при}}\quad \delta \to + 0.$
Поэтому
(8.4)
$\int\limits_0^t {\kern 1pt} \int\limits_{\partial {{\Omega }_{\delta }}} v(\xi ,\tau ){{\mathfrak{N}}_{{\xi ,\tau }}}[u](\xi ,\tau ){\kern 1pt} d{{S}_{\xi }}{\kern 1pt} d\tau \to \int\limits_0^t {\kern 1pt} \int\limits_{\partial \Omega } v(\xi ,\tau ){{\mathfrak{N}}_{{\xi ,\tau }}}[u](\xi ,\tau ){\kern 1pt} d{{S}_{\xi }}{\kern 1pt} d\tau $
$\begin{gathered} \int\limits_{{{\Omega }_{\delta }}} \left[ {v(\xi ,t)\left[ {\Delta \frac{{\partial u}}{{\partial \tau }}(\xi ,t) - \frac{{\partial u}}{{\partial \tau }}(\xi ,t)} \right] - v(\xi ,0)\left[ {\Delta \frac{{\partial u}}{{\partial \tau }}(\xi ,0) - \frac{{\partial u}}{{\partial \tau }}(\xi ,0)} \right]} \right]{\kern 1pt} d\xi \to \\ \to \int\limits_\Omega \left[ {v(\xi ,t)\left[ {\Delta \frac{{\partial u}}{{\partial \tau }}(\xi ,t) - \frac{{\partial u}}{{\partial \tau }}(\xi ,t)} \right] - v(\xi ,0)\left[ {\Delta \frac{{\partial u}}{{\partial \tau }}(\xi ,0) - \frac{{\partial u}}{{\partial \tau }}(\xi ,0)} \right]} \right]{\kern 1pt} d\xi , \\ \end{gathered} $
(8.5)
$\begin{gathered} \int\limits_{{{\Omega }_{\delta }}} \left[ {\frac{{\partial v}}{{\partial \tau }}(\xi ,t)\left[ {\Delta u(\xi ,t) - u(\xi ,t)} \right] - \frac{{\partial v}}{{\partial \tau }}(\xi ,0)\left[ {\Delta u(\xi ,0) - u(\xi ,0)} \right]} \right]{\kern 1pt} d\xi \to \\ \to \int\limits_\Omega \left[ {\frac{{\partial v}}{{\partial \tau }}(\xi ,t)\left[ {\Delta u(\xi ,t) - u(\xi ,t)} \right] - \frac{{\partial v}}{{\partial \tau }}(\xi ,0)\left[ {\Delta u(\xi ,0) - u(\xi ,0)} \right]} \right]{\kern 1pt} d\xi , \\ \end{gathered} $
$\begin{gathered} \int\limits_{\partial {{\Omega }_{\delta }}} \left[ {\frac{{\partial v}}{{\partial \tau }}(\xi ,t)\frac{{\partial u}}{{\partial {{n}_{\xi }}}}(\xi ,t) - \frac{{\partial v}}{{\partial \tau }}(\xi ,0)\frac{{\partial u}}{{\partial {{n}_{\xi }}}}(\xi ,0)} \right]{\kern 1pt} d{{S}_{\xi }} \to \int\limits_{\partial \Omega } \left[ {\frac{{\partial v}}{{\partial \tau }}(\xi ,t)\frac{{\partial u}}{{\partial {{n}_{\xi }}}}(\xi ,t) - \frac{{\partial v}}{{\partial \tau }}(\xi ,0)\frac{{\partial u}}{{\partial {{n}_{\xi }}}}(\xi ,0)} \right]{\kern 1pt} d{{S}_{\xi }}, \\ \int\limits_{\partial {{\Omega }_{\delta }}} \left[ {v(\xi ,t)\frac{{{{\partial }^{2}}u}}{{\partial \tau \partial {{n}_{\xi }}}}(\xi ,t) - v(\xi ,0)\frac{{{{\partial }^{2}}u}}{{\partial \tau \partial {{n}_{\xi }}}}(\xi ,0)} \right]{\kern 1pt} d{{S}_{\xi }} \to \int\limits_{\partial \Omega } \left[ {v(\xi ,t)\frac{{{{\partial }^{2}}u}}{{\partial \tau \partial {{n}_{\xi }}}}(\xi ,t) - v(\xi ,0)\frac{{{{\partial }^{2}}u}}{{\partial \tau \partial {{n}_{\xi }}}}(\xi ,0)} \right]{\kern 1pt} d{{S}_{\xi }} \\ \end{gathered} $
при $\delta \to + 0.$ Теперь рассмотрим интеграл
(8.6)
${{I}_{{3\delta }}}: = \int\limits_0^t {\kern 1pt} \int\limits_{\partial O(x,\delta )} u(\xi ,\tau ){{\mathfrak{N}}_{{\xi ,\tau }}}[v](x - \xi ,t - \tau ){\kern 1pt} d{{S}_{\xi }}{\kern 1pt} d\tau .$(8.7)
$\begin{gathered} \int\limits_0^t \,u(\xi ,\tau )f(x - \xi ,t - \tau ){\kern 1pt} d\tau = \int\limits_0^t \,u(\xi ,t - \tau )f(x - \xi ,\tau ){\kern 1pt} d\tau = \\ = {{u}_{0}}(\xi )\int\limits_0^t \,f(x - \xi ,s){\kern 1pt} ds - \int\limits_0^t \frac{{\partial u(\xi ,t - \tau )}}{{\partial \tau }}\int\limits_0^\tau \,f(x - \xi ,s){\kern 1pt} ds{\kern 1pt} d\tau , \\ f(x - \xi ,t - \tau ) = {{\mathfrak{N}}_{{\xi ,\tau }}}[v](x - \xi ,t - \tau ). \\ \end{gathered} $
${{I}_{{3\delta }}}: = \int\limits_{\partial O(0,\delta )} {{u}_{0}}(x - \xi )\int\limits_0^t \,f(\xi ,s){\kern 1pt} ds{\kern 1pt} d\xi - \int\limits_{\partial O(0,\delta )} {\kern 1pt} \int\limits_0^t \frac{{\partial u(x - \xi ,t - \tau )}}{{\partial \tau }}\int\limits_0^\tau \,f(\xi ,s){\kern 1pt} ds{\kern 1pt} d\tau {\kern 1pt} d\xi = $
(8.8)
$ = \int\limits_{\partial O(0,\delta )} [{{u}_{0}}(x - \xi ) - {{u}_{0}}(x)]{\kern 1pt} \int\limits_0^t \,f(\xi ,s){\kern 1pt} ds{\kern 1pt} d\xi + {{u}_{0}}(x)g(t) - \int\limits_{\partial O(0,\delta )} {\kern 1pt} \int\limits_0^t \frac{{\partial \left[ {u(x - \xi ,t - \tau ) - u(x,t - \tau )} \right]}}{{\partial \tau }} \times $
$ \times \;\int\limits_0^\tau \,f(\xi ,s){\kern 1pt} ds{\kern 1pt} d\tau {\kern 1pt} d\xi - \int\limits_0^t \frac{{\partial u(x,t - \tau )}}{{\partial \tau }}g(\tau )d\tau : = {{I}_{{31\delta }}} + {{I}_{{32\delta }}} + {{I}_{{33\delta }}} + {{I}_{{34\delta }}},$
где
(8.9)
$g(t): = \int\limits_0^t {\kern 1pt} {\kern 1pt} \int\limits_{\partial O(0,\delta )} f(\xi ,s){\kern 1pt} d\xi {\kern 1pt} ds.$(8.11)
${{I}_{{32\delta }}},\;{{I}_{{34\delta }}} \to 0\quad {\text{при}}\quad \delta = \frac{1}{n} \to + 0,\quad n \to + \infty .$
$\int\limits_0^t {\kern 1pt} \int\limits_{\partial O(x,\delta )} u(\xi ,\tau ){{\mathfrak{N}}_{{\xi ,\tau }}}[v](x - \xi ,t - \tau ){\kern 1pt} d{{S}_{\xi }}{\kern 1pt} d\tau \to 0\quad {\text{при}}\quad \delta = \frac{1}{n} \to + 0,\quad n \to + \infty .$
Поэтому
(8.12)
$\begin{gathered} \int\limits_0^t {\kern 1pt} \int\limits_{\partial {{\Omega }_{\delta }}} {\kern 1pt} u(\xi ,\tau ){{\mathfrak{N}}_{{\xi ,\tau }}}[v](x - \xi ,t - \tau ){\kern 1pt} d{{S}_{\xi }}{\kern 1pt} d\tau \to \\ \to \int\limits_0^t {\kern 1pt} \int\limits_{\partial \Omega } u(\xi ,\tau ){{\mathfrak{N}}_{{\xi ,\tau }}}[v](x - \xi ,t - \tau ){\kern 1pt} d{{S}_{\xi }}{\kern 1pt} d\tau \quad {\text{при}}\quad \delta = \frac{1}{n} \to + 0,\quad n \to + \infty . \\ \end{gathered} $
$\int\limits_0^t {\kern 1pt} \int\limits_\Omega \,{v}(\xi ,\tau ){{\mathfrak{M}}_{{\xi ,\tau }}}[u](\xi ,\tau ){\kern 1pt} d\xi {\kern 1pt} d\tau = \int\limits_0^t {\kern 1pt} \int\limits_{\partial \Omega } \left[ {{v}(\xi ,\tau ){{\mathfrak{N}}_{{\xi ,\tau }}}[u](\xi ,\tau ) - u(\xi ,\tau ){{\mathfrak{N}}_{{\xi ,\tau }}}[v](x - \xi ,t - \tau )} \right]{\kern 1pt} d{{S}_{\xi }}{\kern 1pt} d\tau + $
(8.13)
$\begin{gathered} + \;\int\limits_\Omega \left[ {v(\xi ,t)\left[ {\Delta \frac{{\partial u}}{{\partial \tau }}(\xi ,t) - \frac{{\partial u}}{{\partial \tau }}(\xi ,t)} \right] - v(\xi ,0)\left[ {\Delta \frac{{\partial u}}{{\partial \tau }}(\xi ,0) - \frac{{\partial u}}{{\partial \tau }}(\xi ,0)} \right]} \right]{\kern 1pt} d\xi - \\ - \;\int\limits_\Omega \left[ {\frac{{\partial v}}{{\partial \tau }}(\xi ,t)\left[ {\Delta u(\xi ,t) - u(\xi ,t)} \right] - \frac{{\partial v}}{{\partial \tau }}(\xi ,0)\left[ {\Delta u(\xi ,0) - u(\xi ,0)} \right]} \right]{\kern 1pt} d\xi + \\ \end{gathered} $
$ + \;\int\limits_{\partial \Omega } \left[ {\frac{{\partial v}}{{\partial \tau }}(\xi ,t)\frac{{\partial u}}{{\partial {{n}_{\xi }}}}(\xi ,t) - \frac{{\partial v}}{{\partial \tau }}(\xi ,0)\frac{{\partial u}}{{\partial {{n}_{\xi }}}}(\xi ,0)} \right]{\kern 1pt} d{{S}_{\xi }} - \int\limits_{\partial \Omega } \left[ {v(\xi ,t)\frac{{{{\partial }^{2}}u}}{{\partial \tau \partial {{n}_{\xi }}}}(\xi ,t) - v(\xi ,0)\frac{{{{\partial }^{2}}u}}{{\partial \tau \partial {{n}_{\xi }}}}(\xi ,0)} \right]{\kern 1pt} d{{S}_{\xi }}.$
Отметим, что в силу (5.9) имеем
(8.14)
$\begin{gathered} \int\limits_\Omega \left[ {v(\xi ,t)\left[ {\Delta \frac{{\partial u}}{{\partial \tau }}(\xi ,t) - \frac{{\partial u}}{{\partial \tau }}(\xi ,t)} \right] - v(\xi ,0)\left[ {\Delta \frac{{\partial u}}{{\partial \tau }}(\xi ,0) - \frac{{\partial u}}{{\partial \tau }}(\xi ,0)} \right]} \right]{\kern 1pt} d\xi = \\ \, = - \int\limits_\Omega \,\mathcal{E}(x - \xi ,t)\left[ {{{\Delta }_{\xi }}{{u}_{1}}(\xi ) - {{u}_{1}}(\xi )} \right]{\kern 1pt} d\xi , \\ \end{gathered} $
$\begin{gathered} - \int\limits_\Omega \left[ {\frac{{\partial v}}{{\partial \tau }}(\xi ,t)\left[ {\Delta u(\xi ,t) - u(\xi ,t)} \right] - \frac{{\partial v}}{{\partial \tau }}(\xi ,0)\left[ {\Delta u(\xi ,0) - u(\xi ,0)} \right]} \right]{\kern 1pt} d\xi = \\ = - \int\limits_\Omega \frac{{\exp ( - {\text{|}}x - \xi {\kern 1pt} {\text{|}})}}{{4\pi {\text{|}}x - \xi {\kern 1pt} {\text{|}}}}\left[ {{{\Delta }_{\xi }}u(\xi ,t) - u(\xi ,t)} \right]{\kern 1pt} d\xi - \int\limits_\Omega \frac{{\partial{ \mathcal{E}}(x - \xi ,t)}}{{\partial t}}\left[ {{{\Delta }_{\xi }}{{u}_{0}}(\xi ) - {{u}_{0}}(\xi )} \right]{\kern 1pt} d\xi , \\ \end{gathered} $
$\int\limits_{\partial \Omega } \left[ {\frac{{\partial v}}{{\partial \tau }}(\xi ,t)\frac{{\partial u}}{{\partial {{n}_{\xi }}}}(\xi ,t) - \frac{{\partial v}}{{\partial \tau }}(\xi ,0)\frac{{\partial u}}{{\partial {{n}_{\xi }}}}(\xi ,0)} \right]{\kern 1pt} d{{S}_{\xi }} = \int\limits_{\partial \Omega } \frac{{\exp ( - {\text{|}}x - \xi {\kern 1pt} {\text{|}})}}{{4\pi {\text{|}}x - \xi {\kern 1pt} {\text{|}}}}\frac{{\partial u(\xi ,t)}}{{\partial {{n}_{\xi }}}}{\kern 1pt} d{{S}_{\xi }} + \int\limits_{\partial \Omega } \frac{{\partial{ \mathcal{E}}(x - \xi ,t)}}{{\partial t}}\frac{{\partial {{u}_{0}}(\xi )}}{{\partial {{n}_{\xi }}}}{\kern 1pt} d{{S}_{\xi }},$
(8.15)
$ - \int\limits_{\partial \Omega } \left[ {v(\xi ,t)\frac{{{{\partial }^{2}}u}}{{\partial \tau \partial {{n}_{\xi }}}}(\xi ,t) - v(\xi ,0)\frac{{{{\partial }^{2}}u}}{{\partial \tau \partial {{n}_{\xi }}}}(\xi ,0)} \right]{\kern 1pt} d{{S}_{\xi }} = \int\limits_{\partial \Omega } \mathcal{E}(x - \xi ,t)\frac{{\partial {{u}_{1}}(\xi )}}{{\partial {{n}_{\xi }}}}{\kern 1pt} d{{S}_{\xi }}.$(8.16)
$u(x,t)\, = \, - {\kern 1pt} \int\limits_\Omega \,(\Delta u(\xi ,t) - u(\xi ,t))\frac{{\exp ( - {\text{|}}x - \xi {\text{|}}{\kern 1pt} )}}{{4\pi {\text{|}}x - \xi {\text{|}}}}{\kern 1pt} d\xi \, + \,\int\limits_{\partial \Omega } \left[ {\frac{{\exp ( - {\text{|}}x - \xi {\kern 1pt} {\text{|}})}}{{4\pi {\text{|}}x - \xi {\kern 1pt} {\text{|}}}}\frac{{\partial u(\xi ,t)}}{{\partial {{n}_{\xi }}}} - u(\xi ,t)\frac{\partial }{{\partial {{n}_{\xi }}}}\frac{{\exp ( - {\text{|}}x - \xi {\kern 1pt} {\text{|}}{\kern 1pt} )}}{{4\pi {\text{|}}x - \xi {\kern 1pt} {\text{|}}}}} \right]{\kern 1pt} d{{S}_{\xi }}$
$\begin{gathered} u(x,t) = \int\limits_0^t {\kern 1pt} \int\limits_\Omega \,\mathcal{E}(x - \xi ,t - \tau ){{\mathfrak{M}}_{{\xi ,\tau }}}[u](\xi ,\tau ){\kern 1pt} d\xi {\kern 1pt} d\tau + \\ + \;\int\limits_0^t {\kern 1pt} \int\limits_{\partial \Omega } \left[ {u(\xi ,\tau ){{\mathfrak{N}}_{{\xi ,\tau }}}[\mathcal{E}](x - \xi ,t - \tau ) - \mathcal{E}(x - \xi ,t - \tau ){{\mathfrak{N}}_{{\xi ,\tau }}}[u](\xi ,\tau )} \right]{\kern 1pt} d{{S}_{\xi }}{\kern 1pt} d\tau - \\ \end{gathered} $
(8.17)
$ - \;\int\limits_{\partial \Omega } u(\xi ,t)\frac{\partial }{{\partial {{n}_{\xi }}}}\frac{{\exp ( - {\text{|}}x - \xi {\text{|}})}}{{4\pi {\text{|}}x - \xi {\text{|}}}}{\kern 1pt} d{{S}_{\xi }} + $
$\begin{gathered} + \;\int\limits_\Omega \left[ {\mathcal{E}(x - \xi ,t)[{{\Delta }_{\xi }}{{u}_{1}}(\xi ) - {{u}_{1}}(\xi )] + \frac{{\partial{ \mathcal{E}}(x - \xi ,t)}}{{\partial t}}[{{\Delta }_{\xi }}{{u}_{0}}(\xi ) - {{u}_{0}}(\xi )]} \right]{\kern 1pt} d\xi - \\ \, - \int\limits_{\partial \Omega } \left[ {\mathcal{E}(x - \xi ,t)\frac{{\partial {{u}_{1}}(\xi )}}{{\partial {{n}_{\xi }}}} + \frac{{\partial{ \mathcal{E}}(x - \xi ,t)}}{{\partial t}}\frac{{\partial {{u}_{0}}(\xi )}}{{\partial {{n}_{\xi }}}}} \right]{\kern 1pt} d{{S}_{\xi }}. \\ \end{gathered} $
Таким образом, доказана
Теорема 2. Для любой функции $u(x,t) \in {{\mathbb{C}}^{{(2 + 2)}}}(\bar {\Omega } \times [0,T])$ справедливо равенство (8.17), в котором использованы обозначения ${{u}_{0}}(x) = u(x,0)$ и ${{u}_{1}}(x) = u{\kern 1pt} '(x,0)$.
9. ТРЕТЬИ ФОРМУЛЫ ГРИНА ВО ВСЕМ ПРОСТРАНСТВЕ
Справедлива следующая
Теорема 3. Для любой функции $u(x,t) \in \mathbb{C}_{b}^{{(2 + 2)}}({{\mathbb{R}}^{3}} \times [0,T])$ справедливо следующее равенство:
(9.1)
$\begin{gathered} u(x,t) = \int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \mathcal{E}(x - \xi ,t - \tau ){{\mathfrak{M}}_{{\xi ,\tau }}}[u](\xi ,\tau ){\kern 1pt} d\xi {\kern 1pt} d\tau + \\ + \;\int\limits_{{{\mathbb{R}}^{3}}} \left[ {\mathcal{E}(x - \xi ,t)[{{\Delta }_{\xi }}{{u}_{1}}(\xi ) - {{u}_{1}}(\xi )] + \frac{{\partial{ \mathcal{E}}(x - \xi ,t)}}{{\partial t}}[{{\Delta }_{\xi }}{{u}_{0}}(\xi ) - {{u}_{0}}(\xi )]} \right]{\kern 1pt} d\xi . \\ \end{gathered} $Доказательство. Доказательство основано на оценках (6.6) и (6.7) фундаментального решения $\mathcal{E}(x,t)$ и третьей формуле Грина (8.17), в которой нужно положить $\Omega = O(0,R)$ при $R > 0$ и перейти к пределу при $R \to + \infty $. Тогда все интегралы по поверхности шара $\partial O(0,R)$ в пределе при $R \to + \infty $ обратятся в ноль.
Отметим, что можно получить один нестандартный вариант третьей формулы Грина для рассматриваемого оператора ${{\mathfrak{M}}_{{x,t}}}$. С этой целью введем в рассмотрение две функции $\chi (t),\;\eta (t) \in {{\mathbb{C}}^{{(2)}}}[0,T],$ которые удовлетворяют условиям
(9.2)
$\chi (0) = 1,\quad \chi {\kern 1pt} '(0) = 0,\quad \eta (0) = 0,\quad \eta {\kern 1pt} {\kern 1pt} '{\kern 1pt} (0) = 1.$
$F(x,t): = \chi (t){{u}_{0}}(x) + \eta (t){{u}_{1}}(x) \in \mathbb{C}_{b}^{{(2 + 2)}}({{\mathbb{R}}^{3}} \times [0,T])$
при условии, что ${{u}_{0}}(x),\;{{u}_{1}}(x) \in \mathbb{C}_{b}^{{(2)}}({{\mathbb{R}}^{3}})$. Кроме того, эта функция удовлетворяет следующим равенствам:
(9.3)
$F(x,0) = {{u}_{0}}(x),\quad F{\kern 1pt} '(x,0) = {{u}_{1}}(x)\quad {\text{для каждого}}\quad x \in {{\mathbb{R}}^{3}}.$
$u(x,t) - F(x,t)\quad {\text{для любой функции}}\quad u(x,t) \in \mathbb{C}_{b}^{{(2 + 2)}}({{\mathbb{R}}^{3}} \times [0,T]).$
Заметим, что в силу (9.3) имеем
(9.4)
$u(x,0) - F(x,0) = 0,\quad u{\kern 1pt} '(x,0) - F{\kern 1pt} '(x,0) = 0\quad {\text{для всех}}\quad x \in {{\mathbb{R}}^{3}}.$(9.5)
$\begin{gathered} u(x,t) = \chi (t){{u}_{0}}(x) + \eta (t){{u}_{1}}(x) + \int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \mathcal{E}(x - \xi ,t - \tau ){{\mathfrak{M}}_{{\xi ,\tau }}}[u](\xi ,\tau ){\kern 1pt} d\xi {\kern 1pt} d\tau + \\ + \;\int\limits_0^t {\kern 1pt} \int\limits_{{{\mathbb{R}}^{3}}} \mathcal{E}(x - \xi ,t - \tau )(\chi {\kern 1pt} '{\kern 1pt} '(t)[{{\Delta }_{\xi }}{{u}_{0}}(\xi ) - {{u}_{0}}(\xi )] + \eta {\kern 1pt} '{\kern 1pt} '(t)[{{\Delta }_{\xi }}{{u}_{1}}(\xi ) - {{u}_{1}}(\xi )] + \\ \, + \sum\limits_{j = 1}^3 \,\omega _{j}^{2}[\chi (t){{u}_{{0{{\xi }_{j}}{{\xi }_{j}}}}}(\xi ) + \eta (t){{u}_{{1{{\xi }_{j}}{{\xi }_{j}}}}}(\xi )]){\kern 1pt} d\xi {\kern 1pt} d\tau . \\ \end{gathered} $Теорема 4. Для любой функции $u(x,t) \in \mathbb{C}_{b}^{{(2 + 2)}}({{\mathbb{R}}^{3}} \times [0,T])$ и для любых функций $\chi (t)$ и $\eta (t)$ из ${{\mathbb{C}}^{{(2)}}}[0,T],$ удовлетворяющих условиям (9.2), справедливо равенство (9.5).
10. О НЕКОТОРЫХ ИНТЕГРАЛАХ
Рассмотрим следующий интеграл:
(10.1)
$g(t) = \int\limits_0^t {\kern 1pt} \int\limits_{\partial O(0,\delta )} \left[ {\frac{{{{\partial }^{2}}}}{{\partial {{\tau }^{2}}}}\frac{{\partial{ \mathcal{E}}(x,\tau )}}{{\partial {{n}_{x}}}} + \sum\limits_{j = 1}^3 \,\omega _{j}^{2}\frac{{\partial{ \mathcal{E}}(x,\tau )}}{{\partial {{x}_{j}}}}\cos ({{n}_{x}},{{e}_{j}})} \right]{\kern 1pt} d{{S}_{x}}{\kern 1pt} d\tau ,$
(10.2)
${\text{|}}z{\text{|}}: = \sqrt {x_{1}^{2}({{p}^{2}} + \omega _{2}^{2})({{p}^{2}} + \omega _{3}^{2}) + x_{2}^{2}({{p}^{2}} + \omega _{3}^{2})({{p}^{2}} + \omega _{1}^{2}) + x_{3}^{2}({{p}^{2}} + \omega _{1}^{2})({{p}^{2}} + \omega _{2}^{2})} ,$
$\alpha (p) = \frac{p}{{\sqrt {({{p}^{2}} + \omega _{1}^{2})({{p}^{2}} + \omega _{2}^{2})({{p}^{2}} + \omega _{3}^{2})} }}.$
Применим преобразование Лапласа к обеим частям равенства (10.1) и получим выражение
С учетом явного вида (10.2) мы можем переписать равенство (10.3) в виде следующей
суммы:
${{I}_{1}} = - \frac{1}{p}\int\limits_{\partial O(0,\delta )} \frac{1}{{4\pi {\text{|}}z{\kern 1pt} {\text{|}}}}\sum\limits_{j = 1}^3 \,({{p}^{2}} + \omega _{j}^{2})\frac{\partial }{{\partial {{x}_{j}}}}\left( {{{e}^{{( - \alpha (p)|z|)}}}} \right)\cos ({{n}_{x}},{{e}_{j}}){\kern 1pt} d{{S}_{x}},$
${{I}_{2}} = - \frac{1}{p}\int\limits_{\partial O(0,\delta )} \left[ {{{e}^{{ - \alpha (p)|z|}}} - 1} \right]\sum\limits_{j = 1}^3 \,({{p}^{2}} + \omega _{j}^{2})\frac{\partial }{{\partial {{x}_{j}}}}\left( {\frac{1}{{4\pi {\text{|}}z{\kern 1pt} {\text{|}}}}} \right)\cos ({{n}_{x}},{{e}_{j}}){\kern 1pt} d{{S}_{x}},$
${{I}_{3}} = - \frac{1}{p}\int\limits_{\partial O(0,\delta )} \sum\limits_{j = 1}^3 \,({{p}^{2}} + \omega _{j}^{2})\frac{\partial }{{\partial {{x}_{j}}}}\left( {\frac{1}{{4\pi {\text{|}}z{\kern 1pt} {\text{|}}}}} \right)\cos ({{n}_{x}},{{e}_{j}}){\kern 1pt} d{{S}_{x}},$
${{N}_{1}} = \frac{1}{p}\int\limits_{O(0,\delta )} \left[ {{{e}^{{ - |x|}}} - 1} \right]\frac{\partial }{{\partial {{n}_{x}}}}\left( {\frac{1}{{4\pi {\text{|}}{\kern 1pt} x{\text{|}}}}} \right){\kern 1pt} d{{S}_{x}},$
${{N}_{2}} = \frac{1}{p}\int\limits_{O(0,\delta )} \frac{1}{{4\pi {\text{|}}x{\text{|}}}}\frac{\partial }{{\partial {{n}_{x}}}}({{e}^{{ - |x|}}}){\kern 1pt} d{{S}_{x}}.$
${{N}_{3}} = \frac{1}{p}\int\limits_{O(0,\delta )} \frac{\partial }{{\partial {{n}_{x}}}}\left( {\frac{1}{{4\pi {\text{|}}x{\text{|}}}}} \right){\kern 1pt} d{{S}_{x}}.$
С учетом результата леммы 5.1 в работе [30] имеем
Рассмотрим интеграл ${{I}_{1}}$. Справедлива следующая цепочка равенств:
$\sum\limits_{j = 1}^3 \,({{p}^{2}} + \omega _{j}^{2})\frac{\partial }{{\partial {{x}_{j}}}}\left( {\exp ( - \alpha (p){\text{|}}z{\kern 1pt} {\text{|}}{\kern 1pt} )} \right)\cos ({{n}_{x}},{{e}_{j}}) = - {{p}^{2}}\frac{{\exp ( - \alpha (p){\text{|}}z{\kern 1pt} {\kern 1pt} {\text{|}})}}{{\alpha (p){\text{|}}z{\kern 1pt} {\text{|}}}}\sum\limits_{j = 1}^3 \,{{x}_{j}}\cos ({{n}_{x}},{{e}_{j}}) - {{p}^{2}}{\text{|}}x{\kern 1pt} {\text{|}}\frac{{\exp ( - \alpha (p){\text{|}}z{\kern 1pt} {\text{|}})}}{{\alpha (p){\text{|}}z{\kern 1pt} {\text{|}}}}.$
Таким образом, для интеграла ${{I}_{1}}$ имеем следующее выражение:
${{I}_{1}} = \delta \frac{1}{p}\int\limits_{\partial O(0,\delta )} \left( {\frac{{{{p}^{2}}}}{{\alpha (p){\text{|}}z{\kern 1pt} {\text{|}}}}} \right)\left( { - \frac{{\exp ( - \alpha (p){\text{|}}z{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{4\pi {\text{|}}z{\kern 1pt} {\text{|}}}}} \right){\kern 1pt} d{{S}_{x}}.$
Причем справедливы следующие равенства:
${{\bar {\psi }}_{1}}(x,p): = \frac{{{{p}^{2}}}}{{\alpha (p){\text{|}}z{\kern 1pt} {\text{|}}}}\frac{{p\sqrt {({{p}^{2}} + \omega _{1}^{2})({{p}^{2}} + \omega _{2}^{2})({{p}^{2}} + \omega _{3}^{2})} }}{{\sqrt {{{p}^{4}}{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}} + {{\beta }_{1}}(x){{p}^{2}}{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}} + {{\beta }_{2}}(x){\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}} }} = $
(10.5)
$ = \frac{1}{{{\text{|}}x{\kern 1pt} {\text{|}}}}\sqrt {1 + \frac{{\omega _{1}^{2}}}{{{{p}^{2}}}}} {\kern 1pt} \sqrt {1 + \frac{{\omega _{2}^{2}}}{{{{p}^{2}}}}} {\kern 1pt} \sqrt {1 + \frac{{\omega _{3}^{2}}}{{{{p}^{2}}}}} {{\left( {1 + \frac{{{{\beta }_{1}}(x)}}{{{{p}^{2}}}} + \frac{{{{\beta }_{2}}(x)}}{{{{p}^{4}}}}} \right)}^{{ - 1/2}}} = $
$ = \frac{1}{{{\text{|}}x{\kern 1pt} {\text{|}}}}\sum\limits_{{{k}_{1}} = 0}^{ + \infty } \left( {\begin{array}{*{20}{c}} {1{\text{/}}2} \\ {{{k}_{1}}} \end{array}} \right)\frac{{\omega _{1}^{{2{{k}_{1}}}}}}{{{{p}^{{2{{k}_{1}}}}}}}\sum\limits_{{{k}_{2}} = 0}^{ + \infty } \left( {\begin{array}{*{20}{c}} {1{\text{/}}2} \\ {{{k}_{2}}} \end{array}} \right)\frac{{\omega _{2}^{{2{{k}_{2}}}}}}{{{{p}^{{2{{k}_{2}}}}}}}\sum\limits_{{{k}_{3}} = 0}^{ + \infty } \left( {\begin{array}{*{20}{c}} {1{\text{/}}2} \\ {{{k}_{3}}} \end{array}} \right)\frac{{\omega _{3}^{{2{{k}_{3}}}}}}{{{{p}^{{2{{k}_{3}}}}}}}\sum\limits_{k = 0}^{ + \infty } \left( {\begin{array}{*{20}{c}} { - 1{\text{/}}2} \\ k \end{array}} \right){{\left[ {{{\beta }_{1}}(x) + \frac{{{{\beta }_{2}}(x)}}{{{{p}^{2}}}}} \right]}^{k}}\frac{1}{{{{p}^{{2k}}}}},$
где
${{\beta }_{1}}(x): = \frac{{(\omega _{2}^{2} + \omega _{3}^{2})x_{1}^{2} + (\omega _{1}^{2} + \omega _{3}^{2})x_{2}^{2} + (\omega _{1}^{2} + \omega _{2}^{2})x_{3}^{2}}}{{{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}}},$
${{\beta }_{2}}(x): = \frac{{\omega _{2}^{2}\omega _{3}^{2}x_{1}^{2} + \omega _{1}^{2}\omega _{3}^{2}x_{2}^{2} + \omega _{1}^{2}\omega _{2}^{2}x_{3}^{2}}}{{{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}}}.$
Воспользовавшись обратным преобразованием Лапласа, мы из выражения (10.5) получим
равенство
(10.6)
$\begin{gathered} {{\psi }_{1}}(x,t) = \frac{1}{{{\text{|}}x{\kern 1pt} {\text{|}}}}\sum\limits_{{{k}_{1}} = 0}^{ + \infty } \left( {\begin{array}{*{20}{c}} {1{\text{/}}2} \\ {{{k}_{1}}} \end{array}} \right)\frac{{\omega _{1}^{{2{{k}_{1}}}}{{t}^{{2{{k}_{1}}}}}}}{{(2{{k}_{1}})!}}\sum\limits_{{{k}_{2}} = 0}^{ + \infty } \left( {\begin{array}{*{20}{c}} {1{\text{/}}2} \\ {{{k}_{2}}} \end{array}} \right)\frac{{\omega _{2}^{{2{{k}_{2}}}}{{t}^{{2{{k}_{2}}}}}}}{{(2{{k}_{2}})!}}\sum\limits_{{{k}_{3}} = 0}^{ + \infty } \left( {\begin{array}{*{20}{c}} {1{\text{/}}2} \\ {{{k}_{3}}} \end{array}} \right)\frac{{\omega _{3}^{{2{{k}_{3}}}}{{t}^{{2{{k}_{3}}}}}}}{{(2{{k}_{3}})!}} \times \\ \times \;\sum\limits_{k = 0}^{ + \infty } \left( {\begin{array}{*{20}{c}} { - 1{\text{/}}2} \\ k \end{array}} \right){{\left[ {{{\beta }_{1}}(x){\kern 1pt} {\text{id}} + {{\beta }_{2}}(x)\frac{{{{t}^{2}}}}{2}} \right]}^{k}} * \frac{{{{t}^{{2k}}}}}{{(2k)!}}. \\ \end{gathered} $(10.7)
${{\widehat I}_{1}}(t) = \delta {\kern 1pt} \int\limits_0^t {\kern 1pt} \int\limits_{\partial O(0,\delta )} {{\psi }_{1}}(x,\tau ) * \mathcal{E}(x,\tau ){\kern 1pt} d{{S}_{x}}{\kern 1pt} d\tau .$
$\left| {\int\limits_0^t {\kern 1pt} \int\limits_{\partial O(0,\delta )} {{\psi }_{1}}(x,\tau ) * \mathcal{E}(x,\tau ){\kern 1pt} d{{S}_{x}}{\kern 1pt} d\tau } \right|\;\leqslant \;A(T) < + \infty ,$
где постоянная $A(T) > 0$ и не зависит от $\delta \in (0,1].$ Поэтому из (10.7) приходим к выводу, что равномерно по $t \in [0,T]$ справедливо предельное равенство
Теперь рассмотрим интеграл ${{I}_{2}}.$ Прежде всего заметим, что справедливо следующее равенство:
(10.9)
$\frac{\partial }{{\partial {{x}_{j}}}}\left( {\frac{1}{{{\text{|}}z{\kern 1pt} {\text{|}}}}} \right) - \frac{1}{{\sqrt {({{p}^{2}} + \omega _{1}^{2})({{p}^{2}} + \omega _{2}^{2})({{p}^{2}} + \omega _{3}^{2})} }}\frac{1}{{{{{\left( {\frac{{x_{1}^{2}}}{{{{p}^{2}} + \omega _{1}^{2}}} + \frac{{x_{2}^{2}}}{{{{p}^{2}} + \omega _{2}^{2}}} + \frac{{x_{3}^{2}}}{{{{p}^{2}} + \omega _{3}^{2}}}} \right)}}^{{3/2}}}}}\frac{{{{x}_{j}}}}{{{{p}^{2}} + \omega _{j}^{2}}}.$
$\sum\limits_{j = 1}^3 \,({{p}^{2}} + \omega _{j}^{2})\frac{\partial }{{\partial {{x}_{j}}}}\left( {\frac{1}{{{\text{|}}z{\kern 1pt} {\text{|}}}}} \right)\cos ({{n}_{x}},{{e}_{j}}) = - \frac{{{\text{|}}x{\kern 1pt} {\text{|}}}}{{{\text{|}}z{\kern 1pt} {{{\text{|}}}^{3}}}}({{p}^{2}} + \omega _{1}^{2})({{p}^{2}} + \omega _{2}^{2})({{p}^{2}} + \omega _{3}^{2}).$
Тогда для интеграла ${{I}_{2}}$ справедливо следующее равенство:
(10.10)
${{I}_{2}} = \delta \frac{1}{p}({{p}^{2}} + \omega _{1}^{2})({{p}^{2}} + \omega _{2}^{2})({{p}^{2}} + \omega _{3}^{2})\int\limits_{\partial O(0,\delta )} \left[ {\exp ( - \alpha (p){\text{|}}z{\kern 1pt} {\text{|}}{\kern 1pt} ) - 1} \right]\frac{1}{{4\pi {\text{|}}z{\kern 1pt} {{{\text{|}}}^{3}}}}{\kern 1pt} d{{S}_{x}}.$(10.11)
$\exp ( - \alpha (p){\text{|}}z{\kern 1pt} {\text{|}}{\kern 1pt} ) - 1 = \int\limits_0^1 \frac{{\partial \exp ( - s\alpha (p){\text{|}}z{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{\partial s}}{\kern 1pt} ds = - \alpha (p){\text{|}}z{\kern 1pt} {\text{|}}{\kern 1pt} \int\limits_0^1 \exp ( - s\alpha (p){\text{|}}z{\kern 1pt} {\text{|}}{\kern 1pt} ){\kern 1pt} ds.$(10.12)
${{I}_{2}} = \delta \sqrt {({{p}^{2}} + \omega _{1}^{2})({{p}^{2}} + \omega _{2}^{2})({{p}^{2}} + \omega _{3}^{2})} \int\limits_0^1 {\kern 1pt} \int\limits_{\partial O(0,\delta )} \left( { - \frac{{\exp ( - s\alpha (p){\text{|}}z{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{4\pi {\text{|}}z{\kern 1pt} {\text{|}}}}} \right)\left( {\frac{1}{{{\text{|}}z{\kern 1pt} {\text{|}}}}} \right){\kern 1pt} d{{S}_{x}}{\kern 1pt} ds.$(10.13)
${{I}_{2}} = \delta \frac{1}{p}\int\limits_0^1 {\kern 1pt} \int\limits_{\partial O(0,\delta )} \left( { - \frac{{\exp ( - s\alpha (p){\text{|}}z{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{4\pi {\text{|}}z{\kern 1pt} {\text{|}}}}} \right){{\bar {\psi }}_{1}}(x,p){\kern 1pt} d{{S}_{x}}{\kern 1pt} ds.$(10.14)
${{\widehat I}_{2}} = \delta \int\limits_0^t {\kern 1pt} \int\limits_0^1 {\kern 1pt} \int\limits_{\partial O(0,\delta )} s\mathcal{E}(sx,\tau ) * {{\psi }_{1}}(x,\tau ){\kern 1pt} d{{S}_{x}}{\kern 1pt} ds{\kern 1pt} d\tau .$(10.15)
${\kern 1pt} \left| {\int\limits_0^t {\kern 1pt} \int\limits_0^1 \int\limits_{\partial O(0,\delta )} s\mathcal{E}(sx,\tau ) * {{\psi }_{1}}(x,\tau ){\kern 1pt} d{{S}_{x}}{\kern 1pt} ds{\kern 1pt} d\tau } \right|\;\leqslant \;B(T) < + \infty ,$(10.17)
${{\widehat N}_{1}}(t) = \theta (t)\int\limits_{O(0,\delta )} \left[ {{{e}^{{ - |x|}}} - 1} \right]\frac{\partial }{{\partial {{n}_{x}}}}\left( {\frac{1}{{4\pi {\text{|}}x{\kern 1pt} {\text{|}}{\kern 1pt} }}} \right){\kern 1pt} d{{S}_{x}} \to 0\quad {\text{при}}\quad \delta \to + 0,$(10.18)
${{\widehat N}_{2}}(t) = \theta (t)\int\limits_{O(0,\delta )} \frac{1}{{4\pi {\text{|}}x{\kern 1pt} {\text{|}}}}\frac{\partial }{{\partial {{n}_{x}}}}({{e}^{{ - |x|}}}){\kern 1pt} d{{S}_{x}} \to 0\quad {\text{при}}\quad \delta \to + 0$Справедлива
Теорема 5. Для любых $\beta \; \geqslant \;0$ и $\gamma > 0$ справедлива следующая оценка интеграла:
(10.20)
$I = \int\limits_{{{\mathbb{R}}^{3}}} \frac{{\exp ( - \gamma {\text{|}}x - y{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{{\text{|}}x - y{\kern 1pt} {\text{|}}}}\frac{1}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{\beta /2}}}}}{\kern 1pt} dy\;\leqslant \;\frac{A}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{\beta /2}}}}},$Доказательство. Шаг 1. Случай $\beta \in [0,2)$.
Сначала предположим, что ${\text{|}}x{\text{|}}\; \geqslant \;1$. Переходя к сферической системе координат, интеграл (10.20) можно привести к следующему виду:
(10.21)
$I = 2\pi \int\limits_0^{ + \infty } {\kern 1pt} \int\limits_0^\pi \,\rho \exp ( - \gamma \rho )\frac{{\sin \theta }}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}} + {{\rho }^{2}} - 2{\text{|}}x{\kern 1pt} {\text{|}}\rho \cos \theta )}}^{{\beta /2}}}}}{\kern 1pt} d\theta {\kern 1pt} d\rho .$(10.22)
$J = 2\pi \int\limits_0^\pi \frac{{\sin \theta }}{{{{{(1 + \;{\text{|}}{\kern 1pt} x{{{\text{|}}}^{2}} + {{\rho }^{2}} - 2{\text{|}}x{\kern 1pt} {\text{|}}\rho \cos \theta )}}^{{\beta /2}}}}}{\kern 1pt} d\theta = \frac{{2\pi }}{b}\int\limits_{a - b}^{a + b} \frac{{ds}}{{{{s}^{{\beta /2}}}}} = \frac{{2\pi }}{{1 - \beta {\text{/}}2}}\frac{1}{b}\left[ {{{{(a + b)}}^{{1 - \beta /2}}} - {{{(a - b)}}^{{1 - \beta /2}}}} \right],$
$a = 1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}} + {{\rho }^{2}},\quad b = 2{\text{|}}x{\kern 1pt} {\text{|}}\rho .$
Из выражений (10.21) и (10.22) приходим к следующей цепочке равенств:
(10.23)
$\begin{gathered} I = \frac{\pi }{{1 - \beta {\text{/}}2}}\frac{1}{{{\text{|}}x{\kern 1pt} {\text{|}}}}\int\limits_0^{ + \infty } \exp ( - \gamma \rho )\left[ {{{{(a + b)}}^{{1 - \beta /2}}} - {{{(a - b)}}^{{1 - \beta /2}}}} \right]{\kern 1pt} d\rho = \\ = \frac{\pi }{{1 - \beta {\text{/}}2}}\frac{1}{{{\text{|}}x{\kern 1pt} {\text{|}}}}\int\limits_0^{ + \infty } \exp ( - \gamma \rho ){{a}^{{1 - \beta /2}}}\left[ {{{{\left( {1 + \frac{b}{a}} \right)}}^{{1 - \beta /2}}} - {{{\left( {1 - \frac{b}{a}} \right)}}^{{1 - \beta /2}}}} \right]{\kern 1pt} d\rho . \\ \end{gathered} $
$t = \frac{b}{a} = \frac{{2{\text{|}}x{\kern 1pt} {\text{|}}\rho }}{{1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}} + {{\rho }^{2}}}} \Rightarrow t \in [0,1).$
Действительно, всегда $t \ne 1$, поскольку в противном случае справедлива следующая цепочка равенств:
$1 = t = \frac{{2{\text{|}}x{\kern 1pt} {\text{|}}\rho }}{{1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}} + {{\rho }^{2}}}} \Rightarrow 1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}} + {{\rho }^{2}} - 2{\text{|}}x{\kern 1pt} {\text{|}}\rho = 0 \Rightarrow 1 + {{({\text{|}}x{\kern 1pt} {\text{|}} - \rho )}^{2}} = 0.$
Получаем противоречие.
Рассмотрим следующие две функции:
Воспользуемся разложением в ряд Тейлора в окрестности точки $t = 0$ с остаточным слагаемым в форме Лагранжа. Действительно, имеют место следующие равенства:(10.24)
${{f}_{1}}(t) = (1 + t{{)}^{{1 - \beta /2}}} = 1 + \frac{{1 - \beta {\text{/}}2}}{{{{{(1 + {{\varepsilon }_{1}})}}^{{\beta /2}}}}}t = 1 + {{c}_{1}}({{\varepsilon }_{1}})t,\quad {{\varepsilon }_{1}} \in (0,1),$(10.25)
${{f}_{2}}(t) = (1 - t{{)}^{{1 - \beta /2}}} = 1 - \frac{{1 - \beta {\text{/}}2}}{{{{{(1 - {{\varepsilon }_{2}})}}^{{\beta /2}}}}}t = 1 + {{c}_{2}}({{\varepsilon }_{2}})t,\quad {{\varepsilon }_{2}} \in (0,1).$(10.26)
$\begin{gathered} I = {{c}_{3}}\frac{\pi }{{1 - \beta {\text{/}}2}}\frac{1}{{{\text{|}}x{\kern 1pt} {\text{|}}}}\int\limits_0^{ + \infty } \exp ( - \gamma \rho )\frac{b}{a}{{a}^{{1 - \beta /2}}}{\kern 1pt} d\rho = \frac{{2\pi {{c}_{3}}}}{{(1 - \beta {\text{/}}2)}}\frac{1}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{\beta /2}}}}}\int\limits_0^{ + \infty } \rho \exp ( - \gamma \rho ){\kern 1pt} d\rho , \\ {{c}_{3}} = {{c}_{1}}({{\varepsilon }_{1}}) + {{c}_{2}}({{\varepsilon }_{2}}). \\ \end{gathered} $(10.27)
$\begin{gathered} I = \int\limits_{{{\mathbb{R}}^{3}}} \frac{{\exp ( - \gamma {\text{|}}x - y{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{{\text{|}}x - y{\kern 1pt} {\text{|}}}}\frac{1}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{\beta /2}}}}}{\kern 1pt} dy\;\leqslant \;\int\limits_{{{\mathbb{R}}^{3}}} \frac{{\exp ( - \gamma {\text{|}}x - y{\kern 1pt} {\text{|}})}}{{{\text{|}}x - y{\kern 1pt} {\text{|}}}}{\kern 1pt} dy = \\ = \int\limits_{{{\mathbb{R}}^{3}}} \frac{{\exp ( - \gamma {\text{|}}z{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{{\text{|}}z{\kern 1pt} {\text{|}}}}{\kern 1pt} dz\;\leqslant \;2{{\pi }^{2}}\int\limits_0^{ + \infty } \exp ( - \gamma \rho )\rho {\kern 1pt} d\rho . \\ \end{gathered} $Шаг 2. Случай $\beta > 2.$ Пусть сначала ${\text{|}}x{\kern 1pt} {\text{|}}\; \geqslant \;1.$ Воспользуемся равенством (10.23), которое справедливо и в данном случае. Тогда справедливы равенства:
$\begin{gathered} I = \frac{\pi }{{1 - \beta {\text{/}}2}}\frac{1}{{{\text{|}}x{\kern 1pt} {\text{|}}}}\int\limits_0^{ + \infty } \exp ( - \gamma \rho )\left[ {{{{(a + b)}}^{{1 - \beta /2}}} - {{{(a - b)}}^{{1 - \beta /2}}}} \right]{\kern 1pt} d\rho = \\ = \frac{\pi }{{1 - \beta {\text{/}}2}}\frac{1}{{{\text{|}}x{\kern 1pt} {\text{|}}}}\int\limits_0^{ + \infty } \exp ( - \gamma \rho )\left[ {{{{(1 + {{{({\text{|}}x{\kern 1pt} {\text{|}} + \rho )}}^{2}})}}^{{1 - \beta /2}}} - {{{(1 + {{{({\text{|}}x{\kern 1pt} {\text{|}} - \rho )}}^{2}})}}^{{1 - \beta /2}}}} \right]{\kern 1pt} d\rho = {{I}_{1}} + {{I}_{2}} + {{I}_{3}}, \\ \end{gathered} $
(10.28)
${{I}_{1}} = \frac{\pi }{{1 - \beta {\text{/}}2}}\frac{1}{{{\text{|}}x{\kern 1pt} {\text{|}}}}\int\limits_0^{\varepsilon |x|} \exp ( - \gamma \rho )\left[ {{{{(1 + {{{({\text{|}}x{\kern 1pt} {\text{|}} + \rho )}}^{2}})}}^{{1 - \beta /2}}} - {{{(1 + {{{({\text{|}}x{\kern 1pt} {\text{|}} - \rho )}}^{2}})}}^{{1 - \beta /2}}}} \right]{\kern 1pt} d\rho ,$(10.29)
${{I}_{2}} = \frac{\pi }{{1 - \beta {\text{/}}2}}\frac{1}{{{\text{|}}x{\kern 1pt} {\text{|}}}}\int\limits_{\varepsilon |x|}^{|x|/\varepsilon } \exp ( - \gamma \rho )\left[ {{{{(1 + {{{({\text{|}}x{\kern 1pt} {\text{|}} + \rho )}}^{2}})}}^{{1 - \beta /2}}} - {{{(1 + {{{({\text{|}}x{\kern 1pt} {\text{|}} - \rho )}}^{2}})}}^{{1 - \beta /2}}}} \right]{\kern 1pt} d\rho ,$(10.30)
${{I}_{3}} = \frac{\pi }{{1 - \beta {\text{/}}2}}\frac{1}{{{\text{|}}x{\kern 1pt} {\text{|}}}}\int\limits_{|x|/\varepsilon }^{ + \infty } \exp ( - \gamma \rho )\left[ {{{{(1 + {{{({\text{|}}x{\kern 1pt} {\text{|}} + \rho )}}^{2}})}}^{{1 - \beta /2}}} - {{{(1 + {{{({\text{|}}x{\kern 1pt} {\text{|}} - \rho )}}^{2}})}}^{{1 - \beta /2}}}} \right]{\kern 1pt} d\rho ,$
${{f}_{3}}(t) = \frac{1}{{{{{\left( {1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{{\left( {1 + t} \right)}}^{2}}} \right)}}^{{\beta /2 - 1}}}}},\quad {{f}_{4}}(t) = \frac{1}{{{{{\left( {1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{{\left( {1 - t} \right)}}^{2}}} \right)}}^{{\beta /2 - 1}}}}},$
$t = \frac{\rho }{{{\text{|}}x{\kern 1pt} {\text{|}}}} \in [0,\varepsilon ]\quad {\text{при}}\quad \rho \in [0,\varepsilon {\text{|}}x{\kern 1pt} {\text{|}}{\kern 1pt} ].$
При фиксированном ${\text{|}}x{\text{|}}\; \geqslant \;1$ обе функции непрерывно дифференцируемы на отрезке $t \in [0,\varepsilon ]$. Поэтому можно воспользоваться формулой Тейлора с остаточным слагаемым в форме Лагранжа:
(10.31)
${{f}_{3}}(t) = \frac{1}{{{{{\left( {1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{{\left( {1 + t} \right)}}^{2}}} \right)}}^{{\beta /2 - 1}}}}} = \frac{1}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{\beta /2 - 1}}}}} + \left( {1 - \beta {\text{/}}2} \right)\frac{{2(1 + {{\varepsilon }_{3}}){\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}}}{{{{{\left( {1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{{\left( {1 + {{\varepsilon }_{3}}} \right)}}^{2}}} \right)}}^{{\beta /2}}}}}\frac{\rho }{{{\text{|}}x{\kern 1pt} {\text{|}}}},\quad {{\varepsilon }_{3}} \in (0,\varepsilon ),$(10.32)
${{f}_{4}}(t) = \frac{1}{{{{{\left( {1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{{\left( {1 - t} \right)}}^{2}}} \right)}}^{{\beta /2 - 1}}}}} = \frac{1}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{\beta /2 - 1}}}}} + \left( {1 - \beta {\text{/}}2} \right)\frac{{2(1 - {{\varepsilon }_{4}}){\text{|}}x{{{\text{|}}}^{2}}}}{{{{{\left( {1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{{\left( {1 - {{\varepsilon }_{4}}} \right)}}^{2}}} \right)}}^{{\beta /2}}}}}\frac{\rho }{{{\text{|}}x{\kern 1pt} {\text{|}}}},\quad {{\varepsilon }_{4}} \in (0,\varepsilon ).$(10.33)
$\left| {{{f}_{3}}(t) - {{f}_{4}}(t){\kern 1pt} } \right|\;\leqslant \;{{D}_{1}}\left[ {\beta {\text{/}}2 - 1} \right]\frac{{\rho {\text{|}}x{\kern 1pt} {\text{|}}}}{{{{{(4 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{\beta /2}}}}}.$
${\text{|}}{{I}_{1}}{\kern 1pt} {\text{|}}\;\leqslant \;\frac{{{{D}_{2}}}}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{\beta /2}}}}}\int\limits_0^{ + \infty } \rho \exp ( - \gamma \rho ){\kern 1pt} d\rho \frac{{{{D}_{3}}}}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{\beta /2}}}}}.$
Рассмотрим теперь выражение (10.29) для интеграла ${{I}_{2}}$. Справедлива оценка
$\begin{gathered} {\text{|}}{{I}_{2}}{\kern 1pt} {\text{|}}\;\leqslant \;\frac{{2\pi }}{{\beta {\text{/}}2 - 1}}\frac{1}{{{\text{|}}x{\kern 1pt} {\text{|}}}}\int\limits_{\varepsilon |x|}^{|x|/\varepsilon } \exp ( - \gamma \rho ){\kern 1pt} d\rho = \{ \rho = {\text{|}}x{\kern 1pt} {\text{|}}s\} = \\ = \frac{{2\pi }}{{\beta {\text{/}}2 - 1}}\int\limits_\varepsilon ^{1/\varepsilon } \exp ( - s\gamma {\text{|}}x{\kern 1pt} {\text{|}}{\kern 1pt} ){\kern 1pt} ds\;\leqslant \;\frac{{2\pi }}{{\beta {\text{/}}2 - 1}}\exp ( - \gamma {\text{|}}x{\kern 1pt} {\text{|/}}\varepsilon )\frac{{1 - {{\varepsilon }^{2}}}}{\varepsilon }\;\leqslant \;{{D}_{4}}\exp ( - 4\gamma {\text{|}}x{\kern 1pt} {\text{|}}{\kern 1pt} ). \\ \end{gathered} $
Перейдем теперь к рассмотрению интеграла ${{I}_{3}}.$ Для этого введем следующие функции:
${{f}_{5}}(\tau ) = \frac{1}{{{{{\left( {1 + {{\rho }^{2}}{{{(1 + \tau )}}^{2}}} \right)}}^{{\beta /2 - 1}}}}},$
${{f}_{6}}(\tau ) = \frac{1}{{{{{\left( {1 + {{\rho }^{2}}{{{(1 - \tau )}}^{2}}} \right)}}^{{\beta /2 - 1}}}}},$
$\tau = \frac{{{\text{|}}x{\kern 1pt} {\text{|}}}}{\rho },\quad \rho \; \geqslant \;\frac{{{\text{|}}x{\kern 1pt} {\text{|}}}}{\varepsilon } \Rightarrow \tau \in [0,\varepsilon ].$
Разложим функции ${{f}_{5}}(\tau )$ и ${{f}_{6}}(\tau )$ в ряд Тейлора с остаточным слагаемым в форме Лагранжа:
${{f}_{5}}(\tau ) = \frac{1}{{{{{(1 + {{\rho }^{2}})}}^{{\beta /2 - 1}}}}} + \left( {1 - \beta {\text{/}}2} \right)\frac{{2(1 + {{\varepsilon }_{5}}){{\rho }^{2}}}}{{{{{(1 + {{\rho }^{2}}{{{(1 + {{\varepsilon }_{5}})}}^{2}})}}^{{\beta /2}}}}}\frac{{{\text{|}}x{\kern 1pt} {\text{|}}}}{\rho },\quad {{\varepsilon }_{5}} \in (0,\varepsilon ),$
${{f}_{6}}(\tau ) = \frac{1}{{{{{(1 + {{\rho }^{2}})}}^{{\beta /2 - 1}}}}} + \left( {1 - \beta {\text{/}}2} \right)\frac{{2(1 - {{\varepsilon }_{6}}){{\rho }^{2}}}}{{{{{(1 + {{\rho }^{2}}{{{(1 - {{\varepsilon }_{6}})}}^{2}})}}^{{\beta /2}}}}}\frac{{{\text{|}}x{\kern 1pt} {\text{|}}}}{\rho },\quad {{\varepsilon }_{6}} \in (0,\varepsilon ).$
Справедлива оценка
(10.34)
$\left| {{{f}_{5}}(\tau ) - {{f}_{6}}(\tau )} \right|\;\leqslant \;{{D}_{5}}\frac{{\rho {\text{|}}x{\kern 1pt} {\text{|}}}}{{{{{(4 + {{\rho }^{2}})}}^{{\beta /2}}}}}\;\leqslant \;{{D}_{5}}\frac{{\rho {\text{|}}x{\kern 1pt} {\text{|}}}}{{{{{(4 + 4{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{\beta /2}}}}}\quad {\text{при}}\quad \rho \; \geqslant \;{\text{|}}x{\kern 1pt} {\text{|/}}\varepsilon \; \geqslant \;2{\text{|}}x{\kern 1pt} {\text{|}}.$
${\text{|}}{{I}_{3}}{\kern 1pt} {\text{|}}\;\leqslant \;\frac{{{{D}_{6}}}}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{\beta /2}}}}}\int\limits_0^{ + \infty } \,\rho \exp ( - \gamma \rho ){\kern 1pt} d\rho \frac{{{{D}_{7}}}}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{\beta /2}}}}}.$
Случай ${\text{|}}x{\kern 1pt} {\text{|}} < 1$ рассматривается точно так же, как и на шаге 1.
Шаг 3. Случай $\beta = 2.$ Пусть ${\text{|}}x{\kern 1pt} {\text{|}}\; \geqslant \;1.$ В этом случае выражение для интеграла $I$ примет следующий вид:
$I = \frac{\pi }{{{\text{|}}x{\kern 1pt} {\text{|}}}}\int\limits_0^{ + \infty } \exp ( - \gamma \rho )\left[ {{{f}_{6}} - {{f}_{7}}} \right]{\kern 1pt} d\rho ,$
где
${{f}_{6}} = \ln \left( {1 + {{{({\text{|}}x{\kern 1pt} {\text{|}} + \rho )}}^{2}}} \right),\quad {{f}_{7}} = \ln \left( {1 + {{{({\text{|}}x{\kern 1pt} {\text{|}} - \rho )}}^{2}}} \right).$
Теперь представим интеграл $I$ в виде следующей суммы трех интегралов:
(10.35)
$\begin{gathered} {{I}_{4}} = \frac{\pi }{{{\text{|}}x{\kern 1pt} {\text{|}}}}\int\limits_0^{\varepsilon |x|} \exp ( - \gamma \rho )\left[ {{{f}_{6}} - {{f}_{7}}} \right]{\kern 1pt} d\rho , \\ {{I}_{5}} = \frac{\pi }{{{\text{|}}x{\kern 1pt} {\text{|}}}}\int\limits_{\varepsilon |x|}^{|x|/\varepsilon } \exp ( - \gamma \rho )\left[ {{{f}_{6}} - {{f}_{7}}} \right]{\kern 1pt} d\rho , \\ \end{gathered} $
${{I}_{6}} = \frac{\pi }{{{\text{|}}x{\kern 1pt} {\text{|}}}}\int\limits_{|x|/\varepsilon }^{ + \infty } \exp ( - \gamma \rho )\left[ {{{f}_{6}} - {{f}_{7}}} \right]{\kern 1pt} d\rho ,$
где $\varepsilon \in [1{\text{/}}4,1{\text{/}}2]$. Сначала рассмотрим интеграл ${{I}_{4}}$. С этой целью рассмотрим следующие функции:
${{f}_{6}}(t) = \ln (1 + {{({\text{|}}x{\kern 1pt} {\text{|}} + \rho )}^{2}}) = \ln (1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{(1 + t)}^{2}}),$
${{f}_{7}}(t) = \ln (1 + {{({\text{|}}x{\kern 1pt} {\text{|}} - \rho )}^{2}}) = \ln (1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{(t - 1)}^{2}}),\quad t = \frac{\rho }{{{\text{|}}x{\kern 1pt} {\text{|}}}},\quad t \in [0,\varepsilon ],$
при условии, что $\rho \in [0,\varepsilon {\text{|}}x{\text{|}}].$ Тогда справедливы следующие разложения в ряд Тейлора с остаточными слагаемыми в форме
Лагранжа:
(10.36)
${{f}_{6}}(t) = \ln (1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}) + \frac{{2{\text{|}}x{\kern 1pt} {\text{|}}\rho (1 + {{\varepsilon }_{6}})}}{{1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{{(1 + {{\varepsilon }_{6}})}}^{2}}}},\quad {{\varepsilon }_{6}} \in (0,\varepsilon ),$(10.37)
${{f}_{7}}(t) = \ln (1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}) - \frac{{2{\text{|}}x{\kern 1pt} {\text{|}}\rho (1 - {{\varepsilon }_{7}})}}{{1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{{(1 - {{\varepsilon }_{7}})}}^{2}}}},\quad {{\varepsilon }_{7}} \in (0,\varepsilon ).$
$\left| {{{f}_{6}} - {{f}_{7}}} \right|\;\leqslant \;{{D}_{8}}\frac{{{\text{|}}x{\kern 1pt} {\text{|}}\rho }}{{1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}}}.$
Тогда для интеграла ${{I}_{4}}$ мы получаем следующую оценку:
(10.38)
${\text{|}}{{I}_{4}}{\kern 1pt} {\text{|}}\;\leqslant \;\frac{{{{D}_{9}}}}{{1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}}}\int\limits_0^{ + \infty } {\kern 1pt} \rho \exp ( - \gamma \rho ){\kern 1pt} d\rho \frac{{{{D}_{{10}}}}}{{1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}}}.$
$\begin{gathered} {{I}_{5}} = \pi \int\limits_\varepsilon ^{1/\varepsilon } \exp ( - \gamma {\text{|}}x{\kern 1pt} {\text{|}}s)\left[ {\ln (1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{{(1 + s)}}^{2}}) - \ln (1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{{(1 - s)}}^{2}})} \right]{\kern 1pt} ds = \\ = \pi \int\limits_\varepsilon ^{1/\varepsilon } \exp ( - \gamma {\text{|}}x{\kern 1pt} {\text{|}}s)\ln (1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{(1 + s)}^{2}}){\kern 1pt} ds - \pi \int\limits_\varepsilon ^{1/\varepsilon } \exp ( - \gamma {\text{|}}x{\kern 1pt} {\text{|}}s)\ln (1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{(1 - s)}^{2}}){\kern 1pt} ds = {{I}_{{51}}} + {{I}_{{52}}}. \\ \end{gathered} $
Для интеграла ${{I}_{{51}}}$ справедлива следующая оценка:
(10.39)
${\text{|}}{{I}_{{51}}}{\kern 1pt} {\text{|}}\;\leqslant \;\exp ( - \gamma {\text{|}}x{\kern 1pt} {\text{|/}}\varepsilon )\ln \left( {1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{{(1 + 1{\text{/}}\varepsilon )}}^{2}}} \right)\frac{{1 - {{\varepsilon }^{2}}}}{\varepsilon },\quad \varepsilon \in [1{\text{/}}4,1{\text{/}}2].$
${{I}_{{52}}} = - \pi \int\limits_\varepsilon ^1 \exp ( - \gamma {\text{|}}x{\kern 1pt} {\text{|}}s)\ln (1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{(1 - s)}^{2}}){\kern 1pt} ds - \pi \int\limits_1^{1/\varepsilon } \exp ( - \gamma {\text{|}}x{\kern 1pt} {\text{|}}s)\ln (1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{(1 - s)}^{2}}){\kern 1pt} ds = {{I}_{{521}}} + {{I}_{{522}}}.$
Справедливы следующие оценки:
(10.40)
$\begin{gathered} {\text{|}}{{I}_{{521}}}{\kern 1pt} |\;\leqslant \;\pi \exp ( - \gamma {\text{|}}x{\kern 1pt} {\text{|}})(1 - \varepsilon )\left| {\ln \left( {1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{{(1 - \varepsilon )}}^{2}}} \right)} \right|, \\ {\text{|}}{{I}_{{522}}}{\text{|}}\;\leqslant \;\pi \exp ( - \gamma {\text{|}}x{\kern 1pt} {\text{|/}}\varepsilon )(1{\text{/}}\varepsilon - 1)\left| {\ln \left( {1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}{{{(1 - 1{\text{/}}\varepsilon )}}^{2}}} \right)} \right|. \\ \end{gathered} $(10.41)
${\text{|}}{{I}_{5}}{\kern 1pt} {\text{|}}\;\leqslant \;{{D}_{{11}}}\exp ( - 4\gamma {\text{|}}x{\kern 1pt} {\text{|}}{\kern 1pt} )\ln \left( {1 + 25{\kern 1pt} {\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}} \right)\;\leqslant \;\frac{{{{D}_{{12}}}}}{{1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}}},\quad {\text{|}}x{\kern 1pt} {\text{|}}\; \geqslant \;1.$
${{f}_{6}}(\tau ) = \ln \left( {1 + {{\rho }^{2}}{{{(1 + \tau )}}^{2}}} \right),\quad {{f}_{7}}(\tau ) = \ln \left( {1 + {{\rho }^{2}}{{{(1 - \tau )}}^{2}}} \right),\quad \tau = \frac{{{\text{|}}x{\kern 1pt} {\text{|}}}}{\rho },\quad \tau \in [0,\varepsilon ],$
при условии $\rho \; \geqslant \;{\text{|}}x{\text{|/}}\varepsilon $. Справедливы следующие формулы разложения в ряд Тейлора с остаточным слагаемым в
форме Лагранжа:
(10.42)
${{f}_{6}}(\tau ) = \ln (1 + {{\rho }^{2}}) + \frac{{2{\text{|}}x{\kern 1pt} {\text{|}}\rho (1 + {{\varepsilon }_{8}})}}{{1 + {{\rho }^{2}}{{{(1 + {{\varepsilon }_{8}})}}^{2}}}},\quad {{\varepsilon }_{8}} \in (0,\varepsilon ),$(10.43)
${{f}_{7}}(\tau ) = \ln (1 + {{\rho }^{2}}) - \frac{{2{\text{|}}x{\kern 1pt} {\text{|}}\rho (1 - {{\varepsilon }_{9}})}}{{1 + {{\rho }^{2}}{{{(1 - {{\varepsilon }_{9}})}}^{2}}}},\quad {{\varepsilon }_{9}} \in (0,\varepsilon ).$(10.44)
${\text{|}}{{f}_{6}} - {{f}_{7}}{\kern 1pt} {\text{|}}\;\leqslant \;{{D}_{{13}}}\frac{{{\text{|}}x{\kern 1pt} {\text{|}}\rho }}{{1 + {{\rho }^{2}}}}.$(10.45)
${\text{|}}{{I}_{6}}{\kern 1pt} {\text{|}}\;\leqslant \;{{D}_{{14}}}\int\limits_{|x|/\varepsilon }^{ + \infty } \frac{\rho }{{1 + {{\rho }^{2}}}}\exp ( - \gamma \rho ){\kern 1pt} d\rho \;\leqslant \;{{D}_{{15}}}\frac{{{{\varepsilon }^{2}}}}{{{{\varepsilon }^{2}} + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}}}\int\limits_0^{ + \infty } \rho \exp ( - \gamma \rho ){\kern 1pt} d\rho \;\leqslant \;\frac{{{{D}_{{16}}}}}{{1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}}}}.$Аналогичным образом можно доказать несколько более сильное утверждение.
Теорема 6. Для любых $\beta \; \geqslant \;0,$ $\gamma > 0,$ ${{\gamma }_{2}}\; \geqslant \;0,$ $3 > {{\gamma }_{1}}\; \geqslant \;0$ справедлива следующая оценка интеграла:
$I = \int\limits_{{{\mathbb{R}}^{3}}} {\kern 1pt} {{(1 + \;{\text{|}}x - y{\kern 1pt} {{{\text{|}}}^{2}})}^{{{{\gamma }_{2}}/2}}}\frac{{\exp ( - \gamma {\text{|}}x - y{\kern 1pt} {\text{|}}{\kern 1pt} )}}{{{\text{|}}x - y{\kern 1pt} {{{\text{|}}}^{{{{\gamma }_{1}}}}}}}\frac{1}{{{{{(1 + \;{\text{|}}y{\kern 1pt} {{{\text{|}}}^{2}})}}^{{\beta /2}}}}}{\kern 1pt} dy\;\leqslant \;\frac{B}{{{{{(1 + \;{\text{|}}x{\kern 1pt} {{{\text{|}}}^{2}})}}^{{\beta /2}}}}},$
где постоянная $B > 0$ и не зависит от $x \in {{\mathbb{R}}^{3}}.$
Список литературы
Al’shin A.B., Korpusov M.O., Sveshnikov A.G. Blow-up in nonlinear Sobolev type equations. De Gruyter: Ser. Nonlinear Anal. Appl., 2011.
Korpusov M.O., Ovchinnikov A.V., Sveshnikov A.G., Yushkov E.V. Blow-Up in Nonlinear Equations of Mathematical Physics: Theory and Methods. De Gruyter: Ser. Nonlinear Anal. Appl., 2018.
Корпусов М.О. Разрушение решений неклассических нелокальных нелинейных модельных уравнений // Ж. вычисл. матем. и матем. физ. 2019. Т. 59. № 4. С. 621–648.
Корпусов М.О. Разрушение и глобальная разрешимость в классическом смысле задачи Коши для формально гиперболического уравнения с некоэрцитивным источником // Изв. РАН. Сер. матем. 2020. Т. 84. № 5. С. 119–150.
Похожаев С.И., Митидиери Э. Априорные оценки и отсутствие решений нелинейных уравнений и неравенств в частных производных // Тр. МИАН. 2001. Т. 234. С. 3–383.
Korpusov M.O., Lukyanenko D.V., Panin A.A., Shlyapugin G.I. On the blow-up phenomena for a one-dimensional equation of ion-sound waves in a plasma: analytical and numerical investigation // MMAS. 2018. V. 41. № 8. P. 2906–2929.
Korpusov M.O., Lukyanenko D.V. Instantaneous blow-up versus local solvability for one problem of propagation of nonlinear waves in semiconductors // J. Math. Anal. Appl. 2018. V. 459. № 1. P. 159–181.
Корпусов М.О., Лукьяненко Д.В., Панин А.А., Юшков Е.В. О разрушении решений одного полного нелинейного уравнения ионно-звуковых волн в плазме с некоэрцитивными нелинейностями // Изв. РАН. Сер. матем. 2018. Т. 82. № 2. С. 43–78.
Панин А.А., Шляпугин Г.И. О локальной разрешимости и разрушении решений одномерных уравнений типа Ядзимы–Ойкавы–Сацумы // Теор. и матем. физ. 2017. Т. 193. № 2. С. 179–192.
Корпусов М.О., Панин А.А. О непродолжаемом решении и разрушении решения одномерного уравнения ионно-звуковых волн в плазме // Матем. заметки. 2017. Т. 102. № 3. С. 383–395.
Корпусов М.О., Лукьяненко Д.В., Овсянников Е.А., Панин А.А. Локальная разрешимость и разрушение решения одного уравнения с квадратичной некоэрцитивной нелинейностью // Вестн. ЮУрГУ. Сер. Матем. моделирование и программирование. 2017. Т. 10. № 2. С. 107–123.
Korpusov M.O., Lukyanenko D.V., Panin A.A., Yushkov E.V. Blow-up phenomena in the model of a space charge stratification in semiconductors: analytical and numerical analysis // MMAS. 2017. V. 40. № 7. P. 2336–2346.
Лукьяненко Д.В., Панин А.А. Разрушение решения уравнения стратификации объемного заряда в полупроводниках: численный анализ при сведении исходного уравнения к дифференциально-алгебраической системе // Вычисл. методы и программирование. 2016. Т. 17. № 1. С. 437–446.
Korpusov M.O., Lukyanenko D.V., Panin A.A., Yushkov E.V. Blow-up for one Sobolev problem: theoretical approach and numerical analysis // J. Math. Anal. Appl. 2016. V. 442. № 2. P. 451–468.
Корпусов М.О., Овсянников Е.А. Взрывная неустойчивость в нелинейных волновых моделях с распределенными параметрами // Изв. РАН. Сер. матем. 2020. Т. 84. № 3. С. 15–70.
Капитонов Б.В. Теория потенциала для уравнения малых колебаний вращающейся жидкости // Матем. сб. 1979. Т. 109(151). № 4(8). С. 607–628.
Габов С.А., Оразов Б.Б. Об уравнении $\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\left( {{{u}_{{xx}}} - u} \right) + {{u}_{{xx}}} = 0$ и некоторых связанных с ним задачах // Ж. вычисл. матем. и матем. физ. 1986. Т. 26. № 1. С. 92–102.
Габов С.А., Свешников А.Г. Линейные задачи теории нестационарных внутренних волн. М.: Наука, 1990. С. 344.
Габов С.А. Новые задачи математической теории волн. М.: Физматлит, 1998. С. 448.
Плетнер Ю.Д. Фундаментальные решения операторов типа Соболева и некоторые начально-краевые задачи // Ж. вычисл. матем. и матем. физ. 1992. Т. 32. № 12. С. 1885–1899.
Свиридюк Г.А. К общей теории полугрупп операторов // Успехи матем. наук. 1994. Т. 49. № 4. С. 47–74.
Загребина С.А. Начально-конечная задача для уравнений соболевского типа с сильно $(L,p)$–радиальным оператором // Матем. заметки ЯГУ. 2012. Т. 19. № 2. С. 39–48.
Zamyshlyaeva A.A., Sviridyuk G.A. Nonclassical equations of mathematical physics. Linear Sobolev type equations of higher order // Вестн. ЮУрГУ. Сер. Матем. Мех. Физ. 2016. V. 8. № 4. P. 5–16.
Корпусов М.О., Плетнер Ю.Д., Свешников А.Г. О нестационарных волнах в средах с анизотропной дисперсией // Ж. вычисл. матем. и матем. физ. 1999. Т. 39. № 6. С. 1006–1022.
Кудашев В.Р., Михайловский А.Б., Шарапов С.Е. К нелинейной теории дрейфовой моды, индуцированной тороидальностью // Физ. плазмы. 1987. Т. 13. № 4. С. 417–421.
Каменец Ф.Ф., Лахин В.П., Михайловский А.Б. Нелинейные электронные градиентные волны // Физ. плазмы. 1987. Т. 13. № 4. С. 412–416.
Ситенко А.П., Сосенко П.П. О коротковолновой конвективной турбулентности и аномальной электронной теплопроводности плазмы // Физ. плазмы. 1987. Т. 13. № 4. С. 456–462.
Корпусов М.О. Нелинейные уравнения теории ионно-звуковых волн в плазме // Ж. вычисл. матем. и матем. физ. 2021. Т. 21. № 11.
Крылов Н.В. Лекции по эллиптическим и параболическим уравнениям в пространствах Гёльдера. Новосибирск: Научная Книга, 1998. С. 178.
Корпусов М.О., Шляпугин Г.И. О разрушении решений задач Коши для одного класса нелинейных уравнений теории ферритов // Итоги науки и техн. Сер. Соврем. мат. и ее прил. Темат. обз. 2020. Т. 185. С. 79–131.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики
Пн.-пт.: 10.00-19.00