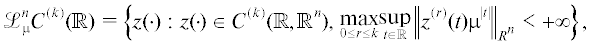Журнал вычислительной математики и математической физики, 2022, T. 62, № 6, стр. 933-950
Вопрос существования ограниченных солитонных решений в задаче о продольных колебаниях упругого бесконечного стержня в поле с нелинейным потенциалом общего вида
А. Л. Бекларян 1, *, Л. А. Бекларян 2, **
1 Центральный экономико-математический институт РАН
117418 Москва, Нахимовский пр-т, 47, Россия
2 Национальный исследовательский университет
“Высшая школа экономики”
101000 Москва, Мясницкая ул., 20, Россия
* E-mail: lbeklaryan@outlook.com
** E-mail: abeklaryan@hse.ru
Поступила в редакцию 24.12.2021
После доработки 15.01.2022
Принята к публикации 15.01.2022
- EDN: DKYGFU
- DOI: 10.31857/S0044466922060035
Аннотация
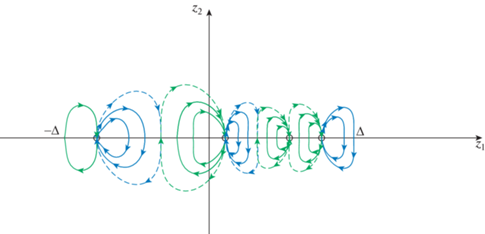
Установлено существование семейства ограниченных солитонных решений для конечно-разностного аналога волнового уравнения с нелинейным потенциалом общего вида. Доказательство проводится в рамках формализма, устанавливающего взаимно однозначное соответствие между солитонными решениями бесконечномерной динамической системы и решениями семейства функционально-дифференциальных уравнений точечного типа. При доказательстве существования ограниченных солитонных решений ключевым является наличие теоремы существования и единственности солитонных решений в случае квазилинейного потенциала. Другим важным обстоятельством для рассматриваемого класса систем уравнений является наличие у них ряда симметрий вследствие малой размерности (одномерности) пространства в каждой точке решетки. Библ. 18. Фиг. 4.
1. ВВЕДЕНИЕ
Для уравнений математической физики, являющихся уравнениями Эйлера–Лагранжа соответствующих вариационных задач, важный класс решений – это решения типа бегущей волны (солитонные решения) (см. [1], [2]). В ряде моделей такие решения хорошо приближаются решениями типа бегущей волны для конечно-разностных аналогов исходных уравнений, которые взамен непрерывной среды описывают взаимодействие сгустков среды, помещенных в вершинах решетки (см. [1], [3]). Возникающие системы относятся к классу бесконечномерных динамических систем. К наиболее широко рассматриваемым классам подобных задач относятся бесконечномерные системы с потенциалами Френкеля–Конторовой (периодические и медленно растущие потенциалы) и Ферми–Паста–Улама (потенциалы экспоненциального роста), широкий обзор которых приведен в [4].
В теории пластической деформации изучается бесконечномерная динамическая система
(1)
$m{{\ddot {y}}_{i}} = {{y}_{{i - 1}}} - 2{{y}_{i}} + {{y}_{{i + 1}}} + \phi ({{y}_{i}}),\quad i \in \mathbb{Z},\quad {{y}_{i}} \in \mathbb{R},\quad t \in \mathbb{R},$Определение 1. $\{ {{y}_{i}}({\kern 1pt} \cdot {\kern 1pt} )\} _{{ - \infty }}^{{ + \infty }}$ называется решением системы (1), если для любого $i \in \mathbb{Z}$ функция ${{y}_{i}}({\kern 1pt} \cdot {\kern 1pt} )$ непрерывно дифференцируема, ее производная является абсолютно непрерывной функцией и почти всюду удовлетворяет системе (1).
Изучение таких систем с различными потенциалами является одним из интенсивно развивающихся направлений в теории динамических систем. Для них центральной задачей является изучение солитонных решений (решений типа бегущей волны) как одного из наблюдаемых классов волн.
Определение 2. Будем говорить, что решение $\{ {{y}_{i}}({\kern 1pt} \cdot {\kern 1pt} )\} _{{ - \infty }}^{{ + \infty }}$ системы (1), определенное для всех $t \in \mathbb{R}$, имеет тип бегущей волны (является солитонным решением), если существует $\tau > 0$, не зависящая от $t$ и $i$, что при всех $i \in \mathbb{Z}$ и $t \in \mathbb{R}$ выполнено равенство
Константу $\tau $ будем называть характеристикой бегущей волны.Таким образом, для рассматриваемого конечно-разностного аналога волнового уравнения изучение солитонных решений сводится к исследованию пространства решений краевой задачи
(2)
$m{{\ddot {y}}_{i}}(t) = {{y}_{{i - 1}}}(t) - 2{{y}_{i}}(t) + {{y}_{{i + 1}}}(t) + \phi ({{y}_{i}}(t)),\quad i \in \mathbb{Z},\quad {{y}_{i}} \in \mathbb{R},\quad t \in \mathbb{R},$Фазовым пространством системы уравнений (2) является пространство бесконечных последовательностей
(4)
$\mathcal{K}_{\mathbb{Z}}^{2} = \overline {\mathop \prod \limits_{q \in \mathbb{Z}} } {\kern 1pt} \mathbb{R}_{q}^{2},\quad \mathbb{R}_{q}^{n} = {{\mathbb{R}}^{2}},\quad \varkappa \in \mathcal{K}_{\mathbb{Z}}^{2},\quad \varkappa = \{ {{x}_{i}}{{\} }_{{i \in \mathbb{Z}}}},\quad {{x}_{i}} = ({{x}_{{i1}}},{{x}_{{i2}}}){\kern 1pt} ',$Определим линейный оператор $\mathbb{A}$, оператор сдвига $\mathbb{T}$ и нелинейный оператор $\mathbb{F}$, действующие непрерывно из пространства ${{\mathcal{K}}^{2}}$ в себя по следующему правилу: для любых $i \in \mathbb{Z}$, $\varkappa \in {{\mathcal{K}}^{2}}$
Система (2), (3), задающая солитонные решения, может быть переписана в следующей операторной форме:
и является краевой задачей с линейными нелокальными краевыми условиями. Краевые условия (6) означают, что сдвиг решения по времени равен сдвигу по пространству.Одним из методов исследования таких систем является конструктивное построение решений, использующее явный вид потенциала и, далее, методами теории возмущений установление факта существования солитонных решений для близких потенциалов. Другим часто применяемым способом является использование наличия симметрий у исходных уравнений. Важным является не только вопрос существования солитонных решений, но и вопрос их единственности. Для этого одним из подходов служит локализация решений в пространстве бесконечно дифференцируемых или аналитических функций. Как правило, в пространстве бесконечно дифференцируемых функций удается показать существование решения, а в пространстве аналитических функций показать их единственность (см. [4]).
В представленной работе используются возможности иного подхода и созданного на его основе формализма (см. [5]–[8]). В рамках такого подхода предлагается локализация солитонных решений заданием их асимптотики как по пространству (параметризированное семейство бесконечномерных фазовых пространств в форме гильбертовых пространств $\mathcal{K}_{{\mathbb{Z}2\mu }}^{2}$, $\mu \in (0,\;1)$), так и по времени. Возможности такого подхода основаны на существовании взаимно однозначного соответствия солитонных решений для бесконечномерных динамических систем с решениями семейства индуцированных функционально-дифференциальных уравнений точечного типа (см. [7], [9]–[12]).
В случае рассматриваемой задачи солитонные решения, решения системы (2), (3), находятся во взаимно однозначном соответствии с решениями семейства индуцированных функционально-дифференциальных уравнений точечного типа
(7)
${{\dot {z}}_{1}}(t) = {{z}_{2}}(t),\quad ({{z}_{1}},{{z}_{2}}){\text{'}} \in {{\mathbb{R}}^{2}},\quad t \in \mathbb{R},$(8)
${{\dot {z}}_{2}}(t) = {{m}^{{ - 1}}}\left[ {{{z}_{1}}(t - \tau ) - 2{{z}_{1}}(t) + {{z}_{1}}(t + \tau ) + \Phi ({{z}_{1}}(t))} \right].$Для изучения вопросов существования и единственности солитонных решений предлагается локализация решений индуцированных функционально-дифференциальных уравнений точечного типа (в случае рассматриваемой задачи это уравнения (7), (8)) в пространствах функций, мажорируемых функциями заданного экспоненциального роста с показателем экспоненты в качестве параметра:
При минимальных ограничениях на потенциал $\phi ({\kern 1pt} \cdot {\kern 1pt} )$ в виде наличия условия Липщица (квазилинейные потенциалы) отмеченная задача была исследована в монографии [8]. Соответствующую константу Липщица для потенциала $\phi ({\kern 1pt} \cdot {\kern 1pt} )$ будем обозначать через ${{L}_{\phi }}$.
Рассмотрим трансцендентное уравнение относительно двух переменных $\tau \in (0, + \infty )$ и $\mu \in (0,\;1)$:
где Множество решений уравнения (11) описывается функциями ${{\mu }_{1}}(\tau )$, ${{\mu }_{2}}(\tau )$, представленными на фиг. 1. Для величины $\hat {\tau }$ имеет место некоторая абсолютная оценка $\hat {\tau } \leqslant {{(2{{C}_{\phi }})}^{{ - 1}}}$ и, в частности, $\hat {\tau } \leqslant 1{\text{/}}2$.Сформулируем теорему существования и единственности решения для индуцированных функционально-дифференциальных уравнений (7), (8).
Tеорема 1 (см. [8]). Пусть потенциал $\Phi $ удовлетворяет условию Липщица с константой ${{L}_{\Phi }}$. Тогда при любых начальных данных $a,b \in \mathbb{R}$, $\bar {t} \in \mathbb{R}$, и характеристиках $\tau > 0$, удовлетворяющих условию $0 < \tau < \hat {\tau }\;{\text{в}}\;{\text{пространстве}}\;L_{\mu }^{2}{{C}^{{(0)}}}(\mathbb{R})$, ${{\mu }^{\tau }} \in ({{\mu }_{1}}(\tau ),{{\mu }_{2}}(\tau ))$ для системы функционально-дифференциальных уравнений (7), (8), существует и причем единственное решение $({{z}_{1}}(t),{{z}_{2}}(t))$, $t \in \mathbb{R}$, такое, что оно удовлетворяет начальным условиям ${{z}_{1}}\left( {\bar {t}} \right) = a$, ${{z}_{2}}\left( {\bar {t}} \right) = b$. Такое решение, как элемент пространства $\mathcal{L}_{\mu }^{2}{{C}^{{(0)}}}(\mathbb{R})$, непрерывно зависит от начальных данных $a,b \in \mathbb{R}$, а также массы $m$, характеристики $\tau $ и потенциала $\Phi ({\kern 1pt} \cdot {\kern 1pt} )$.
Теорема 1 не только гарантирует существование решения, но и задает ограничение его возможного роста по времени $t$. Очевидно, что при каждом $0 < \tau < \hat {\tau }$ пространства $\mathcal{L}_{{(\sqrt[\tau ]{{{{\mu }_{2}}(\tau )}} - \varepsilon )}}^{2}{{C}^{{(0)}}}(\mathbb{R})$ при малых $\varepsilon > 0$ намного уже, чем пространства $\mathcal{L}_{{(\sqrt[\tau ]{{{{\mu }_{1}}(\tau )}} + \varepsilon )}}^{2}{{C}^{{(0)}}}(\mathbb{R})$. Теорема гарантирует существование решения в более узких пространствах и единственность в более широких пространствах.
Теорема 1 допускает переформулировку в терминах решений типа бегущей волны (солитонных решений) для исходного волнового уравнения (в терминах системы (2), (3)).
Tеорема 2 (см. [8]). Пусть потенциал $\Phi $ удовлетворяет условию Липщица с константой ${{L}_{\Phi }}$. Тогда при любых начальных данных $\bar {i} \in \mathbb{Z}$, $a,b \in \mathbb{R}$, $\bar {t} \in \mathbb{R}$, и характеристиках $\tau > 0$, удовлетворяющих условию $0 < \tau < \hat {\tau }$, для исходной системы дифференциальных уравнений (2) существует единственное решение $\left\{ {{{y}_{i}}({\kern 1pt} \cdot {\kern 1pt} )} \right\}_{{ - \infty }}^{{ + \infty }}$ типа бегущей волны (солитонное решение) с характеристикой $\tau $ такое, что оно удовлетворяет начальным условиям ${{y}_{{\bar {i}}}}(\bar {t}) = a$, ${{\dot {y}}_{{\bar {i}}}}(\bar {t}) = b$. Для любого параметра $\mu ,{{\mu }^{\tau }} \in ({{\mu }_{1}}(\tau ),{{\mu }_{2}}(\tau ))$ значения вектор-функции
при любом $t \in \mathbb{R}$ принадлежат пространству $\mathcal{K}_{{\mathbb{Z}2\mu }}^{2}$, а функция принадлежит пространству $\mathcal{L}_{\mu }^{1}{{C}^{{(0)}}}(\mathbb{R})$. Такое решение непрерывно зависит от начальных данных $a,b \in \mathbb{R}$, а также от массы $m$, характеристики $\tau $ и потенциала $\Phi ( \cdot )$.Среди солитонных решений важный класс составляют ограниченные солитонные решения, соответствующие ограниченным решениям индуцированных функционально-дифференциальных уравнений точечного типа. В [15] для функционально-дифференциального уравнения точечного типа с квазилинейной правой частью получена теорема существования ограниченного решения. В ней представлены условия нового типа, использующие средние по некоторому периоду для правых частей функционально-дифференциального уравнения точечного типа. Такие условия являются новыми и для обыкновенных дифференциальных уравнений. На их основе получен результат о существовании ограниченного солитонного решения для систем с квазилинейным потенциалом, а также осуществлена численная реализация таких солитонных решений (см. [16]). Более того, в рамках такого подхода в [17] получена теорема существования ограниченного решения для функционально-дифференциального уравнения точечного типа с сильно нелинейной правой частью.
Вместе с тем условия из упомянутой работы [17] оказываются неприменимыми при изучении ряда систем и, в частности, для конечно-разностного волнового уравнения с нелинейным потенциалом. Причина в том, что у таких систем, а также индуцированных ими функционально-дифференциальных уравнений точечного типа, имеется ряд симметрий вследствие малой размерности (одномерности) пространства в каждой точке решетки, которые препятствуют реализации нужных условий из отмеченной работы.
В свою очередь, наличие симметрий, поведение векторного поля для такого индуцированного функционально-дифференциального уравнения точечного типа, наличие теорем существования и единственности решения, а также непрерывной зависимости от начальных данных и параметров (теоремы 1 и 2) позволяют установить существование семейства ограниченных солитонных решений (решения системы (2), (3)) и в случае нелинейных потенциалов общего вида.
Отмеченный подход был реализован в [18], где для конечно-разностного аналога волнового уравнения с квадратичным потенциалом описаны семейства ограниченных решений. Большинство приведенных там предварительных результатов получены без учета конкретного вида нелинейного потенциала. Поэтому представленный подход носит универсальный характер и может быть применен к изучению широкого класса систем с нелинейным потенциалом, что и будет продемонстрировано далее.
2. НЕКОТОРЫЕ ПРЕДВАРИТЕЛЬНЫЕ РЕЗУЛЬТАТЫ ДЛЯ СИСТЕМЫ С НЕЛИНЕЙНЫМ ПОТЕНЦИАЛОМ ОБЩЕГО ВИДА
Рассмотрим солитонные решения системы (решения системы (2), (3)) с нелинейным потенциалом общего вида. В рамках данной задачи установим ряд универсальных свойств, присущих таким системам. Соответствующее индуцированное функционально-дифференциальное уравнение точечного типа имеет вид
(12)
${{\dot {z}}_{1}}(t) = {{z}_{2}}(t),\quad ({{z}_{1}},{{z}_{2}}){\text{'}} \in {{\mathbb{R}}^{2}},\quad t \in \mathbb{R},$(13)
${{\dot {z}}_{2}}(t) = {{m}^{{ - 1}}}\left[ {{{z}_{1}}(t - \tau ) - 2{{z}_{1}}(t) + {{z}_{1}}(t + \tau ) + \Phi ({{z}_{1}})} \right].$Утверждение 1. Точки замкнутого множества
(14)
$S = \left\{ {z:z = ({{z}_{1}},{{z}_{2}}){\text{'}},\;({{z}_{1}},{{z}_{2}}){\text{'}} \in {{\mathbb{R}}^{2}};\;{{z}_{2}} = 0,\;\Phi ({{z}_{1}}) = 0} \right\}$Для изучения иных решений индуцированного функционально-дифференциального уравнения с условием ограниченности по первой координате построим семейство вспомогательных функционально-дифференциальных уравнений точечного типа.
Для любого $\Delta > 0$ определим потенциал ${{\Phi }_{\Delta }}$:
(15)
$\Phi (\xi ) = \left\{ \begin{gathered} \Phi ( - \Delta ),\quad {\text{если}}\quad \xi {\text{ < }} - \Delta , \hfill \\ \Phi (\xi ),\quad {\text{если}}\quad \xi \in \Delta , \hfill \\ \Phi (\Delta ),\quad {\text{если}}\quad \xi {\text{ > }}\Delta . \hfill \\ \end{gathered} \right.$Константа Липшица для такой функции ${{\Phi }_{\Delta }}$ равна константе Липщица для функции ${{\left. \Phi \right|}_{{[ - \Delta ,\Delta ]}}}$, как ограничения потенциала $\Phi $ на интервал $[ - \Delta ,\Delta ]$. Будем обозначать ее через ${{L}_{{{{\Phi }_{\Delta }}}}}$. Очевидно, что ${{L}_{{{{\Phi }_{\Delta }}}}}$ является монотонно возрастающей по параметру $\Delta > 0$. Рассмотрим вспомогательное функционально-дифференциальное уравнение точечного типа
(16)
${{\dot {z}}_{1}}(t) = {{z}_{2}}(t),\quad ({{z}_{1}},{{z}_{2}}){\text{'}} \in {{\mathbb{R}}^{2}},\quad t \in \mathbb{R},$(17)
${{\dot {z}}_{2}}(t) = {{m}^{{ - 1}}}\left[ {{{z}_{1}}(t - \tau ) - 2{{z}_{1}}(t) + {{z}_{1}}(t + \tau ) + {{\Phi }_{\Delta }}({{z}_{1}}(t))} \right].$По аналогии с уравнением (11) рассмотрим трансцендентное уравнение относительно двух переменных $\tau \in (0, + \infty )$ и $\mu \in (0,\;1)$
гдеРешение уравнения (18) описывается функциями ${{\mu }_{{\Delta 1}}}(\tau )$, ${{\mu }_{{\Delta 2}}}(\tau )$. Качественное поведение функций ${{\mu }_{{\Delta 1}}}(\tau )$, ${{\mu }_{{\Delta 2}}}(\tau )$ такое же, как поведение функций ${{\mu }_{1}}(\tau ),{{\mu }_{2}}(\tau )$ на фиг. 1, а величина $\hat {\tau }$ заменяется соответствующей величиной ${{\hat {\tau }}_{\Delta }}$, которая является монотонно убывающей по параметру $\Delta > 0$.
Для вспомогательного функционально-дифференциального уравнения точечного типа (16), (17) также верна теорема 1, в которой следует потенциал $\Phi $ заменить на ${{\Phi }_{\Delta }}$, функции ${{\mu }_{1}}(\tau )$, ${{\mu }_{2}}(\tau )$ заменить на функции ${{\mu }_{{\Delta 1}}}(\tau )$, ${{\mu }_{{\Delta 2}}}(\tau )$, а величину $\hat {\tau }$ – на ${{\hat {\tau }}_{\Delta }}$. Всякое решение $({{z}_{1}}(t),{{z}_{2}}(t)){\text{'}}$, $t \in \mathbb{R}$, вспомогательного функционально-дифференциального уравнения (16), (17) со свойством ограниченности по первой координате $\left| {{{z}_{1}}(t)} \right| \leqslant \Delta $, $t \in \mathbb{R}$, является решением индуцированного функционально-дифференциального уравнения точечного типа (12), (13) с нелинейным потенциалом и тем же условием ограниченности по первой координате. Таким образом, в силу сформулированного выше правила согласования, нам достаточно установить существование решений вспомогательного функционально-дифференциального уравнения точечного типа (16), (17), удовлетворяющих свойству ограниченности по первой координате $\left| {{{z}_{1}}(t)} \right| \leqslant \Delta $, $t \in \mathbb{R}$.
Определим множества
(20)
${{B}^{\Delta }} = \{ a:{{\Phi }_{\Delta }}(a) = 0\} ,\quad {{D}^{\Delta }} = \mathbb{R}{{\backslash }}{{B}^{\Delta }}.$(21)
$D = \bigcup\limits_{i \in I} {{{d}_{i}}} ,\quad {{d}_{i}} = ({{\alpha }_{i}},{{\beta }_{i}}),\quad i \in I,$(22)
${{D}^{\Delta }} = \bigcup\limits_{i \in {{I}^{\Delta }}} {d_{i}^{\Delta }} ,\quad d_{i}^{\Delta } = (\alpha _{i}^{\Delta },\beta _{i}^{\Delta }),\quad i \in {{I}^{\Delta }},$Лемма 1. Решения $({{z}_{1}}(t),{{z}_{2}}(t)){\text{'}}$, $t \in \mathbb{R}$, вспомогательного функционально-дифференциального уравнения точечного типа (16), (17) инвариантны относительно сдвига по времени.
Доказательство данного свойства инвариантности является следствием автономности рассматриваемой системы дифференциальных уравнений.
Лемма 2. Если $({{z}_{1}}(t),{{z}_{2}}(t)){\text{'}}$, $t \in \mathbb{R}$, является решением вспомогательного функционально-дифференциального уравнения точечного типа (16), (17), то $\left( {{{{\hat {z}}}_{1}}(t),{{{\hat {z}}}_{2}}(t)} \right){\text{'}}$, $t \in \mathbb{R}$, где ${{\hat {z}}_{1}}(t) = {{z}_{1}}( - t)$, ${{\hat {z}}_{2}}(t) = - {{z}_{2}}( - t)$, $t \in \mathbb{R}$, также является решением.
Это свойство инвариантности может быть получено непосредственной проверкой.
Лемма 3. Пусть $({{z}_{1}}(t),{{z}_{2}}(t)){\text{'}}$, $t \in \mathbb{R}$, является решением вспомогательного функционально-дифференциального уравнения точечного типа (16), (17). Рассматриваемое решение при прохождении замкнутой верхней полуплоскости ${{z}_{2}} \geqslant 0$ фазового пространства имеет монотонно возрастающее поведение координаты ${{z}_{1}}(t)$. Аналогично, при прохождении замкнутой нижней полуплоскости ${{z}_{2}} \leqslant 0$ фазового пространства имеется монотонно убывающее поведение координаты ${{z}_{1}}(t)$.
Доказательство утверждения непосредственно следуeт из вида правой части первого уравнения (16).
Утверждение 2. Пусть $({{z}_{1}}(t),{{z}_{2}}(t)){\text{'}}$, $t \in \mathbb{R}$, является решением вспомогательного функционально-дифференциального уравнения точечного типа (16), (17). Если рассматриваемое решение является периодическим, то найдется момент $\hat {t}$, при котором выполняется условие ${{z}_{2}}\left( {\hat {t}} \right) = 0$.
Доказательство данного утверждения непосредственно следует из леммы 3.
Лемма 4. Пусть $\tau \in (0,{{\hat {\tau }}_{\Delta }})$, $\mu \in ({{\mu }_{{\Delta 1}}}(\tau ),{{\mu }_{{\Delta 2}}}(\tau ))$, а $({{z}_{1}}( \cdot ),{{z}_{2}}( \cdot )){\text{'}} \in \mathcal{L}_{\mu }^{2}{{C}^{{(0)}}}(\mathbb{R})$ – решение вспомогательного функционально-дифференциального уравнения точечного типа (16), (17), для которого существует момент $\hat {t}$ со свойством ${{z}_{2}}\left( {\hat {t}} \right) = 0$. Тогда фазовый портрет такого решения симметричен относительно горизонтальной оси ${{z}_{2}} = 0$. Более того, для такого решения каждая пара отмеченных симметричных точек задается в терминах самого решения следующим образом: $\left( {{{z}_{1}}(\hat {t} + t),{{z}_{2}}(\hat {t} + t)} \right){\kern 1pt} {\text{'}}$, $\left( {{{z}_{1}}( - \hat {t} - t), - {{z}_{2}}( - \hat {t} - t)} \right){\kern 1pt} {\text{'}}$, $t \in \mathbb{R}$.
Доказательство. Пусть решение $\left( {{{z}_{1}}(t),{{z}_{2}}(t)} \right){\kern 1pt} {\text{'}}$, $t \in \mathbb{R}$, удовлетворяет всем условиям из леммы, т.е. найдется такое $\hat {t}$, что ${{z}_{2}}(\hat {t}) = 0$. Так как решения инвариантны относительно сдвига по времени (лемма 2, то не нарушая общности, можем положить $\hat {t} = 0$. По лемме 2 $\left( {{{{\hat {z}}}_{1}}(t),{{{\hat {z}}}_{2}}(t)} \right){\kern 1pt} {\text{'}}$, $t \in \mathbb{R}$, где ${{\hat {z}}_{1}}(t) = {{z}_{1}}( - t)$, ${{\hat {z}}_{2}}(t) = - {{z}_{2}}( - t)$, $t \in \mathbb{R}$, также является решением. Заметим, что при этом ${{\hat {z}}_{1}}(0) = {{z}_{1}}(0)$, ${{\hat {z}}_{2}}(0) = - {{z}_{2}}(0) = 0$. Тогда по теореме существования и единственности решения в пространстве функций $\mathcal{L}_{\mu }^{2}{{C}^{{(0)}}}(\mathbb{R})$ следует, что решения $\left( {{{z}_{1}}(t),{{z}_{2}}(t)} \right){\kern 1pt} {\text{'}}$, $\left( {{{{\hat {z}}}_{1}}(t),{{{\hat {z}}}_{2}}(t)} \right){\kern 1pt} {\text{'}}$, $t \in \mathbb{R}$, совпадают. Тогда для любого $t \in \mathbb{R}$ из условия ${{z}_{1}}(t) = {{\hat {z}}_{1}}(t)$, ${{z}_{2}}(t) = {{\hat {z}}_{2}}(t)$ следует, что ${{z}_{1}}(t) = {{z}_{1}}( - t)$, ${{z}_{2}}(t) = - {{z}_{2}}( - t)$. Полученные результаты и доказывают лемму, и фазовый портрет такого решения будет симметричен относительно горизонтальной оси ${{z}_{2}} = 0$.
Лемма 5. Пусть $\tau \in \left( {0,{{{\hat {\tau }}}_{\Delta }}} \right)$, $\mu \in ({{\mu }_{{\Delta 1}}}(\tau ),{{\mu }_{{\Delta 2}}}(\tau ))$, а $\left( {{{z}_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{z}_{2}}({\kern 1pt} \cdot {\kern 1pt} )} \right){\text{'}} \in \mathcal{L}_{\mu }^{2}{{C}^{{(0)}}}(\mathbb{R})$ – решение вспомогательного функционально-дифференциального уравнения точечного типа (16), (17) с начальными данными $\left( {{{z}_{1}}(0),{{z}_{2}}(0)} \right){\kern 1pt} {\text{'}} = (a,0){\text{'}}$. Такое решение является периодическим, но не стационарным, тогда и только тогда, когда найдутся $\hat {t} \ne 0$ с условием ${{z}_{2}}(\hat {t}) = 0$, и минимальное значение таких $\hat {t}$ не равно нулю. Такое минимальное значение равно полупериоду решения.
Доказательство. Если решение является периодическим, то значение периода обозначим через $2\hat {t}$. По лемме 4 справедливы условия ${{z}_{2}}(t) = - {{z}_{2}}( - t)$, $t \in \left[ {0,\hat {t}} \right]$. Так как $\hat {t}$ равно значению минимального полупериода, то для всех $t \in \left[ {0,\hat {t}} \right)$ должны выполняться условия ${{z}_{2}}(t) = - {{z}_{2}}( - t) \ne 0$. Тогда из непрерывности решения и условия симметрии решения относительно оси ${{z}_{2}} = 0$ следует, что ${{z}_{2}}\left( {\hat {t}} \right) = 0$.
Доказательство проведем от обратного. Пусть найдется точка $\hat {t}$, для которой выполняется условие ${{z}_{2}}(\hat {t}) = 0$. С одной стороны, в силу условия симметрии ${{z}_{2}}(t) = - {{z}_{2}}( - t)$, $t \in \left[ {0,\hat {t}} \right]$, из леммы 4 следует, что имеет место условие ${{z}_{2}}(\hat {t}) = - {{z}_{2}}( - \hat {t})$. С другой стороны, имеет место и условие симметрии ${{z}_{1}}(\hat {t}) = {{z}_{1}}( - \hat {t})$, что ведет к выполнению равенства $\left( {{{z}_{1}}(\hat {t}),{{z}_{2}}(\hat {t})} \right) = \left( {{{z}_{1}}( - \hat {t}),{{z}_{2}}( - \hat {t})} \right)$. Следовательно, такое решение является периодическим, а минимальное значение таких $\hat {t}$ равно полупериоду решения.
Лемма 6. Пусть $\tau \in \left( {0,{{{\hat {\tau }}}_{\Delta }}} \right)$, $\mu \in \left( {{{\mu }_{{\Delta ,1}}}(\tau )} \right.$, ${{\mu }_{{\Delta ,2}}}(\tau ))$, а $({{z}_{1}}( \cdot ),z\left. {_{2}( \cdot )} \right){\text{'}} \in \mathcal{L}_{\mu }^{2}{{C}^{{(0)}}}(\mathbb{R})$ – решение вспомогательного функционально-дифференциального уравнения точечного типа (16), (17) с начальными данными $\left( {{{z}_{1}}(0),{{z}_{2}}(0)} \right){\text{'}} = (a,0){\text{'}}$. Тогда справедливо одно из следующих условий.
(a) Либо решение периодическое с полупериодом $\hat {t}$, для которого выполняется одно из условий:
1) ${{z}_{1}}(\hat {t}) \leqslant {{z}_{1}}(t) \leqslant a$, $t \in \left[ { - \hat {t},\hat {t}} \right]$, и при $t \in \left[ {0, - \hat {t}} \right]$ функция ${{z}_{1}}({\kern 1pt} \cdot {\kern 1pt} )$ монотонно возрастающая, а при $t \in \left[ {0,\hat {t}} \right]$ функция ${{z}_{1}}( \cdot )$ монотонно убывающая;
2) $a \leqslant {{z}_{1}}(t) \leqslant {{z}_{1}}(\hat {t})$ при $t \in \left[ { - \hat {t},\hat {t}} \right]$, и при $t \in \left[ {0, - \hat {t}} \right]$ функция ${{z}_{1}}({\kern 1pt} \cdot {\kern 1pt} )$ монотонно убывающая, а при $t \in \left[ {0,\hat {t}} \right]$ функция ${{z}_{1}}( \cdot )$ монотонно возрастающая.
(б) либо решение не периодическое и выполняется одно из условий:
1) ${{z}_{1}}(t) \leqslant a$, $t \in \mathbb{R}$, и при $t \in ( - \infty ,0)$ функция ${{z}_{1}}({\kern 1pt} \cdot {\kern 1pt} )$ монотонно возрастающая, а при $t \in (0,\infty )$ функция ${{z}_{1}}( \cdot )$ монотонно убывающая;
2) $a \leqslant {{z}_{1}}(t)$, $t \in \mathbb{R}$, и при $t \in ( - \infty ,0)$ функция ${{z}_{1}}({\kern 1pt} \cdot {\kern 1pt} )$ монотонно убывающая, а при $t \in (0,\infty )$ функция ${{z}_{1}}( \cdot )$ монотонно возрастающая.
Доказательство. В силу леммы 3, леммы 4 (наличие симметрии для такого решения) и леммы 5, решение имеет следующее поведение.
Случай периодического решения. При положительных моментах времени полупериода ($t \in \left[ {0,\hat {t}} \right]$) решение находится в замкнутой нижней полуплоскости ${{z}_{2}} \leqslant 0$ и выполняется первое двойное неравенство. Если при $t \in \left[ {0,\hat {t}} \right]$ решение находится в замкнутой верхней полуплоскости ${{z}_{2}} \geqslant 0$, то выполняется второе двойное неравенство. Соответствующие условия монотонности решения следуют из вида правой части уравнения (16).
Случай непериодического решения. При положительных моментах времени ($t > 0$) решение находится в замкнутой нижней полуплоскости ${{z}_{2}} \leqslant 0$, а при отрицательных моментах времени ($t < 0$) решение находится в замкнутой верхней полуплоскости ${{z}_{2}} \geqslant 0$, либо с точностью до наоборот. Так как в условиях первого расположения в замкнутой нижней полуплоскости имеет место ограничение ${{z}_{2}} \leqslant 0$, то в силу первого уравнения (16) оно будет монотонно убывающим и будет выполняться ограничение ${{z}_{1}}(t) \leqslant {{z}_{1}}(0)$ при $t < 0$. Точно так же в замкнутой верхней полуплоскости имеет место ограничение ${{z}_{2}} \geqslant 0$ и в силу первого уравнения (16) оно будет монотонно возрастающим, и будет выполняться соотношение ${{z}_{1}}(t) \leqslant {{z}_{1}}(0)$ при $t > 0$. Следовательно, первая координата решения удовлетворяет ограничению ${{z}_{1}}(t) \leqslant {{z}_{1}}(0)$ при $t \in \mathbb{R}$. Точно так же в условиях второго способа расположения решения можно показать, что первая координата решения удовлетворяет ограничению ${{z}_{1}}(t) \geqslant {{z}_{1}}(0)$ при $t \in \mathbb{R}$ и соответствующим условиям монотонности.
Утверждение 3. Любые два периодических не стационарных решения либо не имеют точек пересечения для внутренних областей, которые они выделяют, либо эти области вложены одна в другую. Для периодического решения и внутренней области, которую она выделяет, всякое решение с начальным условием, принадлежащим этой области, также является периодическим.
Данное утверждение следует из теоремы существования и единственности решения, а также непрерывной зависимости от начальных данных.
Сформулируем результат, устанавливающий знак производной ${{\dot {z}}_{2}}(0)$ для решения $({{z}_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{z}_{2}}({\kern 1pt} \cdot {\kern 1pt} )){\text{'}}$ вспомогательного функционально-дифференциального уравнения точечного типа (16), (17) с начальными данными $({{z}_{1}}(0),{{z}_{2}}(0)){\text{'}} = (a,0){\text{'}}$.
Лемма 7. Пусть $\Delta > 0$, $\tau \in \left( {0,{{{\hat {\tau }}}_{\Delta }}} \right)$, $\mu \in ({{\mu }_{{\Delta 1}}}(\tau ),{{\mu }_{{\Delta 2}}}(\tau ))$, а $({{z}_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{z}_{2}}( \cdot {\kern 1pt} )){\text{'}} \in \mathcal{L}_{\mu }^{2}{{C}^{{(0)}}}(\mathbb{R})$ – нестационарное решение вспомогательного функционально-дифференциального уравнения точечного типа (16), (17) с начальными данными $\left( {{{z}_{1}}(0),{{z}_{2}}(0)} \right){\text{'}} = (a,0){\text{'}}$. Тогда
1) если $a \in (\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })$, $i - \in I_{ - }^{\Delta }$, то выполняется условие ${{\dot {z}}_{2}}(0) < 0$;
2) если $a \in (\alpha _{{i + }}^{\Delta },\beta _{{i + }}^{\Delta })$, $i + \in I_{ + }^{\Delta }$, то выполняется условие ${{\dot {z}}_{2}}(0) > 0$.
Доказательство. В силу уравнения (17) и леммы 4 для рассматриваемого решения выполнено условие ${{z}_{1}}(\tau ) = {{z}_{1}}( - \tau )$. Поэтому справедливо соотношение
(23)
$\begin{gathered} {{{\dot {z}}}_{2}}(0) = {{m}^{{ - 1}}}\left[ {{{z}_{1}}( - \tau ) - 2{{z}_{1}}(0) + {{z}_{1}}(\tau ) + {{\Phi }_{\Delta }}({{z}_{1}}(0))} \right] = \\ = \;{{m}^{{ - 1}}}\left[ {{{z}_{1}}( - \tau ) - 2a + {{z}_{1}}(\tau ) + {{\Phi }_{\Delta }}(a)} \right] = {{m}^{{ - 1}}}\left[ {2{{z}_{1}}(\tau ) - 2a + {{\Phi }_{\Delta }}(a)} \right]. \\ \end{gathered} $(25)
${{\ddot {z}}_{1}}(t) = {{m}^{{ - 1}}}\left[ {{{z}_{1}}(t - \tau ) - 2{{z}_{1}}(t) + {{z}_{1}}(t + \tau ) + {{\Phi }_{\Delta }}({{z}_{1}}(t))} \right]$Докажем п. 1). Пусть $a \in [\alpha ,\beta ] \subseteq (\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })$, $i - \in I_{ - }^{\Delta }$. При таких $a$ значение потенциала ${{\Phi }_{\Delta }}(a)$ отрицательное. Поэтому при достаточно малых характеристиках $\tau $ выполняется неравенство ${{\dot {z}}_{2}}(0) < 0$. Из последнего неравенства и начального условия ${{z}_{2}}(0) = 0$ следует, что при малых $t > 0$ выполняется условие ${{z}_{2}}(t) < 0$, а при малых $t < 0$ – условие ${{z}_{2}}(t) > 0$. Если решение не периодическое, то дополнительно будут выполняться более сильные соотношения: ${{z}_{1}}(t) < a$ при $t < 0$ и монотонно возрастает, ${{z}_{1}}(t) < a$ при $t > 0$ и монотонно убывает. Если решение периодическое, то имеют место оценки ${{z}_{1}}(t) \leqslant a$.
Покажем, что условие ${{\dot {z}}_{2}}(0) < 0$ будет выполняться при всех характеристиках $\tau \in (0,{{\hat {\tau }}_{\Delta }})$. Докажем от противного. Пусть найдется $\tau \in (0,{{\hat {\tau }}_{\Delta }})$, при котором для решения выполняется условие ${{\dot {z}}_{2}}(0) = 0$, а $\underline \tau $ – нижняя грань таких значений. Очевидно, что $\underline \tau \in (0,{{\hat {\tau }}_{\Delta }})$.
Из равенства (23) и отрицательности значения потенциала будет следовать условие ${{z}_{1}}(\underline \tau ) > a$. Это противоречит непрерывной зависимости решения системы (16), (17) от начальных данных и характеристики $\tau $ (теорема 1), которая нарушается при значении характеристики, равной $\underline \tau $. Следовательно, ${{\dot {z}}_{2}}(0) < 0$ будет выполняться при всех характеристиках $\tau \in (0,{{\hat {\tau }}_{\Delta }})$. Так как это справедливо для всех интервалов $[\alpha ,\beta ]$ таких, что $[\alpha ,\beta ] \subseteq (\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })$, $i - \in I_{ - }^{\Delta }$, то условие их п. 1) будет выполняться для всех $a \in (\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })$, $i - \in I_{ - }^{\Delta }$.
Точно так же доказывается п. 2).
В действительности мы можем получить более сильную оценку для производной ${{\dot {z}}_{2}}(0)$.
Следствие 1. Пусть $\Delta > 0$, $\tau \in (0,{{\hat {\tau }}_{\Delta }})$, $\mu \in ({{\mu }_{{\Delta ,1}}}(\tau ),{{\mu }_{{\Delta ,2}}}(\tau ))$, а $({{z}_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{z}_{2}}({\kern 1pt} \cdot {\kern 1pt} )){\text{'}} \in \mathcal{L}_{\mu }^{2}{{C}^{{(0)}}}(\mathbb{R})$ – нестационарное решение вспомогательного функционально-дифференциального уравнения точечного типа (16), (17) с начальными данными $\left( {{{z}_{1}}(0),{{z}_{2}}(0)} \right){\text{'}} = (a,0){\text{'}}$. Тогда
1) если $a \in (\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })$, $i - \in I_{ - }^{\Delta }$, то выполняется условие ${{\dot {z}}_{2}}(0) < {{\Phi }_{\Delta }}(a)$;
2) если $a \in (\alpha _{{i + }}^{\Delta },\beta _{{i + }}^{\Delta })$, $i + \in I_{ + }^{\Delta }$, то выполняется условие ${{\dot {z}}_{2}}(0) > {{\Phi }_{\Delta }}(a)$.
Доказательство. Докажем п. 1). Для рассматриваемых $a$ по лемме 6 имеет место оценка ${{z}_{1}}(0) < a$. Тогда из соотношения (23) и отрицательности потенциала ${{\Phi }_{\Delta }}(a)$ будет следовать оценка ${{\dot {z}}_{2}}(0) < {{\Phi }_{\Delta }}(a)$.
Докажем п. 2). Для рассматриваемых $a$ по предложению 1 имеет место оценка ${{z}_{1}}(0) > a$. Тогда из соотношения (23) и положительности потенциала ${{\Phi }_{\Delta }}(a)$ будет следовать оценка ${{\dot {z}}_{2}}(0) > {{\Phi }_{\Delta }}(a)$. Следствие доказано.
Опишем характер точек пересечения периодического нестационарного решения с горизонтальной осью ${{z}_{1}}$.
Лемма 8. Пусть $\tau \in (0,{{\hat {\tau }}_{\Delta }})$, $\mu \in ({{\mu }_{{\Delta ,1}}}(\tau ),{{\mu }_{{\Delta ,2}}}(\tau ))$, а $({{z}_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{z}_{2}}({\kern 1pt} \cdot {\kern 1pt} )){\text{'}}$ – периодическое нестационарное решение вспомогательного функционально-дифференциального уравнения точечного типа (16), (17) с полупериодом $\hat {t} \ne 0$. Тогда
1) $B \ne \not {0}$ и при некоторых $\bar {t},i - \in I_{ - }^{\Delta }$, $i + \in I_{ + }^{\Delta }$ будут выполняться равенства $\left( {{{z}_{1}}(\bar {t}),{{z}_{2}}(\bar {t})} \right){\text{'}} = (a,0){\text{'}}$, $\left( {{{z}_{1}}(\bar {t} + \hat {t}),{{z}_{2}}(\bar {t} + \hat {t})} \right) = (b,0){\text{'}}$, а также либо включения ${{z}_{1}}(\bar {t}) \in (\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })$, ${{z}_{1}}(\bar {t} + \hat {t}) \in (\alpha _{{i + }}^{\Delta },\beta _{{i + }}^{\Delta })$, либо включения ${{z}_{1}}(\bar {t}) \in (\alpha _{{i + }}^{\Delta },\beta _{{i + }}^{\Delta })$, ${{z}_{1}}(\bar {t} + \hat {t}) \in (\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })$;
2) взаимное расположение интервалов $(\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })$, $(\alpha _{{i + }}^{\Delta },\beta _{{i + }}^{\Delta })$ такое, что $\beta _{{i + }}^{\Delta } \leqslant \alpha _{{i - }}^{\Delta }$.
Доказательство. Очевидно, что для такого периодического решения при любом $\mu \in ({{\mu }_{{\Delta ,1}}}(\tau ),{{\mu }_{{\Delta ,2}}}(\tau ))$ выполняется условие $({{z}_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{z}_{2}}({\kern 1pt} \cdot {\kern 1pt} )){\text{'}} \in \mathcal{L}_{\mu }^{2}{{C}^{{(0)}}}(\mathbb{R})$. По утверждению 3 через каждые начальные значения $(\tilde {a},0){\text{'}}$, $\tilde {a} \in [a,b]$ (либо $\tilde {a} \in [b,a]$) проходит периодическое решение. Множество таких решений индуцирует отображение интервала $[a,b]$ (либо $\tilde {a} \in [b,a]$) в себя. В силу теоремы существования и единственности, а также непрерывной зависимости от начальных условий такое отображение является гомеоморфизмом и имеет неподвижную точку, что и означает условие $B \cap [a,b] \ne \not {0}$ ($B \cap [b,a] \ne \not {0}$). Остальные условия п. 1) следуют из периодичности решения и леммы 7.
Взаимное расположение интервалов из п. 2) следует из леммы 7.
Сформулируем результат о пучке периодических решений.
Лемма 9. Пусть $\tau \in (0,{{\hat {\tau }}_{\Delta }})$, $\mu \in ({{\mu }_{{\Delta ,1}}}(\tau ),{{\mu }_{{\Delta ,2}}}(\tau ))$, а $({{z}_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{z}_{2}}({\kern 1pt} \cdot {\kern 1pt} )){\text{'}}$ – периодическое нестационарное решение вспомогательного функционально-дифференциального уравнения точечного типа (16), (17) с начальными данными $({{z}_{1}}(0),{{z}_{2}}(0)){\text{'}} = (a,0){\text{'}}$, $a \in (\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })$, $i - \in I_{ - }^{\Delta }\left( {a \in (\alpha _{{i + }}^{\Delta },\beta _{{i + }}^{\Delta }),\;i + \in I_{ + }^{\Delta }} \right)$. Тогда для любого $(\bar {a},0)',\bar {a} \in (\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })(\bar {a} \in (\alpha _{{i + }}^{\Delta },\beta _{{i + }}^{\Delta }))$ решение $\left( {{{{\bar {z}}}_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{{\bar {z}}}_{2}}({\kern 1pt} \cdot {\kern 1pt} )} \right){\text{'}} \in \mathcal{L}_{\mu }^{2}{{C}^{{(0)}}}(\mathbb{R})$ с начальными данными $({{\bar {z}}_{1}}(0),{{\bar {z}}_{2}}(0)){\text{'}} = (\bar {a},0){\text{'}}$ также является периодическим.
Доказательство. Очевидно, что для такого периодического решения при любом $\mu \in ({{\mu }_{{\Delta ,1}}}(\tau ),{{\mu }_{{\Delta ,2}}}(\tau ))$ выполняется условие $({{z}_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{z}_{2}}({\kern 1pt} \cdot {\kern 1pt} )){\text{'}} \in \mathcal{L}_{\mu }^{2}{{C}^{{(0)}}}(\mathbb{R})$. По утверждению 3 через каждые начальные значения $(\bar {a},0){\text{'}},\bar {a} \in (\alpha _{{i - }}^{\Delta },a]$ ($\bar {a} \in [a,\beta _{{i + }}^{\Delta })$) проходит периодическое решение. Остается установить этот факт для решений с начальными значениями $(\bar {a},0){\text{'}}$, $\bar {a} \in (a,\beta _{{i - }}^{\Delta })$, ($\bar {a} \in (\alpha _{{i + }}^{\Delta },a)$).
Доказательство проведем для случая $(\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })$. Пусть $\hat {a}$ – верхняя грань таких значений, что через каждое $(\bar {a},0){\text{'}},\bar {a} \in (\hat {a},\beta _{{i - }}^{\Delta })$ проходит периодическое решение. Если $\hat {a} = \beta _{{i - }}^{\Delta }$, то все доказано. Остается рассмотреть случай, когда $\alpha _{{i - }}^{\Delta } < \hat {a} < \beta _{{i - }}^{\Delta }$.
Предположим, что решение $\left( {{{{\hat {z}}}_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{{\hat {z}}}_{2}}({\kern 1pt} \cdot {\kern 1pt} )} \right){\text{'}}$ с начальными значениями $({{\hat {z}}_{1}}(0),{{\hat {z}}_{2}}(0)){\text{'}} = (\hat {a},0){\text{'}}$ также является периодическим с полупериодом $\hat {t}$. Тогда найдется монотонно убывающая последовательность $\alpha _{{i - }}^{\Delta } < {{\bar {a}}^{k}} < \beta _{{i - }}^{\Delta }$, $k = 1,\;2,\; \ldots $, такая, что она стремится к значению $\hat {a}$, и решения $\left( {\bar {z}_{1}^{k}({\kern 1pt} \cdot {\kern 1pt} ),\bar {z}_{2}^{k}({\kern 1pt} \cdot {\kern 1pt} )} \right){\kern 1pt} {\text{'}}$ с начальными значениями $\left( {\bar {z}_{1}^{k}(0),\bar {z}_{2}^{k}(0)} \right){\kern 1pt} {\text{'}} = ({{\bar {a}}^{k}},0){\text{'}}$ не являются периодическими.
В силу п. б) леммы 6 и п. 1) леммы 7 найдется малое $\varepsilon > 0$, что для таких решений при значениях $k$, больших некоторого достаточно большого значения $\underline k $, будут выполняться условия $\bar {z}_{1}^{k}(2\hat {t}) < \hat {a} - \varepsilon $. Тогда в окрестности периодического решения $\left( {{{{\hat {z}}}_{1}}({\kern 1pt} {\kern 1pt} \cdot ),{{{\hat {z}}}_{2}}({\kern 1pt} \cdot {\kern 1pt} )} \right){\text{'}}$ нарушается условие непрерывной зависимости решений от начальных данных. Следовательно, такого периодического решения нет.
Предположим, что решение $\left( {{{{\hat {z}}}_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{{\hat {z}}}_{2}}({\kern 1pt} \cdot {\kern 1pt} )} \right){\text{'}}$ с начальными значениями $\left( {{{{\hat {z}}}_{1}}(0),{{{\hat {z}}}_{2}}(0)} \right){\text{'}} = (\hat {a},0){\text{'}}$ не является периодическим. В силу п. б) леммы 6 и п. 1) леммы 7 для такого решения будут выполняться условия ${{\hat {z}}_{1}}(t) \leqslant \hat {a}$, $t \in \mathbb{R}$, и такое решение при $t > 0$ монотонно убывает. Тогда в окрестности непериодического решения $({{\hat {z}}_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{\hat {z}}_{2}}({\kern 1pt} \cdot {\kern 1pt} )){\text{'}}$ также нарушается условие непрерывной зависимости решений от начальных данных. Следовательно, условие $\alpha _{{i - }}^{\Delta } < \hat {a} < \beta _{{i - }}^{\Delta }$ не выполнимо, и $\hat {a} = \beta _{{i - }}^{\Delta }$.
Доказательство для случая $a \in (\alpha _{{i + }}^{\Delta },\beta _{{i + }}^{\Delta })$ проводится аналогичным образом. Лемма доказана.
Следствие 2. Пусть $\tau \in (0,{{\hat {\tau }}_{\Delta }}),\mu \in ({{\mu }_{{\Delta ,1}}}(\tau ),{{\mu }_{{\Delta ,2}}}(\tau ))$, а $({{z}_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{z}_{2}}({\kern 1pt} \cdot {\kern 1pt} )){\text{'}}$ – периодическое нестационарное решение вспомогательного функционально-дифференциального уравнения точечного типа $(16)$, $(17)$ с полупериодом $\hat {t}$. Тогда справедливы условия 1) и 2) леммы 8. Для любого $a{\text{'}} \in (\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })$ ($a{\text{'}} \in (\alpha _{{i + }}^{\Delta },\beta _{{i + }}^{\Delta })$) существует периодическое решение $({{z}_{1}}( \cdot ),{{z}_{2}}( \cdot )){\text{'}}$ с начальными данными $\left( {{{z}_{1}}(\bar {t}),{{z}_{2}}(\bar {t})} \right){\kern 1pt} {\text{'}} = (a{\text{'}},0){\text{'}}$ и полупериодом ${{\hat {t}}_{{a'}}}$ такое, что $\left( {{{z}_{1}}(\bar {t} + {{{\hat {t}}}_{{a'}}}),{{z}_{2}}(\bar {t} + {{{\hat {t}}}_{{a'}}})} \right){\kern 1pt} {\text{'}} = (b{\text{'}},0){\text{'}}$, $b{\text{'}} \in (\alpha _{{i + }}^{\Delta },\beta _{{i + }}^{\Delta })$, $\left( {b{\text{'}} \in (\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })} \right)$, и такое соответствие точек интервала $(\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })$ точкам интервала $(\alpha _{{i + }}^{\Delta },\beta _{{i + }}^{\Delta })$ задает гомеоморфизм.
Доказательство следствия непосредственно следует из лемм 1, 8, 9, а также теоремы существования и единственности решения системы (16), (17) и их непрерывной зависимости от начальных данных.
Теперь мы можем уточнить утверждения леммы 8.
Лемма 10. Пусть $\tau \in (0,{{\hat {\tau }}_{\Delta }})$, $\mu \in ({{\mu }_{{\Delta ,1}}}(\tau ),{{\mu }_{{\Delta ,2}}}(\tau ))$, а $({{z}_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{z}_{2}}({\kern 1pt} \cdot {\kern 1pt} )){\text{'}}$ – периодическое нестационарное решение вспомогательного функционально-дифференциального уравнения точечного типа (16), (17) с полупериодом $\hat {t} \ne 0$. Тогда
1) $B \ne \not {0}$ и при некоторых $\bar {t},i - \in I_{ - }^{\Delta }$, $i + \in I_{ + }^{\Delta }$ будут выполняться равенства $\left( {{{z}_{1}}(\bar {t}),{{z}_{2}}(\bar {t})} \right){\text{'}} = (a,0){\text{'}}$, $\left( {{{z}_{1}}(\bar {t} + \hat {t}),{{z}_{2}}(\bar {t} + \hat {t})} \right){\kern 1pt} {\text{'}} = (b,0){\text{'}}$, а также либо включения ${{z}_{1}}(\bar {t}) \in (\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })$, ${{z}_{1}}(\bar {t} + \hat {t}) \in (\alpha _{{i + }}^{\Delta },\beta _{{i + }}^{\Delta })$, либо включения ${{z}_{1}}(\bar {t}) \in (\alpha _{{i + }}^{\Delta },\beta _{{i + }}^{\Delta })$, ${{z}_{1}}(\bar {t} + \hat {t}) \in (\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })$;
2) взаимное расположение интервалов $(\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })$, $(\alpha _{{i + }}^{\Delta },\beta _{{i + }}^{\Delta })$ такое, что $\beta _{{i + }}^{\Delta } \leqslant \alpha _{{i - }}^{\Delta }$;
3) для любого $(\bar {a},0){\text{'}}$, $\bar {a} \in (\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })(\bar {a} \in (\alpha _{{i + }}^{\Delta },\beta _{{i + }}^{\Delta }))$ решение $\left( {{{{\bar {z}}}_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{{\bar {z}}}_{2}}({\kern 1pt} \cdot {\kern 1pt} )} \right){\kern 1pt} {\text{'}} \in \mathcal{L}_{\mu }^{2}{{C}^{{(0)}}}(\mathbb{R})$ с начальными данными $({{\bar {z}}_{1}}(0),{{\bar {z}}_{2}}(0)){\text{'}} = (\bar {a},0){\text{'}}$ также является периодическим;
4) $\alpha _{{i + }}^{\Delta } = - \infty ,\beta _{{i - }}^{\Delta } = + \infty $.
Доказательство. Доказательства пунктов 1) и 2) следуют из леммы 8, п. 3) – из леммы 9. Остается показать справедливость п. 4).
Предположим, что значение $\alpha _{{i + }}^{\Delta }$ конечно. Тогда в окрестности стационарного решения $(\alpha _{{i + }}^{\Delta },0){\kern 1pt} '$ нарушается непрерывная зависимость от начальных значений. Аналогично проводится доказательство и для значения $\beta _{{i - }}^{\Delta }$. Лемма доказана.
Опишем свойства как периодических, так и непериодических пучков решений.
Лемма 11. Пусть $\Delta > 0$, $\tau \in \left( {0,{{{\hat {\tau }}}_{\Delta }}} \right)$, $\mu \in ({{\mu }_{{\Delta ,1}}}(\tau ),{{\mu }_{{\Delta ,2}}}(\tau ))$, а $({{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z} }_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z} }_{2}}({\kern 1pt} \cdot {\kern 1pt} )){\text{'}} \in \mathcal{L}_{\mu }^{2}{{C}^{{(0)}}}(\mathbb{R})$ – нестационарное решение вспомогательного функционально-дифференциального уравнения точечного типа (16), (17) с начальными данными $({{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z} }_{1}}(0),{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z} }_{2}}(0)){\text{'}} = (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} ,0){\text{'}}$.
Если $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} \in (\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })$, $i - \in I_{ - }^{\Delta }$, то
1) либо для любого $a \in (\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })$ решение $({{z}_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{z}_{2}}({\kern 1pt} \cdot {\kern 1pt} )){\text{'}} \in \mathcal{L}_{\mu }^{2}{{C}^{{(0)}}}(\mathbb{R})$ с начальными данными $({{z}_{1}}(0),{{z}_{2}}(0)){\text{'}} = (a,0){\text{'}}$ является нестационарным периодическим с полупериодом ${{\hat {t}}_{a}}$, и выполняются условия ${{\dot {z}}_{2}}(0) < 0$, ${{z}_{1}}({{\hat {t}}_{a}}) \leqslant {{z}_{1}}(t) \leqslant a$, $t \in [ - {{\hat {t}}_{a}},{{\hat {t}}_{a}}]$, причем при $t \in [0, - {{\hat {t}}_{a}}]$ функция ${{z}_{1}}( \cdot )$ монотонно возрастающая, а при $t \in [0,{{\hat {t}}_{a}}]$ функция ${{z}_{1}}( \cdot )$ монотонно убывающая;
2) либо для любого $a \in (\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })$ решение $({{z}_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{z}_{2}}({\kern 1pt} \cdot {\kern 1pt} )){\text{'}} \in \mathcal{L}_{\mu }^{2}{{C}^{{(0)}}}(\mathbb{R})$ с начальными данными $({{z}_{1}}(0),{{z}_{2}}(0)){\text{'}} = (a,0){\text{'}}$ является непериодическим, и выполняется условие ${{\dot {z}}_{2}}(0) < 0$; для $t \in ( - \infty ,0)$ выполнены оценки ${{z}_{2}}(t) > 0$, ${{z}_{1}}(t) < a$ и первая координата ${{z}_{1}}(t)$ монотонно возрастает; для $t \in (0,\infty )$ выполнены оценки ${{z}_{2}}(t) < 0$, ${{z}_{1}}(t) < a$ и первая координата ${{z}_{1}}(t)$ монотонно убывает.
Если $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} \in (\alpha _{{i + }}^{\Delta },\beta _{ + }^{\Delta })$, $i + \in I_{ + }^{\Delta }$, то
1) либо для любого $a \in (\alpha _{{i + }}^{\Delta },\beta _{{i + }}^{\Delta })$ решение $({{z}_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{z}_{2}}({\kern 1pt} \cdot {\kern 1pt} )){\text{'}} \in \mathcal{L}_{\mu }^{2}{{C}^{{(0)}}}(\mathbb{R})$ с начальными данными $({{z}_{1}}(0),{{z}_{2}}(0)){\text{'}} = (a,0){\text{'}}$ является нестационарным периодическим с полупериодом ${{\hat {t}}_{a}}$, и выполняются условия ${{\dot {z}}_{2}}(0) > 0$, $a \leqslant {{z}_{1}}(t) \leqslant {{z}_{1}}({{\hat {t}}_{a}})$ при $t \in [ - {{\hat {t}}_{a}},{{\hat {t}}_{a}}]$, причем, при $t \in [0, - {{\hat {t}}_{a}}]$ функция ${{z}_{1}}( \cdot )$ монотонно убывающая, а при $t \in [0,{{\hat {t}}_{a}}]$ функция ${{z}_{1}}( \cdot )$ монотонно возрастающая;
2) либо для любого $a \in (\alpha _{{i + }}^{\Delta },\beta _{{i + }}^{\Delta })$ решение $({{z}_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{z}_{2}}({\kern 1pt} \cdot {\kern 1pt} )){\text{'}} \in \mathcal{L}_{\mu }^{2}{{C}^{{(0)}}}(\mathbb{R})$ с начальными данными $({{z}_{1}}(0),{{z}_{2}}(0)){\text{'}} = (a,0){\text{'}}$ является непериодическим, и выполняется условие ${{\dot {z}}_{2}}(0) > 0$; для $t \in ( - \infty ,0)$ выполнены оценки ${{z}_{2}}(t) < 0$, ${{z}_{1}}(t) > a$ и первая координата ${{z}_{1}}(t)$ монотонно убывает; для $t \in (0,\infty )$ выполнены оценки ${{z}_{2}}(t) > 0$, ${{z}_{1}}(t) > a$ и первая координата ${{z}_{1}}(t)$ монотонно возрастает.
Доказательство непосредственно следует из лемм 6 и 9.
Теперь мы можем описать качественное поведение непериодических решений $({{z}_{1}}({\kern 1pt} \cdot ),{{z}_{2}}({\kern 1pt} \cdot {\kern 1pt} )){\text{'}} \in \mathcal{L}_{\mu }^{2}{{C}^{{(0)}}}(\mathbb{R})$ вспомогательного функционально-дифференциального уравнения точечного типа с начальными данными $({{z}_{1}}(0),{{z}_{2}}(0)){\text{'}} = (a,0){\text{'}}$, $a \in \mathbb{R}$.
Предложение 1. Пусть заданы $\Delta > 0$ и $\tau \in \left( {0,{{{\hat {\tau }}}_{\Delta }}} \right)$, $\mu \in ({{\mu }_{{\Delta 1}}}(\tau ),{{\mu }_{{\Delta 2}}}(\tau ))$, а $({{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z} }_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z} }_{2}}({\kern 1pt} \cdot {\kern 1pt} )){\text{'}} \in \mathcal{L}_{\mu }^{2}{{C}^{{(0)}}}(\mathbb{R})$ – непериодическое решение вспомогательного функционально-дифференциального уравнения точечного типа (16), (17) с начальными данными $({{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z} }_{1}}(0),{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{z} }_{2}}(0)){\text{'}} = (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} ,0){\text{'}}$.
1) Если $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} \in (\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })$, $i - \in I_{ - }^{\Delta }$, то при любых $a \in (\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })$ решение $({{z}_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{z}_{2}}({\kern 1pt} \cdot {\kern 1pt} )){\text{'}} \in \mathcal{L}_{\mu }^{2}{{C}^{{(0)}}}(\mathbb{R})$ с начальными данными $({{z}_{1}}(0),{{z}_{2}}(0)){\text{'}} = (a,0){\text{'}}$ является непериодическим, по первой координате ${{z}_{1}}$ не покидает интервал $(\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })$, выполняются соотношения $\mathop {\lim }\nolimits_{t \to \pm \infty } {{z}_{1}}(t) = \alpha _{{i - }}^{\Delta }$, а также соотношения $\mathop {\lim }\nolimits_{t \to \pm \infty } {{z}_{2}}(t) = 0$ при конечном $\alpha _{{i - }}^{\Delta }$. В случае конечности одной из величин $\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta }$ граница области фазовых кривых таких решений состоит из двух сепаратрис $({{\bar {z}}_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{\bar {z}}_{2}}({\kern 1pt} \cdot {\kern 1pt} )){\text{'}} \in \mathcal{L}_{\mu }^{2}{{C}^{{(0)}}}(\mathbb{R})$, $({{\underline z }_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{\underline z }_{2}}({\kern 1pt} \cdot {\kern 1pt} )){\text{'}} \in \mathcal{L}_{\mu }^{2}{{C}^{{(0)}}}(\mathbb{R})$ со свойствами
(27)
$\mathop {\lim }\limits_{t \to - \infty } {{\bar {z}}_{1}}(t) = \mathop {\lim }\limits_{t \to + \infty } {{\underline z }_{1}}(t) = \alpha _{{i - }}^{\Delta },\quad \mathop {\lim }\limits_{t \to + \infty } {{\bar {z}}_{1}}(t) = \mathop {\lim }\limits_{t \to - \infty } {{\underline z }_{1}}(t) = \beta _{{i - }}^{\Delta },$(28)
$\mathop {\lim }\limits_{t \to - \infty } {{\bar {z}}_{2}}(t) = \mathop {\lim }\limits_{t \to + \infty } {{\underline z }_{2}}(t) = 0\quad \left( {\mathop {\lim }\limits_{t \to + \infty } {{{\bar {z}}}_{2}}(t) = \mathop {\lim }\limits_{t \to - \infty } {{{\underline z }}_{2}}(t) = 0} \right).$2) Если $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} \in (\alpha _{{i + }}^{\Delta },\beta _{{i + }}^{\Delta })$, $i + \in I_{ + }^{\Delta }$, то при любых $a \in (\alpha _{{i + }}^{\Delta },\beta _{{i + }}^{\Delta })$ решение $({{z}_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{z}_{2}}({\kern 1pt} \cdot {\kern 1pt} )){\text{'}} \in \mathcal{L}_{\mu }^{2}{{C}^{{(0)}}}(\mathbb{R})$ с начальными данными $({{z}_{1}}(0),{{z}_{2}}(0)){\text{'}} = (a,0){\text{'}}$ является непериодическим, по первой координате ${{z}_{1}}$ не покидает интервал $(\alpha _{{i + }}^{\Delta },\beta _{{i + }}^{\Delta })$, и выполняются соотношения $\mathop {\lim }\nolimits_{t \to \pm \infty } {{z}_{1}}(t) = \beta _{{i + }}^{\Delta }$, а также соотношения $\mathop {\lim }\nolimits_{t \to \pm \infty } {{z}_{2}}(t) = 0$ при конечном $\beta _{{i + }}^{\Delta }$. В случае конечности одной из величин $\alpha _{{i + }}^{\Delta }$, $\beta _{{i + }}^{\Delta }$ граница области фазовых кривых таких решений состоит из двух сепаратрис $({{\bar {z}}_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{\bar {z}}_{2}}({\kern 1pt} \cdot {\kern 1pt} )){\text{'}} \in \mathcal{L}_{\mu }^{2}{{C}^{{(0)}}}(\mathbb{R})$, $({{\underline z }_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{\underline z }_{2}}({\kern 1pt} \cdot {\kern 1pt} )){\text{'}} \in \mathcal{L}_{\mu }^{2}{{C}^{{(0)}}}(\mathbb{R})$ со свойствами
(29)
$\mathop {\lim }\limits_{t \to - \infty } {{\bar {z}}_{1}}(t) = \mathop {\lim }\limits_{t \to + \infty } {{\underline z }_{1}}(t) = \alpha _{{i + }}^{\Delta },\quad \mathop {\lim }\limits_{t \to + \infty } {{\bar {z}}_{1}}(t) = \mathop {\lim }\limits_{t \to - \infty } {{\underline z }_{1}}(t) = \beta _{{i + }}^{\Delta },$(30)
$\mathop {\lim }\limits_{t \to - \infty } {{\bar {z}}_{2}}(t) = \mathop {\lim }\limits_{t \to + \infty } {{\underline z }_{2}}(t) = 0\quad (\mathop {\lim }\limits_{t \to + \infty } {{\bar {z}}_{2}}(t) = \mathop {\lim }\limits_{t \to - \infty } {{\underline z }_{2}}(t) = 0).$Доказательство. Сформулируем ряд утверждений относительно качественного поведения решений. Пусть заданы $a \in (\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })$, $i - \in I_{ - }^{\Delta }$ ($a \in (\alpha _{{i + }}^{\Delta },\beta _{{i + }}^{\Delta })$, $i + \in I_{ + }^{\Delta }$).
Утверждение (i). Пусть решение с начальными значениями $({{z}_{1}}(0),{{z}_{2}}(0)){\text{'}} = (a,0){\text{'}}$, $a \in (\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })$, $i - \in I_{ - }^{\Delta }$ ($a \in (\alpha _{{i + }}^{\Delta },\beta _{{i + }}^{\Delta })$, $i + \in I_{ + }^{\Delta }$) по первой координате ${{z}_{1}}$ не покидает интервал ($(\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })$ $(\alpha _{{i + }}^{\Delta },\beta _{{i + }}^{\Delta })$). Тогда для такого решения справедливы утверждения доказываемого предложения.
Доказательство утверждения (i). Рассматриваемое решение будет удовлетворять всем условиям монотонности из леммы 6. Тогда функция ${{z}_{1}}(t)$, $t \in \mathbb{R}$, монотонна на полупрямых $t \in ( - \infty ,0)$, $t \in (0, + \infty )$ и соответственно конечные пределы $\mathop {\lim }\nolimits_{t \to \pm \infty } {{z}_{1}}(t) = A$ существуют и при $\alpha _{{i - }}^{\Delta } = - \infty $ ($\beta _{{i + }}^{\Delta } = + \infty $) имеет место равенство $A = - \infty $ ($A = + \infty $). Наличие сепаратрис с отмеченными свойствами является следствием теоремы о непрерывной зависимости решения от начальных данных. Остается рассмотреть случай конечного $\alpha _{{i - }}^{\Delta }$ ($\beta _{{i + }}^{\Delta }$). Если для такого решения вторая координата ${{z}_{2}}(t)$, $t \in \mathbb{R}$, окажется ограниченной, то утверждения о предельных переходах будет следовать из теоремы существования и единственности решения для рассматриваемого функционально-дифференциального уравнения точечного типа и теоремы о продолжении решения до непродолжаемого, основанной на ней.
Покажем ограниченность координаты ${{z}_{2}}(t)$, $t \in \mathbb{R}$. Мы уже отмечали, что функция ${{z}_{1}}(t)$, $t \in \mathbb{R}$, монотонна на полупрямых $t \in ( - \infty ,0)$, $t \in (0, + \infty )$ и соответственно пределы $\mathop {\lim }\nolimits_{t \to \pm \infty } {{z}_{1}}(t) = A$ существуют. При больших $\left| t \right| > N$ величина $\left[ {{{z}_{1}}(t - \tau ) - 2{{z}_{1}}(t) + {{z}_{1}}(t + \tau )} \right]$ будет сколь угодно малой. Если $A \ne \alpha _{{i - }}^{\Delta }$ при $i - \in I_{ - }^{\Delta }$ ($A \ne \beta _{{i + }}^{\Delta }$ при $i + \in I_{ + }^{\Delta }$), то потенциал ${{\Phi }_{\Delta }}({{z}_{1}}(t))$ при больших $\left| t \right| > N$ не равен нулю и в силу системы (16), (17) условия $\mathop {\lim }\nolimits_{t \to \pm \infty } {{z}_{1}}(t) = A$ при $i - \in I_{ - }^{\Delta }$ ($\mathop {\lim }\nolimits_{t \to \pm \infty } {{z}_{1}}(t) = A$ при $i + \in I_{ + }^{\Delta }$) нарушаются. Следовательно, $A = \alpha _{{i - }}^{\Delta }$ при $i - \in I_{ - }^{\Delta }$ и $A = \beta _{{i + }}^{\Delta }$ при $i + \in I_{ + }^{\Delta }$. Поэтому при больших $\left| t \right| > N$ правая часть уравнения (17) будет сколь угодно малой и в силу уравнения (16) при $\left| t \right| > N$ значения ${{z}_{2}}(t)$ будут не только ограниченными, но будут удовлетворять также и условию $\mathop {\lim }\nolimits_{t \to \pm \infty } {{z}_{2}}(t) = 0$.
Наличие сепаратрис с отмеченными свойствами является следствием теоремы о непрерывной зависимости решения от начальных данных. Качественное поведение решений, описанное в предложении 1, показано на фиг. 2. Утверждение (i) доказано.
Остается показать, что решения с начальными значениями $({{z}_{1}}(0),{{z}_{2}}(0)){\text{'}} = (a,0){\text{'}}$, $a \in (\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })$, $i - \in I_{{i - }}^{\Delta }$ ($a \in (\alpha _{{i + }}^{\Delta },\beta _{{i + }}^{\Delta })$, $i + \in I_{{i + }}^{\Delta }$) по первой координате ${{z}_{1}}$ не покидают интервал $(\alpha _{i}^{\Delta },\beta _{i}^{\Delta })$. Сформулируем результат о структуре решений, если известен характер одного из рассматриваемых решений.
Утверждение (ii). Пусть задано решение $({{\tilde {z}}_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{\tilde {z}}_{2}}({\kern 1pt} \cdot {\kern 1pt} )){\text{'}} \in \mathcal{L}_{\mu }^{2}{{C}^{{(0)}}}(\mathbb{R})$ с начальными значениями
Доказательство утверждения (ii) следует из теоремы существования и единственности решения для рассматриваемого функционально-дифференциального уравнения точечного типа.
Теперь мы можем окончательно сформулировать результат о структуре решений с начальными данными $(a,0)'$, где $a$ принадлежит интервалам $(\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta }),i - \in I_{ - }^{\Delta }$ ($(\alpha _{{i + }}^{\Delta },\beta _{{i + }}^{\Delta })$, $i + \in I_{ + }^{\Delta }$).
Утверждение (iii). В условиях доказываемого предложения всякое решение $({{z}_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{z}_{2}}({\kern 1pt} \cdot {\kern 1pt} )){\text{'}} \in \mathcal{L}_{\mu }^{2}{{C}^{{(0)}}}(\mathbb{R})$ с начальными условиями
Доказательство утверждения (iii). Для определенности будем рассматривать случай $i - \in I_{ - }^{\Delta }$. Предположим, что при каком-либо $\tilde {a} \in (\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })$ решение по первой координате ${{z}_{1}}$ покидает рассматриваемый интервал $(\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })$. В утверждении (ii) описан характер целого семейства решений, связанного с таким решением. Через $\underline a $ обозначим минимальное среди таких $\tilde {a}$.
Если $\underline a = \alpha _{{i - }}^{\Delta }$, то в силу непериодичности решений с начальными данными $(a,0){\text{'}}$, $a \in (\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })$ в окрестности стационарного решения $(\alpha _{{i - }}^{\Delta },0){\kern 1pt} {\text{'}}$ нарушается непрерывная зависимость от начальных значений.
Если $\underline a \in (\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })$, то по утверждению (ii) при каждом $\tilde {a} \in (\underline a ,\beta _{{i - }}^{\Delta })$ решение по первой координате ${{z}_{1}}$ также покидает интервал $(\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })$, а при каждом $\tilde {a} \in (\alpha _{{i - }}^{\Delta },\underline a )$ решение по первой координате ${{z}_{1}}$ не покидает интервал $(\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })$ и его поведение описано в пункте (i).
В случае, если само решение $({{\underline z }_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{\underline z }_{2}}({\kern 1pt} \cdot {\kern 1pt} )){\text{'}}$ с начальными значениями $({{\underline z }_{1}}(0),{{\underline z }_{2}}(0)){\text{'}} = (\underline a ,0){\text{'}}$ по первой координате ${{\underline z }_{1}}$ также покидает интервал $(\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })$, то в окрестности такого решения нарушается непрерывная зависимость от начальных значений. Остается рассмотреть случай, когда решение $({{\underline z }_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{\underline z }_{2}}({\kern 1pt} \cdot {\kern 1pt} )){\text{'}}$ с начальными значениями $({{\underline z }_{1}}(0),{{\underline z }_{2}}(0)){\text{'}} = (\underline a ,0){\text{'}}$ по первой координате ${{\underline z }_{1}}$ не покидает интервал $(\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })$. В окрестности такого решения также нарушается непрерывная зависимость от начальных значений. Следовательно, $\underline a = \beta _{{i - }}^{\Delta }$ и при всех $\tilde {a} \in (\alpha _{{i - }}^{\Delta },\beta _{{i - }}^{\Delta })$ решение по первой координате ${{z}_{1}}$ не покидает рассматриваемый интервал. Такое же утверждение может быть доказано и для случая $i + \in I_{ + }^{\Delta }$.
Завершим доказательство предложения. По утверждению (iii) решения с начальными условиями $({{z}_{1}}(0),{{z}_{2}}(0)){\text{'}} = (a,0){\text{'}}$ по первой координате ${{z}_{1}}$ не покидают интервал, которому принадлежит $a$. Тогда, в силу утверждения (i), для таких решений справедливы все утверждения доказываемого предложения.
Дадим комментарий к фиг. 3. Малыми кругами обозначены стационарные решения, имеющие гиперболический тип. Крестиками обозначены стационарные решения, являющиеся стоками и истоками для одних и тех же решений и имеющие также гиперболический тип. Штриховыми линиями обозначены сепаратрисы, а коричневым цветом обозначены решения, неограниченные по первой координате ${{z}_{1}}$.
3. ВОПРОСЫ СУЩЕСТВОВАНИЯ ОГРАНИЧЕННЫХ СОЛИТОННЫХ РЕШЕНИЙ ПРИ НЕЛИНЕЙНОМ ПОТЕНЦИАЛЕ. ОСНОВНОЙ РЕЗУЛЬТАТ
Сформулируем предложение об отсутствии при любом $\Delta > 0$ решения, ограниченного по первой координате ${{z}_{1}}$, для вспомогательного функционально-дифференциального уравнения точечного типа (16), (17) с квазилинейным потенциалом ${{\Phi }_{\Delta }}$.
Предложение 2. Если нули нелинейного потенциала $\Phi $ отсутствуют, т.е. $B = \not {0}$, то при любом $\Delta > 0$ для вспомогательного функционально-дифференциального уравнения точечного типа $(16)$, $(17)$ с квазилинейным потенциалом ${{\Phi }_{\Delta }}$ для любых $\tau \in \left( {0,{{{\hat {\tau }}}_{\Delta }}} \right)$ и $\mu ,{{\mu }^{\tau }} \in ({{\mu }_{{\Delta 1}}}(\tau ),{{\mu }_{{\Delta 2}}}(\tau ))$ не существует решения $({{z}_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{z}_{2}}({\kern 1pt} \cdot {\kern 1pt} )){\text{'}} \in \mathcal{L}_{\mu }^{2}{{C}^{{(0)}}}(\mathbb{R})$, ограниченного по первой координате ${{z}_{1}}$ с условием ограниченности $\left| {{{z}_{1}}(t)} \right| < \Delta $, $t \in \mathbb{R}$.
Доказательство. Так как отсутствуют нули у нелинейного потенциала $\Phi $, то такой потенциал знакопостоянный. Тогда при любом $\Delta > 0$ имеется либо единственный интервал $(\alpha _{ - }^{\Delta },\beta _{ - }^{\Delta })$, $\alpha _{ - }^{\Delta } = - \infty $, $\beta _{ - }^{\Delta } = + \infty $ в случае отрицательного потенциала, либо единственный интервал $(\alpha _{ + }^{\Delta },\beta _{ + }^{\Delta })$, $\alpha _{ + }^{\Delta } = - \infty $, $\beta _{ + }^{\Delta } = + \infty $ в случае положительного потенциала.
Рассмотрим случай отрицательного нелинейного потенциала $\Phi $. По лемме 10 в силу условия $B = \not {0}$ у вспомогательного функционально-дифференциального уравнения точечного типа (16), (17) с квазилинейным потенциалом ${{\Phi }_{\Delta }}$ не существует периодического решения. Предположим, что у вспомогательного функционально-дифференциального уравнения точечного типа (16), (17) с квазилинейным потенциалом ${{\Phi }_{\Delta }}$ при некоторых $\tau \in \left( {0,{{{\hat {\tau }}}_{\Delta }}} \right)$ и $\mu ,{{\mu }^{\tau }} \in ({{\mu }_{{\Delta 1}}}(\tau ),{{\mu }_{{\Delta 2}}}(\tau ))$ существует решение $({{\bar {z}}_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{\bar {z}}_{2}}({\kern 1pt} \cdot {\kern 1pt} )){\text{'}} \in \mathcal{L}_{\mu }^{2}{{C}^{{(0)}}}(\mathbb{R})$, ограниченное по первой координате ${{z}_{1}}$ с условием ограниченности $\left| {{{{\bar {z}}}_{1}}(t)} \right| < \Delta $, $t \in \mathbb{R}$. В силу уравнения (16) найдутся $\bar {a},\bar {t} \in \mathbb{R}$, такие, что $({{\bar {z}}_{1}}(\bar {t}),{{\bar {z}}_{2}}\left( {\bar {t}} \right)){\text{'}} = (\bar {a},0){\text{'}}$. Для данного решения в силу предложения 1 должны выполняться условия $\mathop {\lim }\nolimits_{t \to \pm \infty } {{\bar {z}}_{1}}(t) = \alpha _{ - }^{\Delta } = - \infty $, что противоречит ограниченности решения по первой координате. Следовательно, такого ограниченного решения не существует. Точно так же доказательство проводится и в случае положительного нелинейного потенциала $\Phi $.
Сформулируем результат о существовании ограниченного по первой координате решения индуцированного функционально-дифференциального уравнения.
Tеорема 3. Пусть задано $\Delta > 0$ и $B \cap [ - \Delta ,\Delta ] \ne \not {0}$. Тогда для любых $\tau \in \left( {0,{{{\hat {\tau }}}_{\Delta }}} \right)$ и $\mu ,{{\mu }^{\tau }} \in ({{\mu }_{{\Delta 1}}}(\tau ),{{\mu }_{{\Delta 2}}}(\tau ))$ решение $({{z}_{1}}({\kern 1pt} \cdot {\kern 1pt} ),{{z}_{2}}({\kern 1pt} \cdot {\kern 1pt} )){\text{'}} \in \mathcal{L}_{\mu }^{2}{{C}^{{(0)}}}(\mathbb{R})$ индуцированного функционально-дифференциального уравнения точечного типа (12), (13) с нелинейным потенциалом и начальными значениями $({{z}_{1}}(0),{{z}_{2}}(0)){\text{'}} = (a,0){\text{'}}$ существует и единственно при всех таких $a$, что
Доказательство. В силу лемм 8 и 10, а также предложения 1, для соответствующего вспомогательного функционально-дифференциального уравнения точечного типа (16), (17) с начальными условиями
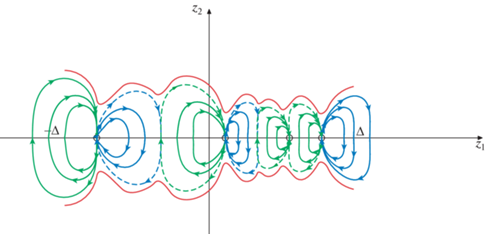
Дадим комментарий к фиг. 4. На фиг. 4 по сравнению с фиг. 3 сохранены только те ограниченные по координате ${{z}_{1}}$ решения, которые принадлежат цилиндру $\{ ({{z}_{1}},{{z}_{2}}):{{z}_{1}} \in [ - \Delta ,\Delta ]\} $, так как только такие решения вспомогательного функционально-дифференциального уравнения точечного типа с квазилинейным потенциалом ${{\Phi }_{\Delta }}$ являются одновременно и решениями индуцированного функционально-дифференциального уравнения точечного типа c нелинейным потенциалом общего вида.
Фиг. 4.
Качественная картина ограниченных решений для индуцированного функционально-дифференциального уравнения точечного типа с нелинейным потенциалом $\Phi $ общего вида.
Теперь мы можем привести эквивалентную переформулировку теоремы 3 о существовании решения индуцированного функционально-дифференциального уравнения точечного типа (системы (12), (13)), ограниченного по первой координате. Такая переформулировка примет форму основного результата о существовании ограниченных солитонных решений для исходного волнового уравнения (для системы (2), (3)).
Tеорема 4. Пусть задано $\Delta > 0$ и $B \cap [ - \Delta ,\Delta ] \ne \not {0}$. Тогда для системы (2), (3) с нелинейным потенциалом $\Phi $ общего вида для любых $\tau $, $0 < \tau < {{\hat {\tau }}_{\Delta }}$ и $\mu ,{{\mu }^{\tau }} \in ({{\mu }_{1}}(\tau ),{{\mu }_{2}}(\tau ))$ существует и единственное солитонное решение $\omega (t) = \{ ({{y}_{i}}(t),{{\dot {y}}_{i}}(t))\} _{{ - \infty }}^{{{\text{'}} + \infty }}$, $t \in \mathbb{R}$ с характеристикой $\tau $ и начальными данными
Доказательство. По теореме 3 для каждого рассматриваемого начального данного $(a,0)'$ существует, причем единственное, решение $({{z}_{1}}(t),{{z}_{2}}(t)){\text{'}}$, $t \in \mathbb{R}$, индуцированного функционально-дифференциального уравнения точечного типа (12), (13) с нелинейным потенциалом $\Phi $ общего вида, с начальным условием $({{z}_{1}}(0),{{z}_{2}}(0))' = (a,0)'$ и условием ограниченности по первой координате $\left| {{{z}_{1}}(t)} \right| \leqslant \Delta ,\;t \in \mathbb{R}$. В силу соотношений (9) решению $({{z}_{1}}(t),{{z}_{2}}(t)){\text{'}}$, $t \in \mathbb{R}$, с начальными данными $({{z}_{1}}(0),{{z}_{2}}(0)){\text{'}} = (a,0){\text{'}}$ соответствует солитонное решение $\{ ({{y}_{i}}(t),{{\dot {y}}_{i}}(t))\} _{{ - \infty }}^{{' + \infty }}$, $t \in \mathbb{R}$, системы (2), (3) с нелинейным потенциалом $\Phi $ общего вида, характеристикой $\tau $, начальными условиями $({{y}_{0}}(0),{{\dot {y}}_{0}}(0)){\text{'}} = (a,0){\text{'}}$ и условием ограниченности $\left| {{{y}_{0}}(t)} \right| \leqslant \Delta $, $t \in \mathbb{R}$.
Список литературы
Toda M. Theory of nonlinear lattices. Berlin: Springer, 1989. https://doi.org/10.1007/978-3-642-83219-2
Miwa T., Jimbo M., Date E. Solitons: differential equations, symmetries and infinite dimensional algebras. Cambridge Univer. Press, UK, 2000.
Frenkel Y.I., Contorova T.A. On the theory of plasti deformation and twinning // J. Exp. Theor. Phys. 1938. V. 8. P. 89–95.
Pustyl'nikov L.D. Infinite-dimensional non-linear ordinary differential equations and the KAM theory // Rus. Math. Surveys. 1997. V. 52. P. 551–604. https://doi.org/10.1070/RM1997v052n03ABEH001810
Beklaryan L.A. A boundary value problem for a differential equation with deviating argument // Dokl. Akad. Nauk. SSSR 1986. V. 291. P. 19–22.
Beklaryan L.A. A differential equation with deviating argument as an infinite-dimensional dynamical system // Rep. Appl. Math., Akad. Nauk SSSR, Vychisl. Tsentr. Moscow, 1989.
Beklaryan L.A. Introduction to the theory of functional differential equations and their applications. Group approach // J. of Math. Sci. 2006. V. 13. P. 2813–2954. https://doi.org/10.1007/s10958-006-0145-3
Beklaryan L.A. Introduction to the theory of functional differential equations. Group approach. Moscow: Factorial Press, 2007.
Keener J.P. Propagation and its failure in coupled systems of discrete excitable cells // SIAM J. on Appl. Math. 1987. V. 47. P. 556–572. https://doi.org/10.1137/0147038
Zinner B. Existence of traveling wavefront solutions for the dis rete Nagumo equation // J. of Different. Equat. 1992. V. 96. P. 1–27. https://doi.org/10.1016/0022- 0396(92)90142-A
Mallet-Paret J. The global structure of traveling waves in spatially dis rete dynamical systems // J. of Dynamic. and Different. Equations 1999. V. 11. P. 49–127. https://doi.org/10.1023/A:1021841618074
Van Vleck E.S., Mallet-Paret J., Cahn J.W. Traveling wave solutions for systems of ODEs on a two-dimensional spatial lattice // SIAM J. on Appl. Math. 1998. V. 59. P. 455–493. https://doi.org/10.1137/S0036139996312703
Beklaryan L.A. Quasitravelling waves // Sbornik: Mathematics. 2010. V. 201. P. 1731–1775. https://doi.org/10.1070/SM2010v201n12ABEH004129
Beklaryan L.A. Quasi-travelling waves as natural extension of lass of traveling waves // Tambov Univer. Rep. Ser. Natural and Technic. Sci. 2014. V. 19. P. 331–340.
Beklaryan L.A. A new approa h to the question of the existence of bounded solutions of functional differential equations of point type // Izvestiya: Mathematics 2020. V. 84. P. 209–245. https://doi.org/10.1070/IM8896
Beklaryan A.L. Numerical methods for constructing solutions of functional differential equations of pointwise type // Adv. Systems Sci. Appl. 2020. V. 20. P. 56–70. https://doi.org/10.25728/assa.2020.20.2.878
Beklaryan L.A., Beklaryan A.L. On the existence of periodic and bounded solutions for functional differential equations of pointwise type with a strongly nonlinear righthand side // Lobachevskii J. of Math. 2020. V. 41. P. 2136–2142. https://doi.org/10.1134/S1995080220110062
Beklaryan L.A., Beklaryan A.L. The question of the existence of bounded soliton solutions in the problem of longitudinal vibrations of an elastic infinite rod in a eld with a strongly nonlinear potential // Comput. Math. and Math. Phys. 2021. V. 61. P. 2024–2039. https://doi.org/10.31857/S0044466921120061
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики