Журнал вычислительной математики и математической физики, 2022, T. 62, № 8, стр. 1269-1287

Трансфинитная барицентрическая интерполяция через минимизацию энергии дирихле для конических поверхностей

А. Г. Беляев^1, *, П.-А. Файоль^2, **

¹ Институт Cенсоров, Cигналов и Cистем, Школа Инженерных и Физических наук, Университет Хериота-Уатта
Эдинбург, Великобритания

² Лаборатория компьютерной графики, Университет Айдзу
Фукушима кен, Айдзу-Вакамацу, Япония

^* E-mail: a.belyaev@hw.ac.uk
^** E-mail: fayolle@u-aizu.ac.jp

Поступила в редакцию 15.04.2021
После доработки 15.04.2021
Принята к публикации 11.04.2022

EDN: URYONZ
DOI: 10.31857/S0044466922080038

Полный текст (PDF)

Аннотация

Мы анализируем общую конструкцию для трансфинитных барицентрических координат (также известных как непрерывные или интегральные барицентрические координаты) и рассматриваем простой вариационный принцип для получения трансфинитной версии барицентрических координат Лапласа. Показываем, что наш подход приводит к общему описанию трансфинитных барицентрических координат и устанавливаем связь с задачами минимизации энергии Дирихле для конических поверхностей. Рассматриваем как двумерные, так и трехмерные случаи и обсуждаем связи трансфинитной барицентрической интерполяции с классическими обратными задачами Минковского и Кристоффеля в дифференциальной геометрии. Библ. 32. Фиг. 8.

Ключевые слова: интегральные (трансфинитные, непрерывные) барицентрические координаты, обобщенные барицентрические координаты, интегральные координаты Лапласа, минимизация энергии Дирихле.

1. ВВЕДЕНИЕ

Начало современным активным исследованиям обобщенных барицентрических координат и их приложений было положено работами Вокспресса (см. [1]), Воррена (см. [2]) и Флотера (см. [3]) и в настоящее время подпитывается многочисленными приложениями обобщенных схем барицентрической интерполяции в вычислительной механике, компьютерной графике и геометрическом моделировании (см. [4]–[7]). В настоящей работе основное внимание уделяется анализу трансфинитных координат Лапласа, являющихся непрерывной версией популярной схемы обобщенной барицентрической интерполяции, которая известна под названиями координат Лапласа (см. [8]), несибсоновских координат (см. [9]), котангенсных весов (см. [10]), дискретных гармонических координат (см. [11]), а также координат Вороного (см. [12], а также более ранние работы [13]–[16]). Высокая популярность координат Лапласа обусловлена тем, что они аппроксимируют оператор Лапласа (отсюда и название) на полигональных сетках (см. [10], [17]).

Трансфинитные (использующие интегрирование, непрерывные) барицентрические координаты были первоначально разработаны Ворреном и соавт. (см. [18]). Хотя в настоящее время трансфинитная барицентрическая интерполяция представляет собой активную область исследований (см. [19]–[27]), очень мало известно о трансфинитных версиях координат Лапласа. В данной работе мы рассматриваем простой вариационный принцип для трансфинитных барицентрических координат Лапласа и показываем, как он приводит к общему описанию трансфинитных барицентрических координат.

Один из наших основных результатов может быть сформулирован следующим образом. Пусть $\Omega $ – строго выпуклая ограниченная область в ${{\mathbb{R}}^{N}}$ с $N = 2$ или $N = 3$. Рассмотрим функцию $u(y)$, определенную для каждого $y \in \partial \Omega $. Зафиксируем $x \in \Omega $ и предположим, что $u(x)$ известно. Рассмотрим коническую поверхность ${{U}_{x}}(z)$, порожденную прямыми отрезками, соединяющими внутреннюю точку $\left( {x,u(x)} \right)$ с граничными точками $\left( {y,u(y)} \right)$, $y \in \partial \Omega $. На фиг. 1а видно, как строится коническая поверхность $\left\{ {\left( {z,{{U}_{x}}(z)} \right) \in {{\mathbb{R}}^{{N + 1}}},z \in \Omega } \right\}$.

Фиг. 1.

(а) – Точка $x \in \Omega $ параметризует семейство конических поверхностей $\left\{ {\left( {z,{{U}_{x}}(z)} \right) \in {{\mathbb{R}}^{{N + 1}}},z \in \Omega \subset {{\mathbb{R}}^{N}}} \right\}$, каждая из которых состоит из отрезков, соединяющих $\left( {y,u(y)} \right)$, $y \in \partial \Omega $, с вершиной $\left( {x,u(x)} \right)$. (б) – Обозначения, которые мы используем для определения трансфинитных барицентрических координат.

Пусть величина $u(x)$ определяется минимизацией энергии Дирихле

(1)

$\int {\int\limits_\Omega {{{{\left| {\nabla {{U}_{x}}} \right|}}^{2}}} } dz \to \min .$

Тогда, как будет показано ниже, значение $u(x)$ получается трансфинитной интерполяцией Лапласа

(2)

$u(x) = {{\int\limits_{{{S}_{x}}} {\frac{{u(y)w(x,{{e}_{\theta }})}}{{\left| {x - y} \right|}}} d\theta } \mathord{\left/ {\vphantom {{\int\limits_{{{S}_{x}}} {\frac{{u(y)w(x,{{e}_{\theta }})}}{{\left| {x - y} \right|}}} d\theta } {\int\limits_{{{S}_{x}}} {\frac{{w(x,{{e}_{\theta }})}}{{\left| {x - y} \right|}}} }}} \right. \kern-0em} {\int\limits_{{{S}_{x}}} {\frac{{w(x,{{e}_{\theta }})}}{{\left| {x - y} \right|}}} }}d\theta $

с весовой функцией, заданной

(3)

$w(x,\theta ) = {{\Delta }_{S}}f + (N - 1)f,\quad f = {{\left| {x - y} \right|}^{{N - 1}}},$

и определенной с точностью до мультипликативной константы. Здесь ${{S}_{x}}$ – это единичная сфера с центром в точке $x$, интегрирование проводится относительно сферических координат $\theta $ (точка $\theta \;{{S}_{x}}$ соответствует единичному вектору $\theta $ и получается как радиальная проекция $y \in \partial \Omega $ на ${{S}_{x}}$), а ${{\Delta }_{S}}$ обозначает сферический оператор Лапласа.

Для двумерного случая мы демонстрируем, как предложенная конструкция, основанная на минимизации энергии Дирихле для конических поверхностей, может быть использована для вывода ставших классическими координат среднего значания (“mean value coordinates”) (см. [3]), которые не аппроксимируют Лапласиан (см. [28]), но обладают замечательными интерполяционными свойствами.

Статья организована следующим образом. В разд. 2 представлена общая конструкция трансфинитных барицентрических координат для выпуклой области. В разд. 3 показано, как двумерные трансфинитные барицентрические координаты могут быть получены как предельный случай метода конструкции Флотера–Хорманна–Коса (см. [11]), которая дает общее описание двумерных барицентрических координат для выпуклых многоугольников. В разд. 4 демонстрируется, как (2), (3) для $N = 2$ получены из (1) и как это приводит к общему построению трансфинитных барицентрических координат в двумерном пространстве. Аналогичные результаты для $N = 3$ представлены в разд. 6. В разд. 5 мы связываем классические “mean value coordinates” (см. [3]) с задачами минимизации энергии Дирихле для конических поверхностей. В разд. 7 показано, как наша кострукция трансфинитных барицентрических координат связана с классическими обратными задачами Минковского и Кристоффеля в дифференциальной геометрии. В разд. 8 приведены итоги нашего исследования.

Настоящая статья является расширенной версией нашей работы, доложенной на NUMGRID 2020 (см. [29]).

2. ВВЕДЕНИЕ В ТРАНСФИНИТНЫЕ БАРИЦЕНТРИЧЕСКИЕ КООРДИНАТЫ

Пусть $\Omega $ – ограниченная выпуклая область в ${{\mathbb{R}}^{N}}$, и $x$ – точка внутри $\Omega $. Предположим, что нам известны значения функции $u( \cdot )$ на $\partial \Omega $. Трансфинитная барицентрическая интерполяция $T$ интерполирует $u( \cdot )$ с $\partial \Omega $ на $\Omega $:

$T:{{\left. u \right|}_{{\partial \Omega }}} \to u(x),$

с сохранением линейных функций.

Рассмотрим единичную сферу ${{S}_{x}}$ с центром в $x$. Предполагаем, что ${{S}_{x}}$ параметризована внешней единичной нормалью ${{e}_{\theta }}$, где $\theta $ обозначает сферические координаты (см. фиг. 1а для наглядного объяснения используемых обозначений). Общая форма интерполяции $T$ дается в виде

(4)

где $w(x,{{e}_{\theta }})$ – весовая функция, удовлетворяющая условия ортогональности

(5)

$0 = \int\limits_{{{S}_{x}}} {{{e}_{\theta }}} w(x,{{e}_{\theta }})d\theta \quad \forall \;x \in \Omega .$

Отметим, что (5) необходимо и достаточно для линейной точности. Действительно, полагая $u(x) \equiv x$, получаем

$u({\mathbf{y}}) \equiv {\mathbf{y}} = {\mathbf{x}} + \rho {\kern 1pt} {{{\mathbf{e}}}_{\theta }},\quad \rho = \left| {{\mathbf{x}} - {\mathbf{y}}} \right|,$

что после подстановки в (4) дает (5).

Если $w(x,{{e}_{\theta }}) \equiv 1$, то мы приходим к трансфинитной версии “mean value coordinates”

(6)

$u({\mathbf{x}}) = {{\int\limits_{{{S}_{{\mathbf{x}}}}} \frac{{u({\mathbf{y}})d\theta }}{{\left| {{\mathbf{x}} - {\mathbf{y}}} \right|}}} \mathord{\left/ {\vphantom {{\int\limits_{{{S}_{{\mathbf{x}}}}} \frac{{u({\mathbf{y}})d\theta }}{{\left| {{\mathbf{x}} - {\mathbf{y}}} \right|}}} {\int\limits_{{{S}_{{\mathbf{x}}}}} \frac{{d\theta }}{{\left| {{\mathbf{x}} - {\mathbf{y}}} \right|}}}}} \right. \kern-0em} {\int\limits_{{{S}_{{\mathbf{x}}}}} \frac{{d\theta }}{{\left| {{\mathbf{x}} - {\mathbf{y}}} \right|}}}},$

которaя была первоначально предложена в [3] для двумерных многоугольников, а затем в [30], [19] для простых многогранников и непрерывного случая.

Двумерный случай

В двумерном случае ${{e}_{\theta }} = (\cos \theta ,\sin \theta )$ и, следовательно, для каждого $x \in \Omega $ (5) упрощается до системы двух уравнений

(7)

$\int\limits_0^{2\pi } w (x,\theta )\cos \theta d\theta = 0 = \int\limits_0^{2\pi } w (x,\theta )\sin \theta d\theta .$

Разложим $w(x,\theta )$ в ряд Фурье

$w(x,\theta ) = \sum {{{c}_{n}}} (x){{e}^{{jn\theta }}},\quad j = \sqrt { - 1} .$

Заметим, что (7) эквивалентно ${{c}_{{ - 1}}} = 0 = {{c}_{1}}$, и поэтому $w(x,\theta )$ можно представить как

(8)

$h_{{\theta \theta }}^{{{\text{''}}}}(x,\theta ) + h(x,\theta ) = w(x,\theta )$

для некоторой периодической по $\theta $ функции $h(x,\theta )$. Действительно, разлaгая $h(x,\theta )$ в ряд Фурье

$h(x,\theta ) = \sum {{{h}_{n}}} (x){{e}^{{jn\theta }}}$

и подставляя это разложение в (8), получаем

$ - {{n}^{2}}{{h}_{n}}(x) + {{h}_{n}}(x) = {{c}_{n}}(x),\quad {{h}_{n}}(x) = {{c}_{n}}(x){\text{/}}(1 - {{n}^{2}}),\quad {\text{где}}\quad n \ne \pm 1,$

что определяет $h(x,\theta )$ однозначно, если дополнительно положить ${{h}_{{ - 1}}}(x) = 0 = {{h}_{1}}(x)$.

Мы можем интерпретировать (8) геометрически. Для каждой точки $x \in \Omega $ рассмотрим замкнутую кривую ${{\Sigma }_{x}}$, чья опорная функция $h(x,\theta )$ задается (8). Радиус кривизны ${{\Sigma }_{x}}$ задается левой частью (8), и условия ортогональности (7) можно записать как

(9)

$\int\limits_0^{2\pi } n \frac{{d\theta }}{k} \equiv \int\limits_{{{\Sigma }_{x}}} {ndl} = 0,$

где $n = {{e}_{\theta }} = (\cos \theta ,\sin \theta )$ – внешняя единичная нормаль к ${{\Sigma }_{x}}$, $k$ – кривизна ${{\Sigma }_{x}}$, и $l$ – натуральная параметризация кривой ${{\Sigma }_{x}}$. Например, если для каждого $x$ кривая ${{\Sigma }_{x}}$ является единичной окружностью с центром в $x$, то $w(x,\theta ) \equiv 1$, и мы получаем двумерный вариант трансфинитных “mean value coordinates” (6).

N-мерный случай

Известно, что $N$ компонентов единичной нормали ${{e}_{\theta }}$ являются собственными функциями, соответствующими минимальному ненулевому собственному значению ${{\lambda }_{{\min }}} = N - 1$ сферического лапласиана $ - {{\Delta }_{S}}$. Таким образом, если весовая функция $w(x,\theta )$ в (4) задается

(10)

$w(x,\theta ) = {{\Delta }_{S}}h + (N - 1)h$

для некоторой функции $h(x,\theta )$, то условия ортогональности (5) выполняются. Действительно, простое интегрирование по частям на единичной сфере ${{S}_{x}}$ дает

$\begin{gathered} \int\limits_{{{S}_{x}}} {{{e}_{\theta }}} w(x,{{e}_{\theta }})d\theta = \int\limits_{{{S}_{x}}} {{{e}_{\theta }}} \left[ {{{\Delta }_{S}}h + (N - 1)h} \right]d\theta = \\ = \;\int\limits_{{{S}_{x}}} {\left[ {{{\Delta }_{S}}{{e}_{\theta }} + (N - 1){{e}_{\theta }}} \right]h(x,\theta )d\theta } = 0. \\ \end{gathered} $

3. ДВУМЕРНЫЕ ТРАНСФИНИТНЫЕ БАРИЦЕНТРИЧЕСКИЕ КООРДИНАТЫ КАК ПРЕДЕЛЬНЫЙ СЛУЧАЙ ИХ ДИСКРЕТНЫХ АНАЛОГОВ

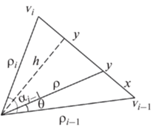
Начнем с общей конструкции обобщенных барицентрических координат, введенной в [11]. Пусть $A(x,y,z)$ обозначает ориентированную площадь треугольника, образованного точками $x$, $y$ и $z$. Рассмотрим выпуклый многоугольник с вершинами ${{v}_{1}}$, …, ${{v}_{n}}$, точку $x$ внутри многоугольника и ориентированные площади треугольников ${{A}_{i}}(x) = A(x,{{v}_{i}},{{v}_{{i + 1}}})$ и ${{B}_{i}}(x) = A(x,{{v}_{{i - 1}}},{{v}_{{i + 1}}})$. Тогда, как показано в [11], веса

(11)

${{w}_{i}} = \frac{{{{c}_{{i + 1}}}{{A}_{{i - 1}}} - {{c}_{i}}{{B}_{i}} + {{c}_{{i - 1}}}{{A}_{i}}}}{{{{A}_{{i - 1}}}{{A}_{i}}}},$

где ${{c}_{i}}(x)$ – некоторые вещественные функции, определяют систему обобщенных барицентрических координат. Более того, любая система обобщенных барицентрических координат может быть представлена в виде ((11)) для некоторых функций ${{c}_{i}}({\mathbf{x}})$, $i = 1,2, \ldots ,n$.

Следуя [11], можно переписать (11) в виде

(12)

${{w}_{i}} = \frac{2}{{{{\rho }_{i}}}}\left( {\frac{{{{h}_{{i + 1}}} - {{h}_{i}}\cos {{\theta }_{i}}}}{{\sin {{\theta }_{i}}}} + \frac{{{{h}_{{i - 1}}} - {{h}_{i}}\cos {{\theta }_{{i - 1}}}}}{{\sin {{\theta }_{{i - 1}}}}}} \right),$

где ${{h}_{i}}(x) = {{c}_{i}}(x){\text{/}}{{\rho }_{i}}(x)$, ${{\rho }_{i}}(x) = \left| {x - {{v}_{i}}} \right|$, и ${{\theta }_{i}}$ – угол между лучами $\left[ {{\mathbf{x}}{{v}_{i}}} \right)$ и $\left[ {{\mathbf{x}}{{v}_{{i + 1}}}} \right)$.

Предположим теперь, что функции ${{h}_{i}}(x)$, $i = 1,\;2,\; \ldots ,\;n$, являются достаточно гладкими, число вершин многоугольника стремится к бесконечности, а все углы ${{\theta }_{i}}$ равномерно стремятся к нулю: ${{\theta }_{i}} \approx d\theta \to 0$. Переходя к пределу, мы получаем гладкую функцию $h(x,\theta )$, удовлетворяющую следующим условиям:

$\frac{{{{h}_{{i + 1}}} - {{h}_{i}}\cos {{\theta }_{i}}}}{{\sin {{\theta }_{i}}}} \approx \frac{{{{h}_{{i + 1}}} - {{h}_{i}} + {{h}_{i}}\theta _{i}^{2}{\text{/}}2}}{{{{\theta }_{i}}}} \approx {{\left[ {h(x,\theta )_{\theta }^{'} + h(x,\theta )\frac{{{{\theta }_{i}}}}{2}} \right]}_{{\theta = \sum\limits_{k = 1}^{i + 1} {{{\theta }_{k}}} }}},$

$\frac{{{{h}_{{i - 1}}} - {{h}_{i}}\cos {{\theta }_{{i - 1}}}}}{{\sin {{\theta }_{{i - 1}}}}} \approx \frac{{{{h}_{{i - 1}}} - {{h}_{i}} + {{h}_{i}}\theta _{{i - 1}}^{2}{\text{/}}2}}{{{{\theta }_{{i - 1}}}}} \approx {{\left[ { - h(x,\theta )_{\theta }^{'} + h(x,\theta )\frac{{{{\theta }_{{i - 1}}}}}{2}} \right]}_{{\theta = \sum\limits_{k = 1}^i {{{\theta }_{k}}} }}}.$

Сложение правых сторон этих формул дает

${{\left[ {\frac{{h(x,\theta + d\theta )_{\theta }^{'} - h(x,\theta )_{\theta }^{'}}}{{d\theta }} + h(x,\theta )} \right]}_{{\theta = \sum\limits_{k = 1}^i {{{\theta }_{k}}} }}}d\theta + {\text{члены}}\;{\text{высшего}}\;{\text{порядка}}.$

Поэтому (12) приблизительно равно

${{\left. {\frac{2}{{{{\rho }_{i}}}}\left[ {h(x,\theta )_{{\theta \theta }}^{{''}} + h(x,\theta )} \right]} \right|}_{{\theta = \sum\limits_{k = 1}^i {{{\theta }_{k}}} }}}d\theta ,$

и мы получаем (8). Теперь можно сформулировать наш результат как утверждение, которое обобщает результат из [5, section 3.2.2].

Утверждение 1. В двумерном случае трансфинитные барицентрические координаты (4), (8) получаются как предельный случай для конструкции Флотера–Хормана–Коса (11).

По сравнению с работой Косинки и Бартона [25], где квадратичная скорость сходимости обобщенных барицентрических координат к их непрерывным аналогам, барицентрическим ядрам была доказана и численно проверена, новизна и важность Утверждения 1 состоит в выявлении связи между функциями ${{c}_{i}}(x)$ в (11) и опорной функцией $h(x)$, заданной (8).

4. ДВУМЕРНЫЕ ТРАНСФИНИТНЫЕ БАРИЦЕНТРИЧЕСКИЕ КООРДИНАТЫ И МИНИМИЗАЦИЯ ЭНЕРГИИ ДИРИХЛЕ

Трансфинитные координаты Лапласа в двумерном пространстве

Под двумерными трансфинитными координатами Лапласа мы понимаем непрерывную версию дискретных гармонических координат. Как показано в [11], задание ${{c}_{i}} = \rho _{i}^{2}$ в (11) дает дискретные гармонические координаты. Таким образом, в соответствии с утверждением 1, трансфинитные координаты Лапласа описываются уравнением

(13)

$w(x,\theta ) = \rho _{{\theta \theta }}^{{''}} + \rho .$

Если вес $w(x,\theta )$ в (4) положителен, то интерполяция посредством (4) следует из [24, теорема 1]. Однако (13) не обязательно положительно и интерполяционные свойства (4), (13) требуют обоснования. Начнем с самого простого случая, когда $\Omega $ – это единичный круг с центром в начале координат, а точка $x$ имеет координаты $( - a,\;0)$, где $0 < a < 1$. Простые аналитические вычисления показывают, что ядро

(14)

$k(x,\theta ) = {{(\rho _{{\theta \theta }}^{{''}} + \rho )} \mathord{\left/ {\vphantom {{(\rho _{{\theta \theta }}^{{''}} + \rho )} \rho }} \right. \kern-0em} \rho }$

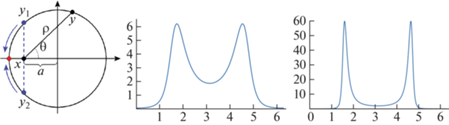
имеет два одинаковых максимума, достигаемых при ${{\theta }_{1}}$ и ${{\theta }_{2}}$, которые приближаются к $\pi {\text{/}}2$ и $3\pi {\text{/}}2$ соответственно, когда $a \to 1$ (см. фиг. 2а). Эти максимумы равны ${{32} \mathord{\left/ {\vphantom {{32} {[27(1 - {{a}^{2}})]}}} \right. \kern-0em} {[27(1 - {{a}^{2}})]}}$ и становятся все более резкими и острее, по мере того, как $x$ приближается к границе, когда $a \to 1$, как демонстрируют фиг. 2б, в. Граничные точки ${{y}_{1}}$ и ${{y}_{2}}$, соответствующие ${{\theta }_{1}}$ и ${{\theta }_{2}}$, становятся все ближе и ближе друг к другу, когда $a \to 1$, и в пределе сливаются с $x$ на границе. Таким образом, подобно классической интерполяции Шепарда (см. [31]),

(15)

$u(x) = {{\int\limits_{{{S}_{x}}} k (x,\theta )u(y)d\theta } \mathord{\left/ {\vphantom {{\int\limits_{{{S}_{x}}} k (x,\theta )u(y)d\theta } {\int\limits_{{{S}_{x}}} k (x,\theta )d\theta }}} \right. \kern-0em} {\int\limits_{{{S}_{x}}} k (x,\theta )d\theta }}$

обеспечивает граничную интерполяцию. Общий случай строго выпуклых $\Omega $ легко сводится к вышеприведенному случаю круга, если для данной точки $y \in \partial \Omega $ мы рассмотрим окружность, соприкасающуюся с $\partial \Omega $ в точке $y$.

Фиг. 2.

(а) – Иллюстрация обозначений, используемых для демонстрации интерполяционных свойств (14), (15) для окружности. Графики ядра $k(x,\theta )$, определенного (14) для $x = ( - 0.9,\;0)$ (б) и $x = ( - 0.99,\;0)$ (в).

Оказывается, что (13) также может быть выведено путем имитации свойства минимизации энергии Дирихле гармоническими функциями (см. [20], [21]). Пусть $u(y)$ задана для каждого $y \in \partial \Omega $. Возьмем $x \in \Omega $ и предположим, что $u(x)$известно. Рассмотрим конический участок поверхности, образованный прямыми отрезками, соединяющими внутреннюю точку $\left( {x,u(x)} \right)$ с граничными точками $\left( {y,u(y)} \right)$. В полярных координатах $(r,\theta )$ с центром в точке $x$ граница $\partial \Omega $ задается $r = \rho (\theta )$, $\rho = \left| {x - y} \right|$, а коническая поверхность, связанная с точкой $x$, определяется уравнением

(16)

${{U}_{x}}(z) = \frac{{(\rho - r)u(x) + ru(y)}}{\rho },$

где $r = \left| {x - z} \right|$ и $y \in \partial \Omega $ обозначает точку пересечения $\partial \Omega $ с лучом, выходящим из $x$ и проходящим через $z$. На фиг. 1 продемонстрировано построение конической поверхности $\left( {z,{{U}_{x}}(z)} \right)$, $z \in \Omega $, и используемые обозначения.

Теперь значение $u(x)$ выбирается так, что энергия Дирихле построенной конической поверхности достигает своего минимального значения:

$\int {\int\limits_\Omega {{{{\left| {\nabla {{U}_{x}}} \right|}}^{2}}} } dz \to \min .$

Утверждение 2. В двумерном случае, минимум энергии Дирихле для конической поверхности, состоящей из прямых отрезков, соединяющих внутреннюю точку $\left( {x,u(x)} \right)$, $x \in \Omega $, с граничными точками $\left( {y,u(y)} \right)$, $y \in \partial \Omega $, достигается на поверхности, определяемой 2D трансфинитной барицентрической интерполяцией (4), (13).

Краткий вывод этого утверждения приведен в [20] (см. также [29]). Для полноты изложения мы приводим здесь подробный вывод результата для интеграла Дирихле с весом

$\int {\int\limits_\Omega {{{{\left| {\nabla {{U}_{x}}} \right|}}^{2}}} } a(x,\theta )dz,$

где $a(x,\theta )$ – положительная весовая функция.

Доказательство. Для функции $f(r,\theta )$ ее градиент и магнитуда градиента в полярных координатах задаются формулами

$\nabla f(r,\theta ) = \frac{{\partial f}}{{\partial r}}{{e}_{r}} + \frac{1}{r}\frac{{\partial f}}{{\partial \theta }}{{e}_{\theta }},\quad {{\left| {\nabla f} \right|}^{2}} = {{\left| {\frac{{\partial f}}{{\partial r}}} \right|}^{2}} + \frac{1}{{{{r}^{2}}}}{{\left| {\frac{{\partial f}}{{\partial \theta }}} \right|}^{2}}.$

Поэтому

$\frac{{\partial {{U}_{x}}}}{{\partial r}} = \frac{{u(y) - u(x)}}{\rho }\quad {\text{и}}\quad \frac{{\partial {{U}_{x}}}}{{\partial \theta }} = r\left[ {(u(y) - u(x))\left( {\frac{1}{\rho }} \right)_{\theta }^{'} + \frac{1}{\rho }u_{\theta }^{'}(y)} \right].$

Таким образом, мы приходим к следующей задаче минимизации:

$\begin{gathered} \min \leftarrow \int {\int\limits_\Omega {{{{\left| {\nabla {{U}_{x}}} \right|}}^{2}}} } a(x,\theta )dz = \int\limits_0^{2\pi } a (x,\theta )d\theta \int\limits_0^\rho r dr\left\{ {{{{\left[ {\frac{{u(x) - u(y)}}{\rho }} \right]}}^{2}} + {{{\left[ {(u({\mathbf{y}}) - u({\mathbf{x}}))\left( {\frac{1}{\rho }} \right)_{\theta }^{'} + \frac{1}{\rho }u_{\theta }^{'}({\mathbf{y}})} \right]}}^{2}}} \right\} = \\ = \frac{1}{2}\int\limits_0^{2\pi } a (x,\theta )d\theta \left\{ {{{{[u(x) - u(y)]}}^{2}} + {{{\left[ {u_{\theta }^{'}(y) + (u(x) - u(y))\frac{{\rho _{\theta }^{'}}}{\rho }} \right]}}^{2}}} \right\}, \\ \end{gathered} $

где последний интеграл является квадратичной функцией от $u(x)$. Отсюда для оптимального значения $u(x)$ получаем

$\int\limits_0^{2\pi } u (x)\left\{ {1 + {{{\left( {\frac{{\rho _{\theta }^{'}}}{\rho }} \right)}}^{2}}} \right\}a(x,\theta )d\theta = \int\limits_0^{2\pi } {\left\{ {u(y) - u_{\theta }^{'}(y)\frac{{\rho _{\theta }^{'}}}{\rho } + u(y){{{\left( {\frac{{\rho _{\theta }^{'}}}{\rho }} \right)}}^{2}}} \right\}} a(x,\theta )d\theta $

и, следовательно, $u(x)$ получается в виде дроби

(17)

$u(x) = \frac{{\int\limits_0^{2\pi } {\left\{ {u(y) - u_{\theta }^{'}(y)\frac{{\rho _{\theta }^{'}}}{\rho } + u({\mathbf{y}}){{{\left( {\frac{{\rho _{\theta }^{'}}}{\rho }} \right)}}^{2}}} \right\}} a(x,\theta )d\theta }}{{\int\limits_0^{2\pi } {\left\{ {1 + {{{\left( {\frac{{\rho _{\theta }^{'}}}{\rho }} \right)}}^{2}}} \right\}} a(x,\theta )d\theta }}.$

Рассмотрим знаменатель парвой части в (17). Интегрирование по частям дает

$\int\limits_0^{2\pi } {{{{\left( {\frac{{\rho _{\theta }^{'}}}{\rho }} \right)}}^{2}}} a(x,\theta )d\theta = \int\limits_0^{2\pi } {\left\{ {\frac{{(a\rho _{\theta }^{'})_{\theta }^{'}}}{\rho } - \left( {\frac{{a\rho _{\theta }^{'}}}{\rho }} \right)_{\theta }^{'}} \right\}} d\theta = \int\limits_0^{2\pi } {\frac{{(a\rho _{\theta }^{'})_{\theta }^{'}}}{\rho }} d\theta ,$

а знаменатель в (17) определяется как

$\int\limits_0^{2\pi } {\frac{{(a\rho _{\theta }^{'})_{\theta }^{'} + a\rho }}{\rho }} d\theta .$

Теперь рассмотрим числитель (17). Мы имеем

$ - \int\limits_0^{2\pi } {u_{\theta }^{'}({\mathbf{y}})} \frac{{a\rho _{\theta }^{'}}}{\rho }d\theta = \int\limits_0^{2\pi } {u({\mathbf{y}})} \left( {\frac{{a\rho _{\theta }^{'}}}{\rho }} \right)_{\theta }^{'}d\theta = \int\limits_0^{2\pi } {u({\mathbf{y}})} \left( {\frac{{(a\rho _{\theta }^{'})_{\theta }^{'}}}{\rho } - \frac{{a{{{(\rho _{\theta }^{'})}}^{2}}}}{{{{\rho }^{2}}}}} \right)d\theta .$

Таким образом, (17) может быть записано как

(18)

$u(x) = {{\int\limits_0^{2\pi } {u(y)} \frac{{w(x,\theta )}}{\rho }d\theta } \mathord{\left/ {\vphantom {{\int\limits_0^{2\pi } {u(y)} \frac{{w(x,\theta )}}{\rho }d\theta } {\int\limits_0^{2\pi } {\frac{{w(x,\theta )}}{\rho }} d\theta }}} \right. \kern-0em} {\int\limits_0^{2\pi } {\frac{{w(x,\theta )}}{\rho }} d\theta }},\quad w(x,\theta ) = (a\rho _{\theta }^{'})_{\theta }^{'} + a\rho .$

Теперь видно, что (18) с $a(x,\theta ) \equiv 1$ соответствует (4) с (13). Утверждение 2 доказано.

Общая конструкция в 2D

Здесь мы покажем, что, подобно трансфинитным координатам Лапласа, общая конструкция двумерных трансфинитных барицентрических координат (4), (8) также может быть получена как решение задачи минимизации энергии Дирихле.

Опять же, рассматриваем точку $x$ внутри выпуклой области $\Omega $ и предполагаем, что $\partial \Omega $ задается $r = \rho (\theta )$ в полярных координатах с центром в $x$. Таким образом, $\Omega $ может быть описана $\left\{ {(r\cos \theta ,r\sin \theta )} \right\}$ с $0 \leqslant r < \rho (\theta )$. Рассмотрим теперь другую область $G$, определяемую неравенством $0 \leqslant r < g(x,\theta )$, где $g(x,\theta )$ – некоторая функция. Тогда $\partial G$ задается $r = g(x,\theta )$.

Предположим, что мы знаем $u(x)$ и, как и раньше, используем линейную интерполяцию между $u(x)$ и $u(y)$, где $y \in \partial \Omega $ для определения $u( \cdot )$. Тогда значения $u( \cdot )$ на $\partial G$ даются в виде

(19)

$v = \frac{{u(y)g(x,\theta ) + u(x)(\rho - g(x,\theta ))}}{\rho }.$

Теперь применим трансфинитную интерполяцию Лапласа к области $G$. Имеем

$\int\limits_0^{2\pi } {\frac{{g_{{\theta \theta }}^{{''}} + g}}{g}vd\theta } = u({\mathbf{x}})\int\limits_0^{2\pi } {\frac{{g_{{\theta \theta }}^{{''}} + g}}{g}d\theta } $

и, подставляя функцию $v( \cdot )$, определенную в (19), получаем

$\int\limits_0^{2\pi } {\frac{{g_{{\theta \theta }}^{{''}} + g}}{\rho }u({\mathbf{y}})d\theta } + u({\mathbf{x}})\int\limits_0^{2\pi } {\left( {1 - \frac{g}{\rho }} \right)} \frac{{g_{{\theta \theta }}^{{''}} + g}}{g}d\theta = u({\mathbf{x}})\int\limits_0^{2\pi } {\frac{{g_{{\theta \theta }}^{{''}} + g}}{g}d\theta } ,$

что сразу же приводит к следующему общему представлению двумерных трансфинитных координат

(20)

$u({\mathbf{x}}) = {{\int\limits_0^{2\pi } {\frac{{g_{{\theta \theta }}^{{''}} + g}}{\rho }u(y)d\theta } } \mathord{\left/ {\vphantom {{\int\limits_0^{2\pi } {\frac{{g_{{\theta \theta }}^{{''}} + g}}{\rho }u(y)d\theta } } {\int\limits_0^{2\pi } {\frac{{g_{{\theta \theta }}^{{''}} + g}}{\rho }} }}} \right. \kern-0em} {\int\limits_0^{2\pi } {\frac{{g_{{\theta \theta }}^{{''}} + g}}{\rho }} }}d\theta $

и дает общую двумерную трансфинитную барицентрическую интерполяцию (4), (8).

5. ТРАНСФИНИТНЫЕ КООРДИНАТЫ ДЛЯ МНОГОУГОЛЬНЫХ ОБЛАСТЕЙ

Теперь рассмотрим случай, когда область $\Omega $ является многоугольником с границей $\partial \Omega $, определяемой вершинами ${{v}_{1}},\; \ldots ,\;{{v}_{n}}$, и вычислим барицентрические координаты, соответствующие (20), для конкретных примеров вспомогательных областей $G$.

Вспомогательная область $G$ является единичным диском

Сначала рассмотрим случай, когда $G$ является единичным диском с центром в точке $x$. В этом случае $g(x,\theta ) = {\text{cst}} = 1$, $g_{{\theta \theta }}^{{''}}(x,\theta ) = 0$ и (20) становится

$u(x) = {{\int\limits_0^{2\pi } {\frac{{u(y)d\theta }}{\rho }} } \mathord{\left/ {\vphantom {{\int\limits_0^{2\pi } {\frac{{u(y)d\theta }}{\rho }} } {\int\limits_0^{2\pi } {\frac{{d\theta }}{\rho }} }}} \right. \kern-0em} {\int\limits_0^{2\pi } {\frac{{d\theta }}{\rho }} }},$

где $y \in \partial \Omega $. Мы получили (6). Так как $\partial \Omega $ – это граница многоугольника с вершинами ${{v}_{1}},\; \ldots ,\;{{v}_{n}}$, то приходим к хорошо известным весам, соответствующим “mean value coordinates”. А именно, вес ${{w}_{i}}$, соответствующий вершине ${{v}_{i}}$, задается уравнением

(21)

${{w}_{i}}(x) = \frac{{\operatorname{tg} {{\alpha }_{{i - 1}}}{\text{/}}2 + \operatorname{tg} {{\alpha }_{i}}{\text{/}}2}}{{{{\rho }_{i}}}},$

где ${{\rho }_{i}} = \left| {{\mathbf{x}} - {{{\mathbf{v}}}_{i}}} \right|$, а ${{\alpha }_{i}}$ – угол между лучами $\left[ {{\mathbf{x}},{{v}_{i}}} \right)$ и $\left[ {{\mathbf{x}},{{{\mathbf{v}}}_{{i + 1}}}} \right)$.

Вспомогательная область $G$ ограничена дискретным набором касательных к единичной окружности

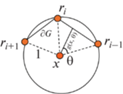
В этом примере рассмотрим касательные к единичной окружности с центром в точке $x$, которые перпендикулярны лучам $\left[ {{\mathbf{x}},{{{\mathbf{v}}}_{i}}} \right)$, как показано на фиг. 3.

Фиг. 3.

Вспомогательная область $\partial G$ задается касательными к единичной окружности, которые перпендикулярны лучам $[x,{{v}_{i}})$ (дискретная огибающая).

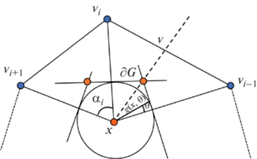
Утверждение 3. Пусть $\Omega $ является многоугольником с вершинами ${{v}_{1}},\; \ldots ,\;{{v}_{n}}$, а $G$ – многоугольник, образованный касательными к единичной окружности с центром в $x$, которые перпендикулярны лучам $[x,{{v}_{i}}]$. Тогда $(20)$ дает дискретную интерполяцию с весами, заданными $(21)$.

Доказательство. Пусть $g(x,\theta )$ обозначает расстояние от $x$ до $\partial G$ в направлении ${{e}_{\theta }}$. Мы хотим оценить

$\int\limits_0^{2\pi } {\frac{{g_{{\theta \theta }}^{{''}} + g}}{\rho }u(y)d\theta } ,$

где $y \in \partial \Omega $. Видно, что

$g({\mathbf{x}},\theta ) = \left\{ \begin{gathered} 1{\text{/}}\cos \theta ,\quad 0 < \theta < {{\alpha }_{{i - 1}}}{\text{/}}2, \hfill \\ 1{\text{/}}\cos ({{\alpha }_{{i - 1}}} - \theta ),\quad {{\alpha }_{{i - 1}}}{\text{/}}2 < \theta < {{\alpha }_{{i - 1}}}, \hfill \\ \end{gathered} \right.$

$g_{\theta }^{'}({\mathbf{x}},\theta ) = \left\{ \begin{gathered} \frac{{\sin \theta }}{{{{{\cos }}^{2}}\theta }},\quad 0 < \theta < {{\alpha }_{{i - 1}}}{\text{/}}2, \hfill \\ - \frac{{\sin ({{\alpha }_{{i - 1}}} - \theta )}}{{{{{\cos }}^{2}}({{\alpha }_{{i - 1}}} - \theta )}},\quad {{\alpha }_{{i - 1}}}{\text{/}}2 < \theta < {{\alpha }_{{i - 1}}}, \hfill \\ \end{gathered} \right.$

$g_{{\theta \theta }}^{{''}}({\mathbf{x}},\theta ) = \left\{ \begin{gathered} \frac{{2{{{\sin }}^{2}}\theta }}{{{{{\cos }}^{3}}\theta }} + \frac{1}{{\cos \theta }},\quad 0 < \theta < {{\alpha }_{{i - 1}}}{\text{/}}2, \hfill \\ \frac{{2{{{\sin }}^{2}}({{\alpha }_{{i - 1}}} - \theta )}}{{{{{\cos }}^{3}}({{\alpha }_{{i - 1}}} - \theta )}} + \frac{1}{{\cos ({{\alpha }_{{i - 1}}} - \theta )}},\quad {{\alpha }_{{i - 1}}}{\text{/}}2 < \theta < {{\alpha }_{{i - 1}}}. \hfill \\ \end{gathered} \right.$

Поскольку $g_{\theta }^{'}({\mathbf{x}},\theta )$ имеет разрыв, нам нужно сначала оценить вклад этого разрыва.

Вклад разрыва. Мы используем здесь обозначения, показанные на фиг. 3. Пусть $v$ обозначает пересечением луча, соответствующего углу ${{\alpha }_{{i - 1}}}{\text{/}}2$, с отрезком $[{{v}_{{i - 1}}},{{v}_{i}}]$. Так как $g_{\theta }^{'}(x,\theta )$ имеет разрыв (скачок) при $\theta = {{\alpha }_{{i - 1}}}{\text{/}}2$, вычисление $g_{{\theta \theta }}^{{''}}(x,\theta )$ создает масштабированную дельта-функцию при $\theta = {{\alpha }_{{i - 1}}}{\text{/}}2$. Скачок $g_{\theta }^{'}(x,\theta )$ при $\theta = {{\alpha }_{{i - 1}}}{\text{/}}2$ это

(22)

$g_{\theta }^{'}\left( {x,\frac{{{{\alpha }_{{i - 1}}}}}{2} + } \right) - g_{\theta }^{'}\left( {x,\frac{{{{\alpha }_{{i - 1}}}}}{2} - } \right) = - {{2\sin \frac{{{{\alpha }_{{i - 1}}}}}{2}} \mathord{\left/ {\vphantom {{2\sin \frac{{{{\alpha }_{{i - 1}}}}}{2}} {{{{\cos }}^{2}}\frac{{{{\alpha }_{{i - 1}}}}}{2}}}} \right. \kern-0em} {{{{\cos }}^{2}}\frac{{{{\alpha }_{{i - 1}}}}}{2}}}.$

Теперь давайте вычислим $u(v)$. Нам даны $u({{v}_{{i - 1}}})$, и $u({{v}_{i}})$ и известно, что $u( \cdot )$ линейно на отрезке $[{{v}_{{i - 1}}},{{v}_{i}}]$. Используем обозначения, показанные на фиг. 4. Пусть ${{\rho }_{{i - 1}}}$ обозначает длину $[x,{{v}_{{i - 1}}}]$, а ${{\rho }_{i}}$ – длину $[x,{{v}_{i}}]$. Обозначим также длины $[{{v}_{{i - 1}}},v]$ и $[{{v}_{i}},v]$ через $x$ и $y$ соответственно. Получаем

$\frac{x}{y} = \frac{{{{\rho }_{{i - 1}}}}}{{{{\rho }_{i}}}},\quad u(v) = \frac{{u({{v}_{i}})x + u({{v}_{{i - 1}}})y}}{{x + y}} = \frac{{u({{v}_{i}}){{\rho }_{{i - 1}}} + u({{v}_{{i - 1}}}){{\rho }_{i}}}}{{{{\rho }_{{i - 1}}} + {{\rho }_{i}}}},$

${{\rho }_{{i - 1}}}{{\rho }_{i}}\sin {{\alpha }_{{i - 1}}} = {{\rho }_{{i - 1}}}l\sin \frac{{{{\alpha }_{{i - 1}}}}}{2} + {{\rho }_{i}}l\sin \frac{{{{\alpha }_{{i - 1}}}}}{2},$

$\frac{1}{\rho } = \frac{1}{l} = \frac{{{{\rho }_{{i - 1}}}\sin \frac{{{{\alpha }_{{i - 1}}}}}{2} + {{\rho }_{i}}\sin \frac{{{{\alpha }_{{i - 1}}}}}{2}}}{{{{\rho }_{{i - 1}}}{{\rho }_{i}}\sin {{\alpha }_{{i - 1}}}}} = \frac{1}{{2\cos \frac{{{{\alpha }_{{i - 1}}}}}{2}}}\left( {\frac{1}{{{{\rho }_{{i - 1}}}}} + \frac{1}{{{{\rho }_{i}}}}} \right),$

$\frac{{u(v)}}{\rho } = \frac{1}{l}\frac{{u({{v}_{i}})x + u({{v}_{{i - 1}}})y}}{{x + y}}\frac{1}{{2\cos \frac{{{{\alpha }_{{i - 1}}}}}{2}}}\left[ {\frac{{u({{v}_{i}})}}{{{{\rho }_{i}}}} + \frac{{u({{v}_{{i - 1}}})}}{{{{\rho }_{{i - 1}}}}}} \right].$

Комбинируя это с (22), получаем

$\frac{{\sin \frac{{{{\alpha }_{{i - 1}}}}}{2}}}{{{{{\cos }}^{3}}\frac{{{{\alpha }_{{i - 1}}}}}{2}}}\left[ {\frac{{u({{v}_{i}})}}{{{{\rho }_{i}}}} + \frac{{u({{v}_{{i - 1}}})}}{{{{\rho }_{{i - 1}}}}}} \right]$

и после перегруппировки слагаемых получаем

(23)

$ - \frac{{u({{v}_{i}})}}{{\left| {{{v}_{i}} - x} \right|}}\left[ {{{\sin \frac{{{{\alpha }_{{i - 1}}}}}{2}} \mathord{\left/ {\vphantom {{\sin \frac{{{{\alpha }_{{i - 1}}}}}{2}} {{{{\cos }}^{3}}\frac{{{{\alpha }_{{i - 1}}}}}{2}}}} \right. \kern-0em} {{{{\cos }}^{3}}\frac{{{{\alpha }_{{i - 1}}}}}{2}}} + {{\sin \frac{{{{\alpha }_{i}}}}{2}} \mathord{\left/ {\vphantom {{\sin \frac{{{{\alpha }_{i}}}}{2}} {{{{\cos }}^{3}}\frac{{{{\alpha }_{i}}}}{2}}}} \right. \kern-0em} {{{{\cos }}^{3}}\frac{{{{\alpha }_{i}}}}{2}}}} \right].$

Фиг. 4.

Влияние разрыва при $\theta = {{\alpha }_{{i - 1}}}{\text{/}}2$. Используемые обозначения.

Вклад регулярной точки. Теперь рассмотрим вклад регулярной точки на $[{{v}_{{i - 1}}},{{v}_{i}}]$. Используемые обозначения показаны на фиг. 5. Обозначим через $h$ высоту от неотмеченной вершины до отрезка $[{{v}_{{i - 1}}},{{v}_{i}}]$.

Фиг. 5.

Вклад регулярной точки отрезка $[{{v}_{{i - 1}}},{{v}_{i}}]$. Используемые обозначения.

Имеем

$u(y) = \frac{{u({{v}_{{i - 1}}})y + u({{v}_{i}})x}}{{x + y}},$

${{\rho }_{{i - 1}}}{{\rho }_{i}}\sin {{\alpha }_{{i - 1}}} = h(x + y),\quad xh = {{\rho }_{{i - 1}}}\rho \sin \theta ,\quad yh = {{\rho }_{i}}\rho \sin ({{\alpha }_{{i - 1}}} - \theta ),$

$\frac{x}{{x + y}} = \frac{{{{\rho }_{{i - 1}}}\rho \sin \theta }}{{{{\rho }_{{i - 1}}}{{\rho }_{i}}\sin {{\alpha }_{{i - 1}}}}},\quad \frac{y}{{x + y}} = \frac{{{{\rho }_{i}}\rho \sin ({{\alpha }_{{i - 1}}} - \theta )}}{{{{\rho }_{{i - 1}}}{{\rho }_{i}}\sin {{\alpha }_{{i - 1}}}}},$

$\frac{{u(y)}}{\rho } = \frac{{u({{v}_{{i - 1}}})}}{{{{\rho }_{{i - 1}}}}}\frac{{\sin ({{\alpha }_{{i - 1}}} - \theta )}}{{\sin {{\alpha }_{{i - 1}}}}} + \frac{{u({{v}_{i}})}}{{{{\rho }_{i}}}}\frac{{\sin \theta }}{{\sin {{\alpha }_{{i - 1}}}}}.$

Теперь нам нужно оценить сумму двух интегралов:

${{I}_{1}} = \int\limits_0^{{{\alpha }_{{i - 1}}}/2} {\left( {\frac{{2{{{\sin }}^{2}}\theta }}{{{{{\cos }}^{3}}\theta }} + \frac{2}{{\cos \theta }}} \right)} \left[ {\frac{{u({{v}_{{i - 1}}})}}{{{{\rho }_{{i - 1}}}}}\frac{{\sin ({{\alpha }_{{i - 1}}} - \theta )}}{{\sin {{\alpha }_{{i - 1}}}}} + \frac{{u({{v}_{i}})}}{{{{\rho }_{i}}}}\frac{{\sin \theta }}{{\sin {{\alpha }_{{i - 1}}}}}} \right]d\theta ,$

${{I}_{2}} = \int\limits_{{{\alpha }_{{i - 1}}}/2}^{{{\alpha }_{{i - 1}}}} {\left( {\frac{{2{{{\sin }}^{2}}({{\alpha }_{{i - 1}}} - \theta )}}{{{{{\cos }}^{3}}({{\alpha }_{{i - 1}}} - \theta )}} + \frac{2}{{\cos ({{\alpha }_{{i - 1}}} - \theta )}}} \right)} \left[ {\frac{{u({{v}_{{i - 1}}})}}{{{{\rho }_{{i - 1}}}}}\frac{{\sin ({{\alpha }_{{i - 1}}} - \theta )}}{{\sin {{\alpha }_{{i - 1}}}}} + \frac{{u({{v}_{i}})}}{{{{\rho }_{i}}}}\frac{{\sin \theta }}{{\sin {{\alpha }_{{i - 1}}}}}} \right]d\theta ,$

которые становятся

${{I}_{1}} = \int\limits_0^{{{\alpha }_{{i - 1}}}/2} {\frac{2}{{{{{\cos }}^{3}}\theta }}} \left[ {\frac{{u({{v}_{{i - 1}}})}}{{{{\rho }_{{i - 1}}}}}\frac{{\sin ({{\alpha }_{{i - 1}}} - \theta )}}{{\sin {{\alpha }_{{i - 1}}}}} + \frac{{u({{v}_{i}})}}{{{{\rho }_{i}}}}\frac{{\sin \theta }}{{\sin {{\alpha }_{{i - 1}}}}}} \right]d\theta ,$

${{I}_{2}} = \int\limits_{{{\alpha }_{{i - 1}}}/2}^{{{\alpha }_{{i - 1}}}} {\frac{2}{{{{{\cos }}^{3}}({{\alpha }_{{i - 1}}} - \theta )}}} \left[ {\frac{{u({{v}_{{i - 1}}})}}{{{{\rho }_{{i - 1}}}}}\frac{{\sin ({{\alpha }_{{i - 1}}} - \theta )}}{{\sin {{\alpha }_{{i - 1}}}}} + \frac{{u({{v}_{i}})}}{{{{\rho }_{i}}}}\frac{{\sin \theta }}{{\sin {{\alpha }_{{i - 1}}}}}} \right]d\theta $

после упрощений.

Интегралы ${{I}_{1}}$ и ${{I}_{2}}$ вычисляются в явном виде

${{I}_{1}} = \frac{{\operatorname{tg} {{\alpha }_{{i - 1}}}{\text{/}}2}}{{1 + \cos {{\alpha }_{{i - 1}}}}}\left[ {\frac{{u({{v}_{{i - 1}}})}}{{{{\rho }_{{i - 1}}}}}(2 + \cos {{\alpha }_{{i - 1}}}) + \frac{{u({{v}_{i}})}}{{{{\rho }_{i}}}}} \right],$

${{I}_{2}} = \frac{{\operatorname{tg} {{\alpha }_{{i - 1}}}{\text{/}}2}}{{1 + \cos {{\alpha }_{{i - 1}}}}}\left[ {\frac{{u({{v}_{{i - 1}}})}}{{{{\rho }_{{i - 1}}}}} + \frac{{u({{v}_{i}})}}{{{{\rho }_{i}}}}(2 + \cos {{\alpha }_{{i - 1}}})} \right].$

После суммирования членов, соответствующих вершине ${{v}_{i}}$, и с учетом скачка (23), мы получаем

$\begin{gathered} \frac{{u({{v}_{i}})}}{{\left| {{{v}_{i}} - x} \right|}}\left\{ {\frac{{\operatorname{tg} {{\alpha }_{{i - 1}}}{\text{/}}2}}{{1 + \cos {{\alpha }_{{i - 1}}}}}(3 + \cos {{\alpha }_{{i - 1}}}) + \frac{{\operatorname{tg} {{\alpha }_{i}}{\text{/}}2}}{{1 + \cos {{\alpha }_{i}}}}(3 + \cos {{\alpha }_{i}})} \right. - \\ \left. {\; - \left[ {{{\sin \frac{{{{\alpha }_{{i - 1}}}}}{2}} \mathord{\left/ {\vphantom {{\sin \frac{{{{\alpha }_{{i - 1}}}}}{2}} {{{{\cos }}^{3}}\frac{{{{\alpha }_{{i - 1}}}}}{2}}}} \right. \kern-0em} {{{{\cos }}^{3}}\frac{{{{\alpha }_{{i - 1}}}}}{2}}} + {{\sin \frac{{{{\alpha }_{i}}}}{2}} \mathord{\left/ {\vphantom {{\sin \frac{{{{\alpha }_{i}}}}{2}} {{{{\cos }}^{3}}\frac{{{{\alpha }_{i}}}}{2}}}} \right. \kern-0em} {{{{\cos }}^{3}}\frac{{{{\alpha }_{i}}}}{2}}}} \right]} \right\}. \\ \end{gathered} $

Дальнейшие упрощения этого выражения приводят к

$\frac{{u({{v}_{i}})}}{{{{\rho }_{i}}}}\left( {\operatorname{tg} {{\alpha }_{{i - 1}}}{\text{/}}2 + \operatorname{tg} {{\alpha }_{i}}{\text{/}}2} \right).$

Таким образом, вес ${{w}_{i}}(x)$, соответствующий вершине ${{v}_{i}}$, дается обычным выражением для “mean value coordinates”. Утверждение 3 доказано.

Вспомогательная область $G$ получается проекцией вершин $\partial \Omega $ на единичную окружность

В качестве последнего примера рассмотрим случай, когда $G$ – многоугольник, чьи вершины ${{p}_{1}},\; \ldots ,\;{{p}_{n}}$ являются проекциями вершин ${{v}_{1}},\; \ldots ,\;{{v}_{n}}$ $\partial \Omega $ на единичную окружность с центром в $x$. На фиг. 6 демонстрируется построение многоугольника $G$.

Фиг. 6.

Случай, когда вершины $\partial G$ определяются из проекции ${{v}_{1}},\; \ldots ,\;{{v}_{n}}$ на единичную окружность с центром в $x$.

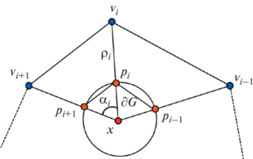
Утверждение 4. Пусть $\Omega $ является многоугольником с вершинами ${{v}_{1}},\; \ldots ,\;{{v}_{n}}$, а $G$ – многоугольник, чьи вершины получены радиальной проекцией вершин $\Omega $ на единичную окружность с центром в $x$. Тогда $(20)$ снова дает веса, соответствующие “mean value coordinates” $(21)$.

Доказательство. Вычислим

$\int\limits_0^{2\pi } {\frac{{g_{{\theta \theta }}^{{''}} + g}}{\rho }u(y)d\theta ,} $

где $y \in \partial \Omega $, a $g(x,\theta )$ обозначает расстояние от $x$ до $\partial G$ в направлении ${{e}_{\theta }}$.

Для треугольника $(x,{{v}_{{i - 1}}},{{v}_{i}})$ имеем

${{\rho }_{{i - 1}}}{{\rho }_{i}}\sin {{\alpha }_{{i - 1}}} = {{\rho }_{{i - 1}}}\rho \sin \theta + {{\rho }_{{i + 1}}}\rho \sin ({{\alpha }_{{i - 1}}} - \theta ),$

что приводит к

$\rho (\theta ) = \frac{{{{\rho }_{{i - 1}}}{{\rho }_{i}}\sin {{\alpha }_{{i - 1}}}}}{{{{\rho }_{{i - 1}}}\sin \theta + {{\rho }_{i}}\sin ({{\alpha }_{{i - 1}}} - \theta )}}.$

Аналогичнo,

Теперь рассмотрим треугольник $(x,{{p}_{{i - 1}}},{{p}_{i}})$ (фиг. 7), имеем

$\sin {{\alpha }_{{i - 1}}} = g(x,\theta )\sin \theta + g(x,\theta )\sin ({{\alpha }_{{i - 1}}} - \theta ),$

что приводит к

$g(x,\theta ) = \frac{{\sin {{\alpha }_{{i - 1}}}}}{{\sin \theta + \sin ({{\alpha }_{{i - 1}}} - \theta )}}.$

Фиг. 7.

Вычисление $g(x,\theta )$ для отрезка $[{{p}_{{i - 1}}},{{p}_{i}}]$.

Нам надо вычислить

$\int\limits_{\theta = 0}^{2\pi } {\frac{{g_{{\theta \theta }}^{{''}}(x,\theta ) + g(x,\theta )}}{{\rho (\theta )}}u(y)d\theta } .$

Рассмoтрим вклад одного отрезка $[{{p}_{{i - 1}}},{{p}_{i}}]$

$I = \int\limits_{\theta = 0}^{{{\alpha }_{{i - 1}}}} \frac{{g_{{\theta \theta }}^{{''}}(x,\theta ) + g(x,\theta )}}{{\rho (\theta )}}u(y)d\theta .$

Этот интеграл вычисляется аналитически:

$I = 2\operatorname{tg} \frac{{{{\alpha }_{{i - 1}}}}}{2}\left\{ {\frac{{u({{v}_{{i - 1}}})}}{{{{\rho }_{{i - 1}}}}} + \frac{{u({{v}_{i}})}}{{{{\rho }_{i}}}}} \right\}.$

Суммируя вклады для данной вершины ${{v}_{i}}$, приходим к

${{w}_{i}}(x) = 2\frac{{u({{v}_{i}})}}{{{{\rho }_{i}}}}\left( {\operatorname{tg} \frac{{{{\alpha }_{{i - 1}}}}}{2} + \operatorname{tg} \frac{{{{\alpha }_{i}}}}{2}} \right).$

Таким образом, с точностью до коэффициента $2$, который исчезает при нормализации весов, мы снова получили веса, соответствующие “mean value coordinates”. Утверждение 4 доказано.

6. ТРЕХМЕРНЫЕ ТРАНСФИНИТНЫЕ КООРДИНАТЫ И МИНИМИЗАЦИЯ ЭНЕРГИИ ДИРИХЛЕ

Трансфинитные координаты Лапласа в 3D

Определим трехмерные трансфинитные координаты Лапласа как барицентрическую интерполяцию (4), которая для каждого $x \in \Omega $ минимизирует энергию Дирихле:

$\int {\int {\int\limits_\Omega {{{{\left| {\nabla {{U}_{x}}} \right|}}^{2}}} } } dz \to \min ,$

для конической поверхности (16), связанной с $x$.

Утверждение 5. В трехмерном случае минимум энергии Дирихле для конической поверхности, состоящей из прямых отрезков, соединяющих внутреннюю точку $\left( {x,u(x)} \right)$, $x \in \Omega $, с граничными точками $\left( {y,u(y)} \right)$, $y \in \partial \Omega $, достигается на трансфинитной барицентрической интерполяции $(4)$ с весовой функцией, заданной

(24)

$w(x,{{e}_{\omega }}) = {{\Delta }_{S}}({{\rho }^{2}}{\text{/}}2) + 2({{\rho }^{2}}{\text{/}}2),$

где ${{\Delta }_{S}}$ обозначает сферический лапласиан, а $\rho (\omega )$ описывает $\partial \Omega $ в сферических координатах с центром в $x$ $($т.е. для каждого $y \in \partial \Omega $ $\rho = \left| {x - y} \right|$ и ${{e}_{\omega }} = (y - x){\text{/}}\rho $$)$.

Ниже мы выведем более общий результат, полученный для энергии Дирихле с весом

(25)

$\int {\int {\int\limits_\Omega {{{{\left| {\nabla {{U}_{x}}} \right|}}^{2}}} } } a(x,\omega )dz,$

где $a(x,\omega )$ – положительная весовая функция и $\omega = (\theta ,\varphi )$ обозначает сферические координаты. Мы покажем, что минимизация взвешенной энергии Дирихле с весом (плотностью) $a(x,\omega )$ приводит к (4) с весовой функцией

$w(x,\omega ) = \Delta _{S}^{a}f + 2af,$

где $f = {{\rho }^{2}}{\text{/}}2$ и

$\Delta _{S}^{a} = {\text{di}}{{{\text{v}}}_{S}}\left( {a{{\nabla }_{S}}} \right).$

Здесь ${\text{di}}{{{\text{v}}}_{S}}$ и ${{\nabla }_{S}}$ обозначают дивергенцию и градиент сферы соответственно.

Доказательство. Пусть задана точка $x \in \Omega $, мы рассматриваем стандартные сферические координаты с центром в точке $x$: радиальное расстояние $r$ и сферические координаты $\omega = (\theta ,\varphi )$ с полярным углом $\theta $ и азимутальным углом $\varphi $. Для функции $f(r,\theta ,\varphi )$ ее градиент и магнитуда градиента в сферических координатах задаются формулами

$\nabla f(r,\theta ,\varphi ) = \frac{{\partial f}}{{\partial r}}{{e}_{r}} + \frac{1}{r}\frac{{\partial f}}{{\partial \theta }}{{e}_{\theta }} + \frac{1}{{r\sin \theta }}\frac{{\partial f}}{{\partial \varphi }}{{e}_{\varphi }},$

${{\left| {\nabla f} \right|}^{2}} = {{\left| {\frac{{\partial f}}{{\partial r}}} \right|}^{2}} + \frac{1}{{{{r}^{2}}}}{{\left| {\frac{{\partial f}}{{\partial \theta }}} \right|}^{2}} + \frac{1}{{{{r}^{2}}{{{\sin }}^{2}}\theta }}{{\left| {\frac{{\partial f}}{{\partial \varphi }}} \right|}^{2}}.$

Аналогично плоскому случаю, мы имеем

${{U}_{x}}(z) = \frac{{(\rho - r)u(x) + ru(y)}}{\rho }$

и, следовательно,

$\frac{{\partial {{U}_{x}}}}{{\partial r}} = \frac{{u(y) - u(x)}}{\rho },$

$\frac{{\partial {{U}_{x}}}}{{\partial \theta }} = r\left[ {(u(y) - u(x))\left( {\frac{1}{\rho }} \right)_{\theta }^{'} + \frac{1}{\rho }u_{\theta }^{'}(y)} \right],$

$\frac{{\partial {{U}_{x}}}}{{\partial \varphi }} = r\left[ {(u(y) - u(x))\left( {\frac{1}{\rho }} \right)_{\varphi }^{'} + \frac{1}{\rho }u_{\varphi }^{'}(y)} \right].$

Как и в двумерном случае определим $u(x)$ таким образом, чтобы для построенной конической поверхности ${{U}_{x}}(z)$ энергия Дирихле с плотностью $a(x,\omega )$ достигла своего минимального значения. Рассмотрим следующую задачу минимизации:

$\min \leftarrow \int {\int {\int\limits_\Omega {{{{\left| {\nabla {{U}_{x}}} \right|}}^{2}}} } } a(x,\theta ,\varphi )dz = \int\limits_0^\pi {\int\limits_0^{2\pi } {\int\limits_0^\rho a } } (x,\theta ,\varphi ){{r}^{2}}\sin \theta drd\varphi d\theta \left\{ {{{{\left[ {\frac{{u(x) - u(y)}}{\rho }} \right]}}^{2}}\mathop + \limits_{\mathop {}\limits_{}^{} }^{} } \right.$

$ + \;{{\left[ {(u(y) - u(x))\left( {\frac{1}{\rho }} \right)_{\theta }^{'} + \frac{1}{\rho }u_{\theta }^{'}(y)} \right]}^{2}} + \left. {\frac{1}{{{{{\sin }}^{2}}\theta }}{{{\left[ {(u(y) - u(x))\left( {\frac{1}{\rho }} \right)_{\varphi }^{'} + \frac{1}{\rho }u_{\varphi }^{'}(y)} \right]}}^{2}}} \right\} = $

$ = \;\frac{1}{3}\int\limits_0^\pi {\int\limits_0^{2\pi } a } (x,\theta ,\varphi )\rho (\theta ,\varphi )\sin \theta d\varphi d\theta \left\{ {{{{[u(x) - u(y)]}}^{2}}\mathop + \limits_{\mathop {{}_{{}}}\limits_{} }^{} } \right.$

$ + \;{{\left[ {u_{\theta }^{'}(y) + (u(x) - u(y))\frac{{\rho _{\theta }^{'}}}{\rho }} \right]}^{2}} + \left. {\frac{1}{{{{{\sin }}^{2}}\theta }}{{{\left[ {u_{\varphi }^{'}(y) + (u(x) - u(y))\frac{{\rho _{\varphi }^{'}}}{\rho }} \right]}}^{2}}} \right\}.$

Таким образом, для оптимального значения $u(x)$ получаем

(26)

$\begin{gathered} \int\limits_0^\pi {\int\limits_0^{2\pi } {u(x)} } \left\{ {1 + {{{\left( {\frac{{\rho _{\theta }^{'}}}{\rho }} \right)}}^{2}} + {{{\left( {\frac{{\rho _{\varphi }^{'}}}{{\rho \sin \theta }}} \right)}}^{2}}} \right\}a\rho \sin \theta d\theta d\varphi = \int\limits_0^\pi {\int\limits_0^{2\pi } {\left\{ {u(y) - u_{\theta }^{'}(y)\frac{{\rho _{\theta }^{'}}}{\rho } - u_{\varphi }^{'}(y)\frac{{\rho _{\varphi }^{'}}}{{\rho \mathop {\sin }\nolimits^2 \theta }}\mathop + \limits_{\mathop {_{{_{{}}}}}\limits_{} }^{} } \right.} } \\ \left. { + \;u(y){{{\left( {\frac{{\rho _{\theta }^{'}}}{\rho }} \right)}}^{2}} + u(y){{{\left( {\frac{{\rho _{\varphi }^{'}}}{{\rho \sin \theta }}} \right)}}^{2}}} \right\}a\rho \sin \theta d\theta d\varphi . \\ \end{gathered} $

Сначала рассмотрим

(27)

$\int\limits_0^\pi {\int\limits_0^{2\pi } {\left\{ {1 + {{{\left( {\frac{{\rho _{\theta }^{'}}}{\rho }} \right)}}^{2}} + {{{\left( {\frac{{\rho _{\varphi }^{'}}}{{\rho \sin \theta }}} \right)}}^{2}}} \right\}} } a\rho \sin \theta d\theta d\varphi $

и покажем, что этот интеграл равен

(28)

$\int\limits_0^\pi {\int\limits_0^{2\pi } {\frac{{\Delta _{S}^{a}f + 2af}}{\rho }} } \sin \theta d\theta d\varphi ,\quad f = {{\rho }^{2}}{\text{/}}2.$

Имеем

(29)

$\begin{gathered} \int\limits_0^\pi {\int\limits_0^{2\pi } {\frac{{\Delta _{S}^{a}f + 2af}}{\rho }} } \sin \theta d\theta d\varphi = \int\limits_0^\pi {\int\limits_0^{2\pi } {\left\{ {\rho _{\theta }^{'}\sin \theta a_{\theta }^{'} + a\frac{{{{{(\rho _{\theta }^{'})}}^{2}}}}{\rho }\sin \theta + a\sin \theta \rho _{{\theta \theta }}^{{''}} + a\rho _{\theta }^{'}\cos \theta } \right\}} } + \\ + \;\frac{1}{{\sin \theta }}\left\{ {\rho _{\varphi }^{'}a_{\varphi }^{'} + a\frac{{{{{(\rho _{\varphi }^{'})}}^{2}}}}{\rho } + a\rho _{{\varphi \varphi }}^{{''}}} \right\}d\theta d\varphi . \\ \end{gathered} $

Рассмотрим

(30)

$\int\limits_0^\pi {\int\limits_0^{2\pi } {\left\{ {\rho _{\theta }^{'}\sin \theta a_{\theta }^{'} + a\frac{{{{{(\rho _{\theta }^{'})}}^{2}}}}{\rho }\sin \theta + a\sin \theta \rho _{{\theta \theta }}^{{''}} + a\rho _{\theta }^{'}\cos \theta } \right\}} } d\theta d\varphi .$

Интегрируя по частям

$\int\limits_0^\pi a \sin \theta \rho _{{\theta \theta }}^{{''}}d\theta ,$

покажем, что

$\int\limits_0^\pi {\int\limits_0^{2\pi } {\left\{ {\rho _{\theta }^{'}\sin \theta a_{\theta }^{'} + a\sin \theta \rho _{{\theta \theta }}^{{''}} + a\rho _{\theta }^{'}\cos \theta } \right\}} } d\theta d\varphi = 0,$

и поэтому (30) равно

(31)

$\int\limits_0^\pi {\int\limits_0^{2\pi } a } \frac{{{{{(\rho _{\theta }^{'})}}^{2}}}}{\rho }\sin \theta d\theta d\varphi = \int\limits_0^\pi {\int\limits_0^{2\pi } {{{{\left( {\frac{{\rho _{\theta }^{'}}}{\rho }} \right)}}^{2}}} } a\rho \sin \theta d\theta d\varphi .$

Далее рассмотрим

(32)

$\int\limits_0^\pi {\int\limits_0^{2\pi } {\frac{1}{{\sin \theta }}} } \left\{ {\rho _{\varphi }^{'}a_{\varphi }^{'} + a\frac{{{{{(\rho _{\varphi }^{'})}}^{2}}}}{\rho } + a\rho _{{\varphi \varphi }}^{{''}}} \right\}d\theta d\varphi .$

Интегрирование по частям

$\int\limits_0^{2\pi } {\rho _{\varphi }^{'}} a_{\varphi }^{'}d\varphi $

дает

$\int\limits_0^{2\pi } {\left\{ {\rho _{\varphi }^{'}a_{\varphi }^{'} + a\rho _{{\varphi \varphi }}^{{''}}} \right\}} d\varphi = 0.$

Таким образом, (32) становится

(33)

$\int\limits_0^\pi {\int\limits_0^{2\pi } {\frac{1}{{\sin \theta }}} } \left\{ {a\frac{{{{{(\rho _{\varphi }^{'})}}^{2}}}}{\rho }} \right\}d\theta d\varphi .$

Теперь, используя (30)–(33), мы видим, что (27) и (28) совпадают.

Далее рассмотрим

(34)

$\int\limits_0^\pi {\int\limits_0^{2\pi } {\left\{ {u(y) - u_{\theta }^{'}(y)\frac{{\rho _{\theta }^{'}}}{\rho } - u_{\varphi }^{'}(y)\frac{{\rho _{\varphi }^{'}}}{{\rho \mathop {\sin }\nolimits^2 \theta }} + u(y){{{\left( {\frac{{\rho _{\theta }^{'}}}{\rho }} \right)}}^{2}} + u(y){{{\left( {\frac{{\rho _{\varphi }^{'}}}{{\rho \sin \theta }}} \right)}}^{2}}} \right\}} } a\rho \sin \theta d\theta d\varphi .$

Интегрирование по частям дает

$\int\limits_0^\pi {\int\limits_0^{2\pi } {\left\{ { - u_{\theta }^{'}(y)\frac{{\rho _{\theta }^{'}}}{\rho }} \right\}} } a\rho \sin \theta d\theta d\varphi = \int\limits_0^\pi {\int\limits_0^{2\pi } {\left\{ {u(y)\frac{{(a\rho _{\theta }^{'}\sin \theta )_{\theta }^{'}}}{{\sin \theta }}} \right\}} } \sin \theta d\theta d\varphi $

и аналогично

$\int\limits_0^\pi {\int\limits_0^{2\pi } {\left\{ { - u_{\varphi }^{'}({\mathbf{y}})\frac{{\rho _{\varphi }^{'}}}{{\rho \mathop {\sin }\nolimits^2 \theta }}} \right\}} } a\rho \sin \theta d\theta d\varphi = \int\limits_0^\pi {\int\limits_0^{2\pi } {\left\{ {u({\mathbf{y}})\frac{{(a\rho _{\varphi }^{'})_{\varphi }^{'}}}{{\mathop {\sin }\nolimits^2 \theta }}} \right\}} } \sin \theta d\theta d\varphi .$

Таким образом, (34) становится

$\int\limits_0^\pi {\int\limits_0^{2\pi } {u(y)} } \left\{ {a\rho + \frac{{(a\rho _{\theta }^{'}\sin \theta )_{\theta }^{'}}}{{\sin \theta }} + a\rho {{{\left( {\frac{{\rho _{\theta }^{'}}}{\rho }} \right)}}^{2}} + \frac{{(a\rho _{\varphi }^{'})_{\varphi }^{'}}}{{\mathop {\sin }\nolimits^2 \theta }} + a\rho {{{\left( {\frac{{\rho _{\varphi }^{'}}}{{\rho \sin \theta }}} \right)}}^{2}}} \right\}\sin \theta d\theta d\varphi .$

Используя (29), мы видим, что это выражение равняется

$\int\limits_0^\pi {\int\limits_0^{2\pi } {u(y)} } \left\{ {\frac{{\Delta _{S}^{a}f + 2af}}{\rho }} \right\}\sin \theta d\theta d\varphi .$

Таким образом, мы показали, что (26) соответствует

$u(x) = {{\int\limits_0^\pi {\int\limits_0^{2\pi } {\frac{{u(y)w(x,\theta ,\varphi )}}{\rho }} } \sin \theta d\theta d\varphi } \mathord{\left/ {\vphantom {{\int\limits_0^\pi {\int\limits_0^{2\pi } {\frac{{u(y)w(x,\theta ,\varphi )}}{\rho }} } \sin \theta d\theta d\varphi } {\int\limits_0^\pi {\int\limits_0^{2\pi } {\frac{{w(x,\theta ,\varphi )}}{\rho }} } }}} \right. \kern-0em} {\int\limits_0^\pi {\int\limits_0^{2\pi } {\frac{{w(x,\theta ,\varphi )}}{\rho }} } }}\sin \theta d\theta d\varphi ,$

где

$w(x,\theta ,\varphi ) = \Delta _{S}^{a}f + 2af,\quad f = {{\rho }^{2}}{\text{/}}2.$

Теперь утверждение (5) получается, если положить $a(x,\theta ,\varphi ) \equiv 1$.

Общее построение в 3D

Аналогично двумерному случаю, введем в рассмотрение область $G$, определяемую радиальной функцией $g(x,\omega )$, $\omega = (\theta ,\varphi )$, и применим трансфинитную интерполяцию Лапласа к $G$, где значения $u( \cdot )$ на $\partial G$ находятся путем линейной интерполяции

$v = \frac{{u(y)g + u(x)(\rho - g)}}{\rho }.$

Тогда имеем

$\int\limits_{{{S}_{x}}} {\frac{{{{\Delta }_{S}}({{g}^{2}}{\text{/}}2) + 2({{g}^{2}}{\text{/}}2)}}{g}vd\omega } = u(x)\int\limits_{{{S}_{x}}} {\frac{{{{\Delta }_{S}}({{g}^{2}}{\text{/}}2) + 2({{g}^{2}}{\text{/}}2)}}{g}d\omega ,} $

где $d\omega = \sin \theta d\theta d\varphi $ – элемент площади ${{S}_{x}}$ единичной сферы с центром в $x$. Аналогично двумерному случаю, это приводит к

$\begin{gathered} \int\limits_{{{S}_{x}}} {\frac{{{{\Delta }_{S}}({{g}^{2}}{\text{/}}2) + 2({{g}^{2}}{\text{/}}2)}}{\rho }u(y)d\omega } + u(x)\int\limits_{{{S}_{x}}} {\left( {1 - \frac{g}{\rho }} \right)} \frac{{{{\Delta }_{S}}({{g}^{2}}{\text{/}}2) + 2({{g}^{2}}{\text{/}}2)}}{g}d\omega = \\ = \;u(x)\int\limits_{{{S}_{x}}} {\frac{{{{\Delta }_{S}}({{g}^{2}}{\text{/}}2) + 2({{g}^{2}}{\text{/}}2)}}{g}d\omega } , \\ \end{gathered} $

и мы получаем

$u(x) = {{\int\limits_{{{S}_{x}}} \frac{{{{\Delta }_{S}}({{g}^{2}}{\text{/}}2) + 2({{g}^{2}}{\text{/}}2)}}{\rho }u(y)d\omega } \mathord{\left/ {\vphantom {{\int\limits_{{{S}_{x}}} \frac{{{{\Delta }_{S}}({{g}^{2}}{\text{/}}2) + 2({{g}^{2}}{\text{/}}2)}}{\rho }u(y)d\omega } {\int\limits_{{{S}_{x}}} \frac{{{{\Delta }_{S}}({{g}^{2}}{\text{/}}2) + 2({{g}^{2}}{\text{/}}2)}}{\rho }}}} \right. \kern-0em} {\int\limits_{{{S}_{x}}} \frac{{{{\Delta }_{S}}({{g}^{2}}{\text{/}}2) + 2({{g}^{2}}{\text{/}}2)}}{\rho }}}d\omega .$

Таким образом, мы пришли к общей трехмерной трансфинитной барицентрической интерполяции (4), (8) с $h(x,\omega ) = g{{(x,\omega )}^{2}}{\text{/}}2$.

7. ОБОБЩЕННЫЕ БАРИЦЕНТРИЧЕСКИЕ КООРДИНАТЫ И ОБРАТНЫЕ ЗАДАЧИ МИНКОВСКОГО И КРИСТОФФЕЛЯ

Рассмотрим трансфинитную барицентрическую интерполяционную схему (4) , которая удовлетворяет свойству линейной точности, т.е. точна на линейных функциях. Тогда, как мы знаем, весовая функция $w(x,{{e}_{\theta }})$, определенная на ${{S}_{x}}$, удовлетворяет условиям ортогональности (5). Оказывается, что условие (5) связано с классическими проблемами Минковского и Кристоффеля в дифференциальной геометрии.

В разд. 2 мы уже исследовали геометрическую интерпретацию весовой функции $w(x,\theta )$ в двумерном случае: ее можно рассматривать как радиус кривизны вспомогательной замкнутой кривой ${{\Sigma }_{x}}$, связанной с точкой $x \in \Omega $. Теперь мы попытаемся распространить это геометрическое наблюдение на трехмерный случай.

Проблема Минковского – это обратная задача, посвященная восстановлению замкнутой выпуклой поверхности из ее гауссовой кривизны, заданной как функция внешней нормали поверхности ${{e}_{\theta }}$ (см. [32]). Если задана положительная функция $K(\theta )$, определенная на единичной сфере $S$, то необходимым и достаточным условием существования решения проблемы Минковского с гауссовой кривизной $K(\theta )$ является условие

(35)

$\int\limits_\Sigma {{{e}_{\omega }}dA} \equiv \int\limits_S \frac{{{{e}_{\omega }}d\omega }}{{K(\omega )}} = 0,$

где $\Sigma $ – реконструированная поверхность, а $dA$ – ее элемент площади ($dA = d\omega {\text{/}}K$ по определению гауссовой кривизны). Необходимость (35) следует сразу же из теоремы Гаусса–Остроградского о дивергенции. Проблема Минковского может быть сведена к решению нелинейного уравнения Монжа–Ампера

$\det \left[ {\nabla _{S}^{2}h(\omega ) + h(\omega )I} \right] = K(\omega ),$

где $h(\omega )$ – опорная функция $\Sigma $, а $\nabla _{S}^{2}h(\omega )$ обозначает матрицу вторых частных производных (гессиан) опорной функции $h(\omega )$.

Проблема Кристоффеля – это еще одна классическая обратная задача в дифференциальной геометрии. Она состоит в нахождении выпуклой поверхности $\Sigma $ с заданной суммой главных радиусов кривизны. Проблема Кристоффеля проще проблемы Минковского и может быть решена через решение эллиптического дифференциального уравнения второго порядка

(36)

${\text{trace}}\left[ {\nabla _{S}^{2}h(\omega ) + h(\omega )I} \right] \equiv {{\Delta }_{S}}h(\omega ) + (N - 1)h(\omega ) = R(\omega ),$

где ${{\Delta }_{S}}$ – лапласиан сферы, а

$R(\omega ) = \sum\limits_{i = 1}^{N - 1} \,{{R}_{i}}(\omega )$

есть сумма главных радиусов кривизны. Так как $\lambda = (N - 1)$ является первым ненулевым собственным значением функции $ - {{\Delta }_{S}}$ и компоненты вектора ${{e}_{\omega }}$ являются соответствующими $N - 1$ собственными функциями, то необходимым и достаточным условием разрешимости (36) является

(37)

$\int\limits_\Sigma {{{e}_{\omega }}} R(\omega )ds = 0.$

Теперь для каждого $x \in \Omega $ мы можем положить

$R(x,\omega ) = w(x,{{e}_{\omega }})$

и решить (36). После чего поверхность ${{\Sigma }_{x}}$ восстанавливается из опорной функции $h(x,\omega )$. Один из способов решения (36) состоит в разложении $w(x,{{e}_{\omega }})$ по сферическим гармоникам и построения опорной функции $h(x,\omega )$ в виде ряда по сферическим гармоникам.

Если $N = 2$, то $\omega = \theta $, и задачи Минковского и Кристоффеля совпадают, так как $R(\theta ) = 1{\text{/}}k(\theta )$. Опорная функция $h(\theta )$ для ${{\Sigma }_{x}}$ удовлетворяет уравнению

(38)

$h_{{\theta \theta }}^{{''}}(\theta ) + h(\theta ) = w(x,\theta )$

с периодическими граничными условиями. Например, трансфинитные координаты Лапласа и координаты Вокспресса–Воррена получаются из

$w(x,\theta ) = \rho _{{\theta \theta }}^{{''}} + \rho \quad {\text{и}}\quad w(x,\theta ) = (1{\text{/}}\rho )_{{\theta \theta }}^{{''}} + 1{\text{/}}\rho $

соответственно.

На фиг. 8 показан пример плоской кривой, восстановленной по заданной опорной функции.

Фиг. 8.

(а) – График в полярных координатах заданной опорной функции $h(\theta )$. (б) – График радиуса кривизны $R(\theta ) = h{\text{''}}(\theta ) + h(\theta )$. (в) – Кривая, восстановленная по опорной функции $h(\theta )$. Кривая имеет шесть вершин, соответствующих нулям ее радиуса кривизны $R(\theta )$.

В трехмерном пространстве ситуация сложнее. Пусть сферические координаты задаются $\omega = (\theta ,\varphi )$. Мы уже видели, что трансфинитные координаты Лапласа задаются с помощью весовой функции

$w(x,\theta ,\varphi ) = {{\Delta }_{S}}({{\rho }^{2}}{\text{/}}2) + 2({{\rho }^{2}}{\text{/}}2)$

и, следовательно, согласно обратной задаче Кристоффеля, определяют поверхность ${{\Sigma }_{x}}$, чья опорная функция задается уравнением $h(x,\omega ) = {{\rho }^{2}}{\text{/}}2$. Далее для каждого $x \in \Omega $, если функция $w(x,\theta ,\varphi )$ удовлетворяет условию ортогональности (5), то решение уравнения

${{\Delta }_{S}}h + 2h = w(x,\theta ,\varphi )$

определяет опорную функцию $h(x,\omega )$ поверхности ${{\Sigma }_{x}}$, соответствующей точке $x$. Более того, как мы видели во второй части разд. 6, обратная задача Кристоффеля естественным образом связана с любой системой трансфинитных барицентрических координатами, если мы положим $h = {{g}^{2}}{\text{/}}2$ и для каждого $x \in \Omega $ будем рассматривать область $G$, определяемую радиальной функцией $g(x,\omega )$.

8. ЗАКЛЮЧЕНИЕ

В настоящей работе мы использовали простой вариационный принцип (минимизация энергии Дирихле конической поверхности) для получения трансфинитной версии барицентрических координат Лапласа и расширили этот подход для получения общего описания трансфинитных барицентрических координат в двумерном и трехмерном случаях. Мы привели выражения этих координат для многоугольных областей на плоскости для некоторых конкретных случаев. Наконец, обсудили связи между трансфинитными барицентрическими координатами и классическими обратными задачами Минковского и Кристоффеля в дифференциальной геометрии.

Авторы благодарны организаторам конференции NUMGRID 2020, где была представлена предварительная версия этой работы. Авторы также хотели бы поблагодарить рецензентов за полезные и конструктивные замечания.

Список литературы

Wachspress E.L. A rational finite element basis. Acad. Press, New York, 1975.
Warren J. Barycentric coordinates for convex polytopes // Adv. in Comput. Math. 1996. V. 6. № 2. P. 97–108.
Floater M.S. Mean value coordinates // Comput. Aided Geometric Design. 2003. V. 20. № 1. P. 19–27.
Floater M.S. Generalized barycentric coordinates and applications // Acta Numer. 2015. V. 24. P. 161–214.
Hormann K., Sukumar N. ed. Generalized barycentric coordinates in computer graphics and computational mechanics. CRC Press, 2017.
Budninskiy M., Liu B., Tong Y., Desbrun M. Power coordinates: A geometric construction of barycentric coordinates on convex polytopes // ACM Transact. on Graph. 2016. V. 35. № 6. P. 241.
Yan Z., Schaefer S. A family of barycentric coordinates for co-dimension 1 manifolds with simplicial facets // Comput. Graph. Forum. 2019. V. 38. № 5. P. 75–83. SGP 2019 Special Issue.
Bobach T., Bertram M., Umlauf G. Issues and implementation of C¹ and C² natural neighbor interpolation. Inter. Symp. on Visual Comput. 2006. P. 186–195.
Belikov V.V., Ivanov V.D., Kontorovich V.K., Korytnik S.A., Semenov A.Y. The non-Sibsonian interpolation: a new method of interpolation of the values of a function on an arbitrary set of points // Comput. Math. Math. Phys. 1997. V. 37. № 1. P. 9–15.
Pinkall U., Polthier K. Computing discrete minimal surfaces and their conjugates // Experiment. Math. 1993. V. 2. № 1. P. 15–36.
Floater M.S., Hormann K., K’os G. A general construction of barycentric coordinates over convex polygons // Adv. in Comput. Math. 2006. V. 24. № 1–4. P. 311–331.
Ju T., Liepa P., Warren J. A general geometric construction of coordinates in a convex simplicial polytope // Comput. Aided Geometr. Design. 2007. V. 24. № 3. P. 161–178.
MacNeal R.H. An asymmetrical finite diﬀerence network // Quart. of Appl. Math. 1953. V. 11. № 3. P. 295–310.
Christ N.H., Friedberg R., Lee T.D. Weights of links and plaquettes in a random Lattice // Nucl. Phys. B 1982. V. 210. № 3. P. 337–346.
Eck M., DeRose T., Duchamp T., Hoppe H., Lounsbery M., Stuetzle W. Multiresolution analysis of arbitrary meshes // In Siggraph. 1995. V. 95. P. 173–182.
Sugihara K. Surface interpolation based on new local coordinates // Computer-Aided Design. 1999. V. 31. № 1. P. 51–58.
Meyer M., Lee H., Barr A., Desbrun M. Generalized barycentric coordinates on irregular polygons // J. of Graph. Tools. 2002. V. 7. № 1. P. 13–22.
Warren J., Schaefer S., Hirani A., Desbrun M. Barycentric coordinates for convex sets // Adv. in Comput. Math. 2007. V. 27. № 3. P. 319–338.
Ju T., Schaefer S., Warren J. Mean value coordinates for closed triangular meshes // ACM Transact. on Graph. 2005. V. 24. № 3. P. 561–566. Proceed. of SIGGRAPH. 2005.
Belyaev A. On transfinite barycentric coordinates. Proceed. of the Fourth Eurographics Symp. on Geometry Processing (SGP 2006). P. 89–99. 2006.
Schaefer S., Ju T., Warren J. A unified, integral construction for coordinates over closed curves // Comput. Aided Geometr. Design. 2007. V. 24. № 8–9. P. 481–493.
Dyken C., Floater M.S. Transfinite mean value interpolation // Comput. Aided Geometr. Design. 2009. V. 26. P. 117–134.
Bruvoll S., Floater M.S. Transfinite mean value interpolation in general dimension // J. Comp. Appl. Math. 2010. V. 233. P. 1631–1639.
Floater M.S., Kosinka J. Barycentric interpolation and mappings on smooth convex domains. Proceed. of the 14th ACM Symp. on Solid and Phys. Model. 2010. P. 111–116.
Kosinka J., Barton M. Convergence of barycentric coordinates to barycentric Kernels // Comput. Aided Geometr. Design. 2016. V. 43. P. 200–210.
Chen R., Gotsman C. Complex transfinite barycentric mappings with similarity Kernels // Comput. Graph. Forum. 2016. V. 35. № 5. P. 41–53. SGP 2016 Special Issue.
Floater M.S., Patrizi F. Transfinite mean value interpolation over polygons, 2019. arXiv:1906.08358 [math.NA].
Zayer R. Numerical and variational aspects of mesh parameterization and editing. PhD thesis, Saarland Univer., 2007.
Belyaev A., Fayolle P.-A. On integral-based (transfinite) laplace coordinates. Numeric. Geometry, Grid Generat. and Sci. Comput. NUMGRID 2020. Springer, 2020.
Floater M.S., K’os G., Reimers M. Mean value coordinates in 3D // Comput. Aided Geometr. Design. 2005. V. 22. № 7. P. 623–631.
Shepard D. A two-dimensional interpolation function for irregularly-spaced data. Proceed. of the 1968 23rd ACM Nation. Conf. P. 517–524. ACM Press, 1968.
Minkowski H. Volumen und Oberfläsche // Math. Ann. 1903. V. 57. P. 447–495.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал вычислительной математики и математической физики

Архивы выпусков Информация о журнале Отправить рукопись в журнал