Журнал вычислительной математики и математической физики, 2022, T. 62, № 8, стр. 1300-1322
Движение и деформация квазиизометрической сетки с геометрически адаптированной метрикой
В. А. Гаранжа 1, 2, *, Л. Н. Кудрявцева 1, 2, **
1 ВЦ им. А.А. Дородницына ФИЦ ИУ РАН
119333 Москва, ул. Вавилова, 40, Россия
2 МФТИ
141701 М.о., Долгопрудный, Институтский пер., 9, Россия
* E-mail: garan@ccas.ru
** E-mail: liukudr@yandex.ru
Поступила в редакцию 11.10.2021
После доработки 03.03.2022
Принята к публикации 11.04.2022
- EDN: MVYOSV
- DOI: 10.31857/S0044466922080063
Аннотация
Предложен алгоритм, который позволяет строить движущуюся адаптивную сетку с фиксированной связностью на основе квазиизометрического сеточного функционала в соответствии с нестационарной геометрически адаптивной управляющей метрикой в расчетной области. На каждом шаге по времени используется предобусловленный метод градиентного спуска для сеточного функционала, чтобы построить большие смещения вершин сетки. Промежуточные сетки, использующие простую линейную интерполяцию между начальным и смещенным состояниями с использованием времени в качестве параметра, гарантированно являются невырожденными деформациями начальной сетки. Следовательно, для численного моделирования с малыми временными шагами можно использовать один сравнительно дорогостоящий шаг вариационного алгоритма деформации сетки на 5–10 временных шагов, что значительно повышает эффективность алгоритма перестроения сетки применительно к алгоритмам вычислительной физики на подвижных сетках. Управляющая метрика обеспечивает анизотропное сгущение сетки вблизи границы движущегося тела по нормали и специальный выбор сгущения сетки в переходных зонах. Алгоритм вычисления целевых касательных растяжений сетки имеет решающее значение для реализуемости управляющей метрики. Он учитывает кривизну границы тела, а мелкие геометрические детали разрешаются с помощью медиальных осей. Дополнительные данные кодируются на фоновой движущейся сетке. Библ. 25. Фиг. 30.
1. ВВЕДЕНИЕ
Принцип равномерного распределения (см. [1]) является одной из основ алгоритмов подвижных адаптирующихся сеток (см. [2], [3]). Его идея состоит в том, чтобы вычислить распределение шага сетки, используя информацию из уравнений в частных производных или из оценки ошибки интерполяции. В одномерном случае принцип равномерного распределения приводит к решению линейного эллиптического уравнения второго порядка со скалярной управляющей функцией. Заметим, что для задач, зависящих от времени, обычно приходится использовать различные адаптивные фильтры для подавления неустойчивости подвижной сетки, которые были описаны в 1986 г. в известной работе [4].
Способ обобщения на несколько измерений до сих пор вызывает споры. Широко используемое обобщение основано на решении уравнений типа Лапласа для координат вершин сетки с помощью скалярной функции управления (см. [5], [6]).
В начале 1990-х гг. С.К. Годунов сформулировал следующие основные принципы вариационного метода построения расчетных сеток:
– сетка сама по себе должна быть квазиизометрической деформацией и должна сходиться к определенному квазиизометрическому отображению при измельчении;
– квазиизометрическое отображение должно быть единственным и устойчивым решением вариационной задачи;
– вариационная задача должна использовать меры искажения, основанные на главных инвариантах метрического тензора деформации;
– дискретизированная вариационная задача также должна иметь единственное и устойчивое решение.
К сожалению, методов построения сеток, удовлетворяющих одновременно всем этим принципам, не существует.
Напомним, что по определению квазиизометрического отображения отношение длины любой простой выпрямляемой кривой к длине ее образа ограничено сверху некоторой константой $K > 1$, а снизу – $1{\text{/}}K$.
Первая реализация этих идей была представлена в [7] с использованием метода конформных отображений в двумерных областях простой формы. Эти идеи получили развитие в ряде работ, включая [8], [9], где был предложен и обоснован теоретически и численно вариационный принцип для построения многомерных квазиизометрических отображений.
В настоящей работе, которая является расширенной версией статьи в трудах конференции NUMGRID2020 (см. [10]), предлагается новый алгоритм, позволяющий строить подвижную адаптивную сетку с фиксированной связностью с помощью нестационарной управляющей метрики в вычислительной области. Рассматриваются методы построения управляющей метрики и расчетных сеток, позволяющих повысить точность численного моделирования вязких течений с использованием погруженных граничных условий (IBC – Immersed Boundary Conditions) (см. [11]) для системы движущихся тел, задаваемых функцией расстояния со знаком.
Используется следующий принцип оптимальности: каждая ячейка идеальной сетки в данный момент времени преобразуется к локальным координатам, в которых локальный метрический тензор является единичным. В результате этого преобразования ячейка должна быть конгруэнтна ячейке с тем же номером в начальной сетке. Квазиизометрический функционал из [8] используется для измерения и управления соответствием между реальной и идеальной сетками. Мы обнаружили, что когда глобальные большие деформации начальной сетки необходимы для удовлетворения критерия сжатия сетки внутри тонких движущихся слоев вблизи границ областей, простые явные методы оптимизации не позволяют сетке точно следовать за метрикой. К сожалению, алгоритм предобусловленного градиентного спуска для квазиизометрического функционала является довольно дорогим, и поэтому его использование на каждом временном шаге расчета вязкого течения неэффективно. Другая проблема заключается в том, что из-за нелинейности уравнений Эйлера–Лагранжа мы не можем предполагать, что норма невязки равна нулю на каждом временном шаге. Таким образом, непрерывность по времени движущейся сетки не гарантируется, поскольку итерационная минимизация функционала с обновленной метрикой может привести к значительным смещениям даже для бесконечно малых временных шагов за счет остаточной невязки, а пространственно-временные траектории ячеек сетки могут стать сильно скошенными. Для решения этой проблемы мы предлагаем простой и эффективный алгоритм, основанный на прямой интерполяции сетки. Используя алгоритм минимизации из [12], мы вычисляем предиктор, который определяет направление минимизации (поле смещения) для каждой вершины сетки для большого приращения времени. Каждая промежуточная сетка, вычисленная с помощью этого смещения посредством линейной интерполяции, гарантированно корректна. Мы обнаружили, что длина вычисленного поля смещений сильно превосходит смещения, допускаемые численным алгоритмом для течений вязкой жидкости (см. [11]), поэтому количество дорогостоящих неявных минимизаций может быть значительно сокращено. Предполагая, что временная зависимость метрики определяется гладкой функцией, получаем алгоритм деформации/адаптации сетки, который требует только 1–2 применений линейного решателя за, скажем, 5–10 временных шагов, что делает его довольно эффективным компонентом решателя потока движущейся сетки. Мы обнаружили, что линейный решатель, основанный на так называемой неполной факторизации Холецкого второго порядка (IC2) (см. [13], [14]), является очень эффективным компонентом алгоритма минимизации, особенно, для параллельной версии алгоритма. Наш опыт с более простыми алгоритмами, такими как метод сопряженных градиентов со стандартной неполной факторизацией Холецкого IC(k) в качестве предобусловливателя, не оправдал ожиданий.
2. КВАЗИИЗОМЕТРИЧЕСКИЙ ФУНКЦИОНАЛ
Квазиизометрический функционал был предложен в [8], [9]. Здесь мы используем упрощенную версию этого функционала для контролируемой деформации сетки.
Пусть ${{\xi }_{1}}, \ldots ,{{\xi }_{d}}$ обозначают лагранжевы координаты, связанные с упругим материалом, а ${{x}_{1}}, \ldots ,{{x}_{d}}$ – эйлеровы координаты материальной точки. Пространственное отображение $x(\xi ,t):{{\mathbb{R}}^{d}} \to {{\mathbb{R}}^{d}}$ задает зависящую от времени упругую деформацию, где параметр $t$ – время, а ${{\xi }_{i}}$ – координаты в области с начальной сеткой. Таким образом, ${{\xi }_{i}}$ вморожены в ячейки исходной сетки, а эйлеровы координаты – это координаты точек сетки в расчетной области.
Матрица Якоби отображения $x(\xi , \cdot )$ обозначается через $C$, где ${{c}_{{ij}}} = \partial {{x}_{i}}{\text{/}}\partial {{\xi }_{j}}$.
Пусть ${{G}_{\xi }}(\xi ,t)$ и ${{G}_{x}}(x,t)$ – метрические тензоры, определяющие линейные элементы и длины кривых в лагранжевых и эйлеровых координатах в областях ${{\Omega }_{\xi }}$ и ${{\Omega }_{x}}$ соответственно. Тогда $x(\xi ,t)$ – это отображение между метрическими многообразиями ${{M}_{\xi }}$ и ${{M}_{x}}$.
Определим следующий поливыпуклый упругий потенциал (внутреннюю энергию), который служит мерой искажения и записывается как взвешенная сумма мер искажения формы и объема (см. [8]):
(1)
$W(C) = (1 - \theta )\frac{{\frac{1}{d}tr({{C}^{{\text{т}}}}C)}}{{\det {{C}^{{2/d}}}}} + \frac{1}{2}\theta \left( {\frac{1}{{\det C}} + \det C} \right).$Ищем деформацию сетки $x(\xi ,t)$, которая является решением вариационной задачи
(3)
$F(x(\xi ,t)) = \int\limits_{{{\Omega }_{\xi }}} \,W(Q(x,t){{\nabla }_{\xi }}x(\xi ,t)H{{(\xi )}^{{ - 1}}})\det H{\kern 1pt} d\xi .$В текущей версии алгоритма деформации сетки мы не рассматриваем вариацию функционала (3) в зависимости от времени $t$.
Матрицы $H(\xi )$ и $Q(x,t)$ задают факторизации метрических тензоров ${{G}_{\xi }}$ и ${{G}_{x}}$ соответственно, определяемые как
Предполагаем, что сингулярные значения матриц $Q$ и $H$ равномерно ограничены снизу и сверху.
Нестационарная деформация сетки вводится через зависящий от времени метрический тензор ${{G}_{x}}(x,t) = {{Q}^{{\text{т}}}}(x,t)Q(x,t)$. Из (2) следует, что абсолютный минимум функционала (3) равен
и достигается при $Q(x,t){{\nabla }_{\xi }}x(\xi ,t)H{{(\xi )}^{{ - 1}}} = U$, где $U$ – ортогональная матрица. Это означает, что в “изотропной” системе координат $y = Qx$, в которой метрический тензор ${{G}_{x}}(x,t)$ является единичным, отображение $x(x,t)$ локально изометрично отображению $x(\xi ,0)$, когда $H(\xi ) = {{\nabla }_{\xi }}x(\xi ,0)$.Предположим, что область ${{\Omega }_{\xi }}$ может быть разбита на выпуклые многогранники ${{D}_{k}}$. Строим непрерывную кусочно-гладкую деформацию ${{x}_{h}}(\xi , \cdot )$, которая регулярна на каждом многограннике. На практике мы используем линейные и полилинейные конечные элементы для того, чтобы собрать глобальную деформацию. Интеграл $F({{x}_{h}}(\xi ),t)$ по этой деформации мы называем полудискретным функционалом.
Для аппроксимации интеграла по выпуклой ячейке ${{D}_{k}}$ требуются определенные квадратурные правила. В результате полудискретный функционал заменяется дискретным:
3. ПРЕДОБУСЛОВЛЕННЫЙ АЛГОРИТМ МИНИМИЗАЦИИ И СТРАТЕГИЯ ИНТЕРПОЛЯЦИИ ПО ВРЕМЕНИ ДВИЖУЩЕЙСЯ СЕТКИ
Удобно записать дискретный функционал в виде функции $F(Z,Y,t)$ с пространственным аргументом ${{Z}^{{\text{т}}}} = (z_{1}^{{\text{т}}}{\kern 1pt} z_{2}^{{\text{т}}}{\kern 1pt} \ldots {\kern 1pt} z_{{{{n}_{v}}}}^{{\text{т}}})$, где ${{z}_{k}} \in {{\mathbb{R}}^{d}}$, $k = 1,2, \ldots ,{{n}_{{v}}}$, являются положениями вершин сетки. Зависимость от времени $t$ вводится через зависящую от времени метрику ${{G}_{x}}(y,t)$. Вектор $Y$ соответствует аргументу $y$ метрики ${{G}_{x}}$.
Матрица Гессе $\tilde {H}$ функции $F$ относительно $Z$ строится из $d \times d$ блоков ${{\tilde {H}}_{{ij}}} = {{\partial }^{2}}F{\text{/}}(\partial {{z}_{i}}\partial z_{j}^{T})$. Здесь матрица ${{\tilde {H}}_{{ij}}}$ находится на пересечении $i$-й блочной строки блока и $j$-го блочного столбца. Мы фильтруем матрицу Гессе во время процедуры сборки конечных элементов, чтобы сделать ее положительно определенной и уменьшить количество ненулевых элементов в 2 раза (см. [12]). Ниже мы используем те же обозначения $\tilde {H}$ для фильтрованной матрицы Гессиана. Градиент $F$ по $Z$ обозначается через $R$. Этот вектор состоит из подвекторов ${{r}_{i}}$ размера $d$. Он является приближенным градиентом функционала, так как мы не дифференцируем метрику ${{G}_{x}}$, следовательно, зависимость от $Y$ не учитывается.
Поскольку точное решение вариационной задачи на временном слое ${{t}^{{n + 1}}} = {{t}^{n}} + \Delta {{t}^{n}}$ слишком дорого, мы используем специальные 1- или 2-шаговые эвристические схемы интегрирования по времени.
Один шаг метода Ньютона для нахождения стационарной точки функции может быть записан как
(5)
$\sum\limits_{j = 1}^{{{n}_{v}}} \,{{\tilde {H}}_{{ij}}}({{Z}^{n}},{{Z}^{n}},{{t}^{{n + 1}}})\delta {{z}_{j}} + {{r}_{i}}({{Z}^{n}},{{Z}^{n}},{{t}^{{n + 1}}}) = 0.$(6)
$\tilde {H}({{Z}^{n}},{{Z}^{n}},{{t}^{{n + 1}}})\delta Z + R({{Z}^{n}},{{Z}^{n}},{{t}^{{n + 1}}}) = 0$(8)
${{\tau }_{n}} = \arg \mathop {\min }\limits_\tau F({{Z}^{n}} + \tau \delta Z,{{Z}^{n}},{{t}^{{n + 1}}}).$Для приближенного решения линейной системы (6) используется метод сопряженных градиентов с предобусловливанием на основе приближенной факторизации Холецкого второго порядка (см. [13]). Для параллельной версии решателя мы используем аддитивную версию приближенной факторизации Холецкого второго порядка, основанную на разбиении на подобласти с перекрытиями (см. [14]). Полученная нелинейная схема оказалась очень устойчивой и достаточно эффективной.
Можно попытаться упростить структуру матрицы Гессе, задав ${{\tilde {H}}_{{ij}}} = 0$, когда $i \ne j$ (см. [15]) или даже рассматривая только диагональную часть матрицы Гессиана в качестве предусловия. Мы обнаружили, что если для удовлетворения критерия сжатия сетки внутри тонких движущихся слоев необходимы глобальные большие деформации исходной сетки, то простые “явные” (т.е. не требующие решения линейных систем с глобальными матрицами) методы оптимизации сетки не могут точно следовать метрике. Наш линейный решатель основан на извлечении $d$ независимых линейных систем с симметричными положительно-определенными ${{n}_{v}} \times {{n}_{v}}$ матрицами (см. [12]) из линейной системы (6), которые по существу эквивалентны конечно-элементным аппроксимациям скалярных уравнений Пуассона с тензорными коэффициентами.
Простейший одношаговый алгоритм интегрирования по времени формулируется так:
Наблюдаемый парадокс вариационного метода заключается в том, что мы можем приписать любую разумную константу $K$ в диапазоне $(0,1{\text{/}}2]$ шагу ${{\tau }_{n}}$ и после короткого переходного периода алгоритм в конечном итоге отмасштабирует приращение $\delta Z$ таким образом, что значение ${{\tau }_{n}}{\text{|}}\delta Z{\kern 1pt} {\text{|}}$ будет почти неизменным, поскольку в противном случае слой сетки будет отставать от заданного положения. Задание $K = 1{\text{/}}2$ оказалось хорошим экспериментальным компромиссом между точностью и устойчивостью. Для улучшения точности был опробован следующий двухшаговый алгоритм:– вычислить
– найти новое приращение $\delta \tilde {Z}$ такое, что
(11)
$\tilde {H}({{Z}^{{n + 1/2}}},{{Z}^{{n + 1/2}}},{{t}^{{n + 1}}})\delta Z + R({{Z}^{{n + 1/2}}},{{Z}^{{n + 1/2}}},{{t}^{{n + 1}}}) = 0,$– присвоить
Для обеспечения устойчивости алгоритма в случае, когда полученное ${{Z}^{{n + 1}}}$ не является допустимым решением, необходимо найти новое ${{\tau }_{n}}$ через(13)
${{\tau }_{n}} = \arg \mathop {\min }\limits_\tau F({{Z}^{n}} + \tau \delta \tilde {Z},{{Z}^{{n + 1/2}}},{{t}^{{n + 1}}}),$4. РАСТЯЖЕНИЕ СЕТКИ И УПРАВЛЕНИЕ ГРАДАЦИЕЙ РАЗМЕРОВ В НОРМАЛЬНОМ И КАСАТЕЛЬНОМ НАПРАВЛЕНИЯХ
Система из одного или нескольких движущихся и деформирующихся тел обозначается как область $B \in {{\mathbb{R}}^{d}}$, определяемая неявной функцией ${{d}_{s}}(x,t)$ таким образом, что функция ${{d}_{s}}$ отрицательна внутри тела, положительна вне его, а изоповерхность ${{d}_{s}}(x,t) = 0$ определяет границу $\partial B$ в момент времени $t$. Мы предполагаем, что ${{d}_{s}}(x,t)$ напоминает функцию расстояния со знаком для мгновенной границы области. Теоретически можно предположить существование квазиизометрического отображения $x(y):{{\mathbb{R}}^{d}} \to {{\mathbb{R}}^{d}}$ такого, что функция ${{d}_{s}}(x(y),t)$ является именно функцией расстояния. На практике мы предполагаем, что вектор ${{\nabla }_{x}}{{d}_{s}}$ в окрестности границы определен, и его норма ограничена снизу и сверху некоторыми глобальными константами.
Метрический тензор $G(x,t)$ определяется как функция ${{d}_{s}}(x,t)$ таким образом, что он достигает наибольшего значения на границе области и уменьшается внутри и снаружи тела (по разным законам). Сетка внутри тела в общем случае довольно грубая, так как решение расчетного модуля с погруженной границей внутри тела не имеет физического смысла. Важно иметь высокоразрешенную сетку, покрывающую внутреннюю и внешнюю части пограничного слоя таким образом, чтобы внешняя (физически осмысленная) часть слоя и внутренняя (искусственная) часть слоя описывались близкими законами, а сгущенная сетка была бы гладкой по всему слою, что значительно повышает точность и устойчивасть реализации условий погруженной границы (IBC) (см. [16]).
Для достижения плавной градации размера сетки мы используем вспомогательное логарифмическое отображение, которое позволяет достичь почти постоянного коэффициента роста размера сетки в нормальном направлении от тела. Рассмотрим одномерное вспомогательное отображение $y(\xi ):[0,1] \to [0,1]$. Определим равномерную сетку в координатах $\xi $ с размером ячейки $h = 1{\text{/}}N$, где $N$ – число ячеек. Вершины ${{y}_{i}}$ распределены в предположении постоянной скорости роста
Это равенство можно рассматривать как конечно-разностную аппроксимацию уравнения Меняя местами зависимые и независимые переменные, получаем Решение этого уравнения выглядит следующим образом:(14)
$\xi = \phi (y) = \frac{h}{\varepsilon }\ln \left[ {1 + \frac{{A\varepsilon }}{h}(y - \delta )} \right] + \delta A.$Фиг. 1.
(а) – Вспомогательное одномерное отображение, определяющее растяжение. (б) – Целевой коэффициент сжатия сетки $A$ слишком велик и должен быть уменьшен.

Производные этого отображения определяются следующим образом:
(15)
$\gamma (y,\delta ,A) = \dot {\phi } = \frac{1}{{\frac{1}{A} + \frac{\varepsilon }{h}(y - \delta )}},\quad \ddot {\phi } = - \frac{\varepsilon }{h}\frac{1}{{{{{\left[ {\frac{1}{A} + \frac{\varepsilon }{h}(y - \delta )} \right]}}^{2}}}}.$Набор управляющих параметров $\delta $, $A$, $\kappa $, $h$ может быть противоречивым, так как при слишком больших значениях коэффициента сжатия $A$ можно получить ${{\phi }^{{ - 1}}}(1) > 1$ или даже ${{\phi }^{{ - 1}}}(D) > 1$. В этом случае мы итерационно уменьшаем значение $A$ с $\kappa = 2$, пока не будет выполнено равенство ${{\phi }^{{ - 1(1)}}} = 1$.
Для вычисления безразмерных управляющих параметров функции $\phi $ мы используем радиус ${{R}_{{\max }}}$ зоны влияния тела, истинную толщину слоя сетки ${{\delta }_{R}}$, и средний размер сетки ${{l}_{R}}$ в направлении нормали к телу.
Тогда
(16)
${{\sigma }_{1}}(x,t) = \gamma ({\text{|}}{{d}_{s}}(x,t){\text{|/}}{{R}_{{\max }}},\delta ,{{A}_{n}}),$Обозначим через ${{u}_{1}} = \nabla {{d}_{s}}{\text{/|}}\nabla {{d}_{s}}{\text{|}}$ единичный вектор нормали к изоповерхности функции расстояния. Мы можем получить полный ортонормированный базис $U = ({{u}_{1}}, \ldots ,{{u}_{d}})$, используя векторы ${{u}_{2}}, \ldots ,{{u}_{d}}$, определяющие локальный касательный базис на изоповерхности ${{d}_{s}}$. Метрический тензор ${{G}_{x}}(x,t)$ определяется следующим образом:
Выбор тангенциальных растяжений, а именно, растяжений в направлениях, ортогональных градиенту неявной функции, не является тривиальным. Он очень важен для того, чтобы получить деформацию сетки без скачков размера и разрывов. Здесь “разрыв” означает появление длинных и перекошенных ячеек сетки, что напоминает приближение разрыва упругого материала.Изотропный выбор ${{\sigma }_{i}} = {{\sigma }_{1}}$ или ${{G}_{x}} = \sigma _{1}^{2}I$ кажется самым простым. К сожалению, его применимость очень ограничена, поскольку прообраз пограничного слоя в начальных координатах $\xi $ масштабируется в ${{A}_{n}}$ раз, как показано на фиг. 2 для ${{A}_{n}} = 6$. Увеличенный прообраз может покрыть всю начальную область или даже выйти за пределы границы, значит, большинство ячеек сетки попадут в пограничный слой, делая результирующую сетку непригодной для использования. Сетка в фиг. 2 содержит 22 531 вершину и 44 610 треугольников, однако геометрическое увеличение слоя практически не зависит от сетки.
Фиг. 2.
Изотропная метрика: внутренний слой в вычислительной области и его прообраз в параметрической области.

Если задать максимальное тангенциальное сжатие ${{A}_{t}}$, то линейный размер прообраза увеличится в ${{A}_{t}}$ раз, а толщина слоя прообраза увеличится в ${{A}_{n}}$ раз, как показано на фиг. 3 для ${{A}_{n}} = 6$, ${{A}_{t}} = 2$ и той же начальной сетки.
Фиг. 3.
Анизотропная метрика: внутренний слой в вычислительной области и его прообраз в параметрической области.

Максимальный коэффициент анизотропии ${{A}_{n}}{\text{/}}{{A}_{t}}$ задается в пограничном слое и ${{\sigma }_{i}}$ выбираются для постепенного уменьшения анизотропии вдали от слоя. В некоторых случаях постоянный коэффициент ${{A}_{t}}$ не позволяет разрешить граничные особенности, в частности, при наличии острых или сильно изогнутых фрагментов границы. Общая идея состоит в том, что когда тангенциальное разрешение недостаточно, следует использовать разумные значения тангенциальных растяжений $A_{{t\,i}}^{*}$, $i = 2, \ldots ,d$, в различных направлениях в диапазоне ${{A}_{t}} \leqslant A_{{t\,i}}^{*} \geqslant {{A}_{n}}$.
Обозначим метрику с постоянными растяжениями в пограничном слое через ${{G}_{1}}$, а метрику около особенностей поверхности через ${{G}_{2}}$. Используем то же представление (16) и (17) для ${{G}_{2}}$, главное отличие – радиус влияния ${{R}_{2}}$, который должен быть меньше по сравнению с глобальным радиусом влияния ${{R}_{{\max }}}$ для ${{G}_{1}}$. Тогда окончательная метрика определяется следующим образом:
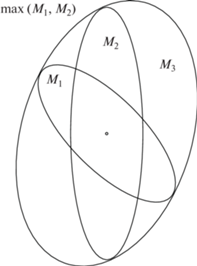
Операция максимума основана на построении общего описанного эллипсоида и близка к предложенной в [17] (см. фиг. 4). Рассмотрим два концентрических эллипсоида ${{M}_{1}}$ и ${{M}_{2}}$, заданных квадратичными формами ${{x}^{{\text{т}}}}G_{1}^{{ - 1}}x = 1$ и ${{x}^{{\text{т}}}}G_{2}^{{ - 1}}x = 1$ соответственно. Общий описанный эллипсоид ${{M}_{3}}$ определяет матрицу ${{G}_{3}}$. Построить эллипсоид ${{M}_{3}}$ просто: достаточно найти аффинное отображение, которое преобразует один из эллипсоидов в сферу. В преобразованных координатах тривиально строится описанный эллипсоид и отображается обратно в исходные координаты. Поскольку каждая из метрик определяется своим спектральным разложением, это построение сводится к ряду произведений ортогональных и диагональных матриц.Основной недостаток этого подхода заключается в том, что он по сути является ручным: необходимо отметить определенные зоны на поверхности как особенности. Это может быть сделано относительно легко на плоскости, но очевидно невозможно в трехмерном случае. Для построения полностью автоматического алгоритма мы предлагаем новую процедуру вычисления целевых касательных растяжений. Она основана на оценке радиусов приближенных главных кривизн граничной поверхности и расстояния до медиальной оси. Напомним, что медиальная ось определяется множеством центров шаров, которые принадлежат области или ее дополнению и касаются границы области хотя бы в двух точках.
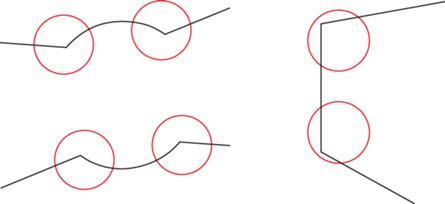
На фиг. 5 показана медиальная ось для простого гладкого контура 2г; фиг. 5в иллюстрирует идею аппроксимации медиальной оси ребрами Вороного (ребрами и гранями в 3г). Эта идея была предложена в известном алгоритме Powercrust, разработанном Н. Амента и соавт. в 2001 г. (см. [18]). Поясним, как медиальные оси сочетаются с данными о кривизне для определения анизотропной локальной функции размера на поверхности тела. Предположим, что в каждой граничной точке $p$ нашего тела мы знаем главные кривизны и главные направления, а также расстояние до медиальной оси. Обозначим через ${{\kappa }_{1}},\;{{\kappa }_{2}}$ главные кривизны и через ${{u}_{1}},\;{{u}_{2}}$ ортогональные главные направления на касательной плоскости. Мы всегда предполагаем, что ${{u}_{1}},\;{{u}_{2}},\;n$ – правый ортонормированный базис, где $n$ – внешняя единичная нормаль в точке $p$. Обозначим через ${{R}_{1}}(p) = 1{\text{/|}}{{\kappa }_{1}}{\text{|}},$ ${{R}_{2}}(p) = 1{\text{/|}}{{\kappa }_{2}}{\text{|}}$ радиусы главных кривых в точке $p$, предполагая, что ${{R}_{1}} \leqslant {{R}_{2}}$, а ${{R}_{{ma}}}(p)$ обозначает минимальное расстояние от точки $p$ до медиальной оси. Обозначим через s отношение масштабов медиальной оси и кривизны:
Тогда локальные радиусы ${{r}_{1}}(p),\;{{r}_{2}}(p)$ определяются следующим образом:Фиг. 5.
Концепция медиальной оси на плоскости: (a) – контур тела, (б) – медиальная ось, (в) – аппроксимация медиальной оси ребрами Вороного, (г) – выбор локального касательного размера на границе тела.

Покажем, как локальные радиусы ${{r}_{{1,2}}}$ переходят в касательные растяжения ${{\sigma }_{{2,3}}}$ в произвольной точке $x$ расчетной области. Для вычисления целевых касательных растяжений на поверхности тела используется простая идея: каждый радиус задает умозрительную окружность в плоскости, заданной нормалью поверхности и одним из векторов касательного базиса. Эта окружность должна быть образом окружности в параметрической области, на окружности которой мы помещаем $m \geqslant 12$ шагов параметрической сетки. Отношение радиуса параметрической окружности и вычисленного локального радиуса определяет локальное тангенциальное растяжение вдоль базисного вектора. Это растяжение усекается сверху заданным значением нормального растяжения. Таким образом, делается умозрительная попытка отобразить, по крайней мере локально, границу тела сложной формы на шар в параметрической области.
Переведем приведенные выше аргументы в алгоритм. Предположим, что масштабированная функция расстояния со знаком
и координата $b(x)$ ближайшей точки на границе известны. Присваиваем касательные базисные векторы ${{u}_{1}}(b),\;{{u}_{2}}(b)$ точке $x$. Нормальное растяжение ${{\sigma }_{1}}(x)$ вычисляется с помощью (16). Для вычисления ${{\sigma }_{{2,3}}}(x)$ для дополнения тела мы предлагаем следующую эвристику. Определим вспомогательную функциюОкончательные формулы выглядят следующим образом:
(18)
${{\sigma }_{2}}(x) = \min ({{\sigma }_{1}}(b),{{\tilde {\sigma }}_{2}}(x)),\quad {{\tilde {\sigma }}_{2}}(x) = \psi ({{r}_{1}},y),$(19)
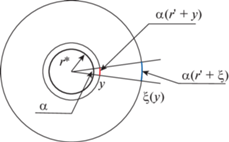
${{\sigma }_{3}}(x) = \min ({{\sigma }_{1}}(b),{{\tilde {\sigma }}_{3}}(x)),\quad {{\tilde {\sigma }}_{3}}(x) = \psi ({{r}_{2}},y),$Рассмотрим одномерное растяжение (14) вдоль радиальных направлений для полярных координат вокруг окружности радиусом $r{\kern 1pt} * = r{\text{/}}{{R}_{{\max }}}$. Предполагаем, что $y = 0$ на границе окружности. Тогда длина внешней границы сектора с углом $\alpha $ равна $\alpha (r{\kern 1pt} *\; + y)$, а после растяжения длина его изображения равна $\alpha (r{\kern 1pt} '\; + \xi )$, $\xi = \phi (y)$, $r{\kern 1pt} ' = {{r}_{r}}{\text{/}}{{R}_{{\max }}}$. Отношение длин определяет целевое касательное растяжение. Для упрощения постановки задачи используем независимое построение касательных для ортогональных направлений, подставляя вместо $r{\kern 1pt} *$ значения ${{r}_{{1,2}}}{\text{/}}{{R}_{{\max }}}$.
Как следует из (18) и (19), касательные растяжения во всей области не могут превышать нормальное растяжение на границе, значит, генерируемая анизотропная метрика ограничена сверху изотропной адаптивной метрикой. В переходной зоне мы добавляем дополнительное ограничение
Это равенство означает, что нас не интересуют ячейки сетки, которые анизотропны в тангенциальном направлении.Формально те же законы (18) и (19) используются внутри тела. Мы обнаружили, что потенциально это может привести к появлению довольно крупных ячеек внутри тела, что не является критическим недостатком алгоритма деформации сетки, так как IBC-решатель (см. [16]) предположительно слабо чувствителен к размеру искусственных ячеек внутри тела. Важно гарантировать симметрию и плавный переход размеров внутри пограничного слоя сетки.
5. ПАРАЛЛЕЛЬНАЯ РЕАЛИЗАЦИЯ НА ОСНОВЕ MPI
Для построения параллельного алгоритма мы используем пространственную декомпозицию сетки. Поскольку степенями свободы, определяющими деформацию сетки, являются вершины сетки, мы строим последовательное разделение ячеек и вершин сетки: параметрическая область ${{\Omega }_{x}}i$ разбивается на связные подобласти, состоящие из целых ячеек сетки. Вершины сетки, принадлежащие границам между подобластями, распределяются между подобластями. Для вычисления направления минимизации используем параллельный итерационный решатель на основе ILU2 (см. [13], [14]). Входными данными решателя являются правая часть (разбитая на блоки) и разреженная матрица (разбитая на блочные строки). Каждый блок в точности соответствует разбиению вершин сетки. Наша реализация итерационной схемы основана на расширенных подобластях, определяющих двухклеточное перекрытие подобластей. В начале каждой итерации минимизации (7) мы используем обмен данными для сборки текущей итерации в каждой из расширенных подобластей. Такое расширение делает сборку функционала, его градиента, матрицы Гессе полностью локальными операциями. Дополнительный обмен данными для нахождения оптимального значения $\tau $ путем приближенного решения задачи одномерной минимизации (8) не требуется, нужно лишь вычислить глобальные суммы. Все операции алгоритма построения сетки полностью масштабируемы. Следовательно, можно ожидать, что общая масштабируемость определяется масштабируемостью параллельного линейного решателя. Заметим, что линейный решатель использует собственные перекрытия и схему обмена данными (см. [14]).
6. ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ
Алгоритм управляемой деформации применен для геометрической адаптации расчетной сетки с целью улучшения разрешения расчетного кода NOISETTE (см. [16]) в задаче для численного моделирования турбулентного течения вокруг винта квадрокоптера. Мы тестируем численную технологию в двух измерениях, используя двумерную проекцию реалистичной геометрии пропеллера (см. [19]) с основной целью применить ее в дальнейшем для моделирования реального трехмерного пропеллера. На данном этапе проводятся несколько упрощенные трехмерные тесты, чтобы проверить начальную геометрическую адаптацию, сравнить вычисленное положение слоя сетки с целевым положением движения, а также проверить эффективность и масштабируемость трехмерного алгоритма. На фиг. 7а показана геометрия пропеллера. Из-за естественных геометрических ограничений сетка деформируется только внутри круга, который на 10% больше самого пропеллера, значит, адаптация сетки вблизи кончика лопасти становится нетривиальной задачей. Пропеллер определяется приближенной функцией расстояния со знаком. Мы вводим коэффициент сжатия 30 в нормальном направлении внутри тонкого слоя вблизи лопастей. Чтобы инициировать деформацию, зависящую от времени, мы стартуем с начальной стационарной адаптации сетки (фиг. 7б).
Для того чтобы разрешить углы и сильно изогнутый фрагмент границы, мы вводим локально изотропные зоны влияния метрики, показанные кругами на фиг. 8. Изотропная метрика определяется по тому же закону (16), где считается расстояние до центра окружности, а ${{R}_{{\max }}}$ – радиус окружности. Коэффициент ${{A}_{n}}$ такой же, как для глобальной метрики и ${{\sigma }_{2}} = {{\sigma }_{1}}$. Для вычисления ${{G}_{x}}$ применяется операция максимума для метрики.
На фиг. 9 показаны фрагменты начальной сетки вблизи зон влияния изотропной метрики.
На фиг. 10 показан общий контур сетки после первого и второго оборотов винта.
На фиг. 11 и 12 показаны фрагменты сетки после первого и второго оборотов.
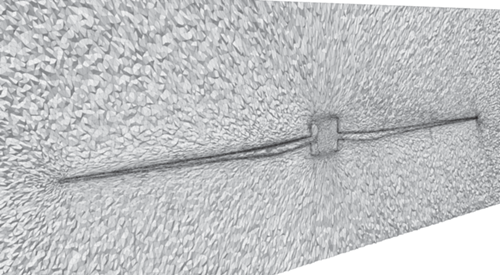
Вычисление долговременной деформации сетки демонстрирует поведение, близкое к периодическому. На фиг. 13 показаны траектории выбранных ячеек в переменных ${{x}_{1}}$, ${{x}_{2}}$ и $t$. Мы выбираем несколько треугольников, сохраняем их координаты каждые 500 шагов по времени и соединяем последовательные позиции, создавая пространственно-временные призмы. Получающиеся “жгуты” треугольного сечения иллюстрируют пространственно-временную деформацию сетки.
Фиг. 13.
Пространственно-временные траектории трех выбранных треугольников для 14 оборотов винта, показанные с разных ракурсов.
На фиг. 14 показана деформация подобластей сетки, когда винт перемещается на четверть оборота.
Отметим, что при расчете используется декомпозиция области на основе вершин, поэтому вершины сетки, лежащие на границах цветных областей, фактически отнесены к той или иной подобласти.
На фиг. 15 показаны деформация сетки и перемещение границ подобластей в системе координат, связанной с пропеллером. Количество подобластей больше, чем в фиг. 14. Выделенные слои шириной в одну ячейку показывают треугольники с вершинами, принадлежащими разным подобластям.
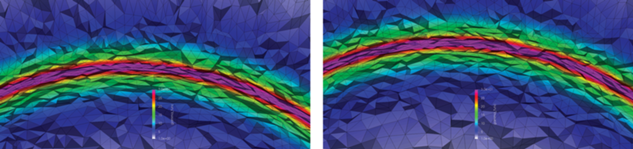
На фиг. 16 показано распределение целевого значения ${{\sigma }_{1}}$ во вращающейся системе координат для двух различных временных уровней. Красным цветом обозначено максимальное значение. Можно заметить, что положение слоя сетки довольно точно следует за управлением. Интересный эффект связан с группами ячеек сетки, которые притягиваются к лопасти, затем некоторое время перемещаются по пограничному слою в сжатом состоянии и, в конце концов, покидают пропеллер. Другая группа ячеек в середине области притягивается к лопастям, пересекает их и выходит с другой стороны. Фигура 16б слегка наклонена в координатах ${{x}_{1}}$, ${{x}_{2}}$ и $t$, чтобы сделать траектории ячеек более заметными.
Фиг. 16.
Локализация слоя сетки в сравнении с управлением ${{\sigma }_{1}}$ (а) и траектории ячеек во вращающейся системе координат (б).
Чтобы оценить масштабируемость параллельной реализации, мы запустили несколько двух- и трехмерных тестовых примеров. В двухмерном примере мы рассматриваем “маленькую” задачу с 357 781 вершинами и 713 760 треугольниками и “умеренную” задачу с 1 429 321 вершинами и 2 855 040 треугольниками. В трехмерном случае мы рассматриваем деформацию тетраэдральной сетки с 9 586 347 вершинами и 56 715 408 тетраэдрами.
Эксперименты по масштабируемости проводились на параллельном кластере Московского физико-технического института. Это кластер на базе процессоров Intel с 24 ядрами на плату и сетью Infiniband. Фигура 17 иллюстрирует масштабируемость алгоритма деформации сетки. Отдельный график посвящен линейному решателю. Как и следовало ожидать, общая масштабируемость определяется линейным решателем. Обратите внимание, что масштабируемость по отношению к одному ядру не впечатляет, в то время как результаты очень хорошо масштабируются, если стартовать с 24 ядер. Мы не смогли объяснить это наблюдение. Это может быть недостатком алгоритма или артефактом неправильной конфигурации программного/аппаратного обеспечения кластера.
Фиг. 17.
Зависимость ускорения от количества вычислительных ядер для двумерной задачи умеренного размера: (a) – ускорение по отношению к одному ядру, (б) – ускорение по отношению к 24 ядрам.
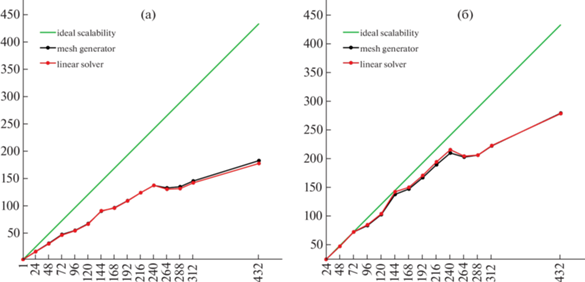
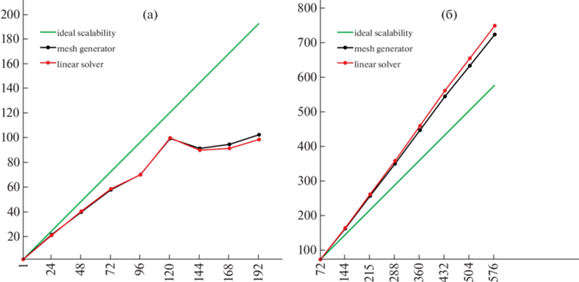
На фиг. 18а показано ускорение для небольшой двумерной задачи, где насыщение достаточно выражено для более чем 120 ядер, в то время как для трехмерного случая на фиг. 18б масштабируемость вполне разумна и насыщение не наблюдается до 600 ядер. Отметим, что наблюдается суперускорение, которое можно объяснить более низкой производительностью трехмерного кода при малом количестве ядер и большом размере локальной сетки на ядро. Мы планируем запустить трехмерный алгоритм на более крупных конфигурациях.
Фиг. 18.
Зависимость скорости от количества вычислительных ядер: (a) – небольшая двумерная задача, (б) – трехмерная задача.
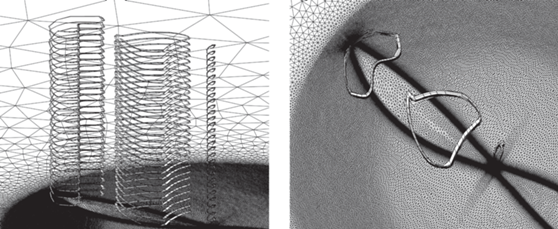
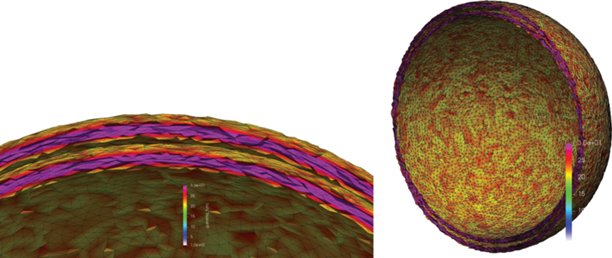
Фигура 19 иллюстрирует подобласти для трехмерной задачи в случае 144 ядер. Показаны след подобластей на границе, сечение исходной равномерной сетки и сечение сетки, адаптированной к движущейся сфере.
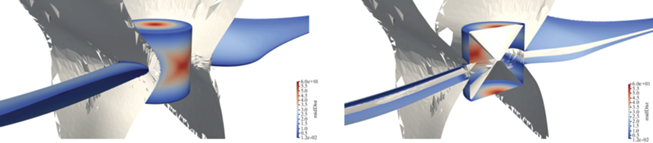
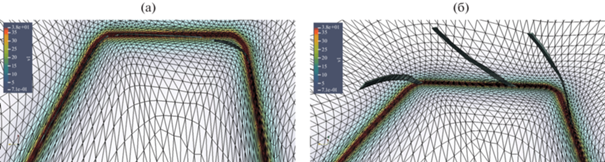
На фиг. 20а показаны исходная адаптированная сетка и целевое распределение ${{\sigma }_{1}}$; фиг. 20б – прообраз сжатого пограничного слоя на исходной равномерной трехмерной сетке. В данном примере в пограничном слое задано ${{\sigma }_{1}} = 30$ и ${{\sigma }_{{2,3}}} \approx 3$.
Фиг. 20.
Распределение коэффициента сжатия сетки в нормальном направлении (а) и его прообраз на исходной сетке (б).

На фиг. 21 показаны фрагменты сетки с двумя положениями вычисленного слоя сетки в процессе движения сферы.
На фиг. 22 показаны два положения слоя сетки, выделенного из глобальных сеток с использованием порога 20 для целевого распределения ${{\sigma }_{1}}$.
Фиг. 22.
Два положения сжатого слоя, извлеченные с использованием порога 20 для коэффициента сжатия по нормали.
В следующей задаче мы тестируем полностью автоматическую технологию адаптации трехмерной сетки для реалистичной модели ротора (см. [20]). Из-за сложности задачи мы показываем результаты только для стационарной сетки. Технологическую цепочку можно кратко описать так: строится треугольная поверхностная сетка с использованием САПР модели ротора, которая показана на фиг. 23.
Затем вычисляем приблизительную кривизну поверхности, используя алгоритм нелинейной параболической подгонки из [21], [22] и строим медиальные оси с помощью алгоритма PowerCrust, используя реализацию из [18]. На фиг. 24 показаны распределение наибольшей главной кривизны по триангулированной поверхности и расстояние до медиальной оси на поверхности ротора. На фиг. 25 показаны фрагменты зашумленных медиальных осей для модели ротора.
Фиг. 24.
(а) – Распределение наибольшей главной кривизны на поверхности, (б) – расстояние от поверхности до медиальной оси.
Адаптивная фоновая восьмеричная сетка строится по алгоритму, описанному в [23]. На этой сетке в вершинах кубических восьмеричных ячеек хранятся значения функции расстояния со знаком от поверхности ротора (фиг. 26). Для вычисления функции расстояния в произвольных точках используется трилинейная интерполяция. Этот простой алгоритм приводит к иззубренным изоповерхностям приближенной функции расстояния вблизи резких особенностей и сильно искривленных фрагментов поверхности, поэтому в узком слое около границы тела вычисляется точное расстояние до поверхностной триагуляции. Важно, что алгоритм вычисления расстояния выдает также положение ближайшей точки на поверхности.
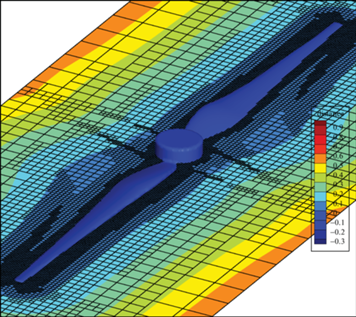
Анизотропная управляющая метрика строится путем комбинирования предписанного закона растяжения вблизи границы, приближенной кривизны поверхности и данных о медиальных осях, и в итоге вычисляется деформация сетки. Нормальный коэффициент сжатия вблизи поверхности в этом тесте равен ${{\sigma }_{1}} = 10$. На фиг. 27 показано поперечное сечение деформированной сетки.
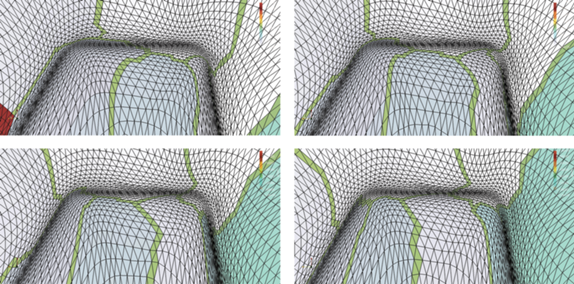
На фиг. 28 и 29 показаны увеличенные фрагменты адаптированной сетки около втулки и около законцовки лопасти.
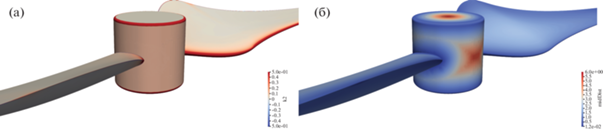
Фиг. 30.
(а) – Призматическая сетка, охватывающая поверхность ротора внутри и снаружи расчетной области, (б) – адаптивная сетка.

Заметим, что касательные растяжения автоматически регулируются для разрешения линий негладкости и зон высокой кривизны на границе ротора. Реальный численный коэффициент нормального сжатия довольно близок к контрольному. Несмотря на то что медиальные оси являются весьма зашумленными, они позволяют извлечь ключевую информацию о локальном размере и передать ее на поверхность модели. Геометрический шум был существенно сглажен во время этой процедуры.
7. ВЫВОДЫ И ОБСУЖДЕНИЕ
Мы описали алгоритм, который позволяет строить нестационарные деформации сеток высокого качества посредством приближенной минимизации квазиизометрического функционала. Представленный алгоритм все еще медленнее по сравнению с построителями сеток, основанных на линейных эллиптических уравнениях (см., например, [5]). Разница, однако, уже не имеет решающего значения, поскольку мы используем $d$ линейных решений с линейными системами, соответствующими конечно-элементным аппроксимациям скалярных уравнений типа Лапласа на несколько шагов по времени. Известно, что алгоритмы, основанные на линейных эллиптических уравнениях, могут достичь приемлемого качества двумерной сетки за счет тщательного выбора метрического тензора/весовых функций (см. [6]), поэтому может оказаться, что преимущество представленного метода в качестве сетки не перевешивает вычислительных затрат. Однако, в отличие от линейных сеточных решателей, представленный алгоритм не накладывает никаких ограничений на размерность и форму области и тип элементов сетки. Он допускает намного более сильное сгущение сетки и может применяться для элементов высокого порядка. Благодаря усовершенствованному параллельному линейному решателю, была продемонстрирована разумная параллельная масштабируемость численного алгоритма.
Используя управляющую метрику, мы продемонстрировали способность алгоритма адаптивной деформации сетки автоматически разрешать геометрические особенности довольно сложных трехмерных тел.
Хотя данная работа не имеет прямого отношения к численному моделированию течений вязкой жидкости с использованием концепции погруженных граничных условий, необходимо четко понимать ограничения метода деформации сетки. Очевидно, что при сильном сжатии деформация сетки при фиксированной связности приведет к сильно искаженным ячейкам сетки в ключевых областях расчетной области, где форма и ориентация ячеек сетки оказывают решающее влияние на качество численных решений. Вопрос заключается в том, возможно ли сохранить преимущество параллельного численного моделирования с фиксированной связностью и совместить ее с гибкостью гибридной сетки? Отметим, что в расчетном коде Noisette (см. [16]) данные из фоновой сетки интерполируются на вершины движущейся деформирующейся сетки. Эта операция полностью локальна, так как фоновая восьмеричная сетка хранится в локальной памяти каждого MPI-процесса. Такую же идею можно использовать для призматического слоя около тела с очень малым количеством ячеек по нормали. Алгоритм, предложенный в [24], позволяет строить достаточно толстые фоновые призматические слои. На фиг. 30 показан призматический слой у поверхности ротора, который довольно толстый с геометрической точки зрения, но имеет ширину всего в одну ячейку в направлении внутрь и наружу.
Видно, что размер ячеек в движущейся деформирующейся сетке достаточен для реализации решателя типа Химера на перекрывающихся сетках (см. [25]), связывающего алгоритм IBC на движущейся сетке с призматическим слоем, который привязан к телу и достигает заданного разрешения пограничных слоев. Отметим, что толстый фоновый слой, показанный на фиг. 30, может служить носителем очень подробного расчетного призматического слоя, который может быть получен одномерным доразбиением. Поскольку различные сетки в зоне перекрытия имеют сопоставимый размер ячеек, устраняется основной недостаток метода Химеры – потеря точности на разномасштабных перекрывающихся сетках. Более того, обмен данными между подобластями на призматических слоях и подобластями на движущейся деформируемой сетке можно сделать простым и асинхронным, используя фоновую призматическую сетку в качестве отсчетного пространства, доступного всем процессам. Мы считаем такую редуцированную версию алгоритма Химера перспективным развитием предложенного алгоритма.
Список литературы
de Boor C. Good approximation by splines with variable knots II. Springer Lecture Notes Series 363, Springer-Verlag, Berlin (1973).
Huang W., Ren Y., Russell R.D. Moving mesh partial differential equations (MMPDES) based on the equidistribution principle // SIAM J. Numer. Anal. 1994. V. 31. № 3. P. 709–730.
Budd C.J., Huang W., Russell R.D. Adaptivity with moving grids // Acta Numerica. 2009. V. 18. P. 111–241.
Coyle J.M., Flaherty J.E., Ludwig R. On the stability of mesh equidistribution strategies for time-dependent partial differential equations // J. Comput. Phys. 1986. V. 62. P. 26–39.
Tang H.Z., Tang T. Adaptive mesh methods for one- and two-dimensional hyperbolic conservation laws // SIAM J. Numer. Anal. 2003. V. 41. № 2. P. 487–515.
Van Dam A., Zegeling P.A. Balanced monitoring of flow phenomena in moving mesh methods // Comm. Comput. Phys. 2010. V. 7. № 1. P. 138–170.
Godunov S.K., Gordienko V.M., Chumakov G.A. Quasi-isometric parametrization of a curvilinear quadrangle and a metric of constant curvature // Siber. Adv. Math. 1995. V. 5. № 2. P. 1–20.
Garanzha V.A. The barrier method for constructing quasi-isometric grids // Comput. Math. Math. Phys. 2000. V. 40. P. 1617–1637.
Garanzha V.A., Kudryavtseva L.N., Utyzhnikov S.V. Untangling and optimization of spatial meshes // J. Comput. Appl. Math. 2014. V. 269. P. 24–41.
Garanzha V.A., Kudryavtseva L. Moving deforming mesh generation based on the quasi-isometric functional // In: Garanzha V.A., Kamenski L., Si H. (eds) Numerical Geometry, Grid Generation and Scientific Computing. Lect. Not. Comput. Sci. Engineer. 2021. V. 143. Springer, Cham, P. 157–178.
Abalakin I., Bakhvalov P., Kozubskaya T. Edge-based reconstruction schemes for unstructured tetrahedral meshes // Inter. J. Numer. Meth. Fluid. 2016. V. 81. № 6. P. 331–356.
Garanzha V.A., Kudryavtseva L.N. Hyperelastic springback technique for construction of prismatic mesh layers // Procedia Engineer. 2017. V. 203. P. 401–413.
Kaporin I.E. High quality preconditioning of a general symmetric positive definite matrix based on its UTU4Edecomposition // Numer. Linear Algebra Appl. 1998. V. 5. № 6. P. 483–509.
Kaporin I.E., Milyukova O.Yu. MPI+OpenMP parallel implementation of explicitly preconditioned conjugate gradient method // Keldysh Inst. Preprint. 2018. V. 008. Mi ipmp2369.
Ivanenko S.A. Construction of nondegenerate grids // Comput. Math. and Math. Phys. 1988. V. 28. P. 141–146.
Tsvetkova V.O., Abalakin I.V., Bobkov V.G., Zhdanova N.S., Kozubskaya T.K., Kudryavtseva L.N. Simulation of flow near rotating propeller on adaptive unstructured meshes using immersed boundary method // Matem. Mod. 2021. V. 33. № 8. P. 59–82.
Castro-Díaz M.J., Hecht F., Mohammadi B., Pironneau O. Anisotropic unstructured mesh adaption for flow simulations // Inter. J. Numer. Meth. Fluid. 1997. V. 25. № 4. P. 475–491.
Amenta N., Choi S., Kolluri R. The power crust, unions of balls, and the medial axis transform // Comput. Geometry: Theory and Appl. 2001. V. 19. P. 127–153.
Brandt J.B. Small-scale propeller performance at low speeds. PhD Thesis. Univer. of Illinois at Urbana-Champaign, 2005.
Bobkov V., Gorobets A., Kozubskaya T., Zhang X., Zhong S. Supercomputer simulation of turbulent flow around isolated UAV rotor and associated acoustic fields // Comm. Comput. Informat. Sci., Springer Inter. Publ., 2021. P. 256–269.
Petitjean S., Boyer E. Regular and non-regular point sets: properties and reconstruction // Comput. Geometry. 2001. V. 19. P. 101–126.
Garimella R., Swartz B. Curvature estimation for unstructured triangulations of surfaces, 2015.
Soukov S.A. Combined signed distance calculation algorithm for numerical simulation of physical processes and visualization of solid bodies movement // Scientif. Visualizat. 2020. V. 12. № 5. P. 86–101.
Garanzha V.A., Kudryavtseva L.N., Belokrys-Fedotov A.I. Single and multiple springback technique for construction and control of thick prismatic mesh layers // Russ. J. Numer. Anal. Math. Model. 2021. V. 36. № 1. P. 1–15.
Steger J., Dougherty F.C., Benek J.A. A chimera grid scheme // Adv. Grid Generat. 1983 V. 5. P. 59–69.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики