Журнал вычислительной математики и математической физики, 2022, T. 62, № 8, стр. 1374-1385
Граничное условие на давление для решения стационарных уравнений Навье–Стокса методом конечных объемов с совмещенным расположением степеней свободы
1 Институт вычислительной математики им. Г.И. Марчука РАН
119333 Москва, ул. Губкина, 8, Россия
2 Московский физико-технический институт
141701 М.о., Долгопрудный, Институтский пер., 9, Россия
* E-mail: terekhov@inm.ras.ru
Поступила в редакцию 10.10.2021
После доработки 21.01.2022
Принята к публикации 11.04.2022
- EDN: YKBHGZ
- DOI: 10.31857/S0044466922080142
Аннотация
Предложены граничные условия на давление для решения стационарных несжимаемых уравнений Навье–Стокса методом конечных объемов с совмещенным расположением степеней свободы. Работа основана на inf-sup устойчивом методе аппроксимации совмещенного потока импульса и массы. На основе предположения о линейности неизвестных скорости и давления выводятся односторонние выражения совмещенного потока. Обеспечивая непрерывность этих выражений на внутренних гранях, получаем скорость и давление на грани и единственное выражение для совмещенного потока. В результате сохранение импульса и массы является дискретно точным. Однако для восстановления давления и расчета совмещенного потока на границе области требуется дополнительное граничное условие на давление. Библ. 28. Фиг. 2. Табл. 3.
1. ВВЕДЕНИЕ
В работе [1] был представлен полностью неявный конечно-объемный метод с совмещенным расположением степеней свободы и кусочно-линейной аппроксимацией скорости и давления. В указанной работе применялось простое искусственное граничное условие для давления, предложенное Грешо (см. [2]): отсутствие изменения градиента давления в нормальном направлении между текущим и следующим временными шагами. Из-за этого условия предложенный метод ограничен нестационарными задачами. В [3] был представлен полностью неявный конечно-объемный метод с совмещенным расположением степеней свободы и кусочно-постоянной аппроксимацией поля давления. Он не требовал никаких граничных условий на давление и позволял моделировать стационарную постановку задачи, но требовал настраиваемого параметра для компенсации ошибки давления в течениях с преобладанием адвекции. Основной мотивацией для полностью неявного подхода является совмещение жесткого каскада реакций в единую систему с уравнениями течения жидкости в модели свертываемости крови (см. [4], [5]). В данной работе мы исследуем улучшение метода конечных объемов (см. [1], [3]) и рассматриваем граничные условия давления, которые позволяют линейно реконструировать поле давления в стационарной постановке.
Типичной проблемой методов с совмещенным расположением степеней свободы является проблема неустойчивости inf-sup (см. [6]). Обычным подходом к решению этой проблемы является использование разнесенного расположения скоростей (см. [7]–[9]). Однако при использовании разнесенной схемы трудно удовлетворить свойствам консервативности (см. [10]). Другим решением является использование метода интерполяции Ри–Чоу (см. [11]) с совмещенным расположением неизвестных. Он является стандартным в промышленных приложениях (см. [12]–[16]).
В настоящей работе используется гипотеза о том, что inf-sup устойчивость удовлетворяется, если все матричные коэффициенты в выражении векторного потока имеют положительные собственные значения. Ранее мы применяли эту гипотезу к смешанной постановке задачи Дарси с седловой точкой (см. [17]), задаче Навье–Стокса (см. [3]) и к задаче гидроразрыва пласта, заданной уравнениями Дарси и пороупругости в разных областях (см. [18]).
Схема, предложенная в [1], [3], получена с использованием метода осреднения в гармонической точке. Первоначально концепция гармонической точки была предложена для задачи анизотропной диффузии (см. [19], [20]). Позже она была расширена для задач анизотропной упругости и поромеханики (см. [21], [22]). Выражение осреднения в гармонической точке вытекает из непрерывности совмещенного потока импульса и массы на границе раздела. Оно позволяет получить единственное выражение для совмещенного потока.
Статья организована следующим образом. В разд. 2 определяется задача и описывается метод конечных объемов. В разд. 3 подробно описаны отдельные нюансы дискретизации одностороннего совмещенного потока. Единственное выражение аппроксимации потока выводится из непрерывности односторонних приближений в разд. 4. Граничные условия и аппроксимация потока на границе объясняются в разд. 5. В разд. 6 подробно описывается метод восстановления градиента, а в разд. 7 – шаги по сборке и решению нелинейной системы. Численные тесты проводятся в разд. 8.
2. ПОСТАНОВКА ЗАДАЧИ И МЕТОД КОНЕЧНЫХ ОБЪЕМОВ
Мы ищем решение системы стационарных уравнений Навье–Стокса:
(1)
$\begin{gathered} {\text{div}}{\kern 1pt} \left( {\rho {\mathbf{u}}{{{\mathbf{u}}}^{{\text{т}}}} - \tau ({\mathbf{u}}) + p\mathbb{I}} \right) = {\mathbf{f}}, \hfill \\ \operatorname{div} {\kern 1pt} \left( {\mathbf{u}} \right) = 0,\quad \quad \quad \quad \quad {\text{в}}\;\;\Omega , \hfill \\ {\text{граничные условия}}\quad {\text{на}}\;\;\partial \Omega . \hfill \\ \end{gathered} $Система (1) замкнута с соответствующими граничными условиями, которые вводятся в разд. 5. В (1) ${\mathbf{u}} = {{\left[ {u,v,w} \right]}^{{\text{т}}}}$ – вектор скорости, $p$ – давление, $u,v,w,p \in {{H}^{1}}(\Omega )$ с соответствующей поправкой на пространство на границе, $\rho = {\text{const}}{\kern 1pt} $ – плотность жидкости, постоянная из-за несжимаемости, $\tau ({\mathbf{u}})$ – тензор напряжений:
(2)
$\tau ({\mathbf{u}}) = 2\mu {\mathbf{D}}({\mathbf{u}}),\quad {\mathbf{D}}({\mathbf{u}}) = \frac{1}{2}\left[ {{\mathbf{u}}{{\nabla }^{{\text{т}}}} + \nabla {{{\mathbf{u}}}^{{\text{т}}}}} \right],$(3)
${\kern 1pt} div{\kern 1pt} \left( {\mathbf{u}} \right) = \nabla \cdot {\mathbf{u}} = {{\nabla }^{{\text{т}}}}{\mathbf{u}} = {{{\mathbf{u}}}^{{\text{т}}}}\nabla = \left[ {\begin{array}{*{20}{c}} u&{v}&w \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\partial }_{x}}} \\ {{{\partial }_{y}}} \\ {{{\partial }_{z}}} \end{array}} \right] = \frac{{\partial u}}{{\partial x}} + \frac{{\partial {v}}}{{\partial y}} + \frac{{\partial w}}{{\partial z}} = 0.$(4)
$\begin{gathered} {\kern 1pt} {\text{div}}{\kern 1pt} \left( {\tau ({\mathbf{u}})} \right) = \mu \left( {{\mathbf{u}}{{\nabla }^{{\text{т}}}} + \nabla {{{\mathbf{u}}}^{{\text{т}}}}} \right)\nabla = \mu {\mathbf{u}}{{\nabla }^{{\text{т}}}}\nabla + \mu \nabla {{{\mathbf{u}}}^{{\text{т}}}}\nabla = \mu \left[ {\begin{array}{*{20}{c}} u \\ v \\ w \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\partial }_{x}}}&{{{\partial }_{y}}}&{{{\partial }_{z}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\partial }_{x}}} \\ {{{\partial }_{y}}} \\ {{{\partial }_{z}}} \end{array}} \right] + \mu \left[ {\begin{array}{*{20}{c}} {{{\partial }_{x}}} \\ {{{\partial }_{y}}} \\ {{{\partial }_{z}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} u&v&w \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\partial }_{x}}} \\ {{{\partial }_{y}}} \\ {{{\partial }_{z}}} \end{array}} \right] = \\ \, = \mu \left[ {\begin{array}{*{20}{c}} {\frac{{{{\partial }^{2}}u}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}u}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}u}}{{\partial {{z}^{2}}}}} \\ {\frac{{{{\partial }^{2}}{v}}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}{v}}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}{v}}}{{\partial {{z}^{2}}}}} \\ {\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} + \frac{{{{\partial }^{2}}w}}{{\partial {{y}^{2}}}} + \frac{{{{\partial }^{2}}w}}{{\partial {{z}^{2}}}}} \end{array}} \right] + \mu \left[ {\begin{array}{*{20}{c}} {{{\partial }_{x}}\left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial {v}}}{{\partial y}} + \frac{{\partial u}}{{\partial z}}} \right)} \\ {{{\partial }_{y}}\left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial {v}}}{{\partial y}} + \frac{{\partial w}}{{\partial z}}} \right)} \\ {{{\partial }_{z}}\left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial {v}}}{{\partial y}} + \frac{{\partial w}}{{\partial z}}} \right)} \end{array}} \right], \\ \end{gathered} $В методе конечных объемов мы используем формулу Остроградского–Гаусса для оператора дивергенции на каждой ячейке $V \in \mathcal{V}(\Omega )$, что приводит к
(5)
$\begin{gathered} \int\limits_V \,\nabla \cdot \left( {\rho {\mathbf{u}}{{{\mathbf{u}}}^{{\text{т}}}} - \tau ({\mathbf{u}}) + p\mathbb{I}} \right){\text{d}}V \approx \sum\limits_{\sigma \in \mathcal{F}(V)} \,{\text{|}}\sigma {\kern 1pt} {\text{|}}{{\left. {\left[ {\rho {\mathbf{u}}{{{\mathbf{u}}}^{{\text{т}}}} - \tau ({\mathbf{u}}) + p} \right]{\kern 1pt} } \right|}_{{{{{\mathbf{x}}}_{\sigma }}}}}{\mathbf{n}}, \\ \int\limits_V \,\nabla \cdot {\mathbf{u}}{\text{d}}V \approx \sum\limits_{\sigma \in \mathcal{F}(V)} {\text{|}}\sigma {\kern 1pt} {\text{|}}{{\left. {\left[ {{\mathbf{u}} \cdot {\mathbf{n}}} \right]{\kern 1pt} } \right|}_{{{{{\mathbf{x}}}_{\sigma }}}}}. \\ \end{gathered} $3. АППРОКСИМАЦИЯ ПОТОКА НА ГРАНИ
Уравнения в (5) вводят потоки импульса ${\mathbf{t}}$ и непрерывности $q$:
(6)
${\mathbf{t}} = \rho {\mathbf{uu}} \cdot {\mathbf{n}} - \tau ({\mathbf{u}}){\mathbf{n}} + p{\mathbf{n}},\quad q = {\mathbf{u}} \cdot {\mathbf{n}},$Адвективная часть ${{{\mathbf{t}}}_{A}}$ потока импульса ${\mathbf{t}}$ линеаризуется для получения эффективного тензора скорости. Пусть ${{{\mathbf{u}}}_{1}} = {{\left[ {{{u}_{1}},{{{v}}_{1}},{{w}_{1}}} \right]}^{{\text{т}}}}$ – вектор скорости, расположенный в барицентре ${{{\mathbf{x}}}_{1}}$ ячейки ${{V}_{1}}$. Используя простую формулу разложения Тейлора, аппроксимация второго порядка адвективной части ${{{\mathbf{t}}}_{A}}$ потока импульса в барицентре ${{{\mathbf{x}}}_{\sigma }}$ грани $\sigma $ имеет следующий вид:
(7)
${{\left. {{{{\mathbf{t}}}_{A}}} \right|}_{{{{{\mathbf{x}}}_{\sigma }}}}} \approx \rho {{\left. {{\mathbf{uu}} \cdot {\mathbf{n}}} \right|}_{{{{{\mathbf{x}}}_{1}}}}} + {{\left. {\frac{{\rho {\mathbf{uu}} \cdot {\mathbf{n}}}}{{\partial {\mathbf{u}}}}} \right|}_{{{{{\mathbf{x}}}_{1}}}}}{{\left. {\left( {{\mathbf{u}}{{\nabla }^{{\text{т}}}}} \right)} \right|}_{{{{{\mathbf{x}}}_{1}}}}}\left( {{{{\mathbf{x}}}_{\sigma }} - {{{\mathbf{x}}}_{1}}} \right),$(8)
${{\left. {{{{\mathbf{t}}}_{A}}} \right|}_{{{{{\mathbf{x}}}_{\sigma }}}}} \approx \frac{\rho }{2}\left( {{{{\mathbf{u}}}_{1}}{{{\mathbf{n}}}^{{\text{т}}}} + {{{\mathbf{u}}}_{1}} \cdot {\mathbf{n}}\mathbb{I}} \right)\left( {2{{{\mathbf{u}}}_{\sigma }} - {{{\mathbf{u}}}_{1}}} \right).$Аппроксимация вязкостной части ${{{\mathbf{t}}}_{T}}$ формулируется следующим образом:
(9)
${{\left. {{{{\mathbf{t}}}_{T}}} \right|}_{{{{{\mathbf{x}}}_{\sigma }}}}} \approx - {{\left. {\tau ({\mathbf{u}})} \right|}_{{{{{\mathbf{x}}}_{1}}}}}{\mathbf{n}} \approx - \mu \left( {\mathbb{I} \otimes {{{\mathbf{n}}}^{{\text{т}}}} + {{{\mathbf{n}}}^{{\text{т}}}} \otimes \mathbb{I}} \right){{\left. {\left( {{\mathbf{u}} \otimes \nabla } \right)} \right|}_{{{{{\mathbf{x}}}_{1}}}}}.$(10)
${\mathbf{u}} \otimes \nabla = \left[ {\begin{array}{*{20}{c}} {\nabla u} \\ {\nabla {v}} \\ {\nabla w} \end{array}} \right],\quad \mathbb{I} \otimes {{{\mathbf{n}}}^{{\text{т}}}} + {{{\mathbf{n}}}^{{\text{т}}}} \otimes \mathbb{I} = \left[ {\begin{array}{*{20}{c}} {2{{n}_{x}}}&{{{n}_{y}}}&{{{n}_{z}}}&{{{n}_{y}}}&{}&{}&{{{n}_{z}}}&{}&{} \\ {}&{{{n}_{x}}}&{}&{{{n}_{x}}}&{2{{n}_{y}}}&{{{n}_{z}}}&{}&{{{n}_{z}}}&{} \\ {}&{}&{{{n}_{x}}}&{}&{}&{{{n}_{y}}}&{{{n}_{x}}}&{{{n}_{y}}}&{2{{n}_{z}}} \end{array}} \right].$При предположении линейности разложение для градиента является точным:
(11)
${{{\mathbf{u}}}_{1}} \otimes \nabla = r_{1}^{{ - 1}}\left( {\mathbb{I} \otimes {\mathbf{n}}} \right)\left( {{{{\mathbf{u}}}_{\sigma }} - {{{\mathbf{u}}}_{1}}} \right) + \left( {\mathbb{I} - r_{1}^{{ - 1}}\left( {\mathbb{I} \otimes {\mathbf{n}}} \right)\mathbb{I} \otimes {{{\left( {{{{\mathbf{x}}}_{\sigma }} - {{{\mathbf{x}}}_{1}}} \right)}}^{{\text{т}}}}} \right){{{\mathbf{u}}}_{1}} \otimes \nabla .$Применим (11) к (9) и получим
(12)
${{\left. {{{{\mathbf{t}}}_{T}}} \right|}_{{{{{\mathbf{x}}}_{\sigma }}}}} \approx \mu r_{1}^{{ - 1}}\left( {\mathbb{I} + {\mathbf{n}}{{{\mathbf{n}}}^{{\text{т}}}}} \right)\left( {{{{\mathbf{u}}}_{1}} - {{{\mathbf{u}}}_{\sigma }}} \right) - \mu \left( {\mathbb{I} \otimes {{{\mathbf{n}}}^{{\text{т}}}} + {{{\mathbf{n}}}^{{\text{т}}}} \otimes \mathbb{I} - r_{1}^{{ - 1}}\left( {\mathbb{I} + {\mathbf{n}}{{{\mathbf{n}}}^{{\text{т}}}}} \right) \otimes {{{\left( {{{{\mathbf{x}}}_{\sigma }} - {{{\mathbf{x}}}_{1}}} \right)}}^{{\text{т}}}}} \right){{{\mathbf{u}}}_{1}} \otimes \nabla ,$Вклад давления в поток импульса ${{{\mathbf{t}}}_{P}}$ и поток непрерывности $q$ образуют систему с седловой точкой:
(13)
${{\left. {\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{t}}}_{P}}} \\ q \end{array}} \right]} \right|}_{{{{{\mathbf{x}}}_{\sigma }}}}} = \left[ {\begin{array}{*{20}{c}} {{{p}_{\sigma }}{\mathbf{n}}} \\ {{{{\mathbf{u}}}_{\sigma }} \cdot {\mathbf{n}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {}&{\mathbf{n}} \\ {{{{\mathbf{n}}}^{T}}}&{} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{\sigma }}} \\ {{{p}_{\sigma }}} \end{array}} \right] = S({\mathbf{n}})\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{\sigma }}} \\ {{{p}_{\sigma }}} \end{array}} \right],$(14)
${{\left. {\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{t}}}_{P}}} \\ q \end{array}} \right]} \right|}_{{{{{\mathbf{x}}}_{\sigma }}}}} \approx A\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{1}}} \\ {{{p}_{1}}} \end{array}} \right] - \left( {A - S({\mathbf{n}})} \right)\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{\sigma }}} \\ {{{p}_{\sigma }}} \end{array}} \right] + A \otimes {{\left( {{{{\mathbf{x}}}_{\sigma }} - {{{\mathbf{x}}}_{1}}} \right)}^{{\text{т}}}}\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{1}}} \\ {{{p}_{1}}} \end{array}} \right] \otimes \nabla ,$(15)
$\begin{gathered} A({\mathbf{u}},{\mathbf{v}},{\mathbf{n}}) = \left[ {\begin{array}{*{20}{c}} {a\left( {\mathbb{I} + {\mathbf{n}}{{{\mathbf{n}}}^{{\text{т}}}}} \right)}&{c{\mathbf{n}}} \\ {c{{{\mathbf{n}}}^{{\text{т}}}}}&b \end{array}} \right],\quad Q({\mathbf{u}},{\mathbf{n}}) = \left[ {\frac{\rho }{2}({\mathbf{u}}{{{\mathbf{n}}}^{{\text{т}}}} + {\mathbf{u}} \cdot {\mathbf{n}}\mathbb{I})} \right], \\ W({\mathbf{n}}) = \left[ {\mu \left( {\mathbb{I} \otimes {{{\mathbf{n}}}^{{\text{т}}}} + {{{\mathbf{n}}}^{{\text{т}}}} \otimes \mathbb{I}} \right)} \right], \\ T({\mathbf{u}},{\mathbf{v}},{\mathbf{n}}) = A({\mathbf{u}},{\mathbf{v}},{\mathbf{n}}) + \left[ {\mu {{r}^{{ - 1}}}\left( {\mathbb{I} + {\mathbf{n}}{{{\mathbf{n}}}^{{\text{т}}}}} \right)} \right], \\ \end{gathered} $(16)
${{\left. {\left[ {\begin{array}{*{20}{c}} {\mathbf{t}} \\ q \end{array}} \right]} \right|}_{{{{{\mathbf{x}}}_{\sigma }}}}} \approx ({{T}_{1}} - {{Q}_{1}})\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{1}}} \\ {{{p}_{1}}} \end{array}} \right] - \left( {{{T}_{1}} - {{S}_{1}} - 2{{Q}_{1}}} \right)\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{\sigma }}} \\ {{{p}_{\sigma }}} \end{array}} \right] + \left( {{{T}_{1}} \otimes {{{\left( {{{{\mathbf{x}}}_{\sigma }} - {{{\mathbf{x}}}_{1}}} \right)}}^{{\text{т}}}} - {{W}_{1}}} \right)\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{1}}} \\ {{{p}_{1}}} \end{array}} \right] \otimes \nabla .$Мы требуем положительности собственных значений в $T({\mathbf{u}},{\mathbf{v}},{\mathbf{n}}) - Q({\mathbf{u}},{\mathbf{n}})$ и $T({\mathbf{u}},{\mathbf{v}},{\mathbf{n}}) - S({\mathbf{u}},{\mathbf{n}}) - 2Q({\mathbf{u}},{\mathbf{n}})$ путем выбора параметров $a,\;b,\;c$ с минимальными абсолютными значениями. Для краткости опускаем анализ и ссылаемся на [1], но для полноты представляем выбор параметров. Пусть $\nu = \rho {{{\mathbf{n}}}^{{\text{т}}}}{\mathbf{u}}{\text{/}}2$, тогда
(17)
$a = \max \left( {2\nu - \mu {{r}^{{ - 1}}},0} \right) + \rho \sqrt {{{{\mathbf{u}}}^{{\text{т}}}}\left( {\mathbb{I} - {\mathbf{n}}{{{\mathbf{n}}}^{{\text{т}}}}} \right){\mathbf{u}} + {{\varepsilon }^{2}}} > 0.$Пусть $\zeta = a + \mu {{r}^{{ - 1}}} - 2\nu > 0$ и $\zeta + \nu \geqslant 0$, тогда $b$ и $c$ даются в виде
(18)
$c = \left\{ \begin{gathered} 1 + t - \sqrt {t + {{t}^{2}}} ,\quad \nu > 0, \hfill \\ 1{\text{/}}2,\quad \nu = 0, \hfill \\ 1 + t + \sqrt {t + {{t}^{2}}} ,\quad \nu < 0, \hfill \\ \end{gathered} \right.\quad b = \left\{ \begin{gathered} \left( {1{\text{/}}2 + t - \sqrt {t + {{t}^{2}}} } \right){\text{/}}\nu ,\quad \nu > 0, \hfill \\ 1{\text{/}}(8\zeta ),\quad \nu = 0, \hfill \\ \left( {1{\text{/}}2 + t + \sqrt {t + {{t}^{2}}} } \right){\text{/}}\nu ,\quad \nu < 0, \hfill \\ \end{gathered} \right.$4. НЕПРЕРЫВНОСТЬ ПОТОКА НА ВНУТРЕННЕЙ ГРАНИ
Определим ${{p}_{i}},\;\nabla {{p}_{i}},\;{{{\mathbf{u}}}_{i}},\;\nabla {{{\mathbf{u}}}_{i}}$, давление, скорость и градиент скорости в ячейке ${{V}_{i}}$ с барицентром ${{{\mathbf{x}}}_{i}}$. Пусть внутренняя грань $\sigma \in \mathcal{F}(\Omega {{\backslash }}\partial \Omega )$ является общей для двух ячеек ${{V}_{1}}$ и ${{V}_{2}}$, т.е. $\sigma = {{V}_{1}} \cap {{V}_{2}}$, ${{V}_{1}},{{V}_{2}} \in \mathcal{V}(\Omega )$. Мы предполагаем, что нормаль ${\mathbf{n}}$ ориентирована из ${{V}_{1}}$ в ${{V}_{2}}$.
Пусть ${{T}_{2}} = T({{{\mathbf{u}}}_{2}},{{{\mathbf{x}}}_{\sigma }} - {{{\mathbf{x}}}_{2}}, - {\mathbf{n}})$, ${{Q}_{2}} = Q({{{\mathbf{u}}}_{2}}, - {\mathbf{n}})$, ${{S}_{2}} = S( - {\mathbf{n}})$ и ${{W}_{2}} = W( - {\mathbf{n}})$, тогда аппроксимация потока со стороны ячейки ${{V}_{2}}$ имеет вид
(19)
${{\left. {\left[ {\begin{array}{*{20}{c}} {\mathbf{t}} \\ q \end{array}} \right]} \right|}_{{{{{\mathbf{x}}}_{\sigma }}}}} \approx \left( {{{T}_{2}} - {{S}_{2}} - 2{{Q}_{2}}} \right)\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{\sigma }}} \\ {{{p}_{\sigma }}} \end{array}} \right] - ({{T}_{2}} - {{Q}_{2}})\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{2}}} \\ {{{p}_{2}}} \end{array}} \right] - \left( {{{T}_{2}} \otimes {{{\left( {{{{\mathbf{x}}}_{\sigma }} - {{{\mathbf{x}}}_{2}}} \right)}}^{{\text{т}}}} - {{W}_{2}}} \right)\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{2}}} \\ {{{p}_{2}}} \end{array}} \right] \otimes \nabla .$Подход к выбору параметров сохраняется для матричных коэффициентов в (19) с учетом обратного направления нормали. Приравнивая приближения потоков (16) и (19), получим вектор неизвестных на грани:
(20)
$\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{\sigma }}} \\ {{{p}_{\sigma }}} \end{array}} \right] = {{\left( {{{T}_{1}} + {{T}_{2}} - {{S}_{1}} - {{S}_{2}} - 2{{Q}_{1}} - 2{{Q}_{2}}} \right)}^{{ - 1}}}\left( {\begin{array}{*{20}{l}} {({{T}_{1}} - {{Q}_{1}})\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{1}}} \\ {{{p}_{1}}} \end{array}} \right] + \left( {{{T}_{1}} \otimes {{{({{{\mathbf{x}}}_{\sigma }} - {{{\mathbf{x}}}_{1}})}}^{{\text{т}}}} - {{W}_{1}}} \right)\left( {\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{1}}} \\ {{{p}_{1}}} \end{array}} \right] \otimes \nabla } \right) + } \\ { + \;({{T}_{2}} - {{Q}_{2}})\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{2}}} \\ {{{p}_{2}}} \end{array}} \right] + \left( {{{T}_{2}} \otimes {{{({{{\mathbf{x}}}_{\sigma }} - {{{\mathbf{x}}}_{2}})}}^{{\text{т}}}} - {{W}_{2}}} \right)\left( {\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{2}}} \\ {{{p}_{2}}} \end{array}} \right] \otimes \nabla } \right)} \end{array}} \right).$Единственное выражение для аппроксимации потока получается путем подстановки (20) в (16) или (19):
(21)
$\begin{gathered} {{\left. {\left[ {\begin{array}{*{20}{c}} {\mathbf{t}} \\ q \end{array}} \right]} \right|}_{{{{{\mathbf{x}}}_{\sigma }}}}} \approx \left( {{{T}_{2}} - {{S}_{2}} - 2{{Q}_{2}}} \right){{\left( {{{T}_{1}} + {{T}_{2}} - {{S}_{1}} - {{S}_{2}} - 2{{Q}_{1}} - 2{{Q}_{2}}} \right)}^{{ - 1}}} \times \\ \, \times \left( {({{T}_{1}} - {{Q}_{1}})\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{1}}} \\ {{{p}_{1}}} \end{array}} \right] + ({{T}_{1}} \otimes {{{({{{\mathbf{x}}}_{\sigma }} - {{{\mathbf{x}}}_{1}})}}^{{\text{т}}}} - {{W}_{1}})\left( {\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{1}}} \\ {{{p}_{1}}} \end{array}} \right] \otimes \nabla } \right)} \right) - \\ \, - \left( {{{T}_{1}} - {{S}_{1}} - 2{{Q}_{2}}} \right){{\left( {{{T}_{1}} + {{T}_{2}} - {{S}_{1}} - {{S}_{2}} - 2{{Q}_{1}} - 2{{Q}_{2}}} \right)}^{{ - 1}}} \times \\ \, \times \left( {({{T}_{2}} - {{Q}_{2}})\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{2}}} \\ {{{p}_{2}}} \end{array}} \right] + ({{T}_{2}} \otimes {{{({{{\mathbf{x}}}_{\sigma }} - {{{\mathbf{x}}}_{2}})}}^{{\text{т}}}} - {{W}_{2}})\left( {\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{2}}} \\ {{{p}_{2}}} \end{array}} \right] \otimes \nabla } \right)} \right). \\ \end{gathered} $5. ГРАНИЧНЫЕ УСЛОВИЯ
Граничные условия на грани $\sigma \in \mathcal{F}(\partial \Omega )$ заданы следующим образом:
(22)
$\begin{gathered} {{{\mathbf{n}}}^{{\text{т}}}}{{\left. {\left( {{{\alpha }_{ \bot }}{\mathbf{u}} + {{\beta }_{ \bot }}\left( {\tau ({\mathbf{u}}) - p\mathbb{I}} \right){\mathbf{n}}} \right)} \right|}_{{{{{\mathbf{x}}}_{\sigma }}}}} = {{r}_{ \bot }}, \hfill \\ \left( {\mathbb{I} - {\mathbf{n}}{{{\mathbf{n}}}^{{\text{т}}}}} \right){{\left. {\left( {{{\alpha }_{\parallel }}{\mathbf{u}} + {{\beta }_{\parallel }}\left( {\tau ({\mathbf{u}}) - p\mathbb{I}} \right){\mathbf{n}}} \right)} \right|}_{{{{{\mathbf{x}}}_{\sigma }}}}} = {{{\mathbf{r}}}_{\parallel }}. \hfill \\ \end{gathered} $Граничные условия (22) используются для вывода выражения для вектора неизвестных на грани. Для этого граничные условия дополняются условием на давление:
(23)
${{\left. {\left( {{{\alpha }_{p}}p + {{\beta }_{p}}{\mathbf{n}} \cdot \nabla p} \right)} \right|}_{{{{{\mathbf{x}}}_{\sigma }}}}} = {{r}_{p}}.$В (23) ${{r}_{p}} = {{\alpha }_{p}}{{p}_{b}} + {{\beta }_{p}}\xi $ с предписанным граничным давлением ${{p}_{b}}$. В [1] для простоты мы использовали граничное условие для давления $\xi = {\mathbf{n}} \cdot \nabla {{p}^{n}}$, предложенное в [2], где ${{p}^{n}}$ – давление на предыдущем временном шаге. Такой выбор невозможен в настоящей работе из-за отсутствия времени. Прямой подход определения граничных условий состоит в том, чтобы вывести $\xi $ из уравнения импульса или непрерывности (см. [23]). Воспользуемся первым вариантом и из первого уравнения в (1) получим
(24)
$\xi = {\mathbf{n}} \cdot {\text{div}}{\kern 1pt} \left( {p\mathbb{I}} \right) = {\mathbf{n}} \cdot \nabla p = {\mathbf{n}} \cdot {\mathbf{f}} - {\mathbf{n}} \cdot {\text{div}}{\kern 1pt} \left( {\rho {\mathbf{u}}{{{\mathbf{u}}}^{{\text{т}}}} - \tau ({\mathbf{u}})} \right).$В силу предположения о локальной линейности ${\mathbf{u}}$ и с учетом (4) член ${\mathbf{n}} \cdot {\text{div}}{\kern 1pt} \left( {\tau ({\mathbf{u}})} \right)$, состоящий из вторых производных вектора скорости, обращается в нуль в (24).
Учитывая вклад адвективного члена в (24) и используя условие бездивергентности (3), получаем
(25)
$\begin{gathered} {\mathbf{n}} \cdot {\text{div}}{\kern 1pt} \left( {\rho {\mathbf{u}}{{{\mathbf{u}}}^{{\text{т}}}}} \right) = \rho {{{\mathbf{n}}}^{{\text{т}}}}{\mathbf{u}}{{{\mathbf{u}}}^{{\text{т}}}}\nabla = \rho {{{\mathbf{n}}}^{{\text{т}}}}\left[ {\begin{array}{*{20}{c}} {{{u}^{2}}}&{u{v}}&{uw} \\ {u{v}}&{{{{v}}^{2}}}&{{v}w} \\ {uw}&{{v}w}&{{{w}^{2}}} \end{array}} \right]\nabla = \rho {{{\mathbf{n}}}^{{\text{т}}}}\left[ {\begin{array}{*{20}{c}} {u\left( {2\frac{{\partial u}}{{\partial x}} + \frac{{\partial {v}}}{{\partial y}} + \frac{{\partial w}}{{\partial z}}} \right) + {v}\frac{{\partial u}}{{\partial y}} + w\frac{{\partial u}}{{\partial z}}} \\ {u\frac{{\partial {v}}}{{\partial x}} + {v}\left( {\frac{{\partial u}}{{\partial x}} + 2\frac{{\partial {v}}}{{\partial y}} + \frac{{\partial w}}{{\partial z}}} \right) + w\frac{{\partial {v}}}{{\partial z}}} \\ {u\frac{{\partial w}}{{\partial x}} + {v}\frac{{\partial w}}{{\partial z}} + w\left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial {v}}}{{\partial y}} + 2\frac{{\partial w}}{{\partial z}}} \right)} \end{array}} \right] = \\ \, = \rho {{{\mathbf{n}}}^{{\text{т}}}}\left[ {\begin{array}{*{20}{c}} {u\frac{{\partial u}}{{\partial x}} + {v}\frac{{\partial u}}{{\partial y}} + w\frac{{\partial u}}{{\partial z}}} \\ {u\frac{{\partial {v}}}{{\partial x}} + {v}\frac{{\partial {v}}}{{\partial y}} + w\frac{{\partial {v}}}{{\partial z}}} \\ {u\frac{{\partial w}}{{\partial x}} + {v}\frac{{\partial w}}{{\partial z}} + w\frac{{\partial w}}{{\partial z}}} \end{array}} \right] = \rho \left( {{{{\mathbf{n}}}^{{\text{т}}}} \otimes {{{\mathbf{u}}}^{{\text{т}}}}} \right){\mathbf{u}} \otimes \nabla . \\ \end{gathered} $Наконец, отметим, что $\xi $ является кусочно-постоянным из-за кусочно-линейности давления. В результате мы оцениваем $\xi $ в барицентре ${{{\mathbf{x}}}_{1}}$ ячейки, смежной с $\sigma $. Это упрощает вычисление проекции объемной силы ${\mathbf{n}} \cdot {\mathbf{f}}$, которая обычно задана в центре ячейки, а адвективный член (25) превращается в $\rho \left( {{{{\mathbf{n}}}^{{\text{т}}}} \otimes {\mathbf{u}}_{1}^{{\text{т}}}} \right){{{\mathbf{u}}}_{1}} \otimes \nabla $.
Окончательное приближение для $\xi $ имеет вид
(26)
$\xi \approx {\mathbf{n}} \cdot {{\left. {\mathbf{f}} \right|}_{{{{{\mathbf{x}}}_{1}}}}} - \rho \left( {{{{\mathbf{n}}}^{{\text{т}}}} \otimes {\mathbf{u}}_{1}^{{\text{т}}}} \right){{{\mathbf{u}}}_{1}} \otimes \nabla .$Выбор коэффициентов для граничных условий типа Дирихле ${{\Gamma }_{D}}$, условия без проскальзывания ${{\Gamma }_{{NS}}}$, условия скольжения ${{\Gamma }_{S}}$, условия без трения ${{\Gamma }_{{TF}}}$, условия предписанного давления ${{\Gamma }_{P}}$ и условия типа Максвелла–Навье ${{\Gamma }_{{MN}}}$ с длиной скольжения $\lambda $ представлены в табл. 1.
Таблица 1.
Коэффициенты для распространенных типов граничных условий
| Коэффициенты ${{\Gamma }_{D}}$ | ${{\Gamma }_{{NS}}}$ | ${{\Gamma }_{S}}$ | ${{\Gamma }_{{TF}}}$ | ${{\Gamma }_{P}}$ | ${{\Gamma }_{{MN}}}$ | |
|---|---|---|---|---|---|---|
| ${{\alpha }_{ \bot }}$ | 1 | 1 | 1 | 0 | 0 | 1 |
| ${{\alpha }_{\parallel }}$ | 1 | 1 | 0 | 0 | 0 | $\lambda $ |
| ${{\beta }_{ \bot }}$ | 0 | 0 | 0 | 1 | 1 | 0 |
| ${{\beta }_{\parallel }}$ | 0 | 0 | 1 | 1 | 1 | 1 |
| ${{\alpha }_{p}}$ | 0 | 0 | 0 | 0 | 1 | 0 |
| ${{\beta }_{p}}$ | 1 | 1 | 1 | 1 | 0 | 1 |
| ${{r}_{ \bot }}$ | ${\mathbf{n}} \cdot {{{\mathbf{u}}}_{b}}$ | 0 | 0 | 0 | $ - {{p}_{b}}$ | 0 |
| ${{{\mathbf{r}}}_{\parallel }}$ | ${{{\mathbf{u}}}_{b}} - {\mathbf{nn}} \cdot {{{\mathbf{u}}}_{b}}$ | 0 | 0 | 0 | 0 | 0 |
Объединим (22) и (23) в единую блочную систему, чтобы получить
(27)
$D\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{\sigma }}} \\ {{{p}_{\sigma }}} \end{array}} \right] + N{{\left. {\left[ {\begin{array}{*{20}{c}} {\tau ({\mathbf{u}}){\mathbf{n}}} \\ {{\mathbf{n}} \cdot \nabla p} \end{array}} \right]} \right|}_{{{{{\mathbf{x}}}_{\sigma }}}}} = \left[ {\begin{array}{*{20}{c}} {{\mathbf{n}}{{r}_{ \bot }} + {{{\mathbf{r}}}_{\parallel }}} \\ {{{r}_{p}}} \end{array}} \right],$(28)
$D = \left[ {\begin{array}{*{20}{c}} {{{\alpha }_{\parallel }}\mathbb{I} + \left( {{{\alpha }_{ \bot }} - {{\alpha }_{\parallel }}} \right){\mathbf{n}}{{{\mathbf{n}}}^{{\text{т}}}}}&{ - {{\beta }_{ \bot }}{\mathbf{n}}} \\ {}&{{{\alpha }_{p}}} \end{array}} \right],\quad N = \left[ {\begin{array}{*{20}{c}} {{{\beta }_{\parallel }}\mathbb{I} + \left( {{{\beta }_{ \bot }} - {{\beta }_{\parallel }}} \right){\mathbf{n}}{{{\mathbf{n}}}^{{\text{т}}}}}&{} \\ {}&{{{\beta }_{p}}} \end{array}} \right].$Используя приближения (12), ${{\left. {{\mathbf{n}} \cdot \nabla p} \right|}_{{{{{\mathbf{x}}}_{\sigma }}}}} \approx {\mathbf{n}} \cdot \nabla {{p}_{1}}$ и расширяя ${{r}_{p}}$ с помощью (26), получаем
(29)
$D\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{\sigma }}} \\ {{{p}_{\sigma }}} \end{array}} \right] + N{{W}_{b}}\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{1}}} \\ {{{p}_{1}}} \end{array}} \right] \otimes \nabla = \left[ {\begin{array}{*{20}{c}} {{\mathbf{n}}{{r}_{ \bot }} + {{{\mathbf{r}}}_{\parallel }}} \\ {{{\beta }_{p}}{\mathbf{n}} \cdot {\mathbf{f}} + {{\alpha }_{p}}{{p}_{b}}} \end{array}} \right],$(30)
${{W}_{b}} = \left[ {\begin{array}{*{20}{c}} {\mu \left( {\mathbb{I} \otimes {{{\mathbf{n}}}^{{\text{т}}}} + {{{\mathbf{n}}}^{{\text{т}}}} \otimes \mathbb{I}} \right)}&{} \\ {\rho {{{\mathbf{n}}}^{{\text{т}}}} \otimes {\mathbf{u}}_{1}^{{\text{т}}}}&{{{{\mathbf{n}}}^{{\text{т}}}}} \end{array}} \right].$Мы используем разложение для градиента, аналогичное (11), но для скорости и давления:
(31)
$\begin{gathered} \left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{1}}} \\ {{{p}_{1}}} \end{array}} \right] \otimes \nabla = r_{1}^{{ - 1}}\left( {\mathbb{I} \otimes {\mathbf{n}}} \right)\left( {\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{\sigma }}} \\ {{{p}_{\sigma }}} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{1}}} \\ {{{p}_{1}}} \end{array}} \right]} \right) + \left( {\mathbb{I} - r_{1}^{{ - 1}}\left( {\mathbb{I} \otimes {\mathbf{n}}} \right)\mathbb{I} \otimes {{{\left( {{{{\mathbf{x}}}_{\sigma }} - {{{\mathbf{x}}}_{1}}} \right)}}^{{\text{т}}}}} \right)\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{1}}} \\ {{{p}_{1}}} \end{array}} \right] \otimes \nabla , \hfill \\ \hfill \\ \end{gathered} $(32)
${{T}_{b}} = r_{1}^{{ - 1}}{{W}_{b}}\left( {\mathbb{I} \otimes {\mathbf{n}}} \right) = r_{1}^{{ - 1}}\left[ {\begin{array}{*{20}{c}} {\mu \left( {\mathbb{I} + {\mathbf{n}}{{{\mathbf{n}}}^{{\text{т}}}}} \right)}&{} \\ {\rho {\mathbf{n}} \cdot {{{\mathbf{u}}}_{1}}{{{\mathbf{n}}}^{{\text{т}}}}}&1 \end{array}} \right].$Используя (31) и (32) в (29), получаем выражение для скорости и давления на грани:
(33)
$\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{\sigma }}} \\ {{{p}_{\sigma }}} \end{array}} \right] = {{\left( {D + N{{T}_{b}}} \right)}^{{ - 1}}}\left( {\left[ {\begin{array}{*{20}{c}} {{\mathbf{n}}{{r}_{ \bot }} + {{{\mathbf{r}}}_{\parallel }}} \\ {{{\beta }_{p}}{\mathbf{n}} \cdot {\mathbf{f}} + {{\alpha }_{p}}{{p}_{b}}} \end{array}} \right] + N{{T}_{b}}\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{1}}} \\ {{{p}_{1}}} \end{array}} \right] + N\left( {{{T}_{b}} \otimes {{{\left( {{{{\mathbf{x}}}_{\sigma }} - {{{\mathbf{x}}}_{1}}} \right)}}^{{\text{т}}}} - {{W}_{b}}} \right)\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{1}}} \\ {{{p}_{1}}} \end{array}} \right] \otimes \nabla } \right).$Для аппроксимации потока на границе подставим выражение (33) в формулу (16).
6. ВОССТАНОВЛЕНИЕ ГРАДИЕНТА
Для численного расчета потоков остается вычислить градиент скорости и давления в каждой ячейке ${{V}_{i}}$. Рассмотрим ячейку ${{V}_{1}}$ с набором граней $\sigma \in \mathcal{F}({{V}_{1}})$. Для внутренней грани $\sigma \in \mathcal{F}(\Omega {{\backslash }}\partial \Omega ),$ $\sigma = {{V}_{1}} \cap {{V}_{2}}$ мы накладываем следующее условие на градиент:
(34)
$\mathbb{I} \otimes {{\left( {{{{\mathbf{x}}}_{2}} - {{{\mathbf{x}}}_{1}}} \right)}^{{\text{т}}}}\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{1}}} \\ {{{p}_{1}}} \end{array}} \right] \otimes \nabla = \left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{2}}} \\ {{{p}_{2}}} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{1}}} \\ {{{p}_{1}}} \end{array}} \right],$(35)
$\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{1}}} \\ {{{p}_{1}}} \end{array}} \right] + \mathbb{I} \otimes {{\left( {{{{\mathbf{x}}}_{\sigma }} - {{{\mathbf{x}}}_{1}}} \right)}^{{\text{т}}}}\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{1}}} \\ {{{p}_{1}}} \end{array}} \right] \otimes \nabla = \left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{\sigma }}} \\ {{{p}_{\sigma }}} \end{array}} \right],$(36)
$\left( {D \otimes {{{\left( {{{{\mathbf{x}}}_{\sigma }} - {{{\mathbf{x}}}_{1}}} \right)}}^{{\text{т}}}} + N{{W}_{b}}} \right)\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{1}}} \\ {{{p}_{1}}} \end{array}} \right] \otimes \nabla = \left[ {\begin{array}{*{20}{c}} {{\mathbf{n}}{{r}_{ \bot }} + {{{\mathbf{r}}}_{\parallel }}} \\ {{{\beta }_{p}}{\mathbf{n}} \cdot {\mathbf{f}} + {{\alpha }_{p}}{{p}_{b}}} \end{array}} \right] - D\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{1}}} \\ {{{p}_{1}}} \end{array}} \right].$Дополняем систему условием бездивергентности:
(37)
$\left[ {\begin{array}{*{20}{c}} 1&0&0&0&1&0&0&0&1&0&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{1}}} \\ {{{p}_{1}}} \end{array}} \right] \otimes \nabla = 0.$Условия (34) и (36) по всем интерфейсам ${{V}_{1}}$ и (37) образуют линейную систему с матрицей $A \in {{\Re }^{{4|\mathcal{F}({{V}_{1}})| + 1 \times 12}}}$ и правой частью $B \in {{\Re }^{{4|\mathcal{F}({{V}_{1}})| + 1 \times 1}}}$. Прямоугольная система решается методом наименьших квадратов:
(38)
$\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{1}}} \\ {{{p}_{1}}} \end{array}} \right] \otimes \nabla = {{\left( {{{A}^{{\text{т}}}}A} \right)}^{{ - 1}}}{{A}^{T}}B,$Мы обнаружили, что на практике для точности полезно масштабировать на ${{r}_{1}}$ строку, соответствующую давлению в (36).
7. РЕШЕНИЕ ЗАДАЧИ
Для определения стационарного состояния нелинейной задачи используется метод Ньютона. На каждой итерации $k$ метода Ньютона соберем вектор правой части ${{\mathcal{R}}^{k}}$ размером $4{\text{|}}\mathcal{V}(\Omega ){\text{|}} \times 1$ и соответствующую матрицу ${{\mathcal{J}}^{k}}$ размером $4{\text{|}}\mathcal{V}(\Omega ){\kern 1pt} {\text{|}} \times 4{\text{|}}\mathcal{V}(\Omega ){\kern 1pt} {\text{|}}$. В данной работе используется автоматическое дифференцирование для сборки разреженных матриц, в результате чего рассматривается только сборка невязки. Сборка происходит следующим образом:
1. Предварительно вычислим градиенты скорости и давления ${{\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}_{i}}}&{{{p}_{i}}} \end{array}} \right]}^{{\text{т}}}} \otimes \nabla $ вместе с производными по каждой ячейке ${{V}_{i}} \in \mathcal{V}(\Omega )$, собирая и решая систему (38).
2. Соберем невязку в ячейке ${{V}_{i}} \in \mathcal{V}(\Omega )$, вычисляя (5):
(39)
$\mathcal{R}_{{{{V}_{i}}}}^{k} = \sum\limits_{\sigma \in \mathcal{F}({{V}_{i}})} {\text{|}}\sigma {\kern 1pt} {\text{|}}{{\left. {\left[ {\begin{array}{*{20}{c}} {\mathbf{t}} \\ q \end{array}} \right]{\kern 1pt} } \right|}_{{{{{\mathbf{x}}}_{\sigma }}}}},$3. Для каждой ячейки ${{V}_{i}} \in \mathcal{V}(\Omega )$ вычтем правую часть из невязки $\mathcal{R}_{{{{V}_{i}}}}^{k}$.
Скорость и давление на следующей итерации Ньютона $k + 1$ получаются из решения системы
(40)
${{\mathcal{J}}^{k}}\left( {\left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}^{{k + 1}}}} \\ {{{p}^{{k + 1}}}} \end{array}} \right] - \left[ {\begin{array}{*{20}{c}} {{{{\mathbf{u}}}^{k}}} \\ {{{p}^{k}}} \end{array}} \right]} \right) = - {{\mathcal{R}}^{k}},$8. ЧИСЛЕННЫЕ ЭКСПЕРИМЕНТЫ
Сначала мы продемонстрируем влияние новых граничных условий для давления на аналитическом решении для уравнений Навье–Стокса, предложенном Эшером и Штейнманом (см. [27]). Аналитическое решение имеет вид
(41)
$v(x,y,z) = - \frac{\pi }{4}\left( {{{e}^{{\frac{{\pi y}}{4}}}}\sin {\kern 1pt} \left( {\frac{\pi }{4}(z + 2x)} \right) + {{e}^{{\frac{{\pi x}}{4}}}}\cos {\kern 1pt} \left( {\frac{\pi }{4}(y + 2z)} \right)} \right){{e}^{{\frac{{ - \mu {{\pi }^{2}}t}}{4}}}},$(42)
$\begin{gathered} \begin{array}{*{20}{l}} {p(x,y,z)}&{ = - \frac{{{{\pi }^{2}}}}{{32}}\left( {{{e}^{{\frac{{\pi x}}{2}}}} + {{e}^{{\frac{{\pi y}}{2}}}} + {{e}^{{\frac{{\pi z}}{2}}}} + 2\sin {\kern 1pt} \left( {\frac{\pi }{4}(x + 2y)} \right)\cos {\kern 1pt} \left( {\frac{\pi }{4}(z + 2x)} \right){{e}^{{\frac{{\pi (y + z)}}{4}}}}} \right.} \end{array} + \\ \left. {\, + 2\sin {\kern 1pt} \left( {\frac{\pi }{4}(y + 2z)} \right)\cos {\kern 1pt} \left( {\frac{\pi }{4}(x + 2y)} \right){{e}^{{\frac{{\pi (z + x)}}{4}}}} + 2\sin {\kern 1pt} \left( {\frac{\pi }{4}(z + 2x)} \right)\cos {\kern 1pt} \left( {\frac{\pi }{4}(y + 2z)} \right){{e}^{{\frac{{\pi (x + y)}}{4}}}}} \right){{e}^{{\frac{{ - \mu {{\pi }^{2}}t}}{2}}}}. \\ \end{gathered} $Мы вводим множитель Лагранжа и накладываем ограничение на интеграл давления, следуя [3] для единственного решения по давлению:
(43)
$\sum\limits_{{{V}_{i}} \in \mathcal{V}(\Omega )} \,{{p}_{i}}\left| {{{V}_{i}}} \right| = \sum\limits_{{{V}_{i}} \in \mathcal{V}(\Omega )} \,p({{x}_{i}},{{y}_{i}},{{z}_{i}})\left| {{{V}_{i}}} \right| \approx \int\limits_\Omega \,p(x,y,z){\text{d}}V.$Задача решается в единичном кубе $\Omega \in {{[0,1]}^{3}}$ до стационарного состояния для невязкой жидкости с $\rho = 1$ и $\mu = 0$. Заметим, что для невязкой жидкости аналитическое решение не зависит от времени. Аналитическое решение удовлетворяет ${\mathbf{f}} = {\mathbf{0}}$. По всей границе накладываются граничные условия типа Дирихле $\partial \Omega = {{\Gamma }_{D}}$. Скорость на границе ${{{\mathbf{u}}}_{b}}$ определяется из аналитического решения в центрах граней. Для ускорения сходимости мы задаем аналитическое решение в качестве начального решения как для давления, так и для скорости.
Введем декомпозицию $\Omega $ на регулярную $N \times N \times N$ кубическую сетку и рассмотрим три варианта задания граничных условий на давление. Первый вариант – $\xi = 0$, второй – $\xi = {{\left. {{\mathbf{n}} \cdot \nabla p(x,y,z)} \right|}_{{{{{\mathbf{x}}}_{\sigma }}}}}$ и в третьем варианте $\xi $ определяется по формуле (26).
Результаты для всех трех вариантов приведены в табл. 2 при различном сгущении сетки. В таблице $\theta = \mathop {{\text{log}}}\nolimits_2 \left( {{{\mathcal{E}}_{{32}}}{\text{/}}{{\mathcal{E}}_{{16}}}} \right)$ обозначает скорость сходимости, где ${{\mathcal{E}}_{N}}$ – ${{L}_{2}}$-норма ошибки на $N \times N \times N$ кубической сетке. Полученные результаты явно мотивируют использование формулы (26) для $\xi $. Хотя аналитически заданное $\xi $ дает немного лучшие результаты, скорость сходимости восстанавливается с $\xi $, определенным по формуле (26).
Таблица 2.
Нормы ошибок для задачи Эшера–Штейнмана
| $\xi $ | $0$ | ${{\left. {{\mathbf{n}} \cdot \nabla p(x,y,z)} \right|}_{{{{{\mathbf{x}}}_{\sigma }}}}}$ | по (26) | |||
|---|---|---|---|---|---|---|
| Ошибка | ${{\left\| {{{{\mathbf{u}}}_{h}} - {\mathbf{u}}} \right\|}_{{{{L}_{2}}}}}$ | ${{\left\| {{{p}_{h}} - p} \right\|}_{{{{L}_{2}}}}}$ | ${{\left\| {{{{\mathbf{u}}}_{h}} - {\mathbf{u}}} \right\|}_{{{{L}_{2}}}}}$ | ${{\left\| {{{p}_{h}} - p} \right\|}_{{{{L}_{2}}}}}$ | ${{\left\| {{{{\mathbf{u}}}_{h}} - {\mathbf{u}}} \right\|}_{{{{L}_{2}}}}}$ | ${{\left\| {{{p}_{h}} - p} \right\|}_{{{{L}_{2}}}}}$ |
| $N = 4$ | 0.04 | 0.25 | 0.025 | 0.14 | 0.026 | 0.21 |
| $N = 8$ | 0.023 | 0.083 | 0.01 | 0.027 | 0.011 | 0.037 |
| $N = 16$ | 0.012 | 0.034 | 0.0035 | 0.0054 | 0.0037 | 0.0077 |
| $N = 32$ | 0.006 | 0.016 | 0.001 | 0.0012 | 0.0011 | 0.0017 |
| $\theta $ | 0.97 | 1.06 | 1.74 | 2.17 | 1.74 | 2.17 |
Нелинейная задача на каждом временном шаге требует до трех итераций для падения нормы невязки к точности ${{\tau }_{{{\text{abs}}}}}{{ = 10}^{{ - 7}}}$ и ${{\tau }_{{{\text{rel}}}}}{{ = 10}^{{ - 4}}}$. Для сравнения наименьшая начальная норма невязки составляет $ 1.6 \times {{10}^{{ - 4}}}$, что соответствует аналитическому граничному условию на самой мелкой сетке.
Далее мы рассмотрим двумерную версию задачи о каверне с подвижной крышкой (см. [28]). Как и в [3] область единичного куба $\Omega \in {{[0,1]}^{3}}$ аппроксимируется полигональной призматической сеткой с одним слоем ячеек в $z$-направлении. Узлы исходной регулярной сетки искажены для улучшения разрешения вблизи границ. Формула преобразования для координат исходной сетки ${{x}_{i}},({{x}_{1}},{{x}_{2}},{{x}_{3}}) = (x,y,z)$ имеет вид
(44)
${{\tilde {x}}_{i}} = \frac{1}{2} + \left( {{{x}_{i}} - \frac{1}{2}} \right){{\left( {\frac{1}{4} + {{\gamma }^{2}}} \right)}^{1}}{\text{/}}2{{\left[ {{{{\left( {{{x}_{i}} - \frac{1}{2}} \right)}}^{2}} + {{\gamma }^{2}}} \right]}^{{ - 1/2}}},$Фиг. 1.
Полигональная призматическая сетка с $280$ элементами в единичном кубе, оригинальная регулярная сетка (а), после искажения (44) с $\gamma = 1{\text{/}}4$ (б).
Граничное условие типа Дирихле ${{\Gamma }_{D}}$ с ${{{\mathbf{u}}}_{b}}{{ = (1,0,0)}^{{\text{т}}}}$ предписано на верхней стороне куба на ${{\Gamma }_{1}} = \partial \Omega \cap \{ y = 1\} $, граничные условия скольжения ${{\Gamma }_{S}}$ заданы на фронтальной и тыловой сторонах куба ${{\Gamma }_{2}} = \partial \Omega \cap \{ z = 0 \cup z = 1\} $ и отсутствие скольжения ${{\Gamma }_{{NS}}}$ на левой, правой и нижней сторонах ${{\Gamma }_{3}} = \partial \Omega {{\backslash }}{{\Gamma }_{1}} \cup {{\Gamma }_{2}}$. Интересующие нас числа Рейнольдса ${\text{Re}} \in \{ 100,400,1000,3200,10\,000\} $, вязкость $\mu = 1{\text{/}}Re$ и плотность $\rho = 1$. Для единственного решения по давлению система дополнена множителем Лагранжа и ограничением (43).
Стационарная задача для ${\text{R}}{{{\text{e}}}_{i}} \in \{ 100,400,1000,3200,10\,000\} $ решается с $\xi $, определяемым (26). Начальным состоянием задачи при ${\text{R}}{{{\text{e}}}_{0}} = 100$ являются нулевая скорость и давление, затем для ускорения сходимости мы повторно используем стационарное решение предыдущей задачи с ${\text{R}}{{{\text{e}}}_{{i - 1}}}$ для определения начального состояния для каждой последующей задачи с более высоким числом Рейнольдса ${\text{R}}{{{\text{e}}}_{i}}$. Решение стационарных задач требует до восьми итераций Ньютона с параметром точности ${{\tau }_{{{\text{abs}}}}}{{ = 10}^{{ - 5}}}$.
Сравнение с эталонными данными [28] представлено на фиг. 2. Детальное сравнение в нескольких контрольных точках с различным выбором $\xi $ для наиболее вязкого случая $Re = 100$ приведено в табл. 3. В результате при $\xi = 0$ метод немного сглаживает отрицательную вершину при $y = 0.4531$, а новый метод немного проскакивает ее. Метод Ньютона не сходится к стационарному состоянию при $Re = 10\,000$ и $\xi = 0$.
Фиг. 2.
Сравнение $u$-компоненты скорости для ${\text{Re}} = \{ 100,400,1000,10\,000\} $ вдоль $y = 0.5$ с данными из [28].
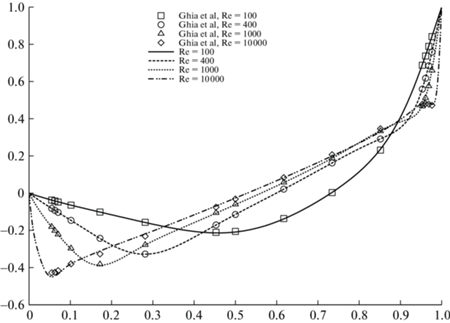
Таблица 3.
Сравнение $u$-компоненты скорости для ${\text{Re}} = 100$ вдоль $y = 0.5$ с данными из [28] и с различным выбором граничного условия $\xi $
| $y$ | 0.9766 | 0.9531 | 0.7344 | 0.4531 | 0.1719 | 0.0547 |
|---|---|---|---|---|---|---|
| Данные [28] | 0.84123 | 0.68717 | 0.00332 | –0.21090 | –0.10150 | –0.03717 |
| $\xi $ из (26) | 0.84443 | 0.69016 | 0.00357 | –0.21367 | –0.10155 | –0.03707 |
| $\xi = 0$ | 0.84256 | 0.68682 | 0.00068 | –0.20823 | –0.10424 | –0.03737 |
9. ВЫВОДЫ
В настоящей работе предложен и исследован подход к определению искусственных граничных условий на давление для стационарных уравнений Навье–Стокса. Новый подход достаточно прост для интеграции в конечно-объемную схему. Он демонстрирует явное улучшение скорости сходимости на задаче с известным аналитическим решением и работает в нескольких сложных эталонных задачах.
В дальнейших работах будет рассмотрен другой подход к аппроксимации диффузионного члена, учитывающий условие бездивергентности и применимый к неньютоновским жидкостям. Другим возможным направлением исследований является метод восстановления градиента с меньшим шаблоном.
Список литературы
Terekhov K. Fully-implicit collocated finite-volume method for the unsteady incompressible navier-stokes problem. In Numerical Geometry, Grid Generation and Scientific Computing, Lect. Not. in Comput. Sci. and Engineer. Springer, Cham, 2021.
Gresho P.M. On the theory of semi-implicit projection methods for viscous incompressible ow and its implementation via a nite element method that also introduces a nearly consistent mass matrix. part 1: Theory // Inter. J. Numer. Meth. Fluid. 1990. V. 11. № 5. P. 587–620.
Terekhov K. Collocated finite-volume method for the incompressible Navier Stokes problem // J. of Numer. Math. 2021. V. 29. № 1. P. 63–79.
Bouchnita A., Terekhov K., Nony P., Vassilevski Yu., Volpert V. A mathematical model to quantify the effects of platelet count, shear rate, and injury size on the initiation of blood coagulation under venous ow conditions // Plos one. 2020. V. 15. № 7. e0235392.
Vassilevski Yu., Terekhov K., Nikitin K., Kapyrin I. Parallel finite volume computation on general meshes. Springer Inter. Publ., 2020.
Ladyzhenskaya O.A. The mathematical theory of viscous incompressible flow, V. 12. Gordon & Breach, New York, 1969.
Lebedev V.I. Difference analogues of orthogonal decompositions, basic differential operators and some boundary problems of mathematical physics // USSR Comput. Math. and Math. Phys. 1964. V. 4, № 3. P. 69–92.
Harlow F.H., Welch J.E. Numerical calculation of time-dependent viscous incompressible ow of fluid with free surface // Phys. Fluid. 1965. V. 8. № 12. P. 2182–2189.
Olshanskii M.A., Terekhov K.M., Vassilevski Yu.V. An octree-based solver for the incompressible Navier Stokes equations with enhanced stability and low dissipation // Comput. Fluid. 2013. V. 84. P. 231–246.
Perot B. Conservation properties of unstructured staggered mesh schemes // J. of Comput. Phys. 2000. V. 159. № 1. P. 58–89.
Rhie C.M., Chow W.L. Numerical study of the turbulent ow past an airfoil with trailing edge separation // AIAA J. 1983. V. 21. № 11. P. 1525–1532.
Brewster R., Carpenter C., Volpenhein E., Baglietto E., Smith J. Application of cd-adapco best practices to nestor omega mvg benchmark exercises using star-ccm+,” // Proc. of NURETH-16. Chicago. IL. 2015.
ANSYS CFX-Solver. Theory guide. Release ll, 2006.
Markovic J.D., Lukic N.L., Ilic J.D., Nikolovski B.G., Milan N Sovilj M.N., Sijacki I.M. Using the ansys fluent for simulation of two-sided lid- driven ow in a staggered cavity // Acta Period. Technolog. 2012. V. 43. P. 169–178.
Rutkowski D.R., Roldan-Alzate A., Johnson K.M. Enhancement of cerebrovascular 4d flow mri velocity fields using machine learning and computational fluid dynamics simulation data // Sci. Rep. 2021. V. 11. № 1. P. 1–11.
Karrholm F.P. Rhie-chow interpolation in openfoam. Depart.t of Appl. Mech., Chalmers Univer. of Technology: Goteborg, Sweden, 2006.
Terekhov K., Vassilevski Yu. Finite volume method for coupled subsurface ow problems, I: Darcy problem // J. of Comput. Phys. 2019. V. 395. P. 298–306.
Terekhov K. Multi-physics flux coupling for hydraulic fracturing modelling within INMOST platform // Rus. J. of Numer. Analys. and Math. Model. 2020. V. 35. № 4. P. 223–237.
Agelas L., Eymard R., Herbin R. A nine-point nite volume scheme for the simulation of di usion in heterogeneous media // Comptes Rendus Math. 2009. V. 347. P. 673–676.
Terekhov K., Mallison B., Tchelepi H. Cell-centered nonlinear finite-volume methods for the heterogeneous anisotropic diffusion problem // J. of Comput. Phys. 2017. V. 330. P. 245–267.
Terekhov K. Cell-centered finite-volume method for heterogeneous anisotropic poromechanics problem // J. of Comput. and Appl. Math. 2020. V. 365. P. 112357.
Terekhov K., Tchelepi H. Cell-centered finite-volume method for elastic deformation of heterogeneous media with full-tensor properties // J. of Comput. and Appl. Math. 2020. V. 364. P. 112331.
Gresho P.M., Sani R.L. On pressure boundary conditions for the incompressible navier-stokes equations // Inter. J. Numer. Meth. Fluid. 1987. V. 7. № 10. P. 1111–1145.
Terekhov K. Parallel multilevel linear solver within INMOST platform. In Voevodin V., Sobolev S. (eds) Supercomputing. RuSCDays 2020. Comm. in Comput. and Inform. Sci. Springer, Cham, 2020.
Terekhov K., Vassilevski Yu. INMOST parallel platform for mathematical modeling and applications. In Voevodin V., Sobolev S. (eds) Supercomputing. RuSCDays 2018. Comm. in Comput. and Inform. Sci. V. 965. P. 230–241. Springer, Cham, 2018.
Terekhov K., Vassilevski Yu. Mesh modification and adaptation within INMOST programming platform. In Numer. Geometry, Grid Generat. and Sci. Comput. P. 243–255. Springer, 2019.
Ethier C.R., Steinman D.A. Exact fully 3D Navier Stokes solutions for benchmarking // Inter. J. Numer. Meth. Fluid. 1994. V. 19. № 5. P. 369–375.
Ghia U., Ghia K.N., Shin C.T. High-re solutions for incompressible ow using the navier-stokes equations and a multigrid method // J. Comput. Phys. 1982. V. 48. № 3. P. 387–411.
Дополнительные материалы отсутствуют.
Инструменты
Журнал вычислительной математики и математической физики


