Журнал вычислительной математики и математической физики, 2023, T. 63, № 4, стр. 657-666

ВВЕДЕНИЕ

В последние годы методы исследования и численного решения задач вариационного усвоения данных, представляющих собой конкретные задачи оптимального управления, получили большое развитие в метеорологии и океанографии, где данные наблюдений усваиваются в моделях атмосферы и океана с целью получения начальных, граничных условий или других параметров модели для последующего моделирования и прогноза (см. [1–9]).

При исследовании задач вариационного усвоения данных наблюдений важную роль играет анализ чувствительности оптимального решения и его функционалов по отношению к входным данным (см. [10–17]). Настоящая работа обобщает результаты предыдущих работ авторов на случай задачи вариационного усвоения данных с целью восстановления потоков тепла на поверхности моря при одновременном использовании ковариационных матриц ошибок данных наблюдений и ошибок начального приближения (бэкграунда). Проведено исследование чувствительности функционалов от оптимального решения задачи вариационного усвоения данных о температуре поверхности для модели термодинамики моря по отношению к входным данным о потоке тепла. С учетом свойств гессиана функции стоимости доказана теорема о представлении градиента функционала по отношению к данным бэкграунда, сформулирован алгоритм вычисления градиента функционала и приведены результаты численных экспериментов для модели динамики Черного моря, разработанной в ИВМ РАН.

1. ЗАДАЧА ВАРИАЦИОННОГО УСВОЕНИЯ ДАННЫХ ДЛЯ МОДЕЛИ ТЕРМОДИНАМИКИ МОРЯ

Рассмотрим задачу термодинамики моря в виде (см. [18], [19])

где $T = T(x,y,z,t)$ – неизвестная функция температуры, $t \in (0,\bar {t})$, $(x,y,z) \in D = \Omega \times (0,H)$, $\Omega \subset {{R}^{2}}$, $H = H(x,y)$ – функция рельефа дна, $Q = Q(x,y,t)$ – суммарный приток тепла, $\bar {U} = (u,{v},w)$, ${{\hat {a}}_{T}} = {\text{diag}}(({{a}_{T}}{{)}_{{ii}}})$, ${{({{a}_{T}})}_{{11}}} = ({{a}_{T}}{{)}_{{22}}} = {{\mu }_{T}}$, ${{({{a}_{T}})}_{{33}}} = {{\nu }_{T}}$, ${{f}_{T}} = {{f}_{T}}(x,y,z,t)$ – заданные функции. Скорости $u,\;{v},\;w$ зависят в общем случае от пространства и времени, а коэффициенты ${{\mu }_{T}},{{\nu }_{T}}$ предполагаются зависящими только от пространственных переменных на рассматриваемом интервале по времени. Граница области $\Gamma \equiv \partial D$ представляется как объединение четырех непересекающихся частей ${{\Gamma }_{S}}$, ${{\Gamma }_{{w,op}}}$, ${{\Gamma }_{{w,c}}}$, ${{\Gamma }_{H}}$, где ${{\Gamma }_{S}} = \Omega $ (невозмущенная поверхность моря), ${{\Gamma }_{{w,op}}}$ – жидкая (открытая) часть вертикальной боковой границы, ${{\Gamma }_{{w,c}}}$ – твердая часть вертикальной боковой границы, ${{\Gamma }_{H}}$ – дно моря. Другие обозначения и детальное описание постановки задачи можно найти в работах [20–22].

Запишем задачу (1.1) в форме операторного уравнения в $\left( {W_{2}^{1}(D)} \right){\kern 1pt} *$:

где равенство понимается в обобщенном смысле, а именно, а операторы $L$, $F,B$ определяются интегральными соотношениями при этом функции ${{\hat {a}}_{T}}$, ${{Q}_{T}}$, ${{f}_{T}}$, $Q$ таковы, что равенство (1.3) имеет смысл.

Рассмотрим задачу об усвоении данных о температуре поверхности моря, следуя [21], [23]. Предположим, что в задаче (1.1) функция $Q \in {{L}_{2}}(\Omega \times (0,\bar {t}))$ не известна. Пусть задана функция данных наблюдений ${{T}_{{{\text{obs}}}}}(x,y,t)$ на $\bar {\Omega } \equiv \Omega \cup \partial \Omega $ при $t \in (0,\bar {t})$, которая по своему физическому смыслу есть приближение к функции поверхностной температуры на $\Omega $, т.е. к ${{\left. T \right|}_{{z = 0}}}$. Считаем, что ${{T}_{{{\text{obs}}}}} \in {{L}_{2}}(\Omega \times (0,\bar {t}))$. Допускается случай, когда ${{T}_{{{\text{obs}}}}}$ имеется лишь на некотором подмножестве из $\Omega \times (0,\bar {t})$, характеристическую функцию которого обозначим через ${{m}_{0}}$. Вне этого подмножества для определенности считаем ${{T}_{{{\text{obs}}}}}$ нулевой.

Будем предполагать, что данные наблюдений ${{T}_{{{\text{obs}}}}}$ заданы с ошибками, а именно,

где ${{T}^{t}}$ – точное решение задачи (1.1) при некотором $Q = {{Q}^{t}}$, а ${{\xi }_{{{\text{obs}}}}} \in {{Y}_{{{\text{obs}}}}} = {{L}_{2}}\left( {\Omega \times \left( {0,\bar {t}} \right)} \right)$ рассматривается как ошибка наблюдений в пространстве наблюдений ${{Y}_{{{\text{obs}}}}}$. Предполагается, что ошибки ${{\xi }_{{{\text{obs}}}}}$ случайные и они распределены по нормальному закону (гауссовские) с нулевым математическим ожиданием и ковариационным оператором $R \cdot = E[( \cdot ,{{\xi }_{{{\text{obs}}}}}){{\xi }_{{{\text{obs}}}}}]$, $R:{{Y}_{{{\text{obs}}}}} \to {{Y}_{{{\text{obs}}}}}$, где $E$ – математическое ожидание. Ковариационные матрицы ошибок наблюдений играют важную роль при вариационном усвоении данных: обратные к ним матрицы включаются в качестве весовых операторов в исходный функционал стоимости [8]. В дальнейшем мы будем предполагать, что $R$ положительно определен и, значит, обратим.

Рассмотрим следующую задачу вариационного усвоения данных: найти $T$ и $Q$ такие, что

где ${{Q}^{{(0)}}} = {{Q}^{{(0)}}}(x,y,t)$ – заданная функция, $\mathcal{B}:{{Y}_{{{\text{obs}}}}} \to {{Y}_{{{\text{obs}}}}}$ – ковариационный оператор ошибок бэкграунда. Функция ${{Q}^{{(0)}}}$ обычно выбирается в качестве начального приближения для неизвестного потока $Q$ (так называемый бэкграунд или фоновый поток). Цель вариационного усвоения данных – используя ${{Q}^{{(0)}}}$, найти лучшую оценку для $Q$, согласованную с решением модели и наблюдениями для дальнейшего моделирования и прогноза.

Слагаемое с весовым оператором ${{\mathcal{B}}^{{ - 1}}}$ играет роль регуляризации по Тихонову (см. [24]), он считается заданным при рассмотрении задачи. Если оператор $\mathcal{B}$ положительно определен, то поставленная задача вариационного усвоения данных имеет единственное решение. Существование оптимального решения следует из классических результатов теории экстремальных задач (см. [2]), так как можно показать, что решение задачи (1.2) непрерывно зависит от потока $Q$ (имеют место априорные оценки в соответствующих функциональных пространствах).

Необходимое условие оптимальности $\operatorname{grad} J = 0$, которое определяет решение сформулированной задачи вариационного усвоения данных, приводит к так называемой системе оптимальности (см. [2]):

где $L{\kern 1pt} *,\;B{\kern 1pt} *$ – операторы, сопряженные к $L,B$ соответственно.

2. ЧУВСТВИТЕЛЬНОСТЬ К ДАННЫМ О ПОТОКЕ ТЕПЛА

Рассмотрим функцию $G(T,Q)$, зависящую от $T,\;Q$, которая предполагается вещественнозначной и может рассматриваться как функционал на $X = {{L}_{2}}(D \times (0,\bar {t})) \times {{L}_{2}}(\Omega \times (0,\bar {t}))$. Нас интересует чувствительность функционала $G(T,Q)$ к данным бэкграунда ${{Q}^{{(0)}}}$ при условии, что $T,\;Q$ получены после вариационного усвоения из системы оптимальности (1.5)–(1.7). Как известно из [1], [25], чувствительность функционала определяется градиентом по ${{Q}^{{(0)}}}$, который является производной Гато:

Обозначим через $\delta {{Q}^{{(0)}}}$ вариацию функции ${{Q}^{{(0)}}}$. Из (1.5)–(1.7) выводим систему оптимальности для вариаций:

Отметим, что данные наблюдений ${{T}_{{{\text{obs}}}}}$ уже не входят в систему (2.2)–(2.4), в отличие от (1.5)–(1.7). Система (2.2)–(2.4) эквивалентна следующей задаче усвоения данных для определения $\delta T,\delta Q$ таких, что где

Справедлива

Лемма 1. Гессиан $\mathcal{H}$ функционала (2.6) определяется на $v \in {{L}_{2}}(\Omega \times (0,\bar {t}))$ последовательным решением задач

Доказательство. Согласно системе оптимальности (2.2)–(2.4), градиент функционала (2.6) определяется по формуле

где $\delta T{\kern 1pt} *$ – решение сопряженной задачи (2.3). Продифференцируем последнюю формулу еще раз по $\delta Q$, чтобы получить правило действия гессиана: где $v$ – вариация $\delta Q$, а $\psi {\kern 1pt} *$ – решение сопряженной задачи (2.8), которая есть не что иное, как продифференцированная задача (2.3). При этом $\psi $ – решение задачи (2.7), которая получена из (2.2) дифференцированием по $\delta Q$. Лемма доказана.

Используя (2.7)–(2.9), нетрудно видеть (см. [26]), что система (2.2)–(2.4) эквивалентна уравнению для вариации оптимального решения $\delta Q$:

Гессиан $\mathcal{H}$ действует в ${{L}_{2}}(\Omega \times (0,\bar {t}))$ с областью определения $D(\mathcal{H}) = {{L}_{2}}(\Omega \times (0,\bar {t}))$, он ограничен, самосопряжен и неотрицательно определен. Если ${{\mathcal{B}}^{{ - 1}}}$ положительно определен, то $\mathcal{H}$ положительно определен, поскольку $(\mathcal{H}v,v) \geqslant \left( {{{\mathcal{B}}^{{ - 1}}}v,v} \right)$. В последнем случае уравнение (2.10) имеет единственное решение

Формула (2.11) дает в явном виде выражение для вариаций оптимального решения $\delta Q$ через вариацию функции начального приближения (бэкграунда) $\delta {{Q}^{{(0)}}}$. Уравнение вида (2.11) может быть положено в основу исследования чувствительности оптимального решения и его функционалов к ошибкам бэкграунда.

Справедлива

Теорема 1. Градиент функционала $G(T,Q)$ по ${{Q}^{{(0)}}}$ имеет вид

где$\mathcal{H}$ – гессиан, определенный формулами (2.7)–(2.9), а $\phi {\kern 1pt} *$ – решение сопряженной задачи

Доказательство. Рассмотрим значение градиента (2.1) на вариации $\delta {{Q}^{{(0)}}}$:

где $\delta {{Q}^{{(0)}}}$ – вариация функции ${{Q}^{{(0)}}}$, $\delta T = \frac{{\partial T}}{{\partial {{Q}^{{(0)}}}}}\delta {{Q}^{{(0)}}}$, $\delta Q = \frac{{\partial Q}}{{\partial {{Q}^{{(0)}}}}}\delta {{Q}^{{(0)}}}$ – решения системы (2.2)–(2.4), $Y = {{L}_{2}}\left( {D \times \left( {0,\bar {t}} \right)} \right)$.

Задача (2.14) является сопряженной по отношению к (2.2), поэтому в силу соотношения сопряженности

Из (2.15)–(2.16) получаем где $\mathcal{F}$ определяется по формуле (2.13).

Уравнение для $\delta Q$ определяется формулой (2.11), отсюда

Таким образом, из (2.15)–(2.18) заключаем, что

откуда следует утверждение теоремы.

Реальное (практическое) использование теоремы 1 может быть сформулировано в виде следующего алгоритма для вычисления градиента функционала. Градиент $dG{\text{/}}d{{Q}^{{(0)}}}$ определяется последовательным выполнением следующих шагов:

1) решить сопряженную задачу

полагая

2) найти $u$ как решение уравнения с гессианом

3) вычислить градиент функционала по формуле

Алгоритм (2.20)–(2.22) с учетом конкретного вида производных $\partial G{\text{/}}\partial T,\;\partial G{\text{/}}\partial Q$ использовался при численных расчетах для оценки чувствительности функционалов, связанных с температурой после усвоения данных наблюдений, по отношению к изменениям функции бэкграунда ${{Q}^{{(0)}}}$.

Отметим, что в процессе отыскания градиента функционала нет необходимости вычислять обратный гессиан ${{\mathcal{H}}^{{ - 1}}}$, который фигурирует в (2.12), достаточно просто решить задачу $\mathcal{H}u = \mathcal{F}$ вида (2.21), например, итерационным методом.

Отметим также, что данные наблюдений ${{T}_{{{\text{obs}}}}}$ предполагаются случайными величинами, их случайность учитывается в функции стоимости $J(Q)$ через ковариационный оператор $R$, который входит в дальнейшем в определение гессиана (2.7)–(2.9).

3. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ ЭКСПЕРИМЕНТОВ

Численные эксперименты проводились с использованием трехмерной численной модели гидротермодинамики Черного и Азовского морей, разработанной в ИВМ РАН на основе метода расщепления (см. [22]) и дополненной процедурой усвоения температуры поверхности моря (ТПМ) для восстановления тепловых потоков $Q$ с учетом ковариационных матриц ошибок наблюдений и ошибок бэкграунда.

Объектом моделирования является акватория Черного и Азовского морей. Параметры рассматриваемой области и ее географические координаты можно описать следующим образом: $\sigma $-сетка $306 \times 200 \times 27$ (широта, долгота и глубина соответственно). Первая точка “сетки C” (см. [27]) имеет координаты $26.65^\circ $ E и $40.15^\circ $ N. Шаги сетки по $x$ и $y$ постоянны и равны 0.05 и 0.036 градуса соответственно. Шаг по времени равен $\Delta t$ = 2.5 мин.

Данные наблюдений ТПМ предоставлены спутниковой службой “See the Sea”, входящей в состав ЦКП “ИКИ Мониторинг”, которая занимается сбором и обработкой различных данных о состоянии земной поверхности и ориентируется на работу со спутниковыми наблюдениями (см. [28]). В качестве ${{T}_{{{\text{obs}}}}}$ в данном эксперименте были выбраны данные ТПМ спектрометра VIIRS на спутнике SNPP и спектрометра MODIS на спутнике Aqua (несколько измерений в сутки в определенные моменты времени). Данные ТПМ за период с 1 января по 30 июня 2019 г. были пересчитаны на сетку численной модели (см. [29]). Для расчета атмосферного воздействия в модели использовались метеорологические характеристики, в том числе, балк-формулы для расчета турбулентных течений на поверхности моря. Рассчитанные таким же образом значения среднего климатического теплового потока ${{Q}^{{(0)}}}$ использовались в процедуре усвоения данных в качестве начального приближения (бэкграунда).

Для расчета диагональных элементов ковариационной матрицы $\mathcal{B}$ были получены данные о тепловом потоке на поверхности моря. Поток тепла на поверхности моря рассчитан по данным реанализа Era 5 (www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era5) (см. [30]) за период с 1979 по 2020 г. Данные Era 5 загружались с временным разрешением 12 ч, что позволяет учитывать суточный ход изменений, разделять дневные и ночные потоки тепла. По данным за 1979–2020 гг. рассчитаны средние значения и дисперсии теплового потока по дневным и ночным данным для каждого дня года. Полученные дисперсии представляют собой диагональные элементы ковариационной матрицы ошибок бэкграунда $\mathcal{B}$. Аналогичным образом (см. [31]) на основе данных сервиса Copernicus (период с 1982 по 2019 г.) и данных ЦКП “ИКИ Мониторинг” о температуре поверхности моря рассчитывались элементы ковариационной матрицы ошибок данных наблюдений $R$.

В численных примерах рассматривались функционалы вида

где $F{\kern 1pt} *(x,y,t)$ – некая весовая функция, связанная с полем температуры на поверхности $z = 0$. Так, для определения средней температуры в избранной акватории океана $\omega $ при $z = 0$ в интервале ${{t}_{1}} - \tau \leqslant t \leqslant {{t}_{1}}$ в качестве $F{\kern 1pt} *$ выбирается функция где ${\text{mes}}{\kern 1pt} {\kern 1pt} \omega $ означает площадь района $\omega $. В этом случае функционал (3.1) представляется в виде

С использованием обозначений, введенных выше, функционал (3.1) записывается в виде скалярного произведения

В силу производные от $G$ по $T,Q$, входящие в (2.20)–(2.22), определяются по формулам

Приведем результаты численных расчетов. При реализации алгоритма усвоения данных использовалась система (1.5)–(1.7). Расчет чувствительности выбранного функционала происходил на одном шаге по времени $({{t}_{k}},{{t}_{{k + 1}}})$, где ${{t}_{{k + 1}}} = \bar {t} = {{t}_{k}} + \Delta t$. На каждом из таких шагов была рассчитана чувствительность функционала к данным бэкграунда. Были выбраны два момента времени для расчета чувствительности функционала к данным бэкграунда: 31 мая 2019 г. 10 ч 25 мин (86 655 временных шагов модели) и 1 июля 2019 г. 23 ч 30 мин (104 820 временных шагов модели). Выбор данных моментов времени обусловлен тем, что в эти моменты времени данные со спутников покрывали почти всю исследуемую акваторию Черного и Азовского морей.

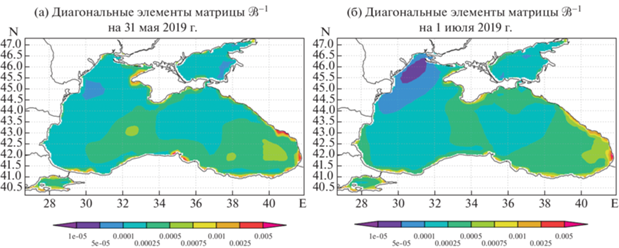
На фиг. 1 представлены значения диагональных элементов матрицы ${{\mathcal{B}}^{{ - 1}}}$ в разные моменты времени. Так, диагональные элементы, рассчитанные на 31 мая 2019 г., показаны на фиг. 1а, а 1 июля 2019 г. – на фиг. 1б.

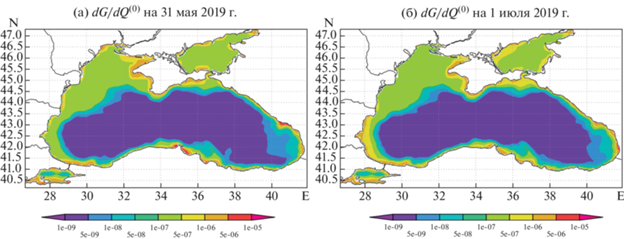
Значения диагональных элементов ${{R}^{{ - 1}}}$ на эти же даты приведены на фиг. 2. Результаты расчета чувствительности к данным бэкграунда для 31 мая и 1 июля 2019 г. представлены на фиг. 3а и 3б соответственно, где даны градиенты функции отклика в разные моменты времени.

Стоит отметить, что результаты, полученные в эксперименте в рассматриваемые моменты времени, не сильно отличаются друг от друга. Характерной особенностью является малая чувствительность функционала к данным бэкграунда в центральной, наиболее глубокой, области Черного моря. В областях с меньшей глубиной прослеживается возрастание чувствительности, которая принимает максимальные значения в некоторых точках на границе области как в Черном, так и в Азовском морях.

В целом чувствительность рассматриваемого функционала к данным бэкграунда намного меньше, чем чувствительность к данным наблюдений, исследованная в [23].

Этот результат подтверждается прямым вычислением функционала $G(T,Q)$ в соответствии с (3.3), полученным после вариационного усвоения, путем введения возмущений в данные бэкграунда ${{Q}^{{(0)}}}$, следуя работе [23].

Таким образом, сформулированный алгоритм (2.20)–(2.22) позволяет оценивать чувствительность функционалов, связанных с температурой поверхности моря после усвоения, по отношению к ошибкам данных бэкграунда.

ЗАКЛЮЧЕНИЕ

С использованием трехмерной модели гидротермодинамики Черного моря, разработанной в ИВМ РАН, в настоящей работе проведено исследование чувствительности функционалов от решения задачи вариационного усвоения данных с восстановлением потоков тепла на поверхности моря. Разработанный алгоритм позволяет вычислять градиенты функционалов от решения задачи после усвоения по отношению к входным данным о потоке тепла. Вычисление градиента функционала требует однократного решения уравнения с гессианом функции стоимости и решения сопряженной задачи. Для решения этого уравнения нет необходимости вычислять обратный гессиан в явном виде, тем не менее, было бы интересно в будущем провести аналитические оценки обратного гессиана, например, через собственные значения, и использовать их для оценки чувствительности. Численные эксперименты для модели динамики Черного моря подтверждают работоспособность предложенного алгоритма. Проведенные исследования могут быть полезны для решения проблемы определения районов моря, в которых функционалы от оптимального решения являются наиболее чувствительными к произвольным возмущениям в исходных данных бэкграунда при использовании процедуры вариационного усвоения, в том числе в случаях, когда значения этих возмущений заранее не известны.

Авторы благодарны рецензенту за полезные замечания, которые позволили улучшить представление результатов и изложение материала в статье.