Журнал вычислительной математики и математической физики, 2023, T. 63, № 8, стр. 1367-1379

ВВЕДЕНИЕ

Метод прямого статистического моделирования (ПСМ) был разработан в начале 60-х годов прошлого столетия Г. Бердом для моделирования течений разреженного газа. Впоследствии он получил дальнейшее развитие, в частности были разработаны эффективные процедуры моделирования столкновений частиц (схема No Time Counter (NTC) [1] и метод мажорантной частоты [2]). В настоящее время, несмотря на развитие альтернативных подходов (см., например, [3–6]), метод ПСМ [7], [8] сохраняет свои лидирующие позиции среди численных методов решения задач динамики разреженного газа.

В основе “классического” алгоритма метода ПСМ лежит расщепление непрерывного движения частиц и их столкновений на два последовательных этапа, определяемых временным интервалом Δt.

Этап 1. Все частицы перемещаются на расстояние, определяемое их скоростями и временем Δt. Проводятся определенные действия, если частицы пересекают граничные поверхности.

Этап 2. Моделируются столкновения между частицами, соответствующие интервалу Δt. Скорости частиц до столкновения заменяются скоростями, приобретенными ими после столкновения.

При этом обычно моделируемый объем физического пространства разбивается на ячейки и в каждой ячейке моделируется некоторое количество частиц. Изменение времени проводится дискретными шагами Δt, малыми по сравнению со средним временем между столкновениями частиц. На каждом временном шаге производится суммирование информации, необходимой для вычисления макропараметров течения газа.

Несмотря на продолжительное и активное использование метода ПСМ, работа по изучению влияния на точность вычисления макропараметров течения отдельных параметров алгоритма (шага по времени, размера ячейки, количества шагов по времени, количества частиц в ячейке, соотношения числа реальных и моделируемых частиц) ввиду очевидной сложности метода далека от завершения. Различными исследователями проделан большой объем работы по изучению погрешности алгоритма и получен ряд важных результатов (см., например, [9–18]). Развитие компьютерной техники и появление пакетов программ для расчетов методом ПСМ стимулируют интерес к разработке новых подходов к моделированию течений газа, дальнейшему анализу погрешности метода и выбору оптимальных параметров [19–22].

Для дальнейшего анализа удобно разделить погрешность метода на внутреннюю и внешнюю [23]. Внутренняя погрешность метода обусловлена тем, что непрерывный процесс движения и столкновений частиц заменяется дискретным по времени и пространству процессом, а также тем, что каждая моделируемая частица представляет собой тысячи реальных частиц. Кроме того, для ускорения расчета при реализации столкновений частиц используется вероятностный процесс выбора партнера. Поэтому внутренняя погрешность зависит от шага по времени, количества моделируемых частиц и способа реализации столкновений частиц, в частности выбора партнера для столкновения (пространственной регуляризации). Внешняя погрешность связана со сбором информации для оценки макропараметров течения. Как правило, требуется пространственное распределение макропараметров течения, поэтому в интересующей области строится сетка, в узлах которой оцениваются макропараметры, а затем производится интерполяция на всю область. Поэтому внешняя погрешность зависит от объема выборки, выбора сетки и способа восполнения.

Одной из составляющих внутренней погрешности метода ПСМ является погрешность, обусловленная регуляризацией столкновения двух частиц по пространственным переменным. В “классическом” алгоритме метода ПСМ (см., например [7]) выбор партнеров для столкновения на каждом временном шаге осуществляется среди частиц, находящихся в одной ячейке. При этом не рассматривается возможность столкновения частиц, находящихся в разных ячейках, даже если они расположены близко друг к другу. Естественно, что такая реализация алгоритма приводит к возникновению дополнительной погрешности. В [15] проведено численное исследование модификации алгоритма ПСМ, основанной на использовании ячеек различного размера для моделирования столкновений и сбора информации. В частности показано, что введение ячеек уменьшенного размера для моделирования столкновений позволяет существенно улучшить точность вычислений. В работе [24] проведен теоретический анализ погрешности метода ПСМ, обусловленной пространственной регуляризацией. В работе [19] предложен имитационный метод с расщеплением (ИМР), в котором этап столкновений разбивается на два этапа. При этом на втором этапе производится поправка на столкновения частиц, принадлежащих на первом этапе к различным группам. В [25] на примере задачи о продольном обтекании пластины показано различие в макропараметрах течения, рассчитанных “классическим” алгоритмом метода ПСМ и методом ИМР.

Представленная работа направлена на исследование влияния погрешности, обусловленной пространственной регуляризацией, на точность вычислений методом ПСМ. Рассматривается решение стационарных задач, в которых для нахождения решения суммируются данные о частицах вдоль одной траектории. Построена верхняя граница погрешности (с учетом регуляризации) метода ПСМ в метрике пространства непрерывных функций и получены условно-оптимальные параметры алгоритма, гарантирующие по вероятности заданный уровень погрешности.

1. СТАТИСТИЧЕСКИЕ ОЦЕНКИ МЕТОДА ПСМ

Макропараметры течения разреженного газа представимы в виде математического ожидания Eξ(X) некоторой функции ξ(X) от состояния N частичной системы X или в виде рациональной функции от таких математических ожиданий. Так, числовая плотность n в некоторой точке r представима в виде

где C_n – нормирующая константа, Δr – мера ячейки, h(r) – индикатор ячейки, ${{r}_{l}}$– точка пространственного расположения частицы с номером l. Отметим, что в представленной работе размерность физического пространства может принимать значения d = 1, 2, 3, а пространство скоростей частиц трехмерно. Полная температура течения в некоторой точке области складывается из трех покоординатных компонент T = (T₁ + T₂ + T₃)/3. Для скорости течения v = (${{{v}}_{1}},{{{v}}_{2}},{{{v}}_{3}}$) и температуры T используются следующие представления: Здесь (v_l)_i есть i-я компонента скорости частицы с номером l, R – газовая постоянная.

При решении стационарных задач основу метода ПСМ составляет предположение об эргодичности рассматриваемого стационарного процесса. В этом случае математические ожидания оцениваются осреднением значений функций от состояний N-частичной системы, взятых через равные интервалы времени Δt. Для определенности зафиксируем три параметра метода, определяющих непосредственно процесс моделирования: полное число частиц N, размер ячейки Δr и шаг по времени Δt. Пусть X_k обозначает состояние N-частичной системы в момент времени t_k = kΔt, k = 1, 2, …, K. Тогда осредненная по времени оценка математического ожидания, например, для вычисления числовой плотности (1.1) имеет вид

Аналогичные выражения получаются для вычисления скорости и температуры (1.2), (1.3).

2. ПРОСТРАНСТВЕННАЯ РЕГУЛЯРИЗАЦИЯ И ВНОСИМАЯ ЕЮ ПОГРЕШНОСТЬ

Пусть расчетная область $D\; \subset \;{{{\mathbf{R}}}^{d}}$ ограниченная, с кусочно-гладкой границей. Обозначим через ΔJ разность между оценками функционала от решения, полученными с использованием регуляризации и без нее. Рассмотрим два подхода к регуляризации парного взаимодействия частиц по пространственным переменным.

1. Расчетная область D разбивается на непересекающиеся ячейки, каждая из которых представляет собой выпуклое множество. Обозначим через h максимальный диаметр ячеек. Выбор партнеров для столкновения на каждом временном шаге осуществляется среди частиц, находящихся в одной ячейке. Такая регуляризация соответствует “классической” реализации метода ПСМ [7], [8].

2. Для произвольной частицы с координатами ${{r}_{1}}\; \in \;D$ партнер для столкновения выбирается среди частиц, попадающих в шар заданного радиуса h с центром в точке ${{r}_{1}}.$

В работе [24] для трехмерного случая расчетной области получены следующие оценки погрешности регуляризации:

для первого и второго подхода соответственно. Здесь C₁ и C₂ – некоторые константы.

Для случая использования расчетной области размерности d = 1 и 2 по аналогии с рассуждениями [24] можно получить следующие оценки:

Отметим, что аналитические выражения для констант C₁ и C₂, позволяющие вычислить их значения для конкретных задач, в [24] не получены, поэтому далее будем использовать оценки этих констант, вычисленные в ходе предварительных расчетов.

3. ТРИ АЛГОРИТМА МЕТОДА ПСМ

Для численного исследования влияния регуляризации на точность вычислений в представленной работе рассмотрим три алгоритма метода ПСМ на основе схемы столкновений NTC [1], [7]. Кратко сформулируем эти алгоритмы, уделяя основное внимание реализации регуляризации.

Алгоритм 1 (первый подход к регуляризации) [7].

Область разбивается на непересекающиеся ячейки. На каждом временном шаге частицы сортируются по ячейкам. Для каждой ячейки номера m вычисляется число столкновений ${{N}_{{{\text{col}},m}}}$ за временной шаг Δt; далее из числа частиц в ячейке ${{N}_{{{\text{col}},m}}}$ раз равновероятно выбираются пары партнеров для столкновения, для каждой пары с некоторой вероятностью происходит реальное столкновение, в противном случае – фиктивное.

Алгоритм 2 (второй подход к регуляризации) [26].

Для числа частиц N во всей расчетной области вычисляется число столкновений N_col за временной шаг Δt. Далее из общего числа частиц N_col раз равновероятно выбираются партнеры для столкновения. Если расстояние между выбранными частицами больше заданного h, то происходит фиктивное столкновение. Если расстояние между ними меньше заданного, то с некоторой вероятностью реализуется реальное столкновение, в противном случае – фиктивное.

Второй алгоритм был реализован на основе алгоритма 6 из [26], сформулированного для схемы столкновений на основе мажорантной частоты. Отметим, что использование ячеек для регуляризации позволяет получить более эффективные алгоритмы (см., например [26]). Проведенные нами расчеты (см. ниже разд. 5) также подтвердили этот вывод. Поэтому нами был сформулирован приближенный комбинированный алгоритм метода ПСМ для второго подхода к регуляризации.

Алгоритм 3 (второй подход к регуляризации).

Область разбивается на непересекающиеся ячейки. На каждом временном шаге частицы сортируются по ячейкам. Для каждой ячейки m вычисляется число столкновений ${{N}_{{{\text{col}},m}}}$ за временной шаг Δt; из числа частиц в ячейке равновероятно выбирается частица для столкновения и далее равновероятно выбирается партнер для столкновения из ее окрестности. Для выбранной таким образом пары с некоторой вероятностью происходит реальное столкновение, в противном случае – фиктивное. Вклад в число столкновений по ячейкам вносится согласно принадлежности выбранных для столкновения частиц ячейкам.

4. ВЕРХНИЕ ГРАНИЦЫ ПОГРЕШНОСТИ И УСЛОВНО-ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ АЛГОРИТМОВ

Для построения верхней границы погрешности и выбора оптимальных параметров метода ПСМ будем использовать теорию функциональных алгоритмов статистического моделирования [27]. Методы статистического моделирования (Монте-Карло) позволяют вычислять отдельные функционалы от решений интегральных и дифференциальных уравнений, в том числе значения решений в выбранных точках. Для построения решения уравнения на всей области необходимо сначала построить сетку, оценить решения в узлах сетки методом Монте-Карло, а затем восполнить решения по полученным приближенным значениям в узлах. Такие алгоритмы будем называть функциональными алгоритмами статистического моделирования. Особенностью таких алгоритмов является наличие детерминированных и стохастических компонент погрешности, что приводит к некоторым сложностям в исследовании сходимости и оптимизации. Важной задачей является выбор оптимальных параметров функциональных алгоритмов статистического моделирования, например, числа узлов сетки и объема выборки, позволяющих достичь заданного уровня погрешности. Здесь мы используем подход к оптимизации из [27], т.е. предполагаем, что верхняя граница погрешности достаточно точно воспроизводит зависимость погрешности от параметров. В этом случае мы приравниваем верхнюю границу к заданному уровню погрешности и минимизируем функцию трудоемкости, зависящую от параметров.

С точки зрения внешней погрешности метод ПСМ можно рассматривать и исследовать как функциональный алгоритм статистического моделирования. Пусть $u\left( r \right)$ один из макропараметров течения, который должен быть аппроксимирован на некоторой ограниченной области $D\; \subset \;{{{\mathbf{R}}}^{d}}.$ Тогда в общем виде функциональный алгоритм метода Монте-Карло строится следующим образом.

1. В области D строится сетка $\left\{ {{{r}^{{\left( i \right)}}}} \right\}_{{m = 1}}^{M}.$

2. Значения функции $u\left( r \right)$в узлах сетки оцениваются методом Монте-Карло:

3. Для приближения функции $u\left( r \right)$на области D применяется процедура интерполяции:

где ${{\chi }_{m}}\left( r \right)$ – базисные функции интерполяции. Здесь мы используем мультилинейную интерполяцию [27], т.е. ${{\chi }_{m}}\left( r \right)\; = \;\chi \left( {{r \mathord{\left/ {\vphantom {r h}} \right. \kern-0em} h}\; - \;m} \right)$ в случае d = 1, где$\chi \left( s \right)$ – кусочно-линейная финитная образующая функция: В случае d = 2, 3 базисные функции ${{\chi }_{m}}\left( r \right)$являются покоординатными произведениями соответствующих функций типа $\chi \left( s \right)$.

Для выбора оптимальных параметров функционального алгоритма, т.е. объема выборки K и числа узлов M, позволяющих достичь заданного уровня погрешности, нужно выполнить два шага.

1. Построить верхнюю границу погрешности аппроксимации (4.1). Здесь мы рассматриваем верхнюю границу погрешности в метрике пространства непрерывных функций со сходимостью по вероятности, т.е. строим отношения вида

где $T\left( {M,K} \right) \to 0\quad {\text{при}}\quad M,K \to \infty ,$ а $\varepsilon \; > \;0$ – малая величина.

2. Решить задачу оптимизации, т.е. найти условно-оптимальные значения параметров функционального алгоритма, минимизирующих функцию трудоемкости при заданном уровне погрешности:

где $S\left( {M,K} \right)$ – функция трудоемкости, $T\left( {M,K} \right)$ – верхняя граница погрешности, а $\alpha > 0$ – заданный уровень погрешности.

При решении стационарных задач методом ПСМ сбор информации на каждом временном шаге приводит к возникновению корреляции данных, собранных с близких временных шагов [28]. В работе [23] при построении верхней границы внешней погрешности метода ПСМ была показана важность использования разреженного сбора информации для уменьшения статистической погрешности оцениваемых макропараметров. Разреженный сбор информации подразумевает суммирование информации с каждого J-го шага по времени, что уменьшает корреляции и соответственно статистическую погрешность. В [23] были построены верхние границы внешней погрешности функционального алгоритма ПСМ для плотности, скорости и температуры:

Здесь первое слагаемое в правой части неравенства соответствует погрешностям интерполяции и смещения, а второе – статистической погрешности. Константы H_I, H_V и β_ξ оцениваются на основе предварительных вычислений. Константа H_I выражается через частные производные решения Константа H_V оценивается через максимум дисперсии статистической оценки ξ по формуле Константа β_ξ оценивается через максимум корреляций статистической оценки ξ по формуле где ${{{{\rho }}}_{{{{\xi }},k}}}$ – корреляции стационарного стохастического процесса ξ(X_k): Величина θ_M(ε) определяется по формуле где Ф_0,1 – стандартная нормальная функция распределения.

По аналогии с выкладками из [23] учет погрешности регуляризации приводит к формулам

для первого подхода к регуляризации и для второго подхода.

Здесь ${{M}_{R}}$ – число ячеек для моделирования столкновений частиц для первого подхода к регуляризации. Для второго подхода ${{M}_{R}}$ – целое число, определяемое диаметром окрестности h: ${{M}_{R}} = {{\operatorname{mes} D} \mathord{\left/ {\vphantom {{\operatorname{mes} D} {{{h}^{d}}}}} \right. \kern-0em} {{{h}^{d}}}}$. Для нахождения оптимальных параметров алгоритма метода ПСМ нужно решить оптимизационную задачу вида

для верхней границы погрешности из формул (4.2) и (4.3): и соответственно.

Для рассматриваемых алгоритмов функция трудоемкости имеет вид:

Здесь ${{t}_{1}}$ – время, затрачиваемое на моделирование процесса переноса частиц за один шаг Δt, $\left( {{{t}_{2}}\; + \;{{t}_{3}}M} \right)$ – время, затрачиваемое на сбор информации за один шаг выборки, ${{t}_{4}}\left( {{{M}_{R}}} \right)$ – время, затрачиваемое на моделирование процесса столкновений частиц за один шаг Δt. Предварительные расчеты показали, что величина ${{t}_{4}}$ зависит от выбранного алгоритма: для первого и второго алгоритмов она прямо пропорциональна ${{M}_{R}},$ ${{t}_{4}}\left( {{{M}_{R}}} \right) = {{t}_{5}}{{M}_{R}}$, а для третьего алгоритма – обратно пропорциональна ${{M}_{R}},$ ${{t}_{4}}\left( {{{M}_{R}}} \right) = {{{{t}_{5}}} \mathord{\left/ {\vphantom {{{{t}_{5}}} {{{M}_{R}}}}} \right. \kern-0em} {{{M}_{R}}}}.$ Для первого алгоритма рост ${{t}_{4}}$ с увеличением ${{M}_{R}}$ связан с необходимостью затрат на сортировку по ячейкам для столкновений, для второго алгоритма – с большим количеством фиктивных столкновений. Для третьего алгоритма рост ${{t}_{4}}$ с уменьшением ${{M}_{R}}$ связан с необходимостью затрат на выбор партнера для столкновения из окрестности.

Чтобы решить задачу оптимизации, мы выражаем K из условия (4.4) и подставляем его в функцию затрат (4.5). Таким образом, мы получаем следующие функции в зависимости от J, M и ${{M}_{R}}$:

для первого подхода к регуляризации и для второго подхода.

Значения M_opt, M_Ropt, K_opt, J_opt, минимизирующие функции (4.6), (4.7), можно найти численно путем перебора всех возможностей. Конечно, для каждого макропараметра течения газа эти значения могут быть разными.

5. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ ЭКСПЕРИМЕНТОВ

Тестирование разработанных подходов проводилось на примере классической задачи Фурье о теплопередаче между двумя бесконечными параллельными пластинами. Введем декартову систему координат XYZ. Пусть газ со средней числовой плотностью n₀ заключен между двумя бесконечными пластинами, расположенными в плоскостях z = 0 и z = H, температуры пластин T₀ и T_H постоянны. Предполагается, что отражение частиц от пластин является диффузным с полной аккомодацией энергии и импульса. Для моделирования межмолекулярных столкновений применяется модель твердых сфер [7]. Для приведения задачи к безразмерному виду использовались следующие величины: числовая плотность n₀, средняя длина свободного пробега L частиц в газе при плотности n₀, температура T₀ и наиболее вероятная тепловая скорость газа ${{c}_{m}}\; = \;\sqrt {{{2k{{T}_{0}}} \mathord{\left/ {\vphantom {{2k{{T}_{0}}} m}} \right. \kern-0em} m}} $ (здесь k – постоянная Больцмана, m – масса частицы). После перехода к безразмерным переменным задача определяется только отношением температур ${{{{T}_{H}}} \mathord{\left/ {\vphantom {{{{T}_{H}}} {{{T}_{0}}}}} \right. \kern-0em} {{{T}_{0}}}}$ и числом Кнудсена Kn = L/H. Требуется определить распределение макропараметров газа (плотность, скорость и температура) между пластинами при заданном отношении температур пластин ${{{{T}_{H}}} \mathord{\left/ {\vphantom {{{{T}_{H}}} {{{T}_{0}}}}} \right. \kern-0em} {{{T}_{0}}}}$и степени разреженности газа. Расчеты проводились для следующего набора параметров: Kn = 0.025; три отношения температур: ${{{{T}_{H}}} \mathord{\left/ {\vphantom {{{{T}_{H}}} {{{T}_{0}}}}} \right. \kern-0em} {{{T}_{0}}}} = 1$, ${{{{T}_{H}}} \mathord{\left/ {\vphantom {{{{T}_{H}}} {{{T}_{0}}}}} \right. \kern-0em} {{{T}_{0}}}} = 4$ и ${{{{T}_{H}}} \mathord{\left/ {\vphantom {{{{T}_{H}}} {{{T}_{0}}}}} \right. \kern-0em} {{{T}_{0}}}} = 9$; Δt = 0.05. При ${{{{T}_{H}}} \mathord{\left/ {\vphantom {{{{T}_{H}}} {{{T}_{0}}}}} \right. \kern-0em} {{{T}_{0}}}}$= 1 известно точное решение: n = 1, T_x = T_y = T_z = 1, u_x = u_y = u_z = 0.

Численные эксперименты проводились также для двумерной задачи Фурье. Для двумерного случая (d = 2) отражающие пластины были расположены в плоскостях z = 0, z = H, y = 0, y = H. Температура пластин z = H и y = H равнялась T_H, а пластин z = 0 и y = 0 – T₀. Расчеты проводились для следующего набора параметров: Kn = 0.2; ${{{{T}_{H}}} \mathord{\left/ {\vphantom {{{{T}_{H}}} {{{T}_{0}}}}} \right. \kern-0em} {{{T}_{0}}}} = 2$; Δt = 0.05; полное число частиц в расчетной области N = 32 000.

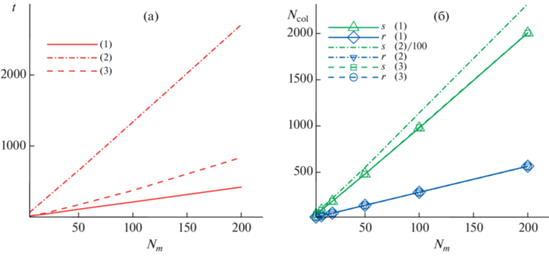
На первом этапе был выполнен ряд расчетов для тестирования рассматриваемых алгоритмов. На фиг. 1 для одномерной задачи приведены зависимости полного времени расчета, количества реальных столкновений и полного количества столкновений (суммы реальных и фиктивных) за один временной шаг от числа частиц в ячейке N_m. Моделировалась задача для ${{{{T}_{H}}} \mathord{\left/ {\vphantom {{{{T}_{H}}} {{{T}_{0}}}}} \right. \kern-0em} {{{T}_{0}}}} = 1$, число ячеек для сбора информации равнялось 100; размер ячейки для моделирования столкновений (размер окрестности) h = 0.4, полное число частиц в расчетной области $N = 100 \cdot {{N}_{m}},$число временных шагов K = 200 000. Второй алгоритм существенно проигрывает по вычислительным затратам первому из-за большого количества фиктивных столкновений, поэтому и был разработан приближенный комбинированный алгоритм 3. Отметим, что количество реальных столкновений фактически совпадает для всех трех алгоритмов, что подтверждает корректность их реализации.

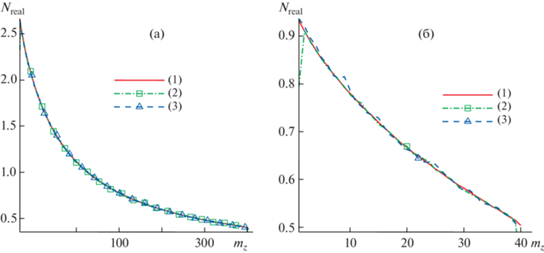
На фиг. 2а для одномерной задачи приведено пространственное распределение количества реальных столкновений за временной шаг. На фиг. 2б для двумерной задачи приведено пространственное распределение (вдоль диагонали области от самой холодной точки (y = z = 0) до самой горячей (y = z = H)) количества реальных столкновений за временной шаг. Отметим хорошее совпадение количества реальных столкновений для всех алгоритмов, за исключением области у границ для второго алгоритма. Это отклонение связано с влиянием границы (уменьшением размера области для выбора партнера для столкновения).

На втором этапе проводилось исследование погрешности, обусловленной пространственной регуляризацией. Для этого вместо неизвестного точного решения задачи использовалось численное решение, насчитанное с заведомо большей точностью. Отметим, что в настоящее время развита методика, позволяющая оценить уровень внешней погрешности (детерминированной и стохастической) [23]. Использование этой методики позволило вычислить “точное” решение с контролируемым малым уровнем внешней погрешности. В табл. 1 приведены параметры алгоритмов, использованные для расчета “точных” решений и полученные при этом уровни внешней погрешности. Здесь δ_i и δ_s – погрешность интерполяции и стохастическая погрешность соответственно. Выбранные временной шаг, размер ячейки и количество частиц в ячейке позволяют рассчитывать на минимальный уровень внутренней погрешности, вносимый этими параметрами алгоритма ПСМ. Отметим, что для каждого алгоритма было получено свое “точное” решение для минимизации возможных других погрешностей.

На фиг. 3а для одномерной задачи представлена зависимость максимума погрешности вычисления плотности n и температуры T_x от размера ячейки (окрестности) регуляризации. Под максимумом погрешности мы подразумеваем максимум модуля разности между “точным” и полученным решением в узлах (т.е. в центрах ячеек для сбора информации). Отметим, что здесь при проведении расчетов использовался тот же набор параметров процесса моделирования (число частиц N, шаг по времени Δt и размер ячейки для сбора информации), что и при вычислении “точного” решения. Это было сделано для того, чтобы исключить из анализа погрешность, обусловленную этими параметрами (см. более подробно в [23]).

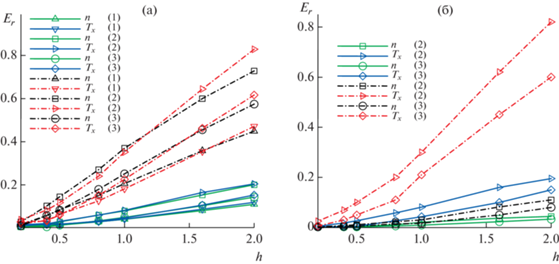
Видим, что максимум погрешности убывает с уменьшением размера ячейки (окрестности) (фиг. 3а). Причем характер убывания близок к линейному. Для первого подхода к регуляризации (алгоритм 1) это соответствует формуле (2.2). Для второго подхода к регуляризации (алгоритмы 2 и 3) ожидалось уменьшение погрешности согласно квадратичному закону в соответствии с формулой (2.3). Возможно, что такое поведение максимума погрешности для второго подхода к регуляризации в проведенных расчетах связано с влиянием граничных условий. Характер изменения погрешности в центральной области близок к квадратичному закону (фиг. 3б).

Из аналитических выкладок при построении оценок (2.1) в [24] можно сделать вывод о том, что константы C₁ и С₂ зависят от градиента решения. Увеличение отношения температур пластин приводит к росту градиента плотности и температуры. Этим можно объяснить рост величины максимума погрешности с увеличением отношения температур пластин (фиг. 3).

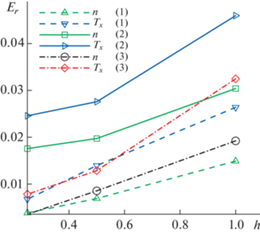
На фиг. 4 представлена зависимость максимума погрешности от размера ячейки (окрестности) регуляризации для двумерной задачи. Погрешность для всех трех алгоритмов убывает с уменьшением размера ячейки (окрестности), причем характер убывания близок к линейному. Анализ изменения погрешности в центральной точке расчетной области показал похожий характер изменения, что возможно связано с более существенным влиянием граничных условий в силу малых размеров области (Kn = 0.2).

На третьем этапе было проведено тестирование полученных в разд. 4 условно-оптимальных параметров. Исходя из близкого к линейному характера изменения погрешности регуляризации условно-оптимальные параметры определялись по формуле (4.6). Константа H_R была оценена из данных, представленных на фиг. 3а и 4. В табл. 2–4 представлены результаты расчетов числовой плотности газа с использованием условно-оптимальных параметров. Здесь M_opt и M_Ropt – количество оптимальных ячеек для сбора информации и столкновений соответственно, K_opt – оптимальное количество шагов по времени, δ_i и δ_s – погрешность интерполяции и стохастическая погрешность, δ = δ_i + δ_s – полная погрешность, t – время расчета в секундах. Сбор информации для оценки макропараметров газа осуществлялся через J_opt временных шагов.

Отметим, что в формуле (4.6) для алгоритма 3 имеем ${{t}_{4}}\left( {{{M}_{R}}} \right)\; = \;{{{{t}_{5}}} \mathord{\left/ {\vphantom {{{{t}_{5}}} {{{M}_{R}}}}} \right. \kern-0em} {{{M}_{R}}}}.$ Из этого следует, что чем больше ${{M}_{R}},$ тем меньше трудоемкость. Однако в представленном подходе к оценке погрешности не учитывается часть внутренней погрешности, обусловленная числом частиц в ячейке. Уменьшение среднего по времени числа частиц в ячейке до величины менее единицы начинает вносить вклад во внутреннюю погрешность и, соответственно, в точность расчетов [15]. Поэтому в расчетах для третьего алгоритма было использовано значение ${{M}_{R}},$ соответствующее расчету “точного” решения.

Видим, что использование условно-оптимальных параметров позволяет оценивать числовую плотность с погрешностью δ, не превышающей заданный уровень α. Также отметим, что самым эффективным с точки зрения затрат компьютерного времени для данной задачи является первый алгоритм, далее идет третий алгоритм. Второй алгоритм требует существенно большего времени.

ЗАКЛЮЧЕНИЕ

Метод ПСМ широко применяется для решения задач динамики разреженного газа. Несмотря на продолжительное и широкое использование метода ПСМ, работа по изучению влияния отдельных параметров алгоритма (шаг по времени, размер ячейки, количество шагов по времени, количество частиц в ячейке, соотношение числа реальных частиц и моделируемых частиц) на точность вычислений макропараметров течения газа ввиду очевидной сложности метода далека от завершения.

В представленной работе проведено исследование влияния погрешности, вносимой регуляризацией взаимодействия двух частиц по пространственным переменным, на точность вычислений методом ПСМ. Рассматриваются два подхода к регуляризации: столкновение частиц, находящихся в одной ячейке, и выбор второго партнера для столкновения из окрестности первой частицы. Для численного исследования реализованы три алгоритма метода ПСМ, использующих эти регуляризации. Проведено численное исследование влияния погрешности, вносимой пространственной регуляризацией, на результаты расчетов на примере классической задачи Фурье (одномерной и двумерной).

Построена верхняя граница погрешности метода ПСМ, учитывающая погрешность регуляризации, в метрике пространства непрерывных функций. Получены условно-оптимальные параметры алгоритма, гарантирующие по вероятности уровень заданной погрешности. Проведено тестирование полученных условно-оптимальных параметров на примере задачи Фурье.