Химия высоких энергий, 2019, T. 53, № 5, стр. 339-348
Кинетика радикально-цепной полимеризации. II. Линейные волны роста макрорадикалов
И. П. Ким a, В. А. Бендерский a, *
a Институт проблем химической физики РАН
142432 Черноголовка, Россия
* E-mail: bender@icp.ac.ru
Поступила в редакцию 23.04.2019
После доработки 29.04.2019
Принята к публикации 08.05.2019
Аннотация
Рост цепи радикально-цепной полимеризации сопоставлен с волной превращения первичных радикалов в макрорадикалы. Изменение длины цепи $n$ и молекулярно-массового распределения $R(t,n)$ со временем $t$ соответствует движению волнового пакета с зависящими от концентрации мономера $M(t)$ скоростью ${{dn} \mathord{\left/ {\vphantom {{dn} {dt}}} \right. \kern-0em} {dt}}$ и шириной $\Delta (n).$ Рассмотрено образование макрорадикалов в отсутствие передачи цепи, когда константы скорости роста цепи $K(n)$ зависят от n, и показано, что пакет описывается распределением Пуассона с зависящей от $K(n)$ и $t$ вероятностью события. При уменьшении $K(n)$ $R(t,n)$ сужается, а его максимум смещается в область минимума $K(n).$ Найдены соотношения между $K(n),$ $M(t),$ $R(t,n)$ и ${{dn} \mathord{\left/ {\vphantom {{dn} {dt,}}} \right. \kern-0em} {dt,}}$ $\Delta (n).$
I. ВВЕДЕНИЕ
Кинетические уравнения радикально-цепной полимеризации (УРП) аналогичны подробно изученным уравнениям Смолуховского (УС) и Беккера–Деринга (УБД), описывающим агрегацию и фрагментацию разнообразных наноразмерных объектов [1–10]. Универсальность этих уравнений обусловлена возможностью их применения в кинетике фазовых переходов (в том числе золь–гель переходов в коллоидных растворах) и образования анизотропных фрактальных структур на начальных стадиях разрушения твердых тел, образования неоднородных поверхностей, пористых материалов и полимеров. Широкие возможности УС и УБД в описании явлений, сопутствующих агрегации и фрагментации, позволяют предположить, что изучение УРП также способно выявить малоизученные особенности радикально-цепной полимеризации, сопровождающейся образованием наноразмерных мицелл и их дальнейшего превращения в коллоидные частицы микронного размера и гели.
Отличие УРП от УС и УБД состоит в том, что они описывают кинетику двух связанных подсистем (радикалов–макрорадикалов и мономеров–олигомеров), изменяющихся в различных масштабах времени и концентраций [11]. Наличие двух подсистем приводит к кинетическим особенностям, которые остаются вне области рассмотрения УС и УБД.
Возродившийся интерес к кинетике радикальной полимеризации [12–16] обусловлен возможностями изменять состав и надмолекулярную структуру образующихся олигомеров, изменяя условия полимеризации. Получение олигомеров с управляемым ММР и специальной архитектурой основано на зависимости этих характеристик от входящих в УРП параметров: концентрации первичных радикалов и переносчиков цепи, констант скорости роста и передачи цепи, зависящих, в свою очередь, от условий инициирования, а также свойств и состава среды, в которой происходит превращение мономеров и которые изменяются в процессе полимеризации. Эти зависимости еще теоретически и экспериментально мало изучены. Периодическое изменение концентрации первичных радикалов (скорости инициирования), как способ управления ММР, предложено в [12]. Изменение константы скорости роста цепи, как реакции, ограниченной диффузией мономеров к малоподвижным макрорадикалам, достигается изменением вязкости среды [14–16]. Резкое изменение вязкости происходит в области золь–гель переходов [17–19] и в условиях эмульсионной полимеризации [20–23], так что скорость полимеризации и фазовый переход взаимно связаны.
Дополнительные возможности для образования надмолекулярных структур с управляемой неоднородностью открывает полимеризация с участием нескольких первичных радикалов, способных участвовать в реакциях переноса [24–27]. Сочетание указанных факторов позволяет, в принципе, подобрать требуемые зависимости скоростей полимеризации от монотонных до экстремальных. Чтобы экспериментально использовать эти возможности, необходимо теоретически установить как характеристики образующихся продуктов зависят от перечисленных параметров, входящих в константы скорости, что, в свою очередь, означает необходимость кинетической теории, в которой обе подсистемы рассматриваются вне рамок обычно используемого квазистационарного приближения [4]. Этой малоизученной проблеме посвящена настоящая серия работ, начиная с [11]. В [11] показано, что начальный баллистический рост цепи за счет начальной концентрации первичных радикалов переходит в диффузионный, в котором участвуют первичные радикалы следующих поколений, регенерируемые в результате передачи цепи. Баллистический рост является близким аналогом волн превращения в автокаталитических системах [28–30], для которых характерны эффекты самоорганизации. Можно предположить существование еще не установленной связи между самоорганизующейся и управляемой полимеризацией.
В этой статье рост макрорадикалов в отсутствие передачи цепи, когда константа скорости роста произвольно зависит от ее длины, представлен как волновой процесс. Подобное описание самоорганизующихся процессов [23–25] показывает, что волновые представления существенно обогащают понимание сложных автокаталитических реакций, к которым следует отнести и управляемую радикальную полимеризацию. Во втором разделе статьи дано решение УРП, когда константы скорости макрорадикалов постоянны, найдены связь УРП с волновым уравнением и зависящие от времени ММР и характеристики волны роста макрорадикалов. В третьем разделе решение обобщено на случай констант скорости роста, зависящих от длины цепи, и показано, что ММР определяется областями медленного движения волнового пакета в окрестности минимумов константы скорости. Изменяя положение и ширину областей с минимальными константами скорости, можно изменять среднюю длину цепи и ширину ММР. В четвертом разделе рассмотрен рост цепи, когда константы скорости экспоненциально уменьшаются или растут с ростом ее длины. Пятый раздел посвящен обсуждению результатов и выводам.
II. РОСТ ЦЕПИ С ПОСТОЯННОЙ КОНСТАНТОЙ СКОРОСТИ
УРП включают уравнение для концентрации мономеров $M$
(1)
$\dot {M} = - {{K}_{0}}MR - \sum\limits_{n = 1}^N {{{K}_{n}}{{R}_{n}}M,\,\,\,M(0) = {{M}_{0}},} $в котором точкой сверху обозначена производная по времени в безразмерных единицах, относящихся к минимальной константе скорости роста цепи ${1 \mathord{\left/ {\vphantom {1 {\min ({{k}_{g}}),}}} \right. \kern-0em} {\min ({{k}_{g}}),}}$ ${{K}_{0}}$ и ${{K}_{n}}$ – безразмерные константы скорости роста и передачи цепи, в тех же единицах $\min ({{k}_{g}}),$ обусловленные присоединением мономера к растущим макрорадикалам ${{R}_{n}}$ с длиной цепи $n$ и взаимодействием макрорадикала с переносчиком цепи с константой скорости ${{k}_{n}},$ регенерирующим первичный радикал [11], $N$-максимальная длина цепи, определяемая не рассматриваемыми процессами обрыва цепи. Уравнения для концентраций первичных радикалов и макрорадикалов имеют вид
(2)
$\begin{gathered} \dot {R} = - {{K}_{0}}MR + \sum\limits_{n = 1}^N {{{k}_{n}}{{R}_{n}}} , \\ {{{\dot {R}}}_{n}} = {{K}_{{n - 1}}}{{R}_{{n - 1}}}M - ({{K}_{n}}M + {{k}_{n}}){{R}_{n}}, \\ R(0) = a,\,\,\,\,{{R}_{n}}(0) = 0. \\ \end{gathered} $В этом разделе мы рассмотрим решение (1) и (2) в отсутствие передачи цепи и одинаковых константах роста всех макрорадикалов
(3)
$\begin{gathered} {{K}_{0}} = {{K}_{1}} = ... = {{K}_{{N - 1}}} = 1, \\ {{k}_{1}} = {{k}_{2}} = ... = {{k}_{N}} = 0. \\ \end{gathered} $Как показано в [11], из условия сохранения полного числа радикалов следует, что расход мономера описывается соотношением
(4)
${{M(t)} \mathord{\left/ {\vphantom {{M(t)} {{{M}_{0}}}}} \right. \kern-0em} {{{M}_{0}}}} = \exp ( - at).$Если зависимость $M(t)$ известна, система уравнений (2) становится линейной, и концентрации первичных радикалов и макрорадикалов можно найти, последовательно решая эти уравнения
(5)
$\begin{gathered} R = \exp ( - F(t)), \\ {{R}_{n}}(t) = \exp ( - F(t))\frac{{{{{\left( {F(t)} \right)}}^{n}}}}{{n!}}, \\ \end{gathered} $где
является характеристической функцией всех УРП (2). Отметим, что (6) справедливо для произвольной зависимости $M(t),$ а (5) является распределением Пуассона, в котором вместо вероятности события (роста цепи на одно звено) за время $t$ входит интеграл $F(t),$ связанный с концентрацией мономера, уменьшающейся в процессе роста. В максимуме концентрации
(7)
${{R}_{n}}\left( {t_{n}^{*}} \right) = a{{e}^{{ - n}}}{{{{n}^{n}}} \mathord{\left/ {\vphantom {{{{n}^{n}}} {n!,}}} \right. \kern-0em} {n!,}}\,\,\,\,F\left( {t_{n}^{*}} \right) = n.$Из (5) следует, что при известной функции $M(t)$ и условии (3) зависящее от времени ММР полностью определено. При достаточно больших $n$ и дополнительном условии $an < 1$ распределение (5) можно преобразовать в гауссиан
где
(9)
$\begin{gathered} {{n}_{0}}(t) = F(t) + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2},\,\,\,\,\beta = \frac{1}{{2{{n}_{0}}}}(1 - \frac{1}{{2{{n}_{0}}}}), \\ A = {{\left( {2\pi {{n}_{0}}} \right)}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}{{\left( {{F \mathord{\left/ {\vphantom {F {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}}} \right)}^{{{{n}_{0}}}}}. \\ \end{gathered} $Коэффициенты в (8) находятся из условия равенства производных первого и второго порядка этим производным в (7) при замене факториала по формуле Стирлинга. Как показывают численные расчеты, точность преобразования (7) в (8) при ${{0.95} \mathord{\left/ {\vphantom {{0.95} a}} \right. \kern-0em} a} > n > 50$ лучше 3%.
Согласно (6)–(9), последовательность превращений ${{R}_{n}} \to {{R}_{{n + 1}}}$ соответствует движению гауссова волнового пакета по оси $n$ с зависящими от $t$ скоростью и шириной ${1 \mathord{\left/ {\vphantom {1 {\sqrt {\beta (t)} }}} \right. \kern-0em} {\sqrt {\beta (t)} }}.$ Групповая скорость гауссова пакета (интервал времени, в котором длина цепи увеличивается на одно звено (от $n$ до $(n + 1)$)) соответствует скорости смещения его максимума и, согласно (6) и (8), определяется расходом мономера
(10)
${{d{{n}_{0}}} \mathord{\left/ {\vphantom {{d{{n}_{0}}} {dt}}} \right. \kern-0em} {dt}} = {{dF} \mathord{\left/ {\vphantom {{dF} {dt}}} \right. \kern-0em} {dt}} = m(t),\,\,\,\,m(t) = {{M(t)} \mathord{\left/ {\vphantom {{M(t)} {{{M}_{0}}}}} \right. \kern-0em} {{{M}_{0}}}}.$Из (4) следует, что степень превращения и положение максимума связаны законом сохранения полного числа мономеров: расход свободных мономеров равен их количеству в составе макрорадикалов
Для перехода от УРП (системы обыкновенных дифференциальных уравнений) к волновому уравнению в частных производных совокупность $\left\{ {{{R}_{n}}(t)} \right\}$ следует заменить непрерывной функцией двух переменных $R(n,t)$ и заменить конечные разности ${{d}_{n}} = {{R}_{n}} - {{R}_{{n + 1}}},$ входящие в (2), производными по $n.$ Это преобразование означает, что при сохранении только производные первого порядка, УРП преобразуются в однородное волновое уравнение
в котором скорость смещения вершины гауссова пакета (9) является характеристикой уравнения (12), так что ${{n}_{0}}(t)$ – траектория движения. Гауссова ширина пакета также зависит от $F(t)$ и определяется степенью превращения. В системе координат, движущейся со скоростью (10), уширение пакета описывается уравнением диффузии из гауссова источника. Рост цепи соответствует потоку мономеров ${{J}_{n}}$ при сохранении суммарной концентрации радикалов
(13)
${{J}_{n}} = {{K}_{n}}{{R}_{n}}M,\,\,\,{{K}_{0}}R + \sum\limits_{n = 1}^\infty {{{K}_{n}}{{R}_{n}} = a} .$Из (13) следует условие
(14)
${{K}_{n}}\int\limits_0^\infty {{{R}_{n}}(t)M(t)dt = {{K}_{n}}\int\limits_0^\infty {{{R}_{n}}(F)dF = a} } ,$которое при всех ${{K}_{n}} = 1$ сводится к нормировке полного числа событий. (14) показывает, что средняя концентрация радикала ${{R}_{n}}\sim {1 \mathord{\left/ {\vphantom {1 {{{K}_{n}}}}} \right. \kern-0em} {{{K}_{n}}}},$ т.е. в волне роста наибольшей концентрацией обладают макрорадикалы с наименьшими константами роста цепи.
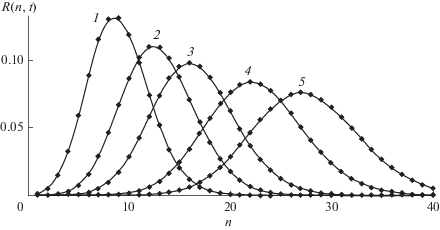
Найденное решение иллюстрируют рис. 1 и 2. На первом из них приведены зависимости от времени концентраций макрорадикалов ${{R}_{n}}(t)$ с растущей длиной цепи, показывающие, что рост $n$ вызывает уширение, вызванное расходом мономера. На рис. 2 показано зависящее от времени ММР, которое характеризует смещение и уширение волнового пакета со временем.
Рис. 1.
Зависящие от времени концентрации макрорадикалов с растущей длиной цепи ${{R}_{n}}(t),$ n = 3, 5, 8, 12, 17, 23 (кривые 1–6 соответственно). Константы скорости роста цепи постоянны, все ${{K}_{n}} = 1,$ $a$ = 0.02.
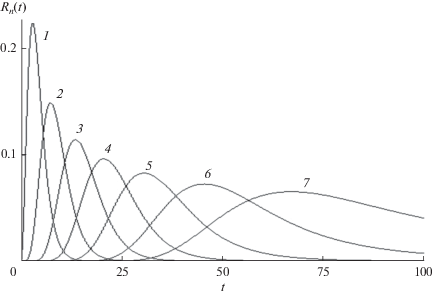
Рис. 2.
Зависящее от времени молекулярно-массовое распределение макрорадикалов $R(n,t)$ в фиксированные моменты времени t = 10, 15, 20, 30, 40 (кривые 1–5 соответственно). ${{K}_{n}} = 1,$ $a = 0.02.$
Когда $at \gg 1,$ $F(t)\sim {1 \mathord{\left/ {\vphantom {1 a}} \right. \kern-0em} a} \gg 1,$ рост цепи замедляется, а ее длина достигает максимального значения, определяемого отношением начальных концентраций мономера и первичного радикала: $n \to N = {1 \mathord{\left/ {\vphantom {1 a}} \right. \kern-0em} a}.$ В пределе все первичные радикалы превращаются в макрорадикалы с максимальной длиной цепи, ${{R}_{N}}\left( \infty \right) \approx a.$ Скорость роста цепи, следующая из закона сохранения (10), равна
Для гауссова пакета (8) групповая скорость и ширина определяются отношениями зависящих от времени моментов распределения макрорадикалов
(16)
$\begin{gathered} \bar {n}(t) = {{S}_{1}}(t){\text{/}}{{S}_{0}}(t), \\ \Delta (t) = \sqrt {{{S}_{2}}(t){\text{/}}{{S}_{0}}(t)} ,\,\,\,\,{{S}_{p}}(t) = \sum\limits_{n = 1}^\infty {{{n}^{p}}{{R}_{n}}(t)} , \\ \end{gathered} $причем смещение усредненного по ММР значения и максимума распределения $R\left( {n,t} \right)$ для гауссиана совпадают: $\bar {n}(t) = {{n}_{0}}(t).$ Соотношения (12)–(16) с единственным параметром $a$ устанавливают связь между зависящей от времени степенью превращения и характеристикой волны роста. Отметим, что эти соотношения следуют из законов сохранения и справедливы при произвольной зависимости $m(t)$ и моментах распределения (16).
В заключение этого раздела перечислим зависимости характеристик волны роста от кинетических характеристик полимеризации. Из (1), (2) и (16) следует, что скорость волны равна
где длина цепи связана со степенью превращения мономера условием сохранения массы (10). Основной параметр волны роста $F(t),$ определенный в (5), связан с моментами ММРГауссов волновой пакет с зависящими от времени смещением максимума и шириной является решением уравнения диффузии в однородном силовом поле. Для волны роста цепи коэффициент диффузии определяет уширение пакета и, согласно (9), пропорционален $F(t).$
III. РОСТ ЦЕПИ С КОНСТАНТАМИ СКОРОСТИ, ЗАВИСЯЩИМИ ОТ ЕЕ ДЛИНЫ
Метод решения УРП, рассмотренный в предыдущем разделе, обобщим на случай констант скорости роста $K(n),$ зависящих от длины цепи. Функцию $K(n)$ общего вида характеризует совокупность значений ${{K}_{n}}$ при целочисленных значениях $n$ и минимальном значении $\min ({{K}_{n}}) = 1,$ в соответствие с выбранной единицей измерения $t.$ Модуль разности соседних значений ${{K}_{n}}$ представим в виде
Если функция $M(t)$ задана (например, найдена экспериментально), концентрация первичных радикалов равна
где характеристическая функция $F(t)$ связана с $M(t)$ тем же соотношением (6). Концентрация радикала ${{R}_{1}}(t)$ имеет вид(21)
${{R}_{1}}(t) = a{{K}_{0}}\exp ( - {{K}_{1}}F(t))\frac{{1 - \exp ( - {{x}_{0}}F(t))}}{{{{x}_{0}}}}.$Отличие (21) от рассмотренного в предыдущем разделе случая одинаковых констант (все ${{K}_{n}} = 1$) состоит в том, что ${{R}_{1}}$ зависит не только от $F(t),$ но и от констант ${{K}_{{0`}}}$ и ${{K}_{1}}.$ Концентрации радикалов ${{R}_{2}}(t)$ и ${{R}_{3}}(t)$ равны
(22)
$\begin{array}{*{20}{c}} \begin{gathered} {{R}_{2}}(t) = a{{K}_{0}}\exp ( - {{K}_{2}}F) \times \\ \times \,\,\left( {\frac{{1 - \exp ( - {{x}_{1}}F)}}{{{{x}_{0}}{{x}_{1}}}} - \frac{{1 - \exp ( - ({{x}_{0}} + {{x}_{1}})F)}}{{{{x}_{0}}({{x}_{0}} + {{x}_{1}})}}} \right) \\ \end{gathered} \\ \begin{gathered} {{R}_{3}}(t) = a{{K}_{0}}\exp ( - {{K}_{3}}F) \times \\ \times \,\,\left( {\frac{{1 - \exp ( - {{x}_{2}}F)}}{{({{x}_{0}} + {{x}_{1}}){{x}_{1}}{{x}_{2}}}} - \frac{{1 - \exp ( - ({{x}_{1}} + {{x}_{2}})F)}}{{{{x}_{0}}{{x}_{1}}({{x}_{1}} + {{x}_{2}})}}} \right. + \\ + \left. {\frac{{1 - \exp ( - ({{x}_{0}} + {{x}_{1}} + {{x}_{2}})F)}}{{{{x}_{0}}({{x}_{0}} + {{x}_{1}})({{x}_{0}} + {{x}_{1}} + {{x}_{2}})}}} \right). \\ \end{gathered} \end{array}$Выражения (21) и (22) легко обобщить для произвольных значений $n$ ${{R}_{n}}(t)$
(23)
$\begin{gathered} {{R}_{n}}(t) = a{{K}_{0}}\exp ( - {{K}_{n}}F(t))U\left( {F(t),{{X}_{n}}} \right), \\ {{X}_{n}} = {{X}_{n}}({{x}_{0}},{{x}_{1}},....,{{x}_{n}}) \\ \end{gathered} $и представить ${{R}_{n}}(t)$ в виде
(24)
${{{{R}_{n}}(t)} \mathord{\left/ {\vphantom {{{{R}_{n}}(t)} {a{{K}_{0}}}}} \right. \kern-0em} {a{{K}_{0}}}} \approx \left\{ {\begin{array}{*{20}{c}} {\exp ( - {{K}_{n}}F){{{{F}^{n}}} \mathord{\left/ {\vphantom {{{{F}^{n}}} {n!,\,\,(\min {{x}_{n}})F < 1}}} \right. \kern-0em} {n!,\,\,(\min {{x}_{n}})F < 1}}} \\ {\exp ( - {{K}_{n}}F)x_{{n - 1}}^{{ - 1}}{{{({{x}_{{n - 1}}} + {{x}_{{n - 2}}})}}^{{ - 1}}}...{{{({{x}_{{n - 1}}} + ... + {{x}_{0}})}}^{{ - 1}}},\,\,({{x}_{{n - 1}}} + ... + {{x}_{0}})F > 1} \end{array}} \right..$Выражения (24) отличается от (5) тем, что начальный рост ${{R}_{n}}(t)$ описывается распределением Пуассона, в котором вероятность события определяет не $F(t),$ а ${{K}_{n}}F(t),$ но число событий по-прежнему не зависит от ${{K}_{n}}.$ Спад ${{R}_{n}}(t)$ при $\left| {{{K}_{0}} - {{K}_{n}}} \right|F \gg 1$ определяет экспоненциальный сомножитель
(25)
${{R}_{1}} \approx \left\{ {\begin{array}{*{20}{c}} {a{{K}_{0}}F(t)\exp ( - {{K}_{0}}F(t))\left( {1 - {{\gamma }_{0}}{{K}_{0}}{{F(t)} \mathord{\left/ {\vphantom {{F(t)} 2}} \right. \kern-0em} 2}} \right),\,\,{{\gamma }_{0}}{{K}_{0}}F(t) < 1} \\ {a\gamma _{0}^{{ - 1}}\exp ( - {{K}_{0}}F(t))\left( {1 - {1 \mathord{\left/ {\vphantom {1 {{{\gamma }_{0}}}}} \right. \kern-0em} {{{\gamma }_{0}}}}{{K}_{0}}F(t)} \right),\,\,{{\gamma }_{0}}{{K}_{0}}F(t) > 1} \end{array}} \right..$Согласно (25), при ${{K}_{n}} \gg 1$ переход ${{R}_{n}} \to {{R}_{{n + 1}}}$ происходит с более высокой вероятностью $\sim {{K}_{n}}a,$ но в течение более короткого времени $\Delta t\sim {1 \mathord{\left/ {\vphantom {1 {a{{x}_{n}}{{K}_{n}}}}} \right. \kern-0em} {a{{x}_{n}}{{K}_{n}}}}.$ Чем больше значение константы скорости, тем меньше $\max ({{R}_{n}}).$ Наибольшие значения ${{R}_{n}}$ соответствуют минимумам $K(n).$ Это поведение ${{R}_{n}}$ непосредственно следует из условия сохранения потока (13). При немонотонной зависимости $K(n)$ совокупность переходов разделяется на две группы – быстрых и медленных переходов, расположенные в окрестности максимумов и минимумов $K(n).$ Из (17) следует, что, помимо характеристической функции (6) свойства ${{R}_{n}}(t)$ в бегущей волне, когда $F \gg n \gg 1$ и концентрации радикалов экспоненциально малы вне этого интервала, определяет интеграл движения в подсистеме макрорадикалов, равный
Чтобы найти волновое уравнение, необходимо заменить дискретный набор значений констант функцией непрерывной переменной, что осуществляет преобразование сдвига, имеющее вид [31]
С помощью (27) УРП (2) преобразуются в уравнение в частных производных для $R(n,t),$ как непрерывной функции двух переменных $(n,t)$
(28)
$\frac{{\partial R}}{{\partial t}} + \left( {1 - \exp \left( { - \frac{\partial }{{\partial n}}} \right)} \right)M(t)K(n)R(n,t) = 0.$Для медленно изменяющихся констант, удовлетворяющих условию
оператор в (27) можно разложить в степенной ряд. Сохраняя только производные первого и второго порядка, получаем уравнение
(30)
$\begin{gathered} \frac{{\partial R}}{{\partial t}} + M(t)Q(n)\frac{{\partial R}}{{\partial n}} = \\ = \frac{1}{2}M(t)K(n)\frac{{{{\partial }^{2}}R}}{{\partial {{n}^{2}}}} - M(t)\frac{{dQ}}{{dn}}R(n,t) \\ Q(n) = K(n) - \frac{1}{2}\frac{{dK}}{{dn}}. \\ \end{gathered} $Как указано в предыдущем разделе, (30) является зависящим от времени уравнением диффузии во внешнем поле, в котором коэффициент диффузии, равный $M(t)K(n){\text{/}}2,$ и подвижность $M(t)Q(n)$ зависят от $(n,t).$ Диффузионный член мал по сравнению с дрейфовым, если справедливо (29), что позволяет заменить (30) квазилинейным уравнением первого порядка, характеристика которого имеет вид
Уравнение (31) определяет траекторию $\bar {n}(t)$ при произвольной зависимости $K(n).$ Из условий сохранения массы мономера и числа радикалов следует, что траектория совпадает с зависящей от времени средне-массовой длиной цепи, равной отношению первого и нулевого моментов (16)
(32)
$\bar {n}(t) = {{{{S}_{1}}(t)} \mathord{\left/ {\vphantom {{{{S}_{1}}(t)} {{{S}_{0}}(t)}}} \right. \kern-0em} {{{S}_{0}}(t)}}.$Подчеркнем, что (31) и (32), связывающие скорость волны роста цепи с макроскопическими характеристиками УРП, справедливы при произвольных $K(n).$ Формулы (6) и (30) позволяют переписать уравнение траектории в виде зависимости длины цепи от характеристической функции (6) и распределения констант в волновом уравнении (30)
IV. ВОЛНЫ С МОНОТОННО ИЗМЕНЯЮЩИМИСЯ КОНСТАНТАМИ СКОРОСТИ РОСТА
Формулы (32) и (33) являются точными, только если волновой пакет – гауссиан. Для произвольной зависимости K(n) они являются приближенными: (32) не учитывает изменение формы пакета, влияющую на отношение моментов, а (33) – вклад производных порядка выше первого, вклад которых в решения УРП следует из (22)–(24). По этой причине необходимо проверить точность (32) и (33) численными расчетами.
В численных расчетах, выполненных в кодах MATLAB R2018 по программе ODE 113, рассмотрены две модельных зависимости $K(n)$ – падающая
и растущая
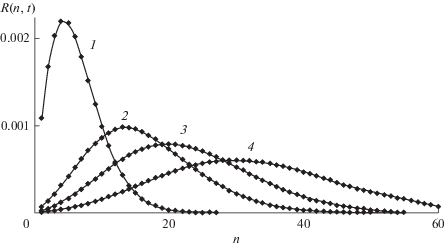
По сравнению с программой, примененной в [11], изменено граничное условие при $n = N.$ Вместо полного отражения (${{K}_{N}} = 0$), поток в бегущей волне из конечного состояния принят равным $ - {{K}_{N}}M(t){{R}_{N}}(t),$ что соответствует отсутствию отражения. Результаты представлены на рис. 3–6. Когда константа скорости уменьшается, $K(n) = {{K}^{ - }}(n)$ и ${{K}_{0}} \gg 1,$ начальный быстрый рост коротких цепей замедляется по мере увеличения их длины не только из-за расхода мономера, но и уменьшения ${{K}^{ - }}(n).$ Уменьшение скорости волны характеризует резкое увеличение с ростом $n$ времен $t = t*,$ при которых ${{R}_{n}}(t*)$ максимальны (верхняя панель рис. 3). В отличие от ${{R}_{n}}(t*)$ при ${{K}_{n}} = 1$ (рис. 1), значения ${{R}_{n}}(t*)$ почти не зависят от n, а число мономеров в их составе $n{{R}_{n}}(t*)$более резко увеличивается (нижняя панель). Зависящие от времени ММР (рис. 4) становятся заметно более узкими, чем на рис. 2. Когда ${{K}_{n}} = {{K}^{ + }}(n),$ скорость волны возрастает с ростом n, что резко уменьшает ${{R}_{n}}(t*)$ (верхняя панель рис. 5). Поскольку длинные радикалы растут быстрее коротких, даже $n{{R}_{n}}(t*)$ изменяется на порядок медленнее, чем длина цепи (нижняя панель). Движение волнового пакета преимущественно сводится к его уширению: передний фронт движется быстрее, чем хвост. Скорость смещения пакета как целого становится меньше, чем его уширение. По терминологии [23], волна роста цепи, которую при уменьшающейся константе роста следует назвать волной возбуждения, в которой все радикалы увеличивают свою длину с приблизительно одинаковой скоростью, при растущей константе скорости рост скорее становится волной превращения, в которой преимущественно растут длинные радикалы на переднем фронте, а рост коротких радикалов за фронтом замедляется (рис. 6). Таким образом, при $K(n) = {{K}^{ - }}(n)$ подавляется уширение волнового пакета и увеличивается его групповая скорость, а при ${{K}_{n}} = {{K}^{ + }}(n),$ напротив, скорость пакета уменьшается, а его уширение возрастает.
Рис. 3.
Зависящие от времени концентрации макрорадикалов, когда константы скорости экспоненциально уменьшаются с ростом длины цепи по соотношению (34), где ${{K}_{0}}$ = 100, $\gamma $ = 0.14. Верхняя панель: ${{R}_{n}}(t),$ n = 4, 8.
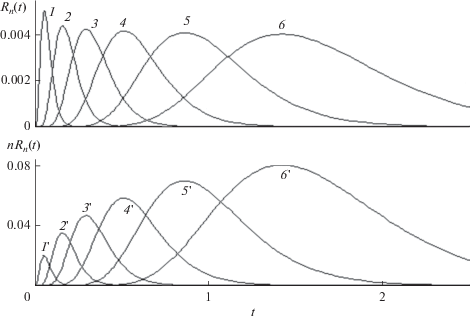
Рис. 4.
Зависящее от времени молекулярно-массовое распределение макрорадикалов $R(n,t)$ в фиксированные моменты времени t = 10, 15, 20, 30, 40 (кривые 1–5 соответственно), когда константы скорости экспоненциально уменьшаются с ростом длины цепи по соотношению (34), где ${{K}_{0}}$ = 100, $\gamma $ = 0.14. ${{R}_{n}}(t),$ $t$ = 0.05, 0.3, 1, 5, 20 (кривые 1–5 соответственно). $a$ = 0.02.
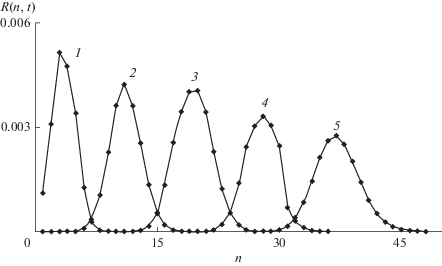
Рис. 5.
Концентрации макрорадикалов при экспоненциально растущей константе скорости роста цепи (35). ${{K}_{0}}$ = 10, $\gamma $ = 0.03. Верхняя панель: ${{R}_{n}}(t),$ $n$ = 1, 3, 5, 8, 15, 25, 35, 45 (кривые 1–8 соответственно). Нижняя панель: $n{{R}_{n}}(t)$ при тех же значениях $n$ (кривые 1'–8').
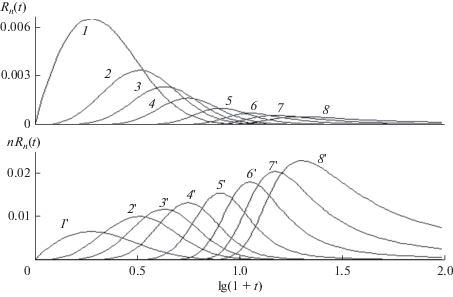
Рис. 6.
Зависящее от времени молекулярно-массовое распределение макрорадикалов $R(n,t)$ в фиксированные моменты времени $t$ = 10, 15, 20, 30, 40 (кривые 1–5 соответственно), когда константы скорости экспоненциально растут с ростом длины цепи по соотношению (35), где ${{K}_{0}}$ = 10, $\gamma $ = 0.03. ${{R}_{n}}(t),$ $t$ = 4, 8, 10, 14 (кривые 1–4 соответственно). $a$ = 0.02.
Это качественное описание изменений кинетики баллистического роста цепи количественно характеризует изменение траектории (31)–(33). Интегрируя (33), находим траектории роста цепи при падающих и растущих константах скорости (34) и (35).
(36)
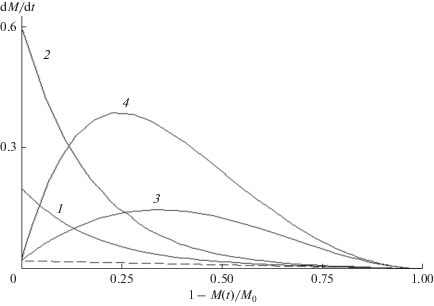
$F(t) = \left\{ {\begin{array}{*{20}{c}} {\bar {n} + {{\gamma }^{{ - 1}}}\ln \frac{{1 + p\exp ( - \gamma \bar {n})}}{{1 + p}},\,\,p = ({{K}_{0}} - 1)(1 + \gamma {\text{/}}2),\,\,{{K}_{n}} = {{K}^{ - }}(n)} \\ {K_{0}^{{ - 1}}\left( {\bar {n} + {{\gamma }^{{ - 1}}}\ln \frac{{1 - q\exp ( - \gamma \bar {n})}}{{1 - q}}} \right),\,\,q = (1 - {1 \mathord{\left/ {\vphantom {1 {{{K}_{0}}}}} \right. \kern-0em} {{{K}_{0}}}})(1 + \gamma {\text{/}}2),\,\,{{K}_{n}} = {{K}^{ + }}(n)} \end{array}} \right..$Траектории (36) связаны законами сохранения с зависимостью скорости расхода мономера $dM{\text{/}}dt$ от степени превращения мономера $(1 - {{M(t)} \mathord{\left/ {\vphantom {{M(t)} {{{M}_{0}}}}} \right. \kern-0em} {{{M}_{0}}}}),$ показанной на рис. 7 при различных значениях параметров ${{K}_{0}}$ и γ. При уменьшающейся константе скорости (34) ${{dM} \mathord{\left/ {\vphantom {{dM} {dt}}} \right. \kern-0em} {dt}}$ монотонно уменьшается от начального значения ${{\left( {{{dM} \mathord{\left/ {\vphantom {{dM} {dt}}} \right. \kern-0em} {dt}}} \right)}_{{t = 0}}} = {{K}_{0}}aM$ до зависимости при ${{K}_{n}}$ = 1, показанной пунктиром. При растущей константе скорости ${{dM} \mathord{\left/ {\vphantom {{dM} {dt}}} \right. \kern-0em} {dt}}$ сначала возрастает, а затем падает из-за расхода мономера. Значения $\bar {n}(t),$ найденные из (11), (32) и (36) и $d\bar {n}{\text{/}}dt$ из (15), (31) и (33), вполне удовлетворительно совпадают, что свидетельствует о том, что волновое представление процесса радикально-цепной полимеризации справедливо в широкой области констант скорости роста цепи.
Рис. 7.
Скорость расхода мономера ${{dM} \mathord{\left/ {\vphantom {{dM} {dt}}} \right. \kern-0em} {dt}}$ в зависимости от степени превращения ($1 - {{M(t)} \mathord{\left/ {\vphantom {{M(t)} {{{M}_{0}}}}} \right. \kern-0em} {{{M}_{0}}}}$) при зависящих от длины цепи константах скорости роста цепи (34) и (35) – кривые 1, 2 и 3, 4 соответственно. 1 – ${{K}_{0}}$ = 10, $\gamma $ = 0.1, 2 – ${{K}_{0}}$ = 30, $\gamma $ = 0.1, 3 – ${{K}_{0}}$ = 30, $\gamma $ = 0.03, 4 – ${{K}_{0}}$ = 100, $\gamma $ = 0.04. Пунктиром показана та же зависимость при ${{K}_{n}}$ = 1. $a$ = 0.02.
V. ВЫВОДЫ
1. Предложен метод аналитического решения кинетических уравнений, описывающих баллистический рост цепи радикальной полимеризации. В предположении, что изменение концентрации мономеров во времени известно, найдены зависящие от времени концентрации макрорадикалов.
2. Показано, что совокупность кинетических уравнений, описывающих радикально-цепную полимеризацию, эквивалентна уравнению первого порядка в частных производных, характеристика которого определяет скорость роста средне-массовой длины цепи и зависящее от времени молекулярно-массовое распределение (ММР) макрорадикалов.
3. Показано, что оба указанных параметра полимеризации однозначно связаны со скоростью движения и шириной волнового пакета при произвольной зависимости константы скорости роста цепи от ее длины.
4. Когда константа скорости возрастает, скорость волны увеличивается с длиной цепи. Поскольку длинные радикалы растут быстрее коротких, движение волнового пакета преимущественно сводится к его уширению.
5. Когда константа скорости уменьшается, начальный быстрый рост коротких цепей замедляется по мере увеличения их длины. Уменьшение скорости волны сужает ММР.
6. Указанные изменения ММР показывают, что изменяя константы скорости роста цепи в нано-размерном пространственном масштабе, можно в том же масштабе направленно изменять надмолекулярную структуру образующихся олигомеров. Зависимость констант скорости полимеризации от концентраций первичных радикалов и переносчиков цепи, а также вязкости среды, делает возможным управлять ММР.
7. Анализ линейной волны роста цепи открывает принципиальную возможность применения волновых представлений к малоизученным нелинейным процессам самоорганизующейся полимеризации.
Список литературы
Ziff R.M. // J. Stat. Phys. 1980. V. 23. P. 241.
Hendriks E.M., Ziff R.M., Ernst M.H. // J. Stat. Phys. 1983. V. 31. P. 519.
Kuchanov S.I. // Adv.Polym. Sci. 1992. V. 103. P. 3.
Spicer P.T., Pratsinis S.E. // AIChE Journal 1996. V. 42. P. 1612.
Davies S.C., King J.R., Wattis J.A.D. // J. Phys. A. 1999. V. 32. P. 7745.
Leyvraz F. // Phys. Reps. 2003. V. 383. P. 95.
Kuchanov S.I., Slot H., Stroeks A. // Progr. Polym. Sci. 2004. V. 29. P. 513.
Wattis J.A.D., Bolton C.D., Coveney P.V. // J. Phys. A. 2004. V. 37. P. 2895.
Wattis J.A.D. // J. Phys. A. 2006. V. 39. P. 7283.
Wattis J.A.D. // Physica D. 2006. V. 222. P. 1.
Ким И.П., Кац Е.И., Бендерский В.А. // Химия высоких энергий. 2019. Т. 53. № 4. С. 255.
Gentekos D.T., Dupuis L.N., Fors B.P. // J. Am. Chem. Soc. 2016. V. 138. P. 1848.
Lynd N.A., Hillmyer M.A. // Macromolecules 2005. V. 38. P. 8803.
Lynd N.A., Hillmyer M.A. // Macromolecules 2007. V. 40. P. 8050.
Matyjaszewski K. // Science 2011. V. 333. P. 1104.
Plichta A., Zhong M., Li W., Elsen A.M., Matyjaszewski K. // Macromol. Chem. Phys. 2012. V. 134. P. 3834.
Ким И.П., Бендерский В.А. // Химия высоких энергий. 2010. Т. 44. № 5. С. 387.
Ким И.П., Бендерский В.А. // Химия высоких энергий. 2011. Т. 45. № 5. С. 406.
Ким И.П., Бендерский В.А. // Химия высоких энергий. 2015. Т. 49. № 1. С. 3.
Ким И.П., Мартыненко В.М., Черняк А.В., Бендерский В.А. // Химия высоких энергий. 2017. Т. 51. № 4. С. 300.
Gao C., Yan D. // Progress Polymer Sci. 2004. V. 29. P. 183.
Thickett S.C., Gilbert R.G. // Polymer. 2007. V. 48. P. 6965.
Zhao T., Zheng Y., Poly J., Wang W. // Nature Commun. 2013.
Tobita H. // Processes. 2018. V. 6. P. 1.
Liu S., Srinivasan S., Grady M.C., Soroush M., Rap-pe A.M. // Intern. J. Quantum Chem. 2014. V. 114. P. 345.
Yu Q., Zhou M., Ding Y., Jiang B., Zhu S. // Polymer 2007. V. 48. P. 7058.
Ким И.П., Бендерский В.А. // Химия высоких энергий. 2019. Т. 53. № 3. С. 178.
Лоскутов А.Ю., Михайлов А.С. Введение в синергетику. М.: Наука. 1990.
Mikhailov A.S., Ertl G. // Chem. Phys. Chem. 2009. V. 10. P. 86.
Engineering of Chemical Complexity. Lecture Notes in Complex Systems. V. 11. Mikhailov S.A. (eds). 2013. World Scientific. Singapore.
Додд Р., Эйлбек Д., Гиббон Д., Моррис Х. Солитоны и нелинейные волновые уравнения. М.: Москва. 1988.
Дополнительные материалы отсутствуют.
Инструменты
Химия высоких энергий


