1. На главную
  2. Электронные версии
  3. Химия высоких энергий
  4. T. 54, № 2, 2020

Химия высоких энергий, 2020, T. 54, № 2, стр. 87-96

Кинетика поликонденсации. I. Бифункциональные кремнийорганические мономеры

И. П. Ким a, Е. И. Кац b, В. А. Бендерский a, *

a Институт проблем химической физики РАН
142432 Московская обл., Черноголовка, просп. Академика Семенова, 1, Россия

b Институт Теоретической Физики им. Л.Д. Ландау РАН
142432 Московская обл., Черноголовка, просп. Академика Семенова, 1, Россия

* E-mail: bender@icp.ac.ru

Поступила в редакцию 20.09.2019
После доработки 21.10.2019
Принята к публикации 21.10.2019

Полный текст (PDF)

Аннотация

Поликонденсация бифункциональных кремнийорганических мономеров, как цепной неразветвленный процесс, включает инициирование (гидролиз нереактивных концевых групп), рост (последовательное присоединение мономеров и бимолекулярная агрегация $n$-меров) и обрыв цепи (циклизация и запутывание концевых групп в нереактивном окружении). Предложены кинетические модели этих стадий c минимальным числом констант скорости. Показано, что каналы роста цепи с участием различных концевых групп перемешиваются, а конкуренция каналов роста и обрыва цепи определяет молекулярно-массовое распределение олигомеров и их фрактальную упаковку в наноразмерных агрегатах.

Ключевые слова: поликонденсация, бифункциональные мономеры, гидролиз, присоединение мономеров, агрегация, циклизация, запутывание цепей

I. ВВЕДЕНИЕ

Поликонденсация (ПК) – один из основных методов получения кремнийорганических полимеров и пористых материалов на основе силикагеля [1–4], – является цепным процессом, в котором добавление инициатора переводит исходные мономеры в реактивное состояние. Постоянный интерес к этим объектам обусловлен не только широкой областью их применений, но и их уникальными свойствами – разнообразием структурных переходов наноразмерных агрегатов типа клубок–глобула в процессе ПК [5–8]. В отличие от радикально-цепной полимеризации (РЦП), в которой низкие концентрации первичных радикалов (10–5–10–3моль/л), на несколько порядков меньшие концентрации мономеров, инициируют быстрый рост цепи (с константами скорости, порядка констант, ограниченных диффузией 109–107 л/моль · с), в процессе ПК концентрации исходных и активных мономеров соизмеримы (~1 моль/л), но рост цепи происходит на много порядков медленнее из-за низких констант скорости (10–5–10–4 л/моль ⋅ с), обусловленных высокими энергиями активации $\Delta {{E}^{\# }}$ > 20 Ккал/моль и сложной структурой переходного состояния. В результате этих различий, рост цепи в РЦП происходит в масштабе времен, на несколько порядков короче, чем фазовые переходы, связанные с образованием коллоидных частиц и гелей, а в ПК эти процессы протекают одновременно, так что рост цепей и образование их агрегатов оказываются взаимосвязанными. В кинетике РЦП возникает неоднородное пространственное распределение длинных олигомеров, которые, обладая низкой подвижностью, образуют наноразмерные агрегаты (“блобы”) в окрестности первичных радикалов, как точечных источников пространственного роста, а последующие фазовые переходы обусловлены агрегацией блобов с образованием субмикронных критических зародышей [9–11]. Из-за низкой концентрации первичных радикалов блобы растут изолированно друг от друга, так что их структура зависит от констант скорости роста и передачи цепи, но слабо влияет на последующие процессы агрегации. Напротив, в ПК концентрация цепей одного порядка с концентрацией мономеров, и структурные переходы происходят не только в одном временном, но и в одном пространственном масштабе.

Кинетические особенности ПК качественно подтверждают данные светорассеяния, рассеяния нейтронов, малоуглового рентгеновского рассеяния [2, 3, 12–14] и разрешенной по времени ИК-спектроскопии [15], согласно которым образующиеся наноразмерные агрегаты силикагеля являются случайными поверхностными и объемными структурами, характерные размеры и фрактальная размерность которых зависят от условий линейного рост цепей, их разветвления и обрыва. Основу для кинетического анализа обеспечили экспериментальные исследования спектров ЯМР 29Si с высоким спектральным разрешением [2, 3, 16–23], изменяющиеся в процессе ПК. Эти данные позволили идентифицировать многообразие олигомеров с длиной цепи n ≤ 5 различного строения, от линейных до циклических, образующихся при малых степенях превращения.

В моделях [3, 17, 19] рассматривались измеряемые зависящие от времени концентрации атомов кремния с различным числом силикатных связей –Si–O–Si– и концевых ОН- и OR-групп. Однако эти характеристики не являются независимыми переменными в нелинейных кинетических уравнениях, описывающих ПК, а лишь линейными комбинациями концентраций ограниченного числа n-меров. Кинетические уравнения, рассмотренные в этих работах, не согласуются с уравнениями Смолуховского (УС) и Беккера–Деринга (УБД) [24–30], решение которых является основой анализа кинетики процессов полимеризации и агрегации. Насколько нам удалось установить, анализ данных ЯМР 29Si с помощью этих уравнений еще не проведен. Последовательное решение кинетической задачи должно включать определение зависящих от времени концентраций n-меров (в частности, их моментов) из решения УС или УБД, а затем, определив эти концентрации, можно найти измеряемые характеристики. Модели [3, 19–23] в лучшем случае применимы при низких степенях превращения, когда ПК ограничивается образованием коротких олигомеров. В общем случае они не воспроизводят ни зависящие от времени распределения олигомеров по длинам цепи, ни образование наноразмерных агрегатов от рыхлых клубков до плотных глобул с различной фрактальной размерностью [5–9] и их превращения в коллоидные частицы и гели. Все перечисленные эффекты наблюдаются в силикагелях, но еще остаются вне рассмотрения данных ЯМР [22, 23]. Хотя одних кинетических уравнений для описания структурных изменений агрегатов в процессе ПК недостаточно и требуется дополнительное пространственное рассмотрение, основанное на решеточных моделях роста цепей и соотношениях подобия [6, 31, 32], решение кинетических уравнений необходимо, как один из элементов такого описания. Сравнение результатов кинетических исследований процессов полимеризации, основанных на общем подходе, с результатами, которые удалось получить из анализа спектров ЯМР 29Si в [17–23], позволяет придти к выводу, что необходимо повторное рассмотрение этих данных. К этому призывает и недавно возникший интерес к исследованию УС и УБД, связанный с возможностью подобрать константы скорости и условия полимеризации для получения полимеров с управляемыми молекулярно-массовым распределением (ММР) и фрактальной архитектурой [33–35].

Цель нашего исследования состоит в том, чтобы найти решение модельных кинетических задач для ПК. Метод решения представлен в наших предыдущих работах [28–30], посвященных кинетике РЦП. В первой статье мы рассмотрим наиболее простой процесс ПК с участием билинейных мономеров, когда образуются только линейные цепи и отсутствует разветвление.

В следующих разделах последовательно рассмотрены следующие задачи. Во втором разделе описана модель инициирования ПК при обратимом двухступенчатом гидролизе концевых групп, создающем совокупность каналов роста цепи, инициируемых реакциями между различными концевыми группами, и показано, что достаточно быстрое перемешивание этих каналов и гидролиз n-меров, позволяют ввести суммарные концентрации n-меров со всеми концевыми группами и, тем самым, уменьшить число констант в кинетических уравнениях. В третьем разделе предложена модель, в которой присоединение мономеров к растущей цепи конкурирует с агрегацией олигомеров, что приводит к ММР, резко зависящему от соотношения констант скорости этих процессов. В четвертом разделе рассмотрены два конкурирующих механизма обрыва цепи, обусловленных циклизацией коротких и запутыванием длинных n-меров, когда рост цепи заканчивается из-за захвата концевой группы в нереактивное окружение. Выводы собраны в пятом разделе.

II. ОБРАТИМЫЙ ГИДРОЛИЗ И РОСТ КОРОТКИХ ЦЕПЕЙ

Инициирование цепей различных алкилсилоксанов обусловлено обратимым ${{{\text{S}}}_{{\text{N}}}}2$-гидролизом алкоксигрупп OR (R = CH3, C2H5, ..), катализируемым ионами Н+ и ОН–

(1)
$ \equiv {\kern 1pt} {\text{Si}}{\kern 1pt} - {\kern 1pt} {\text{OR}} + {{{\text{H}}}_{{\text{3}}}}{{{\text{O}}}^{ + }}({\text{O}}{{{\text{H}}}^{ - }})\overset \Gamma \longleftrightarrow {\text{OH}}{\kern 1pt} - {\kern 1pt} {\text{Si}}{\kern 1pt} \equiv + \,{\text{OR}}.$

Согласно квантово-химическим расчетам [36], переходное состояние в реакции (1) содержит несколько молекул воды, так что низкая скорость гидролиза связана не только с высокой энтальпией активации, но и энтропийным барьером. Последующий рост линейных и разветвленных цепей силикатных связей [2, 3] происходит в бимолекулярных реакциях между концевыми ОН- и OR-группами

(2)
$\begin{gathered} \equiv {\kern 1pt} {\text{Si}}{\kern 1pt} - {\kern 1pt} {\text{OH}} + {\text{HO}}{\kern 1pt} - {\kern 1pt} {\text{Si}}{\kern 1pt} \equiv \xrightarrow{{{{K}_{1}}}} \equiv {\kern 1pt} {\text{Si}}{\kern 1pt} - {\kern 1pt} {\text{O}}{\kern 1pt} - {\kern 1pt} {\text{Si}}{\kern 1pt} \equiv + \,{{{\text{H}}}_{2}}{\text{O}}, \\ \equiv {\kern 1pt} {\text{Si}}{\kern 1pt} - {\kern 1pt} {\text{OR}} + {\text{HO}}{\kern 1pt} - {\kern 1pt} {\text{Si}}{\kern 1pt} \equiv \xrightarrow{{{{K}_{2}}}} \equiv {\kern 1pt} {\text{Si}}{\kern 1pt} - {\kern 1pt} {\text{O}}{\kern 1pt} - {\kern 1pt} {\text{Si}}{\kern 1pt} \equiv + \,{\text{ROH}}. \\ \end{gathered} $

Обратимый последовательный гидролиз бифункциональных мономеров (f = 2) определяют 4 константы скорости прямых $\left( {\Gamma _{{1(2)}}^{ + }} \right)$ и обратных $\left( {\Gamma _{{1(2)}}^{ - }} \right)$ реакций

(3)
$D_{0}^{0}\overset {\Gamma _{1}^{ \pm }} \longleftrightarrow D_{0}^{1}\overset {\Gamma _{2}^{ \pm }} \longleftrightarrow D_{0}^{2},$
где, в согласие с принятыми обозначениями [2, 3, 16, 17], $D_{i}^{j}$ – концентрация атомов кремния, имеющих $j$ силикатных связей и $i$ ОН-групп, т.е. $D_{0}^{j},$ j = 0, 1, 2 обозначает концентрацию исходных и активных мономеров. Необратимое образование димеров происходит по 7 каналам и его определяют две константы скорости реакций (2) и совокупность стехиометрических коэффициентов, равных числу различных комбинаций в реакциях между концевых групп мономеров
(4)
$\begin{array}{*{20}{c}} {} \\ {} \\ {} \end{array}$$\begin{gathered} D_{0}^{0} + D_{0}^{1}\xrightarrow{{2K{}_{2}}}D_{1}^{0} - D_{1}^{0}, \\ D_{0}^{1} + D_{0}^{1}\xrightarrow{{K{}_{1}}}D_{1}^{0} - D_{1}^{0}, \\ D_{0}^{1} + D_{0}^{1}\xrightarrow{{2K{}_{2}}}D_{1}^{0} - D_{1}^{1}, \\ D_{0}^{0} + D_{0}^{2}\xrightarrow{{4K{}_{2}}}D_{1}^{1} - D_{1}^{0}, \\ D_{0}^{1} + D_{0}^{2}\xrightarrow{{2K{}_{1}}}D_{1}^{0} - D_{0}^{1}, \\ D_{0}^{1} + D_{0}^{2}\xrightarrow{{2K{}_{2}}}D_{1}^{1} - D_{1}^{1}, \\ D_{0}^{2} + D_{0}^{2}\xrightarrow{{4K{}_{1}}}D_{1}^{1} - D_{1}^{1}, \\ \end{gathered} $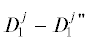
где означает димер. В (4) учтено, что бимолекулярная реакция с участием двух OR-групп не происходит. В дальнейшем мы используем более простое обозначение n-меров $D_{n}^{k},$ которое учитывает, что атомы кремния внутри цепи не связаны с ОН- и OR-группами

(5)
$D_{1}^{j}{{({{D}_{2}})}_{{n - 2}}}D_{1}^{{j'}} = D_{n}^{s},\,\,\,\,s = j + j{\kern 1pt} ' = 0,{\text{1}},{\text{2}}.$

Образование $(n + 1)$-меров из n-меров $\left( {n \geqslant 2} \right)$ происходит по 11 каналам с теми же константами скорости, но другими стехиометрическими коэффициентами

(6)
$\begin{gathered} D_{n}^{0} + D_{0}^{1}\xrightarrow{{2K{}_{2}}}D_{{n + 1}}^{0},\,\,\,\,D_{n}^{0} + D_{0}^{2}\xrightarrow{{4K{}_{2}}}D_{{n + 1}}^{0}, \\ D_{n}^{1} + D_{0}^{0}\xrightarrow{{2K{}_{2}}}D_{{n + 1}}^{1},\,\,\,\,D_{n}^{1} + D_{0}^{1}\xrightarrow{{K{}_{1}}}D_{{n = 1}}^{0}, \\ D_{n}^{1} + D_{0}^{1}\xrightarrow{{2K{}_{2}}}D_{{n + 1}}^{0},\,\,\,\,D_{n}^{1} + D_{0}^{2}\xrightarrow{{2K{}_{1}}}D_{{n + 1}}^{1}, \\ D_{n}^{1} + D_{0}^{2}\xrightarrow{{2K{}_{2}}}D_{{n + 1}}^{1},\,\,\,\,D_{n}^{2} + D_{0}^{0}\xrightarrow{{4K{}_{2}}}D_{{n + 1}}^{1}, \\ D_{n}^{2} + D_{0}^{1}\xrightarrow{{2K{}_{1}}}D_{{n + 1}}^{1},\,\,\,\,D_{n}^{2} + D_{0}^{1}\xrightarrow{{2K{}_{2}}}D_{{n + 1}}^{1}, \\ D_{n}^{2} + D_{0}^{2}\xrightarrow{{4K{}_{1}}}D_{{n + 1}}^{2}. \\ \end{gathered} $

Следует отметить, что в значительной части реакций (6) образуются неактивные n-меры с концевыми группами OR, и для их дальнейшего участия в ПК необходим, как и для мономеров, двухступенчатый гидролиз

(7)
$D_{n}^{0}\overset {\Gamma _{{n1}}^{ \pm }} \longleftrightarrow D_{n}^{1}\overset {\Gamma _{{n2}}^{ \pm }} \longleftrightarrow D_{n}^{2}.$

Ниже мы предположим, что для коротких n-меров константы скорости их гидролиза и гидролиза мономеров (3), определяемые локальной структурой переходного состояния концевых групп, не зависят от длины цепи $\Gamma _{{n1(n2)}}^{ \pm }$ = $\Gamma _{{1(2)}}^{ \pm }.$ Поскольку для коротких цепей реакциями агрегации можно пренебречь (см. раздел III), совокупность реакций (3), (4), (6) и (7) полностью описывает гидролиз и рост коротких цепей $n \leqslant $ 6 в процессе ПК. Следует отметить, что образование n-мера $D_{1}^{0}{{({{D}_{2}})}_{{n - 2}}}D_{1}^{0}$ на каждой стадии роста означает обрыв цепи: новая цепь может появиться только после его гидролиза. Таким образом, кинетическая схема ПК, инициируемой гидролизом, описывается совокупностью $3N$ нелинейных кинетических уравнений для концентраций $D_{n}^{s},$ s = 0, 1, 2, в которых 4 константы скорости характеризуют двухступенчатый обратимый гидролиз (1), а две константы – рост цепи. Только две константы достаточны для описания многоканального роста цепи, следуя гипотезе Флори [37], согласно которой эти константы определяются локальным окружением концевых групп, участвующих в реакциях (2) и не зависят от длины цепи. Кинетические уравнения для n-меров $\left( {n \geqslant 3} \right)$ имеют вид

(8)
$\begin{gathered} \dot {D}_{n}^{0} = - \Gamma _{1}^{ + }D_{n}^{0} + \Gamma _{1}^{ - }D_{n}^{1} + 2{{K}_{2}}D_{{n - 1}}^{0}D_{0}^{1} + \\ + \,\,2{{K}_{2}}D_{{n - 1}}^{1}D_{0}^{1} + {{K}_{1}}D_{{n - 1}}^{1}D_{0}^{1} - 2{{K}_{2}}D_{n}^{0}D_{0}^{1} - 4{{K}_{2}}D_{n}^{0}D_{0}^{2}, \\ \dot {D}_{n}^{1} = \Gamma _{1}^{ + }D_{n}^{0} - (\Gamma _{1}^{ - } + \Gamma _{2}^{ + })D_{n}^{1} + \Gamma _{2}^{ - }D_{n}^{2} + \\ + \,\,4{{K}_{2}}D_{{n - 1}}^{0}D_{0}^{2} + 2{{K}_{2}}D_{{n - 1}}^{1}D_{0}^{1} + 2{{K}_{1}}D_{{n - 1}}^{1}D_{0}^{2} + \\ + \,\,4{{K}_{2}}D_{{n - 1}}^{2}D_{0}^{0} - 2{{K}_{2}}D_{n}^{0}D_{0}^{1} - \\ - \,\,({{K}_{1}} + 2{{K}_{2}})D_{n}^{1}D_{0}^{1} - 2{{K}_{2}}D_{n}^{1}D_{0}^{2}, \\ \dot {D}_{n}^{2} = \Gamma _{2}^{ + }D_{n}^{1} - \Gamma _{2}^{ - }D_{n}^{2} + 2{{K}_{2}}D_{{n - 1}}^{2}D_{0}^{1} + 4{{K}_{1}}D_{{n - 1}}^{2}D_{0}^{2} + \\ + \,\,{{K}_{1}}D_{{n - 1}}^{1}D_{0}^{1} - 4{{K}_{2}}D_{n}^{2}D_{0}^{1} - \\ - \,\,2({{K}_{1}} + {{K}_{2}})D_{n}^{2}D_{0}^{1} - 4{{K}_{1}}D_{n}^{2}D_{n}^{2}. \\ \end{gathered} $

Компьютерное решение системы нелинейных уравнений (8) осуществлено в кодах MATLAB-R2018 по программе ODE113 и обладает следующими свойствами. Концентрации n-меров максимальны в окрестности квазистационарных точек $\dot {D}_{n}^{s}\left( {t_{{ns}}^{*}} \right) = 0,$ где $t_{{ns}}^{*}$ слабо зависят от s, так что кривые $D_{n}^{s}(t)$ синхронно смещаются с ростом $t$ по оси n как пространственной координате (рис. 1). Зависящие от длины цепи и времени концентрации ${{D}^{j}}(n,t)$ имеют вид волновых пакетов, фазовая скорость и ширина которых зависят от времени, т.е. уравнения (6) преобразуются в нелинейное волновое уравнение, описывающее процесс ПК как волну превращения мономеров в олигомеры [29]. Концентрации мономеров в процессе обратимого гидролиза (3) имеют вид

(9)
$D_{0}^{j} = {{A}_{j}} + {{B}_{j}}\exp ( - {{\lambda }_{1}}t) + {{C}_{j}}\exp ( - {{\lambda }_{2}}t),$
где ${{\lambda }_{1}},$ ${{\lambda }_{2}}$ – ненулевые корни векового определителя

(10)
$\begin{gathered} \Delta (\lambda ) = \left| {\begin{array}{*{20}{c}} {\lambda + \Gamma _{1}^{ + }}&{ - \Gamma _{1}^{ - }}&0 \\ { - \Gamma _{1}^{ + }}&{\lambda + \Gamma _{1}^{ - } + \Gamma _{2}^{ + }}&{ - \Gamma _{2}^{ - }} \\ 0&{ - \Gamma _{2}^{ + }}&{\lambda + \Gamma _{2}^{ - }} \end{array}} \right| = \\ = \lambda (\lambda - {{\lambda }_{1}})(\lambda - {{\lambda }_{2}}) = 0, \\ \end{gathered} $
Рис. 1.

Зависящие от времени суммарные концентрации n-меров с концевыми группами OH и OR (жирные линии) и вспомогательные переменные ${{X}_{n}}(t)$ и ${{Y}_{n}}(t),$ введенные в (13) и показанные тонкими и пунктирными линями. Значения ${{X}_{n}}(t)$ и ${{Y}_{n}}(t)$ увеличены в 2 и в 4 раза соответственно. Сравнение ${{P}_{n}}(t)$ с ${{X}_{n}}(t)$ и ${{Y}_{n}}(t)$ иллюстрирует точность исключения из рассмотрения констант гидролиза (7), удовлетворяющих условию (11). $\Gamma _{1}^{ + }$ = 50, $\Gamma _{1}^{{ - {\kern 1pt} '}}$ = 25, $\Gamma _{2}^{ + }$ = 30, $\Gamma _{2}^{ - }$ = 10.

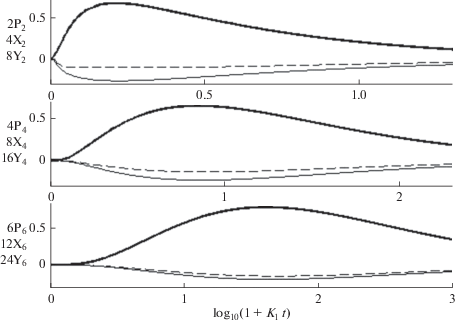
а коэффициенты ${{A}_{j}},$ ${{B}_{j}},$ ${{C}_{j}}$определяются начальными условиями (см., напр., [40]).

Скорость гидролиза, много больше скорости роста цепи, если

(11)
${{\lambda }_{m}} = \min ({{\lambda }_{1}},{{\lambda }_{2}}) \gg \max ({{K}_{1}},{{K}_{2}}).$

При условии (11) три волновых пакета с различными значениями $s$ синхронно смещаются по оси n, изменяя относительные амплитуды и переходя друг в друга за счет быстрого обратимого гидролиза и мономеров и олигомеров. Перемешивание приводит к тому, что три пакета можно заменить одним и для достаточно длинных цепей (n > 4) ввести вместо четырех констант скорости гидролиза в (3) одну эффективную константу. Когда константы скорости обеих прямых реакций намного больше (меньше) чем обратных, преобладает стационарная концентрация $D_{n}^{2}\left( {D_{n}^{0}} \right),$ тогда как $D_{n}^{{(1)}}$ доминирует в случае С

(12)
$\begin{gathered} A:\Gamma _{1}^{ + } \gg \Gamma _{1}^{ - },\,\,\,\,\Gamma _{2}^{ + } \gg \Gamma _{2}^{ - },\,\,\,\,D_{n}^{0} \ll D_{n}^{1} \ll D_{n}^{2}, \\ B:\Gamma _{1}^{ + } \ll \Gamma _{1}^{ - },\,\,\,\,\Gamma _{2}^{ + } \ll \Gamma _{2}^{ - },\,\,\,\,D_{n}^{0} \gg D_{n}^{1} \gg D_{n}^{2}, \\ C:\Gamma _{1}^{ + } \gg \Gamma _{1}^{ - },\,\,\,\,\Gamma _{2}^{ + } \ll \Gamma _{2}^{ - },\,\,\,\,D_{n}^{1} \gg D_{n}^{0},D_{n}^{2}. \\ \end{gathered} $

В общем случае вместо трех концентраций (5) удобно ввести новые независимые переменные: суммарную концентрацию n-меров ${{P}_{n}}(t)$ и две вспомогательных переменных

(13)
$\begin{gathered} {{P}_{n}}(t) = D_{n}^{0}(t) + D_{n}^{1}(t) + D_{n}^{2}(t), \\ {{X}_{n}}(t) = D_{n}^{0}(t) - (\Gamma _{1}^{ - } + \Gamma _{2}^{ + }){{D_{n}^{1}(t)} \mathord{\left/ {\vphantom {{D_{n}^{1}(t)} {\Gamma _{1}^{ + }}}} \right. \kern-0em} {\Gamma _{1}^{ + }}} + \\ + \,\,{{\Gamma _{2}^{ - }D_{n}^{2}(t)} \mathord{\left/ {\vphantom {{\Gamma _{2}^{ - }D_{n}^{2}(t)} {\Gamma _{1}^{ + }}}} \right. \kern-0em} {\Gamma _{1}^{ + }}},\,\,\,\,{{Y}_{n}}(t) = D_{n}^{0}(t) - \left( {\Gamma _{1}^{ - } + \Gamma _{2}^{ + } + \Gamma _{2}^{ - }} \right) \times \\ \times \,\,{{D_{n}^{1}(t)} \mathord{\left/ {\vphantom {{D_{n}^{1}(t)} {\Gamma _{1}^{ + }}}} \right. \kern-0em} {\Gamma _{1}^{ + }}} + \Gamma _{2}^{ - }\left( {\Gamma _{2}^{ + } + \Gamma _{2}^{ - }} \right){{D_{n}^{2}(t)} \mathord{\left/ {\vphantom {{D_{n}^{2}(t)} {\Gamma _{1}^{ + }\Gamma _{2}^{ + }}}} \right. \kern-0em} {\Gamma _{1}^{ + }\Gamma _{2}^{ + }}}. \\ \end{gathered} $

При условии (11) максимумы $D_{n}^{1}(t)$ и $\dot {D}_{n}^{2}(t)$ близки, так что вторая производная $\ddot {D}_{n}^{2}({{t}_{2}})$ = 0 при ${{t}_{2}} \approx t_{{ns}}^{*}.$ Вспомогательные переменные ${{X}_{n}}(t)$ и ${{Y}_{n}}(t),$ пропорциональные $\dot {D}_{n}^{1}(t)$ и $\ddot {D}_{n}^{2}(t),$ уменьшаются настолько быстрее, чем суммарная концентрация мономеров ${{P}_{n}}(t),$ что при $t > {1 \mathord{\left/ {\vphantom {1 {{{\Gamma }_{m}}}}} \right. \kern-0em} {{{\Gamma }_{m}}}}$ ими можно пренебречь в правых частях кинетических уравнений и заменить (8) системой $N$ кинетических уравнений для ${{P}_{n}}(t)$ с эффективными константами скорости роста цепи, явно не зависящими от констант скорости гидролиза. Пользуясь обратным преобразованием $D_{n}^{k}({{P}_{n}},{{X}_{n}},{{Y}_{n}}),$ можно найти систему уравнений в новых переменных (13) и построить приближенное решение, учитывающее, что при выполнении (11) $\left| {{{X}_{n}}(t)} \right|,$ $\left| {{{Y}_{n}}(t)} \right| \ll {{P}_{n}}(t).$ Зависимость от $\left\{ {\Gamma _{n}^{j}} \right\}$ входит в уравнения для ${{X}_{n}}(t),$ ${{Y}_{n}}(t)$ и исчезает в нулевом приближении, где ${{X}_{n}}(t)$ = 0 и ${{Y}_{n}}(t)$ = 0, так что уравнения для ${{\dot {P}}_{n}}(t)$ сводятся к уравнениям с эффективными константами, зависящими только от констант роста цепи

(14)
$\begin{gathered} {{{\dot {P}}}_{1}} = {{{\tilde {K}}}_{1}}P_{1}^{1} - {{{\tilde {K}}}_{2}}{{P}_{1}}\sum\limits_{n = 1}^{N - 1} {{{P}_{n}}} ,\,\,\,\,{{{\dot {P}}}_{2}} = {{{{{\tilde {K}}}_{1}}P_{1}^{2}} \mathord{\left/ {\vphantom {{{{{\tilde {K}}}_{1}}P_{1}^{2}} 2}} \right. \kern-0em} 2} - \\ - \,\,{{{\tilde {K}}}_{2}}{{P}_{1}}{{P}_{2}},\,\,\,\,{{{\dot {P}}}_{n}} = {{{\tilde {K}}}_{2}}{{P}_{1}}({{P}_{{n - 1}}} - {{P}_{n}}),\,\,\,\,n \geqslant 3, \\ \end{gathered} $
где

(15)
${{\tilde {K}}_{1}} = {{7{{K}_{1}}} \mathord{\left/ {\vphantom {{7{{K}_{1}}} 9}} \right. \kern-0em} 9} + {{10{{K}_{2}}} \mathord{\left/ {\vphantom {{10{{K}_{2}}} 9}} \right. \kern-0em} 9},\,\,\,\,{{\tilde {K}}_{2}} = {{K}_{1}} + {{16{{K}_{2}}} \mathord{\left/ {\vphantom {{16{{K}_{2}}} 9}} \right. \kern-0em} 9}.$

В (14) учитывается только последовательное присоединение мономеров к коротким олигомерам. Рекомбинация n-меров $n,n{\kern 1pt} ' \geqslant 3$ будет учтена в следующем разделе. Коэффициент 1/2 во втором уравнении (14) обеспечивает сохранение полного числа мономеров в процессе ПК [30]. Следует указать, что эффективные константы ${{\tilde {K}}_{1}} < {{\tilde {K}}_{2}}$ учитывают обрыв цепи, связанный с накоплением олигомеров с концевыми группами RO. Решение кинетических уравнений (8) и (14) показывает, что во всех трех случаях (12), когда константы скорости гидролиза расположены в интервале $5 \leqslant \Gamma _{1}^{ \pm },$ $\Gamma _{2}^{ \pm } \leqslant 100,$ отклонения приближенных решений (14) от (8) не превышает 10%. Учитывая низкую точность определения констант в таких сложных процессах, эту точность можно признать достаточной и сделать вывод, что при быстром обратимом гидролизе, его константы скорости можно исключить из кинетических уравнений для суммарных концентраций n-меров. Поскольку одну из эффективных констант (15) можно выбрать в качестве масштаба безразмерного времени (напр. $\tilde {t} = {{\tilde {K}}_{1}}t$), кинетику начального роста цепей можно описать, используя только еще одну константу ${{\tilde {K}}_{1}}.$ Зависимости переменных (13) от времени, подтверждающие справедливость нулевого приближения, показана на рис. 1.

III. ПРИСОЕДИНЕНИЕ МОНОМЕРОВ И АГРЕГАЦИЯ ОЛИГОМЕРОВ

Простая кинетическая модель, воспроизводящая два конкурирующих канала роста линейной цепи – последовательное присоединение мономеров

(16)
${{P}_{n}} + {{P}_{1}}\xrightarrow{{{{{\tilde {K}}}_{1}}}}{{P}_{{n + 1}}}$

и агрегацию, – учитывает бимолекулярную рекомбинацию образовавшихся ранее n- и n'-меров

(17)
${{P}_{n}} + {{P}_{{n{\kern 1pt} '}}}\xrightarrow{k}{{P}_{{n + n{\kern 1pt} '}}}.$

Если считать константу скорости агрегации $k$ не зависящей от $n$ и n', эта модель содержит только одну дополнительную константу. Важное отличие этой модели от обычно рассматриваемого неограниченного роста цепи состоит в том, что рост цепи предполагается ограниченным ее максимальной длиной $n \leqslant N,$ такой что ${{K}_{1}}(n) = {{K}_{2}}(n) = 0,$ $n \geqslant N,$ $k(n,n{\kern 1pt} ') = 0,$ $n + n{\kern 1pt} ' \geqslant N.$ Ограничение означает, что рост рыхлых агрегатов происходит в ограниченном объеме (полости) размером порядка среднеквадратичного радиуса инерции и учитывает исключенный объем, занятый цепями [31, 38].

Макроскопические характеристики ПК (расход мономеров и моменты распределения концентраций n-меров) приведены на рис. 2, на котором и всюду ниже использована безразмерная единица времени ${1 \mathord{\left/ {\vphantom {1 {{{{\tilde {K}}}_{1}}}}} \right. \kern-0em} {{{{\tilde {K}}}_{1}}}}$ и безразмерные концентрации, отнесенные к начальной концентрации мономеров. Концентрация мономеров и первый момент связаны законом сохранения числа мономерных единиц

(18)
${{P}_{1}}(t) + {{S}_{1}}(t) = 1,\,\,\,{{S}_{{\alpha }}} = \sum\limits_{n = 2}^N {{{n}^{{\alpha }}}{{P}_{n}}(t)} ,\,\,\,\alpha = 0,1,2.$
Рис. 2.

Зависящие от времени макроскопические характеристики ПК бифункциональных мономеров. 1 – концентрация мономеров, 2–6 – нулевой момент распределения n-меров, 2'–6' – средняя массо-взвешенная длина цепи, отнесенная к максимальной (21). $k$ = 0, 0.001, 0.01, 0.1, 1 – кривые 2(2 ')–6(6 ') соответственно. $N$ = 30. Пунктиром показано сохранение полного числа мономеров (18).

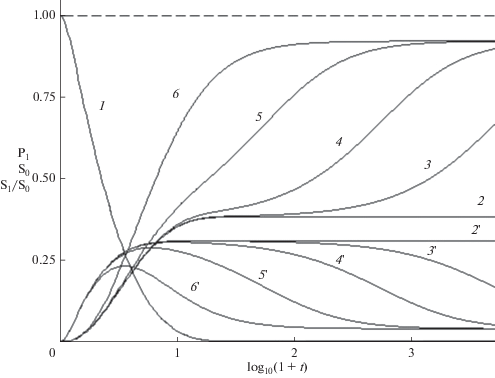
Из (14) следует, что концентрацию мономеров и нулевой момент $\left( {\alpha = 0} \right)$ связывают два уравнения

(19)
$\begin{gathered} {{{\dot {P}}}_{1}} = - P_{1}^{2} - b{{P}_{1}}{{S}_{0}},\,\,\,{{{\dot {S}}}_{0}} = {{ - P_{1}^{2}} \mathord{\left/ {\vphantom {{ - P_{1}^{2}} 2}} \right. \kern-0em} 2}, \\ {{P}_{1}}(0) = 1,\,\,\,{{S}_{0}}(0) = 0, \\ \end{gathered} $
где

(20)
$b = {{{{{\tilde {K}}}_{2}}} \mathord{\left/ {\vphantom {{{{{\tilde {K}}}_{2}}} {{{{\tilde {K}}}_{1}} - 1}}} \right. \kern-0em} {{{{\tilde {K}}}_{1}} - 1}} = {{(2{{K}_{1}} + 3{{K}_{2}})} \mathord{\left/ {\vphantom {{(2{{K}_{1}} + 3{{K}_{2}})} {(7{{K}_{1}} + 10{{K}_{2}})}}} \right. \kern-0em} {(7{{K}_{1}} + 10{{K}_{2}})}}.$

Уравнения (19) решается следующей подстановкой в (14)

(21)
${{P}_{n}}(t) = \phi (t){{\chi }^{{n - 1}}}(t),$
где ${{P}_{1}}(t)$ и ${{S}_{0}}(t)$ связаны с $\phi (t)$ и $\chi (t)$ соотношением

(22)
$\begin{gathered} {{P}_{1}}(t) = \phi (t),\,\,\,{{S}_{0}}(t) = \phi (t)\sum\limits_{n = 1}^N {{{\chi }^{n}}(t)} \approx \\ \approx \phi (t)\frac{{\chi (t)}}{{1 - \chi (t)}},\,\,\,N \gg 1 \\ \end{gathered} $

и подчиняются уравнениям

(23)
$\dot {\phi } = - {{\phi }^{2}}\frac{{1 + (b - 1)\chi }}{{1 - \chi }},\,\,\,\dot {\chi } = \frac{1}{2}\phi \left( {1 + (2b - 1){{\chi }^{2}}} \right).$

Уравнение (23) отличается от УС, описывающих ПК при одинаковых константах скорости роста цепи и агрегации (15), когда ${{K}_{1}} = {{K}_{2}} = k$ [24, 27] и

(24)
$\begin{gathered} {{{\dot {\phi }}}_{0}} = - \phi _{0}^{2}{{(1 - {{\chi }_{0}})}^{{ - 1}}},\,\,\,\dot {\chi } = {{{{\phi }_{0}}} \mathord{\left/ {\vphantom {{{{\phi }_{0}}} 2}} \right. \kern-0em} 2}, \\ {{P}_{{10}}} = {{({{1 + t} \mathord{\left/ {\vphantom {{1 + t} 2}} \right. \kern-0em} 2})}^{{ - 2}}},\,\,\,{{S}_{{00}}} = ({t \mathord{\left/ {\vphantom {t 2}} \right. \kern-0em} 2}){{({{1 + t} \mathord{\left/ {\vphantom {{1 + t} 2}} \right. \kern-0em} 2})}^{{ - 2}}}. \\ \end{gathered} $

Формулы (23) и (24) описывают два различных кинетических режима, когда $k = 0$ и $k = $1 соответственно. Из сравнения решений следует, что агрегация слабо влияет на начальный рост коротких цепей, когда $t < 2$ и рост ${{S}_{0}}$ в обоих режимах описывает (24). Различие появляется при $t \gg 1.$ В отсутствие агрегации нулевой момент достигает постоянного значения

(25)
$\begin{gathered} {{S}_{0}}\left( \infty \right) = {{b}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}\exp ( - {{(2b - 1)}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}} \times \\ \times \,\,\tan {}^{{ - 1}}((2b - 1){{b}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}})), \\ \end{gathered} $

так как рост прекращается из-за полного расхода мономера и длинные цепи не образуются. При быстрой агрегации $\left( {k \geqslant 1} \right)$ образуются длинные цепи и нулевой момент уменьшается до нуля, ${{S}_{{00}}}\sim {{t}^{{ - 1}}}.$ На рис. 2 показано, что между этими двумя режимами расположена промежуточная область, в которой скорость последовательного роста уменьшается, а скорость агрегации растет.

В начальной области $t < 2$ (y < y1 ≈ 0.5), $y = {{\log }_{{10}}}(1 + t),$ $\chi \approx {{\chi }_{0}}$ = ${t \mathord{\left/ {\vphantom {t 2}} \right. \kern-0em} 2}({{1 + t} \mathord{\left/ {\vphantom {{1 + t} 2}} \right. \kern-0em} 2}) \ll 1,$ концентрации мономеров в n-мерах

(26)
$n{{P}_{n}}(t) \approx n{{\left( {{t \mathord{\left/ {\vphantom {t 2}} \right. \kern-0em} 2}} \right)}^{{n - 1}}}{{\left( {{{1 + t} \mathord{\left/ {\vphantom {{1 + t} 2}} \right. \kern-0em} 2}} \right)}^{{ - (n + 1)}}}$

уменьшаются с ростом $n$ при всех $k.$ В промежуточной области ${{y}_{2}} \geqslant y > {{y}_{1}}$ следом за мономерами медленно исчезают короткие n-меры. При $y > {{y}_{2}}$ $n{{P}_{n}}$ растет, заканчиваясь образованием длинных цепей, с максимумом при $n = N$ и уменьшающейся с ростом $k$ шириной. Изменяющиеся во времени средняя длина цепи и дисперсия распределения приведены на рис. 5.

Рис. 3.

Зависящие от времени концентрации мономеров в n-мерах, $nP{}_{n}(t).$ $N$ = 30, $k$ = 0.1. Кривые 1–11, n = 2, 4, 6, 8, 10, 14, 18, 24, 26, 28, 30 соответственно.

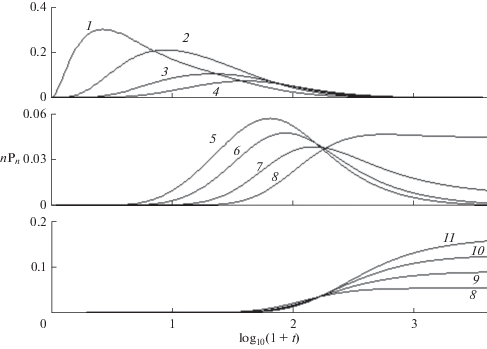
Рис. 4.

Молекулярно-массовые распределения мономеров в n-мерах, $nP{}_{n}(t).$ $N$ = 31 в различные моменты времени ${{y}_{s}} = {{\log }_{{10}}}(1 + {{t}_{s}}).$ Верхняя панель: $k$ = 0.05, ${{y}_{1}}$ = 1.5, ${{y}_{2}}$ = 2.5, ${{y}_{3}}$ = 4. Средняя панель: $k$ = 0.25, ${{y}_{1}}$ = 1, ${{y}_{2}}$ = 1.75,${{y}_{3}}$ = 3. Нижняя панель : $k$ = 1, ${{y}_{1}}$ = 0.75, ${{y}_{2}}$ = 1.5,${{y}_{3}}$ = 3.

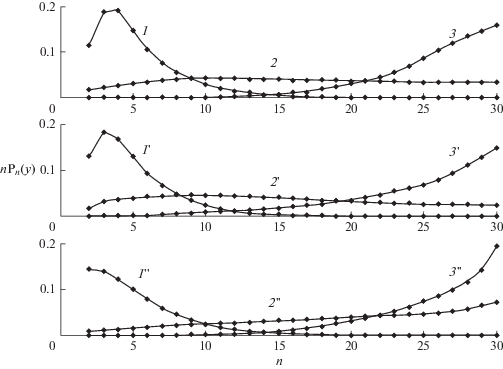
Рис. 5.

Влияние обрыва на среднюю длину цепи, кривые 1–3, и дисперсию (27), кривые 1'–3 '. 1, 1' – ${{g}_{1}} = {{g}_{2}} = 0,$ 2, 2' – ${{g}_{1}}$ = 0, ${{g}_{2}}$ = 0.2, 3, 3' – ${{g}_{1}}$ = 0.01, ${{g}_{2}}$ = 0.2. $k$ = 1, $N$ = 31.

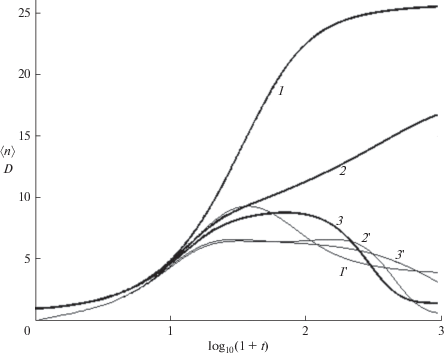
Следует отметить различие механизмов РЦП и ПК в режиме $k = 0.$ В процессе РЦП реакционный объем разбивается на ячейки Вигнера–Зейтца (см., напр., [39]) диаметром ${{R}_{{WZ}}}\sim {{N}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 3}} \right. \kern-0em} 3}}}}$ ~100 нм, каждая из которых содержит один радикал ($N$ ~ ~ 10–5 моль/л). В каждой ячейке изолированно растет один блоб в виде рыхлого клубка, состоящего из $n$-олигомеров и молекул растворителя [31, 37, 38], присоединяя диффундирующие к макрорадикалу мономеры. Диффузионные потоки приходящих мономеров и уходящих олигомеров, создают пространственно неоднородное распределение: плотный блоб из длинных олигомеров окружен “опушкой” гомогенного раствора с низкой концентрацией мономеров и коротких олигомеров. В отличие от РЦП, в процессе ПК реакции (16) происходят статистически равномерно во всем объеме, где ближайшие партнеры расположены на расстоянии ~1 нм ($N\sim 1$ моль/л), так что расход мономера сохраняет однородность распределения. Агрегация начинается после почти полного превращения мономеров в короткие n-меры, что показываeт уменьшение нулевого и рост второго моментов на рис. 2. Максимально длинная цепь, в которую объединены все мономеры, за конечное время не образуется, а средняя массовзвешенная длина цепи, отнесенная к максимальной, и дисперсия распределения олигомеров

(27)
${{\left\langle {n(t)} \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {n(t)} \right\rangle } N}} \right. \kern-0em} N} = {{{{S}_{1}}(t)} \mathord{\left/ {\vphantom {{{{S}_{1}}(t)} {{{S}_{0}}(t)}}} \right. \kern-0em} {{{S}_{0}}(t)}},\,\,\,\Delta (t) = {{\left( {{{{{S}_{2}}} \mathord{\left/ {\vphantom {{{{S}_{2}}} {{{S}_{0}} - {{{\left\langle n \right\rangle }}^{2}}}}} \right. \kern-0em} {{{S}_{0}} - {{{\left\langle n \right\rangle }}^{2}}}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$

остаются малой, ${{\left\langle n \right\rangle } \mathord{\left/ {\vphantom {{\left\langle n \right\rangle } N}} \right. \kern-0em} N}$ < 0.15 и конечной соответственно. Как показывают рис. 2 и 5, скорость агрегации (значения $k$) практически не влияет на расход мономеров (кривая 1), но резко уменьшает нулевой момент (т.е. число олигомеров) и увеличивает среднюю длину цепей (кривые 2–6 и 2 '–6 ' соответственно) в области $y > {{y}_{2}}.$ При $k$ ≤ 0.3 средняя длина цепи остается малой в широком интервале времени. При $k$ ≥ 1, этот интервал исчезает и ${{\left\langle n \right\rangle } \mathord{\left/ {\vphantom {{\left\langle n \right\rangle } N}} \right. \kern-0em} N}$ стремится к 1. Зависящие от времени концентрации мономеров в n-мерах $n{{P}_{n}}(t)$ различны в трех интервалах времени. Вначале $0 < y \leqslant {{y}_{1}}$ образуются короткие n-меры (n < 6), в которых $n{{P}_{n}}(t)$ уменьшаются с ростом длины цепи n. Изменение макроскопических характеристик соответствует распространению волны превращения мономеров в n-меры. При росте цепи концентрация коротких n-меров уменьшается (верхняя панель рис. 3). В интервале ${{y}_{1}} \leqslant y \leqslant {{y}_{2}}$ образуется широкое распределение, близкое к равномерному $n{{P}_{n}}(t)$ ≈ $P{\text{*}}\sim {{N}^{{ - 1}}}.$ В этом интервале расположена точка $y{\text{*,}}$ в которой наибольшее число n-меров имеют одинаковые значения $n{{P}_{n}}(t)$ ≈ $P*\sim {{N}^{{ - 1}}}$ (средняя панель). При $y > {{y}_{2}}$ (нижняя панель) распределение сужается, сохраняются только n-меры с длиной цепи, близкой к $N$. Значения ${{y}_{1}}$ слабо зависят от $k$ при $k$ ≤ 0.1, а ${{y}_{2}}$ уменьшаются пропорционально $ - {{\log }_{{10}}}k,$ показывая, что в начальном росте цепи доминирует реакция (16), а в заключительной стадии роста – агрегация (17). В промежуточной области $\left( {{{y}_{1}} \leqslant y \leqslant {{y}_{2}}} \right)$ скорость роста минимальна, поскольку мала как концентрация мономеров, так и длинных n-меров. Три различных механизма роста цепей приводят к зависящим от времени ММР (рис. 4) для различных значений $k.$

IV. ОБРЫВ ЦЕПИ: ЦИКЛИЗАЦИЯ И ЗАПУТЫВАНИЕ

По данным [3, 16–20], при малых степенях превращения продуктами ПК являются не только линейные, но и циклические n-меры, n = 3 и 4, причем тримеры $D_{{3c}}^{2}$ неустойчивы и исчезают в процессе ПК за несколько часов, а тетрамеры $D_{{4c}}^{2}$ стабильны. Циклические структуры с более длинными цепями не идентифицированы. Поскольку циклизация наблюдалась и в ПК би- и трифункциональных алкоксисиланов с более длинными заместителями, чем метильные и этильные группы [21–23], можно предположить, что циклизация является одним из механизмов обрыва цепи и для более длинных цепей.

В решеточной модели, где рост цепи рассматривается как равновероятное образование силикатных связей между соседними узлами, циклизация происходит, если концы цепи оказываются в этих узлах. Вероятность циклизации определяется из расчета числа соответствующих конформеров. В простой кубической решетке из атомов кремния, моделирующих структуру коллоидных частиц силикагеля [41], линейный рост цепи возможен по 5 ребрам, выходящим из одной вершины (вдоль одного из ребер образовалась цепь). Константа скорости циклизация в такой решетке определяется долей таких конформеров, равной 4/25 (для n = 4 число конформеров с концами на соседних узлах – 4, а их полное число – 25), и относительной вероятностью образования связи межу его концами и по сравнению с ростом цепи по четырем другим ребрам, т.е. 1/5. Следующая возможность циклизации возникает при n = 6, когда доля конформеров, способных образовать цикл, равна 32/625. Этот простой расчет показывает, что вероятность циклизации быстро уменьшается с ростом $n$ и не может привести к обрыву длинных цепей. Мы предлагаем другой механизм обрыва, эффективный при высоких степенях превращения, когда часть узлов, через которые проходит конец растущей цепи, оказываются занятыми в составе образовавшихся ранее олигомеров. Когда занятыми оказываются все соседние узлы, происходит обрыв: цепь запутывается в нереактивном окружении. Таким образом, обрыв коротких цепей может вызвать циклизация, а длинных – запутывание. В кинетических уравнениях (14) оба механизма приводят к мономолекулярной гибели мономеров, которые с учетом агрегации и обрыва имеют вид

(28)
$\begin{gathered} {{{\dot {P}}}_{n}} = {{P}_{{n - 1}}}{{P}_{1}} + \frac{k}{2}\sum\limits_{n{\kern 1pt} ' = 2}^{n - 2} {{{P}_{{n{\kern 1pt} '}}}{{P}_{{n - n{\kern 1pt} '}}}} - \\ - \,\,{{P}_{n}}{{P}_{1}} - k{{P}_{n}}\sum\limits_{n{\kern 1pt} ' = 2}^{N - n{\kern 1pt} '} {{{P}_{{n{\kern 1pt} '}}} - {{g}_{n}}{{P}_{n}}} , \\ \end{gathered} $
где gn =${{g}_{1}}$ и ${{g}_{2}}$– константы скорости циклизации коротких $(n \leqslant {{n}_{1}})$ и запутывания длинных $\left( {n > {{n}_{1}}} \right)$ цепей. Влияние обрыва на среднюю длину цепи и дисперсию (27) показано на рис 5. В согласие с приведенной выше оценкой констант скорости обрыва в решеточной модели, уменьшение средней длины цепи по сравнению с максимальной, происходит при ${{g}_{1}}$, ${{g}_{2}}$ $ \ll $ 1. Хотя вместе с длиной цепи уменьшается и дисперсия, обрыв, связанный с запутыванием цепей, сохраняет широкое распределение олигомеров. Эффективный обрыв обеспечивает ${{g}_{1}} \ll {{g}_{2}},$ поскольку циклизация блокирует рост цепи в промежуточной области, где его скорость минимальна, а запутывание конкурирует с быстрой агрегацией.

V. ВЫВОДЫ

1. Начальный рост цепи обусловлен преимущественным присоединением мономеров к образовавшимся ранее олигомерам по схеме (16) .

2. В промежуточной области времени происходит смена механизма поликонденсации от последовательного роста (16) к агрегации (17), приводящая к ММР, близкому к равномерному.

3. В области глубокого превращения доминирует агрегация, при которой образуются цепи с длиной, близкой к максимальной, и меньшей дисперсией, чем в промежуточной области.

4. Поскольку механизм (16) реализуется при росте изолированных цепей в форме рыхлых клубков, смена механизма ПК означает переход клубок-глобула, заканчивающийся при глубоком превращении образованием плотных глобул из максимально длинных n-меров.

5. В промежуточной области скорость ПК минимальна (последовательный рост блокирует полный расход мономера, а агрегация коротких мономеров слабо влияет на среднюю длину цепи), и образуются глобулы с неоднородным пространственно-временным распределением, радиальная плотность которых увеличивается с ростом степени превращения.

6. Два конкурирующих механизма обрыва цепи (циклизация и запутывание) эффективно влияют на рост цепи при малых и больших степенях превращения соответственно.

7. Конкуренция указанных процессов инициирования, роста и обрыва цепи в процессе ПК обеспечивает принципиальную возможность получения олигомеров с управляемым ММР и наноразмерной архитектурой.

Работа выполнена при финансовой поддержке Программы Президиума РАН П22 и по теме Государственного задания № 0089-2019-0008.

Список литературы

  1. Voronkov M.G., Mileshkevich V.P., Yuzhelevsky Y.A. The Siloxane Bond. Consultant Bureau. N.Y. 1978.

  2. Issa A.A., Luyt A.S. // Popymers .2019. V. 11. № 537.

  3. Brinker C.J., Scherer G.W. Sol-Gel Science. 1990. Academic Press. Boston.

  4. Cypryk M.,Apeloig Y. // Organometallics. 2002. V. 21. P. 2165.

  5. Rabin Y., Grosberg A.Yu., Tanaka T. // Europhys. Lett. 1995. V. 32. P. 505.

  6. Halperin A., Goldbart P.M. // Phys. Rev. E. 2000. V. 61. P. 565.

  7. Guo J., Liang H., Wang Z-G.J. // Chem. Phys. 2011. V. 134. № 244904.

  8. Dai L., Renner C.B., Yan J., Doyle P.S. // Sci. Reports. 2015. V. 5. № 18438.

  9. McCoy B.J. // Ind. Engin. Chem. Res. 2001. V. 40. P. 5147.

  10. Frenkel D., Schilling T. // Phys. Rev. E. 2002. V. 66. P. 041606.

  11. Ким И.П., Бендерский В.А. // Химия высоких энергий. 2015. Т.49. С. 3.

  12. Schaefer D.W., Keefer K.D. // Phys. Rev. Lett. 1984. V. 53. P. 1383.

  13. Koga T., Hashimoto T., Takenaka M., Aizawa K., Nakamura M., Yamaguchi D., Kouzami S. // Macromolecules. 2006. V. 41. P. 453.

  14. Voile D.R., Donnatti D.A., Ruiz A.I., Gatto R. // Phys. Rev. B. 2006. V.74. № 024208.

  15. Zhai Q., Zhou C., Zhao S., Peng C., Han Y. // Ind. Eng. Chem. Res. 2014. V. 53. P. 13598.

  16. Sugahara Y., Okada S., Kuroda K., Kato C. // J. Non-Cryst. Solids 1992. V. 139. P. 25.

  17. Sanchez J., Rankin S.E., McCormick A.V. // Ind. Eng. Chem. Res. 1996. V. 35. P. 117.

  18. Alam T.M., Assink R.A., Loy D.A. // Chem. Mater. 1996. V. 8. P. 2366.

  19. Rankin S.E., Macosko C.W. // AIChE Journal. 1998. V. 44. P. 1141.

  20. Alam T.M., Henry M. // Phys. Chem.Chem.Phys. 2000. V. 2. P. 23.

  21. Dong H., Brook M.A., Brennan J.D. // Chem. Mater. 2006. V. 18. P. 541.

  22. Bennevault-Celton V., Maciejax O., Desmazieres B., Cherdam H. // Polymer Intern. 2010. V. 59. P. 43.

  23. Shi X., Grainer D., Narayan R. // Silicon 2012. V. 4. P. 109.

  24. Ziff R.M., Stell G. // J. Chem. Phys. 1980. V. 73. P. 3492.

  25. Leyvraz F. // Phys. Reps. 2003. V. 383. P. 95.

  26. Kuchanov S.I., Slot H., Stroeks A. // Progr. Polym. Sci. 2004. V. 29. P. 513.

  27. Wattis J.A.D. // Physica. D. 2006. V. 222. P. 1.

  28. Ким И.П., Кац Е.И., Бендерский В.А. // Химия высоких энергий. 2019. Т.53. С. 255.

  29. Ким И.П., Бендерский В.А. // Химия высоких энергий. 2019. Т. 53. № 5. С. 339.

  30. Ким И.П., Кац Е.И., Бендерский В.А. // Химия высоких энергий. 2020. Т. 54. № 1. С. 3.

  31. де Жен П. Идеи скейлинга в физике полимеров. М.: Мир, 1982.

  32. Wattis J.A.D. // J.Phys. A. 2006. V. 39. P. 7283.

  33. Wang W., Zheng Y., Roberts E., Duxbury C.J., Ding L., Irvine D.J., Howdle S.M. // Macromolecules. 2007. V. 40. P. 7184.

  34. Zhao T., Zheng Y., Poly J., Wang W. // Nature Comun. 2013. V. 4. P. 1873.

  35. Gentekos D.T., Dupuis L.N., Fors B.P. // J. Am. Chem. Soc. 2016. V. 138. P. 1848.

  36. Ignatyev I.S., Montejo M., Gonsalez J.J.L. // Dalton Transaction 2010. V. 39. P. 6967.

  37. Flory P.J. // Principles of Polymer Chemistry. Cornell Univ. Press. Ithaka. 1953.

  38. Гросберг А.Ю., Хохлов А.Р. Статистическая физика макромолекул. М.: Наука, 1989.

  39. Ovchinnikov A.A., Timashev S.F., Belyy A.A. Kinetic of diffusion controlled chemical processes. Nova Science Publ. N.Y. 1986.

  40. Арнольд В.И. Обыкновенные дифференциальные уравнения. М.: Наука, 1984.

  41. Jethmalane J.M., Ford W.T. // Langmuir. 1997. V. 13. P. 3338.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Химия высоких энергий

Архивы выпусков Информация о журнале Отправить рукопись в журнал