1. На главную
  2. Электронные версии
  3. Химия высоких энергий
  4. T. 54, № 6, 2020

Химия высоких энергий, 2020, T. 54, № 6, стр. 433-442

Фотоэффект в органических солнечных элементах на основе фталоцианинов. II. Захват молекулярных экситонов примесями

В. А. Бендерский a, *, И. П. Ким a

a Институт проблем химической физики РАН
142432 Московская обл., Черноголовка, просп. Академика Семенова, 1, Россия

* E-mail: bender@icp.ac.ru

Поступила в редакцию 15.06.2020
После доработки 15.06.2020
Принята к публикации 06.07.2020

Полный текст (PDF)

Аннотация

Захват молекулярных экситонов ионизующимися примесями является быстрой начальной стадией фотоэффекта в органических солнечных элементах. Константы скорости захвата МЭ при постоянной концентрации примеси ${{N}_{I}}$ найдены в модели ограниченных диффузией бимолекулярных реакций. Модель учитывает два канала квазистационарного захвата МЭ – контактный и объемный (обусловленный диполь-дипольным взаимодействием с примесью), определяемые диффузионной длиной МЭ ${{l}_{S}}$, минимальным радиусом сближения партнеров ${{a}_{0}}$ и радиусом Фёрстера ${{R}_{S}}$. Квантовый выход захвата при ${{R}_{S}} > {{a}_{0}}$ равен ${{Y}_{S}} = {{\left( {1 + b} \right)}^{{ - 1}}}\;$, ${{b}^{{ - 1}}}$ ≈ $4\pi {{\left( {2{{l}_{D}}{{R}_{S}}} \right)}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}{{N}_{I}}$. Обсуждаются возможные условия легирования, когда ${{Y}_{S}}\sim 1$ при ${{N}_{I}}\sim $1018см-3.

Ключевые слова: молекулярные экситоны, ограниченные диффузией бимолекулярные реакции, контактный радиус, радиус Фёрстера

I. ВВЕДЕНИЕ

В предыдущей статье [1] рассмотрена термически активированная ионизация молекулярных экситонов (МЭ) в кристаллах фталоцианинов (Рс) и показано, что в этом механизме фотоэффекта квантовый выход электронов и дырок (~10–4 при 300 К) одинаков, вероятность ионизации подчиняется аррениусовской зависимости с энергией активации (0.20–0.25 эВ), равной разности ширины запрещенной зоны и энергии основного колебательного состояния, и частотный фактор (~1011 c–1) одного порядка с обратным временем собственной аннигиляции МЭ. Фотоэффект с такими свойствами наблюдается в кристаллах высокой степени чистоты (с концентрацией активных примесей $ \leqslant $10–3 мол. %), когда проводимость близка к собственной [2, 3]. Кристаллы Рс, легированные различными донорами и акцепторами, становятся соответственно полупроводниками n- и p‑типа, в которых квантовый выход возрастает пропорционально концентрации примеси $N{}_{I}$ в интервале ~1016–1018 см–3, слабо зависит от температуры и для электронов и дырок может отличаться по порядку величины. Участие МЭ в примесном фотоэффекте в слоях Рс доказывает то, что его спектр действия совпадает со спектром экситонного поглощения. Известно множество примеров передачи энергии МЭ примесным центрам c основным электронным состоянием ${{I}_{0}},$ вызывающее их переход в возбужденное синглетное электронное состояние $I{}_{1},$ спонтанное излучение которого регистрируется как флуоресценция [4–7]

(1)
${{S}_{1}} + {{I}_{0}} \to {{S}_{0}} + {{I}_{1}},\,\,\,\,{{I}_{1}}\xrightarrow{{\hbar {\omega }}}{{I}_{0}}.$

При интенсивностях солнечного света, генерирующего МЭ, акты передачи энергии (1) происходят настолько редко в масштабе времени аннигиляции ${{I}_{1}},$ что концентрацию собирающих МЭ примесных центров ${{I}_{0}}$ считают постоянной. Образование носителей тока при взаимодействии МЭ с донорными (акцепторными) примесями в органических солнечных элементах (ОСЭ) отличается от этого процесса тем, что передаваемая энергия МЭ тратится не на внутримолекулярные излучательные переходы, а на последующую безызлучательную ионизацию $I{}_{1},$ при которой возбужденная примесь (донор или акцептор $I = D(A)$) превращается в носители тока ${{e}^{ - }},$ ${{h}^{ + }}$ и долгоживущий заряд противоположного знака, локализованный на примесном узле ${{D}^{ + }},$ ${{A}^{ - }}$

(2)
${{A}_{1}} \to {{A}^{ - }} + {{h}^{ + }},\,\,\,\,{{D}_{1}} \to {{D}^{ + }} + {{e}^{ - }}.$

Обратные переходы, восстанавливающие концентрации ${{I}_{0}},$ определяются процессами рекомбинации носителей тока, характеристические времена которых, согласно экспериментальным данным [2, 3, 8, 9], на несколько порядков больше, чем МЭ. Благодаря различному масштабу времен жизни ${{S}_{1}},$ как быстрой подсистемы (~10–11), и изменения концентрации нейтральных и ионизованных примесей и носителей тока, как медленной подсистемы ($ \geqslant $10–7 с), концентрация МЭ адиабатически следует за медленно изменяющимися населенностями примесных центров, так что фотоэффект в ОСЭ можно рассмотреть, как последовательность (1) и (2), и его квантовый выход равен произведению их квантовых выходов. При бимолекулярном захвате и медленно изменяющейся концентрации примеси квантовый выход (1) равен

(3)
${{Y}_{S}} = {{\left( {{{1 + 1} \mathord{\left/ {\vphantom {{1 + 1} {{{\gamma }_{S}}{{\tau }_{S}}{{N}_{I}}(t)}}} \right. \kern-0em} {{{\gamma }_{S}}{{\tau }_{S}}{{N}_{I}}(t)}}} \right)}^{{ - 1}}},$
где ${{\gamma }_{S}}$ – константа скорости (1), ${{\tau }_{S}}$ – время аннигиляции МЭ по всем каналам, кроме захвата, ${{N}_{I}}(t)$ – концентрация, которую при решении кинетической задачи (1) можно считать постоянной (${{N}_{I}}(t) = {{N}_{I}}$), а затем найти ее изменение из решения кинетической задачи для носителей тока и заполнения примесных уровней. Решение первой задачи определяет концентрацию МЭ как функцию ${{\gamma }_{S}},$ ${{\tau }_{S}}$ и позволяет найти значения ${{N}_{I}},$ при которых ${{Y}_{S}}$ ∼ 1, что необходимо для оценки эффективности ОСЭ в целом. Такая оценка для легированных органических кристаллов с высоким квантовым выходом собственной и примесной флуоресценции не представляет трудностей. Однако для большинства фоточувствительных материалов, используемых в ОСЭ, в том числе фталоцианинов (Рс), значения ${{\tau }_{S}}$ (обычно 10–11–10–10 с) более чем на порядок короче излучательного времени жизни, рассчитанного, исходя из дипольного момента оптического перехода, и составляющего ~10–9 c при среднем коэффициенте поглощения в экситонной полосе ~105 cм–1 [4, 7, 10, 11]. Высокая скорость безызлучательных переходов обусловлена сильным экситон-фононным взаимодействием в больших молекулах и связана с факториально быстрым ростом плотности низкочастотных внутримолекулярных колебаний с увеличением числа атомов в молекуле.

Значение ${{\gamma }_{S}}$ не превышает константу скорости, ограниченную диффузией

(4)
${{\gamma }_{S}} = 4\pi {{D}_{S}}R,$
где $R$ – эффективный радиус взаимодействия, ${{D}_{S}}$ – коэффициент диффузии МЭ, измеренные значения которого в ОСЭ лежат в широком интервале 10–5–10–2 см2 с–1, от присущих гидродинамической диффузии молекул в слабо вязкой среде [11–13] до значений, соответствующих когерентному переносу МЭ в кристаллах [6, 10–14]. Низкие измеряемые значения дрейфовой подвижности МЭ, по-видимому, обусловлены не только малыми матричными элементами межмолекулярного переноса [6, 10–14], но и морфологией некристаллических структур с высоким содержанием примесей, состоящих из наноразмерных агрегатов различного состава и строения [15–17]. Наибольшие значения ${{D}_{S}}$ соответствуют матричным элементам диполь–дипольного переноса вдоль оси $b$ (между плоскими молекулами в стопках [1, 6, 8, 9]). Значения ${{D}_{S}}$ того же порядка характерны для собирающих свет молекулярных агрегатов с плоско-параллельной упаковкой молекул, напоминающей ближний порядок в молекулярных кристаллах [18–20]. Для разрешенных дипольных переходов значения $R$ определяются перекрыванием спектров флуоресценции МЭ и электронного поглощения примеси [4–7, 10, 21–23] и в несколько раз превышают межмолекулярное расстояние ${{a}_{0}}$ = 0.5–1.5 нм, достигая 4–5 нм [4–6, 10, 24]. Широко применяемый метод определения ${{\gamma }_{S}}$ по зависимости квантового выхода примесной флуоресценции от ее концентрации [4], как правило, приводит к значениям, меньшим предсказываемых (4), что, возможно, обусловлено уменьшением коэффициента диффузии в окрестности примеси, вызываемым деформацией кристаллической решетки при легировании. Наиболее высокие значения констант измерены для бимолекулярной рекомбинации двух МЭ (синглет-синглетной рекомбинации), наблюдаемой при высоких концентрациях экситонов, создаваемой интенсивным импульсным освещением, когда искажения решетки отсутствуют. В кристаллах антрацена ${{\gamma }_{S}}$ = 1 × 10–8 см3 с–1 [10, 11], чему при независимо измеренном коэффициенте диффузии ${{D}_{S}}$ ≈ 10–2 см2 с–1, соответствует $R$ ≈ 4 нм. В [6, 24–28] приведены примеры молекулярных агрегатов, в которых измеренные значения достигают 4–6 нм. Эти данные свидетельствуют о дальнодействующем механизме, обусловленном диполь-дипольным взаимодействием МЭ с примесью, когда захват происходит в объеме кристалла и его вероятность зависит от расстояния между партнерами
(5)
$W\left( r \right) = \tau _{S}^{{ - 1}}{{({{{{R}_{S}}} \mathord{\left/ {\vphantom {{{{R}_{S}}} r}} \right. \kern-0em} r})}^{6}},$
где ${{R}_{S}}$ – радиус Фёрстера [4–7]. Благодаря диффузии короткоживущих частиц их поверхностный и объемный захват становятся конкурирующими: при быстрой диффузии часть МЭ избегает захвата в объеме и достигает поверхности захвата $r = {{a}_{0}},$ тогда как при медленной диффузии доминирует объемный захват. Хотя экспериментальные данные для молекулярных кристаллов доказывают, что достижимы значения ${{\gamma }_{S}}$ ∼ 10–8–10–9 см3 с–1 и ${{\tau }_{S}}$ ∼ 10–9 с, при которых, согласно (3), квантовый выход захвата ${{Y}_{S}}$ ~ 1, когда ${{N}_{I}}$ ∼ 1018 см–3, концентрацию примеси, необходимую для получения высокого квантового выхода передачи энергии в ОСЭ, нельзя считать надежно установленной. Этот ключевой вопрос для создания эффективных ОСЭ определяет их наноразмерную структуру, которая с ростом уровня легирования изменяется от структуры основного кристалла при ${{{{N}_{I}}} \mathord{\left/ {\vphantom {{{{N}_{I}}} {{{N}_{0}}}}} \right. \kern-0em} {{{N}_{0}}}}$ ≤ 10–3 к структуре смешанного кристалла при ${{{{N}_{I}}} \mathord{\left/ {\vphantom {{{{N}_{I}}} {{{N}_{0}}}}} \right. \kern-0em} {{{N}_{0}}}}$ ∼ 1, где ${{N}_{0}}$ ∼ 1021 см–3– число молекул основного вещества. Между этими двумя пределами расположена широкая область неоднородных молекулярных агрегатов, внутри которых перенос энергии зависит не только от межмолекулярных расстояний, но и границ между агрегатами. Поэтому еще не решенный вопрос о степени легирования, обеспечивающей ${{Y}_{S}}$ ~ 1, можно сформулировать иначе: какие размеры собирающих свет молекулярных агрегатов обеспечивают возможность создать эффективные ОСЭ? Многочисленные современные исследования эффективных ОСЭ показывают, что коэффициент преобразования, выросший за последние 10 лет от 3 до 17% [29–35], достигается в структурах с объемными гетеропереходами, в которых размеры агрегатов одного порядка с радиусом экситонного переноса. Эти данные не отвечают на поставленный выше вопрос, поскольку необходимость такой структуры может быть связана как с условиями эффективной передачи энергии ионизующимся примесям, так и условиями эффективного разделения заряда.

Модель ограниченного диффузией захвата МЭ разработана почти 50 лет назад [7, 10, 11, 36–38]. Однако в ней сформулированный выше вопрос о конечных размерах агрегатов, в которых происходит передача энергии, не был рассмотрен.

Цель этой статьи – восполнить этот пробел в теории ОСЭ, рассмотрев кинетику примесного фотоэффекта и найдя минимальные концентрации донорных и акцепторных уровней, при которых квантовый выход ~1. Статья состоит из следующих разделов. Во втором разделе кинетическая задача о диффузионно-ограниченной аннигиляции МЭ в изотропной непрерывной среде решена в пределе низкой концентрации примеси, учитывая контактный (при минимальном расстоянии между партнерами) и объемный (при диполь-дипольном взаимодействии, характеризуемом радиусом Фёрстера) захват примесями. В третьем разделе расчет эффективности захвата обобщен на случай сферических агрегатов, радиус которых одного порядка с радиусом Фёрстера и диффузионной длиной, и оптимальные параметры кинетической модели сопоставлены с измеренными параметрами МЭ (временами аннигиляции, коэффициентами диффузии, радиусами захвата) и примесей (концентрациями и энергиями уровней), легирующих Рс. Обсуждение результатов и выводы собраны в четвертом разделе. Детали расчета даны в Приложении, где введены безразмерные параметры, являющиеся комбинацией четырех характеристических длин ${{a}_{0}},{{l}_{D}},{{R}_{S}},L.$

II. МОДЕЛЬ ДИФФУЗИОННО-ОГРАНИЧЕННОГО ЗАХВАТА МОЛЕКУЛЯРНЫХ ЭКСИТОНОВ ПРИМЕСЯМИ

В молекулярном кристалле с примесями, являющимися центрами захвата МЭ, зависящая от координаты $\vec {r}$ концентрация МЭ ${{n}_{S}}(\vec {r})$ в условиях однородного поглощения света постоянной интенсивности описывается уравнением [7]

(6)
$\frac{{\partial {{n}_{S}}}}{{\partial t}} = {{D}_{S}}\Delta {{n}_{S}} + I - \left( {\tau _{S}^{{ - 1}} + {{N}_{I}}W\left( r \right)} \right){{n}_{S}} = 0,$
где ${{D}_{S}}$ – коэффициент диффузии МЭ в изотропной трехмерной среде, $W(r)$ – усредненная по ориентациям партнеров вероятность захвата (5), зависящая только от расстояния r между МЭ и центром захвата [5–7], ${{N}_{I}}$ – концентрация примеси, $I$ – объемная скорость генерации, равная интенсивности падающего света, умноженной на коэффициент поглощения $k,$ с размерностью [см–3 с–1], ${{\tau }_{s}}$ – время аннигиляции МЭ по всем каналам, не связанным с примесью. Уравнение (6) соответствует модели Смолуховского, определяющей константу скорости бимолекулярной рекомбинации, ограниченной диффузией МЭ. В этой модели полный объем разбивается на ${{N}_{I}}$ сферических ячеек, число которых на несколько порядков меньше числа основных молекул в кристалле (${{{{N}_{1}}} \mathord{\left/ {\vphantom {{{{N}_{1}}} {{{N}_{0}}}}} \right. \kern-0em} {{{N}_{0}}}} < \ll 1$). Каждая ячейка содержит один центр захвата, так что радиус ячейки равен половине среднего расстояния между примесями

(7)
$L = {{\left( {{{4\pi {{N}_{I}}} \mathord{\left/ {\vphantom {{4\pi {{N}_{I}}} 3}} \right. \kern-0em} 3}} \right)}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 3}} \right. \kern-0em} 3}}}}.$

Модель была предложена для описания коагуляции субмикронных частиц в коллоидных растворах и аэрогелях, где $L$ ≥ 10–5 см и бимолекулярные реакции происходят при контакте поверхностей частиц, когда расстояние между ними минимально. Многочисленные исследования молекулярной диффузии и ограниченных диффузией бимолекулярных реакций в растворах, а также молекулярно-динамические расчеты [39–41] надежно установили, что модель Смолуховского применима в наноразмерном масштабе расстояний, если дополнить захват на поверхности захватом в объеме, обусловленным межмолекулярным взаимодействием и определяющим $W(r)$ в (5). Следует подчеркнуть, что при переходе к объемному захвату МЭ, как короткоживущих частиц, необходимы поправки к модели Смолуховского, связанные с тем, что минимальное расстояние между центром захвата и МЭ ${{a}_{0}},$ диффузионная длина ${{l}_{D}} = \sqrt {{{D}_{S}}{{\tau }_{S}}} $ и радиус захвата ${{R}_{S}}$ одного порядка.

Разделение объема на ячейки позволяет представить аннигиляцию МЭ в виде суммы двух потоков – спонтанной аннигиляции ${{J}_{0}},$ определяемой временем жизни ${{\tau }_{S}}$ и не зависящей явно от ${{N}_{I}},$ и захвата ${{J}_{I}},$ пропорционального ${{N}_{I}}.$ В квазистационарных условиях сумма двух потоков равна скорости генерации

(8)
$\begin{gathered} {{J}_{0}} + {{N}_{I}}{{J}_{I}} = I,\,\,\,\,{{J}_{I}} = {{J}_{s}} + {{J}_{{v}}}, \\ {{J}_{0}} = \tau _{S}^{{ - 1}}\int\limits_{{{a}_{0}}}^L {{{n}_{S}}(r)4\pi {{r}^{2}}dr} ,\,\,\,\,{{J}_{s}} = {{\left. {4\pi {{r}^{2}}\frac{{d{{n}_{S}}}}{{dr}}} \right|}_{{r = {{a}_{0}}}}}, \\ {{J}_{{v}}} = \tau _{S}^{{ - 1}}\int\limits_{{{a}_{0}}}^L {W(r){{n}_{S}}(r)4\pi {{r}^{2}}dr} . \\ \end{gathered} $

Чтобы ввести бимолекулярную константу скорости аннигиляции на примесях ${{\gamma }_{S}},$ необходимо перейти от определяемой (6) локальной концентрации МЭ к входящей в ${{J}_{0}}$ усредненной по объему концентрации

(9)
$\begin{gathered} {{J}_{0}} = {{{{{\bar {n}}}_{S}}} \mathord{\left/ {\vphantom {{{{{\bar {n}}}_{S}}} {{{\tau }_{S}}}}} \right. \kern-0em} {{{\tau }_{S}}}},\,\,\,{{J}_{I}} = {{\gamma }_{S}}{{N}_{I}}{{{\bar {n}}}_{S}}, \\ {{\gamma }_{S}} = {{{{{({{N}_{I}}\tau {}_{S})}}^{{ - 1}}}{{J}_{I}}} \mathord{\left/ {\vphantom {{{{{({{N}_{I}}\tau {}_{S})}}^{{ - 1}}}{{J}_{I}}} {{{J}_{0}}}}} \right. \kern-0em} {{{J}_{0}}}}. \\ \end{gathered} $

Согласно (9), константа скорости ${{\gamma }_{S}}$ равна отношению введенных в (8) потоков аннигиляции.

Поскольку ${{\tau }_{S}}$ не зависит от $r$ и (7) связывает объем ячейки с ${{N}_{I}},$ из уравнения непрерывности следует равенство светового потока $I$ и потоков собственной и примесной аннигиляции в объеме и на поверхности всех ячеек. Поверхностная аннигиляция МЭ происходит на поверхности сферы захвата, создавая поток ${{J}_{s}},$ а объемная примесная аннигиляция создает дополнительный поток ${{J}_{{v}}},$ изменяющий также ${{J}_{s}},$ поскольку гибель МЭ в объеме уменьшает их концентрацию на сфере захвата. В отсутствие объемной аннигиляции ($W = 0$) (9) преобразуется в уравнение

(10)
${{{{d}^{2}}\Phi } \mathord{\left/ {\vphantom {{{{d}^{2}}\Phi } {d{{r}^{2}}}}} \right. \kern-0em} {d{{r}^{2}}}} - l_{D}^{{ - 2}}\Phi = - I{{\tau }_{S}}r,\,\,\,\,\Phi = rn(r)$

с граничными условиями

(11)
${{D}_{S}}{{\left. {\frac{{d{{n}_{S}}}}{{dr}}} \right|}_{{r = {{a}_{0}}}}} = sn({{a}_{0}}) = 0,\,\,\,\,{{\left. {{{dn} \mathord{\left/ {\vphantom {{dn} {dr}}} \right. \kern-0em} {dr}}} \right|}_{{r = L}}} = 0,$
где $s$ – скорость поверхностной рекомбинации. Первое из условий (11) учитывает частичное отражения МЭ от “серой” сферы захвата при конечных значениях $s.$ Второе условие предполагает отсутствие потоков между ячейками, соответствующее независимым изменениям в них концентраций. В пределе низких концентраций примеси (${{L}^{{ - 1}}} = $ 0) это условие можно заменить условием постоянной концентрации МЭ на границе ячейки $n(\infty ) = I{{\tau }_{s}}.$ Решение (10), не учитывающее экспоненциально малые поправки $O(\exp ({{ - 2L} \mathord{\left/ {\vphantom {{ - 2L} {{{l}_{D}}}}} \right. \kern-0em} {{{l}_{D}}}})),$ рассмотренные в следующем разделе, имеет вид
(12)
$n(r) = I{{\tau }_{S}}\left( {1 - \frac{{{{{\tilde {a}}}_{0}}}}{r}\exp \left( { - \frac{{r - {{a}_{0}}}}{{{{l}_{D}}}}} \right)} \right),\,\,\,\,L \gg {{l}_{D}},$
где эффективный радиус захвата ${{\tilde {a}}_{0}}$ становится меньше ${{a}_{0}}$ из-за конечной скорости поверхностной рекомбинации

(13)
${{\tilde {a}}_{0}} = {{a}_{0}}({{1 + D} \mathord{\left/ {\vphantom {{1 + D} {{{a}_{0}}s}}} \right. \kern-0em} {{{a}_{0}}s}}).$

Бимолекулярная константа скорости равна

(14)
${{\gamma }_{S}} = 4\pi {{D}_{S}}{{\tilde {a}}_{0}}({{1 + {{a}_{0}}} \mathord{\left/ {\vphantom {{1 + {{a}_{0}}} {{{l}_{D}}}}} \right. \kern-0em} {{{l}_{D}}}}).$

Согласно (13) и (14), поперечник захвата становится меньше ${{a}_{0}}$ с ростом диффузионной длины и скорости поверхностной рекомбинации. По сравнению с захватом стабильных частиц, для которых $l_{D}^{{ - 1}}$ = 0, $n\left( r \right)$ = ${{n}_{0}}({{1 - {{{\tilde {a}}}_{0}}} \mathord{\left/ {\vphantom {{1 - {{{\tilde {a}}}_{0}}} r}} \right. \kern-0em} r}),$ конечная длина диффузии в (12) уменьшает область $r,$ в которой захват уменьшает $n(r).$ Для стабильных частиц поток $J(r) = {{4\pi {{D}_{S}}{{r}^{2}}dn} \mathord{\left/ {\vphantom {{4\pi {{D}_{S}}{{r}^{2}}dn} {dr}}} \right. \kern-0em} {dr}}$ = $4\pi {{D}_{S}}{{\tilde {a}}_{0}}{{n}_{0}}$ не зависит от $r,$ тогда как для МЭ поток экспоненциально мал при $r > {{a}_{0}} + {{l}_{D}}.$

(15)
$\begin{gathered} {{J}_{s}}(r) = {{{{N}_{I}}4\pi {{D}_{S}}{{r}^{2}}dn} \mathord{\left/ {\vphantom {{{{N}_{I}}4\pi {{D}_{S}}{{r}^{2}}dn} {dr}}} \right. \kern-0em} {dr}} = \\ = {{N}_{I}}4\pi l_{D}^{2}{{{\tilde {a}}}_{0}}I({{1 + r} \mathord{\left/ {\vphantom {{1 + r} {{{l}_{D}}}}} \right. \kern-0em} {{{l}_{D}}}})\exp ({{ - (r - {{a}_{0}})} \mathord{\left/ {\vphantom {{ - (r - {{a}_{0}})} {{{l}_{D}}}}} \right. \kern-0em} {{{l}_{D}}}}) \\ \end{gathered} $

выражения (15) показывают, что отношение ${{{{J}_{s}}} \mathord{\left/ {\vphantom {{{{J}_{s}}} I}} \right. \kern-0em} I}$ равно отношению объема области захвата $\sim {\kern 1pt} 4\pi l_{D}^{2}{{\tilde {a}}_{0}},$ в которой доминирует захват, к полному объему ячейки (7).

Вероятность объемного захвата характеризует радиус Фёрстера ${{R}_{S}}$ (5). Как и в случае поверхностного захвата, для решения (6) вводятся новые безразмерные переменные [38]

(16)
$z = {\alpha \mathord{\left/ {\vphantom {\alpha {{{r}^{2}}}}} \right. \kern-0em} {{{r}^{2}}}},\,\,\,\,\Phi = {{r}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0em} 2}}}}y,\,\,\,\,\alpha = {{R_{S}^{3}} \mathord{\left/ {\vphantom {{R_{S}^{3}} {2{{l}_{D}}}}} \right. \kern-0em} {2{{l}_{D}}}}$

преобразующие (6) в уравнение

(17)
$\begin{gathered} {{{{z}^{2}}{{d}^{2}}\Phi } \mathord{\left/ {\vphantom {{{{z}^{2}}{{d}^{2}}\Phi } {d{{z}^{2}}}}} \right. \kern-0em} {d{{z}^{2}}}} + {{zd\Phi } \mathord{\left/ {\vphantom {{zd\Phi } {dz}}} \right. \kern-0em} {dz}} - ({{{{z}^{2}} + 1} \mathord{\left/ {\vphantom {{{{z}^{2}} + 1} {16}}} \right. \kern-0em} {16}} + {q \mathord{\left/ {\vphantom {q z}} \right. \kern-0em} z})y = \\ = - q{{\alpha }^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}{{z}^{{{{ - 5} \mathord{\left/ {\vphantom {{ - 5} 4}} \right. \kern-0em} 4}}}},\,\,\,\,q = {{({{{{R}_{S}}} \mathord{\left/ {\vphantom {{{{R}_{S}}} {{{l}_{D}}}}} \right. \kern-0em} {{{l}_{D}}}})}^{3}}. \\ \end{gathered} $

Решение (17) рассмотрено в Приложении. Радиальное распределение МЭ в окрестности центра захвата представлено на рис. 1. В случае поверхностной аннигиляции (жирная кривая) концентрация МЭ уменьшается в области захвата ${{a}_{0}} \leqslant r \leqslant {{l}_{D}}$ и равна $I{{\tau }_{S}}\,(y = 1)$ при $r \gg {{l}_{D}}.$ При ${{R}_{s}} \leqslant {{a}_{0}}$ вероятность объемного захвата остается меньше, чем поверхностного. При ${{R}_{s}} > {{a}_{0}}$ область захвата расширяется с ростом радиуса Фёрстера (кривые 1–5). Рисунок 1 показывает, что радиальное распределение характеризует эффективная полуширина области захвата, определяемая условием $y\left( {R_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{*}} \right)$ = 1/2, которая при ${{R}_{S}},{{l}_{D}} \gg {{a}_{0}}$ зависит только от одного безразмерного параметра $q$ в (17).

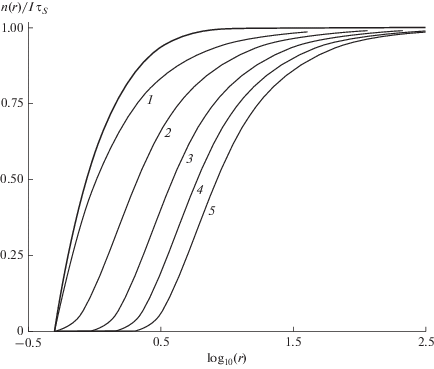
Рис. 1.

Радиальное распределение концентрации МЭ в окрестности центра захвата. Жирная линия соответствует поверхностной аннигиляции с радиусом ${{a}_{0}} = $ 0.5 нм. Кривые 1–5 относятся к поверхностно-объемному захвату при ${{a}_{0}} = $ 0.5 нм и радиусе Фёрстера ${{R}_{S}}$ = 1, 2, 3, 4, 5 нм (кривые 1–5 соответственно). Диффузионная длина ${{l}_{d}}$ = 3 нм. Значения $R_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{*}$ соответствуют значениям $r,$ при которых ${{n(r)} \mathord{\left/ {\vphantom {{n(r)} {I{{\tau }_{S}}}}} \right. \kern-0em} {I{{\tau }_{S}}}}$ = 1/2.

Потоки поверхностной и объемной аннигиляции в переменных (16) равны

(18)
$\begin{gathered} {{{{J}_{s}}} \mathord{\left/ {\vphantom {{{{J}_{s}}} {I{{N}_{I}}}}} \right. \kern-0em} {I{{N}_{I}}}} = 4\pi l_{D}^{2}{{a}_{0}}z_{0}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}{{\left. {{{dy} \mathord{\left/ {\vphantom {{dy} {dz}}} \right. \kern-0em} {dz}}} \right|}_{{z = z{}_{{_{0}}}}}}, \\ {{{{J}_{{v}}}} \mathord{\left/ {\vphantom {{{{J}_{{v}}}} {I{{N}_{I}}}}} \right. \kern-0em} {I{{N}_{I}}}} = 2\pi {{\left( {2{{l}_{D}}{{R}_{S}}} \right)}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}\int\limits_0^{{{z}_{0}}} {{{z}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}y(z)dz} . \\ \end{gathered} $

Соотношение поверхностной и объемной аннигиляции определяется безразмерным параметром

(19)
${{{{J}_{{v}}}} \mathord{\left/ {\vphantom {{{{J}_{{v}}}} {{{J}_{s}}}}} \right. \kern-0em} {{{J}_{s}}}} = {{{{z}_{0}}} \mathord{\left/ {\vphantom {{{{z}_{0}}} 2}} \right. \kern-0em} 2},\,\,\,\,{{z}_{0}} = {{R_{S}^{3}} \mathord{\left/ {\vphantom {{R_{S}^{3}} {2{{l}_{D}}a_{0}^{2}}}} \right. \kern-0em} {2{{l}_{D}}a_{0}^{2}}}$

и представлено на рис. 2. Согласно (19), поверхностный захват (кривая 1) существенен при ${{z}_{0}} \leqslant 1$ и мал при ${{z}_{0}} > 2$. Из (18) следует наличие трех областей захвата, где

(20)
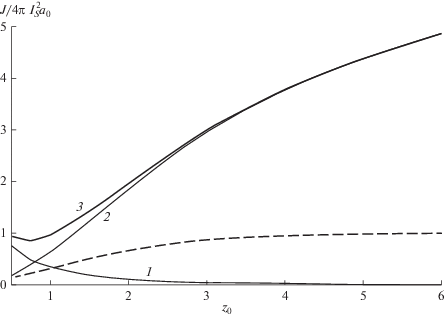
${{({{J}_{s}} + {{J}_{{v}}}({{z}_{0}}))} \mathord{\left/ {\vphantom {{({{J}_{s}} + {{J}_{{v}}}({{z}_{0}}))} {I{{N}_{I}}}}} \right. \kern-0em} {I{{N}_{I}}}} \approx \left\{ {\begin{array}{*{20}{c}} {{{4\pi R_{S}^{3}} \mathord{\left/ {\vphantom {{4\pi R_{S}^{3}} 3}} \right. \kern-0em} 3},\,\,\,{{R}_{S}},\,\,\,{{a}_{0}} \gg {{l}_{D}}} \\ {2\pi {{{\left( {{{R}_{S}}{{l}_{D}}} \right)}}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}},\,\,\,{{z}_{0}}\sim 1} \\ {4\pi l_{D}^{2}{{a}_{0}},\,\,\,{{R}_{S}} < {{l}_{D}},\,\,\,{{a}_{0}}} \end{array}} \right..$
Рис. 2.

Зависимость квантового выхода поверхностного, объемного и суммарного захвата (кривая 1, 2, 3 соответственно) от параметра ${{z}_{0}} = {{R_{S}^{3}} \mathord{\left/ {\vphantom {{R_{S}^{3}} {2{{l}_{D}}a_{0}^{2}}}} \right. \kern-0em} {2{{l}_{D}}a_{0}^{2}}}.$ Пунктиром показана радиальная плотность МЭ, как функция того же параметра ${{n({{z}_{0}})} \mathord{\left/ {\vphantom {{n({{z}_{0}})} {I{{\tau }_{s}}}}} \right. \kern-0em} {I{{\tau }_{s}}}}.$

При малой диффузионной длине доминирует объемный захват с вероятностью (5), в промежуточной области ${{z}_{0}}\sim 1$ захват зависит от трех параметров, а поверхностный захват, обусловленный диффузией, преобладает при малых ${{R}_{S}}.$

III. ЗАХВАТ ЭКСИТОНОВ В СФЕРИЧЕСКИХ ЯЧЕЙКАХ КОНЕЧНОГО РАДИУСА

Эффективность преобразования МЭ в ОСЭ определяет отношение (20), зависящее не только от ${{z}_{0}},$ но и радиуса ячейки $L,$ входящего в граничное условие (11). Рост КПД ОСЭ возможен, если $L$ уменьшается настолько, что объем ячейки, в котором преобладает собственная аннигиляция становится меньше области захвата МЭ примесью.

При поверхностном захвате решение (6) имеет вид

(21)
$\begin{gathered} y(r) = {{1 + (A\exp ({{ - r} \mathord{\left/ {\vphantom {{ - r} {{{l}_{D}}}}} \right. \kern-0em} {{{l}_{D}}}}) + B\exp ({r \mathord{\left/ {\vphantom {r {{{l}_{D}}}}} \right. \kern-0em} {{{l}_{D}}}}))} \mathord{\left/ {\vphantom {{1 + (A\exp ({{ - r} \mathord{\left/ {\vphantom {{ - r} {{{l}_{D}}}}} \right. \kern-0em} {{{l}_{D}}}}) + B\exp ({r \mathord{\left/ {\vphantom {r {{{l}_{D}}}}} \right. \kern-0em} {{{l}_{D}}}}))} r}} \right. \kern-0em} r}, \\ {{a}_{0}} \leqslant r \leqslant L, \\ \end{gathered} $
где коэффициенты $A$ и $B$ решений однородного уравнения удовлетворяют граничным условиям

(22)
$\begin{gathered} A\exp ({{ - {{a}_{0}}} \mathord{\left/ {\vphantom {{ - {{a}_{0}}} {{{l}_{D}}}}} \right. \kern-0em} {{{l}_{D}}}}) + B\exp ({{{{a}_{0}}} \mathord{\left/ {\vphantom {{{{a}_{0}}} {{{l}_{D}}}}} \right. \kern-0em} {{{l}_{D}}}}) = \\ = - {{a}_{0}},\,\,\,\,A\left( {{{1 + L} \mathord{\left/ {\vphantom {{1 + L} {{{l}_{D}}}}} \right. \kern-0em} {{{l}_{D}}}}} \right)\exp ({{ - L} \mathord{\left/ {\vphantom {{ - L} {{{l}_{D}}}}} \right. \kern-0em} {{{l}_{D}}}}) + \\ + \,\,B\left( {{{1 - L} \mathord{\left/ {\vphantom {{1 - L} {{{l}_{D}}}}} \right. \kern-0em} {{{l}_{D}}}}} \right)\exp ({L \mathord{\left/ {\vphantom {L {{{l}_{D}}}}} \right. \kern-0em} {{{l}_{D}}}}) = 0. \\ \end{gathered} $

Радиальное распределение в ячейке конечного радиуса кардинально изменяется с ростом ${{{{l}_{D}}} \mathord{\left/ {\vphantom {{{{l}_{D}}} L}} \right. \kern-0em} L}.$ Когда ${{{{l}_{D}}} \mathord{\left/ {\vphantom {{{{l}_{D}}} L}} \right. \kern-0em} L} \ll 1,$ $y(r)$ на границе ячейки близка к 1, как в пределе низких концентраций, рассмотренном в предыдущем разделе. Напротив, при ${{{{l}_{D}}} \mathord{\left/ {\vphantom {{{{l}_{D}}} L}} \right. \kern-0em} L} \gg 1$ МЭ захватывается примесью во всем объеме ячейки, так что концентрация МЭ уменьшается всюду, вплоть до $y(L) \ll 1$ (рис. 3) и квантовый выход захвата резко увеличивается по сравнению с пределом ${{L}^{{ - 1}}} = 0$ (рис. 4).

Рис. 3.

Радиальное распределение МЭ в сферической ячейке радиусом $L$ = 5 нм при поверхностном захвате и диффузионной длине ${{l}_{D}}$ = 1, 3, 5, 7, 10 нм (кривые 1–5 соответственно). ${{a}_{0}}$ = 0.5 нм.

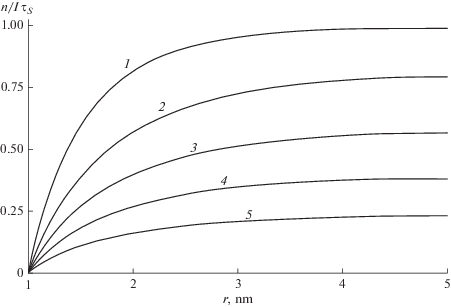
Рис. 4.

Зависимость квантового выхода поверхностного захвата МЭ от концентрации примеси ${{N}_{I}},$ определяющей радиус ячейки $L = {{\left( {{{4\pi {{N}_{I}}} \mathord{\left/ {\vphantom {{4\pi {{N}_{I}}} 3}} \right. \kern-0em} 3}} \right)}^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 3}} \right. \kern-0em} 3}}}}.$ $L$ = 5 нм. ${{a}_{0}}$ = 1 нм. Диффузионная длина МЭ ${{l}_{D}}$ = 1, 3, 5, 8, 12 нм (кривые 1–5 соответственно).

Для расчета скорости объемного захвата решим уравнение (17) при $z = {{z}_{0}}$ и

(23)
${{z}_{L}} = {{R_{S}^{3}} \mathord{\left/ {\vphantom {{R_{S}^{3}} {2{{l}_{D}}{{L}^{2}}}}} \right. \kern-0em} {2{{l}_{D}}{{L}^{2}}}}.$

Как показано в Приложении, решение имеет вид

(24)
$\begin{gathered} y(z) = {{\left( {\frac{z}{\alpha }} \right)}^{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}(A({{z}_{0}},{{z}_{L}}){{K}_{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}(z) + \\ + \,\,B({{z}_{0}},{{z}_{L}}){{I}_{{{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0em} 4}}}}(z)) + q{{(q + {z \mathord{\left/ {\vphantom {z {16}}} \right. \kern-0em} {16}} + {{z}^{3}})}^{{ - 1}}}, \\ \end{gathered} $
где $A$ и $B$ – решения уравнений (П1), $q$ дано в (17). Радиальное распределение МЭ в ячейке показано на рис. 5. Как и при поверхностном захвате, сильное легирование уменьшает концентрацию МЭ во всем объеме ячеек. Когда ${{R}_{S}} \approx L,$ концентрация МЭ становится слабо зависящей от диффузионной длины в широкой области ее изменения ${{l}_{D}} \leqslant {L \mathord{\left/ {\vphantom {L 2}} \right. \kern-0em} 2},$ чему соответствует бездиффузионный захват (${{l}_{D}} = 0$), противоположный поверхностному:

(25)
$\begin{gathered} {{{{J}_{{v}}}} \mathord{\left/ {\vphantom {{{{J}_{{v}}}} {I{{N}_{I}}}}} \right. \kern-0em} {I{{N}_{I}}}} = 4\pi \int\limits_{{{a}_{0}}}^L {y(r)W(r){{r}^{2}}dr} = \\ = {{\left( {\frac{R}{L}} \right)}^{3}}{{\tan }^{{ - 1}}}\left( {{{{\left( {\frac{R}{L}} \right)}}^{3}}\left( {{{{\left( {\frac{L}{{{{a}_{0}}}}} \right)}}^{3}} - 1} \right){{{\left( {1 + \frac{{{{R}^{6}}}}{{{{L}^{3}}a_{0}^{3}}}} \right)}}^{{ - 1}}}} \right). \\ \end{gathered} $
Рис. 5.

Радиальное распределение при захвате МЭ примесью в ячейке радиусом $L$ = 5 нм с радиусом захвата ${{a}_{0}}$ = 1 нм. Радиус Фёрстера ${{R}_{S}}$ = 2, 3, 3.5, 4, 4.5 нм (кривые 1–5' соответственно).

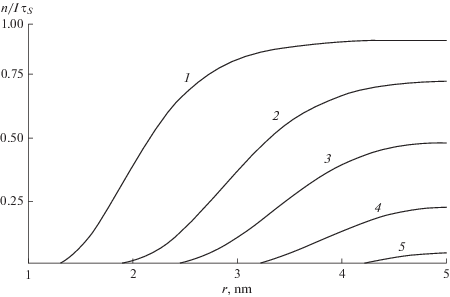
Рис. 6.

Квантовый выход объемного захвата в отсутствие диффузии в зависимости от ${{({{{{R}_{S}}} \mathord{\left/ {\vphantom {{{{R}_{S}}} L}} \right. \kern-0em} L})}^{3}}$ и ${{({{{{R}_{S}}} \mathord{\left/ {\vphantom {{{{R}_{S}}} {{{a}_{0}}}}} \right. \kern-0em} {{{a}_{0}}}})}^{3}}$ = 2, 4, 7, 10, 15 – кривые 1–5 соответственно.

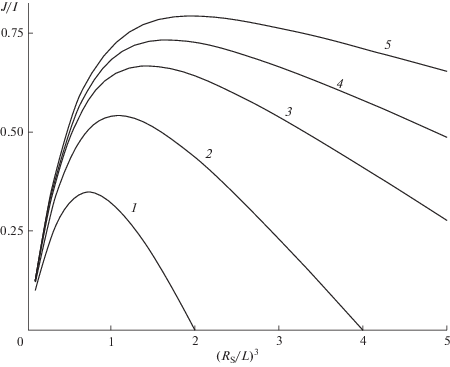
Зависимость (25) имеет максимум, в котором вероятность захвата в несколько раз больше, чем при собственной аннигиляции (рис. 6).

Таким образом, (21) и (25) описывают две области захвата с двумя различными управляющими параметрами – ограниченный диффузией поверхностный захват, когда ${{a}_{0}},{{R}_{S}} \ll {{l}_{D}},L,$ и объемный захват, когда ${{a}_{0}},{{l}_{D}} \ll {{R}_{S}},L.$ В обоих пределах квантовый выход захвата увеличивается с ростом концентрации примеси, стремясь к 1, когда либо ${{l}_{D}} > L,$ либо ${{R}_{S}} > L$ соответственно. В общем случае (24), квантовый выход возрастает до 1, когда возрастают оба параметра, так что${{R}_{S}},{{l}_{D}} \approx L.$

Однако два возможных пути повышения квантового выхода захвата – увеличение подвижности экситонов и концентрации примеси – практически исключают друг друга, поскольку рассеяние на примесях подавляет когерентный перенос МЭ. Для увеличения радиуса Фёрстера необходим рост размеров молекул, при котором растет плотность низкочастотного колебательного спектра, увеличивающая экситон-фононное взаимодействие, также уменьшающее матричные элементы переноса. По этим причинам более доступно увеличивать не ${{l}_{D}},$ а $R{}_{S},$ значения которого 4–5 нм уже известны [24–27]. Расчет общего случая показывает, что при ${{R}_{s}} \geqslant L$ высокий квантовый выход передачи энергии достигает 0.7–0.8 даже в отсутствие диффузии МЭ (рис. 6, кривые 4, 5), если концентрация примесей ~1018 см–3.

IV. ВЫВОДЫ

1. Решение задачи об ограниченном диффузией захвате МЭ примесями в фоточувствительных материалах, применяемых в ОСЭ, показывает, что близкая к 1 вероятность захвата возникает, когда среднее расстояние между примесями $L$ становится сравнимым с диффузионная длиной ${{l}_{D}}$ и/или радиусом Фёрстера ${{R}_{S}}.$

2. Поскольку эти длины не превышают 5 нм, выполнение этого условия означает, что в ОСЭ должны применяться сильно легированные материалы, в которых концентрации донорных и акцепторных примесей должны превышать 1018 см–3.

3. В сильно легированных материалах пространственное квазистационарное пространственное распределение МЭ в сферической ячейке радиусом $L$ становится неоднородным и значительно меньшим, чем в собственном материале. Радиус обедненной области, окружающей примесные центры, близка к $L,$ и вероятность передачи энергии ионизующимся примесям превышает вероятность собственной аннигиляции МЭ. $L$-области в ОСЭ играют роль поглощающих свет наноразмерных агрегатов, захватывающих основную часть образующихся МЭ.

4. Показано, что при ${{R}_{S}} \approx L$ квантовый выход захвата МЭ слабо зависит от ${{l}_{D}},$ так что для повышения эффективности ОСЭ поиск примесей, спектр поглощения которых максимально перекрывается со спектром флуоресценции основного вещества, является более перспективным и достижимым, чем поиск основного вещества с высоким коэффициентом диффузии МЭ.

5. Можно предположить, что вследствие неоднородного пространственного распределения МЭ в сильно легированных ОСЭ возникает неоднородное распределение зарядов, образующихся при ионизации примесей, и появление скачков потенциала на границах наноразмерных ячеек.

Список литературы

  1. Бендерский В.А., Ким И.П. // Химия высоких энергий. 2020. Т. 54. № 6. С. 423.

  2. Usov N.N., Benderskii V.A. // Phys.Stat. Solidi (b) 1970. V. 37. P. 535.

  3. Бендерский В.А., Белкинд А.И., Федоров М.И., Александров С.Б. // ФТТ. 1972. Т. 14. С. 790.

  4. Lakowicz J.R. Principles of fluorescence spectroscopy. 2006. Springer. N.Y.

  5. Loura L.M.S. // Int. J. Mol. Sci. 2012. V. 13. P. 15252.

  6. Muller S.M., Galliardi H., Schneider J., Barisa G., Seidel T. // Front. Plant Sci. 2013. V. 4. № 00413.

  7. Agranovich V.M. Excitations in Organic Solids. 2008. AIP Press. N.Y.

  8. Milan R., Selopal G.S., Cavazzini M., Orlandi S., Boaretto P., Caranioni S., Concina I., Pazzi G. // Scientific Rep. 2010. V. 10. № 1176.

  9. Pereira M.L., da Cuncha W.F., da Sousa R.T., Silva G.M., Ribeira L.A. // J. Phys. Chem. C. 2019. V. 123. P. 13410.

  10. Benderskii V.A., Brikenshtein V.K., Lavrushko A.G., Filippov P.G. // Phys. Stat. Solidi (b). 1978. V. 86. P. 449.

  11. Benderskii V.A., Brikenshtein V.K., Filippov P.G. // Phys. Stat. Solidi (b). 1983. V. 117. P. 9.

  12. Akselrod G.M., Deotare P.B., Thompson N., Lee J., Tisdale W.A., Baldo M.A., Menon V.M., Bulovic V. // Nature Commun. 2014. V. 5. № 3642.

  13. Smith M.B., Michl J. // Annu. Rev. Phys. Chem. 2013. V. 64. P. 361.

  14. Bardeen C.J. // Annu. Rev. Phys. Chem. 2014. V. 65. P. 127.

  15. Chen L., Shenai P., Zhang F., Somoza A., Zhao Y. // Molecules. 2015. V. 20. P. 15224.

  16. Sakaribara Y., Bera R.N., Mizutani T., Ishida K., Tokumoto M., Tami T. // J. Phys. Chem. B. 2001. V. 105. P. 1547.

  17. Hestand N.J., Spako F.C. // Chem.Rev. 2018. V. 118. P. 7069.

  18. Khan A., Wang M., Usman R., Sun H., Du M., Xu C. // Cryst. Growth Design. 2017. V. 17. P. 1251.

  19. Guerrini M., Cocchi C., Calzolari A., Varsano D., Corni S. // J. Phys. Chem. 2019. V. 123. P. 6831.

  20. Wang J., Li A., Xu S., song C., Geng Y., Ye L., Zhang H., Xu W. // ACS Omega. 2019. V. 4. P. 10424.

  21. Shi L., Willard A.P. // J. Chem. Phys. 2018. V. 149. N094110.

  22. Allen L.R., Paci E. // J. Chem. Phys. 2009. V. 131. № 065101.

  23. Deplazes E., Jayatilaka D., Corry B. // Phys.Chem. Chem. Phys. 2011. V. 13. P. 11045.

  24. Ginsberg N.S., Tisdale W.A. // Annu. Rev. Phys. Chem. 2019. V. 71. P. 1.

  25. Jones G.A., Bradshaw D.S. // Front. Phys. 2019. V. 7. P. 100.

  26. Walter M.G., Rudine A.B., Wamser C.C. // J. Porphyrins Phthalocyanines 2010. V. 14. P. 759.

  27. Kim I., Havarinen H.M., Wang Z., Madakumi S., Kim Y., Labbour G.E. // Chem. Mater. 2009. V. 221. P. 4256.

  28. Iwasi M., Suzuki A., Akiyama T., Oku T. Mater Sci. Ap-pl. 2014. V. 5. P. 278.

  29. Yuen A.P., Jovanovic S.M., Hoi A.-M., Klenkler R.A., Devenyi G.A., Loutfy R.O., Preston J.S. // Solar Energy. 2012. V. 86. P. 1683.

  30. Guanes S., Neugebauer H., Saisiftci N.S. // Chem. Rev. 2007. V. 107. P. 1324.

  31. Fan B., Zhong W., Ying L., Zhang D., Li M., Lin Y., Xia R., Liu P., Yip H.-L., Li N., Ma Y., Brabec C.J., Huang F., Cao Y. // Nature Commun. 2019. V. 10. № 41001.

  32. Ganesamoorty R., Sathiyan G., Sarthivel P. // Soar Energy Mater. Solar Cells. 2017. V. 161. P. 102.

  33. Pandey R., Gunavan A.A., Mkhoyan K.A., Holmes R.J. // Adv. Funct. Mater. 2012. V. 22. P. 617.

  34. Kang h., Kim C., Kim J., Kwon S., Kim H., Lee K. // Adv. Mater. 2016. V. 28. P. 7821.

  35. Zhang M., Ma Y., Zheng C. // Front. Chem. 2018. V. 6. P. 427.

  36. Gaspar H., Figueira F., Pereira L., Mendes A., Viana J.C., Bernardo D. // Materials 2018. V. 11. P. 2560.

  37. Luceno-Sanchez J.A., Diez-Pascual A.M., Capilla R.P. // Int. J. Mol. Sci. 2019. V. 20. P. 976.

  38. Yokota M., Tanimoto O. // J. Phys. Soc. Japan. 1967. V. 22. P. 779.

  39. Golubov S.I., Konobeev Y.V. // Phys.Stat. Solidi (b). 1973. V. 56. P. 69.

  40. Gosele U., Hauser M., Klein U.K.A., Frey R. // Chem.Phys.Lett. 1975. V. 34. P. 519.

  41. Hannewold K., Bobbert P.A. // Phys. Rev. B. 2005. V. 72. № 113202.

  42. Giannini S., Carof A., Ellis M., Yang H., Ziogros O.G., Ghosh S., Blumberg J. // Nature Commun. 2019. V. 10. P. 3843.

  43. Ortmann F., Bechstead F., Hannewold K. // Phys.Status Solidi (b). 2011. V. 248. P. 511.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Химия высоких энергий

Архивы выпусков Информация о журнале Отправить рукопись в журнал