1. На главную
  2. Электронные версии
  3. Известия РАН. Физика атмосферы и океана
  4. T. 56, № 4, 2020

Известия РАН. Физика атмосферы и океана, 2020, T. 56, № 4, стр. 418-427

Случайные процессы со стационарными приращениями и композитные спектры

Г. С. Голицын a, *, М. И. Фортус a, **

a Институт физики атмосферы им. А.М. Обухова РАН
119017 Москва, Пыжевский пер., 3, Россия

* E-mail: gsg@ifaran.ru
** E-mail: mfortus@yandex.ru

Поступила в редакцию 08.10.2019
После доработки 13.12.2019
Принята к публикации 05.02.2020

Полный текст (PDF)

Аннотация

Настоящая статья описывает методику получения и интерпретации фрактальных геофизических процессов со степенными спектрами различной природы. Примерами являются спектры энергии атмосферных процессов и их роль в перемешивании примесей, частотные спектры морских ветровых волн, пространственные спектры рельефа поверхностей небесных тел Солнечной системы. Отмечается важнейшее значение для приложений работ А.Н. Колмогорова начала 1930-х гг., получивших впоследствии развитие в работах его учеников А.М. Обухова, А.С. Монина, А.М. Яглома и др. Вероятностные законы Колмогорова служат в качестве модели для анализа изучаемых процессов методами теории подобия и размерности.

Ключевые слова: методы, случайные процессы, структурные функции, спектры, атмосферная турбулентность, различные природные процессы

1. ВВЕДЕНИЕ

В создании современной теории случайных процессов важнейшую роль сыграла серия работ А.Н. Колмогорова под общим названием “Аналитические методы теории вероятностей”, венцом которой является работа “Случайные движения” (Zufällige Bewegungen), 1934 ([1], далее АНК34). Она исходит из задания ускорений как последовательности некоррелированных случайных величин. В современной теоретической физике они называются δ-коррелированными по времени. Аналитическое решение уравнения типа Фоккера–Планка, предложенное Колмогоровым в [1], обсуждено в деталях в книге А.С. Монина и А.М. Яглома [2] в применении к теории турбулентности, развитой в 1941 г. Колмогоровым и его аспирантом А.М. Обуховым. Последний в середине 1950-х гг. начал исследовать уравнение для функции распределения вероятностей вида:

(1)
$\frac{{\partial p}}{{\partial t}} + {{u}_{i}}\frac{{\partial p}}{{\partial {{x}_{i}}}} = \frac{D}{2}\frac{{{{\partial }^{2}}p}}{{\partial u_{i}^{2}}},$

называемое в нашей научной литературе уравнением Фоккера–Планка–Колмогорова ((УФПК34), где $D$ – это коэффициент диффузии). Это уравнение действует и в двух, и в трех измерениях (предполагается только однородность по координатам функции распределения вероятностей (ФРВ). Это уравнение подробно исследовано в §24.4 книги [2]. А.М. Обухов указал в [3], что в уравнении (1) коэффициент диффузии $D$ пропорционален скорости диссипации кинетической энергии ε/2, т.е. описывает диффузию в пространстве скоростей. Это уравнение имеет три масштаба [3], даваемых его общим решением для плотности распределения вероятностей

(2)
${{p}_{t}}\left( {X,U} \right) = {{\left( {\frac{{\sqrt 3 }}{{2\pi D{{t}^{2}}}}} \right)}^{3}}\exp \left[ { - \frac{{3{{X}^{2}}}}{{D{{t}^{3}}}} + \frac{{3UX}}{{D{{t}^{2}}}} - \frac{{{{U}^{2}}}}{{Dt}}} \right].$

Отсюда видно, что распределение является нормальным, у которого локальные экстремумы зависят от времени.

Преобразование

$t = \tilde {t}\tau ,\,\,\,\,U = \tilde {U}{{\left( {\varepsilon \tau } \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},\,\,\,\,X = \tilde {X}{{\left( {\varepsilon {{\tau }^{3}}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}},$
где $\tau $ – произвольная величина, сводит уравнение (1) к универсальному, т.е. автомодельному, виду

(3)
$\frac{{\partial p}}{{\partial{ \tilde {t}}}} + {{\tilde {u}}_{i}}\frac{{\partial p}}{{\partial {{{\tilde {x}}}_{i}}}} = \frac{1}{2}\frac{{{{\partial }^{2}}p}}{{\partial{ \tilde {u}}_{i}^{2}}},$

имеющему решение, не зависящее от внешних параметров, если их нет в начальных или граничных условиях.

А.М. Обухов (1958) показал, что $\varepsilon $ – скорость генерации кинетической энергии в случае турбулентности, а в других ситуациях – коэффициент диффузии в пространстве скоростей. Уравнение (3) является асимптотикой для большого числа природных процессов и явлений. Примером может служить процесс изменения координаты и скорости фиксированной жидкой частицы, который можно считать марковским случайным процессом (для него “ускорения” практически не коррелированы, подробнее см. [2], стр. 506).

В размерных переменных масштабы рассматриваемой системы имеют вид

(4)
$\left\langle {{{x}^{2}}} \right\rangle = \varepsilon {{t}^{3}},$
(5)
$\left\langle {xu} \right\rangle = \varepsilon {{t}^{2}},$
(6)
$\left\langle {{{u}^{2}}} \right\rangle = \varepsilon t.$

Если из (4) исключить $t = {{\left( {{{{{r}^{2}}} \mathord{\left/ {\vphantom {{{{r}^{2}}} \varepsilon }} \right. \kern-0em} \varepsilon }} \right)}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}},$ где ${{r}^{2}} = x_{i}^{2},$ и подставить в (5) и (6), то получается закон Ричардсона–Обухова для турбулентного перемешивания и закон для структурной функции скорости Колмогорова (1941) с нулевыми начальными условиями. Действительно, $\left\langle {{{x}_{i}}{{u}_{i}}} \right\rangle = \left\langle {{{x}_{i}}\frac{{d{{x}_{i}}}}{{dt}}} \right\rangle $ = = $\left\langle {\frac{d}{{dt}}\frac{{x_{i}^{2}}}{2}} \right\rangle $ = $\left\langle {\frac{d}{{dt}}\frac{{{{r}^{2}}}}{2}} \right\rangle = \frac{{dS}}{{dt}},$где $S$ – площадь, пропорциональная размеру ${{r}^{2}},$ производная которой есть коэффициент диффузии, и тогда с помощью (5) получаем для коэффициента диффузии

$K = \varepsilon {{t}^{2}} = \varepsilon {{\left( {\left\langle {{{{{r}^{2}}} \mathord{\left/ {\vphantom {{{{r}^{2}}} \varepsilon }} \right. \kern-0em} \varepsilon }} \right\rangle } \right)}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} = {{\varepsilon }^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}{{\left\langle {{{r}^{2}}} \right\rangle }^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}.$

Точно так же из (6) получаем выражение для структурной функции скорости

${{D}_{u}}\left( r \right) = \left\langle {{{{\left[ {u\left( r \right) - u\left( 0 \right)} \right]}}^{2}}} \right\rangle = \varepsilon t = {{\varepsilon }^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}{{\left\langle {{{r}^{2}}} \right\rangle }^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}.$

Масштабы (4)–(6) объясняют частотный спектр морского ветрового волнения и ряд других статистических природных закономерностей, что описано в статье [4]. Здесь важно, что результаты АНК34 и их методическое развитие учениками А.Н. Колмогорова – А.М. Обуховым, А.С. Мониным, А.М. Ягломом, Г.И. Баренблаттом [2, 5, 6] и др. – не только дают практическую основу для статистического анализа стохастических процессов, но и служат моделью для их описания в терминах теории подобия и размерности [2, 5, 6]. Существенным моментом в этих книгах является понятие промежуточной асимптотики, предложенное в 1971 г. Г.И. Баренблаттом и Я.Б. Зельдовичем [7]. Оно является отражением того известного факта, что степенные закономерности наблюдаются в ограниченных масштабах пространства и/или времени. Эти закономерности отражают тот факт, что явления и процессы в этих масштабах автомодельны [6, 8], т.е. повторяют друг друга в измененных надлежащим образом координатах, как это было показано при получении формулы (3).

2. ТУРБУЛЕНТНОСТЬ

Перейдем от общих положений к конкретным примерам, начав с атмосферной турбулентности в области масштабов от сантиметра до нескольких тысяч километров. Здесь надо вспомнить первое экспериментальное подтверждение законов Колмогорова–Обухова 1941 г. для поперечной структурной функции скорости в интервале от 1 мм до 1 м по данным немецких измерений 1935 г. [8], что воспроизведено в §23.3 книги [2] на рис. 62 . Там же есть полученный в 1965 г. в разнообразных условиях рисунок, показывающий спектр ${{k}^{{{{ - 5} \mathord{\left/ {\vphantom {{ - 5} 3}} \right. \kern-0em} 3}}}}$ в гораздо большем интервале масштабов и в автомодельных переменных (см. рис. 76 книги [2]). Этот же рисунок есть и в главе 6 недавней книги [9].

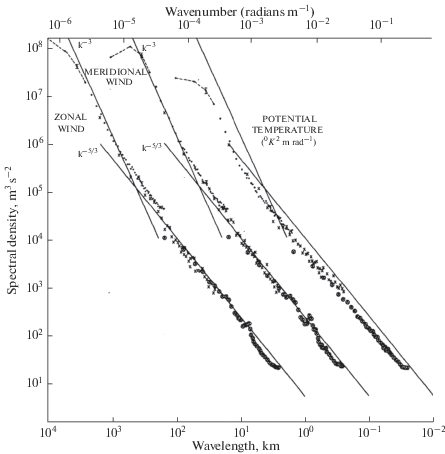
Во второй половине 1970-х гг. в США был осуществлен GASP-проект измерения атмосферной турбулентности на коммерческих авиалиниях. Всего было свыше 6000 полетов. Самолеты были оборудованы датчиками перегрузок, измерявших ускорения, осредненные по объему и размерам их тел. Интегрирование записей по времени давало скорость за вычетом скорости самого самолета. В итоге были получены записи относительной скорости в воздухе в интервале масштабов от 2 до 3000 км [10]. В 1990-х гг. аналогичный проект MOZAIC был осуществлен в Европе [11]. Полученные данные были осреднены по 36 тыс. ч полетного времени. Результаты обоих проектов одинаковы: от 2 до приблизительно 500 км спектры горизонтальных флуктуаций скорости следуют закону степени –5/3, а далее вплоть до 2500 км они плавно переходят к закону ${{k}^{{ - 3}}}.$ Эти данные представлены на рис. 1.

Рис. 1.

Спектры флуктуаций зональной и меридиональной компонент скорости (сдвинут на одну декаду вправо) и потенциальной температуры (сдвинут на две декады вправо). Рисунок заимствован из публикации [10].

Последний закон близок к спектру двумерной турбулентности, установленному в 1960-х гг. Бэтчелором [12] и Крейкнаном [13]. В двумерном потоке сохраняется средний квадрат вихря

(7)
$\Omega = {{\left\langle {{{\omega }^{2}}} \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {{{\omega }^{2}}} \right\rangle } 2}} \right. \kern-0em} 2},$

названный энстрофией. Вихри возбуждаются в некотором промежуточном масштабе [13]. От них в сторону малых вязких масштабов распространяется поток завихренности – поток энстрофии

(8)
${{\varepsilon }_{\omega }} = \frac{{d\Omega }}{{dt}},$

а в сторону больших масштабов (малых волновых чисел) идет поток кинетической энергии со скоростью $\varepsilon .$ Тогда соображения размерности дают спектр кинетической энергии в интервале переноса энстрофии [12, 13]

$S\left( k \right) = \varepsilon _{{\omega }}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}{{k}^{{ - 3}}}.$

Многочисленные лабораторные эксперименты, тщательно задуманные и исполненные, подтверждали основные результаты двумерной турбулентности (см. [14]). Однако натурные самолетные измерения [10, 11] меняли местами спектральные масштабы переноса энергии (спектр ${{k}^{{{{ - 5} \mathord{\left/ {\vphantom {{ - 5} 3}} \right. \kern-0em} 3}}}}$) и масштабы переноса завихренности (спектр ${{k}^{{ - 3}}}$). Это приводило в недоумение тех, кто не воспринял или просто забыл замечательную работу Чарни [15]. Дело в том, что при геострофических движениях, выполняющихся при малых числах Россби ${\text{Ro}} = {U \mathord{\left/ {\vphantom {U {{{L}_{0}}{{l}_{c}}}}} \right. \kern-0em} {{{L}_{0}}{{l}_{c}}}}$ (U и ${{L}_{0}}$ – характерные значения горизонтальной скорости и горизонтального размера потока, ${{l}_{c}}$ – параметр Кориолиса), сохраняется потенциальный вихрь

(9)
${{\Omega }_{p}} = \left( {\Omega + 2\omega } \right){{\nabla s} \mathord{\left/ {\vphantom {{\nabla s} \rho }} \right. \kern-0em} \rho },$
где $\Omega $ – абсолютный вихрь, связанный с вращением планеты, $\rho $ – плотность среды, $\nabla s$ – градиент энтропии по направлению “термодинамической вертикали”, а основное изменение температуры в атмосфере идет по высоте.

Аргументация Чарни, сходная с Бэтчелором и Крейкнаном, также дает закон ${{k}^{{ - 3}}}$ для геострофической турбулентности, а движения в масштабах от 500 до нескольких тысяч километров при скорости ветра $U = 10$ м/с и параметре Кориолиса ${{l}_{c}} \approx {{10}^{{ - 4}}}\,\,{{{\text{c}}}^{{ - 1}}}$ имеют число Россби Ro < 0.2, так что все спектры встают на свои места согласно [15].

В работе Линдборга [11] результаты статистической обработки данных по скорости в эксперименте MOZAIC представлены в виде трехчленных структурных функций, продольных и поперечных:

(10)
${{D}_{{ll}}}\left( r \right) = {{a}_{1}}{{r}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} + {{b}_{1}}{{r}^{2}} - {{c}_{1}}{{r}^{2}}\ln r,$
(11)
${{D}_{{nn}}}\left( r \right) = {{a}_{2}}{{r}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} + {{b}_{2}}{{r}^{2}} - {{c}_{2}}{{r}^{2}}\ln r,$
где численные коэффициенты в системе СИ при глобальном осреднении равны

$\begin{gathered} {{a}_{1}} = 3.6 \times {{10}^{{ - 3}}},\,\,\,\,{{b}_{1}} = 2.4 \times {{10}^{{ - 9}}}, \\ {{c}_{1}} = 0.16 \times {{10}^{{ - 9}}},\,\,\,\,{{a}_{2}} = 4.0 \times {{10}^{{ - 3}}}, \\ {{b}_{2}} = 6.5 \times {{10}^{{ - 9}}},\,\,\,\,{{c}_{2}} = 0.43 \times {{10}^{{ - 9}}}. \\ \end{gathered} $

Линдборг подробно анализировал свои структурные функции, отмечая, что их интервал $ \sim {{k}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}}$ при тщательном рассмотрении короче, чем соответствующий спектральный интервал $ \sim {{k}^{{{{ - 5} \mathord{\left/ {\vphantom {{ - 5} 3}} \right. \kern-0em} 3}}}}.$ Статистическая обработка была проведена им в интервале 2–2500 км.

Выясним, насколько трехчленные структурные функции (10), (11) соответствуют экспериментальному спектру [10], состоящему из двух степенных участков, о чем говорилось выше. Первые слагаемые в (10), (11) соответствуют спектру Колмогорова–Обухова ${{k}^{{{{ - 5} \mathord{\left/ {\vphantom {{ - 5} 3}} \right. \kern-0em} 3}}}},$ вторые – спектру ${{k}^{{ - 3}}},$ логарифмический член появляется от поправок Крейкнана [16], учитывающих нелокальность взаимодействия спектральных компонент отдельных вихрей в интервале переноса энстрофии. Характерно, что в [11] практически нет упоминания работы Чарни [15] и что интервалы переноса энергии и энстрофии в результатах полетов поменялись местами в сравнении с первоначальной теорией [13].

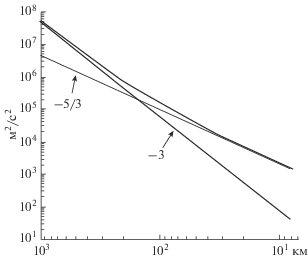
Чтобы сравнить результаты работ [10] и [11], перейдем от структурных функций к их спектрам. Спектры, соответствующие эмпирическим структурным функциям Линдборга ${{D}_{{ll}}}$ (10) и ${{D}_{{nn}}}$ (11) – это суммы двух спектров, отвечающих первому и сумме второго и третьего слагаемых. На рис. 2 изображен полученный нами спектр, соответствующий функции ${{D}_{{ll}}}$ (10) (сплошная линия), а также два спектра, отвечающие первому и сумме второго и третьего слагаемых (тонкие линии). Этот суммарный спектр вполне схож с эмпирическими спектрами (рис. 1), полученными в 70–90-е годы [10]. Это придает уверенности в реалистичности структурной функции Линдборга. Отметим, что такую же структуру имеет и эмпирический спектр потенциальной температуры (см. рис. 1), что неудивительно, поскольку она связана с потенциальным вихрем (9). В проекте GASP [10] подобные спектры с весьма небольшими различиями наблюдались в разных широтах и сезонах. Надо отметить, что эти спектры были воспроизведены в модели атмосферы высокого разрешения [17] до 80 км на различных высотах не только тропосферы, но и стратосферы и мезосферы.

Рис. 2.

Спектр, соответствующий функции Dll (формула (10)) – сплошная линия и два спектра, отвечающие первому и сумме второго и третьего слагаемых – тонкие линии.

Зная структурные функции (10) и (11), можно определить дисперсию относительных скоростей, равную

(12)
${{\sigma }^{2}} = {{D}_{{ll}}}\left( r \right) + {{D}_{{nn}}}\left( r \right) = D\left( r \right),$

а по ней коэффициент относительной вихревой (турбулентной) диффузии, как произведение размера пятна на разность скоростей на его краях [18]:

(13)
$\begin{gathered} K\left( r \right) = r{{\sigma }_{u}}\left( r \right) = r{{\left[ {D\left( r \right)} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = r\left[ {7.6 \times {{{10}}^{{ - 3}}}{{r}^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}}}} + } \right. \\ {{\left. { + \,\,8.9 \times {{{10}}^{{ - 9}}}{{r}^{2}} - 0.59 \times {{{10}}^{{ - 9}}}{{r}^{2}}\ln r} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} = \\ = 0.087{{r}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}~{{\left[ {1 + 1.17 \times {{{10}}^{{ - 6}}}{{r}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}\left( {1 - 0.066\ln r} \right)} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}, \\ \end{gathered} $

где сомножитель перед квадратной скобкой во второй строке описывает турбулентную диффузию Ричардсона–Обухова согласно масштабу (5). Корень из квадратной скобки описывает отклонения от последней вследствие геострофической турбулентности, следы которой начинают проявляться при $r > 30$ км, если предположить, что значения Линдборга для коэффициентов в (10), (11) действуют на всем интервале масштабов 2–2500 км. Конечно, это сильное предположение для 36 тысяч летных часов в самых разных сезонах, местах и т.п. Чтобы оценить роль геострофической турбулентности в перемешивании, вычислим корень из второй квадратной скобки в (13). Его отклонения от единицы в зависимости от расстояния представлены в табл. 1.

Таблица 1.  

Значения функции ${{\left[ {1 + 1.17 \times {{{10}}^{{ - 6}}}{{r}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}\left( {1 - 0.066\ln r} \right)} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$

        r, км 30 60 100 300 1000 2500
${{\left[ {1 + 1.17 \cdot {{{10}}^{{ - 6}}}{{r}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}\left( {1 - 0.066\ln r} \right)} \right]}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ 1.16 1.32 1.51 2.20 3.29 3.20

Начавшееся уменьшение при $r = 2500$ соответствует уменьшению показателя степени у структурной функции ${{D}_{{ll}}}\left( r \right).$

Рисунок 3 показывает, что наша формула (13) для коэффициента перемешивания неплохо согласуется с восемью точками Ричардсона [19, 20], которые были получены в разные времена и для разных высот (формула (13) относится к данным MOZAIC на высотах порядка 10 км).

Рис. 3.

Цифрами обозначены графики: 1 – коэффициента турбулентной диффузии K(r); 2 – зависимости 0.087r4/3. Черные кружки – данные Ричардсона [19, 20].

3. МОРСКОЕ ВОЛНЕНИЕ

Степенные спектры с высокими показателями встречаются при анализе морcких ветровых волн. Технику обращения с ними дал А.М. Яглом [21]. Частотный спектр возвышений морской поверхности пропорционален ${{\omega }^{{ - 4}}}.$ Такая степень сразу следует из первого масштаба Колмогорова (4) $\left\langle {{{x}^{2}}} \right\rangle = \varepsilon {{t}^{3}}{\text{:}}$ если правую часть этой формулы рассматривать как временную структурную функцию с нулевыми начальными условиями, то ее преобразование типа Фурье (см. Приложение, формула (П3) при $n = 3$) соответствует спектру $S\left( \omega \right) = \varepsilon {{\omega }^{{ - 4}}}.$ Такую же степень имеют участки сейсмического шума в интервале 1–10 с. Как показал Лонге–Хиггинс [22], именно эти периоды характерны для волн прибоя, обрушивающихся на берега и возбуждающих микросейсмы.

Спектр ${{\omega }^{{ - 4}}}$ – это основная мода, впервые открытая С.А. Китайгородским в 1962 г. [23] с помощью соображений размерности, затем в 1966 г. В.Е. Захаровым [24] “из первых принципов” и в 1973 г. Тоба [25]. Анализируя законы разгона, полученные в многолетнем проекте JONSWAP М, Тоба [26] представил график, показывающий четкую корреляцию квадрата высоты основного пика и куба периода. Это следует из частотной зависимости спектра возвышений волн ${{\omega }^{{ - 4}}}$ и непосредственно из соотношения (4). Однако если результаты получаются путем анализа размерностей параметров, определяющих явления, то при сравнении с экспериментальными данными всегда возникают численные множители. Эти множители могут зависеть от безразмерных параметров, определяющих процесс. Даже в таких устоявшихся в общем понимании процессах, как турбулентный пограничный слой или структура мелкомасштабной турбулентности, в последнее время были обнаружены слабые зависимости от логарифма числа Рейнольдса (см. [27] и литературу там).

Однако вернемся к ветровым волнам, весьма сложному и комплексному явлению. Одним из плохо освещенных моментов в теории их роста остается влияние стратификации атмосферы. Давно замечено, что рост волн замедляется в несколько раз, если атмосфера стратифицирована устойчиво по сравнению со случаями близости ее к нейтральной стратификации или даже конвекции. Давно отмечалось, что осенью вода теплее воздуха и волны при одном и том же ветре выше, чем весной и летом [28–30]. Устойчивость атмосферы характеризуется числом Ричардсона ${\text{Ri}} = {{{{N}^{2}}} \mathord{\left/ {\vphantom {{{{N}^{2}}} {{{S}^{2}}}}} \right. \kern-0em} {{{S}^{2}}}},$ которое в работах по эволюции волнения нигде не упоминается. Здесь $S = {{\partial{ \bar {U}}} \mathord{\left/ {\vphantom {{\partial{ \bar {U}}} {\partial z}}} \right. \kern-0em} {\partial z}}$ – вертикальный сдвиг среднего ветра, а

(14)
${{N}^{2}} = - \frac{g}{T}\left( {\frac{{dT}}{{dz}} - {{\gamma }_{a}}} \right),$
где $T$ – температура воздуха, ${{\gamma }_{a}} = {{ - g} \mathord{\left/ {\vphantom {{ - g} {{{c}_{p}}}}} \right. \kern-0em} {{{c}_{p}}}}$ – ее адиабатический градиент, ${{c}_{p}}$ – ее теплоемкость. При ${{N}^{2}}$ > 0 в атмосфере присутствуют внутренние гравитационные волны.

В условиях, близких к нейтральности, процесс волнообразования более или менее устойчив. В этой ситуации были давно предложены два параметра подобия [31]. Первый из них – это безразмерный разгон

(15)
$F = \frac{{gx}}{{{{U}^{2}}}},$
где $x$ – это расстояние, например, от подветренного берега, $U$ – скорость ветра, обычно измеряемая, или относимая к высоте 10 м над поверхностью моря. Второй безразмерный параметр – это возраст волнения

(16)
$\Omega = \frac{{U{{\omega }_{p}}}}{g} = 2\pi \frac{{U{{f}_{p}}}}{g}.$

Здесь ${{f}_{p}}$ – частота пика волны в герцах, т.е. отношение скорости ветра к фазовой скорости пика, определяемой (для простоты) из дисперсионного соотношения для случая глубокой воды:

(17)
${{\omega }^{2}} = gk,$
где $k = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0em} \lambda }$ – волновое число. Численные коэффициенты, получаемые при натурных измерениях спектров ветровых волн, могут (и должны!) зависеть от обоих параметров подобия (15) и (16), т.е. от разгона и возраста.

Энергия волны определяется как

(18)
$E = {{\rho }_{w}}\frac{{gh_{s}^{2}}}{{16}} = {{\rho }_{w}}g\frac{{{{U}^{4}}\tilde {h}_{s}^{2}}}{{16{{g}^{2}}}},$
где ${{\rho }_{w}}$ – плотность воды, ${{\tilde {h}}_{s}}$ – так называемая существенная высота волны, равная 1/4 от ее полной высоты в пике волнения (знак тильда означает безразмерное значение соответствующей переменной, например, безразмерная энергия $e = {{\tilde {h}_{s}^{2}} \mathord{\left/ {\vphantom {{\tilde {h}_{s}^{2}} {16}}} \right. \kern-0em} {16}}$).

Многочисленные эксперименты по наблюдению развития волн в пространстве и времени проводились в разных местах. Первые и наиболее полные эксперименты были проведены в начале 1970-х гг. в Северном море под руководством К. Хасссельмана. Они четко выявили так называемые законы разгона [32]. В безразмерном виде частота основного пика волнения зависит от разгона (15)

(19)
$\frac{{U{{f}_{p}}}}{g} = A{{F}^{{ - \alpha }}},$

а энергия основного пика $e \sim {{h}^{2}}$ (пропорциональна квадрату его высоты):

(20)
$\frac{{{{g}^{2}}e}}{{{{U}^{4}}}} = B{{F}^{{\beta }}},$
где $A,$ $\alpha ,$ $B,$ $\beta $ – положительные константы, определяемые на больших рядах наблюдений; $U$ – скорость ветра, измеряемая обычно на высоте 10 м от поверхности воды. В [9, 33] показана связь этих величин с возрастом волнения (16). В [32] найдены показатели степени $\alpha = 0.33$ и $\beta = 1.0,$ обзор данных других экспериментов можно найти в [33, 34]. С ростом устойчивости атмосферы оба значения $\alpha $ и β пропорционально снижаются, но всегда в пределах 10%:

(21)
$3\alpha \approx \beta ,$

а это прямое следствие соотношения (4) служит вероятностным обоснованием эмпирического закона Тоба [26]: ${{h}_{p}} \sim T_{p}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}.$

Более или менее детальная нелинейная теория развития ветрового волнения разработана только для нейтральной стратификации [33, 34] и подкреплена подробными расчетами [35]. В зависимости от развития волнения, т.е. от его возраста, выделяются асимптотически три вида частотного спектра волн. При $\Omega > 2,$ т.е. для молодых коротких и крутых волн, наблюдается спектр вида $ \sim {\kern 1pt} {{\omega }^{{{{ - 13} \mathord{\left/ {\vphantom {{ - 13} 3}} \right. \kern-0em} 3}}}},$ ветер передает свой импульс молодым крутым волнам на их рост. При $1.2 < \Omega < 2$ передается энергия и спектр имеет вид $ \sim {\kern 1pt} {{\omega }^{{ - 4}}},$ а при $0.83 < \Omega < 1.2$ передается действие и тогда частотный спектр $ \sim {\kern 1pt} {{\omega }^{{{{ - 11} \mathord{\left/ {\vphantom {{ - 11} 3}} \right. \kern-0em} 3}}}}.$ В последнем интервале частотный спектр волн приближается к насыщению и вблизи нижнего предела волны обрушиваются. Волны с их частотным спектром осуществляют рост пятен примеси на их поверхности. Подробное сравнение теории с наблюдениями роста пятен дано в [36, 37]. Конечно, преобразование спектра со временем происходит плавно у функции ${{\omega }^{{ - n}}},$ где $n = 4 \pm 1{\text{/}}3,$ и меняется в процессе эволюции волн от 13/3 до 11/3, но основное значение базисного показателя $n = 4$ сразу видно из (4), первого масштаба Колмогорова [1] $\left\langle {{{x}^{2}}} \right\rangle = \varepsilon {{t}^{3}}.$ Отметим, что средний возраст волн в Мировом океане близок к 1.2 (см. [9, 35]).

4. СПЕКТРЫ РЕЛЬЕФА ПОВЕРХНОСТЕЙ НЕБЕСНЫХ ТЕЛ

Еще один характерный пример, совсем недавний, это объяснение пространственного спектра Каулы [38] cлучайного рельефа поверхностей небесных тел (и флуктуаций их гравитационного поля) – Земли, Луны, Марса, Венеры и некоторых астероидов. Все их случайные возвышения с некоторых начальных (некоторых первых) сферических гармоник выявляют зависимость ${{k}^{{ - 2}}},$ т.е. обратную квадратичную зависимость от номера гармоники. По имени ученого, открывшего в 1963 г. эту зависимость для Земли, она называется правилом Каулы [39]. Для названных тел измеряется случайная временная зависимость $h\left( t \right).$ Знание скорости регистрирующего аппарата позволяет перевести временную зависимость $h\left( t \right)$ в пространственную зависимость $h\left( y \right).$ При отсутствии движений, ${{u}_{i}} = 0,$ уравнение (1) принимает вид обычного уравнения для броуновского движения, т.е. типа теплопроводности

$\frac{{\partial p}}{{\partial y}} = \frac{D}{2}\frac{{{{\partial }^{2}}p}}{{\partial {{h}^{2}}}}.$

Здесь $p = p\left( {h,t} \right)$ = $p\left( {h,y} \right),$ $t = \frac{u}{y},$ а коэффициент диффузии $D$ имеет размерность длины; для него известно, что $\left\langle {{{h}^{2}}} \right\rangle = Dy.$

Считая правую часть этого равенства структурной функцией с нулевыми начальными условиями, получим пространственный спектр такого процесса, пропорциональный ${{k}^{{ - 2}}}.$ Для такого рельефа спектр углов, т.е. производной рельефа, будет постоянной величиной (спектром белого шума), а сам процесс дельта-коррелирован по пространству. Наблюдаемое для небольших по сравнению с радиусом небесного тела участков поверхности “укручение” спектра в малых масштабах получается, если предположить, что пространственная корреляция углов начинает действовать. Для простейшего вида такой корреляции $\exp \left( { - \frac{y}{{{{y}_{0}}}}} \right)$ спектр равен ${{\left( {1 + {{k}^{2}}y_{0}^{2}} \right)}^{{ - 1}}}.$ Если $k{{y}_{0}} \ll 1,$ то спектр рельефа остается обратно квадратичным, а в противном случае он переходит в ${{k}^{{ - 2}}}{{\left( {k{{y}_{0}}} \right)}^{{ - 2}}} \sim {{k}^{{ - 4}}}.$ Константа ${{y}_{0}}$ определяется свойствами материала и внешними воздействиями. Для Луны ${{y}_{0}} \approx 3$ км, а для Земли с такого масштаба укручение спектра только начинается [38]. Вопрос требует дальнейшего теоретического анализа, связывающего величину ${{y}_{0}}$ с механическими свойствами материала поверхности и с характерными воздействиями на нее.

5. ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Эта работа несет в основном методический характер и излагает в принципе известные, но мало употребляемые на практике конкретные правила при анализе случайных процессов со степенными спектрами. Численные константы, определяемые для таких спектров путем сравнения с экспериментальными данными, реальными или численными, могут меняться в зависимости от конкретных ситуаций, характеризуемых параметрами подобия, например, безразмерным возрастом, как в случае ветрового волнения.

Флуктуации ветра в атмосфере в масштабах до 2500 км определяются разными причинами, и их спектр можно назвать композитным как сумму спектра типа Колмогорова–Обухова 1941 г. и спектра геострофической турбулентности Чарни 1971 г. Замечательно, что такой спектр воспроизводится в численной модели общей циркуляции высокого разрешения [17]. Последний пример – спектр рельефа поверхности небесных тел, как и первые два, – является хорошей иллюстрацией действия вероятностных законов А.Н. Колмогорова в природных условиях, а структура рельефа в самых мелких масштабах является естественным обобщением основного предположения классика науки XX в. о характере сил, определяющих случайный процесс. Предположение о коррелированности углов рельефа на малых пространственных масштабах делает его спектр в этой области более крутым. Характер спектра позволяет судить о корреляционной функции воздействий сил, порождающих процесс. Когда воздействие дельта-коррелировано, то спектр рельефа на малых масштабах обратно пропорционален квадрату частоты, а соответствующее распределение вероятности нормально [2], § 24. Дальнейшее, более сильное, спадание спектра энергии в сторону высоких частот говорит о некоррелированности воздействий на соответствующих масштабах. Такие масштабы определяются свойствами материи и характером воздействий. Иллюстрацией к этому выводу, ранее авторами не встречавшемуся, служит раздел 4 данной работы.

Другие примеры проявления в природе законов Колмогорова 1934 г. приведены в [4]. Например, при анализе дискретной совокупности, такой как числа $N$ литосферных плит, составляющих земную поверхность, в зависимости от их площадей $N\left( S \right),$ $S = \left\langle {{{x}^{2}}} \right\rangle ,$ $\left\langle {{{x}^{2}}} \right\rangle = \left\langle {\varepsilon {{t}^{3}}} \right\rangle ,$ используют кумулятивное распределение $P\left\{ {N \geqslant S} \right\}.$ Было найдено, что $N\left( S \right)$ пропорционально ${{S}^{{ - 0.33}}},$ и формула (4) сразу дает $N \geqslant S = {{\left( {\varepsilon {\text{/}}S} \right)}^{{1{\text{/}}3}}}.$

Данная работа посвящена памяти наших общих учителей в образовании и в науке А.Н. Колмогорова, А.М. Обухова, А.М. Яглома, А.С. Монина.

Авторы признательны рецензенту за внимательное прочтение и полезные замечания.

Работа была частично поддержана программой президиума Российской академии наук “Нелинейная динамика фундаментальные проблемы и приложения”.

Список литературы

  1. Kolmogorov A.N. Zufällige Bewegungen // Ann Math 1934. V. 35. P. 116–117. (см. также Колмогоров А.Н. Труды по теории вероятностей и математической статистике М.: Наука, 1983 и более поздние издания).

  2. Монин А.С., Яглом А.М. Статистическая гидродинамика. Т. 2. М.: Наука, 1965.

  3. Obukhov A.M. Description of turbulence in terms of lagrangian variables // Adv. Geophys. 1959. V. 6. P. 117–119.

  4. Голицын Г.С. Законы случайных блужданий А.Н. Колмогорова 1934 г. // Метеорология и гидрология. 2018. № 3. С. 5–15.

  5. Barenblatt G.I. Scaling. Cambridge Univ. Press. 2003. 171 p.

  6. Баренблатт Г.И. Автомодельные явления – анализ размерностей и скейлинг. Долгопрудный: изд. Интеллект, 2009. 216 с.

  7. Баренблатт Г.И., Зельдович Я.Б. // Промежуточные асимптотики в математической физике. // Успехи матем. наук. 1971. Т. 26. № 2. С. 45–61.

  8. Обухов А.М. Локальная структура атмосферной турбулентности // Докл. АН СССР. 1949. Т. 67. № 4. С. 643–646.

  9. Голицын Г.С. Статистика и динамика природных процессов и явлений. М.: Красанд, 2013. 400 с.

  10. Nastrom G.D., Gage K.S. A climatology of atmospheric wave-numder spectra of wind and temperature observed by commercial aircraft // J. Atmos. Sci. 1984. V. 42. № 4. P. 950–960.

  11. Lindborg E. Can the atmospheric kinetic energy spectrum be explained by two-dimensional turbulence? // J. Mech. 1999. V. 388. P. 259–288.

  12. Batchelor G.K. Computation of the energy spectrum in homogeneous two-dimensional turbulence // Phys. Fluids. 1969. Suppl. II. V. 12. № 12. P. 233–239.

  13. Kraichnan R.H. Inertial ranges in two-dimensional turbulence // Phys. Fluids 1967. V. 10. № 7. P. 1417–1423.

  14. Kelley H., Goldberg W.I. Two-dimensional turbulence:a review of some recent experiments // Rep. Prog. Phys. 2002. V. 65. P. 845–894.

  15. Charney J. Geostrophic turbulence // J. Atmos. Sci. 1971. V. 29. № 6. P. 1087–1095.

  16. Kraichnan R.H. Inertial-range transfer in two- and three-dimensional turbulence. J. Fluid Mech. 1971. V. 47. № 3. P. 525–536.

  17. Koshyk J.N., Hamilton R. The horizontal kinetic energy spectrum and spectral budget simulated by a troposphere-stratosphere-mesosphere GCM. // J. Atmos. Sci. 2001. V. 58. № 4. P. 329–348.

  18. Taylor G.I. Eddy motion in the atmosphere. Phil. Trams. Roy. Soc. 1915. V. A215. P. 1–26.

  19. Richardson L.F. Atmospheric diffusion shown on a distance-neighbour graph. // Proc. Soc. London. 1926. V. A110. № 756. P. 708–731.

  20. Richardson L.F. A search for the law of atmospheric diffusion. // Beiträge Phys. für Atmosph. 1929. B. XV. P. 24–29.

  21. Yaglom A.M. Correlation theory of stationary and related random functions. I Basic Results. N.Y.: Springer-Verlag, 1986. 526 p. II Supplementary Notes and References. N.Y.: Springer-Verlag, 1987. 258 p.

  22. Longuet-Higgins M.A. A theory of the origin of microseisms // Phil. Trans. Roy. Soc. London. 1953. V. 243. P. 1–35.

  23. Китайгородский С.А. Применение теории подобия к анализу волн, возбуждаемых ветром, как случайному процессу // Изв. АН СССР сер. геофиз. 1962. № 1. С. 73–82.

  24. Захаров В.Е., Филоненко Н.Н. Спектр энергии для стохастических колебаний поверхности жидкости // Докл. АН СССР. 1966. Т. 170. № 6. С. 1292–1295.

  25. Toba Y. Total balance in the air-sea boundary processes: III. On the spectrum of wind waves // J. Oceanogr. Soc. Japan. 1973. V. 29. № 3. P. 209–229.

  26. Toba Y. Stochastic form of the growth of wind waves in a single parameter representation with physical implications // J. Oceanogr. 1978. V. 8. № 5. P. 494–507.

  27. Баренблатт Г.И., Корин А.Дж., Простокишин В.М. Турбулентные течения при очень больших числах Рейнольдса: уроки новых исследований // Успехи физ. наук. 2014. Т. 184. № 3. С. 265–272.

  28. Давидан И.Н., Лопатухин Л.И., Рожков В.А. Ветровое волнение как вероятностный гидродинамический процесс. Л.: Гидрометеоиздат, 1978. 288 с.

  29. Phillips O.M. Dynamics of the Upper Ocean. Cambridge Univ. Press, 1977. 336 p.

  30. Доронина Ю.Л. Взаимодействие атмосферы и океана. Л.: Гидрометеоиздат. 1981. 288 с.

  31. Титов Л.Ф. Ветровые волны. Л.: Гидрометеоиздат., 1969. 292 с.

  32. Hasselmann K., Barnett T.P., Bows E. et al. Measurements of wind-wave growth and swell decay during Joint North Sea Wave Project (JONSWAP). Deutche Hydrograph. Z. Suppl, 1973. V. 12(A8). 95 p.

  33. Zakharov V.E. Analytic theory of a wind driven sea. Proc. IUTAM, 2018. V. 26 Symposium Wind Waves, September, 2017, London, UK.

  34. Komen G.J., Cavaleri L., Donelan M., Hasselmann K., Hasselmann S., Janssen P.A.E.M. Dynamics and Modelling of Ocean Waves. N.Y.: Cambridge Univ. Press., 1994. 532 p.

  35. Gagnaire–Renou E., Benoit M., Badulin S.I. On weakly turbulent scaling of wind sea in simulations of fetch-limited growth // J. Fluid Mech. 2011. V. 669. P. 178–213.

  36. Голицын Г.С. Коэффициент турбулентной диффузии примеси на водной поверхности в зависимости от стадии развития волнения. // Изв. РАН. Физика атмосферы и океана. 2011. Т. 47. № 3. С. 426–432.

  37. Голицын Г.С., Чхетиани О.Г. Влияние вязкости на коэффициент диффузии в поле морских ветровых волн // Изв. РАН. Физика атмосферы и океана. 2014. Т. 50. № 6. С. 545–553.

  38. Гледзер Е.Б., Голицын Г.С. Структура рельефа и гравитационного поля планет: правило Каулы – следствие законов теории вероятностей А.Н. Колмогорова и его школы // Докл. РАН. 2019. Т. 485. № 4. С. 391–395.

  39. Kaula W.M. Theory of Satellite Geodesy. Bleisdell. Mass. 1966. 71 p.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Физика атмосферы и океана

Архивы выпусков Информация о журнале Отправить рукопись в журнал