1. На главную
  2. Электронные версии
  3. Прикладная математика и механика
  4. T. 87, № 1, 2023

Прикладная математика и механика, 2023, T. 87, № 1, стр. 36-44

О задаче определения положения источника внутренних волн

В. Г. Байдулов 1, *

1 Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

* E-mail: bayd@ipmnet.ru

Поступила в редакцию 20.09.2022
После доработки 10.11.2022
Принята к публикации 14.11.2022

Полный текст (PDF)

Аннотация

При движении тел в непрерывно стратифицированной жидкости с постоянной скоростью волновое поле движется вместе с телом и образует поле так называемых присоединенных внутренних волн. Набегающий на тело поток обычно предполагается постоянным, нестационарными волнами, порождаемыми на начальном этапе движения, пренебрегается. Тело при этом моделируется точечными массовыми источниками, а волновое поле находится с помощью функции Грина с последующим использованием асимптотических разложений на основе метода стационарной фазы [1]. В работе рассмотрена задача определения положения источника по известному волновому полю, генерируемому движущимся в стратифицированной жидкости телом.

Ключевые слова: внутренние волны, массовый источник, стратифицированная жидкость

1. Введение. Движению тел в стратифицированной жидкости посвящено большое количество исследований. В линейной постановке решались задачи обтекания двумерных тел (цилиндра) [2], исследовалось поле присоединенных внутренних волн [3, 4]. Широкое распространение получила техника моделирования поля движущегося тела массовыми и силовыми источниками [5], которая была систематически развита в [6–9] в том числе и для случая нестационарного набегающего потока, а также тел движущихся под углом к горизонту [8, 9]. В последние годы изучались задачи о движении тел в ограниченном пространстве и взаимодействия внутренних волн со свободой поверхностью [10]. Несмотря на то, что расчету поля присоединенных внутренних волн посвящено большое число работ, обратная задача определения положения источника по известному волновому полю не ставилась. В то же время в гидроакустике широко разрабатываются методы пространственной обработки сигналов с последующим решением задачи определения положения и параметров их источников. Построение методов локации источника по полю внутренних волн создаст дополнительные возможности в областях параметров движения, для которых гидроакустические методы оказываются неэффективными.

2. Постановка задачи. В реальных морских условиях поле течения жидкости определяется многими параметрами. В зависимости от постановки задачи необходимо учитывать многокомпонентный состав среды, диссипативные эффекты (вязкость, теплопроводность, диффузию), а также нелинейный характер уравнений гидродинамики. В этих условиях построение максимально простой модели течения представляется основой для успешного решения поставленной задачи.

Приближение несжимаемости. Традиционным важным упрощением, используемым, например, в гидродинамике океана, является предположение о несжимаемости жидкости, приводящее к условию бездивергентности (соленоидальности) поля скоростей течений. В рамках модели идеальной жидкости энтропия жидких частиц не изменяется в процессе течения, диффузия примеси отсутствует, и несжимаемость среды, понимаемая формально как неограниченность величины скорости звука, приводит к неизменности плотности материальных частиц. Такое постоянство полной (материальной) производной плотности по времени вместе с уравнением сохранения массы дает упомянутое условие бездивергентности скорости. В итоге одно уравнение сохранения массы распадается на два соотношения, делающие излишним уравнение состояния среды. Однако подобный формальный подход к условию несжимаемости требует уточнения рамок его применимости.

Наиболее просто физический смысл приближения несжимаемости выявляется на примере идеальной двухпараметрической модели сжимаемой жидкости. Малые возмущения плотности в этом случае распространяются со скоростью звука, а относительная величина плотностных пульсаций оказывается пропорциональной отношению скорости пульсаций к (адиабатической) скорости звука. Так что несжимаемость подразумевает малость скоростей течения по сравнению со скоростью звука, которая при нормальных условиях в воде близка к 1.5 × 103 м/с.

В случае более общей модели идеальной сжимаемой стратифицированной жидкости для монохроматических плоских волн малой амплитуды в предположении однородной стратификации (постоянной частоты плавучести) и в пренебрежении остальными изменениями плотности основного состояния (в приближении Буссинеска) получается биквадратное по частоте дисперсионное уравнение. Это дисперсионное уравнение внутренних акустикогравитационных волн при больших (по сравнению с частотой плавучести) частотах сводится к квадратному дисперсионному уравнению для обычных акустических волн, которыми при обсуждавшемся ограничении на скорости можно пренебречь. Что касается волн низких частот, меньших частоты плавучести, с фазовыми скоростями гораздо меньшими скорости звука, дисперсионное уравнение упрощается до уравнения внутренних волн второй степени частоты, пропорциональной квадрату частоты плавучести. Общий вид этого соотношения не зависит (в первом приближении) от степени сжимаемости жидкости, поскольку колебания частиц жидкости определяются неоднородностью плотности среды и силой Архимеда. Однако сжимаемость (конечность скорости звука) существенно отражается на виде выражения для частоты плавучести $N$

${{N}^{2}} = g\frac{{d\ln {{\rho }_{0}}}}{{dz}} - {{\left( {\frac{g}{{{{{v}}_{s}}}}} \right)}^{2}}$

В этой формуле ${{\rho }_{0}}(z)$, $g$, ${{{v}}_{s}}$ и z – плотность основного возмущаемого состояния, величина ускорения свободного падения, адиабатическая величина скорости звука, и вертикальная координата, отсчитываемая в направлении силы тяжести, соответственно.

Поскольку для воды отношение ускорения свободного падения к скорости звука составляет 7 × 10–3 1/с, а частота плавучести в океане не превосходит 2 × 10–2 1/с, то вклад в изменение плотности, связанный с конечностью скорости звука, является значительным при глубинах, меньших 50 м или больших 200 м. В то же время в области термо- и халоклина на глубинах порядка 100 м для описания внутренних волн может быть использована модель несжимаемой жидкости с соленоидальным полем скорости.

Баланс плотностных изменений существенно изменяется при учете диссипативных (вязких и других) свойств жидкости. В модели неоднородной жидкости плотность материального объема изменяется в отличие от однородной не только за счет изменения давления, но и из-за производства энтропии, порождаемого диффузией скорости и вещества (изменения концентрационного состава среды). Эти дополнительные изменения могут быть важными даже тогда, когда изменениями плотности в силу изменения давления можно пренебречь.

Для малых возмущений уравнения баланса энтропии и диффузии примеси позволяют свести скорости изменения температуры и концентрации примеси к дивергенциям потоков, так что в силу закона сохранения массы дивергенция скорости будет определяться оператором Лапласа линейной комбинации температуры и концентрации примеси

$\operatorname{div} v = \nabla \left[ {\left( {\alpha \chi - \gamma D\frac{{{{k}_{T}}}}{T}} \right)\nabla T - \gamma D\nabla c - \gamma D\frac{{{{k}_{p}}}}{p}\nabla p} \right] \approx \Delta (\alpha \chi T - \gamma Dc),$
где ${\mathbf{v}}$ – скорость, $T$ – температура, $c$ – концентрация примеси, $\alpha $ и $\gamma $ – коэффициенты теплового расширения и соленостного сжатия, $\chi $ и $D$ – коэффициенты температуропроводности и диффузии, ${{k}_{T}}$ и ${{k}_{p}}$ – коэффициенты термо- и бародиффузии.

Здесь приведено также уточненное выражение, принимающее во внимание перекрестные термодинамические эффекты. Выше важность такого влияния устанавливалась на основе относительно крупномасштабных оценок. Однако полученный результат содержит высокие производные, и потому можно ожидать наибольших эффектов от областей с повышенными градиентами при тонкоструктурных изменениях и в пограничных слоях.

Большое различие в скоростях диффузионной, тепловой и вязкой релаксации заставляет в случае вязкой стратифицированной жидкости традиционно принимать во внимание только вязкую диффузию, и в приближении несжимаемости упрощать модель, используя одновременно условия бездивергентности скорости и постоянства плотности материальных частиц.

Поскольку изменения плотности относительно невелики (не превышают нескольких процентов) далее будет использоваться приближение Буссинеска, в рамках которого неоднородностью среды пренебрегается везде за исключением членов содержащих ускорение свободного падения (силы плавучести).

Экспериментальные наблюдения. Простейшим примером стратификации является свободная поверхность, когда плотность меняется на конечную величину на границе раздела воздух–вода. Как известно при движении тела по границе среды в этом случае формируется поле волн (корабельные волны) и картина течения в случае движения тела с постоянной скоростью движется вместе с источником, а поверхности постоянной фазы имеют вид клина (рис. 1).

Рис. 1.

Корабельные волны на поверхности воды.

Экспериментальные наблюдения движения тел (цилиндра и сферы) в однородно стратифицированной жидкости [11–13] показали, что за ограниченное время (порядка 2–3 периода плавучести) позади тела формируется волновое поле, движущееся вместе с источником. При этом существующие благодаря эффектам диффузии конвективные течения вблизи покоящегося тела оказываются настолько слабыми, что после начала движения тела экспериментально не наблюдаются.

Проведенные детальные исследования показали, увеличение скорости движения тела приводит благодаря совместному влиянию нелинейных членов уравнений гидродинамики и вязкости к возникновению возмущений волнового поля в области спутного течения вначале в виде присоединенных донных вихрей, а затем и вихревой дорожки. Тем не менее, волновое поле на больших расстояниях от тела значительное изменение не претерпевает, а сама картина течения определяется эффективным размером источника, скоростью его движения и частотой плавучести. Область спутного течения при этом ограничена в вертикальном направлении размерами тела [11–13], а интенсивность волнового поля, создаваемого вихревой дорожкой, значительно уступает полю присоединенных внутренних волн [14].

Таким образом представляется обоснованной задача определения положения источника по полю присоединенных внутренних волн в рамках линеаризованной модели идеальной несжимаемой линейно стратифицированной жидкости.

Теоретическая модель. Рассматривается наиболее типичное горизонтальное движение тела с постоянной скоростью ${{{\mathbf{v}}}_{0}}$ в неограниченной экспоненциально стратифицированной жидкости (ρ = ${{\rho }_{0}}\exp \left( { - \beta z} \right)$ + $\rho {\kern 1pt} '\left( {{\mathbf{r}},t} \right)$, $\beta g = {{N}^{2}}$, $N$ – частота плавучести). В качестве модели выбрана модель идеальной жидкости. Поскольку изменения плотности жидкости по отношению к базовой стратификации обычно малы, и уравнения движения записываются в приближении Буссинеска. Основным безразмерным параметром является число Фруда $\operatorname{Fr} = {{{v}}_{0}}{\text{/}}Na$, где $a$ – размер тела.

(2.1)
$\begin{gathered} \frac{{\partial {\mathbf{v}}}}{{\partial t}} = - \nabla P + {\mathbf{g}}\frac{{\rho {\kern 1pt} '}}{{{{\rho }_{0}}}} \\ \frac{{\partial \rho {\kern 1pt} '}}{{\partial t}} = \beta {{{v}}_{z}} \\ \operatorname{div} {\mathbf{v}} = 0 \\ \end{gathered} $

Движущееся тело моделируется массовым источником $m\left( {{\mathbf{r}},t} \right)$ = ${{m}_{0}}\delta \left( {{\mathbf{r}} - {{{\mathbf{v}}}_{0}}t} \right)$. Динамическое давление $P$ и скорость могут быть переписаны в терминах внутреннего потенциала $\psi \left( {{\mathbf{r}},t} \right)$ [1]

(2.2)
$P = - {{\rho }_{0}}\left( {\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}} + {{N}^{2}}} \right)\frac{\partial }{{\partial t}}\psi ,\quad {\mathbf{v}} = \left( {\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}\nabla + {{N}^{2}}{{\nabla }_{h}}} \right)\frac{\partial }{{\partial t}}\psi ,$
где ${{\nabla }_{h}} = \left( {{{\partial }_{x}},{{\partial }_{y}},0} \right)$, а внутренний потенциал удовлетворяет уравнению

$\left( {\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}{{\nabla }^{2}} + {{N}^{2}}\nabla _{h}^{2}} \right)\psi = m$

Для источника, движущегося с постоянной скоростью, поле течения оказывается стационарным в системе координат, связанной с источником. Асимптотическое решение задачи [1] на больших расстояниях от источника дает выражение для вертикального смещения частиц жидкости в системе координат источника

(2.3)
$\zeta \left( {{\mathbf{r}},t} \right)\sim H\left( x \right)\frac{{N{{m}_{0}}}}{{2\pi {v}_{0}^{2}}}\frac{{xz}}{{r_{ \bot }^{3}{{r}^{2}}}}\sqrt {{{x}^{2}}{{y}^{2}} + r_{ \bot }^{4}} \cos \left( {\frac{N}{{{{{v}}_{0}}}}\frac{z}{{{{r}_{ \bot }}}}r} \right),$
где $r_{ \bot }^{2} = {{y}^{2}} + {{z}^{2}}$, ${{r}^{2}} = {{x}^{2}} + r_{ \bot }^{2}$ – координаты точки наблюдения в системе отсчета $\left( {x,y,z} \right)$, связанной с источником, $H\left( x \right)$ – функция Хевисайда.

Выражение для вертикальных смещений частиц жидкости позволяет рассчитать горизонтальные карты смещений на различных вертикальных расстояниях от движущегося источника (рис. 2). Эти поля могу быть измерены лабораторно и в натурных условиях традиционными средствами гидрофизических измерений. Таким образом, актуальной оказывается задача определения положения источника по полю вертикальных смещений.

Рис. 2.

Вертикальные (a) и горизонтальные (б) карты вертикальных смещений жидкости $\zeta $ в системе координат, связанной с движущимся источником.

Пусть существует возможность измерять вертикальные смещения в горизонтальной плоскости, над которой двигается источник и по данным измерений требуется определить его положение и скорость. Выберем измерительные устройства в виде горизонтальных концентрических окружностей (рис. 3). Пусть измерения вертикального смещения производятся в центре и вдоль концентрических окружностей.

Рис. 3.

Схема определения скорости движения источника $S$ относительно неподвижной системы координат. Плоскость $\left( {X{\kern 1pt} ',Y{\kern 1pt} '} \right)$ – горизонтальная.

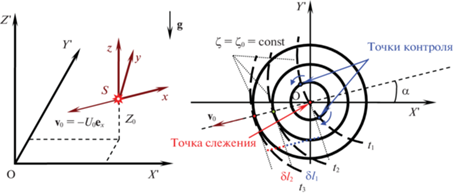
Измеряя в момент времени ${{t}_{1}}$ смещение в центре $O$ (красная точка $\zeta = {{\zeta }_{0}}$) найдем положения точек на первой от центра окружности (расстояние от центра $\delta {{l}_{1}}$), смещения в которых будут равны ${{\zeta }_{0}}$. Тогда определяя момент времени ${{t}_{2}}$ в который эти точки сойдутся в одной точке первой окружности, определим направление движения источника и его скорость ${{{v}}_{0}} = \delta {{l}_{1}}{\text{/}}\left( {{{t}_{2}} - {{t}_{1}}} \right)$.

Чтобы определить положение источника выберем систему отсчета $\left( {X,Y,Z} \right)$, движущуюся вместе с источником, начало отсчета которой с положением источника не совпадает (рис. 4). При этом координаты источника и точки наблюдения имеют значения $\left( {{{X}_{0}},{{Y}_{0}},{{Z}_{0}}} \right)$ и $\left( {x + {{X}_{0}},y + {{Y}_{0}},z + {{Z}_{0}}} \right)$. Обращая внимание, что нули вертикального смещения определяется нулями косинуса, входящего в выражение (2.3) для первого и второго нуля, положения которых определяются выражениями

(2.4)
$\frac{{{{z}_{1}}}}{{{{r}_{{ \bot ,1}}}}}{{r}_{1}} = \frac{{{{{v}}_{0}}}}{N}\frac{\pi }{2}\quad {\text{и}}\quad \frac{{{{z}_{2}}}}{{{{r}_{{ \bot ,2}}}}}{{r}_{2}} = 3\frac{{{{{v}}_{0}}}}{N}\frac{\pi }{2},$
То есть в точках с координатами $\left( {x,y,z} \right)$, которые связаны соотношением
(2.5)
$x = k\sqrt {{{y}^{2}} + {{z}^{2}}} ,$
где $k = \sqrt {\frac{{{{\pi }^{2}}}}{{4{{a}^{2}}{{z}^{2}}}}{{{\left( {2n - 1} \right)}}^{2}} - 1} $ ($n$ – номер нуля $\zeta $), вертикальное смещение частиц жидкости обращается в нуль. Для двух значений высот ${{z}_{1}}$ и ${{z}_{2}}$ такие зависимости изображены на рис. 4 (сверху). Из рисунка следует, что уже на некотором удалении от источника зависимость $x\left( y \right)$ становится близкой к прямолинейной вида $x = ky$. Эти прямые для двух соседних нулей $\zeta $ порядков $n$ и $n + 1$ пересекаются в месте расположения источника, что позволяет определить связь между горизонтальными координатами источника $\left( {{{X}_{0}},{{Y}_{0}}} \right)$, номером нуля и глубиной погружения источника ${{Z}_{0}}$. Таким образом, общее число неизвестных оказывается равным четырем, что позволяет решить задачу определения положения источника по данным измерения нулей вертикального смещения жидкости в четырех точках, расположенных в горизонтальной плоскости.

Рис. 4.

Для двух вертикальных горизонтов z = z1 и z = z2 показаны расположения нулей смещений (порядков n = 1, 2, 3) в системе координат источника (сверху), а также их расположение относительно систем координат Sxyz и ОXYZ (внизу).

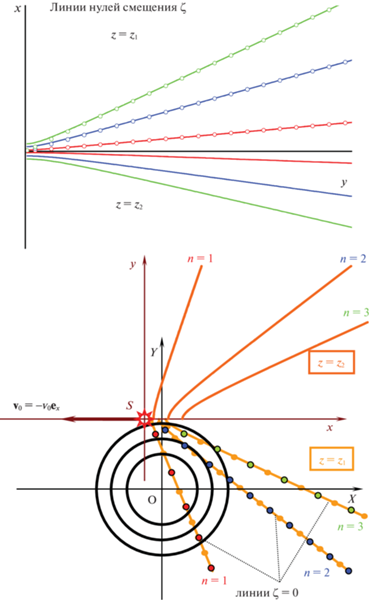
Обозначая координаты нулей порядков $m = n$ и $n + 1$, через $\left( {X_{{i,m}}^{{}},Y_{{i,m}}^{{}},Z} \right)$; $i = 1,2$, а определяя коэффициенты наклона прямых как

${{k}_{m}} = \frac{{\Delta {{X}_{m}}}}{{\Delta {{Y}_{m}}}},$
приходим к выражениям
(2.6)
${{X}_{0}} = \frac{{{{k}_{n}}{{k}_{{n + 1}}}\left( {Y_{{i,n + 1}}^{{}} - Y_{{i,n}}^{{}}} \right) + {{k}_{{n + 1}}}X_{{i,n}}^{{}} - {{k}_{n}}Xi,_{{n + 1}}^{{}}}}{{{{k}_{{n + 1}}} - {{k}_{n}}}}$
(2.7)
${{Y}_{0}} = \frac{{{{k}_{{n + 1}}}Y_{{i,n + 1}}^{{}} - {{k}_{n}}Y_{{i,n}}^{{}} + X_{{i,n}}^{{}} - X_{{i,n + 1}}^{{}}}}{{{{k}_{{n + 1}}} - {{k}_{n}}}}$
(2.8)
${{Z}_{0}} = Z - \frac{{\pi {\text{/}}a}}{{{{b}_{{n + 1}}} - {{b}_{n}}}},\quad n = \frac{1}{2}\frac{{{{b}_{{n + 1}}} + {{b}_{n}}}}{{{{b}_{{n + 1}}} - {{b}_{n}}}},$
где $b_{n}^{2} = k_{n}^{2} + 1$.

Решение задачи без использования асимптотических выражений зависимостей (2.5) можно получить, воспользовавшись выражением для производной $x{\kern 1pt} ' = {{k}^{2}}y{\text{/}}x$. В этом случае для полного решения достаточно знать положение четырех точек и четырех производных x′ в этих точках.

В отличие от асимптотического, точное решение может быть построено по данным измерения восьми нулевых точек двух соседних нулей вертикального смещения $\left( {X_{{i,m}}^{{}},Y_{{i,m}}^{{}},Z} \right)$, $m = n,n + 1$; $i = 1,4$. Выбирая в качестве неизвестных величины ${{X}_{0}}$, $k_{m}^{2}{{Y}_{0}}$, $k_{m}^{2}$ приходим к линейной системе уравнений

(2.9)
$2\left( {X_{{i,m}}^{{}} - X_{{i + 1,m}}^{{}}} \right){{X}_{0}} - 2\left( {Y_{{i,m}}^{{}} - Y_{{i + 1,m}}^{{}}} \right)k_{m}^{2}{{Y}_{0}} + \left( {Y_{{i,m}}^{2} - Y_{{i + 1,m}}^{2}} \right)k_{m}^{2} = X_{{i,m}}^{2} - X_{{i + 1,m}}^{2},$
решение которой однозначно определяет положение источника.

Работа выполнена за счет гранта Российского научного фонда (проект № 21-11-00151).

Список литературы

  1. Voisin B. Internal wave generation in uniformly stratified fluids. Part 2. Moving point sources // J. Fluid Mech. 1994. V. 261. P. 333–374.

  2. Bretherton F.P. The time-dependent motion due to a cylinder moving in an unbounded rotating or stratified fluid // J. Fluid Mech. 1967. V. 28. P. 545–570.

  3. Стурова И.В. Волновые движения, возникающие в стратифицированной жидкости при обтекании погруженного тела // ПМТФ. 1974. № 6. С. 80–91.

  4. Аксенов А.В., Можаев В.В., Скороваров В.Е., Шеронов А.А. Фазовая структура трехмерных внутренних волн в канале // Изв. АН СССР. МЖГ. 1989. № 1. С. 129–135.

  5. Городцов В.А., Теодорович Э.В. Плоская задача для внутренних волн, порождаемых движущимися сингулярными источниками // Изв. АН СССР. МЖГ. 1981. № 2. С. 77–83.

  6. Voisin B. Internal wave generation in uniformly stratified fluids. Part 1. Green’s function and point sources // J. Fluid Mech. 1991. V. 231. P. 439–480.

  7. Dupont P., Voisin B. Internal waves generated by a translating and oscillating sphere // Dyn. Atmos. Oceans. 1996. V. 23. P. 289–298.

  8. Scase M.M., Dalziel S.B. Internal wave fields and drag generated by a translating body in a stratified fluid // J. Fluid Mech. 2004. V. 498. P. 289–313.

  9. Scase M.M., Dalziel S.B. Internal wave fields generated by a translating body in a stratified fluid: an experimental comparison // J. Fluid Mech. 2006. V. 564. P. 305–331.

  10. Stetsyuk I.V. The development of a stratified flow following over a sphere inside the viscous fluid in the presence of internal or surface waves // J. Phys.&Math. 2015. № 1. P. 293–298.

  11. Сысоева Е.Я., Чашечкин Ю.Д. Вихревые системы спутного стратифицированного течения за сферой // Изв. АН СССР. МЖГ. 1991. № 4. С. 82–90.

  12. Миткин В.В., Чашечкин Ю.Д. Экспериментальное исследование поля скорости около цилиндра в непрерывно стратифицированной жидкости // Изв. РАН. МЖГ. 2000. № 5. С. 20–30.

  13. Чашечкин Ю.Д. Гидродинамика сферы в стратифицированной жидкости // Изв. АН СССР. МЖГ. 1989. № 1. С. 3–9.

  14. Voisin B. Internal wave generation by turbulent wakes // In: Mixing in Geophysical Flows / Ed. by Redondo J.M., Métais O. 1995. P. 291–301. CIMNE.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал