Прикладная математика и механика, 2023, T. 87, № 1, стр. 45-52

1. Определяющие соотношения и материальные функции. Рассмотрим интегральные определяющие соотношения между напряжениями ${{\sigma }_{{ij}}} = {{s}_{{ij}}} + \sigma {{\delta }_{{ij}}}$ и малыми деформациями ${{\varepsilon }_{{ij}}} = {{e}_{{ij}}} + \theta {{\delta }_{{ij}}}{\text{/}}3$ для линейных изотропных вязкоупругих сред с ядрами разностного типа:

где $R(t)$ и ${{R}_{1}}(t)$ – функции сдвиговой и объемной релаксации, $\Pi (t)$ и ${{\Pi }_{1}}(t)$ – функции сдвиговой и объемной ползучести [1–4]. Эти функции служат ядрами разностных операторов $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{R} $, ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{R} }_{1}}$, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\Pi } $ и ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\Pi } }_{1}}$, таких что $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{R} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\Pi } $ = $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\Pi } \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{R} $ = $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{I} $, ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{R} }_{1}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\Pi } }_{1}}$ = ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\Pi } }_{1}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{R} }_{1}}$ = $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{I} $. Единичный оператор $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{I} $ в дальнейшем для простоты будет обозначаться единицей.

Для описания поведения сред во времени помимо упомянутых привлекаются безразмерные операторы $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\nu } $ (оператор Пуассона), $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } $ и $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\pi } $:

а также оператор Юнга $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{E} $:

2. Оператор ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{g} }_{\beta }}$. Набор $\left\{ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{R} ,{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{R} }}_{1}},\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\Pi } ,{{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\Pi } }}_{1}}} \right\}$ составляет множество так называемых основных операторов, легко подлежащих расшифровке в силу того, что их ядра определяются из стандартных установочных экспериментов на релаксацию и ползучесть. Для расширения числа операторных функций, представимых в виде суммы произведений основных операторов, а следовательно, допускающих точную интегральную расшифровку, вводится оператор ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{g} }_{\beta }}$ Ильюшина

Его свойства подробно освещены в монографиях [1, 2].

Приведем пример задачи теории вязкоупругости, в которой введение ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{g} }_{\beta }}$ в число основных операторов позволяет избежать аппроксимационных методов и найти точное решение.

Пусть сплошной диск радиуса $b$ из материала с определяющими соотношениями (1.1), (1.2) плотности $\rho $ вращается вокруг своей оси с угловой скоростью $\Omega (t)$. Требуется определить возникающее в результате центрифужного эффекта кольцевое напряжение ${{\sigma }_{{\theta \theta }}}(b,t)$ в точках границы диска.

Решение соответствующей задачи теории упругости о вращении тяжелого диска следующее (см., напр., ([5], с. 47)):

Согласно принципу Вольтерры и связи операторов $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } $ и $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\nu } $ в задаче для вязкоупругого диска

Дробно-линейную функцию $\phi (\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\omega } )$ нельзя представить конечной суммой произведений из набора $\{ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{R} ,{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{R} }_{1}},\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\Pi } ,{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\Pi } }_{1}}\} $. Но в то же время

с параметрами $N = 1$, ${{\beta }_{0}} = 0$, ${{c}_{0}} = 2$, ${{\beta }_{1}} = 1{\text{/}}2$, ${{c}_{1}} = - 3{\text{/}}2$. Таким образом, можно дать точное выражение для кольцевого напряжения:

Возможные установочные эксперименты для непосредственного определения функции ${{g}_{\beta }}(t)$ описаны в ([1], с. 112; [2], с. 109). В общем случае связи шаровых частей (1.2) они достаточно сложны в осуществлении и различны для разных диапазонов изменения $\beta $. Так, для $0 \leqslant \beta \leqslant 1{\text{/}}2$ к исследуемому образцу необходимо последовательно присоединить скручиваемый образец, изготовленный из того же материала, что и основной, и одной и той же силой растягивать первый и скручивать второй образец.

Проще ситуация в случае вязкоупругой модели с нерелаксирующим объемом (${{R}_{1}}(t) \equiv K$, ${{\Pi }_{1}}(t) \equiv 1{\text{/}}K$), в которой шаровые части $\sigma (t)$ и $\theta (t)$ связаны упругим законом

с модулем объемного сжатия $K = \operatorname{const} $. Тогда вместо скручиваемого второго образца в предыдущем эксперименте можно взять работающую на растяжение пружину заданной в зависимости от параметра $\beta $ жесткости.

Остановимся в дальнейшем подробнее на случае (2.6) и предложим дополнительные возможные установочные эксперименты для определения ядра ${{g}_{\beta }}(t)$. Заметим, что операторы (1.3) и (1.4) примут вид

а сам оператор (2.1) будет выглядеть следующим образом:

Если две функции $x(t)$ и $y(t)$ связаны между собой операторным соотношением

то обратная связь имеет вид

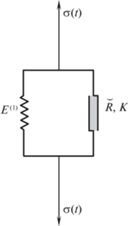
Эксперимент 1. Соединим параллельно упругий элемент с модулем Юнга ${{E}^{{(1)}}}$ и слой из исследуемого вязкоупругого материала с определяющими соотношениями (1.1) и (2.6) (рис. 1). При действии осевым напряжением $\sigma (t)$ упругий элемент работает на растяжение, а слой на сдвиг. Так как деформация упругого элемента $\varepsilon (t)$ при параллельном соединении совпадает с деформацией сдвига слоя, то

Из сравнения выражений в (2.10) и (2.11) видно, что при переобозначении $x(t) = \sigma (t)$, $y(t) = {{E}^{{(1)}}}\varepsilon (t)$, ${{E}^{{(1)}}} = 3K{\text{/}}\beta $ они совпадут, а, следовательно, согласно (2.9)

Прикладывая напряжение ступенькой Хевисайда $\sigma (t) = {{\sigma }_{0}}h(t)$ и измеряя в эксперименте деформацию ${{\varepsilon }_{0}}(t)$, получим искомую функцию

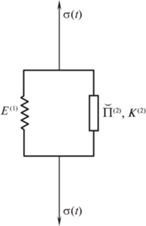
Эксперимент 2. Заменим в предыдущем эксперименте работающий на сдвиг слой из исследуемого материала на работающий на растяжение образец из другого (вспомогательного) вязкоупругого материала с нерелаксирующим объемом и материальными функциями, которые будем обозначать верхним индексом (2). Упругий элемент в другом колене параллельного соединения оставим прежним (рис. 2).

Как следует из (2.11), вспомогательный материал должен быть таким, чтобы ядро ${{E}^{{(2)}}}(t)$ оператора Юнга ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{E} }^{{(2)}}}$ для него совпадало с известной функцией $R(t)$ сдвиговой релаксации. Нетрудно показать, что это требование приводит к следующей связи материальных операторов исследуемой и вспомогательной сред:

В частности, если вспомогательный материал несжимаем, то

Результаты эксперимента 2 можно интерпретировать и в обратную сторону. Если имеется образец из материала с нерелаксирующим объемом, функцией сдвиговой ползучести $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\Pi } _{{(t)}}^{{(2)}}$ и модулем объемного сжатия ${{K}^{{(2)}}}$, то, проведя серию экспериментов с упругими элементами с различными модулями Юнга ${{E}^{{(1)}}}$, можно построить серию функций ${{g}_{\beta }}(t)$ для материала с функцией сдвиговой ползучести $\Pi (t)$, вид которой следует из (2.14), и модулем объемного сжатия $K = \beta {{E}^{{(1)}}}{\text{/}}3$. Поскольку величины $K$ и $\beta $ везде входят только своим отношением, то для любого $a > 0$ ядро ${{g}_{\beta }}(t)$ вязкоупругой среды с материальными функциями $\Pi (t)$ и $K$ будет совпадать с ядром ${{g}_{{a\beta }}}(t)$ среды с функциями $\Pi (t)$ и $aK$.

3. Оператор ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h} }_{\gamma }}$. С оператором ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{g} }_{\beta }}$ Ильюшина тесно связан другой оператор, который по аналогии с ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{g} }_{\beta }}$ назовем ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h} }_{\gamma }}$:

Эта связь устанавливается взаимообратными соотношениями

Так, решение (2.3) упоминаемой ранее задачи о вращении тяжелого диска можно записать и по-другому:

Точное решение (2.5) представимо и в терминах операторов ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h} }_{\gamma }}$:

В случае нерелаксирующего объема из (3.1) имеем

Предложим ряд экспериментов по непосредственному (безотносительно к ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{g} }_{\beta }}$) нахождению ядра ${{h}_{\gamma }}(t)$. Заметим, что если две функции $x(t)$ и $y(t)$ удовлетворяют операторному уравнению

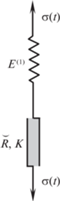
с функцией ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{h} }_{\gamma }}$ в виде (3.5), то

Эксперимент 3. Последовательно соединим упругий элемент с модулем Юнга ${{E}^{{(1)}}}$ и слой из исследуемого материала с определяющими соотношениями (1.1), (2.6) (рис. 3). Так как напряжение $\sigma (t)$ в упругом элементе при последовательном соединении равно сдвиговому напряжению в слое, то

Соотношения (3.7) и (3.8) тождественно совпадут при переобозначении $x(t) = \varepsilon (t)$, $y(t) = \sigma (t){\text{/}}{{E}^{{(1)}}}$, ${{E}^{{(1)}}} = 3K\gamma $, так что согласно (3.6)

Если фиксировать деформацию ступенькой Хевисайда $\varepsilon (t) = {{\varepsilon }_{0}}h(t)$ и измерять в эксперименте осевое напряжение ${{\sigma }_{0}}(t)$ всей системы, то искомая функция ${{h}_{\gamma }}(t)$ вычисляется по формуле

По заданному $\gamma > 0$ упругий элемент выбирается так, чтобы его модуль Юнга был равен $3K\gamma $.

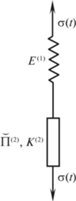
Эксперимент 4. Воспользуемся, как и в эксперименте 2, работающим на растяжение образцом из вспомогательного материала с нерелаксирующим объемом и соединим его последовательно с упругим элементом, имеющим модуль Юнга ${{E}^{{(1)}}}$ (рис. 4). Оператор $1{\text{/}}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{E} }^{{(2)}}}$ для этого материала должен совпадать с известным оператором $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\Pi } $, а, следовательно, ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{E} }^{{(2)}}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{R} $. Таким образом, связь материальных операторов (2.14) исследуемой и вспомогательной сред остается такой же, как в эксперименте 2.

Проводя серию экспериментов на релаксацию с упругими элементами с различными модулями Юнга ${{E}^{{(1)}}}$, принципиально можно построить серию функций ${{h}_{\gamma }}(t)$ для материала с функцией сдвиговой ползучести, следующей из (2.14), и модулем объемного сжатия $K = {{E}^{{(1)}}}{\text{/}}(3\gamma )$. Так как $K$ и $\gamma $ входят только комбинацией своего произведения, то ядро ${{h}_{\gamma }}(t)$ вязкоупругой среды с материальными функциями $\Pi (t)$ и $K$ не будет отличаться от ядра ${{h}_{{a\gamma }}}(t)$ среды, характеризующейся $\Pi (t)$ и $K{\text{/}}a$, $a > 0$.

4. Использование температурно-временнóй аналогии. Естественно, встает вопрос о подборе в экспериментах 2 и 4 реального вспомогательного материала с фиксированными реологическими свойствами, определяемыми связью (2.14) либо (2.15). Здесь на помощь может прийти температурно-временнáя аналогия, позволяющая в определенных случаях в качестве вспомогательного материала выбирать сам исследуемый материал.

Положим в (2.14) ${{K}^{{(2)}}} = K$ и запишем

Используем тот факт, что при повышении температуры $T > {{T}_{0}}$ явление ползучести во времени протекает быстрее, чем при $T = {{T}_{0}}$, и тем самым значение функции ползучести в каждый момент становится больше. Надлежащим образом устанавливая температурный режим $T(t)$ при проведении экспериментов 2 и 4, добьемся того, чтобы с удовлетворительной точностью выполнялось соотношение

Тогда в качестве ядра ${{\Pi }^{{(2)}}}(t)$ оператора ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\Pi } }^{{(2)}}}$ в (4.1) можно взять функцию $\Pi (t,T(t))$.

Заметим, что проведенные рассуждения, связанные с приближенным подбором оператора ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\Pi } }^{{(2)}}}$ в (2.14) и (2.15), имеют место и в случаях, когда в качестве вспомогательного выбирается не сам исследуемый материал, а другой вязкоупругий материал, но эксперимент проводится при вычисленном для него температурном режиме $T(t)$.

Работа выполнена при поддержке Российского научного фонда (проект 22-21-00077).