Прикладная математика и механика, 2023, T. 87, № 1, стр. 3-18

1. Введение. Прецессионные движения тела, имея достаточно широкий диапазон применения в приложениях (например, в теории гироскопических систем [1]), большой интерес представляют в теоретических исследованиях, поскольку они дают возможность моделировать эти движения под действием различного класса сил. В динамике тяжелого твердого тела существуют регулярные прецессии гироскопа Лагранжа относительно вертикали [2], регулярные прецессии тела относительно наклонной оси [3], полурегулярные прецессии [4] и прецессии общего вида в решении В. Гесса [5] и прецессии общего вида [6]. Но, как показано в [4], тяжелое твердое тело не может совершать полурегулярную прецессию второго типа. В обобщенных задачах динамики твердого тела (задаче о движении гиростата под действием потенциальных и гироскопических сил с постоянным и переменным гиростатическим моментом, задаче о движении гиростата в магнитном поле с учетом эффекта Барнетта–Лондона) получены многочисленные классы прецессий [7–9]. Определенный интерес представляют и исследования прецессий системы связанных твердых тел [10], состоящей из гироскопа Лагранжа и Гесса, а также в задаче о движении твердого тела с жидким заполнением [11–14].

В задаче о движении твердого тела в силовом поле, которое является суперпозицией трех однородных силовых полей, известны результаты, посвященные рассмотрению только регулярных прецессий [15–17]. В данной статье изучается класс прецессий общего вида при дополнительном предположении о том, что скорость прецессии тела в два раза больше скорости собственного вращения (он может быть отнесен к резонансным прецессиям тела). Из трех направлений, которые характеризуют результирующие силы однородных полей, выделено приоритетное направление с единичным вектором ${\mathbf{\gamma }}$. Поскольку движение тела является прецессией, то постоянен угол между вектором ${\mathbf{\gamma }}$ и вектором ${\mathbf{a}}$, неизменно связанным с твердым телом. В результате проведенных исследований по нахождению условий существования резонансных прецессионных движений установлено, что векторы, определяющие центры приложения сил других направлений ${\mathbf{\gamma }}_{1}^{{}}$, ${\mathbf{\gamma }}_{2}^{{}}$ ортогональны. Получено алгебраическое уравнение второго порядка на угол нутации, коэффициенты которого зависят от главных моментов инерции тела. Если тело имеет сферическое распределение масс, то этот угол равен $\arccos \frac{1}{4}$. Нахождение основных переменных уравнений движения сведено к обращению эллиптических интегралов.

2. Постановка задачи. Рассмотрим движение твердого тела, имеющего неподвижную точку, в силовом поле, которое является суперпозицией трех однородных и постоянных силовых полей. Обозначим через ${\mathbf{\gamma }}$, ${\mathbf{\gamma }}_{{}}^{{(1)}}$, ${\mathbf{\gamma }}_{{}}^{{(2)}}$ единичные векторы, характеризующие направления сил ${\mathbf{P}},{{{\mathbf{P}}}_{1}},{{{\mathbf{P}}}_{2}}$ каждого из полей; $C,{{C}_{1}},{{C}_{2}}$ – центры приведения сил; ${\mathbf{s}} = P\,{\mathbf{OC}}$, ${\mathbf{r}} = {{P}_{1}}\,{\mathbf{O}}{{{\mathbf{C}}}_{1}}$, ${\mathbf{p}} = {{P}_{2}}\,{\mathbf{O}}{{{\mathbf{C}}}_{2}}$; $Oxyz$ – подвижная система координат, $O$ – неподвижная точка. Пусть тензор инерции тела в системе $Oxyz$ имеет значение $A = {\text{(}}A_{{ij}}^{{}}{\text{)}}$ $(i,j = \overline {1,3} )$. Тело вращается вокруг точки $O$ с угловой скоростью ${\mathbf{\omega }} = {\text{(}}\omega _{1}^{{}}{\mathbf{i}}_{1}^{{}} + \omega _{2}^{{}}{\mathbf{i}}_{2}^{{}} + \omega _{3}^{{}}{\mathbf{i}}_{3}^{{}}{\text{)}}$ (${\mathbf{i}}_{1}^{{}},{\mathbf{i}}_{2}^{{}},{\mathbf{i}}_{3}^{{}}$ – единичные векторы системы $Oxyz$). Для векторов ${\mathbf{s}},{\mathbf{r}},{\mathbf{p}}$ запишем соотношения

Тогда уравнения движения тела представим в виде

где точка над переменными ${\mathbf{\omega }},{\mathbf{\gamma }},{\mathbf{\gamma }}_{{}}^{{(1)}},{\mathbf{\gamma }}_{{}}^{{(2)}}$ обозначает дифференцирование по времени $t$. В формулах (2.2), (2.3) полагаем то есть направления силовых полей будут характеризоваться тройкой ${\mathbf{\gamma }},{\mathbf{\gamma }}_{{}}^{{(i)}}$ $(i = 1,2)$. Тогда очевидны равенства ${\mathbf{P}} = P\,{\mathbf{\gamma }}$, ${\mathbf{P}}_{i}^{{}} = P_{i}^{{}}{\mathbf{\gamma }}_{{}}^{{(i)}}$ $(i = 1,2)$.

Рассмотрим прецессии тела относительно вектора ${\mathbf{\gamma }}$. Они характеризуются инвариантным соотношением (ИС)

где $\theta _{{\text{0}}}^{{}}$ – угол между векторами ${\mathbf{a}}$ и ${\mathbf{\gamma }}$ (${\mathbf{\dot {a}}} = {\mathbf{0}}$, $\left| {\mathbf{a}} \right| = 1$). Вектор угловой скорости тела на ИС (2.5) представим так [7]:

Переменные $\varphi ,\psi $ и постоянную $\theta _{{\text{0}}}^{{}}$ можно трактовать, как углы Эйлера. Используя метод [7], запишем значение вектора ${\mathbf{\gamma }}_{{}}^{{(i)}}$:

где $b_{0}^{{}} = \frac{1}{{a_{0}^{'}}}$ ($a_{0}^{'} = \sin {{\theta }_{0}}$), $\psi _{0}^{{}}$ – постоянная.

Значение вектора ${\mathbf{\gamma }}_{{}}^{{(2)}}$ найдем по второй формуле системы (2.4):

Таким образом, при получении (2.7), (2.8) полагалось, что ${\mathbf{a}} \times {\mathbf{\gamma }} \ne {\mathbf{0}}$, то есть случай равномерных вращений тела исключаем из рассмотрения. Подвижную систему координат выберем следующим образом: направим вектор $\,{\mathbf{i}}_{3}^{{}}$ по вектору ${\mathbf{a}}$. Тогда на основании ИС (2.5), первого уравнения из (2.3) имеем [6, 7]

На основании (2.6), (2.9) запишем компоненты $\omega _{1}^{{}},\omega _{2}^{{}},\omega _{3}^{{}}$ вектора ${\mathbf{\omega }}$:

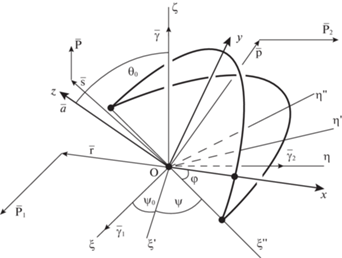
На рис. 1 приведена геометрическая трактовка прецессий тела относительно вектора ${\mathbf{\gamma }}$ ($O\xi \eta \zeta $ – неподвижная система координат).

Замечание 1. При описании кинематических свойств в виде соотношений (2.5)–(2.10) использован метод [7, 8], который отличается от методов, применяемых в [11, 14–17].

Замечание 2. Уравнения (2.2), (2.3) имеют интеграл энергии

где $E$ – постоянная. Как было показано [6, 7], нахождение условий существования прецессий в задачах динамики твердого тела на основании (2.11) значительно упрощается.

3. Преобразование уравнения (2.2) на ИС (2.5). Внесем в уравнение (2.2) значение ${\mathbf{\omega }}$ из (2.6) и рассмотрим полученное уравнение в базисе ${\mathbf{a}},{\mathbf{\gamma }},{\mathbf{a}} \times {\mathbf{\gamma }}$ с учетом (2.7), (2.8):

где ${\text{Sp}}(A) = A_{{11}}^{{}} + A_{{22}}^{{}} + A_{{33}}^{{}}$ – след матрицы $A$.

По аналогии с (3.1)–(3.3) распишем интеграл (2.11) на ИС (2.5), (2.6):

Введем обозначения

Сначала запишем интеграл (3.4) в силу (3.5):

Затем обратимся к уравнениям (3.1)–(3.3). На основании (3.5) имеем

Представление соотношений (3.1)–(3.4) в виде (3.6)–(3.9) связано с решением задачи о замене одного из уравнений (3.7)–(3.9) интегралом (3.6). Вычислим производную по времени от левой части уравнения (3.6), используя соотношения

Если учесть в полученном уравнении соотношения (3.7), (3.8), то имеем тождество. Данное свойство выполняется в случае, когда одно из уравнений (3.7), (3.8) не вырождается в тождество (см. разд. 6, уравнения (6.2)). Исключая этот вариант, можно рассматривать интеграл (3.6) совместно с одним из указанных уравнений, но уравнение (3.9) необходимо учитывать всегда.

4. Исследование уравнений (3.6)–(3.9) в случае $\psi = 2\varphi $. В динамике твердого тела известны решения, описывающие прецессии при условии

Из (4.1) следует, что $\dot {\psi } = 2\dot {\varphi }$, то есть скорость прецессии в два раза больше скорости собственного вращения. Введем обозначения

В силу (4.2) функции $f_{i}^{{}}(\varphi )$ $(i = \overline {1,\,3} )$ преобразуем к виду

На основании (4.1)–(4.3) найдем функции

где

Здесь

Рассмотрим уравнения (3.6)–(3.9) при условиях (4.1) и $A = {\text{(}}A_{{ij}}^{{}}{\text{)}}$. Тогда на первом этапе распишем уравнение (3.6). Положим

где

Уравнение (3.6), в силу условия (4.1) и обозначений (4.7), (4.9), таково:

где

На основании (4.1), (4.4), (4.10) уравнение (3.8) представим в развернутом виде. Для этой цели введем обозначения

где $Q_{2}^{{}},L_{2}^{{}}$ имеют значения (4.10), а $\tilde {L}_{1}^{{}},\tilde {Q}_{1}^{{}},Q_{0}^{{}}$ зависят от параметров следующим образом:

В силу соотношений (4.4), (4.13) и учете (4.1), из уравнения (3.8) получим

Уравнения (4.11), (4.15) записаны в полном представлении, что связано с необходимостью использовать их в дальнейших преобразованиях. Но для исследования конкретных условий на параметры задачи, при которых уравнения совместны, целесообразно представить их в компактном виде. Обозначим правую часть уравнения (4.11) через $2{{R}_{1}}$, где

Тогда, на основании (4.11), (4.16) имеем

Аналогично запишем (4.15), учтя формулы (4.4), (4.15):

Продифференцируем обе части уравнения (4.17) по $t$ и внесем в него $\ddot {\varphi }$ из (4.18). В результате получим уравнение, содержащее $\dot {\varphi }_{{}}^{2}$. Поэтому в нем необходимо избавиться от $\dot {\varphi }_{{}}^{2}$ с помощью уравнения (4.17). Тогда найдем алгебраическое уравнение

Если учесть в (4.19) функции (4.6), (4.9), (4.13), то имеем тригонометрический многочлен пятого порядка

где $M_{i}^{{}}$ $(i = \overline {0,5} )$, $N_{i}^{{}}$ $(i = \overline {1,\,4} )$ – постоянные, не зависящие от φ, должны быть равны нулю. Рассмотрим равенства $M_{5}^{{}} = 0$, $N_{5}^{{}} = 0$. Они приводят к условиям

Изучим вариант $G_{3}^{2} + H_{3}^{2} \ne 0$. Тогда из (4.21) получим

Используя в равенствах (4.22) обозначения (4.10), находим условия на тензор инерции $A$:

Запишем функции $F_{1}^{{}}(\varphi )$, $F_{2}^{{}}(\varphi )$, $F_{3}^{{}}(\varphi )$, $R_{1}^{{}}(\varphi )$, $R_{1}^{'}(\varphi )$, сохраняя члены, имеющие максимальные аргументы тригонометрических функций

Обратимся к уравнению (4.19). Для его представления в наглядном виде вычислим $2F_{1}^{{}}(\varphi )F_{3}^{{}}(\varphi )$ + $F_{2}^{{}}(\varphi )F_{1}^{'}(\varphi )$. Используя (4.24), а также (4.10), (4.14), имеем

Преобразуем выражение в квадратных скобках во втором слагаемом уравнения (4.19). На основании принятых ранее обозначений имеем

Запишем уравнение (4.19), в силу (4.16), (4.24)–(4.26)

Рассмотрим случай $1 + 2a_{0}^{{}} = 0$. Тогда из (4.27) следует, что коэффициенты при $\sin 5\varphi $, $\cos 5\varphi $ равны нулю. Для дальнейшего изучения уравнения (4.19) положим в (4.9), (4.13), (4.14) $a_{0}^{{}} = - \frac{1}{2}$:

Функции $R_{1}^{{}}(\varphi )$, $R_{1}^{'}(\varphi )$, $\Phi _{1}^{{}}(\varphi )$, в силу предположения $H_{3}^{{}} \ne 0$, $G_{3}^{{}} \ne 0$ имеют прежний вид. На основании (4.28) формул для $\,R_{1}^{{}}(\varphi )$ и $R_{1}^{'}(\varphi )$ из (4.24) можно сделать заключение о том, что коэффициенты при $\sin 4\varphi $, cos4φ в уравнении (4.19) обращаются в нуль при условии $a_{0}^{{}} = 0$, что невозможно, так как $a_{0}^{{}} = - \frac{1}{2}$, или при выполнении равенств $A_{{23}}^{{}} = 0$, $A_{{13}}^{{}} = 0$. Рассмотрение уравнения (4.19) в последнем случае приведет к заключению о том, что оно может быть тождеством по $\varphi $ только при $H_{3}^{{}} = 0$, $G_{3}^{{}} = 0$.

Распишем уравнение (4.27) при $1 + 2a_{0}^{{}} \ne 0$, приняв во внимание только коэффициенты при $\sin 5\varphi $, cos 5φ:

где

Если в (4.29) полагать $a_{0}^{{}} \ne 0$, то в силу предположения $H_{3}^{{}} \ne 0$, $G_{3}^{{}} \ne 0$, из (4.25), (4.30) получим

Пусть в (4.29) $a_{0}^{{}} = 0$. Тогда, на основании (4.10), (4.13), (4.24), из уравнения (4.19) установим его вид, указанный в (4.20):

Из (4.32) следуют равенства $A_{{13}}^{{}} = 0$, $A_{{23}}^{{}} = 0$. Тогда ${{F}_{1}} = {{L}_{0}}$, ${{F}_{2}} = {{Q}_{0}}$, ${{F}_{3}} = 0$. Уравнение (4.19) упрощается:

где

Приравнивая к нулю коэффициенты при $\sin 3\varphi $, $\cos 3\varphi $ в уравнении (4.33), в силу (4.34) получим уравнение

Других условий из (4.33) не следует. Поэтому обратимся к уравнению (3.9), полагая в нем $A_{{12}}^{{}} = 0$, $A_{{22}}^{{}} = A_{{11}}^{{}}$, $A_{{13}}^{{}} = 0$, $A_{{23}}^{{}} = 0$. Очевидно, что коэффициент при производной $\ddot {\varphi }$ равен нулю. Для того, чтобы расписать (3.9), запишем основные формулы. В силу (3.5), (4.5), (4.24), имеем

где

Тогда, в силу (4.36), (4.37) и принятых ранее условий из (3.9), для слагаемых, содержащих $\sin 3\varphi $ и $\cos 3\varphi $, имеем

Из данного соотношения следует условие на параметры

Очевидно, что уравнения (4.35), (4.38) относительно параметра $a_{0}^{{}}$ не совместны. Итак, в равенствах (4.29), (4.30) необходимо принять $H_{3}^{{}} = 0$, $G_{3}^{{}} = 0$. Тогда в равенствах (4.21) необходимо принять

5. Случай $H_{3}^{{}} = 0$, $G_{3}^{{}} = 0$. В дальнейшем, на основании результатов разд. 4 и формул (4.39), полагаем, что $Q_{2}^{2} + L_{2}^{2} \ne 0$. Из обозначений для $H_{3}^{{}}$, $G_{3}^{{}}$ из системы (4.7), в силу (4.8), получим

При условиях (5.1) значения $\Phi _{i}^{{}}(\varphi )$ $(i = \overline {1,\,4} )$ таковы:

где на основании (4.7), (5.1) коэффициенты многочленов (5.2) имеют вид

Если в (5.3) параметры $H_{2}^{{}} = 0$, $G_{2}^{{}} = 0$, то должны выполняться условия $p_{3}^{{}} = 0$, $r_{3}^{{}} = 0$. Тогда на основании равенств (5.1) векторы ${\mathbf{p}} = (r_{2}^{{}}, - r_{1}^{{}},0)$, ${\mathbf{r}} = (r_{1}^{{}},r_{2}^{{}},0)$ ортогональны. Когда выполнены равенства $H_{1}^{{}} = 0$, $G_{1}^{{}} = 0$, то из (5.3) следует, что векторы ${\mathbf{p}}$ и ${\mathbf{r}}$ направлены по оси, содержащей вектор ${\mathbf{a}}$.

Рассмотрим уравнения (4.11), (4.15), полагая в них $A_{{11}}^{{}} \ne A_{{22}}^{{}}$, $A_{{12}}^{{}} \ne 0$, то есть $Q_{2}^{{}} \ne 0$, $L_{2}^{{}} \ne 0$. В силу условий (4.38), функция $R_{1}^{{}}(\varphi )$ из (4.16) упрощается, а функции $F_{i}^{{}}(\varphi )$ $(i = \overline {1,\,3} )$ сохраняют прежний вид. Запишем их так:

Как показывают вычисления, в данном случае целесообразно рассматривать не уравнение (3.8), а уравнение (3.7) (совместно с уравнением (3.6)).

На основании соотношения (4.6) при условии $\dot {\psi } = 2\dot {\varphi }$ уравнение (3.7) представим в виде

где где

Запишем уравнение (4.11), полагая в нем $H_{3}^{{}} = 0$, $G_{3}^{{}} = 0$

где

Если $F_{4}^{{}}(\varphi ) \ne 0$, то из (5.5), (5.7) следует

В особом случае $F_{4}^{{}}(\varphi ) \equiv 0$ из (5.5), (5.7) следует

Из уравнения (5.10) в силу $A_{{12}}^{{}} \ne 0$, $A_{{22}}^{{}} \ne A_{{11}}^{{}}$ получим $H_{2}^{{}} = 0$, $G_{2}^{{}} = 0$. Таким образом, $F_{4}^{{}}(\varphi ) \equiv 0$ и справедливо уравнение (5.9), в котором $R_{1}^{{}}(\varphi )$ при $H_{2}^{{}} = 0$, $G_{2}^{{}} = 0$ принимает вид

Подставляя в уравнение (5.9) $F_{1}^{{}}(\varphi )$ из (5.4), $F_{4}^{{}}(\varphi )$ и $F_{5}^{{}}(\varphi )$ из (5.6), $R_{1}^{{}}(\varphi )$ из (5.11), потребуем, чтобы полученное уравнение было тождеством по $\varphi $. Тогда, приравнивая к нулю коэффициенты при $\sin 5\varphi $ и $\cos 5\varphi $, найдем равенства

из которых, в силу предположения $Q_{2}^{{}} \ne 0$, $L_{2}^{{}} \ne 0$, следуют условия $S_{1}^{{}} = 0$, $S_{2}^{{}} = 0$. Рассматривая уравнение (5.9) при данных равенствах, получим $S_{0}^{{}} = 0$, то есть $\dot {\varphi }_{{}}^{2}$ из (5.7) обращается в нуль, что невозможно. Итак, установлено, что должны выполняться условия (4.22), (4.23), (5.1).

6. Случай $H_{3}^{{}} = 0$, $G_{3}^{{}} = 0$, $Q_{2}^{{}} = 0$, $L_{2}^{{}} = 0$. Запишем необходимые соотношения для дальнейших преобразований:

Функция $R_{1}^{{}}(\varphi )$ из (5.8) не изменяет своего значения. В силу (5.5) случай $F_{4}^{{}}(\varphi ) = 0$, $F_{5}^{{}}(\varphi ) = 0$ является особым. Для него в (6.1) необходимо положить $A_{{13}}^{{}} = 0$, $A_{{23}}^{{}} = 0$, $a_{0}^{{}} = - \frac{1}{2}$, а в (5.10) – $S_{1}^{{}} = 0$, $S_{2}^{{}} = 0$. Уравнения (5.7), (4.15) примут вид

Из уравнений (6.2) на основании значений $L_{0}^{{}} = 4a_{0}^{{'2}}A_{{11}}^{{}}$, $Q_{0}^{{}} = 2a_{0}^{{'2}}A_{{11}}^{{}}$ положим, что $H_{1}^{{}} = 0$, $G_{1}^{{}} = 0$. Тогда из (5.3) следует $r_{1}^{{}} = 0$, $r_{2}^{{}} = 0$. В исследуемом случае уравнение (3.7) вырождается и поэтому необходимо обращаться к уравнению (3.9). На основании принятых условий и обозначений (3.5) получим

Если это уравнение рассматривать совместно с первым уравнением из (6.2) при условии ${{a}_{0}} = - \frac{1}{2}$, то получим $H_{2}^{{}} = 0$, $G_{2}^{{}} = 0$. Следовательно, в силу первого уравнения из (6.2) установим для $\dot {\varphi }$ постоянное значение, что исключается в данной статье.

Рассмотрим уравнение (5.9) в случае (6.1) и потребуем, чтобы при подстановке (6.1) в (5.9) последнее будет тождеством по $\varphi $. Тогда, исключая случай ${{a}_{0}} = - \frac{1}{2}$, получим два независимых варианта условий на параметры:

Изучим вариант (6.3). Рассмотрим уравнение (5.9) при $A_{{13}}^{2} + A_{{23}}^{2} \ne 0$, тогда из (5.9) найдем $S_{1}^{{}} = 0$, $S_{2}^{{}} = 0$. Учитывая эти условия, а также равенства (6.3), из (5.8) установим $R_{1}^{{}}(\varphi ) = S_{0}^{{}}$, то есть $R_{1}^{'}(\varphi ) = 0$. Покажем, что параметр $S_{0}^{{}} = 0$. Обратимся к уравнению (5.9), полагая в нем R₁(φ) = S₀ ($R_{1}^{'}(\varphi ) = 0$). Тогда указанное свойство следует из (5.9), если

Функцию $F{\kern 1pt} *{\kern 1pt} (\varphi )$ из (6.5) будем изучать при значениях (6.1). Поскольку $A_{{13}}^{2} + A_{{23}}^{2} \ne 0$, то $F{\kern 1pt} *{\kern 1pt} (\varphi ) = 0$ в случае, когда параметр $a_{0}^{{}} = - \frac{1}{4}$ и выполняется следующее условие на $a_{0}^{{}}$ и другие параметры $2L_{0}^{{}} = A_{{33}}^{{}}$:

Подставляя ${{a}_{0}} = - \frac{1}{4}$ в уравнение (6.6), получим $A_{{33}}^{{}} = 15A_{{11}}^{{}}$. Так как в силу неравенств треугольника на главные моменты тела $A_{{33}}^{{}} < {\text{2}}A_{{11}}^{{}}$, то условие $A_{{33}}^{{}} = 15A_{{11}}^{{}}$ выполняться не может. Следовательно, $S_{0}^{{}} = 0$ и из (6.2) следует $\dot {\varphi }_{{}}^{2} = 0$, что невозможно. Это свойство означает, что, наряду с равенствами $H_{2}^{{}} = 0$, $L_{2}^{{}} = 0$, необходимо полагать $Q_{1}^{{}} = 0$, $L_{1}^{{}} = 0$. Так как $H_{2}^{{}} = 0$, $L_{2}^{{}} = 0$, то из (5.3) следуют равенства $r_{3}^{{}} = 0$, $p_{3}^{{}} = 0$.

7. Случай динамической симметрии тела. Результаты, полученные ранее, показывают, что исследуемое решение имеет место при следующих условиях:

которые, в силу обозначений, отвечают равенствам

Запишем (4.17) с учетом условий (7.2), (7.3):

где

Обратимся к уравнению (4.19), в котором $F{\kern 1pt} *{\kern 1pt} (\varphi ) = 0$, $F_{3}^{{}}(\varphi ) = 0$:

где

Используя значения $H_{1}^{{}}{\text{,}}G_{1}^{{}}$, полученные из (4.7) в силу (7.3):

а также параметры (4.12), из (7.6) получим где

Рассмотрим уравнение (3.9) с учетом условий (7.2), (7.3). Потребуем, чтобы оно было тождеством по $\varphi $. Тогда, учитывая равенства (7.4), (7.5), (7.7)–(7.10), найдем функцию $E = E\left( {a_{0}^{{}},\psi _{0}^{{}},A_{{11}}^{{}},A_{{33}}^{{}}} \right)$ (явное значение не выписываем в силу сложности формулы) и равенства

где

Так как условия $r_{1}^{{}}\sin \psi _{0}^{{}} - r_{2}^{{}}\cos \psi _{0}^{{}} = 0$, $r_{1}^{{}}\cos \psi _{0}^{{}} + r_{2}^{{}}\sin \psi _{0}^{{}} = 0$ при $r_{1}^{{}} \ne 0$, $r_{2}^{{}} \ne 0$ не выполняются, то в формулах (7.11), (7.12) $\tilde {F}(a_{0}^{{}}) = 0$, то есть, в силу (7.12), параметр $a_{0}^{{}}$ удовлетворяет уравнению

Представляет интерес случай $A_{{33}}^{{}} = A_{{11}}^{{}}$, для которого эллипсоид инерции тела является сферой. Тогда из (7.13) следует

то есть ${{\theta }_{0}} = {\text{arccos}}\frac{1}{4}$. В общем случае, в силу неравенств на главные моменты инерции, из уравнения (7.13) получим

Если в (7.13) положить обобщенные условия Ковалевской $A_{{22}}^{{}} = A_{{11}}^{{}} = 2A_{{33}}^{{}}$, то из (7.13) следует, что $a_{0}^{{}} = 0$ (θ₀ = 90°). При этом особенностей в выполненных преобразованиях не возникает. Можно в (7.13) принять и обобщенные условия Горячева–Чаплыгина: $A_{{22}}^{{}} = A_{{11}}^{{}} = 4A_{{33}}^{{}}$, тогда значение параметра таково: $a_{0}^{{}} \approx 0.94$.

Покажем, что в формуле (7.4) $S_{1}^{{}} \ne 0$, $S_{2}^{{}} \ne 0$. Внесем значения $s_{1}^{{}}$, $s_{2}^{{}}$ из (7.9) в формулы из (4.12):

В силу значения $L_{0}^{{}}$ из (7.5) получим $S_{1}^{{}} \ne 0$, $S_{2}^{{}} \ne 0$, а из формулы (7.4) следует, что $\varphi (t)$ – эллиптическая функция времени $\left( {\psi (t) = 2\varphi (t)} \right)$. Величина $S_{0}^{{}}$ определяется из последней формулы системы (4.12): $S_{0}^{{}} = a_{0}^{{}}s_{3}^{{}}$ + $E(a_{0}^{{}},\psi _{0}^{{}},A_{{11}}^{{}},A_{{33}}^{{}})$. Запишем (7.4) в интегральной форме:

Нахождение $\varphi (t)$ из (7.16) проводится стандартным образом.

Обсудим условия (7.2), (7.3). Равенства (7.2) означают, что прямая, содержащая вектор ${\mathbf{a}}$, является осью, относительно которой тело имеет динамически симметричное распределение. Но, в силу $s_{1}^{{}} \ne 0$, $s_{2}^{{}} \ne 0$, центр масс тела не лежит на этой оси. На основании равенств (7.3) приходим к выводу о том, что векторы ${\mathbf{r}} = (r_{1}^{{}},r_{2}^{{}},0)$, ${\mathbf{p}} = (r_{2}^{{}}, - r_{1}^{{}},0)$ ортогональны и расположены в плоскости, ортогональной вектору ${\mathbf{a}}$. Из полученных в разд. 7 результатов следует, что условий на параметры $r_{1}^{{}}$, $r_{2}^{{}}$, $\psi _{0}^{{}}$ нет.

Заключение. В статье рассмотрена задача об условиях существования прецессионных движений твердого тела под действием сил трех однородных силовых полей. Полагается, что скорость прецессии тела в два раза больше его скорости собственного вращения. Доказано, что необходимым условием таких движений является ортогональность векторов, задающих центры притяжения сил двух однородных силовых полей. Параметр в (7.13) $a_{0}^{{}} \in \left( { - \frac{1}{6},\frac{1}{2}} \right)$. Если тело имеет распределение масс, для которого эллипсоид инерции является сферой, то угол нутации равен ${\text{arccos}}\frac{{\text{1}}}{{\text{4}}}$. Угол собственного вращения находится путем обращения эллиптического интеграла (угол прецессии в два раза больше угла собственного вращения). Тело обладает свойством динамической симметрии относительно оси, образующей постоянный угол с одним из направлений действующих сил.

Представляет интерес привести примеры рациональных значений угла нутации в динамике твердого тела. В классической задаче о движении тела в решении Д. Гриоли [3] угол ${{\theta }_{0}}$ = 90°. В задаче о движении гиростата под действием потенциальных и гироскопических сил известно решение [18], в котором ${{\theta }_{0}}$ = 120°. Можно анонсировать и результат, который относится к анализу прецессионно-изоконических движений ($\dot {\psi } = \dot {\varphi }$) в рассматриваемой задаче. Он для сферического гиростата характеризуется значением ${{\theta }_{0}}$ = 60°.