Прикладная математика и механика, 2023, T. 87, № 1, стр. 19-25

1. Введение. Модели, приводящие к системам с интегральной памятью.

В последние примерно 15–20 лет большое распространение получили исследования в области механических систем с т.н. “памятью” или интегральным последействием. Первые из них были посвящены уравнению Гуртина–Пипкина [1]:

В данном уравнении ядро $K(t)$ может иметь различный вид, отражающий природу физических процессов, которые описывают данное уравнение. В двух простейших случаях это ядро может быть тождественно равно единице или равняться дельта-функции. В первом случае уравнение сводится к волновому уравнению посредством дифференцирования по временной переменной, во втором случае (1.1) превращается в уравнение теплопроводности. Ниже мы рассмотрим ядра более сложного вида.

После (1.1) изучались уравнения классического вида с добавлением интегральных членов (памяти). Эти дополнительные члены в ряде случаев позволяют более эффективно описывать те или иные процессы механики и физики. Кроме этого можно, например, записать уравнение “запаздывающей реакции”:

Уравнение (1.2) можно рассматривать как модификацию закона Гука, в котором действующая сила пропорциональна смещению.

Кратко опишем еще один способ получения большого класса моделей с интегральной памятью. Этот способ связан с т.н. “наивной механикой” и подробно изложен в [2]. Суть дела состоит в записи определяющего соотношения между напряжением и деформацией (здесь рассматривается одномерный по пространственной переменной случай). Это соотношение, в свою очередь, записывается исходя из различных способов соединения “пружин” и “поршеньков”. В результате этого соединения образуется элемент, который является простейшей ячейкой сплошной среды и определяющее соотношение для этого элемента затем в ряде случаев (при определенном типе соединения между собой этих элементов) переносится на всю сплошную среду. Если таким элементом является “пружина”, то определяющее соотношение для него имеет вид:

если элемент – “поршень”, то

Здесь $\sigma $ – напряжение, $\varepsilon $ – деформация, $E > 0$ – это модуль упругости и $\mu > 0$ коэффициент вязкости.

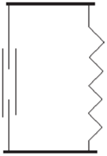
Приведем примеры известных простых моделей. Рассмотрим модель (элемент) Максвелла (рис. 1). Она состоит в последовательном соединении пружины и поршня. Составим теперь цепочку из последовательного соединения этих элементов (моделей Максвелла), рис. 2:

Для данной цепочки определяющее соотношение имеет вид:

Заметим, что параллельное соединение элементов Максвелла приводит уже к другому определяющему соотношению.

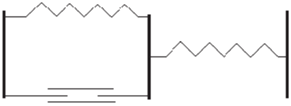
Рассмотрим теперь модель (элемент) Фойгхта. Она состоит из параллельного соединения “пружины” и “поршня” (рис. 3). В свою очередь, составим из параллельного соединения этих элементов цепочку Фойгхта (рис. 4). Для этой цепочки определяющее соотношение имеет вид:

Рассмотрим теперь более сложную модель. Она состоит из последовательного соединения элемента Фойгхта и пружины (рис. 5). Далее соединим эти элементы последовательно, получаем цепочку из сложных элементов (рис. 6). Для этой последней цепочки определяющее соотношение записывается следующим образом:

Из (1.3) формально выразим $\sigma $:

Пусть $\theta (t,x)$ – состояние системы, тогда его связь с напряжением и деформацией имеет вид:

Продифференцируем (1.4) по переменной $x$ и воспользуемся (1.5):

Уравнение (1.6) представляет собой уравнение колебания струны с дополнительным интегральным членом и ядром в виде убывающей экспоненциальной функции.

Рассмотрим теперь общий случай. Доказано [2], что в рамках “наивной механики” определяющее соотношение имеет вид:

где ${{a}_{i}} > 0$, ${{b}_{i}} > 0$, $i = 1,2, \ldots ,n$, ${{b}_{{n + 1}}} \geqslant 0$. Рассмотрим многочлен

Пусть корни ${{\lambda }_{1}},{{\lambda }_{2}}, \ldots ,{{\lambda }_{n}}$ полинома $P(\lambda )$ вещественные, отрицательные и попарно различны, причем среди них нет нулевого. Тогда (см. [2]) формально выразим $\sigma (t,x)$ из определяющего соотношения (1.7):

Здесь ядро $K(t)$ имеет вид:

Здесь и далее предположим, что ${{C}_{0}} \geqslant 0$, ${{C}_{1}} \geqslant 0$ и все постоянные ${{K}_{i}}$, $i = 1,2, \ldots ,n$, меньше либо равны нулю. Данное условие связано с тем, что во всех подобных вязкоупругих моделях знаки берутся именно такими.

Используя (1.5), получим из (1.8) интегро-дифференциальное уравнение:

Предположим, что в уравнении (1.10) переменная $x$ принадлежит интервалу $(0,\pi )$ и $t > 0$.

2. Задачи граничного управления для систем с памятью

Уравнение (1.10) описывает достаточно широкий класс моделей в механике. Более того, в этот класс прямо или косвенно входят основные классические уравнения (уравнения колебания струны, теплопроводности, телеграфное).

Для (1.10) можно поставить задачу управления. Например, рассмотрим нулевое условие для решения $\theta $ на правом конце отрезка $[0,\pi ]$ и функцию ${v}(t) \in L_{2}^{{\operatorname{loc} }}(0, + \infty )$ (управление) на левом конце. В нулевой момент времени имеется два начальных условия ${{\xi }_{1}}$, ${{\xi }_{2}}$ (смещение, скорость соответственно). Для этой начально-краевой задачи дадим важное определение управляемости.

Будем говорить, что система управляема в покой, если для любых заданных начальных условий ${{\xi }_{1}}$ и ${{\xi }_{2}}$, можно найти управление ${v}(t)$ и момент времени $T > 0$ такой, что ${v}(t)$ равно нулю для любого $t > T$ и соответствующее решение $\theta (t,{v})$ задачи также равно нулю для любого $t > T$.

В противоположность, система называется неуправляемой в покой, если существуют начальные условия ${{\xi }_{1}}$, ${{\xi }_{2}}$ такие, что для любого управления ${v}(t)$, которое равно нулю тождественно вне некоторого конечного отрезка $[0,T]$, соответствующее решение не равно тождественно нулю вне любого конечного отрезка (по $t$). В этом случае мы также будем говорить, что управляемость в покой отсутствует.

В изучении вопросов управляемости ключевую роль играет исследование спектра задачи. Например, в работе [3] для некоторого случая, который попадает в класс уравнений (1.10), спектр хорошо изучен. Это делает возможным рассматривать не только задачи граничного, но и распределенного управления (см. [4, 5]). Еще отметим работу [6], где рассматриваются похожие интегро-дифференциальные уравнения с более широким, чем (1.9) классом ядер.

Докажем следующую теорему.

Теорема. В задаче управления для уравнения (1.10) заведомо отсутствует граничная управляемость в покой во всех случаях, кроме трех:

a) ${{C}_{0}} > 0,\quad {{C}_{1}} = {{K}_{1}} = {{K}_{2}} = \ldots = {{K}_{n}} = 0$

б) ${{C}_{1}} > 0,\quad {{C}_{0}} = {{K}_{1}} = {{K}_{2}} = \ldots = {{K}_{n}} = 0$

в) ${{K}_{1}} < 0,\quad {{C}_{0}} = \frac{{{{K}_{1}}}}{{{{\lambda }_{1}}}},\quad {{C}_{1}} = {{K}_{2}} = \ldots = {{K}_{n}} = 0$

Случай (а) дает уравнение колебания струны, хорошо известно, что для этого уравнения имеет место граничная управляемость. Для (б) и (в) ситуация несколько сложнее. Граничная управляемость для уравнений, описываемых этими случаями, формально отсутствует, если определение управляемости понимать так, как оно было введено выше. Между тем, если мы будем рассматривать более узкий класс начальных данных: положим равным нулю второе начальное условие ${{\xi }_{2}}$, то уравнение в случае (б) интегрированием по переменной t сводится к уравнению теплопроводности, а в случае (в) к уравнению Гуртина–Пипкина, которые можно дополнительно исследовать на предмет управляемости. Заметим, что уравнение в случае (в) при ${{\xi }_{2}} = 0$ может быть также сведено к телеграфному уравнению.

Доказательство. Определим функции комплексного переменного λ:

где $\hat {K}(\lambda )$ – преобразование Лапласа от ядра $K(t)$. В дальнейшем совокупность всех корней уравнений ${{G}_{n}}(\lambda ) = 0$ для каждого натурального $n$ будем называть спектром задачи для уравнения (1.10). Предположим, что (а), (б) и (в) не выполнены и, дополнительно, пусть не выполнен случай ${{K}_{1}} \ne 0$, ${{C}_{0}} = {{C}_{1}} = {{K}_{2}}$ = … = K_n = 0 (случай (г)). Тогда нетрудно видеть, что $N(\lambda )$ имеет по крайней мере один нуль ${{\lambda }_{0}}$. Используя методы работы [7], для очень похожего уравнения, нетрудно доказать, что для ${{\lambda }_{0}} \ne 0$ существуют нули ${{\lambda }_{n}}$ функций ${{G}_{n}}(\lambda )$, причем построенная последовательность $\{ {{\lambda }_{n}}\} $ имеет предельную точку. Последнее является препятствием к управляемости. Если ${{\lambda }_{0}} = 0$, то это также является препятствием к управляемости, так как в этом случае преобразование Лапласа от функции управления, т.е. ${\hat {v}}(\lambda )$, не будет целой функцией.

Осталось рассмотреть случай (г), это уравнение вида (1.2). Доказательство отсутствия управляемости для похожего уравнения приведено в ([7], теорема 3), для случая (г) доказательство отсутствия граничной управляемости проводится совершенно аналогичным методом. Этот метод основан на том, что спектр задачи растет достаточно медленно, именно это и является препятствием к управляемости в покой. Теорема доказана.

Таким образом, среди всех моделей “наивной механики” неуправляемыми в покой заведомо являются все модели, кроме только трех классических систем.

Доказано [8], что для уравнения Гуртина–Пипкина также отсутствует управляемость в покой, если управление приложено к фиксированной подобласти (там рассматривается двумерная система). Остается открытым вопрос, можно ли привести в покой данную систему, если управляющее воздействие приложено к подмножеству, которое движется по некоторому закону. Для более простых уравнений положительный ответ на данный вопрос дан в работах [9–11]. Сделаем важное замечание: пусть ядро $K(t)$ в уравнении (1.1) представляет собой ряд из убывающих экспоненциальных функций, при этом на коэффициенты и показатели этих экспонент наложены дополнительные ограничения, тогда управляемость в покой отсутствует даже, если управляющее воздействие приложено ко всей области. Точное изложение этого результата содержится в работе [12].

В заключение заметим, что интерес представляет перенесение полученных результатов на многомерный случай. Представляется, что это можно сделать, используя методы [8].

Исследование выполнено за счет гранта Российского научного фонда (проект № 21-11-00151).