Прикладная математика и механика, 2023, T. 87, № 1, стр. 53-62
Двоякопериодические контактные задачи для слоя с неизвестной зоной контакта
Н. Б. Золотов 1, Д. А. Пожарский 1, *
1 Донской государственный технический университет
Ростов-на-Дону, Россия
* E-mail: pozharda@rambler.ru
Поступила в редакцию 17.07.2022
После доработки 29.10.2022
Принята к публикации 01.11.2022
- EDN: HVZBFR
- DOI: 10.31857/S0032823523010101
Аннотация
Рассматриваются двоякопериодические контактные задачи для упругого слоя с неизвестной областью контакта. Одна грань слоя находится в условиях скользящей или жесткой заделки. Задачи сводятся к интегральным уравнениям, ядра которых не содержат квадратур. Для случая полного контакта другой грани слоя с двумерной синусоидальной жесткой поверхностью задачи имеют точное решение, которое используется для отладки программ, реализующих численный метод нелинейных интегральных уравнений Галанова, позволяющий одновременно определить область контакта и контактные давления. Рассчитаны механические характеристики при внедрении системы эллиптических параболоидов, изучен переход от дискретной к непрерывной области контакта.
Пионерской работой в области периодического контакта является решение Вестергаарда для одномерной волнистой поверхности [1]. Основная доля публикаций по данной тематике относится к плоским задачам [2]. Для исследования пространственного периодического контакта для круговых инденторов разработан метод локализации [3, 4]. Асимптотические [5, 6] и численные [7] результаты получены для контакта двумерной волнистой поверхности с полупространством. На основе регулярного асимптотического метода изучались двоякопериодические контактные задачи для упругого слоя при заданной области контакта [8]. Учитывалось влияние трения, износа, сцепления, микрогеометрии и адгезии при периодическом контакте упругих тел [9–13], было получено точное решение задачи о полном контакте волнистого штампа со слоем [13]. Исследовались периодические контактные задачи для вязкоупругого полупространства [14], а также для полупространства с частично закрепленной границей [15].
В настоящей статье для решения трехмерных периодических контактных задач для слоя с неизвестной зоной контакта применяется численный метод нелинейных граничных интегральных уравнений [16]. Для верификации результатов используется точное решение для полного контакта двумерной синусоидальной жесткой поверхности и упругого слоя, которое обобщает известное решение Джонсона и соавторов для полупространства [5, 6]. В отличие от прямого численного метода быстрого преобразования Фурье [7] метод интегральных уравнений [16] позволяет получать приемлемые результаты при существенно меньшем числе узлов. Показано, что переход от дискретного к непрерывному двоякопериодическому контакту (перколяция) связан с образованием новых интегрируемых особенностей ядра интегрального уравнения на линиях перехода. Качественные выводы согласуются с известными результатами метода локализации для полупространства [3, 4].
1. Постановка задач, интегральные уравнения. В декартовых координатах рассмотрим слой {|x| < ∞, |y| < ∞, 0 ≤ z ≤ h} с параметрами упругости G (модуль сдвига) и ν (коэффициент Пуассона). Изучим контактные задачи без учета сил трения, когда контактное давление
является двоякопериодической функцией с полупериодами l1 и l2 соответственно вдоль осей x и y. Контакт осуществляется на верхней грани слоя z = 0, а нижняя грань z = –h подчинена условиям скользящей или жесткой заделки (задачи А и Б соответственно). Давление (1.1) порождено двоякопериодической системой одинаковых жестких штампов, внедренная подошва которых не имеет острых кромок, поэтому зона контакта заранее неизвестна и содержится в прямоугольных ячейках размера 2l1 × 2l2. Пусть ячейка S содержит начало координат и единичную область контакта Ω (рис. 1). Форма оснований штампов описывается функциейК каждому штампу приложена нормальная сила P так, что штампы вдавливаются без перекоса и испытывают осадку δ.
Граничные условия контактных задач имеют вид
При заданных параметрах упругости G, ν, величинах l1, l2, δ, h и функции f(x, y) требуется определить область контакта Ω и давление q(x, y) = –σz(0, 0, h), (x, y) ∈ Ω. Затем при использовании интегрального условия равновесия штампов может быть найдена сила P.
Интегральные уравнения задач А и Б относительно контактного давления, используя известные функции Грина для слоя и периодичность, можно записать, интегрируя по единичной области контакта Ω, в виде (θ = G/(1 – ν))
(1.2)
$\iint\limits_\Omega {q(\xi ,\eta )K(\xi ,\eta ,x,y)d\xi d\eta = 2\pi \theta [\delta - f(x,y)]};\quad (x,y) \in \Omega $(1.3)
$\begin{gathered} {{Q}_{{nm}}} = R_{{nm}}^{{ - 1}} - {{\left( {4{{h}^{2}} + R_{{nm}}^{2}} \right)}^{{ - 1{\text{/}}2}}},\quad {{R}_{{nm}}} = {{\left[ {{{{(s + 2n{{l}_{1}})}}^{2}} + {{{(t + 2m{{l}_{2}})}}^{2}}} \right]}^{{1{\text{/}}2}}} \\ {\text{А)}}\;{{G}_{0}} = 3{\text{/}}2,\quad {\text{Б)}}\;{{G}_{0}} = 2 - 4(\kappa - 1){\text{/}}{{(\kappa + 1)}^{2}},\quad \kappa = {\text{3}} - 4\nu \\ \end{gathered} $Cходимость рядов в выражениях для Fk. (k = 1, 2, 3) улучшается при уменьшении толщины слоя h. Функция M(r) на бесконечности убывает, как exp(–2r), обеспечивая сходимость рядов в выражениях для Gk. (k = 1, 2, 3), а в нуле стремится к G0.
2. Точное решение. Интегральное уравнение (1.2) имеет точное решение, когда единичная область контакта Ω совпадает с ячейкой S (полный контакт), а к функции f(x, y) применимо преобразование Фурье. Для определенности рассмотрим полный контакт грани упругого слоя с жесткой двоякопериодической синусоидальной поверхностью амплитуды A и длинами волн (периодами) 2l1 и 2l2. В рамках линейной теории упругости предполагается, что амплитуда мала по сравнению с длинами волн [6]. В этом случае уравнение (1.2) преобразуется к виду [8]
(2.1)
$\begin{gathered} \int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {q(\xi ,\eta )d\xi d\eta } } \int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {\frac{{L\left( {\sqrt {{{u}^{2}} + {{w}^{2}}} } \right)}}{{\sqrt {{{u}^{2}} + {{w}^{2}}} }}\cos \left( {u\frac{{\xi - x}}{h}} \right)\cos \left( {w\frac{{\eta - y}}{h}} \right)dudw = } } \\ = 4{{\pi }^{2}}\theta h{\text{ }}\left[ {\delta - \left( {A - A\cos \frac{{\pi x}}{{{{l}_{1}}}}\cos \frac{{\pi y}}{{{{l}_{2}}}}} \right)} \right]{\text{;}}\quad - {\kern 1pt} \infty < x,\;y < \infty \quad (\delta \geqslant 2A) \\ \end{gathered} $Условие $\delta \geqslant 2A$ не является достаточным для полного контакта ввиду несогласованности деформаций поверхности слоя с жесткой поверхностью. Как показывают расчеты по методу Галанова, при $\delta = 2A$ могут оставаться малые зоны в S вне контакта. В этом случае полный контакт возникает лишь при $\delta \geqslant {{\delta }_{1}} > 2A$, где ${{\delta }_{1}}$ – некоторое критическое значение.
Пусть l1 ≥ l2. Введем безразмерные обозначения (штрихи далее опускаем)
(2.2)
$\begin{gathered} x{\kern 1pt} ' = \frac{x}{{{{l}_{1}}}},\quad \xi {\kern 1pt} ' = \frac{\xi }{{{{l}_{1}}}},\quad y{\kern 1pt} ' = \frac{y}{{{{l}_{1}}}},\quad \eta {\kern 1pt} ' = \frac{\eta }{{{{l}_{1}}}},\quad A{\kern 1pt} ' = \frac{A}{{{{l}_{1}}}},\quad \lambda = \frac{h}{{{{l}_{1}}}},\quad \delta {\kern 1pt} ' = \frac{{\delta - A}}{{{{l}_{1}}}} \\ q{\kern 1pt} '\left( {x{\kern 1pt} ',y{\kern 1pt} '} \right) = \frac{{q(x,y)}}{{2\pi \theta }},\quad \varepsilon = \frac{{{{l}_{2}}}}{{{{l}_{1}}}},\quad P{\kern 1pt} ' = \frac{P}{{2\pi \theta l_{1}^{2}}},\quad S{\kern 1pt} ' \leftrightarrow S,\quad \Omega {\kern 1pt} ' \leftrightarrow \Omega \\ \end{gathered} $Параметр λ характеризует относительную толщину упругого слоя, а параметр ε ≤ 1 – отношение периодов.
В обозначениях (2.2) уравнение (2.1) примет вид
(2.3)
$\begin{gathered} \int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {q(\xi ,\eta )d\xi d\eta } } \int\limits_{ - \infty }^\infty {\int\limits_{ - \infty }^\infty {\frac{{L\left( {\sqrt {{{u}^{2}} + {{w}^{2}}} } \right)}}{{\sqrt {{{u}^{2}} + {{w}^{2}}} }}\cos \left( {u\frac{{\xi - x}}{\lambda }} \right)\cos \left( {w\frac{{\eta - y}}{\lambda }} \right)dudw = } } \\ = 2\pi \lambda {\text{ }}\left( {\delta + A\cos (\pi x)\cos \frac{{\pi y}}{\varepsilon }} \right){\text{;}}\quad - {\kern 1pt} \infty < x,y < \infty \quad (\delta \geqslant A) \\ \end{gathered} $Точное решение интегрального уравнения (2.3) находится при помощи двойного преобразования Фурье. В результате получим
(2.4)
$\begin{gathered} q(x,y) = \frac{{\delta {{L}_{0}}}}{{2\pi \lambda }} + \frac{{A\sqrt {1 + {{\varepsilon }^{{ - 2}}}} }}{{2L\left( {\pi \lambda \sqrt {1 + {{\varepsilon }^{{ - 2}}}} } \right)}}\cos (\pi x)\cos \frac{{\pi y}}{\varepsilon } \\ {{L}_{0}} = \mathop {\lim }\limits_{u \to 0} \frac{u}{{L(u)}};\quad {\text{А)}}\;{{L}_{0}} = 2,\quad {\text{Б)}}\;{{L}_{0}} = \frac{{2{{{(1 - \nu )}}^{2}}}}{{1 - 2\nu }} \\ \end{gathered} $В задаче Б при приближении материала слоя к несжимаемому (ν → 0.5) контактные давления неограниченно возрастают (полный контакт становится затруднительным).
При λ → ∞ решение (2.4) переходит в решение Джонсона и соавторов [5, 6] для упругого полупространства
Для слоя из решения (2.4) найдем вдавливающую силу
(2.5)
$P = \int\limits_{ - 1}^1 {\int\limits_{ - 1}^1 {q(x,y)dxdy = \frac{{2\delta {{L}_{0}}}}{{\pi \lambda }}} } $Для задачи Б сила P чувствительна к значению коэффициента Пуассона. При ν = = 0.25 значение P (2.5) для задачи Б на 12.5% превышает соответствующее значение для задачи А.
3. Численный анализ. Для численного решения контактных задач применим метод, предложенный Галановым [16], позволяющий одновременно определить область контакта и давления в этой области. В этом методе интегрирование в уравнении (1.2), (1.3) распространяется на ячейку S, содержащую область Ω. Предположения об отсутствии контакта и обращения в нуль давления в дополнительной области S \Ω приводят к системе интегрального уравнения и интегрального неравенства (снова используем размерные величины)
(3.1)
$\begin{gathered} \int\limits_S {q(N)K(N,M)dN = d(M);\quad q(M) \geqslant 0,\quad M \in \Omega } \\ \int\limits_S {q(N)K(N,M)dN > d(M);\quad q(M) = 0,\quad M \in S{{\backslash }}\Omega } \\ N = \xi ,\eta ,\quad M = x,y,\quad d(M) = 2\pi \theta \left[ {\delta - f(M)} \right] \\ \end{gathered} $После введения нелинейных операторов
и представления искомого давления в форме система (3.1) сводится к решению нелинейного операторного уравнения типа Гаммерштейна(3.2)
$\Theta p = 0\quad {\text{(}}M \in \Omega {\text{),}}\quad \Theta p \equiv {{p}^{ - }} + K{{p}^{ + }} - d,$При этом интегральное неравенство (3.1) удовлетворяется автоматически. Можно доказать эквивалентность системы (3.1) и уравнения (3.2) [16].
При численном решении уравнения (3.2) применяется модифицированный метод Ньютона, основанный на построении последовательных приближений по формулам
В отличие от задач для одного штампа ядра (1.3) в ячейке S имеют не только классическую особенность R–1, но и дополнительные интегрируемые особенности $R_{{ \pm 1,0}}^{{ - 1}}$, $R_{{0, \pm 1}}^{{ - 1}}$, $R_{{ \pm 1, \pm 1}}^{{ - 1}}$, $R_{{ \pm 1, \mp 1}}^{{ - 1}}$ соответственно в точках $(\xi = x \mp 2{{l}_{1}}$, $\eta = y)$, $(\xi = x$, $\eta = y \mp 2{{l}_{2}})$, $(\xi = x \mp 2{{l}_{1}}$, $\eta = y \mp 2{{l}_{2}})$ и $(\xi = x \mp 2{{l}_{1}}$, $\eta = y \pm 2{{l}_{2}})$ на сторонах и в вершинах прямоугольника S. При расчете значений ядра оператора (3.3) в этих точках особенности сглаживались по формулe (n, m = 0; ±1)
Отладку программ проведем при помощи сравнения интегральной характеристики с точным значением (2.5) при A = 0.001, ε = 1, ν = 0.25. В силу симметрии достаточно интегрировать по четверти S. В табл. 1 даны значения P, рассчитанные при разных λ, δ и изменении числа узлов равномерной сетки в первой четверти S (сетка 9 × 9 соответствует 289 узлам в S; сетка 13 × 13 – 625 узлам в S). Видно, что при сгущении сетки численное решение приближается к точному. Для сетки 13 × 13 погрешность расчета интегральной характеристики не превосходит 3%. В табл. 1 неполный (почти полный) контакт осуществляется для задачи А при λ = 1, δ × 103 = 2. При почти полном контакте численное решение также стремится к точному.
Таблица 1.
Сравнение значений силы P(δ) × 103 для сеток 9 × 9, 13 × 13 с (2.5) при A = 0.001, ε = 1, ν = 0.25
| Задача | А | Б | |||
|---|---|---|---|---|---|
| δ × 103 | 2 | 3 | 2 | 3 | |
| λ = 0.25 | 9 × 9 | 10.50 | 15.75 | 11.86 | 17.78 |
| 13 × 13 | 10.40 | 15.60 | 11.73 | 17.59 | |
| (2.5) | 10.19 | 15.28 | 11.46 | 17.19 | |
| λ = 1 | 9 × 9 | 2.58 | 3.87 | 2.91 | 4.36 |
| 13 × 13 | 2.57 | 3.86 | 2.90 | 4.35 | |
| (2.5) | 2.55 | 3.82 | 2.86 | 4.30 | |
Рассмотрим внедрение двоякопериодической системы эллиптических параболоидов, когда
Далее используем безразмерные обозначения (2.2), заменяя формулы для A и δ на
Значения силы P в зависимости от осадки δ0 при разных λ приведены в табл. 2 для случая A0 = B0 = 0.001 (круговые параболоиды), ε = 1, ν = 0.25. В задаче А (скользящая заделка) значения силы меньше, чем в задаче Б (жесткая заделка). В обеих задачах, как видно из табл. 2, вдавливающая сила снижается при увеличении λ. В задаче Б, как правило, площадь области контакта немного больше, чем в задаче А.
Таблица 2.
Значения силы P × 103 при A0 = B0 = 0.001, ε = 1, ν = 0.25
| δ0 × 103 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
|---|---|---|---|---|---|
| λ = 1 | |||||
| Задача А | 0.172 | 0.575 | 1.124 | 1.734 | 2.365 |
| Задача Б | 0.183 | 0.634 | 1.257 | 1.948 | 2.663 |
| λ = 2 | |||||
| Задача А | 0.119 | 0.337 | 0.605 | 0.897 | 1.205 |
| Задача Б | 0.127 | 0.369 | 0.671 | 1.004 | 1.352 |
| λ = 3 | |||||
| Задача А | 0.0935 | 0.247 | 0.426 | 0.619 | 0.820 |
| Задача Б | 0.101 | 0.271 | 0.473 | 0.691 | 0.920 |
Для изучения зависимости интегральной характеристики от ν введем безразмерную силу
На рис. 2 представлены зависимости силы P0 от ν для задач А и Б при δ0 = A0 = B0 = = 0.001, ε = 1, λ = 0.25 и для соответствующих случаев вдавливания одного штампа (задачи А1 и Б1). Для задач А и А1 зависимость P0(ν) имеет гиперболический тип. Значения силы (3.4) для двоякопериодической системы больше, чем для случая одного штампа. Труднее становится вдавить двоякопериодическую систему для задачи Б, когда материал приближается к несжимаемому.
Рис. 2.
Зависимость безразмерной вдавливающей силы P0 от коэффициента Пуассона ν для задач А и А1 (а) и Б и Б1 (б); δ0 = A0 = B0 = 0.001, ε = 1, λ = 0.25, пунктир для задач А1 и Б1.
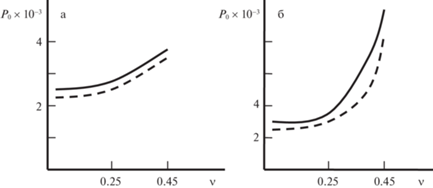
При сближении штампов (уменьшении ε) растет их взаимодействие, которое проявляется в уменьшении интегральной характеристики контактных давлений.
Для вытянутых вдоль оси x эллиптических параболоидов (A0 = 0.0005, B0 = 0.001, ε = 1, ν = 0.25) значения P больше, чем соответствующие значения для круговых параболоидов из табл. 2.
Отметим, что в случае периодической контактной задачи для упругого полупространства на основе метода локализации были сделаны выводы о том, что учет взаимного влияния пятен контакта уменьшает контактный радиус и увеличивает давление в центральной части области контакта по сравнению со случаем единичного штампа [17]. Для слоя можно сделать аналогичные выводы. Хотя интегральная характеристика (номинальная сила) для единичного штампа, как правило, больше, чем для двоякопериодической системы, давление в центре области контакта больше для двоякопериодической системы. При этом номинальная площадь области контакта меньше для двоякопериодической системы. Например, для задач А1 и Б1 при δ0 = 0.0025, A0 = B0 = = 0.001, ε = λ = 1, ν = 0.25 область контакта заполняет S, а для аналогичных значений параметров в задачах А и Б имеются узлы вне контакта; контактное давление в точке первоначального касания q0 × 103 = 0.833 для задачи А1 и q0 × 103 = 0.885 для задачи А, аналогично q0 × 103 = 0.928 для задачи Б1 и q0 × 103 = 0.970 для задачи Б.
В табл. 3 даны минимальные значения осадки и соответствующие значения силы, при которых начинается перколяция (сразу в двух направлениях), а также при наступлении полного контакта для двоякопериодической системы равноотстоящих друг от друга круговых параболоидов. В начале перколяции для обеих задач зависимость от minδ0 × 103 от λ близка к линейной. Отметим, что значения номинальной силы в табл. 3 с ростом λ выходят на постоянный одинаковый для обеих задач уровень.
Таблица 3.
Минимальные значения осадки и силы для начала перколяции и полного контакта при A0 = B0 = 0.001, ε = 1, ν = 0.25
| Задача | λ | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
|---|---|---|---|---|---|---|
| Начало перколяции | ||||||
| А | δ0 × 103 | 1.41 | 2.14 | 2.87 | 3.61 | 4.33 |
| А | P × 103 | 1.97 | 1.91 | 1.90 | 1.91 | 1.90 |
| Б | δ0 × 103 | 1.33 | 1.97 | 2.62 | 3.27 | 3.91 |
| Б | P × 103 | 2.00 | 1.91 | 1.90 | 1.90 | 1.90 |
| Полный контакт | ||||||
| А | δ0 × 103 | 2.82 | 4.49 | 6.34 | 8.22 | 10.09 |
| А | P × 103 | 5.67 | 4.93 | 4.88 | 4.88 | 4.88 |
| Б | δ0 × 103 | 2.67 | 4.09 | 5.71 | 7.37 | 9.03 |
| Б | P × 103 | 5.84 | 4.97 | 4.88 | 4.88 | 4.89 |
Заключение. Согласование численного решения с точным подтверждает корректность ядра в форме (1.3). Метод Галанова эффективен и в предельном случае полного контакта, когда интегральное неравенство (3.1) исчезает. По сравнению с прямым численным методом [7] приемлемая точность достигается при небольшом числе узлов сетки. Жесткая заделка одной грани упругого слоя из несжимаемого материала препятствует полному двоякопериодическому контакту по другой грани. При двоякопериодическом контакте для слоя выявлены эффекты аналогичные обнаруженным ранее методом локализации для полупространства.
Работа выполнена при поддержке Российского научного фонда (код проекта 22-21-00013) и посвящается столетию прикладного математика академика Е.В. Золотова (1922–1990 гг.).
Список литературы
Westergaard H.M. Bearing pressure and cracks // ASME. J. Appl. Mech. E. 1939. V. 6. № 1. P. 43–53.
Пожарский Д.А. Периодические контактные и смешанные задачи теории упругости (обзор) // Изв. вузов. Сев.-Кавк. регион. Естеств. науки. 2021. № 2. С. 22–33.
Горячева И.Г. Периодическая контактная задача для упругого полупространства // ПММ. 1998. Т. 62. Вып. 6. С. 1036–1044.
Goryacheva I.G. Contact Mechanics in Tribology. Berlin: Springer, 1998. 360 p.
Johnson K.L., Greenwood J.A., Higginson J.G. The contact of elastic regular wavy surfaces // Int. J. Mech. Sci. 1985. V. 27. № 6. P. 383–396.
Джонсон К. Механика контактного взаимодействия. М.: Мир, 1989. 510 с.
Yastrebov V.A., Anciaux G., Molinari J.-F. The contact of elastic regular wavy surfaces revisited // Tribol. Lett. 2014. V. 56. P. 171–183.
Александров В.М. Двоякопериодические контактные задачи для упругого слоя // ПММ. 2002. Т. 66. Вып. 2. С. 307–315.
Солдатенков И.А. Периодическая контактная задача теории упругости. Учет трения, износа и сцепления // ПММ. 2013. Т. 77. Вып. 2. С. 337–351.
Goryacheva I.G., Torskaya E.V. Modeling of fatigue wear of a two-layered elastic half-space in contact with periodic system of indenters // Wear. 2010. V. 268. № 11–12. P. 1417–1422.
Jin F., Wan Q., Guo X. A double-Westergaard model for adhesive contact of a wavy surface // Int. J. Solids Struct. 2016. V. 102–103. P. 66–76.
Goryacheva I.G., Makhovskaya Y. Combined effect of surface microgeometry and adhesion in normal and sliding contacts of elastic bodies // Friction. 2017. V. 5. № 3. P. 339–350.
Солдатенков И.А. Пространственная контактная задача для упругого слоя и волнистого штампа при наличии трения и износа // ПММ. 2014. Т. 78. Вып. 1. С. 145–155.
Goryacheva I., Yakovenko A. The periodic contact problem for spherical indenters and viscoelastic half-space // Tribol. Int. 2021. V. 161. P. 107078.
Золотов Н.Б., Пожарский Д.А. Периодические контактные задачи для полупространства с частично закрепленной границей // ПММ. 2022. Т. 86. № 3. С. 394–403.
Галанов Б.А. Метод граничных уравнений типа Гаммерштейна для контактных задач теории упругости в случае неизвестных областей контакта // ПММ. 1985. Т. 49. Вып. 5. С. 827–835.
Яковенко А.А. Моделирование дискретного контакта упругих и вязкоупругих тел. Дисс. на соиск. уч. степ. канд. физ.-мат. н. М.: Институт проблем механики им. А.Ю. Ишлинского РАН, 2022. 127 с.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика



