Прикладная математика и механика, 2023, T. 87, № 2, стр. 124-156

1. Введение, анализ проблемы регуляризации и обоснование использования регулярных кватернионных уравнений в переменных Кустаанхеймо–Штифеля (KS-переменных) для решения задач прогноза и коррекции орбитального движения космического аппарата. В настоящее время в механике космического полета активно разрабатываются проблемы прогноза и коррекции орбитального движения космических аппаратов с использованием уравнений и соотношений в вариациях. Изучение влияния изменений начальных условий движения (или их неточного выполнения) на орбитальное движение играет важную роль в механике космического полета. На это обращается внимание, в частности, еще в книге Эльясберга 1965 года [1], посвященной теории полета искусственных спутников Земли (предисловие, введение, глава X “Связь между вариациями текущих характеристик и начальных условий движения”). В этой главе говорится, что “Более трудной задачей является установление связи между вариациями $\Delta {{p}_{i}}$ и $\Delta {{q}_{j}}$ (между вариациями текущих характеристик (вариациями каких-либо координат и составляющих вектора скорости центра масс) и вариациями начальных условий движения)”. Приводятся не только общие соотношения, устанавливающие связи между вариациями $\Delta {{p}_{i}}$ и $\Delta {{q}_{j}}$ с использованием частных производных и их матриц (матриц изохронных производных), но и рассматриваются частные производные (изохронные производные) от модуля радиус-вектора, от продольной и радиальной составляющих вектора скорости, от времени полета и от других параметров орбитального движения для эллиптического кеплеровского движения. Приводится матрица частных производных от текущих характеристик по начальным условиям (матрица изохронных производных) для эллиптического кеплеровского движения.

Дополнительно отметим, что в работе Чарного (1963) [2] получена матрица изохронных производных на кеплеровой дуге (для отклонений вдоль радиус-вектора, вдоль трансверсали и бинормали, а также для отклонений радиальной, трансверсальной и боковой скоростям), получившая впоследствии широкое распространение в практических вычислениях. В работе Алферьева (2011) [3], посвященной изучению свойств матриц частных производных, выписан удобный для программирования вид матриц частных производных от радиус-вектора и вектора скорости центра масс космического объекта на кеплеровой дуге.

В основе небесной механики и механики космического полета лежит векторное ньютоновское дифференциальное уравнение возмущенной пространственной задачи двух тел и соответствующие им скалярные дифференциальные уравнения в прямоугольных декартовых координатах. Эти уравнения широко используются не только в теоретических исследованиях, но и для решения многих технических задач. Это связано с большой наглядностью декартовых координат, компактностью уравнений в декартовых координатах и их удобством при решении многих прикладных задач, в том числе задач, решаемых с помощью навигационных спутников. Так, в документе “Глобальная навигационная спутниковая система ГЛОНАСС. Интерфейсный контрольный документ” говорится (П. 3.1.1. Алгоритм пересчета эфемерид НКА на текущий момент времени): “Пересчет эфемерид потребителем с момента t_э их задания … проводится методом численного интегрирования дифференциальных уравнений движения КА, в правых частях которых учитываются ускорения, определяемые константой гравитационного поля Земли μ, второй зональной гармоникой с индексом С20, характеризующей полярное сжатие Земли, а также ускорения от лунно-солнечных гравитационных возмущений. Уравнения движения интегрируются в прямоугольной абсолютной геоцентрической системе координат OX₀Y₀Z₀, связанной с текущими экватором и точкой весеннего равноденствия, методом Рунге–Кутта четвертого порядка и имеют вид…”. Приводятся дифференциальные уравнения движения КА в декартовых координатах (дифференциальные уравнения возмущенной пространственной задачи двух тел, в которой изучаемое (второе) тело малой массы – КА), в которых учитываются указанные возмущающие ускорения.

Уравнения возмущенной пространственной задачи двух тел в декартовых координатах вырождаются при соударении второго тела, например КА (тела с пренебрежимо малой массой), с центральным телом (при равенстве нулю расстояния между телами), что делает использование этого уравнения неудобным при изучении движения второго тела в малой окрестности центрального тела или его движения по сильно вытянутым орбитам. Сингулярность в начале координат (особенность типа деления на ноль, порождаемая действием ньютоновской гравитационной силой) создает не только теоретические, но и практические (вычислительные) трудности использования этих уравнений. В работе Бордовицыной [4] отмечается, что “В практических задачах небесной механики прямые соударения тел, как правило, не рассматриваются. Однако в рамках этих задач наличие особенностей в уравнениях движения оказывают заметное (негативное) влияние на процесс их численного решения”.

Проблема устранения указанной особенности, известная в небесной механике и механике космического полета (астродинамике) как проблема регуляризации дифференциальных уравнений возмущенной задачи двух тел, восходит к Эйлеру (1765) [5] и Леви-Чивита (Levi-Civita) (1920) [6–8], которые дали решения одномерной и двумерной задач о соударении двух тел (в случаях прямолинейного и плоского движений). Процедуру, позволяющую устранить указанную особенность дифференциальных уравнений движения, следуя [7], называют регуляризацией. Эффективная регуляризация уравнений возмущенной пространственной задачи двух тел, так называемая спинорная или KS-регуляризация, была предложена Кустаанхеймо (Kustaanheimo) и Штифелем (Stiefel) (1964–1965) [9, 10]. Она наиболее полно изложена в широко цитируемой монографии Штифеля и Шейфеле (Scheifele) (1971, 1974) [11].

Отметим следующие основные достоинства уравнений Кустаанхеймо–Штифеля [4, 11–19]:

• они, в отличие от ньютоновских, существенно нелинейных, уравнений, регулярны в центре притяжения (не имеют особенностей типа деления на ноль, порождаемых действующей ньютоновской гравитационной силой);

• линейны для невозмущенных кеплеровских движений в новом времени τ, определяемым дифференциальным соотношением dt = rdτ (преобразованием времени Зундмана), в котором r – расстояние до центра притяжения, и имеют в этом случае вид системы четырех независимых линейных дифференциальных уравнений второго порядка относительно KS-переменных u_j с одинаковыми постоянными коэффициентами, равными половинной кеплеровской энергии h:

• для эллиптического кеплеровского движения, когда кеплеровская энергия h < 0, эти уравнения эквивалентны уравнениям движения четырехмерного одночастотного гармонического осциллятора, квадрат частоты которого равен половине кеплеровской энергии, взятой со знаком минус (это свойство позволяет построить регулярные уравнения в оскулирующих элементах (медленно изменяющихся переменных), удобные для изучения возмущенного кеплеровского эллиптического движения);

• позволяют выработать единый подход к изучению всех трех типов кеплеровского движения;

• близки к линейным уравнениям для возмущенных кеплеровских движений;

• позволяют представить правые части дифференциальных уравнений движения небесных и космических тел в полиномиальной форме, удобной для их решения с помощью ЭВМ.

Эти свойства регулярных уравнений в KS-переменных позволили разработать эффективные методы нахождения решений в аналитической или численной форме таких трудных для классических методов задач как исследование движения вблизи притягивающих масс или движения по орбитам с большими эксцентриситетами.

Штифелем, Шейфеле, Бордовицыной, Шарковским и др. [4, 11, 13] показано, что использование регулярных уравнений в KS-переменных позволяет повысить точность численного решения ряда задач небесной механики и астродинамики, например, задачи о движении искусственного спутника Земли (ИСЗ) по орбитам с большими эксцентриситетами, от трех до пяти порядков по сравнению с решениями, полученными при использовании классических ньютоновских уравнений. В книге Бордовицыной и Авдюшева [13] говорится: “методы теории специальных возмущений весьма эффективны и могут быть рекомендованы к применению для численного моделирования спутниковых орбит. Впечатляющие результаты получаются при использовании KS-уравнений (u, δu) и уравнений Роя (ry). Так, при сохранении точности интегрирования с их помощью удается повысить быстродействие в 3–4 раза. Кроме того, метод Энке в KS-переменных (δu) за счет ослабления влияния ошибок округления позволяет повысить уровень наивысшей точности почти на 1–2 порядка”. Здесь речь идет о спутниковых орбитах с эксцентриситетом равным нулю или 0.01 (типа орбит спутниковой навигационной группировки ГЛОНАСС, близких к круговым орбитам). Отметим, что для этих круговых или слабоэллиптичеких орбит численное интегрирование уравнений движения КА в KS-переменных дает существенно меньший выигрыш в смысле точности в сравнении с интегрированием уравнений движения КА в декартовых координатах, чем для высокоэллиптических орбит (орбит с большими эксцентриситетами).

В работах Fukushima (2005, 2007) [18, 19] также показано, что KS-регуляризация приводит к очень эффективной схеме интегрирования уравнений орбитального движения, повышающей точность и скорость численного интегрирования. Это связано не только со структурой уравнений, но также с использованием нескольких методов, которые приносят важные преимущества численной схеме: “The KS regularization resulted in a very efficient integration scheme, improving the accuracy and speed of numerical integration. This comes not only from the structure of the equations, but also from the use of several techniques that bring important advantages to the numerical scheme”. В работе [19] приводится численное сравнение четырех схем регуляризации трехмерной задачи двух тел в условиях возмущения: регуляризации Шперлинга–Бюрде (Sperling–Burdet) (SB), Кустаанхеймо–Штифеля (KS), Бюрде–Феррандиса (Burdet–Ferrfindiz) (BF) и трехмерное расширение регуляризации Леви-Чивита (LC). В аннотации статьи [19] сказано: “the KS and the extended LC regularizations with Kepler energy scaling provide the best cost performance in integrating almost all the perturbed two-body problems” (КS и расширенная LС регуляризация с масштабированием энергии Кеплера обеспечивают наилучшую экономическую эффективность при интеграции почти всех возмущенных задач двух тел). Подчеркнем, что и Fukushima сравнивает семь схем, описанных в § 1 его статьи, а также “нерегуляризованную обработку, а именно прямое интегрирование в декартовых координатах”. Для каждой из этих формулировок им проводится тестовая интеграция Икара, охватывающая около 1 миллиона лет, и измеряется время его выполнения: “We compare the seven schemes described in § 1, as well as the unregularized treatment, namely, direct integration in Cartesian coordinates. For each of these formulations, we conduct a test integration of Icarus covering about 1 million years and measure its execution time”.

В основе регуляризации Кустаанхеймо–Штифеля лежит нелинейное неоднозначное преобразование декартовых координат. Оно состоит в переходе от трехмерного пространства декартовых координат x_k к четырехмерному пространству новых координат u_j. Поэтому вскоре после открытия KS-преобразования было рассмотрено использование кватернионов (четырехмерных гиперкомплексных чисел) и четырехмерных кватернионных матриц для регуляризации уравнений пространственной задачи двух тел. Однако Штифель и Шейфеле полностью отвергли эту идею, написав в своей книге ([11], c. 288) (1971): “Любая попытка заменить теорию KS-матриц более популярной теорией кватернионных матриц приводит поэтому к неудаче или, во всяком случае, к очень громоздкому формализму”. Позже (в конце 70-х и начале 80-х годах) Челноковым было показано [20, 21] (в работе [20] (1981) с использованием классических кватернионных матриц, а в работе [21] (1984) с использованием кватернионов Гамильтона), что в действительности кватернионный подход к регуляризации

• позволяет дать прямой и наглядный вывод регулярных уравнений в KS-переменных (что ставилось Штифелем и Шейфеле под сомнение ([11], c. 29) из-за неоднозначности KS-преобразования: “единственный путь избежать этой трудности (неоднозначности) состоит в постулировании матричных уравнений в KS-переменных и проверки того, что при этом удовлетворяются старые ньютоновские уравнения”);

• позволяет дать наглядные геометрическую и кинематическую интерпретации регуляризующему KS-преобразованию;

• раскрывает геометрический смысл его неоднозначности;

• позволяет получить более общие регулярные уравнения возмущенной пространственной задачи двух тел, частным случаем которых являются регулярные уравнения Кустаанхеймо–Штифеля.

В работах [20, 21] было показано, что регуляризующее нелинейное преобразование координат Кустаанхеймо–Штифеля

фактически означает переход от трехмерных декартовых координат x_k центра масс второго тела в инерциальной системе координат к новым четырехмерным переменным (KS-переменным) u_j, определяемым формулами где λ_j ( j = 0, 1, 2, 3) – параметры Эйлера (Родрига–Гамильтона), характеризующие ориентацию вращающейся в инерциальном пространстве системы координат η, ось η₁ которой направлена вдоль радиус-вектора r центра масс второго тела, а проекция ω₁ вектора ω абсолютной угловой скорости которой на направление радиус-вектора r равна нулю: ω₁ = 0. Такая система координат называется в механике неголономной или азимутально-свободной.

Следовательно, для получения регулярных уравнений Кустаанхеймо–Штифеля необходимо записать векторное уравнение возмущенной пространственной задачи двух тел (в декартовых координатах) в этой вращающейся системе координат η, используя в качестве параметров ориентации этой системы координат четырехмерные параметры Эйлера ${{\lambda }_{j}}$, являющиеся компонентами кватерниона поворота λ этой системы координат. Дальнейшие преобразования этих уравнений связаны [20, 21] с нормировкой параметров Эйлера (кватерниона поворота) с помощью множителя $\sqrt r $ и с переходом в полученных уравнениях к KS-переменным u_j по выше приведенным формулам, а также с введением в качестве дополнительных зависимых переменных кеплеровской энергии h и времени t и с переходом к новой независимой переменной τ с помощью преобразования времени Зундмана dt = rdτ.

Подчеркнем, что использование четырехмерных параметров Эйлера естественным образом приводит к использованию в теории регуляризации четырехмерных кватернионных матриц и четырехмерных гиперкомплексных переменных – кватернионов Гамильтона.

В работах [20, 21] было также показано, что билинейное соотношение Кустаанхеймо–Штифеля

связывающее между собой KS-переменные u_j и их первые производные $u_{j}^{'}$ (верхний штрих “'” означает дифференцирование по новой независимой переменной τ) и играющее, по словам Штифеля и Шейфеле, основную роль в их построении регулярной небесной механики ([11], с. 29), имеет ясный геометрический и механический смысл и не является обязательным условием получения регулярных уравнений в KS-переменных. Более того, отказ от его выполнения позволил получить в работах [20, 21] более общие регулярные матричные (в четырехмерных кватернионных матрицах) и кватернионные (в кватернионах Гамильтона) уравнения возмущенной пространственной задачи двух тел в KS-переменных, которые, возможно, также найдут практическое приложение.

Объясняется это тем, что билинейное соотношение Кустаанхеймо–Штифеля эквивалентно равенству нулю проекции ω₁ вектора абсолютной угловой скорости неголономной системы координат η на направление радиус-вектора r. Проекция ω₁ для такой системы координат является произвольно задаваемым параметром (может быть задана произвольно). В случае Кустаанхеймо–Штифеля она равна нулю: ω₁ = 0. Отказ от выполнения этого условия и позволил Челнокову построить более общие регулярные кватернионные уравнения.

Позднее (в 1983–2008 годах) эффективность применения кватернионов для решения проблемы регуляризации уравнений возмущенной пространственной задачи двух тел была продемонстрирована также в работах ряда зарубежных авторов [22–26]. Так, Вальдфогель (Waldvogel) (2008) [26] утверждает, что “кватернионы для регуляризации небесной механики – верный путь”, и что кватернионы “являются идеальным инструментом для описания и разработки теории пространственной регуляризации в небесной механике”. Вальдфогелем отмечается приоритет Челнокова в области кватернионной регуляризации со ссылкой на его статью [20] 1981 г. и другие его работы в этой области и в области практических приложений регулярных кватернионных уравнений в механике космического полета.

Отметим также вышедшую в 2011 г. книгу [16], обзорные работы [17, 27] по проблеме регуляризации уравнений небесной механики и астродинамики и недавний обширный обзор на английском языке Челнокова [28] работ по кватернионной регуляризации дифференциальных уравнений возмущенной пространственной задачи двух тел и возмущенного центрального движения материальной точки с использованием четырехмерных KS-переменных и модифицированных четырехмерных переменных, параметров Эйлера (Родрига–Гамильтона), переменных Леви-Чивита. В этой работе также дается обзор приложений регулярных кватернионных уравнений к построению и исследованию регулярных уравнений орбитального движения космических аппаратов, уравнений движения спутника Земли в ее гравитационном поле с учетом зональных, тессеральных и секториальных гармоник, к решению задач оптимального управления орбитальным движением космического аппарата с использованием принципа максимума и к решению задач автономной инерциальной навигации в космосе.

Во всех работах по проблеме регуляризации дифференциальных уравнений возмущенной пространственной задачи двух тел, известных авторам статьи, рассматривается регуляризация уравнений движения центра масс второго (изучаемого) тела, описывающих движение этого тела относительно системы координат, движущейся в инерциальной системе координат поступательно, т.е. рассматривается регуляризация уравнений абсолютного движения центра масс изучаемого тела. Дальнейшее развитие кватернионной регуляризации дифференциальных уравнений возмущенной пространственной задачи двух тел дано Челноковым в работе (2018) [29], в которой в рамках возмущенной пространственной задачи двух тел предложены регулярные кватернионные дифференциальные уравнения возмущенного движения второго (изучаемого) тела относительно системы координат, вращающейся в инерциальной системе координат по произвольно заданному закону, а также относительно системы координат, связанной с Землей, принимаемой за первое (центральное) тело. Эти кватернионные уравнения относительного движения целесообразно использовать для решения задач прогноза и коррекции движения КА относительно Земли (т.е. не относительно инерциальной системе координат, а относительно системы координат, связанной с вращающейся Землей).

В настоящее время регулярные кватернионные уравнения в KS-переменных нашли широкое применение в задачах прикладной небесной механики и механики космического полета. Это объясняется не только указанными достоинствами этих уравнений, но и тем, что кватернионный аппарат является более мощным и гибким средством решения этих задач (в том числе и изучаемых в статье задач прогноза и коррекции орбитального движения КА) в сравнении с аппаратом специальных KS-матриц, введенных Штифелем и Шейфеле и широко используемых в их книге, а также в работах других исследователей. Поэтому многие отечественные и зарубежные исследователи используют регулярные кватернионные уравнения для решения задач прикладной небесной механики и механики космического полета.

Отметим, что в настоящее время в Центральном научно-исследовательском институте машиностроения (АО ЦНИИМАШ, г. Королев) ведутся исследования [30] (с участием авторов статьи) по использованию регулярных кватернионных уравнений орбитального движения космических аппаратов в KS-переменных совместно с использованием уравнений в декартовых координатах для решения задач оценивания параметров движения, прогноза и коррекции орбитального движения КА.

В нашей статье решение задач прогноза и коррекции орбитального движения КА предлагается решать с использованием предложенных нами ранее регулярных кватернионных уравнений орбитального движения, приведенных в разд. 2.1, и новых регулярных кватернионных орбитального движения КА, полученных в статье, а также с помощью кватернионных уравнений и соотношений в вариациях, полученных в статье из кватернионных уравнений орбитального движения КА. Перспективность такого подхода к решению задач прогноза и коррекции орбитального движения была обоснована нами выше.

В разд. 2.1 статьи рассмотрены известные, предложенные нами ранее, регулярные кватернионные уравнения возмущенной пространственной задачи двух тел и регулярные кватернионные уравнения орбитального движения КА в четырехмерных KS-переменных, построенные на основе этих уравнений. Эти уравнения используются в статье для построения новых уравнений и соотношений, предлагаемых нами для решения задач прогноза и коррекции орбитального движения.

В разд. 2.2 приведены результаты сравнительного исследования точности численного интегрирования классических ньютоновских дифференциальных уравнений пространственной ограниченной задачи трех тел (Земля, Луна и КА) в декартовых координатах и предложенных Челноковым [31] регулярных кватернионных дифференциальных уравнений этой задачи в KS-переменных, которые показывают, что точность численного интегрирования регулярных кватернионных уравнений значительно выше (на несколько порядков) точности численного интегрирования уравнений в декартовых координатах, и которые говорят в пользу использования регулярных кватернионных уравнений орбитального движения для решения задач прогноза и коррекции орбитального движения КА. Эти результаты докладывались Логиновым и Челноковым [32] на XXVIII Санкт-Петербургской международной конференции по интегрированным навигационным системам в 2021 году. Здесь они дополнены графиками, иллюстрирующими погрешности численного интегрирования кватернионных уравнений и уравнений в декартовых координатах, пояснениями графиков и более подробным описанием моделирования.

В разделах 2–6 статьи излагаются новые, полученные нами, результаты:

1) Формулы, устанавливающие связи вариаций декартовых координат и проекций вектора скорости центра масс КА в инерциальной системе координат с вариациями KS-переменных и их первых производных по новой независимой переменной Зундмана (“фиктивному” времени τ).

2) Формулы для нахождения вариаций KS-переменных, их первых производных и реального времени t для фиксированного времени τ по вариациям этих переменных, кеплеровской энергии и времени τ для начального момента времени τ(0) = 0, найденные прямым путем.

3) Матрицы изохронных производных от KS-переменных, их первых производных по времени τ и кеплеровской энергии для эллиптического кеплеровского движения КА.

4) Линеаризованные регулярные дифференциальные кватернионные уравнения возмущенного орбитального движения КА в вариациях KS-переменных и их первых производных по времени $\tau $, а также дифференциальные уравнения в вариациях кеплеровской энергии и времени t, обусловленные вариациями начальных условий и вариацией действующего на КА возмущающего ускорения.

5) Различные формы новых дифференциальных регулярных кватернионных уравнений орбитального движения КА, в которых в качестве независимой переменной используется не время τ (независимая переменная Зундмана), а безразмерное время $\tau {\kern 1pt} *$. Эта независимая переменная равна половинной обобщенной эксцентрической аномалии, широко используемой в небесной механике и механике космического полета. Эти уравнения, также как и наши известные уравнения, изложенные в разд. 2.1, могут быть эффективно использованы для решения задач прогноза и коррекции орбитального движения.

6) Формулы для вариаций KS-переменных и их первых производных в безразмерном времени $\tau {\kern 1pt} *$.

7) Система дифференциальных кватернионных уравнений орбитального движения КА в регулярных кватернионных оскулирующих элементах (медленно изменяющихся переменных) с использованием в качестве независимой переменной безразмерного времени $\tau {\kern 1pt} *$.

Полученные в статье кватернионные уравнения и соотношения в вариациях позволяют изучать и оценивать влияние изменений начальных условий движения КА и действующих возмущений на изменение текущих характеристик его движения для текущего момента времени, а также позволяют эффективно решать задачи прогноза и коррекции орбитального движения КА, используя описание движения центра масс КА в регулярных четырехмерных KS-переменных и в соответствующих им кватернионных переменных, а также в кватернионных оскулирующих элементах.

2. Регулярные кватернионные дифференциальные уравнения возмущенной пространственной задачи двух тел и возмущенного орбитального движения космического аппарата.

2.1. Регулярные кватернионные уравнения возмущенной пространственной задачи двух тел и орбитального движения космического аппарата в KS-переменных. В основе небесной механики и астродинамики лежит векторное ньютоновское дифференциальное уравнение возмущенной пространственной задачи двух тел

В уравнении (2.1) r – радиус-вектор центра масс второго (изучаемого) тела, проведенный из центра масс первого (центрального) тела; $r = \left| {\mathbf{r}} \right|$ – расстояние от центра масс второго тела до центра масс первого тела, m и M – массы второго и первого тел; f – гравитационная постоянная; p – вектор возмущающего ускорения центра масс второго тела, t – время.

При m = 0 уравнением (2.1) описывается возмущенное движение центра масс космического аппарата (второго тела пренебрежимо малой массы) в поле тяготения центрального тела (например, Земли).

Уравнение (2.1) вырождается при соударении второго тела с центральным телом (при равенстве нулю расстояния r между телами), что делает использование этого уравнения неудобным при изучении движения второго тела в малой окрестности центрального тела или его движения по сильно вытянутым орбитам. Сингулярность в начале координат создает не только теоретические, но и практические (вычислительные) трудности использования уравнения (2.1). Эффективная регуляризация уравнений возмущенной пространственной задачи двух тел, так называемая спинорная или KS-регуляризация, была предложена, как уже отмечалось, Кустаанхеймо и Штифелем (1964–1965) [9, 10].

В основе регуляризации Кустаанхеймо–Штифеля лежит нелинейное неоднозначное преобразование декартовых координат изучаемого тела, так называемое KS-преобразование, обобщающее преобразование Леви-Чивита и имеющее вид

где x_k (k = 1, 2, 3) – координаты центра масс изучаемого тела в инерциальной системе координат X, имеющей начало в центре масс центрального тела и координатные оси, направленные на удаленные звезды, u_j ( j = 0, 1, 2, 3) – новые переменные (KS-переменные), L(u_KS) – обобщенная матрица Леви-Чивита, называемая KS-матрицей, содержащая в левом верхнем углу двухмерную квадратную матрицу Леви-Чивита.

В скалярной записи преобразование (2.2) имеет вид

и с точностью до перестановки индексов совпадает с отображением Хопфа (1931) [33].

Регулярные дифференциальные уравнения Кустаанхеймо–Штифеля возмущенной пространственной задачи двух тел имеют в скалярной записи следующий вид [11]:

Здесь верхний штрих, как уже отмечалось, символ дифференцирования по новой независимой переменной Зундмана τ, называемой фиктивным временем и связанной со временем t дифференциальным уравнением (2.6): dt/dτ = r; h – кеплеровская энергия, рассматриваемая как дополнительная переменная и определяемая соотношением

p_k (k = 1, 2, 3) – проекции вектора возмущающего ускорения p центра масс второго тела на оси инерциальной системы координат. Время t также рассматривается как дополнительная (зависимая) переменная.

Уравнения (2.4)–(2.6) образуют систему десяти обыкновенных нелинейных и нестационарных (для возмущенного движения второго тела) дифференциальных уравнений относительно четырех KS-переменных u_j, кеплеровской энергии h и времени t.

Эти скалярные уравнения эквивалентны матричным уравнениям [11]

где ${{{\mathbf{u}}}_{{ks}}}$ – четырехмерный вектор-столбец KS-переменных, L(u_KS) – KS-матрица, определяемая соотношением (2.2), ${{{\mathbf{P}}}_{{ks}}}$ – четырехмерный вектор-столбец, сопоставляемый трехмерному вектору возмущающего ускорения p, $\left( {{\mathbf{a}},{\mathbf{b}}} \right)$ – скалярное произведение четырехмерных вектор-столбцов a и b.

Основные достоинства уравнений Кустаанхеймо–Штифеля (2.4)–(2.6) или (2.7) были указаны выше.

Билинейное соотношение Кустаанхеймо–Штифеля

связывает между собой KS-переменные и их первые производные и играет, по словам Штифеля и Шейфеле, основную роль в их построении регулярной небесной механики ([11], с. 29). Оно является первым частным интегралом дифференциальных уравнений (2.4)–(2.6) или (2.7).

Кватернионные регулярные уравнения возмущенной пространственной задачи двух тел в KS-переменных в случае, когда выполняется выше приведенное билинейное соотношение (2.8), имеют следующий вид [21] (см. также [16, 17]):

Здесь

p_x – отображение вектора p возмущающего ускорения центра масс изучаемого тела на инерциальный базис X, символ “$ \circ $” означает кватернионное умножение; верхняя черта означает символ кватернионного сопряжения; scal(•) – скалярная часть кватерниона, стоящего в круглых скобках; u – кватернионная регулярная переменная, определяемая соотношениями где ${\mathbf{\lambda }} = {{\lambda }_{0}} + {{\lambda }_{1}}{\mathbf{i}} + {{\lambda }_{2}}{\mathbf{j}} + {{\lambda }_{3}}{\mathbf{k}}$ – кватернион ориентации выше описанной системы координат η, вращающейся в инерциальной системе координат X, $\bar {\lambda }$ – сопряженный кватернион: $\bar {\lambda } = {{\lambda }_{0}} - {{\lambda }_{1}}{\mathbf{i}} - {{\lambda }_{2}}{\mathbf{j}} - {{\lambda }_{3}}{\mathbf{k}}$; i, j, k – векторные мнимые единицы Гамильтона.

В подвижной системе координат η Челноковым записывается [20, 21] исходное векторное ньютоновское дифференциальное уравнение возмущенной пространственной задачи двух тел (2.1) с целью дальнейшей его регуляризации и получения кватернионных уравнений (2.9).

Отметим, что в наших работах [20, 21] получены более общие матричные и кватернионные регулярные уравнения возмущенной пространственной задачи двух тел в KS-переменных в общем случае, когда билинейное соотношение (2.8) не выполняется.

В кватернионных уравнениях (2.9) в качестве переменных выступают кватернион u, компонентами которого являются регулярные KS-переменные u_j, кеплеровская энергия h и время t. Эти уравнения имеют все ранее указанные достоинства матричных регулярных уравнений (2.7), предложенных Кустаанхеймо и Штифелем. Однако, как уже отмечалось, в отличие от них, они позволяют использовать кватернионный аппарат, который является более мощным и гибким средством решения изучаемых в статье задач по сравнению с аппаратом специальных KS-матриц $L\left( {{{{\mathbf{u}}}_{{ks}}}} \right)$, введенных Штифелем и Шейфеле и широко используемых в их книге, а также в работах других исследователей. Поэтому регулярные кватернионные уравнения в KS-переменных в настоящее время также широко используются для решения задач прикладной небесной механики и астродинамики.

Дополнительно отметим, что линейность кватернионных уравнений (2.9) для кеплеровских движений позволяет эффективно построить новые регулярные кватернионные уравнения орбитального движения в кватернионных оскулирующих элементах (медленно изменяющихся переменных), удобные для исследования и прогноза возмущенного движения космических тел и аппаратов.

Для нахождения декартовых координат x_k изучаемого тела в инерциальной системе координат X и проекций ${{{v}}_{k}}$ = dx_k/dt вектора его скорости v на оси этой системы координат служат кватернионные соотношения

где r_x и v_x – отображения векторов r и v на инерциальный базис, ${{{v}}_{k}}$ – проекции вектора скорости v оси инерциальной системы координат X.

В скалярной записи выражения для проекций ${{{v}}_{k}}$ вектора скорости v имеют вид соотношений

где верхняя точка – символ производной по времени t.

2.2. Исследование точности численного интегрирования регулярных кватернионных уравнений возмущенной пространственной ограниченной задачи трех тел (уравнений орбитального движения космического аппарата) в переменных Кустаанхеймо–Штифеля. Логиновым и Челноковым проведено [32] сравнительное исследование точности численного интегрирования классических ньютоновских дифференциальных уравнений пространственной ограниченной задачи трех тел (Земля, Луна и космический аппарат) в декартовых координатах и построенных нами [31] регулярных кватернионных дифференциальных уравнений этой задачи в четырехмерных KS-переменных, принимающих вид регулярных кватернионных уравнений (2.9) возмущенной пространственной задачи двух тел в случае отсутствия поля тяготения Луны.

Исследована точность определения траектории орбитального движения космического аппарата в поле тяготения Земли и Луны для четырех орбит: круговой (влияние поля тяготения Луны не учитывается), двух возмущенных эллиптических с малым эксцентриситетом 0.05 и одной возмущенной эллиптической с большим эксцентриситетом 0.85 (учитываются возмущения от силы гравитации Луны). Траектория КА определялась численным интегрированием классических ньютоновских дифференциальных уравнений в декартовых координатах и предложенных нами регулярных кватернионных дифференциальных уравнений в KS-переменных методом Рунге–Кутты 4-го порядка. Уравнения в KS-переменных интегрировались в “фиктивном” времени τ. Оно является новой независимой переменной в регулярных уравнениях и связано с реальным временем t дифференциальным соотношением (2.6), содержащим расстояние от КА до центра масс Земли. В реальном времени шаги интегрирования регулярных кватернионных и классических ньютоновских дифференциальных уравнений совпадали.

На интервале времени в 50 оборотов КА выполнялось прямое, а затем обратное интегрирование уравнений движения. При прямом интегрировании реальное время t нарастает от нуля до конечного значения ${{t}_{{{\text{end}}}}}$, а фиктивное время τ – от нуля до конечного значения ${{\tau }_{{{\text{end}}}}}$, соответствующего конечному реальному времени ${{t}_{{{\text{end}}}}}$. При этом КА движется по траектории, которую будем называть прямой траекторией.

При обратном интегрировании реальное время t и фиктивное время τ убывает от своих соответствующих значений ${{t}_{{{\text{end}}}}}$ и ${{\tau }_{{{\text{end}}}}}$ до нуля, в качестве начальных условий интегрирования выступают параметры движения КА в конечной точке прямой траектории (т.е. параметры, полученные при прямом интегрировании для моментов времени ${{t}_{{{\text{end}}}}}$ и ${{\tau }_{{{\text{end}}}}}$), а КА из этой точки движется в обратную сторону по траектории, которую будем называть обратной траекторией.

Эти прямую и обратную траектории, полученные путем численного интегрирования уравнений движения, будем называть численными траекториями.

В результате прямого интегрирования классических ньютоновских уравнений для каждого момента реального времени $t \in [0,{{t}_{{{\text{end}}}}}]$ вычисляется радиус-вектор КА $r_{{{\text{frw}}}}^{{{\text{clas}}}}$. Каждому моменту реального времени $t \in [0,{{t}_{{{\text{end}}}}}]$ соответствует момент фиктивного времени $\tau \in [0,{{\tau }_{{{\text{end}}}}}]$, для которого в результате прямого интегрирования кватернионных уравнений вычисляется радиус-вектор КА $r_{{{\text{frw}}}}^{{KS}}$.

В результате обратного интегрирования классических ньютоновских уравнений для каждого момента реального времени $t \in [{{t}_{{{\text{end}}}}},0]$ вычисляется радиус-вектор КА $r_{{{\text{rev}}}}^{{{\text{clas}}}}$. Каждому моменту реального времени $t \in [{{t}_{{{\text{end}}}}},0]$ соответствует момент фиктивного времени $\tau \in [{{\tau }_{{{\text{end}}}}},0]$, для которого в результате обратного интегрирования кватернионных уравнений вычисляется радиус-вектор КА $r_{{{\text{rev}}}}^{{KS}}$.

В силу погрешностей методов численного интегрирования прямая и обратная траектории (т.е. радиус-векторы КА, вычисленные для каждого момента времени в результате прямого и обратного интегрирования) не совпадают между собой.

Первая орбита представляет особый случай, так как является круговой, а влияние поля тяготения Луны для нее не учитывается, поэтому для этой орбиты известен аналитический закон движения КА. С помощью этого аналитического закона вычислялась траектория, которую будем называть истинной траекторией. Каждому моменту времени t при движении по истинной траектории соответствует радиус-вектор КА $r_{{{\text{true}}}}^{{}}$, не зависящий от направления движения (прямого или обратного) вдоль этой траектории.

Радиус-векторы $r_{{{\text{frw}}}}^{{{\text{clas}}}}$, $r_{{{\text{frw}}}}^{{KS}}$, $r_{{{\text{rev}}}}^{{{\text{clas}}}}$, $r_{{{\text{rev}}}}^{{KS}}$, $r_{{{\text{true}}}}^{{}}$ проведены из центра масс Земли.

Приведем описания орбит, методы сравнения точности интегрирования, а также условия и результаты моделирования для каждой из них. Первая орбита – круговая. По этой орбите объект движется вокруг Земли на расстоянии 10 000 км от ее центра. Период обращения объекта вокруг Земли составил 2.8 часа, интервал интегрирования – 50 оборотов (около 139 часов), шаг интегрирования в реальном времени – 30 с.

Для первой орбиты точность численного решения дифференциальных уравнений движения определялась с помощью отклонения $\Delta r{\kern 1pt} *$ прямой и обратной численных траекторий от истинной траектории. Отклонение $\Delta r{\kern 1pt} *$ в каждый момент времени определяется для классических ньютоновских уравнений соотношением $\Delta r{\kern 1pt} * = \left| {r_{{{\text{frw}}}}^{{{\text{clas}}}} - r_{{{\text{true}}}}^{{}}} \right|$ при прямом интегрировании и соотношением $\Delta r{\kern 1pt} * = \left| {r_{{{\text{rev}}}}^{{{\text{clas}}}} - r_{{{\text{true}}}}^{{}}} \right|$ при обратном интегрировании, а для кватернионных уравнений – соотношением $\Delta r{\kern 1pt} * = \left| {r_{{{\text{frw}}}}^{{KS}} - r_{{{\text{true}}}}^{{}}} \right|$ при прямом интегрировании и соотношением $\Delta r{\kern 1pt} * = \left| {r_{{{\text{rev}}}}^{{KS}} - r_{{{\text{true}}}}^{{}}} \right|$ при обратном интегрировании.

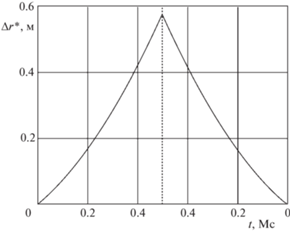
Результаты исследования точности численного решения для первой орбиты представлены на рис. 1 и 2 графиками, показывающими зависимость отклонения $\Delta r{\kern 1pt} *$ от времени при прямом и обратном интегрировании классических ньютоновских уравнений (рис. 1) и кватернионных уравнений (рис. 2). Здесь и далее на всех графиках для кватернионных уравнений вместо значений фиктивного времени τ представлены соответствующие значения реального времени t.

Область слева от вертикальной пунктирной линии соответствует прямому интегрированию, в этой области при движении слева направо по оси абсцисс время t нарастает. Для оценки точности интегрирования использовано значение $\Delta r{\kern 1pt} *$ на вертикальной пунктирной линии, то есть в конечный момент времени прямого интегрирования.

Область справа от пунктирной линии соответствует обратному интегрированию, в ней при движении слева направо по оси абсцисс время t, напротив, убывает. Эта область приведена для демонстрации существенного различия поведения отклонения $\Delta r{\kern 1pt} *$ для классических ньютоновских и регулярных кватернионных уравнений.

Видно, что для классических уравнений отклонение $\Delta r{\kern 1pt} *$ достигает максимума в конечный момент времени обратного интегрирования. Для кватернионных уравнений отклонение $\Delta r{\kern 1pt} *$ достигает максимума в конечный момент времени прямого интегрирования, а при обратном интегрировании убывает, достигая в конечный момент времени обратного интегрирования значения, близкого к нулю. Причина такого различия в том, что регулярные кватернионные уравнения в KS-переменных для невозмущенной круговой орбиты линейны, а классические ньютоновские уравнения – нелинейны.

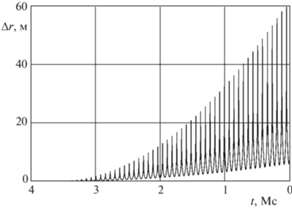
Параметры второй, третьей и четвертой невозмущенных орбит взяты из книги Бордовицыной [4] (с. 95, табл. 2 для начальных значений декартовых координат КА и проекций его вектора начальной скорости). Эксцентриситет второй невозмущенной орбиты – 0.05, период оборота – 2 часа, интервал интегрирования уравнений возмущенного движения – 100 часов, шаг интегрирования в реальном времени – 30 секунд. Эксцентриситет третьей невозмущенной орбиты – 0.05, период оборота – 20 часов, интервал интегрирования уравнений возмущенного движения – 1000 часов, шаг интегрирования в реальном времени – 360 секунд. Эксцентриситет четвертой невозмущенной орбиты – 0.85, период оборота – 20 часов, интервал интегрирования уравнений возмущенного движения – 1000 часов, шаг интегрирования в реальном времени – 60 секунд.

Для этих трех орбит аналитический закон движения неизвестен, поэтому точность численного решения дифференциальных уравнений движения определялась с помощью отклонения $\Delta r$ обратной численной траектории КА от его прямой численной траектории. Подобный метод использован в книге Бордовицыной [4]. Отклонение $\Delta r$ в каждый момент времени определяется для классических ньютоновских уравнений соотношением $\Delta r = \left| {r_{{{\text{rev}}}}^{{{\text{clas}}}} - r_{{{\text{frw}}}}^{{{\text{clas}}}}} \right|$, а для кватернионных уравнений – соотношением $\Delta r = \left| {r_{{{\text{rev}}}}^{{KS}} - r_{{{\text{frw}}}}^{{KS}}} \right|$.

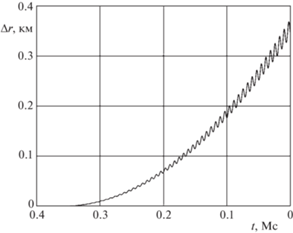
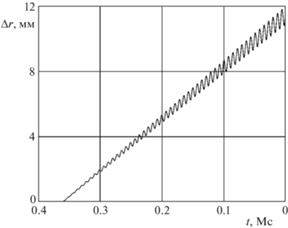
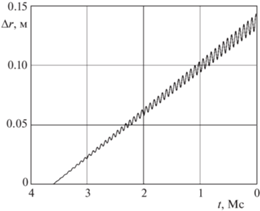
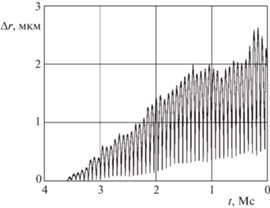
Результаты исследования точности интегрирования классических ньютоновских дифференциальных уравнений и кватернионных уравнений в KS-переменных для второй орбиты представлены графиками на рис. 3 и 4, для третьей орбиты – на рис. 5 и 6, для четвертой орбиты – на рис. 7 и 8. На этих графиках представлена зависимость отклонения $\Delta r$ от времени. В отличие от графиков для первой (круговой) орбиты, здесь представлено только обратное интегрирование, поэтому при движении слева направо по оси абсцисс время t убывает. Для оценки точности численного решения использовано максимальное на интервале интегрирования значение $\Delta r$.

Из графиков на рис. 3 и 4 видно, что в случае второй орбиты отклонение $\Delta r$ для классических ньютоновских уравнений нарастает по закону, близкому к экспоненциальному, а для уравнений в KS-переменных – по закону, близкому к линейному.

Графики на рис. 5 и 6 показывают, что в случае третьей орбиты отклонение $\Delta r$ для классических ньютоновских уравнений нарастает по закону, близкому к экспоненциальному, а для уравнений в KS-переменных – по закону, близкому к линейному.

Графики на рис. 7 и 8 для четвертой орбиты демонстрируют колебательные составляющие с гораздо большей, чем для остальных орбит, амплитудой, что связано с большим эксцентриситетом орбиты. На рис. 8 видно, что для кватернионных уравнений абсолютные значения амплитуды колебаний $\Delta r$ на интервале интегрирования являются минимальными из всех рассмотренных случаев и не превышают $2.7 \times {{10}^{{ - 6}}}$ м, однако нарастание амплитуды не является монотонным. Отсутствие монотонности нарастания амплитуды, по всей видимости, объясняется ограниченностью разрядной сетки вычислителя, реализующего алгоритм численного интегрирования.

По результатам моделирования регулярные кватернионные уравнения в KS-переменных показали значительно более высокую точность, чем уравнения в декартовых координатах. Графики на рис. 1–8 показывают, что для круговой орбиты точность оказалась выше на два порядка, для возмущенных эллиптических орбит со средним эксцентриситетом – на четыре порядка, для возмущенной эллиптической орбиты с высоким эксцентриситетом – на семь порядков. Отметим, что в книге Бордовицыной [4] приведены результаты численных исследований решений уравнений невозмущенной и возмущенной пространственной задачи двух тел (решений уравнений невозмущенного и возмущенного движения ИСЗ) ряда авторов с использованием других известных (канонических) уравнений в KS-переменных, построенных с использованием соответствующего гамильтониана, и уравнений в декартовых координатах, демонстрирующие преимущество уравнений в KS-переменных перед уравнениями в декартовых координатах (в смысле точности их численного интегрирования). Сравнение этих результатов с нашими результатами показало, что они в целом согласуются между собой.

Полученные нами результаты численного исследования подтверждают значительные преимущества регулярных кватернионных уравнений в KS-переменных в задачах прогноза движения небесных и космических тел, а также в задачах коррекции параметров орбитального движения КА и инерциальной навигации в космосе перед уравнениями в декартовых координатах. Они обосновывают перспективность использования регулярных кватернионных уравнений для решения задач прогноза и коррекции орбитального движения КА.

3. Связи вариаций декартовых координат и проекций вектора скорости космического аппарата с вариациями KS-переменных и их первых производных. Вариации δx_k (k = 1, 2, 3) декартовых координат x_k КА могут быть найдены через вариации δu_j ( j = 0, 1, 2, 3) KS-переменных u_j по формулам

Используя формулы (3.1) и (2.3), получаем следующие скалярные выражения для нахождения вариаций δx_k через вариации δu_j:

В кватернионной записи соотношения (3.2) примут вид (3.3):

где вариация $\delta {{{\mathbf{r}}}_{x}}$ отображения ${{{\mathbf{r}}}_{x}}$ радиус-вектора r центра масс КА на инерциальный базис X и вариация $\delta {\mathbf{u}}$ кватернионной регулярной переменной u определяются соотношениями а ${\text{vect}}\left( {\mathbf{a}} \right)$ означает векторную часть кватерниона a, заключенного в круглые скобки.

Вариации $\delta {{{v}}_{k}}$ (k = 1, 2, 3) проекций ${{{v}}_{k}}$ вектора скорости v центра масс КА на оси инерциальной системы координат X могут быть найдены через вариации δu_j ( j = 0, 1, 2, 3) KS-переменных u_j и вариации $\delta u_{j}^{'} = \delta {{s}_{j}}$ их первых производных $u_{j}^{'} = {{s}_{j}}$ по формулам

Используя формулы (3.5) и (2.12), получаем выражения (3.6) или (3.7) для нахождения вариаций $\delta {{{v}}_{k}}$ через вариации δu_j и $u_{j}^{'} = {{s}_{j}}$:

где

В кватернионной записи соотношения (3.6) и (3.7) принимают вид соотношений (2.9) и (2.10) соответственно:

где $\delta {{{\mathbf{v}}}_{x}} = \delta {{v}_{1}}{\mathbf{i}} + \delta {{v}_{2}}{\mathbf{j}} + \delta {{v}_{3}}{\mathbf{k}}$ – отображение вариации вектора скорости v на инерциальный базис X, ${\mathbf{s}} = {\mathbf{u}}{\kern 1pt} '$, $\delta {\mathbf{s}} = \delta {\mathbf{u}}{\kern 1pt} '$.

Отметим, что скалярная часть суммы кватернионных произведений в соотношениях (3.9) и (3.10) равна нулю:

в силу билинейного соотношения (2.8).

Поэтому

Для круговой орбиты, когда модуль радиус-вектора КА r = const, вариация δr = 0. Соотношения (3.9) и (3.10) упрощаются и принимают вид

4. Решения регулярных кватернионных уравнений орбитального движения КА в вариациях для эллиптического кеплеровского движения в KS-переменных и изохронные производные. Получим соотношения, позволяющие изучать и оценивать влияние изменений начальных условий движения КА на изменения текущих характеристик его движения для текущего момента времени, используя описание движения центра масс КА в KS-переменных. Другими словами, найдем вариации δu_j(τ) ( j = 0, 1, 2, 3) KS-переменных u_j и вариации $\delta u_{j}^{'}\left( \tau \right) = \delta {{s}_{j}}\left( \tau \right)$ их первых производных $u_{j}^{'} = {{s}_{j}}$ для фиксированного времени τ по вариациям δu_j(τ₀) и $\delta u_{j}^{'}\left( {{{\tau }_{0}}} \right) = \delta {{s}_{j}}\left( {{{\tau }_{0}}} \right)$ этих переменных для начального момента времени τ₀ в случае эллиптического кеплеровского движения КА.

Для решения этой задачи воспользуемся прямым путем – варьированием кватернионных конечных соотношений, описывающих общее решение кватернионных регулярных дифференциальных уравнений движения центра масс КА в KS-переменных для его невозмущенного кеплеровского движения

получающихся из уравнений (1.9) в случае невозмущенного кеплеровского движения КА (при отсутствии возмущающего ускорения центра масс КА, когда кватернион q = 0).

В скалярной записи эти уравнения имеют следующий вид:

(получаются из уравнений (2.4) и (2.5) при q_j = 0).

В случае движения КА по эллиптической орбите, когда кеплеровская энергия h < 0, кватернионное уравнение системы уравнений (4.1) принимает вид уравнений движения одночастотного четырехмерного гармонического осциллятора. Общее решение системы (4.1) или (4.2) имеет вид

Переменные u и ${\mathbf{s}} = {\mathbf{u}}{\kern 1pt} '$ в этом случае – гармонические функции переменной τ, k – частота осциллятора.

Отметим, что в случае круговой орбиты время t и фиктивное время τ связаны прямо пропорциональной зависимостью: t = rτ.

Соотношения (4.3) запишем также в виде

Запишем кватернионные соотношения (4.6) (общее решение системы (4.1)) в скалярном виде

Вариации δu_j(τ) ( j = 0, 1, 2, 3) KS-переменных u_j и вариации $\delta u_{j}^{'}(\tau ) = \delta {{s}_{j}}(\tau )$ их первых производных $u_{j}^{'} = {{s}_{j}}$ для фиксированного времени τ могут быть найдены по вариациям δu_j(τ₀) и $\delta u_{j}^{'}({{\tau }_{0}}) = \delta {{s}_{j}}({{\tau }_{0}})$ этих переменных, а также по вариации $\delta {{h}_{0}}$ кеплеровской энергии h для начального момента фиктивного времени τ₀ = 0 в случае эллиптического кеплеровского движения КА, описываемого соотношениями (4.7), по формулам

где ${{u}_{{j0}}} = {{u}_{j}}({{\tau }_{0}}) = {{u}_{j}}(0)$, ${{s}_{{j0}}} = {{s}_{j}}({{\tau }_{0}}) = {{s}_{j}}(0)$, ${{h}_{0}} = h({{\tau }_{0}}) = h(0)$.

Подставляя соотношения (4.7) в формулы (4.8) и (4.9), получаем следующие соотношения для нахождения вариаций KS-переменных и их первых производных для фиксированного времени τ по вариациям этих переменных для начального момента времени τ₀ = 0 в случае эллиптического кеплеровского движения КА:

В кватернионной записи формулы (4.10) и (4.11) принимают вид

где ${{{\mathbf{u}}}_{0}} = {\mathbf{u}}({{\tau }_{0}}) = {\mathbf{u}}(0)$, ${{{\mathbf{s}}}_{0}} = {\mathbf{s}}({{\tau }_{0}}) = {\mathbf{s}}(0)$, частота k определяется формулой (4.5).

Соотношения (4.10), (4.11) или (4.12), (4.13) – решение уравнений орбитального движения КА в вариациях KS-переменных и их первых производных для эллиптического кеплеровского движения КА. В этом решении постоянные интегрирования определены для начального момента времени τ₀ = 0.

В матричной записи это решение принимает вид

где E – единичная матрица размерами 4 × 4, а $\delta {\mathbf{u}}$, $\delta {\mathbf{s}}$; $\delta {{{\mathbf{u}}}_{0}}$, $\delta {{{\mathbf{s}}}_{0}}$ и ${{{\mathbf{u}}}_{0}}$, ${{{\mathbf{s}}}_{0}}$ – четырехмерные вектор-столбцы с элементами $\delta {{u}_{j}}$, $\delta {{s}_{j}}$; $\delta {{u}_{{j0}}}$, $\delta {{s}_{{j0}}}$ и ${{u}_{{j0}}}$, ${{s}_{{j0}}}$, соответственно.

Отметим, что слагаемые в соотношениях (4.12) и (4.13) или в (4.14), содержащие в качестве множителей величины $\tau \sin (k\tau )$ и $\tau \cos (k\tau )$ перед вариацией δh кеплеровской энергии h, показывают, что при неточном задании кеплеровской энергии h (при наличии ее вариации δh) вариации $\delta {\mathbf{u}}$ и $\delta {\mathbf{s}}$ KS-переменных и их первых производных для эллиптического кеплеровского движения КА растут во времени τ и, следовательно, вариации $\delta {\mathbf{u}}$ и $\delta {\mathbf{s}}$ неустойчивы в смысле Ляпунова во времени τ. При отсутствии вариации δh (при точном задании кеплеровской энергии h) эта неустойчивость исчезает (в этом случае вариации $\delta {\mathbf{u}}$ и $\delta {\mathbf{s}}$ ведут себя как гармонические функции времени τ). Известно, что движение материальной точки в ньютоновском гравитационном поле по эллиптической траектории неустойчиво по отношению к декартовым координатам (показано еще Ляпуновым) в смысле Ляпунова. Также известно, что неустойчивость по декартовым координатам развивается быстрее, чем неустойчивость по KS-переменным.

Решение (4.14) можно также записать в другой матричной форме

где матричный элемент ${{0}_{4}} = (\begin{array}{*{20}{c}} 0&0&0&0 \end{array})$,

В соответствии с формулами (4.15) и (4.16) матрица изохронных производных в KS-переменных и их первых производных для эллиптического кеплеровского движения КА имеет следующий вид (при отсутствии вариации времени τ):

С использованием формул (3.3), (3.4) и (3.9) (или (3.8), (3.10)) находятся вариации декартовых координат КА и проекций его орбитальной скорости через вариации KS-переменных их первых производных для эллиптического кеплеровского движения.

5. Изохронные производные в KS-переменных и их первых производных для эллиптического кеплеровского движения: учет вариации фиктивного времени. Общее решение (4.6) системы дифференциальных уравнений (4.1) орбитального движения КА по эллиптической орбите в KS-переменных запишем с учетом начальных условий при τ₀ = 0 (t = 0) в следующем виде:

Здесь

Физическое время t выражается через фиктивное время τ и начальные значения KS-переменных u_j и их первых производных $u_{j}^{'} = {{s}_{j}}$ по фиктивному времени по формуле (4.4), которую запишем в следующем виде:

где $\left( {{\mathbf{u}}(0),{\mathbf{s}}(0)} \right) = {\text{scal}}\left( {{\mathbf{u}}(0) \circ {\mathbf{\bar {s}}}(0)} \right)$ – скалярное произведение четырехмерных векторов u(0) и s(0).

Согласно (5.4) физическое время $t = t(\tau ,{\mathbf{u}}(0),{\mathbf{s}}(0),h(0))$. Следовательно, фиктивное время $\tau = \tau (t,{\mathbf{u}}(0),{\mathbf{s}}(0),h(0))$.

Между переменными u_j и s_j во все время движения имеет место следующая связь (билинейное соотношение):

Таким образом, между переменными u, s и h во все время движения имеют место соотношения (5.2) и (5.5).

Уравнение (5.4) легко решается численно относительно τ по заданным t, ${\mathbf{u}}(0)$, ${\mathbf{s}}(0)$, так как зависимость от времени t монотонная. Тогда в любой момент t определяются переменные u и s по формулам (5.1), а по их значениям – положение в декартовых координатах и скорость КА в этот момент времени по формулам (1.11) и (2.10).

5.1. Вариации для KS-переменных, их первых производных и времени t по всем вариациям переменных u(0), s(0), h(0) и времени τ. Вариации δu, δs и δt для KS-переменных, их первых производных и времени t находятся по всем вариациям δu(0), δs(0), δh(0) и δτ переменных u(0), s(0), h(0) и “времени” τ из соотношений (5.1) и (5.4) и имеют следующий вид:

Введем обозначения A(τ) и D(τ) для двух скалярных и обозначения B(τ), C(τ), E_u(τ), E_s(τ) для четырех кватернионных функций:

С учетом обозначений (5.9)–(5.14) соотношения (5.6)–(5.8) для вариаций δu, δs и δt KS-переменных, их первых производных и времени t записываются в следующем виде:

5.2. Вычисление изохронных производных от KS-переменных. Для вычисления изохронных производных в соотношении (5.17) положим δt = 0. Из полученного соотношения определяется δτ:

Вариация фиктивного времени δτ, которая определяется по формуле (5.18), показывает изменение фиктивного времени за счет изменения начальных условий u(0), s(0) и h(0) на величины δu(0), δs(0) и δh(0), при котором физическое время, определяемое формулой (5.4), в первом приближении не изменяется, т.е.

Если выражение (5.18) для вариации δτ фиктивного времени подставить в соотношения (5.15) и (5.16), записывая скалярные произведения кватернионов, заключенные в круглые скобки, через суммы произведений соответствующих компонент кватернионов, и выделить в них коэффициенты при компонентах вариаций δu(0), δs(0) и при вариации δh(0), то эти коэффициены будут определять изохронные производные от KS-переменных и их первых производных по компонентам кватернионов u(0), s(0) и по энергии h(0), имеющие вид

Здесь ${{\sigma }_{{ij}}}$ – символ Кронекера: ${{\sigma }_{{ij}}}$ = 1, если i = j и ${{\sigma }_{{ij}}}$ = 0, если i ≠ j.

Отметим, что между вариациями δh(0) и δu(0), δs(0) имеется связь, которая в соответствии с соотношением (5.3), имеет вид

Кроме того, между вариациями δu(0) и δs(0) имеется связь, получаемая из соотношения (5.5) и имеющая вид

5.3. Вычисление приращений KS-переменных. Вычисление приращений $\delta {{u}_{j}}$, $\delta {{s}_{j}}$ KS-переменных в момент времени t за счет их приращений $\delta {{u}_{j}}(0)$, $\delta {{s}_{j}}(0)$ в начальный момент времени через изохронные производные, определяемые соотношениями (5.19)–(5.21), будет производиться по формулам

Гораздо проще после того, как вычислено δτ по формуле (5.18), вычислить приращения KS-переменных по формулам (5.6) и (5.7) или (5.15) и (5.16) без вычисления изохронных производных. После того, как вычислено δτ по формуле (5.18), можно вычислить значения KS-переменных при измененных начальных условиях по формулам (5.1)–(5.3), заменив в них u(0) на u(0) + δu(0), s(0) на s(0) + δs(0), h(0) на h(0) + δh(0), τ на τ + δτ.

Несмотря на то, что δh(0) выражается через δu(0) и δs(0) по формуле (5.22), нет необходимости исключать h(0) из числа аргументов кватернионных переменных u и s. Первый дифференциал функции многих переменных обладает свойством инвариантности относительно зависимости между аргументами функции. Исключение h(0) усложнит выражения для изохронных производных, так как в этом случае в производные

войдут в качестве основных частей выражения для δh(0).

6. Кватернионные дифференциальные уравнения орбитального движения в вариациях KS-переменных, их первых производных, а также в вариациях кеплеровской энергии и времени. Линеаризованные дифференциальные регулярные кватернионные уравнения возмущенного орбитального движения КА в вариациях δu и δs KS-переменных и их первых производных по времени $\tau $, а также уравнения в вариациях $\delta h$ и $\delta t$ кеплеровской энергии и времени t, обусловленные вариациями начальных условий и действующего возмущающего ускорения, получаются из уравнений (2.9) и имеют вид

Здесь

$\delta {{{\mathbf{p}}}_{x}}$ – вариация возмущающего ускорения p, которая обусловлена вариациями переменных $t,{\mathbf{u}},{\mathbf{s}}$ и зависит от конкретного вида действующих возмущений.

При отсутствии возмущающего ускорения p уравнения возмущенного орбитального движения КА в вариациях (6.1) принимают вид

Формулы (4.12) и (4.13) для вариаций KS-переменных их первых производных для фиксированного времени τ по вариациям этих переменных для начального момента времени τ₀ = 0 в случае эллиптического кеплеровского движения КА получаются интегрированием первого кватернионного дифференциального уравнения из этих уравнений при $h = \operatorname{const} $, $\delta h = \delta {{h}_{0}}$.

7. Регулярные кватернионные дифференциальные уравнения возмущенного орбитального движения космического аппарата с использованием в качестве независимой переменной половинной обобщенной эксцентрической аномалии. Для решения задач прогноза и коррекции орбитального движения космического аппарата целесообразно также использовать регулярные кватернионные уравнения орбитального движения, в которых в качестве независимой переменной используется переменная $\tau {\kern 1pt} *$. Эта переменная равна половинной обобщенной эксцентрической аномалии и определяется дифференциальными соотношениями

Получены следующие различные дифференциальные регулярные кватернионные уравнения орбитального движения КА с использованием независимой переменной $\tau {\kern 1pt} *$.

Первая форма уравнений:

Вторая форма уравнений:

Третья форма уравнений:

Здесь, по-прежнему, возмущение ${\mathbf{q}} = - {\mathbf{i}} \circ {\mathbf{u}} \circ {{{\mathbf{p}}}_{x}}$.

Для невозмущенного эллиптического кеплеровского движения КА кватернион возмущения q = 0 и основное дифференциальное кватернионное уравнение орбитального движения центра масс КА принимает во времени $\tau {\kern 1pt} *$ вид уравнения движения четырехмерного одночастотного гармонического осциллятора

частота колебаний которого в безразмерном времени $\tau {\kern 1pt} *$ равна 1.

Для движения по круговой орбите расстояние r и кеплеровская энергия h – постоянные величины. Поэтому время t и новое время $\tau {\kern 1pt} *$ связаны прямо пропорциональной зависимостью

С другой стороны для круговой орбиты

где E – эксцентрическая аномалия.

Поэтому для круговой орбиты $\tau {\kern 1pt} * = E{\text{/}}2$, то есть, новое время $\tau {\kern 1pt} *$ для круговой орбиты равно половинной эксцентрической аномалии E.

В новом времени $\tau {\kern 1pt} *$ эллиптическое кеплеровское движение центра масс КА описывается кватернионными соотношениями

где ${\mathbf{u}}(0)$ и ${{\left( {\frac{{d{\mathbf{u}}}}{{d\tau {\kern 1pt} *}}} \right)}_{0}}$– значение кватернионов ${\mathbf{u}}$ и $\frac{{d{\mathbf{u}}}}{{d\tau {\kern 1pt} *}}$ при $\tau {\kern 1pt} * = 0$.

Вариации δu и δs для KS-переменных и их первых производных в безразмерном времени $\tau {\kern 1pt} *$ (с учетом вариации $\delta \tau {\kern 1pt} *$ этого времени) имеют вид

где ${\mathbf{s}}{\kern 1pt} *{\kern 1pt} \left( {\tau {\kern 1pt} *} \right) = \frac{{d{\mathbf{u}}\left( {\tau {\kern 1pt} *} \right)}}{{d\tau {\kern 1pt} *}}$.

Эти вариации формально имеют более простой вид в сравнении с вариациями δu и δs во “времени” τ (5.6) и (5.7), однако следует иметь в виду, что выражение для вариации $\delta \tau {\kern 1pt} *$ гораздо сложнее выражения для вариации $\delta \tau $, присутствующей в вариациях δu и δs во времени τ.

Вместо переменных u и ${\mathbf{s}}{\kern 1pt} *$ для решения задач прогноза и коррекции орбитального движения космического аппарата можно также использовать кватернионные дифференциальные уравнения в кватернионных оскулирующих (медленно изменяющихся) переменных α и β.

Для их вывода используем метод вариации постоянных. Запишем решение первого кватернионного дифференциального уравнения орбитального движения КА из системы уравнений (7.1) в следующем виде:

где α и β – новые кватернионные переменные.

Продифференцируем это соотношение по времени $\tau {\kern 1pt} *$:

Потребуем, чтобы выражение в скобках было равно нулю:

Тогда предпоследнее выражение приводит к тому же результату, что и в случае постоянных α и β.

Используя соотношения

как формулы замены кватернионных переменных u и ${\mathbf{s}}{\kern 1pt} *$ на новые кватернионные переменные α и β, получим из первого кватернионного дифференциального уравнения системы уравнений (7.1) следующую систему кватернионных дифференциальных уравнений в регулярных кватернионных элементах α и β и в безразмерном времени $\tau {\kern 1pt} *$: где возмущение ${\mathbf{q}} = - {\mathbf{i}} \circ {\mathbf{u}} \circ {{{\mathbf{p}}}_{x}}$, кватернионы ${\mathbf{u}}$ и $d{\mathbf{u}}{\text{/}}d\tau {\kern 1pt} *$ определены в новых переменных соотношениями (7.2).

Кватернионные оскулирующие переменные α и β находятся через переменные u и ${\text{s}}{\kern 1pt} * = d{\mathbf{u}}{\text{/}}d\tau {\kern 1pt} *$ по формулам

Отметим, что дифференциальные уравнения (7.3) в регулярных кватернионных оскулирующих элементах α и β справедливы для возмущенного эллиптического кеплеровского движения центра масс КА.

Заключение. В статье получены основные уравнения и соотношения, необходимые для решения задач прогноза и коррекции орбитального движения КА с использованием регулярных кватернионных уравнений орбитального движения КА в KS-переменных и соответствующих им уравнений в вариациях. Была обоснована перспективность такого подхода к решению задач прогноза и коррекции орбитального движения.

Рассмотрены известные, предложенные нами ранее, регулярные кватернионные уравнения возмущенной пространственной задачи двух тел и регулярные кватернионные уравнения орбитального движения КА в четырехмерных KS-переменных, построенные на основе этих уравнений. Уравнения орбитального движения КА включают дифференциальные уравнения второго порядка относительно четырехмерных KS-переменных u_j осцилляторного типа, имеющие в случае возмущенного эллиптического кеплеровского движения вид дифференциальных уравнений движения возмущенного четырехмерного одночастотного гармонического осциллятора, квадрат частоты которого равен половине кеплеровской энергии h, взятой со знаком минус, а также включают дифференциальные уравнения первого порядка относительно кеплеровской энергии и реального времени t.

Приведены результаты нашего сравнительного исследования точности численного интегрирования классических ньютоновских уравнений пространственной ограниченной задачи трех тел (Земля, Луна и космический аппарат) в декартовых координатах и предложенных нами регулярных кватернионных уравнений этой задачи в KS-переменных. Точность численного интегрирования регулярных кватернионных уравнений в KS-переменных оказалась значительно выше точности численного интегрирования уравнений в декартовых координатах: для круговой орбиты точность оказалась выше на два порядка, для возмущенных эллиптических орбит со средним эксцентриситетом – на четыре порядка, для возмущенной эллиптической орбиты с высоким эксцентриситетом – на семь порядков. Эти результаты согласуются с результатами, приведенными в книге Бордовицыной [4], где приводится другая (каноническая) форма регулярных уравнений в KS-переменных, выведенных с использованием соответствующего гамильтониана, и результаты точности их численного интегрирования. Наши результаты численного исследования говорят о перспективности использования регулярных кватернионных уравнений орбитального движения в KS-переменных для решения задач прогноза и коррекции орбитального движения КА.

Получены формулы, устанавливающие связи вариаций δx_k и $\delta {{{v}}_{k}}$ декартовых координат и проекций вектора скорости центра масс КА в инерциальной системе координат с вариациями δu_j и δs_j KS-переменных u_j и их первых производных s_j = du_j/dτ по новому (“фиктивному”) времени τ.

Найдены прямым путем вариации δu_j, δs_j и δt KS-переменных u_j, их первых производных s_j и времени t для фиксированного времени τ по вариациям δu_j(0), δs_j(0), δh(0) и δτ переменных u_j(0), s_j(0), кеплеровской энергии h(0) и времени τ для начального момента времени τ(0) = 0 (как без учета, так и с учетом вариации времени τ). Найдены также матрицы изохронных производных от KS-переменных u_j, их первых производных s_j и кеплеровской энергии h по компонентам u_j(0) и s_j(0) регулярных кватернионных переменных u(0), s(0) и по энергии h(0) для эллиптического кеплеровского движения КА.

Получены линеаризованные дифференциальные регулярные кватернионные уравнения возмущенного орбитального движения КА в вариациях δu и δs KS-переменных и их первых производных по времени $\tau $, а также дифференциальные уравнения в вариациях $\delta h$ и $\delta t$ кеплеровской энергии и реального времени, обусловленные вариациями начальных условий и вариацией действующего возмущающего ускорения. Формулы (4.12) и (4.13) для вариаций KS-переменных, их первых производных для фиксированного времени τ по вариациям этих переменных для начального момента времени τ₀ = 0 в случае эллиптического кеплеровского движения КА получаются интегрированием первого кватернионного уравнения из этих полученных уравнений в случае, когда $h = {\text{const}}$, $\delta h = \delta {{h}_{0}}$.

Получены также для решения задач прогноза и коррекции орбитального движения КА другие различные регулярные кватернионные дифференциальные уравнения орбитального движения, в которых в качестве независимой переменной используется безразмерное время $\tau {\kern 1pt} *$. Эта переменная равна половинной обобщенной эксцентрической аномалии E. Для невозмущенного эллиптического кеплеровского движения основное дифференциальное кватернионное уравнение орбитального движения центра масс КА принимает во времени $\tau {\kern 1pt} *$ вид уравнения движения четырехмерного одночастотного гармонического осциллятора, частота колебаний которого в этом безразмерном времени $\tau {\kern 1pt} *$ равна 1.

Получены вариации δu и δs для KS-переменных и их первых производных в безразмерном времени $\tau {\kern 1pt} *$ (с учетом вариации $\delta \tau {\kern 1pt} *$ этого времени). Построена система кватернионных дифференциальных уравнений орбитального движения КА в регулярных кватернионных оскулирующих элементах α и β с использованием в качестве независимой переменной безразмерного времени $\tau {\kern 1pt} *$. Эти уравнения справедливы для возмущенного эллиптического кеплеровского движения центра масс КА.

Полученные уравнения и соотношения позволяют изучать и оценивать влияние изменений начальных условий движения КА и действующих возмущений на изменение текущих характеристик его движения для текущего момента времени, а также позволяют эффективно решать задачи прогноза и коррекции орбитального движения КА, используя описание движения центра масс КА в регулярных KS-переменных и в соответствующих им кватернионных переменных, а также в кватернионных оскулирующих элементах.

Этому способствуют следующие достоинства уравнений Кустаанхеймо–Штифеля и предложенных нами регулярных кватернионных уравнений орбитального движения КА:

• регулярность в центре притяжения (в отличие от нерегулярных ньютоновских уравнений);

• линейность для невозмущенных кеплеровских движений (в отличие от существенно нелинейных ньютоновских уравнений) (в этом случае кватернионные уравнения имеют вид системы четырех независимых линейных дифференциальных уравнений второго порядка с одинаковыми постоянными коэффициентами, равными отрицательной половинной кеплеровской энергии h при использовании безразмерной независимой переменной τ или равными 1, при использовании безразмерной независимой переменной $\tau {\kern 1pt} *$ (половинной обобщенной эксцентрической аномалии);

• возможность выработать единый подход к изучению всех трех типов кеплеровского движения;

• близость к линейным уравнениям для возмущенных кеплеровских движений;

• возможность представить правые части дифференциальных уравнений движения небесных и космических тел в полиномиальной форме, удобной для их решения с помощью ЭВМ.

Линейность кватернионных уравнений (2.9) для кеплеровских движений позволила нам эффективно построить новые регулярные кватернионные уравнения орбитального движения в кватернионных оскулирующих элементах (медленно изменяющихся переменных), удобные для исследования и прогноза возмущенного движения космических тел и аппаратов.