Прикладная математика и механика, 2023, T. 87, № 2, стр. 157-175
Асимптотики длинных стоячих волн в одномерных бассейнах с пологими берегами: теория и эксперимент
С. Ю. Доброхотов 1, *, В. А. Калиниченко 1, **, Д. С. Миненков 1, ***, В. Е. Назайкинский 1, ****
1 Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
* E-mail: s.dobrokhotov@gmail.com
** E-mail: vakalin@mail.ru
*** E-mail: minenkov.ds@gmail.com
**** E-mail: nazaikinskii@yandex.ru
Поступила в редакцию 28.11.2022
После доработки 03.02.2023
Принята к публикации 03.02.2023
- EDN: TZCFHT
- DOI: 10.31857/S0032823523020066
Аннотация
В статье построены периодические по времени асимптотические решения одномерной нелинейной системы уравнений мелкой воды в бассейне переменной глубины $D(x)$ с двумя пологими берегами (что означает обращение в нуль функции $D(x)$ в точках, задающих берег) или с одним пологим берегом и вертикальной стенкой. Такие решения описывают стоячие волны, аналогичные известным волнам Фарадея в бассейнах с вертикальными стенками. В частности, они приближенно описывают сейши в протяженных бассейнах. Конструкция таких решений состоит из двух этапов. Сначала определяются гармонические по времени точные и асимптотические решения линеаризованной системы, порожденные собственными функциями оператора $d{\text{/}}dxD(x)d{\text{/}}dx$, а затем с помощью недавно развитого подхода, основанного на упрощении и модификации преобразования Кэрриера–Гринспена, по ним в параметрической форме восстанавливаются решения нелинейных уравнений. Полученные асимптотические решения сравниваются с результатами эксперимента, основанного на возбуждении волн в бассейне с помощью параметрического резонанса.
1. Введение. Нелинейная система уравнений мелкой воды [1–4] описывает длинные необрушающиеся волны различной природы, включая волны в бассейнах ограниченных размеров. В случае протяженных бассейнов можно ограничиться одномерной по пространственной переменной $x$ системой, которая в простейшем случае имеет вид
(1.1)
$\begin{gathered} {{\eta }_{t}} + {{((D(x) + \eta )u)}_{x}} = 0,\quad {{u}_{t}} + g{{\eta }_{x}} + u{{u}_{x}} = 0 \hfill \\ \end{gathered} $Здесь неизвестными функциями являются возвышение свободной поверхности $\eta $ и горизонтальная компонента $u$ скорости потока, $g$ – ускорение свободного падения, а функция $D(x)$ описывает глубину дна. Будем считать, что $D(x)$ – гладкая функция. При наличии наклонных берегов функция $D(x)$ обращается в нуль в некоторых точках $x = a$ и $x = b$, определяющих границу бассейна в отсутствие возмущений; в точках, где $D(x) > 0$, решения описывают волны внутри бассейна, а при $D(x) < 0$ – набегание на берег. Система (1.1) рассматривается на переменном интервале ${{\Omega }_{t}} = (a(t),b(t))$, границы которого $a(t)$ и $b(t)$ определяются соотношениями
Система мелкой воды хорошо моделирует такие явления как цунами (см. [1, 4, 5]) и сейши (см. [2, 6–8], недавний обзор [9] и анализ натурных данных, напр., [10–12])), причем одномерную систему можно рассматривать для волн в вытянутых водоемах, как например озеро Байкал. Исследованию подобных волн и посвящена данная статья.
Для постановки корректной задачи к уравнениям (1.1) и условиям (1.2) следует добавить, например, начальные условия для функций $\eta $ и $u$ или условия периодичности по времени $t$. В последнем случае построенные решения являются нелинейными аналогами гармонических колебаний линеаризованной системы мелкой воды
эквивалентной волновому уравнениюЛинеаризованные уравнения задаются на фиксированном интервале $[a,b]$, на концах которого волновая скорость $c{{(x)}^{2}} = gD(x)$ вырождается. Для таких уравнений не требуются обычные граничные условия типа Дирихле или Неймана [13], вместо которых налагается естественное условие ограниченности интеграла энергии [14–16]
(1.5)
$E_{{{\text{sw}}}}^{2} = {{\left\| {g\eta } \right\|}^{2}} + {{\left\| {c(x)u} \right\|}^{2}} < \infty ,\quad {\text{или}}\quad E_{{{\text{wave}}}}^{2} = {{\left\| {{{\eta }_{t}}} \right\|}^{2}} + {{\left\| {c(x){{\eta }_{x}}} \right\|}^{2}} < \infty $Гармонические по времени $t$ решения уравнения (1.3) имеют вид
(1.6)
$\eta (x,t) = {v}(x)\cos (\omega t),\quad u(x,t) = - \frac{g}{\omega }{v}{\kern 1pt} '(x)\sin (\omega t),$Вопрос об асимптотических собственных функциях оператора $\hat {L}$ детально обсуждался в статье [17], где для них также построены явные формулы, которые будут использованы ниже.
Подчеркнем, что поскольку далее рассматриваются необрушающиеся волновые решения нелинейных уравнений, их амплитуда предполагается малой. Формально эту малость будем характеризовать безразмерным малым параметром $\varepsilon $ и считать, что $\eta = O(\varepsilon )$, $u = O(\varepsilon )$. Такое предположение естественно, поскольку, например, большая часть цунами не обрушается [5] и тем более отсутствие обрушения характерно для сейшей [10–12]. Возникает идея, что изучаемые задачи можно решать с помощью теории возмущений, стартуя с линейного приближения. Применение теории возмущений оказывается нетривиальным, поскольку исходная задача – это задача с подвижной границей. Отметим также, что просто ограничиться решением линеаризованного уравнения в рассматриваемой ситуации нельзя, поскольку наиболее интересные эффекты в поведении волн в окрестности берега линейная задача не описывает. Также нужно отметить, что, как правило, амплитуда решения в окрестности береговой линии оказывается существенно больше, чем внутри бассейна, поскольку береговая линия представляет собой “нестандартную” каустику (в одномерном случае – фокальную точку). В работе [18] с помощью замены переменных, основанной на использовании параметрически заданных функций и мотивированной известным в одномерном случае преобразованием Кэрриера–Гринспена [19], эта задача (как в одномерном, так и в двумерном случае) сведена к задаче с неподвижной границей (в одномерном случае – на отрезке $[a,b]$), в которой уже можно применять идеи стандартной теории возмущений. При этом алгоритм нахождения наиболее интересной с точки зрения приложений главной части решения становится очень эффективным и состоит из двух шагов:
1) построение решения (возможно, приближенного) линеаризованной задачи, которое достаточно хорошо работает во внутренних точках бассейна;
2) восстановление приближенного решения нелинейной задачи по решению линеаризованной задачи в окрестности береговой линии с помощью соответствующей обратной замены.
Под “приближенным решением” нелинейной задачи понимается пара, состоящая из вектор-функции $(\eta ,{v})$ и переменной области ее определения, такая, что на границе области выполнены условия (1.2), а внутри области подстановка функции в уравнения (1.1) дает малую невязку (строгое определение такого формального асимптотического решения дано в [18]).
Построение решений линеаризованной системы нетривиально, из-за вырождения на границе скорости $c = \sqrt {gD} $. Ее точные решения удается найти в исключительных случаях, например, для линейной и квадратичной функции $D(x)$. Следовательно, для линеаризованной системы речь может идти о приближенных (асимптотических), как правило, быстроменяющихся решениях. Поэтому возникает вопрос о применимости теории возмущений по нелинейности в том случае, если в качестве нулевого приближения выступает асимптотическое решение линеаризованной системы. Фактически речь идет о построении асимптотических решений, зависящих от двух параметров, один из которых, $\varepsilon $, характеризует амплитуду решения, а второй, $\mu $, – скорость изменения решения (причем числа $a,b$ от этих параметров не зависят). Применимость развитого в [18] подхода и основанного на нем практического алгоритма зависит от соотношения между указанными параметрами. Этот вопрос обсудим на примере периодических по времени и быстроосциллирующих по пространственной переменной решений, которые не только, как уже говорилось выше, моделируют сейши в протяженных бассейнах, но и удобны для сравнения с экспериментом, поскольку в Институте проблем механики им. А.Ю. Ишлинского РАН имеется экспериментальная установка [20, 21], которая благодаря параметрическому резонансу воспроизводит стоячие волны на свободной поверхности жидкости в сосуде – волны Фарадея (см. [22–25]).
Наряду с задачей о волнах в бассейне с двумя наклонными берегами, рассмотрим задачу, когда с одной стороны бассейн вместо наклонного берега ограничен вертикальной стенкой. В этом случае вместо условий (1.2) ставятся условия
Основная цель данной работы – применение (и иллюстрация) развитого в [18] подхода к сформулированным выше задачам в одномерном случае и сравнение полученных решений с результатами эксперимента.
Статья организована следующим образом. Сначала в разд. 2 для случая плоского наклонного дна кратко напомним преобразование Кэрриера–Гринспена, представленное в форме [26], и представим его приближенную модификацию, а также сравним точное решение нелинейной задачи с асимптотиками. В разд. 3 рассмотрены примеры, когда линеаризованная задача в ограниченном бассейне решается точно (разд. 3.1 и 3.2), и случай произвольной функции дна (разд. 3.3), когда в линейном случае требуется построение асимптотик. В разд. 4 обсуждается эксперимент, сравниваются экспериментальные и аналитические результаты.
2. Конструктивная приближенная линеаризация одномерных нелинейных уравнений мелкой воды.
2.1. Преобразование Кэрриера–Гринспена. Для полноты изложения напомним в удобной для нас форме [26] (см. также [27, 28]) простые формулы, определяющие преобразование Кэрриера–Гринспена [19], сводящее одномерные нелинейные уравнения мелкой воды над наклонным дном $D(x) = \gamma x$ к линейному волновому уравнению. Всюду далее в линейной системе возвышение свободной поверхности и скорость обозначаются через $N$ и $U$, а координата и время – через $y$ и $\tau $.
Утверждение 1. Пусть $N(y,\tau )$, $U(y,\tau )$ – некоторое решение линеаризованной системы (1.3) с $D(x) = \gamma x$, и предположим, что замена переменных $(y,\tau ) \to (x,t)$:
(2.1)
$\begin{gathered} t = T(y,\tau ) \equiv \tau + \frac{1}{{\gamma g}}U,\quad x = X(y,\tau ) \equiv y - \frac{1}{\gamma }N + \frac{1}{{2\gamma g}}{{U}^{2}} \hfill \\ \end{gathered} $(2.2)
$\begin{gathered} J \equiv \frac{{\partial (x,t)}}{{\partial (y,\tau )}} = 1 - \frac{1}{\gamma }{{N}_{y}} + \frac{1}{{\gamma g}}({{U}_{\tau }} + {{N}_{\tau }}{{U}_{y}} - {{N}_{y}}{{U}_{\tau }} + U{{U}_{y}}) \hfill \\ \end{gathered} $Тогда параметрически заданные функции
(2.3)
$\eta = N(y,\tau ) - {{U}^{2}}(y,\tau ){\text{/}}2g,\quad u = U(y,\tau ),\quad t = T(y,\tau ),\quad x = X(y,\tau )$Отметим, что обратная к (2.3) замена имеет вид
(2.4)
$\tau = t - \frac{1}{{\gamma g}}u,\quad y = x + \frac{1}{\gamma }\eta ,\quad N = \eta + \frac{1}{{2g}}{{u}^{2}},\quad U = u$Формулы (2.3), (2.4) связывают точным точечным преобразованием одномерные линейную и нелинейную системы с наклонным дном $D = \gamma x$. В работах [29–31] этот результат обобщен на случай волн в каналах с “U” или “V”-образным сечением и равномерным изменением глубины, в недавней работе [32] представлены результаты для каналов произвольного сечения. Замена Кэрриера–Гринспена также послужила отправной точкой ряда работ, где исследуются приближенные решения в случае неровного дна. В одномерном случае в работе [33] рассмотрен численный алгоритм, когда вблизи берега осуществляется переход к римановым инвариантам, в [34] построены нелинейные асимптотики в предположении небольших изменений дна с использованием приближенной замены, в [35] авторы рассмотрели случай произвольного дна и построили приближенное решение с помощью упрощенной замены $y = x - a(t)$, где в главном члене $a(t) = N(0,t){\text{/}}D{\kern 1pt} '(0)$. В [36] для двумерного случая с функцией дна $D({{x}_{1}},{{x}_{2}}) = {{x}_{1}}$ для получения асимптотик использованы непосредственно формулы Кэрриера–Гринспена вдоль координаты, нормальной к береговой линии. Наконец, в [18] рассмотрен двумерный бассейн с функцией дна $D(x)$ общего вида, градиент которой не вырождается на границе области ($\nabla D(x) \ne 0$, когда $D(x) = 0$), и доказаны строгие утверждения касательно нелинейных асимптотик. На последние результаты мы и будем опираться в данной работе.
2.2. Модифицированное преобразование. Некоторая сложность реализации формул (2.3) состоит в их зависимости от скорости $U$, особенно при пересчете времени $\tau $ в $t$. С другой стороны, поскольку рассматриваются достаточно малые решения (для которых, в частности, невырождена замена (2.1)), естественно попытаться упростить формулы (2.1), (2.3), отбрасывая в их правых частях слагаемые наиболее высокого порядка малости, – а это слагаемые, содержащие $U$. Итак, упрощенные формулы имеют вид
(2.5)
$\eta = N(y,\tau ),\quad u = U(y,\tau ),\quad t = \tau ,\quad x = y - N(y,\tau ){\text{/}}\gamma \quad \Rightarrow $Выясним, какова эффективность такого подхода на примере точных решений двух типов.
1) Построенные в [26] решения вида набегающих на берег уединенных волн основаны на решениях линейного волнового уравнения (1.4) с $D(x) = \gamma x$ специального вида
(2.7)
$\begin{gathered} N(y,\tau ) = \varepsilon \gamma \mu \operatorname{Re} {{e}^{{i\theta }}}\left( {{{c}_{0}}\frac{{\tau - {{\tau }_{0}}}}{\mu } - i} \right){{\left[ {\frac{{4y}}{\mu } - {{{\left( {{{c}_{0}}\frac{{\tau - {{\tau }_{0}}}}{\mu } - i} \right)}}^{2}}} \right]}^{{ - 3/2}}} \\ U(y,\tau ) = 2\varepsilon {{c}_{0}}\operatorname{Re} {{e}^{{i\theta }}}{{\left[ {\frac{{4y}}{\mu } - {{{\left( {{{c}_{0}}\frac{{\tau - {{\tau }_{0}}}}{\mu } - i} \right)}}^{2}}} \right]}^{{ - 3/2}}} \\ \end{gathered} $Здесь $\mu $ – длина волны, $\varepsilon > 0$ – безразмерный малый параметр, отвечающий за амплитуду волны, ${{c}_{0}} = \sqrt {\gamma \mu g} $ – волновая скорость на расстоянии $\mu $ от берега, параметр $\theta $ влияет на форму профиля, а $t = {{\tau }_{0}}$ – время прихода волны на берег.
2) Решения вида стоячих волн [6, 7, 19] получаются из решений
(2.8)
$\begin{gathered} N(y,\tau ) = \varepsilon \gamma \mu \cos (\omega \tau ){{{\mathbf{J}}}_{0}}\left( {2\omega \sqrt {\frac{y}{{\gamma g}}} } \right),\quad U(y,\tau ) = \varepsilon {{c}_{0}}\sin (\omega \tau )\sqrt {\frac{\mu }{y}} {{{\mathbf{J}}}_{1}}\left( {2\omega \sqrt {\frac{y}{{\gamma g}}} } \right) \hfill \\ \end{gathered} $Сравнение точных решений нелинейной задачи, полученных из (2.7) и (2.8) преобразованием Кэрриера–Гринспена, с приближенными решениями, полученными параметрически заданным упрощенным преобразованием (2.5) или с помощью явного итерационного преобразования (2.10), показывает, что указанные преобразования дают в этих примерах достаточно хорошее приближение к точному решению (см. рис. 1, 2).
Рис. 1.
Сравнение точного решения нелинейной задачи с асимптотическим для бегущей волны (a) и сравнение графиков замены переменных (б). Используется решение (2.7) линейной задачи в безразмерных переменных (γ = 1, g = 1, μ = 1, c0 = 1), значения параметров: τ0 = 0, θ = –π/4, ε = 0.17, а графики построены для моментов времени t = –2, –1, 0, 1. Нелинейные решения отвечают замене Кэрриера–Гринспена (2.4) (серые кривые), а асимптотики – параметрической замене (2.5) (черные сплошные) и явной замене (2.10) с одной итерацией (черный пунктир). Соответствующие кривые для замены y =Y(x, t) изображены в момент времени t = 0. График замены (2.10) с двумя итерациями (серый пунктир на (б)) неотличим от параметрической замены.
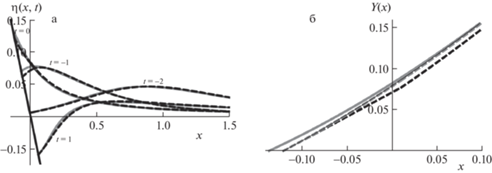
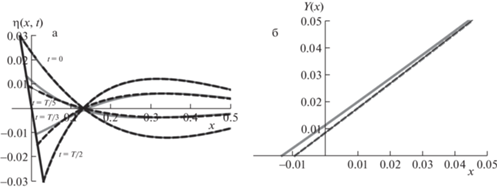
Рис. 2.
а: Сравнение точного решения нелинейной задачи с асимптотиками для стоячей волны и б: сравнение графиков замены переменных. Используется решение линейной задачи (2.8) в безразмерных переменных (γ = 1, g = 1, μ = 1, c0 = 1) при значениях параметров: ε = 0.03, ω = 3.3, T = 2πω–1 , в моменты времени t = 0, T/5, T/3 и T/2 . Нелинейные решения отвечают замене Кэрриера–Гринспена (2.4) (серые кривые), а асимптотики – параметрической замене (2.5) (черные сплошные) и явной замене (2.10) с одной итерацией (черный пунктир). Соответствующие кривые для замены y =Y(x,t) изображены в момент времени t =T/5. График замены (2.10) для одной итерации уже неотличим от параметрической замены.
Замена (2.5) хороша тем, что она легко обобщается на случай нелинейной функции $D(x)$ и на двумерный случай (в предположении, что на береговой линии $\nabla D \ne 0$). Именно, в этой замене следует заменить $x$ и $y$ соответственно на $D(x)$ и $D(y)$. При этом нужно учесть, что такую замену следует делать лишь в окрестности точек берега $a,b$, во внутренних точках она может не работать. Аккуратная реализация этого соображения состоит во введении гладкой срезающей функции $\rho (x)$, равной единице в окрестности берега и нулю вдали от берега, например, $\rho (x) = 1$ при $x - a < \delta $ или $b - x < \delta $, $\rho (x) = 0$ при $x - a > 2\delta $ и $b - x > 2\delta $, где $\delta $ – некоторое достаточно малое расстояние. В результате получается замена
(2.9)
$\eta = N(y,\tau ),\quad u = U(y,\tau ),\quad t = \tau ,\quad D(x) = D(y) - N(y,\tau )\rho (y),$Далее предлагается использовать замену вычислительно даже более простую, чем (2.9) – определяемую явно с помощью итерационных формул. Именно, в одномерном случае решение $y = Y(x,t)$ уравнения (2.9) можно искать следующим образом (в окрестности левого берега $y = a$):
(2.10)
$\begin{gathered} {{Y}_{0}} = \max \{ a + {{\delta }_{0}},x\} ,\quad {{Y}_{n}} - a = ({{Y}_{{n - 1}}} - a)\frac{{D(x) + N(a,t)}}{{D({{Y}_{{n - 1}}}) - \rho ({{Y}_{{n - 1}}})N({{Y}_{{n - 1}}},t) + N(a,t)}} \\ Y(x,t) = {{Y}_{n}}(x,t) + O\left( {{{{\left| {{{Y}_{n}} - x} \right|}}^{{n + 1}}}} \right), \\ \end{gathered} $Предложенная формула входит в рассмотренный в [18] класс замен, и из результатов [18] вытекает следующее утверждение. Пусть параметр $\varepsilon \to 0 + $ характеризует амплитуду решения линеаризованной системы: $N(y,t) = O(\varepsilon )$, $U(y,t) = O(\varepsilon )$.
Утверждение 2. При достаточно малом $\varepsilon $ функции $\eta (x,t)$, $u(x,t)$, полученные из точного решения линеаризованной задачи (например, (2.7) или (2.8)) посредством обратной параметрической замены (2.9) (или явной (2.10)), определяют главный член формального асимптотического решения системы (1.1), (1.2).
На рис. 1 рассматривается случай полубесконечной области и плоского наклонного дна, для которого нелинейные асимптотики сравниваются с точными решениями нелинейной задачи, полученными с помощью замены Кэрриера–Гринспена (2.4). Как видно из графика, асимптотики, полученные с помощью параметрической и явной замены практически не отличаются уже для первой итерации ${{Y}_{1}}(x)$. Также можно видеть, что асимптотики довольно хорошо совпадают с точным решением, а отклонения связаны в первую очередь с тем, что не учитываются поправки по времени, т.е. профиль точного решения практически точно повторяется асимптотикой, но в слегка измененный момент времени.
Замечание 1. Замена Кэрриера–Гринспена (2.3) корректно определена, когда якобиан (2.2) не обращается в нуль. Это же условие гарантирует отсутствие обрушения решения нелинейной системы. “Упрощенная” замена (2.5) существует, когда не обращается в нуль якобиан ${{J}_{1}} = \partial x{\text{/}}\partial y$ = $1 - \gamma {{N}_{y}}$, что не совпадает с условием необрушения $J \ne 0$. Тем не менее, вырождение ${{J}_{1}}$ и $J$ происходит при одном и том же порядке отношения амплитуды $\varepsilon $ линейной волны к длине волны $\mu $. В частности, для стоячих волн (2.8) над плоским наклонным дном ${{J}_{1}}$ не вырождается при
Для бегущей волны (2.7) условие необрушения можно получить аналогично [37].
В случае неровного дна $D(x)$ для точного условия необрушения эффективные формулы нам не известны, но естественно ожидать, что обрушение происходит при примерно тех же соотношениях амплитуды и длины волны, при которых вырождается замена (2.9) ${{J}_{2}}: = \partial x{\text{/}}\partial y$ = 0, что вблизи берега равносильно условию $D{\kern 1pt} '(y)$ – ${{N}_{y}}(y,t)$ = 0.
3. Асимптотические решения типа стоячих волн в ограниченном бассейне. В предыдущем пункте были построены некоторые точные решения системы уравнений мелкой воды над плоским наклонным дном в неограниченном бассейне. Выше оговаривалось, что для построения решений этой нелинейной системы в ограниченном бассейне следует задать либо начальные условия, либо потребовать выполнения каких-то других условий, например, условие периодичности решения по времени. В линейном случае многие такие решения выражаются через собственные функции ${v}(y)$ и значения ${{\omega }^{2}}$ заданного на отрезке $[a,b]$ оператора $\hat {L}$ (1.7) по формулам (1.6), аналогичным (2.8).
Такие решения могут служить базой для построения $t$-периодических решений с малой амплитудой (мы, напомним, характеризуем ее малым параметром $\varepsilon $) нелинейных уравнений, точнее их асимптотик в предположении об их малости, с помощью методов теории возмущений, например бесконечномерных аналогов метода осреднения Крылова–Боголюбова [38] или метода КАМ [39, 40]. Если иметь в виду эти методы, соответствующие частоты $\omega $ следует считать зависящими от $\varepsilon $, предполагая что $\omega = \omega (\varepsilon )$ = ${{\omega }_{0}} + \varepsilon {{\omega }_{1}} + {{\varepsilon }^{2}}{{\omega }_{2}}$ + …. В рассматриваемых здесь задачах нелинейные эффекты сильно сказываются только в окрестности берега и согласно [18] слабо влияют на значения $\omega $, поэтому при определении главного члена асимптотики достаточно взять ${{\omega }_{0}}$, что будет сделано в дальнейшем, при этом для упрощения обозначений вместо ${{\omega }_{0}}$ пишем $\omega $.
3.1. Стоячие волны в бассейне с плоским наклонным дном и вертикальной стенкой. Рассмотрим уравнение (1.1) с плоским наклонным дном $D(x) = x$ и с граничными условиями (1.8) (вертикальная стенка при $x = b$). Замена Кэрриера–Гринспена (2.3) переводит нелинейное уравнение в линейное уравнение (1.3), когда соответствующий якобиан $J$ не обращается в нуль. При этой замене переменная левая граница $x = a(t)$, определяемая соотношением (1.2), переходит в фиксированную: $y \in [0,\infty )$, но правая граница $x = b$ переходит в подвижную $y = {{y}_{b}}(\tau )$
Таким образом, при наличии стенки замена Кэрриера–Гринспена не обеспечивает точную линеаризацию задачи даже в случае плоского наклонного дна, хотя и линеаризует системы уравнений. С другой стороны, замена (2.9) или (2.10), где срезающая функция $\rho (y) = 0$ в окрестности стенки, приводит к нелинейной задаче в фиксированной области $y \in [0,b]$, при этом условие на стенке $y = b$ остается без изменений, а вместо условия на подвижной границе $a(t)$ нужно потребовать конечность энергии решения (1.5) (при ${{c}^{2}}(x) = x$). Методы решения второй задачи представляются нам более развитыми и эффективными. Более того, если считать решение малым и ввести характеризующий амплитуду решения малый параметр $\varepsilon $, то как уже отмечалось, согласно Утверждению 2, главный член формального асимптотического (по параметру $\varepsilon $) решения полностью определяется решением линейной задачи, задаваемой уравнением (1.3), условием (1.5) и краевым условием ${{\left. U \right|}_{{y = b}}}$ = 0.
Очевидно, линейная задача (1.3), (1.5), ${{\left. u \right|}_{{y = b}}}$ = 0 допускает семейство точных стационарных решений (в виде стоячей волны), задаваемых формулами (2.8) [6, 7, 9], где частоты принимают дискретные значения $\omega = {{\omega }_{n}}$, которые определяются равенствами
(3.1)
${{\omega }_{n}} = \frac{1}{2}{{\alpha }_{n}}\sqrt {\frac{{\gamma g}}{b}} ;\quad n \in \mathbb{N}$Здесь ${{\alpha }_{n}}$ – нули функции Бесселя ${{{\mathbf{J}}}_{1}}$, (при больших $n$: ${{\alpha }_{n}} \approx \pi (n + 1{\text{/}}4)$).
Аналогично ([18], теор. 2), можно доказать следующее утверждение.
Утверждение 3. Функции ${{\eta }_{n}}(x,t)$, ${{u}_{n}}(x,t)$, полученные из (2.8), (3.1) с помощью замены (2.10), определяют формальное асимптотическое решение нелинейной задачи.
Замечание 2. Главный член асимптотики применим (дает малую невязку при подстановке в уравнение) на временах порядка $t = O(1)$ при $\varepsilon \to 0 + $. На больших временах начинает играть роль зависимость частоты нелинейных колебаний от амплитуды, т.е. нелинейное дисперсионное соотношение (см. [38]), и частоту нужно соответствующим образом подправлять.
3.2. Стоячие волны в бассейне с параболическим дном. Еще один пример точных решений линеаризованных уравнений дает случай дна $D(x)$, имеющего форму параболы, которую без уменьшения общности можно представить в виде $D(x)$ = $\mathcal{D} - {{\mathcal{H}}^{{ - 1}}}{{x}^{2}}$ = = ${{\mathcal{H}}^{{ - 1}}}\left( {{{\mathcal{A}}^{2}} - {{x}^{2}}} \right)$, где $\mathcal{D}$ – максимальная глубина и $2\mathcal{A}$ – ширина невозмущенной поверхности. В этом случае соответствующая задача о собственных функциях – сводится к уравнению, определяющему полиномы Лежандра ${{P}_{n}}(y)$ (по-видимому, впервые этот факт отмечен Лэмбом в 1895 г., см. ([6], sec. 182)):
(3.2)
$\hat {L}{{P}_{n}} \equiv - \frac{d}{{d\tilde {y}}}\left( {\left( {1 - {{{\tilde {y}}}^{2}}} \right)\frac{{d{{P}_{n}}}}{{d\tilde {y}}}(\tilde {y})} \right) = \tilde {\omega }_{n}^{2}{{P}_{n}}(\tilde {y});\quad \tilde {\omega }_{n}^{2} = n(n + 1),\quad n \in \mathbb{N}$Перейти от физического волнового уравнения (1.3) к безразмерному (3.2) можно с помощью подстановки: $x = \mathcal{A}\tilde {x}$, $t = \mathcal{T}\tilde {t}$, $\eta = \tilde {\eta }{{\mathcal{H}}^{{ - 1}}}{{\mathcal{A}}^{2}}$, $u = \tilde {u}\sqrt {g{{\mathcal{H}}^{{ - 1}}}{{\mathcal{A}}^{2}}} $, где характерный масштаб времени $\mathcal{T} = \sqrt {\mathcal{H}{\text{/}}g} $, так что частота меняется как $\omega = \tilde {\omega }\sqrt {g{{\mathcal{H}}^{{ - 1}}}} $. Таким образом гармонические по времени решения линейной задачи (1.3) с двумя берегами при условии конечности энергии (1.5) определяются формулой
(3.3)
$\begin{gathered} {{N}^{n}}(y,\tau ) = \frac{{\varepsilon {{\mathcal{A}}^{2}}}}{\mathcal{H}}\cos ({{\omega }_{n}}\tau ){{P}_{n}}\left( {\frac{y}{\mathcal{A}}} \right),\quad {{U}^{n}}(y,\tau ) = - \frac{{\varepsilon \mathcal{A}g}}{{{{\omega }_{n}}\mathcal{H}}}sin({{\omega }_{n}}\tau ){{P}_{{n'}}}\left( {\frac{y}{\mathcal{A}}} \right) \\ {{\omega }_{n}} = \sqrt {n(n + 1)g{{\mathcal{H}}^{{ - 1}}}} \\ \end{gathered} $Утверждение 4. Согласно ([18], теор. 2), при достаточно малой амплитуде $\varepsilon $ применение замены (2.9) к точному решению (3.3) даст асимптотику $modO(\varepsilon )$ при $\varepsilon \to 0{\kern 1pt} + $ исходной нелинейной задачи (1.1) с двумя подвижными границами (1.2).
В случае, когда область ограничена двумя берегами $\Omega = (a,b)$, итерационная процедура (2.10) заменяется на следующую (срезающая функция $\rho (y)$ равна нулю в точке $c \in (a,b)$):
(3.4)
$\begin{gathered} {{Y}_{0}} = \left\{ \begin{gathered} \max \{ a + \delta ,x\} ,\quad x \leqslant c \hfill \\ \min \{ b - \delta ,x\} ,\quad x \geqslant c \hfill \\ \end{gathered} \right. \\ {{Y}_{1}} = \left\{ \begin{gathered} a + ({{Y}_{0}} - a)\frac{{D(x) + N(a,t)}}{{D({{Y}_{0}}) - \rho ({{Y}_{0}})N({{Y}_{0}},t) + N(a,t)}},\quad x \leqslant c \hfill \\ b + ({{Y}_{0}} - b)\frac{{D(x) + N(b,t)}}{{D({{Y}_{0}}) - \rho ({{Y}_{0}})N({{Y}_{0}},t) + N(b,t)}},\quad x \geqslant c \hfill \\ \end{gathered} \right. \\ \end{gathered} $3.3. Стоячие волны в бассейне с произвольным неровным дном. Формулы для решения линейной задачи. Рассмотрим задачу о построении периодических по времени решений типа стоячих волн в случае, когда функция $D(x)$ достаточно произвольно зависит от $x$. Ограничимся случаем бассейна с двумя пологими берегами и будем предполагать, что $D(x)$ – гладкая функция, заданная на интервале $[a - \delta ,b + \delta ]$, $D(a) = D(b) = 0$, $D{\kern 1pt} '(a) < 0$, $D{\kern 1pt} '(b) > 0$, $D(x) > 0$ при $x \in (a,b)$, $D(x) < 0$ вне отрезка $[a,b]$. Здесь $a < b$ – числа, определяющие берега бассейна, $\delta $ – положительное число. Как отмечалось, описанный выше подход позволяет, по крайней мере, задачу о старшей части асимптотики решения по параметру $\varepsilon $ свести к линейной задаче (1.3) и, более точно, к задаче о собственных функциях оператора $\hat {L}$ вида (1.7).
Будем строить асимптотические решения задачи (1.7). Большим параметром здесь является номер $n$ соответствующей собственной функции ${{\psi }_{n}}$, который связан с малой характерной длиной волны $\mu = \left( {b - a} \right){\text{/}}n$ функции ${{\psi }_{n}}$. Такие асимптотики были построены в [17] с помощью модифицированного канонического оператора Маслова и последующей его реализации в виде функций Бесселя (историю вопроса и библиографию можно найти в этой статье). Приведем соответствующие формулы. Определим функцию, имеющую размерность времени
(3.5)
$S(x,y) = \int\limits_x^y {\frac{{dy}}{{\sqrt {gD(y)} }}} ;\quad a \leqslant x \leqslant y \leqslant b$Решение в виде стоячей волны существует при выполнении условия квантования
(3.6)
$\begin{gathered} {{\omega }_{n}} = \frac{\pi }{{S(a,b)}}\left( {\frac{m}{4} + n} \right)\left( {1 + O\left( {{{n}^{{ - 1}}}} \right)} \right);\quad n \in \mathbb{N}, \hfill \\ \end{gathered} $(3.7)
$\begin{gathered} {{N}^{n}} = \varepsilon \cos ({{\omega }_{n}}\tau + {{\tau }_{0}}){{{\hat {N}}}^{n}}(y),\quad {{U}^{n}} = - \frac{{\varepsilon g}}{{{{\omega }_{n}}}}\sin ({{\omega }_{n}}\tau + {{\tau }_{0}})\frac{{\partial {{{\hat {N}}}^{n}}(y)}}{{\partial y}}, \hfill \\ \end{gathered} $(3.8)
$\begin{gathered} {{{\hat {N}}}^{n}} = \frac{{{{\mathcal{A}}^{2}}}}{\mathcal{H}}\left\{ \begin{gathered} {{{\mathbf{J}}}_{0}}({{\omega }_{n}}S(a,y)){{\left( {\frac{{\mathcal{A}\sqrt g S(a,y)}}{{\mathcal{H}\sqrt {D(y)} }}} \right)}^{{1{\text{/}}2}}},\quad y \in [a,b - \delta ] \hfill \\ {{( - 1)}^{n}}{{{\mathbf{J}}}_{0}}({{\omega }_{n}}S(y,b)){{\left( {\frac{{\mathcal{A}\sqrt g S(y,b)}}{{\mathcal{H}\sqrt {D(y)} }}} \right)}^{{1{\text{/}}2}}},\quad y \in [a + \delta ,b] \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $В случае одного берега и вертикальной стенки асимптотика определяется на всем интервале $y \in [a,b]$ с помощью функции $S(a,y)$ по (3.8).
Условия существования приближенного решения и согласование малых параметров. Следуя предложенному алгоритму, возьмем асимптотику (3.6)–(3.8) линейной задачи (1.3) и применим к ней замену (2.10); получатся приближенные формулы для волны с соответствующей переменной областью.
Строгое доказательство того утверждения, что в результате получится асимптотическое решение нелинейной задачи, существенно сложнее проведенного в [18]. Дело в том, что при использовании асимптотики линейной задачи, помимо амплитуды $\varepsilon $, возникает дополнительный малый параметр – относительная длина волны $\mu {{\mathcal{A}}^{{ - 1}}}$, и применимость линейной асимптотики доказывается в пределе при малых $\mu \to {{0}_{ + }}$ (в случае стоячих волн удобнее рассматривать большой параметр – номер гармоники $n\sim \mathcal{A}{\text{/}}\mu $). Чтобы провести строгое доказательство, что для нелинейной задачи построенные формулы дают малую невязку, необходимо рассмотреть пределы сразу по двум параметрам $\mu \to {{0}_{ + }}$ (характеризующим длину волны) и $\varepsilon \to {{0}_{ + }}$ (характеризующим амплитуду), причем эти параметры должны быть согласованы.
Для точных решений (2.8) и (3.3) можно вычислить критическую амплитуду ${{\varepsilon }_{0}}$, когда происходит “обрушение” замены (2.9), а именно вырождается якобиан ${{J}_{2}}(y) = \partial x{\text{/}}\partial y$. В первую очередь якобиан обнуляется в точке берега $y = a$, причем происходит это в момент $t = T{\text{/}}2 = \pi {\text{/}}\omega $ максимального откатывания волны (наименьшего уровня уреза воды):
(3.9)
$\begin{gathered} {{\kappa }_{1}} = \frac{{\varepsilon \mu {{\omega }^{2}}}}{{\gamma g}} < 1,\quad {{\kappa }_{2}} = \frac{{\varepsilon n(n + 1)}}{4} \hfill \\ \end{gathered} $Наша гипотеза заключается в том, что условия существования замены (2.9) по порядку величин совпадают с условиями необрушения, а также, что если амплитуда $\varepsilon $ много меньше критической, то и невязка будет мала.
Поскольку при моделировании конкретных волн “малые параметры” всегда принимают некоторые конечные значения, то предлагаемый алгоритм заключается в том, чтобы проверить корректность замены (2.10), и если соответствующие нелинейные формулы не обрушаются, то использовать их как приближенные для моделируемых волн.
Проиллюстрируем сказанное на следующем примере. Выберем функцию дна в виде
(здесь все выкладки приведены в безразмерных переменных). Асимптотики линейной задачи для такой функции глубины можно найти в [17]. Обозначим невязку, возникающую при подстановке линейной асимптотики в первое и второе уравнение из (1.3), через ${{\delta }_{1}}(y,\tau ),{{\delta }_{2}}(y,\tau )$ соответственно и положимЧисленные расчеты показывают, что при амплитуде $\varepsilon = 0.3$, в ситуации, близкой к обрушению, когда якобиан ${{J}_{2}}$ очень близок к нулю, невязка становится сравнимой с самой асимптотикой. При уменьшении амплитуды невязка уменьшается: ${{\left\| \delta \right\|}_{{{{L}_{2}}[a,b]}}}{\text{/}}{{\left\| {{{\xi }_{\tau }}} \right\|}_{{{{L}_{2}}[a,b]}}}$ = $O\left( {\varepsilon {{\omega }^{2}}} \right)$.
4. Экспериментальные методы и результаты. В лабораторных условиях исследованы длинные поверхностные волны в жидкости в прямоугольных сосудах с переменной глубиной. Эксперименты проводились на стенде “Динамики и структуры осциллирующих течений” (ДСО) [20], который входит в уникальный исследовательский комплекс “ГФК ИПМех РАН”. Цель – верификация результатов теоретической модели на экспериментальных данных.
Экспериментально изучались стоячие волны в сосудах с линейным и вогнутым параболическим профилем дна с пологими берегами. Наличие пологого берега позволяет наблюдать набегание волн и его влияние на колебания жидкости. В этом состоит отличие представленного эксперимента от исследований стоячих волн в сосуде с параболическим [22] или линейным [24, 25] дном и вертикальными стенками.
4.1. Описание эксперимента. При создании волнового движения жидкости использовался параметрический резонанс, при котором образуются стоячие волны (волны Фарадея) из-за дестабилизации горизонтальной свободной поверхности жидкости в сосуде, колеблющемся вертикально. Поскольку волны Фарадея возбуждаются без использования каких-либо волнопродукторов, их наблюдение и измерение оказываются более простыми и точными, чем при использовании других методов. Более того, профили волн аналогичны профилям свободных стоячих волн, что позволяет сравнить результаты измерений с выводами теории.
Сосуд с жидкостью помещался на платформу электромеханического вибростенда (см. [20]), обеспечивающего его гармонические вертикальные колебания. Двумерные волновые движения исследовались в режиме основного резонанса Фарадея [23], когда частота колебаний сосуда $\Omega $ в два раза превышает частоту $\omega $ возбужденных волн ($\Omega \sim 2\omega $). Точность измерения периода колебаний резервуара составляла 2 мс. При фиксированной амплитуде колебаний сосуда $\mathcal{S} = 0.75$ см изменение частоты $\Omega $ обеспечивало возбуждение соответствующей волновой моды с номером $n$ и высотой волны $\mathcal{H}$. Сейши моделировались третьей и четвертой модами ($n = 3,4$) двумерных стоячих гравитационных волн на свободной поверхности воды в прямоугольном сосуде размером $60 \times 14 \times 40$ или $50 \times 4 \times 50$ см, колеблющемся в вертикальном направлении [23–25]. Сосуд изготовлен из прозрачного оргстекла. Волновая картина регистрировалась цифровой камерой DIMAGE Z2 и Canon PowerShot SX50HS (частота кадров составляла 30 и 120 к/с) в движущейся системе отсчета, жестко связанной с сосудом. Разрешение видеоизображений составляло 0.15 мм/пиксель. Последующая обработка видеокадров осуществлялась с использованием программы ImageJ. Все эксперименты проводились при комнатной температуре 21–22°C.
В качестве рабочей жидкости использовалась вода и рассматривались две различные конфигурации дна сосуда: плоское наклонное и параболическое.
Конфигурация I: плоское наклонное дно. Используя монолитную трапециевидную вставку из оргстекла на дне сосуда размером $60 \times 14 \times 40$ см, создана емкость с плоским дном $D(x) = \gamma x$ с уклоном $\gamma = 4.8:60$ или с углом наклона 0.08 радиана – рис. 3,а. При максимальной глубине воды $\mathcal{D} = 4.5$ см длина невозмущенной свободной поверхности составляла $\mathcal{X} = 56$ см. Экспериментальные исследования ограничивались двумерными стационарными колебаниями жидкости (рис. 3,б), создаваемыми четвертой волновой модой ($n = 4$). Параметрическое возбуждение этих волн осуществлялось при частоте колебаний сосуда $\Omega $ ~ 19.64–22.67 с–1.
Рис. 3.
Конфигурация I. а: Сосуд с плоским наклонным дном, фронтальная камера, и б: четвертая мода двумерных стоячих волн, угловая камера. Конфигурация II. в: Сосуд с вогнутым параболическим дном, фронтальная камера, и г: третья мода двумерных стоячих волн, угловая камера, показаны волны максимального развития.

Конфигурация II: вогнутое параболическое дно. В этом случае вогнутое параболическое дно в сосуде размером $50 \times 4 \times 50$ см изготовлено из технического пластилина – рис. 3,в. Для формирования дна, описываемого функцией $D(x)$ = $\mathcal{D} - {{\mathcal{H}}^{{ - 1}}}{{x}^{2}}$ = = ${{\mathcal{H}}^{{ - 1}}}\left( {{{\mathcal{A}}^{2}} - {{x}^{2}}} \right)$, использовался соответствующий пластиковый шаблон. В результате при максимальной глубине воды $\mathcal{D} = 3.2$ см длина поверхности неподвижной воды составляла $\mathcal{X} = 2\mathcal{A}$ = $2\sqrt {\mathcal{H}\mathcal{D}} $ = 35.6 см ($\mathcal{H} = 100$ см). В диапазоне частот $\Omega \sim 18.85{\kern 1pt} - {\kern 1pt} 26.39$ с–1 возбуждалась третья мода двумерных стоячих волн – рис. 3,г.
На рис. 4 показаны профили четвертой волновой моды, возбуждаемой на свободной поверхности воды в сосуде с линейным берегом. Видеокадры, представленные на рисунках, полностью отражают динамику волны в течение ее периода, причем производилась высокоскоростная видеозапись (120 к/с) с фронтальной стенки сосуда (а) и обычная запись (30 к/с) с направления под углом к сосуду (б). Разница в скорости съемки определяет неизбежную незначительную временную десинхронизацию, наблюдаемую при сравнении кадров (а) и (б) на этих рисунках. Несмотря на очень низкую амплитуду колебаний (едва заметную глазом) вблизи берега происходит обрушение волны (см. [41]).
Рис. 4.
Профиль стоячих колебаний над плоским наклонным дном с частотой колебаний сосуда $\Omega = 20.47$ с$^{{ - 1}}$, соответствующий четвертой волновой моде во фронтальной (а) и изометрической (б) проекциях. Время в секундах отмечено в левом верхнем углу кадра.

На рис. 5 показаны типичные профили третьей волновой моды, возбуждаемой на свободной поверхности воды в сосудах с параболическим дном в случае двух частот $\Omega $ и разные по амплитуде. Сравнение профилей волн (а) и (б) позволяет сделать вывод о наличии безобрушающихся волн в одном случае и существенно нелинейных колебаний – в другом.
Рис. 5.
Третья мода стоячих волн над вогнутым параболическим дном с малой (а) и большой (б) амплитудой, частота колебаний сосуда соответственно $\Omega = 25.23$ и 24.26 с–1; съемка на фронтальную камеру с частотой 120 к/с, время (с) указано в левом верхнем углу кадра.

Эксперимент с линейным дном оказался неудобен для сравнения, поскольку необрушающиеся волны настолько малы, что их тяжело наблюдать: для волн, изображенных на рис. 4, безразмерное отношение, определяющее условие обрушения равно (3.9) ${{\kappa }_{1}} \approx 18 > 1$, так что якобиан обнуляется около берега. Эта проблема преодолевается в эксперименте с дном параболического профиля, когда при той же глубине можно получить больший наклон дна у границы жидкости и соответственно существенно меньшее требование на амплитуду необрушающихся волн. Учитывая указанную разницу в экспериментах, сравнение с теорией проводилось для случая вогнутого параболического дна, см. рис. 5,б.
4.2. Сравнение с экспериментом: случай вогнутого параболического дна. Рассмотрим систему мелкой воды в размерных величинах (1.1). В соответствии с параметрами эксперимента в конфигурации II, зададим характерный масштаб $\mathcal{A} = 17.8$ см, так что длина невозмущенной поверхности воды $\mathcal{X} = 2\mathcal{A}$ = 35.6 см и функция дна $D(x)$ = = $\mathcal{D} - \mathcal{H}_{0}^{{ - 1}}{{x}^{2}}$ = $\mathcal{H}_{0}^{{ - 1}}\left( {{{\mathcal{A}}^{2}} - {{x}^{2}}} \right)$, где максимальная глубина $\mathcal{D} = 3.2$ см и $\mathcal{H}_{0}^{{ - 1}}$ = 0.01 см–1. Чтобы перейти от системы мелкой воды (1.1) к безразмерной системе с $\tilde {g} = 1$ и функцией дна $\tilde {D}(\tilde {x})$ = $1 - {{\tilde {x}}^{2}}$, характерный масштаб времени выберем равным $\mathcal{T} = \sqrt {{{\mathcal{H}}_{0}}{\text{/}}g} $ и сделаем подстановку $x = \mathcal{A}\tilde {x}$, $t = \mathcal{T}\tilde {t}$, $\eta $ = $\tilde {\eta }\mathcal{H}_{0}^{{ - 1}}{{\mathcal{A}}^{2}}$, $u = \tilde {u}\sqrt {g\mathcal{H}_{0}^{{ - 1}}{{\mathcal{A}}^{2}}} $, что приведет к
(4.1)
${{\tilde {\eta }}_{{\tilde {t}}}} + {{((\tilde {D}(\tilde {x}) + \tilde {\eta })\tilde {u})}_{{\tilde {x}}}} = 0,\quad {{\tilde {u}}_{{\tilde {t}}}} + {{\tilde {\eta }}_{{\tilde {x}}}} + \tilde {u}{{\tilde {u}}_{{\tilde {x}}}} = 0,\quad \tilde {D}(\tilde {x}) = 1 - {{\tilde {x}}^{2}}$Для трехузловой моды $n = 3$, наблюдаемой в эксперименте (рис. 5,а), период колебаний, предсказываемый теорией, равен ${{T}^{{(3)}}} = 2\pi \omega _{3}^{{ - 1}}$ ≈ 0.58 с (см., напр, [2]). Период волн в эксперименте $T_{{{\text{exper}}}}^{{(3)}}$ = 0.50 с отличался от теоретического (это связано с особенностями параметрического возбуждения волн), но при этом профили волны довольно хорошо совпали с теорией.
На рис. 6 сравнивается асимптотика возвышения свободной поверхности с экспериментом в моменты максимального и минимального отклонения уреза воды. Амплитуда волны в максимальной точке $\mathcal{H} \approx 1$ см, и критерий необрушения (3.9) выполняется: ${{\kappa }_{2}} = 0.9 < 1$.
Рис. 6.
Сравнение асимптотических формул (сплошные кривые) с волной в эксперименте (прозрачные и сплошные кружочки) в моменты времени, соответствующие максимальному и минимальному отклонению уреза воды: $t = T$ и $t = T{\text{/}}2$, где $T$ – период колебаний.

Заключение. Предложен метод моделирования одномерных периодических (стоячих) волн в бассейнах с двумя берегами и берегом и стенкой. При построении приближенного решения нелинейной задачи используются асимптотики решения линейной задачи и замена вроде замены Кэрриера–Гринспена. Проведено сравнение с модельными примерами плоского наклонного дна и параболического дна, а также сравнение с экспериментом, в котором стоячие волны возбуждаются при основном параметрическом резонансе. Сравнение показало хорошее соответствие. Полученные аналитические формулы легко реализуются на компьютере и позволяют проводить расчеты в режиме реального времени.
Работа выполнена при поддержке Российского научного фонда, грант № 21-1100341.
Список литературы
Stoker J.J. Water Waves: The Mathematical Theory with Applications. New York: Wiley, 1958. 609 p.
Сретенский Л.Н. Теория волновых движений жидкости. М.: Наука, 1977. 816 с.
Mei C.C. The Applied Dynamics of Ocean Surface Waves. Singapore: World Sci., 1989. 768 p.
Пелиновский Е.Н. Гидродинамика волн цунами. Н. Новгород: ИПФ РАН, 1996. 276 с.
Pelinovsky E.N., Mazova R.Kh. Exact analytical solutions of nonlinear problems of tsunami wave run-up on slopes with different profiles // Natural Hazards, 1992. V. 6. P. 227–249.
Lamb H. Hydrodynamics. Cambridge: Univ. Press, 1932. 738 p.
Chrystal G. XXV. On the hydrodynamical theory of seiches // Trans. Roy. Soc. Edinburgh. 1906. V. 41. P. 599–649.
Оболенский В.Н. Сейши и их теория // Записки по гидрографии. 1919. Т. 42. № 2. С. 13–76.
Rabinovich A.B. Seiches and harbor oscillations // Handbook of Coastal&Ocean Engng. 2009. P. 193–236.
Арсеньева Н.М., Давыдов Л.К., Дубровина Л.Н., Конкина Н.Г. Сейши на озерах СССР. Л.: Изд-во Ленингр. ун-та, 1963. 184 с.
Зырянов В.Н. Сейши подо льдом // Водные ресурсы. 2011. Т. 38. № 3. С. 259–271.
Смирнов С.В., Кучер К.М., Гранин Н.Г., Стурова И.В. Сейшевые колебания Байкала // Изв. РАН. ФАО. 2014. Т. 50. № 1. С. 105–116.
Олейник О.А., Радкевич Е.В. Уравнения второго порядка с неотрицательной характеристической формой // в: Итоги науки. Сер. Матем. Матем. анал. 1969. М.: ВИНИТИ, 1971. 252 с.
Vukašinac T., Zhevandrov P. Geometric asymptotics for a degenerate hyperbolic equation // Russ. J. Math. Phys. 2002. V. 9. № 3. P. 371–381.
Владимиров В.С. Уравнения математической физики. М.: Наука, 1981. 512 с.
Бирман М.Ш., Соломяк М.З. Спектральная теория самосопряженных операторов в гильбертовом пространстве. СПб.: Лань, 2010. 457 с.
Доброхотов С.Ю., Назайкинский В.Е. Нестандартные Лагранжевы особенности и асимптотические собственные функции вырождающегося оператора $d{\text{/}}dxD(x)d{\text{/}}dx$ // Тр. МИАН. 2019. Т. 306. С. 83–99.
Dobrokhotov S.Yu., Minenkov D.S., Nazaikinskii V.E. Asymptotic solutions of the Cauchy problem for the nonlinear shallow water equations in a basin with a gently sloping beach // Russ. J. Math. Phys. 2022. V. 29. P. 28–36.
Carrier G.F., Greenspan H.P. Water waves of finite amplitude on a sloping beach // J. Fluid Mech. 1958. V. 4. P. 97–109.
http://www.ipmnet.ru/uniqequip/gfk/#aboutDSO
Калиниченко В.А., Нестеров С.В., Секерж-Зенькович С.Я., Чайковский А.А. Экспериментальное исследование поверхностных волн при резонансе Фарадея // Изв. РАН. МЖГ. 1995. № 1. С. 122–129.
White P., Watson W. Some experimental results in connection with the hydrodynamical theory of seiches // Proc. R. Soc. Edinb. 1906. V. 26. № 01. P. 142–156.
Калиниченко В.А., Секерж-Зенькович С.Я. Экспериментальное исследование волн Фарадея максимальной высоты // Изв. РАН. МЖГ. 2007. № 6. С. 120–126.
Калиниченко В.А., Нестеров С.В., Со А.Н. Волны Фарадея в прямоугольном сосуде с локальными нерегулярностями дна // Изв. РАН. МЖГ. 2015. № 4. С. 83–91.
Калиниченко В.А., Нестеров С.В., Со А.Н. Стоячие поверхностные волны в прямоугольном сосуде с локальными нерегулярностями стенок и дна // Изв. РАН. МЖГ. 2017. № 2. С. 65–74.
Доброхотов С.Ю., Тироцци Б. Локализованные решения одномерной нелинейной системы уравнений мелкой воды со скоростью $c = \sqrt x $ // УМН. 2010. Т. 65. № 1 (391). С. 185–186.
Доброхотов С.Ю., Медведев С.Б., Миненков Д.С. О заменах, приводящих одномерные системы уравнений мелкой воды к волновому уравнению со скоростью звука ${{c}^{2}} = x$ // Матем. зам. 2013. Т. 93. № 5. С. 725–736.
Чиркунов Ю.А., Доброхотов С.Ю., Медведев С.Б., Миненков Д.С. Точные решения одномерных уравнений мелкой воды над ровным и наклонным дном // ТМФ. 2014. Т. 178. № 3. С. 322–345.
Didenkulova I., Pelinovsky E. Non-dispersive traveling waves in inclined shallow water channels // Phys. Lett. A. 2009. V. 373. № 42. P. 3883–3887.
Rybkin A., Pelinovsky E., Didenkulova I. Non-linear wave run-up in bays of arbitrary cross-section: generalization of the Carrier–Greenspan approach // J. Fluid Mech. 2014. V. 748. P. 416–432.
Anderson D., Harris M., Hartle H. et al. Run-up of long waves in piecewise sloping U-shaped bays // Pure Appl. Geophys. 2017. V. 174. P. 3185–3207.
Rybkin A., Nicolsky D., Pelinovsky E., Buckel M. The generalized Carrier–Greenspan transform for the shallow water system with arbitrary initial and boundary conditions // Water Waves. 2021. V. 3. № 1. P. 267–296.
Antuono M., Brocchini M. The boundary value problem for the nonlinear shallow water equations // Studies in Appl. Math. 2007. V. 119. № 1. P. 73–93.
Миненков Д.С. Асимптотики решений одномерной нелинейной системы уравнений мелкой воды с вырождающейся скоростью // Матем. зам. 2012. Т. 92. № 5. С. 721–730.
Chugunov V.A., Fomin S.A., Noland W., Sagdiev B.R. Tsunami runup on a sloping beach // Comp.&Math. Meth. 2020. № 2. P. e1081.
Minenkov D.S. Asymptotics near the shore for 2D shallow water over sloping planar bottom // Days on Diffraction (DD). 2017. P. 240–243.
Аксенов А.В., Доброхотов С.Ю., Дружков К.П. Точные решения типа “ступеньки” одномерных уравнений мелкой воды над наклонным дном // Матем. зам. 2018. Т. 104. № 6. С. 930–936.
Боголюбов Н.Н., Митропольский Ю.А. Асимптотические методы в теории нелинейных колебаний. М.: Наука, 1974. 504 с.
Арнольд В.И. Математические методы классической механики. М.: Ленанд, 2017. 416 с.
Арнольд В.И., Козлов В.В., Нейштадт А.И. Математические аспекты классической и небесной механики. М.: УРСС, 2002. 414 с.
Galvin C.J. Breaker type classification on three laboratory beaches //J. Geophys. Res. 1968. V. 73. P. 12. P. 3651–3659.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика


