Прикладная математика и механика, 2023, T. 87, № 2, стр. 327-336
Собственные частоты и формы продольных и крутильных колебаний стержней переменного поперечного сечения
И. С. Никитин 1, *, Н. Г. Бураго 1, 2, **, А. Д. Никитин 1, ***
1 Институт автоматизации проектирования РАН
Москва, Россия
2 Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
* E-mail: i_nikitin@list.ru
** E-mail: buragong@yandex.ru
*** E-mail: nikitin_alex@bk.ru
Поступила в редакцию 09.01.2023
После доработки 02.03.2023
Принята к публикации 02.03.2023
- EDN: UAJFFL
- DOI: 10.31857/S003282352302011X
Аннотация
Рассматривается задача определения частоты и формы собственных продольных или крутильных колебаний для стержня переменного сечения на основе теории возмущений. Предполагается, что упругие свойства и площадь поперечного сечения прямого стержня меняются достаточно медленно и слабо отклоняются от некоторых средних значений по продольной координате. С использованием метода асимптотических разложений по малому параметру, получены аналитические формулы для поправок к собственным частотам и формам стационарных гармонических колебаний стержня. Работоспособность формул проверена сравнением с точными решениями для некоторых зависимостей площади поперечного сечения от продольной координаты. Показано, что приближенные формулы хорошо работают даже для стержней, у которых отношение максимального и минимального радиуса сечения достигает 2.5–3. Численные расчеты ориентированы на оценку геометрических и упругих свойств образцов для проведения экспериментальных исследований усталостной прочности металлических сплавов при высокочастотном циклическом нагружении на растяжение-сжатие и кручение. Пьезоэлектрические установки для проведения таких высокочастотных испытаний основаны на общем принципе резонансного нагружения корсетных образцов с частотой порядка 20 кГц.
1. Введение. Уравнения продольных, крутильных и поперечных колебаний стержней с переменным сечением приведены в различных учебниках и монографиях, в частности, в [1]. Задача определения собственных частот и форм продольных и крутильных колебаний стержней с переменным сечением исследовалась многими авторами [2–6]. Обзор работ по определению собственных частот и форм изгибных колебаний можно найти в [7], решение конкретных задач дано в [8–12]. Основные приложения связаны с определением поправок к резонансным частотам и формам колебаний, обусловленных дефектами поверхности – при продольных колебаниях [2–4], при крутильных колебаниях [5, 6], при изгибных колебаниях [10, 11], при наличии внутренних дефектов (трещин) [12].
Стержни переменного сечения используются при проведении экспериментальных исследований усталостной прочности металлических сплавов при высокочастотном циклическом нагружении образцов на растяжение-сжатие, кручение или трехточечный изгиб [13]. Пьезоэлектрические установки для проведения высокочастотных СВМУ испытаний осуществляют циклическое нагружение: растяжением–сжатием и кручением [13]. Эти испытательные установки обладают общим принципом резонансного нагружения с частотой порядка 20 кГц. Испытания на растяжение-сжатие и кручение контролируются и программируются с использованием одного и того же программного комплекса. Различие между машинами состоит лишь в типе пьезоэлектрического конвертера и геометрии волновода. Для реализации осевых нагружений используется конвертер, обеспечивающий продольные смещения малой амплитуды (10–30 мкм). Для крутильного нагружения используется конвертер, обеспечивающий непосредственно вращательные колебания с амплитудой 0.10–0.25 миллирадиан. Для случая кручения резонансные длины оказываются меньше, чем для осевых испытаний [13]. Базовая корсетная форма осесимметричного стержня имеет вид “песочных часов” для создания квазиоднородного напряженного состояния с повышенным уровнем напряжений в центральной, узкой части образца.
В данной работе основной интерес представляет исследование влияния геометрии стержня на первую резонансную частоту и антисимметричную форму продольных или крутильных колебаний при исследовании сверхмногоциклового усталостного разрушения (СВМУ) с числом циклов N > 108.
Пьезоэлектрические установки с несущей частотой порядка 20 кГц имеют достаточно узкий частотный диапазон отклонений при эксплуатации, составляющий ±500 Гц. Поэтому оценка и определение чувствительности и влияния геометрических параметров образца (общей длины, длины участка переменного сечения и характеристик его изменчивости) на резонансную частоту является необходимой при проектировании экспериментальных установок и образцов из различных металлических сплавов.
Для определения поправок к резонансной частоте и форме собственных продольных и крутильных колебаний для стержня переменного сечения используется теория возмущений [14]. Теория возмущений использовалась в [4] при решении обратной задачи восстановления распределения плотности и модуля Юнга для неоднородного стержня переменного сечения по частотам собственных колебаний. В данной работе рассматривается прямая задача нулевого и первого приближений для упрощенного, но достаточно общего представления формы стержня, для которой удалось получить явные решения в удобной аналитической форме.
2. Постановка задачи. Рассмотрим уравнение колебаний общего вида:
Пусть параметры колебательной системы зависят от продольной координаты x. Для продольных колебаний $I(x)$ = $E(x)S(x)$, $A(x)$ = $S(x)$,E – модуль Юнга стержня, S – переменная площадь сечения. Для крутильных колебаний $I(x)$ = $\mu (x)J(x)$, $A(x)$ = = $J(x)$, где $\mu $ – модуль сдвига стержня, $J$ – полярный момент инерции. Поскольку уравнения продольных и крутильных колебаний отличаются только обозначениями, далее будем вести изложение для случая продольных колебаний стержня.
Рассматривая гармонические колебания $w(x,t)$ = $u(x){{e}^{{i\omega t}}}$, приходим к уравнению для амплитуды
с граничными условиями2.1. Построение общего решения методом разложения по малому параметру. Рассмотрим случай малого изменения параметров стержня по длине
Тогда, решение для функций смещений и собственной частоты также будем искать в виде асимптотического ряда по степеням малого параметра $\varepsilon $:
Подставим разложения в уравнение (2.1) и в граничные условия (2.2) и, приравнивая члены при одинаковых степенях малого параметра $\varepsilon $, получаем задачи нулевого а) и первого б) порядков для определения собственных частот и форм колебаний. Введя обозначение k2 = $\rho {{S}_{0}}\omega _{0}^{2}{\text{/}}{{I}_{0}}$ и безразмерные геометрические и упругие параметры стержня, получим
Тогда, учитывая, что
2.2. Решение для поправок к собственным частотам и формам колебаний. Будем рассматривать антисимметричное решение задачи а) нулевого приближения, которое имеет простой вид:
Отсюда получаем значения параметра $k$ (нулевого приближения собственных частот):
Отметим, что наименьшее значение ${{k}_{n}}$ равно ${{k}_{0}} = \pi {\text{/}}(2l)$.
С учетом решения для нулевого приближения задача б) для первого приближения запишется в виде неоднородного дифференциального уравнения с граничными условиями:
Будем решать эту задачу методом вариации постоянных:
Коэффициентные функции ${{A}_{{i,n}}}$ находятся из системы уравнений:
Учитывая граничные условия при x = ±l
имеем:Тогда, из граничных условий при находим:
Таким образом, поправка к частоте равна:
Если фиксировать полную амплитуду колебаний величиной Un, то константу В2n можно положить равной нулю. Тогда поправка к собственной форме колебаний примет вид:
Если переменные по длине стержня площадь сечения и модуль Юнга являются четными функциями пространственной координаты, то функция ${{f}_{n}}(\xi )$ = $\bar {I}_{1}^{'}\cos {{k}_{n}}\xi $ – ${{k}_{n}}{{\bar {E}}_{1}}\sin {{k}_{n}}\xi $ является нечетной. Тогда поправка к собственной частоте колебаний будет равна:
Подставляя выражение для ${{f}_{n}}(\xi )$, получим окончательно:
2.3. Случай однородного стержня переменного сечения. Для однородного по модулю упругости стержня E1= 0, ${{\bar {I}}_{1}} = {{\bar {S}}_{1}}$. Для этого случая первые поправки
Проводя интегрирование по частям, в этом случае получим
Для первой моды ${{k}_{0}} = \pi {\text{/}}(2l)$:
поправка к собственной частоте равна
(2.3)
${{\bar {\omega }}_{1}} = \frac{1}{l}\int\limits_0^l {{{{\bar {S}}}_{1}}\cos \left( {\frac{{\pi \xi }}{l}} \right)d\xi } = \frac{1}{{2l}}\int\limits_{ - l}^l {{{{\bar {S}}}_{1}}\cos \left( {\frac{{\pi \xi }}{l}} \right)d\xi } $(2.4)
${{u}_{1}}(x) = \frac{{\pi U}}{{2l}}\left\{ {\int\limits_{ - l}^l {{{{\bar {S}}}_{1}}\cos \left( {\frac{{\pi x}}{{2l}}} \right)\cos \left( {\frac{{\pi \xi }}{l}} \right)d\xi } \frac{{(x + l)}}{{2l}} - \int\limits_{ - l}^x {{{{\bar {S}}}_{1}}\cos \left( {\frac{{\pi x}}{{2l}} - \frac{{\pi \xi }}{l}} \right)d\xi } } \right\}$3. Примеры аналитических расчетов собственной частоты и формы колебаний.
3.1. Тригонометрическое представление формы стержня. Рассмотрим конкретную форму осесимметричного стержня радиуса $r\left( x \right)$ = ${{r}_{0}} + \varepsilon {{r}_{1}}\left( x \right)$, $S\left( x \right)$ = ${{S}_{0}} + \varepsilon {{S}_{1}}\left( x \right)$, ${{S}_{0}} = \pi r_{0}^{2}$, ${{S}_{1}}\left( x \right)$ = $2\pi {{r}_{0}}{{r}_{1}}\left( x \right)$, ${{\bar {S}}_{1}}$ = $2{{r}_{1}}\left( x \right){\text{/}}{{r}_{0}}$.
Пусть радиус стержня может быть представлен в следующем виде:
Определим первую собственную частоту и антисимметричную моду колебаний при ${{k}_{0}} = \pi {\text{/}}(2l)$ по формуле (2.3).
Поправка к частоте равна:
Собственная частота определится формулой:
Вычисляя интегралы (2.4), находим поправку к собственной форме:
Первая антисимметричная собственная форма колебаний имеет вид:
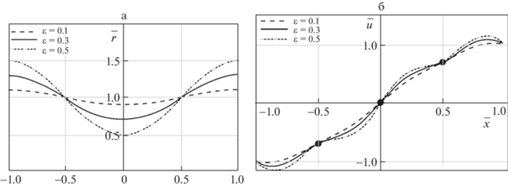
Для наглядной иллюстрации поведения решений задачи для конкретных функций переменного радиуса поперечного сечения на рис. 1,а представлены безразмерные формы стержня $\bar {r} = r(\bar {x}){\text{/}}{{r}_{0}}$, а на рис. 1,б безразмерные собственные формы колебаний $\bar {u} = u(\bar {x}){\text{/}}U$ при различных значениях малого параметра $\varepsilon $ = 0.1, 0.3, 0.5 в зависимости от безразмерной продольной координаты $\bar {x} = x{\text{/}}l$.
Рис. 1.
Форма стержня – а) и собственная форма колебаний – б) при различных значениях малого параметра $\varepsilon $ = 0.1 – штрихованная, $\varepsilon $ = 0.3 – сплошная, $\varepsilon $ = 0.5 – штрих-пунктир.
3.2. Экспериментальные корсетные образцы в форме “песочных часов”. Выберем следующее, часто используемое для образцов в высокочастотных усталостных испытаниях, представление переменного радиуса осесимметричного стержня [8]:
Выберем срединный радиус стержня равным ${{R}_{0}} = \left( {{{R}_{1}} + {{R}_{2}}} \right){\text{/}}2$, что соответствует горизонтальной координате ${{l}_{0}}$ (${{R}_{0}} = {{R}_{1}}\operatorname{ch} \left( {\alpha {{l}_{0}}} \right)$). Далее считаем, что отклонение наружного и внутреннего радиусов стержня от среднего радиуса невелико R2 = R0(1 + ε), R1 = R0(1 – ε).
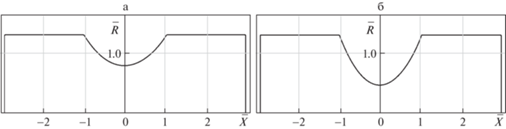
Характерная форма такого стержня со значительным изменением поперечного сечения показана на рис. 2,а для ε = 0.3 и на рис. 2,б для ε = 0.5, введены безразмерные переменные $\bar {R} = r(\bar {X}){\text{/}}{{R}_{0}}$ для формы стержня и $\bar {X} = x{\text{/}}{{l}_{2}}$ для продольной координаты.
Рис. 2.
Форма стержня при различных значениях малого параметра $\varepsilon $ = 0.3 (а), $\varepsilon $ = 0.5 (б).
Определим унифицированные представления этой формы стержня с учетом малости параметра $\varepsilon $
С учетом этих оценок определим поправки к собственной частоте для первой антисимметричной моды:
Введя обозначение δ = πl2/l, получим компактную формулу для поправки к собственной частоте:
Частота первого резонанса будет вычисляться по следующей формуле:
Для данной формы стержня существует точная формула для первой частоты собственных колебаний [8], которая позволяет оценить точность полученной приближенной асимптотической формулы в зависимости от отношения R2/R1.
Точная формула связи геометрии стержня с первой резонансной частотой $\omega $ в безразмерных переменных имеет вид:
В этих же обозначениях асимптотическая формула для безразмерной частоты p
Для оценки точности асимптотических формул построим графики зависимостей l/l2(р) для точной и приближенной формул при различных значениях R2/R1 и $\varepsilon $. Эти графики попарно представлены на рис. 3–5, где прерывной линией изображены кривые, соответствующие точному решению, а сплошной линей – решению по асимптотическим формулам.
Рис. 3.
Зависимость геометрических характеристик стержня от безразмерной частоты а) R2/R1 = 1.5, $\varepsilon $ = 0.2, $\gamma $ = 0.96, б) R2/R1 = 2.1, $\varepsilon $ = 0.355, $\gamma $ = 1.38.
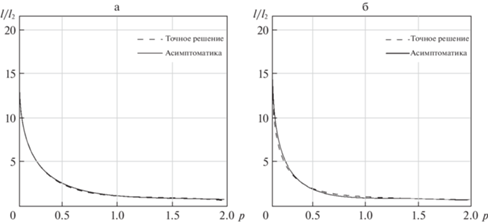
Рис. 4.
Зависимость геометрических характеристик стержня от безразмерной частоты а) R2/R1 = 2.5, $\varepsilon $ = 0.429, $\gamma $ = 1.56, б) R2/R1 = 3, $\varepsilon $ = 0.5, $\gamma $ = 1.76.
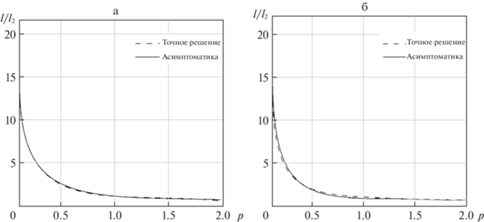
Рис. 5.
Зависимость геометрических характеристик стержня от безразмерной частоты а) R2/R1 = 4, $\varepsilon $ = 0.6, $\gamma $ = 2.06, б) R2/R1 = 5, $\varepsilon $ = 0.67, $\gamma $ = 2.30.
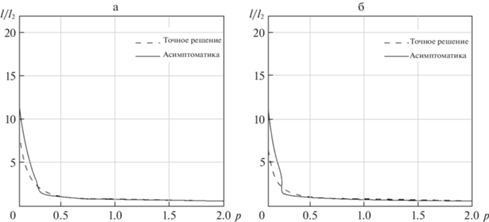
Из рис. 3–4 видно, что при значениях малого параметра $\varepsilon $ = 0.2 решения на графике неотличимы, даже при не малых значениях $\varepsilon $ = 0.35–0.43 ошибка не превышает 2.5%.
Только при более высоких значениях $\varepsilon $ > 0.5, когда параметр $\varepsilon $ ни в коем случае не может считаться малым, графики серьезно расходятся в диапазоне 0 < p < 0.4 (рис. 5).
Однако можно отметить такой любопытный факт. Для типичных образцов из титанового сплава, применяемых в пьезоэлектрической испытательной установке с эксплуатационной частотой 20 кГц, E = 115 ГПа, ρ = 4500 кг/м3, с = 5055 м/c и геометрическим параметром l2 = 1.5 см, величина р = 0.373. Как видно из рис. 3–5, в окрестности этой точки графики точного и приближенного решения пересекаются, и точность асимптотического решения резко возрастает до величин <1%. Поэтому использование полученных асимптотических формул при типичных значениях параметров установки и экспериментальных образцов обеспечивает высокую точность в доли процента для определения их геометрических характеристик.
Заключение. Решена задача определения частоты и формы собственных продольных или крутильных колебаний для стержня переменного сечения на основе теории возмущений. В предположении, что упругие свойства и площадь поперечного сечения прямого стержня меняются достаточно медленно и слабо отклоняются от некоторых средних значений по продольной координате, получены аналитические формулы для поправок к собственным частотам и формам стационарных гармонических колебаний стержня. Работоспособность формул проверена сравнением с точными решениями для некоторых зависимостей площади поперечного сечения от продольной координаты. Показано, что приближенные формулы для первой антисимметричной моды хорошо работают даже для стержней, у которых отношение максимального и минимального радиуса сечения достигает 2.5–3.
Проведены численные расчеты геометрических и упругих свойств образцов для проведения экспериментальных исследований усталостной прочности металлических сплавов при высокочастотном циклическом нагружении на растяжение-сжатие.
Исследование выполнено в рамках госзадания ИАП РАН.
Список литературы
Бабаков И.М. Теория колебаний. М.: Наука, 1965. 560 с.
Акуленко Л.Д., Гавриков А.А., Нестеров С.В. Идентификация дефектов поперечного сечения стержня по собственным частотам и особенностям формы продольных колебаний // Изв. РАН. МТТ. 2019. № 6. С. 98–107.
Акуленко Л.Д., Байдулов В.Г., Георгиевский Д.В., Нестеров С.В. Эволюция собственных частот продольных колебаний стержня при увеличении дефекта поперечного сечения // Изв. РАН. МТТ. 2017. № 6. С. 136–144.
Ватульян А.О., Бочарова О.В. О реконструкции плотности и модуля Юнга для неоднородного стержня // Акуст. ж. 2009. Т. 55. № 3. С. 275–282.
Павлов В.П., Нусратуллина Л.Р. Крутильные колебания стержня непостоянного сечения // Вестн. УГАТУ. Машиностр. и технич. науки. 2022. Т. 26. № 1 (95). С. 22–30.
Хакимов А.Г. О собственных колебаниях вала с моделью искусственного дефекта // Дефектоскопия. 2010. № 6. С. 93–98.
Гусев Б.В., Саурин В.В. О колебаниях неоднородных балок // Инжен. вестн. Дона. 2017. № 3.
Павлов В.П., Нусратуллина Л.Р. Точные решения уравнения, описывающего поперечные колебания стержня с переменным поперечным сечением и их применение // Вестн. Башк. ун-та. Машиностр. и технич. науки. 2019. Т. 23. № 4. С. 774–779.
Гусев Б.В., Саурин В.В. О свободных изгибных колебаниях бетонных балок переменного поперечного сечения // Промышл. и гражд. строит. 2019. № 8. С. 93–98.
Ватульян А.О., Осипов А.В. Об одном подходе при определении параметров дефекта в балке // Дефектоскопия. 2014. № 11. С. 37–47.
Ильгамов М.А., Хакимов А.Г. Диагностика повреждений консольной балки с надрезом // Дефектоскопия. 2009. № 6. С. 83–89.
Лебедев И.М., Шифрин Е.И. Идентификация поперечных трещин в стержне по собственным частотам поперечных колебаний // Изв. РАН. МТТ. 2020. № 4. С. 50–70.
Найфэ А.Х. Введение в методы возмущений. М.: Мир, 1984. 535 с.
Bathias C., Paris P.C. Gigacycle Fatigue in Mechanical Practice. New York: Marcel Dekker, 2005. 328 p.
Дополнительные материалы отсутствуют.
Инструменты
Прикладная математика и механика


