Прикладная математика и механика, 2023, T. 87, № 2, стр. 314-326

К теории метода “эхоскопии” призабойной зоны скважины в низкопроницаемом пласте, подверженным ГРП

Р. А. Башмаков^1, 2, *, Э. В. Галиакбарова^1, 3, **, З. Р. Хакимова^1, 3, ***, В. Ш. Шагапов^1, ****

¹ Институт механики им. Р.Р. Мавлютова Уфимского федерального исследовательского центра РАН
Уфа, Россия

² Уфимский университет науки и технологий,
Уфа, Россия

³ Уфимский государственный нефтяной технический университет
Уфа, Россия

^* E-mail: Bashmakov_Rustem@mail.ru
^** E-mail: Emi.galiakbar@yandex.ru
^*** E-mail: Zulfya.hakimova@yandex.ru
^**** E-mail: Shagapov@rambler.ru

Поступила в редакцию 05.12.2022
После доработки 01.03.2023
Принята к публикации 01.03.2023

EDN: TZACKT
DOI: 10.31857/S0032823523020042

Полный текст (PDF)

Аннотация

Строится математическая модель, описывающая эволюцию импульсного сигнала в скважине при наличии продольной или поперечной трещины ГРП в призабойном участке. Полагается, что из устья скважины сигнал посылается с длиной волны большей диаметра скважины и длины открытого участка скважины. По динамике “эха” импульсного сигнала, возвратившегося к устью скважины, можно судить о качестве гидроразрыва пласта. Приведены результаты численных расчетов для импульса колоколообразной формы. Показано, что при диагностике трещин в качестве флюида, по которому распространяется сигнал, более предпочтительна вода, чем нефть.

Ключевые слова: импульсный сигнал, гидроразрыв пласта, нефтяная скважина, фаза волны, коэффициент отражения, гармонические волны

1. Введение. Для исследования призабойной зоны скважин могут быть использованы различные методы: гидродинамические, акустические, сейсмические, термодинамические. Наиболее активно применяются исследования скважин при установившихся отборах (снятие индикаторных диаграмм); исследование скважин при неустановившихся режимах (снятие кривых восстановления давления, кривых восстановления уровня), исследование скважин на взаимодействие (гидропрослушивание) (см., напр., [1]). Гидроразрыв пласта (ГРП) зарекомендовал себя, как один из наиболее эффективных методов интенсификации добычи высоковязкой нефти или нефти из низкопроницаемых пластов [2].

Существующие способы оценки высоты трещины ГРП после ее образования (акустический, температурный, импульсный нейтрон-нейтронный каротаж с использованием нейтроно-поглощающего проппанта) имеют высокую погрешность. Применение новых способов добычи нефти и необходимость более точного прогнозирования процесса эксплуатации скважин, совершенствование приборов и способов наблюдения за режимами работы требуют новых подходов для определения состояния призабойной зоны скважин.

В работах [3, 4] изучаются собственные колебания жидкости в скважине с трещиной ГРП. При этом период колебаний, а также, особенно, интенсивность затухания колебаний определяются не только протяженностью столба жидкости в скважине, ее диаметром и реологическими свойствами жидкости, но и коллекторскими характеристиками призабойной зоны пласта (в частности, коэффициентами проницаемости, качеством перфорации скважин и свойствами образованных трещин ГРП).

В работе [5] предложен метод гидравлического импедансного тестирования, идея которого заключается в интерпретации фактического изменения гидравлического сопротивления между стволом скважины и открытой трещиной ГРП. Для этого искусственно создается импульс давления в скважину и анализируется отраженный сигнал.

В работе [6] приведены результаты полевых измерений изменения давления в различных точках скважины при резком изменении скорости потока жидкости. Скважинные датчики фиксировали изменение давления в зависимости от времени со скоростью 100 проб в секунду.

В статье [7] исследована динамика импульсного сигнала, распространяющегося в кольцевом зазоре между диагностирующим зондом и открытой скважиной, окруженной низкопроницаемым пластом, подвергаемым гидроразрыву. В [8] изучено влияние на дисперсию сигнала влияния фильтрационных характеристик призабойной зоны скважины.

В данной работе рассматривается метод эхоскопии призабойной зоны скважины: из устья скважины посылается сигнал распространяющийся по жидкости с длиной волны большей диаметра скважины и большей, чем длина открытого участка скважины.

Термин “эхоскопия” используется в основном в медицинской литературе и означает исследование органов и тканей с помощью ультразвуковых волн. Особенностью ультразвуковых волн является способность отражаться от границ сред, отличающихся друг от друга по плотности. Использование этого термина применительно к диагностике трещин ГРП оправдывается использованием идеи анализа изменения волнового сигнала при изменении параметров трещины. Для решения поставленной задачи строится математическая модель, описывающая распространение импульсного сигнала в скважине и для описания распространения волн в трещине используются интегро-дифференциальное уравнение фильтрации жидкости в вертикальной трещине ГРП (плоской трещине, идущей параллельно стволу скважины) [9] и радиальной трещине, перпендикулярной стволу скважины в виде, представленном в работе [10]. Изменение импульсного сигнала в скважине изучается с применением преобразования Фурье, для численной реализации используется быстрое преобразование Фурье [11].

2. Основные уравнения. Рассмотрим систему “вертикальная скважина–пласт–трещина ГРП” (рис. 1). Предполагается, что скважина через открытый участок длины ${{l}_{p}}$ сообщается с пластом, а также трещинами, имеющими симметричное продольное или радиальное расположение относительно вскрытого участка скважины. Кроме того, длина открытого участка скважины значительно меньше длины его закрытого участка $l$ $\left( {{{l}_{p}} \ll l} \right)$. Примем, что в исходном состоянии жидкость, находящаяся в системе “скважина–пласт” покоится, т.е. течение в вертикальной скважине и горизонтальном пласте отсутствует.

Рис. 1.

Схема скважины, сообщающейся с пластом (а) и призабойной зоны с продольными (б) и радиальными (в) трещинами ГРП. Обозначения: ${{a}_{{\text{c}}}}$ – радиус скважины, a – радиус обсадной колонны скважины, $l$ – протяженность скважины, ${{l}_{p}}$ – протяженность призабойной зоны пласта.

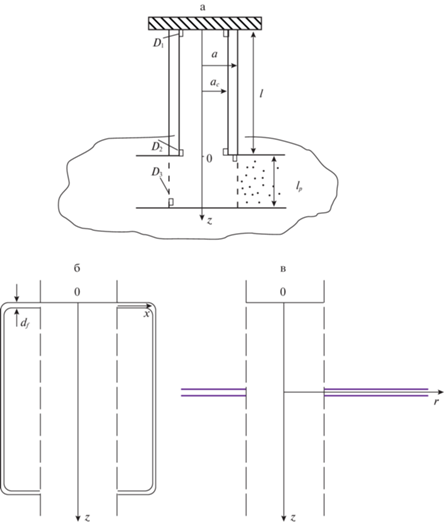
Пусть на устье скважины (точка D₁ на рис. 1) создается импульсный сигнал давления, который будет распространяться по жидкости в скважине. Принимается приближение акустически сжимаемой жидкости. Ось $Oz$ направим вертикально вниз, начало координат поместим на забое скважины.

Рассмотрим распространение волн давления малой амплитуды в скважине при следующих допущениях: длина сканирующей волны $\lambda $ больше радиуса скважины ${{a}_{с}}$ и длины открытого участка скважины, но значительно меньше длины скважины ($\lambda > {{a}_{с}}$, $\lambda > {{l}_{p}}$, $\lambda \ll l$); при распространении акустической волны по каналу вязкость проявляется в тонком пограничном слое, и означает, что для частоты возмущения выполняется условие: ${{a}_{с}} \gg 2\sqrt {{\nu \mathord{\left/ {\vphantom {\nu \omega }} \right. \kern-0em} \omega }} $, где $\nu $ – коэффициент кинематической вязкости жидкости; $\omega $ – круговая частота.

Система основных уравнений, описывающая распространение импульсного сигнала в скважине, представляющая собой законы сохранения масс и импульса, в линеаризованном приближении имеет вид [8]:

(2.1)

$\begin{gathered} \frac{1}{{{{С}^{2}}}}\frac{{\partial P}}{{\partial t}} + {{\rho }_{0}}\frac{{\partial w}}{{\partial z}} = 0 \\ {{\rho }_{0}}\frac{{\partial w}}{{\partial t}} + \frac{{\partial P}}{{\partial z}} = - \frac{{2\sigma }}{{{{a}_{с}}}},\quad \sigma = {{\rho }_{0}}\sqrt {\frac{\nu }{\pi }} \int\limits_{ - \infty }^t {\frac{{\left( {{{\partial w} \mathord{\left/ {\vphantom {{\partial w} {\partial \tau }}} \right. \kern-0em} {\partial \tau }}} \right)}}{{\sqrt {t - \tau } }}d\tau } \quad \left( {\nu = {\mu \mathord{\left/ {\vphantom {\mu {{{\rho }_{0}}}}} \right. \kern-0em} {{{\rho }_{0}}}}} \right) \\ \end{gathered} $

Здесь $P$ и w – возмущения давления и скорости; ${{\rho }_{0}}$ – плотность жидкости в невозмущенном состоянии; C – скорость звука в жидкости; $\mu $ – динамическая вязкость жидкости; $\sigma $ – касательное напряжение на стенках канала [12].

Поскольку длина ${{l}_{p}}$ открытого участка $0 < z < {{l}_{p}}$ значительно меньше длины закрытого участка $ - l < z < 0$, то можем принять, что возмущение давления в открытом участке однородное. Поэтому в качестве граничного условия для системы (2.1) при $z = 0$ примем

(2.2)

$P(0,t) = {{P}_{{(l)}}}(t)$

Второе граничное условие получим из закона сохранения массы жидкости на открытом участке, которое с учетом однородности возмущений давления в призабойной зоне скважины для продольной и радиальной трещин, соответственно, запишется в виде:

(2.3)

$\pi a_{с}^{2}{{l}_{p}}\frac{1}{{{{С}^{2}}}}\frac{{\partial {{P}_{{(l)}}}}}{{\partial t}} = \pi a_{с}^{2}{{\rho }_{0}}{{w}_{{(l)}}} - 2\pi a{{l}_{p}}{{\rho }_{0}}{{u}_{p}} - 2{{d}_{f}}{{l}_{p}}{{\rho }_{0}}{{u}_{f}}$

(2.4)

где ${{w}_{{(l)}}}$ – скорость жидкости в скважине при $z = 0$; ${{u}_{p}}$ и ${{u}_{f}}$ – скорости фильтрации жидкости в пласт через стенку открытого участка скважины и в трещину шириной ${{d}_{f}}$; ${{a}_{с}}$ и $a$ – радиусы скважины и обсадной трубы.

Для определения значений ${{u}_{p}}$ и ${{u}_{f}}$, в свою очередь, необходимо рассмотреть внешнюю, от открытого участка скважины, фильтрационную задачу в пласте и трещине. Уравнения упругой фильтрации жидкости из открытого участка скважины в пласт в процессе отражения импульса давления от забойного участка запишем в виде:

(2.5)

${{u}_{p}} = - \frac{{{{k}_{p}}}}{\mu }\frac{{\partial {{P}_{p}}}}{{\partial r}},\quad \frac{{\partial {{P}_{p}}}}{{\partial t}} = \frac{{{{\unicode{230} }_{p}}}}{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial {{P}_{p}}}}{{\partial r}}} \right)\quad (0 < z < {{l}_{p}},\;a < r < \infty )$

Для фильтрации в продольную трещину примем уравнения [9]:

(2.6)

$\begin{gathered} {{u}_{f}} = - \frac{{{{k}_{f}}}}{\mu }\frac{{\partial {{P}_{f}}}}{{\partial x}},\quad \frac{{\partial {{P}_{f}}}}{{\partial t}} = {{\unicode{230} }_{f}}\frac{{{{\partial }^{2}}{{P}_{f}}}}{{\partial {{x}^{2}}}} - 2\frac{{{{m}_{p}}}}{{{{m}_{f}}}}\frac{{\sqrt {{{\unicode{230} }_{p}}} }}{{{{d}_{f}}}}\int\limits_{ - \infty }^t {\frac{{{{\partial {{P}_{f}}\left( {\tau ,x} \right)} \mathord{\left/ {\vphantom {{\partial {{P}_{f}}\left( {\tau ,x} \right)} {\partial \tau }}} \right. \kern-0em} {\partial \tau }}}}{{\sqrt {\pi \left( {t - \tau } \right)} }}} d\tau \\ (0 < z < {{l}_{p}},\;0 < x < \infty ), \\ \end{gathered} $

а для радиальной трещины используем [10]:

(2.7)

$\begin{gathered} {{u}_{f}} = - \frac{{{{k}_{f}}}}{\mu }\frac{{\partial {{P}_{f}}}}{{\partial r}},\quad \frac{{\partial {{P}_{f}}}}{{\partial t}} = \frac{\unicode{230} }{r}\frac{\partial }{{\partial r}}\left( {r\frac{{\partial {{P}_{f}}}}{{\partial r}}} \right) - 2\frac{{{{m}_{p}}}}{{{{m}_{f}}}}\frac{{\sqrt {{{\unicode{230} }_{p}}} }}{{{{d}_{f}}}}\int\limits_{ - \infty }^t {\frac{{{{\partial {{P}_{f}}\left( {\tau ,r} \right)} \mathord{\left/ {\vphantom {{\partial {{P}_{f}}\left( {\tau ,r} \right)} {\partial \tau }}} \right. \kern-0em} {\partial \tau }}}}{{\sqrt {\pi \left( {t - \tau } \right)} }}} d\tau \\ (0 < z < {{l}_{p}},\;a < r < \infty ), \\ \end{gathered} $

где $r$ – расстояние от оси скважины, ${{P}_{p}}$ и ${{P}_{f}}$ – возмущения давления в пласте и трещине; ${{m}_{s}}\,$, ${{k}_{s}}\,$ и ${{\unicode{230} }_{s}} = \frac{{{{k}_{s}}\,{{\rho }_{0}}{{C}^{2}}}}{{{{m}_{s}}\mu }}$ $\left( {s = f,p} \right)$ – пористость, коэффициенты проницаемости и пьезопроводности.

Начальные и граничные условия запишутся как:

(2.8)

${{\left. P \right|}_{{t \to - \infty }}} = 0,\quad {{\left. w \right|}_{{t \to - \infty }}} = 0$

(2.9)

${{\left. P \right|}_{{z = - l}}} = f(t)$

(2.10)

${{P}_{p}}\left( {r \to + \infty } \right) = 0,\quad {{P}_{p}}\left( {r = a} \right) = {{P}_{{(l)}}}(t)$

(2.11)

${{P}_{f}}\left( {x \to + \infty } \right) = 0,\quad {{P}_{f}}\left( {x = 0} \right) = {{P}_{{(l)}}}(t)\quad {\text{для продольной трещины}}$

(2.12)

${{P}_{f}}\left( {r \to + \infty } \right) = 0,\quad {{P}_{f}}\left( {r = a} \right) = {{P}_{{(l)}}}(t)\quad {\text{для радиальной трещины}}$

Условие (2.9) задает форму импульса давления характерной длительности $\Delta t$ и амплитуды $\Delta {{P}_{0}}$, создаваемого в устье ($z = - l$) скважины.

3. Дисперсионные выражения для гармонических волн в скважине. Решения системы уравнений (2.1) ищем в виде затухающих гармонических волн:

(3.1)

$P,w = {{A}^{{(p)}}}(z),{{A}^{{(w)}}}(z)\left[ {\exp \left[ {i\left( {Kz - \omega t} \right)} \right]} \right],$

где $\omega $ – круговая частота, $K = k + i\delta $ – волновой вектор, ${{C}_{p}} = {\omega \mathord{\left/ {\vphantom {\omega k}} \right. \kern-0em} k}$ и $\delta $ – фазовая скорость и коэффициент затухания, ${{A}^{{(p)}}}$ – амплитуда параметра $p$, ${{A}^{{(w)}}}$ – амплитуда параметра $w$.

Подставляя (3.1) в систему (2.1), получим

(3.2)

$\begin{gathered} - \frac{{i\omega }}{{{{C}^{2}}}}{{A}^{{(p)}}} + iK{{\rho }_{0}}{{A}^{{(w)}}} = 0 \\ - {{\rho }_{0}}\omega {{A}^{{(w)}}} + K{{A}^{{(p)}}} = \left( {\frac{2}{{{{a}_{c}}}}\sqrt {{{\rho }_{0}}\mu } \sqrt {\frac{\omega }{2}} \left( {1 + i} \right)} \right){{A}^{{(w)}}} \\ \end{gathered} $

Из этой системы уравнений (3.2), при условии существования нетривиального решения вида (3.1), получим дисперсионное уравнение:

(3.3)

$K = \pm \frac{\omega }{C}{{\left( {1 + \frac{1}{{{{a}_{c}}}}\sqrt {\frac{{2\nu }}{\omega }} \left( {1 + i} \right)} \right)}^{{1{\text{/}}2}}}$

Учитывая, что длина сканирующей волны $\lambda $ больше длины открытого участка скважины ${{l}_{p}}$ ($\lambda > {{l}_{p}}$), открытый участок скважины принимается отражающей поверхностью с координатой $z = 0$.

Для гармонической волны вида (3.1), падающей на отражающую поверхность ($z = 0$) положим, что на участке $ - l < z < 0$ формируется отраженная волна для которой соответствующее волновое число из (3.3) берется со знаком “–”. Причем, в забое скважины (на отражающей поверхности $z = 0$) давление определяется как сумма давлений, соответствующих падающей и отраженной волнам

(3.4)

${{P}_{{(o)}}} + {{P}_{{(r)}}} = {{P}_{{(l)}}}$

Здесь нижние индексы ${\text{(}}o{\text{)}}$ и ${\text{(}}r{\text{)}}$ указывают значениям давления для падающей и отраженной волнам при $z = 0$.

Тогда для решения вида (3.1) условие (3.4) можно записать как

(3.5)

$A_{{(o)}}^{{(p)}} + A_{{(r)}}^{{(p)}} = A_{{(l)}}^{{(p)}}$

Скорость жидкости ${{w}_{{(l)}}}$ на границе колонны скважины ($z = 0$) складывается из ${{w}_{{(o)}}}$ и ${{w}_{{(r)}}}$, соответствующим падающей и отраженным волнам (${{w}_{{(l)}}} = {{w}_{{(o)}}} + {{w}_{{(r)}}}$). Причем для гармонической волны следует

(3.6)

${{w}_{{(o)}}} = A_{{(o)}}^{{(w)}}{{e}^{{ - i\omega t}}},\quad {{w}_{{(r)}}} = A_{{(r)}}^{{(w)}}{{e}^{{ - i\omega t}}}$

Для амплитуд скорости $A_{{(o)}}^{{(w)}}$ и $A_{{(r)}}^{{(w)}}$, соответствующих падающей и отраженной волнам, на основе первого уравнения из (3.2) с учетом (3.3) можно записать

(3.7)

$A_{{(o)}}^{{(w)}} = \frac{{A_{{(o)}}^{{(p)}}}}{{{{\rho }_{0}}C}}{{\left( {1 + \frac{1}{{{{a}_{c}}}}\sqrt {\frac{{2\nu }}{\omega }} (1 + i)} \right)}^{{ - 1{\text{/}}2}}},\quad A_{{(r)}}^{{(w)}} = - \frac{{A_{{(r)}}^{{(p)}}}}{{{{\rho }_{0}}C}}{{\left( {1 + \frac{1}{{{{a}_{c}}}}\sqrt {\frac{{2\nu }}{\omega }} (1 + i)} \right)}^{{ - 1{\text{/}}2}}}$

Граничные условия при $z = 0$, следующие из (2.3) и (2.4) для продольной трещины и радиальной трещины с учетом уравнений фильтрации в пласт (2.4) и трещины ((2.6) – продольная и (2.7) – радиальная), можно привести к виду:

(3.8)

$\frac{1}{{{{\rho }_{0}}{{С}^{2}}}}\frac{{\partial {{P}_{{(l)}}}}}{{\partial t}} = \frac{{{{w}_{{(l)}}}}}{{{{l}_{p}}}} + \frac{{2a}}{{{{a}_{c}}^{2}}}\frac{{{{k}_{p}}}}{\mu }{{\left. {\left( {\frac{{\partial {{P}_{p}}}}{{\partial r}}} \right)} \right|}_{{\begin{subarray}{l} r = a \\ z = 0 \end{subarray}} }} + \frac{{2{{d}_{f}}}}{{\pi {{a}_{c}}^{2}}}\frac{{{{k}_{f}}}}{\mu }{{\left. {\left( {\frac{{\partial {{P}_{f}}}}{{\partial x}}} \right)} \right|}_{{\begin{subarray}{l} x = 0 \\ z = 0 \end{subarray}} }}$

(3.9)

$\frac{1}{{{{\rho }_{0}}{{С}^{2}}}}\frac{{\partial {{P}_{{(l)}}}}}{{\partial t}} = \frac{{{{w}_{{(l)}}}}}{{{{l}_{p}}}} + \frac{{2a}}{{{{a}_{c}}^{2}}}\frac{{{{k}_{p}}}}{\mu }{{\left. {\left( {\frac{{\partial {{P}_{p}}}}{{\partial r}}} \right)} \right|}_{{\begin{subarray}{l} r = a \\ z = 0 \end{subarray}} }} + \frac{{2a{{d}_{f}}}}{{{{a}_{c}}^{2}{{l}_{p}}}}\frac{{{{k}_{f}}}}{\mu }{{\left. {\left( {\frac{{\partial {{P}_{f}}}}{{\partial r}}} \right)} \right|}_{{\begin{subarray}{l} r = a \\ z = 0 \end{subarray}} }}$

Решения для распределения давления и скорости в призабойной зоне для гармонического закона изменения давления в забое скважины будем искать в виде:

(3.10)

${{P}_{p}} = A_{p}^{{(p)}}(r)\exp \left[ { - i\omega t} \right],\quad {{u}_{p}} = A_{p}^{{(u)}}(r)\exp \left[ { - i\omega t} \right],$

где ${{A}^{{(u)}}}$ – амплитуда параметра $u$.

Тогда из уравнений (2.5) для закона распределения давления и скорости фильтрации получим следующие уравнения

(3.11)

$A_{p}^{{(u)}}(r) = - \frac{{{{k}_{p}}}}{\mu }\frac{{dA_{p}^{{(p)}}}}{{dr}}\quad {\text{и}}\quad \frac{1}{r}\frac{d}{{dr}}\left( {r\frac{{dA_{p}^{{(p)}}}}{{dr}}} \right) = q_{p}^{2}A_{p}^{{(p)}},$

где $q_{p}^{2} = - i\omega {\text{/}}{{\unicode{230} }_{p}}$.

Из граничного условия (2.10) следует

$A_{p}^{{(p)}}(a) = A_{{(l)}}^{{(p)}}\quad {\text{и}}\quad A_{p}^{{(p)}}(r) \to {{\left. 0 \right|}_{{r \to \infty }}}$

Тогда для решения уравнений (3.11) можно записать

(3.12)

$A_{p}^{{(p)}}(r) = A_{{(l)}}^{{(p)}}\frac{{{{K}_{0}}({{q}_{p}}r)}}{{{{K}_{0}}({{q}_{p}}a)}},\quad A_{p}^{{(u)}}(r) = \frac{{{{k}_{p}}}}{\mu }{{q}_{p}}A_{{(l)}}^{{(p)}}\frac{{{{K}_{1}}({{q}_{p}}r)}}{{{{K}_{0}}({{q}_{p}}a)}},$

где ${{K}_{0}}(S) = \int_0^\infty {{{e}^{{ - S\operatorname{ch} \xi }}}d\xi } $ и ${{K}_{1}}(S) = - \frac{{d\,{{K}_{0}}(S)}}{{d\,S}}$ – функции Макдональда нулевого и первого порядков

Для распределения давления и скорости фильтрации в продольной трещине решение будем искать в виде:

${{P}_{f}} = A_{f}^{{(p)}}(x)\exp \left[ { - i\omega t} \right],\quad {{u}_{f}} = A_{f}^{{(u)}}(x)\exp \left[ { - i\omega t} \right],$

из уравнения (2.6) получим:

(3.13)

$A_{f}^{{(u)}}(x) = - \frac{{{{k}_{f}}}}{\mu }\frac{{dA_{f}^{{(p)}}}}{{dx}}\quad {\text{и}}\quad \frac{{{{d}^{2}}A_{f}^{{(p)}}}}{{d{{x}^{2}}}} = q_{f}^{2}A_{f}^{{(p)}},$

где $q_{f}^{2} = - i\left( {\frac{\omega }{{{{\unicode{230} }_{f}}}} + 2\frac{{{{m}_{p}}}}{{{{m}_{f}}}}\;\frac{{\sqrt {{{\unicode{230} }_{p}}} }}{{{{\unicode{230} }_{f}}}}\frac{{\sqrt {i\omega } }}{{{{d}_{f}}}}} \right)$.

С учетом граничных условий (2.11) решения уравнений (3.13) имеют вид:

(3.14)

$A_{f}^{{(p)}}(x) = A_{{(l)}}^{{(p)}}\exp \left[ { - {{q}_{f}}x} \right],\quad A_{f}^{{(u)}}(x) = \frac{{{{k}_{f}}}}{\mu }{{q}_{f}}A_{{(l)}}^{{(p)}}\exp \left[ { - {{q}_{f}}x} \right]$

Аналогично предыдущему (3.10) решения уравнений (2.7) для радиальной трещины при условии (2.12) запишем как

(3.15)

$A_{f}^{{(p)}}(r) = A_{{(l)}}^{{(p)}}\frac{{{{K}_{0}}({{q}_{f}}r)}}{{{{K}_{0}}({{q}_{f}}a)}},\quad A_{f}^{{(u)}}(r) = \frac{{{{k}_{f}}}}{\mu }{{q}_{f}}A_{{(l)}}^{{(p)}}\frac{{{{K}_{1}}({{q}_{f}}r)}}{{{{K}_{0}}({{q}_{f}}a)}}$

Тогда, подставляя (3.12) и (3.14) в уравнение (3.8) и принимая во внимание (3.5), получим

(3.16)

$\frac{{ - i\omega }}{{{{\rho }_{0}}{{C}^{2}}}}\left( {A_{{(o)}}^{{(p)}} + A_{{(r)}}^{{(p)}}} \right) = \frac{{A_{{(l)}}^{{(w)}}}}{{{{l}_{p}}}} - \frac{{2a}}{{a_{c}^{2}}}\frac{{{{k}_{p}}}}{\mu }{{q}_{p}}\frac{{{{K}_{1}}({{q}_{p}}a)}}{{{{K}_{0}}({{q}_{p}}a)}}A_{{(l)}}^{{(p)}} - \frac{{2{{d}_{f}}}}{{\pi a_{c}^{2}}}\frac{{{{k}_{f}}}}{\mu }{{q}_{f}}A_{{(l)}}^{{(p)}}$

Из (3.16) с учетом (3.7) можем записать

(3.17)

$\begin{gathered} A_{{(o)}}^{{(p)}} - A_{{(r)}}^{{(p)}} = A_{{(l)}}^{{(p)}}{{\Delta }_{\parallel }} \\ {{\Delta }_{\parallel }} = {{\rho }_{0}}C{{l}_{p}}{{\left( {1 + \frac{1}{{{{a}_{c}}}}\sqrt {\frac{{2\nu }}{\omega }} (1 + i)} \right)}^{{1{\text{/}}2}}}\left( {\frac{{ - i\omega }}{{{{\rho }_{0}}{{C}^{2}}}}\left. { + \frac{{2{{k}_{p}}}}{\mu }{{q}_{p}}\frac{a}{{a_{c}^{2}}}\frac{{{{K}_{1}}({{q}_{p}}a)}}{{{{K}_{0}}({{q}_{p}}a)}} + \frac{{2{{d}_{f}}}}{{\pi a_{c}^{2}}}\frac{{{{k}_{f}}}}{\mu }{{q}_{f}}} \right)} \right. \\ \end{gathered} $

Из совместного решения (3.5) и (3.17) получим выражение для коэффициента отражения $N$ $\left( {N = A_{{(r)}}^{{(p)}}{\text{/}}A_{{(o)}}^{{(p)}}} \right)$ от забоя скважины в случае продольной трещины

(3.18)

$N = 1 - \frac{{2{{\Delta }_{\parallel }}}}{{1 + {{\Delta }_{\parallel }}}}$

После аналогичных преобразований из (3.9) с учетом (3.12) и (3.15) найдем коэффициент отражения в случае радиальной трещины:

(3.19)

$\begin{gathered} N = 1 - \frac{{2{{\Delta }_{r}}}}{{1 + {{\Delta }_{r}}}} \\ {{\Delta }_{r}} = {{\rho }_{0}}C{{l}_{p}}{{\left( {1 + \frac{1}{{{{a}_{c}}}}\sqrt {\frac{{2\nu }}{\omega }} (1 + i)} \right)}^{{1/2}}}\left( {\frac{{ - i\omega }}{{{{\rho }_{0}}{{C}^{2}}}}\left. { + \frac{{2{{k}_{p}}}}{\mu }{{q}_{p}}\frac{a}{{a_{c}^{2}}}\frac{{{{K}_{1}}({{q}_{p}}a)}}{{{{K}_{0}}({{q}_{p}}a)}} + \frac{{2{{d}_{f}}a}}{{{{l}_{p}}a_{c}^{2}}}\frac{{{{k}_{f}}}}{\mu }{{q}_{f}}\frac{{{{K}_{1}}({{q}_{f}}a)}}{{{{K}_{0}}({{q}_{f}}a)}}} \right)} \right. \\ \end{gathered} $

4. Численные анализ. Динамика импульсного сигнала в скважине изучается с применением преобразования Фурье и программы быстрого преобразования, для численной реализации [11, 13], а в качестве импульсного сигнала в момент времени ${{t}_{0}}$ возьмем давление колоколообразной формы длительности $\Delta t$ с амплитудой $\Delta {{P}_{0}}$:

(4.1)

${{\tilde {P}}^{{(0)}}} = \Delta {{P}_{0}}\exp \left( { - {{{\left( {6\frac{{t - {{t}_{0}}}}{{\Delta t}}} \right)}}^{2}}} \right)$

Для сигнала, дошедшего и отраженного от сечения $z = 0$ канала имеем:

(4.2)

${{P}_{{(o)}}}(t) = \frac{1}{\pi }\int\limits_0^\infty {\int\limits_{ - \infty }^\infty {{{{\tilde {P}}}^{{(0)}}}(\tau ){\kern 1pt} \exp (iK(\omega )l)\exp \left[ {i\omega (t - \tau )} \right]} } d\omega d\tau $

(4.3)

${{P}_{{(r)}}}(t) = \frac{1}{\pi }\int\limits_0^\infty {\int\limits_{ - \infty }^\infty {{{P}_{{(l)}}}(\tau )N(\omega )\exp \left[ {i\omega (t - \tau )} \right]} } d\omega d\tau $

Согласно выражениям (4.2) с учетом (3.3) и (4.3) с учетом (3.18) и (3.19) следует, что наличие гидроразрывных трещин, продольных и радиальных вскрытому участку скважины, приводит к дисперсии в динамике импульсного сигнала по скважине.

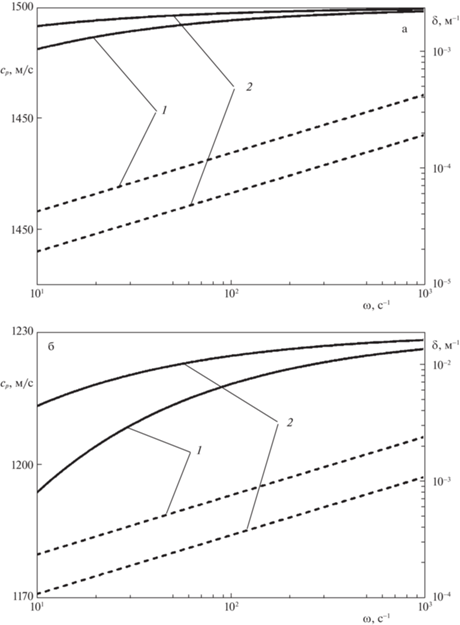
На рис. 2 представлено влияние вида жидкости в скважине на зависимости фазовой скорости и коэффициента затухания от частоты. Для параметров скважины и жидкости (воды или нефти) приняты следующие величины: $l$ = 2.6 × 10³ м; ${{a}_{c}}$ = 3.5 × 10^–2 м; $a$ = 7.75 × 10^–2 м; ρ₀ = 10³, 890 кг/м³; C = 1.5 × 10³, 1.23 × 10³ м/с; μ = 10^–3, 2 × 10^–2 Па с. Заметно снижение фазовой скорости, которое для воды составляет менее 10 м/с, а для нефти в обсаженной скважине может уменьшаться на 15 м/с при круговой частоте $\omega = {{10}^{2}}$ c^–1 и на 40 м/с при круговой частоте $\omega = 10$ с^–1. Коэффициенты затухания в обсаженной скважине для воды и нефти отличаются более, чем в 6 раз. Например, при круговой частоте $\omega = {{10}^{2}}$ с^–1 коэффициент затухания примерно равен $\delta = 1.5 \times {{10}^{{ - 4}}}{\kern 1pt} $ м^–1 в воде и $\delta = {{10}^{{ - 3}}}{\kern 1pt} $ м^–1 в нефти, а характерное расстояние затухания примерно равно ${{z}_{\delta }} = 6.6 \times {{10}^{3}}$ м для воды и ${{z}_{\delta }} = {{10}^{3}}{\kern 1pt} $ м для нефти.

Рис. 2.

Зависимости фазовой скорости (сплошные) и коэффициента затухания (пунктирные) от частоты. Линии 1 и 2 соответствуют обсаженной и не обсаженной (a_c = a) скважине. Скважина и пласт заполнены водой – а, нефтью – б.

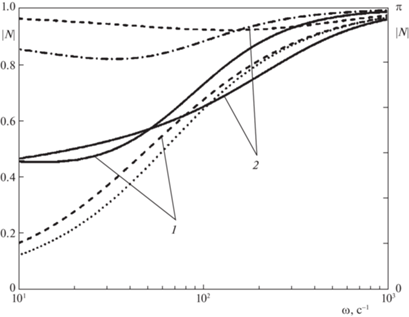
На рис. 3, 4 показано влияние трещины проводимости ${{C}_{f}} = {{d}_{f}}{{k}_{f}}$ пористостью ${{m}_{f}}$ = 0.2 на модуль и аргумент коэффициента отражения сигнала, рассчитанных для продольной и радиальной трещины по выражению (3.18) и (3.19) соответственно. Принято, что обсаженная скважина и пласт ${{k}_{p}} = {{10}^{{ - 15}}}$ м², ${{m}_{p}}$ = 0.1, ${{l}_{p}}$ = 20 м заполнены водой. Из рисунков следует, что при отсутствии трещины значение модуля коэффициента отражения примерно равно 0.9, аргумент близок к углу $\pi {\text{/}}2$ для круговой частоты $\omega = {{10}^{2}}$ с^–1. Наличие трещины проводимости ${{C}_{f}} = 5 \times {{10}^{{ - 12}}}$ м³ изменяет фазу сигнала, поскольку аргумент коэффициента отражения становится близкий к углу $\pi $ для круговой частоты $\omega = {{10}^{2}}$ с^–1. Для радиальной трещины проводимости ${{C}_{f}} = 5 \times {{10}^{{ - 13}}}$ м³ несмотря на некоторое снижение модуля коэффициента отражения, его аргумент близок к углу $\pi {\text{/}}2$, также как и при отсутствии трещины. Это позволяет предположить, что “эхоскопия” будет менее чувствительна к трещинам, перпендикулярным вскрытому участку скважины.

Рис. 3.

Зависимости модуля коэффициента отражения (сплошные и штрихпунктирные линии) и аргумента (пунктирные и точечные линии) от частоты. Штрихпунктирные и точечные линии – при отсутствии трещины. Линии 1, 2 и 3 соответствуют продольной трещине проводимости С_f = 5 × 10^–13; 5 × 10^–12; 5 × 10^–11 м³.

Рис. 4.

Зависимости модуля коэффициента отражения (сплошные и штрихпунктирные линии) и аргумента (пунктирные и точечные линии) от частоты. Штрихпунктирные и точечные линии – при отсутствии трещины. Линии 1 и 2 соответствуют радиальной трещине проводимости С_f = 5 × 10^–13 и 5 × 10^–12 м³.

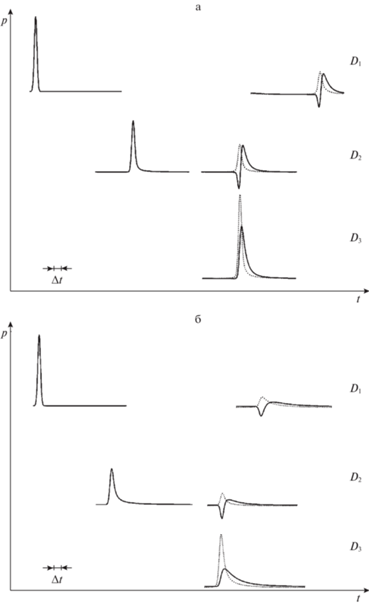
На рис. 5 представлена динамика импульсного сигнала длительности $\Delta t = 5 \times {{10}^{{ - 2}}}$ с в обсаженной скважине с водой. Расчетные параметры совпадают с параметрами рис. 2–4 . Алгоритмические датчики D₁, D₂ и D₃ расположены на устье, забое и дне скважины. Видно, наличие трещины приводит к качественному изменению эволюции импульсного сигнала в скважине. Образуется импульс сжатия от забоя без трещины или импульс разгрузки при наличии трещины в забое. Для обнаружения радиальной трещины малой проводимости можно использовать более короткие сигналы (рис. 6,б). Заметим, что на дне вскрытой скважины при отсутствии трещины в забое происходит усиление сигнала, т.к. из-за низкой проницаемости пласта призабойная зона ведет себя как жесткая стенка.

Рис. 5.

Динамика сигнала длительности Δt = 5 × 10^–2 c в обсаженной скважине. Сплошная линия соответствует наличию продольной трещины проводимости ${{C}_{f}}$ = 5 × 10^–13 м³ , точечная линия – при отсутствии трещины.

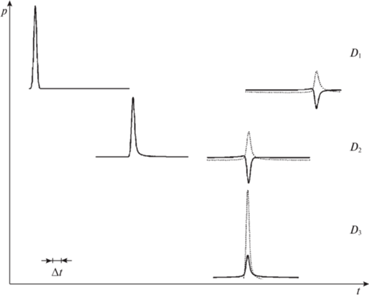
Рис. 6.

Расчетные осциллограммы импульсного сигнала длительности Δt = 5 × 10^–2 c – а и Δt = 8 × 10^–3 c – б в обсаженной скважине с радиальной трещиной (сплошные линии) проводимости ${{C}_{f}}$ = 5 × 10^–13 м³ и без трещины (точечные линии) на вскрытом участке.

Заключение. Предложен метод “эхоскопии” для обнаружения трещин гидроразрыва в низкопроницаемых пластах, проницаемостью порядка миллидарси. По динамике импульсного сигнала в обсаженной скважине с открытым участком, заполненным водой можно судить качественно о наличии ГРП трещин. Для более детального определения фильтрационных характеристик гидроразрывных трещин следует запускать еще более короткие импульсные сигналы конкретно на вскрытом участке скважины, соответствующая теория акустического “телевизора” предложена в работах [7, 8]. Эволюция импульсного сигнала более четко прослеживается, если в роли фильтрующейся жидкости используется вода. Наблюдается импульс сжатия от забоя без трещины или импульс разгрузки при наличии трещины в забое. Для обнаружения радиальной трещины малой проводимости целесообразно использовать более короткие сигналы.

Исследование выполнено за счет гранта Российского научного фонда № 21-11-00207, https://rscf.ru/project/21-11-00207/

Список литературы

Кременецкий М.И., Ипатов А.И. Гидродинамические и промыслово-технологические исследования скважин. М.: МАКС Пресс, 2008. 475 с.
Экономидес М. Унифицированный дизайн гидроразрыва пласта: от теории к практике. М.; Ижевск: Институт компьютерных технологий, 2007. 237 с.
Байков В.А., Булгакова Г.Т., Ильясов А.М., Кашапов Д.В. К оценке геометрических параметров трещины гидроразрыва пласта // Изв. РАН. МЖГ. 2018. № 5. С. 64–75.
Башмаков Р.А., Насырова Д.А., Шагапов В.Ш. Собственные колебания жидкости в скважине, сообщающейся с пластом, при наличии трещины ГРП // ПММ. 2022. Т. 86. № 1. С. 88–104.
Holzhausen G.R., Gooch R.P. Impedance of Hydraulic Fractures: Its Measurement and Use for Estimating Fracture Closure Pressure and Dimensions // Paper presented at the SPE/DOE Low Permeability Gas Reservoirs Symp., Denver / Colorado, May 1985. Paper Number: SPE- SPE-13892-MS.
Wang X., Hovem K., Moos D., Quan Y. Water Hammer Effects on Water Injection Well Performance and Longevity // SPE Int. Symp. Exhib. on Formation Damage Control, 2008, SPE-112282-MS. https://doi.org/10.2118/112282-MS
Шагапов В.Ш., Галиакбарова Э.В., Хакимова З.Р. К теории локального зондирования трещин, образовавшихся при гидроразрыве пласта, с использованием импульсных волн давления // ПМТФ. 2021. Т. 62. № 4. С. 46–56.
Галиакбарова Э.В. Влияние проводимости гидроразрывной трещины на возможность диагностирования с помощью акустического “телевизора”// Вестн. Башкирск. ун-та. 2021. Т. 26. № 4. С. 866–870.
Шагапов В.Ш., Нагаева З.М., Аносова Е.П. Упругий режим фильтрации жидкости к скважине через перпендикулярную ей трещину, образовавшуюся при гидроразрыве пласта // ПМТФ. 2022. Т. 63. № 4 (374). С. 105–115.
Нагаева З.М., Шагапов В.Ш. Об упругом режиме фильтрации в трещине, расположенной в нефтяном или газовом пласте // ПММ. 2017. Т. 81. № 3. С. 319–329.
Лайонс Р. Цифровая обработка сигналов. М.: ООО “Бином-Пресс”, 2006. 656 с.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. VI. Гидродинамика. М.: Наука, 1986. 736 с.
Айфичер Э.C., Джервис Б.У. Цифровая обработка сигналов: практический подход. М.: Издат. дом “Вильямс”, 2004. 992 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал