Прикладная математика и механика, 2023, T. 87, № 2, стр. 240-253

Волны седиментации в двухфазной гранулированной жидкости

В. В. Шелухин^1, *, В. В. Неверов¹

¹ Институт гидродинамики им. М.А. Лаврентьева СО РАН
Новосибирск, Россия

Поступила в редакцию 01.02.2023
После доработки 05.03.2023
Принята к публикации 05.03.2023

EDN: UBHIWW
DOI: 10.31857/S0032823523020145

Аннотация

Рассматривается вопрос математического моделирования течений суспензии твердых частиц без предположений о малых концентрациях. Различие скоростей частиц и связующей жидкости учитывается путем применения двухконтинуального подхода, в рамках которого частицы и жидкость трактуются как две различные вязкие жидкости. Исследуется роль сил плавучести и гравитационной мобильности на оседание частиц. Проводится качественное сравнение с теорией концентрационных волн Кинча для случая одномерных вертикальных течений. Отмечена роль вихрей на поперечную миграцию частиц при седиментации в двумерном сосуде.

Ключевые слова: суспензии, седиментация, силы плавучести, поперечная миграция частиц

1. Введение. Двухфазные гранулированные жидкости отличаются от сыпучей среды тем, что фаза сухих частиц является смоченной и допускается различие скоростей между частицами и связующей жидкостью. Важно отметить, что в таких жидкостях нет гипотезы о слабой концентрации частиц; они также называются слабо смоченным сыпучим материалом, если доля связующей жидкости мала [1]. Хотя гранулированные жидкости изучались и раньше [2], в последнее время они стали вновь привлекать внимание [3]. Тематика реологии смоченных сыпучих сред [4] играет важную роль в геотехническом и геофизическом контексте [5], в технологических процессах в связи с образованием агломератов [6], изготовлением пресс-форм [7], в технологиях литья металлических форм с пустотами путем заполнения форм сыпучим материалом и последующим плавлением [8]. В последнем примере связующая жидкость занимает всего несколько процентов от смеси. Как показывают эксперименты по своей реологии смоченные сыпучие материалы отличаются от сухих сыпучих сред и относятся к неньютоновским жидкостям [9].

Данная работа посвящена формулировке новой математической модели двухфазной гранулированной жидкости и исследованию на ее основе проблемы седиментации частиц. При оседании скорости частиц и связующей жидкости различаются существенно, поэтому уместен подход, основанный на взаимодействии двух континуумов. Известно несколько методов построения двухскоростных математических моделей. Как правило, они выводятся либо усреднением по объему [10], либо по ансамблю частиц [11, 12]. Одно из применений двухскоростных моделей – изучение поперечной миграции частиц относительно главного потока [13]. С этой целью вводятся силы Магнуса или Саффмана, которые оцениваются, исходя из движения одиночной частицы в потоке. Установлено, что такие силы обязаны эффектам инерции и присутствия стенок [14]. Однако согласование этих сил с законами термодинамики до сих пор не выяснено. Проблеме гравитационной конвекции посвящено много публикаций. Некоторый обзор содержится в работах [15, 16].

Уравнения в настоящей работе получены другим методом, который первоначально был разработан в работах Е.М. Халатникова и Л.Д. Ландау для термодинамики сверхтекучего гелия 2He [17]. По этому методу неизвестные потоки в законах сохранения сначала определяются для обратимых процессов согласованно с термодинамикой ввиду того, что закон сохранения энергии делает всю систему уравнений переопределенной; при этом учитывается инвариантность законов сохранения относительно преобразований Галилея. Затем находятся необратимые добавки к потокам в диссипативных процессах путем согласования законов сохранения с принципами де Гроот–Мазура необратимой термодинамики.

Развитие термодинамического метода Халатникова–Ландау для двухфазной гранулированной жидкости предложено в недавней работе [18], где в отличие от [17] к законам сохранения добавлен закон Фика для потока концентрации частиц, который учитывает не только диффузию концентрации частиц, но и гравитационную мобильность, бародиффузию и температурную диффузию. При этом закон Фика согласован с неотрицательным производством энтропии. Область применимости диффузионного подхода [18] ограничена случаем очень мелких частиц. Цель настоящей работы – отказаться от этого ограничения. С этой целью к межфазным силам будет добавлена сила плавучести, а задача седиментации будет исследована при подавлении эффекта гравитационной мобильности в законе Фика.

Для теоретической валидации модели мы устанавливаем, что в одномерном случае, когда учитываются только вертикальные течения, теория Кинча [19, 20] для седиментационных волн концентрации вытекает из разработанных уравнений как частный случай. Двумерные течения в вертикальном сосуде исследуются численно с помощью FreeFem++. Показно, что массовая концентрация частиц $c$ не выходит за пределы интервала $0 < c < 1$, несмотря на то, что ее динамика описывается не уравнением переноса, как это предполагается в большинстве работ, а более сложным уравнением с матричным коэффициентом диффузии. Хотя твердые и жидкие частицы вовлечены в вихревые течения, тем не менее, осадочный слой растет таким образом, что его верхняя граница остается всегда почти горизонтальной. Это, в частности, означает, что эффект поперечной миграции частиц воспроизводится предложенной моделью.

2. Модель двухфазной гранулированной жидкости в диффузионном приближении. Рассматривается смесь двух взаимопроникающих сред [21], т.е. в произвольном объеме $V$ содержатся и жидкость (индекс $f$) и гранулированная фаза (индекс $s$). Объем, масса и давление жидкой и гранулированной фаз обозначим ${{V}_{f}},{{m}_{f}},{{p}_{f}}$ и ${{V}_{s}},{{m}_{s}},{{p}_{s}}$ соответственно. Предполагается, что гранулированная фаза представляет собой смесь сухих частиц и несущей жидкости, например гель с проппантом. При этом ${{V}_{s}} = {{V}_{M}} + {{V}_{p}}$ и ${{m}_{s}} = {{m}_{M}} + {{m}_{p}}$. Частицы “вморожены” в несущую жидкость, т.е. гранулированная фаза характеризуется всего одной скоростью ${{{\mathbf{v}}}_{s}}$, одной вязкостью и одним тензором напряжений.

Перейдем к переменным, определенным для единичного объема

(2.1)

$\rho = \frac{m}{V},\quad {{\rho }_{s}} = \frac{{{{m}_{s}}}}{V},\quad {{\rho }_{f}} = \frac{{{{m}_{f}}}}{V},\quad {{\rho }_{p}} = \frac{{{{m}_{p}}}}{V},\quad {{\varphi }_{k}} = \frac{{{{V}_{k}}}}{V},\quad {{\rho }_{M}} = \frac{{{{m}_{M}}}}{V},\quad c = \frac{{{{m}_{p}}}}{m}$

Здесь $c = {{\rho }_{p}}{\text{/}}\rho $ – массовая концентрация частиц в смеси, а ${{\varphi }_{k}}$ – объемная доля фазы $k$, где $k = f,p,M$. Из введенных определений следует, что парциальные плотности ρ_kсвязаны с физическими плотностями ${{\bar {\rho }}_{k}}$ по следующим формулам

${{\rho }_{k}} = {{\phi }_{k}}{{\bar {\rho }}_{k}},\,\;{{\bar {\rho }}_{k}} \equiv \frac{{{{m}_{k}}}}{{{{V}_{k}}}},\,\,{{\phi }_{f}} + {{\phi }_{s}} = 1,\,\,{{\phi }_{s}} = {{\phi }_{p}} + {{\phi }_{M}},\,\,\rho = {{\rho }_{f}} + {{\rho }_{p}} + {{\rho }_{M}}$

В общем случае давления в фазах ${{p}_{s}}$ и ${{p}_{f}}$ различны. Далее в работе предполагается, что силы поверхностного натяжения на границах между фазами пренебрежимо малы и можно использовать приближение ${{p}_{s}} = {{p}_{f}} = p$, аналогично тому, как это было сделано в [21].

Введем обозначения: ${{{\mathbf{v}}}_{f}}$ – скорость жидкой фазы; ${\mathbf{l}}$ – вектор потока концентрации; ${{T}_{i}}$ – вязкая часть тензора напряжения фазы $i$; ${\mathbf{g}}$ – вектор гравитации; $k$ – коэффициент межфазного трения.

Если пренебречь вращением частиц и тепловыми эффектами, то из работы [21] можно получить следующую математическую модель для шести неизвестных функций ${{\rho }_{s}}$, ${{\rho }_{f}}$, $p$, $c$, ${{{\mathbf{v}}}_{s}}$, ${{{\mathbf{v}}}_{f}}$:

(2.2)

$\frac{{\partial ({{\rho }_{s}}{{{\mathbf{v}}}_{s}})}}{{\partial t}} + \operatorname{div} ({{\rho }_{s}}{{{\mathbf{v}}}_{s}} \otimes {{{\mathbf{v}}}_{s}}) = - \frac{{{{\rho }_{s}}}}{\rho }\nabla p - \frac{{{{\rho }_{s}}{{\rho }_{f}}}}{{2\rho }}\nabla {{{\mathbf{u}}}^{2}} - k{\mathbf{u}} + \operatorname{div} {{T}_{s}} + {{\rho }_{s}}{\mathbf{g}}$

(2.3)

$\frac{{\partial ({{\rho }_{f}}{{{\mathbf{v}}}_{f}})}}{{\partial t}} + \operatorname{div} ({{\rho }_{f}}{{{\mathbf{v}}}_{f}} \otimes {{{\mathbf{v}}}_{f}}) = - \frac{{{{\rho }_{f}}}}{\rho }\nabla p + \frac{{{{\rho }_{s}}{{\rho }_{f}}}}{{2\rho }}\nabla {{{\mathbf{u}}}^{2}} + k{\mathbf{u}} + \operatorname{div} {{T}_{f}} + {{\rho }_{f}}{\mathbf{g}}$

(2.4)

$\frac{{\partial (\rho c)}}{{\partial t}} + \operatorname{div} (c{\mathbf{j}} + {\mathbf{l}}) = 0,\quad p = p(\rho )$

(2.5)

${{\rho }_{{st}}} + \operatorname{div} ({{\rho }_{s}}{{{\mathbf{v}}}_{s}}) = 0,\quad {{\rho }_{{ft}}} + \operatorname{div} ({{\rho }_{f}}{{{\mathbf{v}}}_{f}}) = 0,$

где $p = p(\rho )$ – заданное уравнение состояния и

${\mathbf{j}} = {{\rho }_{s}}{{{\mathbf{v}}}_{s}} + {{\rho }_{f}}{{{\mathbf{v}}}_{f}},\quad \rho = {{\rho }_{s}} + {{\rho }_{f}},{\mathbf{u}} = {{{\mathbf{v}}}_{s}} - {{{\mathbf{v}}}_{f}},\quad {{{\mathbf{u}}}^{2}} = {\mathbf{u}} \cdot {\mathbf{u}} \equiv {{u}_{k}}{{u}_{k}}$

Здесь использованы следующие обозначения. Тензорное произведение ${\mathbf{a}} \otimes {\mathbf{b}}$ векторов ${\mathbf{a}}$ и ${\mathbf{b}}$ представляет собой матрицу с компонентами ${{({\mathbf{a}} \otimes {\mathbf{b}})}_{{ij}}}$ = ${{a}_{i}}{{b}_{j}}$. Для заданной матрицы $A({\mathbf{x}})$ обозначим через $A({\mathbf{x}}){\kern 1pt} *$ сопряженную матрицу ${{\left( {A({\mathbf{x}}){\kern 1pt} *} \right)}_{{ij}}}$ = ${{\left( {A({\mathbf{x}})} \right)}_{{ji}}}$. Компоненты вектора $\operatorname{div} A$ определяются формулой ${{(\operatorname{div} A)}_{i}}$ = $\partial {{A}_{{ij}}}{\text{/}}\partial {{x}_{j}}$.

Фаза $f$ считается вязкой ньютоновской жидкостью. Фаза $s$ содержит частицы, $c$ – их массовая концентрация по отношению ко всему двухскоростному континууму. В реологических соотношениях

(2.6)

${{T}_{i}} = 2{{\eta }_{i}}{{D}_{i}},\quad 2{{D}_{i}} = \nabla {{{\mathbf{v}}}_{i}} + (\nabla {{{\mathbf{v}}}_{i}}){\kern 1pt} *;\quad i = f,s,$

${{D}_{j}}$ – тензор скоростей деформаций, ${{\eta }_{i}}$ – вязкость. Параметры $k,{{\eta }_{s}}$ – обычно зависят от концентрации $c$, а ${{\eta }_{f}}$ является константой. Напомним определение дифференциального оператора $\nabla $:

${{\left( {\nabla {\mathbf{u}}} \right)}_{{ks}}} = \frac{{\partial {{u}_{k}}}}{{\partial {{x}_{s}}}},\quad {{\left( {{\mathbf{v}} \cdot \nabla {\mathbf{u}}} \right)}_{k}} = {{{v}}_{s}}\frac{{\partial {{u}_{k}}}}{{\partial {{x}_{s}}}}$

Скалярное произведение матриц $A$ и $B$ обозначается через $A:B = {{A}_{{ij}}}{{B}_{{ij}}}$.

Модель содержит еще одно реологическое соотношение, это закон Фика для потока концентрации:

(2.7)

${\mathbf{l}} = - \left( {{{\gamma }_{2}}\nabla c + {{\gamma }_{1}}\nabla p + {{\gamma }_{3}}\nabla {{{\mathbf{u}}}^{2}}} \right) + \rho cB{\mathbf{g}},$

где ${{\gamma }_{i}}$ – коэффициенты диффузии, а $B$ – мобильность [17].

Для решения задачи о седиментации преобразуем систему уравнений (2.2)–(2.7). С помощью уравнений неразрывности (2.5) законы сохранения импульса (2.2) и (2.3) можно записать в виде

(2.8)

${{\rho }_{s}}\left( {\frac{{\partial {{{\mathbf{v}}}_{s}}}}{{\partial t}} + {{{\mathbf{v}}}_{s}} \cdot \nabla {{{\mathbf{v}}}_{s}}} \right) = - \frac{{{{\rho }_{s}}}}{\rho }\nabla p - \frac{{{{\rho }_{s}}{{\rho }_{f}}}}{{2\rho }}\nabla {{{\mathbf{u}}}^{2}} - k{\mathbf{u}} + \operatorname{div} {{T}_{s}} + {{\rho }_{s}}{\mathbf{g}}$

(2.9)

${{\rho }_{f}}\left( {\frac{{\partial {{{\mathbf{v}}}_{f}}}}{{\partial t}} + {{{\mathbf{v}}}_{f}} \cdot \nabla {{{\mathbf{v}}}_{f}}} \right) = - \frac{{{{\rho }_{f}}}}{\rho }\nabla p + \frac{{{{\rho }_{s}}{{\rho }_{f}}}}{{2\rho }}\nabla {{{\mathbf{u}}}^{2}} + k{\mathbf{u}} + \operatorname{div} {{T}_{f}} + {{\rho }_{f}}{\mathbf{g}}$

Как и в работе [18] введем следующие предположения:

1. Физические плотности каждой фазы постоянны ${{\bar {\rho }}_{k}} \equiv {\text{const}}$, где $k = f,p,M,$

2. Объемная доля геля ${{\varphi }_{M}}$ мала.

Тогда из определений (2.1) получим, что:

(2.10)

${{\rho }_{s}} \approx c\rho ,\quad {{\rho }_{f}} \approx (1 - c)\rho ,\quad {{\varphi }_{s}}(c) = \frac{c}{{{{R}_{0}} + c(1 - {{R}_{0}})}},\quad {{R}_{0}} = \frac{{{{{\bar {\rho }}}_{s}}}}{{{{{\bar {\rho }}}_{f}}}}$

Следует отметить, что в отличие от физических плотностей, парциальные плотности фаз ${{\rho }_{i}}$ и средняя плотность суспензии $\rho $ не являются постоянными. Далее объемные доли ${{\varphi }_{s}}$ и ${{\varphi }_{f}}$, а также и функции ${{\rho }_{s}}$, ${{\rho }_{f}}$, $\rho $ рассматриваются как известные функции от массовой концентрации $c$:

(2.11)

$\frac{{{{\rho }_{s}}}}{{{{{\bar {\rho }}}_{f}}}} = c[1 + ({{R}_{0}} - 1){{\varphi }_{s}}(c)] \equiv {{r}_{s}}(c),\quad \frac{{{{\rho }_{f}}}}{{{{{\bar {\rho }}}_{f}}}} = 1 - {{\varphi }_{s}}(c) \equiv {{r}_{f}}(c),\quad \rho = \frac{{{{{\bar {\rho }}}_{s}}}}{{{{R}_{0}} + c(1 - {{R}_{0}})}}$

Функции ${{r}_{s}}(c)$ и ${{r}_{f}}(c)$ – безразмерные парциальные плотности.

Разделив первое уравнение (2.5) на ${{\bar {\rho }}_{s}}$, второе уравнение (2.5) на ${{\bar {\rho }}_{f}}$ и сложив их, приходим к уравнению неразрывности для среднеобъемной скорости

(2.12)

$\operatorname{div} {\mathbf{v}} = 0,$

где

${\mathbf{v}} \equiv {{\varphi }_{s}}(c){{{\mathbf{v}}}_{s}} + {{\varphi }_{f}}(c){{{\mathbf{v}}}_{f}},\quad {{\varphi }_{f}} = \frac{{{{R}_{0}}(1 - c)}}{{{{R}_{0}} + c(1 - {{R}_{0}})}}$

Используя законы сохранения массы (2.5) и гипотезу (2.10), можно переписать (2.4) в виде

(2.13)

$\frac{{\partial c}}{{\partial t}} + \operatorname{div} (c{\mathbf{v}}) + {{\rho }^{{ - 1}}}(c)\operatorname{div} {\mathbf{l}} = 0$

Теперь модель сводится к отысканию четырех неизвестных функций $p$, $c$, ${{{\mathbf{v}}}_{s}}$ ${{{\mathbf{v}}}_{f}}$, удовлетворяющих четырем уравнениям (2.8), (2.9), (2.12), (2.13). Параметры ${{\eta }_{s}}$, ${{\eta }_{f}}$, $k$, ${{\gamma }_{j}}$ считаются известными функциями от $c$. Заметим, что в условиях постоянства физических плотностей давление уже не является термодинамическим параметром и не удовлетворяет уравнению состояния, а находится из решения уравнений также как и в случае модели Навье–Стокса вязкой несжимаемой жидкости. Соотношения (2.10) заменяют законы сохранения масс фаз.

Вязкость суспензии для плотных суспензий определяется по формуле Krieger–Douhgerty [22]:

(2.14)

${{\eta }_{s}}{\text{/}}{{\eta }_{{s0}}} = (1 - {{\varphi }_{s}}{\text{/}}\varphi _{s}^{*}{{)}^{{ - 5/2}}},$

где ${{\eta }_{{s0}}}$ – вязкость несущей жидкой фазы гранулированной жидкости при отсутствии частиц, $\varphi _{s}^{*}$ – концентрация плотной упаковки. Коэффициенты диффузии ${{\gamma }_{j}}$ обращаются в ноль, когда исчезает какая-либо фаза. Для коэффициента межфазного трения известна корреляция [23]

(2.15)

$k = \frac{3}{4}{{C}_{D}}\frac{{{{\varphi }_{s}}{{{\bar {\rho }}}_{s}}\left| {\mathbf{u}} \right|}}{{{{d}_{p}}}},$

где ${{d}_{p}}$ – диаметр частиц, ${{C}_{D}}$ – коэффициент трения частицы о жидкость,

(2.16)

${{C}_{D}} = \left\{ \begin{gathered} \frac{{24}}{{{\text{R}}{{{\text{e}}}_{p}}}}\left( {1 + 0.15{\text{Re}}_{p}^{{0.678}}} \right)\quad {\text{при}}\quad {\text{R}}{{{\text{e}}}_{p}} < 1000, \hfill \\ 0.44\quad {\text{при}}\quad {\text{R}}{{{\text{e}}}_{p}} > 1000, \hfill \\ \end{gathered} \right.\quad {\text{R}}{{{\text{e}}}_{p}} = \frac{{{{d}_{p}}{{{\bar {\rho }}}_{s}}\left| {\mathbf{u}} \right|}}{{{{\eta }_{f}}}}$

Отметим, что в задачах седиментации число Рейнольдса для частиц очень мало ${{\operatorname{Re} }_{p}} \ll 1$, что позволяет использовать приближенные соотношения

(2.17)

${{C}_{D}} = \frac{{24}}{{{{{\operatorname{Re} }}_{p}}}},\quad k = \frac{{18{{\eta }_{f}}{{\varphi }_{s}}}}{{d_{p}^{2}}}$

3. Модель двухфазной гранулированной жидкости с пренебрежимо малыми диффузией и диссипацией. Если пренебречь диффузией и вязкостью, то диффузионная модель c условием несжимаемости смеси для функций $c$, ${{{\mathbf{v}}}_{f}}$, ${{{\mathbf{v}}}_{s}}$, $p$ примет вид

(3.1)

${{\rho }_{f}}\left( {\frac{{\partial {{{\mathbf{v}}}_{f}}}}{{\partial t}} + {{{\mathbf{v}}}_{f}} \cdot \nabla {{{\mathbf{v}}}_{f}}} \right) = - \frac{{{{\rho }_{f}}}}{\rho }\nabla p + \frac{{{{\rho }_{s}}{{\rho }_{f}}}}{{2\rho }}\nabla {{{\mathbf{u}}}^{2}} + {{{\mathbf{f}}}_{d}} - {{{\mathbf{f}}}_{b}} + {{\rho }_{f}}{\mathbf{g}}$

(3.2)

${{\rho }_{s}}\left( {\frac{{\partial {{{\mathbf{v}}}_{s}}}}{{\partial t}} + {{{\mathbf{v}}}_{s}} \cdot \nabla {{{\mathbf{v}}}_{s}}} \right) = - \frac{{{{\rho }_{s}}}}{\rho }\nabla p + \frac{{{{\rho }_{s}}{{\rho }_{f}}}}{{2\rho }}\nabla {{{\mathbf{u}}}^{2}} - {{{\mathbf{f}}}_{d}} + {{{\mathbf{f}}}_{b}} + {{\rho }_{s}}{\mathbf{g}}$

(3.3)

$\frac{{\partial \left( {c\rho } \right)}}{{\partial t}} + \operatorname{div} \left( {c{\mathbf{j}}} \right) = 0,\quad {\mathbf{j}} = {{\rho }_{f}}{{{\mathbf{v}}}_{f}} + {{\rho }_{s}}{{{\mathbf{v}}}_{s}}$

(3.4)

$\operatorname{div} {\mathbf{v}} = 0,\quad {\mathbf{v}} \equiv {{\varphi }_{s}}(c){{{\mathbf{v}}}_{s}} + {{\varphi }_{f}}(c){{{\mathbf{v}}}_{f}},$

где

(3.5)

$\begin{gathered} {{\varphi }_{s}} + {{\varphi }_{f}} = 1,\quad {{\rho }_{s}} = {{{\bar {\rho }}}_{s}}{{\varphi }_{s}}(c),\quad {{\rho }_{f}} = {{{\bar {\rho }}}_{f}}{{\varphi }_{f}}(c) \\ \rho = {{\rho }_{s}} + {{\rho }_{f}},\quad {{\varphi }_{f}} = \frac{{{{R}_{0}}(1 - c)}}{{{{R}_{0}} + c(1 - {{R}_{0}})}}, \\ \end{gathered} $

а плотности материалов ${{\bar {\rho }}_{f}}$ и ${{\bar {\rho }}_{s}}$ считаются постоянными. Здесь ${{{\mathbf{f}}}_{d}} = k({{{\mathbf{v}}}_{s}} - {{{\mathbf{v}}}_{f}})$ – сила межфазного трения и ${{{\mathbf{f}}}_{b}}$ – сила плавучести. Отметим, что в литературе нет однозначного вида для ${{{\mathbf{f}}}_{b}}$. Например, в [24] эта сила пропорциональна градиенту объемной доли жидкой фазы, а в [15] она пропорциональна дивергенции тензора вязких напряжений жидкой фазы. Отметим, что в указанных работах законы сохранения импульсов фаз также различаются. Поскольку в данной работе уравнения импульсов тоже другие, то естественно предположить, что и вид межфазной силы плавучести будет другим. Далее приводится формула для ${{{\mathbf{f}}}_{b}}$ и излагаются аргументы в пользу этого выбора.

В терминах скорости проскальзывания ${\mathbf{u}} = {{{\mathbf{v}}}_{s}} - {{{\mathbf{v}}}_{f}}$ можно записать следствия уравнений (3.1)–(3.4):

(3.6)

$\frac{{\partial (c\rho )}}{{\partial t}} + {\text{div}}(c\rho {{{\mathbf{v}}}_{f}} + c{{\rho }_{s}}{\mathbf{u}}) = 0$

(3.7)

$\frac{{\partial {\mathbf{u}}}}{{\partial t}} + ({{{\mathbf{v}}}_{s}} \cdot \nabla ){\mathbf{u}} + ({\mathbf{u}} \cdot \nabla ){{{\mathbf{v}}}_{f}} = - \frac{{\nabla {{{\left| {\mathbf{u}} \right|}}^{2}}}}{2} + {{{\mathbf{f}}}_{b}}\left( {\frac{1}{{{{\rho }_{s}}}} + \frac{1}{{{{\rho }_{f}}}}} \right) - {{{\mathbf{f}}}_{d}}\left( {\frac{1}{{{{\rho }_{s}}}} + \frac{1}{{{{\rho }_{f}}}}} \right)$

Будем искать ${{{\mathbf{f}}}_{b}}$ в таком виде, чтобы выполнялась формула

(3.8)

${{{\mathbf{f}}}_{b}}\left( {\frac{1}{{{{\rho }_{s}}}} + \frac{1}{{{{\rho }_{f}}}}} \right) = \varepsilon {\mathbf{g}},\quad \varepsilon = \frac{{{{{\bar {\rho }}}_{s}} - {{{\bar {\rho }}}_{f}}}}{{{{{\bar {\rho }}}_{s}}}},$

где $\varepsilon $ – параметр плавучести. Поэтому

(3.9)

${{{\mathbf{f}}}_{b}} = \varepsilon \frac{{{{\rho }_{s}}{{\rho }_{f}}}}{\rho }{\mathbf{g}}$

В случае стационарных течений линеаризация уравнения (3.7) приводит к формуле

(3.10)

${\mathbf{u}} = \varepsilon {\mathbf{g}}\frac{{{{\rho }_{s}}{{\rho }_{f}}}}{{k\rho }}$

Воспользуемся представлением (2.17) для коэффициента трения $k$ и перейдем к пределу при ${{\varphi }_{s}} \to 0$, тогда с помощью (3.10) получим формулу Стокса для скорости оседания одиночной частицы:

(3.11)

$\left| u \right| = \frac{{g({{{\bar {\rho }}}_{s}} - {{{\bar {\rho }}}_{f}})d_{p}^{2}}}{{18{{\eta }_{f}}}}$

4. Одномерная седиментация с малыми диффузией и вязкостью. Рассмотрим одномерные вертикальные течения вдоль оси $z$, направленной вверх. В этом случае

(4.1)

${{{\mathbf{v}}}_{s}} = (0,0,{{{v}}^{s}}{{)}^{T}},\quad {{{\mathbf{v}}}_{f}} = (0,0,{{{v}}^{f}}{{)}^{T}},\quad {\mathbf{g}} = - g{{{\mathbf{e}}}_{z}},$

где ${{{\mathbf{e}}}_{z}}$ – единичный вектор оси $z$. Для таких течений условие соленоидальности (3.4) для среднеобъемной скорости эквивалентно уравнению:

(4.2)

$\frac{\partial }{{\partial z}}({{\varphi }_{f}}{{{v}}^{f}} + {{\varphi }_{s}}{{{v}}^{s}}) = 0$

При граничных условиях на дне

(4.3)

$z = 0{\kern 1pt} :{{{v}}^{f}} = {{{v}}^{s}} = 0$

в области $z > 0$ уравнение (4.2) сводится к следующему:

(4.4)

${{\varphi }_{f}}{{{v}}^{f}} + {{\varphi }_{s}}{{{v}}^{s}} = 0,\quad {{{v}}^{s}} = {{\varphi }_{f}}(c)u,\quad {{{v}}^{f}} = - {{\varphi }_{s}}(c)u$

Поэтому систему (3.1)–(3.3), (4.4) можно записать в виде

(4.5)

$\frac{{\partial u}}{{\partial t}} + {{{v}}^{s}}\frac{{\partial u}}{{\partial z}} + u\frac{{\partial {{{v}}^{f}}}}{{\partial z}} = - \frac{1}{2}\frac{{\partial {{u}^{2}}}}{{\partial z}} - u\frac{{k\rho }}{{{{\rho }_{s}}{{\rho }_{f}}}} - g\varepsilon $

(4.6)

$\frac{{\partial (c\rho )}}{{\partial t}} + \frac{{\partial (c\rho {{{v}}^{f}} + c{{\rho }_{s}}u)}}{{\partial z}} = 0$

для двух функций $u$ и $c$. Давление восстанавливается из уравнения

(4.7)

$\frac{{\partial {{{v}}^{s}}}}{{\partial t}} + {{{v}}^{s}}{\kern 1pt} \frac{{\partial u}}{{\partial z}} + u\frac{{\partial {{{v}}^{f}}}}{{\partial z}} = - \frac{1}{\rho }\frac{{\partial p}}{{\partial z}} - \frac{{{{\rho }_{f}}}}{{2\rho }}\frac{{\partial {{u}^{2}}}}{{\partial z}} + g - \frac{{ku}}{{{{\rho }_{s}}}} - \frac{{\varepsilon {{\rho }_{f}}g}}{\rho }$

Опираясь на формулы (2.10), (2.11), введем приведенную массовую концентрацию $r$:

$r = \frac{{\rho c}}{{{{{\bar {\rho }}}_{f}}}} = \frac{c}{{1 - \varepsilon c}},\quad 0 \leqslant r \leqslant {{R}_{0}} = \frac{1}{{1 - \varepsilon }}$

Выполняются следующие представления:

$c = \frac{r}{{1 + \varepsilon r}},\quad {{\varphi }_{s}}(r) = r(1 - \varepsilon )$

Тогда функции $u$ и $r$ удовлетворяют системе уравнений

(4.8)

$\frac{{\partial u}}{{\partial t}} + \frac{{\partial ({{u}^{2}}{{\varphi }_{f}})}}{{\partial z}} = - \frac{{k\rho }}{{{{\rho }_{s}}{{\rho }_{f}}}}u - g\varepsilon $

(4.9)

$\frac{{\partial r}}{{\partial t}} + \varepsilon \frac{\partial }{{\partial z}}\left( {\frac{{u{{r}^{2}}(1 + \varepsilon r - r)}}{{1 + \varepsilon r}}} \right) = 0$

5. Теория седиментации Кинча. Теория Кинча основана на эмпирическом соотношении [25]

(5.1)

${\mathbf{u}} = - {{V}_{{St}}}H(c){{{\mathbf{e}}}_{z}},\quad {{V}_{{{\text{St}}}}} = \frac{{2({{{\bar {\rho }}}_{s}} - {{{\bar {\rho }}}_{f}})g{{{({{d}_{p}}{\text{/}}2)}}^{2}}}}{{9\eta _{f}^{2}}},$

для скорости проскальзывания, где ${{\eta }_{f}}$ – вязкость жидкой фазы, ${{\bar {\rho }}_{s}}$ – плотность фазы частиц, ${{d}_{p}}$ – диаметр частицы, ${{V}_{{{\text{St}}}}}$ – скорость оседания Стокса. Для экспериментов в ньютоновской жидкости подходит эмпирическая функция торможения $H$ в форме Ричардсона–Заки [26]:

(5.2)

$H(c) = - {{(1 - c)}^{m}};\quad m = 4.6$

В этом случае $u = - {{(1 - c)}^{m}}{{V}_{{{\text{St}}}}}$ и уравнение (4.9) для приведенной концентрации принимает вид

(5.3)

$\frac{{\partial r}}{{\partial t}} + \frac{{\partial f(r)}}{{\partial z}} = 0,\quad f = - \tilde {\varepsilon }{{r}^{2}}{{\left( {\frac{{1 + \varepsilon r - r}}{{1 + \varepsilon r}}} \right)}^{{m + 1}}},\quad \tilde {\varepsilon } = \varepsilon {{V}_{{{\text{St}}}}},\quad 0 < r < \frac{1}{{1 - \varepsilon }}$

Для построения решения зададим начальные и граничные условия

(5.4)

${{\left. r \right|}_{{t = 0}}} = {{r}_{0}},\quad {{\left. r \right|}_{{z = 0}}} = 1$

Решение задачи (5.3), (5.4) определяется следующими свойствами функции $f(r)$ на рис. 1. Существует единственное значение ${{r}_{1}}$ переменной $r$, такое что $f{\kern 1pt} '({{r}_{1}}) = 0$. При $0 < {{r}_{0}} < {{r}_{1}}$ существует единственное значение ${{r}_{2}}$ переменной $r$, такое что

(5.5)

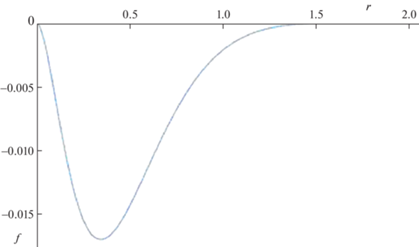
$\frac{{f({{r}_{2}}) - f({{r}_{0}})}}{{{{r}_{2}} - {{r}_{0}}}} = f{\kern 1pt} '{\kern 1pt} ({{r}_{2}})$

Рис. 1.

Зависимость $f\left( r \right)$ на интервале $0 < r < {{\left( {1 - \varepsilon } \right)}^{{ - 1}}}$ при $\tilde {\varepsilon } = 1$, $\varepsilon = 0.5$, $m = 4.6$.

Поэтому существует единственное энтропийное решение [27], задаваемое формулой

(5.6)

$r(z,t) = \left\{ \begin{gathered} {{r}_{0}},\quad {\text{при}}\quad z > h(t) \hfill \\ r(\xi ),\quad \xi = z{\text{/}}t,\quad {\text{при}}\quad z < h(t) \hfill \\ \end{gathered} \right.$

Решение имеет следующий смысл. Снизу вверх идет ударная волна $z = h\left( t \right)$ с постоянной скоростью $h{\kern 1pt} '\left( t \right)$, значение которой задано уравнением (5.5) ввиду условия Гюгонио на разрыве $h{\kern 1pt} '\left( t \right)\left( {{{r}_{2}} - {{r}_{0}}} \right)$ = $f\left( {{{r}_{2}}} \right) - f\left( {{{r}_{0}}} \right)$. Значения концентрации $r$ перед фронтом и за ним равны ${{r}_{0}}$ и ${{r}_{2}}$ соответственно. За фронтом решение имеет вид центрированной волны разрежения $r\left( \xi \right)$, $\xi = z{\text{/}}t$. Оно определяется путем решения уравнения $\xi = f{\kern 1pt} '\left( {r\left( \xi \right)} \right)$. Функция $r\left( \xi \right)$ растет монотонно от ${{r}_{2}}$ до ${{\left( {1 - \varepsilon } \right)}^{{ - 1}}}$, когда ξ уменьшается от $h{\kern 1pt} '\left( t \right)$ до 0. Заметим, что решение с ударной волной существует и для тех ${{r}_{0}} \geqslant {{r}_{1}}$, для которых формула (5.5) остается в силе.

6. Численное решение. Рассмотрим одномерную систему (4.8), (4.9) для неизвестных $\left( {u,r} \right)$, которая описывает седиментацию без гипотез о скорости проскальзывания. Поскольку используется решатель FreeFem++, то вводятся малые коэффициенты диффузии ${{D}_{1}},{{D}_{2}}$ и численно исследуется регуляризованная система

(6.1)

$\frac{{\partial u}}{{\partial t}} + \frac{\partial }{{\partial z}}\left( {{{u}^{2}}(1 + \varepsilon r - r)} \right) + \frac{{k\rho (r)}}{{{{\rho }_{s}}(r){{\rho }_{f}}(r)}}u + g\varepsilon = {{D}_{1}}\frac{{{{\partial }^{2}}u}}{{\partial {{z}^{2}}}}$

(6.2)

$\frac{{\partial r}}{{\partial t}} + \varepsilon \frac{\partial }{{\partial z}}\left( {\frac{{u{{r}^{2}}(1 + \varepsilon r - r)}}{{1 + \varepsilon r}}} \right) = {{D}_{2}}\frac{{{{\partial }^{2}}r}}{{\partial {{z}^{2}}}}$

Уравнения (6.1)–(6.2) рассматриваются на интервале $\Omega = 0 < z < 8$ со следующими начальными и граничными условиями:

(6.3)

${{\left. r \right|}_{{t = 0}}} = {{r}_{0}} = {\text{const}},\quad {{\left. u \right|}_{{t = 0}}} = 0,$

(6.4)

$r = 0,\quad u = 0,\quad {\text{на верхней границе}}\;z = 8$

(6.5)

$r = {{\left( {1 - \varepsilon } \right)}^{{ = 1}}},\quad u = 0,\quad {\text{на нижней границе}}\;z = 0$

На рис. 2,a показано распределение по высоте массовой концентрации частиц c = = $r{\text{/}}(1 + \varepsilon r)$ для следующих значений параметров:

(6.6)

$\varepsilon = 0.5,\quad {{r}_{0}} = 0.2,\quad {{D}_{1}} = 0.001,\quad {{D}_{2}} = 0.001$

Рис. 2.

а. Распределение массовой концентрации в различные моменты времени для одномерной модели вертикальных течений без условия на скорость проскальзывания. б. Распределение средней по горизонтальному сечению концентрации в различные моменты времени для 2D-седиментации.

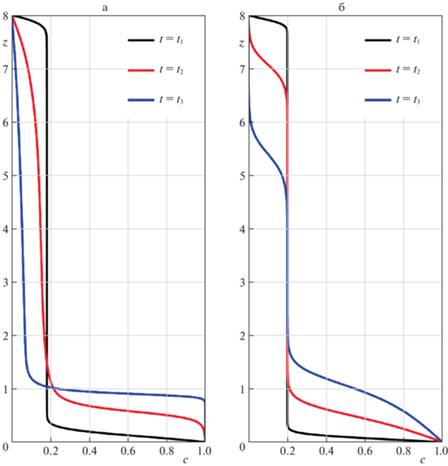
Со временем нарастает слой осадка $c = 1$, причем концентрация при переходе от осадка к смеси меняется скачком, что соответствует разрывному решению. Однако, в отличие от уравнения Кинча (4.9) с эмпирической корреляцией для скорости проскальзывания, в верхней части сосуда концентрация убывает плавно.

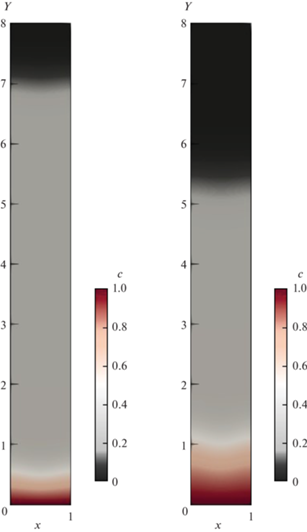
Также с помощью FreeFem++ находилось численное решение двумерной задачи седиментации в прямоугольной области $\Omega = [0,\;1] \times [0,\;8]$ переменных $x$ и $z$, где $x$ – горизонтальная переменная. Для сравнения с диффузионной моделью система (3.1)–(3.4) рассматривалась в следующей модификации:

(6.7)

${{\rho }_{s}}\left( {\frac{{\partial {{{\mathbf{v}}}_{s}}}}{{\partial t}} + {{{\mathbf{v}}}_{s}} \cdot \nabla {{{\mathbf{v}}}_{s}}} \right) = - \frac{{{{\rho }_{s}}}}{\rho }\nabla p - \frac{{{{\rho }_{s}}{{\rho }_{f}}}}{{2\rho }}\nabla {{{\mathbf{u}}}^{2}} + \operatorname{div} {{T}_{s}} - {{{\mathbf{f}}}_{d}} + {{{\mathbf{f}}}_{b}} + {{\rho }_{s}}{\mathbf{g}}$

(6.8)

${{\rho }_{f}}\left( {\frac{{\partial {{{\mathbf{v}}}_{f}}}}{{\partial t}} + {{{\mathbf{v}}}_{f}} \cdot \nabla {{{\mathbf{v}}}_{f}}} \right) = - \frac{{{{\rho }_{f}}}}{\rho }\nabla p + \frac{{{{\rho }_{s}}{{\rho }_{f}}}}{{2\rho }}\nabla {{{\mathbf{u}}}^{2}} + \operatorname{div} {{T}_{f}} + {{{\mathbf{f}}}_{d}} - {{{\mathbf{f}}}_{b}} + {{\rho }_{f}}{\mathbf{g}}$

(6.9)

$\frac{{\partial \left( {\rho c} \right)}}{{\partial t}} + \operatorname{div} \left( {c{\mathbf{j}} + {\mathbf{l}}} \right) = 0,\quad {\mathbf{j}} = {{\rho }_{f}}{{{\mathbf{v}}}_{s}} + {{\rho }_{f}}{{{\mathbf{v}}}_{s}}$

(6.10)

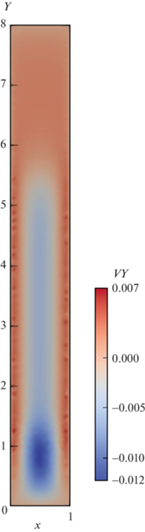
$\operatorname{div} {\mathbf{v}} = 0,\quad {\mathbf{v}} = {{\varphi }_{s}}\left( c \right){{{\mathbf{v}}}_{s}} + {{\varphi }_{f}}\left( c \right){{{\mathbf{v}}}_{f}},$

где тензоры вязких напряжений ${{T}_{i}}$, диффузионный поток ${\mathbf{l}}$ определяются формулами (2.6) и (2.7) соответственно. Вязкость жидкой фазы ${{\eta }_{f}}$ считается постоянной, а вязкость гранулированной фазы ${{\eta }_{s}}$ зависит от концентрации частиц по формуле (2.14). Плотности и объемные доли фаз зависят от концентрации по формулам (3.5). Граничные условия на $\partial \Omega $ есть условия прилипания для скоростей фаз и условие отсутствия диффузионного потока: ${\mathbf{l}} \cdot {\mathbf{n}} = 0$, где ${\mathbf{n}}$ – вектор внешней нормали. В начальный момент скорости фаз считаются нулевыми, а концентрация выбирается постоянной.

Иллюстрации вычислений, приведенные на рис. 2,б–рис. 4, относятся к случаю, когда гравитационная мобильность на порядок меньше, чем параметр плавучести. Зависимость от вертикальной переменной усредненных по горизонтальной координате значений концентрации изображены на рис. 2,б для разных моментов времени. Если не усреднять по переменной $x$, а наблюдать полную картину концентрации, то можно увидеть на рис. 3, что линии уровня концентрации локально искривляются в середине 2D сосуда. Это связано с образованием вихрей, рис. 4.

Рис. 3.

Распределение концентрации в различные моменты времени. Двумерный расчет.

Рис. 4.

Распределение средней скорости смеси. Цветом обозначена вертикальная компонента среднеобъемной скорости ${\mathbf{v}}$.

Заключение. Предложена математическая модель двухфазной гранулированной жидкости, в которой учитываются два механизма гравитационной седиментации. Первый механизм связан с силами плавучести, а второй обязан гравитационной мобильности в диффузионном законе Фика для потока концентрации. Для течений в вертикальном 2D сосуде вычисления показывают, что линии уровня концентрации образуют локальную ямку посредине. Ямка отсутствует, если доминирует диффузионный эффект. Для валидации модели показано, что теория гравитационных волн Кинча для одномерных вертикальных потоков вытекает из нее как частный случай, если воспользоваться известными эмпирическими корреляциями для скорости проскальзывания. Еще одно следствие теории – вывод новой одномерной модели гравитационной седиментации для вертикальных течений, которая не опирается на эмпирические корреляции для скорости проскальзывания. В этой новой модели скорость проскальзывания определяется одновременно с концентрацией частиц. Вычисления показывают, что полная одномерная модель и одномерное уравнение Кинча качественно дают одну и ту же картину оседания частиц.

Работа поддержана грантом Российского научного фонда, проект № 20-19-00058.

Список литературы

Schwarze R., Gladkyy A., Uhlig F., Luding S. Rheology of weakly wetted granular materials: a comparison of experimental and numerical data // Granular Matter. 2013. V. 15. P. 455–465.
Herminghaus S. Dynamics of wet granular matter // Adv. Phys. 2005. V. 54. P. 221–261.
Hsiau S.S., Liao C.C., Tai C.H., Wan C.Y. The dynamics of wet granular matter under a vertical vibration bed // Granul. Matter. 2013. V. 15. P. 437–446.
Jop P., Forterre Y., Pouliquen O. A constitutive law for dense granular flows // Nature. 2006. V. 441. P. 727–730.
Gabrieli F., Lambert P., Cola S., Calvetti F. Micromechanical modelling of erosion due to evaporation in a partially wet granular slope // Int. J. Numer. Anal. Meth. Geomech. 2012. V. 36. P. 918–943.
Pietsch W. Agglomeration Processes. Weinheim: Wiley, 2002.
Guo Y., Wu C.Y., Thornton C. The effects of air and particle density difference on segregation of powder mixtures during die filling // Chem. Eng. Sci. 2011. V. 66. P. 661–673.
Beeley P.R. Foundry Technology. Oxford: Elsevier, 2001.
Schwarze R., Rudert A., Tilch W., Bast J. Rheological behavior of sand-binder mixtures measured by a coaxial cylinder rheometer // I. Foundry Res. 2008. V. 60. № 3. P. 2–6.
Anderson T., Jackson R. Fluid mechanical description of fluidized beds. Equations of motion // Ind. Eng. Chem. Fundamen. 1967. V. 6. P. 527–539.
Buyevich Y., Shchelchkova I. Flow of dense suspensions // Prog. Aerosp. Sci. 1978. V. 18. P. 121–150.
Zhang D., Prosperetti A. Momentum and energy equations for disperse two-phase flows and their closure for dilute suspensions // Int. J. Multiphase Flow. 1997. V. 23. P. 425–453.
Miller R., Singh J., Morris J. Suspensions flow modeling for general geometries // Chem. Eng. Sci. 2009. V. 64. P. 4597–4610.
Crowe C., Schwarzkopf J., Sommerfield M., Tsuji Y. Multiphase Flows with Droplets and Particles. Boca Raton: CRC Press, 2011.
Dontsov E.V., Peirce A.P. Slurry flow, gravitational settling and a proppant transport model for hydraulic fracture // J. Fluid Mech. 2014. V. 760. P. 567–590.
Nevskii Yu.A., Osiptsov A.N. Slow gravitational convection of disperse systems in domain with inclined boundaries // Fluid Dyn. 2011. V. 46. № 2. P. 225–239.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. VI. Гидродинамика. М.: Наука, 1986. 736 с.
Shelukhin V.V., Neverov V.V. Dense suspension flows: a mathematical model consistent with thermodynamics // J. Fluids Eng. ASME. 2022. V. 144. Iss. 021402. P. 1–13.
Kynch G.F. A theory of sedimentation // Trans. Faraday Soc. 1952. V. 48. P. 166–176.
Bustos M.C., Concha F., Bürger R., Tory E.M. Sedimentation and Thickening Phenomenological Foundation and Mathematical Theory. Dordrecht: Springer, 1999.
Shelukhin V.V. Thermodynamics of two-phase granular fluids // J. Non-Newton. Fluid Mech. 2018. V. 262. P. 25–37.
Krieger I.M., Dougerty T. A mechanism for non-Newtonian flow in suspensions of rigid spheres // Trans. Soc. Rheol. 1959. V. 3. P. 137–152.
Ishii V., Mishima K. Two-fluid model and hydrodynamic constitutive relations // Nucl. Eng.&Des. 1984. V. 82. P. 107–126.
Baumgarten A.S., Kamrin K. A general fluid-sediment mixture model and constitutive theory validated in many flow regimes // J. Fluid Mech. 2018. V. 861. P. 721–764.
Acrivos A., Herbolzheimer E. Enhanced sedimentation in settling tanks with inclined walls // J. Fluid Mech. 1979. V. 92. P. 435–457.
Richardson J.F., Zaki W.N. The sedimentation of a suspension of uniform spheres under conditions of viscous flow // Chem. Eng. Sci. 1954. V. 3. P. 65–73.
Шелухин В.В. Квазистационарная седиментация с адсорбцией // ПМТФ. 2005. Т. 46. № 4. С. 66–77.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Прикладная математика и механика

Архивы выпусков Информация о журнале Отправить рукопись в журнал