Прикладная математика и механика, 2023, T. 87, № 2, стр. 226-239

1. Введение. Пристенные струи изучены намного хуже свободных. Единственное известное аналитическое решение построено только для плоских, бьющих из удлиненной щели ламинарных пристенных струй в рамках уравнений пограничного слоя [1, 2]. Оказалось, что в этом случае в любом поперечном сечении струи сохраняется величина – инвариант Акатнова, которая имеет смысл произведения импульса на расход. Таким образом, в отличие от свободных плоской и осесимметричной струй [3, 4], которые можно создать за счет привнесения в поток импульса, для пристенных струй важны при их создании как начальный (через выходное сечение струи) импульс, так и начальный расход. Наличие инварианта в плоской пристенной ламинарной струе позволило построить автомодельное решение и определить, что толщина струи при увеличении продольной координаты $x$ растет как ${{x}^{{{3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}}}}$.

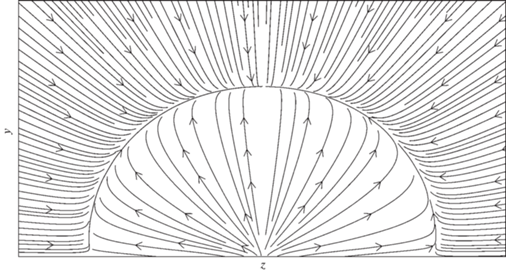
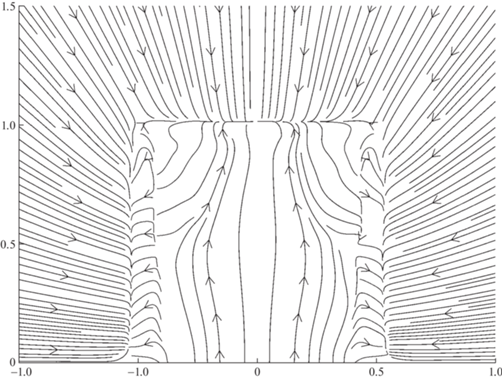
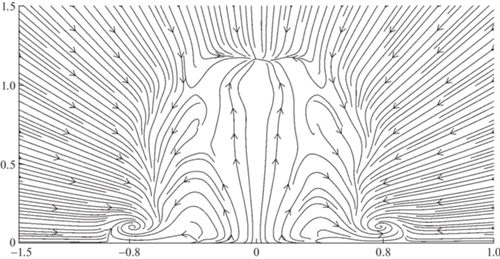
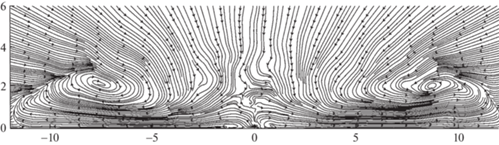
Если струя выдувается в затопленное пространство параллельно бесконечной плоскости из не удлиненного выходного сечения, то такая струя называется трехмерной пристенной струей. Течение в дальнем поле трехмерной ламинарной пристенной струи выходит на автомодельный режим, но, поскольку инвариантный интеграл еще не найден, параметр автомодельности, определяющий изменение размера струи, в работе [5] был найден численно. Оказалось, что характерные размеры струи растут пропорционально ${{x}^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3}}}}$. В [5, 6] также определена структура линий тока автомодельного течения (рис. 1), которая указывает на то, что всю область течения можно условно разбить на две подобласти: внутреннего и внешнего течения. Разделяет эти две подобласти овальная предельная линия тока. Во внутренней области с ростом координаты $x$ продольная скорость уменьшается, что приводит к вытесняющему действию: линии тока направлены от центра струи. Во внешней области линии тока направлены к центру – струя, подсасывая, разгоняет внешнее течение. Практически во всей области течения, за исключением окрестности разделительной линии тока, азимутальная скорость намного меньше радиальной.

Исследования трехмерных турбулентных пристенных струй велись в двух направлениях: экспериментальное [7–17] и немногочисленное расчетное [18–20].

Экспериментально было обнаружено, что в поперечном сечении турбулентной пристенной струи ее толщина существенно различна в перпендикулярном и параллельном к твердой поверхности направлениях. Этот факт в [7] подтвержден визуализацией течения в струе. В [8] в ближнем поле струи такое аномальное поведение было объяснено образованием в потоке подковообразных вихрей. В [7, 9–17] изучается автомодельное изменение характеристик струи. В этих работах было показано, что, несмотря на различие формы выходных сечений, из которых вытекает пристенная струя, и расположения этих сечений, течение в струе выходит на автомодельный режим. Вместе с тем, выход на автомодельный режим, по-видимому, зависит от многих факторов, например, геометрии и расположения выходного сечения, уровня турбулентных пульсаций на экспериментальной установке, числа Рейнольдса и др. В разных экспериментальных исследованиях координата выхода на автомодельный режим колеблется от 15 до 60 диаметров. Следует заметить, что выход на автомодельный режим различных величин происходит в разных сечениях струи: сначала выходит осредненная скорость, затем турбулентные напряжения и т.д.

В одной из первых работ по численному расчету характеристик трехмерной турбулентной пристенной струи результаты были получены с помощью решения осредненных уравнений Рейнольдса [18]. Хотя, как отмечают сами авторы, сравнение результатов численных расчетов с экспериментальными данными оказалось не очень хорошим, им все же удалось численно подтвердить, что различие в толщинах струи в параллельном и перпендикулярном к твердой поверхности направлениях вызвано продольными вихрями. Примерно такое же соответствие численных и экспериментальных данных продемонстрировано в работе [19], в которой также производилось численное интегрирование уравнений Рейнольдса.

Лучшее совпадение получено в работе [20], в которой численное решение получено с помощью метода крупных вихрей (LES). В качестве подсеточной модели использовалась модель Смагоринского, поправленная вблизи твердой поверхности эмпирическим демпфирующим множителем. В работе [20] была еще раз продемонстрирована определяющая роль продольных вихрей в эволюционном развитии пристенной струи.

В данной работе проведен расчет характеристик трехмерной пристенной струи с помощью метода LES. В отличие от метода RANS, для которого необходима полуэмпирическая модель турбулентной вязкости для всего течения, в LES необходимо задание модели турбулентности лишь на масштабах, не превышающих размера ячеек сетки. При этом крупные масштабы, несущие значительную долю энергии, разрешаются достаточно точно. При измельчении сетки LES, в отличие от RANS, переходит в прямое численное моделирование уравнений Навье–Стокса. Кроме того, в настоящей работе предпринята попытка получения наиболее достоверных с позиций сегодняшнего дня результатов с различных точек зрения: подсеточной модели турбулентности, численной схемы, мелкости разбиения расчетной области.

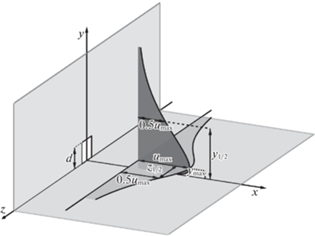
2. Постановка задачи. Линию пересечения двух полубесконечных плоскостей определим как $x = 0$, $y = 0$. В вертикальной плоскости имеется квадратное отверстие (рис. 2, длина стороны квадрата $d$), из которого выдувается струя со скоростью ${{u}_{0}}$ в пространство, заполненное покоящейся жидкостью. Отверстие своим основанием примыкает к горизонтальной плоскости. Введем систему координат. Струя распространяется вдоль оси $x$. Ось $y$ направлена перпендикулярно горизонтальной плоскости, третья ось – ось $z$. Компоненты скорости $u,\,v,w$ направлены вдоль осей $x,\,y,\,z$. Жидкость будем считать несжимаемой. Основной характеристикой струи является число Рейнольдса, образованное по скорости ${{u}_{0}}$, размеру $d$ и кинематическому коэффициенту вязкости $\nu $.

Будем описывать характеристики течения в рамках метода LES. Уравнения неразрывности и движения запишем в тензорном виде:

Здесь $\bar {f}$ – осредненная (отфильтрованная) по ячейке величина

интегрирование проводится по объему ячейки $\Delta V$, ${{x}_{1}} = x$, ${{x}_{2}} = y$, ${{x}_{3}} = z$, ${{\bar {u}}_{1}} = \bar {u}$, ${{\bar {u}}_{2}} = {\bar {v}}$, ${{\bar {u}}_{3}} = \bar {w}$, $\bar {p}$ – осредненное по ячейке давление, $\rho $ – плотность. Вследствие процедуры осреднения по ячейке появляются дополнительные подсеточные напряжения ${{\tau }_{{ij}}} = \overline {{{u}_{i}}{{u}_{j}}} - {{\bar {u}}_{i}}{{\bar {u}}_{j}}$.

Тензор подсеточных напряжений можно переписать в следующем виде:

где $\operatorname{dev} \left( \tau \right) = {{\tau }_{{ij}}} - {{{{\delta }_{{ij}}}{{\tau }_{{kk}}}} \mathord{\left/ {\vphantom {{{{\delta }_{{ij}}}{{\tau }_{{kk}}}} 3}} \right. \kern-0em} 3}$ – девиаторная часть этого тензора. Выражения для ${{k}_{{sgs}}}$, $\operatorname{dev} \left( \tau \right)$ представляют собой подсеточную модель. В настоящей работе используется адаптированная к моделированию пристенных течений модель WALE [21], основанная на гипотезе Буссинеска о турбулентной подсеточной вязкости ${{\nu }_{{sgs}}}$:

В этой формуле $\bar {S}$ – тензор скоростей деформации с элементами

Величина ${{k}_{{sgs}}}$, необходимая для подсеточной модели, связана с турбулентной вязкостью соотношением

где $\Delta = \sqrt[3]{{\Delta V}}$ – линейный масштаб ячейки.

Кроме того, турбулентную подсеточную вязкость, задают соотношением, которое, в отличие от модели Смагоринского, дает “правильное” асимптотическое ее поведение в окрестности стенки без использования эмпирических демпфирующих множителей:

где $\bar {g}_{{ij}}^{2} = {{\bar {g}}_{{ik}}}{{\bar {g}}_{{kj}}}$, ${{\bar {g}}_{{ij}}} = \frac{{\partial {{{\bar {u}}}_{i}}}}{{\partial {{x}_{j}}}}$ – компоненты тензора градиента скорости. При заданных константах ${{C}_{k}}$ и ${{C}_{w}}$ формулы (2.3) и (2.4) определяют ${{\nu }_{{sgs}}}$ и ${{k}_{{sgs}}}$. В проведенных в данной работе вычислениях принято:

Зададим граничные условия для уравнений (2.1), (2.2). На твердых поверхностях ставится условие прилипания. На квадратном отверстии – $u = {{u}_{0}}$, ${v} = 0$, $w = 0$. На большом расстоянии от источника струи должно обеспечиваться затухание компонент вектора скорости.

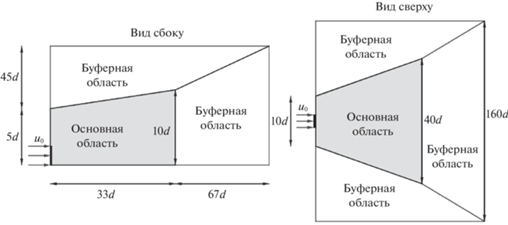
Численное интегрирование уравнений (2.1), (2.2) проводится в расширяющейся с ростом $x$ области. Продольный размер расчетной области выбран равным 33d, что позволяет провести расчет в обозримое время. Во избежание проблем, вызванных отражением возмущений от границ расчетной области, к основной расчетной области была пристроена вспомогательная буферная область, размер ячеек которой намного больше размера ячеек основной области. Назначение буферной области – диссипация вихрей до достижения ими границ расчетной области. Продольные сечения расчетной области представлены на рис. 3.

На верхней, задней и боковых границах расчетной области ставятся “мягкие” условия – равенство нулю нормальной производной вектора скорости.

3. Особенности численной схемы и достоверность результатов. Задача, поставленная в предыдущем разделе, решается методом конечного объема. Для интегрирования по времени используется неявная схема второго порядка точности с разностями назад. Интерполяция конвективных членов на гранях расчетных ячеек проводится с помощью схемы центральных разностей второго порядка, интерполяция давления – с помощью взвешенной противопоточной схемы первого и второго порядков точности. Градиенты вычисляются по схеме, основанной на теореме Гаусса. Для решения системы (2.1), (2.2) используется алгоритм SIMPLEC [22], сводящий ее к последовательному итерационному решению уравнений импульса и уравнения Пуассона для давления.

Моделирование истечения струи было проведено для $\operatorname{Re} = 7500$ на сетке, содержащей 14.6 млн ячеек, построенной в соответствии с требованиями к LES-моделированию пристенных течений [23]: $\Delta {{x}^{ + }} < 40$, $\Delta {{z}^{ + }} < 20$, размер пристенных ячеек удовлетворяет требованию $\Delta {{y}^{ + }} < 1$.

После установления статистически стационарного режима на протяжении достаточно большого промежутка времени было проведено осреднение характеристик течения. Такое осреднение величины $a$ по времени обозначается далее треугольными скобками $\left\langle a \right\rangle $.

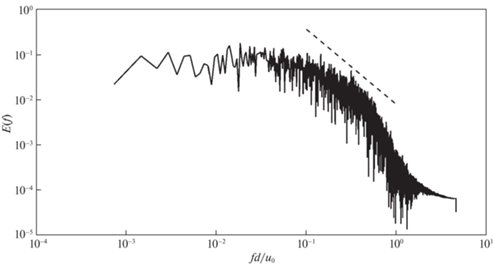
Качественный расчет методом LES должен разрешать значительную долю турбулентной энергии. На рис. 4 приведен временной спектр разрешаемой части кинетической энергии турбулентных пульсаций $k = 0.5(u{\kern 1pt} {{'}^{2}}\; + v{\kern 1pt} {{'}^{2}}\; + w{\kern 1pt} {{'}^{2}})$ в точке $x = 20d$, $y = 2d$, находящейся в плоскости симметрии. Наличие инерционного интервала на рис. 4 дает основание полагать, что разрешение достаточно высокое. Пунктиром изображена линия, соответствующая закону инерционного интервала $E\sim {{f}^{{ - 5{\text{/}}3}}}$.

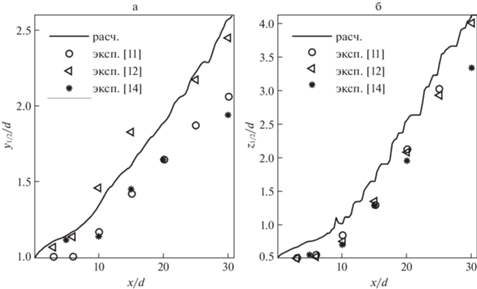
4. Результаты. В пристенной струе продольная компонента скорости в сечении $x = const$ плоскости симметрии имеет максимум ${{\left\langle u \right\rangle }_{{\max }}}(x)$ на некотором расстоянии ${{y}_{{\max }}}\left( x \right)$ от поверхности (рис. 2). Координату точки, в которой скорость в два раза меньше ${{\left\langle u \right\rangle }_{{\max }}}(x)$ в плоскости симметрии принято обозначать ${{y}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\left( x \right)$, а в выделенной на рис. 2 горизонтальной плоскости, проходящей через точку ${{y}_{{\max }}}\left( x \right)$, обозначают ${{z}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\left( x \right)$ (ввиду симметрии таких точек две).

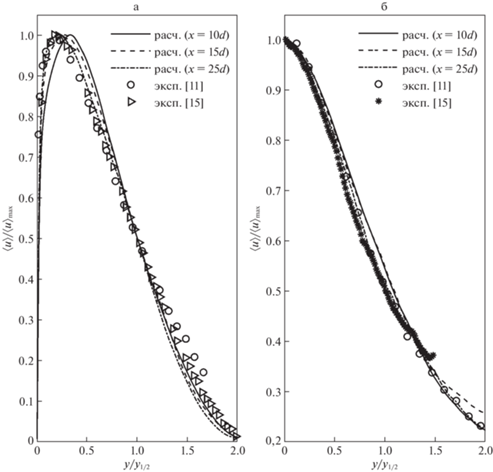
Как было отмечено во введении, профили осредненной скорости становятся автомодельными на некотором удалении от источника струи. На рис. 5 приведены профили продольной компоненты скорости в различных поперечных сечениях $x = const$ плоскости симметрии и выделенной горизонтальной плоскости (для определенности здесь и в дальнейшем нарисована часть профиля, соответствующая положительным значениям $z$). Профили продольной компоненты скорости начинают подчиняться автомодельному изменению при $x \approx 15d$, начиная с которого они довольно точно совпадают с экспериментальными данными. Возможно, такой быстрый выход на автомодельный режим достигается из-за того, что выходное отверстие струи располагается непосредственно над твердой поверхностью, а не на некотором расстоянии от нее.

Согласно экспериментальным и расчетным данным [8, 9, 11–15, 17, 20] характерные размеры струи ${{y}_{{1{\text{/}}2}}}(x)$, ${{z}_{{1{\text{/}}2}}}(x)$ в перпендикулярном и параллельном к твердой поверхности направлениях при выходе на автомодельный режим растут линейно по координате $x$, но с разной скоростью (рис. 6).

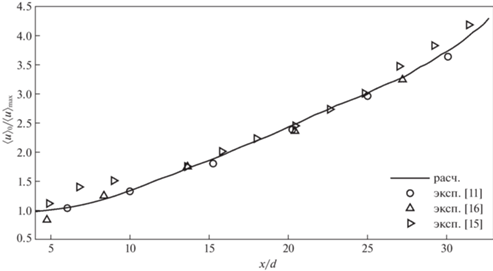
На рис. 7 представлено изменение максимума продольной компоненты скорости ${{\left\langle u \right\rangle }_{{\max }}}(x)$, полученное в расчете при $x \gg d$. Видно, что ${{\left\langle u \right\rangle }_{{\max }}}\sim {{x}^{{ - 1}}}$, что также совпадает с выводами [16].

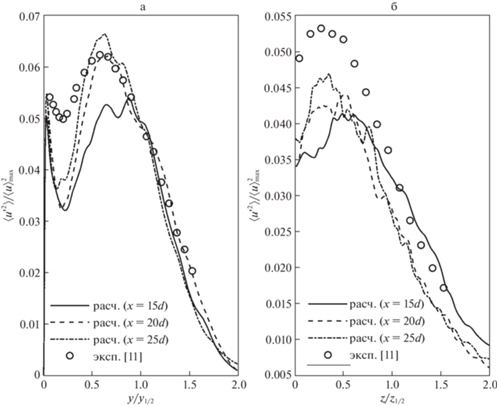
Выход на автомодельный режим профиля осредненной скорости, еще не означает, что такой же выход наблюдается и в других величинах. На рис. 8 представлено изменение $\langle u{\kern 1pt} {{'}^{2}}\rangle $, которое выходит на автомодельный режим при $x > 20d$.

Трехмерная пристенная струя представляет собой пример существенного различия структуры в случаях ламинарного и турбулентного течений. Дело тут не столько в неустойчивости течения, сколько в отношении диффузионных членов к инерционным. Запишем уравнение Гельмгольца для изменения завихренности $\omega = \operatorname{rot} V$ в несжимаемой жидкости:

Если компоненты завихренности $\omega $ обозначить ${{\omega }_{x}},\,{{\omega }_{y}},\,{{\omega }_{z}}$, то

В начальном выходном сечении струи компонента скорости $u$ терпит разрыв, а ${{\omega }_{x}} = 0$. Внутри струи $u = {{u}_{0}}$, вне $u = 0$. Это означает, что в начальном сечении внешний контур струи представляет собой поверхность разрыва тангенциальной компоненты скорости. На вертикальных ребрах струи возникает ненулевая величина ${{\omega }_{y}}$, а на горизонтальных – ${{\omega }_{z}}$. Далее включаются механизмы образования завихренности ${{\omega }_{x}}$ в основном из-за разворота остальных компонент завихренности (первые три слагаемых в правой части уравнения (4.1)), и диффузии завихренности. В случае малых чисел $\operatorname{Re} $ (ламинарные струи) диффузия превалирует над образованием завихренности, сколь-либо существенные продольные вихри не образуются, и схема течения соответствует приведенной на рис. 1.

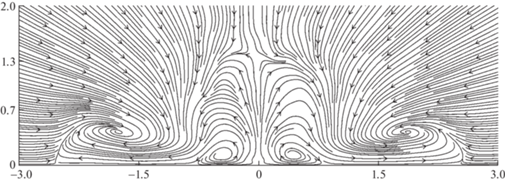
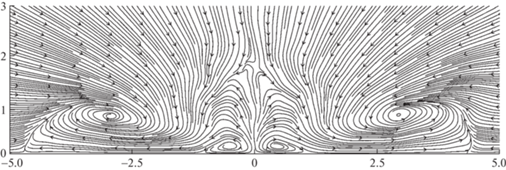
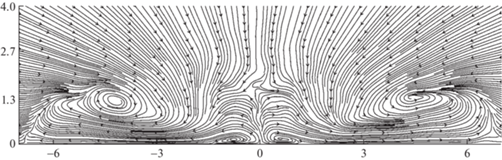
Для турбулентных течений в начальном сечении ненулевая завихренность присутствует только на ребрах квадрата. Именно вдоль ребер появляются продольные вихри различного знака, которые с ростом координаты x усиливаются благодаря слабой диффузии. Особое значение имеют вихревые пары, которые образуются в углах квадрата вблизи твердой поверхности (рис. 9, $x = 0.2d$). Далее эти вихревые пары усиливаются, индуцируют скорость в местах их расположения, направленную от линии симметрии, и таким образом “растаскивают” струю (рис. 10–14, $x = d$, $5d$, $10d$, $15d$, $25d$).

Заключение. Современные вычислительные комплексы позволяют при сравнительно небольших числах $\operatorname{Re} $ моделировать течения в турбулентных структурах. Хотя, по-прежнему, турбулентную вязкость необходимо учитывать для адекватного получения результатов, ее значение уже становится сравнимым с молекулярной вязкостью. Модель для подсеточной вязкости, которая применялась в данной работе, позволяет проводить расчеты без введения демпфирующих около твердой поверхности множителей.

Проведен расчет трехмерной пристенной турбулентной струи. Результаты расчетов согласуются и с экспериментальными, и с расчетными данными других исследователей. Показан выход течения на автомодельный режим.

Выявлены члены уравнения, которые приводят к образованию продольной завихренности, благодаря влиянию которой структура течения в трехмерных ламинарной и турбулентной пристенных струях кардинально различна. Если в ламинарном случае струя имеет предельную разделительную линию тока, отделяющую внутреннюю и внешнюю области течения, а толщина струи в поперечных направлениях не сильно различается, то в турбулентном случае образуются продольные вихри, “растаскивающие” течение в струе; размер струи вдоль твердой поверхности превалирует над размером в перпендикулярном направлении.