Сенсорные системы, 2022, T. 36, № 1, стр. 61-89

ВВЕДЕНИЕ

В статье описываются и с привлечением компьютерных симуляций обсуждаются новые аспекты (сценарии задач, методы и численные схемы их решения) развития темы, отраженной в цикле авторских работ по распознаванию овальной фигуры о по плоской центральной ее проекции инвариантно к группе дробно линейных (иначе – проективных) преобразований плоского контура о в пространстве сцены. Объект этого исследования – кривые семейства о – плоские гладкозамкнутые фигуры (не предполагающие формул аналитического описания, единых для семейства о и не имеющие опорных элементов контура о, традиционно используемых в распознавании фигур по особенностям их геометрии, – наподобие точек излома, перегиба, спрямления, двойного касания и прочего).

Эти соображения делают понятными трудности в попытках получить устойчивое описание о, не зависящее от ракурса оптической регистрации о технической системой распознавания: исключительно дифференциальные методы анализа о, обеспечивающие ее инвариантное описание (эти приемы давно предложены в теории плоских кривых (Картан, 1933)), не пригодны для дискретного входного задания о – в силу точностных требований к оценке локальных производных высокого порядка у “поточечно” описываемой кривой, каковые абсолютно нереализуемы практически (при любых технически возможных характеристиках камер). По упомянутым причинам для инвариантной (и не затратной, как это, в принципе, реализуемо полнопереборными методами для дискретно заданного о) репрезентации о необходимо получить какие-то дополнительные данные о его структуре. Ресурсно экономные методы анализа и проективно инвариантного опознания о возможны в случае задания о совместно с линейным элементом (точкой либо прямой произвольной ориентации относительно о (Николаев, 2011; 2019)) в плоскости о. Если же про о априори известно, что ему присущи свойства симметрии, то таким дополнительным атрибутам его описания может послужить линия горизонта HL, однозначно связанная позиционно для любых о неявной центральной симметрии разных типов (радиальной, поворотной либо совмещающей аксиальные и центральные ее аспекты, как это присуще кривым Ламе). Схемы и быстрые алгоритмы поиска элементов симметрии (полного набора ее вариантов) разработаны, численно промоделированы и описаны (Николаев, 2014; 2016). Согласно теореме 1 об инваринтных свойствах прямой extL, внешней относительно о (Балицкий и др., 2017) на extL имеется не менее двух пар точек (именуемых здесь “дуальными парами” ДП), где каждая ДП в терминах Плюккерова “полюс-полярного соответствия” дуально симметрична по полюсам, инцидентным extL. Каждая ДП детерминирует на контуре о свой квартет проективно инвариантных вершин, что для двух ДП однозначно задает сет из восьми упорядоченных точек контура (октет о). Если же от произвольной extL перейти к HL для о (вычисляемой для центрально симметричных о либо регистрируемых оптически камерой с фиксацией линии горизонта как функции ракурса съемки), то в этой постановке представляется целесообразным найденный по HL октет вершин использовать в задаче инвариантного описания о, не требующего расширения “атрибутов сцены” до композиций “о + extL” либо “о + intP” (вариант с тестовым полюсом), производя репрезентацию о в категориях, имманентных исключительно особенностям его геометрии. Эта идея имеет дополнительный бонус в части “эталонирования формы о”: малоразмерным дескриптором (циклическим 8-вершинным графом на плоскости вурфов) либо перепроецированием о на некий правильный n-вершинник, для чего мы предлагаем новый вид репрезентации – “на ромб и квадрат” (8-вершинный стандарт), о важных преимуществах какового в сравнении с предложенным нами ранее вариантом проекции на 4-вершинник будет сообщено далее. В соответствующих разделах обсудим методы и модельные реализации, формирующие сеты ДП, октеты для о и “конструкты его инвариантной репрезентации” (дескрипторы и “двойные эталонные проекции”) для сценических вариантов: аксиально симметричный о, центрально (и “поворотно”) симметричный о, кривые Ламе (подсемейство суперэллипсов, принадлежащее семейству о) и, наконец, о общего вида, симметриями не обладающий.

Немалый объем текста посвящен также рассмотрению двух гипотез, вызванных “логически внятным стремлением”: произвести универсализацию идеи о наличии у любых о октета проективно инвариантных вершин (если локализация HL обеспечена) и показать возможности оптимизации поиска ДП на HL в предположении, что позиции ДП связаны неким дополнительным условием в случаях о с симметриями. Первая гипотеза выглядела априори провальной, поскольку именно для аксиально симметричных о относительно “их потенциала” в реконструкции расположения HL “теория недвусмысленно декларирует” возможность вычисления лишь одной точки, HL принадлежащей: ей соответствует полюс P плюккеровой поляры, являющейся “по совместительству” неявной осью о (а положение оси всегда можно оценить в универсальной переборной схеме, с асимптотикой сложности n log n), т.е. вместо точной локации HL гарантирован шанс получения проективного пучка “гипотез о HL” с центром в P. Если бы получила подтверждение вторая гипотеза “о связи позиций двух ДП”, то “положительные вычислительные примеры” могли бы стать побудительным мотивом для расширения декларций упомянутой теоремы 1 относительно конкретных свойств HL. В силу этих интуитивных ожиданий модельный эксперимент в направлении “выбор истинной HL из пучка гипотез в анализе позиционных оценок ДП” представлялся вполне осмысленным (он проведен на материале четырех сгенерированных вариантов о с аксиальной симметрией (рис. 1), итоги чего рассмотрены в разд. 1).

Рис. 1.

Вид ортоформ, использованных в модельных демонстрациях, осесимметричных о Ф1–Ф4 и о С1, С2 радиальной симметрии (разд. 1 и 3). Остальные пояснения в тексте.

Следует коснуться истории вопроса (октет на контуре о) в связи с 10-й (X) статьей данного цикла исследований, где термин “октет” фигурирует в подзаголовке (Николаев, 2017). Рассмотрение 8-точечных конфигурций, возникающих на овальной кривой, не было там связано со свойствами HL, а привлекало внимание к возможному единообразию для схем дескрипторов в примерах сцен с о разного генезиса: при экспериментальном анализе идеи об односвязной проективной природе траекторий для триад “эллиптических точек” (содержание теоремы 2 о точках пересечения введенных ранее H- и T-поляр (Савчик, Николаев, 2016)), где октет соотнесен с позициями восьми экстремальных кривизн триады траекторий; на о общего вида, в вариантах, фиксированных для них контурной M либо внутренней intP позиций, для которых в соответствии с теоремой 2 вычисляется триада эллиптических точек, позволяющая по ним аппроксимировать некую прямую, что в свою очередь дает шанс оценить координаты двух ДП, детерминирующих сет восьми вершин контура о. Переход от найденной диспозиции октета к схеме дескриптора обосновывался заявлениями теоремы 3 (Депутатов, 1926) о существовании набора из двух независимых вурфов (названного “плоскостным вурфом” – как антитеза “линейному” (Глаголев, 1963), вычисляемому на прямой) для любой упорядоченной пятерки точек, принадлежащих гладкой выпуклой дуге (два вурфа – это пара координат точки на числовой плоскости вурфов). Производя для ансамбля из пяти соседствующих вершин циклический обход октета, получаем замкнутый 8-вершинник дескриптора. Схемы вычисления пары вурфов (шаблоны) для описываемой вершины октета можно предложить во многих вариантах. В последующих разделах (на примерах о разного типа) будут рассмотрены и иллюстративно предъявлены дескрипторы с минимальным (5-шаблон) и максимально возможным (8-шаблон) привлечением вершин о для задания описываемой вершины графа.

Дальнейшее повествование исключает обсуждение аспектов, обеспечивающих (методами обнаружения, подчеркивания и сглаживания “регистрируемых границ фигур”, – в их качечстве стандартных фаз обработки изображений) получение “продукта анализа” для нашего исследования – в виде “контура о” (тем более, при изложении развиваемых теоретических тезисов, конкретно соотносимых с разделами проективной геометрии плоских кривых). Итак, граница о и ее инвариантные геометрические характеристики фигурируют в качестве “данных автоматического анализа о в практической задаче по его опознанию/классификации”. Нас будут интересовать численно реализуемые подходы (с устойчиво воспроизводимми особенностями), где координаты, задающие границу о сетом вершин “оцифровки”, итогом дискретной обработки о формируют инвариантное его описание, создавая механизм классификации разнообразных гладких фигур методами проективно эквивалентных выборок, либо производят “эталонное описание” о – для последующих технических нужд (практических задач автономного опознания объектов).

Как и в предшествующих статьях цикла, под неявной формой представительства элементов симметрии (ЭС) подразумеваются особенности их проявления в проективной форме, не совпадающей с признаками ЭС в геометрии Декарта (где осевую симметрию описывает правило “хорды, перпендикулярные оси, делятся ею пополам”, а радиальная – задается свойством: “хорды, включающие центр, разделяются им на равные части”). В проективной геометрии неопределимы “перпендикулярность” и операция деления отрезка пополам. Методы поиска ЭС, опирающиеся на проективно инвариантные признаки, эффективны в широком диапазоне смены “ракурсов регистрации” о, в математической модели следуя законам лучевой оптики для камеры-обскуры. Простейшую разновидность наличия свойств симметрии у о (декартовы признаки) будем называть его ортоформой. В терминах ракурса ввода ее продуцирует камера ортогональной ориентации к плоскости о. Прежде чем перейти к обсуждению задачи выбора наилучшей гипотезы об HL (из числа возможных в пучке для полюса P) в случае осесимметричного о, традиционно уведомим читателя, что данный текст адресуется интересующимся вопросами автономного анализа формы, не предполагая навыков профессиональной подготовки в этой сфере. Для уяснения сути обсуждаемых проблем и понимания модельных итогов работы достаточно ориентироваться в общих вопросах естественнонаучного плана. Мысли автора донесены здесь в образной геометрической форме. Точное понимание деталей в вводимых далее нотациях, схемах и приемах обработки не обязательно для знакомства с миром образов и логикой обсуждаемых идей. Текст насыщен подробными иллюстрациями (“графическими копиями продуктов компьютерного моделирования”, полученных для разных сценариев с о), снабженных комментариями, что, возможно, удовлетворит и неспециалистов. Тема “как полюс-полярный дуализм коник и теорема взаимности помогают понять идеи и методы проективного анализа о”, доходчиво рассмотрена в статье (Акимова и др., 2014).

1. АНАЛИЗ СВОЙСТВ ДП В ЗАДАЧЕ ПОИСКА HL ПО НЕЯВНОЙ ОСИ СИММЕТРИИ О

Кратко о генезисе “конструкта” ДП. Особенность “дуальная”, в нашем случае присущая паре точек прямой, – имеет истоком теорию полюс-полярного соответствия для квадратичных кривых (коник) и базовую “теорему взаимности” для них (Глаголев, 1963; Моденов, 1969). Тезисы теоремы подсказали продуктивность введения в аппарат анализа о двух инструментов: H-поляры, следующей правилам гармонических отношений, и “на языке касательных формируемой” T-поляры. Детализируем взаимосвязь полюса и поляры “из мира коник”: плюккерова прямолинейная поляра соответствует прямой, проходящей через точки касания к эллипсу из внешнего полюса (потому связь их позиций взаимно однозначна). Точка (на кривой) T-поляры и задающая ее хорда на о, образуют комплекс “точка+отрезок”, соответствующий паре “полюс+поляра”. В работе (Акимова и др., 2014) сказано, что в диспозиции “внешний полюс, внутренняя поляра” однозначная их связь для о общего вида неизменна при любых проективных трансформациях о, что теряет свою приложимость для о в ситуации “внешняя поляра, внутренний полюс”. Тем не менее из идеи теоремы взаимности удается вычленить “условное правило дуальности отношений”. “Вариативная” (одна степень позиционной свободы) связь позиций двух полюсов и двух плюккеровых поляр, гарантированная для коник, редуцируется в случае с о к связи уже уникальной: для некоторой позиции полюса P1 при о можно искать такую позицию P2, что поляра p1 пройдет через P2, а полюс P1 будет принадлежать поляре p2. Эти два полюса нефиксированного внешнего расположения стали исходным носителем дуальных свойств в теореме 1, заявляющей, что на прямой extL произвольного ориентирования по отношению ко всякому о всегда существует не менее двух проективно инвариантных ДП.

Уточнив природу ДП, перейдем к описанию компьютерных экспериментов, целью которых был поиск устойчивых признаков, позволяющих для осесимметричного о – к точке полюса P симметрии, заведомо локализуемой на HL (по уже вычисленной позиции оси, являющейся плюккеровой полярой для P, что обеспечивают универсальные быстрые алгоритмы ее поиска (Николаев, 2015б)), добавить координаты любой второй точки, принадлежащей HL (например, F – в пересечении HL с осью E-D, см. рис. 2). Эта иллюстрация воспроизводит численно смоделированную сцену для о Ф1, вид ортоформы которого показан на врезке слева вверху, тогда как основные построения отображают ту “пластичность” проективных свойств лучей из P к о (в альтернативе вариантов выбора искомой вершины А, симметричная хорда=поляра A-B которой имела бы полюс F на HL), что и в ложной позиции избранной вершины a демонстрирует “гармонизм” проективных инвариантов (вурфов), присущий истинному положению A: например, для “верного луча” к A справедлива оценка W(P, M, F, N) = 1 (врезка справа вверху), но и для версии с ложной a (врезка слева под ортоформой) показан аналогичный итог: W(n, P, m, f) = 1 (где n, m, f заданы на врезках цепочкой определений: n ⇒ 1'–2' × P–f, f ⇒ t(a) × × t(b), 1' ⇒ f–b × P–D, 2' ⇒ f–a × P–E, 3' ⇒ f–b × × P–E, m ⇒ o-3' × P–f, демонстрируя проективную аналогию тройки n, m, f, соотносимую с триадой N, M, F, где N ⇒ 1–2 × P–F, M ⇒ O-3 × P–F, F ⇒ t(A) × t(B), O ⇒ 1–2 × E–D, 1 ⇒ t(B) × P–D, 2 ⇒ t(A) × P–E, 3 ⇒ F–B × P–E. Здесь и всюду далее значки “⇒”, “t(X)” и “×” следует понимать соответственно как операции “вычисляется”, “касательная в точке X” и “на пересечении”, а цифры “1”, “2”, …, “7” – это “имена” вспомогательных точек. Позиции контура I, R, J, L определены на врезках рис. 2, как и рецепты расчета служебных точек “4”, “5”, “6”, “7”, а также точки S, “связующей ДП”.

Рис. 2.

Демонстрация альтернативности решений (на примере о Ф1 осевой симметрии) в задаче локализации линии горизонта HL. На врезке слева показан вид ортоформы Ф1, а на остальных врезках приведены структурные формулы позиционной оценки для служебных точек и прямых. Построение для ложной гипотезы об HL выполнено штрихпунктирными прямыми: оно начинается с вершины-конкурента a. Показана схема детерминации октета {A, R, D, J, B, L, E, I} дуальными парами P..F, M..N на HL. Остальные пояснения в тексте.

Для внятности описываемых далее процедурных решений, на некоторой стадии вычисления использующих понятие “гармонизма”, приведем “формулу гармонического отношения”, в качестве важнейшего выражения для фундаментального проективного инварианта, здесь именуемого вурф (в современных математических работах его чаще называют “сложным отношением четверки точек на прямой”). Для простоты определения ограничимся заданием вурфа через длины отрезков, на которые прямую разбивает квартет ее точек (т.е. определим модуль вурфа, где знак при численном инварианте, формируемом из ориентированных отрезков, нами проигнорирован). Обозначив через a, b и c длины отрезков в маркировке их следования на несущей прямой, получим значение вурфа w в виде w[a, b, c] ≡ a * c/((a + + b + c) * b), что и дает всегда “безразмерное” число при любой размерности длин. Гармоническим (в этой форме задания) называется вурф, следующий условию w[a, b, c] ≡ 1, что реализуется, к примеру, радикально отличающимися композициями w[3, 1, 2 ] и w[x, x, ∞] с близкими и бесконечно далекой позицией одной из точек квартета (ее называют несобственной). В нашем случае “прыжки из бесконечности” в окрестность о являются характерной особенностью сцен при переходе от явного задания свойств симметрии (т.е. ортоформой) к неявному их представительству (реализующему требование независимости результатов анализа о от оптического ракурса его регистрации, как – ортогональной – для ортоформы, так и для любой неортогональной). Вернемся к трактовке модельных (численных) процедур, геометрия о в которых задавалась напрямую цепью вершин аппроксимации (с управляемой плотностью представительства на контуре).

Продолжим рассмотрение осесимметричного Ф1 в неортогональной проекции, для которого вычислены координаты E, D оси и позиция полюса P, а объектами исследования являются положения двух ДП на прямой, целевая установка для которой – “быть линией горизонта” HL. В рамках той же задачи проследим, не поможет ли выбрать “истинный азимут для A” гипотеза о позиционной связи двух ДП (“дуальность” неких пар P, F и M, N будем теперь фиксировать в виде P..F и M..N), задаваемой через “связующие координаты” S (S ⇒ t(A) × t(D) эквивалентно S ⇒ A–F × D–P)), что выражает реализация условия: “если найдена пара P..F (т.е. определено пересечение оси с HL), то M пары M..N принадлежит пересечению HL с S-3 (напомним: 3 ⇒ F–B × P–E), а N – пересечению c прямой “1–2”.

Вурф-оценки, связывающие гармонически координаты симметричных вершин, не могут помочь верной фиксации HL: W(P, A, C, B) = W(P, a, c, b) = 1. Равно бесплодны и попытки привлечь проективно связанные с ними оценки (верхняя врезка справа на рис. 2): W(P, 2, E, 3) = W(P, S, D, 1) = 1. Это же относится и к “осевым” негармоническим вурфам: W(F, D, C, E) = W(F, S, A, 2) = W(F, 1, B, 3) ≠ ≠ 1. Отметив, что адекватное задаче положение поляры A-B (означающее принадлежность ее полюса F “истинной” HL) действительно детерминирует искомый октет {A, R, D, J, B, L, E, I}, сосредоточим внимание на узловых фрагментах построенной сети касательных и хорд, где положение “пересечений” может изменять координатную привязку в зависимости от альтернативы вычисления позиции того или иного узла (например, M можно локализовать не только по “схеме” O-3 × × P–F, но и производя операцию t(I) × t(J); см. нижнюю левую врезку рис. 1). Целесообразно теперь обратиться к рис. 3, изображающему узловые места “карты проб” (и схемы оценок для них), для которой метод поиска желательных связей между элементами построения имел отправной точкой априорный список гипотез Г (с акцентацией узлов, предположительно устойчиво локализующих искомую позицию A в ходе перебора вершин на дуге контура “без малого” от E до D), и список этих гипотез, интуитивно нами выбранных для серии тестовых экспериментов, “исчерпался” набором {Г1÷Г7} (а самая эффективная из них – Г7 – была предложена в финале “прогностического штурма”).

Рис. 3.

Демонстрация узловых позициий (на примере с Ф1) для семи гипотез Г1÷Г7 (при переборе по n позиций вершины a(n) оценивается их близость к A для альтернативных построений, производимых в семи узлах) и показ условий У1, У2 и вурф-соотношений, не дающих отбраковать ложные варианты позиции HL в силу их универсального характера. Штриховой прямой выделен “особый” отрезок G-6, где проверяются Г2, Г4, Г5, У1 (с ним проективно связан пунктирный S-6 с оцениваемой Г6). Остальные пояснения в тексте.

Кратко прокомментируем (рис. 3 исполнен в стиле адресации активному читателю и содержит существенно больше информации, чем будет обсуждено в тексте) суть гипотез в допущении, что связь для S проверяется в M единственно по Г1 (O–S × P–F〉 〈t(I) × t(J), см. правую верхнюю врезку, где значок “〉 〈” имеет трактовку: “оценивается степень позиционного сближения левого и правого продукта операций”), тогда как серия гипотез Г2, Г4, Г5 “троекратно тестирует” прямую “5–6” (в узлах “6”, “8” и G), представляющую собой “индикатор гипотетически уникального сета свойств проективно стабильной точки на оси E–D, детерминируемого фиксированной триадой {P, E, D}” (Николаев, 2017). Г6 (с узлом V, не принадлежащим штриховому отрезку “5–6”) также косвенно связана с проверками существования “стабильной точки”, являясь нелинейно зависимой от Г2 (что подтвеждают эпюры, демонстрируемые в конце раздела).

В качестве дополнительного свидетельства трудностей выбора между “целью” и “шумом” (где A среди конкурентных a?) рис. 3 включает и два универсальных условия У тождественного позиционного задания узлов “7” и S “вроде бы” независимыми методами: “P–A × 5–6 ≡ P–A × Q–S” и “t(A) × t(D) ≡ O-3 × Q-7” (правая верхняя врезка рис. 3). В этот перечень логично включить и “не вполне очевидное” свойство: W(P, 6, 2, E)*W(P, 5, S, D) = 1. Не будем воспроизводить в тексте схемы операций всех Г, вынесенные в верхнюю правую врезку; ограничимся записью для “лидера” Г7 (ее узел H): E–D × I–R〉 〈E–D × J–L (нижняя врезка). Уточним: на каждом шаге перебора позиций A(n) по номерам n вершин о к квартету {E, D, A(n), B(n)} по координатам “текущего” 4-вершинника {1, 2, 3, S} – в пересечениях контура о с его диагоналями – определяется и квартет {I(n), J(n), L(n), R(n)}, что завершает комплектацию текущего октета. Имея полную его карту, можно вычислять экстремумы сближений в паре тестируемых операций для семи узлов по списку {Г1÷Г7} (о полученных результатах – чуть ниже, до этого полезно упомянуть о ситуации с о Ф4).

Аналогичные численные эксперименты были проведены на сгенерированных “по случайным” (не выбранным с целью “утвердить правоту” проверяемого тезиса) правилам осесимметричных Ф2, Ф3, Ф4. Результаты для Ф2 и Ф3 не привнесли ничего нового, лишь подтвердив приемлемую погрешность ошибки для предположения о “связующей роли” S (для задания ДП M..N по диспозиции P..T, что в дальнейшем было оценено примерно с той же позиционной ошибкой для о всех остальных типов симметрии и о общего вида), и потому не приводятся в качестве иллюстраций. “Печальную неожиданность подарил” о Ф4, развеяв надежды на Г7, бывшую абсолютным лидером на материале проб с Ф1÷Ф3. Графическая информативность рис. 4 основным образом сконцентрирована на четырех врезках, показывающих схему 5 -шаблона дескриптора и результат его привлечения для найденного по “истинной” HL октета {A, R, D, J, B, L, E, I} (врезки внизу, слева и справа), а также распределение октета на ортоформе, помогающее понять организацию и вид для нового (“двойного”) эталонного описания о по схеме проецирования “на ромб и квадрат”, в случае безошибочной локализации HL (верхние врезки, соответственно слева и справа). На основном поле рис. 4 изображена сеть построений, в которой произошло нарушение эмпирического правила – о доволно точном совпадении хорды R-L с диагональю S-F (что произошло в ситуации, когда T принадлежит HL, а S успешно аппроксимирует результат t(A) × t(D); это отображается на левой верхней врезке для ортоформы и на основном поле рис. 4). Если в примерах с Ф1, Ф2 и Ф3 “вторичный” квартет {R, J, L, I} локализовался на пересечениях контура о с диагоналями описанного 4-вершинника (образованного на касательных к “первичному” квартету {A, D, B, E} и на рис. 3 имевшего маркировку вершин не {S, G, F, K}, а {S, 1, 3, 2}), то для Ф4 “правильная” диагональ октета L-R (синяя тонкая прямая) уже не совпадала с диагональю S–F пересечений касательных в A, D и B, E. Этот “сбой” и повлек ряд существенных сдвигов в окрестностях L, I, M, N. По той же причине “не оправдала себя” Г7: прямые I–R и J–L не пересекались более на оси E–D (что легко заметить на левой верхней врезке рис. 4 – в виде отчетливой непараллельности этой триады прямых для ортоформы). Прежде чем будет кратко обсуждена “динамика оценок сближениия в узлах” по всем {Г1÷Г7} на материале тестов для сета Ф1÷Ф4, коснемся вопроса о проективно инвариантных эталонах для них.

Рис. 4.

Вид: двойной эталонной проекции о (показана на верхней врезке справа на примере Ф4, давшем опровержение всех Г), графа дескриптора Ф4 (в версии 5-шаблона; врезка в середине внизу), схемы вычисления 5-шаблона (врезка рядом, внизу) и ортоформы Ф4, где показан гипотетический источник ошибок локализации HL по факту расхождения поляры L–R и диагонали S–F (верхняя врезка слева), в два цвета фиксируемый на основном поле рис. вариантами позиций для M и N. Остальные пояснения в тексте.

Поясним вычислительную схему дескриптора по 5-шаблону. Если на октете заданы пять соседcтвующих вершин {1, 2, 3, 4, 5}, то позицию “3” можно проективно стабильно представить точкой на плоскости вурфов, используя упорядоченные квартеты {1, 6, 7, 4} и {5, 6, 8, 2} в качестве вурф-оценок w1 и w2 для них (на левой нижней врезке рис. 3 показано, как введение внутренних точек 6, 7, 8 по правилам 6 ⇒ 1–4 × 2–5, 7 ⇒ 3–5 × × 1–4, 8 ⇒ 2–5 × 1–3 создает условия вычисления требуемых квартетов). Просканировав сетом из пяти точек все вершины описываемого октета, получим циклический граф дескриптора, “отчетливо” классифицирующий роли вершин в октете: пара {E, D}, репрезентирующая ось, лежит на диагонали графика, а проективно симметричные пары {A, B}, {I, L} и {J, R} расположились на плоскости W вурфов точно симметрично относительно диагонали ее положительного квадранта (по причине перегруженности рис. 4 схема 8 -шаблона будет показана и описана в разд. 3 на примере центрально симметричного о С1, однако в рамках этого раздела целесообразно продемонстрировать форму дескрипторов для о типа Ф).

На рис. 5 и 6 приведены графики дескрипторов Ф1 и Ф2 соответственно (по схемам 5 - и 8-шаблонов). 8-шаблонные графы, как правило, имеют на плоскости вурфов масштаб существенно меньший, по этой причине они изображены на рисунках в пропорционально увеличенном размере. Поэтому граф для 8-шаблона неизменно симметричен относительно диагонали плоскости вурфов в координатах (kw1, kw2), где k коэффициент гомотетии, т.е. масштабирования. Для Ф1 k = 11.4, он намеренно был выбран таким для “эстетичной” компоновки рис. 5, так что условие d ≡ E не является законом “зависимости шаблонов”. У Ф2 k = = 12.5, и этот выбор обусловлен оптимизацией компоновки рис. 6. Так же как и по схеме 5 -шаблона, 8-шаблонные графы строго симметричны относительно диагонали, при этом ей самой всегда инцидентны образы осевых вершин E, D. Не приведены аналогичные графики для Ф3 – они мало отличаются от графов для Ф2. Рисунок 7 изображает дескриптор по 8-шаблону для “анархиста” Ф4. Его дублер по схеме 5 -шаблона уже показан на врезке рис. 4. Осталось заметить, что осесимметричность подсемейства Ф характерным образом выделяет их по дескриптору в 8-шаблонной форме: все опробованные в компьютерных тестах представители Ф имеют для графов этого шаблона строго квадратный фрагмент, а его вершины, ортогональные главной диагонали плоскости вурфов, являют собой образы вершин A и B, лежащих на луче из полюса симметрии P.

Рис. 5.

Вид на W-плоскости 8-вершинного циклического графа дескриптора Ф1 в формах 5-шаблона (черный график слева) и 8-шаблона (синий справа вверху). Пояснения в тексте.

Рис. 6.

Вид на W-плоскости 8-вершинного циклического графа дескриптора Ф2 в формах 5-шаблона (черный график слева) и 8-шаблона (синий справа вверху). Пояснения в тексте.

Рис. 7.

Вид на W-плоскости 8-вершинного циклического графа дескриптора Ф2 в форме 8-шаблона. Выделены диагонали A–B и I–L квадратных фрагментов. Пояснения в тексте.

Осталось обсудить нововведение в части непрерывного проективно инвариантного описания о, ставшее “естественным” следствием развиваемой здесь концепции “октета вершин о, имманентных проективным особенностям его геометрии”. Требует разъяснения утверждение о существенном улучшении схемы эталонного представления о проекцией на “правильную” композицию ромба и квадрата (с общим для них центром и равными площадями, так что восемь их вершин принадлежат окружности, а ромб – это повернутый на 45^о квадрат) в сравнении с прежней схемой, когда “вполне успешной” оценивалась инвариантная репрезентация одного стабильного квартета вершин о на квадрат эталона. Старая схема имела известный недостаток – “низкой чувствительности к проективным нюансам формы” сформированного эталонного описания вблизи каждой угловой точки квадрата (доходящей до нулевой – в четверке вершин). Предлагаемая нами методика этого четырежды происходящего “обнуления вариативности репрезентации” нацело лишена: будучи удвоенной, проекция на любой из вершин каждого правильного 4-вершинника имеет “дублера” на второй ветви со свободой выражения “нюанса формы” для того же (по полярному углу) участка представляемой ортоформы. И уточнение “того же участка” не является гиперболой, так как октет позиционно детерминирован двумя ДП, которые в соответствии с законами их генезиса не могут не только совпасть, но и сблизиться на HL, а стало быть, и вершины двух квартетов ({A, D, B, E} и {R, J, L, I}), регулярно чередуясь, маркируют контур о без значительных сближений, нивелирующих “информативность” репрезентации, как это с “неизбежностью свойственно” прежней манере эталонирования. Возвращаясь к рис. 4, отметим, что на крайней нижней врезке слева показан повернутый и увеличенный (×2.5) фрагмент двойного эталона для Ф4 от образа вершины J до образа D, на котором видно расхождение “квадратной” и “ромбической” ветвей в окрестности D (ветвь с узлом D выделена лазурным цветом, чтобы расхождение ветвей было отчетливее).

Вернемся к демонстрации результатов тестирования сгенерированной четверки о типа Ф на эффективность (в итоге – на целесообразность привлечения) набора {Г1÷Г7}. На рис. 8 приведены графики меняющейся (при последовательной смене номеров вершин о для текущей точки контура a(n)) оценки расстояния между “позициями, вычисляемыми по заданной альтернативной схеме для каждой из семи Г на роль наилучшего (в ареале своего узла) индикатора соответствия искомой позиции A для позиции HL, задаваемой априори точным ее расположением”. Для каждой из Г формируется своя кривая, минимум ординат расстояния d которой чем ближе к заранее известному номеру “истинной” A, тем эффективнее проверяемая Г для данного Ф (на рис. 8 верхний график отображает тесты для Ф1, нижний – для Ф2). Рисунок 9 демонстрирует динамику оценок d для того же набора гипотез при обработке Ф3 и Ф4. Сводка достижений: Г1 и Г3 дали хорошие оценки для Ф2 и Ф3, Г2, Г4 и Г6 оказались неэффективными, Г5 дала хорошие оценки для Ф1 и точные – для Ф2, Г7 дала наилучшие показатели для Ф1, Ф2 и Ф3 (при массиве вершин на полупериметре в 1200 дискрет, погрешности оценок колебались от одной до четырех дискрет, т.е. не достигали уровня в полпроцента). На тестировании Ф4 ни одна из гипотез не дала даже удовлетворительного результата. Дополнительные эксперименты показали, что дескрипторы для разнообразных Ф, вычисленные по ДП на “ошибочных” HL (хотя и принадлежащих пучку с центром P), обладают на плоскости вурфов (w1, w2) точно той же симметрией относительно диагонали ее положительного квадранта, так что и по свойству осевой симметрии графа “отбраковать ложные” HL не получится. Вне подхода, только и возможного для о общего вида (считывать положение HL при оптической регистрации о в условиях технической эксплуатации системы автоматического распознавания), остается шанс набрать статистику случаев нарушения эмпирического правила “квартет {R, J, L, I} инцидентен диагоналям 4-вершинника {S, G, F, K}” (рис. 4), для “нарушивших” – попыток инвариантной обработки не производить, прочих о (по типу Ф) – подвергать тесту по Г7.

Рис. 8.

Поведение функций-оценок по семи гипотезам Г, фиксирующих эффективность Г (через позиционную близость к целевой A) минимумом по d. Верхний блок эпюр – тесты для Ф1, нижний – для Ф2. Остальные пояснения в тексте.

Рис. 9.

Поведение функций-оценок по семи гипотезам Г, фиксирующих эффективность Г (через позиционную близость к целевой A) минимумом по d. Верхний блок эпюр – тесты для Ф3, нижний – для Ф4. Остальные пояснения в тексте.

2. НОВЫЕ МЕТОДЫ ПОИСКА ЦЕНТРА O У О СКРЫТОЙ РАДИАЛЬНОЙ СИММЕТРИИ

Представилось целесообразным – до обсуждения метода с привлечением позиции HL в задаче поиска октета стабильных вершин у радиально симметричных о – сообщить о произведенной в этой связи существенной оптимизации в схеме оценки позиции центра симметрии O, поскольку координаты O однозначно задают расположение HL, и ускорение (плюс упрощение, при увеличении точности) этапа детекции O делает более мобильной процедуру получения октета по ДП. Чтобы уяснить суть оптимизации поиска O (нами предложены два новых метода решения этой важной задачи), логично охарактеризовать прежнюю схему поиска (Николаев, 2014), которая ныне модернизирована. Заметим, что в работе (Николаев, 2021) также был предложен и испытан универсальный алгоритм поиска O, привлекающий ДП, но отличие его в том, что природа последнего не итерационная (как в обсуждаемых процедурах с общим генезисом), а переборная, и до тех пор, пока не будет разработана (и проверена в компьютерных тестах) его итерационная версия, он не конкурентен обсуждаемому тут подходу к общей задаче.

Идейная подоплека старого и нового подходов в целом общая и различается мерой сервисной поддержки (в оценке, насколько громоздок ресурс, требуемый для проведения итерационной процедуры поиска), а их общность может быть выражена двумя тезисами, связанными с природой инструмента анализа о, названного гармоническим контуром HC (он был предложен нами ранее, являясь для о клоном H-поляры внутренней локализации (Николаев, 2011), и использовался для получения ивариантных вурф-отображений о):

1. HC, вычисленный для центра симметрии O, представляет собой овальную кривую, с его вмещающим о (общего вида) связанную преобразованием Ω гомографии (то же, что и “проективное преобразование плоскости в декартовом 3D пространстве”; восемь его независимых коэффициентов через решение линейной системы восьми уравнений связывают произвольный квартет вершин о с идентичным квартетом на овале HC). Это единственный (уникальный) случай совпадающей с O позиции детерминирующего форму HC тестового полюса s, когда H- и T-поляра становятся прямыми, совмещенными с HL.

2. Если же тестовый полюс s, задающий HC, сдвигается из O, проективная связь HC и контура о теряется, а по мере приближения s к контуру о форма HC претерпевает некую регулярную деформацию (законы которой можно пытаться использовать для организации итерационной процедуры “обратной динамики”: сдвига s в направлении O).

Интуитивный отклик на сформулированные тезисы можно выразить так: для того, чтобы организовать “управляемый сдвиг s в сторону O”, следует озаботиться созданием механизма управления пошаговым сдвигом s, использующим “неведомые закономерности деформации” HC. Именно этими блоками “контроля и управления сдвига” сравниваемые методы и отличаются. В старой схеме “управление и проверка” возлагались на случайным образом избранный октет вершин о. Два новых метода привлекают для той же цели три (“трехточечный” метод 1) либо четыре вершины о (“четырехточечный” метод 2). Очень быстрая работа старого и двух новых алгоритмов имеет причиной отсутствие требования на каждом шаге итеративного процесса вычислять текущую версию овала HC: достаточно производить вурф-оценки для малого (от трех-четырех – теперь, до восьми – для прежней методы) числа квартетов на прямых, связывающих вершины HC с “точками управления” на контуре о. Формулы для вурфов просты, уравнения – линейны, счет – стремителен.

Для большей внятности дальнейших комментариев обратимся к рис. 10. Общий момент имеется и у двух новых схем: на контуре о случйным образом выбирается пара вершин A и B, а во внутреннем поле фигуры о (на рис. 10 овал о получает обозначение S) рандомно выбирается стартовая позиция s. Так, на контуре S появляется третья точка C (ее положение вычисляется на пересечении луча s-z с контуром S, где z ⇒ t(A) × t(B) (см. эту и прочие структурные формулы на врезках, в уже знакомой нотации). Далее пути решения расходятся (а конкретика трехточечной схемы проста, хотя и объемна в деталях), потому сосредоточимся на методе 1 (его функциональный узел показан в верхней врезке слева). Контурная триада {A, C, B}, благодаря наличию s, обеспечивает детекцию новой триады {E, D, F} в пересечениях лучей A–s, B–s, C–s с контуром S, а те, в свою очередь, дают возможность оценить позиции внешних P и T (где P ⇒ t(F) × t(B), а T ⇒ t(A) × t(E)), что в итоге позволяет локализовать по их координатам прямую (названную “гипотеза о HL”), на пересечениях с которой лучей A-s, B-s и C-s определяется тройка {H, R, M}. На трех прямых H–E, R–F, M–D фиксированы теперь три коллинеарные тройки точек: {H, A, E}, {R, B, F} и {M, C, D}. Для каждой предписано вычисление четвертой точки, с условием получения гармонического квартета (т.е. требуется найти позиции e, f, o, решая линейные уравнения W(H, A, e, E) = 1, W(R, B, f, F) = 1 и W(M, C, o, D) = 1; эти выражения вынесены в правую нижнюю врезку рис. 10). Теперь созданы все условия для завершения первого итерационного шага, поскольку сформирован треугольник “f–o–e”, во внутреннем поле которого можно объявлять новую позицию тестового полюса s' (сдвигаемой точки; на левой маленькой врезке слева этот шаг показан как сдвиг из позиции s(n) в точку s(n + 1)). Правило для локализации нового полюса было выбрано в виде операции определения центра масс f–o–e. Хотя этот прием и не является проективно инвариантным переходом от s(n) к s(n + 1), “свобода” в организации траектории по нежесткому правилу “смещаться в сторону O” оказалась допустимой в модельных испытаниях итерационной схемы, выводя траектории к целевой O из разных стартовых позиций. На рис. 11 продемонстрирована карта траекторий поиска O из пяти различных стартовых позиций s (они помечены в виде начальных точек s1, s2, s3, s4, s5 для пяти траекторий, а также маркируют на врезке с изображением S фиксированные вершины A, B и центр O в едином масштабе совместно со стартовым сетом {s1÷s5}), полученная нами в модельном эксперименте. Нижний график рис. 11 показывает, как для каждой из пяти траекторий менялись пошагово расстояния до O. Положение о допустимости непроективной операции (с вычислением центра масс) для “текущих f–o–e” убедительно иллюстрируют траектории из стартовых s1 и s2, где “путь к O” выглядит на начальных стадиях процесса “весьма окольным”.

Рис. 10.

О двух новых итерационных методах поиска неявного центра O у о радиальной симметрии. Слева – схема организации шага итерации, сдвигающего стартовую позицию s “в сторону O” согласно “трехточечному методу 1”. На основном поле рис. показано, как по рандомно заданным A, B и s выстраивается вся композиция элементов, требуемая для сдвига s, в том числе и по HC, привлекаемому в методе 2. Комментарии в тексте.

Рис. 11.

Демонстрация пошаговых сдвигов (от стартовых точек s1–s5) в итеративном цикле поиска O по методу 1 в модельном тесте с о радиальной симметрии – с показом (врезка вверху слева) на фигуре C позиций: центра O, рандомно заданных A, B и пятерки s1–s5. Нижний график изображает пошаговое сближение s_j  с  O. Большой окружностью (слева внизу) очерчена зона вокруг O, где эффективность методов падает. Комментарии в тексте.

Дополним идеологическую часть описания метода 1 объяснением, почему прямая через точки P и T названа “гипотезой о HL”. Для этого надо “мысленно перенестись” в финальную стадию процедуры поиска O. При условии, что траектория привела s в O, оказываются выполненными условия, связывающие позицию центра O с положением HL: плюккеровы поляры A–s–E и B–s–F, став в финале хордами A–O–E и B–O–F, имеют теперь полюсами окончательные позиции P и T, действительно (по тангенциальным законам связи полюса и поляры) принадлежащие HL. По законам гармоническим (из теоремы взаимности следующим) факт своей принадлежности HL дублируют и три коллинеарных квартета {H, A, O, E}, {M, C, O, D} и {R, B, O, F}, вурфы w для которых “обязаны приобрести” оценку w ≡ 1 (как и требуется для прямых пучка из O, пересекающих HL).

Целесообразен еще один комментарий принципиального характера, проясняющий необходимость сделать процесс поиска O двухстадийным (что свойственно всем здесь обсуждаемым методам – старому и новым). Процедура вычисления сдвига s имеет такую особенность: по мере приближения к цели (когда корректирующий сигнал становится все более неустойчивым, падая по амплитуде) цепь позиционных смен теряет однажды черты “траектории”, являя “хаотическое блуждание в статичной зоне”. Подобный ареал “потери эффективности метода” на рис. 11 выделен окружностью, где в среднем после 35-го шага итераций продолжение описанной процедуры лишено функционального смысла. С этого момента надо “менять парадигму”, переходя к известной технике “уплотняемых сеток”, когда, например, для девяти точек квадратной решетки “3 × 3” по четырем направлениям (вертикаль, горизонталь и две диагонали) для трех точек (это s и пара вершин пересечения с контуром S) – по каждому из них вычисляется позиция четвертой – с целью получения гармонического вурфа (вспомним уравнение для оценки e: W(H, A, e, E) = 1), после чего формируется “квартет из оных четвертых точек”, для которого оценивается “степень коллинеарности” (в целевой точке O она абсолютная, позиционно принадлежа HL), узел максимальной коллинеарности объявляется центром в три раза более плотной решетки и выбор “лучшего из девяти” повторяется той же схемой. Если алгоритм первого этапа мы назвали быстрым, то финальный – следует наименовать “молниеносным” (он не требует не только формирования кривых HC, но и существенно менее громоздкого “вычисления по полюсу – его поляры”, где нужна оценка касательных, и без чего не обойтись при детекции ДП). Варианты реализаций подобных пирамидально-переборных 2D подходов (как и “схемы спуска” – для первого этапа) давно изучены и стали “классикой итерационной идеи”. Казалось важным сообщить детали организации вектора сдвига, что и делает метод 1 новацией. Все три метода чувствительны к выбору опорных вершин контура: неудачная их композиция по отношению к рандомно зафиксированному стартовому s приводит “иногда” к спиральной траектории (либо ее финишу на контуре о). Сменить позицию s при фиксированных A и B (либо раздвинуть/сдвинуть эту пару) легче, чем варьировать композицию “октет на контуре + s”, как это приходилось делать в старой процедуре, и дело тут не в комбинаторном навале проб, а в разы более понятной причине неудачи. Уже со второго-третьего перезапуска траектория “выводит” к O (для метода 1 подобные ситуации были единичными в статистике проб в десятки стартов). Осталось аттестовать метод 2 (что будет сделано максимально лаконично – по причине ясности его новационной составляющей – в сравнении с техническими нюансами работы программы).

Вернемся к образам и “мантрам” рис. 10. На контуре S фигурируют десять вершин. Из этого набора для дела понадобится компактная четверка {A, G, U, B} (и служебная пара K, Q), из числа которых позиционные особенности еще не объявлены для {G, U, K, Q}. Их положение детерминируют на S описанные выше полюсы P и T, задавшие позиционно уточняемую “гипотезу о HL”. Лучи P–s и T–s на пересечениях с S задают пары G, K и U, Q. Далее для уяснения целевой установки метода 2 понадобятся принцип вычисления HC и основная мысль, объединяющая ранее сформулированные тезисы 1 и 2. Закономерности формирования HC поможет понять прочтение структурных формул из списка “Свойства HC” (на правой врезке рис. 10), суть которых в решении уже не один раз упоминавшейся вычислительной задачи: по координатам трех коллинеарных точек (это s и пара вершин S в пересечениях с прямой, через s проходящей) найти четвертую при условии получения гармонического квартета. Тезисы ориентируют мысль двумя конструктивными аспектами. В целевой позиции поиска (в центре O) для произвольной четверки вершин S – в итоге решения линейной системы восьми уравнений, связывающих восемь ее координат (4 точки, каждая с парой координат x, y) с аналогичным набором чисел для квартета на HC, будут получены 8 коэффициентов преобразования гомографии Ω, которые свяжут любую точку плоскости S c точками плоскости HC (как если бы это были разные плоскости). Мобилизуем тезисы 1, 2. Для s, совмещенного с O, преобразование Ω точку s никуда не сместит (случай тождественного преобразования), тогда как для любого иного положения s (когда проективная связь внешнего S и внутреннего HC овалов заведомо отсутствует) коэффициенты Ω, найденные по данным проективно независимых квартетов на S и HC, “непременно сдвинут” s в направлении, обусловленном “неведомой деформацией” HC. В методе 2 итерационные сдвиги s детерминированы коэффициентами Ω, получаемыми из уравнений связи (отсутствующей, хотя и “примерно закономерной” в части деформаций тем больших, чем ближе к контуру S форму HC задающая позиция s) между квартетами вершин {A, G, U, B} на S и набором {a, g, u, b} для HC. Идея подхода сформулирована “квази-математическим языком” в нижней части рис. 10 справа. Обсуждение модельной реализации метода 2, по мнению автора, мало соответствует тематическому профилю публикующего издания, но на ноте “уклонения от изложения” нельзя заканчивать тему новаций. Пусть заключительной позитивной мыслью станет декларация: новый метод 1, к этапу работы с ДП на HL поставляющий найденное положение центра O, финальным “побочным” продуктом имеет точную диспозицию востребованной “линии горизонта”.

3. О ВЫЧИСЛЕНИИ ОКТЕТА ВЕРШИН О РАДИАЛЬНОЙ СИММЕТРИИ И ЕГО ПРИМЕНЕНИИ

Согласно принципу дуальности плюккеровых полюса и поляры и уникальной роли центра симетрии O (явного у ортоформы и скрытого – в общем случае) H-поляра для O утрачивает криволинейность, трансформируясь непосредственно в интересующий нас носитель ДП – в прямую HL. Для ортоформы о разновидности радиально симметричных (представителей семейства которых будем в этом разд. классифицировать литерой С), HL из понятного нематематикам образа “линия горизонта” (что “присуще” общему случаю) становится бесконечно удаленным объектом – математической абстракцией под именем “несобственная прямая проективной плоскости”. В силу этих обстоятельств вид ортоформ для фигур семьи C напрямую иллюстрирует проективные особенности своей геометрии, давая возможность использования свойства “параллельность” и облегчая “интуитивное” понимание бесконечно удаленного объекта HL – посредством применения гармонического описания свойств его хорд, разделяемых центром O пополам, – на языке формулы “вурф в отрезках” (вспомним Введение): w[x, x, ∞] ≡ 1, где фрагмент x, x и означает разделение произвольной хорды у ортоформы о на две равные половины длины х. И, поскольку этот тип симметрии (что ясно геометру априори) обеспечивает для о однозначно простую связь с HL, то не потребуется “мудреных подозрений списка Г”, чтобы проследить путь и идею получения октета стабильных вершин кривой С посредством локализации двух ДП на HL.

В правой части рис. 1 приведен конкретный вид двух ортоформ разновидности С (им назначены имена: С1 и С2), на материале численных экспериментов с которыми будут иллюстрированы особенности и итоги задачи проектвно инвариантного распознавания фигур С по ходу поиска элементов (от ДП – через октет – к стабильным эталонам), эту задачу реализующих. Обсудим материал, скомпанованный на рис. 12. В правой верхней врезке в терминах плюккеровой дуальной пары “полюс, поляра” расклассифицированы для ДП D..T и H..M геометрические их связи, делающие отношения полюсов {D, T, H, M} и их поляр (хорд на С1 через точки касания, детерминируемые полюсами) дуальными. В уже стандартной нотации в верхней левой врезке даны структурные определения десятка внешних вспомогательных точек, а ниже – с привлечением свойства параллельности рубрицированы отношения элементов ортоформы, объединяющие триады вида “хорда и две касательных к С1” в группы, являющиеся для S общего вида проективными пучками с центром на HL. Дополнительные свойства, обнаруженные на примере С1, выражаются в добавлении к пучкам с центрами H, D, M, T пар хорд, не проходящих через O (а на ортоформе образующих ромб I–Q–J–G), дооснащающих каждый пучок в виде сета из пяти элементов (например, в D сходятся лучи B–L, I–J, A–B и касательные tG, tQ). На ортоформе с большой точностью композиции 1–3–5–7, 2–4–6–8, A–R–B–L и I–Q–J–G образовали ромбы (параллелограммы), а четверка “0, 1, 2, 9” (где “0 ⇒ B–L × 1–2”, а “9 ⇒ J–Q × 1–2”) проявила свойство коллинеарности. Был замечен факт W(i, I, Q, q) = 1/3 (i ⇒ I–Q × t(G), q ⇒ I–Q × × t(J)), для ортоформы о, свидетельствуя о равенстве трех отрезков, где средний I–Q, а крайние отсекаются прямыми “6–4” и “6–8”. Следует отметить важное свойство элементов ДП для о с симметрией осевой (Ф) и радиальной (С). Если узлом ДП называть точку пересечения ее поляр, то Ф и С различаются его “поведением”: у Ф узлы двух ДП не совпадают (принадлежат оси симметрии; на рис. 3 они обозначены как O и C), тогда как у С узел O общий. Свойство совпадения узлов ДП сохраняется и у кривых Ламе (будет рассмотрено в разд. 4), “несмотря на то”, что у них имеются оси симметрии (числом более одной; определяющим фактором является все же центрально симметричный характер о).

Рис. 12.

Схема оценки позиций ДП на найденной HL для о С1 радиальной симметрии – с показом: вида его ортоформы (врезка слева внизу) с двуцветной разметкой чередующихся квартетов вершин контура, структурных формул вычисления вспомогательных элементов схемы и правил для ДП (на прочих врезках), роли позиций “1” и “3” в гипотезе связи квартета H..M, D..T (основное поле, с двуцветным показом элементов, задаваемых каждой ДП, компонующих искомый октет {A, Q, R, J, B, G, L, I}). Остальные пояснения в тексте.

Рисунок 12 дополнительным образом информирует на примере фигуры С1 о ситуации продолжающихся (начало положено о типа Ф) проверок гипотезы о позиционной связи двух ДП. Как и ранее, предположение о координатной зависимости пар формулируется в виде альтернативы: если точно вычислена пара H..M, то найти D..T можно по положению точки “1” (1 ⇒ t(A) × t(L)), поскольку ожидается, что D ⇒ H–M × O–1, следовательно, локализуемы I и J, после чего окажется возможной оценка T (T ⇒ t(I) × t(J)), тогда как при известном расположении D..T пару H..M может “симметричным образом” локализовать точка “2” (2 ⇒ t(I) × t(Q)), задавая M. По координатам M определятся L и R (полюс M задаст поляру L–R), а вслед за тем – H (H ⇒ L–R × D–T)). Этот же альтернативный тезис на средней врезке справа объединен с констатацией зафиксированной погрешности вурфа на HL для ДП: W(H, D, M, T) = = 1.002. Сам же тезис сформулирован “косвенным” образом: MO ⇒ D–Q × t(I), HO ⇒ D–G × t(I) (где MO и HO записаны как плюккеровы поляры, лучи для которых из O фиксируются касательной в I на пересечениях с D–Q и D–G). Ошибка в оценке вурфа на HL – из-за сдвига позиций H и M. Она – в пределах координатного шума, порождаемого неточным заданием касательных в L и R для M, а также у A и B – для H (которые вычислялись программой, сгенерировавшей рис. 12, по правилам для коник – с использованием пяти соседних вершин, где средняя – в роли точки касания). При этом для M (на рис. 12 рядом с ее меткой надпись “погрешность оценки”) в масштабе рисунка позиционная ошибка – в толщину тонкой линии (вариант печати). Итак, связь ДП (случай – H..M по D..T) фиксирована в границах, допустимых для вывода “позиции ДП связаны”.

Неточности связанного позиционирования ДП для о С2 (рис. 13) были столь же незначительны (они намеренно нами усилены, чтобы показать источник расхождения в направлении на “далекий” полюс H (он за пределами поля рис.) в соотнесении с позицией L–R, по которой вычислялась M. Факт неточной гармоничности квартета ДП (на верхней врезке справа) зафиксирован “формулой” W(D, M, T, H) ~ 1. Переходя к описанию итогов инвариантного эталонирования о типа С, имеем теперь возможность продемонстрировать схему задания 8-шаблона дескриптора о (врезка на рис. 13 внизу справа). Его особенность – в полноте данных, привлекаемых для оценки координат каждой вершины полученного октета о (весь октет привлекается 8 раз в циклической смене ролей), и в топологической симметричности композиции, реализующей оценку пары вурф-координат. Чуть подробнее (о правилах вычисления w1 = W(2, 0, c, 5) и w2 = W(8, 9, х, 5)) коснемся участия четырех внутренних точек {0, 9, x, c}. Они необходимы для формирования композиции из двух коллинеарных квартетов (для вычисления вурфа нужна зафиксированная четверка точек прямой): {2, 0, c, 5} и {8, 9, х, 5}. Поэтому программа должна 8 раз пересчитать позиции дополнительных точек: 0 ⇒ 1–3 × 2–5, 9 ⇒ ⇒ 1–7 × 5–8, с ⇒ 4–6 × 2–5, х ⇒ 4–6 × 5–8. Теперь обратимся к рис. 14 и 15, где показаны для С1 и С2 (черными и синими прямыми) графы дескрипторов обеих версий шаблонов. Свойство радиальной симметрии (даже в неявной форме ее проявления, поскольку вурфы инвариантны относительно смены коэффициентов матрицы Ω) отразилось в особенностях организации дескрипторов: все они – двойного покрытия, т.е. вычисляемый граф, сформировав четыре вершины, далее “идет по своим следам”. Поэтому вершины графа (для обеих схем шаблона) идентично соотносятся с парами вершин октета о, радиально симметричных у C1 и C2: 4-вершинник объединяет в вершине пары: A/B, I/J, L/R и G/Q. Отметим черту, общую у шаблонов обоих типов: переход от С1 к С2 сопровождается поворотом “выпуклой оболочки” графа. Для схемы 5 -шаблона (при повороте) можно усмотреть и сдвиг, тогда как 4-вершинник 8-шаблонной версии при смене объекта С инвариантного описания совершает “чистый” поворот вокруг общего центра на W-плоскости (на рис. 15 это свойство показано наглядно при помощи пар тонких прямых черного и синего цветов с единым центром их пересечения), причем граф у С2 это квадрат, а у дескриптора С1 форма неправильная, – это 4-вершинник общего вида.

Рис. 13.

Дополнительная демонстрация (на модельном о С2) причин погрешности для гипотезы связей ДП по позициям “2” либо “3” с показом: распределения вершин октета на ортоформе о (врезка слева вверху), схемы вычисления графа дескриптора о согласно 8-шаблону по восьми вершинам в цикле (врезка справа внизу). Комментарии в тексте.

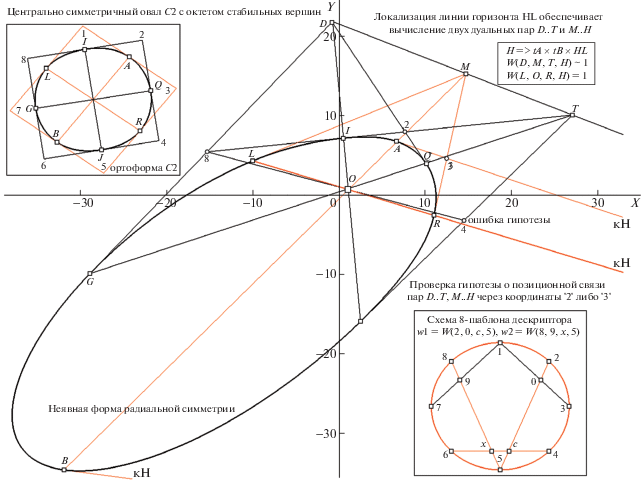
Рис. 14.

Вид графа дескрипторов С1, С2 по схеме 5 -шаблона, с двойной репрезентацией вершин октета в квартете вершин графа. Остальные пояснения в тексте.

Рис. 15.

Вид графа дескрипторов С1, С2 по схеме 8 -шаблона, с двойной репрезентацией вершин октета в четырех вершинах графа. Остальные пояснения в тексте.

Осталось продемонстрировать полученные (в тех же, что и ранее, компьютерных симуляциях) образцы двойных эталонных проекций для овалов С1 и С2 (рис. 16, слева – образ С1, справа – С2). Для лучшей “визуализации” свойств ДП разным цветом показаны ромб эталона {A, B, L, R}, порождаемый дуальной парой M..H, и квадрат {I, J, G, Q}, что детерминирован парой D..T. “Ромбическая” и “квадратная” ветви проекций нигде не соприкасаются (как это было у Ф4 при образе вершин J и R, см. рис. 4) и не пересекаются (как это “будет” показано в разд. 5 для о общего вида). “Комбинаторную задачу” выбора осей и вершин для дескрипторов и двойных проекций обсудим в Заключении, переходя далее к обсуждению свойств (в рамках концепции “роль ДП в детекции октета вершин о и формы его участия в инвариантной репрезентации о”) “специфического” объекта из того же семейства о, совмещающего особенности осевой и радиальной симметрии.

Рис. 16.

Вид двойной эталонной проекции фигур С1 и С2. Остальные пояснения в тексте.

4. СУПЕРЭЛЛИПСЫ И КОНЦЕПЦИЯ СТАБИЛЬНЫХ ОКТЕТОВ

Рассмотрим теперь, как согласно выдвинутой концепции о роли распределения ДП на HL (в итоге – октета вершин), детерминируемого самой геометрией кривой, проективно инвариантные ее свойства проявляются на примере популярного представителя семейства о, для которого известно (в отличие от уже рассмотренных случаев о с симметриями) аналитическое задание. В середине XX века под именем “суперэллипс” была переоткрыта кривая (спустя век после того, как она уже была описана Габриелем Ламе), имеющая в декартовых координатах вид (x/a)^m + (y/b)^m = 1, где показатель – m любое рациональное число, a и b – положительные коэффициенты; причем к семейству о имеют отношение лишь образцы, удовлетворяющие условию m ≥ 2 (при m < 2 контур фигуры теряет свойства выпуклости и гладкости, следовательно, – и принадлежность к о (Савелов, 1960; Gardner, 1977)). Будем оба эти названия фигуры использовать как синонимы, отводя кривой Ламе роль ортоформы. Поскольку “формулу суперэллипса расширяли” (включив, к примеру, вид “треугольное колесо”), в нашем рассмотрении мы не выйдем за пределы формализма, подразумевающего для кривой Ламе “обобщенную трактовку эллиптических свойств” в рамках определения: фигура с четырьмя либо с двумя осями симметрии, вписываемая в прямоугольник. При m = 2 это эллипс (либо окружность при a = b), в остальных случаях – алгебраическая кривая, не имеющая индекса аналитического порядка.

На рис. 17 показано (ставшее уже стандартным в части правила связей между ДП, где на рис. парам присвоены обозначения P..T и M..N) распределение на контуре фигуры (данный модельный образец маркирован литерой “Э”) октета {A, R, D, J, B, L, E, I}. Слева вверху на врезке предъявлена ортоформа Э с ее плюккеровыми полярами A–B, E–D, L–R и I–J (L–R и I–J это псевдо-оси симметрии). На основном поле рис. 17 в тех же обозначениях (с добавлением участка HL от P до T – в качестве неполного набора ДТ) демонстрируется вид проекции Э. Матрица преобразования Ω выбрана обеспечивающей расположение HL вблизи от Э (хотя N, как четвертая в наборе ДП, за пределами поля рис.). Не изменилась и нотация задания определяющих точек построенной сети (все важные структурные формулы вынесены во врезки с правой стороны рис. 17, в том числе внизу показана связь канонического образа о при задании ортоформой со стандартными коэффициентами матрицы Ω, меняющими ее к общему виду).

Рис. 17.

Схема вычисления октета стабильных вершин {A, R, D, J, B, L, E, I} суперэллипса, задаваемых согласно диспозиции ДП P..T и M..N, с показом: вида ортоформы кривой Ламе с ее четырьмя полярами в роли “осей” (двуцветная врезка вверху слева), структурных формул для элементов схемы и установочных правилах для нее (на прочих врезках) и роли точки S в качестве связующей для позиций ДП на HL. Остальные пояснения в тексте.

Наличие двух осей симметрии (явных у ортоформы), а также – двух диагональных псевдо-осей, в действительности являющихся “хордами разреза” в границах “поворотной симметрии” о (т.е. они должны быть классифицированы как принадлежащие виду R₂, об этом семействе подробнее будет раcсказано в разд. 6; а реальные четыре оси кривая Ламе имеет в случае равенства параметров a = b), и обусловило дополнительное проявление новых “попарно симметричных” отношений у вершин октета: концевые точки осей-хорд стали полностью определяющим фактором для диспозиции октета. Дадим пример. Хорда L–R симметризует на ортоформе позиции трех пар: I–J, A–D и B–E, что на схеме рис. 17, как проекции общего вида для суперэллипса Э, реализовалось в выполнении правил, задающих позицию N (образующую совместно с M одну из ДП) в виде пучка трех прямых I–J, A–D, B–E и двух касательных t(L) и t(R) (шестым элементом пучка можно считать саму HL). В пользу проверяемой гипотезы о позиционной связи ДП (из геометрических соображений ее для кривых Ламе можно считать доказанной) говорит и факт тройных пересечений, тестами подтверждаемых (в виде истинности не только симметрии позиций у вершин октета, но и симметризованных направлений касательных в них) для моделей суперэллипсов: на маленькой врезке справа подобное свойство зафиксировано для общей схемы в виде пары позиционных условий “t(R) × t(J) × T–O” и “t(R) × t(I) × × P–O”, а сами эти две точки показаны на лучах T–O и P–O метками “малый кружок” (без литер при них).

Указанные выше обстоятельства “усиления свойств симметрии” для кривых Ламе выразительнейшим образом проявили себя через свойства графа дескриптора в варианте 8-шаблонной схемы (рис. 18). Образ графа объединил особенности “двойного покрытия” и форму ромба 4-вершинника, выявленные у центрально симметричных представителей о (рис. 15), со свойством иметь “квадратный фрагмент”, присущим графу осесимметричной разновидности Ф (рис. 7), “монопольно” представляя собой квадрат двойного покрытия, с симметричным его расположением относительно диагонали положительного квадранта W-плоскости. События на ней (при 8-кратном увеличении масштаба для графа-квадрата) отображены с указанием пар октета, совмещаемых (для обеих схем шаблона) в четырех вершинах графа, причем для удобства визуального отслеживания вершин Э, отображаемых на графе, на врезке справа внизу показана маркировка вершин Э для проекции, общей с рис. 17. На верхней врезке слева (рис. 18) для Э (с той же разметкой) воспроизведена его “двойная эталонная проекция” (цвет ветви соответствует ромбу либо квадрату эталона). Данный вид репрезентации о сохранил проективные свойства симметрии суперэллипса: двойную осевую и радиальную (ситуация с диагональными осями обсуждается ниже).

Рис. 18.

Вид эталонных описаний для модельного суперэллипса Э – в форме дескриптора, по схемам шаблонов для пяти (черный график) и восьми (синий) вершин и в виде двойной проекции, с эталонами ромб (черный) и квадрат (синий), чередующими на двух ветвях (черной и синей) позиции найденного октета (врезка вверху слева), а также демонстрация распределения октета на контуре Э (врезка внизу справа). Остальные пояснения в тексте.

Вторым о для иллюстрации численных экспериментов с кривыми Ламе выбрана дискретная модель З с меньшим степенным показателем m (т.е. ортоформа у З ближе к окружности, чем у Э, а сами ортоформы – с общим центром – показаны на нижней правой врезке рис. 19). Поскольку никаких неожиданностей с поиском ДП и детерминацией по ним октета не произошло (да и не предполагалось), равно как и погрешность при проверке гипотезы о позиционной связи ДП не возросла (а в среднем по серии тестов суперэллипсы проявили себя как наиболее точно следующие условиям связи – в сравнении с остальными типами “о с симметриями”), для З не приводится карта поиска, аналогичная таковой для рис. 17. Так как все модельные тесты для Э и З проводились “по идентичной программе, но с попыткой показать различия двух избранных образцов”, то для задания З параметры о были выбраны таким образом, чтобы подчеркнуть нетождественность проявления осевой и радиальной симметрии. На двойных эталонных проекциях это отличие выразилось в том, что диагональные псевдо-осевые направления L–R и I–J не только не совпадали, но и с существенной визуально разной точностью годились на роль осей, при этом оба образца имели идентично расположенные ортогональные оси симметрии – по A–B и E–D. Более явственным это отличие заметно при совмещении ортоформ (врезка внизу справа на рис. 19; слово “ось” там имеет смысл псевдо-ось). В завершение темы “октеты кривых Ламе” осталось уточнить, что масштабный коэффициент для 8-шаблонного дескриптора З равен 8.4, а на правой верхней врезке рис. 19 показан “почти в три раза” увеличенный фрагмент двойной эталонной проекции З (на интервале от I до A) – для демонстрации отсутствия слияния ветвей в окрестности вершины A (что трудно различить на полной проекции). По уже доложенному материалу (за вычетом финальной фазы исследования; раздел 5 работы посвящен рассмотрению проективно инвариантных свойств о общего вида) можно сделать предварительный вывод: для о со свойствами симметрии – идея поиска (методами дискретной обработки) октета стабильных вершин его контура обеспечивает получение двух новых форм репрезентации проективно инвариантных свойств о, каждая из которых несет информацию, дающую однозначно произвести классификацию типов симметрии о. Переходим к рассмотрению о, не имеющего свойств симметрии, а потому согласно теории гладких выпуклых кривых о может быть приведен преобразованием Ω к любому иному о'.

Рис. 19.

Вид графа дескриптора З (двойного покрытия) для шаблонов с пятью (черный график) и восемью (синий) вершинами в цикле и вид для З двойной проекции, с эталонами ромб и квадрат (черный и синий), чередующими на ветвях позиции найденного октета (врезка вверху слева). На врезке справа внизу – вид ортоформ Э и З. Пояснения в тексте.

5. ОВАЛЬНАЯ ФИГУРА ОБЩЕГО ВИДА И ДВА МЕТОДА ЕЕ ИНВАРИАНТНОЙ РЕПРЕЗЕНТАЦИИ

Ведущиеся более четверти века попытки предложить методы и схемы дискретной обработки о общего вида, приемлемые (по устойчивости, точности и вычислительным затратам) в рамках проективно инвариантного их представления в задачах автономного распознавания, не увенчались, по мнению исследователей, внушающим надежды успехом (Olver, 2001; Hann, Hickman, 2002; Musso, Nicolodi, 2009; Hoff, Olver, 2013). Громоздкость полнопереборных схем (с их неутешительной асимптотикой сложности алгоритмов), а главное, координатный шум оптической регистрации о, лишают проблему перспектив разрешения. Ситуацию усугубляет известный запрет на использование универсальных идей дифференциальной обработки, давно предложенных математиками (Картан, 1933; Faugeras, 1993), но технически нереализуемых в принципе – по причинам недостижимости требуемой точности оценок производных высокого порядка для кривой в ее задании на дискретной сетке. Описанный идейный тупик “рушит искусственный прием” расширения сценария задачи – образованием композиции “о + L” либо “о + P” (фиксированного при о задания прямой L или же точки P – для любых вариантов их расположения относительно о), рассмотренной в работе (Николаев, 2019). Вариант “о + extL”, согласно декларациям теоремы 1 (см. Введение), устраняет препятствия в попытке быстро и точно организовать инвариантную репрезентацию о привлечением сета ДП, локализуемого на внешней L.

По причинам отсутствия возможности “извлечь данные” о диспозиции HL из самой геометрии о, как это предлагалось делать для симметричных фигур (особенности разных типов симметрии использовались, благодаря теоретически найденному способу “опоры на инвариантные их свойства”), приходится сменить подход к задаче, сделав ее постановку с учетом реальных технических аспектов ввода изображения регистрирующей его камерой. Для аэрофотосъемок земного рельефа (методы картографии) известна задача опознания контуров озер (Савчик, Саблина, 2018; Savchik et al., 2018), при реализации которой для серии снимков угол отклонения оптической оси от вертикали без труда трансформируется в позицию линии горизонта (при заданном направлении оси на “середину” опознаваемого озера). Контур овального озера при этом “комплектуется” диспозицией HL. Далее будем считать, что прямая HL и контур о образуют входную карту, и перейдем к схеме рис. 20.

Рис. 20.

Схема построений, задающих позиции стабильного октета вершин у о общего вида, связывающих через диспозицию HL, полученную с оптического входа регистратора, координаты ДП на ней с детерминируемым по ДП октетом. На врезках показаны: вид двойной проекции с пересекающимися ветвями (справа вверху) и граф дескриптора о в двух формах шаблона (слева внизу), оценки вурфов на полярах (и на HL), позволяющие избежать вариаций проецирования о на эталонный 8-вершинник. Разъяснения в тексте.

На поле рис. внизу справа изображен контур овального объекта, каким бы он был на снимке при ортогональной регистрации (назовем этот ракурс “ортоформой”). Снятый не под прямым углом (к “плоскости Земли”), он приобрел вид, который уже может теперь рассматриваться в компоновке с HL (основное поле рис.). После успешной оценки сета ДП, стандартная процедура фиксирует на контуре о октет {A, R, E, I, B, L, D, J}, позиции которого задают граф дескриптора (для двух шаблонов; врезка слева внизу) и могут быть привлечены (через оценку матриц Ω для эталонов ромба и квадрата) для формирования двойной проекции о (двуцветная карта ветвей – на верхней врезке справа). Инвариантные репрезентации имеют особенности, отличающие их от полученных на о с симметриями: дескрипторы утеряли осесимметричную форму (относительно диагонали W-плоскости), а ветви на двойной эталонной проекции асимметрично пересекаются. Осталось заметить, что проверка на связь ДП (на рис. 20 они обозначены как P..T и M..N) также приобрела новый аспект, нивелирующий оценку ее достоверности: узлы каждой из ДП в “постановке общего вида” (позиции C и c) стали теперь разнесенными, поэтому оценки положения S уже недостаточно для задания поляры D–S, требуется оценка позиции c (чисто случайно лучи S–C и S–c оказались близки, а сама S удовлетворяла условию связи S ⇒ t(I) × t(R)). Не собираясь усложнять гипотезу о связи ДП, отвергаем ее адекватность для общего случая. Разбором этого варианта геометрии о (в рамках применимости предложенной “концепции о стабильном октете”) мы собирались завершить изложение модельных экспериментов. Желание достичь “большей репрезентативности тестов на численных моделях” побудило добавить короткий раздел, в котором рассмотрен о, имеющий “особую (вращательную) симметрию и не требующий привнесения данных об HL”, однако, по причине отсутствия у него на эталонных отображениях (и на ортоформе) свойств симметрии уже описанного нами вида (осевой либо радиальный вариант), он близок к о, обсуждавшемуся выше.

6. АНАЛИЗ СЦЕНЫ С ОВАЛОМ НЕЯВНОЙ ПОВОРОТНОЙ СИММЕТРИИ R₃

Фигуры, ортоформы которых обладают поворотной (ротационной) симметрией с нечетным индексом (когда индекс у о четный, он формально неотличим от о радиальной симметрии, а сам индекс n фиксирует количество идентичных фрагментов дуг, которые гладко сопрягаются, имитируя образование замкнутой фигуры “склеиванием поворотом” n раз вокруг центра O), рассмотрены в работах (Николаев, 2015а; 2017), где был описан ряд универсальных процедур (тесты по индексам n “3” и “5”) поиска неявного центра O фигуры R_n, а для о R₃ был предложен и испытан метод реконструкции HL по данным о позиции O. Эти алгоритмы описать лаконично (без потери внятности изложения) вряд ли возможно, поэтому сразу же приступим к изложению деталей и выводов по данным серии модельных экспериментов с R₃, иллюстрируя материал на примере одного из тестовых образцов (объекты R₅ не рассматриваются тут по причине ограничений объема текста).

На поле рис. 21 внизу справа показана тестовая ортоформа R₃ (подобные объекты типа сглаженный треугольник стали ныне в компьютерной графике популярной фигурой – из клона обобщенного семейства суперэллипсов, и это уже не “исходная кривая Ламе”). На основном поле изображен о, гомографически трансформированный к виду с близко от него расположенной HL (центр O при этом приобрел столь сильный сдвиг, что визуально особенности симметрии вращения у O уже не воспринимаются даже “приблизительно”), на которой стандартная процедура поиска фиксирует квартет позиций двух ДП (это M..N и T..P, причем P локализуется за пределами поля рис.). Найденные ДП детерминируют для R₃ октет вершин {A, R, E, I, B, L, D, J}, позиции которых используются для дискретного (дескриптор в двух форматах графа; верхняя врезка справа) и гладко непрерывного (слева на большой врезке – двуцветная двойная проекция) инвариантного представления R₃. Из числа особенностей, эмпирически уникальных (теорем на тему “вурфы ДП для HL” автор не знает, поэтому поспешный вывод о всеобщем для R₃ свойстве W(M, T, N, P) ≠ 1 “рухнет однажды у контрпримера”), можно указать на нарушаемое представителями R₃ правило: “иметь оценку вурфа для квартета точек ДП на HL, близкую к гармонической”. Хотя у R₃ симметрия центральной природы, она столь непрямая, что дескрипторы “являют хаос”, а двойной образ проекций стирает след правил, регуляризующих композицию ветвей. Уже на ортоформе R₃ связь ее узлов c1, c2 с O “не проста”. Этими ремарками завершим раздел.

Рис. 21.

Схема получения позиционных оценок стабильного октета {A, R, E, I, B, L, D, J} вершин о ротационной симметрии типа R₃, с показом вида: ортоформы R₃ и некоторой ее трансформации под действием Ω (основное поле рис.), двойной проекции (слева вверху) и графа дескриптора R₃ (для двух форм шаблона; справа вверху). Комментарии в тексте.

ЗАКЛЮЧЕНИЕ

Одной из адекватных форм стабильной репрезентации о ранее заявлена операция проецирования о на стандартный 4-вершинник (фигуру фиксированного расположения и формы), что однозначно реализуется решением линейной системы восьми уравнений (Николаев, 2011), так как позиции проективно инвариантной четверки вершин контура о можно связать с шаблоном 4-вершинного эталона, произведя проективное преобразование Ω плоскости исходного о (его задают восемь неизвестных независимых коэффициентов) проецированием на 4-вершинник эталона, с условием совмещения найденной стабильной четверки вершин о с вершинами эталона. О слабых местах этого подхода сказано в разд. 1 (а в разд. 2 тот же прием перепроецирования на 4-вершинник обсуждается в связи со схемой “4-точечного метода 2” в итерационном процессе поиска центра O). Подчеркнем эволюцию “качества эталонирования”: схема двойной проекции лишена происходившего (по прежней методике – в каждой вершине эталона,) “обнуления свободы репрезентации”. Будучи удвоенной, проекция в любой из вершин каждого эталонного 4-вершинника имеет “резерв описания нюансов формы о” для того же локуса представляемой ортоформы на парной ей ветви. Наконец, кратко о выборе для членов октета их позиций на “квадрате” и “ромбе”. Стандартизации порядка вершин у о общего вида и R_n могут помочь различия оценок вурфов на полярах ДП с несовпадающими узлами (см. рис. 20 и 21). Для аксиально симметричных о диаду вершин оси следует проецировать на горизонталь ромба (рис. 4).

Во Введении была сформулирована задача проективно инвариантного описания гладких выпуклых фигур (о), имеющих некие ЭС и регистрируемых массивом вершин в произвольном ракурсе. Такая постановка подразумевает быстрое вычисление дискретного описания (устойчивого к трансформирующим влияниям проективного преобразования гомографии Ω плоскости о) – в виде получения графа дескриптора (Николаев, 2016; 2019), формирование которого реализует идея плоскостного вурфа (Депутатов, 1926). Интерес к вурфу, как к ключевому элементу производной Шварца, описанной более века назад, до сих пор не угас у математиков (Овсиенко, Табачников, 2008). Элемент эволюции в развиваемых нами подходах не только в том, что плюккеровы поляры у ДП на HL для о радиальной симметрии гарантируют наличие признака гармоничности вурфа для них, а новые эталонные схемы имеют главным узлом процедур вычисление вурфа, но одним из актуальных следствий описываемой концепции можно считать обеспечение однозначной типизации особенностей симметрии о по геометрически проявляемым свойствам его дескриптора (в обеих версиях). Перед “расшифровкой типа о – по правилам для графа” уточним: исследование проективно стабильной презентации фигур семейства о включило немало работ, где анализировались законы проявления неявной симметрии различных типов (Николаев, 2014; 2016; 2017; 2019), при этом в них не был предложен единый носитель=классификатор симметрий. Дескриптор о индицирует (на плоскости W) тип симметрии: аксиальной – по 8 вершинам, где 6 “разбиты” диагональю d на пары, у о симметричные, а пара осевых лежит на d; радиальной – по четверке вершин двойного покрытия, “cливших” симметричные пары о; у R_n и о общего вида – по беспорядку на W.

Востребованность задач автоматического опознания объектов типа о побуждает искать приемлемые подходы с предложениями различных “полуинвариантов” (Olver, 2001; Hann, Hickman, 2002; Musso, Nicolodi, 2009; Hoff, Olver, 2013). Например, Карлсон (Carlsson, 1996) предложил метод сопоставления о по пяти точкам касания вписанного в о эллипса либо по четырем точкам касания к о, образующим гармоническое отношение, которое можно доопределить для четырех точек на эллипсе. Следует отметить, что в этих работах схемы и методы детекции проективно устойчивых свойств симметрии выпуклой гладкой кривой не рассматриваются. Свойства симметрии плоских гладких фигур если и исследуются, то, как правило, это относится к кривым заданного аналитического порядка. Примером можно привести исследование аспектов симметрии у алгебраических объектов шестого порядка (Itenberg, Itenberg, 2004), добавив работу (Brugalle, 2007), где обсуждены свойства и особенности кривых седьмого порядка. Интересны и современные работы по параметризации и нормализации кривых ротационной симметрии (Lebmeir, Jurgen, 2008), а также – по разработке теоретических подходов и реализации задач попарного сравнения аффинно и проективно эквивалентных симметричных кривых (Hauer, Jüttler, 2018). Все процитированые работы не имели объектом иcследования представителей семейства о.

Сформулируем выводы по рассмотренной теме Привлечение ДП на HL для оценки октета проективно стабильных вершин о, обеспечивающего решение задачи эталонного описания о в форме, удобной для классификации типов симметрии о (плюс сепарации образцов, лишенных этого свойства). Разработаны и испытаны в сериях модельных тестов численные методы решения задачи инвариантного описания о, не требующие расширения входного сценария заданием композиций “о + intP” либо “о + extL”, так как декларации теоремы 1 (о ДП на extL) предложено использовать для носителя HL в качестве объекта, диспозицию которого (в плоскости о) можно оценить, исходя из свойств симметрии о (неявной, центральной природы). Предложенные приемы обработки кривых семейства о с получением для них эталонных описаний оригинальны. Прямые и косвенные аналоги схем привлечения ДП в формирование инвариантных эталонов о двух видов (дискретного и непрерывного) не обнаружены нами в доступных базах цитирования.

Работа выполнена при поддержке РФФИ (грант № 19-29-09075).