1. На главную
  2. Электронные версии
  3. Сенсорные системы
  4. T. 36, № 1, 2022

Сенсорные системы, 2022, T. 36, № 1, стр. 90-98

Учет гетероскедастичности в измеряемых томографических проекциях при реализации алгебраического подхода в томографической реконструкции

М. В. Чукалина 1, 2, *, А. С. Ингачева 2, 3, А. В. Бузмаков 1, 2, И. В. Якимчук 4, И. А. Варфоломеев 4, П. А. Кулагин 5, Д. П. Николаев 2, 3

1 ФНИЦ Кристаллография и фотоника
119333 Москва, Ленинский проспект, 59, Россия

2 Смарт Энджинс Сервис
117312 Москва, проспект 60-летия Октября, 9, Россия

3 Институт проблем передачи информации РАН
127051 Москва, Большой каретный пер., 19, Россия

4 Московский научно-исследовательский центр Шлюмберже
125171 Москва, Ленинградское шоссе, д.16 А, стр. 3, Россия

5 Московский физико-технический институт
141707 Долгопрудный, Институтский пер, 9, Россия

* E-mail: chukalinamarina@gmail.com

Поступила в редакцию 20.10.2021
После доработки 29.10.2021
Принята к публикации 09.11.2021

Полный текст (PDF)

Аннотация

Метод компьютерной томографии, являясь неразрушающим методом искусственного интеллекта, позволяет восстанавливать внутреннюю морфологическую структуру объектов по набору зарегистрированных под разными углами проекций. Объект зондируется рентгеновским излучением, которое при прохождении через него ослабляется. Ослабленное излучение регистрируется позиционно чувствительным детектором. Время экспозиции является важным параметром измерительной системы и наряду с поглощающими свойствами самого образца определяет вероятностные характеристики регистрируемых величин. Статистическая модель формирования сигнала в ячейке детектора базируется на распределении Пуассона, поэтому, чем меньше значение регистрируемого сигнала, тем больше его дисперсия, т.е. значения гетероскедастичны. Гетероскедастичность порождает на восстановленных изображениях искажения, которые мешают правильной интерпретации получаемых результатов. В данной работе предлагается метод реконструкции, базирующийся на алгебраическом подходе, основная идея которого состоит в добавлении матрицы “доверия” в решаемую систему линейных алгебраических уравнений (СЛАУ). Матрица рассчитывается на основе результатов анализа дисперсии зарегистрированных сигналов. Выписан шаг градиентного метода оптимизации, используемого для решения СЛАУ. Результаты экспериментов на синтетических данных показывают увеличение точности реконструкции при учете гетероскедастичности.

Ключевые слова: рентгеновская томография, метод искусственного интеллекта, методы реконструкции, гетероскедастичность

ВВЕДЕНИЕ

Рентгеновская томография – это метод восстановления внутренней морфологической структуры объекта по набору его рентгеновских изображений (проекций) (Withers et al., 2021; Arlazarov et al., 2021). Современные томографические комплексы востребованы во многих областях человеческой жизни, начиная с медицины, где в отделениях кардиологии изучаются проблемы самой важной для человека динамической системы (Sartini et al., 2017), и заканчивая исследованиями динамики поведения наноматериалов, применяемых для создания новейших возобновляемых источников энергии (Pietsch, Wood, 2017). Для реконструкции изображений из собранных томографами проекций применяются разные группы методов, различающиеся по быстродействию (Agulleiro, Fernandez, 2011; Saha et al., 2012), требованиям к используемым вычислительным ресурсам (Inoue, 2016), устойчивостью к наличию шума в проекциях (Balasubramani, 2021). По существу, эти комплексы превращаются, а где-то уже и превратились в реальные системы с искусственным интеллектом, в которых выбор метода реконструкции осуществляется автоматически. Несмотря на большое количество существующих подходов к реконструкции, работы по созданию новых не прекращаются. Это связано с несколькими причинами. Жесткие требования к дозовой нагрузке диктуют появление схем сбора проекций с критически малым числом ракурсов или малой экспозицией. Увеличение пространственного разрешения понижает уровень сигнала, регистрируемого ячейкой позиционно-чувствительного детектора, что, соответственно, ведет к сильному ухудшению отношения сигнал-шум на проекциях (Grigoriev et al., 2021). Создание автоматических систем классификации (Гладилин и др., 2014) результатов реконструкции задает высокие требования к качеству реконструкции. Не все методы способны работать в таких жестких условиях.

В данной работе предлагается новый подход к реконструкции. Регистрация рентгеновских квантов, попадающих в ячейку позиционно-чувствительного детектора за время экспозиции, является стохастическим процессом и описывается распределением Пуассона (Lasio et al., 2007). Дисперсия сигнала в каждом пикселе детектора зависит от математического ожидания сигнала в этом пикселе, т.е. значения гетероскедастичны. Модификация алгебраического подхода к томографической реконструкции, в который добавлен учет гетероскедастичности в виде дополнительного множителя – “доверительной матрицы”, описана в данной статье.

МЕТОДИКА ИССЛЕДОВАНИЙ

Вычисление дисперсии линеаризованных зарегистрированных значений

В компьютерной томографии при зондировании монохроматическим излучением регистрируемое пикселем детектора значение I1 формируется потоком рентгеновских квантов, прошедших через исследуемый объект в направлении “источник-детектор” l за определенное время экспозиции, и описывается следующим выражением (Kak, Slaney, 1988):

(1)
${{I}_{1}} = {{I}_{0}}\int { - \;\mu (l)} dl.$

Здесь I0 – число квантов зонда, μ – линейный коэффициент ослабления рентгеновского излучения используемой длины волны материалом объекта. После регистрации текущей проекции объект поворачивается на некоторый угол, называемый проекционным углом, и снимается следующая проекция. Процедура сбора проекций может быть организована с использованием вращающейся вокруг объекта системы “источник-детектор”, что не меняет математической модели формирования сигнала. Результатом решения задачи томографической реконструкции является рассчитанное по набору зарегистрированных проекций пространственное распределение линейного коэффициента ослабления.

Процесс регистрации, являясь стохастическим процессом, может быть описан распределением Пуассона с плотностью вероятности:

(2)
$p({{I}_{1}} = k) = \frac{{{{\lambda }^{k}}{{e}^{{ - \lambda }}}}}{{k!}},$
где математическое ожидание, равное дисперсии, описывается параметром λ. Чтобы решить задачу реконструкции, т.е. восстановить распределение μ, первым этапом необходимо линеаризовать задачу (1):

(3)
$y = \ln ({{I}_{0}}) - \ln ({{I}_{1}}).$

Здесь y – случайная величина.

Без ограничения описанного далее метода рассмотрим 2D случай задачи реконструкции, т.е. будем говорить о реконструкции одного сечения объекта, причем в параллельной или веерной геометрии были собраны томографические проекции принципиального значения не имеет. В алгебраическом подходе к реконструкции дискретизация задачи проводится на первом этапе ее решения, интеграл заменяется суммированием, формируя СЛАУ вида

(4)
$Ax = y.$

Здесь А – так называемая проекционная матрица, размер которой равен N × M, где N = n × n – количество пикселей восстанавливаемого объема x, M – число проекционных углов. Обратим внимание, что x – оценка линейного коэффициента ослабления. Компоненты вектора y – значения, зарегистрированные всеми ячейками детектора для всех проекционных углов.

Сведем решение СЛАУ к решению оптимизационной задачи следующего вида:

(5)
$||{\kern 1pt} Ax - y{\kern 1pt} |{{|}_{2}}\xrightarrow{x}\min .$

Поскольку значение y есть результат монотонного преобразования I1 (3), то функция вероятности дискретных случайных величин не меняется относительно используемой для регистрируемых значений. Тогда математическое ожидание рассчитывается согласно выражению:

(6)
$M = \sum\limits_{i = 1}^\infty {{{y}_{i}}{{p}_{i}}} ,$
где индекс i указывает на реализацию случайной величины. Подставляя в явном виде выражение для плотности вероятности, выпишем выражение для математического ожидания
(7)
$M = \sum\limits_{i = 1}^\infty {(\ln ({{I}_{0}}) - \ln ({{k}_{i}}))} \frac{{{{\lambda }^{{{{k}_{i}}}}}{{e}^{{ - \lambda }}}}}{{{{k}_{i}}!}}$
и выражение для дисперсии

(8)
$D = \sum\limits_{i = 1}^\infty {{{{(\ln ({{I}_{0}}) - \ln ({{k}_{i}}) - M)}}^{2}}} \frac{{{{\lambda }^{{{{k}_{i}}}}}{{e}^{{ - \lambda }}}}}{{{{k}_{i}}!}}.$

Найти сумму ряда как для математического ожидания, так и для дисперсии аналитически не удается, поэтому предлагается для поиска значений математического ожидания и дисперсии численно рассчитывать суммы рядов до N-го члена, где N достаточно велико.

На рис. 1 приведены результаты расчета. Результат расчета, проведенного согласно (8), представлен штриховой линией. Результат расчета с использованием генератора случайных величин (СВ) – серая кривая. В качестве генератора СВ использовался генератор для распределения Пуассона numpy.random.poisson (lam=i, size=5000). Модельные расчеты проводились для значений в интервале от 30 до 500 с шагом 0.5. Для каждого значения было сгенерировано 5000 значений.

Рис. 1.

Сравнение теоретического результата с результатом моделирования.

Визуальное сравнение кривых позволяет сделать вывод о корректности выбранного приближения. Чтобы учесть свойство гетероскедастичности наблюдений при решении задачи реконструкции, припишем вес, равный обратному среднеквадратическому отклонению (корень из дисперсии) каждому наблюдаемому значению:

(9)
$y* = y^\circ \frac{1}{{\sqrt D }}.$

Здесь $\frac{1}{{\sqrt D }}$ – вектор обратного среднеквадратического отклонения, ° – оператор поэлементного умножения. Тогда СЛАУ (4) перепишется в следующем виде

(10)
$\frac{1}{{\sqrt D }}^\circ Ax = y*,$
и оптимизационная задача будет переформулирована как

(11)
$F = {{\left\| {\frac{1}{{\sqrt D }}^\circ Ax - y{\kern 1pt} *} \right\|}_{2}}\xrightarrow{x}\min .$

Для ее решения воспользуемся методом наискорейшего спуска. После выписывания в явном виде градиента минимизируемого функционала

(12)
$\nabla F = 2{{A}^{T}}\left( {\frac{1}{{\sqrt D }}^\circ \left[ {\frac{1}{{\sqrt D }}^\circ Ax - y{\kern 1pt} *} \right]} \right),$
стало возможным записать шаг к + 1-й итерации метода
(13)
${{x}_{{k + 1}}} = {{x}_{k}} - {{\gamma }_{k}}\nabla F({{x}_{k}}),$
где γk – это шаг спуска. Оптимальное значение шага рассчитывается одним из методов решения оптимизационной задачи
(14)
${{\gamma }_{k}} = \arg \min ({{x}_{k}} - \gamma \nabla F({{x}_{k}})),$
например, (Коднянко, 2018).

РЕЗУЛЬТАТЫ РЕКОНСТРУКЦИИ

Примеры работы на модельных данных

Чтобы проиллюстрировать работу предложенного метода, проведены расчеты с использованием изображения фантома размером 50 × 50 пикселов (рис. 2), промоделировав несколько ситуаций, возникающих в ходе измерений.

Рис. 2.

Изображение фантома, использованное в экспериментах.

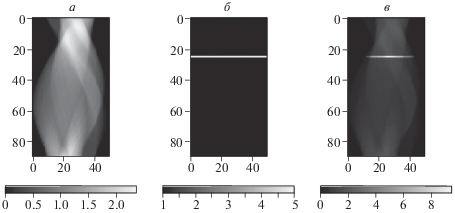
Первый проведенный эксперимент моделирует ситуацию, в которой время экспозиции (время регистрации одной проекции) различалось для первой и второй половины проекционных данных. На рис. 3, а представлена синограмма, рассчитанная с учетом различающегося времени экспозиции. Иллюстрация границы раздела времен экспозиции представлена картой распределения значений величины обратного стандартного отклонения (б). Значения на карте равны 10.0 в первой половине синограммы и 1.0 – во второй половине соответственно. Взвешенные значения синограммы, используемые в записи СЛАУ, представлены на (в).

Рис. 3.

а – синограмма с переменным временем экспозиции; б – иллюстрация границы раздела времен экспозиции; в – взвешенные значения синограммы.

Томографическая реконструкция выполнялась двумя алгебраическими методами: методом SIRT (Gilbert, 1972) (рис. 4, а) и предложенным методом с учетом гетероскедастичности (б). Итерационный процесс был остановлен после 100 итераций.

Рис. 4.

а – результат реконструкции методом SIRT и б – предложенным методом.

Среднеквадратическое отклонение результата реконструкции от использованного для расчета проекций фантома при реконструкции методом SIRT составило 6.8E-1, при реконструкции описанным методом – 4.4Е-6. Значения различаются на три порядка и визуально это хорошо видно (рис. 4).

Второй пример иллюстрирует ситуацию, в которой сбой отклика детектора случился при одном из проекционных углов. На рис. 5, а представлена модельная синограмма, на (б) – распределение стандартного отклонения и на (в) – взвешенные значения синограммы, используемые при реконструкции предлагаемым методом.

Рис. 5.

а – модельная синограмма; б – иллюстрация процесса сбоя в детектировании; в – использованная в СЛАУ синограмма.

Для реконструкции были использованы SIRT (рис. 6, а) и предлагаемый новый метод (б). Итерационный процесс был остановлен после 100 итераций.

Рис. 6.

Результаты реконструкции: а – методом SIRT, б – предлагаемым методом.

Среднеквадратическое отклонение от фантома при реконструкции методом SIRT составило 2.4E-4, при реконструкции описанным методом – 1.6Е-6. По-прежнему визуальное различие результатов велико.

Рассмотрим поведение предлагаемого к реконструкции подхода в ситуации, когда к значениям идеальной синограммы добавлен нормально распределенный аддитивный шум (рис. 7, а). Карта дисперсии различается для верхней и нижней половин изображения (б). На (в) представлены откорректированные значения синограммы, используемые в СЛАУ.

Рис. 7.

а – модельная синограмма; б – карта распределения дисперсии аддитивного шума; в – взвешенная синограмма.

Результаты реконструкции методом SIRT (рис. 8, а) и предлагаемым методом (б) приведены ниже. Итерационный процесс остановлен после 100 итераций. Полученные результаты демонстрируют высокую чувствительность нового подхода к наличию аддитивного нормально распределенного шума. Это следует учитывать при выборе метода реконструкции, если томографирование проведено в нестабильных условиях. Источник нестабильности не имеет значения. Это могут быть небольшие случайные движения самого объекта или биения держателя образца. На рисунке представлен результат выполнения 50 итераций.

Рис. 8.

Результаты реконструкции алгебраическими методами: а – методом SIRT, б – предлагаемым методом.

Последний модельный пример является иллюстрацией случая, когда время регистрации одной проекции (время экспозиции) мало. Расчет модельных значений синограммы (рис. 9, а) проводился с учетом распределения Пуассона. Распределение значений стандартного отклонения представлено на (б). Взвешенные на обратную величину стандартного отклонения значения синограммы, использованные при решении СЛАУ, даны на (в).

Рис. 9.

а – модельная синограмма; б – распределение дисперсии в поле вида; в – использованная в СЛАУ синограмма.

Томографическая реконструкция была методом SIRT (рис. 10, а) и предложенным методом с учетом гетероскедастичности (б). Итерационный процесс был остановлен после 100 итераций.

Рис. 10.

Результаты реконструкции алгебраическими методами: а – методом SIRT, б – предлагаемым методом.

На изображении, восстановленном с учетом гетероскедастичности (рис. 10, б), визуально наблюдается большая однородность фона, чем при использовании метода SIRT для реконструкции (а). Это свойство оказывается важным при применении автоматических методов оценки качества реконструкции, в которых привлечены интегральные метрики сравнения с опорным (идеальным) изображением (Bulatov et al., 2020). Среднеквадратическое отклонение результатов реконструкции от фантома, использованного для расчета синограммы, при реконструкции методом SIRT составило 1.8E-4, при реконструкции описанным методом – 1.2Е-4.

ЗАКЛЮЧЕНИЕ

В данной работе представлен новый подход к решению задачи томографической реконструкции, в котором учитывается гетероскедастичность шума, присутствующего на регистрируемых позиционно-чувствительным детектором проекциях. Абсолютные значения могут различаться на несколько порядков. Природа такого разброса значений имеет несколько принципиально разных причин. Она может быть обусловлена существенной разницей величин коэффициентов линейного ослабления включений, содержащихся в объекте, и коэффициентов так называемого матрикса (Zschech et al., 2018). Причина может скрываться в сбое работы регистрирующего оборудования или требованием сильного ограничения дозовой нагрузки. Полученные результаты демонстрируют, что учет гетероскедастичности позволяет повысить качество реконструкции. Величина среднеквадратичного отклонения результата реконструкции от фантома, использованного для расчета модельных проекций, в некоторых случаях достигала нескольких порядков.

Следует отметить, что учет свойства гетероскедастичности шума при создании различных математических инструментов предложен не впервые, поскольку позволяет повысить качество работы математических инструментов. Так, недавно введенное авторами новое пространство цветовых координат proLab (Konovalenko et al., 2021) характеризуется тем, что в этом пространстве гетеро-скедастичность дробового шума меньше, чем в пространстве CAM16-UCS и стандартных цветовых пространствах. Это свойство делает proLab удобной координатной системой для линейного цветового анализа. Еще одним примером работы со свойством гетероскедастичности шума является учет данного свойства в модели, используемой для имитации цветных подводных изображений на основе натуральных (Shepelev et al., 2021). Учет гетероскедастичности позволил не занижать дисперсию шума на имитациях подводных снимков. Такая имитация необходима для создания наборов данных, применяемых для автоматического анализа качества вновь создаваемых или тестируемых алгоритмов оценки подводных изображений. Последнее востребовано при исследовании подводных артефактов, разработке систем предотвращения затоплений, картировании дна водоемов и прочее.

В дальнейшем планируется оценить вклад учета гетероскедастичности при решении задачи реконструкции на реальных данных, собранных с нескольких томографов, различающихся условиями съемки.

Список литературы

  1. Гладилин C.А., Котов А.А., Николаев Д.П., Усилин С.А. Построение устойчивых признаков детекции и классификации объектов, не обладающих характерными яркостными контрастами. ИТиВС. 2014. № 1. С. 53–60.

  2. Коднянко В.А. Условная минимизация слабоунимодальных функций методом бинарного сканирования (бискана). Вестник ЮУрГ, серия Вычислительная математика и информатика. 2018. Т. 7. № 4. С. 59–66. https://doi.org/10.14529/cmse180404

  3. Agulleiro J.I., Fernandez J.J. Fast tomographic reconstruction on multicore computers. Bioinformatics. 2011. V. 27 (4). P. 582–583. https://doi.org/10.1093/bioinformatics/btq692

  4. Arlazarov V.L., Nikolaev D.P., Arlazarov V.V., Chukalina M.V. X-ray tomography: the way from layer-by-layer radiography to computed tomography. Computer Optics. 2021. V. 45 (6). Р. 897–906.

  5. Balasubramani V., Montresor S., Tu H-Y., Huang C-H., Picart P., Cheng C-J. Influence of noise-reduction techniques in sparse-data sample rotation tomographic imaging. Applied Optics. 2021. V. 60. P. B81–B87. https://doi.org/10.1364/AO.415284

  6. Bulatov K., Chukalina M., Buzmakov A., Nikolaev D., Arlazarov V. V. Monitored reconstruction: computed tomography as an anytime algorithm. IEEE Access. 2020. V. 8. P. 110759–110774. https://doi.org/10.1109/ACCESS.2020.3002019

  7. Gilbert P. Iterative methods for the three-dimensional reconstruction of an object from projections. J. Theoretical Biology. 1972. V. 36 (1). P. 105–117.

  8. Grigoriev M., Khafizov A., Kokhan V., Asadchikov V. Robust technique for representative volume element identification in noisy microtomography images of porous materials based on pores morphology and their spatial distribution. Proc. SPIE, Thirteenth International Conference on Machine Vision. 2021. V. 11605. P. 1–10. https://doi.org/10.1117/12.2586785

  9. Inoue H. Efficient tomographic reconstruction for commodity processors with limited memory bandwidth. 13th International Symposium on Biomedical Imaging (ISBI). 2016. P. 747–750. https://doi.org/10.1109/ISBI.2016.7493374

  10. Kak A.C., Slaney M. Principles of Computerized Tomographic Imaging. NY. IEEE Press, 1988. 329 p.

  11. Konovalenko I.A., Smagina A.A., Nikolaev D.P., Nikolaev P.P. ProLab: A Perceptually Uniform Projective Color Coordinate System. IEEE Access. 2021. V. 9. P. 133023–133042. https://doi.org/10.1109/ACCESS.2021.3115425

  12. Lasio G.M., Whiting B.R., Williamson J.F. Statistical reconstruction for x-ray computed tomography using energy-integrating detectors. Physics in Medicine & Biology. 2007. V. 52. (8). P. 2247–2266.

  13. Pietsch P., Wood V. X-Ray tomography for lithium ion battery research: a practical guide. Annual Review of Materials Research. 2017. V. 47. P. 451–479. https://doi.org/10.1146/annurev-matsci-070616-123957

  14. Saha S., Tahtali M., Lambert A., Pickering M. Novel algebraic reconstruction technique for faster and finer CT reconstruction. Proc. SPIE, Fifth International Conference on Machine Vision (ICMV 2012): Computer Vision, Image Analysis and Processing. 2012. V. 8783. P. 1–7. https://doi.org/10.1117/12.2011073

  15. Sartini S., Frizzi J., Borselli M., Sarcoli E., Granai C., Gealli V., Cevenini G., Guazzi G., Bruni F., Gonelli S., Postorelly M. Which method is best for an early accurate diagnosis of acute heart failure? Comparison between lung ultrasound, chest X-ray and NT pro-BNP performance: a prospective study. Internal and Emergency Medicine. 2017. V. 12. P. 861–869. https://doi.org/10.1007/s11739-016-1498-3

  16. Shepelev D.A., Bozhkova V.P., Ershov E.I., Nikolaev D.P. Simulating shot noise of color underwater images. Computer Optics. 2020. V. 44 (4). P. 671–679. https://doi.org/10.18287/2412-6179-CO-754

  17. Withers P.J., Bouman C., Carmignato S., Cnudde V., Grimaldi D., Hagen C.K., Meire E., Manley M., Du Plessis A., Stock S.R. X-ray computed tomography. Nature Reviews Methods Primers. 2021. V. 1. (18). P. 1–21. https://doi.org/10.1038/s43586-021-00015-4

  18. Zschech E., Löffler M., Krüger P., Gluch J., Kutukova K., Zgłobicka, I., Silomon J., Rosenkranz R., Standke Y., Topal E. Laboratory computed X-ray tomography – a nondestructive technique for 3D microstructure analyis of materials. Practical Metallography. 2018. V. 55 (8). P. 539–555. https://doi.org/10.3139/147.110537

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Сенсорные системы

Архивы выпусков Информация о журнале Отправить рукопись в журнал