Теоретические основы химической технологии, 2022, T. 56, № 3, стр. 345-357
Расчет межфазного тепломассообмена в факеле распыла форсунки с учетом кризиса сопротивления и тепломассообмена
Н. Н. Симаков *
Ярославское высшее военное училище противовоздушной обороны
Ярославль, Россия
* E-mail: nik_simakov@mail.ru
Поступила в редакцию 08.04.2021
После доработки 11.06.2021
Принята к публикации 15.02.2022
- EDN: RBJCBM
- DOI: 10.31857/S0040357122030137
Аннотация
В работе представлены детали численной модели и результаты расчета межфазного тепломассообмена в двухфазном потоке, создаваемом при форсуночном распыливании жидкости в газ. В качестве основы предлагаемой математической модели использованы нестационарные дифференциальные уравнения течения сжимаемой среды, дополненные уравнениями тепло- и массопередачи от капель к газу. В разностных аналогах уравнений неразрывности и движения фаз использована известная явная схема Лакса–Вендроффа. Представлены рассчитанные аксиальные и радиальные профили скоростей и температур капель и газа в свободном факеле распыла, а также в двухфазном потоке через цилиндрический аппарат с учетом раннего кризиса сопротивления капель и кризиса тепломассообмена фаз, а также обнаруженных в предшествующих экспериментах особенностей турбулентного трения в газе. В расчетах, в частности, установлены зависимости средних по выходному сечению аппарата температур газа и капель от расхода газа через него.
ВВЕДЕНИЕ. ОСОБЕННОСТИ ГИДРОДИНАМИКИ ФАКЕЛА РАСПЫЛА ФОРСУНКИ
В энергетике и химических технологиях для интенсификации таких процессов, как: сжигание или пиролиз жидких углеводородов, мокрая очистка воздуха от пыли и вредных газовых примесей, сушка и гранулирование полимеров, – за счет увеличения межфазной поверхности используется распыливание жидкости в газе, например, с помощью форсунок.
Основу метода расчета таких тепломассобменных процессов составляют представления о гидродинамической структуре образующегося двухфазного потока, называемого факелом распыла, силах взаимодействия капель с газом, а также об элементарных актах тепло- и/или массообмена между газом и отдельной каплей [1, 2].
Методы удовлетворительного расчета гидродинамики факела распыла и межфазного тепломассообмена в нем до недавнего времени не были разработаны, что обуславливает актуальность данной работы, являющейся продолжением исследований, описанных в работах [1–3].
Очень часто процессы межфазного тепло- и массообмена протекают одновременно и параллельно, что усложняет моделирование и расчет совмещенных процессов переноса. Целью данной работы было моделирование сложного процесса, включающего испарение и охлаждение капель воды, распыленной в воздухе, с учетом кризисов сопротивления капель и межфазного тепломассообмена.
Моделирование и расчет более простого процесса межфазного массообмена (без теплообмена), в качестве которого рассматривался процесс мокрой очистки воздуха от вредных газовых примесей, например, от оксида серы SO2, было выполнено и описано в работе [2].
При математическом моделировании двухфазных потоков используют два основных подхода: метод взаимопроникающих континуумов [4] и теорию турбулентных струй [5]. В первом из них каждую из фаз рассматривают как непрерывно распределенную по пространству сплошную среду с переменной плотностью, усредненной по малому объему, а скорости фаз полагают различными. Во втором – полагают концентрацию дисперсной фазы малой, скорости фаз примерно одинаковыми, но при этом учитывают турбулентность газовой фазы.
Примером одного из первых применений континуального подхода к расчету двухфазного газокапельного потока может служить одномерная модель гидродинамики факела распыла форсунки [6]. Впоследствии эта модель многократно использовалась как основа для моделирования ряда тепло- и массообменных процессов химической технологии с распыливанием жидкости, в частности, процесса испарения жидкого углеводородного сырья в процессе получения технического углерода [7]. Развитием такого подхода должно было стать создание двумерной модели осесимметричного факела распыла. При этом необходимо было учесть ряд его важных особенностей, заключающихся в следующем.
Как было позже установлено в эксперименте, течение газа в факеле распыла представляет собой турбулентную струю [1], которая возникает у корня факела из-за взаимодействия фаз. На достаточном удалении от форсунки она развивается автономно от капельного потока и отличается от однофазной газовой струи структурой и характером турбулентного трения. В частности, было показано, что безразмерные профили аксиальной скорости газа более пологи, чем в однофазной струе, а также установлено заметное различие скоростей фаз и наличие перепадов давления газа порядка 1–10 Па по радиусу и оси факела.
Таким образом, в двумерной модели факела распыла было необходимо и целесообразно использовать сочетание континуального подхода с учетом турбулентности струйного газового потока.
Кроме того, в эксперименте была обнаружена описанная ниже существенная особенность во взаимодействии фаз, названная ранним кризисом сопротивления [1], которую также необходимо учитывать при расчете факела распыла и заключающуюся в следующем.
Классически известный кризис сопротивления шара, движущегося в вязкой среде, заключается в том, что сила и коэффициент сопротивления среды при числе Рейнольдса Re = Recr ≈ (2–3) × × 105 уменьшаются примерно в 4–5 раз [8, 9], что объясняется переходом ламинарного пограничного слоя у поверхности обтекаемого тела в турбулентный, смещением линии отрыва потока вниз по течению и улучшением обтекания тела с уменьшением его сопротивления [11].
Само значение критического числа Рейнольдса Recr зависит от степени турбулентности вязкой среды, обтекающей шар, и уменьшается с ее увеличением. В работе [10] описаны случаи возникновения кризиса сопротивления шара уже при Recr ≈ 400–2200.
При форсуночном распыливании жидкости образуются капли со средним заутеровским диаметром d порядка 10–4 м. С учетом таких размеров и существенного различия динамических коэффициентов вязкости жидкости капель и обтекающего их газа (для воды и воздуха, примерно, в 60 раз) можно пренебречь деформацией капель и внутренним течением жидкости в них и рассматривать их как твердые шарики.
Cилу гидродинамического сопротивления капли, обтекаемой газом, обычно рассчитывают по формуле
(1)
$F~\,\, = \,\,{{~{{C}_{d}}~s~\rho ~{{V}^{2}}} \mathord{\left/ {\vphantom {{~{{C}_{d}}~s~\rho ~{{V}^{2}}} 2}} \right. \kern-0em} 2},$При обтекании шара ламинарным потоком при малых числах Рейнольдса Re = Vdρ/μ $ \ll $ 1 используют зависимость Стокса Cd = 24/Re, а при обтекании в переходном диапазоне 2 < Re < 700 – формулу Клячко
(2)
${{C}_{d}}~~ = ~\,\,{{24} \mathord{\left/ {\vphantom {{24} {{\text{Re}}}}} \right. \kern-0em} {{\text{Re}}}}{\text{\;}} + \,\,~{4 \mathord{\left/ {\vphantom {4 {{\text{R}}{{{\text{e}}}^{{1/3}}}}}} \right. \kern-0em} {{\text{R}}{{{\text{e}}}^{{1/3}}}}},$хорошо аппроксимирующую указанном диапазоне экспериментальные данные, обобщенные стандартной кривой Рэлея [9, 8 ].
В работе [1] экспериментально показано, что в развитом турбулентном потоке факела распыла форсунки при Re = Recr ≈ 100 величина Cd для капель уменьшалась в 4–7 раз по сравнению со значениями, определяемыми формулой (2) Клячко. Это и есть самый ранний кризис сопротивления.
В частности, для капель, движущихся по оси факела, в качестве хорошего приближения при 40 < Re < 110 в работе [1] была предложена формула
(3)
${{C}_{d}}~\,\, = {{2000} \mathord{\left/ {\vphantom {{2000} {{{{\operatorname{Re} }}^{2}}}}} \right. \kern-0em} {{{{\operatorname{Re} }}^{2}}}}.$Последующий анализ экспериментальных данных показал, что формула (3) верна не только для капель на оси факела распыла, но и для всей совокупности капель в объеме факела при z > 0.1 м. Кроме того, для упрощения расчетов можно учесть, что в автомодельной зоне свободного факела распыла, при z > 300 мм и Re > 110,
(4)
${{C}_{d}}\left( {r,~z} \right)~\,\, = \,\,~{{C}_{d}}\left( {\operatorname{Re} } \right)~\,\, \simeq \,\,~0.1,$с приблизительным отклонением ±0.05.
Такой же ранний кризис сопротивления наблюдался при обтекании одиночного твердого шарика газовой струей в конфузоре [3, Sect. 5.1].
Как одна из возможных причин возникновения раннего кризиса сопротивления сферической частицы была рассмотрена гипотеза о влиянии сильной турбулентности газового потока, которую конфузор еще больше усилил по сравнению со свободной струей и сделал достаточной для возникновения раннего кризиса на одиночном твердом шарике [3, Sect. 5.1].
Это предположение подтвердилось численным моделированием обтекания шара как ламинарным, так и сильнотурбулентным потоком газа [3, Sect. 5.3].
Вышесказанное позволило прийти к выводу, что для математического и численного моделирования факела распыла как двухфазного потока, учитывая все его особенности, при описании движения обеих фаз единым образом целесообразно использовать сочетание метода взаимопроникающих континуумов [4] и теории турбулентных струй [5]. Эта идея была использована в двумерной модели для расчета гидродинамики свободного факела распыла и двухфазного потока, ограниченного стенкой корпуса в цилиндрическом аппарате [3, Sect. 7.2].
Для ознакомления с рядом важных обстоятельств, относящихся к рассматриваемой проблеме, в том числе с учетом раннего кризиса сопротивления во взаимодействии фаз в факеле распыла, а также описанием основ математической модели, использованной в данной работе, отсылаем читателя к работам [2, 3].
МОДЕЛИРОВАНИЕ ТЕПЛОМАССООБМЕНА В СВОБОДНОМ ФАКЕЛЕ РАСПЫЛА ФОРСУНКИ
Основу рассматриваемой модели составляют уравнения гидродинамики двухфазного потока. Например, в работе [2] кроме формулы (1) такими являются уравнения (4)–(14). Причем из них два последних учитывают ранний кризис сопротивления капель при их взаимодействии с сильнотурбулентным газовым потоком путем использования полученной в эксперименте зависимости Cd(r, z). Заметим, что в данной работе наряду с ними используются также вышеприведенные формулы (3) и (4).
Для расчета межфазного массообмена (без учета теплообмена) указанная система уравнений гидродинамики (4)–(14) была дополнена в [2] уравнениями (15)–(19), учитывающими конвективный перенос примесного газового компонента в потоке и от газа к каплям жидкости.
Аналогичным образом в данной работе система уравнений (4)–(19) из [2] была дополнена нижеприведенными уравнениями конвективного переноса тепла в каждой из фаз и массы пара как одного из компонентов газовой фазы, а также соотношениями, учитывающими тепло- и массопередачу от капель жидкости в газовый поток.
Для учета теплопереноса внутри газовой фазы математическую модель необходимо и возможно дополнить “уравнением баланса тепла” [11, с. 436], также называемым “общим уравнением переноса тепла” [12, с. 277], которое в работе [3, Sect. 6.1] было представлено под номером (6.8) в виде
(5)
${{\rho ~{{c}_{v}}~dT} \mathord{\left/ {\vphantom {{\rho ~{{c}_{v}}~dT} {d\tau ~}}} \right. \kern-0em} {d\tau ~}} = \,\,~ - ~P~{\text{div}}{\mathbf{w}}~\,\, + ~\,\,{\text{div}}\left( {\lambda ~\nabla T} \right)~\,\, + \,\,~{{\Phi }_{d}}.$В формуле (5) последний член Φd учитывает диссипацию механической энергии газа в тепло. Согласно источникам [11] и [12] при малых скоростях течения и степени сжатия газа этот член можно представить в виде
(6)
${{\Phi }_{d}}\,\,~ = \,\,~{\mu \mathord{\left/ {\vphantom {\mu 2}} \right. \kern-0em} 2}{{\left( {{{\partial {{w}_{i}}} \mathord{\left/ {\vphantom {{\partial {{w}_{i}}} {\partial {{x}_{k}}}}} \right. \kern-0em} {\partial {{x}_{k}}}} + ~{{\partial {{w}_{k}}} \mathord{\left/ {\vphantom {{\partial {{w}_{k}}} {\partial {{x}_{i}}}}} \right. \kern-0em} {\partial {{x}_{i}}}}} \right)}^{2}}.$При небольших различиях температур шара (капли) и обтекающего его газа изменение коэффициентов вязкости μ и теплопроводности λ газа (воздуха) мало. Как показали расчеты [3, Sect. 6.2], влиянием члена Φd на распределения скоростей и температур газа при этом также можно пренебречь. Тогда уравнение (5) можно привести к виду
(7)
$\begin{gathered} \frac{{\partial T}}{{\partial \tau }} + {{w}_{z}}\frac{{\partial T}}{{\partial z}} + {{w}_{r}}\frac{{\partial T}}{{\partial r}} = \\ = - 0.4T~{\text{div}}{\mathbf{w}} + \frac{\lambda }{{\rho ~{{c}_{v}}}}\Delta T + \frac{Q}{{\rho ~{{c}_{v}}}}. \\ \end{gathered} $Переходя от формулы (5) к (7), использовали соотношение P/(ρcv) = R T/(Mcv) ≈ 0.4T, которое следует из уравнения Клапейрона–Менделеева с учетом данных для воздуха, а также учитывали поток тепла Q от всех капель к газу в единице объема факела.
В формулах (5)–(17) обозначено: α − объемная доля жидкости, ρl – физическая плотность капель, wz, wr − аксиальная и радиальная компоненты скорости газа, uz, ur – то же для жидкости, ρsv – плотность насыщенного водяного пара у поверхности капли, ρv= ρv(r, z) – плотность водяного пара в воздухе вдали от капли, сv – удельная теплоемкость газа при постоянном объеме, сp – то же при постоянном давлении, cl – удельная теплоемкость капель, a = λ/(ρсp) – коэффициент температуропроводности газа, Pr = ν/a = 0.71 – число Прандтля, ν = μ/ρ – кинематический коэффициент вязкости газа, D – коэффициент диффузии водяного пара в газе, PrD = ν/D = 0.64 – диффузионное число Прандтля (иногда называемое числом Шмидта Sc), Vd – объем капли, L – удельная теплота испарения капель жидкости, R = 8.31 Дж/(моль К) – универсальная газовая постоянная, M – молярная масса газа. В приведенных числовых оценках использованы данные для воздуха при температуре tg = 20°С.
С учетом результатов, представленных в [3, Sect. 6.3] для упрощения модели межфазного теплообмена температуру во всех точках внутри капли и на ее поверхности можно принять одинаковой Tl = Tl(r, z), зависящей только от координат r и z капли в факеле. При этом мы приходим к внешней задаче межфазного теплообмена. Тогда плотность потока тепла от отдельной капли с температурой на поверхности Tl к окружающему ее газу с температурой Tg = Tg(r, z) мы можем описать уравнением Ньютона–Рихмана
с коэффициентом теплоотдачи
(9)
$~{{k}_{t}} = ~{\text{Nu\;}}{\lambda \mathord{\left/ {\vphantom {\lambda d}} \right. \kern-0em} d}.$Число Нуссельта можно определить по формуле Ранца–Маршалла [13]
(10)
${\text{Nu}} = {\text{\;}}2 + 0.6{\text{R}}{{{\text{e}}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}~{\text{P}}{{{\text{r}}}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}}.$Тогда поток тепла от всех капель к газу в единице объема факела распыла с учетом (9) можно представить в виде
(11)
$Q = \frac{{4q~s~\alpha }}{{{{V}_{{\text{d}}}}}} = \frac{{6q~\alpha }}{d} = \frac{{6{{k}_{t}}~\left( {{{T}_{l}} - {{T}_{g}}} \right)~\alpha }}{d}.$Для учета переноса массы пара в газовом потоке и его массопередачи от капель жидкости к газу по аналогии с работой [2], где уравнениями (15)–(19) учитывался межфазный массообмен примесным газовым компонентом, вышеприведенная система уравнений (5)–(11) была дополнена также следующими уравнениями (12)–(16).
Учитывая аналогию явлений межфазного тепло- и массообмена [11], для плотности потока массы пара от отдельной капли в газ мы можем написать уравнение массопередачи
аналогичное уравнению Ньютона–Рихмана (8) для плотности потока тепла. Также по аналогии с коэффициентом теплоотдачи можно определить коэффициент массопередачи от капли к газу
(13)
$~{{k}_{m}} = ~{\text{\;N}}{{{\text{u}}}_{D}}~{D \mathord{\left/ {\vphantom {D d}} \right. \kern-0em} d},$а диффузионное число Нуссельта определить по аналогии с известной для теплообмена формулой (6) Ранца–Маршалла
(14)
${\text{N}}{{{\text{u}}}_{{D{\text{\;}}}}} = {\text{\;}}2 + 0.6{\text{R}}{{{\text{e}}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{\text{\;Pr}}_{D}^{{{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}}}.$Тогда поток массы пара от всех капель в газ в единице объема факела с учетом (12) можно представить соотношениями
(15)
$J = \frac{{4{{j}_{v}}~s~\alpha }}{{{{V}_{{\text{d}}}}}} = \frac{{6{{j}_{v}}~\alpha }}{d} = \frac{{6{{k}_{m}}~\left( {{{\rho }_{{sv}}} - {{\rho }_{v}}} \right)~\alpha }}{d}.$Уравнение конвективно-диффузионного переноса пара в газовом потоке с учетом его массопередачи от капель жидкости к газу можем написать в виде
(16)
$\frac{{\partial {{\rho }_{v}}}}{{\partial \tau }} + {{w}_{z}}\frac{{\partial {{\rho }_{v}}}}{{\partial z}} + {{w}_{r}}\frac{{\partial {{\rho }_{v}}}}{{\partial r}} = D\Delta {{\rho }_{v}} + J.$В правую часть уравнения неразрывности для газа (4) из работы [2] надо добавить такое же слагаемое J, как последний член в (15) и (16) здесь. В правую часть уравнения (5) из [2] для изменения аксиальной скорости wz газа стоит добавить член uz J/ρ, учитывающий реактивную силу (поток импульса) из-за притока пара со скоростью испаряющихся капель в поток газа, а в правую часть уравнения (6) той же системы (4)–(9) из [2] – аналогичный член ur J/ρ.
Кроме того, для учета теплопереноса дисперсной фазы математическую модель нужно дополнить аналогичным (7), но более простым уравнением
(17)
$\frac{{\partial {{T}_{l}}}}{{\partial \tau }} + {{u}_{z}}\frac{{\partial {{T}_{l}}}}{{\partial z}} + {{u}_{r}}\frac{{\partial {{T}_{l}}}}{{\partial r}} = - \frac{{Q + J~L}}{{\alpha ~{{\rho }_{l}}~{{c}_{l}}}}.$В числителе дроби правой части (17) учтены убыль тепла капель жидкости за счет теплоотдачи газу Q и испарения с их поверхности J L.
Без учета кризиса массообмена, аналогичного кризису теплообмена [3, Sect. 6.2], формулы (10) и (14) дают значения Nu ≈ NuD > 2. Для учета кризиса тепло- и массообмена, обусловленного вместе с кризисом сопротивления капель сильной турбулентностью газового потока, нужно использовать значения Nu = NuD = 2.
Система уравнений (1), (4)–(12) из [2], дополненная представленными здесь формулами (3)–(17), позволяет рассчитывать изменение температур фаз T(r, z) и Tl(r, z) в двухфазном потоке факела распыла форсунки как с учетом кризиса сопротивления капель и кризиса тепломассообмена фаз, так и без учета этих кризисов.
В численной модели факела распыла перед заменой дифференциальных уравнений их разностными аналогами, стоит перейти к безразмерным переменным, поделив значения координат r и z на начальный (минимальный) радиус r0= z0 tg φ факела в расчетной области (z0 = 100 мм расстояние от ее верхней границы до выходного отверстия форсунки), скоростей w, u, V и ws − на начальную скорость капель (струи жидкости) u0, плотность воздуха ρ (а также водяного пара) − на плотность ρ0 покоящегося газа вдали от факела, время τ – на τ0= r0/u0, температуры T и Tl – например, на T0 = 293 K. Вид уравнений (4)–(9) из [2], а также (7), (16), (17) в данной работе при этом не изменится, а у слагаемых в правых частях этих уравнений появятся соответствующие дополнительные коэффициенты.
Также, как в работе [2], при переходе от указанных дифференциальных уравнений к их разностным аналогам с учетом представлений (1), (10)–(12) из [2] и (3)–(4), (8)–(15) в данной статье для аппроксимации конвективных членов на прямоугольной пространственной сетке (i, j) использовалась явная двухшаговая разностная схема Лакса–Вендроффа [14], которая центрирована по времени, из-за чего численные эффекты вязкости и диффузии в ней значительно меньше, чем в одношаговой схеме Лакса, и поэтому профили скоростей каждой из фаз ближе к истинным.
Для устойчивости схемы Лакса–Вендроффа необходимо выполнение условие Куранта–Фридрихса–Леви [14], которое при равных шагах сетки Δz = Δr имеет вид
(18)
$\Delta \tau \leqslant \frac{{\Delta z}}{{\sqrt {2\left( {w_{s}^{2} + w_{z}^{2} + w_{r}^{2}} \right)} }}.$Аппроксимация диффузионных членов в уравнениях (7) и (16) проводилась по явной схеме первого порядка точности [14, с. 107], имеющей на двумерной сетке условие устойчивости в виде
Для обеспечения устойчивости разностной схемы в целом необходимо одновременное выполнение обоих условий (18) и (19), из которых более сильным оказалось первое.
Преимущество предложенной численной модели в том, что она позволяет вычислять все переменные по простой явной схеме.
Определенную трудность при построении численной модели представляет задание подходящих граничных условий, которые сохраняют устойчивость разностной схемы. В граничных узлах сетки разностная схема имеет иной, чем во внутренних точках, вид, так как пространственные производные здесь аппроксимируют односторонними, а не двухсторонними разностями. Кроме того, на оси симметрии (при r = i Δr = 0) радиальные скорости фаз wr = ur = 0, производные по r от некоторых переменных также могут обращаться в нуль.
С учетом экспериментальных данных на верхней (входной) границе расчетной области (j = 0) задают профиль объемной доли жидкости, например, треугольной формы α(r, z0) = 3(rn/r0)2(1 – – r/r0), где rn – радиус выходного отверстия форсунки, r0= z0tgφ. А также здесь нужно задать радиальные профили компонент скорости жидкости uz(r, z0) и ur(r, z0). Первый из них по форме можно взять прямоугольным, трапециевидным или более сложным, второй, с учетом характера истечения жидкости из сопла форсунки, стоит задать в виде функции радиуса: ur(r, z0) = uz(r, z0)r/z0.
В случае свободного факела распыла для определения плотности газа на боковой (внешней) границе расчетной области можно использовать уравнение Бернулли
а для температуры газа – ее начальное значение T0 = 293 К.
При расчете двухфазного потока в цилиндрическом распылительном аппарате на его стенке, служащей боковой границей сетки, задают условия обращения компонент скорости газа в нуль wz = wr = 0, температуру газа и жидкости можно принять одинаковой T = Tl при z ≥ zw = RAPP/tgφ из-за смачивания стенки аппарата жидкостью, стекающей в виде пленки.
РЕЗУЛЬТАТЫ РАСЧЕТА ТЕПЛОМАССООБМЕНА ФАЗ В СВОБОДНОМ ФАКЕЛЕ РАСПЫЛА ФОРСУНКИ
Вышеописанный алгоритм реализован с использованием программных средств Delphi для расчета гидродинамики и межфазного тепломассообмена в симметричном относительно вертикальной оси факеле распыла центробежно-струйной форсунки с диаметром выходного отверстия dh = 2 мм.
В расчетах свободного факела распыла использовались из работы [2] зависимость (11) для напряжения турбулентного трения газа и зависимости (13) и (14) для коэффициента сопротивления капель. При расчете двухфазного потока в аппарате вместо двух последних зависимостей использовались формулы (3) и (4) данной статьи.
В качестве единицы безразмерного пространственного масштаба сетки принят радиус факела на верхней границе расчетной области r0 = z0tgφ (φ = 32.5° – половина корневого угла факела, z0 = = 100 мм), за единицу масштаба скоростей – начальная скорость u0 = 0.75(2Рl/ρl)1/2 жидкости, истекающей из сопла форсунки. В расчетах в качестве d использовался средний объемно-поверхностный диаметр капель d32 = 0.14 мм, измеренный при давлении воды на форсунке Рl = 5 × 105 Па, теплофизические характеристики газа были приняты, как у воздуха, а жидкости, как у воды. Начальная температура воздуха была принята T0 = 293 K, капель воды Tl = 1.1T0 = 322 K.
Расчеты проводились на прямоугольной пространственной области с физическими размерами rmax = h max(i), zmax – z0 = h max(j), h = 4 мм. Число точек сетки в расчетах свободного факела варьировалось до max(i) = max(j) = 200 при безразмерном шаге сетки Δr = Δz = 1/16, что обеспечивало достаточную аппроксимацию разностной схемы.
Интересующее нас (квази)стационарное состояние потока достигалось в результате эволюции нестационарного решения за “сеточное” время, примерно, в 15–20 раз большее характерного времени τs= (zmax − z0)/u0, за которое капли могли пролететь от верхней до нижней границы расчетной области без учета их торможения в газе.
На рис. 1–6 приведены результаты расчетов межфазного тепло- и массообмена в осесимметричном свободном факеле распыла форсунки, выполненных по предлагаемой модели.
Рис. 1.
Расчетные зависимости скоростей газа wz[0, j], капель uz[0, j] и их температур tg[0, j] и tl[0, j] на оси свободного факела. Светлые символы – расчет без учета кризиса сопротивления по формуле (2) Клячко и кризиса тепломассообмена с использованием формул (10) и (14) при Nu ≈ NuD > 2. Темные символы – расчет с учетом кризиса сопротивления по формулам (13)–(14) из работы [2] и кризиса тепломассообмена при Nu = NuD = 2.

Рис. 2.
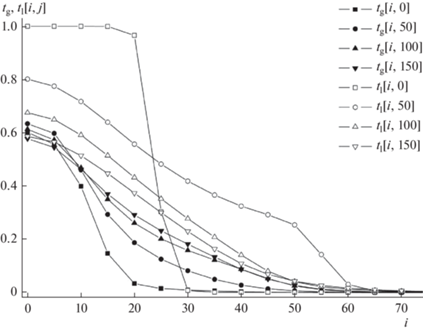
Радиальные профили температур фаз на различных расстояниях z = (100 + 4j) мм от форсунки в свободном факеле распыла с учетом кризисов сопротивления капель и тепломассообмена с газом. Темные символы – приведенная температура газа tg[i, j], светлые символы – то же для капель tl[i, j].

Рис. 3.
То же, что на рис. 2 с учетом кризиса сопротивления капель по формулам (13), (14) из работы [2], но без учета кризиса тепломассообмена при Nu ≈ NuD > 2, обозначения те же, что на рис. 2.

Рис. 4.
То же, что на рис. 2 без учета кризиса сопротивления капель с использованием формулы (2), но с учетом кризиса тепломассообмена фаз при Nu = NuD = 2, обозначения те же, что на рис. 2.

Рис. 6.
Изменение средних по сечению двухфазного потока температур 〈tg[i, j]〉 и 〈tl[i, j]〉 фаз по шкале Цельсия при удалении от форсунки на расстояние z = 100 + 4j мм.

На рис. 1 показаны аксиальные профили скоростей фаз и приведенных температур газа tg[0, j] = = 10(T[0, j]/T0 – 1) и капель tl[0, j] = 10(Tl[0, j]/T0 – 1) на оси свободного факела без учета и с учетом кризисов сопротивления капель и межфазного тепломассообмена. Очевидно, кризис сопротивления заметно влияет на профили скоростей каждой из фаз: газ движется медленнее, а капли быстрее из-за более слабого межфазного обмена импульсом. Аналогичным образом кризис тепломассообмена влияет на изменение температур фаз вблизи оси факела: газ нагревается (на 10 K), а капли остывают (на 9 K) в меньшей степени, чем без кризиса (на 17 и 12 K, соответственно).
На рис. 2–5 представлены радиальные профили приведенных температур газа tg[i, j] = 10(T[i, j]/T0 – 1) и капель tl[i, j] = 10(Tl[i, j]/T0 – 1) на разных расстояниях z = 100 + 4j мм от форсунки, рассчитанные с учетом и без учета кризисов сопротивления капель и тепломассообмена фаз.
Очевидно, кризис сопротивления, примерно, вдвое увеличивает ширину температурных профилей для капель при j = 100–150.
А кризис тепломассообмена настолько же уменьшает максимальную высоту температурных профилей для газа. Без учета кризиса тепломассообмена приведенные температуры фаз вблизи оси факела на большом удалении от форсунки близки по значениям, а с учетом кризиса отличаются, примерно, вдвое. Качественный характер влияния обоих кризисов на изменения температур фаз вполне согласуется с ожиданиями: из-за кризиса сопротивления капли движутся быстрее, а газ медленнее, чем без кризиса, из-за кризиса тепломассообмена капли остывают, а газ нагревается в меньшей степени, чем без него.
На рис. 6 показаны рассчитанные с учетом обоих кризисов зависимости средних по сечению двухфазного потока температур 〈tg[i, j]〉 и 〈tl [i, j]〉 фаз по шкале Цельсия от расстояния z = 100 + 4j мм до форсунки.
Очевидно, несмотря на возникновение обоих кризисов, степень охлаждения теплой воды, распыленной форсункой в воздухе, в свободной струе протяженностью 1.5 м составляет 22.7°С или 77.5% от начальной разности Δt = 29.3°С температур фаз.
РАСЧЕТ МЕЖФАЗНОГО ТЕПЛОМАССООБМЕНА В РАСПЫЛИТЕЛЬНОМ АППАРАТЕ
На рис. 4 в работе [2] представлена используемая в расчетах схема распылительного аппарата-инжектора, в составе которой присутствуют форсунка, формирующая факел распыла, соосная с форсункой цилиндрическая камера смешения фаз и бак-сепаратор для их разделения. Общая ось форсунки и камеры – вертикальна. Камера смешения открыта сверху, расход газа ограничивается вентилем на выходе газа из аппарата. Накопившаяся на дне бака-сепаратора жидкость отводится через вентиль.
Цилиндрическая камера смешения фаз ограничивает двухфазный поток по радиусу (r ≤ RAPP) и высоте H. Последняя связана с положением нижней границы jmax= n расчетной области формулой H = zmax= (z0+ n h). Внутренняя поверхность стенки корпуса камеры является в расчетной области боковой границей imax= m = RAPP/h, на которой обе компоненты скорости газа обращаются в нуль: wr(m, j) = wz(m, j) = 0.
Долетевшие до стенки корпуса капли выпадают на нее, смачивая ее внутреннюю поверхность ниже координаты zw = RAPP/tgφ. Для температуры жидкости, стекающей в виде пленки по внутренней поверхности корпуса аппарата (при r = RAPP), было принято граничное условие вида: Tl(RAPP, z) = = T0 при z < zw – как начальная температура газа, и ∂Tl(RAPP, z)/∂r = 0 при z ≥ zw – как температура выпадающих на стенку капель на данной высоте z.
В предлагаемой модели двухфазного потока расчетная область 0 < j < n целиком располагается в камере смешения фаз.
В расчетах задавался и поддерживался перепад давления ΔP газа между нижним и верхним сечениями камеры смешения – горизонтальными границами расчетной области. По рассчитанным значениям аксиальной скорости газа рассчитывался его объемный расход V через аппарат. Варианты расчета аппарата отличались перепадом давления ΔP газа, радиусом RAPP и высотой H камеры смешения инжектора.
На рис. 7 представлены результаты расчета радиальных профилей приведенных температур фаз tg[i, j] и tl[i, j] в распылительном аппарате с учетом обоих кризисов: гидродинамического сопротивления капель и тепломассообмена фаз.
Рис. 7.
Радиальные профили приведенных температур газа tg[i, j] (темные символы) и жидкости tl [i, j] (светлые символы) на разных расстояниях z = 100 + 4j мм от форсунки в распылительном аппарате, рассчитанные с учетом кризисов сопротивления капель и тепломассообмена фаз, RAPP= 144 мм, H = 1100 мм, перепад давления газа на аппарате ΔP = 7 Па.

Очевидно, различие температур фаз вблизи оси аппарата (при i = 0) заметно больше, чем у стенки его корпуса (при i = n = 36).
На рис. 8 представлены результаты расчета зависимостей от объемного расхода V газа через аппарат для средних значений приведенных температур газа 〈tg[i, n]〉 и жидкости 〈tl[i, n]〉 в выходном для данной фазы сечении камеры смешения. При V > 0 режим течения газа прямоточный, т.е. в том же направлении, что и жидкость, а при V < 0 – противоточный.
Рис. 8.
Расчетные зависимости от расхода V газа через аппарат для средних (по выходному для данной фазы сечению камеры смешения) значений приведенных температур 〈tg[i, n]〉 и 〈tl [i, n]〉 фаз при RAPP= 140 мм, H = 1100 мм.

На графиках с наблюдается, приблизительно, линейное убывание температуры жидкости ростом V, и то же для температуры газа при V < 0, а при V > 0 – максимум (около 30%). Положение максимума температуры газа согласуется со сделанным в [1, Sect. 7.2] предположением, что максимальная эффективность тепло и/или массообмена фаз в прямоточном режиме распылительного аппарата может достигаться при расходе газа, близком к оптимальному значению Vopt, удовлетворяющему условию: Vopt/Vmax= 3–1/2.
На рис. 9 показаны расчетные зависимости от площади S поперечного сечения камеры смешения для максимального расхода Vmax газа (т.е. при малом перепаде давления ΔP = 0.7 Па на аппарате), величин 〈tg[i, n]〉 и 〈tl [i, n]〉, а также для отношения ml(n)/ml(0) – потока массы жидкости в выходном сечении аппарата (т.е. не выпавшей на стенку аппарата) к потоку ее массы во входном сечении.
Рис. 9.
Расчетные зависимости от площади S поперечного сечения аппарата для максимального расхода Vmax газа через аппарат, средних значений приведенных температур 〈tg[i, n]〉 и 〈tl [i, n]〉 фаз и отношения потока массы капель жидкости в выходном сечении аппарата к потоку их массы во входном сечении ml(n)/ml(0), H = 1100 мм, перепад давления газа на аппарате ΔP = 0.7 Па.

Очевидно, с увеличением S средние температуры обеих фаз на выходе из камеры смешения уменьшаются, расход газа Vmax и доля не выпавшей на стенку камеры жидкости возрастают, но более 65% капель все же долетают до стенки.
На рис. 10 представлены расчетные зависимости от высоты H аппарата для тех же величин, что и на рис. 9, но при перепаде давления газа на аппарате ΔP = 7 Па.
Рис. 10.
Расчетные зависимости от высоты H аппарата для тех же величин, что и на рис. 9, при перепаде давления газа на аппарате ΔP = 7 Па, RAPP= 140 мм.

Очевидно, при увеличении H в 3 раза объемный расход V газа уменьшается не более чем в 2 раза, средняя температура газа на выходе из камеры смешения увеличивается приблизительно линейно, у жидкости она изменяется незначительно и нерегулярно, доля жидкости, еще не выпавшей на стенку аппарата, уменьшается приблизительно обратно пропорционально величине H.
ЗАКЛЮЧЕНИЕ
Предложенная в работах [2, 3] модель факела распыла форсунки с учетом раннего кризиса сопротивления капель и межфазного массообмена развита в данной работе путем учета кризиса тепло- и массопередачи от капель к газу, аналогичного кризису теплообмена между шаром и газовым потоком, описанному в [3, Sect. 6.2].
По сравнению с прежними результатами автора, изложенными в работах [2, 3], в данной работе получены новые. В частности, в свободном факеле распыла высотой H до 1.5 м рассчитаны не только аксиальные и радиальные профили скоростей фаз, но и распределения температур фаз Tg(r, z) и Tl(r, z) с учетом и без учета кризисов сопротивления капель и тепломассопередачи от них к газу.
Согласно рис. 6, несмотря на учет в модели обоих кризисов, степень охлаждения воды в свободной распыленной форсункой струе длиной до 1.5 м значительна, составляет 23°С, т.е. почти 80% от начальной разности 29°С температур фаз.
Кроме свободного факела распыла межфазный тепломассообмен был рассчитан также в газокапельном потоке через цилиндрический аппарат. Установлены зависимости средней температуры 〈Tl〉, 〈Tg〉 каждой из фаз на выходе аппарата от ежесекундного объемного расхода V газа через аппарат.
Представленная численная модель позволяет рассчитать зависимости режимных характеристик V, 〈Tl〉, 〈Tg〉 распылительного аппарата от его конструктивных параметров S и H и перепада давления ΔP газа на нем.
Согласно рис. 8–10 из-за кризиса массопередачи в распылительном аппарате степень охлаждения теплой воды, распыленной форсункой в воздухе, невелика: в исследованных условиях не превышает 17.5 K, т.е. около 60% от разности начальных температур воды и воздуха.
Не вполне решенной проблемой пока осталось определение степени охлаждения воды, стекающей по стенке камеры смешения. Предварительная оценка вклада тепломассообмена газа с жидкостью, стекающей в виде пленки, составила около 8% от тепломассообмена газа с каплями в объеме аппарата.
ОБОЗНАЧЕНИЯ
| a = λ/(ρ сp) | коэффициент температуропроводности газа, м2/с |
| Cd | коэффициент гидродинамического сопротивления капли |
| c | удельная теплоемкость, Дж/(кг К) |
| D | коэффициент диффузии водяного пара в газе, м2/с |
| d = d32 | средний объемно-поверхностный диаметр капель, м |
| dh | диаметр выходного отверстия форсунки, мм |
| H | высота аппарата, мм |
| h | шаг расчетной сетки, мм |
| i, j | номера точек расчетной сетки по радиусу и по оси потока |
| J | поток массы пара от всех капель в газ в единице объема, кг/(м3 с) |
| jv | плотность потока массы пара от отдельной капли в газ, кг/(м2 с) |
| kt | коэффициент теплоотдачи от капли к газу, Вт/(м2 К) |
| km | коэффициент массопередачи от капли к газу м/с |
| L | удельная теплота испарения капель жидкости, Дж/кг |
| M | молярная масса газа, кг/моль |
| m, n | максимальные значения величин i, j |
| ml | поток массы капель жидкости через поперечное сечение аппарата, кг/с |
| Pl | избыточное давление воды в форсунке, Па |
| P | давление газа, Па |
| Q | поток тепла от всех капель к газу в единице объема, Вт/м3 |
| q | плотность потока тепла от отдельной капли к газу, Вт/м2 |
| R = 8.31 | универсальная газовая постоянная, Дж/(моль К) |
| RAPP | радиус аппарата, мм |
| r | радиальная координата точек в факеле распыла, м |
| S | площадь сечения аппарата, см2 |
| s | площадь центрального сечения сферической капли, мм2 |
| T, Tl | температура газа, жидкости, K |
| t | то же по шкале Цельсия, °С |
| tg, tl | приведенные температуры газа и жидкости |
| u | скорость жидкости, м/с |
| V = u – w | относительная скорость капли в газе, м/с |
| V | объемный расход газа через аппарат, м3/с |
| Vd | объем капли, м3 |
| Δx | изменение величины x |
| 〈x〉 | среднее значение величины x |
| z | аксиальная координата точек в факеле распыла, м |
| w, ws | скорость газа, скорость звука в газе, м/с |
| α | объемная доля жидкости в данной точке факела распыла |
| λ | коэффициент теплопроводности газа, Вт/(м К) |
| μ | динамический коэффициент вязкости газа, Па с |
| ν = μ/ρ | кинематический коэффициент вязкости газа |
| ρ, ρl, ρv и ρsv | плотность газа, жидкости, пара и насыщенного пара, кг/м3 |
| τ и τs | время и характерное время, с |
| Φd | выделение тепла из-за диссипации механической энергии газа, Вт/м3 |
| φ | половина корневого угла факела распыла форсунки, ° |
| Nu = ktd/λ, NuD = kmd/D | число Нуссельта диффузионное число Нуссельта |
| Pr = ν/a PrD = ν/D | число Прандтля диффузионное число Прандтля |
| Re = Vdρ/μ Recr | число Рейнольдса критическое число Рейнольдса |
ИНДЕКСЫ
Список литературы
Simakov N.N. Crisis of Hydrodynamic Drag of Drops in the Two-Phase Turbulent Flow of a Spray Produced by a Mechanical Nozzle at Transition Reynolds Numbers // Tech. Phys. 2004. V. 49. № 2. P. 188 [Симаков Н.Н. Кризис сопротивления капель при переходных числах Рейнольдса в турбулентном двухфазном потоке факела распыла механической форсунки // Журн. техн. физики. 2004. Т. 74. № 2. С. 46.]
Simakov N.N. Calculation of Interphase Mass Transfer in a Spray Flow Produced by a Nozzle with Account of Crisis // Tech. Phys. 2020. V. 65 № 4. P. 534. [Симаков Н.Н. Расчет межфазного массообмена в факеле распыла форсунки с учетом кризиса // Журн. техн. физики. 2020. Т. 90. № 4. С. 560.]
Simakov N.N. Liquid Spray from Nozzles. Cham: Springer Nature Switzerland AG, 2020.
Нигматулин Р.И. Динамика многофазных систем. Ч. 1. М.: Наука, 1987.
Абрамович Г.Н. Теория турбулентных струй. М.: Наука, 1984.
Гельперин Н.И., Басаргин Б.Н., Звездин Ю.Г. О гидродинамике жидкогазовых инжекторов с диспергированием рабочей жидкости // Теорет. основы хим. технологии. 1972. Т. 6. № 3. С. 434.
Звездин Ю.Г., Симаков Н.Н., Пластинин А.П., Басаргин Б.Н. Гидродинамика и теплообмен при распыливании жидкости в потоке высокотемпературного газа // Теорет. основы хим. технологии. 1985. Т. 19. № 3. С. 354.
Шлихтинг Г. Теория пограничного слоя / Пер. с немецкого. М.: Наука, 1974.
Torobin L.B., Gauvin W.H. Fundamental Aspects of Solids-Gas Flow. Part 1: Introductory Concepts and Idealized Motion in Viscous Regime // Can. J. Chem. Eng. 1959. V. 37. № 4. P. 129–141.
Torobin L.B., Gauvin W.H. Fundamental aspects of solids-gas flow. Part 5: The Effect of Fluid Turbulence on the Particle Drag Coefficient // Can. J. Chem. Eng. 1960. V. 38. No 6. P. 189–200.
Лойцянский Л.Г. Механика жидкости и газа. М.: Наука, 1978.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. IV. Гидродинамика. М.: Наука, 1988.
Ranz W.E., Marshall W.R. Evaporation from drops (Part 2) // Chem. Eng. Progress. 1952. V. 48. № 5. P. 173.
Поттер Д. Вычислительные методы в физике / Пер. с англ. М.: Мир, 1975.
Дополнительные материалы отсутствуют.
Инструменты
Теоретические основы химической технологии